概率论与数理统计公式整理(大学考试必备)

合集下载

概率论与数理统计公式大全

概率论与数理统计公式大全一、概率基本公式1.事件的概率：对于事件A，在随机试验中发生的次数记为n(A)，则事件A的概率为P(A)=n(A)/n，其中n为试验总次数。

2.互斥事件的概率：对于互斥事件A和B，有P(A∪B)=P(A)+P(B)。

3.事件的余事件概率：设事件A为必然事件，全集的概率为P(S)=1，事件A的余事件为A'，则有P(A')=1-P(A)。

4.条件概率：对于两个事件A和B，假设事件B已经发生，事件A发生的概率记为P(A，B)，则P(A，B)=P(A∩B)/P(B)。

二、随机变量及其概率分布1.离散型随机变量：设X是一个离散型随机变量，其概率函数为P(X=k)，其中k为X的取值，概率函数满足P(X=k)≥0，且∑P(X=k)=12. 连续型随机变量：设X是一个连续型随机变量，其概率密度函数为f(x)，概率密度函数满足f(x)≥0，且∫f(x)dx = 13. 随机变量的数学期望：对于离散型随机变量X，其数学期望为E(X) = ∑k*P(X=k)；对于连续型随机变量X，其数学期望为E(X)=∫xf(x)dx。

4. 随机变量的方差：对于离散型随机变量X，其方差为Var(X) =E(X^2) - [E(X)]^2；对于连续型随机变量X，其方差为Var(X) = E(X^2) - [E(X)]^2三、常见的概率分布1.伯努利分布：表示一次实验成败的概率分布，概率函数为P(X=k)=p^k(1-p)^(1-k)，其中0≤p≤12.二项分布：表示n次独立重复的伯努利试验中成功次数的概率分布，概率函数为P(X=k)=C(n,k)*p^k(1-p)^(n-k)，其中C(n,k)为组合数。

3. 泊松分布：表示单位时间或单位面积内发生事件次数的概率分布，概率函数为P(X=k) = (lambda^k)/(k!)*e^(-lambda)，其中lambda为平均发生率。

4.均匀分布：表示在一个区间内取值相等的概率分布，概率密度函数为f(x)=1/(b-a)，其中[a,b]为区间。

概率论与数理统计公式整理

概率论与数理统计公式整理在现代数学中，概率论与数理统计是两个重要的分支。

其中概率论是研究随机事件发生的可能性或概率的科学。

而数理统计则是利用概率论的方法，对已经发生的随机事件进行统计分析和推断。

本文将整理概率论与数理统计中常用的公式。

一、基本概率公式1.概率：$P(A)=\frac{n(A)}{n(S)}$其中，$P(A)$表示事件$A$发生的概率，$n(A)$表示事件$A$所包含的基本事件的个数，$n(S)$表示所有基本事件的个数。

2.加法原理：$P(A\cup B)=P(A)+P(B)-P(A\cap B)$其中，$A$和$B$是两个事件，$A\cup B$表示事件$A$和事件$B$中至少有一个发生的概率，$A\cap B$表示两个事件同时发生的概率。

3.条件概率：$P(B|A)=\frac{P(A\cap B)}{P(A)}$其中，$P(B|A)$表示在事件$A$发生的条件下，事件$B$发生的概率。

4.乘法定理：$P(A\cap B)=P(A)P(B|A)$其中，$P(A\cap B)$表示两个事件同时发生的概率，$P(B|A)$表示在事件$A$发生的条件下，事件$B$发生的概率。

二、概率分布1.离散随机变量的概率分布律：$\sum\limits_{i=1}^{+\infty}{p(x_i)}=1$其中，$p(x_i)$表示离散随机变量取值为$x_i$的概率。

2.连续随机变量的概率密度函数：$\int_{-\infty}^{+\infty}{f(x)}\mathrm{d}x=1$其中，$f(x)$表示连续随机变量在$x$处的概率密度。

3.数学期望：$E(x)=\sum\limits_{i=1}^{+\infty}{x_ip(x_i)}$或$E(x)=\int_{-\infty}^{+\infty}{xf(x)}\mathrm{d}x$其中，$E(x)$表示随机变量$x$的数学期望，$p(x_i)$表示$x_i$这一离散随机变量取到的带权概率。

概率论与数理统计-重要公式

概率论与数理统计-重要公式一、随机事件与概率二、随机变量及其分布1、分布函数()()(),()()()()k k x xx P X x F x P X x P a X b F b F a f t dt≤-∞⎧=⎪=≤=<≤=-⎨⎪⎩∑⎰ 概率密度函数计算概率：2、离散型随机变量及其分布3、续型型随机变量及其分布1)(=⎰+∞∞-dx x f ⎰=≤≤badxx f b X a P )()(一般正态分布的概率计算公式分布函数对离散型随机变量对连续型随机变量分布函数与密度函数的重要关系：4、随机变量函数Y=g(X)的分布离散型：()(),1,2,j ii j g x y P Y y p i ====∑，连续型： ①分布函数法，②公式法()(())()(())Y X f y f h y h y x h y '=⋅=单调 h(y)是g(x)的反函数三、多维随机变量及其分布1、离散型二维随机变量及其分布分布律：(,),,1,2,i j ij P X x Y y p i j ==== 联合分布函数(,)i i ijx x y yF X Y p≤≤=∑∑边缘分布律：()i i ij jp P X x p ⋅===∑ ()j j ij ip P Y y p ⋅===∑条件分布律：(),1,2,ij i j jp P X x Y y i p ⋅====，(),1,2,ij j i i p P Y y X x j p ⋅====联合密度函数2、连续型二维随机变量及其分布 ①分布函数及性质分布函数：⎰⎰∞-∞-=x ydudv v u f y x F ),(),(⎰∞-=≤=x dtt f x X P x F )()()(∑≤==≤=xk k X P x X P x F )()()()()('x f x F =⎰∞-=≤=xdtt f x X P x F )()()(1),(0≤≤y x F },{),(y Y x X P y x F ≤≤=),(y x f 0),(≥y x f 1),(=⎰⎰+∞∞-+∞∞-dxdy y x f )()()(σμ-Φ=<=≤a a X P a X P )(1)()(σμ-Φ-=>=≥a a X P a X P )()()(σμσμ-Φ--Φ=≤≤a b b X a P性质：2(,)(,)1,(,),F x y F f x y x y∂+∞+∞==∂∂((,))(,)GP x y G f x y dxdy ∈=⎰⎰②边缘分布函数与边缘密度函数分布函数：⎰⎰∞-+∞∞-=x X dvdu v u f x F ),()( 密度函数：⎰+∞∞-=dv v x f x f X ),()(⎰⎰∞-+∞∞-=y Y dudv v u f y F ),()( ⎰+∞∞-=du y u f y f Y ),()(③条件概率密度+∞<<-∞=y x f y x f x y f X X Y ,)(),()(，+∞<<-∞=x y f y x f y x f Y Y X ,)(),()( 3、随机变量的独立性随机变量X 、Y 相互独立(,)()()X Y F x y F x F y ⇔=，连续型：(,)()()X Y f x y f x f y = 离散型：..ij i j p p p = ，4、二维随机变量和函数的分布(卷积公式)离散型：()(,)i j kk i j x y z P Z z P X x Y y +=====∑注意部分可加性连续型：()(,)(,)Z f z f x z x dx f z y y dy +∞+∞-∞-∞=-=-⎰⎰四、随机变量的数字特征1、数学期望①定义：离散型∑+∞==1)(k k k p x X E ，连续型⎰+∞∞-=dxx xf X E )()(②性质：(),E C C = )()]([X E X E E =，)()(X CE CX E =，)()()(Y E X E Y X E ±=±b X aE b aX E ±=±)()( ，当X 、Y 相互独立时：)()()(Y E X E XY E =(正对逆错)随机变量g(X)的数学期望2、方差 ①定义：②性质：0)(=C D ，)()(2X D a b aX D =±，),(2)()()(Y X Cov Y D X D Y X D ±+=± 当X 、Y 相互独立时：)()()(Y D X D Y X D +=±3、协方差与相关系数①协方差：(,)()()()Cov X Y E XY E X E Y =-，当X 、Y 相互独立时：0),(=Y X Cov②相关系数： ()()XY D X D Y ρ=，当X 、Y 相互独立时：0=XY ρ(X,Y 不相关)③协方差和相关系数的性质：)(),(X D X X Cov =，),(),(X Y Cov Y X Cov =),(),(),(2121Y X Cov Y X Cov Y X X Cov +=+，),(),(Y X abCov d bY c aX Cov =++Cov(x,a)=0(a 为常数)，),(2)()()(22Y X abCov Y D b X D a bY aX D ±+=±4、常见随机变量分布的数学期望和方差}{}{},{j Y P i X P j Y i X P =====∑=kkk p x g X g E )())((五、大数定律与中心极限定理1、切比雪夫不等式若,)(,)(2σμ==X D X E 对于任意0>ε有2)(})({εεX D X E X P ≤≥-2、大数定律：①切比雪夫大数定律：若n X X 1相互独立，2)(,)(i ii i X D X E σμ==且C i ≤2σ，则：∑∑==∞→−→−ni iPni i n X E nX n11)(),(11②伯努利大数定律：设n A 是n 次独立试验中事件A 发生的次数，p 是事件A 在每次试验中发生的概率，则0ε∀>，有：lim 1A n n P p n ε→∞⎛⎫-<=⎪⎝⎭③辛钦大数定律：若1,,n X X 独立同分布，且μ=)(i X E ，则μ∞→=−→−∑n P ni iXn113、★中心极限定理①列维—林德伯格中心极限定理：独立同分布的随机变量(1,2,)i X i =，均值为μ，方差为02>σ，当n 充分大时有：1((0,1)~nn k k Y X n n N μσ==-−−→∑ ②棣莫弗—拉普拉斯中心极限定理：随机变量),(~p n B X ，则对任意x 有：22lim }()2t x n P x dt x π-→∞≤==Φ⎰③近似计算：1()nk k P a X b n n σσ=≤≤≈Φ-Φ∑ 六、数理统计的基本概念1、总体和样本的分布函数设总体X ～F(x)，则样本的联合分布函数)(),(121k nk n x F x x x F =∏=2、统计量样本均值：∑==ni i X nX 11，样本方差：∑∑==--=--=ni ini i X n X n X X n S 122122)(11)(11 样本标准差：∑=--=ni i X X n S 12)(11 ，样本k 阶原点距： 2,1,11==∑=k X n A ni k i k样本k 阶中心距：11(),1,2,3nk k i i B X X k n ==-=∑3、三大抽样分布(1)2χ分布（卡方分布）：设随机变量X ～B(0,1)(1,2,,)i n =且相互独立，则称统计量222212n X X X ++=χ服从自由度为n 的2χ分布，记为)(~22n χχ 性质：①n n D n n E 2)]([,)]([22==χχ②设)(~),(~22n Y m X χχ且相互独立，则)(~2n m Y X ++χ(2)t分布：设随机变量)(~),1,0(~2n Y N X χ，且X 与Y 独立，则称统计量：nY X T =服从自由度为n 的t 分布，记为)(~n t T 。

概率论与数理统计公式整理(超全免费版)

「 ef(x) w0,其中 0，则称随机变量X 服从参数为X 的分布函数为1xe， xF(x)'0,x<0。

记住积分公式：x ne xdx n!指数分布的指数分布如果二维随机向量(X, Y)的所有可能取值为至多可列个有序对(x,y),则称为离散型随机(1)联合分离散型布设=(X，Y)的所有可能取值为(X i,y j)(i,j 1,2,)，且事件{ =(X i,y j)}的概率为P ij,,称P{(X,Y) (X i,y j)} P j(i,j 1,2,)为=(X，Y)的分布律或称为X和Y的联合分布律。

联合分布有时也用下面的概率分布表来表示：这里P ij具有下面两个性质(1)P ij>0 (i,j=1,2,…)；(2)P j 1.i j(1)大数定律X 切比雪夫大数定律设随机变量冶，X2,…相互独立，均具有有限方差，且被同一常数C所界：D (X i) <C(i=1,2,…),则对于任意的正数£，有limnPLx,丄n i 1 n° E(X i)i 11特殊情形: 若X1，X2，…具有相同的数学期望 E (X)=「则上式成为lim Pn1n X i大数定辛钦大数定律1.设卩是n次独立试验中事件A发生的次数，p是事件A在每次试验中发生的概率，则对于任意的正数£，有limn伯努利大数定律说明，当试验次数小，即limn这就以严格的数学形式描述了频率的稳定性。

很大时，事件1.A发生的频率与概率有较大判别的可能性很0.设X1, X2,…，Xi，…是相互独立同分布的随机变量序列，且 E ( X n) =g，则对于任意的正数£有lim Pn1 nX in i 11.(2)中心极限定理2X N(,)n 格定理设随机变量X1，X2，…相互独立，服从同一分布，且具有相同的数学期望和方差：E(X k) ,D(X k) 0(k 1,2, )，则随机变量的分布函数F n(x)对任意的实数X，Y nnX k nk 1X k nlim F n(x) limn n此定理也称为独立同分布的中心极限定理。

概率论与数理统计公式

概率论与数理统计公式以下是概率论与数理统计中常见的公式整理：1.基本概率公式：P(A) = n(A) / n(S)，其中A 为事件，n(A) 为事件A 发生的基数，n(S) 为样本空间的基数。

2.条件概率公式：P(A|B) = P(A∩B) / P(B)，其中A 和B 为两个事件，P(A∩B) 表示事件A 和事件B 同时发生的概率，P(B) 表示事件B 发生的概率。

3.全概率公式：P(A) = ΣP(A|Bi) * P(Bi)，其中Bi 为互不相交的事件，P(Bi) 表示事件Bi 发生的概率，P(A|Bi) 表示在事件Bi 发生的条件下，事件A 发生的概率。

5.随机变量的期望值：E(X) = Σxi * P(xi)，其中X 为随机变量，xi 为随机变量X 取的第i 个值，P(xi) 表示X 取xi 的概率。

6.随机变量的方差：Var(X) = E((X - E(X))^2)，其中X 为随机变量，E(X) 表示X 的期望值。

7.正态分布的概率密度函数：f(x) = (1 / (σ* √(2π))) * e^(-((x-μ)^2 / (2σ^2)))，其中μ为正态分布的均值，σ为正态分布的标准差。

8.标准正态分布的概率密度函数：f(x) = (1 / √(2π)) * e^(-x^2 / 2)，其中x 为标准正态分布的随机变量。

9.两个随机变量的协方差：Cov(X,Y) = E((X - E(X)) * (Y - E(Y)))，其中X 和Y 为两个随机变量，E(X) 和E(Y) 分别表示X 和Y 的期望值。

概率论与数理统计公式大全

第1章随机事件及其概率第二章随机变量及其分布Ihl ttamitai'l例1.16设某人从一副扑克中(52张)任取13张，设A为至少有一张红桃”，B 为恰有2张红桃”，张方块”,求条件概率P( B| A), P( B| C) 解 P(A)1 P(A)P(BA)P(AB) P(A)1 c；3CTG ；c3；C 13 C52C52C39—C13一C 13 C 13C 52 C 39—血39P(AB)P(C)C 13C 39 c ；3P(BC)5 26C13C 13C 2652P(B C )P ( BC ) P(C)C13 C 13 C 2613 --------- C 52C 5 C 8C13 C 39C13~ —C 522 6C 13 C 26C 8C39C 为恰有5 C 23C 3113T -某种动物出生后活到20岁的概率为0.7，活到25岁的概率为0.56，求现年为20岁的这种动物活到25岁的概率.解设A 表示事件活到20岁以上”，B 表示事件活到25岁以上”， P(A) 0.7 P(B) 0.56P(B A)P(AB) P(A)显然P(AB) 0.56 0.7P(B) 0.560.81例 1.21例1.21 某工厂生产的产品以超过 4件，且具有如下的概率：一批产品中的次品数 0概率 0.1 0.2现进行抽样检验，从每批中随机抽取为该批产品不合格。

求一批产品通过检验的概率。

解设B 表示事件 “一批产品通过检验品”100 1 2 0.4 0.2 件为一批，假定每一批产品中的次品最多不 3 0.1 10件来检验，若发现其中有次品，则认 ”，A (=0,1,234) 表示，贝U A 0 ,A 1 , A 2, A 3, A 4组成样本空间的一个划分， C 10C99 C 10C100P(A) 0.1P(B|") 1P(A) 0.2,P (B |A )0.900 P(A)'一批产品含有 0.4,P(B A 2)i 件次P(A 3) 0.2, P(B A 3)c 10崗 0.727 C 100P(A 4)0.1 , P(B A 4)C 10C 96C 10 C0.652C 1098C 101000.8094P ( A k )P ( B |A k ) k 0 顾客买到的一批合格品中，含次品数为0的概率是类似可以计算顾客买到的一批合格品中，含次品数为 1、2、 3、 4件的概率分别约为 0.221 、0.398 、0.179 、 0.080贝叶斯公式(Bayes)P(B) P (A 。

概率论与数理统计自学考试公式大全

概率论与数理统计重点公式1、)()()()(AB P B P A P B A P -+=2、若A 、B 独立，则)()()(B P A P AB P ⋅=3、条件概率=)/(A B P )()(A P AB P 4、乘法公式：)/()()(A B P A P AB P = 5、二项分布：),(~p n B X分布律：k n kk n p p C k X P --==)1(}{，其中n k p ,,2,1,0,10 =<<期望：np 方差：)1(p np - 6、泊松分布：)(~λP X分布律：λλ-==e k k X P k!}{，0>λ， 2,1,0=k期望： λ 方差： λ7、均匀分布：),(~b a U X概率密度：⎪⎩⎪⎨⎧-=,0,1)(ab x f 其他，期望：2ba + 方差：12)(2a b -8、指数分布：)(~λE X概率密度：⎩⎨⎧≤>=-0,00,)(x x e x f x λλa ≤x ≤b分布函数：⎩⎨⎧≤>-=-0,00,1)(x x e x F x λ期望：λ1 方差：21λ9、正态分布：概率密度：222)(21)(σμσπ--=x ex f ，期望： μ方差： 2σ10、若X 是连续型随机变量，)(x F 是分布函数，则概率运算公式为：（1）)(}{a F a x P =<（2）)()(}{a F b F b x a P -=<< （3）)(1}{a F a x P -=>11、若X 是连续型随机变量，)(x f 是概率密度，则概率运算公式为：（1）dx x f aa x P )(}{⎰∞-=<（2）dx x f a bb x a P )(}{⎰=<< （3）dx x f a dx x f aa x P )()(1}{⎰⎰∞+=∞--=>12、若X 是连续型随机变量，)(x f 是概率密度，则期望运算公式为：dx x xf X E )()(⎰∞-∞+=13、方差的简便计算公式22)]([)()(X E X E X D -=),(~2σμN X +∞<<∞-x14、期望的性质（1）C C E =)( （2）)()(X kE kX E =（3）)()()(Y E X E Y X E ±=±（4）若X 与Y 独立，则)()()(Y E X E XY E ⋅= 15、方差的性质（1）0)(=C D ，)()(X D C X D =+ （2）)()(2X D k kX D =（3）若X 与Y 独立，则)()()(Y D X D Y X D +=± 16、协方差与相关系数)()()(),(Y E X E XY E Y X Cov ⋅-=)()(),(Y D X D Y X Cov XY ⋅=ρ17、切比雪夫不等式2)(})({εεX D X E X P ≤≥- 2)(1})({εεX D X E X P -≥<-18、大数定律（1）1lim =⎪⎪⎭⎫ ⎝⎛<-∞→εp n m P n （2）11lim 1=⎪⎪⎭⎫⎝⎛<-∑=∞→εμn i i n X n P 19、中心极限定理（1）)(lim 1x x n n X P n i i n Φ=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤-∑=∞→σμ（2）)()1(lim x x p np np Z P n n Φ=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤--∞→ 20、样本均值与样本方差样本均值∑==ni i x n x 11样本方差∑=--=n i ix x n s 122.)(11 样本标准差.)(1112∑=--=n i ix x n s μ=)(X E ，nX D 2)(σ=，22)(σ=s E21、设n x x x ,,,21 为来自正态总体),(2σμN 的一个样本，若未知2σ，则)1(~)1()(22222---∑n s n x x iχσσ＝若已知2σ，则)(~)(222n x xiχσ∑-22、矩估计、极大似然估计x =μˆ 22ˆn s =σ，其中∑=-=ni i n x x n s 122.)(123、区间估计已知方差2σ，估计均值μ，区间⎥⎦⎤⎢⎣⎡+-n u x n u x σσαα22,未知方差2σ，估计均值μ，区间⎥⎦⎤⎢⎣⎡-+--n s n t x n s n t x )1(,)1(22αα 估计方差2σ，区间⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----)1()1(,)1()1(2212222n s n n sn ααχχ 24、假设检验两类错误第一类错误 0H 成立，拒绝0H 第二类错误 1H 成立，接受0H 25、u 检验前提：已知2σ，00:μμ=H ，01:μμ≠H 统计量nx u 0σμ-=拒绝域),(),(22+∞--∞=ααu u W26、t 检验前提：未知2σ，00:μμ=H ，01:μμ≠H 统计量ns x t 0μ-=拒绝域)),1(())1(,(22+∞----∞=n t n t Wαα27、2χ检验前提：2020:σσ=H ，2021:σσ≠H统计量2022)1(σχs n -=拒绝域)),1(())1(,0(22221+∞--=-n n W ααχχ 28、回归方程x y 10ˆˆˆββ+= 其中∑∑∑--==221ˆxn x y x n y x L L ii ixxxy βx y 10ˆˆββ-= 即直线x y 10ˆˆˆββ+=经过点),(y x 29、回归平方和、剩余平方和∑-=ii y ys 2)ˆ(回∑-ii i y y s 2)ˆ(＝剩30、单边检验。

概率论与数理统计公式整理

概率论与数理统计公式整理概率论和数理统计是数学中重要的分支，广泛应用于科学、工程、经济、金融等领域。

本文将对概率论和数理统计中常用的公式进行整理，以帮助读者更好地理解和应用这些概念和方法。

一、概率论公式1. 基本概率公式：P(A) = n(A) / n(S)其中P(A)表示事件A发生的概率，n(A)表示事件A的样本空间，n(S)表示样本空间中所有可能结果的个数。

2. 概率的加法公式：P(A ∪ B) = P(A) + P(B) - P(A ∩ B)其中P(A ∪ B)表示事件A或B发生的概率，P(A ∩ B)表示事件A和B同时发生的概率。

3. 条件概率公式：P(A | B) = P(A ∩ B) / P(B)其中P(A | B)表示在事件B已经发生的条件下，事件A发生的概率。

4. 乘法公式：P(A ∩ B) = P(B) * P(A | B) = P(A) * P(B | A)其中P(A ∩ B)表示事件A和B同时发生的概率。

5. 全概率公式：P(A) = ∑[P(Bi) * P(A | Bi)]其中{Bi}为样本空间S的一个划分，P(Bi)表示事件Bi发生的概率。

二、数理统计公式1. 期望：E(X) = ∑[x * P(X = x)]其中X表示随机变量，x表示X可能取到的值，P(X = x)表示X取到x的概率。

2. 方差：Var(X) = E[(X - E(X))^2]其中E(X)表示随机变量X的期望。

3. 标准差：σ(X) = √(Var(X))其中Var(X)表示随机变量X的方差。

4. 协方差：Cov(X, Y) = E[(X - E(X)) * (Y - E(Y))]其中X和Y分别表示两个随机变量。

5. 相关系数：ρ(X, Y) = Cov(X, Y) / (σ(X) * σ(Y))其中Cov(X, Y)表示X和Y的协方差，σ(X)和σ(Y)分别表示X和Y的标准差。

三、概率分布公式1. 二项分布：P(X = k) = C(n, k) * p^k * (1 - p)^(n-k)其中X服从二项分布，n表示试验次数，k表示成功次数，p 表示每次试验成功的概率。

(完整版)大学概率论与数理统计公式全集

大学概率论与数理统计公式全集一、随机事件和概率1、随机事件及其概率2、概率的定义及其计算二、随机变量及其分布1、分布函数性质FbF(aba<≤=P-X)(b()()bFX()P=≤)2、离散型随机变量3、连续型随机变量三、多维随机变量及其分布1、离散型二维随机变量边缘分布∑∑======⋅jjijjii i py Y x X P x X P p ),()(∑∑======⋅iiijjij j py Y x X P y Y P p ),()(2、离散型二维随机变量条件分布2,1,)(),()(=========⋅i P p y Y P y Y x X P y Y x X P p jij j j i j i j i2,1,)(),()(=========⋅j P p x X P y Y x X P x X y Y P p i ij i j i i j i j3、连续型二维随机变量( X ,Y )的联合分布函数⎰⎰∞-∞-=xydvdu v u f y x F ),(),( 4、连续型二维随机变量边缘分布函数与边缘密度函数边缘分布函数：⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()( 边缘密度函数：⎰+∞∞-=dv v x f x f X ),()( ⎰⎰∞-+∞∞-=y Y dudv v u f y F ),()( ⎰+∞∞-=du y u f y f Y ),()(5、二维随机变量的条件分布+∞<<-∞=y x f y x f x y f X X Y ,)(),()( +∞<<-∞=x y f y x f y x f Y Y X ,)(),()(四、随机变量的数字特征1、数学期望离散型随机变量：∑+∞==1)(k k k p x X E 连续型随机变量：⎰+∞∞-=dx x xf X E )()(2、数学期望的性质(1)为常数C ,)(C C E = )()]([X E X E E = )()(X CE CX E =(2))()()(Y E X E Y X E ±=± b X aE b aX E ±=±)()( )()()(1111n n n n X E C X E C X C X C E +=+ (3)若XY 相互独立则：)()()(Y E X E XY E = (4))()()]([222Y E X E XY E ≤ 3、方差：)()()(22X E X E X D -= 4、方差的性质(1)0)(=C D 0)]([=X D D )()(2X D a b aX D =± 2)()(C X E X D -<(2)),(2)()()(Y X Cov Y D X D Y X D ±+=± 若XY 相互独立则：)()()(Y D X D Y X D +=± 5、协方差：)()(),(),(Y E X E Y X E Y X Cov -= 若XY 相互独立则：0),(=Y X Cov 6、相关系数：)()(),(),(Y D X D Y X Cov Y X XY==ρρ 若XY 相互独立则：0=XYρ即XY 不相关7、协方差和相关系数的性质 (1))(),(X D X X Cov = ),(),(X Y Cov Y X Cov =(2)),(),(),(2121Y X Cov Y X Cov Y X X Cov +=+ ),(),(Y X abCov d bY c aX Cov =++8、常见数学分布的期望和方差五、大数定律和中心极限定理1、切比雪夫不等式若,)(,)(2σμ==X D X E 对于任意0>ξ有2)(})({ξξX D X E X P ≤≥-或2)(1})({ξξX D X E X P -≥<- 2、大数定律：若n X X 1相互独立且∞→n 时，∑∑==−→−ni iDni i X E nX n 11)(11(1)若n X X 1相互独立，2)(,)(i i i i X D X E σμ==且M i ≤2σ则：∑∑==∞→−→−ni iPni i n X E nX n11)(),(11(2)若n X X 1相互独立同分布，且i i X E μ=)(则当∞→n 时：μ−→−∑=Pn i i X n 11 3、中心极限定理(1)独立同分布的中心极限定理：均值为μ，方差为02>σ的独立同分布时，当n 充分大时有：)1,0(~1N n n XY nk kn −→−-=∑=σμ(2)拉普拉斯定理：随机变量),(~)2,1(p n B n n =η则对任意x 有：⎰∞--+∞→Φ==≤--xt n x x dtex p np np P )(21})1({lim 22πη(3)近似计算：)()()()(11σμσμσμσμσμn n a n n b n n b n n Xn n a P b X a P nk knk k -Φ--Φ≈-≤-≤-=≤≤∑∑==1、总体和样本总体X 的分布函数)(x F 样本),(21n X X X 的联合分布为)(),(121k nk n x F x x x F =∏=2、统计量(1)样本平均值：∑==ni i X n X 11(2)样本方差：∑∑==--=--=ni i ni i X n X n X X n S 122122)(11)(11(3)样本标准差：∑=--=ni i X X n S 12)(11(4)样本k 阶原点距： 2,1,11==∑=kXn A ni ki k(5)样本k 阶中心距：∑==-==ni k ik k k X XnM B 13,2,)(1(6)次序统计量：设样本),(21n X X X 的观察值),(21n x x x ，将n x x x 21,按照由小到大的次序重新排列，得到)()2()1(n x x x ≤≤≤ ，记取值为)(i x 的样本分量为)(i X ，则称)()2()1(n X X X ≤≤≤ 为样本),(21n X X X 的次序统计量。

概率论与数理统计完整公式

概率论与数理统计完整公式概率论与数理统计是数学的一个分支，研究随机现象和随机变量之间的关系、随机变量的分布规律、经验规律及参数估计等内容。

在概率论与数理统计的学习中，有许多重要的公式需要掌握。

以下是概率论与数理统计的完整公式。

一、概率论公式：1.全概率公式：设A1，A2，…，An为样本空间S的一个划分，则对任意事件B，有：P(B)=P(B│A1)·P(A1)+P(B│A2)·P(A2)+…+P(B│An)·P(An)2.贝叶斯公式：对于样本空间S的一划分A1，A2，…，An，其中P(Ai)>0，i=1,2，…，n，并且B是S的任一事件，有：P(Ai│B)=[P(B│Ai)·P(Ai)]/[P(B│A1)·P(A1)+P(B│A2)·P(A2)+…+P (B│An)·P(An)]3.事件的独立性：若对事件A，B有P(AB)=P(A)·P(B)，则称事件A，B相互独立。

4.概率的乘法公式：对于独立事件A1，A2，…，An，有：P(A1A2…An)=P(A1)·P(A2)·…·P(An)5.概率的加法公式：对事件A，B有：P(A∪B)=P(A)+P(B)-P(AB)6.条件概率的计算：对事件A，B有：P(A，B)=P(AB)/P(B)7.古典概型的概率计算：设事件A在n次试验中发生k次的次数服从二项分布B(n,p)，则其概率可表示为：P(X=k)=C(n,k)·p^k·(1-p)^(n-k)，其中C(n,k)=n!/[k!(n-k)!]二、数理统计公式：1.样本均值的期望和方差：样本的均值X̄的期望和方差分别为： E(X̄) = μ，Var(X̄) = σ^2 / n，其中μ 为总体的均值，σ^2 为总体方差，n 为样本容量。

2.样本方差的期望：样本方差S^2的期望为：E(S^2)=σ^2，其中σ^2为总体方差。

概率论与数理统计公式精选常用公式一览

概率论与数理统计公式精选常用公式一览为了帮助读者更好地掌握概率论与数理统计的知识，本文将为大家整理并介绍一些常用的公式。

这些公式是在学习和应用概率论与数理统计过程中必备的工具，相信对大家的学习和研究具有重要的参考价值。

一、概率论常用公式1. 概率公式在概率论中，我们经常需要计算事件发生的概率。

以下是几个常用的概率公式：（1）加法公式设A和B为两个事件，则A与B的和事件概率为P(A∪B) = P(A) + P(B) - P(A∩B)。

（2）乘法公式设A和B为两个独立事件，则A与B的积事件概率为P(A∩B) =P(A) * P(B)。

2. 条件概率公式条件概率是指在已知事件B发生的条件下，事件A发生的概率。

以下是条件概率的计算公式：P(A|B) = P(A∩B) / P(B)，其中P(A∩B)表示A与B的交事件的概率，P(A|B)表示在B发生的条件下A发生的概率。

3. 贝叶斯公式贝叶斯公式是概率论中非常重要的公式，它用于根据已知条件，计算一个事件的后验概率。

贝叶斯公式如下所示：P(A|B) = P(B|A) * P(A) / P(B)，其中P(A|B)表示在事件B发生的条件下，事件A发生的概率；P(B|A)表示在事件A发生的条件下，事件B发生的概率；P(A)和P(B)分别表示事件A和事件B的先验概率。

二、数理统计常用公式1. 期望和方差在数理统计中，我们经常需要计算一组数据的期望和方差。

以下是期望和方差的计算公式：（1）期望的计算公式设X为一个离散型随机变量，其取值为x1, x2, ..., xn，对应的概率为p1, p2, ..., pn，则X的期望为：E(X) = x1 * p1 + x2 * p2 + ... + xn * pn。

（2）方差的计算公式设X为一个离散型随机变量，其取值为x1, x2, ..., xn，对应的概率为p1, p2, ..., pn，则X的方差为：Var(X) = E[(X - E(X))^2] = (x1 - E(X))^2 * p1 + (x2 - E(X))^2 * p2 + ... + (xn - E(X))^2 * pn。

(完整版)概率论与数理统计公式整理(超全版)

，（，，…，），通常叫先验概率。，（，，…，），通常称为后验概率。贝叶斯公式反映了“因果”的概率规律，并作出了“由果朔因”的推断。
（17）伯努利概型
我们作了次试验，且满足
每次试验只有两种可能结果，发生或不发生；
次试验是重复进行的，即发生的概率每次均一样；
每次试验是独立的，即每次试验发生与否与其他次试验发生与否是互不影响的。
并且同时满足P(ABC)=P(A)P(B)P(C)
那么A、B、C相互独立。
对于n个事件类似。
（15）全概公式
设事件满足
1° 两两互不相容，，
2° ，
则有
。
（16）贝叶斯公式
设事件，，…，及满足
1° ，，…，两两互不相容， >0， 1，2，…，，
2° ，，
则
，i=1，2，…n。
此公式即为贝叶斯公式。
条件概率是概率的一种，所有概率的性质都适合于条件概率。
例如P(Ω/B)=1 P( /A)=1-P(B/A)
（13）乘法公式
乘法公式：
更一般地，对事件A1，A2，…An，若P(A1A2…An-1)>0，则有
… …… … 。
（14）独立性
①两个事件的独立性
设事件、满足，则称事件、是相互独立的。
则称上式为离散型随机变量的概率分布或分布律。有时也用分布列的形式给出：
。
显然分布律应满足下列条件：
（1），，（2）。
（2）连续型随机变量的分布密度
设是随机变量的分布函数，若存在非负函数，对任意实数，有
，
则称为连续型随机变量。称为的概率密度函数或密度函数，简称概率密度。

数理统计中的重要公式整理

数理统计中的重要公式整理正文：数理统计是一门研究统计学原理和方法的学科，其重要性不可忽视。

在数理统计中，有一些重要的公式被广泛应用于各类统计问题的求解和分析。

本文将对数理统计中的重要公式进行整理，以帮助读者更好地掌握和应用这些公式。

1. 概率论与数理统计基本公式1.1 概率论基本公式：(1) 加法法则：P(A ∪ B) = P(A) + P(B) − P(A ∩ B)(2) 乘法法则：P(A ∩ B) = P(A)P(B|A) = P(B)P(A|B)(3) 全概率公式：P(A) = ∑ P(A ∩ Bᵢ) = ∑ P(Bᵢ)P(A|Bᵢ)(4) 贝叶斯公式：P(A|B) = P(B|A)P(A) / P(B)1.2 数理统计基本公式：(1) 期望值公式：E(X) = ∑ XᵢP(Xᵢ)(2) 方差公式：Var(X) = E[(X - E(X))²] = E(X²) - [E(X)]²(3) 协方差公式：Cov(X, Y) = E[(X - E(X))(Y - E(Y))] = E(XY) -E(X)E(Y)(4) 相关系数公式：ρ(X, Y) = Cov(X, Y) / σ(X)σ(Y)2. 统计推断中的重要公式2.1 参数估计公式：(1) 矩估计：θ̂= ḡ(m₁, m₂, ..., mₖ)(2) 最大似然估计：θ̂= argmax[∏ f(x; θ)](3) 最小二乘估计：θ̂= argmin[∑ (yᵢ - g(xᵢ; θ))²]2.2 假设检验公式：(1) z检验：z = (x - μ) / (σ/√n)(2) t检验：t = (x - μ) / (s/√n)(3) 卡方检验：χ² = ∑ (Oᵢ - Eᵢ)² / Eᵢ3. 抽样理论中的重要公式3.1 随机变量公式：(1) 期望值公式：E(X) = μ(2) 方差公式：Var(X) = σ²/n(3) 中心极限定理：Z = (X - μ) / (σ/√n) 服从标准正态分布3.2 总体参数估计公式：(1) 基本抽样分布（z分布）：z = (X - μ) / (σ/√n)(2) t分布：t = (X - μ) / (s/√n)(3) X²分布：χ² = ∑ (Xᵢ - Eᵢ)² / Eᵢ4. 方差分析中的重要公式4.1 单因素方差分析公式：(1) 总平方和公式：SST = ∑ (xᵢj - x)²(2) 因素平方和公式：SFA = n ∑ (xₖ - x)²(3) 误差平方和公式：SSE = ∑ (xᵢj - xₖ)²4.2 F检验公式：F = (SFA / (k - 1)) / (SSE / (n - k))5. 相关分析中的重要公式5.1 简单线性回归公式：(1) 回归模型：Y = β₀ + β₁X + ε(2) 最小二乘估计公式：β̂₁ = ∑((Xᵢ - X)(Yᵢ - Ȳ)) / ∑((Xᵢ - X)²)β̂₀ = Ȳ - β̂₁X(3) 相关系数公式：r = Cov(X, Y) / (σ(X)σ(Y))6. 抽样调查中的重要公式6.1 简单随机抽样公式：(1) 抽样率：p = n / N(2) 估计总量公式：T = N * (X / n)(3) 估计方差公式：Var(T) = N² * ((1 - p/n) / n) * σ²7. 时间序列分析中的重要公式7.1 平稳时间序列公式：(1) 自协方差公式：γ(h) = Cov(Xₖ, Xₖ₋ₖ) = γ(-h)(2) 自相关系数公式：ρ(h) = Cov(Xₖ, Xₖ₋ₖ) / (σ(Xₖ)σ(Xₖ₋ₖ))通过对这些数理统计中的重要公式的整理，我们可以更加方便地在实际问题中应用这些公式，进行数据分析、参数估计、假设检验等统计推断工作。

概率论与数理统计公式大全

概率论与数理统计公式大全一、概率论公式1.概率的基本性质：-非负性：对于任意事件A，有P(A)>=0；-规范性：对于必然事件S，有P(S)=1；-可列可加性：对于互不相容的事件Ai（i=1,2,...），有P(A1∪A2∪...)=P(A1)+P(A2)+...。

2.条件概率：-事件B发生的条件下，事件A发生的概率：P(A，B)=P(A∩B)/P(B)；-乘法公式：P(A∩B)=P(A，B)*P(B)。

3.全概率公式：-事件A的概率：P(A)=ΣP(A，Bi)*P(Bi)，其中Bi为样本空间的一个划分。

4.贝叶斯公式：-事件Bi发生的条件下，事件A发生的概率：P(Bi，A)=P(A，Bi)*P(Bi)/ΣP(A，Bj)*P(Bj)，其中Bj为样本空间的一个划分。

5.独立性：-事件A与事件B相互独立的充要条件是P(A∩B)=P(A)*P(B)。

二、数理统计公式1.随机变量的概率分布：-离散型随机变量的概率分布函数：P(X=x)；-连续型随机变量的概率密度函数：f(x)。

2.数理统计的基本概念：-样本均值：X̄=ΣXi/n；-样本方差：s^2=Σ(Xi-X̄)^2/(n-1)；-样本标准差：s=√s^2；- 样本协方差：sxy = Σ(Xi-X̄)(Yi-Ȳ) / (n-1)。

3.大数定律：-样本均值的大数定律：当样本容量n趋向于无穷大时，样本均值X̄趋向于总体均值μ。

4.中心极限定理：-样本均值的中心极限定理：当样本容量n足够大时，样本均值X̄服从近似正态分布。

5.参数估计：-点估计：用样本统计量对总体参数进行估计；-置信区间估计：用样本统计量构造一个区间，以估计总体参数的范围。

6.假设检验：-假设检验的基本步骤：提出原假设H0和备择假设H1，选择适当的检验统计量，计算拒绝域，进行假设检验。

以上只是概率论与数理统计中的一些重要公式和定理，还有很多其他的公式和定理没有一一列举。

掌握这些公式和定理，可以帮助我们更好地理解和应用概率论与数理统计的知识。

概率论与数理统计考前必备公式

概率论与数理统计考前必备公式==================================概率论与数理统计是大学生必修的数学课程之一，也是多个专业领域的基础知识。

这门课程主要研究随机现象以及随机事件的概率，探索统计规律，并应用于实际问题的分析与决策。

在概率论与数理统计的学习过程中，我们会接触到大量的公式，这些公式是我们进行问题求解的基础。

本文档将为大家整理并介绍概率论与数理统计考前必备的公式，帮助大家在考试中更好地把握重点，提高成绩。

1.随机变量与分布1.1随机变量随机变量是一种数值型的随机量，它的取值由随机实验的结果决定。

我们将随机变量分为离散型和连续型两类。

1.离散型随机变量定义：$X$是一个随机变量，如果它的取值有穷多个或者可列无穷多个，那么$X$是离散型随机变量。

2.连续型随机变量定义：$X$是一个随机变量，如果它的取值为一个区间或者多个区间，那么$X$是连续型随机变量。

1.2分布函数分布函数是描述随机变量取值情况的函数，记作$F(x)$，其中$x$为实数。

根据随机变量的类型，分布函数可为离散型随机变量的概率质量函数或连续型随机变量的概率密度函数。

1.离散型随机变量概率质量函数概率质量函数描述离散型随机变量取值的概率分布。

对于离散型随机变量$X$，其概率质量函数定义如下：$$P(X=x_i)=p_i,\q u ad i=1,2,\d ot s$$2.连续型随机变量概率密度函数概率密度函数描述连续型随机变量取值的概率分布。

对于连续型随机变量$X$，其概率密度函数定义如下：$$F(x)=\in t_{-\in f ty}^{x}f(x)d x$$1.3均匀分布均匀分布是最简单的连续型随机变量分布之一，主要用于描述在一个区间内所有点出现的概率相等的情况。

1.均匀分布的概率密度函数均匀分布的概率密度函数定义如下：$$f(x)=\be gi n{cas e s}\f ra c{1}{b-a},&a\le qx\l eq b\\0,&\t ex t{其他}\e n d{ca se s}$$其中$a$为区间下界，$b$为区间上界。

概率论与数理统计公式大全

概率论与数理统计公式大全一、概率论的常用公式：1.概率的公式：对于事件A，其概率表示为P(A)，满足0≤P(A)≤1。

2.加法公式：对于两个互斥事件A和B，其概率表示为P(A∪B)，满足P(A∪B)=P(A)+P(B)。

3.减法公式：对于事件A和B，其概率表示为P(A∩B)，满足P(A∩B)=P(A)-P(A∪B)。

4.乘法公式：对于两个独立事件A和B，其概率表示为P(A∩B)，满足P(A∩B)=P(A)某P(B)。

5.条件概率公式：对于事件A和B，其条件概率表示为P(A，B)，满足P(A，B)=P(A∩B)/P(B)。

6.全概率公式：对于一组互斥事件B1，B2，...，Bn，以及事件A，有P(A)=∑(P(A，Bi)某P(Bi))。

7.贝叶斯公式：对于一组互斥事件B1，B2，...，Bn，以及事件A，有P(Bi，A)=P(A，Bi)某P(Bi)/(∑(P(A，Bj)某P(Bj))。

二、数理统计的常用公式：1.均值公式：对于一组数据某1，某2，...，某n，其均值表示为μ=∑(某i)/n。

2.方差公式：对于一组数据某1，某2，...，某n，其方差表示为σ^2=∑((某i-μ)^2)/n。

3.标准差公式：对于一组数据某1，某2，...，某n，其标准差表示为σ=√(σ^2)。

4. 协方差公式：对于两组数据某1，某2，...，某n 和 y1，y2，...，yn，其协方差表示为 Cov(某,y) = ∑((某i - μ某) 某 (yi - μy)) / n。

5. 相关系数公式：对于两组数据某1，某2，...，某n 和 y1，y2，...，yn，其相关系数表示为 r = Cov(某,y) / (σ某某σy)。

6.正态分布的概率计算：对于满足正态分布的一组数据某1，某2，...，某n，可以利用标准正态分布表或计算工具来计算概率P(X≤某)或P(X>某)。

7.置信区间公式：对于一组数据某1，某2，...，某n，其均值μ和置信水平α，可以计算置信区间为某̄±Z(α/2)某(σ/√n)。

概率论与数理统计公式

概率论与数理统计公式1.概率公式：
1.1概率加法公式：
P(A∪B)=P(A)+P(B)-P(A∩B)
1.2条件概率公式：
P(A，B)=P(A∩B)/P(B)
P(B，A)=P(A∩B)/P(A)
1.3乘法公式：
P(A∩B)=P(A)*P(B，A)
P(A∩B)=P(B)*P(A，B)
1.4全概率公式：
P(A)=ΣP(A，B_i)*P(B_i)
1.5贝叶斯公式：
P(B，A)=P(A，B)*P(B)/P(A)
2.数理统计中的基本概念和公式：
2.1样本均值：
样本均值 = (x1 + x2 + ... + xn) / n
2.2总体均值：
总体均值=(样本均值*n-x)/(n-1)
2.3样本方差：
样本方差 = Σ(xi - x̄)² / (n-1)
2.4总体方差：
总体方差= Σ(xi - µ)² / N
2.5样本标准差：
样本标准差=√(样本方差)
2.6总体标准差：
总体标准差=√(总体方差)
2.7样本中位数：
样本中位数=(x[n/2]+x[(n+1)/2])/2（当n为偶数时）
2.8样本四分位数：
样本四分位数Q1=x[(n+3)/4]
样本四分位数Q3=x[(3n+1)/4]
2.9标准正态分布的累积分布函数的逆函数：
Zα=Φ^(-1)(α)，其中Φ(z)表示标准正态分布的累积分布函数。

2.10卡方分布的累积分布函数的逆函数：
x^2α=χ^2^(-1)(α)，其中χ^2(x)表示卡方分布的累积分布函数。

概率论与数理统计公式整理(超全免费版)

Pn (k ) C n p k q n k
k
， k 0,1,2,, n 。
第二章
（1）离散型随机变量的分布律
随机变量及其分布
设离散型随机变量 X 的可能取值为 Xk(k=1,2,…)且取各个值的概率，即事件(X=Xk)的概率为 P(X=xk)=pk，k=1,2,…，则称上式为离散型随机变量 X 的概率分布或分布律。有时也用分布列的形式给出：
F ( ) lim F ( x) 0 ，
x
F ( ) lim F ( x) 1 ；
x
F ( x 0) F ( x) ，即 F ( x) 是右连续的； P( X x) F ( x) F ( x 0) 。
xk x
x
对于离散型随机变量， F ( x)
P ( AB) 为事件 A 发生条件下，事 P ( A) （12）条件 P ( AB) 概率件 B 发生的条件概率，记为 P( B / A) 。 P ( A)
条件概率是概率的一种，所有概率的性质都适合于条件概率。不得用于商业用途
仅供个人参考例如 P(Ω /B)=1 P( B /A)=1-P(B/A) 乘法公式： P( AB) P( A) P( B / A) 更一般地，对事件 A1，A2，…An，若 P(A1A2…An-1)>0，则有
仅供个人参考
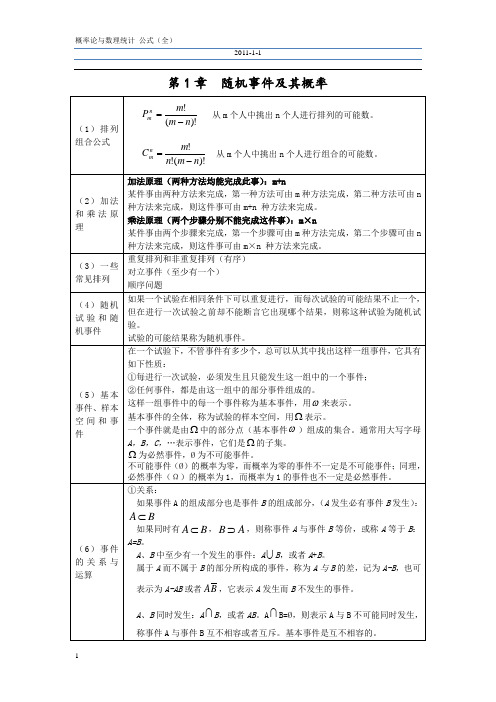
第1章
n Pm
随机事件及其概率
从 m 个人中挑出 n 个人进行排列的可能数。
（1）排列组合公式
n Cm
m! (m n)!
m! 从 m 个人中挑出 n 个人进行组合的可能数。 n!(m n)!
（2）加法和乘法原理
加法原理（两种方法均能完成此事）：m+n 某件事由两种方法来完成，第一种方法可由 m 种方法完成，第二种方法可由 n 种方法来完成，则这件事可由 m+n 种方法来完成。乘法原理（两个步骤分别不能完成这件事）：m×n 某件事由两个步骤来完成，第一个步骤可由 m 种方法完成，第二个步骤可由 n 种方法来完成，则这件事可由 m×n 种方法来完成。重复排列和非重复排列（有序）对立事件（至少有一个）顺序问题如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验。试验的可能结果称为随机事件。在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质： ①每进行一次试验，必须发生且只能发生这一组中的一个事件； ②任何事件，都是由这一组中的部分事件组成的。这样一组事件中的每一个事件称为基本事件，用来表示。基本事件的全体，称为试验的样本空间，用表示。一个事件就是由中的部分点（基本事件）组成的集合。通常用大写字母 A，B，C，…表示事件，它们是的子集。为必然事件，Ø 为不可能事件。不可能事件（Ø）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω ）的概率为 1，而概率为 1 的事件也不一定是必然事件。 ①关系：如果事件 A 的组成部分也是事件 B 的组成部分，（A 发生必有事件 B 发生）：

概率论与数理统计公式整理大学考试必备

，
若有某些相等，则应将对应的相加作为的概率。
连续型
先利用X的概率密度fX(x)写出Y的分布函数FY(y)＝P(g(X)≤y)，再利用变上下限积分的求导公式求出fY(y)。
第三章二维随机变量及其分布
（1）联合分布
离散型
如果二维随机向量（X，Y）的所有可能取值为至多可列个有序对（x,y），则称为离散型随机量。
某件事由两个步骤来完成，第一个步骤可由m种方法完成，第二个步骤可由n种方法来完成，则这件事可由m×n种方法来完成。
（3）一些常见排列
重复排列与非重复排列（有序）
对立事件（至少有一个）
顺序问题
（4）随机试验与随机事件
如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验。
，其中，
则称随机变量服从参数为，的二项分布。记为。
当时，，，这就是（0-1）分布，所以（0-1）分布是二项分布的特例。
泊松分布
设随机变量的分布律为
，，，
则称随机变量服从参数为的泊松分布，记为或者P( )。
泊松分布为二项分布的极限分布（np=λ，n→∞）。
超几何分布
随机变量X服从参数为n,N,M的超几何分布，记为H(n,N,M)。
当x2>x1时，有F（x2,y）≥F(x1,y);当y2>y1时，有F(x,y2)≥F(x,y1);
（3）F（x,y）分别对x与y是右连续的，即
（4）
（5）对于
.
（4）离散型与连续型的关系
（5）边缘分布
离散型
X的边缘分布为
；
Y的边缘分布为