巧用中间时刻速度法求解匀变速直线运动问题
匀变速直线运动的六种解题方法

匀变速直线运动的六种解题方法张岩松(山东省泰安第十九中学ꎬ山东泰安271000)摘㊀要:匀变速直线运动是力学的基础ꎬ在高中物理中具有非常重要的地位ꎬ这部分知识可以说贯穿整个高中物理ꎬ尤其是在力学和电学中使用的频率很高.匀变速直线运动这部分知识ꎬ内容比较少ꎬ可以概括为两个基本公式和三个重要推论ꎬ但是涉及这部分知识的题目却纷繁复杂㊁灵活多变㊁技巧性强ꎬ因此解这部分题目需要掌握一定的解题方法.关键词:比较法ꎻ中间时刻速度法ꎻ逐差法ꎻ比例法ꎻ逆向思维法中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)10-0128-03收稿日期:2023-01-05作者简介:张岩松(1963.6-)ꎬ男ꎬ山东省泰安人ꎬ本科ꎬ中学高级教师ꎬ从事高中物理教学研究.㊀㊀匀变速直线运动问题这部分知识可以高度的概括为:两个基本公式和三个重要推论.两个基本公式是:①速度公式:v=v0+atꎬ②位移公式:x=v0t+12at2ꎻ三个重要推论是:①v2-v02=2axꎬ②Δx=at2ꎬ③v-=vt2=v0+vt2.下面结合典型的例题来探究一下六种最常见的解题方法.1比较法利用物理基本公式和题目中提供的数学表达式进行类比ꎬ从而找到初速度㊁加速度等物理量的方法叫比较法.例1.质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位制单位)ꎬ则该质点(㊀㊀).A.第1s内的位移是5mB.前2s内的平均速度是6m/sC.任意相邻的1s内位移差都是1mD.任意1s内的速度增量都是2m/s解㊀将题目中给出的公式:x=5t+t2与位移基本公式:x=v0t+12at2对照.即:x=5t+t2①x=v0t+12at2②由①㊁②两式对照可知:v0=5m/sꎻ12a=1.ʑa=2m/s2.然后再根据两个基本公式求解ꎬ可以知道只有D正确.故应选D.2中间时刻速度法对于匀变速直线运动ꎬ中间时刻的瞬时速度等于这段时间内的平均速度ꎬ即vt2=v-=xt.例2㊀一物体做匀加速直线运动ꎬ通过一段位移Δx所用的时间为t1ꎬ紧接着通过下一段位移Δx821所用时间为t2.则物体运动的加速度为(㊀㊀).A.2Δx(t1-t2)t1t2(t1+t2)㊀㊀㊀B.Δx(t1-t2)t1t2(t1+t2)C.2Δx(t1+t2)t1t2(t1-t2)D.Δx(t1+t2)t1t2(t1-t2)解㊀第一个Δx内平均速度v1=Δxt1ꎬ第二个x内的平均速度v2=Δxt2.因为中间时刻的瞬时速度等于这段时间内的平均速度ꎬ所以物体的加速度为:a=v2-v1t1+t22=2Δx(t1-t2)t1t2(t1+t2)故A正确.解题策略:(1)某段位移内的平均速度等于其中间时刻的瞬时速度.(2)利用公式a=vt-v0t求解加速度.3逐差法对于匀变速直线运动ꎬ相邻的相等的时间内的位移之差等于恒量ꎬ即:Δx=at2.利用这个推论解题的方法叫逐差法[1].例3㊀一物体做匀变速直线运动ꎬ在连续相等的两个时间间隔内ꎬ通过的位移分别是24m和64mꎬ每一个时间间隔为4sꎬ求物体的初速度和末速度及加速度.解㊀根据Δx=at2ꎬ所以:64-24=aˑ42ꎬ故:a=2.5m/s2.根据:x1=vAt+12at2ꎬ解得:vA=1m/s.同理:vB=21m/s.故答案为:vA=1m/sꎻvB=21m/sꎻa=2.5m/s24比例法对于初速度为零的匀加速直线运动ꎬ从开始运动计时ꎬ相邻相等时间内的位移之比是连续的奇数之比[2]ꎬ即:xⅠʒxⅡʒxⅢ =1ʒ3ʒ5 .例4㊀«简氏防务周刊»最近披露美国政府对阿富汗和伊拉克境内的 中国制穿甲弹 感到担忧ꎬ并正就此事与北京展开 交涉 .假设装甲运兵车的车壳由AB㊁BC两层紧密固定在一起的合金甲板组成ꎬ如图1所示ꎬ甲板AB的长度是BC的三倍ꎬ一颗穿甲弹以初速度v0从A端射入甲板ꎬ并恰能从C端射出ꎬ所用的时间为tꎬ子弹在甲板中的运动可以看成是匀变速运动ꎬ则以下说法中正确的是(㊀㊀).图1A.穿甲弹到B点的速度为v04.B.穿甲弹到B点的速度为v02.C.穿甲弹从A到B的时间为t4.D.穿甲弹从A到B的时间为t2.解㊀因为穿甲弹恰能从C端射出ꎬ所以穿甲弹在C点的速度vc等于零.我们可以把穿甲弹从A到C的匀减速直线运动ꎬ看成是从C到A的初速度为零匀加速直线运动.C到A是穿甲弹运动的逆过程.又因为:xBCʒxAB=1ʒ3ʑtBCʒtAB=1ʒ1ʑtAB=t2.故:D正确C错误.对于穿甲弹运动的逆过程:vB=atBC=aˑt2vo=aˑtʑvB=12v0.故:B正确A错误.对于C㊁D选项ꎬ另一种解法:921ȵv2=2axꎬʑv2B=2axBCꎻv20=2a(xBC+xAB)=2aˑ4xBCʑvB=12v0.故A正确B错误.综上所述:应该选BD.解题策略㊀本题首先是采用逆向思维的方法ꎬ再根据位移之比等于连续的奇数之比进行求解ꎬ非常巧妙ꎬ非常简练.5逆向解题法对于某些匀减速直线运动ꎬ解题的策略是利用逆向解题法.何为 逆向思维法 ?就是将匀减速直线运动的逆过程看成是初速度为零的匀加速直线运动[3].例5㊀以36km/h的速度沿平直公路行驶的汽车ꎬ遇障碍物刹车后获得大小为4m/s2的加速度ꎬ刹车后第3s内汽车的位移大小为(㊀㊀).A.0.5m㊀㊀B.2m㊀㊀C.10m㊀㊀D.12.5m解㊀36km/h=10m/sꎬ设从汽车开始刹车到速度减为零所需的时间为t0ꎬ则:t0=0-v0a=-10-4=2.5s刹车后第3s内的位移等于停止前0.5s内的位移.而正过程的匀减速直线运动ꎬ它的逆过程可以看成是初速度为零的匀加速直线运动.所以x=12at2=12ˑ4ˑ0.52=0.5m.所以A选项是正确的.故答案应选A.解题策略㊀(1)必须先求出汽车从刹车到停止的时间ꎬ这是解这个题的前提和关键ꎬ是解这个题的突破口.不要盲目的利用位移公式x=v0t+12at2去求解ꎬ因为根据实际情况ꎬ汽车刹车速度减为零后就不再运动了ꎬ即停止不动了.(2)注意利用逆过程解题ꎬ因为有时利用逆过程解题比正过程解题要简单的多.(3)本题要求的是 刹车后第3s内的位移 ꎬ而不是 刹车后3s内的位移 ꎬ这两种说法是绝对不一样ꎬ所以一定要仔细审题.6巧选参考系法通常我们选地面为参考系ꎬ但也不尽然ꎬ有时要具体问题具体分析ꎬ为了研究问题的方便ꎬ可以灵活地㊁巧妙地选取参考系ꎬ这种方法叫做巧选参考系法.对于研究对象比较多ꎬ而且具有相对运动的问题ꎬ解题的策略是巧妙选取参考系.例6㊀某航空母舰上的战斗机起飞过程中最大加速度是a=4.5m/s2ꎬ飞机速度要达到v0=60m/s才能起飞ꎬ航空母舰甲板长为L=289mꎬ为使飞机安全起飞ꎬ航空母舰应以一定速度航行以保证起飞安全ꎬ求航空母舰的最小速度v是多少?(设飞机起飞对航空母舰的状态没有影响ꎬ飞机的运动可以看作匀加速运动.)匀变速直线问题所涉及的基本公式和推论不是很多ꎬ很容易记忆ꎬ但是所涉及的题目却是变化万千的ꎬ光记住这些基本公式和推论还是远远不够的ꎬ还需要掌握一定的解题技巧和方法ꎬ而以上六种解题方法便是最常见的解题方法ꎬ必须牢固的掌握.当然ꎬ除此之外还有很多其它的解题技巧和方法ꎬ需要在解题过程中慢慢地去积累和总结ꎬ以便达到孰能生巧.参考文献:[1]沈卫.例谈匀变速直线运动问题中平均速度公式的运用(J).教学考试(高考物理)ꎬ2021(1):57-59.[2]杜馥芬.匀变速直线运动的解题技巧(J).数理化解题研究ꎬ2021(28):98-99.[3]刘军.高中物理中匀变速直线运动的解题技巧(J).高中数理化ꎬ2021(24):45.[责任编辑:李㊀璟]031。
(完整版)匀变速直线运动的推论及推理

罗老师总结匀变速直线运动常用公式 (附匀变速直线运动的推论及推理过程)一、基本公式速度公式 at v v t +=0 当00=v 时,at v t = 位移公式 2021at t v s += 221at s = 二、几个常用的推论1.位移推导公式 2022v v as t -=, t v v s t20+=2.平均速度v 、中间时刻的瞬时速度2/t v 、中间位置的瞬时速度2/s v 为:0/22t t v v xv v t +===, 22202/t s v v v += 3.做匀变速直线运动的物体,在各个连续相等的时间T 内的位移分别是s 1、s 2、s 3…s n ,则Δs =s 2-s 1=s 3-s 2=…=s n -s n-1=aT 2.4.V 0=0的匀加速直线运动中的几个常用的比例公式(1)等分运动时间,以T 为单位时间.①1T 末,2T 末,3T 末…,n T 末的速度之比v 1:v 2:v 3:…:v n =1:2:3…:n②1T 内、2T 内、3T 内…n T 内通过的位移之比s 1:s 2:s 3:…:s n =1:4:9…:n 2③第1个T 内、第2个T 内、第3个T 内…、第n 个T 内通过的位移之比s Ⅰ:s Ⅱ:s Ⅲ:…:s N =1:3:5…:(2n —1)④第1个T 内、第2个T 内、第3个T 内…、第n 个T 内的平均速度之比v Ⅰ:v Ⅱ:v Ⅲ:…:v N =1:3:5…:(2n —1) (2)等分位移,以x 为位移单位. ①通过1x 、2x 、3x …、n x 所需时间之比t 1:t 2:t 3:…:t n =1:3:2…:n②通过第1个x 、第2个x 、第3个x 、…第n 个x 所需时间之比t Ⅰ:t Ⅱ:t Ⅲ:…:t N =1::23:12--…:1--n n③1x 末,2x 末,3x 末…,n x 末的速度之比v 1:v 2:v 3:…:v n =1:3:2…:n对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
匀变速直线运动的规律及应用

(3)第1s内、第2s内、第3s内、…第ns内的位移之比
SI:SII:SIII:…:SN=1:3:5:…:(2n-1)
注意:(1)如何描述这几个规律 (2)时间间隔可扩展到任意t秒
5、做匀变速直线运动的物体,在任意相邻相等时间间隔
例3、一汽车在水平路面上行驶时以v=20m/s,遇到障碍刹车, 加速度的大小为4m/s2,求汽车在6s内通过的位移为多少? (汽车距刹车点多远)
解: S=v0t+ at2=20×6+ ×(-4)×36=48m
注意,以上解法是错误的。原因是刹车过程的最后状态是停下 来,即:vt=0。这类题在解的过程中,应首先判断在所给时 间内,物体是否停下来。如果物体没有停下来,所求过程为匀 变速直线运动,直接代公式求解;如果已经停下来了,过程应 该分为两部分:匀变速过程(停下来以前)和静止过程(停下 来以后),整个过程不再是匀变速直线运动。这种情况下,直 接代公式就不行了。但是前一个过程还是匀变速,可以代公式 求前一个过程的位移(注意这时所代时间不再是全部时间而是 匀变速过程的时间)。我们又知道,后一个过程的位移为0, 所以前一个过程的位移与整个过程的位移相同
设物体运动的初速度为v0,加速度为a,则由位移公式有:
S1=v0t1+
at12
7.2=3v0+ a×32 ①
对后3s,v2=v0+at=v0+2a
②
S2=v2t2+
at22
16.8=3v2+ a×32 ③
三式联立可求得:v0=0 a=1.6m/s2 ∴由S= at2有S总= ×1.6×52=20(m)
可以求出a=-2.5m/s2
几种常见匀变速直线运动解题方法

几种常见匀变速直线运动解题方法一.一般公式法.一般公式法是指选用速度、位移和时间的关系式,它们均是矢量式,使用时应注意方向性.一般以v的方向为正方向,其余与正方向相同者取正,与正方向相反者取负.二.平均速度法.定义式v=xt,对任何性质的运动都适用,而公式v=12(v0+v t)只适用于匀变速直线运动.三.中间时刻速度法.利用“任一段时间t的中间时刻的瞬时速度等于这段时间t内的平均速度”,即v t2=v.此公式适用于任何一个匀变速直线运动.有些题目应用它可以避免常规解法中用位移公式列出的含有t2的复杂式子,从而简化解题过程,提高解题速度.四.比例法.对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动,可利用初速度为零的匀加速直线运动的重要结论的比例关系,用比例法求解问题.五.逆向思维法.逆向过程处理(逆向思维)是把运动过程的“末态”作为“初态”的反向研究问题的方法.如:物体做匀加速运动可看成做反向的匀减速运动,物体做匀减速运动可看成做反向的匀加速运动.该方法一般用在末状态已知的情况中.六.图象法应用v-t图象,可把较复杂的问题转变为较为简单的数学问题解决,尤其是用图象定性分析,可避开繁杂的计算,快速找出答案.七.巧用推论Δx=x n+1-x n=aT2解题.匀变速直线运动中,在连续相等的时间T内的位移之差为一恒量,即x n+1-x n=aT2.对一般的匀变速直线运动问题,出现相等的时间间隔时,应优先考虑用Δx=aT2求解.自由落体运动1.钢球A自塔顶自由落下2 m时,钢球B自离塔顶6 m距离处自由落下,两钢球同时到达地面,不计空气阻力,则塔高为( D )A.24m B.16m C.12m D.8m2.甲、乙两物体分别从10m和20m高处同时自由落下,不计空气阻力,下面描述正确的是( D )A.落地时甲的速度是乙的1/2 B.落地的时间甲是乙的2倍C.甲、乙两物体在最后1s内下落的高度相等 D 下落1s时甲的速度与乙的速度相同3.把自由落体运动总路程从上到下分成相等的两段,则上、下两段路程的平均速度之比为( B )A.1∶4 B.(2-1)∶1 C.1∶2 D.1∶(2-l)4.甲乙两球从同一高度相隔1s先后自由下落,在下落过程中( AD )A.两球速度差始终不变 B.两球速度差越来越大C.两球距离始终不变 D.两球距离越来越大匀变速直线运动提高小练1.(2013·无锡模拟)如图所示,一小球分别以不同的初速度,从光滑斜面的底端A 点向上做直线运动,所能到达的最高点位置分别为a 、b 、c ,它们距斜面底端A 点的距离分别为s 1、s 2、s 3,对应到达最高点的时间分别为t 1、t 2、t 3,则下列关系正确的是( C )A.s 1t 1=s 2t 2=s 3t 3B.s 3t 3>s 2t 2>s 1t 1C.s 1t12=s 2t 22=s 3t 32 D.s 1t 12>s 2t 22>s 3t 32 2.(2014·启东质检)汽车以20m /s 的速度做匀速直线运动,刹车后的加速度大小为 5m/s 2,那么开始刹车后2 s 内与开始刹车后6 s 内汽车通过的位移之比为( C ) A .1∶1 B .1∶3C .3∶4D .4∶33、 一辆公共汽车进站后开始刹车,做匀减速直线运动,开始刹车后的第1s 内和第2s 内位移大小依次为9m 和7m.则刹车后6s 内的位移是( C )A .20mB .24mC .25mD .75m4、小石子从离地某一高度处由静止自由落下,某摄影爱好者恰好拍 到了它下落的一段轨迹AB .该爱好者用直尺量出轨迹的长度,如图所示,已知曝光时间为11 000s ,则小石子出发点离A 点的距离约为( C ) A .6.5 m B .10 mC .20 mD .45 m5、做匀加速直线运动的物体,先后经过A 、B 两点时的速度分别为v 和7v ,经历的时间为t ,则(C D )A .前半程速度增加3.5vB .前t 2时间内通过的位移为11v t 4C .后t 2时间内通过的位移为11v t 4D .后半程速度增加2v6.一位同学在某星球上完成自由落体运动实验:让一个质量为2 kg 的小球从一定的高度自由下落,测得在第5 s 内的位移是18 m ,则( D )A .物体在2 s 末的速度是20 m/sB .物体在第5 s 内的平均速度是3.6 m/sC .物体在第2 s 内的位移是20 mD .物体在5 s 内的位移是50 m7、.(2013·佛山一模)如图1-2-5所示,一小球从A 点由静止开始沿斜面向下做匀变速直线运动,若到达B 点时速度为v ,到达C 点时速度为2v ,则x AB ∶x BC 等于( C )A .1∶1B .1∶2C .1∶3D .1∶48、某列车离开车站后做匀加速直线运动,从某时刻开始计时,前1 s 内的位移为10 m ,前2 s 内的位移为25 m ,则前 3秒内的位移为( B )A .40 mB .45 mC .50 mD .55 m9、一个质点正在做匀加速直线运动,用固定的照相机对该质点进行闪光照相,闪光时间间隔为1 s ,分析照片得到的数据,发现质点在第1次、第2次闪光的时间间隔内移动了0.2 m ;在第3次、第4次闪光的时间间隔内移动了0.8 m ,由上述条件可知( B )A .质点运动的加速度是0.6 m/s 2B .质点运动的加速度是0.3 m/s 2C .第1次闪光时质点的速度是0.1 m/sD .第2次闪光时质点的速度是0.3 m/s| 多阶段匀变速直线运动问题10、(2014·江都模拟)珠海航展现场空军八一飞行表演队两架“歼-10”飞机表演剪刀对冲,上演精彩空中秀。
2021届高考物理:匀变速直线运动的规律含答案

(1)这时出租车离出发点的距离;
(2)出租车继续做匀加速直线运动,当速度计显示速度为108 km/h时,出租车开始做匀速直线运动。10时12分35秒时计价器里程表示数应为多少千米?(车启动时,计价器里程表示数为零)
匀速运动的时间为t=15 s-t′1-t′2
上升的高度为h= (t′1+t′2)+v(15 s-t′1-t′2),联立解得v=4 m/s,另一解不合理,舍去。
[答案](1)12 s (2)4 m/s
解决匀变速直线运动的常用方法[讲典例示法]
解决匀变速直线运动问题常用的六种方法
[典例示法](一题多法)物体以一定的初速度从斜面底端A点冲上固定的光滑斜面,斜面总长度为l,到达斜面最高点C时速度恰好为零,如图所示。已知物体运动到距斜面底端 l处的B点时,所用时间为t,求物体从B滑到C所用的时间。
多过程问题
3.有一部电梯,启动时匀加速上升的加速度大小为2 m/s2,制动时匀减速上升的加速度大小为1 m/s2,中间阶段电梯可匀速运行,电梯运行上升的高度为48 m。问:
(1)若电梯运行时最大限速为9 m/s,电梯升到最高处的最短时间是多少;
(2)如果电梯先加速上升,然后匀速上升,最后减速上升,全程共用时间为15 s,上升的最大速度是多少?
[跟进训练]
1.一物体做匀加速直线运动,通过一段位移Δx所用时间为2t,紧接着通过下一段位移Δx所用时间为t。则物体运动的加速度大小为( )
A. B. C. D.
C[物体做匀加速直线运动,在第一段位移Δx内的平均速度是v1= ;在第二段位移Δx内的平均速度是v2= ;因为某段时间内的平均速度等于中间时刻的瞬时速度,则两个中间时刻的时间差为Δt=t+ = t,则物体加速度的大小a= = ,解得:a= ,故选C。]
(整理)匀变速直线运动.

匀变速直线运动基本公式:末速度Vt=Vo+at 位移S==Vot+at² /2 平均速度V平=s/t(定义式)(1)推论Vt² -Vo²=2as(a为正值时匀加速直线运动,a为负值时匀减速直线运动)(2)中间时刻速度Vt/2=V平=(Vt+Vo)/2=S/t(若为匀变速运动等于这段的平均速度)(3)中间位置速度Vs/2=√[(Vo² +Vt²)/2](4)加速度a=(Vt-Vo)/t{以Vo为正方向,a与Vo同向(加速)a>0;反向则a<0}(5)中间时刻速度Vt/2 =中间位置速度Vs/2时为匀速中间时刻速度Vt/2 ﹤中间位置速度Vs/2时为匀加速或匀减速直线运动(6)初速度为零的匀加速直线运动规律①在前1T末,前2T末,前3T末,.....前nT末的瞬时速度之比为V₁∶V₂∶V₃:……∶Vn=1∶2∶3∶……∶n②在前1T内,前2T内,前3T内,...前nT内的位移之比为xT∶x2T∶x3T∶……:xnT=1∶4∶9∶……∶n²③在第一个T内,第二个T内,第三个T内,......第n个T内的位移之比为x₁∶x₂∶x₃:……∶xn=1∶3∶5∶……∶(2n-1)④在通过第一个∆x,第二个∆x,第三个∆x...第n个∆x所用的时间之比为t₁∶t₂∶t₃:……∶xn=1∶(√2-1)∶(√3-√2)∶……∶(√n﹣√(n-1))(7)匀减速直线运动至停止可等效认为反方向初速为零的匀加速直线运动.(先考虑减速至停止的时间).(8)主要物理量及单位:初速度(Vo):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算:1m/s=3.6km/h。
注:(1)平均速度是矢量;(2)物体速度大,加速度不一定大;(3)a=(Vt-Vo)/t只是量度式,不是决定式;(4)其它相关内容:质点、位移和路程、参考系、时间与时刻/s--t图、v--t图/速度与速率、瞬时速度。
匀变速直线运动的推论整理
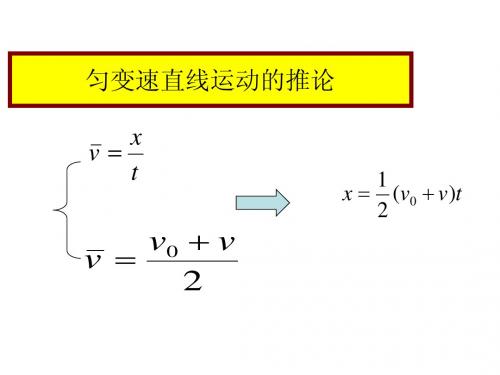
1 2 x2 a 2 2 1 2 x3 a 3 2
故 x1 : x2
: x3 : 1 : 4 : 9 :
(3)第一秒、第二秒、第三秒……位移之比
1 2 x = a 1 第一秒内位移 Ⅰ 2
(m)
1 1 3 2 2 第二秒内位移 xⅡ= a 2 a 1 a 2 2 2 1 1 5 2 2 第三秒内位移 xⅢ = a 3 a 2 = a 2 2 2
②为确定解题结果是否正确,用不同方法求 解是一有效措施。 ③一般应该先用字母代表物理量进行运算, 得出用已知量表达未知量的关系式,然后 再把数值代入。 这样做能够清楚地看出未知量与已知 量的关系,计算也比较简便。
四个比例式:初速为零的匀加速直线运动 的几个常用的比例式:
• • • • • • • (1)1秒末、2秒末、3秒末……瞬时速度 之比
位移公式:
速度位移公式:
v v 2ax
2 2 0
二、3个推论与一种方法
1. 2.
v
v0 v 2
vt
2
Vx
2
V02 V 2 2
2
3. x2 x1 x3 x2 aT 4.
逆向思维法
练习1:一物体做初速为零的匀加速直线运 动。求:
(1)1秒末、2秒末、3秒末……瞬时速度 之比 由速度公式
4.汽车刹车后做匀减速直线运动,经3 s后停止运动,那么,在这 连续的3个1 s内汽车通过的位移之比为( B ) A.1∶3∶5 C.1∶2∶3 B.5∶3∶1 D.3∶2∶1
解析:末速度为零的匀减速直线运动可以看作反向的初速度 为零的匀加速直线运动处理,初速度为零的匀加速直线运动 第1秒内、第2秒内、第3秒内……的位移之比为
专题匀变速直线运动“九大题型与六大方法

专题匀变速直线运动“九大题型与六大方法编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(专题匀变速直线运动“九大题型与六大方法)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为专题匀变速直线运动“九大题型与六大方法的全部内容。
专题 匀变速直线运动中的九大题型与六大解题方法第一部分 基础知识快速回顾知识点1 匀变速直线运动及其公式 1.定义和分类(1)匀变速直线运动:物体在一条直线上运动,且 加速度 不变. (2)匀加速直线运动:a 与v 同向 (3)匀减速直线运动:a 与v 反向 2.三个基本公式(1)速度公式: v =v 0+at(2)位移公式: x =v 0t +错误!at 2(3)位移速度关系式: v 2-v 错误!=2ax 3.两个重要推论(1)物体在一段时间内的平均速度等于这段时间 中间时刻 的瞬时速度,还等于初末时刻速度矢量和的 一半 ,即:v =v 错误!=错误!.(2)任意两个连续相等的时间间隔T 内的位移之差为一恒量,即:Δx =x2-x1=x3-x2=…=xn -xn -1=__aT 2_____可以推广到xm -xn =(m -n)aT 2. 4.初速度为零的匀变速直线运动的四个推论(1)1T 末、2T 末、3T 末……瞬时速度的比为: v1∶v2∶v3∶…∶vn = 1:2:3:…:n (2)1T 内、2T 内、3T 内……位移的比为:x1∶x2∶x3∶…∶xn = 12∶22∶32∶…∶n 2(3)第一个T 内、第二个T 内、第三个T 内……位移的比为:xⅠ∶xⅡ∶xⅢ∶…∶xn =_1:3:5:…:(1n-1)(4)从静止开始通过连续相等的位移所用时间的比为:t1∶t2∶t3∶…∶tn =知识点2 自由落体运动和竖直上抛运动 1。
(2014使用)匀变速直线运动的推论
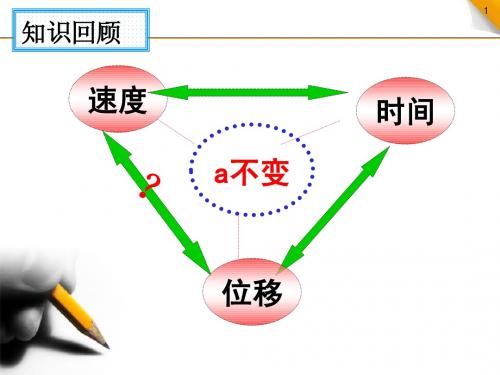
x aT
2
v0
o T T T T t/s
14
匀变速直线运动推论公式:
任意两个连续相等时间间隔T内, 位移之差是常数,即△x=x2-x1=aT2。
拓展:△xM N=xM-xN=(M-N)aT2
15
小试牛刀:有一物体做匀加速直线运动,第一 个2秒内通过的位移为12m,第二个2秒内通过 的位移为24m,求该质点的加速度。
2 2
2
b、第1T内,第2T内,第3T内,…的位移之比
2N 1 x : 3: 5: : Ⅰ: x Ⅱ : xⅢ : : xN 1
匀变速直线运动的推论: ③时间比例(连续相等位移)
25
a、通过前x、前2x、前3x、…的位移所用时间的比
t : tⅡ : tⅢ : : t N 1 : 2 : 3 : : Ⅰ 1 2 3
(A) 1.2m (B) 3.6m (C) 6.0m (D) 10.8m 2、一质点做从静止开始做匀加速直线运动,则 质点在第一个2s,第二个2s和第5s内的三段位 4:12:9 。 移之比为________ 3、一物体做匀减速直线运动,3.5秒后停下来 ,则第1秒内,第2秒内,第3秒内的位移之比 为_________ 3:2:1 。
答案:4m/s2;
7
8
推论二:匀变速直线运动中点 位移速度?
v0 v vx 2 2
2
2
9
v0 v v0 v t v vx v2 2 2 2
2
2
讨论:这两个速度一样吗?试 比较它们的大小
ቤተ መጻሕፍቲ ባይዱ
可以证明, 无论匀加速还是 匀减速, 都有 vt/2 <vs/2 .
10
匀变速直线运动的规律及应用精讲

解析:根据v=v0+at,则a=
-10-10 2
m/s2=-10
m/s2.由于物体
做匀变速运动,所以 v =v+2 v0=0,即C正确,其余均错. 答案:C
3.一个小石块从空中a点自由落下,先后经过b点和c点,不计 空气阻力.已知它经过b点时的速度为v,经过c点时的速度为3v.则ab段 与ac段位移之比为( )
A.1∶3
B.1∶5
C.1∶8
D.1∶9
解析:经过b点时的位移为xab=
v2 2g
,经过c点时的位移为xac=
32vg2,所以xab∶xac=1∶9,故选D. 答案:D
4.以35 m/s的初速度竖直向上抛出一个小球.不计空气阻力, g=10 m/s2,以下判断正确的是( )
A.小球到最大高度时的速度为0 B.小球到最大高度时的加速度为0 C.小球上升的最大高度为61.25 m D.小球上升阶段所用的时间为3.5 s
()
A.240 m B.250 m
C.260 m
解析:汽车从刹车开始直到停下来所需要的时间t=
0-a Dv.=90-0-0m1.20s
=50 s,汽车在1 min内的后10 s静止,故汽车刹车的距离x= v t= 0+210×50 m=250 m.
答案:B
疑难点一.解决一般的匀变速直线运动问题常用公式有v=v0+
解析:以地面为参考系,在t时间内航空母舰的位移设为x,则 飞机位移为x+L,由运动学规律得
x=vt, v02-v2=2a(x+L), v0-v=at, 由以上各式解得v=v0- 2aL, 代入数据解得v=9 m/s. 答案:9 m/s
易错点三 乱套公式引起的错误
自我诊断3 火车上某人用手表估测该火车的加速度.先观测3 min,发现火车前进540 m,隔3 min又观测1 min,发现火车前进360 m.若火车在这7 min内做匀加速直线运动,则火车的加速度为( )
“中间时刻速度等于平均速度”对于匀变速曲线运动也成

龙源期刊网
“中间时刻速度等于平均速度”对于匀变速曲线运动也成
作者:立曹闯
来源:《中学物理·高中》2014年第01期
1问题与证明
“中间时刻速度等于平均速度”是匀变速直线运动的一个重要的结论,这一结论在纸带的处理、运动学的计算中有着广泛的应用.那么,对于匀变速曲线运动该结论是否成立呢?对此做
简要证明如下.
由以上证明过程可以知道,“中间时刻速度等于平均速度”不仅对匀变速直线运动成立,对于匀变速曲线运动也成立.也就是说该结论对于匀变速运动都成立,与轨迹没有关系,但当轨
迹是曲线时要运用平行四边形定则进行矢量合成,换言之匀变速直线运动只是一种特殊情况,所以结论为代数和的形式.
2实例例证
可以看到,两种解法所得到的结果完全一致,利用结论可使解题过程大为简化,不失为解决此类问题的一种快捷方法.。
匀变速直线运动中中间位置的速度公式

匀变速直线运动中中间位置的速度公式匀变速直线运动是物体在相同时间内速度增加的运动。
在这种运动中,物体的速度是随时间而变化的,而中间位置指的是物体运动过程中的某个时间点,即物体在整个运动过程中的中间时刻。
那么,如何计算中间位置的速度呢?我们需要了解匀变速直线运动的速度变化规律。
在匀变速直线运动中,物体的速度随时间变化的规律可以用速度公式来表示。
速度公式是用来计算物体在某一时刻的速度的数学表达式。
在匀变速直线运动中,速度公式可以写为v = v0 + at,其中v表示物体在某一时刻的速度,v0表示物体在起始时刻的速度,a表示物体的加速度,t 表示经过的时间。
假设我们要计算物体在匀变速直线运动过程中的中间位置的速度,首先需要确定中间位置的时间。
假设物体总共运动的时间为T,那么中间位置的时间可以表示为t = T/2。
将中间位置的时间代入速度公式中,即可计算出中间位置的速度。
还需要知道起始时刻的速度和加速度的数值,才能完整地计算出中间位置的速度。
起始时刻的速度可以通过实验或观测得到,而加速度则需要根据具体情况进行计算或给定。
在实际运用中,可以根据物体的运动情况和已知条件,灵活选择适合的速度公式进行计算。
比如,如果已知物体的位移和时间,可以使用位移公式s = v0t + (1/2)at^2来计算中间位置的速度。
如果已知物体的加速度和时间,可以使用加速度公式v = v0 + at来计算中间位置的速度。
计算匀变速直线运动中中间位置的速度,需要根据已知条件选择适合的速度公式,确定中间位置的时间,并代入公式中进行计算。
这样,就可以准确地得到物体在中间位置的速度了。
通过以上的分析,我们可以看出,在匀变速直线运动中,计算中间位置的速度是可行的。
只需要根据已知条件选择适合的速度公式,并代入中间位置的时间,就可以准确地计算出中间位置的速度。
这种方法具有一定的普适性,可以应用于各种匀变速直线运动的问题中。
当然,在实际问题中,可能还会存在其他的条件和限制,需要根据具体情况进行分析和计算。
几种常见匀变速直线运动解题方法

几种常见匀变速直线运动解题方法一.一般公式法.一般公式法是指选用速度、位移和时间的关系式,它们均是矢量式,使用时应注意方向性.一般以v 0的方向为正方向,其余与正方向相同者取正,与正方向相反者取负.1、如图所示,一物体在做匀加速直线运动,加速度为a ,在A 点的速度为v 0,物体从A 到B 和从B 到C 的时间均为T ,则物体在B 点和C 点的速度各是多大?物体在AC 阶段的平均速度多大?此过程平均速度与B 点速度大小有什么关系?x BC 与x AB 的差又是多大?2.如图所示,在倾角θ=30°的足够长的光滑斜面上,一质量为2 kg 的小球自与斜面底端P 点相距0.5 m 处,以4 m /s 的初速度沿斜面向上运动。
在返回P 点之前,若小球与P 点之间的距离为d ,重力加速度g 取10 m/s 2,则d 与t 的关系式为( )A .d =4t +2.5t 2B .d =4t -2.5t 2C .d =0.5+4t +2.5t 2D .d =0.5+4t -2.5t 23.(2013·无锡模拟)如图所示,一小球分别以不同的初速度,从光滑斜面的底端A 点向上做直线运动,所能到达的最高点位置分别为a 、b 、c ,它们距斜面底端A 点的距离分别为s 1、s 2、s 3,对应到达最高点的时间分别为t 1、t 2、t 3,则下列关系正确的是( ) A.s 1t 1=s 2t 2=s 3t 3 B.s 3t 3>s 2t 2>s 1t 1C.s 1t 12=s 2t 22=s 3t 32D.s 1t 12>s 2t 22>s 3t 32 4.(2014·启东质检)汽车以20m /s 的速度做匀速直线运动,刹车后的加速度大小为5 m/s 2,那么开始刹车后2 s 内与开始刹车后6 s 内汽车通过的位移之比为( )A .1∶1B .1∶3C .3∶4D .4∶35.(2011安徽理综卷第16题)一物体做匀加速直线运动,通过一段位移△x 所用的时间为t 1,紧接着通过下一段位移△x 所用时间为t 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧用中间时刻速度法求解匀变速直线运动问题
利用“任何时间t中间时刻的瞬时速度等于这段时间t内平均速度”,即,这个结论适用于任何一个匀变速直线运动。
有些题目应用它可以避免常规解法中用位移公式列出的含有t2的复杂式子,从而简化解题过程,提高解题速度,示例如下:
例一,一个物体以一定初速度沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,求经过b时刻的加速度和速度分别为a和vb是多少?
解析:此题用基本公式解析如下:由于物体做
匀减速运动至停止,故可以将此运动看做反向
的初速度为零的匀加速直线运动。
设第n秒以
后的时间为t,位移为x,b时刻的速度为vb ,
运动加速度为a,根据匀变速直线运动位移公式和速度公式列出方程如下:X= at2-------------------①
S+x= a(t+n)2-------------②
2s+x= a(t+n+m)2----------③
vb=a(t+n)-----------------④
解此方程组可以得出答案,但解的过程相当繁杂,数学基础不好的学生根本解不出正确结果。
如果用中间时刻速度法就很简便,也好理解,解答如下:
根据匀变速直线运动的平均速度和中间时刻的瞬时速度相等,可知m和n 的中点时刻的速度分别为,v1和v2的时间间隔
Δt= ,应用速度公式可知加速度,经过b点时的速度vb=v1+a = .
例二.一辆汽车在笔直的公路上做匀变速直线运动,该公路旁每隔15m安置一个路标.汽车经过A、B两相邻路标用时2s,通过B、C两相邻路标用时3s,求汽车通过A、B、C三个路标时的速度。
解析:汽车做匀变速直线运动,AB段的平均速度v1等于从A点起1s末的瞬时速度,BC段的平均速度v2等于从A点起3.5s末的瞬时速度
由得,
由vt=v0+at得汽车的加速度
所以vA=v1-at1=7.5+1×1=8.5(m/s)
vB=vA+at2=8.5-1×2=6.5(m/s)
vC=vB+at3=6.5-1×3=3.5(m/s).
从以上两例可以看出,巧用中间时刻速度法解答匀变速直线运动问题极为简洁,巧妙,能够去繁就简,收到事半功倍的效果,希望学生学习时加以领悟,很好掌握。
