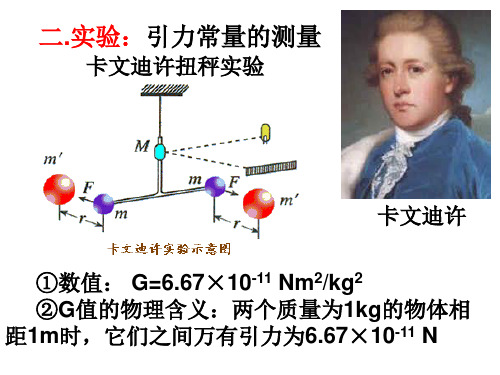
引力常量的测定卡文迪许扭秤实验

库仑扭秤实验和卡文迪许扭秤实验原理和注意事项

库仑扭秤实验和卡文迪许扭秤实验原理和注意事项库仑扭秤实验和卡文迪许扭秤实验，这两个名字听起来就很高级，好像是什么科学家发明的高科技仪器。

其实，它们就是两个简单的实验，用来测量物体之间的相互作用力。

今天，我们就来聊聊这两个实验的原理和注意事项，让你也能轻松掌握这个知识点。

我们来说说库仑扭秤实验。

这个实验的名字听起来有点像是个大家伙，其实它就是一个小小的装置。

它的原理很简单，就是通过测量两个小球之间的相互作用力来计算出它们的质量。

听起来好像很难懂，其实很简单。

比如说，你有两个小球，一个重一点，一个轻一点。

当你把这两个小球放在一起时，它们会互相吸引。

这时候，你就可以用库仑扭秤实验来测量它们之间的相互作用力。

只要知道了相互作用力的大小，就可以根据万有引力定律算出它们的质量了。

接下来，我们来说说卡文迪许扭秤实验。

这个实验的名字也很高级，但是它的原理比库仑扭秤实验简单多了。

卡文迪许扭秤实验的原理是利用杠杆原理来测量物体之间的相互作用力。

具体来说，就是通过测量物体在不同方向上的扭转程度来计算出它们之间的相互作用力。

听起来好像很难懂，其实也很简单。

比如说，你有一个很重的物体和一个很轻的物体。

当你把这两个物体放在一条绳子的两端时，让它们沿着这条绳子滑动。

这时候，你就可以用卡文迪许扭秤实验来测量它们之间的相互作用力了。

只要知道了相互作用力的大小和方向，就可以根据牛顿第二定律算出它们的加速度了。

好了，现在我们已经知道了库仑扭秤实验和卡文迪许扭秤实验的原理，下面我们来说说它们的注意事项。

要注意安全。

这两个实验都是用重力和摩擦力来产生作用力的，所以一定要小心操作，避免受伤。

要注意精度。

这两个实验都需要非常精确地测量物体之间的相互作用力，所以要保证测量工具的质量和精度。

要注意环境条件。

这两个实验都受到环境因素的影响，比如温度、湿度等，所以要在合适的环境下进行实验。

库仑扭秤实验和卡文迪许扭秤实验虽然看起来很高级，但是原理和注意事项都很简单易懂。

卡文迪许扭秤实验法

卡文迪许扭秤实验法
卡文迪许用一根39英寸的镀银铜丝，吊起一根6英尺长的木杆，在杆的两端各固定一个直径2英寸的小铅球，另用两颗直径12英寸的固定着的大铅球吸引它们。

如果能够测出铅球间引力引起的摆动周期，由此计算出两个铅球的引力，就能够推算出地球的质量和密度。

可是，在卡文迪许的实验室里，根本没有那么精确的度量仪器。

两个一公斤重的铝球相距十公分时，相互之间引力只有百万分之一克。

即使空气中的飘尘，也能干扰它的准确度，这怎么能够测量呢？一连几天，卡文迪许都把自己关在实验室里，整天冥思苦想。

走在半路上，他看到几个小孩子，正在作一种有趣的游戏：他们每人手里拿着一面小镜子，用来反射太阳光，互相照着玩。

镜子只要稍一转动，远处光点的位置就发生很大变化。

“真有意思！”看着那些活泼的孩子，卡文迪许想。

突然之间，他茅塞顿开。

他掉头跑回实验室，对自己的实验装置进行了一番革新。

他把一面小镜子固定在石英丝上，用一束光线去照射它。

光线被小镜子反射过来，射在一根刻度尺上。

这样，只要石英丝有一点极小的扭动，反射光就会在刻度尺上明显地表示出来。

扭动被放大了！实验的灵敏度大大提高了，这就是著名的“扭秤”实验法。

历史趣谈卡文迪许扭秤实验如何验证万有引力定律

历史趣谈卡文迪许扭秤实验如何验证万有引力定律
卡文迪许扭秤实验是由美国物理学家卡文迪许（Henry Cavendish）于1798年进行的一组实验，它为我们证明了万有引力定律（Universal Law of Gravitation）。

万有引力定律是牛顿发明的一条定律，它描述了所有物体之间的引力作用，并将其描述为一个简单的方程式。

在1798年，牛顿的学生、物理学家卡文迪许（Henry Cavendish）发现，要证明这条定律，他需要一个更有力的证据。

他因此想出了一种利用机械装置来测量和测算物体之间的引力作用的方法，也就是今天我们所知道的卡文迪许扭秤实验。

卡文迪许扭秤实验是一种基于力平衡的实验，它涉及大量的精确测量和计算，使它具有极高的精度。

实验装置由一个大型扭秤、一个小型扭秤以及一些其它的物体组成，这些物体分别是一根塔形结构、一个支点、一个钩子、一个球形的铅球和一些夹住铅球的把手。

大扭秤上方的钩子固定了一个球形铅球，而小扭秤的一头则固定在塔形结构的支点上，另一头则夹住了铅球上的把手，铅球就悬挂在两部扭秤之间并平衡在一起，这种结构使得小扭秤的大小可以改变。

在进行实验时，卡文迪许使用了一种精密的测量仪器，称为杆计，可以准确测量出小扭秤大小的变化，以及大小扭秤之间在改变时所受的力大小，从而推断出这些铅球之间的引力大小。

引力常量的测定卡文迪许扭秤实验

引力常量的测定——卡文迪许扭秤实验牛顿认为公式中的引力常数G是普适常数，不受物体的形状、大小、地点和温度等因素影响，引力常数的准确测定对验证万有引力定律将提供直接的证据。

英国物理学家卡文迪许（H.Cavendish 1731-1810）根据牛顿提出的直接测量两个物体间的引力的想法,采用扭秤法第一个准确地测定了引力常数。

卡文迪许实验所用的扭秤是英国皇家学会的米歇尔神父制作的。

米歇尔制作扭秤的目的是为了测定地球的密度，并与卡文迪许讨论过这一问题。

但是，米歇尔还未用它来进行测定，便去世了。

米歇尔去世后，这架仪器几经辗转传到了剑桥大学杰可逊讲座教授沃莱斯顿神父手里，他又慷慨地赠送给了卡文迪许，这时卡文迪许已是年近古稀的老人了。

卡文迪许首先根据自己实验的需要对米歇尔制作的扭秤进行的分析，他认为有些部件没有达到他所希望的方便程度，为此，卡文迪许重新制作了绝大部分部件，并对原装置进行了一些改动。

卡文迪许认为大铅球对小铅球的引力是极其微小的，任何一个极小的干扰力就会是实验失败。

他发现最难以防止的干扰力来自冷热变化和空气的流动，为了排除误差来源，卡文迪许把整个仪器安置在一个关闭房间里，通过望远镜从室外观察扭秤臂杆的移动。

扭秤的主要部分是一个轻而坚固的T形架，倒挂在一根金属丝的下端。

T形架水平部分的的两端各装一个质量是m的小球，T形架的竖直部分装一面小平面镜M，它能把射来的光线反射到刻度尺上，这样就能比较精确地测量金属丝地扭转。

实验时，把两个质量都是m'地大球放在如图所示的位置，它们跟小球的距离相等。

由于m受到m'的吸引，T形架受到力矩作用而转动，使金属丝发生扭转，产生相反的扭转力矩，阻碍T形架转动。

当这两个力矩平衡时，T形架停下来不动。

这时金属丝扭转的角度可以从小镜M反射的光点在刻度尺上移动的距离求出，再根据金属丝的扭转力矩跟扭转角度的关系，就可以算出这时的扭转力矩，进而求得m与m'的引力F。

卡文迪许扭秤法测量万有引力常数

卡文迪许扭秤法测量万有引力常数班级核工程82学号 08182022姓名刘勇卡文迪许扭秤法测量万有引力常数一、实验目的1. 掌握在扭秤摆动中求平衡位置的方法。

2. 掌握如何通过卡文迪许扭秤法测量万有引力常数。

二、实验仪器卡文迪许扭秤，激光发射器，光屏，米尺，秒表，电源三、实验原理根据牛顿万有引力定律，间距为r, 质量为 m1 和m2 的两球之间的万有引力F 方向沿着两球中心连线，大小为其中G 为万有引力常数。

实验仪器卡文迪许扭秤法原理图所示。

卡文迪许扭秤是一个高精度的仪器，非常灵敏，为保护仪器和防止外界干扰影响实验测量，扭秤被悬挂在一根金属丝上，装在镶有玻璃板的铝框盒内，固定在底座上。

实验时，把两个大球贴近装有扭秤的盒子，扭秤两端的小球受到大球的万有引力作用而移近大球，使悬挂扭秤的悬丝扭转。

激光器发射的激光被固定在扭秤rm m G F 221上的小镜子反射到远处的光屏上，通过测量光屏上扭秤平衡时光点的位置可以得到对应的扭转角度, 从而计算出万有引力常数 G 。

假设开始时扭秤扭转角度θ0=0，把大球移动贴近盒子放置，大小球之间的万有引力为F ，小球受到力偶矩N =2 Fl 而扭转，悬挂扭秤的金属丝因扭转产生与力偶矩N 相平衡的反向转矩N ’= K(θ/2)，扭秤最终平衡在扭角θ的位置：F=G M m /d 22Fl= K(θ/2)其中 K 是金属悬丝的扭转常数，M 是大球的质量，m 是小球的质量，d 是大球小球的中心的连线距离，l 是小球中心到扭秤中心的距离。

由转动方程可求得悬丝的扭转常数:通过转动惯量I 和测量扭秤扭转周期T 就可以得到金属丝的扭转系数K ：假设小球相对大球是足够轻，那么转动惯量lm I22=因此由上述几式得，扭转角ld222πT2GM θ=。

当大球转动到相反的对称位置后，新平衡位置是-θ, 因此平衡时的总扭转角为ld222πTGM 2θ=通过反射光点在光屏上的位移S 可以得到悬丝扭转角度。

引力常量的测量卡文迪许扭称试验

4．某实心均匀球半径为R，质量为M，在球外壳离球面h高处有一质量为m的质点，则其万有引力大小为( B )
A．GMm／R2 B．GMm/(R+h)2 C．GMm／h2 D．GMm／(R2+h2)
5．有两个大小相同的实心小铁球，它们紧靠
在一起时，相互之间的万有引力为F，若换成两个
半径为原来2倍的实心大铁球紧靠在一起，则它们
2.太阳与行星间的引力
太阳对行星的引力Fቤተ መጻሕፍቲ ባይዱ行星所受的向心力
即：F
v2 m
r 圆周运动中：V=
2πr
则：F
4 2mr

T
开普勒定律变形为 T2

r3
T2
代入上式得到
F 4 2K m
k Fm
r2
r2
这表明：太阳对不同行星的引力，与行星的
质量成正比，与行星和太阳间距离的二次方成反
比。
由牛顿第三定律，行星吸引太阳的力跟太阳吸引行星的力，大小相等且性质相同。
引力常量的测量—卡文迪许扭称实验(1789年)
卡文迪许实验室
卡文迪许
【思考】对于一个十分微小的物理量
该采用什么方法测量？ —放大法
引力常量的测量—卡文迪许扭称实验(1789年)
对万有引力定律的理解
(1)普遍性．它存在于宇宙中任何有质量的物体之间，不管它们之间是否还有其他作用力．
(2)普适性．G是一个仅和m、r、F单位选择有关，而与物体性质无关的恒量．
有两个大小相同的实心小铁球它们紧靠在一起时相互之间的万有引力为f若换成两个半径为原来2倍的实心大铁球紧靠在一起则它们之间的万有引力是a2fb4fc8fd16f物之间的距离减小x两物体仍可视为质点此时两个物体之间的万有引力为f根据上述条件可以计算a

卡文迪许扭秤法测量万有引力常数

位：s）
2. 对测量结果进行分析，分析影响测量结果的主要因素。答：本实验本身是具有高度精确性的，但在光电在屏幕上移动距离和位置时，仿真实验本身模型不够好，会在数据积累的过程中造成很大误差。
七、实验感悟与体会
能够亲手去做这个经典实验让我充分感受到了卡文迪许的智慧和自然的神奇。仿真实验虽说提高效率降低了成本，但调试仪器的过程还是不可复制真是情况的。因此我认为仿真是呀不能完全代替实验室，在实验室里做实验才更加有意义。
二、实验原理
根据牛顿万有引力定律，间距为 r, 质量为 m1 和 m2 的两球之间的万有引力 F 方向沿着两球中心连线，大小为 (1) 其中 G 为万有引力常数。
实验仪器如卡文迪许扭秤法原理图所示。卡文迪许扭秤是一个高精度的仪器，非常灵敏，为保护仪器和防止外界干扰影响实验测量，扭秤被悬挂在一根金属丝上，装在镶有玻璃板的铝框盒内，固定在底座上。
3. 光点位移的测量(单位：cm)
6/8
4. 由以上数据可以求得
标准值相对误差为
六、思考题
1.假设 M= 1kg,
l = 10 cm, d =5cm , m = 15 g
1) 扭秤的周期 T ?
答：由
可得
2) 悬丝的扭转常数
K
? 7/8
答：又由
以及
,可得 T=
,最终结果 T=202.78（单
8/8
打开激光器电源：双击电源弹出放大的激光器电源面板。鼠标单击开关打开电源，可以看见激光被镜子反射到远处的光屏上。确定平衡位置 C：鼠标双击实验窗口中的卡文迪许扭秤进行调节。过右键菜单可打开卡文迪许扭秤顶视图。通过的鼠标调节扭丝转角调节旋钮，可对扭秤初始转角进行粗调。双击锁紧螺钉使得扭秤下落，并且作最大振幅的扭转振动（撞击玻璃板）。记录此时光点在光屏两端最远点的位置 x1, x2 。 Xc = (x1+ x2)/2。

卡文迪许扭秤实验

T形架水平部分的的两端各装一个质量是m的小球,竖直部分装一面小平面镜 M，把射来的光线反射到刻度尺上，比较精确地测量金属丝地扭转。
当万有引力产生的力矩与金属丝扭转力矩平衡时，T形架静止不动，扭转的角度可以从小镜M反射的光点在刻度尺上移动的距离求出，再根据金属丝的扭转力矩跟扭转角度的关系，就可以算出这时的扭转力矩，进而求得m与m'的引力F卡 Nhomakorabea迪许扭秤实验
赵俊林
万有引力定律
G=6.67×10⁻¹¹ N·m²/kg²
G最早如何测得？
卡文迪许扭秤实验
实验原理
用准直的细光束照射镜子，细光束反射到一个很远的地方，标记下此时细光束所在的点。用两个质量一样的铅球同时分别吸引扭秤上的两个铅球。由于万有引力作用。扭秤微微偏转。但细光束所反射的远点却移动了较大的距离。用此计算出了万有引力公式中的常数G。
2.勇于创新
化小为大，将十分微小的变化通过设计实现放大，巧妙设计扭秤实验来测量引力常数，凭借高超的实验技巧和强大的数理基础，为科学界做出卓越的贡献。
THANKS
实验精妙之处
实验巧妙地利用光的反射实现二次放大（微小形变放大） 1. 尽可能地增大了T型架连接两球的长度使两球间万有引力产生较大的力矩，使杆偏转
2. 尽力的增大弧度尺与系统的距离使小镜子的反射光在弧线上转动了较大角度
启发
1.严谨的求知态度
卡文迪许认为大铅球对小铅球的引力是极其微小的，任何一个极小的干扰力就会使实验失败。他发现最难以防止的干扰力来自冷热变化和空气的流动。为了排除误差来源，卡文迪许把整个仪器安置在一个关闭房间里，通过望远镜从室外观察扭秤臂杆的移动。测得引力常量G=6.754×10-11m3kg-1s2，与目前的公认值只差百分之一，在此后得89年间竟无人超过他的测量精度。

【高中物理】引力常量的测定

引力常量的测定●本节教材分析这节课的内容是要让学生知道引力常量G的值的测出使万有引力定律更具有实际意义．可是一般物体间的引力很小,怎样才能够测出呢？要让学生去体会卡文迪许扭秤的“巧妙”所在．这节课的重点是卡文迪许扭秤测量引力常量的原理,难点是扭转力矩平衡问题的理解．在教学中解决重点、难点的同时要渗透对学生的思想教育及“测定微小量的思想方法”．●教学目标一、知识目标1．了解卡文迪许实验装置及其原理．2．知道引力常量的物理意义及其数值．二、能力目标通过卡文迪许如何测定微小量的思想方法,培养学生开动脑筋,灵活运用所学知识解决实际问题的能力．三、德育目标通过对卡文迪许实验的设计思想的学习,启发学生多动脑筋,培养其发散性思维、创造性思维．●教学重点卡文迪许扭秤测引力常量的原理．●教学难点扭转力矩与引力矩平衡问题的理解．●教学方法1．对卡文迪许实验的装置和原理采用直接讲授、介绍的方法．2．对金属丝的扭转角度采用与微小形变实验的对照．●教学用具投影仪、投影片、卡文迪许扭秤模型．●课时安排1课时●教学过程本节课的学习目标1．了解卡文迪许实验装置及其原理． 2．知道引力常量的物理意义及其数值．学习目标完成过程一、导入新课上节我们学习了万有引力定律的有关知识,现在请同学们回忆一下．万有引力定律的内容及公式是什么？公式中的G 又是什么？回答上述问题：内容：自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的平方成反比．公式：F ＝G 221r m m ．公式中的G 是万有引力常量,它在大小上等于质量为1 kg 的两个物体相距1 m 时所产生的引力大小,经测定其值为6.67×10-11 N ·m 2/kg 2．牛顿在前人的基础上,应用他超凡的数学才能,发现了万有引力定律,却没能给出准确的引力常量,使万有引力定律只有其理论意义,而无更多的实际意义,今天我们就来共同学习英国物理学家卡文迪许是如何用实验来测定引力常量的．二、新课教学 A ．基础知识请同学们阅读课文,同时考虑下列几个问题． 1．引力常量为什么难以测量？2．谁设计实验对万有引力常量进行了测定,他使用的装置是什么？ 3．该装置主要由几部分组成？ 4．该实验的实验原理是什么？阅读课文,从课文中找出相关的答案．1．万有引力常量难以测量的原因是其值非常小,很难用实验方法将它显示出来．所以对它的测定必须设计特殊的装置才行．2．英国的物理学家卡文迪许在1789年,巧妙地设计了扭秤装置,把万有引力常量应用实验的方法测量出来．3．扭秤的主要部件有四部分：一个倒置的金属架；一根金属丝；一个固定在T型架上的平面镜；T型架两端各装一质量为m的小球．其结构如图所示：4．该实验的实验原理是应用力矩平衡的知识来设计的．B．深入探究请同学们结合课本知识,分析、讨论下列问题．1．由于一般物体间的引力非常小,导致引力常量难以测量,那么,怎么样就能把引力常量测量出来了呢？2．扭秤装置中的小平面镜起什么作用呢？3．在扭秤装置中,除了平面镜外是否还有其他地方对相互作用的效果进行了放大呢？4．本实验的实验原理是力矩平衡,那么,具体说是哪些力矩相平衡呢？学生分组讨论,结合课文给出的提示,得出相似结论．1．引力常量难以测量的原因是一般物体间的相互作用力很小,产生的作用效果不明显,如果我们能把引力产生的微小效果进行放大的话,就可以用实验来测量引力常量了．2．装置中的小平面镜就起到了放大的作用．当m′与m相互吸引时,引力会使金属丝发生微小的扭转形变,也正是由于形变量非常微小,所以我们很难用眼睛观察到．当固定上一个小镜后,小镜会随金属丝的扭转而转过很小的角度,它的转动会引起刻度尺反射光点的明显移动,从光点位置移动的大小便可反映出金属丝的扭转程度,进而反映出两小球间相互作用力的大小．3．在该装置中,除了平面镜起到的放大作用外,“T”型架也起到了放大的作用．我们从力矩平衡的知识知道,力矩的大小与两个因素有关,一个是力的大小,另一个是力臂的大小．在这一实验中,我们不能增大相互作用的引力,所以考虑去增大力臂,而“T”型架正好起到了增大力臂的作用．当力矩增大后,也就将力的作用效果进行了放大．4．“T ”型架受到力矩的作用产生转动,使金属丝发生扭转,产生相反的扭转力矩,阻碍“T ”型架转动,当这两个力矩平衡时,“T ”型架停止转动．设金属丝的扭转力矩为M 1,引力矩为M 2,即有：M 1＝M 2． C ．教师总结通过前面的学习,我们了解了扭秤装置的组成、结构、二次放大原理以及实验原理．当应用扭秤装置进行实验时,金属丝的扭转力矩M 1可以根据它与扭转角“θ”的关系来求,而扭转角度“θ”可通过平面镜M 反射光点在刻度尺上移动的距离求出．此时M 1便成了已知量．而M 1＝M 2＝F 引·l ＝G 2r m m 'l ．故：G ＝lm m r M '21利用上述原理,再加上可控变量法,经多次测量便可求得：G ＝6.67×10-11 N ·m 2/kg 2．D ．基础知识应用1．________年,________国物理学家________应用________装置,第一次在实验室里巧妙地测出了万有引力常量．2．扭秤装置的巧妙之处在于对作用效果进行了二次放大,这两次放大分别体现在________；________．3．卡文迪许应用扭秤装置测定万有引力常量的实验原理是________．4．一个人的质量是50 kg,他在地面上受到的重力是多大？已知地球半径R ＝6.4×106 m ．地球质量为6.0×1024 kg ．计算一下人与地球之间万有引力的大小．参考答案：1．1789；英；卡文迪许；扭秤2．小平面镜反射；“T ”型架横杆增大力臂3．万有引力产生的力矩与金属丝扭转时产生的扭转力矩相等 4．490 N ；4.89×102 N ．解：G ＝mg ＝50×9.8 N ＝490 N ．由万有引力定律可知：F 引＝G 2R Mm＝6.67×10-11×2624)104.6(50100.6⨯⨯⨯N三、知识反馈1．关于引力常量,下列说法正确的是( )A ．引力常量是两个质量为1 kg 的物体相距1 m 时的相互吸引力B ．牛顿发现了万有引力定律时,给出了引力常量的值C ．引力常量的测出,证明了万有引力的存在D ．引力常量的测定,使人们可以测出天体的质量2．两个行星的质量分别为m 1和m 2,绕太阳运行的轨道半径分别是r 1和r 2,若它们只受万有引力作用,那么这两个行星的向心加速度之比为( ) A ．1B ．m 2r 1/m 1r 2C ．m 1r 2/m 2r 1D ．r 22/r 123．一旦万有引力常量G 值为已知,决定地球质量的数量级就成为可能,若已知万有引力常量G ＝6.67×10-11 N ·m 2/kg 2,则可知地球质量的数量级是( ) A ．1018B ．1020C ．1022D ．10244．已知地球绕太阳公转的轨道半径为1.49×1011 m,公转周期为3.16×107 s,试求： (1)地球绕太阳公转的速度； (2)地球绕太阳公转的向心加速度；(3)如果地球质量为5.89×1024 kg,那么太阳对地球的万有引力应为多大．参考答案： 1．CD 2．D 3．D4．地球绕太阳公转的向心力是太阳对地球的万有引力提供的．设地球质量为m ,轨道半径为r ,公转周期为T ,运行速度为v ,运行的向心加速度为a n ,则(1)v ＝7111016.31049.114.322⨯⨯⨯⨯=T r πm/s ＝2.96×104 m/s (2)a n ＝r v 2＝11241049.1)1096.2(⨯⨯m/s 2＝5.88×10-3 m/s 2(3)F 引＝F 向＝ma n ＝5.89×1024×5.88×10-3 N ＝3.46×1022 N四、小结卡文迪许实验对引力常量的测定,使得万有引力定律有了真正实用性,通过本节学习我们要掌握：1．卡文迪许实验装置及原理．2．知道引力常量测定的意义．3．知道卡文迪许扭秤的设计思想,应该对我们有较大的启迪作用．五、作业1．复习本节内容2．思考题(1)离地面某一高度h处的重力加速度是地球表面重力加速度的一半,则高度h是地球半径的()A．2倍B．2倍C．2＋1倍D．2-1倍(2)设想把物体放到地球中心,则此物体此时与地球间的万有引力是多少？参考答案：(1)D(2)零六、板书设计七、本节优化训练设计1．(1996年上海)已知地球表面重力加速度为g,地球半径为R,引力常量为G,用以上各量表示地球的质量M ＝________．2．(1997年全国)已知地球半径约为6.4×106 m,又知月球绕地球的运动可近似看做圆周运动,则可估算出月球到地心的距离约为________m ．(结果保留一位有效数字)3．某行星半径为R ,其表面附近有一颗卫星,其绕行周期为T ,已知引力常量为G ,写出该行星质量M ,平均密度ρ的表达式．4．如果有一天,因某种原因地球自转加快．则地球上的物体重量将发生变化,当赤道上重力为零时,这时一昼夜有多长？(已知地球半径R ＝6.4×106 m)5．某行星质量是地球质量的一半,半径也是地球半径的一半,某运动员在地球上能举起250 kg 的杠铃,在行星上最多能举起质量为多少的杠铃？参考答案： 1．gR 2/G分析：本题考查的是地面上物体重力mg 近似等于地球对物体的万有引力,即：mg ＝G 2R Mm．所以 M ＝gR 2/G ． 2.3×108 m分析：此题的运动模型是：“月球绕地球做匀速圆周运动”,其规律是：“万有引力提供向心力”．已知常识是：“月球运行周期为30天”．解法1：对月球,万有引力提供向心力,得：G 2r Mm＝m 224T rπ①式中M ,m 分别表示地球和月球的质量,须想法替换M 和G ．对地面上的物体,忽略地球自转的影响,认为其重力等于万有引力,则有m ′g ＝G 2R m M '②式中m ′为地面上某一物体的质量由①②两式消去G 、M 、m 、m ′得：r ＝326233222104)104.6()106.32430(104⨯⨯⨯⨯⨯⨯⨯=πR gT＝4×108 m解法2：利用近地卫星1结合开普勒第三定律求解,即把近地卫星和月球作为地球的两颗卫星则有：3322R r T T 月近月=近地卫星周期T 近＝85分钟月球周期T 月＝30×24×60分钟 R ＝6.4×106 m则：r 月＝R322/近月T T＝6.4×10632285)602430(⨯⨯＝4×108 m 3．M ＝4π2R 3/GT 2ρ＝V M＝3π/GT 24．1600π s解：由于G 2RMm＝m (R T 2)2(π①且G 2R Mm＝mg②由①②两式得：T 2＝gR24π所以T ＝2πgR ＝1600π s5．125 kg解：该运动员在地球上所能举起的杠铃的重力与他在行星上所能举起的杠铃的重力应相等．而重物的重力近似等于万有引力在地球上：m 1g 地＝G21地地R m M •在行星上：m 2g 行＝G 22行行R m M •．因为m 1g 地＝m 2g 行所以G 2221行行地地R m M GR m M =所以m 2＝12)(m R R M M ••地行行地＝250)21(122⨯⨯＝125 kg●备课资料关于引力常量G 的测定牛顿在首次描述万有引力定律时,设定了一个基本常数G ,即关于质量与距离的力,然而G 数值的精确测定却长期困扰着科学家,现在,科学家通过周密而细致的工作,终于揭开了这一神秘面纱．科研人员将一块特别的玻璃块放进一个垂直的真空管中,同时用激光器来跟踪它的运动,由于地球的质量知道得还不精确,研究人员必须排除行星引力对G 的影响．他们在真空管的周围套上一个500 kg 的钨环形套,让其或低于玻璃块,或高于玻璃块,结果,环形磁的引力几乎没有增大或减慢这颗“卫星”的降落速度,通过测定环形套两种位置和玻璃块的加速度差异,研究人员可以推断出仅有环形套时的加速度,然后试验人员进行G 的计算．尽管有着比期望值误差较大的干扰,但是,这颗用来试验G 的“卫星”,其轨迹图展示出接近于最广为公认的数值,这一实验的一致性,将有助于验证人们认为前人的测定因某些原因而不够准确的看法．。

卡文迪许扭秤实验介绍

卡文迪许扭秤实验介绍卡文迪许扭秤实验是历史上最有名的科学实验之一，这个实验是由英国著名科学家卡文迪许设计完成的，并以他的名字命名，这个实验测出了地球引力的常值，下面是为你搜集卡文迪许扭秤实验的相关内容，希望对你有帮助!卡文迪许扭秤实验卡文迪许扭秤实验是历史上最有名的科学实验之一，这个实验是由英国著名科学家卡文迪许设计完成的，并以他的名字命名，这个实验测出了地球引力的常值，证明了牛顿万有引力定律的正确性，可以说是人类科学事业上的伟大成果之一。

卡文迪许扭秤实验的原理非常巧妙，因为在当时没有精密仪器的条件下，要验证物体的微小变化量很不容易，因此卡文迪许扭秤实验的做法就是将不易察觉的微小变化量，转化为较大的显著的变化量，然后再根据计算微小变化量与较大的显著变化量之间的关系，从而成功地测量出了万有引力常数，虽然这个数据并不是非常精准，有后世测出的数据有百分之一的差距，但是在当时，这绝对是一项史无前例的成就，而且此后近百年都无人打破这个记录，更可贵的是卡文迪许证明了牛顿万有引力定律的正确性。

卡文迪许扭秤实验的具体做法虽然显得有些繁琐，普通人可能不太容易领会，不过原理是简单明了的，这个实验同时也运用了光的折射原理，可以说是一项非常符合科学规律的实验。

卡文迪许在做这个实验时已经是古稀老人，但是他依然靠着顽强的毅力和严谨的科学精神，完成了这一伟大的实验，实在非常可贵。

卡文迪许成就卡文迪许成就主要分为两方面，一是物理成就。

在物理方面，他对电学的研究非常深入，在后人发现的很多卡文迪许的手稿中，人们发现他在电学方面的很多研究都走在了时代前列。

而卡文迪许扭秤实验用非常巧妙的用实验的方式测量出万有引力常数，从而证明了牛顿万有引力定律的正确性，而且它还推测出地球的密度，从而称量出地球的质量，卡文迪许因此被称为称量地球的第一人。

卡文迪许成就的第二方面就在化学方面，在化学领域内，他的成就同样突出。

卡文迪许研究出空气的组成成分，指出水是一种化合物。

用英国科学家亨利的扭秤实验证明万有引力就是磁力

用英国科学家亨利•卡文迪许的扭秤实验证明万有引力就是磁力万有引力定律是艾萨克•牛顿在1687年于《自然哲学的数学原理》上发表的。

牛顿的普适的万有引力定律表示如下：任意两个质点有通过连心线方向上的力相互吸引。

该引力大小与它们质量的乘积成正比与它们距离的平方成反比，与两物体的化学组成和其间介质种类无关。

扭秤实验：18世纪末,英国科学家亨利•卡文迪许决定要找出这个引力。

他将小金属铅球系在长为6英尺（1英尺等于0.305米）木棒的两边并用金属线悬吊起来。

这个木棒就像哑铃一样.再将两个350磅（1磅等于0.4536千克）的铅球放在相当近的地方，以产生足够的引力让哑铃转动，并扭转金属线，然后用自制的仪器测量出微小的转动，测量结果惊人地准确。

他测出的万有引力和用质量的乘积成正比与它们距离的平方成反比算出的力总是相差6.67259x10^-11倍。

他测出了万有引力恒量的常数，万有引力常量约为G=6.67259x10^-11 (N•m^2 /kg^2)，通常取G=6.67×10^-11。

地球膨裂说认为，亨利•卡文迪许的扭秤实验其实就是磁力实验。

亨利•卡文迪许的扭秤实验用的是两个350磅（1磅等于0.4536千克）的铅球和两个小铅球，亨利•卡文迪许认为，铅球没有磁力，所以测的是万有引力而不是磁力。

地球膨裂说认为，如果我们把亨利•卡文迪许的扭秤实验中的大小铅球都换成是铁球，然后测出引力常数D。

因为磁力和质量成正比，和距离平方成反比，所以只要证明D就是铁的磁场强度，那么测得的力不就是磁力吗？那么引力公式F=D•m1•m2/r^2不就是磁力公式吗？为简单起见，我们不用证明D是铁的磁场强度来证明测得的力是磁力，只要我们证明G是铅的磁场强度、证明万有引力F=G•m1•m2/r^2是磁力就可以了。

现代科学证明：任何物质都具有磁性，所以任何物质在不均匀磁场中都会受到磁力的作用{1}。

科学家们现已测出，星际空间磁感应强度为10^-10（T）、原子核表面约10^12（T）、中子星表面约10^8（T）、人体表面 3*10^(-10)（T）{1} 。

引力常量的测量----卡文迪许扭秤实验

2020/3/2
F1 可以看成是被挖去部分与质点的万有引力与剩余部分与质点的万有引力的和，即 F1 ＝ F2 ＋ F2′(被挖去部分)． F2′＝GM5′2Rm2 ＝Gρ2V5′4R2m ρ＝43πMR3，V′＝43π(R2 )3，
2020/3/2
M 所以 F2′＝Gቤተ መጻሕፍቲ ባይዱ85Rm2＝G50MRm2
2020/3/2
(3)当物体由赤道向两极移动的过程中，向心力减小，重力增大，只有物体在两极时物体所受
的万有引力才等于重力．
(4)除在两极处外，都不能说重力就是地球对物体的万有引力，但在忽略地球自转时，通常认
为重力等于万有引力，即 mg＝GRM2m(这个关系非常重要，以后要经常用)．
注意：重力只是物体所受万有引力的一个分力，但是由于另一个分力F向特别小，所以一般近似认为地球表面（附近）上的物体，所受重力等于万有引力。
• 三、万有引力与重力的区别与联系：
•
物体与地球的引力：F＝G
Mm R2
• 方向：指向地心。
• 重力:由于地球的吸引而使物体受到的力，
叫做重力。重力与万有引力是同一性质
的力。
2020/3/2
重力与万有引力的关系
• 由于地球自转，静止在地球上的物体也跟着绕地轴作圆周运动，这个作圆周运动的向心力就由万有引力的一个分力来提供。因此，在地球表面上的物体所受的万有引力F可以分解成物体所受的重力mg和随地球自转做圆周运动的向心力F′，如图3－1 －3所示．
Gmm r2
‧L=
kθ
即：G kr2
mml
巧妙之处：
1、把微小力（根本不可能觉察到）转变成力矩来反映（一次放大）

卡文迪什引力常量实验

卡文迪什引力常量实验
科学家卡文迪什曾说过：“真实的奇迹只能通过实验得以证实。

”这句话最能体现他对科学的精神，他致力于揭示万有引力的规律，他的终极目标是实现“定引力常量实验”，也就是在实验中直接测量万有引力的常量。

卡文迪什引力常量实验的始作俑者，是德国力学家路德维希康斯坦丁（Ludwig van Kostantin），他在1802年提出了“定引力常量实验”的想法，但是由于当时的技术水平不足，他的这个想法没有得到实现。

卡文迪什将康斯坦丁的想法付诸实践，他准备用更小的砝码（称为“摆”），在不同的距离下测量万有引力，他担心如果摆太小，那么它会被地球的引力拉向地面，因此，他选择了一个较大的摆，用金属制成，重量超过200克。

在测量过程中，卡文迪什采用“垂直测量”的方法，即以电码为中心，将摆置在电码的不同高度，然后测量摆的位置改变，由此可以得出与摆的距离和摆的角度成正比的规律。

卡文迪什的实验做出了重要结果，实验结果表明，摆deviate 随着距离增大而减小，而且引力常量可以从实验中推导出来。

这是第一次有人从实验中直接得出了宇宙大尺度的定律，也就是卡文迪什定律，这使科学家们更加相信万有引力的存在，它也成为物理学的最基本定律之一。

接下来的几个世纪，卡文迪什定律的解释依然在不断深化，其
原理也被用于许多科学领域。

如今，它已成为宇宙结构的基础，也帮助我们更好地理解宇宙中的物质与能量之间的联系。

总之，卡文迪什引力常量实验是一个重要的科学实验，它揭示了万有引力的定律，为人类科学发展做出了重大贡献，也为我们更加深入地理解宇宙奥秘提供了历史性的机遇。

卡文迪许扭秤实验介绍

卡文迪许扭秤实验介绍卡文迪许扭秤实验是历史上最有名的科学实验之一，这个实验是由英国著名科学家卡文迪许设计完成的，并以他的名字命名，这个实验测出了地球引力的常值，下面是店铺为你搜集卡文迪许扭秤实验的相关内容，希望对你有帮助!卡文迪许扭秤实验卡文迪许扭秤实验是历史上最有名的科学实验之一，这个实验是由英国著名科学家卡文迪许设计完成的，并以他的名字命名，这个实验测出了地球引力的常值，证明了牛顿万有引力定律的正确性，可以说是人类科学事业上的伟大成果之一。

卡文迪许扭秤实验的原理非常巧妙，因为在当时没有精密仪器的条件下，要验证物体的微小变化量很不容易，因此卡文迪许扭秤实验的做法就是将不易察觉的微小变化量，转化为较大的显著的变化量，然后再根据计算微小变化量与较大的显著变化量之间的关系，从而成功地测量出了万有引力常数，虽然这个数据并不是非常精准，有后世测出的数据有百分之一的差距，但是在当时，这绝对是一项史无前例的成就，而且此后近百年都无人打破这个记录，更可贵的是卡文迪许证明了牛顿万有引力定律的正确性。

卡文迪许扭秤实验的具体做法虽然显得有些繁琐，普通人可能不太容易领会，不过原理是简单明了的，这个实验同时也运用了光的折射原理，可以说是一项非常符合科学规律的实验。

卡文迪许在做这个实验时已经是古稀老人，但是他依然靠着顽强的毅力和严谨的科学精神，完成了这一伟大的实验，实在非常可贵。

卡文迪许成就卡文迪许成就主要分为两方面，一是物理成就。

在物理方面，他对电学的研究非常深入，在后人发现的很多卡文迪许的手稿中，人们发现他在电学方面的很多研究都走在了时代前列。

而卡文迪许扭秤实验用非常巧妙的用实验的方式测量出万有引力常数，从而证明了牛顿万有引力定律的正确性，而且它还推测出地球的密度，从而称量出地球的质量，卡文迪许因此被称为称量地球的第一人。

卡文迪许成就的第二方面就在化学方面，在化学领域内，他的成就同样突出。

卡文迪许研究出空气的组成成分，指出水是一种化合物。

万有引力常数——卡文迪许试验的数学分析

万有引力常数——卡文迪许试验的数学分析虽然牛顿推导出了万有引力定律F=GF1F2/r^2。

但是这个常数G 的大小牛顿并不知道。

卡文迪什试验由亨利·卡文迪什于1797年-1798年完成。

这是第一个在实验室里完成的测量两个物体之间万有引力的实验，并且较准确地求出了万有引力常数和地球质量。

该实验是物理学史上的经典实验之一。

有了万有引力常数，对于天体以及地球质量的估计才成为可能。

卡文迪许实验的难点在于如何排除环境的干扰，以及控制扭秤和光标的精度。

卡文迪许在测量技巧上的创造性工作所获得的结果精度，在后续的近百年时间里一直没有人能够超越。

下面就简要介绍相关的实验与数学分析1.细金属线扭动形成的扭力矩一根弹簧被拉伸或者压缩在力的一定的范围内，弹力遵循胡克定律，扭摆是一条一端固定吊起来的细弹性金属线，当金属线被扭转，金属线内部就会产生试图恢复原来形状的弹力。

图1给出了金属线直观变形的情况图2.有限元分析金属线形变图3是一个距离固定点A长度为L的金属线扭转了一个角度，横截面的变形情况。

图3从外观看，下端面各半径直线相对下底面转过一个相同的角度φ，此角称为扭转角；侧面轴向直线倾斜一个相同角度这叫外层的切变角。

距离轴中心坐标为r的切变角则为：恢复弹力可以看成截面之间沿着圆环状表面产生的扭力的合成结果。

图4在一端固定的细弹性金属丝下中点水平吊着一个长度为L水平杆，在水平杆的两端各有一个质量为m的小球。

图5水平杆会绕中心点在水平面上来回转动，假设瞬时的扭转角为θ，水平杆的来回转动的力矩与金属丝线的扭力矩大小相等方向相反。

质量为m的两个小球球心在转动中的运动轨迹是以轴心为圆心，L/2为半径的圆，因此所产生的合力矩是：，F是质点m受到的杆的推力。

现在将两个质量为M的大球与小球相互接近，由于m-M之间的万有引力作用，会改变上面阻尼方程解的θ角，使得摆动中心向M大球偏移图6这个偏移值由m-M之间的万有引力引起。

m-M之间的万有引力产生力矩为卡文迪许试验装置卡文迪许的实验装置如下图，扭摆的转角可以由光线平射到镜面反射到纪录标尺上的刻度转换测得，不加大球M时的振动周期T可以通过通过过刻度的中心位置的次数测得，那么固有角频率可知，I是可以计算的量，结果扭摆的常数k可以测得，图7下图是扭角与光线反射角之间的关系。