南京盐城2018届高三一模数学试题及答案
江苏省南京市、盐城市高三第一次模拟考试 数学 Word版

南京市、盐城市2018届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上) 1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则A B =I ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ . 3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 7.设函数1x x y e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值范围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ .9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值范围是 ▲ . 10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,时间(单位:分钟)50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 第4题图则2017S 的值为 ▲ .11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =-有四个不同的零点,则实数m 的取值范围是 ▲ .12.在平面直角坐标系xOy中,若直线(y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =,则实数k 的最小值为 ▲ . 13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则CD AB ⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分. 解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点. (1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB A C ⊥.16.(本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c已知2c =. (1)若2C B =,求cos B 的值; (2)若AB AC CA CB ⋅=⋅,求cos()4B π+的值.17.(本小题满分14分)有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧»EF,¼GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?第13题图 ABC A 1B 1C 1 MN第15题图F18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N 是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N运动到点处时,点Q的坐标为. (1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =时,求直线BM 的方程.19.(本小题满分16分)设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n …,且n N ∈,λ为常数.(1)若{}n a 是等差数列,且公差0d ≠,求λ的值;(2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-卪对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N ∈均成立. 求所有满足条件的数列{}n a 中T 的最小值.20.(本小题满分16分)设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈). (1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值; (2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值;(3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.南京市、盐城市2018届高三年级第一次模拟考试数学附加题部分(本部分满分40分,考试时间30分钟)21.[选做题](在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)A .(选修4-1:几何证明选讲)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD 垂直DE 于点D . 若4DE =,求切点E 到直径AB 的距离EF .B .(选修4-2:矩阵与变换)已知矩阵 2 00 1⎡⎤=⎢⎥⎣⎦M ,求圆221x y +=在矩阵M 的变换下所得的曲线方程.A B ED F O · 第21(A)图C .(选修4-4:坐标系与参数方程) 在极坐标系中,直线cos()13πρθ+=与曲线r ρ=(0r >)相切,求r 的值.D .(选修4-5:不等式选讲)已知实数,x y 满足2231x y +=,求当x y +取最大值时x 的值.[必做题](第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内) 22.(本小题满分10分)如图,四棱锥P ABCD -的底面ABCD 是菱形,AC 与BD 交于点O ,OP ⊥底面ABCD ,点M 为PC 中点,4,2,4AC BD OP ===.(1)求直线AP 与BM 所成角的余弦值;(2)求平面ABM 与平面PAC 所成锐二面角的余弦值.23.(本小题满分10分)已知n N *∈,()0112112r r n n n n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.(1)求()1,f ()2,f ()3f 的值;(2)试猜想()f n 的表达式(用一个组合数表示),并证明你的猜想.M A CD O P 第22题图南京市、盐城市2018届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分.1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞8.34π 9.1(0,]4 10.4034 11.9[1,)412. 13.24 14.100二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =,又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N . 所以四边形1A NBM是平行四边形,从而1//A M BN . ……………4分又BN ⊄平面1A M C,1A M ⊂平面1A M C ,所以BN ∥面1A MC . ……………6分(2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC .又CA CB =,且M 是AB 的中点,所以CM AB ⊥. 则由侧面11ABB A ⊥底面ABC ,侧面11ABB A 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC,得CM ⊥侧面11ABB A . ……………8分又1AB ⊂侧面11ABB A ,所以1AB CM ⊥. ……………10分又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1A M MC M =,所以1AB ⊥平面1A M C . ……………12分又1AC ⊂平面1A MC,所以11AB A C ⊥. ……………14分16.解:(1)因为c =,则由正弦定理,得sin C B =. ……………2分 又2C B =,所以s i n 2s i n2B B =,即4sn c o s 5sinB B =. ……………4分又B 是ABC ∆的内角,所以s i nB >,故c o s 4B =. ……………6分(2)因为AB AC CA CB ⋅=⋅, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =. ……………10分从而223cos 25a c bB ac+-===, (12)分又0B π<<,所以4sin 5B ==. 从而3c o 44B Bππ+=. ……………14分17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===,在Rt OET∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2RM T O MO T =-=. 从而2R B EMT==,即22R BE ==. ……………2分故所得柱体的底面积OEF OEF S S S ∆=-扇形22114sin120323R R ππ=-︒= ……………4分 又所得柱体的高4EG =,所以V S EG =⨯=163π-答:当BE 长为1分米时,折卷成的包装盒的容积E为163π-. …………………6分 (2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114sin120(323R R x ππ=-︒=.又所得柱体的高62EG x =-,所以V S =⨯=328(3)3x x π--+,其中03x <<. …………………10分令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=,解得2x =. …………………12分答:当BE 的长为2分米时,折卷成的包装盒的容积最大.…………………14分 18.解:(1)由2N Q ,得直线NQ 的方程为32y x =- …………………2分 令0x =,得点B 的坐标为(0,.所以椭圆的方程为22213x y a +=. …………………4分 将点N 的坐标)2代入,得222213a+=,解得24a =. 所以椭圆C 的标准方程为22143x y +=.…………………8分 (2)方法一:设直线BM 的斜率为(0)k k >,则直线BM 的方程为y kx =-.在y kx =-0y =,得P x k =,而点Q 是线段OP 的中点,所以2Q x k =. 所以直线BN的斜率2BN BQ k k k ===. ………………10分联立22143y kx x y ⎧=-⎪⎨+=⎪⎩,消去y,得22(34)0k x +-=,解得M x = 用2k 代k ,得2163316N x k =+. ………………12分 又2DN NM =,所以2(N M N x x x =-,得23M N x x =. ………………14分故222334316k k ⨯=⨯++,又0k >,解得2k =. 所以直线BM的方程为y x =- ………………16分 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为11y y x x =0y =,得P x =.同理,得Q x =.而点Q 是线段OP的中点,所以2P Qx x =,故=. …………………10分 又2DN NM =,所以2122()x x x =-,得21203x x =>4=解得2143y y =+. …………………12分将21212343x x y y ⎧=⎪⎪⎨⎪=+⎪⎩代入到椭圆C的方程中,得2119x =. 又22114(1)3y x =-,所以21214(1)(431927y y -+=21120y +=, 解得1y =(舍)或1y =.又10x >,所以点M 的坐标为(3M .……………14分故直线BM的方程为2y x =- …………………16分 19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+, 化简得2(1)0d λ-=,又0d ≠,所以1λ=. ………………4分(2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=. ……6分欲存在[3,7]r ∈,使得12n m n r -⋅-…,即12n r n m --⋅…对任意*n N ∈都成立,则172n n m --⋅…,所以172n n m --…对任意*n N ∈都成立. ………………8分令172n n n b --=,则11678222n nn n n n n nb b +-----=-=, 所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>.所以n b 的最大值为981128b b ==,所以m 的最小值为1128. ………………10分 (3)因为数列{}n a 不是常数列,所以2T ….①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩, 所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意. ………………12分②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立. ………………14分由2221321()a a a a a λ=+-,得7λ=.则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-;由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-;由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-.所以,数列(*)适合题意. 所以T的最小值为3. ………………16分20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,.当c =时,()b g x ax x=+,所以2()b g x a x '=-,所以(1)g a b '=-. ………………2分因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩. ………………4分 (2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =,则题意可转化为方程3(0)aa x c t t x-+-=>在(0,)+∞上有相异两实根12,x x . ………………6分即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a <<⎧⎪∆=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩, 所以3)c a t >--对(0,),(0,3)t a ∈+∞∈恒成立. ………………8分因为03a <<,所以23=(当且仅当32a =时取等号), 又0t -<,所以t 的取值范围是(,3)-∞,所以3c …. 故c 的最小值为3. ………………10分(3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x c x b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. ………………12分要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--, 即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x xx x x -<<-. ………………14分令21x t x =,则1t >,此时即证11ln 1t t t-<<-. 令1()ln 1t t t ϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t t ϕ=+->,即11ln t t-<成立;再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减,又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立.综上所述,实数12,x x 满足122x x x b x x x -<<-. ………………16分附加题答案21.(A )解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② ………………5分 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4. ………………10分(B )解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即02x x y y =⎧⎨=⎩,解得0012x xy y⎧=⎪⎨⎪=⎩, ………………5分 代入22001x y +=,得2214x y +=,即为所求的曲线方程. ………………10分(C )解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系,由cos()13πρθ+=,得(cos cossin sin )133ππρθθ-=, 得直线的直角坐标方程为20x -=. ………………5分曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.ABE DF O · 第21(A)图因为直线cos()13πρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. ……………10分(D)解:由柯西不等式,得22222[)][1](1x x ++≥⨯+, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y ≤+≤ ………………5分由13x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得x y ⎧=⎪⎪⎨⎪=⎪⎩,所以当且仅当x y ==时,max ()x y += 所以当x y+取最大值时x 的值为2x =. ………………10分 22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系. 则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -. 所以(2,0,4)AP =-,(1,1,2)BM =--,10AP BM ⋅=,||25AP =,||6BM =.则cos ,||||2AP BM AP BM AP BM ⋅<>===. 故直线AP 与BM 所成角的余弦值为6. ………5分 (2)(2,1,0)AB =-,(1,1,2)BM =--.设平面ABM 的一个法向量为(,,)n x y z =,则00n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =.得平面ABM 的一个法向量为(2,4,3)n =.又平面PAC 的一个法向量为(0,1,0)OB =,所以n 4OB ⋅=,||29n =,||1OB =.则cos ,||||29n OB n OB n OB ⋅<>===故平面ABM 与平面PAC 所成锐二面角的余弦值为………………10分 23.解:(1)由条件,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+ ①,C第22题图在①中令1n =,得()011111f C C ==. ………………1分在①中令2n =,得()011222222226f C C C C =+=,得()23f =. ………………2分在①中令3n =,得()011223333333332330f C C C C C C =++=,得()310f =. ………………3分 (2)猜想()f n =21nn C -(或()f n =121n n C --). ………………5分 欲证猜想成立,只要证等式011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+成立.方法一:当1n =时,等式显然成立,当2n …时,因为11!!(1)!==!()!(1)!()!(1)!()!rr n n r n n n rC n nC r n r r n r r n r --⨯-=⨯=-----(),故11111()r r r r r r n n n n n n rC C rC C nC C -----==.故只需证明00111111211111n r r n n n n n n n n n n n nC nC C nC C nC C nC C ---------=++⋅⋅⋅++⋅⋅⋅+. 即证00111111211111n r r n n n n n n n n n n n C C C C C C C C C ---------=++⋅⋅⋅++⋅⋅⋅+.而11r n r n n C C --+=,故即证0111111211111n n n r n r n n n n n n n n n n C C C C C C C C C ---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21n n C -.而右边1(1)n nxx-++()()0111n nn n C C x------=++++++++,所以nx 的系数为01111111111n n r n r n n n n n n n n n C C C C C C C C ---+-----++⋅⋅⋅++⋅⋅⋅+.由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立. 综上,()21nn f n C -=成立. ………………10分方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n 的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1r n rn n C C --,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111n n n n n n nn n C C C C C C -----+++.另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21nn C -.故0111121111n n n n n n n n n n nC C C C C C C ------=++,即②成立. 余下同方法一. ………………10分方法三:由二项式定理,得0122(1)n n n n n n n x C C x C x C x +=++++ ③.两边求导,得112111(1)2n r r n n n n n n n x C C x rC x nC x ---+=+++++ ④.③×④,得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++⑤.左边n x 的系数为21nn nC -.右边nx 的系数为121112n n r n r n n n n n n n n n C C C C rC C nC C --+++⋅⋅⋅++⋅⋅⋅+1021112r r n n n n n n n n n nC C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+0112112r r n nn n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.由⑤恒成立,可得011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+.故()21nn f n C -=成立. ………………10分。
南京市、盐城市2018届高三年级第一次模拟考试数学试题(理)

(2)试猜想 f n 的表达式(用一个组合数表示) ,并证明你的猜想.
南京市、盐城市 2018 届高三年级第一次模拟考试 数学参考答案
一、填空题:本大题共 14 小题,每小题 5 分,计 70 分. 1 . 1 7. ( , 2] 8. 2.1 3 . 1200 4.1 5.
2 3
6.6
0.035 a 0.020 0.010 0.005
y ln x
Else
y ex
End If Print y
50 60 70 80 90 100 时间(单位:分钟)
第 3 题图 4.执行如图所示的伪代码,若 x 0 ,则输出的 y 的值为 ▲
第 4 题图 .
5.口袋中有形状和大小完全相同的 4 个球,球的编号分别为 1,2,3,4,若从袋中一次随 机摸出 2 个球,则摸出的 2 个球的编号之和大于 4 的概率为 ▲ . 6.若抛物线 y 2 px 的焦点与双曲线
高三数学试题第 6页(共 4 页)
所 又
以
四
边
形
A1 NBM
是
平
行
四
边
形
,
从
而
A1M / / BN . A1MC .
……………6 分
……………4 分 ∥ 面
BN 平 面 A1MC , A1M 平 面 A1MC , 所 以 BN
(2)因为 ABC A1B1C1 是直三棱柱,所以 AA1 底面 ABC ,而 AA1 侧面 ABB1 A1 , 所以侧面 ABB1 A1 底面 ABC . 又 CA CB ,且 M 是 AB 的中点,所以 CM AB . 则由侧面 ABB1 A1 底面 ABC ,侧面 ABB1 A1 底面 ABC AB ,
南京市、盐城市2018年高三年级第一次模拟考试数学试题及答案解析

南京市、盐城市2018届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上) 1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则A B =I ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ .3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 7.设函数1x x y e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值范围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ .9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值范围是 ▲ .10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .时间(单位:分钟) 组距 50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 第4题图11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =- 有四个不同的零点,则实数m 的取值范围是 ▲ .12.在平面直角坐标系xOy中,若直线(y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =,则实数k 的最小值为 ▲ .13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分. 解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点.(1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB A C ⊥.16.(本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c已知2c =. (1)若2C B =,求cos B 的值; (2)若AB AC CA CB ⋅=⋅,求cos()4B π+的值.第13题图ABCA 1B 1C 1MN第15题图有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧»EF,¼GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N 是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N 运动到点2处时,点Q的坐标为(,0)3. (1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =时,求直线BM 的方程.第17题-图甲 FH 第17题-图乙设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n …,且n N ∈,λ为常数.(1)若{}n a 是等差数列,且公差0d ≠,求λ的值;(2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-卪对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N ∈均成立.求所有满足条件的数列{}n a 中T 的最小值.20.(本小题满分16分)设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈). (1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值;(2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值;(3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.南京市、盐城市2018届高三年级第一次模拟考试数学附加题部分(本部分满分40分,考试时间30分钟)21.[选做题](在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)A .(选修4-1:几何证明选讲)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD 垂直DE 于点D . 若4DE =,求切点E 到直径AB 的距离EF .B .(选修4-2:矩阵与变换)已知矩阵 2 00 1⎡⎤=⎢⎥⎣⎦M ,求圆221x y +=在矩阵M 的变换下所得的曲线方程.C .(选修4-4:坐标系与参数方程)在极坐标系中,直线cos()13πρθ+=与曲线r ρ=(0r >)相切,求r 的值.D .(选修4-5:不等式选讲)已知实数,x y 满足2231x y +=,求当x y +取最大值时x 的值.A B E D F O · 第21(A)图[必做题](第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内) 22.(本小题满分10分)如图,四棱锥P ABCD -的底面ABCD 是菱形,AC 与BD 交于点O ,OP ⊥底面ABCD ,点M 为PC 中点,4,2,4AC BD OP ===.(1)求直线AP 与BM 所成角的余弦值;(2)求平面ABM 与平面PAC 所成锐二面角的余弦值.23.(本小题满分10分)已知n N *∈,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.(1)求()1,f ()2,f ()3f 的值;(2)试猜想()f n 的表达式(用一个组合数表示),并证明你的猜想.M A C D O P 第22题图南京市、盐城市2018届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分. 1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞ 8.34π 9.1(0,]4 10.4034 11.9[1,)412. 13.24 14.100 二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =,又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N .所以四边形1A NBM 是平行四边形,从而1//A M BN . ……………4分 又BN ⊄平面1A MC ,1A M ⊂平面1A MC ,所以BN ∥面1A MC . ……………6分 (2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC .又CA CB =,且M 是AB 的中点,所以CM AB ⊥.则由侧面11ABB A ⊥底面ABC ,侧面11ABB A 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC ,得CM ⊥侧面11ABB A . ……………8分 又1AB ⊂侧面11ABB A ,所以1AB CM ⊥. ……………10分又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1A MMC M =,所以1AB ⊥平面1A MC . ……………12分又1AC ⊂平面1A MC ,所以11AB A C ⊥. ……………14分 16.解:(1)因为c =,则由正弦定理,得sin C B =. ……………2分 又2C B =,所以sin 22B B =,即4sin cos B B B =. ……………4分 又B 是ABC ∆的内角,所以sin 0B >,故cos 4B =. ……………6分(2)因为AB AC CA CB ⋅=⋅, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =. ……………10分从而2223cos 25a cb B ac +-===, ……………12分又0B π<<,所以4sin 5B ==.从而34cos()cos cos sin sin 444525210B B B πππ+=-=⨯-⨯=-. ……………14分17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===,在Rt OET ∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2R MT OM OT =-=. 从而2RBE MT ==,即22R BE ==. ……………2分 故所得柱体的底面积OEF OEF S S S ∆=-扇形22114sin120323R R ππ=-︒=-. ……………4分又所得柱体的高4EG =,所以V S EG =⨯=163π-答:当BE 长为1分米时,折卷成的包装盒的容积为163π-. …………………6分(2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114sin120(323R R x ππ=-︒=.又所得柱体的高62EG x =-,所以V S EG =⨯=328(3)3x x π--+,其中03x <<. …………………10分令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=,解得2x =. …………………12分列表如下:所以当x =答:当BE 的长为2分米时,折卷成的包装盒的容积最大. …………………14分18.解:(1)由NQ ,得直线NQ的方程为32y x =…………………2分令0x =,得点B 的坐标为(0,. 所以椭圆的方程为22213x y a +=. …………………4分 将点N 的坐标2代入,得222213a +=,解得24a =. 所以椭圆C 的标准方程为22143x y +=. (8)分 (2)方法一:设直线BM 的斜率为(0)k k >,则直线BM 的方程为y kx =-在y kx =0y =,得P x k =,而点Q 是线段OP 的中点,所以2Q x k=.所以直线BN的斜率22BN BQ k k k k===. ………………10分联立22143y kx x y ⎧=⎪⎨+=⎪⎩,消去y,得22(34)0k x +-=,解得234M x k =+. 用2k 代k,得N x =………………12分又2DN NM =,所以2()N M N x x x =-,得23M N x x =. ………………14分故23=0k >,解得k = 所以直线BM的方程为y x =. ………………16分 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为11y y x x +=0y =,得P x =同理,得Q x =.而点Q 是线段OP 的中点,所以2P Q x x ==…………………10分 又2DN NM =,所以2122()x x x =-,得21203x x =>4=,解得21433y y =+. …………………12分将21212343x x y y ⎧=⎪⎪⎨⎪=⎪⎩代入到椭圆C的方程中,得2119x +=. 又22114(1)3y x =-,所以21214(1)(431927y y -++=21120y +=,解得1y =13y =.又10x >,所以点M的坐标为(33M .……………14分 故直线BM的方程为y x =-. …………………16分 19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+,化简得2(1)0d λ-=,又0d ≠,所以1λ=. ………………4分 (2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=. ……6分欲存在[3,7]r ∈,使得12n m n r -⋅-…,即12n r n m --⋅…对任意*n N ∈都成立, 则172n n m --⋅…,所以172n n m --…对任意*n N ∈都成立. ………………8分 令172n n n b --=,则11678222n n n n n n n n b b +-----=-=,所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>.所以n b 的最大值为981128b b ==,所以m 的最小值为1128. ………………10分(3)因为数列{}n a 不是常数列,所以2T ….①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩,所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意. ………………12分②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立. ………………14分由2221321()a a a a a λ=+-,得7λ=. 则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-; 由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-; 由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-.所以,数列(*)适合题意.所以T 的最小值为3. ………………16分20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,. 当0c =时,()b g x ax x =+,所以2()bg x a x'=-,所以(1)g a b '=-. ………………2分 因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩. ………………4分(2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =,则题意可转化为方程3(0)aax c t t x-+-=>在(0,)+∞上有相异两实根12,x x . ………………6分 即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a <<⎧⎪∆=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩,所以c t >对(0,),(0,3)t a ∈+∞∈恒成立. ………………8分因为03a <<,所以23=(当且仅当32a =时取等号), 又0t -<,所以t 的取值范围是(,3)-∞,所以3c …. 故c 的最小值为3. ………………10分 (3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x cx b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. ………………12分 要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--, 即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x x x x x -<<-. ………………14分 令21x t x =,则1t >,此时即证11ln 1t t t-<<-. 令1()ln 1t t t ϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t t ϕ=+->,即11ln t t-<成立;再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减,又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立.综上所述, 实数12,x x 满足122121x x x b x x x -<<-. ………………16分附加题答案21.(A )解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② ………………5分 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4. ………………10分(B )解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,ABE DF O · 第21(A)图设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即002x x y y =⎧⎨=⎩,解得0012x x y y⎧=⎪⎨⎪=⎩, ………………5分代入2201x y +=,得2214x y +=,即为所求的曲线方程. ………………10分 (C )解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系,由cos()13πρθ+=,得(cos cossin sin )133ππρθθ-=,得直线的直角坐标方程为20x --=. ………………5分曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.因为直线cos()13πρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. ……………10分(D)解:由柯西不等式,得22222[)][1(](133x x ++≥⨯⨯, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y ≤+≤ ………………5分由1x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得2x y ⎧=⎪⎪⎨⎪=⎪⎩26x y ==时,max ()x y += 所以当x y +取最大值时x的值为2x =. ………………10分 22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系. 则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -.所以(2,0,4)AP =-,(1,1,2)BM =--,10AP BM ⋅=,||25AP =,||6BM =.则cos ,6||||2AP BM AP BM AP BM ⋅<>===. 故直线AP 与BM 所成角的余弦值为6. ………5分 (2)(2,1,0)AB =-,(1,1,2)BM =--.设平面ABM 的一个法向量为(,,)n x y z =,C第22题图则00n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =.得平面ABM 的一个法向量为(2,4,3)n =.又平面PAC 的一个法向量为(0,1,0)OB =,所以n 4OB ⋅=,||29n =,||1OB =.则cos ,||||29n OBn OB n OB ⋅<>===故平面ABM 与平面PAC ………………10分 23.解:(1)由条件,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+ ①,在①中令1n =,得()011111f C C ==. ………………1分 在①中令2n =,得()011222222226f C C C C =+=,得()23f =. ………………2分 在①中令3n =,得()011223333333332330f C C C C C C =++=,得()310f =. ………………3分(2)猜想()f n =21nn C -(或()f n =121n n C --). ………………5分 欲证猜想成立,只要证等式011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+成立.方法一:当1n =时,等式显然成立,当2n …时,因为11!!(1)!==!()!(1)!()!(1)!()!rr n n r n n n rC n nC r n r r n r r n r --⨯-=⨯=-----(),故11111()r r r r r r n n n n n n rC C rC C nC C -----==.故只需证明00111111211111n r r n n n n n n n n n n n nC nC C nC C nC C nC C ---------=++⋅⋅⋅++⋅⋅⋅+. 即证00111111211111n r r n n n n n n n n n n n C C C C C C C C C ---------=++⋅⋅⋅++⋅⋅⋅+.而11r n r n n C C --+=,故即证0111111211111n n n r n r n n n n n n n n n n C C C C C C C C C ---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21n n C -.而右边1(1)(1)n n x x -++()()01221101221111n n n nnn n n n n n n C C x C x C x C C x C x C x ------=++++++++,所以nx 的系数为01111111111n n r n r n n n n n n n n n C C C C C C C C ---+-----++⋅⋅⋅++⋅⋅⋅+.由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立.综上,()21n n f n C -=成立. ………………10分 方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n 的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1r n rn nC C --,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111n n n n n n nn n C C C C C C -----+++.另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21nn C -.故0111121111n n n n n n n n n n n C C C C C C C ------=++,即②成立. 余下同方法一. ………………10分方法三:由二项式定理,得0122(1)n n n n n n n x C C x C x C x +=++++ ③. 两边求导,得112111(1)2n r r n n n n n n n x C C x rC x nC x ---+=+++++ ④.③×④, 得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++ ⑤.左边n x 的系数为21nn nC -.右边nx 的系数为121112n n r n r n n n n n n n n n C C C C rC C nC C --+++⋅⋅⋅++⋅⋅⋅+1021112r r n n n n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+0112112r r n n n n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.由⑤恒成立,可得011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+.故()21n n f n C -=成立. ………………10分。
2018年江苏省盐城市、南京市高考高三数学一模试卷及解析

2018年江苏省盐城市、南京市高考数学一模试卷一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B=.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p的值为.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是.8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是.10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是.12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为.二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N*都成立,求m的最小值;(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T=a n对任意的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22.23.24四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)[选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.2018年江苏省盐城市、南京市高考数学一模试卷参考答案与试题解析一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B={1} .【试题解答】解:∵集合A={x|x(x﹣4)<0}={x|0<x<4},B={0,1,5},∴A∩B={1}.故答案为:{1}.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为1.【试题解答】解:∵z=a+i,∴(1+i)•z=(1+i)(a+i)=a﹣1+(a+1)i,又(1+i)•z为为纯虚数,∴a﹣1=0即a=1.故答案为:1.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为1200.【试题解答】解:由频率分布直方图得:该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的频率为:1﹣(0.005+0.035+0.020+0.010)×10=0.3,∴估计该县小学六年级4000名学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为:4000×0.3=1200.故答案为:1200.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为1.【试题解答】解:根据题意知,执行程序后,输出函数y=,当x=0时,y=e0=1.故答案为:1.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.【试题解答】解:口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,从袋中一次随机摸出2个球,基本事件总数n==6,摸出的2个球的编号之和大于4包含的基本事件有:(1,4),(2,3),(2,4),(3,4),共4个,∴摸出的2个球的编号之和大于4的概率为p=.故答案为:.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p的值为6.【试题解答】解:∵双曲线的方程,∴a2=4,b2=5,可得c==3,因此双曲线的右焦点为F(3,0),∵抛物线y2=2px(p>0)的焦点与双曲线的右焦点重合,∴=3,解之得p=6.故答案为:6.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是(﹣∞,2] .【试题解答】解:函数y=e x﹣a的值域为A∵e x=2,∴值域为A=[2﹣a,+∞).又∵A⊆[0,+∞),∴2﹣a≥0,即a≤2.故答案为:(﹣∞,2].8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.【试题解答】解:∵(tanα﹣1)(tanβ﹣1)=2,可得:tanα+tanβ+1=tanαtanβ,∴tan(α+β)=═﹣1,∵锐角α,β,可得:α+β∈(0,π),∴α+β=.故答案为:.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是(0,] .【试题解答】解:由函数y=sinωx,图象过原点,可得ω>0在区间[0,2π]上单调递增,∴,即.故答案为:(0,]10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为4034.【试题解答】解:因为S n为等差数列{a n}的前n项和,且{a n}的前2017项中的奇数项和为2018,所以S=a1+a3+a5+…+a2017=1009×(a1+a2017)×=1009×a1009=2018,得奇a1009=2.=a2+a4+a6+…+a2016=1008×(a2+a2016)×=1008×a1009=1008×2=则S偶2016则S2017=S奇+S偶=2018+2016=4034.故答案为:4034.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是[1,).【试题解答】解:由0≤x≤3可得f(x)∈[0,],x>3时,f(x)∈(0,1).画出函数y=f(x)与y=m的图象,如图所示,∵函数y=f(x)﹣m有四个不同的零点,∴函数y=f(x)与y=m的图象有4个交点,由图象可得m的取值范围为[1,),故答案为:[1,).12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为﹣.【试题解答】解:设P(x1,y1),Q(x2,y2);则y1=k(x1﹣3)①,+(y2﹣1)2=1②;由=3,得,即,代入②得+=9;此方程表示的圆心(0,3)到直线kx﹣y﹣3k=0的距离为d≤r;即≤3,解得﹣≤k≤0.∴实数k的最小值为﹣.故答案为:﹣.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为24.【试题解答】解:建立如图的直角坐标系,则A(,),B(0,0),那么容易得到C(0,5)时,D的位置可以有三个位置,其中D1(﹣,),D2(﹣,0),D3(﹣,),此时=(﹣,﹣),=(﹣,﹣),=(﹣,﹣5),=(﹣,﹣),则•=21,•=24,•=22.5,则的最大值为24,故答案为:24.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为100.【试题解答】解:∵ksin2B+sinAsinC>19sinBsinC,由正弦定理可得:kb2+ac>19bc,∴k>,只需k大于右侧表达式的最大值即可,显然c>b时,表达式才能取得最大值,又∵c﹣b<a<b+c,∴﹣b﹣c<﹣a<b﹣c,∴<19+()=20﹣()2=100﹣(﹣10)2,当=10时,20﹣()2取得最大值20×10﹣102=100.∴k≥100,即实数k的最小值为100.故答案为:100二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.【试题解答】证明:(1)因为ABC﹣A1B1C1是直三棱柱,所以AB∥A1B1,且AB=A1B1,又点M,N分别是AB、A1B1的中点,所以MB=A1N,且MB∥A1N.所以四边形A1NBM是平行四边形,从而A1M∥BN.又BN⊄平面A1MC,A1M⊂平面A1MC,所以BN∥平面A1MC;(2)因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥底面ABC,而AA1⊂侧面ABB1A1,所以侧面ABB1A1⊥底面ABC.又CA=CB,且M是AB的中点,所以CM⊥AB.则由侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,CM⊥AB,且CM⊂底面ABC,得CM⊥侧面ABB1A1.又AB1⊂侧面ABB1A1,所以AB1⊥CM.又AB1⊥A1M,A1M、MC平面A1MC,且A1M∩MC=M,所以AB1⊥平面A1MC.又A1C⊂平面A1MC,所以AB⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.【试题解答】解:(1)因为c=,则由正弦定理,得sinC=sinB. …(2分)又C=2B,所以sin2B=sinB,即2sinBcosB=sinB. …(4分)又B是△ABC的内角,所以sinB>0,故cosB=. …(6分) (2)因为=,所以cbcosA=bacosC,则由余弦定理,得b2+c2﹣a2=b2+a2﹣c2,得a=c. …(10分)从而cosB==,…(12分)又0<B<π,所以sinB==.从而cos(B+)=cosBcos﹣sinBsin=. …(14分)17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?【试题解答】解:(1)在图甲中,连接MO交EF于点T.设OE=OF=OM=R,在Rt△OET中,因为∠EOT=∠EOF=60°,所以OT=,则MT=0M﹣OT=.从而BE=MT=,即R=2BE=2.故所得柱体的底面积S=S扇形OEF ﹣S△OEF=πR2﹣R2sin120°=﹣,又所得柱体的高EG=4,所以V=S×EG=﹣4.答:当BE长为1(分米)时,折卷成的包装盒的容积为﹣4立方分米.(2)设BE=x,则R=2x,所以所得柱体的底面积S=S扇形OEF﹣S△OEF=πR2﹣R2sin120°=(﹣)x2,又所得柱体的高EG=6﹣2x,所以V=S×EG=(﹣2)(﹣x3+3x2),其中0<x<3.令f(x)=﹣x3+3x2,0<x<3,则由f′(x)=﹣3x2+6x=﹣3x(x﹣2)=0,解得x=2.列表如下:x(0,2)2(2,3)f′(x)+0﹣f(x)增极大值减所以当x=2时,f(x)取得最大值.答:当BE的长为2分米时,折卷成的包装盒的容积最大.18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.【试题解答】解:(1)由N(),点Q的坐标为(),得直线NQ的方程为y=x﹣,令x=0,得点B的坐标为(0,﹣).所以椭圆的方程为+=1.将点N的坐标(,)代入,得+=1,解得a2=4.所以椭圆C的标准方程为+=1.(2):设直线BM的斜率为k(k>0),则直线BM的方程为y=x﹣.在y=kx﹣中,令y=0,得x P=,而点Q是线段OP的中点,所以x Q=.所以直线BN的斜率k BN=k BQ==2k.联立,消去y,得(3+4k2)x2﹣8kx=0,解得x M=.用2k代k,得x N=.又=2,所以x N=2(x M﹣x N),得2x M=3x N,故2×==3×,又k>0,解得k=.所以直线BM的方程为y=x﹣19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N*都成立,求m的最小值;(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T=a n对任意的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.【试题解答】解:(1)由题意,可得a=(a n+d)(a n﹣d)+λd2,化简得(λ﹣1)d2=0,又d≠0,所以λ=1.(2)将a1=1,a2=2,a3=4,代入条件,可得4=1×4+λ,解得λ=0,所以a=a na n﹣1,所以数列{a n}是首项为1,公比q=2的等比数列,+1所以a n=2n﹣1.欲存在r∈[3,7],使得m•2n﹣1≥n﹣r,即r≥n﹣m•2n﹣1对任意n∈N*都成立,则7≥n﹣m•2n﹣1,所以m≥对任意n∈N*都成立.令b n=,则b n+1﹣b n=﹣=,所以当n>8时,b n+1<b n;当n=8时,b9=b8;当n<8时,b n+1>b n.所以b n的最大值为b9=b8=,所以m的最小值为;(3)因为数列{a n}不是常数列,所以T≥2,①若T=2,则a n+2=a n恒成立,从而a3=a1,a4=a2,所以,所以λ(a2﹣a1)2=0,又λ≠0,所以a2=a1,可得{a n}是常数列,矛盾.所以T=2不合题意.②若T=3,取a n=(*),满足a n+3=a n恒成立.由a22=a1a3+λ(a2﹣a1)2,得λ=7.则条件式变为a n2=a n+1a n﹣1+7.由22=1×(﹣3)+7,知a3k﹣12=a3k﹣2a3k+λ(a2﹣a1)2;由(﹣3)2=2×1+7,知a3k2=a3k﹣1a3k+1+λ(a2﹣a1)2;由12=2×(﹣3)+7,知a3k+12=a3k a3k+2+λ(a2﹣a1)2;所以,数列(*)适合题意.所以T的最小值为3.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.【试题解答】解:(1)由f(x)=lnx,得f(1)=0,又f′(x)=,所以f′(1)=1,当c=0时,g(x)=ax+,所以g′(x)=a﹣,所以g′(1)=a﹣b,因为函数f(x)与g(x)的图象在x=1处有相同的切线,所以,即,解得a=,b=﹣;(2)当x0>1时,则f(x0)>0,又b=3﹣a,设t=f(x0),则题意可转化为方程ax+﹣c=t(t>0)在(0,+∞)上有相异两实根x1,x2. 即关于x的方程ax2﹣(c+t)x+(3﹣a)=0(t>0)在(0,+∞)上有相异两实根x1,x2.所以,得,所以c>2﹣t对t∈(0,+∞),a∈(0,3)恒成立.因为0<a<3,所以2≥2•=3(当且仅当a=时取等号),又﹣t<0,所以2﹣t的取值范围是(﹣∞,3),所以c≥3.故c的最小值为3.(3)当a=1时,因为函数f(x)与g(x)的图象交于A,B两点,所以,两式相减,得b=x1x2(1﹣),要证明x1x2﹣x2<b<x1x2﹣x1,即证x1x2﹣x2<x1x2(1﹣)<x1x2﹣x1,即证<<,即证1﹣<ln<﹣1令=t,则t>1,此时即证1﹣<lnt<t﹣1.令φ(t)=lnt+﹣1,所以φ′(t)=﹣=>0,所以当t>1时,函数φ(t)单调递增.又φ(1)=0,所以φ(t)=lnt+﹣1>0,即1﹣<lnt成立;再令m(t)=lnt﹣t+1,所以m′(t)=﹣1=<0,所以当t>1时,函数m(t)单调递减,又m(1)=0,所以m(t)=lnt﹣t+1<0,即lnt<t﹣1也成立.综上所述,实数x1,x2满足x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22.23.24四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)[选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.【试题解答】解:如图,连接AE,OE,因为直线DE与⊙O相切于点E,所以DE⊥OE,又因为AD⊥DE于D,所以AD∥OE,所以∠DAE=∠OEA,①在⊙O中,OE=OA,所以∠OEA=∠OAE,②…(5分)由①②得∠DAE=∠OAE,即∠DAE=∠FAE,又∠ADE=∠AFE,AE=AE,所以△ADE≌△AFE,所以DE=FE,又DE=4,所以FE=4,即E到直径AB的距离为4.…(10分)[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.【试题解答】解:设P(x0,y0)是圆x2+y2=1上任意一点,则=1,设点P(x0,y0)在矩阵M对应的变换下所得的点为Q(x,y),则=,即,解得,…(5分)代入=1,得=1,∴圆x2+y2=1在矩阵M的变换下所得的曲线方程为=1.…(10分)[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.【试题解答】解:直线ρcos(θ+)=1,转化为:,曲线ρ=r(r>0)转化为:x2+y2=r2,由于直线和圆相切,则:圆心到直线的距离d=.所以r=1.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.【试题解答】解:由柯西不等式,得[x2+()2][12+()2]≥(x•1+)2,即≥(x+y)2.而x2+3y2=1,所以(x+y)2,所以﹣,…(5分)由,得,所以当且仅当x=,y=时,(x+y)max=.所以当x+y取最大值时x值为.…(10分)25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.【试题解答】解:(1)因为ABCD是菱形,所以AC⊥BD.又OP⊥底面ABCD,以O为原点,直线OA,OB,OP分别为x轴,y轴,z轴,建立如图所示空间直角坐标系.则A(2,0,0),B(0,1,0),P(0,0,4),C(﹣2,0,0),M(﹣1,0,2).=(﹣2,0,4),=(01,﹣1,2),cos<,>===.故直线AP与BM所成角的余弦值为.…(5分)(2)=(﹣2,1,0),=(﹣1,﹣1,2).设平面ABM的一个法向量为=(x,y,z),则,令x=2,得=(2,4,3).又平面PAC的一个法向量为=(0,1,0),∴cos<>===.故平面ABM与平面PAC所成锐二面角的余弦值为.…(10分)26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.【试题解答】解:(1)由条件,nf(n)=C C C C①,在①中令n=1,得f(1)=1.在①中令n=2,得2f(2)=6,得f(2)=3.在①中令n=3,得3f(3)=30,故f(3)=10.(2)猜想f(n)=.要证猜想成立,只要证等式n=•+2•+…+n•成立.由(1+x)n=+x+x2+…+x n①,两边同时对x求导数,可得n(1+x)n﹣1=+2x+3x2+n x n﹣1②,把等式①和②相乘,可得n(1+x)2n﹣1=(+x+x2+…+x n)•(+2x+3x2+n x n﹣1 ) ③.等式左边x n的系数为n,等式右边x n的系数为•+•2+•3+…+n•n=•+2•+3•+…+n•=C C C C,根据等式③恒成立,可得n=C C C C.故f(n)=成立.。
南京市、盐城市2018届高三年级第一次模拟考试数学试题(理)含答案
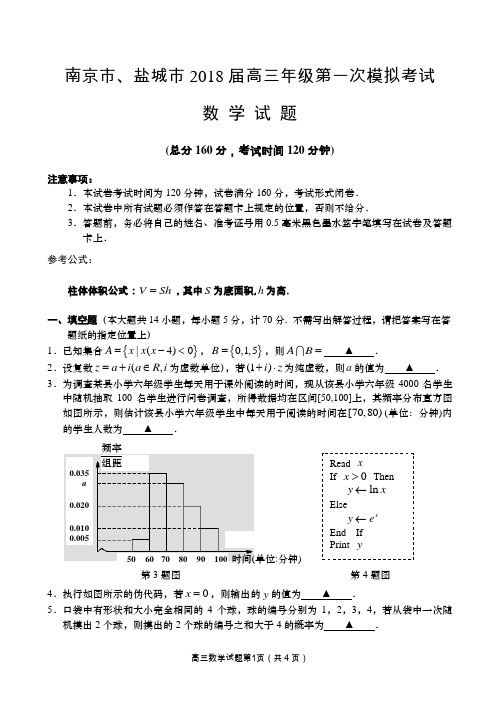
南京市、盐城市2018届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上) 1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则AB = ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ .3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .时间(单位:分钟) 频率组距 50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 Read x If 0x > Then ln y x ← Else x y e ← End If Print y 第4题图6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 7.设函数1x x y e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值范围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ .9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值范围是 ▲ . 10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =-有四个不同的零点,则实数m 的取值范围是 ▲ .12.在平面直角坐标系xOy 中,若直线(33)y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =,则实数k 的最小值为 ▲ . 13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则CD AB ⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分. 解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点. (1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB A C ⊥.16.(本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c 已知52c b =. (1)若2C B =,求cos B 的值; (2)若AB AC CA CB ⋅=⋅,求cos()4B π+的值.A第13题图 ABCA 1B 1C 1MN第15题图17.(本小题满分14分)有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧EF ,GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N 是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N运动到点2处时,点Q的坐标为(3. (1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =时,求直线BM 的方程.第17题-图甲F第17题-图乙19.(本小题满分16分)设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n ,且n N ∈,λ为常数.(1)若{}n a 是等差数列,且公差0d ≠,求λ的值;(2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N ∈均成立. 求所有满足条件的数列{}n a 中T 的最小值.20.(本小题满分16分)设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈). (1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值; (2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值;(3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.南京市、盐城市2018届高三年级第一次模拟考试数学附加题部分(本部分满分40分,考试时间30分钟)21.[选做题](在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内) A .(选修4-1:几何证明选讲)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD 垂直DE 于点D . 若4DE =,求切点E 到直径AB 的距离EF .B .(选修4-2:矩阵与变换)已知矩阵 2 00 1⎡⎤=⎢⎥⎣⎦M ,求圆221x y +=在矩阵M 的变换下所得的曲线方程.C .(选修4-4:坐标系与参数方程)在极坐标系中,直线cos()13πρθ+=与曲线r ρ=(0r >)相切,求r 的值.D .(选修4-5:不等式选讲)已知实数,x y 满足2231x y +=,求当x y +取最大值时x 的值.[必做题](第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内) 22.(本小题满分10分)如图,四棱锥P ABCD -的底面ABCD 是菱形,AC 与BD 交于点O ,OP ⊥底面ABCD ,点M 为PC 中点,4,2,4AC BD OP ===.(1)求直线AP 与BM 所成角的余弦值;(2)求平面ABM 与平面PAC 所成锐二面角的余弦值.A B ED F O· 第21(A)图23.(本小题满分10分)已知n N *∈,()0112112r r n n n n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.(1)求()1,f ()2,f ()3f 的值;(2)试猜想()f n 的表达式(用一个组合数表示),并证明你的猜想.南京市、盐城市2018届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分.1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞ 8.34π 9.1(0,]4 10.4034 11.9[1,)412.3- 13.24 14.100二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =,MABCDOP第22题图又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N . 所以四边形1A NBM是平行四边形,从而1//A M BN . ……………4分又BN ⊄平面1A MC ,1A M ⊂平面1A MC ,所以BN ∥面1A MC . ……………6分(2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC .又CA CB =,且M 是AB 的中点,所以CM AB ⊥.则由侧面11ABB A ⊥底面ABC ,侧面11ABB A 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC,得CM ⊥侧面11ABB A . ……………8分又1AB ⊂侧面11ABB A ,所以1AB CM ⊥. ……………10分又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1A M MC M =,所以1AB ⊥平面1A MC . ……………12分又1AC ⊂平面1A MC,所以11AB A C ⊥. ……………14分16.解:(1)因为c =,则由正弦定理,得sin C B =. ……………2分 又2C B=,所以sin 22B B =,即4sin cos B B B =. ……………4分又B是ABC ∆的内角,所以sin 0B >,故cos 4B =. ……………6分 (2)因为AB AC CA CB ⋅=⋅, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =. ……………10分 从而2223cos 25a cb B ac+-===, (12)分又0B π<<,所以4sin 5B ==. 从而34cos()cos cos sin sin 44455B B B πππ+=-==. (14)分17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===,在Rt OET ∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2RMT OM OT =-=. 从而2R BE MT ==,即22R BE ==. ……………2分故所得柱体的底面积OEF OEF S S S ∆=-扇形22114sin120323R R ππ=-︒= ……………4分又所得柱体的高4EG =,所以V S EG =⨯=163π-答:当BE 长为1分米时,折卷成的包装盒的容积为163π-. …………………6分(2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114sin120(323R R x ππ=-︒=-.又所得柱体的高62EG x =-,所以V S EG =⨯=328(3)3x x π--+,其中03x <<. …………………10分令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=, 解得2x =. …………………12分答:当BE的长为2分米时,折卷成的包装盒的容积最大.…………………14分18.解:(1)由N Q,得直线NQ的方程为32y x=…………………2分令0x=,得点B的坐标为(0,.所以椭圆的方程为22213x ya+=.…………………4分将点N的坐标)2代入,得222213a+=,解得24a=.所以椭圆C的标准方程为22143x y+=.…………………8分(2)方法一:设直线BM的斜率为(0)k k>,则直线BM的方程为y kx=在y kx=0y=,得Pxk=,而点Q是线段OP的中点,所以2Qxk=.所以直线BN的斜率2BN BQkk k===.………………10分联立22143y kxx y⎧=⎪⎨+=⎪⎩,消去y,得22(34)0k x+-=,解得Mx=.用2k代k,得2316Nxk=+.………………12分又2DN NM=,所以2()N M Nxx x=-,得23M Nx x=.………………14分故222334316k k⨯=⨯++,又0k>,解得2k=.所以直线BM的方程为2y x =-. ………………16分 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为1y x =0y =,得P x =.同理,得Q x =.而点Q 是线段OP的中点,所以2P Qx x =,故=…………………10分 又2DN NM =,所以2122()x x x =-,得21203x x =>4=解得21433y y =+. …………………12分将21212343x x y y ⎧=⎪⎪⎨⎪=+⎪⎩代入到椭圆C的方程中,得2211(41927x y ++=. 又22114(1)3y x =-,所以214(1)319y -=21120y +=, 解得1y =(舍)或1y =.又10x >,所以点M 的坐标为(3M .……………14分故直线BM的方程为2y x =-. …………………16分 19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+, 化简得2(1)0d λ-=,又d ≠,所以1λ=. ………………4分(2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=. ……6分欲存在[3,7]r ∈,使得12n m n r -⋅-,即12n r n m --⋅对任意*n N ∈都成立,则172n n m --⋅,所以172n n m --对任意*n N ∈都成立. ………………8分令172n n n b --=,则11678222n n nn n n n nb b +-----=-=, 所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>.所以n b 的最大值为981128b b ==,所以m 的最小值为1128. ………………10分 (3)因为数列{}n a 不是常数列,所以2T .①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩, 所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意. ………………12分②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立. ………………14分由2221321()a a a a a λ=+-,得7λ=. 则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-;由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-; 由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-.所以,数列(*)适合题意. 所以T的最小值为3. ………………16分20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,. 当c =时,()bg x ax x=+,所以2()bg x a x'=-,所以(1)g a b '=-. ………………2分因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩. ………………4分 (2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =,则题意可转化为方程3(0)aax c t t x-+-=>在(0,)+∞上有相异两实根12,x x . ………………6分即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a <<⎧⎪∆=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩, 所以c t>对(0,),(0,3)t a ∈+∞∈恒成立. ………………8分因为03a <<,所以)2(3a +⨯=(当且仅当32a =时取等号), 又0t -<,所以t 的取值范围是(,3)-∞,所以3c .故c 的最小值为3. ………………10分(3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x c x b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. ………………12分要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--,即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x xx x x -<<-. ………………14分 令21x t x =,则1t >,此时即证11ln 1t t t-<<-. 令1()ln 1t t t ϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t tϕ=+->,即11ln t t-<成立; 再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减,又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立.综上所述,实数12,x x 满足122121x x x b x x x -<<-. ………………16分附加题答案21.(A )解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② ………………5分 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4. ………………10分(B )解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即02x x y y =⎧⎨=⎩,解得0012x xy y⎧=⎪⎨⎪=⎩, ………………5分 代入22001x y +=,得2214x y +=,即为所求的曲线方ABE DF O · 第21(A)图程. ………………10分(C )解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系,由cos()13πρθ+=,得(cos cossin sin )133ππρθθ-=, 得直线的直角坐标方程为20x -=. ………………5分曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.因为直线cos()13πρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. ……………10分(D)解:由柯西不等式,得22222[)][1](1x x ++≥⨯, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y ≤+≤ ………………5分由1x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得x y ⎧=⎪⎪⎨⎪=⎪⎩所以当且仅当26x y ==时,max ()x y += 所以当x y+取最大值时x 的值为x =………………10分 22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系. 则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -. 所以(2,0,4)AP =-,(1,1,2)BM =--,10AP BM ⋅=,||25AP =,||6BM =.则cos ,||||2AP BM AP BM AP BM ⋅<>=== C故直线AP 与BM所成角的余弦值为6. ………5分 (2)(2,1,0)AB =-,(1,1,2)BM =--.设平面ABM 的一个法向量为(,,)n x y z =,则00n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =.得平面ABM 的一个法向量为(2,4,3)n =.又平面PAC 的一个法向量为(0,1,0)OB =,所以n 4OB ⋅=,||29n =,||1OB =.则4cos ,||||29n OB n OB n OB ⋅<>===.故平面ABM 与平面PAC 所成锐二面角的余弦值为………………10分 23.解:(1)由条件,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+ ①,在①中令1n =,得()011111f C C ==. ………………1分在①中令2n =,得()011222222226f C C C C =+=,得()23f =. ………………2分在①中令3n =,得()011223333333332330f C C C C C C =++=,得()310f =. ………………3分(2)猜想()f n =21nn C -(或()f n =121n n C --). ………………5分 欲证猜想成立,只要证等式011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+成立.方法一:当1n =时,等式显然成立,当2n 时,因为11!!(1)!==!()!(1)!()!(1)!()!rr n n r n n n rC n nC r n r r n r r n r --⨯-=⨯=-----(),故11111()r r r r r r n n n n n n rC C rC C nC C -----==.故只需证明00111111211111n r r n n n n n n n n n n n nC nC C nC C nC C nC C ---------=++⋅⋅⋅++⋅⋅⋅+. 即证00111111211111n r r n n n n n n n n n n nC C C C C C C C C ---------=++⋅⋅⋅++⋅⋅⋅+. 而11r n r n n C C --+=,故即证0111111211111n n n r n r n n n n n n n n n n C C C C C C C C C ---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21n n C -.而右边1(1)(1)n n x x -++()()01221101221111n n n nnn n n n n n n C C x C x C xC C x C x C x ------=++++++++,所以nx 的系数为01111111111n n r n r n n n n n n n n n C C C C C C C C ---+-----++⋅⋅⋅++⋅⋅⋅+.由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立. 综上,()21nn f n C -=成立. ………………10分方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1r n rn nC C --,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111n n n n n n nn n C C C C C C -----+++.另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21nn C -.故0111121111n n n n n n n n n n nC C C C C C C ------=++,即②成立. 余下同方法一. ………………10分方法三:由二项式定理,得0122(1)n n n n n n n x C C x C x C x +=++++ ③. 两边求导,得112111(1)2n r r n n n n n n n x C C x rC x nC x ---+=+++++ ④.③×④,得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++⑤.左边n x 的系数为21nn nC -.右边nx 的系数为121112n n r n r n n n n n n n n n C C C C rC C nC C --+++⋅⋅⋅++⋅⋅⋅+1021112r r n n n n n n n n n nC C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+0112112r r n nn n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.由⑤恒成立,可得011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+.故()21nn f n C -=成立. ………………10分。
2018年江苏省盐城市、南京市高考数学一模试卷

2018年江苏省盐城市、南京市高考数学一模试卷一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B=.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p 的值为.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是.8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是.10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是.12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点".若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为.二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM 的方程.19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N *都成立,求m的最小值;(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T=a n对任意的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b 的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22。
数学---江苏省南京市、盐城市2018届高三上学期第一次模拟考试试题(理)

江苏省南京市、盐城市2018届高三上学期第一次模拟考试数学试题(理)参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高. 一、填空题(本大题共14小题,每小题5分,计70分.)1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则A B =I ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ . 3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ .7.设函数1x xy e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值范围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ . 9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值范围是 ▲ . 10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =-有四个不同的零点,则实数m 的取值范围是 ▲ .12.在平面直角坐标系xOy 中,若直线(y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =,则实数k 的最小值为 ▲ .13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则CD AB ⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分. 解答应写出必要的文字说明,证明过程或演算 步骤)15.(本小题满分14分)如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点.(1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB AC ⊥.16.(本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c 已知2c =. (1)若2C B =,求cos B 的值;(2)若AB AC CA CB ⋅=⋅ ,求cos()4B π+的值.17.(本小题满分14分)有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰.好.能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧»EF,¼GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N 是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N 运动到点2处时,点Q 的坐标为(3.(1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =时,求直线BM的方程.19.(本小题满分16分)设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n …,且n N ∈,λ为常数.(1)若{}n a 是等差数列,且公差0d ≠,求λ的值; (2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-卪对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N∈均成立. 求所有满足条件的数列{}n a 中T 的最小值.20.(本小题满分16分)设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈).(1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值; (2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值;(3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.数学附加题部分21.[选做题](在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.) A.(选修4-1:几何证明选讲)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD 垂直DE 于点D . 若4DE =,求切点E 到直径AB 的距离EF .B.(选修4-2:矩阵与变换)已知矩阵 2 00 1⎡⎤=⎢⎥⎣⎦M ,求圆221x y +=在矩阵M 的变换下所得的曲线方程.C .(选修4-4:坐标系与参数方程) 在极坐标系中,直线cos()13πρθ+=与曲线r ρ=(0r >)相切,求r 的值.D .(选修4-5:不等式选讲)已知实数,x y 满足2231x y +=,求当x y +取最大值时x 的值.[必做题](第22、23题,每小题10分,计20分.)22.(本小题满分10分)如图,四棱锥P ABCD -的底面ABCD 是菱形,AC 与BD 交于点O ,OP ⊥底面ABCD ,点M 为PC 中点,4,2,4AC BD OP ===.(1)求直线AP 与BM 所成角的余弦值;(2)求平面ABM 与平面PAC 所成锐二面角的余弦值.23.(本小题满分10分) 已知n N *∈,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.(1)求()1,f ()2,f ()3f 的值;(2)试猜想()f n 的表达式(用一个组合数表示),并证明你的猜想.【参考答案】一、填空题1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞8.3π49.1(0,]4 10.4034 11.9[1,)4 12. 13.2414.100 二、解答题15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =, 又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N . 所以四边形1A NBM 是平行四边形,从而1//A M BN .又BN ⊄平面1A MC ,1A M ⊂平面1A MC ,所以BN ∥面1A MC .(2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC . 又CA CB =,且M 是AB 的中点,所以CM AB ⊥.则由侧面11ABB A ⊥底面ABC ,侧面11ABB A 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC ,得CM ⊥侧面11ABB A . 又1AB ⊂侧面11ABB A ,所以1ABCM ⊥. 又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1AM MC M = , 所以1AB ⊥平面1A MC .又1AC ⊂平面1A MC ,所以11AB AC ⊥.16.解:(1)因为c =,则由正弦定理,得sin C B =.又2C B =,所以sin 2B B =,即4sin cos B B B =.又B 是ABC ∆的内角,所以sin 0B >,故cos B =.(2)因为AB AC CA CB ⋅=⋅, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =.从而2223cos 25a cb B ac+-===,又0πB <<,所以4sin 5B ==.从而πππ34cos()cos cossin sin 444525210B B B +=-=⨯-⨯=-. 17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===, 在Rt OET ∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2RM T O M O T =-=. 从而2RBE MT ==,即22R BE ==. 故所得柱体的底面积OEF OEF S S S ∆=-扇形22114ππsin120323R R =-︒=又所得柱体的高4EG =, 所以V S EG =⨯=16π3-答:当BE 长为1分米时,折卷成的包装盒的容积为16π3-.(2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114ππsin120(323R R x =-︒=.又所得柱体的高62EG x =-,所以V S EG =⨯=328π(3)3x x --+,其中03x <<. 令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=,解得2x=. 列表如下:所以当2x=时,()f x取得最大值.答:当BE的长为2分米时,折卷成的包装盒的容积最大.18.解:(1)由N Q,得直线NQ的方程为32y x=-令0x=,得点B的坐标为(0,.所以椭圆的方程为22213x ya+=.将点N的坐标2213+=,解得24a=.所以椭圆C的标准方程为22143x y+=.(2)方法一:设直线BM的斜率为(0)k k>,则直线BM的方程为y kx=在ykx=0y=,得Px=,而点Q是线段OP的中点,所以Qx=所以直线BN的斜率2BN BQk k k===.联立22143y kxx y⎧=⎪⎨+=⎪⎩,消去y,得22(34)0k x+-=,解得234Mxk=+.用2k代k,得2316Nxk=+.又2DN NM=,所以2()N M Nx x x=-,得23M Nx x=.故222334316k k ⨯=⨯++,又0k >,解得2k =. 所以直线BM的方程为2y x =. 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为1y x =0y =,得P x =.同理,得Q x =.而点Q 是线段OP 的中点,所以2P Q x x ==. 又2DN NM = ,所以2122()x x x =-,得21203x x =>4=,解得2143y y =+将212123433x x y y ⎧=⎪⎪⎨⎪=+⎪⎩代入到椭圆C的方程中,得2119x +=. 又22114(1)3y x =-,所以21214(1)(431927y y -+=21120y +=,解得1y =(舍)或1y =.又10x >,所以点M的坐标为M . 故直线BM的方程为2y x =19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+, 化简得2(1)0d λ-=,又0d ≠,所以1λ=.(2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=.欲存在[3,7]r ∈,使得12n m n r -⋅-…,即12n r n m --⋅…对任意*N n ∈都成立,则172n n m --⋅…,所以172n n m --…对任意*N n ∈都成立. 令172n n n b --=,则11678222n n n n n n n n b b +-----=-=,所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>. 所以n b 的最大值为981128b b ==,所以m 的最小值为1128.(3)因为数列{}n a 不是常数列,所以2T …. ①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩, 所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意.②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立.由2221321()a a a a a λ=+-,得7λ=.则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-; 由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-; 由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-. 所以,数列(*)适合题意.所以T 的最小值为3. 20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,. 当0c =时,()b g x ax x =+,所以2()bg x a x'=-,所以(1)g a b '=-. 因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩.(2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =, 则题意可转化为方程3(0)aax c t t x-+-=>在(0,)+∞上有相异两实根12,x x . 即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a ∆<<⎧⎪=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩,所以c t >对(0,),(0,3)t a ∈+∞∈恒成立.因为03a <<,所以23=(当且仅当32a =时取等号), 又0t -<,所以t 的取值范围是(,3)-∞,所以3c ….故c 的最小值为3. (3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x c x b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. 要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--,即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x x x x x -<<-.令21x t x =,则1t >,此时即证11ln 1t t t -<<-.令1()ln 1t t tϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t t ϕ=+->,即11ln t t-<成立; 再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减, 又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立. 综上所述, 实数12,x x 满足122121x x x b x x x -<<-. 21.A .解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4.B .解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦, 即002x x y y =⎧⎨=⎩,解得0012x x y y⎧=⎪⎨⎪=⎩,代入2201x y +=,得2214x y +=,即为所求的曲线方程. C .解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系, 由πcos()13ρθ+=,得ππ(cos cos sin sin )133ρθθ-=,得直线的直角坐标方程为20x -=.曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.因为直线πcos()13ρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. D.解:由柯西不等式,得22222[)][1(](133x x ++≥⨯+⨯, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y ≤+≤,由1x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得x y ⎧=⎪⎪⎨⎪=⎪⎩,26x y ==时,max()x y +=所以当x y +取最大值时x的值为2x =22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系.则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -.所以(2,0,4)AP =- ,(1,1,2)BM =-- ,10AP BM ⋅=,||AP =||BM .则cos ,||||AP BM AP BM AP BM ⋅<>===. 故直线AP 与BM所成角的余弦值为6. (2)(2,1,0)AB =- ,(1,1,2)BM =--.设平面ABM 的一个法向量为(,,)n x y z = ,则00n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =. 得平面ABM 的一个法向量为(2,4,3)n =.又平面PAC 的一个法向量为(0,1,0)OB = ,所以n 4OB ⋅=,||n ||1OB = .则cos ,||||n OB n OB n OB ⋅<>===. 故平面ABM 与平面PAC23.解:(1)由条件,()011211C C 2C C C C C r r n nn n n n n n n n nf n C r n --=++⋅⋅⋅++⋅⋅⋅+ ①, 在①中令1n =,得()01111C C 1f ==.在①中令2n =,得()0112222222C C 2C C 6f =+=,得()23f =. 在①中令3n =,得()01122333333333C C 2C C 3C C 30f =++=,得()310f =. (2)猜想()f n =21C nn -(或()f n =121C n n --). 欲证猜想成立,只要证等式01121121C C C 2C C C C C C n r r n n n n n n n n n n nn r n ---=++⋅⋅⋅++⋅⋅⋅+成立. 方法一:当1n =时,等式显然成立, 当2n …时,因为11!!(1)!C ==C !()!(1)!()!(1)!()!rr n n r n n n r n n r n r r n r r n r --⨯-=⨯=-----(),故11111C C (C )C C C r r r r r r n n n n n nr r n -----==. 故只需证明00111111211111C C C C C C C C C n r r n n n n n n n n n n n n n n n n ---------=++⋅⋅⋅++⋅⋅⋅+. 即证00111111211111C C C C C C C C C n r r n n n n n n n n n n n---------=++⋅⋅⋅++⋅⋅⋅+. 而11C C r n r n n --+=,故即证0111111211111C C C C C C C C C n n n r n r n n n n n n n n n n---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21C n n -. 而右边1(1)(1)n n x x -++()()01221101221111C C C C C C C C n n n n n n n n n n n n x x xx x x ------=++++++++ , 所以nx 的系数为01111111111C C C C C C C C n n r n r n n n n n n n n n---+-----++⋅⋅⋅++⋅⋅⋅+.由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立. 综上,()21C n n f n -=成立. 方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n 的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1C C r n r n n--,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111C C C C C C n n n n n n n n n-----+++ . 另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21C n n -. 故0111121111C C C C C C C n n n n n n n n n n n------=+++ ,即②成立. 余下同方法一.方法三:由二项式定理,得0122(1)C C C C n n nn n n n x x x x +=++++ ③. 两边求导,得112111(1)C 2C C C n r r n n n n n n n x x r x n x---+=+++++ ④. ③×④,得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++ ⑤.左边nx 的系数为21C n n n -. 右边nx 的系数为12111C C 2C C C C C C n n r n r n n n n n n nn n r n --+++⋅⋅⋅++⋅⋅⋅+ 102111C C 2C C C C C C r r n n n n n n n n n n r n --=++⋅⋅⋅++⋅⋅⋅+011211C C 2C C C C C C r r n nn n n n n n n n r n --=++⋅⋅⋅++⋅⋅⋅+. 由⑤恒成立,可得01121121C C C 2C C C C C C n r r n nn n n n n n n n nn r n ---=++⋅⋅⋅++⋅⋅⋅+. 故()21C n n f n -=成立.。
江苏省盐城市南京市高考数学一模试卷

2018年江苏省盐城市、南京市高考数学一模试卷一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B=.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)?z为纯虚数,则a的值为.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p的值为.7.(5分)设函数y=e x﹣a的值域为A,若A?[0,+∞),则实数a的取值范围是.8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是.10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f (x)﹣m 有四个不同的零点,则实数m的取值范围是.12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为.二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m?a n≥n﹣r对任意的n∈N*都成立,求m的最小值;(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n=a n对任意的n∈N*均+T成立.求所有满足条件的数列{a n}中T的最小值.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.[选做题][选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.2018年江苏省盐城市、南京市高考数学一模试卷参考答案与试题解析一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B={1} .【解答】解:∵集合A={x|x(x﹣4)<0}={x|0<x<4},B={0,1,5},∴A∩B={1}.故答案为:{1}.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)?z为纯虚数,则a的值为1.【解答】解:∵z=a+i,∴(1+i)?z=(1+i)(a+i)=a﹣1+(a+1)i,又(1+i)?z为为纯虚数,∴a﹣1=0即a=1.故答案为:1.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为1200.【解答】解:由频率分布直方图得:该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的频率为:1﹣(0.005+0.035+0.020+0.010)×10=0.3,∴估计该县小学六年级4000名学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为:4000×0.3=1200.故答案为:1200.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为1.【解答】解:根据题意知,执行程序后,输出函数y=,当x=0时,y=e0=1.故答案为:1.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.【解答】解:口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,从袋中一次随机摸出2个球,基本事件总数n==6,摸出的2个球的编号之和大于4包含的基本事件有:(1,4),(2,3),(2,4),(3,4),共4个,∴摸出的2个球的编号之和大于4的概率为p=.故答案为:.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p的值为6.【解答】解:∵双曲线的方程,∴a2=4,b2=5,可得c==3,因此双曲线的右焦点为F(3,0),∵抛物线y2=2px(p>0)的焦点与双曲线的右焦点重合,∴=3,解之得p=6.故答案为:6.7.(5分)设函数y=e x﹣a的值域为A,若A?[0,+∞),则实数a的取值范围是(﹣∞,2] .【解答】解:函数y=e x﹣a的值域为A∵e x=2,∴值域为A=[2﹣a,+∞).又∵A?[0,+∞),∴2﹣a≥0,即a≤2.故答案为:(﹣∞,2].8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.【解答】解:∵(tanα﹣1)(tanβ﹣1)=2,可得:tanα+tanβ+1=tanαtanβ,∴tan(α+β)=═﹣1,∵锐角α,β,可得:α+β∈(0,π),∴α+β=.故答案为:.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是(0,] .【解答】解:由函数y=sinωx,图象过原点,可得ω>0在区间[0,2π]上单调递增,∴,即.故答案为:(0,]10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为4034.【解答】解:因为S n为等差数列{a n}的前n项和,且{a n}的前2017项中的奇数项和为2018,=a1+a3+a5+…+a2017=1009×(a1+a2017)×=1009×a1009=2018,得a1009=2.所以S奇=a2+a4+a6+…+a2016=1008×(a2+a2016)×=1008×a1009=1008×2=2016则S偶则S2017=S奇+S偶=2018+2016=4034.故答案为:4034.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f (x)﹣m 有四个不同的零点,则实数m的取值范围是[1,).【解答】解:由0≤x≤3可得f(x)∈[0,],x>3时,f(x)∈(0,1).画出函数y=f(x)与y=m的图象,如图所示,∵函数y=f(x)﹣m有四个不同的零点,∴函数y=f(x)与y=m的图象有4个交点,由图象可得m的取值范围为[1,),故答案为:[1,).12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k﹣.【解答】解:设P(x1,y1),Q(x2,y2);则y1=k(x1﹣3)①,+(y2﹣1)2=1②;由=3,得,即,代入②得+=9;此方程表示的圆心(0,3)到直线kx﹣y﹣3k=0的距离为d≤r;即≤3,解得﹣≤k≤0.∴实数k的最小值为﹣.故答案为:﹣.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为24.【解答】解:建立如图的直角坐标系,则A(,),B(0,0),那么容易得到C(0,5)时,D的位置可以有三个位置,其中D1(﹣,),D2(﹣,0),D3(﹣,),此时=(﹣,﹣),=(﹣,﹣),=(﹣,﹣5),=(﹣,﹣),则?=21,?=24,?=22.5,则的最大值为24,故答案为:24.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为100.【解答】解:∵ksin2B+sinAsinC>19sinBsinC,由正弦定理可得:kb2+ac>19bc,∴k>,只需k大于右侧表达式的最大值即可,显然c>b时,表达式才能取得最大值,又∵c﹣b<a<b+c,∴﹣b﹣c<﹣a<b﹣c,∴<19+()=20﹣()2=100﹣(﹣10)2,当=10时,20﹣()2取得最大值20×10﹣102=100.∴k≥100,即实数k的最小值为100.故答案为:100二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.【解答】证明:(1)因为ABC﹣A1B1C1是直三棱柱,所以AB∥A1B1,且AB=A1B1,又点M,N分别是AB、A1B1的中点,所以MB=A1N,且MB∥A1N.所以四边形A1NBM是平行四边形,从而A1M∥BN.又BN?平面A1MC,A1M?平面A1MC,所以BN∥平面A1MC;(2)因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥底面ABC,而AA1?侧面ABB1A1,所以侧面ABB1A1⊥底面ABC.又CA=CB,且M是AB的中点,所以CM⊥AB.则由侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,CM⊥AB,且CM?底面ABC,得CM⊥侧面ABB1A1.又AB1?侧面ABB1A1,所以AB1⊥CM.又AB1⊥A1M,A1M、MC平面A1MC,且A1M∩MC=M,所以AB1⊥平面A1MC.又A1C?平面A1MC,所以AB⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.【解答】解:(1)因为c=,则由正弦定理,得sinC=sinB.…(2分)又C=2B,所以sin2B=sinB,即2sinBcosB=sinB.…(4分)又B是△ABC的内角,所以sinB>0,故cosB=.…(6分)(2)因为=,所以cbcosA=bacosC,则由余弦定理,得b2+c2﹣a2=b2+a2﹣c2,得a=c.…(10分)从而cosB==,…(12分)又0<B<π,所以sinB==.从而cos(B+)=cosBcos﹣sinBsin=.…(14分)17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大【解答】解:(1)在图甲中,连接MO交EF于点T.设OE=OF=OM=R,在Rt△OET中,因为∠EOT=∠EOF=60°,所以OT=,则MT=0M﹣OT=.从而BE=MT=,即R=2BE=2.故所得柱体的底面积S=S扇形OEF ﹣S△OEF=πR2﹣R2sin120°=﹣,又所得柱体的高EG=4,所以V=S×EG=﹣4.答:当BE长为1(分米)时,折卷成的包装盒的容积为﹣4立方分米.(2)设BE=x,则R=2x,所以所得柱体的底面积S=S扇形OEF﹣S△OEF=πR2﹣R2sin120°=(﹣)x2,又所得柱体的高EG=6﹣2x,所以V=S×EG=(﹣2)(﹣x3+3x2),其中0<x<3.令f(x)=﹣x3+3x2,0<x<3,则由f′(x)=﹣3x2+6x=﹣3x(x﹣2)=0,解得x=2.列表如下:所以当x=2时,f(x)取得最大值.答:当BE的长为2分米时,折卷成的包装盒的容积最大.18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.【解答】解:(1)由N(),点Q的坐标为(),得直线NQ的方程为y=x ﹣,令x=0,得点B的坐标为(0,﹣).所以椭圆的方程为+=1.将点N的坐标(,)代入,得+=1,解得a2=4.所以椭圆C的标准方程为+=1.(2):设直线BM的斜率为k(k>0),则直线BM的方程为y=x﹣.在y=kx﹣中,令y=0,得x P=,而点Q是线段OP的中点,所以x Q=.所以直线BN的斜率k BN=k BQ==2k.联立,消去y,得(3+4k2)x2﹣8kx=0,解得x M=.用2k代k,得x N=.又=2,所以x N=2(x M﹣x N),得2x M=3x N,故2×==3×,又k>0,解得k=.所以直线BM的方程为y=x﹣19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m?a n≥n﹣r对任意的n∈N*都成立,求m的最小值;=a n对任意的n∈N*均(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T成立.求所有满足条件的数列{a n}中T的最小值.【解答】解:(1)由题意,可得a=(a n+d)(a n﹣d)+λd2,化简得(λ﹣1)d2=0,又d≠0,所以λ=1.(2)将a1=1,a2=2,a3=4,代入条件,可得4=1×4+λ,解得λ=0,a n﹣1,所以数列{a n}是首项为1,公比q=2的等比数列,所以a=a n+1所以a n=2n﹣1.欲存在r∈[3,7],使得m?2n﹣1≥n﹣r,即r≥n﹣m?2n﹣1对任意n∈N*都成立,则7≥n﹣m?2n﹣1,所以m≥对任意n∈N*都成立.令b n=,则b n+1﹣b n=﹣=,<b n;当n=8时,b9=b8;当n<8时,b n+1>b n.所以当n>8时,b n+1所以b n的最大值为b9=b8=,所以m的最小值为;(3)因为数列{a n}不是常数列,所以T≥2,=a n恒成立,从而a3=a1,a4=a2,①若T=2,则a n+2所以,所以λ(a2﹣a1)2=0,又λ≠0,所以a2=a1,可得{a n}是常数列,矛盾.所以T=2不合题意.②若T=3,取a n=(*),满足a n+3=a n恒成立.由a22=a1a3+λ(a2﹣a1)2,得λ=7.则条件式变为a n2=a n+1a n﹣1+7.由22=1×(﹣3)+7,知a3k﹣12=a3k﹣2a3k+λ(a2﹣a1)2;由(﹣3)2=2×1+7,知a3k2=a3k﹣1a3k+1+λ(a2﹣a1)2;由12=2×(﹣3)+7,知a3k+12=a3k a3k+2+λ(a2﹣a1)2;所以,数列(*)适合题意.所以T的最小值为3.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.【解答】解:(1)由f(x)=lnx,得f(1)=0,又f′(x)=,所以f′(1)=1,当c=0时,g(x)=ax+,所以g′(x)=a﹣,所以g′(1)=a﹣b,因为函数f(x)与g(x)的图象在x=1处有相同的切线,所以,即,解得a=,b=﹣;(2)当x0>1时,则f(x0)>0,又b=3﹣a,设t=f(x0),则题意可转化为方程ax+﹣c=t(t>0)在(0,+∞)上有相异两实根x1,x2.即关于x的方程ax2﹣(c+t)x+(3﹣a)=0(t>0)在(0,+∞)上有相异两实根x1,x2.所以,得,所以c>2﹣t对t∈(0,+∞),a∈(0,3)恒成立.因为0<a<3,所以2≥2?=3(当且仅当a=时取等号),又﹣t<0,所以2﹣t的取值范围是(﹣∞,3),所以c≥3.故c的最小值为3.(3)当a=1时,因为函数f(x)与g(x)的图象交于A,B两点,所以,两式相减,得b=x1x2(1﹣),要证明x1x2﹣x2<b<x1x2﹣x1,即证x1x2﹣x2<x1x2(1﹣)<x1x2﹣x1,即证<<,即证1﹣<ln<﹣1令=t,则t>1,此时即证1﹣<lnt<t﹣1.令φ(t)=lnt+﹣1,所以φ′(t)=﹣=>0,所以当t>1时,函数φ(t)单调递增.又φ(1)=0,所以φ(t)=lnt+﹣1>0,即1﹣<lnt成立;再令m(t)=lnt﹣t+1,所以m′(t)=﹣1=<0,所以当t>1时,函数m(t)单调递减,又m(1)=0,所以m(t)=lnt﹣t+1<0,即lnt<t﹣1也成立.综上所述,实数x1,x2满足x1x2﹣x2<b<x1x2﹣x1.[选做题][选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.【解答】解:如图,连接AE,OE,因为直线DE与⊙O相切于点E,所以DE⊥OE,又因为AD⊥DE于D,所以AD∥OE,所以∠DAE=∠OEA,①在⊙O中,OE=OA,所以∠OEA=∠OAE,②…(5分)由①②得∠DAE=∠OAE,即∠DAE=∠FAE,又∠ADE=∠AFE,AE=AE,所以△ADE≌△AFE,所以DE=FE,又DE=4,所以FE=4,即E到直径AB的距离为4.…(10分)[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.【解答】解:设P(x0,y0)是圆x2+y2=1上任意一点,则=1,设点P(x0,y0)在矩阵M对应的变换下所得的点为Q(x,y),则=,即,解得,…(5分)代入=1,得=1,∴圆x2+y2=1在矩阵M的变换下所得的曲线方程为=1.…(10分)[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.【解答】解:直线ρcos(θ+)=1,转化为:,曲线ρ=r(r>0)转化为:x2+y2=r2,由于直线和圆相切,则:圆心到直线的距离d=.所以r=1.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.【解答】解:由柯西不等式,得[x2+()2][12+()2]≥(x?1+)2,即≥(x+y)2.而x2+3y2=1,所以(x+y)2,所以﹣,…(5分)由,得,所以当且仅当x=,y=时,(x+y)max=.所以当x+y取最大值时x值为.…(10分)25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.【解答】解:(1)因为ABCD是菱形,所以AC⊥BD.又OP⊥底面ABCD,以O为原点,直线OA,OB,OP分别为x轴,y轴,z轴,建立如图所示空间直角坐标系.则A(2,0,0),B(0,1,0),P(0,0,4),C(﹣2,0,0),M(﹣1,0,2).=(﹣2,0,4),=(01,﹣1,2),cos<,>===.故直线AP与BM所成角的余弦值为.…(5分)(2)=(﹣2,1,0),=(﹣1,﹣1,2).设平面ABM的一个法向量为=(x,y,z),则,令x=2,得=(2,4,3).又平面PAC的一个法向量为=(0,1,0),∴cos<>===.故平面ABM与平面PAC所成锐二面角的余弦值为.…(10分)26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.【解答】解:(1)由条件,nf(n)=C C C C①,在①中令n=1,得f(1)=1.在①中令n=2,得2f(2)=6,得f(2)=3.在①中令n=3,得3f(3)=30,故f(3)=10.(2)猜想f(n)=.要证猜想成立,只要证等式n=?+2?+…+n?成立.由(1+x)n=+x+x2+…+x n①,两边同时对x求导数,可得n(1+x)n﹣1=+2x+3x2+n x n﹣1②,把等式①和②相乘,可得n(1+x)2n﹣1=(+x+x2+…+x n)?(+2x+3x2+n x n ﹣1)③.等式左边x n的系数为n,等式右边x n的系数为?+?2+?3+…+n?n=?+2?+3?+…+n?=C C C C,根据等式③恒成立,可得n=C C C C.故f(n)=成立.。
2018南京盐城高三一模数学

2018届高三年级第一次模拟考试(一)数学(满分160分,考试时间120分钟)参考公式:柱体体积公式:V =Sh ,其中S 为底面积,h 为高.一、 填空题:本大题共14小题,每小题5分,共计70分.1. 已知集合A ={x|x(x -4)<0},B ={0,1,5},则A ∩B =________.2. 设复数z =a +i (a ∈R ,i 为虚数单位),若(1+i)·z 为纯虚数,则a 的值为________.3. 为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4 000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为________.(第3题) (第4题)4. 执行如图所示的伪代码,若x =0,则输出的y 的值为________.5. 口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为________.6. 若抛物线y 2=2px 的焦点与双曲线x 24-y 25=1的右焦点重合,则实数p 的值为________.7. 设函数y =e x +1e x -a 的值域为A ,若A ⊆[0,+∞),则实数a 的取值范围是________.8. 已知锐角α,β满足(tan α-1)(tan β-1)=2,则α+β的值为________.9. 若函数y =sin ωx 在区间[0,2π]上单调递增,则实数ω的取值范围是________. 10. 设S n 为等差数列{a n }的前n 项和,若{a n }的前2 017项中的奇数项和为2 018,则S 2 017的值为________.11. 设函数f(x)是偶函数,当x ≥0时,f(x)=⎩⎪⎨⎪⎧x (3-x ), 0≤x ≤3,-3x +1, x>3,若函数y =f(x)-m 有四个不同的零点,则实数m 的取值范围是________.12. 在平面直角坐标系xOy 中,若直线y =k(x -33)上存在一点P ,圆x 2+(y -1)2=1上存在一点Q ,满足OP →=3OQ →,则实数k 的最小值为________.13. 如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A ,B ,C ,D 四点均位于图中的“晶格点”处,且点A ,B 的位置如图所示,则AB →·CD →的最大值为________.14. 若不等式k sin 2B +sin A sin C>19sin B sin C 对任意△ABC 都成立,则实数k 的最小值为________.二、 解答题:本大题共6小题,共计90分.解答应写出文字说明、证明过程或演算步骤.15. (本小题满分14分)如图,在直三棱柱ABCA 1B 1C 1中,CA =CB ,M ,N 分别是AB ,A 1B 1的中点. (1) 求证:BN ∥平面A 1MC ;(2) 若A 1M ⊥AB 1,求证:AB 1⊥A 1C.16. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知c =52b. (1) 若C =2B ,求cos B 的值;(2) 若AB →·AC →=CA →·CB →,求cos ⎝⎛⎭⎫B +π4的值.有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图1所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图2所示,重叠部分忽略不计),其中OEMF是以O为圆心、∠EOF=120°的扇形,且弧EF,GH分别与边BC,AD相切于点M,N.(1) 当BE为1分米时,求折卷成的包装盒的容积;(2) 当BE的长是多少分米时,折卷成的包装盒的容积最大?图1 图2如图,在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a>b>0)的下顶点为B ,M ,N 是椭圆上异于点B 的动点,直线BM ,BN 分别与x 轴交于点P ,Q ,且Q 是线段OP 的中点.当点N 运动到点⎝⎛⎭⎫3,32处时,点Q 的坐标为⎝⎛⎭⎫233,0. (1) 求椭圆C 的标准方程;(2) 设直线MN 交y 轴于点D ,当点M ,N 均在y 轴右侧,DN →=2NM →时,求直线BM 的方程.设数列{a n}满足a2n=a n+1a n-1+λ(a2-a1)2,其中n≥2,且n∈N,λ为常数.(1) 若{a n}是等差数列,且公差d≠0,求λ的值;(2) 若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m·a n≥n-r对任意的n∈N*都成立,求实数m的最小值;(3) 若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T=a n对任意的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.设函数f(x)=ln x ,g(x)=ax +bx-c(a ,b ,c ∈R).(1) 当c =0时,若函数f (x )与g (x )的图象在x =1处有相同的切线,求a ,b 的值; (2) 当b =3-a 时,若对任意x 0∈(1,+∞)和任意a ∈(0,3),总存在不相等的正实数x 1,x 2,使得g (x 1)=g (x 2)=f (x 0),求c 的最小值;(3) 当a =1时,设函数y =f (x )与y =g (x )的图象交于A (x 1,y 1),B (x 2,y 2)(x 1<x 2)两点.求证:x 1x 2-x 2<b <x 1x 2-x 1.2018届高三年级第一次模拟考试(一)数学附加题(本部分满分40分,考试时间30分钟)21. 【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两小题,并作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A. [选修4-1:几何证明选讲](本小题满分10分)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD ⊥DE ,垂足为D .若DE =4,求切点E 到直径AB 的距离EF .B. [选修4-2:矩阵与变换](本小题满分10分)已知矩阵M =⎣⎢⎡⎦⎥⎤2 00 1,求圆x 2+y 2=1在矩阵M 的变换下所得的曲线方程.C. [选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系中,直线ρcos ⎝⎛⎭⎫θ+π3=1与曲线ρ=r (r >0)相切,求r 的值.D. [选修4-5:不等式选讲](本小题满分10分)已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.【必做题】第22题、第23题,每题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤22. (本小题满分10分)如图,四棱锥PABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,M为PC的中点,AC=4,BD=2,OP=4.(1) 求直线AP与BM所成角的余弦值;(2) 求平面ABM与平面PAC所成锐二面角的余弦值.23. (本小题满分10分)已知n∈N*,nf(n)=C0n C1n+2C1n C2n+…+r C r-1n C r n+…+n C n-1nC n n.(1) 求f(1),f(2),f(3)的值;(2) 试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.。
南京、盐城2018年高三一模数学试题与答案解析

市、市2018届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的、号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上) 1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则AB = ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ .3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 7.设函数1x x y e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值围是 ▲ .时间(单位:分钟)50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 第4题图8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ . 9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值围是 ▲ . 10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =-有四个不同的零点,则实数m 的取值围是 ▲ .12.在平面直角坐标系xOy 中,若直线(33)y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =,则实数k 的最小值为 ▲ .13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则CD AB ⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分. 解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域) 15.(本小题满分14分)如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点.(1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB AC ⊥.16.(本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c 已知52c =. (1)若2C B =,求cos B 的值; (2)若AB AC CA CB ⋅=⋅,求cos()4B π+的值.17.(本小题满分14分)有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截A第13题图 ABC A 1B 1C 1 MN第15题图取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧EF ,GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N 是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N运动到点处时,点Q的坐标为. (1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =时,求直线BM 的方程.第17题-图甲 F 第17题-图乙19.(本小题满分16分)设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n ,且n N ∈,λ为常数.(1)若{}n a 是等差数列,且公差0d ≠,求λ的值;(2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N ∈均成立. 求所有满足条件的数列{}n a 中T 的最小值.20.(本小题满分16分)设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈). (1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值; (2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值;(3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.市、市2018届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分.1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞8.34π 9.1(0,]4 10.4034 11.9[1,)412. 13.24 14.100二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域. 15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =,又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N . 所以四边形1A NBM是平行四边形,从而1//A M BN . ……………4分又BN ⊄平面1A MC ,1A M ⊂平面1A MC ,所以BN ∥面1A MC . ……………6分(2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC .又CA CB =,且M 是AB 的中点,所以CM AB ⊥.则由侧面11ABB A ⊥底面ABC ,侧面11ABB A 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC,得CM ⊥侧面11ABB A . ……………8分又1AB ⊂侧面11ABB A ,所以1AB CM ⊥. ……………10分又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1A M MC M =,所以1AB ⊥平面1A MC . ……………12分又1AC ⊂平面1A MC,所以11AB A C ⊥. ……………14分16.解:(1)因为52c b =,则由正弦定理,得5sin C B =. ……………2分 又2C B=,所以5sin 2B B =,即4sin cos 5B B B =. ……………4分又B是ABC ∆的角,所以sin 0B >,故5cos B =. ……………6分(2)因为AB AC CA CB ⋅=⋅, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =. ……………10分从而2223cos 25a cb B ac+-===, (12)分又0B π<<,所以4sin 5B ==. 从而34cos()cos cos sin sin 444525210B B B πππ+=-=⨯-⨯=-. (14)分17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===,在Rt OET ∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2RMT OM OT =-=. 从而2R BE MT ==,即22R BE ==. ……………2分故所得柱体的底面积OEF OEF S S S ∆=-扇形22114sin120323R R ππ=-︒=……………4分又所得柱体的高4EG =,所以V S EG =⨯=163π-答:当BE 长为1分米时,折卷成的包装盒的容积为163π-. …………………6分(2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114sin120(323R R x ππ=-︒=-.又所得柱体的高62EG x =-,所以V S EG =⨯=328(3)3x x π--+,其中03x <<. …………………10分令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=, 解得2x =. …………………12分答:当BE的长为2分米时,折卷成的包装盒的容积最大. …………………14分18.解:(1)由N Q,得直线NQ的方程为32y x=…………………2分令0x=,得点B的坐标为(0,.所以椭圆的方程为22213x ya+=.…………………4分将点N的坐标)22(213+=,解得24a=.所以椭圆C的标准方程为22143x y+=. (8)分(2)方法一:设直线BM的斜率为(0)k k>,则直线BM的方程为y kx=在y kx=0y=,得Pxk=,而点Q是线段OP的中点,所以2Qxk=.所以直线BN的斜率2BN BQk k k===.………………10分联立22143y kxx y⎧=⎪⎨+=⎪⎩,消去y,得22(34)0k x+-=,解得234Mxk=+.用2k代k,得Nx=.………………12分又2DN NM=,所以2()N M Nxx x=-,得23M Nx x=.………………14分故23=0k>,解得k=.所以直线BM的方程为2y x =-. ………………16分 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为1y x =0y =,得P x =.同理,得Q x =.而点Q 是线段OP的中点,所以2P Qx x =,故=…………………10分 又2DN NM =,所以2122()x x x =-,得21203x x =>4=解得2143y y =+ …………………12分将21212343x x y y ⎧=⎪⎪⎨⎪=+⎪⎩代入到椭圆C的方程中,得2211(41927x y ++=. 又22114(1)3y x =-,所以21214(1)(431927y y -+=21120y +=, 解得1y =(舍)或1y =.又10x >,所以点M 的坐标为M .……………14分故直线BM 的方程为y x =-. …………………16分19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+,化简得2(1)0d λ-=,又d ≠,所以1λ=. ………………4分(2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=. ……6分欲存在[3,7]r ∈,使得12n m n r -⋅-,即12n r n m --⋅对任意*n N ∈都成立,则172n n m --⋅,所以172n n m --对任意*n N ∈都成立. ………………8分令172n n n b --=,则11678222n n nn n n n nb b +-----=-=, 所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>.所以n b 的最大值为981128b b ==,所以m 的最小值为1128. ………………10分 (3)因为数列{}n a 不是常数列,所以2T .①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩, 所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意. ………………12分②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立. ………………14分由2221321()a a a a a λ=+-,得7λ=. 则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-;由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-; 由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-.所以,数列(*)适合题意. 所以T的最小值为3. ………………16分20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,. 当c =时,()bg x ax x=+,所以2()bg x a x'=-,所以(1)g a b '=-. ………………2分因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩. ………………4分 (2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =,则题意可转化为方程3(0)aax c t t x-+-=>在(0,)+∞上有相异两实根12,x x . ………………6分即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a <<⎧⎪∆=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩, 所以c t>对(0,),(0,3)t a ∈+∞∈恒成立. ………………8分因为03a <<,所以)2(3a +⨯=(当且仅当32a =时取等号), 又0t -<,所以t 的取值围是(,3)-∞,所以3c .故c 的最小值为3. ………………10分(3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x c x b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. ………………12分要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--, 即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x xx x x -<<-. ………………14分 令21x t x =,则1t >,此时即证11ln 1t t t-<<-. 令1()ln 1t t t ϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t tϕ=+->,即11ln t t-<成立; 再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减,又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立.综上所述,实数12,x x 满足122121x x x b x x x -<<-. ………………16分附加题答案21.(A )解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② ………………5分 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4. ………………10分(B )解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即002x x y y =⎧⎨=⎩,解得0012x xy y⎧=⎪⎨⎪=⎩, ………………5分 代入22001x y +=,得2214x y +=,即为所求的曲线方程. ………………10分(C )解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系,ABE DF O · 第21(A)图由cos()13πρθ+=,得(cos cossin sin )133ππρθθ-=, 得直线的直角坐标方程为20x -=. ………………5分曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.因为直线cos()13πρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. ……………10分(D)解:由柯西不等式,得22222[)][1](1x x ++≥⨯+, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y ≤+≤ ………………5分由1x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得26x y ⎧=⎪⎪⎨⎪=⎪⎩,所以当且仅当26x y ==时,max ()x y += 所以当x y+取最大值时x 的值为2x =. ………………10分 22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系. 则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -. 所以(2,0,4)AP =-,(1,1,2)BM =--,10AP BM ⋅=,||25AP =,||6BM =.则cos ,6||||2AP BM AP BM AP BM ⋅<>===. 故直线AP 与BM . ………5分 (2)(2,1,0)AB =-,(1,1,2)BM =--.C第22题图设平面ABM 的一个法向量为(,,)n x y z =,则00n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =.得平面ABM 的一个法向量为(2,4,3)n =.又平面PAC 的一个法向量为(0,1,0)OB =,所以n 4OB ⋅=,||29n =,||1OB =.则4cos ,||||29n OB n OB n OB ⋅<>===.故平面ABM 与平面PAC 所成锐二面角的余弦值为………………10分 23.解:(1)由条件,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+ ①,在①中令1n =,得()011111f C C ==. ………………1分在①中令2n =,得()011222222226f C C C C =+=,得()23f =. ………………2分在①中令3n =,得()011223333333332330f C C C C C C =++=,得()310f =. ………………3分(2)猜想()f n =21nn C -(或()f n =121n n C --). ………………5分 欲证猜想成立,只要证等式011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+成立.方法一:当1n =时,等式显然成立,当2n 时,因为11!!(1)!==!()!(1)!()!(1)!()!rr n n r n n n rC n nC r n r r n r r n r --⨯-=⨯=-----(),故11111()r r r r r r n n n n n n rC C rC C nC C -----==.故只需证明00111111211111n r r n n n n n n n n n n n nC nC C nC C nC C nC C ---------=++⋅⋅⋅++⋅⋅⋅+.即证00111111211111n r r n n n n n n n n n n nC C C C C C C C C ---------=++⋅⋅⋅++⋅⋅⋅+. 而11r n r n n C C --+=,故即证0111111211111n n n r n r n n n n n n n n n n C C C C C C C C C ---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21n n C -.而右边1(1)(1)n n x x -++()()01221101221111n n n nnn n n n n n n C C x C x C xC C x C x C x ------=++++++++,所以nx 的系数为01111111111n n r n r n n n n n n n n n C C C C C C C C ---+-----++⋅⋅⋅++⋅⋅⋅+.由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立. 综上,()21nn f n C -=成立. ………………10分方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1r n rn nC C --,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111n n n n n n nn n C C C C C C -----+++.另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21nn C -.故0111121111n n n n n n n n n n n C C C C C C C ------=++,即②成立. 余下同方法一. ………………10分方法三:由二项式定理,得0122(1)n n nn n n n x C C x C x C x +=++++ ③.两边求导,得112111(1)2n r r n n n n n n n x C C x rC x nC x ---+=+++++ ④.③×④,得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++⑤.左边n x 的系数为21nn nC -.右边nx 的系数为121112n n r n r n n n n n n n n n C C C C rC C nC C --+++⋅⋅⋅++⋅⋅⋅+1021112r r n n n n n n n n n nC C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+0112112r r n nn n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.由⑤恒成立,可得011211212n r r n n n n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+.故()21nn f n C -=成立. ………………10分。
江苏省南京市、盐城市2018届高三年级第一次模拟考试数学试题

江苏省南京市、盐城市2018届高三年级第一次模拟考试数学试题一、填空题1. 已知集合,,则____.2. 设复数为虚数单位),若为纯虚数,则的值为____.3. 为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在(单位:分钟)内的学生人数为____.4. 执行如图所示的伪代码,若,则输出的的值为________.5. 口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为________.6. 若抛物线的焦点与双曲线的右焦点重合,则实数的值为____.7. 设函数的值域为,若,则实数的取值范围是________.8. 已知锐角满足,则的值为________.9. 若函数在区间上单调递增,则实数的取值范围是________.10. 设为等差数列的前项和,若的前2017项中的奇数项和为2018,则的值为________.11. 设函数是偶函数,当x≥0时,=,若函数有四个不同的零点,则实数m的取值范围是________.12. 在平面直角坐标系中,若直线上存在一点,圆上存在一点,满足,则实数的最小值为________.13. 如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若四点均位于图中的“晶格点”处,且的位置所图所示,则的最大值为________.14. 若不等式对任意都成立,则实数的最小值为________.二、解答题15. 如图所示,在直三棱柱中,,点分别是的中点.(1)求证:∥平面;(2)若,求证:.16. 在中,角的对边分别为已知.(1)若,求的值;(2)若,求的值.17. 有一矩形硬纸板材料(厚度忽略不计),一边长为6分米,另一边足够长.现从中截取矩形(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中是以为圆心、的扇形,且弧,分别与边,相切于点,.(1)当长为1分米时,求折卷成的包装盒的容积;(2)当的长是多少分米时,折卷成的包装盒的容积最大?18. 如图,在平面直角坐标系中,椭圆的下顶点为,点是椭圆上异于点的动点,直线分别与轴交于点,且点是线段的中点.当点运动到点处时,点的坐标为.(1)求椭圆的标准方程;(2)设直线交轴于点,当点均在轴右侧,且时,求直线的方程.19. 设数列满足,其中,且,为常数.(1)若是等差数列,且公差,求的值;(2)若,且存在,使得对任意的都成立,求的最小值;(3)若,且数列不是常数列,如果存在正整数,使得对任意的均成立. 求所有满足条件的数列中的最小值.20. 设函数,().(1)当时,若函数与的图象在处有相同的切线,求的值;(2)当时,若对任意和任意,总存在不相等的正实数,使得,求的最小值;(3)当时,设函数与的图象交于两点.求证:.南京市、盐城市2018届高三年级第一次模拟考试数学附加题部分21. (选修4-1:几何证明选讲)如图,已知为⊙的直径,直线与⊙相切于点,垂直于点. 若,求切点到直径的距离.22. (选修4-2:矩阵与变换)已知矩阵,求圆在矩阵的变换下所得的曲线方程.23. (选修4-4:坐标系与参数方程)在极坐标系中,直线与曲线()相切,求的值.24. (选修4-5:不等式选讲)已知实数满足,求当取最大值时的值.25. 如图,四棱锥的底面是菱形,与交于点,底面,点为中点,.(1)求直线与所成角的余弦值;(2)求平面与平面所成锐二面角的余弦值.26. 已知,.(1)求的值;(2)试猜想的表达式(用一个组合数表示),并证明你的猜想.南京市、盐城市2018届高三年级第一次模拟考试答案一、填空题1. 已知集合,,则____.【答案】【解析】,所以2. 设复数为虚数单位),若为纯虚数,则的值为____.【答案】1【解析】因为为纯虚数,所以3. 为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在(单位:分钟)内的学生人数为____.【答案】1200【解析】4. 执行如图所示的伪代码,若,则输出的的值为________.【答案】1【解析】因为,所以时5. 口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为________.【答案】【解析】从袋中一次随机摸出2个球,共有 6种基本事件,其中摸出的2个球的编号之和大于4的事件为,四种基本事件数,因此概率为学+科+网...学+科+网...学+科+网...学+科+网...学+科+网...学+科+网...学+科+网...学+科+网...学+科+网...学+科+网...6. 若抛物线的焦点与双曲线的右焦点重合,则实数的值为____.【答案】6【解析】因为双曲线的右焦点为,所以7. 设函数的值域为,若,则实数的取值范围是________.【答案】【解析】因为a,所以8. 已知锐角满足,则的值为________.【答案】【解析】因为,所以因此因为9. 若函数在区间上单调递增,则实数的取值范围是________.【答案】【解析】由题意得,所以10. 设为等差数列的前项和,若的前2017项中的奇数项和为2018,则的值为________.【答案】4034【解析】因为的前2017项中的奇数项和为2018,所以因此点睛:在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.11. 设函数是偶函数,当x≥0时,=,若函数有四个不同的零点,则实数m的取值范围是________.【答案】【解析】作图,由图可得实数m的取值范围是点睛:对于方程解的个数(或函数零点个数)问题,可利用函数的值域或最值,结合函数的单调性、草图确定其中参数范围.从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等.12. 在平面直角坐标系中,若直线上存在一点,圆上存在一点,满足,则实数的最小值为________.【答案】【解析】设因此,即实数的最小值为点睛:判断直线与圆的位置关系的常见方法(1)几何法:利用d与r的关系.(2)代数法:联立方程之后利用Δ判断.(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.13. 如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若四点均位于图中的“晶格点”处,且的位置所图所示,则的最大值为________.【答案】24【解析】先建立直角坐标系,由向量投影知取最大值时 ,即点睛:平面向量数量积的类型及求法(1)求平面向量数量积有三种方法:一是夹角公式a·b=|a||b|cos θ;二是坐标公式a·b=x1x2+y1y2;三是利用数量积的几何意义.(2)求较复杂的平面向量数量积的运算时,可先利用平面向量数量积的运算律或相关公式进行化简.14. 若不等式对任意都成立,则实数的最小值为________.【答案】100【解析】由正弦定理得因此,即的最小值为100点睛:三角形中最值问题,一般转化为条件最值问题:先根据正、余弦定理及三角形面积公式结合已知条件灵活转化边和角之间的关系,利用基本不等式或函数方法求最值. 在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.二、解答题15. 如图所示,在直三棱柱中,,点分别是的中点.(1)求证:∥平面;(2)若,求证:.【答案】(1)见解析(2)见解析【解析】试题分析:(1)先根据平面几何知识证明四边形是平行四边形,得.再根据线面平行判定定理得结论(2)先根据直三棱柱性质得,再根据等腰三角形性质得,由线面垂直判定定理得侧面.即得.再由已知,证得平面,即得结论试题解析:证明:(1)因为是直三棱柱,所以,且,又点分别是的中点,所以,且.所以四边形是平行四边形,从而.又平面,平面,所以∥面.(2)因为是直三棱柱,所以底面,而侧面,所以侧面底面.又,且是的中点,所以.则由侧面底面,侧面底面,,且底面,得侧面.又侧面,所以.又,平面,且,所以平面.又平面,所以.16. 在中,角的对边分别为已知.(1)若,求的值;(2)若,求的值.【答案】(1)(2)【解析】试题分析:(1)由正弦定理得.利用二倍角公式化简得.(2)化简向量得.再根据余弦定理得,最后根据同角三角函数关系以及两角和余弦公式得的值.试题解析:解:(1)因为,则由正弦定理,得.又,所以,即.又是的内角,所以,故.(2)因为,所以,则由余弦定理,得,得.从而,又,所以.从而.17. 有一矩形硬纸板材料(厚度忽略不计),一边长为6分米,另一边足够长.现从中截取矩形(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中是以为圆心、的扇形,且弧,分别与边,相切于点,.(1)当长为1分米时,求折卷成的包装盒的容积;(2)当的长是多少分米时,折卷成的包装盒的容积最大?【答案】(1)当长为1分米时,折卷成的包装盒的容积为立方分米.(2)当的长为2分米时,折卷成的包装盒的容积最大【解析】试题分析:(1)先根据扇形面积减去三角形面积得弓形面积,即为柱体底面积,再根据柱体体积公式求体积(2)同(1)先计算底面积,再表示高,代入柱体体积公式得容积函数关系式,最后利用导数求最值试题解析:解:(1)在图甲中,连接交于点.设,在中,因为,所以,则.从而,即.故所得柱体的底面积.又所得柱体的高,所以.答:当长为1分米时,折卷成的包装盒的容积为立方分米.(2)设,则,所以所得柱体的底面积.又所得柱体的高,所以,其中.令,则由,解得.列表如下:+0 -增极大值减所以当时,取得最大值.答:当的长为2分米时,折卷成的包装盒的容积最大.18. 如图,在平面直角坐标系中,椭圆的下顶点为,点是椭圆上异于点的动点,直线分别与轴交于点,且点是线段的中点.当点运动到点处时,点的坐标为.(1)求椭圆的标准方程;(2)设直线交轴于点,当点均在轴右侧,且时,求直线的方程.【答案】(1)(2)【解析】试题分析:(1)先求直线的方程,即得B坐标,有;再将N坐标代入椭圆方程解得a(2)设直线的斜率为,解得P点坐标,根据中点坐标公式得Q,利用直线方程与椭圆方程联立方程组解得M,N,根据横坐标之间比例关系求k,即得直线的方程.试题解析:解:(1)由,得直线的方程为.令,得点的坐标为.所以椭圆的方程为.将点的坐标代入,得,解得.所以椭圆的标准方程为.(2)方法一:设直线的斜率为,则直线的方程为.在中,令,得,而点是线段的中点,所以.所以直线的斜率.联立,消去,得,解得.用代,得.又,所以,得.故,又,解得.所以直线的方程为.方法二:设点的坐标分别为.由,得直线的方程为,令,得.同理,得.而点是线段的中点,所以,故.又,所以,得,从而,解得.将代入到椭圆C的方程中,得.又,所以,即,解得(舍)或.又,所以点的坐标为.故直线的方程为.19. 设数列满足,其中,且,为常数.(1)若是等差数列,且公差,求的值;(2)若,且存在,使得对任意的都成立,求的最小值;(3)若,且数列不是常数列,如果存在正整数,使得对任意的均成立. 求所有满足条件的数列中的最小值.【答案】(1)(2)(3)3【解析】试题分析:(1)利用等差数列定义将条件转化为公差关系,解方程可得的值;(2)先求的值;即得数列为等比数列,分离变量将不等式恒成立问题转化为对应函数最值问题:,即,最大值,再根据数列单调性确定最大值,即得的最小值;(3)本题由于求周期最小值,可以从小逐个验证即可:为常数列,舍去;时,可推得,舍去;时,可取一个数列满足条件.试题解析:解:(1)由题意,可得,化简得,又,所以.(2)将代入条件,可得,解得,所以,所以数列是首项为1,公比的等比数列,所以.欲存在,使得,即对任意都成立,则,所以对任意都成立.令,则,所以当时,;当时,;当时,.所以的最大值为,所以的最小值为.(3)因为数列不是常数列,所以.①若,则恒成立,从而,,所以,所以,又,所以,可得是常数列.矛盾.所以不合题意.②若,取(*),满足恒成立.由,得.则条件式变为.由,知;由,知;由,知.所以,数列(*)适合题意.所以的最小值为.20. 设函数,().(1)当时,若函数与的图象在处有相同的切线,求的值;(2)当时,若对任意和任意,总存在不相等的正实数,使得,求的最小值;(3)当时,设函数与的图象交于两点.求证:.【答案】(1)(2)(3)见解析【解析】试题分析:(1)由导数几何意义可得,又,解方程组可得的值;(2)先转化条件为对应方程有两个不等实根,再根据实根分布充要条件列不等式组,解得的最小值;(3)先根据零点表示b,代入要证不等式化简得.再构造函数,以及,结合导数研究其单调性,即证得结论试题解析:解:(1)由,得,又,所以,.当时,,所以,所以.因为函数与的图象在处有相同的切线,所以,即,解得.(2)当时,则,又,设,则题意可转化为方程在上有相异两实根.即关于的方程在上有相异两实根.所以,得,所以对恒成立.因为,所以(当且仅当时取等号),又,所以的取值范围是,所以.故的最小值为.(3)当时,因为函数与的图象交于两点,所以,两式相减,得.要证明,即证,即证,即证.令,则,此时即证.令,所以,所以当时,函数单调递增.又,所以,即成立;再令,所以,所以当时,函数单调递减,又,所以,即也成立.综上所述,实数满足.点睛:利用导数证明不等式常见类型及解题策略(1) 构造差函数.根据差函数导函数符号,确定差函数单调性,利用单调性得不等量关系,进而证明不等式.(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.南京市、盐城市2018届高三年级第一次模拟考试数学附加题部分21. (选修4-1:几何证明选讲)如图,已知为⊙的直径,直线与⊙相切于点,垂直于点. 若,求切点到直径的距离.【答案】4【解析】试题分析:根据条件证明三角形全等:,即得切点到直径的距离试题解析:解:如图,连接,,因为直线与⊙相切于点,所以,又因为垂直于,所以,所以,①在⊙中,所以,②由①②得,即,又,,所以,所以,又,所以,即到直径的距离为4.22. (选修4-2:矩阵与变换)已知矩阵,求圆在矩阵的变换下所得的曲线方程.【答案】【解析】试题分析:根据矩阵运算得对于点之间关系,再代入已知动点轨迹,化简可得在矩阵的变换下所得的曲线方程试题解析:解:设是圆上任意一点,则,设点在矩阵对应的变换下所得的点为,则,即,解得,代入,得,即为所求的曲线方程.23. (选修4-4:坐标系与参数方程)在极坐标系中,直线与曲线()相切,求的值.【答案】【解析】试题分析:先根据将直线与曲线极坐标方程化为直角坐标方程,再根据直线与圆相切得,解得的值.试题解析:解:以极点O为原点,极轴为轴建立平面直角坐标系,由,得,得直线的直角坐标方程为.曲线,即圆,所以圆心到直线的距离为.因为直线与曲线()相切,所以,即.点睛:(1)直角坐标方程化为极坐标方程,只要运用公式及直接代入并化简即可; (2)极坐标方程化为直角坐标方程时常通过变形,构造形如的形式,进行整体代换.其中方程的两边同乘以(或同除以)及方程两边平方是常用的变形方法.但对方程进行变形时,方程必须同解,因此应注意对变形过程的检验.24. (选修4-5:不等式选讲)已知实数满足,求当取最大值时的值.【答案】【解析】试题分析:根据柯西不等式,得,化简可得取最大值时的值试题解析:解:由柯西不等式,得,即.而,所以,所以,由,得,所以当且仅当时,.所以当取最大值时的值为.点睛:柯西不等式的一般形式:设为实数,则当且仅当或存在一个数,使时,等号成立.25. 如图,四棱锥的底面是菱形,与交于点,底面,点为中点,.(1)求直线与所成角的余弦值;(2)求平面与平面所成锐二面角的余弦值.【答案】(1)(2)【解析】试题分析:(1)先根据条件建立空间直角坐标系,设立各点坐标,表示直线方向向量,根据向量数量积求向量夹角,最后根据线线角与向量夹角关系得结果(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解出各面法向量,根据向量数量积求法向量夹角,最后根据二面角与向量夹角关系得结果试题解析:解:(1)因为是菱形,所以.又底面,以为原点,直线分别为轴,轴,轴,建立如图所示空间直角坐标系.则,,,,.所以,,,,.则.故直线与所成角的余弦值为.(2),.设平面的一个法向量为,则,得,令,得,.得平面的一个法向量为.又平面的一个法向量为,所以,,.则.故平面与平面所成锐二面角的余弦值为.26. 已知,.(1)求的值;(2)试猜想的表达式(用一个组合数表示),并证明你的猜想.【答案】(1)1,3,10(2)=【解析】试题分析:(1)代入,根据组合数依次求出的值;(2)根据数值猜想=,利用倒序相加法可求出的表达式试题解析:解:(1)由条件,①,在①中令,得.在①中令,得,得.在①中令,得,得.(2)猜想=(或=).欲证猜想成立,只要证等式成立.方法一:当时,等式显然成立,当时,因为,故.故只需证明.即证.而,故即证②.由等式可得,左边的系数为.而右边,所以的系数为.由恒成立可得②成立.综上,成立.方法二:构造一个组合模型,一个袋中装有个小球,其中n个是编号为1,2,…,n的白球,其余n -1个是编号为1,2,…,n-1的黑球,现从袋中任意摸出n个小球,一方面,由分步计数原理其中含有个黑球(个白球)的n个小球的组合的个数为,,由分类计数原理有从袋中任意摸出n个小球的组合的总数为.另一方面,从袋中个小球中任意摸出n个小球的组合的个数为.故,即②成立. 余下同方法一.方法三:由二项式定理,得③.两边求导,得④.③×④,得⑤.左边的系数为.右边的系数为.由⑤恒成立,可得.故成立.。
2018年江苏省盐城市、南京市高考数学一模试卷及答案

2018年江苏省盐城市、南京市高考数学一模试卷一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B=.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p 的值为.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是.8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是.10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是.12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为.二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q 的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N*都成立,求m的最小值;=a n对任意(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b 的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22.23.24四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)[选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.2018年江苏省盐城市、南京市高考数学一模试卷参考答案与试题解析一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B={1} .【解答】解:∵集合A={x|x(x﹣4)<0}={x|0<x<4},B={0,1,5},∴A∩B={1}.故答案为:{1}.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为1.【解答】解:∵z=a+i,∴(1+i)•z=(1+i)(a+i)=a﹣1+(a+1)i,又(1+i)•z为为纯虚数,∴a﹣1=0即a=1.故答案为:1.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为1200.【解答】解:由频率分布直方图得:该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的频率为:1﹣(0.005+0.035+0.020+0.010)×10=0.3,∴估计该县小学六年级4000名学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为:4000×0.3=1200.故答案为:1200.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为1.【解答】解:根据题意知,执行程序后,输出函数y=,当x=0时,y=e0=1.故答案为:1.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.【解答】解:口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,从袋中一次随机摸出2个球,基本事件总数n==6,摸出的2个球的编号之和大于4包含的基本事件有:(1,4),(2,3),(2,4),(3,4),共4个,∴摸出的2个球的编号之和大于4的概率为p=.故答案为:.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p 的值为6.【解答】解:∵双曲线的方程,∴a2=4,b2=5,可得c==3,因此双曲线的右焦点为F(3,0),∵抛物线y2=2px(p>0)的焦点与双曲线的右焦点重合,∴=3,解之得p=6.故答案为:6.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是(﹣∞,2] .【解答】解:函数y=e x﹣a的值域为A∵e x=2,∴值域为A=[2﹣a,+∞).又∵A⊆[0,+∞),∴2﹣a≥0,即a≤2.故答案为:(﹣∞,2].8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.【解答】解:∵(tanα﹣1)(tanβ﹣1)=2,可得:tanα+tanβ+1=tanαtanβ,∴tan(α+β)=═﹣1,∵锐角α,β,可得:α+β∈(0,π),∴α+β=.故答案为:.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是(0,] .【解答】解:由函数y=sinωx,图象过原点,若ω<0,图象在x轴下方单调递减,∴ω>0,因为y=Sinωx在[0,2π]单调递增,说明其至少在[0,2π]单调递增,则其周期至少8π,∴,即.故答案为:(0,]10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为4034.【解答】解:因为S n为等差数列{a n}的前n项和,且{a n}的前2017项中的奇数项和为2018,所以S=a1+a3+a5+…+a2017=1009×(a1+a2017)×=2018,得a1+a2017═4.奇则S2017=(a1+a2017)=2017×2=4034故答案为:4034.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是[1,).【解答】解:由0≤x≤3可得f(x)∈[0,],x>3时,f(x)∈(0,1).画出函数y=f(x)与y=m的图象,如图所示,∵函数y=f(x)﹣m有四个不同的零点,∴函数y=f(x)与y=m的图象有4个交点,由图象可得m的取值范围为[1,),故答案为:[1,).12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为﹣.【解答】解:【解法一】设P(x1,y1),Q(x2,y2);则y1=k(x1﹣3)①,+(y2﹣1)2=1②;由=3,得,即,代入②得+=9;此方程表示的圆心(0,3)到直线kx﹣y﹣3k=0的距离为d≤r;即≤3,解得﹣≤k≤0.∴实数k的最小值为﹣.【解法二】设P(x,y),Q(x0,y0);则+(y0﹣1)2=1①;由=3,得,即,代入①化简得x2+(y﹣3)2=9;∴点P的轨迹是圆心为(0,3),半径为3的圆的方程,又点P在直线kx﹣y﹣3k=0上,如图所示;则直线与该圆有公共点,即圆心到直线的距离为d≤r;∴≤3,解得﹣≤k≤0;∴实数k的最小值为﹣.故答案为:﹣.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为24.【解答】解:建立如图的直角坐标系,则A(,),B(0,0),那么容易得到C(0,5)时,D的位置可以有三个位置,其中D1(﹣,),D2(﹣,0),D3(﹣,),此时=(﹣,﹣),=(﹣,﹣),=(﹣,﹣5),=(﹣,﹣),则•=21,•=24,•=22.5,则的最大值为24,故答案为:24.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为100.【解答】解:∵ksin2B+sinAsinC>19sinBsinC,由正弦定理可得:kb2+ac>19bc,∴k>,又∵c﹣b<a<b+c,∴﹣b﹣c<﹣a<b﹣c,∴<19+()=20﹣()2=100﹣(﹣10)2,当=10时,20﹣()2取得最大值20×10﹣102=100.∴k≥100,即实数k的最小值为100.故答案为:100二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.【解答】证明:(1)因为ABC﹣A1B1C1是直三棱柱,所以AB∥A1B1,且AB=A1B1,又点M,N分别是AB、A1B1的中点,所以MB=A1N,且MB∥A1N.所以四边形A1NBM是平行四边形,从而A1M∥BN.又BN⊄平面A1MC,A1M⊂平面A1MC,所以BN∥平面A1MC;(2)因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥底面ABC,而AA1⊂侧面ABB1A1,所以侧面ABB1A1⊥底面ABC.又CA=CB,且M是AB的中点,所以CM⊥AB.则由侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,CM⊥AB,且CM⊂底面ABC,得CM⊥侧面ABB1A1.又AB1⊂侧面ABB1A1,所以AB1⊥CM.又AB1⊥A1M,A1M、MC平面A1MC,且A1M∩MC=M,所以AB1⊥平面A1MC.又A1C⊂平面A1MC,所以AB⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.【解答】解:(1)因为c=,则由正弦定理,得sinC=sinB.…(2分)又C=2B,所以sin2B=sinB,即2sinBcosB=sinB.…(4分)又B是△ABC的内角,所以sinB>0,故cosB=.…(6分)(2)因为=,所以cbcosA=bacosC,则由余弦定理,得b2+c2﹣a2=b2+a2﹣c2,得a=c.…(10分)从而cosB==,…(12分)又0<B<π,所以sinB==.从而cos(B+)=cosBcos﹣sinBsin=.…(14分)17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?【解答】解:(1)在图甲中,连接MO交EF于点T.设OE=OF=OM=R,在Rt△OET中,因为∠EOT=∠EOF=60°,所以OT=,则MT=0M﹣OT=.从而BE=MT=,即R=2BE=2.故所得柱体的底面积S=S扇形OEF ﹣S△OEF=πR2﹣R2sin120°=﹣,又所得柱体的高EG=4,所以V=S×EG=﹣4.答:当BE长为1(分米)时,折卷成的包装盒的容积为﹣4立方分米.(2)设BE=x,则R=2x,所以所得柱体的底面积S=S扇形OEF﹣S△OEF=πR2﹣R2sin120°=(﹣)x2,又所得柱体的高EG=6﹣2x,所以V=S×EG=(﹣2)(﹣x3+3x2),其中0<x<3.令f(x)=﹣x3+3x2,0<x<3,则由f′(x)=﹣3x2+6x=﹣3x(x﹣2)=0,解得x=2.列表如下:所以当x=2时,f(x)取得最大值.答:当BE的长为2分米时,折卷成的包装盒的容积最大.18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q 的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.【解答】解:(1)由N(),点Q的坐标为(),得直线NQ的方程为y=x﹣,令x=0,得点B的坐标为(0,﹣).所以椭圆的方程为+=1.将点N的坐标(,)代入,得+=1,解得a2=4.所以椭圆C的标准方程为+=1.(2):设直线BM的斜率为k(k>0),则直线BM的方程为y=x﹣.在y=kx﹣中,令y=0,得x P=,而点Q是线段OP的中点,所以x Q=.所以直线BN的斜率k BN=k BQ==2k.联立,消去y,得(3+4k2)x2﹣8kx=0,解得x M=.用2k代k,得x N=.又=2,所以x N=2(x M﹣x N),得2x M=3x N,故2×==3×,又k>0,解得k=.所以直线BM的方程为y=x﹣19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N*都成立,求m的最小值;(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n=a n对任意+T的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.【解答】解:(1)由题意,可得a=(a n+d)(a n﹣d)+λd2,化简得(λ﹣1)d2=0,又d≠0,所以λ=1.(2)将a1=1,a2=2,a3=4,代入条件,可得4=1×4+λ,解得λ=0,所以a=a na n﹣1,所以数列{a n}是首项为1,公比q=2的等比数列,+1所以a n=2n﹣1.欲存在r∈[3,7],使得m•2n﹣1≥n﹣r,即r≥n﹣m•2n﹣1对任意n∈N*都成立,则7≥n﹣m•2n﹣1,所以m≥对任意n∈N*都成立.令b n=,则b n+1﹣b n=﹣=,<b n;当n=8时,b9=b8;当n<8时,b n+1>b n.所以当n>8时,b n+1所以b n的最大值为b9=b8=,所以m的最小值为;(3)因为数列{a n}不是常数列,所以T≥2,=a n恒成立,从而a3=a1,a4=a2,①若T=2,则a n+2所以,所以λ(a2﹣a1)2=0,又λ≠0,所以a2=a1,可得{a n}是常数列,矛盾.所以T=2不合题意.②若T=3,取a n=(*),满足a n+3=a n恒成立.由a22=a1a3+λ(a2﹣a1)2,得λ=7.则条件式变为a n2=a n+1a n﹣1+7.由22=1×(﹣3)+7,知a3k﹣12=a3k﹣2a3k+λ(a2﹣a1)2;由(﹣3)2=2×1+7,知a3k2=a3k﹣1a3k+1+λ(a2﹣a1)2;由12=2×(﹣3)+7,知a3k+12=a3k a3k+2+λ(a2﹣a1)2;所以,数列(*)适合题意.所以T的最小值为3.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b 的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.【解答】解:(1)由f(x)=lnx,得f(1)=0,又f′(x)=,所以f′(1)=1,当c=0时,g(x)=ax+,所以g′(x)=a﹣,所以g′(1)=a﹣b,因为函数f(x)与g(x)的图象在x=1处有相同的切线,所以,即,解得a=,b=﹣;(2)当x0>1时,则f(x0)>0,又b=3﹣a,设t=f(x0),则题意可转化为方程ax+﹣c=t(t>0)在(0,+∞)上有相异两实根x1,x2.即关于x的方程ax2﹣(c+t)x+(3﹣a)=0(t>0)在(0,+∞)上有相异两实根x1,x2.所以,得,所以c>2﹣t对t∈(0,+∞),a∈(0,3)恒成立.因为0<a<3,所以2≤2•=3(当且仅当a=时取等号),又﹣t<0,所以2﹣t的取值范围是(﹣∞,3),所以c≥3.故c的最小值为3.(3)当a=1时,因为函数f(x)与g(x)的图象交于A,B两点,所以,两式相减,得b=x1x2(1﹣),要证明x1x2﹣x2<b<x1x2﹣x1,即证x1x2﹣x2<x1x2(1﹣)<x1x2﹣x1,即证<<,即证<ln<,即证1﹣<ln<﹣1,令=t,则t>1,此时即证1﹣<lnt<t﹣1.令φ(t)=lnt+﹣1,所以φ′(t)=﹣=>0,所以当t>1时,函数φ(t)单调递增.又φ(1)=0,所以φ(t)=lnt+﹣1>0,即1﹣<lnt成立;再令m(t)=lnt﹣t+1,所以m′(t)=﹣1=<0,所以当t>1时,函数m(t)单调递减,又m(1)=0,所以m(t)=lnt﹣t+1<0,即lnt<t﹣1也成立.综上所述,实数x1,x2满足x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22.23.24四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)[选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.【解答】解:如图,连接AE,OE,因为直线DE与⊙O相切于点E,所以DE⊥OE,又因为AD⊥DE于D,所以AD∥OE,所以∠DAE=∠OEA,①在⊙O中,OE=OA,所以∠OEA=∠OAE,②…(5分)由①②得∠DAE=∠OAE,即∠DAE=∠FAE,又∠ADE=∠AFE,AE=AE,所以△ADE≌△AFE,所以DE=FE,又DE=4,所以FE=4,即E到直径AB的距离为4.…(10分)[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.【解答】解:设P(x0,y0)是圆x2+y2=1上任意一点,则=1,设点P(x0,y0)在矩阵M对应的变换下所得的点为Q(x,y),则=,即,解得,…(5分)代入=1,得=1,∴圆x2+y2=1在矩阵M的变换下所得的曲线方程为=1.…(10分)[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.【解答】解:直线ρcos(θ+)=1,转化为:,曲线ρ=r(r>0)转化为:x2+y2=r2,由于直线和圆相切,则:圆心到直线的距离d=.所以r=1.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.【解答】解:由柯西不等式,得[x2+()2][12+()2]≥(x•1+)2,即≥(x+y)2.而x2+3y2=1,所以(x+y)2,所以﹣,…(5分)由,得,所以当且仅当x=,y=时,(x+y)max=.所以当x+y取最大值时x值为.…(10分)25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.【解答】解:(1)因为ABCD是菱形,所以AC⊥BD.又OP⊥底面ABCD,以O为原点,直线OA,OB,OP分别为x轴,y轴,z轴,建立如图所示空间直角坐标系.则A(2,0,0),B(0,1,0),P(0,0,4),C(﹣2,0,0),M(﹣1,0,2).=(﹣2,0,4),=(01,﹣1,2),cos<,>===.故直线AP与BM所成角的余弦值为.…(5分)(2)=(﹣2,1,0),=(﹣1,﹣1,2).设平面ABM的一个法向量为=(x,y,z),则,令x=2,得=(2,4,3).又平面PAC的一个法向量为=(0,1,0),∴cos<>===.故平面ABM与平面PAC所成锐二面角的余弦值为.…(10分)26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.【解答】解:(1)由条件,nf(n)=C C C C①,在①中令n=1,得f(1)=1.在①中令n=2,得2f(2)=6,得f(2)=3.在①中令n=3,得3f(3)=30,故f(3)=10.(2)猜想f(n)=.要证猜想成立,只要证等式n=•+2•+…+n•成立.由(1+x)n=+x+x2+…+x n①,两边同时对x求导数,可得n(1+x)n﹣1=+2x+3x2+n x n﹣1②,把等式①和②相乘,可得n(1+x)2n﹣1=(+x+x2+…+x n)•(+2x+3x2+n x n﹣1)③.等式左边x n的系数为n,等式右边x n的系数为•+•2+•3+…+n•n=•+2•+3•+…+n•=C C C C,根据等式③恒成立,可得n=C C C C.故f(n)=成立.。
南京市、盐城市届高三年级第一次模拟考试数学试题及答案

南京市、盐城市2018届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上) 1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则A B =I ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ .3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 7.设函数1x x y e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值范围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ .9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值范围是 ▲ . 10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .时间(单位:分钟) 组距 50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 Read x If 0x > Then ln y x ← Else x y e ← End If Print y 第4题图11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =- 有四个不同的零点,则实数m 的取值范围是 ▲ .12.在平面直角坐标系xOy 中,若直线(33)y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =u u u r u u u r,则实数k 的最小值为 ▲ .13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分. 解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点.(1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB A C ⊥.16.(本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c 已知52c =. (1)若2C B =,求cos B 的值;(2)若AB AC CA CB ⋅=⋅u u u r u u u r u u u r u u u r ,求cos()4B π+的值.A第13题图ABCA 1B 1C 1MN第15题图有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧»EF,¼GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N 是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N 运动到点2处时,点Q的坐标为(,0)3. (1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =u u u r u u u u r 时,求直线BM 的方程.第17题-图甲 FH 第17题-图乙设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n …,且n N ∈,λ为常数.(1)若{}n a 是等差数列,且公差0d ≠,求λ的值;(2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-卪对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N ∈均成立.求所有满足条件的数列{}n a 中T 的最小值.20.(本小题满分16分)设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈). (1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值;(2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值;(3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.南京市、盐城市2018届高三年级第一次模拟考试数学附加题部分(本部分满分40分,考试时间30分钟)21.[选做题](在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)A .(选修4-1:几何证明选讲)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD 垂直DE 于点D . 若4DE =,求切点E 到直径AB 的距离EF .B .(选修4-2:矩阵与变换)已知矩阵 2 00 1⎡⎤=⎢⎥⎣⎦M ,求圆221x y +=在矩阵M 的变换下所得的曲线方程.C .(选修4-4:坐标系与参数方程)在极坐标系中,直线cos()13πρθ+=与曲线r ρ=(0r >)相切,求r 的值.D .(选修4-5:不等式选讲)已知实数,x y 满足2231x y +=,求当x y +取最大值时x 的值.A B E D F O · 第21(A)图[必做题](第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内) 22.(本小题满分10分)如图,四棱锥P ABCD -的底面ABCD 是菱形,AC 与BD 交于点O ,OP ⊥底面ABCD ,点M 为PC 中点,4,2,4AC BD OP ===.(1)求直线AP 与BM 所成角的余弦值;(2)求平面ABM 与平面PAC 所成锐二面角的余弦值.23.(本小题满分10分)已知n N *∈,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.(1)求()1,f ()2,f ()3f 的值;(2)试猜想()f n 的表达式(用一个组合数表示),并证明你的猜想.M BC D O P 第22题图南京市、盐城市2018届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分. 1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞ 8.34π 9.1(0,]4 10.4034 11.9[1,)412.3- 13.24 14.100 二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =,又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N .所以四边形1A NBM 是平行四边形,从而1//A M BN . ……………4分 又BN ⊄平面1A MC ,1A M ⊂平面1A MC ,所以BN ∥面1A MC . ……………6分 (2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC .又CA CB =,且M 是AB 的中点,所以CM AB ⊥.则由侧面11ABB A ⊥底面ABC ,侧面11ABB A I 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC ,得CM ⊥侧面11ABB A . ……………8分 又1AB ⊂侧面11ABB A ,所以1AB CM ⊥. ……………10分又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1A M MC M =I ,所以1AB ⊥平面1A MC . ……………12分又1AC ⊂平面1A MC ,所以11AB A C ⊥. ……………14分 16.解:(1)因为5c =,则由正弦定理,得5sin C B =. ……………2分 又2C B =,所以5sin 22B B =,即4sin cos 5B B B =. ……………4分 又B 是ABC ∆的内角,所以sin 0B >,故5cos 4B =. ……………6分(2)因为AB AC CA CB ⋅=⋅u u u r u u u r u u u r u u u r, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =. ……………10分从而222()35cos 25c c c a c b B ac +-+-===, ……………12分又0B π<<,所以24sin 1cos 5B B =-=.从而32422cos()cos cos sin sin 444525210B B B πππ+=-=⨯-⨯=-. ……………14分17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===,在Rt OET ∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2R MT OM OT =-=.从而2RBE MT ==,即22R BE ==. ……………2分 故所得柱体的底面积OEF OEF S S S ∆=-扇形22114sin120323R R ππ=-︒=- ……………4分又所得柱体的高4EG =,所以V S EG =⨯=163π-答:当BE 长为1分米时,折卷成的包装盒的容积为163π-. …………………6分(2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114sin120(323R R x ππ=-︒=.又所得柱体的高62EG x =-,所以V S EG =⨯=328(3)3x x π--+,其中03x <<. …………………10分令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=,解得2x =. …………………12分列表如下:所以当x =答:当BE 的长为2分米时,折卷成的包装盒的容积最大. …………………14分18.解:(1)由2NQ ,得直线NQ的方程为32y x = (2)分 令0x =,得点B 的坐标为(0,. 所以椭圆的方程为22213x y a +=. …………………4分 将点N 的坐标2213=,解得24a =. 所以椭圆C 的标准方程为22143x y +=.…………………8分 (2)方法一:设直线BM 的斜率为(0)k k >,则直线BM 的方程为y kx =-在y kx =0y =,得P x =,而点Q 是线段OP的中点,所以Q x = 所以直线BN 的斜率2BN BQk k k ===. ………………10分联立22143y kx x y ⎧=⎪⎨+=⎪⎩,消去y,得22(34)0k x +-=,解得M x =. 用2k 代k,得2316N x k =+. ………………12分又2DN NM =u u u r u u u u r ,所以2()N M N x x x =-,得23M N x x =. ………………14分故222334316k k ⨯=⨯++,又0k >,解得2k =. 所以直线BM的方程为2y x =. ………………16分 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为1y x =0y =,得P x =同理,得Q x =.而点Q 是线段OP 的中点,所以2P Q x x ==…………………10分 又2DN NM =u u u r u u u u r ,所以2122()x x x =-,得21203x x =>4=,解得2143y y =. …………………12分将21212343x x y y ⎧=⎪⎪⎨⎪=⎪⎩代入到椭圆C的方程中,得2211(41927x y +=. 又22114(1)3y x =-,所以214(1)319y -+=21120y +=,解得1y =1y =.又10x >,所以点M的坐标为(3M .……………14分 故直线BM的方程为y x =-. …………………16分 19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+,化简得2(1)0d λ-=,又0d ≠,所以1λ=. ………………4分 (2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=. ……6分欲存在[3,7]r ∈,使得12n m n r -⋅-…,即12n r n m --⋅…对任意*n N ∈都成立,则172n n m --⋅…,所以172n n m --…对任意*n N ∈都成立. ………………8分 令172n n n b --=,则11678222n n n n n n n n b b +-----=-=,所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>.所以n b 的最大值为981128b b ==,所以m 的最小值为1128. ………………10分(3)因为数列{}n a 不是常数列,所以2T ….①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩, 所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意. ………………12分②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立. ………………14分由2221321()a a a a a λ=+-,得7λ=. 则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-;由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-; 由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-.所以,数列(*)适合题意.所以T 的最小值为3. ………………16分20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,. 当0c =时,()b g x ax x =+,所以2()bg x a x'=-,所以(1)g a b '=-. ………………2分 因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩. ………………4分(2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =,则题意可转化为方程3(0)aax c t t x-+-=>在(0,)+∞上有相异两实根12,x x . ………………6分 即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a <<⎧⎪∆=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩,所以c t >对(0,),(0,3)t a ∈+∞∈恒成立. ………………8分因为03a <<,所以23=(当且仅当32a =时取等号), 又0t -<,所以t 的取值范围是(,3)-∞,所以3c …. 故c 的最小值为3. ………………10分 (3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x cx b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. ………………12分 要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--, 即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x x x x x -<<-. ………………14分 令21x t x =,则1t >,此时即证11ln 1t t t-<<-. 令1()ln 1t t t ϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t t ϕ=+->,即11ln t t-<成立;再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减,又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立.综上所述, 实数12,x x 满足122121x x x b x x x -<<-. ………………16分附加题答案21.(A )解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② ………………5分 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4. ………………10分(B )解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,ABE DF O · 第21(A)图设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即002x x y y =⎧⎨=⎩,解得0012x x y y⎧=⎪⎨⎪=⎩, ………………5分代入2201x y +=,得2214x y +=,即为所求的曲线方程. ………………10分 (C )解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系,由cos()13πρθ+=,得(cos cossin sin )133ππρθθ-=,得直线的直角坐标方程为20x --=. ………………5分曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.因为直线cos()13πρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. ……………10分(D)解:由柯西不等式,得22222[)][1(](133x x ++≥⨯+⨯, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y ≤+≤ ………………5分由1x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得2x y ⎧=⎪⎪⎨⎪=⎪⎩26x y ==时,max ()x y += 所以当x y +取最大值时x的值为2x =. ………………10分 22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系. 则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -.所以(2,0,4)AP =-u u u r ,(1,1,2)BM =--u u u u r,10AP BM ⋅=u u u r u u u u r ,||AP =u u u r ,||BM =u u u u r. 则cos ,6||||AP BM AP BM AP BM ⋅<>===u u u u ru u u r u u u u r u u u r u u u u r . 故直线AP 与BM 所成角的余弦值为6. ………5分 (2)(2,1,0)AB =-u u u r ,(1,1,2)BM =--u u u u r.设平面ABM 的一个法向量为(,,)n x y z =r,C第22题图则0n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u u r ,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =.得平面ABM 的一个法向量为(2,4,3)n =r.又平面PAC 的一个法向量为(0,1,0)OB =u u u r ,所以n r 4OB ⋅=u u u r,||n =r ||1OB =u u u r .则cos ,||||n OB n OB n OB ⋅<>===r u u u rr u u u r r u u ur 故平面ABM 与平面PAC………………10分23.解:(1)由条件,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+ ①,在①中令1n =,得()011111f C C ==. ………………1分 在①中令2n =,得()011222222226f C C C C =+=,得()23f =. ………………2分 在①中令3n =,得()011223333333332330f C C C C C C =++=,得()310f =. ………………3分(2)猜想()f n =21nn C -(或()f n =121n n C --). ………………5分 欲证猜想成立,只要证等式011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+成立.方法一:当1n =时,等式显然成立,当2n …时,因为11!!(1)!==!()!(1)!()!(1)!()!rr n n r n n n rC n nC r n r r n r r n r --⨯-=⨯=-----(),故11111()r r r r r r n n n n n n rC C rC C nC C -----==.故只需证明00111111211111n r r n n n n n n n n n n n nC nC C nC C nC C nC C ---------=++⋅⋅⋅++⋅⋅⋅+. 即证00111111211111n r r n n n n n n n n n n nC C C C C C C C C ---------=++⋅⋅⋅++⋅⋅⋅+. 而11r n r n n C C --+=,故即证0111111211111n n n r n r n n n n n n n n n n C C C C C C C C C ---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21n n C -.而右边1(1)(1)n n x x -++()()01221101221111n n n n n n n n n n n n C C x C x C xC C x C x C x ------=++++++++L L , 所以nx 的系数为01111111111n n r n r n n n n n n n n n C C C C C C C C ---+-----++⋅⋅⋅++⋅⋅⋅+.由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立.综上,()21n n f n C -=成立. ………………10分 方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n 的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1r n rn nC C --,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111n n n n n n n n n C C C C C C -----+++L . 另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21n n C -.故0111121111n n n n n n n n n n n C C C C C C C ------=++L ,即②成立. 余下同方法一. ………………10分方法三:由二项式定理,得0122(1)n n nn n n n x C C x C x C x +=++++L ③.两边求导,得112111(1)2n r r n n n n n n n x C C x rC x nC x ---+=+++++L L ④.③×④, 得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++L L L ⑤.左边n x 的系数为21nn nC -.右边nx 的系数为121112n n r n r n n n n n n n n n C C C C rC C nC C --+++⋅⋅⋅++⋅⋅⋅+1021112r r n n n n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+0112112r r n n n n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.由⑤恒成立,可得011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+.故()21n n f n C -=成立. ………………10分。
南京市、盐城市届高三级第一次模拟考试数学试题及答案

南京市、盐城市2018届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上) 1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则A B =I ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ .3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 7.设函数1x x y e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值范围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ .9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值范围是 ▲ . 10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .时间(单位:分钟) 组距 50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 Read x If 0x > Then ln y x ← Else x y e ← End If Print y 第4题图11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =- 有四个不同的零点,则实数m 的取值范围是 ▲ .12.在平面直角坐标系xOy 中,若直线(33)y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =u u u r u u u r,则实数k 的最小值为 ▲ .13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分. 解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点.(1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB A C ⊥.16.(本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c 已知52c =. (1)若2C B =,求cos B 的值;(2)若AB AC CA CB ⋅=⋅u u u r u u u r u u u r u u u r ,求cos()4B π+的值.A第13题图ABCA 1B 1C 1MN第15题图有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧»EF,¼GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N 是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N 运动到点2处时,点Q的坐标为(,0)3. (1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =u u u r u u u u r 时,求直线BM 的方程.第17题-图甲 FH 第17题-图乙设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n …,且n N ∈,λ为常数.(1)若{}n a 是等差数列,且公差0d ≠,求λ的值;(2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-卪对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N ∈均成立.求所有满足条件的数列{}n a 中T 的最小值.20.(本小题满分16分)设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈). (1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值;(2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值;(3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.南京市、盐城市2018届高三年级第一次模拟考试数学附加题部分(本部分满分40分,考试时间30分钟)21.[选做题](在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)A .(选修4-1:几何证明选讲)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD 垂直DE 于点D . 若4DE =,求切点E 到直径AB 的距离EF .B .(选修4-2:矩阵与变换)已知矩阵 2 00 1⎡⎤=⎢⎥⎣⎦M ,求圆221x y +=在矩阵M 的变换下所得的曲线方程.C .(选修4-4:坐标系与参数方程)在极坐标系中,直线cos()13πρθ+=与曲线r ρ=(0r >)相切,求r 的值.D .(选修4-5:不等式选讲)已知实数,x y 满足2231x y +=,求当x y +取最大值时x 的值.A B E D F O · 第21(A)图[必做题](第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内) 22.(本小题满分10分)如图,四棱锥P ABCD -的底面ABCD 是菱形,AC 与BD 交于点O ,OP ⊥底面ABCD ,点M 为PC 中点,4,2,4AC BD OP ===.(1)求直线AP 与BM 所成角的余弦值;(2)求平面ABM 与平面PAC 所成锐二面角的余弦值.23.(本小题满分10分)已知n N *∈,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.(1)求()1,f ()2,f ()3f 的值;(2)试猜想()f n 的表达式(用一个组合数表示),并证明你的猜想.M BC D O P 第22题图南京市、盐城市2018届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分. 1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞ 8.34π 9.1(0,]4 10.4034 11.9[1,)412.3- 13.24 14.100 二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =,又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N .所以四边形1A NBM 是平行四边形,从而1//A M BN . ……………4分 又BN ⊄平面1A MC ,1A M ⊂平面1A MC ,所以BN ∥面1A MC . ……………6分 (2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC .又CA CB =,且M 是AB 的中点,所以CM AB ⊥.则由侧面11ABB A ⊥底面ABC ,侧面11ABB A I 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC ,得CM ⊥侧面11ABB A . ……………8分 又1AB ⊂侧面11ABB A ,所以1AB CM ⊥. ……………10分又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1A M MC M =I ,所以1AB ⊥平面1A MC . ……………12分又1AC ⊂平面1A MC ,所以11AB A C ⊥. ……………14分 16.解:(1)因为5c =,则由正弦定理,得5sin C B =. ……………2分 又2C B =,所以5sin 22B B =,即4sin cos 5B B B =. ……………4分 又B 是ABC ∆的内角,所以sin 0B >,故5cos 4B =. ……………6分(2)因为AB AC CA CB ⋅=⋅u u u r u u u r u u u r u u u r, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =. ……………10分从而222()35cos 25c c c a c b B ac +-+-===, ……………12分又0B π<<,所以24sin 1cos 5B B =-=.从而32422cos()cos cos sin sin 444525210B B B πππ+=-=⨯-⨯=-. ……………14分17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===,在Rt OET ∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2R MT OM OT =-=. 从而2RBE MT ==,即22R BE ==. ……………2分 故所得柱体的底面积OEF OEF S S S ∆=-扇形22114sin120323R R ππ=-︒=-. ……………4分又所得柱体的高4EG =,所以V S EG =⨯=163π-答:当BE 长为1分米时,折卷成的包装盒的容积为163π-. …………………6分(2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114sin120(323R R x ππ=-︒=.又所得柱体的高62EG x =-,所以V S EG =⨯=328(3)3x x π--+,其中03x <<. …………………10分令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=,解得2x =. …………………12分列表如下:所以当x =答:当BE 的长为2分米时,折卷成的包装盒的容积最大. …………………14分18.解:(1)由N Q,得直线NQ的方程为32y x =…………………2分令0x =,得点B 的坐标为(0,. 所以椭圆的方程为22213x y a +=. …………………4分 将点N 的坐标2代入,得222213a +=,解得24a =. 所以椭圆C 的标准方程为22143x y +=. (8)分 (2)方法一:设直线BM 的斜率为(0)k k >,则直线BM 的方程为y kx =-在y kx =0y =,得P x k =,而点Q 是线段OP 的中点,所以2Q x k=.所以直线BN的斜率22BN BQ k k k k===. ………………10分联立22143y kx x y ⎧=⎪⎨+=⎪⎩,消去y,得22(34)0k x +-=,解得234M x k =+. 用2k 代k,得N x =………………12分又2DN NM =u u u r u u u u r,所以2()N M N x x x =-,得23M N x x =. ………………14分故23=0k >,解得k = 所以直线BM的方程为y x =. ………………16分 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为11y y x x +=0y =,得P x =同理,得Q x =.而点Q 是线段OP 的中点,所以2P Q x x ==…………………10分 又2DN NM =u u u r u u u u r ,所以2122()x x x =-,得21203x x =>4=,解得21433y y =+. …………………12分将21212343x x y y ⎧=⎪⎪⎨⎪=⎪⎩代入到椭圆C的方程中,得2119x +=. 又22114(1)3y x =-,所以21214(1)(431927y y -++=21120y +=,解得1y =13y =.又10x >,所以点M的坐标为(33M .……………14分 故直线BM的方程为y x =-. …………………16分 19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+,化简得2(1)0d λ-=,又0d ≠,所以1λ=. ………………4分 (2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=. ……6分欲存在[3,7]r ∈,使得12n m n r -⋅-…,即12n r n m --⋅…对任意*n N ∈都成立, 则172n n m --⋅…,所以172n n m --…对任意*n N ∈都成立. ………………8分 令172n n n b --=,则11678222n n n n n n n n b b +-----=-=,所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>.所以n b 的最大值为981128b b ==,所以m 的最小值为1128. ………………10分(3)因为数列{}n a 不是常数列,所以2T ….①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩,所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意. ………………12分②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立. ………………14分由2221321()a a a a a λ=+-,得7λ=. 则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-; 由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-; 由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-.所以,数列(*)适合题意.所以T 的最小值为3. ………………16分20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,. 当0c =时,()b g x ax x =+,所以2()bg x a x'=-,所以(1)g a b '=-. ………………2分 因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩. ………………4分(2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =,则题意可转化为方程3(0)aax c t t x-+-=>在(0,)+∞上有相异两实根12,x x . ………………6分 即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a <<⎧⎪∆=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩,所以c t >对(0,),(0,3)t a ∈+∞∈恒成立. ………………8分因为03a <<,所以23=(当且仅当32a =时取等号), 又0t -<,所以t 的取值范围是(,3)-∞,所以3c …. 故c 的最小值为3. ………………10分 (3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x cx b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. ………………12分 要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--, 即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x x x x x -<<-. ………………14分 令21x t x =,则1t >,此时即证11ln 1t t t-<<-. 令1()ln 1t t t ϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t t ϕ=+->,即11ln t t-<成立;再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减,又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立.综上所述, 实数12,x x 满足122121x x x b x x x -<<-. ………………16分附加题答案21.(A )解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② ………………5分 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4. ………………10分(B )解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,ABE DF O · 第21(A)图设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即002x x y y =⎧⎨=⎩,解得0012x x y y⎧=⎪⎨⎪=⎩, ………………5分代入2201x y +=,得2214x y +=,即为所求的曲线方程. ………………10分 (C )解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系,由cos()13πρθ+=,得(cos cossin sin )133ππρθθ-=,得直线的直角坐标方程为20x --=. ………………5分曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.因为直线cos()13πρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. ……………10分(D)解:由柯西不等式,得22222[)][1(](133x x ++≥⨯⨯, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y ≤+≤ ………………5分由1x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得2x y ⎧=⎪⎪⎨⎪=⎪⎩26x y ==时,max ()x y += 所以当x y +取最大值时x的值为2x =. ………………10分 22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系. 则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -.所以(2,0,4)AP =-u u u r ,(1,1,2)BM =--u u u u r,10AP BM ⋅=u u u r u u u u r ,||AP =u u u r ,||BM =u u u u r. 则cos ,6||||AP BM AP BM AP BM ⋅<>===u u u u ru u u r u u u u r u u u r u u u u r . 故直线AP 与BM 所成角的余弦值为6. ………5分 (2)(2,1,0)AB =-u u u r ,(1,1,2)BM =--u u u u r.设平面ABM 的一个法向量为(,,)n x y z =r,C第22题图则0n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u u r ,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =.得平面ABM 的一个法向量为(2,4,3)n =r.又平面PAC 的一个法向量为(0,1,0)OB =u u u r ,所以n r 4OB ⋅=u u u r,||n =r ||1OB =u u u r .则cos ,||||n OB n OB n OB ⋅<>===r u u u rr u u u r r u u ur 故平面ABM 与平面PAC………………10分23.解:(1)由条件,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+ ①,在①中令1n =,得()011111f C C ==. ………………1分 在①中令2n =,得()011222222226f C C C C =+=,得()23f =. ………………2分 在①中令3n =,得()011223333333332330f C C C C C C =++=,得()310f =. ………………3分(2)猜想()f n =21nn C -(或()f n =121n n C --). ………………5分 欲证猜想成立,只要证等式011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+成立.方法一:当1n =时,等式显然成立,当2n …时,因为11!!(1)!==!()!(1)!()!(1)!()!rr n n r n n n rC n nC r n r r n r r n r --⨯-=⨯=-----(),故11111()r r r r r r n n n n n n rC C rC C nC C -----==.故只需证明00111111211111n r r n n n n n n n n n n n nC nC C nC C nC C nC C ---------=++⋅⋅⋅++⋅⋅⋅+. 即证00111111211111n r r n n n n n n n n n n n C C C C C C C C C ---------=++⋅⋅⋅++⋅⋅⋅+.而11r n r n n C C --+=,故即证0111111211111n n n r n r n n n n n n n n n n C C C C C C C C C ---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21n n C -.而右边1(1)(1)n n x x -++()()01221101221111n n n n n n n n n n n n C C x C x C xC C x C x C x ------=++++++++L L , 所以nx 的系数为01111111111n n r n r n n n n n n n n n C C C C C C C C ---+-----++⋅⋅⋅++⋅⋅⋅+.由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立.综上,()21n n f n C -=成立. ………………10分 方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n 的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1r n rn nC C --,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111n n n n n n n n n C C C C C C -----+++L . 另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21n n C -.故0111121111n n n n n n n n n n n C C C C C C C ------=++L ,即②成立. 余下同方法一. ………………10分方法三:由二项式定理,得0122(1)n n nn n n n x C C x C x C x +=++++L ③.两边求导,得112111(1)2n r r n n n n n n n x C C x rC x nC x ---+=+++++L L ④.③×④, 得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++L L L ⑤.左边n x 的系数为21nn nC -.右边nx 的系数为121112n n r n r n n n n n n n n n C C C C rC C nC C --+++⋅⋅⋅++⋅⋅⋅+1021112r r n n n n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+0112112r r n n n n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.由⑤恒成立,可得011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+.故()21n n f n C -=成立. ………………10分。
南京市、盐城市2018届高三年级第一次模拟考试数学试卷与答案

市、市2018届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的、号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上) 1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则A B =I ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ .3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 7.设函数1x x y e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ . 9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值围是 ▲ .10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .时间(单位:分钟)50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 第4题图11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =- 有四个不同的零点,则实数m 的取值围是 ▲ .12.在平面直角坐标系xOy 中,若直线(33)y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =u u u r u u u r,则实数k 的最小值为 ▲ .13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分. 解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域) 15.(本小题满分14分)如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点.(1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB A C ⊥.16.(本小题满分14分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c 已知5c =. (1)若2C B =,求cos B 的值;(2)若AB AC CA CB ⋅=⋅u u u r u u u r u u u r u u u r ,求cos()4B π+的值.A第13题图ABCA 1B 1C 1MN第15题图有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧»EF,¼GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N 是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N 运动到点2处时,点Q的坐标为(,0)3. (1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =u u u r u u u u r时,求直线BM 的方程.第17题-图甲 F H 第17题-图乙设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n …,且n N ∈,λ为常数.(1)若{}n a 是等差数列,且公差0d ≠,求λ的值;(2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-卪对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N ∈均成立.求所有满足条件的数列{}n a 中T 的最小值.20.(本小题满分16分)设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈). (1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值;(2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值;(3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.市、市2018届高三年级第一次模拟考试数学附加题部分(本部分满分40分,考试时间30分钟)21.[选做题](在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域)A .(选修4-1:几何证明选讲)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD 垂直DE 于点D . 若4DE =,求切点E 到直径AB 的距离EF .B .(选修4-2:矩阵与变换)已知矩阵 2 00 1⎡⎤=⎢⎥⎣⎦M ,求圆221x y +=在矩阵M 的变换下所得的曲线方程.C .(选修4-4:坐标系与参数方程)在极坐标系中,直线cos()13πρθ+=与曲线r ρ=(0r >)相切,求r 的值.D .(选修4-5:不等式选讲)已知实数,x y 满足2231x y +=,求当x y +取最大值时x 的值.A B ED F O· 第21(A)图[必做题](第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域) 22.(本小题满分10分)如图,四棱锥P ABCD -的底面ABCD 是菱形,AC 与BD 交于点O ,OP ⊥底面ABCD ,点M 为PC 中点,4,2,4AC BD OP ===.(1)求直线AP 与BM 所成角的余弦值;(2)求平面ABM 与平面PAC 所成锐二面角的余弦值.23.(本小题满分10分)已知n N *∈,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.(1)求()1,f ()2,f ()3f 的值;(2)试猜想()f n 的表达式(用一个组合数表示),并证明你的猜想.M B C D O P 第22题图市、市2018届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分. 1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞ 8.34π 9.1(0,]4 10.4034 11.9[1,)412.3.24 14.100 二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域. 15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =,又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N .所以四边形1A NBM 是平行四边形,从而1//A M BN . ……………4分 又BN ⊄平面1A MC ,1A M ⊂平面1A MC ,所以BN ∥面1A MC . ……………6分 (2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC .又CA CB =,且M 是AB 的中点,所以CM AB ⊥.则由侧面11ABB A ⊥底面ABC ,侧面11ABB A I 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC ,得CM ⊥侧面11ABB A . ……………8分 又1AB ⊂侧面11ABB A ,所以1AB CM ⊥. ……………10分又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1A M MC M =I ,所以1AB ⊥平面1A MC . ……………12分又1AC ⊂平面1A MC ,所以11AB A C ⊥. ……………14分 16.解:(1)因为5c =,则由正弦定理,得5sin C B =. ……………2分 又2C B =,所以5sin 22B B =,即4sin cos 5B B B =. ……………4分 又B 是ABC ∆的角,所以sin 0B >,故5cos 4B =. ……………6分(2)因为AB AC CA CB ⋅=⋅u u u r u u u r u u u r u u u r, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =. ……………10分从而222()35cos 25c c c a c b B ac +-+-===, ……………12分又0B π<<,所以24sin 1cos 5B B =-=.从而32422cos()cos cos sin sin 444525210B B B πππ+=-=⨯-⨯=-. ……………14分17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===,在Rt OET ∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2R MT OM OT =-=.从而2RBE MT ==,即22R BE ==. ……………2分 故所得柱体的底面积OEF OEF S S S ∆=-扇形22114sin120323R R ππ=-︒=-分又所得柱体的高4EG =,所以V S EG =⨯=163π-答:当BE 长为1分米时,折卷成的包装盒的容积为163π-分(2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114sin120(323R R x ππ=-︒=.又所得柱体的高62EG x =-,所以V S EG =⨯=328(3)3x x π--+,其中03x <<. …………………10分令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=,解得2x =. …………………12分列表如下:所以当x =答:当BE 的长为2分米时,折卷成的包装盒的容积最大. …………………14分18.解:(1)由2N Q ,得直线NQ 的方程为32y x = …………………2分 令0x =,得点B 的坐标为(0,.所以椭圆的方程为22213x y a +=. …………………4分 将点N的坐标2213=,解得24a =. 所以椭圆C 的标准方程为22143x y +=. …………………8分 (2)方法一:设直线BM 的斜率为(0)k k >,则直线BM 的方程为y kx =-在y kx =0y =,得P x =,而点Q 是线段OP 的中点,所以Q x = 所以直线BN 的斜率2BN BQk k k ===. ………………10分联立22143y kx x y ⎧=⎪⎨+=⎪⎩,消去y,得22(34)0k x +-=,解得M x =. 用2k 代k,得2316N x k =+. ………………12分又2DN NM =u u u r u u u u r ,所以2()N M N x x x =-,得23M N x x =. ………………14分故222334316k k ⨯=⨯++,又0k >,解得2k =. 所以直线BM的方程为2y x =. ………………16分 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为1y x =0y =,得P x =同理,得Q x =.而点Q 是线段OP 的中点,所以2P Q x x ==…………………10分 又2DN NM =u u u r u u u u r ,所以2122()x x x =-,得21203x x =>4=,解得2143y y =. …………………12分将21212343x x y y ⎧=⎪⎪⎨⎪=⎪⎩代入到椭圆C的方程中,得2211(41927x y ++=. 又22114(1)3y x =-,所以214(1)319y -+=21120y +=,解得1y =1y =.又10x >,所以点M的坐标为(3M .……………14分 故直线BM的方程为y x =-. …………………16分 19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+,化简得2(1)0d λ-=,又0d ≠,所以1λ=. ………………4分 (2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=. ……6分欲存在[3,7]r ∈,使得12n m n r -⋅-…,即12n r n m --⋅…对任意*n N ∈都成立,则172n n m --⋅…,所以172n n m --…对任意*n N ∈都成立. ………………8分 令172n n n b --=,则11678222n n n n n n n n b b +-----=-=,所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>.所以n b 的最大值为981128b b ==,所以m 的最小值为1128. ………………10分(3)因为数列{}n a 不是常数列,所以2T ….①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩, 所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意. ………………12分②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立. ………………14分由2221321()a a a a a λ=+-,得7λ=. 则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-;由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-; 由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-.所以,数列(*)适合题意.所以T 的最小值为3. ………………16分20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,. 当0c =时,()b g x ax x =+,所以2()bg x a x'=-,所以(1)g a b '=-. ………………2分 因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩. ………………4分(2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =,则题意可转化为方程3(0)aax c t t x-+-=>在(0,)+∞上有相异两实根12,x x . ………………6分 即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a <<⎧⎪∆=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩,所以c t >对(0,),(0,3)t a ∈+∞∈恒成立. ………………8分因为03a <<,所以23=(当且仅当32a =时取等号), 又0t -<,所以t 的取值围是(,3)-∞,所以3c …. 故c 的最小值为3. ………………10分 (3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x cx b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. ………………12分 要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--, 即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x x x x x -<<-. ………………14分 令21x t x =,则1t >,此时即证11ln 1t t t-<<-. 令1()ln 1t t t ϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t t ϕ=+->,即11ln t t-<成立;再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减,又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立.综上所述, 实数12,x x 满足122121x x x b x x x -<<-. ………………16分附加题答案21.(A )解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② ………………5分 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4. ………………10分(B )解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,ABE DF O · 第21(A)图设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即002x x y y =⎧⎨=⎩,解得0012x x y y⎧=⎪⎨⎪=⎩, ………………5分代入2201x y +=,得2214x y +=,即为所求的曲线方程. ………………10分 (C )解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系,由cos()13πρθ+=,得(cos cossin sin )133ππρθθ-=,得直线的直角坐标方程为20x --=. ………………5分曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.因为直线cos()13πρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. ……………10分(D)解:由柯西不等式,得22222[)][1(](1)33x x ++≥⨯+⨯, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y ≤+≤ ………………5分由1x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得2x y ⎧=⎪⎪⎨⎪=⎪⎩26x y ==时,max ()x y += 所以当x y +取最大值时x的值为2x =. ………………10分 22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系.则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -.所以(2,0,4)AP =-u u u r ,(1,1,2)BM =--u u u u r,10AP BM ⋅=u u u r u u u u r ,||AP =u u u r ,||BM =u u u u r. 则cos ,6||||AP BM AP BM AP BM ⋅<>===u u u u ru u u r u u u u r u u u r u u u u r . 故直线AP 与BM 所成角的余弦值为6. ………5分 (2)(2,1,0)AB =-u u u r ,(1,1,2)BM =--u u u u r.设平面ABM 的一个法向量为(,,)n x y z =r,C第22题图则0n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u u r ,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =.得平面ABM 的一个法向量为(2,4,3)n =r.又平面PAC 的一个法向量为(0,1,0)OB =u u u r ,所以n r 4OB ⋅=u u u r,||n =r ||1OB =u u u r .则cos ,||||n OB n OB n OB ⋅<>===r u u u rr u u u r r u u ur 故平面ABM 与平面PAC………………10分23.解:(1)由条件,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+ ①,在①中令1n =,得()011111f C C ==. ………………1分 在①中令2n =,得()011222222226f C C C C =+=,得()23f =. ………………2分 在①中令3n =,得()011223333333332330f C C C C C C =++=,得()310f =. ………………3分(2)猜想()f n =21nn C -(或()f n =121n n C --). ………………5分 欲证猜想成立,只要证等式011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+成立.方法一:当1n =时,等式显然成立,当2n …时,因为11!!(1)!==!()!(1)!()!(1)!()!rr n n r n n n rC n nC r n r r n r r n r --⨯-=⨯=-----(),故11111()r r r r r r n n n n n n rC C rC C nC C -----==.故只需证明00111111211111n r r n n n n n n n n n n n nC nC C nC C nC C nC C ---------=++⋅⋅⋅++⋅⋅⋅+. 即证00111111211111n r r n n n n n n n n n n nC C C C C C C C C ---------=++⋅⋅⋅++⋅⋅⋅+. 而11r n r n n C C --+=,故即证0111111211111n n n r n r n n n n n n n n n n C C C C C C C C C ---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21n n C -.而右边1(1)(1)n n x x -++()()01221101221111n n n n n n n n n n n n C C x C x C xC C x C x C x ------=++++++++L L , 所以nx 的系数为01111111111n n r n r n n n n n n n n n C C C C C C C C ---+-----++⋅⋅⋅++⋅⋅⋅+.由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立.综上,()21n n f n C -=成立. ………………10分 方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n 的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1r n rn nC C --,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111n n n n n n n n n C C C C C C -----+++L . 另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21n n C -.故0111121111n n n n n n n n n n n C C C C C C C ------=++L ,即②成立. 余下同方法一. ………………10分方法三:由二项式定理,得0122(1)n n nn n n n x C C x C x C x +=++++L ③.两边求导,得112111(1)2n r r n n n n n n n x C C x rC x nC x ---+=+++++L L ④.③×④, 得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++L L L ⑤.左边n x 的系数为21nn nC -.右边nx 的系数为121112n n r n r n n n n n n n n n C C C C rC C nC C --+++⋅⋅⋅++⋅⋅⋅+1021112r r n n n n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+0112112r r n n n n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.由⑤恒成立,可得011211212n r r n nn n n n n n n n n nC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+.故()21n n f n C -=成立. ………………10分。
南京、盐城2018届高三第一次模拟考数学
南京、盐城2018届高三第一次模拟考数 学一、填空题1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则A B =I ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ . 3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 7.设函数1x x y e a e=+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值范围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ .9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值范围是 ▲ . 10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =-有四个不同的零点,则实数m 的取值范围是 ▲ .12.在平面直角坐标系xOy中,若直线(y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =,则实数k 的最小值为 ▲ .13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则CD AB ⋅的最大值为 ▲ . 14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,时间(单位:分钟)50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 第4题图第13题图则实数k 的最小值为 ▲ .二、解答题 15.如图所示,在直三棱柱111ABC A B C -中,CA CB =,点,M N 分别是11,AB A B 的中点. (1)求证:BN ∥平面1A MC ; (2)若11A M AB ⊥,求证:11AB AC ⊥. 16.在ABC ∆中,角,,A B C 的对边分别为,,,a b c已知2c =. (1)若2C B =,求cos B 的值;(2)若AB AC CA CB ⋅=⋅ ,求cos()4B π+的值.17.有一矩形硬纸板材料(厚度忽略不计),一边AB 长为6分米,另一边足够长.现从中截取矩形ABCD (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好..能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O 为圆心、120EOF ∠=︒的扇形,且弧»EF,¼GH 分别与边BC ,AD 相切于点M ,N . (1)当BE 长为1分米时,求折卷成的包装盒的容积;(2)当BE 的长是多少分米时,折卷成的包装盒的容积最大?ABC A 1B 1C 1MN第15题图第17题-图甲F第17题-图乙18.如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ,点,M N是椭圆上异于点B 的动点,直线,BM BN 分别与x 轴交于点,P Q ,且点Q 是线段OP 的中点.当点N运动到点处时,点Q的坐标为. (1)求椭圆C 的标准方程;(2)设直线MN 交y 轴于点D ,当点,M N 均在y 轴右侧,且2DN NM =时,求直线BM 的方程.19.设数列{}n a 满足221121()n n n a a a a a λ+-=+-,其中2n …,且n N ∈,λ为常数. (1)若{}n a 是等差数列,且公差0d ≠,求λ的值;(2)若1231,2,4a a a ===,且存在[3,7]r ∈,使得n m a n r ⋅-卪对任意的*n N ∈都成立,求m 的最小值;(3)若0λ≠,且数列{}n a 不是常数列,如果存在正整数T ,使得n T n a a +=对任意的*n N ∈均成立. 求所有满足条件的数列{}n a 中T 的最小值.20.设函数()ln f x x =,()bg x ax c x=+-(,,a b c R ∈). (1)当0c =时,若函数()f x 与()g x 的图象在1x =处有相同的切线,求,a b 的值; (2)当3b a =-时,若对任意0(1,)x ∈+∞和任意(0,3)a ∈,总存在不相等的正实数12,x x ,使得120()()()g x g x f x ==,求c 的最小值; (3)当1a =时,设函数()y f x =与()y g x =的图象交于11(,),A x y 2212(,)()B x y x x <两点.求证:122121x x x b x x x -<<-.南京、盐城2018届高三第一次模拟考数学附加题部分(本部分满分40分,考试时间30分钟)21.[选做题](在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)A .(选修4-1:几何证明选讲)如图,已知AB 为⊙O 的直径,直线DE 与⊙O 相切于点E ,AD 垂直DE 于点D . 若4DE =,求切点E 到直径AB 的距离EF .B .(选修4-2:矩阵与变换)已知矩阵 2 00 1⎡⎤=⎢⎥⎣⎦M ,求圆221x y +=在矩阵M 的变换下所得的曲线方程.C .(选修4-4:坐标系与参数方程)在极坐标系中,直线cos()13πρθ+=与曲线r ρ=(0r >)相切,求r 的值.D .(选修4-5:不等式选讲)已知实数,x y 满足2231x y +=,求当x y +取最大值时x 的值.A B ED F O · 第21(A)图[必做题](第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内) 22.(本小题满分10分)如图,四棱锥P ABCD -的底面ABCD 是菱形,AC 与BD 交于点O ,OP ⊥底面ABCD ,点M 为PC 中点,4,2,4AC BD OP ===. (1)求直线AP 与BM 所成角的余弦值;(2)求平面ABM 与平面PAC 所成锐二面角的余弦值.23.(本小题满分10分)已知n N *∈,()0112112r r n n n n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.(1)求()1,f ()2,f ()3f 的值;(2)试猜想()f n 的表达式(用一个组合数表示),并证明你的猜想.M CD O P 第22题图南京、盐城2018届高三第一次模拟考数学参考答案一、填空题:本大题共14小题,每小题5分,计70分.1.{}1 2.1 3.1200 4.1 5.236.6 7.(,2]-∞8.34π 9.1(0,]4 10.4034 11.9[1,)412. 13.24 14.100二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.证明:(1)因为111ABC A B C -是直三棱柱,所以11//AB A B ,且11AB A B =,又点,M N 分别是11,AB A B 的中点,所以1MB A N =,且1//MB A N . 所以四边形1A NBM是平行四边形,从而1//A M BN . ……………4分又BN ⊄平面1A M C ,1A M ⊂平面1A M C ,所以BN∥面1A MC . ……………6分(2)因为111ABC A B C -是直三棱柱,所以1AA ⊥底面ABC ,而1AA ⊂侧面11ABB A ,所以侧面11ABB A ⊥底面ABC .又CA CB =,且M 是AB 的中点,所以CM AB ⊥.则由侧面11ABB A ⊥底面ABC ,侧面11ABB A 底面ABC AB =,CM AB ⊥,且CM ⊂底面ABC ,得CM ⊥侧面11ABB A . ……………8分又1AB ⊂侧面11ABB A ,所以1AB CM ⊥. ……………10分又11AB A M ⊥,1,A M MC ⊂平面1A MC ,且1AM MC M = , 所以1AB ⊥平面1A M C . ……………12分 又1AC ⊂平面1A M C ,所以11AB AC ⊥. ……………14分16.解:(1)因为2c =,则由正弦定理,得sin 2C B =. ……………2分又2C B=,所以s in 2s i nB B =,即4sn c o s 5s i nB B =. ……………4分又B是ABC ∆的内角,所以s i n B >,故cos 4B =. ……………6分 (2)因为AB AC CA CB ⋅=⋅, 所以cos cos cb A ba C =,则由余弦定理,得222222b c a b a c +-=+-,得a c =. ……………10分 从而223cos 25a c bB ac+-===, (12)分又0B π<<,所以4sin 5B ==. 从而3c o 44B Bππ+=. ……………14分17.解:(1)在图甲中,连接MO 交EF 于点T .设OE OF OM R ===,在Rt OET∆中,因为1602EOT EOF ∠=∠=︒,所以2ROT =,则2RM T O MO T =-=. 从而2R B EMT==,即22R BE ==. ……………2分故所得柱体的底面积OEF OEF S S S ∆=-扇形22114sin120323R R ππ=-︒=. ……………4分又所得柱体的高4EG =,所以V S EG =⨯=163π-答:当BE 长为1分米时,折卷成的包装盒的容积为163π-. …………………6分 (2)设BE x =,则2R x =,所以所得柱体的底面积OEF OEF S S S ∆=-扇形222114sin120(323R R x ππ=-︒=-.又所得柱体的高62EG x =-,所以V S =⨯=328(3)3x x π--+,其中03x <<. …………………10分令32()3,(0,3)f x x x x =-+∈,则由2()363(2)0f x x x x x '=-+=--=,解得2x =. (12)E分答:当BE的长为2分米时,折卷成的包装盒的容积最大.…………………14分18.解:(1)由2N Q,得直线NQ的方程为32y x=…………………2分令x=,得点B的坐标为(0,.所以椭圆的方程为22213x ya+=.…………………4分将点N的坐标22213+=,解得24a=.所以椭圆C的标准方程为22143xy+=.…………………8分(2)方法一:设直线BM的斜率为(0)k k>,则直线BM的方程为y kx=在y kx=0y=,得Pxk=,而点Q是线段OP的中点,所以2Qxk=.所以直线BN的斜率2BN BQk k k===.………………10分联立22143y kxx y⎧=-⎪⎨+=⎪⎩,消去y,得22(34)0k x+-=,解得Mx=.用2k代k,得2163316Nxk=+.………………12分又2DN NM=,所以2(N M Nx x x=-,得23M Nx x=.………………14分故222334316k k⨯=⨯++,又0k>,解得2k=.所以直线BM的方程为y x =. ………………16分 方法二:设点,M N 的坐标分别为1122(,),(,)x y x y .由(0,B ,得直线BN的方程为1y x =0y =,得P x =.同理,得Q x =.而点Q 是线段OP的中点,所以2P Qx x =,故=. …………………10分 又2DN NM = ,所以2122()x x x =-,得21203x x =>4=,解得2143y y =. …………………12分将212123433x x y y ⎧=⎪⎪⎨⎪=+⎪⎩代入到椭圆C的方程中,得2211(41927x y ++=.又22114(1)3y x =-,所以214(1)319y -=21120y +=,解得1y =(舍)或1y =.又10x >,所以点M 的坐标为(3M .……………14分故直线BM 的方程为y x =. …………………16分 19.解:(1)由题意,可得22()()n n n a a d a d d λ=+-+, 化简得2(1)0d λ-=,又0d ≠,所以1λ=. ………………4分(2)将1231,2,4a a a ===代入条件,可得414λ=⨯+,解得0λ=,所以211n n n a a a +-=,所以数列{}n a 是首项为1,公比2q =的等比数列,所以12n n a -=. ……6分欲存在[3,7]r ∈,使得12n m n r -⋅-…,即12n r n m --⋅…对任意*n N ∈都成立,则172n n m --⋅…,所以172n n m --…对任意*n N ∈都成立. ………………8分令172n n n b --=,则11678222n n nn n n n nb b +-----=-=, 所以当8n >时,1n n b b +<;当8n =时,98b b =;当8n <时,1n n b b +>.所以n b 的最大值为981128b b ==,所以m 的最小值为1128. ………………10分 (3)因为数列{}n a 不是常数列,所以2T …. ①若2T =,则2n n a a +=恒成立,从而31a a =,42a a =,所以22221212221221()()a a a a a a a a λλ⎧=+-⎪⎨=+-⎪⎩, 所以221()0a a λ-=,又0λ≠,所以21a a =,可得{}n a 是常数列.矛盾.所以2T =不合题意. ………………12分②若3T =,取*1,322,31()3,3n n k a n k k N n k =-⎧⎪==-∈⎨⎪-=⎩(*),满足3n n a a +=恒成立. ………………14分由2221321()a a a a a λ=+-,得7λ=. 则条件式变为2117n n n a a a +-=+.由221(3)7=⨯-+,知223132321()k k k a a a a a λ--=+-; 由2(3)217-=⨯+,知223313121()k k k a a a a a λ-+=+-; 由21(3)27=-⨯+,知223133221()k k k a a a a a λ++=+-.所以,数列(*)适合题意.所以T 的最小值为3. ………………16分20.解:(1)由()ln f x x =,得(1)0f =,又1()f x x'=,所以(1)1f '=,. 当c =时,()bg x ax x=+,所以2()bg x a x'=-,所以(1)g a b '=-. ………………2分因为函数()f x 与()g x 的图象在1x =处有相同的切线,所以(1)(1)(1)f g f g ''=⎧⎨=⎩,即10a b a b -=⎧⎨+=⎩,解得1212a b ⎧=⎪⎪⎨⎪=-⎪⎩. ………………4分 (2)当01x >时,则0()0f x >,又3b a =-,设0()t f x =,则题意可转化为方程3(0)aa x c t t x-+-=>在(0,)+∞上有相异两实根12,x x . ………………6分即关于x 的方程2()(3)0(0)ax c t x a t -++-=>在(0,)+∞上有相异两实根12,x x .所以2121203()4(3)030a c t a a c t x x a ax x a <<⎧⎪∆=+-->⎪⎪+⎨+=>⎪⎪-=>⎪⎩,得203()4(3)0a c t a a c t <<⎧⎪+>-⎨⎪+>⎩, 所以3)c a t >--对(0,),(0,3)t a ∈+∞∈恒成立. 8分因为03a <<,所以23=(当且仅当32a =时取等号), 又0t -<,所以t 的取值范围是(,3)-∞,所以3c …. 故c 的最小值为3. ………………10分 (3)当1a =时,因为函数()f x 与()g x 的图象交于,A B 两点,所以111222ln ln b x x c x b x x cx ⎧=+-⎪⎪⎨⎪=+-⎪⎩,两式相减,得211221ln ln (1)x x b x x x x -=--. ………………12分要证明122121x x x b x x x -<<-,即证211221212121ln ln (1)x x x x x x x x x x x x --<-<--,即证212211ln ln 11x x x x x x -<<-,即证1222111ln 1x x xx x x -<<-. ………………14分 令21xt x =,则1t >,此时即证11ln 1t t t -<<-.令1()ln 1t t t ϕ=+-,所以22111()0t t t t tϕ-'=-=>,所以当1t >时,函数()t ϕ单调递增.又(1)0ϕ=,所以1()ln 10t t t ϕ=+->,即11ln t t-<成立;再令()ln 1m t t t =-+,所以11()10tm t t t-'=-=<,所以当1t >时,函数()m t 单调递减,又(1)0m =,所以()ln 10m t t t =-+<,即ln 1t t <-也成立.综上所述, 实数12,x x 满足122121x x x b x x x -<<-. ………………16分附加题答案21.(A )解:如图,连接AE ,OE ,因为直线DE 与⊙O 相切于点E ,所以DE OE ⊥,又因为AD 垂直DE 于D ,所以//AD OE ,所以DAE OEA ∠=∠,① 在⊙O 中OE OA =,所以OEA OAE ∠=∠,② ………………5分 由①②得DAE ∠OAE =∠,即DAE ∠FAE =∠, 又ADE AFE ∠=∠,AE AE =,所以ADE AFE ∆≅∆,所以DE FE =,又4DE =,所以4FE =, 即E 到直径AB 的距离为4. ………………10分(B )解:设()00,P x y 是圆221x y +=上任意一点,则22001x y +=,设点()00,P x y 在矩阵M 对应的变换下所得的点为(),Q x y ,则002 00 1x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即002x x y y =⎧⎨=⎩,解得0012x xy y⎧=⎪⎨⎪=⎩, ………………5分 代入22001x y +=,得2214x y +=,即为所求的曲线方程. ………………10分(C )解:以极点O 为原点,极轴Ox 为x 轴建立平面直角坐标系,由cos()13πρθ+=,得(cos cossin sin )133ππρθθ-=, 得直线的直角坐标方程为20x -=. ………………5分 曲线r ρ=,即圆222x y r +=,所以圆心到直线的距离为1d ==.因为直线cos()13πρθ+=与曲线r ρ=(0r >)相切,所以r d =,即1r =. ……………10分(D)解:由柯西不等式,得22222[)][1](1x x ++≥⨯+, 即2224(3)()3x y x y +≥+. 而2231x y +=,所以24()3x y +≤,所以x y +≤, ………………5分 ABE DF O ·第21(A)图由1x x y ⎧=⎪⎪⎨⎪⎪+=⎩,得x y ⎧=⎪⎪⎨⎪=⎪⎩所以当且仅当x y ==时,max()x y += 所以当x y +取最大值时x的值为x =………………10分 22.解:(1)因为ABCD 是菱形,所以AC BD ⊥.又OP ⊥底面ABCD ,以O 为原点,直线,,OA OB OP 分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系.则(2,0,0)A ,(0,1,0)B ,(0,0,4)P ,(2,0,0)C -,(1,0,2)M -.所以(2,0,4)AP =- ,(1,1,2)BM =--,10AP BM ⋅= ,||AP = ,||BM =.则cos ,||||AP BM AP BM AP BM ⋅<>===. 故直线AP 与BM ………5分 (2)(2,1,0)AB =- ,(1,1,2)BM =--.设平面ABM 的一个法向量为(,,)n x y z = ,则00n AB n BM ⎧⋅=⎪⎨⋅=⎪⎩,得2020x y x y z -+=⎧⎨--+=⎩,令2x =,得4y =,3z =. 得平面ABM 的一个法向量为(2,4,3)n =.又平面PAC 的一个法向量为(0,1,0)OB = ,所以n 4OB ⋅=,||n ||1OB = .则cos ,||||n OB n OB n OB ⋅<>===. 故平面ABM与平面PAC 所成锐二面角的余弦值为………………10分 23.解:(1)由条件,()0112112r r n nn n n n n n n n nf n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+ ①,在①中令1n =,得()011111f C C ==. ………………1分在①中令2n =,得()011222222226f C C C C =+=,得()23f =. ………………2分在①中令3n =,得()011223333333332330f C C C C C C =++=,得()310f =. ………………3分 (2)猜想()f n =21nn C -(或()f n =121n n C --). ………………5分 欲证猜想成立,只要证等式011211212n r r n nn n n n n n n n nnC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+成立. 方法一:当1n =时,等式显然成立,C第22题图当2n …时,因为11!!(1)!==!()!(1)!()!(1)!()!r r n n r n n n rC n nC r n r r n r r n r --⨯-=⨯=-----(),故11111()r r r r r r n n n n n nrC C rC C nC C -----==. 故只需证明00111111211111n r r n n n n n n n n n n nnC nC C nC C nC C nC C ---------=++⋅⋅⋅++⋅⋅⋅+. 即证00111111211111n r r n n n n n n n n n n nC C C C C C C C C ---------=++⋅⋅⋅++⋅⋅⋅+. 而11r n r n n C C --+=,故即证0111111211111n n n r n r n n n n n n n n n n C C C C C C C C C ---+------=++⋅⋅⋅++⋅⋅⋅+ ②. 由等式211(1)(1)(1)n n n x x x --+=++可得,左边nx 的系数为21n n C -. 而右边1(1)n n xx -++()()0111n nn nC C x------=++++++++,所以nx 的系数为01111111111n n r n r n n n n n n n n nC C C C C C C C ---+-----++⋅⋅⋅++⋅⋅⋅+. 由211(1)(1)(1)n n n x x x --+=++恒成立可得②成立. 综上,()21nn f n C -=成立. ………………10分方法二:构造一个组合模型,一个袋中装有21n -个小球,其中n 个是编号为1,2,…,n 的白球,其余n -1个是编号为1,2,…,n -1的黑球,现从袋中任意摸出n 个小球,一方面,由分步计数原理其中含有r 个黑球(n r -个白球)的n 个小球的组合的个数为1r n rn n C C --,01r n ≤≤-,由分类计数原理有从袋中任意摸出n 个小球的组合的总数为01111111n n n n n n n n nC C C C C C -----+++ . 另一方面,从袋中21n -个小球中任意摸出n 个小球的组合的个数为21nn C -. 故0111121111n n n n n n n n n n nC C C C C C C ------=++ ,即②成立. 余下同方法一. ………………10分方法三:由二项式定理,得0122(1)n n n n n n n x C C x C x C x +=++++ ③.两边求导,得112111(1)2n r r n n n n n n n x C C x rC x nC x ---+=+++++ ④.③×④, 得21012212111(1)()(2)n n n r r n n n n n n n n n n n x C C x C x C x C C x rC x nC x ---+=+++++++++⑤.左边nx 的系数为21nn nC -. 右边nx 的系数为121112n n r n r n n n n n n n n n C C C C rC C nC C --+++⋅⋅⋅++⋅⋅⋅+ 1021112r r n n n n n n n n n nC C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+0112112r r n nn n n n n n n n C C C C rC C nC C --=++⋅⋅⋅++⋅⋅⋅+.由⑤恒成立,可得011211212n r r n nn n n n n n n n nnC C C C C rC C nC C ---=++⋅⋅⋅++⋅⋅⋅+. 故()21nn f n C -=成立. ………………10分。
南京、盐城2018届高三一模数学试卷及答案

南京市、盐城市2018届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =,其中S 为底面积,h 为高。
一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上) 1.已知集合{}|(4)0A x x x =-<,{}0,1,5B =,则AB = ▲ .2.设复数(,z a i a R i =+∈为虚数单位),若(1)i z +⋅为纯虚数,则a 的值为 ▲ .3.为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为 ▲ .4.执行如图所示的伪代码,若0x =,则输出的y 的值为 ▲ .5.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为 ▲ .6.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为 ▲ . 时间(单位:分钟) 频率组距 50 60 70 80 90 100 0.035 a0.0200.0100.005第3题图 Read x If 0x > Then ln y x ← Else x y e ← End If Print y 第4题图7.设函数1x xy e a e =+-的值域为A ,若[0,)A ⊆+∞,则实数a 的取值范围是 ▲ .8.已知锐角,αβ满足()()tan 1tan 12αβ--=,则αβ+的值为 ▲ .9.若函数sin y x ω=在区间[0,2]π上单调递增,则实数ω的取值范围是 ▲ . 10.设n S 为等差数列{}n a 的前n 项和,若{}n a 的前2017项中的奇数项和为2018,则2017S 的值为 ▲ .11.设函数()f x 是偶函数,当x ≥0时,()f x =(3),03,31,>3x x x x x-≤≤⎧⎪⎨-+⎪⎩,若函数()y f x m =-有四个不同的零点,则实数m 的取值范围是 ▲ .12.在平面直角坐标系xOy 中,若直线(33)y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =,则实数k 的最小值为 ▲ . 13.如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若,,,A B C D 四点均位于图中的“晶格点”处,且,A B 的位置所图所示,则CD AB ⋅的最大值为 ▲ .14.若不等式2sin sin sin 19sin sin k B A C B C +>对任意ABC ∆都成立,则实数k 的最小值为 ▲ .二、解答题(本大题共6小题,计90分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的
焦点与
双
曲线x42-
y2 5
=
1
的右焦点重合,则实数
p
的值为
________.
7. 设函数 y=ex+e1x-a 的值域为 A,若 A⊆[0,+∞),则实数 a 的取值范围是________.
8. 已知锐角 α,β满足(tanα-1)(tanβ-1)=2,则 α+β 的值为________.
9. 若函数 y=sinωx 在区间[0,2π]上单调递增,则实数 ω 的取值范围是________.
12. 在平面直角坐标系 xOy 中,若直线 y=k(x-3 3)上存在一点 P,圆 x2+(y-1)2=1
上存在一点 Q,满足O→P=3O→Q,则实数 k 的最小值为________.
13. 如图是蜂巢结构图的一部分,正六边形的边长均为 1,正六边形的顶 点称为“晶格点”.若 A,B,C,D 四点均位于图中的“晶格点”处,且点
D. [选修 4-5:不等式选讲](本小题满分 10 分) 已知实数 x,y 满足 x2+3y2=1,求当 x+y 取最大值时 x 的值.
【必做题】第 22 题、第 23 题,每题 10 分,共计 20 分.解答时应写出文字说明、证明 过程或演算步骤
22. (本小题满分 10 分) 如图,四棱锥 PABCD 的底面 ABCD 是菱形,AC 与 BD 交于点 O,OP⊥底面 ABCD, M 为 PC 的中点,AC=4,BD=2,OP=4. (1) 求直线 AP 与 BM 所成角的余弦值; (2) 求平面 ABM 与平面 PAC 所成锐二面角的余弦值.
令 x=0,得点 B 的坐标为(0,- 3). 所以椭圆的方程为xa22+y32=1.(4 分)
32
将点 N 的坐标
3,
23代入,得(
a32)2+
2 3
=1,解得
a2=4.
所以椭圆 C 的标准方程为x42+y32=1.(8 分)
(2) 设直线 BM 的斜率为 k(k>0),则直线 BM 的方程为 y=kx- 3.
令 f(x)=-x3+3x2,x∈(0,3),则由 f′(x)=-3x2+6x=-3x(x-2)=0,解得 x=2.(12 分)
当 x 变化时,f′(x),f(x)的变化情况如下:
所以当 x=2 时,f(x)取得最大值. 故当 BE 的长为 2 分米时,折卷成的包装盒的容积最大.(14 分)
18. 解析:(1) 由 N 3, 23,Q2 3 3,0得直线 NQ 的方程为 y=32x- 3.(2 分)
图1
图2
18. (本小题满分 16 分) 如图,在平面直角坐标系 xOy 中,椭圆 C:xa22+yb22=1(a>b>0)的下顶点为 B,M,N 是椭 圆上异于点 B 的动点,直线 BM,BN 分别与 x 轴交于点 P,Q,且 Q 是线段 OP 的中点.当
点 N 运动到点 3, 23处时,点 Q 的坐标为233,0.
2018 届南京、盐城高三年级第一次模拟考试 数学
(满分 160 分,考试时间 120 分钟) 参考公式: 柱体体积公式:V=Sh,其中 S 为底面积,h 为高. 一、 填空题:本大题共 14 小题,每小题 5 分,共计 70 分.
1. 已知集合 A={x|x(x-4)<0},B={0,1,5},则 A∩B=________. 2. 设复数 z=a+i(a∈R,i 为虚数单位),若(1+i)·z 为纯虚数,则 a 的值为________. 3. 为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级 4 000 名学生中随机抽取 100 名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直 方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟) 内的学生人数为________.
2 1. {1} 2. 1 3. 1 200 4. 1 5. 3 6. 6
7. (-∞,2]
3π 8. 4
9. 0,14
10. 4 034
11. 1,94 12. - 3 13. 24 14. 100
15. 解析:(1) 因为 ABCA1B1C1 是直三棱柱, 所以 AB∥A1B1,且 AB=A1B1. 又 M,N 分别是 AB,A1B1 的中点, 所以 MB=A1N,且 MB∥A1N, 所以四边形 A1NBM 是平行四边形, 从而 A1M∥BN.(4 分) 又 BN⊄平面 A1MC,A1M⊂平面 A1MC, 所以 BN∥平面 A1MC.(6 分) (2) 因为 ABCA1B1C1 是直三棱柱, 所以 AA1⊥底面 ABC,而 AA1⊂侧面 ABB1A1, 所以侧面 ABB1A1⊥底面 ABC. 又 CA=CB,且 M 是 AB 的中点,所以 CM⊥AB. 因为由侧面 ABB1A1⊥底面 ABC,侧面 ABB1A1∩底面 ABC=AB,CM⊥AB,且 CM⊂ 底面 ABC, 所以 CM⊥侧面 ABB1A1.(8 分) 又 AB1⊂侧面 ABB1A1,所以 AB1⊥CM.(10 分) 又 AB1⊥A1M,A1M,MC⊂平面 A1MC,且 A1M∩MC=M, 所以 AB1⊥平面 A1MC.(12 分) 又 A1C⊂平面 A1MC,所以 AB1⊥A1C.(14 分)
A,B 的位置如图所示,则A→B·C→D的最大值为________.
14. 若不等式 ksin2B+sinAsinC>19sinBsinC 对任意△ABC 都成立,则实数 k 的最小值为 ________.
二、 解答题:本大题共 6 小题,共计 90 分.解答应写出文字说明、证明过程或演算步 骤.
15. (本小题满分 14 分) 如图,在直三棱柱 ABCA1B1C1 中,CA=CB,M,N 分别是 AB,A1B1 的中点. (1) 求证:BN∥平面 A1MC; (2) 若 A1M⊥AB1,求证:AB1⊥A1C.
所以 cbcosA=bacosC, 由余弦定理得 b2+c2-a2=b2+a2-c2,得 a=c,(10 分)
从而 cosB=a2+2ca2c-b2=c2+c2- 2c2 25c2=35.(12 分)
又 0<B<π,所以 sinB= 1-cos2B=45,
从而
cosB+π4 =cosBcosπ4 -sinBsinπ4 =35×
B. [选修 4-2:矩阵与变换](本小题满分 10 分)
已知矩阵 M=20 01,求圆 x2+y2=1 在矩阵 M 的变换下所得的曲线方程.
C. [选修 4-4:坐标系与参数方程](本小题满分 10 分)
在极坐标系中,直线 ρcosθ+π3 =1 与曲线 ρ=r(r>0)相切,求 r 的值.
10. 设 Sn 为等差数列{an}的前 n 项和,若{an}的前 2 017 项中的奇数项和为 2 018,则 S2 017 的值为________.
x(3-x), 0≤x≤3,
11. 设函数 f(x)是偶函数,当 x≥0 时,f(x)=-3x+1, x>3,
若函数 y=f(x)-m
有四个不同的零点,则实数 m 的取值范围是________.
2018 届高三年级第一次模拟考试(一) 数学附加题
(本部分满分 40 分,考试时间 30 分钟) 21. 【选做题】本题包括 A、B、C、D 四小题,请选定其中两小题,并作答.若多做, 则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤. A. [选修 4-1:几何证明选讲](本小题满分 10 分) 如图,已知 AB 为⊙O 的直径,直线 DE 与⊙O 相切于点 E,AD⊥DE,垂足为 D.若 DE =4,求切点 E 到直径 AB 的距离 EF.
为163π-4 3立方分米.(6 分)
(2) 设 BE=x,则 R=2x,
所以所得柱体的底面积 S=S 扇形 OEF-S△OEF=13πR2-12R2sin120°=4π3 - 3x2.
因为所得柱体的高 EG=6-2x,
所以 V=S·EG=8π3 -2 3(-x3+3x2),其中 0<x<3.(10 分)
22-45×
22=-
2 10 .(14
分)
17. 解析:(1) 在图 1 中,连结 MO 交 EF 于点 T.
设 OE=OF=OM=R.
在 Rt△OET 中,因为∠EOT=12∠EOF=60°,
所以 OT=R2,则 MT=OM-OT=R2,
从而 BE=MT=R2,即 R=2BE=2.(2 分) 故所得柱体的底面积 S=S 扇形 OEF-S△OEF=13πR2-12R2sin120°=43π- 3.(4 分) 因为所得柱体的高 EG=6-1×2=4, 所以 V=S·EG=163π-4 3. 故当 BE 长为 1 分米时,折卷成的包装盒的容积
(1) 求椭圆 C 的标准方程;
(2) 设直线 MN 交 y 轴于点 D,当点 M,N 均在 y 轴右侧,D→N=2N→M时,求直线 BM 的
方程.
19. (本小题满分 16 分) 设数列{an}满足 a2n=an+1an-1+λ(a2-a1)2,其中 n≥2,且 n∈N,λ为常数. (1) 若{an}是等差数列,且公差 d≠0,求 λ 的值; (2) 若 a1=1,a2=2,a3=4,且存在 r∈[3,7],使得 m·an≥n-r 对任意的 n∈N*都成立, 求实数 m 的最小值; (3) 若 λ≠0,且数列{an}不是常数列,如果存在正整数 T,使得 an+T=an 对任意的 n∈N* 均成立.求所有满足条件的数列{an}中 T 的最小值.
16. 解析:(1) 因为 c= 25b,
所以由正弦定理得
sinC=
5 2 sinB.(2
分)
又 C=2B,所以 sin2B= 25sinB,
即 4sinBcosB= 5sinB.(4 分) 又 B 是△ABC 的内角,
