理想变压器特性及与等效电路的分析
理想变压器

理想变压器理想变压器是实际变压器的理想化模型,是对互感元件的理想科学抽象,是极限情况下的耦合电感。
1.理想变压器的三个理想化条件条件 1 :无损耗,认为绕线圈的导线无电阻,做芯子的铁磁材料的磁导率无限大。
条件 2 :全耦合,即耦合系数条件 3 :参数无限大,即自感系数和互感系数但满足:上式中 N 1 和 N 2 分别为变压器原、副边线圈匝数, n 为匝数比。
以上三个条件在工程实际中不可能满足,但在一些实际工程概算中,在误差允许的范围内,把实际变压器当理想变压器对待,可使计算过程简化。
2. 理想变压器的主要性能满足上述三个理想条件的理想变压器与有互感的线圈有着质的区别。
具有以下特殊性能。
(1)变压关系图 4.15 为满足三个理想条件的耦合线圈。
由于,所以因此图4.15 耦合线圈图 4.16理想变压器模型1 根据上式得理想变压器模型如图4.16所示。
注意:理想变压器的变压关系与两线圈中电流参考方向的假设无关,但与电压极性的设置有关,若 u1、u2 的参考方向的“+”极性端一个设在同名端,一个设在异名端,如图4.17 所示,此时 u1 与 u2 之比为:(2)变流关系根据互感线圈的电压、电流关系(电流参考方向设为从同名端同时流入或同时流出):则图 4.17理想变压器模型2 图 4.18理想变压器的变流关系代入理想化条件:,得理想变压器的电流关系为:注意:理想变压器的变流关系与两线圈上电压参考方向的假设无关,但与电流参考方向的设置有关,若i1、i2的参考方向一个是从同名端流入,一个是从同名端流出,如图4.18所示,此时i1与i2之比为:(3)变阻抗关系设理想变压器次级接阻抗 Z ,如图4.19所示。
由理想变压器的变压、变流关系得初级端的输入阻抗为:图4.19理想变压器的阻抗变换作用图 4.20 理想变压器的初级等效电路由此得理想变压器的初级等效电路如图4.20所示,把Zin称为次级对初级的折合等效阻抗。
电路分析之理想变压器
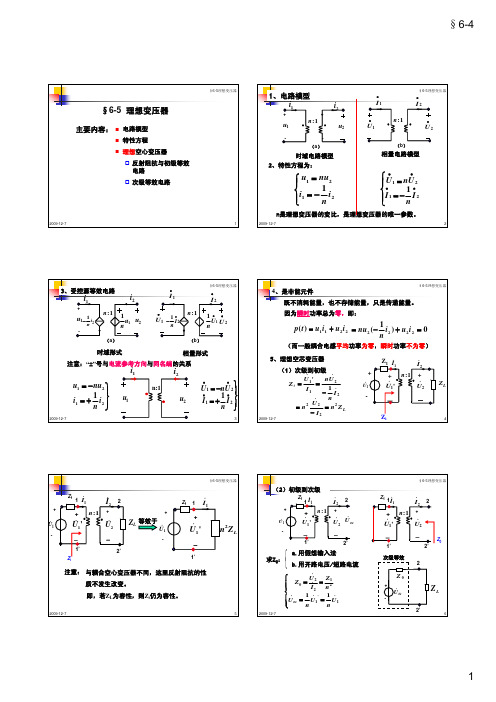
& ⎧ U 2 Z1 ⎪ Z0 = & = 2 ⎪ I2 n ⎨ ⎪U = 1 U ' = 1 U & & & ⎪ oc n 1 n 1 ⎩
Z0
+
& U oc
-
ZL
2’
6
1
§6-4
§6-5理想变压器
§6-5理想变压器
6、几点注意: (1)特性方程只对理想变压器两端而言成立 写出下列电路的
I&1
+
(2)当匝数比为1:n 时,注意这时特性方程为: 一般: & & ⎧ U 1 ≠ nU 2 ⎪ 1 & ⎨& ⎪ I1 ≠ − n I 2 ⎩ 但总有:
2
+
& U1
+
+
& U1'
- Zi
& U2
-
ZL
-
4
§6-5理想变压器
§6-5理想变压器
(2)初级到次级
Z1 +
1
& I1
n :1
& I2
+
2
+
Z1
1
& I1
Z1 +
1 I1
&
& I2
n :1
+
2
Z1
& 1 I1
& I2
n :1
+
2
+
& U1
-
& U1'
-
& U2
-
ZL 等效于
+
理想变压器的性质

理想变压器的性质1.功率性质抱负变压器汲取的瞬时功率为:可以看出,抱负变压器不耗能、不储能,它将能量由原边全部传输到副边输出。
在传输过程中,仅将电压、电流按变比做数值变换,即它在电路中只起传递信号和能量的作用。
抱负变压器是个抱负化的电路模型,实际变压器线圈的电感L1和L2不行能趋于无穷大。
含铁芯的变压器当工作在铁芯不饱和时,它的磁导率很大,因而电感较大,若将铁芯损耗忽视,就可近似为抱负变压器。
2.阻抗变换性质当抱负变压器的副边接入阻抗ZL时,原边输入阻抗为:即n2ZL 为副边折合到原边的等效阻抗:在电子电路中常用具有接近于抱负变压器性能的变压器来转变阻抗以满意电路的需要。
3.两种特别状况(1)输出端短路(2)输出端开路抱负变压器的受控源等效电路例6. 已知RS=1kΩ,RL=10Ω。
为使RL获得最大功率,求抱负变压器的变比n。
解:方法1:戴维宁等效电路。
(1)求开路电压。
uoc=u2=u1/n=us/n(2)求等效电阻。
Req=Rs/n2(3)要使RL上获得最大功率,则:RL=Req=Rs/n2→ 10=1000/n2→ n=10方法2:原边等效电路。
要使n2RL获得最大功率,则:因抱负变压器不耗能,故等效电阻的功率即为负载电阻的功率。
例7. 求解:方法1:列方程。
解得方法2:阻抗变换(原边等效电路)。
方法3:戴维宁等效。
求求Req:小结:变压器的原理本质上都是互感作用,实际上有习惯处理方法。
空心变压器原边等效电路:空心变压器:电路参数L1、L2、M, 储能。
抱负变压器原边等效电路:抱负变压器:电路参数n,不耗能、不储能,变压、变流、变阻抗。
留意:抱负变压器不要与全耦合变压器混为一谈。
理想变压器特性及与等效电路的分析

理想变压器特性及与等效电路的分析
理想变压器特性及与等效电路的分析
谭阳红1,汪沨1,陈五立2
(1.湖南大学电气与信息工程学院,湖南长沙410082;
2.
用,
在此基础上,
掌握特方法。
利用磁路定理来理解理想变压器的特性,只需用以下定律:磁路的基尔霍夫第一定律即磁通连续性原理和磁路的基尔霍夫第二定律,即安培环路定律。
1.双绕组理想变压器电压方程。
考虑如下的变压器(图1(a)所示),设变压器初次级的原边和副边匝数分别为Np和Ns,电流为ip蓸t蔀、is蓸t蔀,铁芯磁导率μ趋近于无穷大,即没有漏磁,磁感应强度全部集中于铁芯。
变压器的初、次级磁链相等,设为ψm。
很明显:
四、结语
本文的分析表明,变压器的特性方程与磁路形式密切相关。
在理想变压器的教学中,采用磁路的分析方法,只有如此,学生才能牢固掌握理想变压器特性方程的本质。
理想变压器等效电路

理想变压器等效电路理想变压器等效电路是电学中的一个重要概念,它可以帮助我们更好地理解电路中电压、电流的变化过程。
理想变压器等效电路是由一个理想变压器和一些标准元件(如电阻、电容、电感等)组成的电路模型。
下面,我们将分步骤地阐述理想变压器等效电路。
第一步,了解理想变压器的特点理想变压器是一种绝缘良好、电感大、电阻小、磁路无损耗的变压器。
理想变压器的特点在于,它是一个完全理想化的变压器,没有任何的漏电感和损耗,可以将电能完全传递。
在实际中,变压器的损耗和漏电感是无法避免的,但理想变压器等效电路中可以将变压器所有的损耗和漏电感都归零,只考虑变压器的转化作用。
第二步,建立理想变压器等效电路理想变压器等效电路是由一个理想变压器和一些标准元件组成的电路模型。
根据理想变压器的特点,我们可以将理想变压器等效电路简化为只有两个端子,分别代表输入端和输出端。
同时,电路中还可以加入一些其他元件,如电阻、电容和电感等元件。
这些元件与理想变压器紧密联系,构成了一个完整的电路模型。
通过这个电路模型,我们可以更好地理解理想变压器的工作原理。
第三步,分析理想变压器等效电路的作用理想变压器等效电路的作用在于将电压和电流传递过来,并通过添加其他元件来调节电路的性能。
在理想变压器等效电路中,输入端可以输入一定的电压,而输出端可以输出一个对应的电压。
通过理想变压器等效电路,我们可以调整输入端的电压和输出端的电压以及电流大小。
还可以通过调整其他元件的参数来改变电路的频率响应和波形形状。
第四步,应用理想变压器等效电路理想变压器等效电路广泛应用于电子电路中的各种电源、放大器和信号处理器中。
这些电路需要一个稳定的电压和电流输出,因此理想变压器等效电路可以作为这些电路的重要组成部分。
此外,在建立模拟电路和数字电路的过程中,理想变压器等效电路也经常被用来模拟实际的变压器。
在理想变压器等效电路中,我们可以通过调整电路的参数来改变电路的性能。
但是需要注意的是,在实际电路中,我们无法完全避免损耗和漏电感。
理想变压器等效电路

理想变压器等效电路
理想变压器是一种非常重要的电子元件。
它可以将电压从一个电路传输到另一个电路,同时保持电流不变。
理想变压器具有非常高的效率和精度,因此在许多应用中得到广泛的应用。
理想变压器的等效电路包含两个部分:主要是一个理想变压器,其次是一个少量的电阻和电感。
在理想变压器中,电势能和电磁能可以完全转化。
这意味着,在理想情况下,变压器不会消耗能量,也不会产生任何损失。
在等效电路中,变压器的主要功能是将电压的大小和方向传递到另一个电路中。
这样,我们可以使用理想变压器来实现不同的电压转换,例如从低电压到高电压或从高电压到低电压。
除了变压器外,等效电路中还包含一些电阻和电感。
这些元件可以模拟理想变压器的一些实际效应,例如漏电感和电阻。
其目的是进一步优化电路的性能,并且可以更好地匹配变压器和其他电子元件。
总的来说,理想变压器等效电路是一种非常有用的电子电路,因为它可以帮助我们实现各种电压转换。
通过了解其基本原理和构造,我们可以更好地理解变压器的工作原理,并且可以更好地设计和优化电子电路。
- 1 -。
变压器等效电路

变压器等效电路变压器是电力系统中常用的重要设备,用于改变交流电压的大小。
在电力系统中,为了进行电路分析和计算,可以采用等效电路模型来表示变压器的工作原理和性能。
本文将介绍变压器等效电路的基本原理和常见模型。
1. 变压器的基本原理变压器是由一个或多个线圈组成的,通过电磁感应的原理来改变电压。
变压器由铁心和绕组组成。
绕组分为初级绕组和次级绕组,通过将电流通过初级绕组,产生的磁场会感应到次级绕组,从而改变输出电压的大小。
变压器的基本原理是基于法拉第电磁感应定律。
2. 变压器的等效电路模型为了简化电路分析和计算,可以采用等效电路模型来代替变压器。
常见的变压器等效电路模型有两种:简化型和精确型。
2.1 简化型等效电路模型简化型等效电路模型将变压器抽象为两个卷绕电感和一个理想变压器,分别代表初级绕组和次级绕组的电感和变压器的变换关系。
在这个模型中,忽略了变压器的内阻和铁芯的磁滞特性。
2.2 精确型等效电路模型精确型等效电路模型更加符合实际变压器的工作原理,考虑了变压器的内阻和铁芯的磁滞特性。
在这个模型中,将变压器抽象为两个卷绕电感、两个卷绕电阻和一个理想变压器。
通过考虑内阻和磁滞特性,可以更加准确地描述变压器的电特性。
3. 变压器等效电路模型的参数无论是简化型还是精确型等效电路模型,都需要知道一些参数来描述变压器的性能。
常见的参数有:3.1 变压器的变比变比是指变压器的输入电压与输出电压的比值。
例如,变比为2:1表示输出电压是输入电压的两倍。
3.2 变压器的电感电感是指变压器的绕组对电流变化的阻抗。
初级绕组和次级绕组的电感分别表示为L1和L2。
3.3 变压器的内阻内阻是指变压器绕组的电阻。
初级绕组和次级绕组的内阻分别表示为R1和R2。
4. 变压器等效电路的应用变压器等效电路模型可以应用于电力系统的分析和计算中。
通过使用等效电路模型,可以更加方便地处理变压器与其他电路元件之间的相互作用。
4.1 电路分析变压器等效电路模型可以与其他电路元件一起进行电路分析,例如,计算电流、电压、功率等参数。
电路分析基础理想变压器的VCR及其特性

变压器的符号
返回
X
初级线圈产生的磁通Φ 11
I1 M
I2
次级线圈产生的磁通 根据条件(1) :
Φ 22
Us
U1
L1
L2 U2
RL
Φ11Φ21, Φ22Φ12
N1 N2
各线圈中的磁链:
11112N 1(Φ 11 Φ 1)2N 1(Φ 11 Φ 2)2 N1Φ 22221N 2(Φ 22 Φ 2)1N 2(Φ 22 Φ 1)1 N2Φ
L1
i1 R1
L1 M us1
L2
us 2
R2 i2
L2 M
us2
8 0 0 j1 2 0 0=9 6 j2 7 2
M
3 j4
X
解(续)
I11R1j(LU 1s1M)Z并 1
1000
200j100(24)96j272
1000 1000 0.3313.67A
296j72 304.6313.67
X
解(续)
I11
R1nn22U RRs221jjLL11
2001010500j200
1000 296j72
150j200
1000 0.3313.67A 304.6313.67
I1'1n2Rj2Lj1L1I11150j20j02000.3313.67
490 0.3313.670.2623.2A 553.13
i1
和i
2
。
i1
R1
k
R2 i2
M L 1L2 284H
u s 1 单独作用 Us11000V
Z并1
j M [R2 j ( L2 M )] j M [R2 j ( L2 M )]
理想变压器模型介绍

理想变压器模型介绍理想变压器是电力系统中广泛使用的一种电力设备,它被用于电能的传输和变换。
在介绍理想变压器模型之前,我们先来了解一下什么是理想变压器。
理想变压器是一种假设性的模型,用于简化实际变压器的复杂性。
它忽略了实际变压器中的损耗、饱和等因素,将其视为没有耗损、无磁滞的理想设备。
这种模型大大简化了电力系统的分析过程,使得电力工程师能够更方便地进行计算和设计。
理想变压器模型的基本原理如下:假设理想变压器的一侧为主侧(Primary Side),另一侧为副侧(Secondary Side)。
主副侧之间通过磁耦合实现能量传输。
主侧和副侧分别由感抗Lp和Ls来表示。
理想变压器忽略了磁耦合的漏阻抗,因此主副侧之间可以无损耗地转移能量。
基于以上原理,我们可以得到理想变压器的等效电路模型。
在该模型中,主侧和副侧分别由电感Lp和Ls表示,电感之间由互感系数K(0 < K ≤ 1)联系起来。
互感系数K是指主副侧磁链之间的耦合程度,它的取值范围决定了理想变压器的变压比。
理想变压器模型的等效电路如下所示:------ ------| Lp |-------- -----------| Ls |Voltage Vin--> ----- -------Source Load在上述电路中,Vin是输入电压,Source是电压源。
Lp和Ls分别表示主副侧的电感,它们之间的连接由互感系数K决定。
在理想变压器模型中,输入电压Vin和输出电压Vout之间的关系由变压比公式决定:Vout / Vin = Ns / Np = K其中,Ns表示副侧匝数,Np表示主侧匝数。
变压比公式表明,当变压器是升压变压器时,副侧匝数大于主侧匝数;当变压器是降压变压器时,副侧匝数小于主侧匝数。
理想变压器模型的应用十分广泛。
在电力系统的稳态分析中,理想变压器模型被广泛应用于电压调节、功率传输等方面。
在电力系统的短路分析和过电流保护中,理想变压器模型可以帮助工程师进行全面的系统计算。
20170419-理想变压器的等效电路模型
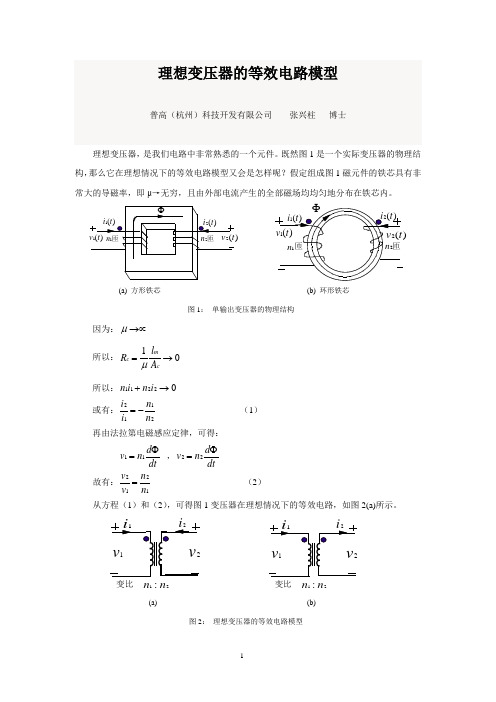
理想变压器的等效电路模型普高(杭州)科技开发有限公司 张兴柱 博士理想变压器,是我们电路中非常熟悉的一个元件。
既然图1是一个实际变压器的物理结构,那么它在理想情况下的等效电路模型又会是怎样呢?假定组成图1磁元件的铁芯具有非常大的导磁率,即μ→无穷,且由外部电流产生的全部磁场均均匀地分布在铁芯内。
(a) 方形铁芯 (b) 环形铁芯图1: 单输出变压器的物理结构因为:→∝µ 所以:01→=cmc A l R µ 所以:02211→+i n i n 或有:2112n n i i −= (1) 再由法拉第电磁感应定律,可得: dt d n v Φ=11 ,dtd n v Φ=22 故有:1212n n v v = (2) 从方程(1)和(2),可得图1变压器在理想情况下的等效电路,如图2(a)所示。
(a) (b)图2: 理想变压器的等效电路模型由于方程(1)中有一个负号,故也可采用图2(b)来表示理想变压器的等效电路模型,它与图2(a)的区别是电流i 2的参考方向,在这种参考方向下,一个理想变压器满足下列电压电流关系:2112//n n i i =1212//n n v v = (3)方程组(3)就是我们在电路中看到的关于变压器元件的电压和电流关系,通过关系,可以看出,由铁芯和两个绕组组成的单输出变压器,其绕组两端的电压之比与绕组的匝数之比成正比,绕组中流过的电流之比与绕组的匝数成反比,如果将两个绕组中的一个看成是输入绕组(或原边绕组),将绕组中的另一个看成是输出绕组(或副边绕组),那么图1的变压器和其等效电路模型就可分别用图3 (a)和图3 (b)来表示,这种变压器的表示方法已被开关电源文献和书籍中所规范,所以本文及后续要介绍的文章,也将以此来表示变压器。
原边或一次侧用下标p 表示,副边或二次侧用下标s 表示。
因此方程组(3)将变成方程组(4):(a) 变压器结构 (b) 等效电路图3: 开关电源中规范化表示的变压器sp p s N N i i //=ps p s N N v v //= (4)当变压器的副边不止一个绕组时,该变压器就是多输出变压器,多输出变压器在理想情况下的电压电流关系可以用方程组(5)表示,其中K 为副边绕组的个数。
理想变压器的综合分析

理想变压器的综合分析理想变压器是电能转换系统中最常用的装置之一。
它通常用于变压、隔离、耦合和功率匹配等应用领域。
理想变压器是一种没有漏抗的模型,其次级侧输出电压与次级施加电压的比值等于它们的匝数比。
理想变压器的原理是基于强磁耦合的电感耦合,通过其交流电磁感应,实现了电压和电流的转换。
理想变压器是在没有能量损失,同时维持磁通连续性的前提下工作的。
因此,它的电流和电压比是完全由匝数比所决定的。
理想变压器的数学模型中,假设两组绕组之间没有漏抗,这意味着所有的磁通都集中于铁心之间。
理想变压器的线圈是不耗散的,没有电阻和电感,因此没有能量损失。
这样,它的工作效率就达到了100%。
理想变压器的性能指标可以通过以下参数来描述:1. 匝数比:变压器的主要功能是转换电压。
匝数比是理想变压器中二者之间相当于给定电压比的表达式。
它为Np/NS (次级匝数÷主级匝数)。
2. 变压度:变压器的工作是在输入和输出侧之间建立电压比。
而变压度是转换器中输入和输出电压的比值。
因此,它是来自绕组的电压比的表征,为VP/VS(输入电压÷输出电压)。
3. 社会电抗率:社会电抗率是描述理想变压器在未激磁情况下的漏磁阻抗的一个术语。
它可以通过复数表达式1/jωL 来描述,其中L为漏感。
理想变压器的分析过程中,需要通过对分压器,分流器和等效电路的分析来确定其性能。
在分析过程中,我们可以将变压器想象成一个含有内部阻抗的电源,是由主线圈的响应直接推导出来的。
由于内部耗散元件的消耗,则需要计算戴入主线圈的热功率。
这种功率损失随着线圈的制造质量和使用条件的影响而发生变化。
需要注意的是,在现实世界中,理想变压器并不存在。
所有变压器都会存在漏抗和铁损耗。
因此,在实际应用中,通常需要考虑压降和损耗等因素。
未考虑损耗时,理想变压器的特征与实际变压器的特征相同,除了在变压器的事实性处理等方面存在差异。
总的来说,理想变压器是在没有能量损失和维持磁通连续性的前提下工作的。
理想变压器的电路分析_OK

求得
n Ro 800 10
RL
8
解:理想变压器端接负载电阻RL时 的等效电阻为
Ri n2 RL
根据最大功率传输定理,Ri获得 最大功率的条件是
Ri n2 RL Ro
pmax
uo2c 4Ro
22 W 1.25m11W 4 800
例6 用结点分析法再求图5-5(a)所示单口网络的等效电阻。
1
2
i2 n i 1
3、阻抗变换作用
•
Zi
U1
•
I1
1 n2
ZL
•
n Z Zo
U2
•
I2
2 S
三大变换需要注意的地方:
①电压变换和电流变换时需要注意正负号与同名异名端的关系。
(这个地方非常容易出错,千万要注意!!!!!!!)
3
②阻抗变换与理想变压器的同名端位置无关!
含理想变压器的电路分析
4
u2 3u1 i1 3i2
用两个相应的受控源代替理想 变压器的两条支路,得到图(b)
列出节点方程:
1 2
u1
1 2
u2
3
1 3
u2
i2
代入 可解得
u2 3u1
Ri
u1 iS
0.2
13
理想变压器的特点:
①只有一个参数n(无L1、L2、M); ②不消耗能量、不储存能量,是无记忆元件, 即:从一次侧进入理想变压器的功率,全部 传输到二次侧的负载中。所以在计算与理想 变压器功率有关的计算题,所消耗的功率一 定是其上的电阻消耗的。
方法:采用外加电流源计算端口
电压的方法求等效电阻。
图5-5
变压器和三相电动机的等效电路

变压器和三相电动机的等效电路变压器和三相电动机是电力系统中常见的电气设备,它们在电能的转换和传输过程中发挥着重要的作用。
本文将从等效电路的角度,对变压器和三相电动机进行介绍和分析。
一、变压器的等效电路变压器是一种用来改变交流电压的装置。
它由一个或多个线圈(即绕组)构成,绕组之间通过磁场耦合而相互影响。
变压器的等效电路是为了简化分析和计算而建立的模型,它将变压器的绕组和磁路抽象为电路元件。
1. 主要元件变压器的等效电路主要由四个元件组成:输入电压源、输出负载、主绕组和副绕组。
其中,输入电压源表示输入电压的大小和相位,输出负载表示输出电压和电流的大小和相位,主绕组和副绕组分别表示主边和副边的线圈。
2. 线圈和磁路主绕组和副绕组通过磁路耦合在一起,构成了变压器的传递路径。
磁路的特性可以用磁感应强度和磁导率来描述。
主绕组和副绕组的线圈可以看作是电感元件,它们的大小和匝数决定了变压器的变比。
3. 等效电路图变压器的等效电路图可以简化为一个理想变压器和一个实际变压器。
理想变压器假设没有能量损耗和磁通泄漏,转换效率为100%;实际变压器考虑了能量损耗和磁通泄漏,转换效率降低。
二、三相电动机的等效电路三相电动机是工业中常用的电动机类型,它通过三相交流电源驱动,将电能转换为机械能。
三相电动机的等效电路是为了分析和计算电动机的性能和特性而建立的模型。
1. 主要元件三相电动机的等效电路主要由三个元件组成:输入电源、定子和转子。
输入电源提供了驱动电动机运转所需的电能,定子是固定不动的部分,转子则是旋转的部分。
2. 定子和转子定子由定子绕组和铁芯构成,绕组一般为三相对称绕组,通过定子绕组产生的旋转磁场与转子上的导体相互作用,产生转矩驱动转子旋转。
转子一般由铁芯和绕组构成,绕组上的导体通过感应电动势产生感应电流,感应电流与定子磁场相互作用,产生转矩。
3. 等效电路图三相电动机的等效电路图可以简化为定子电阻、定子电抗、转子电抗和转矩负载。
变压器的等效电路及相量

根据空载试验和短路试验结果,可以计算出变压器的等效电路参数,包括激磁阻抗Zm、 漏阻抗Zk和负载阻抗ZL等。这些参数可以用于分析变压器的运行特性和设计控制电路。
03
相量图表示方法
相量基本概念及性质
相量定义
01
在正弦交流电路中,用来表示同频率正弦量的复数,称为相量。
相量性质
02
相量具有大小和方向,其大小等于正弦量的有效值,方向等于
变压器并联运行与自耦变 压器简介
并联运行条件及优缺点分析
变压器的阻抗电压应相等
变压器的额定电压和变比应相等
并联运行条件
01
03 02
并联运行条件及优缺点分析
变压器的接线组别应相同 并联运行优点 提高供电的可靠性
并联运行条件及优缺点分析
01 可根据负载的大小调整投入并联运行的变压器台 数,提高运行效率
正弦量在任意时刻的旋转角度。
相量与正弦量的关系
03
相量是正弦量的复数表示,二者具有一一对应的关系。通过相
量可以方便地分析正弦交流电路。
相量图绘制步骤与技巧
1. 确定坐标轴
以实轴为横轴,虚轴为纵轴,建 立复数平面。
2. 标记正弦量
在复数平面上标记出各个正弦量 的相量。
相量图绘制步骤与技巧
• 连接相量:根据电路的连接方式,用直线或箭头连接各个 相量。
02 减少备用容量,便于对变压器进行维护和检修
03
并联运行缺点
并联运行条件及优缺点分析
如不满足并联条件,将产生环流,影 响变压器的出力,甚至烧毁变压器
需要增加相应的保护和控制装置,提 高投资成本
自耦变压器结构特点和工作原理
结构特点
1
初级和次级共用一组线圈
理想变压器等效电路

理想变压器等效电路
理想变压器等效电路是电气工程中常用的一种电路模型,它是指假设变压器没有损耗,可以无限传输功率的模型。
在该模型中,变压器的输入端和输出端可以看作是独立的电路,它们之间的传输效率是完美的。
理想变压器等效电路可以简化复杂的变压器电路问题,例如在电力传输和电子设备中常见的变压器应用。
该模型利用变压器的原理,可以将输入端的电压和输出端的电压按照一定的比例转换,并且可以通过改变变压器的绕组比例来改变电压的大小。
理想变压器等效电路通常由一个电感器和多个旋变器组成,其中电感器模拟变压器的铁芯,而旋变器模拟变压器的绕组。
通过调整旋变器的匝数比例,可以使得输入端和输出端的电压比例发生变化,从而实现变压器的功能。
总之,理想变压器等效电路是电气工程中重要的一种电路模型,它可以有效地简化复杂的变压器电路问题,实现电压的转换和传输。
- 1 -。
2电力线路变压器的参数与等值电路

2电力线路变压器的参数与等值电路电力线路变压器是电力系统中重要的设备,用于将电能从一个电压等级变换至另一个电压等级,以满足不同用电需求。
变压器通过电磁感应原理工作,根据法拉第定律变换电压和电流。
变压器的参数与等值电路可以帮助我们更好地理解和分析变压器的工作特性。
1.变压器的参数:变压器的主要参数有变比、额定容量、额定电压、额定电流等。
(1)变比:变比是指输入线圈和输出线圈之间的线圈匝数比。
变比越高,输出电压越高。
(2)额定容量:指变压器能正常工作的容量大小,通常以千伏安(kVA)为单位。
额定容量表示变压器能够承受的最大功率负载。
(3)额定电压:变压器的额定电压分为输入端额定电压和输出端额定电压。
输入端额定电压表示输入线圈的额定电压,而输出端额定电压表示输出线圈的额定电压。
(4)额定电流:指变压器额定容量时的输入电流和输出电流。
额定电流与额定容量有一定的关系。
2.变压器的等值电路:为了更方便地分析和计算变压器的工作特性,可以将变压器抽象成一个等值电路,该等值电路包含主要参数和特性。
(1)等效电路模型:变压器的等效电路模型主要是由电压源、主线圈(输入线圈)、副线圈(输出线圈)以及相应的电感和电阻等元件组成。
主要包括两种等效电路模型:短路模型和开路模型。
-短路模型:短路模型用于分析变压器在短路状态下的等效电路。
主线圈和副线圈依次串联,其中主线圈的电感和电阻分别为L1和R1,副线圈的电感和电阻分别为L2和R2-开路模型:开路模型用于分析变压器在开路状态下的等效电路。
主线圈和副线圈相互独立地并联,其中主线圈的电感和电阻分别为L1和R1,副线圈的电感和电阻分别为L2和R2(2)理想变压器模型:理想变压器模型是一种特殊的等效电路模型,在该模型中,主要忽略了主线圈和副线圈的电阻和漏磁等损耗,只考虑了电感元件。
-理想变压器的变比为N:1,输出电压与输入电压之间的关系为:V2/V1=N。
-理想变压器的短路阻抗为ZK=(R1+jωL1)/N^2,其中ω为角频率。
2024理想变压器的三个理想条件

理想变压器的三个理想条件•理想变压器基本概念•第一个理想条件:无漏磁通•第二个理想条件:无电阻损耗•第三个理想条件:无铁心损耗目•理想变压器工作特性分析•理想变压器在电路中应用录01理想变压器基本概念变压器定义及作用变压器定义变压器作用理想变压器与实际变压器区别理想变压器实际变压器理想变压器重要性及应用场景重要性理想变压器模型忽略了实际变压器中的非理想因素,从而简化了电路分析和计算过程,方便工程师进行电力系统设计和优化。
应用场景理想变压器模型广泛应用于电路理论、电力系统分析、电机与电力电子等领域。
在分析实际电路时,可以将实际变压器等效为理想变压器模型,从而简化电路结构和计算过程。
同时,在电力系统规划和设计阶段,也需要利用理想变压器模型进行潮流计算、短路计算等分析工作。
02第一个理想条件:无漏磁通漏磁通产生原因及影响磁路不完全闭合由于铁芯的几何形状、磁路长度和铁芯接缝等因素,导致磁路无法完全闭合,从而产生漏磁通。
绕组分布不均绕组在铁芯上的分布不均匀,使得部分区域的磁通密度过高,导致漏磁通增加。
漏磁通的影响漏磁通会在绕组中产生额外的感应电动势和电流,导致变压器效率降低、温升增加,甚至可能引发局部过热和绝缘损坏。
提高效率无漏磁通可以减少绕组中的额外感应电动势和电流,从而降低变压器的损耗,提高效率。
降低温升无漏磁通可以减少绕组中的环流和局部过热现象,从而降低变压器的温升。
提高绝缘性能无漏磁通可以减少绕组中的电压梯度,降低绝缘应力,从而提高变压器的绝缘性能和使用寿命。
无漏磁通对变压器性能影响优化铁芯设计合理布置绕组采用高导磁材料增加屏蔽措施实现无漏磁通技术措施03第二个理想条件:无电阻损耗电阻损耗产生原因及影响绕组电阻磁芯损耗影响效率温升问题无电阻损耗对变压器性能提升提高效率01降低温升02优化设计03降低电阻损耗方法探讨选择优质材料优化绕组结构采用先进技术控制工作条件04第三个理想条件:无铁心损耗铁心损耗产生原因及分类磁滞损耗由于铁心材料在磁化过程中的不可逆性,导致部分能量以热能形式散失。
理想变压器
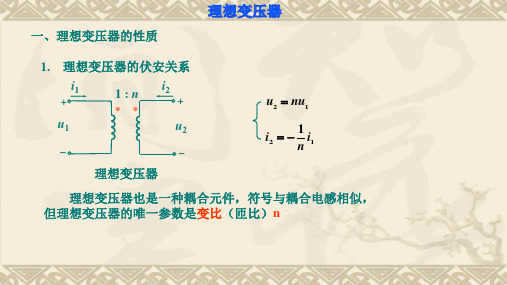
3. 理想变压器的阻抗变换性质:
i1
+
u1
–
1:n i
**
(a)
i2
+
RL u2
–
i1
+
u1
–
1:n
RL * * n2
(b)
i2
+
u2
–
利用伏安关系证明(a),(b)等效:
对(a)有:
i1
ni
n(i2
u2 RL
)
ni2
nu2 RL
u2 nu1
u1 RL / n2
(ni2 )
RL
RL n2
称为RL在初级中的折合阻抗。
功率,求理R想S 变压n器:的变比n。
1
+
**
RS
uS–RL+ NhomakorabeauS
n2RL
–
当 n2RL=RS时匹配,即 10n2=1000
n2=100, n=10 .
小结
理想变压器性质:
(1)变电压
(2)变电流
u1 =
N1 N2
u2
nu2
i1 =-
N2 N1
i2
1 n
i2
(3)变阻抗
Z in
U 1 I1
n2ZL
结论:理想变压器满足以下3个理想条件
(1) 耦合系数k=1,即为全耦合; (2) 自感系数L1、L2为无穷大,但L1/L2为常数;
(3) 无任何损耗,这意味着绕线圈的金属导线无任何电阻,做芯的 铁磁材料的磁导率μ无穷大。
【例】电路如图(a)所示,已知 uS 10 2 cos314t V, R1=1Ω,R2=50Ω。试求u2。
变压器电路分析

变压器电路分析电力系统中的变压器是一种重要的电气设备,用于电能的传输和变换。
在电力系统中,变压器的电路分析是了解其工作性能和状况的关键步骤。
本文将对变压器的电路进行详细分析,以帮助读者更好地理解其原理和应用。
一、变压器基本原理变压器是基于电磁感应原理工作的电气设备。
它由两个或多个线圈(分别称为初级线圈和次级线圈)和一个铁芯组成。
当变压器的初级线圈通电时,它会产生磁场,进而感应次级线圈中的电动势。
通过调整初级线圈和次级线圈的匝数比例,可以实现电压的升降变换。
二、变压器电路模型为了方便分析和计算,变压器可以用电路模型来表示。
最常用的是理想变压器模型和实际变压器模型。
1. 理想变压器模型理想变压器模型假设变压器没有任何损耗,即没有电阻和磁损耗。
在这个模型中,变压器的初级和次级线圈是完美的导线,两者之间只有电动势源和互感电感。
2. 实际变压器模型实际变压器模型考虑了变压器的损耗,包括线圈内阻和铁芯损耗。
在这个模型中,变压器的初级和次级线圈分别通过等效电阻表示,并引入铁芯的磁导抗。
三、变压器电路分析方法变压器电路分析的主要目标是确定变压器的电压比、电流比、变压器效率和功率损耗。
下面介绍几种常用的分析方法。
1. 等效电路法使用等效电路法可以有效地简化复杂的变压器电路,将其转化为简单的等效电路。
通过对等效电路进行分析,可以确定变压器的各种参数。
2. 全电压法全电压法是一种比较常用的变压器电路分析方法。
它基于变压器的电压方程,通过联立各个线圈的电压方程组来求解各个参数。
3. 等级法等级法是一种基于变压器等级的电路分析方法。
它将变压器按照电压等级和额定容量分类,通过分析各等级变压器之间的连接关系和功率传输来实现电路分析。
四、变压器电路分析应用案例变压器电路分析在实际工程中有着广泛的应用。
下面以电力系统中的变压器组为例,介绍其电路分析的应用。
1. 变压器组平衡电路分析在某些电力系统中,会采用多台变压器组接入同一电网,以满足电能传输需求。
电路基础原理理想变压器与变压器的等效电路

电路基础原理理想变压器与变压器的等效电路电路基础原理:理想变压器与变压器的等效电路电路基础原理是学习电气工程的基础,其中一个重要的概念就是电压的变换。
变压器是实现电压变换的重要设备之一,它通过电磁感应的原理,将输入端的电压转换为输出端的电压。
在电路理论中,我们通常会讨论理想变压器和变压器的等效电路。
本文将从深入浅出的角度介绍这些概念,并探讨它们在电路设计中的应用。
首先,我们来了解理想变压器的概念。
理想变压器是一种假设模型,它假设变压器的线圈没有电阻和电感,并且变压器的磁路没有能量损耗。
在理想变压器中,输入端与输出端的电压之比等于输入端与输出端的匝数之比。
这个比例关系可以用下面的公式表示:\[ \frac{V_1}{V_2} = \frac{N_1}{N_2} \]其中,\( V_1 \) 和 \( V_2 \) 分别表示输入端和输出端的电压,\( N_1 \) 和 \( N_2 \) 分别表示输入端和输出端的匝数。
理想变压器的等效电路模型可以通过将理想变压器转化为电路元件来描述。
在这个等效电路模型中,理想变压器被建模为一个变压器符号,其中的变压器匝数比和理想变压器的匝数比相等。
通过这个等效电路模型,我们可以分析电路中的电压变换过程。
接下来,我们来探讨变压器的等效电路。
实际上,真实的变压器在工作过程中会有电阻、电感和磁耗等损耗,因此我们需要考虑这些损耗对电压变换的影响。
变压器的等效电路模型中,通常会引入一个串联电感元件和一个并联电阻元件来描述这些损耗。
通过这个等效电路模型,我们可以更准确地分析变压器的工作性能。
在实际应用中,电路工程师需要根据具体的设计要求选择合适的变压器类型。
理想变压器适用于只关注电压变换比的情况,而变压器的等效电路模型更适用于需要考虑损耗和性能的设计。
根据具体的应用需求,我们可以根据变压器的特性来选择合适的电路模型。
总结起来,电路基础原理中的理想变压器和变压器的等效电路模型是实现电压变换的重要概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理想变压器特性及与等效电路的分
析
理想变压器特性及与等效电路的分析
谭阳红1,汪沨1,陈五立2
(1.湖南大学电气与信息工程学院,湖南长沙410082;
2.湖南信息学院,湖南长沙410151)
摘要:作为电路理论的重要内容,理想变压器的教学重点通常在于理想变压器特性方程及其运用,不涉及磁路分析,这导致学生在分析多绕组变压器时错误运用特性方程。
本文以双绕组和三绕组变压器为例,就磁路形式对理想变压器方程的影响进行分析,导出理想变压器特性方程。
在此基础上,得到其阻抗变换的统一表达式,并得到不同情况
下的实际变压器等效电路,对理想变压器的教学有一定的指导作用。
关键词:理想变压器;特性方程;等效电路
基金项目:本文受国家自然基金及51107034、湖南省自然科学基金资助项目、中央高校基金和湖南省教改课题的资助
器是电路理论教学中的重要部分。
在教学过程中,教学重点往往变压器理想化的条件、掌握特性方程及其运用。
但是,很多学生在分析多绕组变压器时觉得无所适从,甚至错误运用理想变压器的特性方程。
要理解磁路对理想变压器特性方程的影响,必须明确理想化的条件和特性方程的获得方法。
二、双绕组理想变压器特性方程
利用磁路定理来理解理想变压器的特性,只需用以下定律:磁路的基尔霍夫第一定律即磁通连续性原理和磁路的基尔霍夫第二定律,即安培环路定律。
1.双绕组理想变压器电压方程。
考虑
如下的变压器(图1(a)所示),设变压器初次级的原边和副边匝数分别为Np 和Ns,电流为ip 蓸t 蔀、is 蓸t 蔀,铁芯磁导率μ趋近于无穷大,即没有漏磁,磁感应强度全部集中于铁芯。
变压器的初、次级磁链相等,设为ψm。
很明显:
四、结语
本文的分析表明,变压器的特性方程与磁路形式密切相关。
在理想变压器的教学中,采用磁路的分析方法,只有如此,学生才能牢固掌握理想变压器特性方程的本质。
参考文献:
[1]邱关源,罗先觉。
电路[M].第四
版。
北京:高等教育出版社,1999.
[2]于歆杰,朱桂萍,陆文娟。
电路原理[M].北京:清华大学出版社,2007.。
