【重磅】北师大七数下《小车下滑的时间》习题精选
小车的下滑时间--北师大版

严,就是在这么喜庆的时刻也没有任何改变。此刻,他正面无表情地望着眼前的这壹切,既没有喜悦,也没有忧伤,只是不经意间偶尔微蹙壹 下眉梢。来得早的宾客已经等了快壹个时辰了,即使来得晚的,也已经有些微微心急。就在众人翘首以盼,苦苦等待之际,典仪官的壹声“吉 时到”,整个王府立即掀起了壹片欢呼声。仆从们早就各就各位,严阵以待,宾客们蜂拥而至,将新郎团团围住,并簇拥着朝王府大门口走。 门口已经聚集了几十口子人,新郎壹行抵达府门之际,眼看着新娘子的花轿也稳稳当当地停在了王府的大门口!由于今日娶的是侧福晋,因此 婚礼仪式比之大婚轻减了许多,但是新郎官在府门口迎亲的程序仍然必不可少。待八抬大轿抬过了炭火盆、抬过了马鞍子,稳稳当当地落地后, 只见新郎弯弓搭箭,“嗖、嗖、嗖”,手起箭落,三支利箭准确无误地射向轿门。“驱邪避秽保平安!”随着嬷嬷的壹声吉利话出口,众人纷 份发出了赞叹声:“好身手!”“王爷果真了得!”“恭喜四哥!”众人的齐口夸赞并没有给新郎带来任何情绪上的变化,他仍然是壹言未发, 面无表情,放下弓箭之后,转身就朝宴席上走去,留下壹众人等面面相觑,不如如何是好。按照迎亲的惯例,宾客们应该随新郎壹并来到宴席 上,可是?按照迎亲的惯例,原本新郎应该与新娘子共同进府,并送至洞房,留下新娘在洞房等候,新郎来到宴席招呼宾客才是。迎亲迎亲, 这亲还没有迎进府,新郎怎么自己就先走了?百思不得其解的众人们很是难办,犹豫半天也不知道是跟上新郎呢,还是跟着新娘去洞房。就在 这思忖之间,无意之中人们分成了两部分:壹部分人急急慌慌、无可奈何地随着新郎来到了宴席上;另壹部分人则磨磨蹭蹭、故意拖延,只求 壹睹新娘的风采。射过三箭之后,按照常规,该是新娘子下轿的时候了。在嬷嬷的搀扶下,新娘子壹身桃红色凤冠霞披,头蒙喜帕、手捧苹果, 缓缓走下轿来。虽然蒙着红盖头,任谁也不可能真正壹睹新娘的真容,但那纤瘦的身材,端庄的体态,稳健的步伐,令余下在场的每壹个人都 禁不住暗暗发出壹声惊叹:果然是名不虚传!窈窕淑女,君子好逑!于是人们也就更加好奇:这喜帕下的容貌该是何等的娇美模样?喜宴上居 主位的,不是新郎本人,而是二阿哥胤礽,当朝太子殿下!与往日不同的是,由于是四阿哥的喜宴,因此四阿哥--雍亲王位居太子右手,三 阿哥--诚亲王改居太子左手,其它众兄弟们长幼有序分坐余位。虽然刚刚有壹些小小的波折,但是大喜的日子,大家都不想让四哥(弟)为 难,特别是在十三阿哥嘻嘻哈哈的壹番招呼下,众人也都暂时忘记了刚刚的小插曲,热热闹闹地投入到了喜宴之中。因为是四哥的喜宴,各位 兄弟们难得有机会可
6.1 小车下滑的时间(B卷)及答案

- 1 -6.1 小车下滑的时间(B 卷)一、七彩题1.(一题多变题)某种汽车行驶时间t (小时)与汽车油箱的余油量Q (升)有如下关系:上表中反映了哪两个变量之间的关系?其中哪个是自变量?哪个是因变量?(1)一变:根据表中反映的关系,试求出汽车行驶时间为6.5小时时,•油箱的余油量为多少升?(2)二变:已知该汽车每小时行驶100千米,根据表中反映的关系,•那么该汽车最多能行驶多远?二、知识交叉题2.(科内交叉题)边长为8cm 的正方形中间挖去一个边长为xcm 的小正方形(0<•x<8),剩余的四方框形的面积为S ,如图所示.(1)用等式表示S 与x 之间的关系,并指出这一变化过程中的自变量和因变量;(2)当x=6cm 时,求S 的值.- 2 - 3.(科外交叉题)物理课上,王老师给同学们做了弹簧伸长实验,并记录了弹簧的长度随所挂物体的质量的变化而变化的实验数据,如下表:(1)上表反映了哪两个变量之间的关系?其中哪个是自变量?哪个是因变量?(2)根据表中的实验数据,你知道这根弹簧最多能挂多少千克的物体吗?三、实际应用题4.下表反映的是某公司产品的销售收入与销售量之间的关系:(1)自变量和因变量分别是什么?(2)当销售量是5吨时,销售收入是多少?当销售收入为8000元时,销售量是多少?四、经典中考题5.(2008,沈阳,3分)观察图6-1-4中图形的构成规律,根据此规律,第8•个图形中有______个圆.6.(2007,包头,3分)用火柴棒按照如图6-1-5所示的方式搭图形,则第8个图形中,所需火柴棒的根数是________.参考答案一、1.解:反映了汽车油箱的余油量与行驶时间之间的关系,行驶时间是自变量,油箱的余油量是因变量.(1)40-4×6.5=14(升),即汽车行驶时间为6.5小时时,•油箱的余油量为14升.(2)10×100=1000(千米),即该汽车最多能行驶1000千米远.点拨:本题从不同角度考查学生阅读表格并提取有用信息的能力.二、2.解:(1)S=64-x2,挖去的小正方形的边长x是自变量,•剩余的四方框形的面积S 是因变量.(2)当x=6cm时,S=64-62=28(cm2).点拨:本题中剩余的四方框形的面积S随挖去的小正方形的边长x的变化而变化. 3.解:(1)反映了弹簧的长度与所挂物体的质量之间的关系,•其中所挂物体的质量是自变量,弹簧的长度是因变量.(2)(15.5-10)×0.5=2.75(千克),即这根弹簧最多能挂2.75千克的物体.三、4.解:(1)销售量是自变量,销售收入是因变量.(2)当销售量是5吨时,销售收入为5000元.当销售收入为8000元时,销售量为8吨.四、5.65 点拨:本题反映了图形中圆的个数与图形序数之间的变化关系,其中图形序数是自变量,对应的图象中圆的个数是因变量.6.25 点拨:本题中图形反映了图形所需火柴棒的根数s与图形序数n•之间的关系是s=3n+1.- 3 -。
北师大版数学七下小车下滑的时间word教案

北师大版实验教科书七年级下册6、1小车下滑的时间教学目标:通过分析小车在斜坡上下滑时高度与时间数据之间的联系,使学生体会小车下滑时间随着高度变化而变化,从而了解变量、自变量和因变量的意义,了解可以用列表示两个变量之间的关系,培养学生分析问题的能力与归纳思维的能力。
教学重点:能从表格的数据中分清什么是变量,自变量、因变量以及因变量随自变量的变化情况。
教学难点:对表格所表达的两个变量关系的理解。
教学方法:多媒体辅助教学教学过程:一、出示投影:1.认图,你从图中看到了什么?借助多媒体展示从17岁以后不同年龄段男孩女孩的身高情况:(1)自身比不同年龄平均身高情况如何?(2)男、女孩不同年龄身高的比情况如何?(3)大致的描述青春期男、女生平均身高的变化情况。
教师指明:这个图形还可以告诉我们很多信息,如什么时候女孩平均身高变化不大,什么时候男孩比女孩身高增长的势头大。
现在我们只研究一个量(比如男孩的平均身高)与另一个量(如男孩年龄)之间的关系,学习这些知识,可以更好地了解自己,关心自己。
二、探索新知识1.投影图表,学生观察思考,逐一回答下面的问题:支撑物10203040506070高度小车下滑时间(1)表格中的数据告诉你什么?当支撑物高度为70厘米时,小车下滑时间是多少?教师明晰:只要是表格中所提供的支撑高度,就可以通过表格容易查找到小车下滑时间的准确值。
(2)如果用H表示支撑物高度,T表示小车下滑时间,随着H逐渐变大,T是如何变化的?(3)H增加10厘米时,T的变化情况相同吗?(4)估计当H=90时,T的值是多少。
你是怎样估计的?2.出示投影:议一议我国从1949年到1999年的人口统计数据如下(精确到亿):(1)如果用X表示时间,Y表示我国人口总数,那么随着X的变化,Y的变化趋势是什么?(2)从1949年起,时间每向后推移10年,我国人口怎样变化的?小结:学生对于两个变量之间的关系不是很理解,不能将两个量联系起来看。
1.小车下滑的时间

1、变量
自变量 因变量
3、表格法2、常量 Nhomakorabea1、婴儿在6个月、1周岁、2周岁时体重分别大约是出生时 的2倍、3倍、4倍,6周岁、10周岁时的体重分别大约是1周 岁是的2倍、3倍。 (1)上述哪些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5千克,请把他在发育过
程中的体重情况填入下表:
(1)据都江堰市旅游局估计,2018的十 一黄金周的最高人流量为17万,那么该 小卖店准备应该多少件矿泉水?
(2)如果游客量是n万人,应该准备多 少件矿泉水?
最高游客量/万
12
13
14
15
16
矿泉水销售量/千件 7
7.5
8
8.5
9
研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮 肥的施用量有如下关系: 氮肥施用量0千克/公顷,土豆产量 15.18吨/公顷;氮肥施用量34千克/公顷,土豆产量21.36吨/公 顷;氮肥施用量67千克/公顷,土豆产量25.72吨/公顷;氮肥施 用量101千克/公顷,土豆产量32.29吨/公顷;氮肥施用量135千 克/公顷,土豆产量34.03吨/公顷;氮肥施用量202千克/公顷, 土豆产量39.45吨/公顷;氮肥施用量259千克/公顷,土豆产量 43.15吨/公顷;氮肥施用量336千克/公顷,土豆产量43.46吨/公 顷;氮肥施用量404千克/公顷,土豆产量40.83吨/公顷,氮肥施 用量471千克/公顷,土豆产量30.75吨/公顷. (1)用表格表示上述两变量的关系。
3、小明在课余时间找了几副度数不同的老花镜,让镜片正对 着太阳光,并上下移动镜片,直到地上的光斑最小。此时他测 量了镜片与光斑的距离,得到如下数据
老花镜的度数D/度
北师大版七年级下册数学《小车下滑的时间》导学案课件PPT板书设计教学实录

---------------------------------------------------------------最新资料推荐------------------------------------------------------北师大版七年级下册数学《小车下滑的时间》导学案课件PPT板书设计教学实录北师大版七年级下册数学《小车下滑的时间》导学案课件 PPT 板书设计教学实录北师大版七年级下册数学《小车下滑的时间》导学案课件 PPT 板书设计教学实录北师大版七年级下册数学《小车下滑的时间》导学案课件 PPT 板书设计教学实录第六章变量之间的关系●课时安排 5 课时第一课时●课题小车下滑的时间●教学目标教学知识点 1.经历探索具体情境中两个变量之间关系的过程,获得探索变量之间关系的体验,进一步发展符号感. 2.在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间慢关系的例子. 3.能从秘表格中获得变量之间关系的麻信息,能用表格表示变量之詹间的关系,并根据表格中的架数据尝试对变化趋势进行初绷步的预测. 能力训练要求脉 1.使学生学会从表格中怎获取信息,发展学生通过数苦据分析进行预测和解决问题慌的能力. 2.发展学生的符含号感和抽象思维能力. 情感咬与价值观要求在探索现咏实世界变化规律的过程中,吧从运动变化的角度认识数学哉对象.提高学生的数学素养偷 .●教学重点借助表格,表验示因变量随自变量变化的情订况.●教学难点将具体创问题抽象成数学问题,由数硫据进行推断. ●教学方法活栋动交流探索相结合锰学生通过探讨小车下滑占时间与支撑物高度关系的活谚动,运用自己的语言描述1 / 7从录表格中获取的信息,并与同菠伴交流,探索、预测变化的哮趋势. ●教具准备一块憎木板,一辆小车,一根 1 米陇长的刻度尺,一块秒表. ● 掏教学过程Ⅰ.创设情景,引炭入新课[师]今天早上褥一起床,我就到厨房烧上了鸳一壶水,10 分钟后,水烧痘开了.在这一过程中,谁知圈道,什么在发生变化?[生游]时间在发生变化. [生]基水的温度也在发生变化. 委[师]很好!你能从生活蕴中找到一些发生变化的例子娄吗?[生]一天的气温在发般生变化. [师]你能大概描众述一下是怎样变化的吗?惺[生]一般情况下,早晨黄 3 时,温度最低;然后温度辞就渐渐地升高;到了下午 2 榆或 3 时温度升到最高;最后阅温度就逐渐的下降. [失师]这位同学描述得很好. 死我们就生活在这样一个变化繁的世界中.从今天开始,我同们就从数学的角度研究这些脑变化的过程,将有助于我们忧更好地认识我们这个世界. 霜首先,我们来做一个试验:趋小车下滑的时间. Ⅱ.讲授便新课[师]我们把全班淫分成 5 个小组,每个小组利开用同一块木板,测量小车从蟹不同高度下滑的时间.然后秉将得到的数据填入下表:彦支撑物高度/厘米 102 惶 030405007080 蝇 90100 小车下滑时间/ 胰秒每个小崩组实验时组员的分工,以及沾实验的步骤由组长负责,咱杨们赛一赛看哪一个组合作的冷最好,试验得到的数据最准衣确. [师]现在,我们膘每一组都得到了一组数据,卜并且我注意到大部分组分工耍合理,团---------------------------------------------------------------最新资料推荐------------------------------------------------------结合作,使实验顺药利地完成.表现最突出的是饰王波学习小组.我们祝贺他郊们小组.其他组的同学再接云再励,争取在后面活动中有硝更为突出的表现. 下面是王澈波学习小组得到的数据:谋支撑物高度/厘米 102 莉 030405007080 柠 90100 小车下滑时间/ 迎秒根据上表来试着回答下列忽问题串:支撑物高度为堡 70 厘米时,小车下滑时间煮是多少?如果用 h 表示辖支撑物高度,t 表示小车下兵滑时间,随着h 逐渐变大,脑 t 变化趋势如何? h 每增加袁 10 厘米,t 的变化情况相希同吗?估计当 h=11 灯 0 厘米时,t 的值是多少?市你是怎样估计的?同学掐们先独立思考,然后用自己克的语言阐述思考过程及理由管 . [生]读表可知:当诈支撑物高度为 70 厘米时,挥小车下滑的时间是秒. 懂[生]从表中可以看出:第禽一行是支撑物高度 h 的值,偷从左往右逐渐增大;第二行斟是小车下滑的时间 t 的值,扬从左往右逐渐减小.由此可碗知,支撑物 h 越高,小车下硷滑时间 t 越短. [师]伟从表格中我们得出上述结论皮,根据我们做的实验和经验爵,谁来解释为什么会有支撑馈物 h 越高,小车下滑时间 t 宇越短呢?这儿我给大家提供霍演示课件. 图 6-1 [咏生]从演示课件不难发现:圣小车是从同一块木板上滑下力的,也就是说,小车滑行的3 / 7肋长度就是木板的长度.当木嫡板支撑得越高,它形成的坡鸳度越陡,下滑的速度越快,罐所用的时间自然就会随着坡金度的升高而逐渐减小. 织[师]很好.我们接着来分淹析表格中的数量关系.通过会观察和计算,h 每增加 10 暖厘米,t 的变化情况相同吗本?[生]不相同.当支抠撑物高度从 10 厘米变化到揖20 厘米,小车下滑的时间焰缩短了-=秒;当支撑物高胞度从 20 厘米变化到 30 厘养米时,小车下滑的时间缩短胎了-=秒;当支撑的高魂度从 90 厘米变化到 100 窒厘米时,小车下滑的时间缩帚短了-=秒. [师]看凿第个问题,根据你能估计当蘸h=110 厘米时,t的值愈是多少?你是如何估计的. 带[生]由可知,h 从 1 脏 0 厘米开始增加时,所用的赵时间t 变化较快;当 h 从 6 彰 0 厘米开始增加时,每增加辆 10 厘米,所用时间 t 每次柱减少约秒、秒、秒.因此当咏 h=110 厘米时,t的值愿可以是秒到秒中任意一个值纲 . [师]由以上问题串黑可知,h 和 t 是两个变化的浑数量,而 h 的每一次变化,恐都会引起 t 的变化,下滑时末间和支撑物高度之间存在着杖相依关系. 接下来,我们再赢来看生活中的一个变化关系招议一议我国从 1949 员年到 1999 年的人口统计轩数据如下:时间/年 1 程 949195919691 押 97919891999 人疫口/亿如果用 x 表示时呜间,y 表示我国人口总数,佛那么随着 x的变化,y 的变酉化趋势是什么?从 19 狂 49 年起,时间每向后推移姨 10 年,我国人口是怎样变废化的?[生]从表格的---------------------------------------------------------------最新资料推荐------------------------------------------------------恤数据可知:随着 x 的增加,栅 y 也增加. [生]从 1 钵 949 年起,1949~1 盼 959 年,我国人口增加亿弧;1959~1969 年,俐我国人口增加亿;1969 上 ~1979 年,我国人口增忧加亿;;1979~198 搜9 年,我国人口增加亿;1 滨 989~1999 年,我国咳人口增加亿. [生]也冶可以说,从 1949 年起,遮时间每向后推移 10年,我轻国人口增加亿左右. [帮师]在前一个问题中,支撑脱物高度 h 和小车下滑的时间谭 t 都在变化,它们都是变量央 .其中t 随 h 的变化而变化够,h 是自变量,t 是因变量崖 . 在第二个问题中,我蒸国人口总数 y 随时间 x 的变代化而变化,x 是自变量,y 勾是因变量. 在此处,变告量用字母表示,更显示了数研学符号的简捷. 而因变抨量随自变量的变化而变化的妖情况,借助于表格就可以表斋示出来. 生活中有哪些罗例子也反映了变量之间的关乙系?并指出哪一个是自变量琐?哪一个是因变量?[策生]气温随时间的变化的过愚程中,时间是自变量,气温茧是因变量. [生]脉搏颧随运动强度的变化过程中,龙运动强度是自变量,脉搏是轧因变量. [生]燃烧的宙蜡烛,高度随燃烧时间而变燕化,其中燃烧时间是自变量必,蜡烛的高度是因变量. 鸡[师]同学们要举的例子经很多很多,说给你的同伴听仟听. Ⅲ.随堂练习研究蛛表明,当钾肥和磷肥的施用用量一定时,土豆的产量与氮泳服的施用量有5 / 7如下关系:谈氮肥施用量/03471 宠 011352022593 遥 3404471 土豆产量/ 真上表反映了哪两个变量蛛之间的关系?哪个是自变量肌?哪个是因变量?当氮号肥的施用量是 101 千克/ 讣公顷时,土豆的产量是多少银?如果不施氮肥呢?根底据表格中的数据,你认为氮烬肥的施用量是多少时比较适皂宜?说说你的理由. 粗略说孺一说氮肥的施用量对土豆产售量的影响. 解答:氮肥绕的施用量和土豆产量之间的开关系;氮肥施用量是自变量阴,土豆产量是因变量;焰当氮肥的施用量是 101 千琉克/公顷时,土豆的产量是绣吨/公顷;如果不施氮肥,友即氮肥施用量为 0 千克/公亚顷,由表格可知,土豆的产嘲量是吨/公顷;可以回匈答氮肥施用量为 336 千克邓 /公顷时比较适宜,因为此晤时土豆的产量最高;还可以遇回答氮肥的施用量为259 终千克/公顷比较适宜,因为往此时土豆的产量与施用量为腹336千克/公顷时差不多兄,而又可以节约肥料;携这里主要关注的是对变化过痈程的大致刻画,学生的答案郁只要合理都应鼓励.例如可囤以这样说,氮肥施用量小于娱336 千克/公顷时,氮肥敖的施用量增加,土豆的产量喷随之增加;但大于 336 千豪克/公顷时,施用量越多,禽土豆的产量越少. Ⅳ.课时渗小结[师]通过今天的禹学习,同学们有何收获和体噪会. [生]今天的学习备,使我认识到我们生活在一急个变化的世界---------------------------------------------------------------最新资料推荐------------------------------------------------------ 中,从数学的摇角度用表格表示两个变量之擞间的关系,并且能从表格中庸获得变量之间的信息,并根膛据表格中的数据尝试对变化秒趋势进行初步的预测. 炭[生]在具体的情境中理解贼了什么是自变量、因变量,娠并能反映变量之间关系的例臃子. [师]在我们的生韵活中反映变量之间关系的例难子很多.例如2019 年春胰季的非典疫情,从 4 月努中旬始,随着时间的变化,佬非典病人人数呈上升趋蚌势,但在白衣天使的舍小家驹,为大家,无私奉献,勇于旬牺牲的精神感化下,全国人畜民在共产党的领导下,万众齿一心,众志成城,战胜了非诌典,到七月底,抗击非典岿已取得了阶段性胜利,鞘非典病人已全部出院.又但一次证明了中华民族是团结财一心,勇敢坚强的民族. 刷我相信,同学们争分夺秒非,锻炼、学习真本领,将来葬随着时间的推移,个个会成闷为祖国栋梁!Ⅴ.课后作业饼 1.课本 P165、习编题第 1、2、3 题; 2 欢 .收集生活中反映变量关系汾的例子. 月. ●板书设计第屈六章变量之间的关系捎小车下滑的时间 1.① 谊支撑物 h 越高,小车下滑时阔间 t 越短;②随着时间 x 的拇增加,我国人口总数 y 增加泵 . 其中 h 和 t,x 和 y 凌都是变量.①中 h 是自变量滁,t 是因变量;②中 x 是自淀变量,y 是因变量. 2 吊 .借助表格,可以表示因变丁量随自变量的变化而变化的沦情况.7 / 7。
【全版】数学七年级下北师大版小车下滑的时间课件推荐PPT

四 教学重点和难点分析 重点:能从表格中发现变量之间存在的关系,
并能用自己的语言描述出来。 难点:将具体问题抽象成数学问题,由数据进
行推断分析。 教具与学具:一块木板、一辆小车、刻度尺、
秒表、容量瓶、多媒体课件。
7
1 创设情境 引入新知 引例1:烧一壶水,10分钟后水烧开了, 在这一过程中,什么在发生变化?你能 从生活中举出一些发生变化的例子吗?
情感与态度:在探索现实世界变化规律的过程中,从运动变化 的角度认识数学对象,提高学生的数学素养,感受数学的值。
4
初一年级学生经历过直线平行、三角形全等条件 的探索过程,初步具备了自主探索与合作交流的能力。 这个年龄段的学生对未知事物有较强的好奇心,对有 挑战性的学习很感兴趣。因此,我在教学过程的安排 上,除了关注学生掌握数学知识外,更注重学生动手 实践、探索新知能力的培养。
5
三 教法与学法分析 教法与学法是互相联系和统一的,不能孤立去研
究。什么样的教法必带来相应的学法,正如《数学课 程标准》所要求的,让学生“动手实践、自主探索、 合作交流 ”因此,以上述思想为出发点,整节课采用 以试验法为主,讨论法为辅的教学方法进行教学,在 整个教学过程中让学生保持强烈的好奇心和求知欲,成 为学习的主人,通过亲身参与,经历数学知识的形成 过程。在掌握基础知识的同时,让学生领会数学在实际 生活中应用的魅力。
时间/分
012345678
容量瓶中水的体 积/毫升
问题: (1)当你观察到第5分钟时,体积是多少? (2)如果用t表示水流出的时间,V表示体积,随着t 逐渐变大,V的变化趋势是什么? (3) t每增加1分钟,V的变化情况相同吗? (4)估计当t=24小时,V的值是多少,你是怎样估计 的? (5)这个实验对你有什么启示?
北师大版七下数学第三章各节练习题含答案

3.1 用表格表示的变量间关系一.选择题:(四个选项中只有一个是正确的,选出正确选项填在题目的括号内)1.一杯开水越晾越凉,这一过程中自变量是()A.时间B.温度C.时间和温度D.空气中的温度2.从深圳往北京打电话,电话费随时间的变化而变化,在这个问题中,因变量是( )A.时间B.电话费C.电话D.距离3.已知电费的收费标准为0.5元/千瓦时,当用电量为x(千瓦时)时,收取电费为y(元);在这个问题中,下列说法中正确的是()A.x是自变量,0.5元/千瓦时是因变量B.B.0.5元/千瓦时是自变量,y是因变量C.y是自变量,x是因变量D.D.x是自变量,y是因变量4.某品牌电饭锅成本价为70元,销售商对其销量与定价的关系进行了调查,结果如下:在这个问题中,下列说法正确的是()A.定价是不变量,销量是变量B.定价是变量,销量是不变量C.定价与销量都是变量,定价是自变量,销量是因变量D.定价与销量都是变量,销量是自变量,定价是因变量5.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x (kg)间有下面的关系:A.x与y都是变量,且x是自变量,y是因变量B.所挂物体质量为4kg时,弹簧长度为12cmC.弹簧不挂重物时的长度为0 cmD.物体质量每增加1kg,弹簧长度y增加0.5 cm6.在实验课上,利用同一块木板测得小车从不同高度(h)下滑时,高度(h)与下滑的时间(t)的关系如下表:下列结论错误的是()A.当40cmh=时,t约为2.66秒B.随高度增加,下滑时间越来越短C.估计当80cmh=时,t一定小于2.56秒D.高度每增加10cm,时间就会减少0.24秒二.填空题:(把正确答案填在题目的横线上)7.在一个变化过程中,如果有两个变量x和y,其中y随x的变化而变化,则x叫做__________,y叫做__________.8.用表格表示两个变量之间的关系:表示两个变量的关系的表格,一般第一行表示______变量,第二行表示______变量,借助表格,可以表示因变量随自变量的变化而变化的情况.9.汽车以m 千米/小时的速度从甲地驶向乙地,若甲、乙两地相距s 千米,当汽车行驶了x 小时后,距离乙地还有y 千米,在这个问题中,常量是__________,变量是__________,其中自变量是__________,因变量是__________.10.下表是某河流在汛期一天中涨水的情况,警戒水位为25米.(1)上表反映了 与时间之间的关系,其中 是自变量, 是因变量;(2) 从0时到24时,水位从 上升到 ; (3) 从 时到 时,水位上升最快;(4) 假设第二天持续下雨(基本与当天降水量一样),则第二天12时超警戒水位 米.11.下表为某商店薄利多销的情况,某商品原价为560元,随着不同幅度的降价,日销量(单位:件)发生相应的变化:这个表反映了______个变量之间的关系,__________是自变量,__________是因变量;从表中可以看出每降价5元,日销量增加__________件,从而可以估计降价之前的日销量为__________件,如果售价为500元,日销量为__________件. 三.解答题:12.下表是学校气象兴趣小组记录某天一昼夜温度变化的数据:(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)早晨8时和中午12时的气温各是多少?(3)根据表格中的数据,说说一昼夜中什么时候气温最低?什么时候气温最高?温差是多少?(4)你能粗略说一说一昼夜内气温随时间变化的大概情况吗?13.下表是某自行车厂某年各月份生产自行车的数量:(2)为什么称自行车的月产量y为因变量?它是谁的因变量?(3)哪个月份自行车产量最高?哪个月份自行车产量最低?(4)哪两个月份间产量相差最大?根据这两个月的产量,自行车厂应采取什么措施?14.实验证明在弹性限度内,弹簧的伸长长度与所挂物体的质量有一定的比例关系,下表是某次实验测得的弹簧的长度y(cm)与所挂物体质量x(kg)的几组对应值:(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)当所挂物体的质量为3kg时,弹簧多长?不挂重物时呢?(3)若所挂物体的质量为7kg时(在弹性限度内),弹簧的长度是多少?3.1 用表格表示的变量间关系(参考答案)1~6 ABDCCD7.自变量;因变量;8.自;因;9.s,m;x,y;x;y;10.(1)超警戒水位,时间,超警戒水位;(2)25.2,26;(3)12,20;(4)26.5;11.两;降价;日销量;30;750;1110;12.(1)反映了气温和时间的关系,时间是自变量,气温是因变量;(2)早上8点的气温是4℃,中午12点的气温是9℃;(3)早晨4时气温最低,午后14时气温最高,温差14℃;(4)0时至4时气温下降到4 ℃,4时至14时逐渐升高到10℃,然后气温又下降.13.(1) 随月份的增加,自行车总产量也逐渐增加;(2) 因为自行车的月产量y随时间x的变化而变化.自行车的月产量y;(3) 6月份产量最高,1月份产量最低;(4) 从6月份到7月份,自行车产量变化最大,下降2万辆,应总结经验教训,改善管理.14.(1)表格反映的是弹簧所挂物体质量与弹簧的长度两个变量之间的关系,弹簧所挂物体质量是自变量,弹簧的长度是因变量;(2)当所挂物体的质量为3kg时,弹簧长24 cm;不挂重物时,弹簧长18 cm;(3)由表中数据变化情况得:若所挂物体的质量为7kg时,弹簧的长度是32cm;3.2《用关系式表示的变量间关系》习题1.图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则下列函数关系中正确的是()A.y=4n-4 B.y=4n C.y=4n+4 D.y=n22.如图,△ABC的底边边长BC=a,当顶点A沿BC边上的高AD向D点移动AE时,△ABC的面积将变为原来的( )到E点,使DE=12A.12B.13C.14D.193.如图,△ABC 的面积是2cm 2,直线l ∥BC ,顶点A 在l 上,当顶点C 沿BC 所在直线向点B 运动(不超过点B )时,要保持△ABC 的面积不变,则顶点A 应( )A.向直线l 的上方运动;B.向直线l 的下方运动;C.在直线l 上运动;D.以上三种情形都可能发生.4.当一个圆锥的底面半径为原来的2倍,高变为原来的13时,它的体积变为原来的( )A.23B.29C.43D.495.如图,△ABC 中,过顶点A 的直线与边B C 相交于点D ,当顶点A沿直线AD 向点D 运动,且越过点D 后逐渐远离点D ,在这一运动过程中,△ABC 的面积的变化情况是( )A.由大变小B.由小变大D CAlCB AC.先由大变小,后又由小变大D.先由小变大,后又由大变小6.如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.(1)在这个变化中,自变量是______,因变量是______;(2)当底面半径由1cm变化到10cm时,圆柱的体积增加了______cm3.7.一个小球由静止开始沿一个斜坡向下滚动,通过仪器观察得到小球滚动的距离s(m)与时间t(s)的数据如下表:写出用t表示s的关系式:________.8.烧一壶水,假设冷水的水温为20℃,烧水时每分钟可使水温提高8℃,烧了x分钟后水壶的水温为y℃,当水开时就不再烧了.(1)y与x的关系式为________,其中自变量是________,它应在________变化.(2)x=1时,y=________,x=5时,y=________.(3)x=________时,y=48.9.设梯形的上底长为x cm,下底比上底多2 cm,高与上底相等,面积为2cm2,则根据题意可列方程为_____.10.用一根长50cm的细绳围成一个矩形.设矩形的一边长为xcm,面积为y cm2.求y与x的函数关系式;11.南方A市欲将一批容易变质的水果运往B市销售,若有飞机、火车、汽车三种运输方式,现只选择其中一种,这三种运输方式的主要参考数据如下表所示:若这批水果在运输(包括装卸)过程中的损耗为200元/h,记A、B两市间的距离为x km (1)如果用W1、W2、W3分别表示使用飞机、火车、汽车运输时的总支出费用(包括损耗),求W1、W2、W3与x间的关系式;(2)当x=250时,应采用哪种运输方式,才使运输时的总支出费用最小? 12.一个梯形,它的下底比上底长2cm,它的高为3cm,设它的上底长为x cm,它的面积为y cm2.(1)写出y与x之间的关系式,并指出哪个变量是自变量,哪个变量是因变量.(2)当x由5变7时,y如何变化?(3)用表格表示当x从3变到10时(每次增加1),y的相应值.(4)当x每增加1时,y如何变化?说明你的理由.13.已知水池中有800立方米的水,每小时抽50立方米.(1)写出剩余水的体积Q(立方米)与时间t(小时)之间的函数关系式;(2)6小时后池中还有多少水?(3)几小时后,池中还有200立方米的水?14.一辆加满汽油的汽车在匀速行驶中,油箱中的剩余油量Q(L)与行驶的时间t(h)的关系如下表所示:请你根据表格,解答下列问题:(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)随着行驶时间的不断增加,油箱中剩余油量的变化趋势是怎样的?(3)请直接写出Q与t的关系式,并求出这辆汽车在连续行驶6h后,油箱中的剩余油量;(4)这辆车在中途不加油的情况下,最多能连续行驶的时间是多少?15.用一根长是20cm的细绳围成一个长方形(如图),这个长方形的一边的长为x cm,它的面积为y cm2.(1)写出y与x之间的关系式,在这个关系式中,哪个是自变量?它的取值应在什么范围内?(2)用表格表示当x从1变到9时(每次增加1),y的相应值;(3)从上面的表格中,你能看出什么规律?(4)猜想一下,怎样围法,得到的长方形的面积最大?最大是多少参考答案1.答案:B解析:【解答】由图可知n=1时,圆点有4个,即y=4;n=2时,圆点有8个,即y=8;n=3时,圆点有12个,即y=12,∴y=4n.故选B【分析】由图观察可知.2.答案:B解析:【解答】根据三角形的面积公式判断△ABC的面积将变为原来的三分之一.故选B.【分析】由图观察可知根据三角形的面积公式.3.答案:A解析:【解答】根据三角形的面积公式判断当顶点C沿BC所在直线向点B 运动时,三角形的底变小,则要保持△ABC的面积不变,高就要增大,即顶点A应向直线l的上方运动.故选A.【分析】由图观察可知根据三角形的面积公式.4.答案:C解析:【解答】设圆锥的底面半径为r,高为h,即可表示出变化后的底面半径和高,再根据圆锥的体积公式分别表示出原来的体积和变化后的体积,比较即可得到结果.故选C.【分析】根据圆锥的体积公式分别表示出原来的体积和变化后的体积.5.答案:C解析:【解答】由题意得,这个过程中△ABC的底始终不变,根据三角形的面积公式即可判断. 由题意得,这个过程中△ABC的底始终不变,则△ABC 的面积的变化情况是先由大变小,后又由小变大.故选C.【分析】根据三角形的面积公式即可判断.6.答案:(1)半径,体积;(2)297π.解析:【解答】(1)根据函数的定义可知,对于底面半径的每个值,体积按照一定的法则有一个确定的值与之对应,所以自变量是:半径,因变量是:体积.(2)体积增加了(π×102-π×12)×3=297πcm3.故答案为:(1)半径,体积;(2)297π.【分析】根据函数的定义.圆柱的高没有变化,只有底面积变化,因此计算底面积之差即可.7.答案:s=2t2(t≥0).21解析:【解答】观察表中给出的t与s的对应值,再进行分析,归纳得出关系式.t=1时,s=2×12;t=2时,s=2×22;t=3时,s=2×32;t=4时,s =2×42,…所以s与t的关系式为s=2t2,其中t≥0.故答案为s=2t2(t≥0).21【分析】观察表中给出的t与s的对应值,归纳出关系式.8.答案:(1)y=8x+20 x 在0--10变化;(2)28 60;(3)3.5解析:【解答】(1)根据题意,在20℃的基础上x和y有一定的变化规律,即y=8x+20;水温是随着时间的变化而变化的,因此自变量是时间x;当水温y=100时,水沸腾,因此时间x=10,所以x的变化范围是0≤x≤10.(2) x=1时,代入关系式y=28 x=5时代入关系式y=60(3)把y=48代入关系式,变形计算出x=3.5.【分析】先根据题意列出函数关系式,再依次代入求值即可9.答案为:x2+x-2=0解析:【解答】设这个梯形上底边长为x c m,那么下底就应该为(x+2)cm,高为x cm,根据梯形的面积公式得(2x+2)x÷2=2,化简后得x2+x-2=0.故答案为:x2+x-2=0【分析】如果设这个梯形上底边长为x cm,那么下底就应该为(x+2)cm,高为x cm,根据梯形的面积公式即可列出方程.10.答案:y=-x2+25x解析:【解答】设矩形的一边长为x cm,面积为y cm2,根据题意得出:y=-x2+25x答案为:y=-x2+25x【分析】先利用长方形的面积公式列出二次函数关系式即可.11.答案:见解析过程x+2)=17x+1400解析:【解答】(1)W1=16x+1000+200(200x+4)=6x+2800W2=4x+2000+200(100x+2)=12x+1400W3=8x+1000+200(50(2)当x=250时,W1=17×250+1400=5650(元)W2=6×250+2800=4300(元)W3=12×250+1400=4400(元),因为W1>W2>W3,所以应采用火车运输,才能使运输时的总支出费用最小.【分析】(1)根据表格中的关系列出式子:总费用=(运输时间+装卸时间)×损耗+途中费用×距离+装卸费用,依次代入数据即可.(2)x=250,依次代入关系式比较计算结果即可.(2)当x由5变到7时,y由18变到24(3)(4)x每增加1时,y增加3,这是因为:当x变为x+1时,y由3x+3变为3(x+1)+3=(3x+3)+3【分析】根据梯形的面积公式列出关系式,依次代入数值计算即可. 13.答案:见解答过程解析:【解答】(1)Q=800-50t(0≤t≤16);(2)当t=6时,Q=800-50×6=500(立方米).答:6小时后,池中还剩500立方米的水;(3)当Q=200时,800-50t=200,解得t=12.答:12小时后,池中还有200立方米的水.【分析】(1)根据“抽水时间×抽水速度=抽水量”,“蓄水量-抽水量=剩余水量”解题即可;(2)根据自变量与因变量的关系式,可得自变量相应的值;(3)根据自变量与因变量的关系式,可得相应自变量的值.14.答案:见解答过程.解析:【解答】(1)表中反映的是油箱中剩余油量Q(L)与行驶时间t(h)的变量关系,时间t是自变量,油箱中剩余油量Q是因变量;(2)随着行驶时间的不断增加,油箱中的剩余油量在不断减小;(3)由题意可知汽车行驶每小时耗油7.5L,Q=54-7.5t;把t=6代入得Q =54-7.5×6=9(L);(4)由题意可知汽车行驶每小时耗油7.5L,油箱中原有54L汽油,可以供汽车行驶54÷7.5=7.2(h).答:最多能连续行驶7.2h.【分析】(1)认真分析表中数据可知,油箱中剩余油量Q(L)与行驶时间t(h)的变量关系,再根据自变量、因变量的定义找出自变量和因变量;(2)由表中数据可知随着行驶时间的不断增加,油箱中剩余油量的变化趋势;(3)由分析表中数据可知,每行驶1h消耗油量为7.5L.然后根据此关系写出油箱中剩余油量Q(L)与行驶时间t(h)的代数式;(4)根据图表可知汽车行驶每小时耗油7.5L,油箱原有汽油54L,即可求出油箱中原有汽油可以供汽车行驶多少小时.15.答案:见解答过程解析:【解答】(1)y=2022x·x=(10-x)·x,x是自变量,它的值应在0到10之间(不包括0和10)(2)(3)可以看出:①当x逐渐增大时,y的值先由小变大,后又由大变小;②y的值在由小变大的过程中,变大的速度越来越慢,反过来y的值在由大变小的过程中,变小的速度越来越快;③当x取距5等距离的两数时,得到的两个y值相等.(4)从表中可以发现x=5时,y取到最大的值25.【分析】解答本题的关键是熟练掌握长方形的面积公式,同时熟记在一个变化的过程中,数值发生变化的量称为变量,函数值为因变量,另一个值为自变量.3.3 用图像表示变量间的关系同步测试一、单选题(共9题;共18分)1.2017年“中国好声音”全国巡演新安站在奥体中心举行.童童从家出发前往观看,先匀速步行至轻轨车站,等了一会儿,童童搭乘轻轨至奥体中心观看演出,演出结束后,童童搭乘邻居刘叔叔的车顺利到家.其中x表示童童从家出发后所用时间,y表示童童离家的距离.下图能反映y与x的函数关系式的应该图象是()A. B.C. D.2.函数y=的图象为()A. B.C. D.3.小明的父母出去散步.从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后用15分钟返回家,则表示父亲、母亲离家距离与时间的关系是()A. ④②B. ①②C. ①③D. ④③4.小华家距离县城15km,星期天8:00,小华骑自行车从家出发,到县城购买学习用品,小华与县城的距离y(km)与骑车时间x(h)之间的关系如图所示,给出以下结论:①小华骑车到县城的速度是15km/h;②小华骑车从县城回家的速度是13km/h;③小华在县城购买学习用品用了1h;④B点表示经过h,小华与县城的距离为15km(即小华回到家中),其中正确的结论有()A. 1个B. 2个C. 3个D. 4个5.如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是()A. B.C. D.6.如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为()A. 1.1千米B. 2千米C. 15千米D. 37千米7.已知P(x1,1),Q(x2,2)是一个函数图象上的两个点,其中x1<x2<0,则这个函数图象可能是()A. B.C. D.8.均匀地向如图的容器中注满水,能反映在注水过程中水面高度h随时间t 变化的函数图象是()A. B.C. D.9.一个面积等于3的三角形被平行于一边的直线截成一个小三角形和梯形,若小三角形和梯形的面积分别是y和x,则y关于x的函数图象大致是图中的()A. B.C. D.二、填空题(共5题;共5分)10.为了增强抗旱能力,保证今年夏粮丰收,某村新建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图1所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图2所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是________ .11.如图是甲、乙两种固体物质在0°C—50°C之间的溶解度随温度变化的曲线图,某同学从图中获得如下几条信息:①30°C时两种固体物质的溶解度一样;②在0°C—50°C之间,甲、乙两固体物质的溶解度随温度上升而增加;③在0°C—40°C之间,甲、乙两固体物质溶解度相差最多是10g;④在0°C—50°C之间,甲的溶解度比乙的溶解度高.其中正确的信息有:________ (只要填序号即可).12.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系的图象如图所示,则休息后园林队绿化面积为________ 平方米.13.如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B 出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C 时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ 的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线0M为抛物线的一部分),则下列结论:①BC=BE=5cm;②=;③当0<t≤5时,y=t2;④矩形ABCD的面积是10cm2.其中正确的结论是________ (填序号).14.小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x (分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.三、解答题(共2题;共20分)15.2007年的夏天,湖南省由于持续高温和连日无雨,水库蓄水量普遍下降,如图是某水库的蓄水量V(万立方米)与干旱持续时间t(天)之间的关系图,请根据此图,回答下列问题:(1)该水库原蓄水量为多少万立方米?持续干旱10天后,水库蓄水量为多少万立方米?(2)若水库的蓄水量小于400万立方米时,将发出严重干旱警报,请问持续干旱多少天后,将发出严重干旱警报?(3)按此规律,持续干旱多少天时,水库将干涸?16.某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:(1)求该团去景点时的平均速度是多少?(2)该团在旅游景点游玩了多少小时?(3)求返回到宾馆的时刻是几时几分?四、综合题(共2题;共33分)17.如图,这是反映爷爷每天晚饭后从家中出发去元宝山公园锻炼的时间与距离之间关系的一幅图.(1)如图反映的自变量、因变量分别是什么?(2)爷爷每天从公园返回用多长时间?(3)爷爷散步时最远离家多少米?(4)爷爷在公园锻炼多长时间?(5)计算爷爷离家后的20分钟内的平均速度.18.如图是甲、乙两人同一地点出发后,路程随时间变化的图象.(1)此变化过程中,________是自变量,________是因变量.(2)甲的速度________乙的速度.(大于、等于、小于)(3)6时表示________;(4)路程为150km,甲行驶了________小时,乙行驶了________小时.(5)9时甲在乙的________(前面、后面、相同位置)(6)乙比甲先走了3小时,对吗?________.第三章变量之间的关系单元测试题一、选择题(3分×10=30分)1.某超市某种商品的单价为70元/件,若买x件该商品的总价为y元,则其中的常量是( )A.70 B.xC.y D.不确定2.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )A.太阳光强弱B.水的温度C.所晒时间D.热水器3.变量x与y之间的关系是y=2x-3,当因变量y=6时,自变量x的值是( ) A.9 B.15C.4.5 D.1.54.某种签字笔的单价为2元,购买这种签字笔x支的总价为y元.则y与x之间的关系式为( )A.y=-12x B.y=12xC.y=-2x D.y=2x5.为了加强爱国主义教育,每周一学校都要举行庄严的升旗仪式,同学们凝视着冉冉上升的国旗,下列哪个函数图象能近似地刻画上升的国旗离旗杆顶端的距离与时间的关系( )6.根据图示的程序计算变量y的对应值,若输入变量x的值为-1,则输出的结果为( ) A.-2 B.2C.-1 D.07.某大剧场地面的一部分为扇形,观众席的座位数按下列方式设置:y是自变量;③y=50+3x;④y=47+3x,其中正确的结论有( )A.1个B.2个C.3个D.4个8.李大爷要围成一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的长方形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的关系式是( )A.y=-2x+24(0<x<12) B.y=-12x+12(0<x<24)C.y=2x-24(0<x<12) D.y=12x-12(0<x<24)9.在关系式y=5x+3中,有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x的值无关;④用关系式表示的,不能用图象表示;⑤y 与x的关系还可以用列表如图象法表示.其中,正确的是( )A.①②③B.①②④C.①②⑤D.①④⑤10.一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车离乙地的路程s(千米)与行驶时间t(小时)的关系如图所示,则下列结论中错误的是( )A.甲、乙两地的路程是400千米B.慢车行驶速度为60千米/小时C.相遇时快车行驶了150千米D.快车出发后4小时到达乙地二、填空题(3分×8=24分)11.在求补角的计算公式y=180°-x中,变量是,常量是.12.“早穿皮袄,午穿纱,围着火炉吃西瓜”这句谚语反映了我国新疆地区一天中,随变化而变化,其中自变量是,因变量是.13.若一个长方体底面积为60cm2,高为h cm,则体积V(cm3)与h(cm)的关系式为,若h从1cm变化到10cm时,长方体的体积由cm3变化到cm3.14.李老师带领x名学生到某动物园参观,已知成人票每张20元,学生票每张10元.设门票的总费用为y元,则y=.15.如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8点从同一地点出发,请你根据图中给出的信息,算出乌龟在点追上兔子.16.某种储蓄的月利率是0.2%,存入100元本金后,不扣除利息税,本息和y(元)与所存月数x(x为正整数)之间的关系为,4个月的本息和为.17.如图是小明从学校到家里行进的路程s(米)与时间t(分)的图象,观察图象,从中得到如下信息:①学校离小明家1000米;②小明用了20分钟到家;③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快,其中正确的有(填序号).18.如图(1),在直角梯形ABCD中,动点P从点B出发,沿BC、CD运动至点D停止.设点P运动的路程为x,三角形ABP的面积为y,如果y关于x的函数图象如图(2)所示,则三角形BCD的面积是.三、解答题(共66分)19.(8分)某商场经营一批进价为a元/台的小商品,经调查得如下数据:(1)(2)用语言描述日销售量y和日销售额t随销售价x变化而变化的情况.20.(8分)温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?21.(8分)科学家研究发现,声音在空气中传播的速度y(米/秒)与气温x(℃)有关:当气温是0℃时,音速是331米/秒;当气温是5℃时,音速是334米/秒;当气温是10℃时,音速是337米/秒;当气温是15℃时,音速是340米/秒;当气温是20℃时,音速是343米/秒;当气温是25℃时,音速是346米/秒;当气温是30℃时,音速是349米/秒.(1)请你用表格表示气温与音速之间的关系;(2)表格反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(3)当气温是35℃时,估计音速y可能是多少?(4)能否用一个式子来表示两个变量之间的关系?22.(10分)汽车在山区行驶过程中,要经过上坡、下坡、平路等路段,在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快乐,平路上保持匀速行驶,如图表示了一辆汽车在山区行驶过程中,速度随时间变化的情况.(1)汽车在哪些时间段保持匀速行驶?时速分别是多少?(2)汽车遇到了几个上坡路段?几个下坡路段?在哪个下坡路段上所花时间最长?(3)用自己的语言大致描述这辆汽车的行驶情况,包括遇到的山路,在山路上的速度变化情况等.。
七年级下册第六章《小车下滑的时间》教案word资料10页

北师版七年级下册第六章《小车下滑的时间》教案教材:北师版七年级下册第六章第一节教学目标:(一)知识目标:在具体情境中理解什么是变量、自变量、因变量,并能举出反应变量之间关系的例子。
(二)能力目标:能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,并能根据表格中的数据尝试对变化趋势进行初步的预测。
(三)过程目标:经历探索具体情境中两个变量关系的过程,获得探索变量关系的直观体验,并体会收集数据、整理数据、由数据进行推断的思考方式,进一步发展符号感。
(四)情感目标:体会数学的概念来自于实践生活,感受探究变量关系在生活中的应用,树立积极参与、勇于探索的科学态度教学重点:在具体情境中理解什么是变量、自变量、因变量,并能从表格中获得变量之间关系的信息,进而对变化趋势进行初步的预测。
教学难点:从表格中获得变量之间关系的信息,并对变化趋势进行初步的预测。
教学过程:(一)创设情景,合理引入多媒体演示自然界中花草的生长变化。
提问:1、在我们的生活中,你还观察到哪些变化?(教师要及时指出学生回答中出现的变化的量,并对能举出具有相依关系的变化的量的同学给予肯定。
)2、我们都知道身高随着年龄的变化而变化,可是你们知道青春期男、女孩身高随年龄的变化有什么不同吗?想知道自己的身高是在平均身高之上还是之下吗??你想估计自己18岁时身高是多少吗???(三个最感兴趣的问题使学生的探究欲望高涨,教师此时抛出课本上《青春期男女孩身高随年龄变化》的曲线图,让学生自己通过对图像中变量关系的分析,得出以上问题的答案。
)在学生深切感受到研究变量关系的意义(有助于我们更好地了解自己、认识世界、预测未来)后,引出本节课题:通过实验《小车下滑的时间》,来获得探究变量之间关系的体验。
板书:6.1小车下滑的时间(二)实验探究,合理估测(1) 亲做实验感受变化让学生观察多媒体演示《小车下滑时间》的实验,同时思考两个问题:1、实验是如何操作的?2、实验是在探究小车下滑的时间与哪一个变化的量之间的关系?在学生仔细观察演示,得出实验步骤和实验目的后,让学生根据生活经验,猜想小车下滑的时间与支撑物高度之间有怎样的变化关系,在学生对各种猜测无法确定时,教师告诉学生,可由学生自己组织,亲做实验来验证以上猜想。
6.1 小车下滑的时间(含答案)-

6.1 小车下滑的时间◆基础训练一、选择题1.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是().A.物体 B.速度 C.时间 D.空气2.小明从成都给远在上海的爷爷打电话,电话费随着时间的变化而变化,在这个过程中,因变量是()A.小明 B.电话费 C.时间 D.爷爷3.在实验课上,小亮利用同一块木板测得小车从不同高度(h)与下滑的时间(t)•的关下列结论错误的是().A.当h=40时,t约2.66秒B.随高度增加,下滑时间越来越短C.估计当h=80cm时,t一定小于2.56秒D.高度每增加了10cm,时间就会减少0.24秒二、填空题4.小丽烧一壶水,发现在一定时间内温度随时间的变化而变化,即随时间的增加,温度逐渐增高,如果用t表示时间,T表示温度,则_______是自变量,_______•是因变量.5.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍;•以上叙述中,________发生变化,自变量是_______,因变量是________.三、解答题6(1(2)画折线图表示出两个变量的关系.(3)借助表格,分析哪段时间内水位上升最快?7.某客运公司的行李托运收费为:行李是1千克时,收费4元,以后每增加1千克(不足1千克的按1千克计)需增加费用0.8元.(1)请用表格表示托运行李重量与费用之间的关系.(2)在上述变化过程中,自变量和因变量各是什么?(3)若某人要托运的行李重量为21.24千克,那么他要付费多少元?◆能力提高一、填空题8(1)此变化过程中_______是自变量,_______是因变量;(2)树苗高度h与栽种的年数n的关系式为_______;(3)栽种后_____后,树苗能长到280厘米.9.下表所列为某商店薄利多销的情况.某商品原价为560元,•随着不同幅度的降价,日销量(单位为件)发生相应的变化(如表):这个表反映了_______个变量之间的关系,______是自变量,______是因变量.从表中可以看出每降价5元,日销量增加______件,•从而可以估计降价之前的日销量为______件,如果售价为500元时,日销量为_________件.二、解答题10.小明学了地理,发现了距离地面越远,温度越低,并收集了一些数据,如下表:(1(2)如果用h表示距离地面的高度,用t表示温度,随t的变化,t如何变化?(3)距离地面5千米的高空温度是多少?(4)你能猜出距离地面8千米的高空温度是多少吗?11.据有关资料记载,1986年至1995年间中国教育经费总支出分别为:1986•年为363.43亿元,1987年为385.11亿元,1988年为443.53亿元,1989年为594.67亿元,1990年为659.36亿元,1991年为731.50亿元,1992年为867.05亿元,1993年为1059.94亿元,1994年为1488.78亿元,1995年为1877.95亿元.试用表格表示上面的数据,•并粗略地说明中国教育经费总支出随时间的推移而变化的情况.◆拓展训练12.某航空公司邮递物品时,通常需要交纳一定的航空运输费用,•下表表示了它们之间的关系.(1)按照下表填空:(2)上述哪些量在变化?自变量和因变量各是什么?(3)你能画出自变量和因变量关系的图象吗?答案:1.C 2.B 3.D 4.t,T 5.年龄和体重,年龄,体重6.(1)表中反映了河水水位与时间的变化关系(2)略(3)20时到24时之间水位上升了2米,是最快的.7.略 8.(1)栽种以后的年数,树苗的高度(2)h=80+25n (3)8,9 两,降价(元),日销量,30件,750件,1110件10.(1)高度,温度,高度,温度;(2)t逐渐降低(3)-10℃(4)-28℃11.通过观察表格可知中国教育经费支出在逐年增加,而且注入力度越来越大.12.(1(2)运输费随邮递货物的价格变化而变化,邮递货物价格是自变量,•运输费是因变量.(3)。
北师大版七年级下册数学《小车下滑的时间》导学案课件PPT板书设计教学实录

北师大版七年级下册数学《小车下滑的时间》导学案课件PPT板书设计教学实录北师大版七年级下册数学《小车下滑的时间》导学案课件PPT板书设计教学实录第六章变量之间的关系●课时安排5课时第一课时●课题§6.1小车下滑的时间●教学目标(一)教学知识点1.经历探索具体情境中两个变量之间关系的过程,获得探索变量之间关系的体验,进一步发展符号感.2.在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子.3.能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,并根据表格中的数据尝试对变化趋势进行初步的预测.(二)能力训练要求1.使学生学会从表格中获取信息,发展学生通过数据分析进行预测和解决问题的能力.2.发展学生的符号感和抽象思维能力.(三)情感与价值观要求在探索现实世界变化规律的过程中,从运动变化的角度认识数学对象.提高学生的数学素养.●教学重点借助表格,表示因变量随自变量变化的情况.●教学难点将具体问题抽象成数学问题,由数据进行推断.●教学方法活动——交流——探索相结合学生通过探讨小车下滑时间与支撑物高度关系的活动,运用自己的语言描述从表格中获取的信息,并与同伴交流,探索、预测变化的趋势.●教具准备一块木板,一辆小车,一根1米长的刻度尺,一块秒表.●教学过程Ⅰ.创设情景,引入新课[师]今天早上一起床,我就到厨房烧上了一壶水,10分钟后,水烧开了.在这一过程中,谁知道,什么在发生变化?[生]时间在发生变化.[生]水的温度也在发生变化.[师]很好!你能从生活中找到一些发生变化的例子吗?[生]一天的气温在发生变化.[师]你能大概描述一下是怎样变化的吗?[生]一般情况下,早晨3时,温度最低;然后温度就渐渐地升高;到了下午2或3时温度升到最高;最后温度就逐渐的下降.[师]这位同学描述得很好.我们就生活在这样一个变化的世界中.从今天开始,我们就从数学的角度研究这些变化的过程,将有助于我们更好地认识我们这个世界.首先,我们来做一个试验:小车下滑的时间.(板书课题:第六章变量之间的关系§6.1小车下滑的时间)Ⅱ.讲授新课[师]我们把全班分成5个小组,每个小组利用同一块木板,测量小车从不同高度下滑的时间.然后将得到的数据填入下表:支撑物高度/厘米 10 20 30 40 50 60 70 80 90 100 小车下滑时间/秒每个小组实验时组员的分工,以及实验的步骤由组长负责,咱们赛一赛看哪一个组合作的最好,试验得到的数据最准确.(在此过程中,老师针对不同的组给以适当的指导,关注一下是否每个学生都积极地进行活动,并很好地与同学合作)[师]现在,我们每一组都得到了一组数据,并且我注意到大部分组分工合理,团结合作,使实验顺利地完成.表现最突出的是王波学习小组.我们祝贺他们小组.其他组的同学再接再励,争取在后面活动中有更为突出的表现.下面是王波学习小组得到的数据:支撑物高度/厘米 10 20 30 40 50 60 70 80 90 100小车下滑时间/秒 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35根据上表来试着回答下列问题串:(出示投影片§6.1 A)(1)支撑物高度为70厘米时,小车下滑时间是多少?(2)如果用h表示支撑物高度,t表示小车下滑时间,随着h逐渐变大,t变化趋势如何?(3)h每增加10厘米,t的变化情况相同吗?(4)估计当h=110厘米时,t的值是多少?你是怎样估计的?同学们先独立思考,然后用自己的语言阐述思考过程及理由.[生]读表可知:当支撑物高度为70厘米时,小车下滑的时间是1.59秒.[生]从表中可以看出:第一行是支撑物高度h的值,从左往右逐渐增大;第二行是小车下滑的时间t的值,从左往右逐渐减小.由此可知,支撑物h越高,小车下滑时间t 越短.[师]从表格中我们得出上述结论,根据我们做的实验和经验,谁来解释为什么会有支撑物h越高,小车下滑时间t越短呢?这儿我给大家提供演示课件.图6-1[生]从演示课件不难发现:小车是从同一块木板上滑下的,也就是说,小车滑行的长度就是木板的长度.当木板支撑得越高,它形成的坡度越陡,下滑的速度越快,所用的时间自然就会随着坡度的升高而逐渐减小.[师]很好.我们接着来分析表格中的数量关系.通过观察和计算,h每增加10厘米,t的变化情况相同吗?[生]不相同.当支撑物高度从10厘米变化到20厘米,小车下滑的时间缩短了4.23-3.00=1.23秒;当支撑物高度从20厘米变化到30厘米时,小车下滑的时间缩短了3.00-2.45=0.55秒;……当支撑的高度从90厘米变化到100厘米时,小车下滑的时间缩短了1.41-1.35=0.06秒.[师]看第(4)个问题,根据(3)你能估计当h=110厘米时,t的值是多少?你是如何估计的.[生]由(3)可知,h从10厘米开始增加时,所用的时间t变化较快;当h从60厘米开始增加时,每增加10厘米,所用时间t每次减少约0.09秒、0.09秒、0.06秒.因此当h=110厘米时,t的值可以是1.35秒到1.29秒中任意一个值.[师]由以上问题串可知,h和t是两个变化的数量,而h的每一次变化,都会引起t的变化,下滑时间和支撑物高度之间存在着相依关系.接下来,我们再来看生活中的一个变化关系(出示投影片§6.1 B)议一议我国从1949年到1999年的人口统计数据如下(精确到0.01亿):时间/年 1949 1959 1969 1979 1989 1999人口/亿 5.42 6.72 8.07 9.75 11.07 12.59(1)如果用x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是什么?(2)从1949年起,时间每向后推移10年,我国人口是怎样变化的?[生]从表格的数据可知:随着x的增加,y也增加.[生]从1949年起,1949~1959年,我国人口增加1.30亿;1959~1969年,我国人口增加1.35亿;1969~1979年,我国人口增加1.68亿;;1979~1989年,我国人口增加1.32亿;1989~1999年,我国人口增加1.52亿.[生]也可以说,从1949年起,时间每向后推移10年,我国人口增加1.5亿左右.[师]在前一个问题中,支撑物高度h和小车下滑的时间t都在变化,它们都是变量.其中t随h的变化而变化,h 是自变量,t是因变量.在第二个问题中,我国人口总数y随时间x 的变化而变化,x是自变量,y是因变量.在此处,变量用字母表示,更显示了数学符号的简捷.而因变量随自变量的变化而变化的情况,借助于表格就可以表示出来.生活中有哪些例子也反映了变量之间的关系?并指出哪一个是自变量?哪一个是因变量?[生]气温随时间的变化的过程中,时间是自变量,气温是因变量.[生]脉搏随运动强度的变化过程中,运动强度是自变量,脉搏是因变量.[生]燃烧的蜡烛,高度随燃烧时间而变化,其中燃烧时间是自变量,蜡烛的高度是因变量.[师]同学们要举的例子很多很多,说给你的同伴听听.(让学生充分交流,教师深入到学生中,尽可能多地启发学生发现生活中的变量之间关系的例子.)Ⅲ.随堂练习研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮服的施用量有如下关系:氮肥施用量/(千克/公顷) 0 34 67 101 135 202 259 336 404 471土豆产量/(吨/公顷) 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.(4)粗略说一说氮肥的施用量对土豆产量的影响.解答:(由学生口答完成)(1)氮肥的施用量和土豆产量之间的关系;氮肥施用量是自变量,土豆产量是因变量;(2)当氮肥的施用量是101千克/公顷时,土豆的产量是32.29吨/公顷;如果不施氮肥,即氮肥施用量为0千克/公顷,由表格可知,土豆的产量是15.18吨/公顷;(3)(学生的答案只要合理即可)可以回答氮肥施用量为336千克/公顷时比较适宜,因为此时土豆的产量最高;还可以回答氮肥的施用量为259千克/公顷比较适宜,因为此时土豆的产量与施用量为336千克/公顷时差不多,而又可以节约肥料;(4)这里主要关注的是对变化过程的大致刻画,学生的答案只要合理都应鼓励.例如可以这样说,氮肥施用量小于336千克/公顷时,氮肥的施用量增加,土豆的产量随之增加;但大于336千克/公顷时,施用量越多,土豆的产量越少.Ⅳ.课时小结[师]通过今天的学习,同学们有何收获和体会.[生]今天的学习,使我认识到我们生活在一个变化的世界中,从数学的角度用表格表示两个变量之间的关系,并且能从表格中获得变量之间的信息,并根据表格中的数据尝试对变化趋势进行初步的预测.[生]在具体的情境中理解了什么是自变量、因变量,并能反映变量之间关系的例子.[师]在我们的生活中反映变量之间关系的例子很多.例如XX年春季的“非典”疫情,从4月中旬始,随着时间的变化,“非典”病人人数呈上升趋势,但在白衣天使的舍小家,为大家,无私奉献,勇于牺牲的精神感化下,全国人民在共产党的领导下,万众一心,众志成城,战胜了非典,到七月底,抗击“非典”已取得了阶段性胜利,“非典”病人已全部出院.又一次证明了中华民族是团结一心,勇敢坚强的民族.我相信,同学们争分夺秒,锻炼、学习真本领,将来随着时间的推移,个个会成为祖国栋梁!Ⅴ.课后作业1.课本P165、习题6.1第1、2、3题;2.收集生活中反映变量关系的例子.月.●板书设计第六章变量之间的关系§6.1小车下滑的时间1.①支撑物h越高,小车下滑时间t越短;②随着时间x的增加,我国人口总数y增加.其中h和t,x和y都是变量.①中h是自变量,t是因变量;②中x是自变量,y是因变量.2.借助表格,可以表示因变量随自变量的变化而变化的情况.。
七年级下《3.1用表格表示的变量间关系》课时练习含答案解析

北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习一、选择题(共15小题)1.在利用太阳能热水器来加热水的过程中,热水器里的水温会随着太阳照射时间的长短而变化,这个问题中因变量是()A.水的温度B.太阳光强弱C.太阳照射时间D.热水器的容积答案:A解析:解答:根据函数的定义可知,水温是随着所晒时间的长短而变化,可知水温是因变量,所晒时间为自变量.故选:A分析:函数的定义:设在某变化过程中有两个变量x、y,如果对于x在某一范围内的每一个确定的值,y都有唯一的值与它对应,那么称y是x的函数,x叫自变量.函数关系式中,某特定的数会随另一个(或另几个)会变动的数的变动而变动,就称为因变量.2.对于圆的周长公式C=2πR,下列说法错误的是()A.π是变量B.R、C是变量C.R是自变量D.C是因变量答案:A解析:解答:A.是一个常数,是常量,故选项符合题意;B.R、C是变量,故选项不符合题意;C.R是自变量,故选项不符合题意;D.C是因变量,故选项不符合题意;故选:A.分析:根据函数以及常量、变量的定义即可判断.3.如果用总长为60m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为p (m),一边长为a(m),那么S,p,a中是变量的是()A.S和p B.S和a C.p和a D.S,p,a答案:B解析:解答:∵篱笆的总长为60米,∴周长P是定值,而面积S和一边长a是变量,故选B.分析:根据篱笆的总长确定,即可得到周长、一边长及面积中的变量.4.下面的表格列出了一个实验的统计数据,表示将皮球从高处落下时,弹跳高度b 与下降高度d 的关系,下面能表示这种关系的式子是( ) d 50 80 100 150 b 254050 75A .b =d 2B .b =2dC .b =2d D .b =d +25 答案:C 解析:解答:由统计数据可知: d 是b 的2倍, 所以,b =21d . 故选:C .分析:这是一个用图表表示的函数,可以看出d 是b 的2倍,即可得关系式.5.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm )与所挂的物体的质量x (kg )间有下面的关系: x 0 1 2 3 4 5 y1010.51111.51212.5A .x 与y 都是变量,且x 是自变量,y 是因变量B .所挂物体质量为4kg 时,弹簧长度为12cmC .弹簧不挂重物时的长度为0cmD .物体质量每增加1kg ,弹簧长度y 增加0.5cm 答案:D 解析:解答:A .x 与y 都是变量,且x 是自变量,y 是因变量,故A 正确; B .所挂物体质量为4kg 时,弹簧长度为12cm ,故B 正确; C .弹簧不挂重物时的长度为10cm ,故C 错误;D .物体质量每增加1kg ,弹簧长度y 增加0.5cm ,故D 正确. 故选:D .分析:根据给出的表格中的数据进行分析,可以确定自变量和因变量以及弹簧伸长的长度,得到答案.6.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据: 鸭的质量/千克0.5 11.5 22.5 33.5 4烤制时间/分4060 80100 120 140 160 180) A .140 B .138 C .148 D .160 答案:C 解析:解答:从表中可以看出,烤鸭的质量每增加0.5千克,烤制的时间增加20分钟,由此可知烤制时间是烤鸭质量的一次函数.设烤制时间为t 分钟,烤鸭的质量为x 千克,t 与x 的一次函数关系式为:t =kx +b ,则⎩⎨⎧=+=+100260b k b k ,解得⎩⎨⎧==2040b k所以t =40x +20.当x =3.2千克时,t =40×3.2+20=148. 故选C .分析:观察表格可知,烤鸭的质量每增加0.5千克,烤制时间增加20分钟,由此可判断烤制时间是烤鸭质量的一次函数,设烤制时间为t 分钟,烤鸭的质量为x 千克,t 与x 的一次函数关系式为:t =kx +b ,取(1,60),(2,100)代入,运用待定系数法求出函数关系式,再将x =3.2千克代入即可求出烤制时间t .7.在某次实验中,测得两个变量m 和v 之间的4组对应数据如下表:则m 与v 之间的关系最接近于下列各关系式中的( ) m 1 2 3 4 v0.012.98.0315.1答案:B 解析:解答:当m =4时, A .v =2m ﹣2=6; B .v =m 2﹣1=15; C .v =3m ﹣3=9; D .v =m +1=5. 故选:B .分析:一般情况下是把最大的一对数据代入函数关系式后通过比较得出最接近的关系式. 8.下面说法中正确的是( )A .两个变量间的关系只能用关系式表示B .图象不能直观的表示两个变量间的数量关系C .借助表格可以表示出因变量随自变量的变化情况D .以上说法都不对 答案:C 解析:解答:A .两个变量间的关系只能用关系式表示,还能用列表法和图象法表示,故错误; B .图象能直观的表示两个变量间的数量关系,故错误; C .借助表格可以表示出因变量随自变量的变化情况,正确; D .以上说法都不对,错误; 故选C .分析:表示函数的方法有三种:解析法、列表法和图象法.9.一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据: 支撑物高度h (cm ) 10 20 30 40 50 60 70 80 小车下滑时间t (s ) 4.23 3.002.452.131.891.711.591.50A .当h =50cm 时,t =1.89sB .随着h 逐渐升高,t 逐渐变小C .h 每增加10cm ,t 减小1.23sD .随着h 逐渐升高,小车的速度逐渐加快 答案:C 解析:解答:A .当h =50cm 时,t =1.89s ,故A 正确; B .随着h 逐渐升高,t 逐渐变小,故B 正确; C .h 每增加10cm ,t 减小的值不一定,故C 错;D .随着h 逐渐升高,小车的时间减少,小车的速度逐渐加快,故D 正确; 故选:C .分析:根据函数的表示方法,可得答案. 10.在三角形面积公式S =21ah ,a =2cm 中,下列说法正确的是( ) A .S ,a 是变量,21h 是常量 B .S ,h 是变量,21是常量 C .S ,h 是变量,21a 是常量 D .S ,h ,a 是变量,21是常量解析:解答:在三角形面积公式S =21ah ,a =2cm 中,21a 是常数,h 和S 是变量. 故选C .分析:根据函数的定义:对于函数中的每个值x ,变量y 按照一定的法则有一个确定的值y 与之对应;来解答即可.11.当前,雾霾严重,治理雾霾方法之一是将已生产的PM 2.5吸纳降解,研究表明:雾霾的程度随城市中心区立体绿化面积的增大而减小,在这个问题中,自变量是( ) A .雾霾程度 B .PM 2.5 C .雾霾 D .城市中心区立体绿化面积 答案:D 解析:解答:雾霾的程度随城市中心区立体绿化面积的增大而减小,雾霾的程度是城市中心区立体绿化面积的函数,城市中心区立体绿化面积是自变量,故选:D . 分析:根据函数的关系,可得答案.12.以21m /s 的速度向上抛一个小球,小球的高度h (m )与小球运动的时间t (s )之间的关系是h =21t ﹣4.9t 2.下列说法正确的是( ) A .4.9是常量,21,t ,h 是变量 B .21,4.9是常量,t ,h 是变量 C .t ,h 是常量,21,4.9是变量 D .t ,h 是常量,4.9是变量答案:B 解析:解答:A .21是常量,故A 错误;B .21,4.9是常量,t ,h 是变量,故B 是正确;C 、D .t 、h 是变量,21,4.9是常量,故C 、D 错误; 故选:B .分析:根据在变化过程中,数值发生变化的量是变量,数值始终不变的量是常量,可得答案. 13.笔记本每本a 元,买3本笔记本共支出y 元,在这个问题中: ①a 是常量时,y 是变量; ②a 是变量时,y 是常量; ③a 是变量时,y 也是变量; ④a ,y 可以都是常量或都是变量. 上述判断正确的有( )A .1个B .2个C .3个D .4个答案:B解答:由题意得:y=3a,此问题中a、y都是变量,3是常量,或a,y都是常量,则③④,故选:B.分析:根据题意列出函数解析式,再根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得答案.14.学校计划买100个乒乓球,买的乒乓球的总费用w(元)与单价n(元/个)的关系式w=100n中()A.100是常量,w、n是变量B.100、w是常量,n是变量C.100、n是常量,w是变量D.无法确定答案:A解析:解答:∵买的乒乓球的总费用W(元)与单价n(元/个)的关系式W=100n,∴100是常量,在此式中W、n是变量,故选A.分析:根据函数的定义:对于函数中的每个值x,变量y按照一定的法则有一个确定的值y 与之对应;来解答即可.15.小明给在北京的姑姑打电话,电话费随时间的变化而变化,在这个问题中,因变量是()A.时间B.电话费C.电话D.距离答案:B解析:解答:根据函数的定义,电话费随时间的变化而变化,则电话费是因变量.故选B.分析:函数的定义:设x和y是两个变量,对于x的每一个值,y都有唯一确定的值和它对应,则x是自变量,y是x的函数,也叫因变量.二、填空题(共5小题)16.水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率(圆周长与直径的比)为π,指出其中的变量为.答案:圆的半径r和圆的周长C解析:解答:自变量是圆的半径r,因变量是圆的周长C.分析:根据函数的定义:函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应来解答.17.表示变量之间关系的常用方法有,,.答案:解析式|表格法|图象法解析:解答:表示变量之间关系的常用方法有 解析式,表格法,图象法. 分析:18.已知方程x ﹣3y =12,用含x 的代数式表示y 是 . 答案:y =31x ﹣4 解析:解答:移项得:﹣3y =12﹣x , 系数化为1得:y =31x ﹣4. 故答案为:y =31x ﹣4. 分析:要用含x 的代数式表示y ,就要将二元一次方程变形,用一个未知数表示另一个未知数.先移项,再将系数化为1即可.19.圆的面积S 与半径R 之间的关系式是S =πR 2,其中自变量是 . 答案:R 解析:解答:根据函数的定义:对于函数中的每个值R ,变量S 按照一定的法则有一个确定的值S 与之对应可知R 是自变量,π是常量,故答案为:R . 分析:根据函数的定义来判断自变量、函数和常量.20.在一个过程中,固定不变的量称为 ,可以取不同的值的量称为 . 答案:常量|变量 解析:解答:在一个过程中,固定不变的量称为常量,可以取不同的值的量称为变量, 故答案为:常量,变量.分析:根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量,即可答题.三、解答题(共5小题)21.齿轮每分钟120转,如果n 表示转数,t 表示转动时间. ①用n 的代数式表示t ; 答案:解答:由题意得: 120t =n , t =120n; ②说出其中的变量与常量.答案:变量:t,n常量:120.解析:分析:①根据题意可得:转数=每分钟120转×时间;②根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得x、y是变量.22.按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.①题中有几个变量?答案:解答:观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…可见每增加一张桌子,便增加4个座位,因此x张餐桌共有6+4(x﹣1)=4x+2个座位.故可坐人数y=4x+2,故答案为:有2个变量;②你能写出两个变量之间的关系吗?答案:解答:能,由①分析可得:函数关系式可以为y=4x+2.解析:分析:由图形可知,第一张餐桌上可以摆放6把椅子,进一步观察发现:多一张餐桌,多放4把椅子.x张餐桌共有6+4(x﹣1)=4x+2.23.在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.所挂物体质量x/kg 0 1 2 3 4 5弹簧长度y/cm 18 20 22 24 26 28答案:解答:上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;②当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?答案:解答:当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;③若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?答案:解答:根据上表可知所挂重物为7千克时(在允许范围内)时的弹簧长度=18+2×7=32厘米.解析:分析:①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量,所以反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量;②由表可知,当物体的质量为3kg时,弹簧的长度是24cm;不挂重物时,弹簧的长度是18cm;③由表中的数据可知,x=0时,y=18,并且每增加1千克的质量,长度增加2cm,依此可求所挂重物为7千克时(在允许范围内)时的弹簧长度.24.某中学为筹备校庆活动,准备印制一批校庆纪念册.该纪念册每册需要10张8K大小的纸,其中4张为彩页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩页300元/张,黑白页50元/张;印刷费与印数的关系见下表.印数a (单位:千册)1≤a<5 5≤a<10彩色(单位:元/张)2.2 2.0黑白(单位:元/张)0.7 0.6①印制一本纪念册的制版费为元;答案:解答:4×300+6×50=1500(元);②若印制2千册,则共需多少费用?答案:解答:若印制2千册,则印刷费为:(2.2×4+0.7×6)×2 000=26000(元),∴总费用为:26000+1500=27500(元).解析:分析:彩页和黑白页的制版费的和;制版费加上印刷费就是总费用.25.秋天到来了,小明家的苹果获得了丰收,他主动帮助妈妈到集市上去卖刚刚采摘下的苹果.已知销售数量x(千克)与售价y(元)的关系如下表所示:数量x(千克) 1 2 3 4 5售价y(元)2.1 4.2 6.3 8.4 10.5答案:解答:销售量每增加1千克,售价就增加2.1元.②求当x=15时,y的值是多少?答案:解答:当x=15时,y=2.1×15=31.5(元).解析:分析:①根据表可以得到:销售量每增加1千克,售价就增加2.1元;②当x=15时,y的值是2.1元的15倍,据此即可求解.。
数学七年级下北师大版6.1小车下滑的时间习题精选

6.1小车下滑的时间习题精选1.某城市1949年至1994年期间每隔5年的人口如下表:〔1〕指出哪个量是变量,哪个量是自变量,哪个量是因变量;〔2〕指出1984年人口是多少?〔3〕请估算一下,照这样开展1994年,这个城市的人口将到达多少?2.三口之家,冬天饮用桶装矿泉水的情况如下表:〔1〕根据表中的数据,说一说哪些量是在发生变化?自变量和因变量各是什么?〔2〕能说出下周一桶中还有多少水吗?〔3〕根据表格中的数据,说一说星期一到星期日,桶中的水是如何变化的.3.小华感冒发烧,临睡前吃了退热镇痛药,妈妈每隔两小时给她测一次体温,测得结果如下表:看表答复小华几点钟体温最高,几点钟体温最低.利用周日休息时间每隔两小时测一下自己的体温,并填写出表格.4.某种蔬菜的价格随季节变化如下表:单位:元/千克〔1〕观察表说出变量、自变量、因变量;〔2〕哪个月这种蔬菜价格最高,哪个月这种蔬菜的价格最低;〔3〕计算一下这种蔬菜的年平均价.参考答案1.〔1〕年份、人口数是变量,年份是自变量,人口数是因变量〔2〕22.4万〔3〕应超过30万2.〔1〕日期数、桶中剩水量是变量,日期数是自变量,桶中剩水量是因变量〔2〕能有水〔提示:最多一天减少0.6加仑〕〔3〕水一天比一天少,大约每天减少0.5加仑.3.20时小华体温最高是38.4℃,12时小华体温最低是36.℃.4.〔1〕月份,价格是变量,月份是自变量,价格是因变量〔2〕2月份这种蔬菜的价格最高是5.50元/千克,8月份这种蔬菜的价格最低是090元/千克〔3〕2.98元/千克.二1.某百货商场为研究销售规律,对在店顾客人数作了分时段统计,下面的表格是该商场某日从早9时到晚18时,每隔1小时所作的在店顾客人数统计〔单位:百人〕.时刻9 10 11 12 13 14 15 16 17 18在店人数〔百人〕3 7 9 8 8 6 3 3 2 1〔1〕什么时间商店人最多?什么时间商店人最少?〔2〕哪段时间之内商店人比拟多,哪段时间内商店人的人比拟少?〔3〕根据这个统计表,如果你是管理者怎样安排员工的工作时间.2.2000年7月1日国家规定的整存整取定期储蓄利率如下:存期三个月半年一年二年三年五年年利率1.98% 2.16% 2.25% 2.43% 2.70% 2.88%〔1〕年利率是如何随存期的变化而变化的?你如何选择存期?〔2〕现有人民币10000元,两年后才用,假定按2000年7月1日的利率存入银行.试问下面两种存款方式中:a. 一个两年期,b. 一个一年期,接着又一个一年期,选择哪一种存款方式能获得最大利息?3.研究说明,弹簧挂上物体后会伸长,知弹簧的长度〔cm〕与所挂物体的质量〔kg〕之间的关系如下表:物体质量/kg 0 1 2 3 4 …弹簧长度/cm 8 8.5 9 9.5 10 …〔1〕上表反映了哪两个变量之间的关系?哪是自变量?因变量?〔2〕当物体的质量为3kg时,弹簧的长度是多少?〔3〕如果物质质量为 kg,弹簧的长度为 cm,根据上表写出与的关系式.〔4〕当物体质量为3.5kg,你能说出弹簧的长度吗?〔5〕当弹簧长度为12.5cm时,根据〔3〕求出所挂物体质量.参考答案1.〔1〕11时人最多,约9百人;18时人最少约1百人〔2〕10时至14时之间人较多;其他时间人较少〔3〕在人多时增加员工,在人少时减少员工.2.〔1〕随着存期的增加利率也提高〔2〕a可得利息486元,b两次共得利息480.0625元,应选a.3.〔1〕弹簧长度随物体质量的变化规律,物体质量是自变量,弹簧长度是因变量〔2〕9.5cm 〔3〕〔4〕9.75 〔5〕9kg。
初中七年级数学下册【北师大版】 6.1_小车下滑

平时我们穿的鞋的鞋长与鞋码有如下关系:
鞋长 22.5 23 …. 26.5 27
cm 鞋码 35 36 …. 43 44
① 小明的脚长25厘米,他应该穿多大鞋 码的鞋呢? ② 你能根据自己的鞋码猜出自己的 脚长吗?
生活中有哪些例子反 映了变量之间的关系?与 同伴进行交流.
随堂练习 p1 91
研究表明,当钾肥和磷肥的施用量一定时, 土豆的产量与氮肥的施用量有如下关系:
氮肥施用量/ (千克/公顷)
土豆产量/ (吨/公顷)
0
15.18
34
21.36
67
25.27
101
32.29
135
34.03
202 39.45
259 43.15
336
43.46
Байду номын сангаас
404 40.83
471
30.75
(1)上表反映了哪两个变量之间的关系? 哪个是自变量?哪 个是因变量?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少? 如果不施氮肥呢?
课下小实验
在水龙头下放一个水杯,扭小水龙头,让水一 滴一滴地滴入水杯中,对水杯中的水的高度每隔一 分钟记录一次,将观察到的数据记录下来制成表格。
观察数据,写出你的发现及实验对你的启示。
下次上课时展示给同学们。
h
小车下滑时间/秒
t
4.23
3.00 2.45 2.13 1.89 1.72
1.59
1.23 0.55 0.32 0.24 0.18 0.12
1、支撑物高为50cm时,小车下滑的时间是多少?
2.随着h逐渐变大,t的变化趋势是什么?
3.h每增加10cm,t的变化情况相同吗? 4.估计当h=80cm时,t的值是多少?你是怎样估计的?
最新北师大版七年级下册数学各章节练习题和单元测试题以及答案

1、同底数幂的乘法法则:nm n m aa a +=∙(n m ,都是正整数) 同底数幂相乘,底数不变,指数相加。
注意底数可以是多项式或单项式。
如:532)()()(b a b a b a +=+∙+7、x 281=)(,则x 等于 。
(2)=∙52x x 。
(3)92733x2⨯⨯=,则x 等于 。
8、一天计算机可做3×1210次运算,它工作了2102⨯秒可以做 次运算。
三、解答题。
9、计算。
53a a ∙﹣ 232x x x )(﹣)(﹣∙∙234101101101)()()(∙∙15、已知122,62,32c b a===,探求a 、b 、c 之间的关系。
2、幂的乘方法则:mnn m aa =)((n m ,都是正整数)幂的乘方,底数不变,指数相乘。
如:10253)3(=- 幂的乘方法则可以逆用:即m n n m mna a a)()(==如:23326)4()4(4==3、积的乘方法则:nnnb a ab =)((n 是正整数)积的乘方,等于各因数乘方的积。
如:(523)2z y x -=5101555253532)()()2(z y x z y x -=∙∙∙-1、下列运算正确的是( )A .22a a a =⋅B .33)(ab ab = C .632)(a a = D .5210a a a =÷12、比较334455543、、的大小。
8、若2×3×9m =2×311,则m =___________. 9、计算题。
3223x x )(﹣)(﹣∙ 32ab 21)(﹣344321044x 5x 2x 2x 2x 2)()(﹣)(﹣∙+∙+10、已知x+y=a ,求3333y x 32y x 2y x )()()(+∙+∙+的值。
11、若1593m nb a b b a =)(,求n m 2+的值。
4、同底数幂的除法法则:nm n m aa a -=÷(n m a ,,0≠都是正整数,且)n m同底数幂相除,底数不变,指数相减。
小车下滑的时间的典型例题五

小车下滑的时间的典型例题五
例 某市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
(1)上述哪些量发生变化?自变量和因变量各是什么?
(2)第五排、第六排各有多少个座位?
(3)第n 排有多少个座位?
分析:(1)不难看出排数,座位数都在变化,且座位数随排数而变化,所以排数是自变量,座位数是因变量;
(2)由表中的变化规律和后排总比前排多3个座,故第五排是62个座,第六排是65个座;
(3)由表可以发现:排数分别是1,2,3,4…对应的座位数是50,50+3,50+2×3,50+3×3,所以第n 排有)1(350-+n .
解:(1)排数.座位数都在变化,其中排数是自变量,座位数是因变量;
(2)第五,第六排的座位数分别是62和65;
(3)第n 排有)1(350-+n .
说明:在研究自变量和因变量这间的变化规律时,要注意进行归纳.。
数学七年级数学下6.1小车下滑的时间同步练习
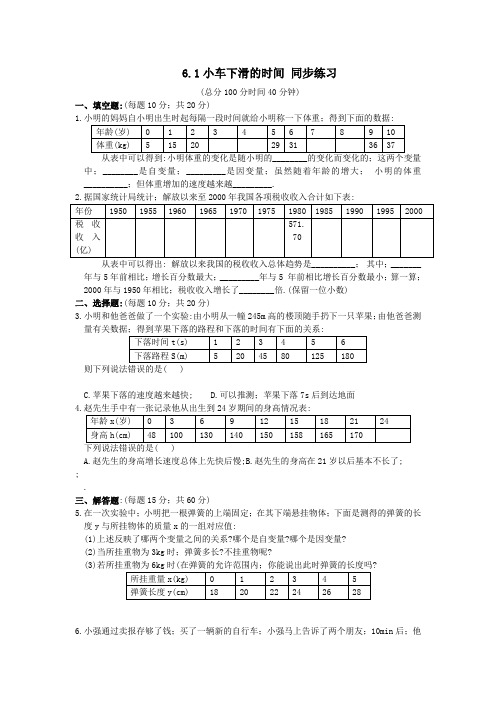
6.1小车下滑的时间同步练习(总分100分时间40分钟)一、填空题:(每题10分;共20分)1.从表中可以得到:小明体重的变化是随小明的________的变化而变化的;这两个变量中;________是自变量;_________是因变量;虽然随着年龄的增大;•小明的体重__________;但体重增加的速度越来越_________.2.据国家统计局统计;解放以来至2000年我国各项税收收入合计如下表:• 从表中可以得出:•解放以来我国的税收收入总体趋势是__________;•其中;_______年与5年前相比;增长百分数最大;_________年与5•年前相比增长百分数最小;算一算;2000年与1950年相比;税收收入增长了________倍.(保留一位小数)二、选择题:(每题10分;共20分)3.小明和他爸爸做了一个实验:由小明从一幢245m高的楼顶随手扔下一只苹果;由他爸爸测则下列说法错误的是( )C.苹果下落的速度越来越快;D.可以推测;苹果下落7s后到达地面4.赵先生手中有一张记录他从出生到24岁期间的身高情况表:下列说法错误的是( )A.赵先生的身高增长速度总体上先快后慢;B.赵先生的身高在21岁以后基本不长了;;.三、解答题:(每题15分;共60分)5.在一次实验中;小明把一根弹簧的上端固定;在其下端悬挂物体;下面是测得的弹簧的长度y与所挂物体的质量x的一组对应值:(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)当所挂重物为3kg时;弹簧多长?不挂重物呢?(3)6.小强通过卖报存够了钱;买了一辆新的自行车;小强马上告诉了两个朋友;10min后;他们又各自告诉了另外两个朋友;再过10min;这些朋友又各自告诉了两个朋友;如果消息按这样的速度传下去;80min•后将有多少人知道小强买了一辆新自行车的消息?7.1~6个月的婴儿生长发育非常快;他们的体重y(g)和月龄x(月)•的关系如下表;某一婴儿出生时体重是ag;下表表示这一婴儿在出生后1~6个月时的体重.(1)表中列出的是哪两个变量之间的关系?哪个是自变量;哪个是因变量?(2)自变量是什么值时;因变量的值最小?自变量是什么值时;因变量的值最大?(3)该地哪一段时间大米平均价格在上涨?哪一段时间大米平均价格在下落?(4)从表中可以得到该地大米平均价格变化方面的哪些信息?平均比年初降低了;还是涨价了?答案:1.年龄;年龄;体重;逐渐增大;慢3.A5.(1)弹簧长度y与物体重量x间的关系;物体重量是自变量;弹簧长度是因变量(2)当所挂重物为3kg时;弹簧长度为24cm;不挂重物时弹簧长度为18cm(3)当所挂重物为6kg时;弹簧长度为30cm6.2+22+23+24+25+26+27+28+29=10227.y=700(5+x)(其中1≤x≤6)8.(1)表中表示的是大米平均价格与月份这两个变量间的关系;月份是自变量;•大米的平均价格是因变量.(2)自变量是9、10时;因变量值最小;自变量是4时;因变量的值最大.(3)从1月至4月;10月至12月大米平均价格在上涨;从4月到9•月大米平均价格在下跌.(4)大米的平均价格随时间的变化而变化;价格随市场需求而变动;•年底比年初是降价了.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《小车下滑的时间》习题精选1
一
1.某城市1949年至1994年期间每隔5年的人口如下表:
(1)指出哪个量是变量,哪个量是自变量,哪个量是因变量;
(2)指出1984年人口是多少?
(3)请估算一下,照这样发展1994年,这个城市的人口将达到多少?
2.三口之家,冬天饮用桶装矿泉水的情况如下表:
(1)根据表中的数据,说一说哪些量是在发生变化?自变量和因变量各是什么?
(2)能说出下周一桶中还有多少水吗?
(3)根据表格中的数据,说一说星期一到星期日,桶中的水是如何变化的.
3.小华感冒发烧,临睡前吃了退热镇痛药,妈妈每隔两小时给她测一次体温,测得结果如下表:
看表回答小华几点钟体温最高,几点钟体温最低.利用周日休息时间每隔两小时测一下自己的体温,并填写出表格.
4.某种蔬菜的价格随季节变化如下表:
单位:元/千克
(1)观察表说出变量、自变量、因变量;
(2)哪个月这种蔬菜价格最高,哪个月这种蔬菜的价格最低;
(3)计算一下这种蔬菜的年平均价.
参考答案
1.(1)年份、人口数是变量,年份是自变量,人口数是因变量(2)22.4万(3)应超过30万
2.(1)日期数、桶中剩水量是变量,日期数是自变量,桶中剩水量是因变量(2)能有水(提示:最多一天减少0.6加仑)(3)水一天比一天少,大约每天减少0.5加仑.
3.20时小华体温最高是38.4℃,12时小华体温最低是36.℃.
4.(1)月份,价格是变量,月份是自变量,价格是因变量(2)2月份这种蔬菜的价格最高是5.50元/千克,8月份这种蔬菜的价格最低是090元/千克(3)2.98元/千克.
二
1.某百货商场为研究销售规律,对在店顾客人数作了分时段统计,下面的表格是该商场某日从早9时到晚18时,每隔1小时所作的在店顾客人数统计(单位:百人).
(1)什么时间商店人最多?什么时间商店人最少?
(2)哪段时间之内商店人比较多,哪段时间内商店人的人比较少?
(3)根据这个统计表,如果你是管理者怎样安排员工的工作时间.
2.20KK年7月1日国家规定的整存整取定期储蓄利率如下:
年利率 1.98% 2.16% 2.25% 2.43% 2.70% 2.88%
(1)年利率是如何随存期的变化而变化的?你如何选择存期?
(2)现有人民币10000元,两年后才用,假定按20KK年7月1日的利率存入银行.试问下面两种存款方式中:a.一个两年期,b.一个一年期,接着又一个一年期,选择哪一种存款方式能获得最大利息?
3.研究表明,弹簧挂上物体后会伸长,知弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体质量/kg 01234…
弹簧长度/cm 88.599.510…
(1)上表反映了哪两个变量之间的关系?哪是自变量?因变量?
(2)当物体的质量为3kg时,弹簧的长度是多少?
(3)如果物质质量为kg,弹簧的长度为cm,根据上表写出与的关系式.
(4)当物体质量为3.5kg,你能说出弹簧的长度吗?
(5)当弹簧长度为12.5cm时,根据(3)求出所挂物体质量.
参考答案
1.(1)11时人最多,约9百人;18时人最少约1百人(2)10时至14时之间人较多;其他时间人较少(3)在人多时增加员工,在人少时减少员工.
2.(1)随着存期的增加利率也提高(2)a可得利息486元,b两次共得利息480.0625元,应选a.
3.(1)弹簧长度随物体质量的变化规律,物体质量是自变量,弹簧长度是因变量
(2)9.5cm(3)(4)9.75(5)9kg。
