对偶理论
02对偶理论

6
对偶关系对应表
第2章 对偶理论
原问题 (对偶问题)
对偶问题(原问题)
目标函数
Max
Min
目标函数系数
约束方程右端常数
n个
变
≥0
量
≤0
无约束
m个
约束
≤
条件
≥
=
约束方程右端常数
目标函数系数
n个
≥
≤ = m个
≥0 ≤0 无约束
-Y1 +2Y2 +Y3 ′- Y3〞 ≥0
Y2 -Y3 ′+Y3〞 ≥2 -Y1 +6Y2 +3Y3 - 3Y3〞≥-5 Y1 ,Y2 ,Y3 ′,Y3〞 ≥0 令Y1 ′ = -Y1 , Y3 = Y3 ′- Y3〞 , 则模型可表示为
Min =2Y1 ′ +6Y2 Y1 ′ +2Y2 +Y3 ≥0
或出售,如何给资源定价才合算?
产Ⅰ产品的单位获利
定价应考虑的问题 1.出卖资源获利应不少于生产获利 2.价格尽可能低,才能有竞争力 设Y1 Y2 Y3分别为3种资源的出卖价格
1Y1+4Y2≥2 同理 2Y1+4Y3≥3 最低价格应使总收入最小
Min z= 8Y1+16Y2+12Y3
1
对偶问题的提出
y1符号不限, y2 0, y3 0 y1符号不限, y2 0, y3 0
√
×
Min Z 4x1 2x2 3x3
4x1 5x2 6x3 7 s.t.182x1x191x32 x2101x43 11
x1 0, x2符 号 不 限, x3 0 9
规划数学对偶理论

理论框架的局限性
当前对偶理论主要基于某些特定的数学框架,对于一些复杂问题 可能无法提供有效的解决方案。
计算复杂度问题
对偶理论中的一些算法具有较高的计算复杂度,对于大规模问题可 能难以在可接受的时间内得出结果。
缺乏实际应用场景
目前对偶理论的应用主要集中在理论研究层面,缺乏在现实世界复 杂问题中的应用实例。
02
线性规划的对偶理论
线性规划问题
定义
线性规划问题是在一组线性不等式约束下,寻找一组 线性变量的最优解的问题。
目标函数
线性规划的目标函数是线性的,我们需要找到一组变 量使得目标函数取得最小值或最大值。
约束条件
线性规划的约束条件也是线性的,通常表示为不等式 或等式。
线性规划的对偶问题
定义
01
线性规划的对偶问题是通过将原问题的约束条件和目标函数进
求解方法
通过递归求解子问题,并记录子问题的最优解,避免重复计算。
动态规的基础上,对某些约
束或目标函数进行变换,从而得到的新问题。
特点
02 对偶问题与原问题具有相同的最优解,但求解难度可
能降低。
应用
03
通过对偶问题可以更有效地求解原问题,特别是在处
理约束优化问题时。
投资组合优化
对偶理论也可以应用于投资组合优化问题,通过 对偶问题的求解,可以找到最优的投资组合方案。
03
非线性规划的对偶理论
非线性规划问题
定义
非线性规划问题是在满足一系列约束条件下,最 小化或最大化一个非线性函数。
类型
包括无约束、有约束、凸优化、非凸优化等。
求解方法
常用的求解方法包括梯度法、牛顿法、拟牛顿法 等。
对偶理论的重要性
线性规划的对偶理论(第一部分

对偶问题的约束条件 对应于原问题的目标 函数和约束条件的系 数。
对偶问题的可行解集 是原问题可行解集的 凸包。
原问题与对偶问题关系
弱对偶性
对于任意一对原问题和对偶问题 的可行解,原问题的目标函数值 总是大于或等于对偶问题的目标
函数值。
强对偶性
当原问题和对偶问题都存在可行 解时,它们的最优解对应的目标
强对偶性定理
若原问题和对偶问题都有可行解,则 它们分别存在最优解,且这两个最优 解的目标函数值相等。
在满足某些约束规格(如Slater条件) 的情况下,强对偶性成立。
互补松弛条件
在原问题和对偶问题的最优解中,如果某个约束条件的对偶变量值为正,则该约束 条件必须是紧的(即取等号)。
如果原问题(对偶问题)的某个变量在最优解中取正值,则其对应的对偶问题(原 问题)的约束条件必须是紧的。
标准形式
通常将线性规划问题转化为标准 形式,即求解目标函数的最小值 ,约束条件为一系列线性不等式 。
对偶问题定义与性质
对偶问题定义:对于 给定的线性规划问题, 可以构造一个与之对 应的对偶问题,该问 题的目标函数和约束 条件与原问题密切相 关。
对偶问题性质
对偶问题的目标函数 是原问题约束条件的 线性组合。
解决对偶间隙等关键问题
在实际应用中,由于原问题和对偶问题之间可能存在对偶间隙,导致对偶理论的实用性受到一定的限制。 未来可以研究如何缩小或消除对偶间隙,提高对偶理论的实用性和应用范围。
THANKS
感谢您的观看
简化了复杂问题的求解过程
对偶理论能够将一些复杂的线性规划问题转化为相对简单的对偶问题进行求解,从而降低了问题 的求解难度和计算量。
揭示了原问题和对偶问题之间的内在联系
对偶理论

第四节
灵敏度分析
灵敏度分析也称为优化后分析,是研究线性规划模型某些系 数或限制量的变化对最优解的影响及其影响程度的分析过程。
一、影子价格及其应用
例7 某企业生产A、B、C三种产品,每吨的利润分别为2000元、3000元和 1000元,生产单位产品所需的工时及原材料如表3-8所示。若供应的原材料每天不 超过3吨,所能利用的劳动力总工时是固定的,应如何制定日生产计划,使三种产 品的总利润最大? 表3-8 生产每吨产品所需资源 所需工时占总工时比例 所需原材料(吨) 产 品 A 1/3 1/3 B 1/3 4/3 C 1/3 7/3
二、对偶问题的基本性质 1.对称性。 对偶问题的对偶是原问题。 2.弱对偶性。 若 X 是原问题的可行解, Y 是对偶问题的可行 解。则存在 C X Yb 3.无界性。 若原问题(对偶问题)为无界解,则其对偶问 题(原问题)无可行解。 ˆ ˆ 4.可行解是最优解时的性质。 设 X 是原问题的可行解, Y ˆ ˆ ˆ Y 是对偶问题的可行解,当 CX Yb 时,X , ˆ 是最优解。 5.对偶定理。 若原问题有最优解,那么对偶问题也有最优 解;且目标函数值相等。 Y 6.互补松弛性。 若 Xˆ ,ˆ 分别是原问题和对偶问题的可行 ˆ ˆ Y 解。那么 YˆX 0 和 Y X 0,当且仅当 X ,ˆ 为最优解。 7.对应基解。 设原问题是
y1 4 y 2 2
同理将生产每件产品Ⅱ的设备台时和原材料出租和 出让的所有收入应不低于生产一件产品Ⅱ的利润, 这就有
2 y1 4 y 3 3
把企业所有设备台时和资源都出租和出让,其收入为 8 y1 16y 2 12y 3
从企业的决策者来看当然ω愈大愈好,但从接受者来看他的支付愈少愈好,所以企 业的决策者只能在满足 所有产品的利润条件下,使其总收入尽可能地小,他才能 实现其意愿,为此需解如下的线性规划问题:
对偶理论知识点总结

对偶理论知识点总结一、一般理解对偶理论是运筹学和数学中的一个重要理论,主要研究优化问题的对偶性质和利用对偶问题来解决原始问题的方法。
优化问题是现实世界中的一种普遍问题,它的目标是在一定的约束条件下找到最优解。
而对偶理论则是研究优化问题的一个重要角度,它告诉我们,对于每一个原始问题都存在一个对偶问题,通过对偶问题我们可以获得原始问题的一些重要信息,比如最优解的下界。
二、对偶问题的定义在深入了解对偶理论之前,我们首先需要了解什么是对偶问题。
对于一个原始优化问题:\[ \begin{cases} inf \ c^T x \\ Ax=b \\ x\geq0 \end{cases}\]它的对偶问题可以定义为:\[ \begin{cases} sup \ b^T y \\ A^Ty+c=y \\ y\geq0 \end{cases}\]其中,\(c,x\)是原始问题的目标函数和解向量,\(A,b\)是原始问题的约束条件,对偶问题的目标函数和解向量分别为\(b,y\)。
原始问题和对偶问题之间存在着一种对偶关系,通过对偶问题我们可以获得原始问题的一些重要信息。
三、对偶性质对偶理论的一个重要性质就是对偶性质,它告诉我们原始问题和对偶问题之间存在着一种非常紧密的联系。
具体来讲,对偶性质包括弱对偶性和强对偶性两个方面。
1. 弱对偶性:对于任意一个优化问题,其对偶问题的目标函数值不会超过原始问题的目标函数值,即对于原始问题的任意可行解x和对偶问题的任意可行解y,有\[c^Tx\geqb^Ty\]2. 强对偶性:若原始问题和对偶问题均存在最优解,则它们的目标函数值相等,即\[inf \c^Tx=sup \ b^Ty\]这两个对偶性质告诉我们,对偶问题的解可以为原始问题的最优解提供一个下界,并且在某些情况下,对偶问题的解可以等于原始问题的最优解。
四、对偶问题的应用对偶理论不仅仅是一种理论概念,更是一种实际问题求解的工具。
在实际问题中,我们经常可以通过对偶问题来求解原始问题,或者通过对偶问题的解来获得原始问题的解。
第二章对偶理论
3 5
x1 , x2 , x3 0
解:首先将原式变形
max Z 2 x1 3 x2 4 x3
2 x 3 x2 5 x3 2
3 x1 x2 7 x3 3
x1 4 x2 6 x3
5
x1 , x2 , x3 0
注意:以后不强调等式右段项 b≥0,原因在对偶单
纯型表中只保证 而j 不0 保证
=(1.1),分别是
(P_)_ 和__(D)的可行解。Z=10 ,W=40,故有
C X < Y b ,弱对偶定理成立。由推论⑴可知,W 的最
小值不能小于10,Z 的最大值不能超过40。
例二、已知
p : max Z x1 2x2
D : minW 2 y1 y2
x1 x2 x3 2
2x1 x2 x3 1
n
j 1
aij
yi
cj
(对偶问题)
yi 0
目标函数 约束条件
原问题
对偶问题
max
min
≤
≥
变量数量 约束条件个数
约束条件个数 变量数量
例三、
23
x1
x2
原问题
12 y1 2
2
≤ 12
8
y2
1
2
≤
8
16 y3 4 0 ≤ 16 12 y4 0 4 ≤ 12
对偶问题 2 3
二、线性规划的对偶理论
原问题 问题无界
无可 行解
对偶问题 无可 行解
问题无界
(对)
y1 y1
y1
y2 y2 0, y2
2 1 0
无可 行解
推论⑶.在一对对偶问题(P)和(D)中,若一个可 行(如P),而另一个不可行,(如D),则该可行的 问题无界。
线性规划的对偶理论2-对偶问题的性质

含多个决策变量的线性规 划问题及其对偶问题的求 解
含不等式约束的线性规划 问题及其对偶问题的求解
经典案例分析:运输问题、生产计划等
通过对偶理论实现资源的最优分 配
对偶理论在生产计划优化中的应 用
如何通过对偶理论求解最小成本 运输问题
运输问题
资源分配问题 生产计划问题
实际应用案例分享
供应链管理
椭球法
通过构造一个包含原问题可行域的椭球,将原问题转化为 一个椭球约束的优化问题,然后利用椭球算法进行求解。
割平面法
通过在原问题的约束条件中不断添加割平面,将原问题转 化为一个更容易求解的问题,然后利用相关算法进行求解。
Part
04
对偶理论在经济学中应用
影子价格概念及计算
影子价格定义
影子价格反映资源在最优配置下 的边际价值,即资源每增加一单
选择一个满足所有约束条 件的初始内点。
迭代过程
通过不断迭代,沿着目标函数 的负梯度方向进行搜索,直到 达到最优解或满足停止准则。
求解最优解
当迭代过程结束时,从最 终迭代点中读取最优解。
其他方法简介
外点法
通过构造一个包含原问题可行域的外点,将原问题转化为 一个无约束优化问题,然后利用无约束优化方法进行求解。
简化问题求解从而降低了 计算复杂度和难度。
揭示问题内在联系
对偶理论揭示了原问题与其对偶问题之间的内在联系,有助于发现 问题的隐藏性质和潜在优化方向。
未来发展趋势预测及挑战分析
拓展应用领域
随着对偶理论的不断完善和发展, 其应用领域将进一步拓展,包括机 器学习、大数据分析等前沿领域。
强对偶性
强对偶性定义
01
存在一组可行解,使得原问题的目标函数值等于其对偶问题的
对偶理论几个性质的证明

对偶理论几个性质的证明
图论的对偶理论指在图论的内容中针对一个特殊的图G建立的另一个
图G*,它们之间的关系满足交换律,即G与G*互为对偶,可以发现的特
性包括:
一、Konig定理:
它是有关其中一种有向图的带宽是否可容的定理,即一个可容的有向
图其最大匹配数等于最大独立集的最小覆盖数。
它的对偶理论表明,一个
图G的最大匹配是邻接矩阵A的最小非零向量的数量加上图G的最小独立
集的数量。
其中,A是G的一个邻接矩阵,反映了图G的一种表示。
证明:
假设G是可容的有向图,则G具有非负的顶点覆盖数V和边覆盖数E,满足V≤E。
而G*是G的对偶图,具有最大匹配数m和最小独立集数f。
我们假设,图G的边覆盖数E等于G*的最小独立集数f,可以说明图
G的顶点覆盖数V等于G*的最大匹配数m。
因此,可以将等式node(V) = edge(E)和node(V) = match(m)结合起
来得到:
edge(E) = match(m)
与Konig定理的含义相同,即:G的最大匹配数等于G*的最小独立集数。
另外,根据等式,我们可以得出:
G具有V顶点和E边的最大匹配数=G*具有f点和m边的最小独立集
数
结论:一个可容的有向图其最大匹配数等于最小独立集的最小覆盖数。
二、Hall定理:
Hall定理指出:若图G有顶点集V和边集E,则G具有最大匹配 M 且,V,<=,M,时,必有一个完全匹配。
第三章对偶理论

目标函数系数与右边项 目标函数各变量系数对应 的对应关系 约束条件右边项的系数 变量个数与约束条件个 变量个数 n 数的对应关系 约束条件个数 m
原问题变量类型与对偶 问题约束条件类型的对 变量类型 应关系
原问题约束条件类型与 对偶问题变量类型的对 约束条件类型 应关系
原始问题有4个变量,3个约束,对偶问题应该有3个变量, 4个约束。根据定义,对偶问题为:
x1 x2 x3 x4
非对称形式的对偶—原始问题有“=”约束
max z=2x1+3x2-x3
s.t. x1+2x2+x3=6 2x1-3x2+2x3≤9
x1, x2, x3≥0
min w=6y1+9y2 s.t. y1+2y2 ≥ 2 2y1- 3y2 ≥ 3 y1+2y2 ≥ -1 y1:Free y2≥0
y1=w2-w1,y1:Free,y2=w3
如果原始问题中一个约束是等号约束,则对偶问题中相应的变 量没有符号限制
非对称形式的对偶—原始问题有“≥”约束
max z=2x1+3x2-x3 s.t. x1+2x2+x3 ≥ 6 2x1-3x2+2x3≤9 x1, x2, x3≥0 max z=2x1+3x2-x3
s.t. -x1-2x2-x3≤-6 2x1-3x2+2x3≤9 x1, x2, x3≥0 min w=-6y1’+9y2 s.t. -y’1+2y2≥2 -2y’1 -3y2≥3 -y’1+2y2≥-1 y’1, y2≥0
min w=6y1+9y2 s.t. y1+2y2≥2 2y1- 3y2≥3 y1+2y2≥-1 y1≤0, y2≥0
对偶理论

第2节 对偶问题解的性质
z c1 x1 c2 x2 cn xn ( z max) a11 x1 a12 x2 a1n xn b1 a21 x1 a22 x2 a2 n xn b2 a x a x a x b m2 2 mn n m m1 1 x1 , x2 , xn 0
第三章 对偶理论
Dual Theory
第1节 对偶问题
一、对偶的含义 对同一事物(问题)从不同的角度(立场) 观察,有两种对立的表述。 例如:“平面中矩形的面积与周长的关系” 有两种表述:周长一定,面积最大的矩形 是正方形;面积一定,周长最短的矩形是 正方形。
第1节 对偶问题
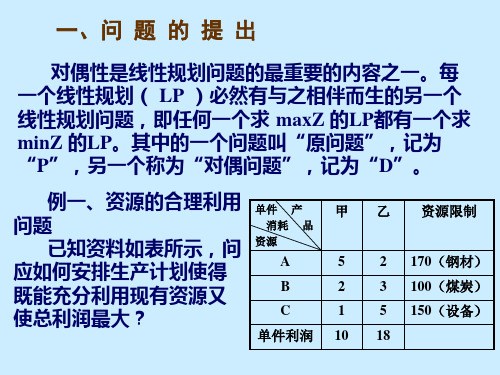
例1:某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产 品,已知生产单位产品所需的设备台时及A、B 两种原材料的消耗,如下表所示。该工厂每生 产一件产品Ⅰ可获利2元,每生产一件产品Ⅱ可 获利3元,问应如何安排计划使该工厂获利最多? 设备 原材料A 原材料B
Ⅰ 1 4 0 Ⅱ 2 0 4
8台时 16kg 12kg
第1节 对偶问题
例1:
解:设计划期内产品Ⅰ、Ⅱ的产量分别为x1、x2 max z =2x1+3x2 x1+2x2≤8 4x1≤16 4x2≤12
x1,x2≥0
第1节 对偶问题
从另一个角度考虑例1。 假设该工厂的决策者决定不生产产品Ⅰ、 Ⅱ,而将其所有资源(设备和原材料)出 租或外售,问应给每种资源如何定价,使 该工厂的收入最合理?
第1节 对偶问题
例5: max z =3x1-7x2 -5x3+8x4+8x5 x2-x3+3x4-4x5=-16 2x1+3x2-3x3-2x4≥2 -x1+2x3-2x4≤-5 -2≤x1≤10 5≤x2≤25 x3,x4≥0,x5无约束
运筹学第2章 对偶理论

2 y1 3 y2 y3 2 3 y1 y2 4 y3 3 5 y1 7 y2 6 y3 4 y , y , y 0 1 2 3
原—对偶问题的相互变换形式
原问题(或对偶问题) 目标函数 max 约 束 条 件 变 量 m个 ≤ ≥ = n个 ≥0 ≤0 无约束 约束条件右端项 目标函数变量的系数 对偶问题(或原问题) 目标函数 min m个 ≥0 ≤0 无约束 n个 ≥ ≤ = 目标函数变量的系数 约束条件右端项 变 量 约 束 条 件
设y1 , y2 , y3分别为三种资源的收费单价,所以 有下式: 5 y1 2 y2 y3 10 2 y1 3 y2 5 y3 18 y1 , y2 , y3 0 就目标而言,用下式可以表达: 170 y1 100 y2 150 y3 W
一般而言,W 越小越好,但因需双方满意,故
变为对称形式
m axZ 2 x1 3 x 2 4 x 3 2 x 3 x 2 5 x 3 2 3 x1 x 2 7 x 3 3 x1 4 x 2 6 x 3 5 x1 , x 2 , x 3 0
min W 2 y1 3 y2 5 y3
B
1 0
M-1
-2
最 终 表
cj cB 3 -1 -1 xB x1 x2 x3 检验数 b 4 1 9
3 x1 1 0 0 0
-1 x2
-1 x3 0 0 1 0
0 x4 1/3 0 2/3 -1/3
I
0 1 0 0
-1/3 1/3-M 2/3- M
所以, X*=(4 , 1 , 9),Z = 2
初 始 表
复代数几何中的对偶性理论

复代数几何中的对偶性理论复代数几何是一门集合代数和几何学思想于一体的数学理论,它的核心概念是对偶性理论。
对偶性理论在复代数几何中扮演着重要的角色,不仅为研究人员提供了深入理解复代数几何结构的工具,还为相关领域的应用研究提供了理论基础。
1. 对偶性理论的起源与发展对偶性理论最早出现在19世纪,由一些杰出的数学家如克勒因、普罗伊斯等人提出,并在20世纪得到进一步发展与丰富。
随着数学领域的不断拓展,对偶性理论也得到了广泛应用。
它在代数几何、代数拓扑、代数编码等领域都有涉及,并且在这些领域都取得了重要的成果。
2. 对偶空间的概念与应用对偶性理论的核心概念之一是对偶空间。
在复代数几何中,对于给定的一个向量空间V,它的对偶空间V*定义为所有线性函数组成的向量空间。
对偶空间在复代数几何中有着广泛的应用,特别是在研究多项式环、代数流形等方面。
通过对偶空间的引入,研究人员可以更深入地理解向量空间的性质与结构。
3. 对偶性的几何解释对偶性理论还有一个重要的几何解释,即通过对偶性可以建立起几何对象之间的对应关系。
在复代数几何中,这种对应关系可以用于研究多项式环的结构、代数流形之间的映射等。
通过对偶性的几何解释,研究人员可以将一些复杂的代数问题转化为几何问题,从而简化了问题的分析与解决过程。
4. 对偶性与代数编码对偶性理论在代数编码领域中也有重要的应用。
代数编码是一门研究如何通过代数方法对信息进行编码和解码的学科。
通过对偶性理论,研究人员可以构造出一些具有纠错能力的代数编码方案,从而保证在信息传输过程中能够对有限的错误进行纠正和恢复。
5. 未来的发展方向对偶性理论作为复代数几何的核心理论之一,目前仍然存在一些问题和挑战。
随着计算机科学的不断发展,对偶性理论在计算代数几何、代数拓扑等领域的应用将会得到进一步拓展。
另外,对偶性理论与其他数学领域的关联性也将成为未来研究的重点之一。
总结:复代数几何中的对偶性理论是一门重要的数学理论,它在代数几何、代数编码等领域发挥着重要作用。
第二章对偶理论11资料讲解

如果原问题无可行解时,对偶问题无可行解或具 有无界解
对偶问题无可行解时,原问题无可行解或具有无 界解
(原问题有可行解,对偶问题无可行解,则原问 题有无界解)
元,生产一件乙产品需两种设备分别为5、1小时,盈利1 元。
从美佳公司来看,出让资源获得的利润应不少于自己组 织生产获得的利润。因此有:
y1 + 6y2 2
5 y1 +2 y2 1
5
要使收买成功,双方的要求都必 须满足,于是得到出让资源问题的 线性规划数学模型: min w=17 y1 +24 y2
显然,该企业愿意出让的条件是,出让的价格不应低
于同等数量资源由自己组织生产活动时获取的利润。
分析:设y1 , y2 分别表示单位时间(h)设备A 、设备B 的出让代价,则从东方公司来看,希望用最小的代价把全
部资源收买过来, 故有: min w=17 y1 +24 y2 因生产一件甲产品需两种设备分别为1、6小时,盈利2
(4)由此可知,原问题目标函数的最大值对应于 对偶问题的目标函数的最小值。CX* Yb
(具体见第三节基本性质)
11
§2 原问题与对偶问题
一、对偶关系(对称形式)
原问题
对偶问题
max z=CX
min w=Yb
st. AX b
st. YA C
X0
Y0
看书上表2.1,验证对应关系
对称性:LP的原问题与对偶问题之间存在对称关系,即 LP对偶问题的对偶是原问题 结论:LP对偶问题与原问题互为对偶。 看例2,通过例子得出结论 第一步,化为对称形式下的原问题形式;第二步,根据对 应关系写出其对偶问题;第三步,做一变换,得到原12问题
第3章 对偶理论

第3章对偶理论第3章对偶理论§3.1 线性规划的对偶理论3.1.1 对偶问题的表述对称形式的对偶:(L ) min cx (D) max wbs.t. Ax ≥b s.t. wA ≤cx ≥0 w ≥0其中c 为n 维行向量,A 为m ⨯n 矩阵,b 为m 维列向量,x 表示n 维列向量,w 表示m 维行向量。
称(D)为线性规划(L)的对偶规划问题。
定理1 (L)与(D)互为对偶规划问题。
――(对合性)例设原问题对偶问题min x 1-x 2s.t. x 1+ x 2≥5x 1-2x 2≥1x 1, x 2≥0非对称形式的对偶:max 5w 1+w 2s.t. w 1+ w 2≤1 w 1-2w 2≤-1 w 1, w 2≥0(LP ) min cx (DP) max wbs.t. Ax =b s.t. wA ≤cx ≥0例设原问题对偶问题min 5x 1+4x 2+3x 3s.t. x 1+ x 2+x 3=43x 1+2x 2+x 3=5x 1, x 2, x 3≥0一般线性规划问题:max 4w 1+5w 2s.t. w 1+ 3w 2≤5 w 1+2w 2≤4 w 1+ w 2≤3可化为上述二者之一讨论其对偶问题,也可直接写出对偶问题,详细的对应法则见教材(陈宝林)124页。
直接写出对偶的弊端之一是对偶最优解不易确定,而对称形式和非对称形式对偶的最优解都可由原问题的单纯形乘子确定出来。
3.1.2 对偶定理(强对偶定理和弱对偶定理)定理2 (弱对偶定理) :设和分别是(L ) min cx 和 (D) max wbs.t. Ax ≥b s.t. wA ≤cx ≥0 w ≥0的可行解,则有下列不等式成立:c ≥b证明:由于A x ≥b 和w ≥0,则有w A x ≥w b 。
由于c ≥w A 和x ≥0,则有c x ≥w A x 。
因此有c ≥b推论1 设和分别是(L)和(D)的可行解,且有c =b ,则和分别是(L)和(D)的最优解。
第三章 对偶理论 第一讲 线性规划的对偶模型,对偶性质

由这个性质可得到下面几个结论:
1) (DP) 的任一可行解的目标值是 (LP)的最优值下界; (LP)的任一可行解的 目标是 (DP)的最优值的上界;
2)在互为对偶的两个问题中,若一个问题可行且具有无界解,则另一个问 题无可行解;
3) 若原问题可行且另一个问题不可行,则原问题具 有无界解。
注意: 上述结论(2)及(3)的条件不能少。一个问题无可行解时,另一个问题可能有可 行解(此时具有无界解)也可能无可行解。
目标函数求极大值时,所有约束条件为≤号,变量非负; 目标函数求极小值时,所有约束条件为≥号,变量非负。
max Z CX
AX b
(2.1)
X
0
min Z CX
AX b
(2.2)
X
0
注: (1)线性规划规范形式与标准型是两种不同形式,但可以 相互转换。
(2)规范形式的线性规划问题的对偶仍然是规范形式.
3.1 对偶线性规划问题
对偶问题的提出
原问题
min CX
AX b
X
0
对偶问题
max ub uA C u 0
原问题
min CX
AX b
X
0
对偶问题
max ub uA C u 0
原问题与对偶问题关系
(1)原问题的约束个数(不含非负约束)等于对 偶变量的个数
对偶问题
【例】写出下列线性规划的对偶问题
min CX
max ub
max Z 5x1 2x2 3x3
AX b
X
0
uA C u 0
对偶理论的原理

对偶理论的原理对偶理论(Duality Theory)是现代线性规划理论的重要组成部分,它与线性规划之间存在深刻的关系。
对偶理论的提出为线性规划问题的求解提供了一种全新的思路,使得原始问题与对偶问题之间能够相互转化和互相补充。
在对偶理论的引导下,线性规划问题的求解不再依赖于具体的算法和技巧,而是通过分析原始问题和对偶问题之间的关系,从而为问题的求解提供了更深入的理论支持。
对偶理论的基本原理来源于线性规划的最优性条件和对偶性原理。
在线性规划问题中,我们常常需要通过确定一组变量的数值来使得目标函数取得最大(或最小)值,并且满足一定的约束条件。
对于一个线性规划问题,我们可以将其分为两个部分,即原始问题(Primal Problem)和对偶问题(Dual Problem)。
原始问题的一般形式为:最大化:c^Tx约束条件:Ax ≤b其中,c为目标函数的系数向量,A为约束条件矩阵,x为决策变量向量,b为约束条件右端向量。
原始问题的最优解被称为原始问题的最优解。
对偶问题的一般形式为:最小化:b^Ty约束条件:A^Ty ≥c其中,y为对偶变量向量。
对偶问题的最优解被称为对偶问题的最优解。
对于线性规划问题的任意一个可行解,我们可以定义一个对应的对偶问题。
原始问题和对偶问题之间存在一种非常重要的关系,即弱对偶性和强对偶性。
弱对偶性指的是,对于原始问题和对偶问题的任意可行解,我们有:c^Tx ≤b^Ty强对偶性指的是,当原始问题和对偶问题都存在有限的最优解时,其最优解相等,即:c^Tx = b^Ty对偶理论的核心思想是通过最大化原始问题的目标函数和最小化对偶问题的目标函数,来求解原始问题和对偶问题的最优解。
具体而言,对偶理论主要包括以下几个方面的内容:1. 对偶定理:对于一个线性规划问题,从弱对偶性和强对偶性的角度出发,我们可以得到一些重要的结论。
例如,弱对偶性可以用来判断某个解是否为原始问题和对偶问题的最优解;而强对偶性则为原始问题和对偶问题的最优解提供了一个等价的刻画方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1
Complementary Slackness
The Strong Duality Theorem tells us that optimality is equivalent to equality in the Weak Duality Theorem. That is, x solves P and y solves D if and only if (x, y ) is a P − D feasible pair and cT x = y T Ax = bT y. We now carefully examine the consequences of this equivalence. Note that the equation cT x = y T Ax implies that
m
(i) either 0 = xj or
i=1 n
aij yi = cj or both for j = 1, . . . , n, and aij xj = bi or both for i = 1, . . . , m.
j =1
(ii) either 0 = yi or
3
Proof: If x solves P and y solves D, then by the Strong Duality Theorem we have equality in the Weak Duality Theorem. But we have just observed that this implies (1.2) and (1.3) which are equivalent to (i) and (ii) above. Conversely, if (i) and (ii) are satisfied, then we get equality in the Weak Duality Theorem. Therefore, by Theorem 1.2, x solves P and y solves D. The Complementary Slackness Theorem can be used to develop a test of optimality for a putative solution to P (or D). We state this test as a corollary. Corollary 1.1 The vector x ∈ Rn solves P if and only if x is feasible for P and there exists a vector y ∈ Rm feasible for D and such that
or both for i = 1, . . . , m.
The two observations (1.2) and (1.3) combine to yield the following theorem. Theorem 1.8 (The Complementary Slackness Theorem) The vector x ∈ Rn solves P and the vector y ∈ Rm solves D if and only if x is feasible for P and y is feasible for D and
The problem on the right is in standard form so we can take its dual to get the LP minimize subject to (−c)T x (−AT )T x ≥ (−b), 0 ≤ x = maximize subject to cT x Ax ≤ b, 0 ≤ x .
1
Duality Theory
maximize subject to cT x Ax ≤ b, 0 ≤ x
Recall from Section 1 that the dual to an LP in standard form (P ) is the LP (D ) minimize subject to bT y AT y ≥ c, 0 ≤ y.
m
aij yi − cj ) ≥ 0
i=1
for
j = 1, . . . , n.
Hence, the only way (1.1) can hold is if
m
xj (
i=1
aij yi − cj ) = 0
for
j = 1, . . . , n.
or equivalently,
m
(1.2)
xj = 0
or
i=1
aij yi = cj
or both for j = 1, . . . , n.
Similarly, (??) implies that
m n
0 = y T (b − Ax) =
i=1
yi (bi −
j =1
aij xj ).
Again, feasibility implies that
n
The primal-dual pair of LPs P − D are related via the Weak Duality Theorem. Theorem 1.1 (Weak Duality Theorem) If x ∈ Rn is feasible for P and y ∈ Rm is feasible for D, then cT x ≤ y T Ax ≤ bT y. Thus, if P is unbounded, then D is necessarily infeasible, and if D is unbounded, then P is necessarily infeasible. Moreover, if cT x ¯ = bT y ¯ with x ¯ feasible for P and y ¯ feasible for D, then x ¯ must solve P and y ¯ must solve D. We now use The Weak Duality Theorem in conjunction with The Fundamental Theorem of Linear Programming to prove the Strong Duality Theorem. The key ingredient in this proof is the general form for simplex tableaus derived at the end of Section 2 in (??). Theorem 1.2 (The Strong Duality Theorem) If either P or D has a finite optimal value, then so does the other, the optimal values coincide, and optimal solutions to both P and D exist. Remark: This result states that the finiteness of the optimal value implies the existence of a solution. This is not always the case for nonlinear optimization problems. Indeed, consider the problem min lem has a finite optimal value, namely zero; however, this value is not attained by any point x ∈ I R. That is, it has a finite optimal value, but a solution does not exist. The existence of solutions when the optimal value is finite is one of the many special properties of linear programs. Proof: Since the dual of the dual is the primal, we may as well assume that the primal has a finite optimal value. In this case, the Fundamental Theorem of Linear Programming says that an optimal basic feasible solution exists. By our formula for the general form of simplex tableaus (??), we know that there exists a nonsingular record matrix R ∈ I Rn×n and m a vector y ∈ I R such that the optimal tableau has the form R 0 −y T 1 A I b cT 0 0 = RA R Rb T T c − y A −y −y T b
n m
(1.1)
0 = x (A y − c) =
j =1
T
T
xj (
i=1
aij yi − cj ).
In addition, feasibility implies that
m
0 ≤ xj
and
0≤
i=1
aij yi − cj 2
for j = 1, . . . , n,
and so xj (
Since the problem D is a linear program, it too has a dual. The duality terminology suggests that the problems P and D come as a pair implying that the dual to D should be P . This is indeed the case as we now show: minimize subject to bT y AT y ≥ c, 0≤y = −maximize subject to (−b)T y (−AT )y ≤ (−c), 0 ≤ y.
