八年级上册数学周测题

合集下载

八年级上册数学周练试卷2.docx

扬州市江都区国际学校初二数学周练试卷2班级学号姓名成绩—一、选择题：（每题3分，计30分）1.下列图形中只有一条对称轴的是（）。

3. 将一正方形纸片按图中（1）、（2）的方式依次对折后，再沿（3）中的虚线裁剪，最后将4. 如图，已知AB = AD,那么添加下列一个条件后，仍无法判定△ABC 丝AADC 的是（）A. CB = CDB. ZBAC = ZDACC. ZBCA = ZDCAD. ZB = ZD=9Q°5. 如图，已知线段a, h,作等腰△ABC,使AB=AC,且BC=a, BC 边上的高AD=h.张红的作法是：（1）作线段BC=a ；（2）作线段BC 的垂直平分线MN, MN 与BC 相交于点D ；（3）在直线MN 上截取线段h ；（4）连结AB, AC, Z\ABC 为所求的等腰三角形.上述作法的四个步骤中，有错误的一步你认为是（）6. 下列线段中能围成三角形的是（）A. 7, 5, 12B. 6, 8, 14C. 4, 5, 6D.3, 4, 82015. 9.117.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为（）C 、7cm 或 3cm A 、7cm B 、3cmD 、5cmB8.如图，已知AABC的六个元素，则下面甲、乙、丙三个三角形中和AABC全等的图形是（）A.甲和乙 B ,乙和丙 C.只有乙 D.只有丙第9题图S如图，把矩形ABCD沿EF对折，若Zl=50°,则ZAEF等于（）A. 115°B. 130°C. 120°D. 65°10.已知ZAOB=30°,点P在ZAOB内部，点Pi与点P关于OA对称，点P2与点P关于OB对称，则左PiOP2是（）A.含30。

角的直角三角形B.顶角是30。

的等腰三角形C.等边三角形D.等腰直角三角形二、填空题：（每题3分，计30分）11.等腰ZXABC 中，若ZA=30°,则ZB=.12.如图，在AABC 中，ZC=90° , AD 平分ZCAB, BC=8cm, BD=5cm,那么D 点到直线AB的距离（图中虚线）是cm013.等腰三角形的两边长分别为5cm和2cm,则它的周长是cm。

八年级数学上册周周练检测试题一(含答案)

八年级数学(上)周周练(1.1～1.3)（满分：100分时间：90分钟）一、选择题(每小题2分，共20分)1．下列图案中，是轴对称图形的是( )2．下列四幅图案中，不是轴对称图形的是( )3．下列图案中，是轴对称图形的有( )A．1个B．2个C．3个D．4个4．下列轴对称图形中，对称轴最多的是( )5．如图是小华在镜子中看到的身后墙上的钟，你认为实际时问最接近8点的是( )6．把一个图形先沿着一条直线进行轴对称变换。

再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换．在自然界和日常生活中，大量地存在这种图形变换(如图①)．结合轴对称变换和平移变换的有关性质，你认为在滑动对称变换过程中，两个对应三角形(如图②)的对应点所具有的性质是( )A．对应点连线与对称轴垂直B．对应点连线被对称轴平分C．对应点连线被对称轴垂直平分D．对应点连线互相平行7．如图，把一张长方形纸片对折，折痕为AB，再以AB的中点O为顶点把平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( )A．正三角形B．正方形C．正五边形D．正六边形8．下列语句：①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③一个轴对称图形不一定只有一条对称轴；④两个轴对称图形的对应点一定在对称轴的两侧，其中正确的是( )A．①B．①③C．①②③D．①③④9．剪纸是中国的民间艺术，剪纸的方法很多，如图是一种剪纸方法的图示，先将纸折叠，然后再剪，展开即得到图案，则下列的四个图案中，不能用上述方法剪出的是( )10．如图，六边形ABCDEF是轴对称图形，CF所在的直线是它的对称轴，若∠AFC+∠BCF=150°，则∠AFE+OBCD的度数为( )A．150°B．300°C．210°D．330°二、填空题(每小题2分，共16分)11．长方形有______条对称轴，正方形有_______条对称轴，圆有______条对称轴．12．在缩写符号SOS、CCTV、BBC、WWW、TNT中，成轴对称图形的是___________．13．计算器上显示的0～9这十个数字中，是轴对称图形的是__________．14．如图，把图中某两个小方格涂上阴影，使整个图形是以虚线为对称轴的轴对称图形．第14题第15题第16题15．星期天小华去书店买书时，从镜子内看到背后墙上普通时钟的时针(粗)与分针(细)的位置如图所示，此时时钟表示的时间是___________________(按12小时制填写)．16．张军是学校足球队的运动员，他在镜子里看到衣服上的号码如图所示，则他是________号运动员．17．如图，桌面上有A、B两个球，若要将B球射向桌面任意一边，使一次反弹后击中A 球，则图中的8个点中，可以瞄准的点有__________个．第17题第18题18．如图，直线l是四边形ABCD的对称轴．若AD∥BC，则下列结论：①AB∥CD；②AB=BC；③A B⊥BC；④AO=OC，其中正确的是____________________(填序号)．三、耐心解一解(共64分)19．(10分)在下列图形中找出轴对称图形，并找出它的两组对应点．20．(8分)已知点A和点B关于某条直线对称，请你画出这条直线．21．(8分)如图是方格纸中画出的树形的一半，请你以树干为对称轴画出图形的另一半．22．(12分)如图是由两个等边三角形组成的图形，它是轴对称图形吗?如果不是，可以移动其中一个三角形，使它与另一个三角形一起组成轴对称图形，那么怎样移动才能使所构成的图形具有尽可能多的对称轴?23．(13分)如图，A是锐角∠MON内的一点，试分别在OM、ON上确定点B、C，使△ABC的周长最小．写出你作图的主要步骤，并标明你所确定的点(要求画出草图，保留作图痕迹)．24．(13分)某居民小区搞绿化，要在一块矩形空地上铺草坪，现征集设计方案，要使设计的图案由圆或正方形组成(圆和正方形的个数、大小不限)，并且使整个矩形场地成轴对称图形，请在矩形中画出你设计的方案．参考答案—、1．C 2．A 3．C 4．A 5．D 6．B 7．D 8．B 9．D 10．B二、11．2 4 无数12．BBC、WWW 13．0、1、3、8 14．如图所示15．下午1：30 16．16 17．2 18．①②④三、19．①、②、③、⑤都是轴对称图形，对应点略20．图略连接AB，作出线段AB 的垂直平分线l，即为它们的对称轴21．如图所示22．不是轴对称图形．将小的等边三角形移动到大的等边三角形内部图略23．分别作点A关于OM、ON的对称点A′、A″，连接A′A″，分别交OM、ON于点B、C，连接AB、AC．则点B、C即为所求．如图所示24．答案不唯一，如图所示。

人教版数学八年级上册周周测(含解析)第7周

第七周1.在平面直角坐标系中，点(2,1)A 与点B 关于x 轴对称，则点B 的坐标是( )A.(2,1)-B.(2,1)-C.(2,1)--D.(2,1)2.如图,AD 是等腰角形ABC 的顶角平分线,5BD = ,则CD 等于( )A.10B.5C.4D.33.如图，在ABC 中，AC BC =，点D 在AC 边上，点E 在CB 的延长线上，DE 与AB 相交于点F ，若50C ∠=︒，25E ∠=︒，则BFD ∠的度数为( )A.100°B.120°C.140°D.150°4.如图，在平面直角坐标系中，对ABC 进行循环往复的轴对称变换，若原来点A 的坐标是(,)m n ，经过2020次变换后所得的点A 的坐标是( )A.(),m n -B.(),m n --C.(,)m n -D.(,)m n5.如图，已知ABC 中，50ABC ∠=︒，P 为ABC 内一点，过点P 的直线MN 分别交AB ，BC 于点M ，N .若M 在PA 的垂直平分线上，N 在PC 的垂直平分线上，则APC ∠的度数为( )A.100°B.105°C.115°D.无法确定6.如图，在ABC △中，20AB =cm ，12AC =cm ，点P 从点B 出发以每秒3cm 的速度向点A 运动，点Q 从点A 同时出发以每秒2cm 的速度向点C 运动，其中一个动点到达终点时，另一个动点也随之停止运动，当APQ △是以PQ 为底边的等腰三角形时，运动的时间是( )A.2.5秒B.3秒C.3.5秒D.4秒7.在平面直角坐标系中，已知点(,3)P a -在第四象限，则点P 关于直线2x =对称的点的坐标是( )A.(,1)aB.(2,3)a -+-C.(4,3)a -+-D.(,3)a --8.如图，在ABC 中，ABC ∠与ACB ∠的平分线交于点I ，过点I 作DE BC 交BA 于点D ，交AC于点E ，且5AB =，3AC =，50A ∠=︒，则下列说法错误的是( )A.DBI 和EIC 是等腰三角形B. 1.5DI IE =C.ADE 的周长是8D.115BIC ∠=︒9.李华同学在求点(,)P a b 关于y 轴对称的点的坐标时，看成了求关于x 轴对称的点的坐标，求得结果是(1,2)，那么正确的结果应该是___________.10.已知ABC △是等腰三角形.若40A ∠=︒，则ABC △的顶角度数是___________.11.如图，AD ，CE 分别是ABC 的中线和角平分线.若AB AC =，25CAD ∠=︒，则ACE ∠的度数为____________.12.如图，在ABC △中,,AB AC D =是BC 边上的中点，连接,AD BE 平分ABC ∠交AC 于点E ，过点E 作//EF BC 交AB 于点F .(1)若36C ∠=，求BAD ∠的度数.(2)求证:FB FE =.答案以及解析1.答案：A 解析：点(2,1)A 与点B 关于x 轴对称，∴点B 的坐标是：(2,1)-.故选：A.2.答案：B解析：AD 是等腰三角形ABC 的顶角平分线，5BD =，5CD BD ∴==.3.答案：C解析：ABC 中，AC BC =，50C ∠=︒，()118050652ABC ∴∠=⨯︒-︒=︒，ABC ∠是BEF 的外角，652540BFE ABC E ∴∠=∠-∠=︒-︒=︒，18040140BFD ∴∠=︒-︒=︒，故选C.4.答案：D解析：点A 第1次关于y 轴对称后在第一象限，点A 第2次关于x 轴对称后在第四象限，点A 第3次关于y 轴对称后在第三象限，点A 第4次关于x 轴对称后在第二象限，即点A 回到原始位置，所以，每4次对称为—个循环. 20204505÷=，所以经过第2020次变换后所得的A 点与原始位置相同，其坐标为(,)m n .故选D.5.答案：C解析：50ABC ∠=︒，130BAC ACB ∴∠+∠=︒，M 在PA 的垂直平分线上，N 在PC 的垂直平分线上，AM PM ∴=，PN CN =，MAP APM ∴∠=∠，CPN PCN ∠=∠，180180APC APM CPN PAC ACP ∠=︒-∠-∠=︒-∠-∠，1130652MAP PCN PAC ACP ∴∠+∠=∠+∠=⨯︒=︒，115APC ∴∠=︒，故选C. 6.答案：D解析：设运动的时间为x 秒，则3BP x =cm ，2AQ x =cm.当APQ 是以PQ 为底边的等腰三角形时，AP AQ =，即2032x x -=，解得4x =.当运动的时间为4秒时，3412BP =⨯=（cm ）AB <，248AQ =⨯=（cm ）AC <，符合题意.故运动的时间为4秒.7.答案：C解析：设(,3)P a -关于直线2x =的对称点为(,3)P m '-，则有22a m +=，4m a ∴=-， (4,3)P a '∴-+-，故选C.8.答案：B解析：BI 平分DBC ∠，DBI CBI ∴∠=∠，DE BC ，DIB IBC ∴∠=∠，DIB DBI ∴∠=∠，BD DI ∴=.同理，CE EI =.DBI ∴和EIC 是等腰三角形.ADE ∴的周长8AD DI IE EA AB AC =+++=+=.50A ∠=︒，130ABC ACB ∴∠+∠=︒，65IBC ICB ∴∠+∠=︒，115BIC ∴∠=︒，故选项A,C,D 说法正确，故选B.9.答案：(1,2)-- 解析：点(,)P a b 关于x 轴对称的点的坐标为(1,2)，∴点(12)P -,，∴点P 关于y 轴对称的点的坐标为(1,2)--.10.答案：40°或100°解析：分两种情况讨论.①当A ∠是顶角时，ABC △的顶角的度数是40°；②当A ∠是底角时，ABC △的顶角的度数是180402100-⨯=.11.答案：32.5° 解析：AD 是ABC 的中线，AB AC =，25CAD ∠=︒，250CAB CAD ∴∠=∠=︒，()1180652B ACB CAB ∠=∠=︒-∠=︒.CE 是ABC 的角平分线，132.52ACE ACB ∴∠=∠=︒.故答案为32.5°.12.答案：(1)54°(2)见解析解析：(1),36AB AC ABC C =∴∠=∠=.又D 是BC 边上的中点，,90AD BC ADB ∴⊥∴∠=,903654BAD ∴∠=-=.(2)证明：BE 平分,ABC FBE CBE ∠∴∠=∠.,//EF BC FEB CBE ∴∠=∠，,FEB FBE FB FE ∴∠=∠∴=.。

人教版八上数学八年级数学上册周周清检测内容：13

检测内容：13.3－13.4得分________卷后分________评价________一、选择题(每小题4分，共32分)1．下列条件中，能判定三角形是等腰三角形的是(C)A．三角形中有两个角为30°，60°B．三角形中有两个角为40°，80°C．三角形中有两个角为50°，80°D．三角形中有两个角为锐角2．若等腰三角形的周长为10 cm，其中一边长为2 cm，则该等腰三角形的底边长为(A) A．2 cm B．6 cmC．2 cm或6 cm D．以上全错3．如图，在△ABC中，点D在BC上，若AD＝BD＝DC，则∠BAC等于(C)A．60°B．80°C．90°D．100°第3题图第4题图4．如图是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC，DE垂直于横梁AC，AB＝6 m，∠A＝30°，则DE等于(A)A．1.5 m B．2 m C．2.5 m D．3 m5．如图，E是等边三角形ABC中AC边上的点，∠1＝∠2，BE＝CD，则△ADE的形状是(B)A．等腰三角形B．等边三角形C．不等边三角形D．不能确定形状第5题图第6题图6．如图，在等边三角形ABC中，D是AB的中点，DE⊥AC于点E，EF⊥BC于点F，已知AB＝8，则BF的长为(C)A．3 B．4 C．5 D．67．(包头中考)如图，在△ABC中，AB＝AC，△ADE的顶点D，E分别在BC，AC上，且∠DAE＝90°，AD＝AE.若∠C＋∠BAC＝145°，则∠EDC的度数为(D) A．17.5°B．12.5°C．12°D．10°第7题图第8题图8．如图，等腰三角形ABC 的底边BC 长为4，面积是16，腰AC 的垂直平分线EF 分别交AC ，AB 边于点E ，F ，若点D 为BC 边的中点，点M 为线段EF 上一动点，则△CDM 周长的最小值为(D )A ．7B ．8C ．9D ．10二、填空题(每小题4分，共24分)9．如图，在△ADC 中，B 是AC 上一点，AD ＝BD ＝BC ，若∠C ＝25°，则∠ADB ＝__80°__．第9题图第10题图10．(白银中考)将一张长方形纸片折叠成如图所示的图形，若AB ＝6 cm ，则AC ＝__6__cm.11．(成都中考)如图，在△ABC 中，AB ＝AC ，点D ，E 都在边BC 上，∠BAD ＝∠CAE ，若BD ＝9，则CE 的长为__9__．第11题图第12题图12．如图，在△ABC 中，AF 平分∠BAC ，AC 的垂直平分线交BC 于点E ，∠B ＝67°，∠FAE ＝19°，则∠C ＝__25__度．13．如图，已知△ABC 中，AB ＝AC ，AD ⊥BC 于点D ，若△ABC ，△ABD 的周长分别为20 cm ，16 cm ，则AD 的长为__6__cm.第13题图第14题图14．如图，已知∠MON ＝30°，点A 1，A 2，A 3……在射线ON 上，点B 1，B 2，B 3……在射线OM 上，△A 1B 1A 2，△A 2B 2A 3，△A 3B 3A 4……均为等边三角形，若OA 1＝12，则△A 6B 6A 7的边长为__16__．三、解答题(共44分)15．(8分)如图，一艘轮船以15海里/小时的速度由南向北航行，在A 处测得小岛P 在北偏西15°方向上，2小时后，轮船在B 处测得小岛P 在北偏西30°方向上，在小岛P 周围18海里内有暗礁，若轮船继续向前航行，有无触礁的危险？解：过点P作PC⊥AB，垂足为C，∵∠PAB＝15°，∠PBC＝30°，∴∠APB＝∠PBC －∠PAB＝30°－15°＝15°.∴PB＝AB.由题意知AB＝15×2＝30(海里)，∴PB＝30海里．在Rt△PBC中，∵∠PBC＝30°，∴PC＝12PB＝15(海里).∴PC<18海里．∴轮船继续向前航行有触礁的危险16．(10分)(重庆中考)如图，在△ABC中，AB＝AC，AD⊥BC于点D.(1)若∠C＝42°，求∠BAD的度数；(2)若点E在边AB上，EF∥AC交AD的延长线于点F.求证：AE＝FE.解：(1)∵AB＝AC，AD⊥BC于点D，∴∠BAD＝∠CAD，∠ADC＝90°，又∠C＝42°，∴∠BAD＝∠CAD＝90°－∠C＝90°－42°＝48°(2)∵EF∥AC，∴∠F＝∠CAD，又∠BAD＝∠CAD，∴∠BAD＝∠F，∴AE＝FE17．(12分)如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，AD平分∠CAB，延长AC至E，使CE＝AC.(1)求证：DE＝DB；(2)连接BE，试判断△ABE的形状，并说明理由．解：(1)证明：∵∠ACB＝90°，∠ABC＝30°，∴∠CAB＝60°.∵AD平分∠CAB，∴∠DAB＝12∠CAB＝30°＝∠ABC.∴DA＝DB.∵CE＝AC，BC⊥AE，∴BC是线段AE的垂直平分线，∴DE ＝DA ，∴DE ＝DB (2)△ABE 是等边三角形，理由如下：∵BC 是线段AE 的垂直平分线，∴BA ＝BE ，即△ABE 是等腰三角形．又∵∠CAB ＝60°，∴△ABE 是等边三角形18．(14分)如图，在Rt △ABC 中，∠C ＝90°，∠A ＝60°，AB ＝10 cm ，若点M 从点B 出发以2 cm/s 的速度向点A 运动，点N 从点A 出发以1 cm/s 的速度向点C 运动，设M ，N 分别从点B ，A 同时出发，运动的时间为t s.(1)用含t 的式子表示线段AM ，AN 的长；(2)当 t 为何值时，△AMN 是以MN 为底边的等腰三角形？(3)当t 为何值时，MN ∥BC ？并求出此时CN 的长.解：(1)由题意知BM ＝2t cm ，AN ＝t cm ，∵∠C ＝90°，∠A ＝60°，∴∠B ＝30°. ∵AB ＝10 cm ，∴AM ＝AB －BM ＝(10－2t )cm ，AN ＝t cm(2)∵△AMN 是以MN 为底的等腰三角形，∴AM ＝AN ，即10－2t ＝t ，解得t ＝103. ∴当t ＝103时，△AMN 是以MN 为底边的等腰三角形 (3)∵∠C ＝90°，∠A ＝60°，∴∠B ＝30°，AC ＝12AB ＝5 cm.∵MN ∥BC ，∴∠NMA ＝∠B ＝30°，∠MNA ＝∠C ＝90°，∴AN ＝12 AM ，∴t ＝12 (10－2t )，解得t ＝52，∴当t ＝52 时，MN ∥BC ，CN ＝5－52 ×1＝52cm。

沪科版八年级数学上单元周周测(三)(12

2．(绍兴中考)如图是我国古代计时器“漏壶”的示意图，在壶内盛一定
量的水，水从壶底的小孔漏出，壶壁内画有刻度．人们根据壶中水面的
位置计时，用 x 表示时间，y 表示壶底到水面的高度，则 y 与 x 的函数关
系的图象是
( C)
第3页
八年级数学上册沪科版
3．已知关于 x 的方程 kx＋b＝3 的解为 x＝5，则直线 y＝kx＋b 的图象一
第9页
八年级数学上册沪科版
10．(鄂州中考)如图，直线 y＝kx＋b 过 A(－1，2)，B(－2，0)两点，则 0≤kx＋b≤－2x 的解集为－－2≤2≤x≤x≤－1－1.
第 10 页
八年级数学上册沪科版
11．某市为提倡居民节约用水，自今年 1 月 1 日起调整居民用水价格，图中 l1，l2 分别表示去年、今年水费 y(元)与用水量 x(m3)之间的关系，小雨家去年用水量为 140 m3，若今年用水量与去年相同，水费将比去年多 18180 0 元．【解析】由函数图象中的数据确定 l1，l2 的表达式，计算出 x＝140 时的函数值，相减即得．
所以k＋b＝4， k＝－1，
解得b＝5，所以直线 AB 的表达式为 y＝－x＋5.
第 17 页
八年级数学上册沪科版
(2)因为直线 y＝2x－4 与直线 AB 相交于点 C，所以－n＋5＝2，解得 n＝ 3，所以点 C 的坐标为(3，2)，由图象可知方程 kx＋b＝2x－4 的解是 x ＝3. (3)根据图象，写出关于 x 的不等式组 2x－4≥kx＋b＞0 的解集．解：由图象可知 x≥3 时，2x－4≥kx＋b，由图象可知 x＜5 时，kx＋b＞0，所以不等式组 2x－4≥kx＋b＞0 的解集是 3≤x＜5.

人教版八上数学八年级数学上册周周清检测内容

检测内容：14.1得分________ 卷后分________ 评价________一、选择题(每小题3分，共24分)1．(温州中考)计算a 6·a 2的结果是(C )A ．a 3B ．a 4C ．a 8D ．a 122．(南通中考)下列计算，正确的是(D )A ．a 2·a 3＝a 6B ．2a 2－a ＝aC ．a 6÷a 2＝a 3D ．(a 2)3＝a 63．下列多项式相乘的结果为x 2＋3x －18的是(D )A ．(x －2)(x ＋9)B ．(x ＋2)(x －9)C ．(x ＋3)(x －6)D ．(x －3)(x ＋6)4．通过计算比较图①，图②中阴影部分的面积，可以验证的计算式子是(D )A ．a (b －x )＝ab －axB ．b (a －x )＝ab －bxC ．(a －x )(b －x )＝ab －ax －bxD ．(a －x )(b －x )＝ab －ax －bx ＋x 25．下列运算中，错误的是(B )A ．(6a 3＋3a 2)÷12a ＝12a 2＋6a B ．(6a 3－4a 2＋2a )÷2a ＝3a 2－2aC ．(9a 7－3a 3)÷(－13a 3)＝－27a 4＋9 D ．(14 a 2＋a )÷(－12 a )＝－12a －2 6．(河北中考)小明总结了以下结论：①a (b ＋c )＝ab ＋ac ；②a (b －c )＝ab －ac ；③(b －c )÷a ＝b ÷a －c ÷a (a ≠0)；④a ÷(b ＋c )＝a ÷b ＋a ÷c (a ≠0).其中一定成立的个数是(C )A ．1个B ．2个C ．3个D ．4个7．当m 为偶数时，(a －b )m ·(b －a )n 与(b －a )m ＋n 的结果(A )A ．相等B ．互为相反数C ．不相等D ．以上说法都不对8．(乐山中考)已知3m ＝4，32m －4n ＝2.若9n ＝x ，则x 的值为(C )A ．8B ．4C ．2 2D ． 2二、填空题(每小题3分，共18分)9．计算：－a 3·(－a )2＝__－a 5__．10．计算：(1)23 ×(π－1)0＝__23 __； (2)[(－a －b )2]5·(a ＋b )3＝__(a ＋b )13__．11．一个多项式与－8x 2的积是多项式－16x 3＋40x 2y ，则这个多项式是__2x －5y __．12．小明在进行两个多项式的乘法运算时，不小心把乘以x ＋y 2 错抄成乘以12，结果得到(3x 2－xy )，则正确的计算结果是__3x 3＋2x 2y －xy 2__．13．已知a x ＋y ＝6，a y ＝3，则a 2x ＝__4__．14．已知(x －12)(x －n )＝x 2＋mx －12，则m －n ＝__－10__．三、解答题(共58分)15．(12分)计算：(1)(－2)3＋(2 )2－(3 －5)0；解：原式＝－8＋2－1＝－7(2)(23)2 020×1.52 018×(－1)2 020；解：原式＝(23 ×32 )2 018×49 ×1＝49(3)(2a 2b )3·(－ab 2)÷(－8a 7b 5)；解：原式＝1(4)(m －n )2·(n －m )3·(n －m )4.解：原式＝(n －m )2·(n －m )3·(n －m )4＝(n －m )916．(8分)解方程或不等式：(1)(x －3)(x ＋8)＝(x ＋4)(x －7)＋2(x ＋5)；解：x 2＋5x －24＝x 2－3x －28＋2x ＋10，∴5x ＋x ＝6，解得x ＝1(2)2x (x －4)>(x ＋4)(x ＋2)＋(x －3)(x ＋6).解：2x 2－8x >x 2＋6x ＋8＋x 2＋3x －18，∴－8x －9x >－10，解得x <101717．(6分)先化简，再求值：[2y (x －1)8－3y 2(x －1)7＋4y 3(x －1)6]÷[－3y (x －1)2]，其中x ＝2，y ＝－1.解：原式＝－23 (x －1)6＋y (x －1)5－43y 2(x －1)4，当x ＝2，y ＝－1时，原式＝－318．(8分)小明想把一个长为60 cm ，宽为40 cm 的长方形硬纸片做成一个无盖的长方体盒子，于是在长方形纸片的四个角各剪去一个相同的小正方形．(1)若设小正方形的边长为x cm ，求图中阴影部分的面积；(2)当x ＝5时，求这个盒子的体积．解：(1)(60－2x )(40－2x )＝4x 2－200x ＋2 400.答：图中阴影部分的面积为(4x 2－200x ＋2 400)cm 2(2)当x ＝5时，4x 2－200x ＋2 400＝1 500(cm 2).这个盒子的体积为1 500×5＝7 500(cm 3)19．(10分)(1)3x ＝4，3y ＝6，求92x －y ＋27x －y 的值；解：92x －y ＋27x －y ＝34x－2y ＋33x －3y ＝(3x )4÷(3y )2＋(3x )3÷(3y )3＝44÷62＋43÷63＝649 ＋827 ＝20027(2)已知10a ＝20，10b ＝15，求3a ÷3b 的值．解：∵10a ＝20，10b ＝15 ，∴10a ÷10b ＝10a －b ＝20÷15＝102.∴a －b ＝2，∴3a ÷3b ＝3a －b ＝32＝920．(14分)阅读材料：一般地，若a x ＝N (a ＞0且a ≠1)，那么x 叫做以a 为底N 的对数，记作x ＝log a N ，比如指数式23＝8可以转化为对数式3＝log 28，对数式2＝log 636可以转化为指数式62＝36.根据以上材料，解决下列问题：(1)计算：log 24＝__2__，log 216＝__4__，log 264＝__6__；(2)观察(1)中的三个数，猜测：log a M ＋log a N ＝__log a MN __(a ＞0且a ≠1，M ＞0，N ＞0)，并加以证明这个结论；(3)已知：log a 3＝5，求log a 9和log a 27的值(a ＞0且a ≠1).解：(2)log a M＋log a N＝log a MN；证明：设log a M＝x，log a N＝y，则a x＝M，a y＝N，∴M·N＝a x·a y＝a x＋y，根据对数的定义，x＋y＝log a MN，即log a M＋log a N＝log a MN(3)由log a3＝5，得a5＝3.∵9＝3×3＝a5·a5＝a10，27＝3×3×3＝a5·a5·a5＝a15，∴根据对数的定义，log a9＝10，log a27＝15。

人教版数学八年级上册周周测(含解析)第4周

第四周1.如图，OA OBC∠等于( )∠=︒，30∠=︒，则OBD=，OC OD=，若45OA.75°B.105°C.90°D.120°2.如图，已知AC DB=，添加下列四个条件：①A D∠=∠；②ABD DCA∠=∠；③ACB DBC∠=∠；④ABC DCB∠=∠中的一个，其中能使ABC DCB≌的有( )A.1个B.2个C.3个D.4个3.如图是作ABC的作图痕迹，则此作图的已知条件是( )A.已知两边及夹角B.已知三边C.已知两角及夹边D.已知两边及一边对角4.要测量圆形工件的外径，工人师傅设计了如图所示的卡钳，点O为卡钳两柄交点，且有===，如果圆形工件恰好通过卡钳AB，则此工件的外径必是CD之长了，其中的OA OB OC OD依据是全等三角形的判定条件( )A.SSSB.SASC.ASAD.AAS5.如图所示，AC 和BD 相交于点O ，AO DO =，AB AC ⊥，CD BD ⊥，那么AB 与CD 的关系是( )A.一定相等B.可能相等也可能不相等C.一定不相等D.增加条件后，它们相等6.如图,D 是AB 上的一点,DF 交AC 于点,,//E DE EF FC AB =.若4,3AB CF ==,则BD 的长是( )A.0.5B.1C.1.5D.27.如图，点B ，C ，E 在同一条直线上，60B E ACF ∠=∠=∠=︒，AB CE =，则与BC 相等的线段是( )A.ACB.AFC.CFD.EF8.在ABC 中，AB AC =，AB BC >，点D 在边BC 上，2CD BD =，点E ，F 在线段AD 上，12BAC ∠=∠=∠，若ABC 的面积为18，则ACF 与BDE 的面积之和是( )A.6B.8C.9D.129.如图所示，已知AF DC≌，则需添加的条件是=，BC EF，若要用“ASA”去证ABC DEF______________.10.如图所示，在ABC中，50∠的度数是B C=，则EDF=，BE CD∠=∠=︒，BD CF____________.11.如图，Rt ABC中，90BAC=，分别过点B、C作过点A的直线的垂线BD、∠=︒，AB ACCE，垂足分别为DE，若4BD=，2CE=，则DE=___________.12.如图①，ABC中，H是高AD和高BE的交点，且AD BD=.（1）请你猜想BH和AC的数量关系，并说明理由；（2）若将图①中的BAC∠改成钝角，请你在图②中画出该题的图形，此时（1）中的结论还成立吗？答案以及解析1.答案：B解析：在AOC 与BOD 中，OA OB O O OC OD =⎧⎪∠=∠⎨⎪=⎩，(SAS)AOC BOD ∴≌，30D C ∴∠=∠=︒，1804530105OBD ∴∠=︒-︒-︒=︒，故选B.2.答案：A解析：已知AC DB =，由题图知BC CB =，则添加条件③，可以使得(SAS)ABC DCB ≅，故选A.3.答案：C解析：观察题图可知：已知线段AB ，CAB α∠=，CBA β∠=，故选C.4.答案：B解析：如图，连接AB 、CD ，在ABO 和DCO 中，OA OD AOB DOC OB OC =⎧⎪∠=∠⎨⎪=⎩，(SAS)ABO DCO ∴≅，AB CD ∴=.故选B.5.答案：A解析：AB AC ⊥，CD BD ⊥，90A D ∴∠=∠=︒.在OAB 和ODC 中，A D OA ODAOB DOC ∠=∠⎧⎪=⎨⎪∠=∠⎩，(ASA)OAB ODC ∴≅，AB CD ∴=，故选A.6.答案：B解析：,/,/FC AB A FCE ADE F ∴∠=∠∠=∠.在ADE △和CFE △中,,,,A FCE ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩, 3.4ADE CFE AD CF AB ∴∴===≌△△,1BD AB AD ∴=-=.7.答案：D 解析：ACE B BAC ACF ECF ∠=∠+∠=∠+∠，60B E ACF ∠=∠=∠=︒，BAC ECF ∴∠=∠.在ABC 和CEF 中，B E AB CEBAC ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩，(ASA)ABC CEF ∴≅，BC EF ∴=.故选D. 8.答案：A解析：12BAC ∠=∠=∠，1BAE ABE ∠=∠+∠，BAC BAE CAF ∠=∠+∠，2FCA CAF ∠=∠+∠，ABE CAF ∴∠=∠，BAE FCA ∠=∠.在ABE 和CAF 中，ABE CAF AB ACBAE ACF ∠=∠⎧⎪=⎨⎪∠=∠⎩，(ASA)ABE CAF ∴≅，ACF ∴的面积ABE =的面积，ACF ∴与BDE 的面积之和ABE =与BDE 的面积之和ABD =的面积.ABC 的面积为18，2CD BD =，ABD ∴的面积为11863⨯=，ACF ∴与BDE 的面积之和ABD =的面积6=. 9.答案：A D ∠=∠解析：需添加A D ∠=∠，理由：AF CD =，AF FC CD FC ∴+=+，AC DF ∴=.BC EF ，BCA EFD ∴∠=∠.在ABC 和DEF 中，A D AC DF BCA EFD ∠=∠⎧⎪=⎨⎪∠=∠⎩，(ASA)ABC DEF ∴≅. 10.答案：50°解析：在BDE 与CFD 中，50BD CF B C BE CD =⎧⎪∠=∠=︒⎨⎪=⎩，(SAS)BDE CFD ∴≅，BDE CFD ∴∠=∠，()180()180()18018050EDF BDE CDF CFD CDF C ∴∠=︒-∠+∠=︒-∠+∠=︒-︒-∠=︒.11.答案：6解析：90BAC ∠=︒，90BAD CAE ∴∠+∠=︒，BD DE ⊥，90BDA ∴∠=︒，90BAD DBA ∴∠+∠=︒，DBA CAE ∴∠=∠，CE DE ⊥，90AEC ∴∠=︒，在BDA 和AEC 中，90ABD CAE BDA AEC AB AC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，(AAS)BDA AEC ∴≅，2AD CE ∴==，4AE BD ==，246DE AD AE ∴=+=+=.12.答案：（1）BH AC =. 理由：AD 和BE 是ABC 的高，90BDH ADC ∴∠=∠=︒，90DBH C CAD C ∠+∠=∠+∠=︒，DBH DAC ∴∠=∠，在BDH 和ADC 中，DBH DAC BD ADBDH ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩， (ASA)BDH ADC ∴≅，BH AC ∴=.（2）成立.如图，AD 和BE 是ABC 的高，90BDH ADC BEC ∴∠=∠=∠=︒，90DBH H DBH C ∴∠+∠=∠+∠=︒，H C ∴∠=∠，在BDH 和ADC 中，H C BDH ADC BD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩，(AAS)BDH ADC ∴≅，BH AC ∴=.。

人教版数学八年级上册周周测(含解析)第8周

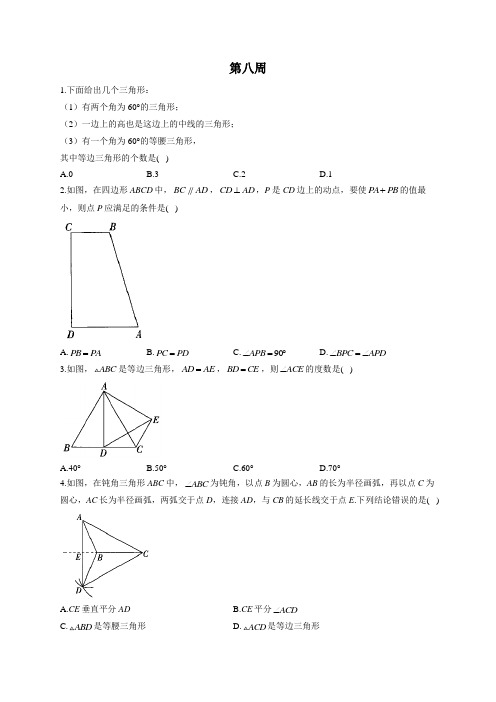
第八周1.下面给出几个三角形：（1）有两个角为60°的三角形；（2）一边上的高也是这边上的中线的三角形；（3）有一个角为60°的等腰三角形，其中等边三角形的个数是( )A.0B.3C.2D.12.如图，在四边形ABCD中，BC AD，CD AD+的值最⊥，P是CD边上的动点，要使PA PB小，则点P应满足的条件是( )A.PB PA= B.PC PD∠=∠∠=︒ D.BPC APD= C.90APB3.如图，ABC是等边三角形，AD AE=，BD CE=，则ACE∠的度数是( )A.40°B.50°C.60°D.70°4.如图，在钝角三角形ABC中，ABC∠为钝角，以点B为圆心，AB的长为半径画弧，再以点C为圆心，AC长为半径画弧，两弧交于点D，连接AD，与CB的延长线交于点E.下列结论错误的是( )A.CE垂直平分ADB.CE平分ACD∠C.ABD是等腰三角形D.ACD是等边三角形5.如图，牧童在A 处放牛，其家在B 处，A 、B 到河岸的距离分别为AC 的长和BD 的长，且AC BD =，若点A 到河岸CD 的中点的距离为500米，则牧童从A 处把牛牵到河边饮水再回家，最短距离是( )A.750米B.1000米C.1500米D.2000米 6.如图，在等边ABC 中，BD 平分ABC ∠交AC 于点D ，过点D 作DE BC ⊥于点E ，且1.5CE =，则AB 的长为( )A.3B.4.5C.6D.7.57.如图，CD 是ABC 的角平分线，ABC 的面积为12，BC 的长为6，点E ，F 分别是CD ，AC 上的动点，则AE EF +的最小值是( )A.6B.4C.3D.28.如图，等边三角形ABC 的边长为4，AD 是BC 边上的中线，F 是AD 上的动点，E 是AC 边上一点.若2AE =，则EF CF +取得最小值时，ECF ∠的度数为( )A.15°B.22.5°C.30°D.45°9.如图，在等边ABC 中，BD 为AC 边上的中线，CE 为ACB ∠的平分线，BD 、CE 交于点M ，则BME ∠=___________°.10.如图，在等边ABC中，9AO=，点P是AB上一动点，连接AC=，点O在AC上，且3OP，将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上，则AP的长是____________.11.如图，直线m是ABC中BC边的垂直平分线，点P是直线m上的动点.若6AC=，AB=，4 BC=，则APC的周长的最小值是_____________.712.如图，A,B,C是平面内三点.（1）按要求作图：①作射线BC，过点B作直线l，使A,C两点在直线l两旁；②点P为直线l上任意一点，点Q为射线BC上任意一点，连接线段AP,PQ.（2）在（1）所作图形中，若点A到直线l的距离为2，点A到直线BC的距离为5，点A,B之间的距离为8，点A,C之间的距离为6，求AP PQ+的最小值，并写出其依据.答案以及解析1.答案：C解析：易知（1）有两个角为60°的三角形的三个内角都是60°，（3）有一个角是60°的等腰三角形是等边三角形，所以（1）（3）为等边三角形，故等边三角形的个数是2.2.答案：D解析：如图所示，作点A 关于CD 的对称点A '，连接A B '，交CD 于点P ，连接AP ，则PA PB +的最小值为A B '的长，点P 即为所求.点A '与点A 关于CD 对称，APD A PD '∴∠=∠，BPC A PD '∠=∠，BPC APD ∴∠=∠，故D 符合题意.由图可知，选项A 和选项B 不成立，而C 只有在PC BC =时才成立，故选项C 不一定成立.故选D.3.答案：C解析：ABC 是等边三角形，AB AC BC ∴==，60B ∠=︒，在ABD 和ACE 中，AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩，ABD ACE ∴≌，60ACE B ∴∠=∠=︒，故选C.4.答案：D解析：由题意可得CA CD =，BA BD =，∴直线CB 是AD 的垂直平分线，即CE 垂直平分AD ，故A 选项结论正确；CE 垂直平分AD ，CAD CDA ∴∠=∠，CEA CED ∠=∠，ACE DCE ∴∠=∠，即CE 平分ACD ∠，故B 选项结论正确；DB AB =，ABD ∴是等腰三角形，故C 选项结论正确；AD 与AC 不一定相等，ACD ∴不一定是等边三角形，故D 选项结论错误.故选D.5.答案：B解析：作A 关于CD 的对称点A '，连接A B '交CD 于P ，则AC A C BD '==，90A CD ACD '∠=∠=︒，A P AP '=，在A CP '和BDP 中，A CP BDP A PC BPD A C BD '∠=∠⎧⎪'∠=∠⎨⎪'=⎩，A CP BDP '∴≅，CP PD ∴=，A P PB '=，∴P 为CD 的中点，500AP A P PB '∴===米，1000A B AP PB '∴=+=米.6.答案：C解析：ABC 是等边三角形，60ABC C ∴∠=∠=︒，AB BC AC ==，DE BC ⊥，30CDE ∴∠=︒， 1.5EC =，23CD EC ∴==，BD 平分ABC ∠，3AD CD ∴==，6AB AC AD CD ∴==+=.7.答案：B解析：如图，作点A 关于CD 的对称点H .CD 是ABC 的角平分线，∴点H 一定在BC 上.过H 作HF AC ⊥于F ，交CD 于E ，此时AE EF +的值最小，AE EF +的最小值HF =.过A 作AG BC ⊥于G .ABC 的面积为12，BC 的长为6，4AG ∴=，CD 垂直平分AH ，AC CH ∴=，1122ACH S AC HF CH AG ∴=-⋅=⋅，4HF AG ∴==，AE EF ∴+的最小值是4，故选B. 8.答案：C解析：如图,连接BE 交AD 于点.F AD 是等边三角形ABC 的中线,,, ,AD BC BD CD FC FB CF EF BF EF BE ∴⊥=∴=∴+=+=,此时CF EF +的值最小.4,2,AC AE E ==∴是AC 的中点.ABC 是等边三角形,,BE AC BE ∴⊥平分,60ABC ABC ACB ∠∠=∠=︒,30FBC ∴∠=︒.,30FC FB FCB FBC =∴∠=∠=︒,603030ECF ACB FCB ∴∠=∠-∠=︒-︒=︒.故选C.9.答案：60解析：ABC 是等边三角形，60ABC ∴∠=︒，BD 为AC 边上的中线，CE 为ACB ∠的平分线，11603022EBD ABC ∴∠=∠=⨯︒=︒，90BEC ∠=︒，180180309060BME EBD BEC ∴∠=︒-∠-∠=︒-︒-︒=︒.10.答案：6解析：A APO POC POD COD ∠+∠=∠=∠+∠，60A POD ∠=∠=︒，APO COD ∴∠=∠.在APO 和COD 中，,,,A C APO COD OP DO ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)APO COD ∴≅，AP CO ∴=，6CO AC AO =-=，6AP ∴=.11.答案：10 解析：直线m 垂直平分BC ，∴B 、C 两点关于直线m 对称，如图，设直线m 交AB 于D ，连接CD ，则BD CD =.当P 和D 重合时，AP CP +的值最小，最小值等于AB 的长，APC ∴的周长的最小值是6410+=.12.答案：（1）（作法不唯一）如图所示，射线BC ，直线l ，线段AP ,PQ 即为所求.（2）如图，过点A 作AQ BC ⊥于点Q ，交直线l 于点P ，此时AP PQ +的值最小.因为点A 到直线BC 的距离为5，所以AP PQ +的最小值为5，依据是垂线段最短.。

bfb数学八年级上册周周清检测卷

bfb数学八年级上册周周清检测卷示例文章篇一：哎呀呀！一提到这八年级上册的BFB 数学周周清检测卷，我这心里可真是像装了个小兔子，七上八下的！你们能想象吗？每周都要来这么一场“数学大战”！那一张张卷子发到手里的时候，感觉就像是接到了一个艰巨的任务，而且还必须得完成得漂漂亮亮的！每次考试前，我都会紧张得不行。

我就问自己：“我真的都复习好了吗？那些公式和定理我真的记住了吗？”心里那叫一个没底儿啊！考试的时候，我眼睛紧紧盯着题目，脑子飞速运转。

这题，哎呀，不就像是上次老师讲过的那种类型吗？赶紧回忆回忆解题步骤。

那题，怎么感觉像个“拦路虎”，横在我面前，不让我前进呢？我咬着笔头，心里着急得要命：“这可怎么办呀？时间可不等人！”看看我旁边的同桌，他倒是一脸淡定，刷刷刷地写着答案。

我忍不住想：“他怎么这么厉害？难道他有什么秘密武器？”再看看前面的学霸，那神情，仿佛这卷子对他来说就是小菜一碟。

我心里那个羡慕哟：“啥时候我也能像他这样轻松应对呢？”好不容易做完了，检查的时候又是一阵紧张。

“这道题我是不是算错了？那道题的步骤有没有写全？”等到交卷的那一刻，我长长地舒了一口气，可心里还是忐忑不安，不知道自己能考个啥样。

等卷子发下来的时候，那心情，就像坐过山车一样。

考得好，那简直要高兴得飞起来，心里想着：“哈哈，我这努力没白费！”要是考得不好，那可就像霜打的茄子——蔫了，垂头丧气地想：“怎么又没考好呢？我得加把劲啦！”其实啊，这BFB 数学八年级上册周周清检测卷就像是一次次的小挑战，虽然有时候让人头疼，让人紧张，但也让我们能发现自己的不足，能让我们不断进步。

只要我们认真对待，努力去克服困难，就一定能在数学的海洋里畅游，你们说对不对？所以呀，不管成绩好坏，每次的周周清都是一次成长的机会。

我们可不能被它打倒，要勇敢地迎接它，战胜它！示例文章篇二：哎呀呀，说起这八年级上册的BFB 数学周周清检测卷，可真是让我又爱又恨呐！每周一到做这个卷子的时候，我就感觉自己像是要上战场的战士，紧张得不行。

八年级上册数学周周清试卷带答案

一、单选题(共32分)1．下列各等式中成立的有（）个．①()a b a bc c---=--；①a b a bc c---=；①a b a bc c-++=-；①a b a bc c-+-=-．A．1B．2C．3D．42．分式434y xa+，2411xx--，22x xy yx y-++，2222a abab b+-中，最简分式有（）A．1个B．2个C．3个D．4个3．下列图形，是中心对称图形的是（）A．B．C．D．4．如图，Rt ABC△中，∠B=90°，12AB=，5BC=，射线AP AB⊥于点A，点E，D分别在线段AB和射线AP上运动，并始终保持DE AC=．要使DAE和ABC全等，则AD的长为（）A．5B．12C．5或12D．5或13第4题第7题第13题第14题5．在实数5-，π2，4，227，3.14159，38，0.232332332……（每相邻两个2之间依次多一个3）中，无理数有（）A．4个B．3个C．2个D．1个6．设2221M a a=++，2327N a a=-+，其中a为实数，则M与N的大小关系是（）A．M N≥B．M N>C．N M≥D．N M>7．如图，已知BAC DAC∠=∠，则下列条件中不一定能使ABC ADC∆∆≌的是（）A．B D∠=∠B．ACB ACD∠=∠C．BC DC=D．AB AD=8．下列说法，错误的是（）．A．0.698精确到0.01的近似值是0.7B．近似数1.205是精确到千分位C．2与2--互为相反数D．3与5-是同类项．9．估算12÷2的运算结果应在（）A．1与2之间B．2与3之间C．3与4之间D．4与5之间10．若111x y z-=，则z等于()A．x y-B．-y xxyC．xyx y-D．xyy x11．下面等式：3242122⨯=①，43271-=②，()222x y x y-=-③，()3412m m=④，()()22222x y x y x y-+=-⑤，1823÷=⑥，其中正确的个数是（）A．1B．2C．3D．412．化简28xy y⋅=（）A．4y x B．16y x C．4x y D．16x y13．如图，在ABC中，90A∠=︒，25AB BC==，，BD是ABC∠的平分线，设ABD△和BDC的面积分别是1S，2S，则12:S S的值为（）A．5:2B．2:5C．1:2D．1:514．如图，ABC中，3AC=，4BC=，5AB=，BD平分ABC∠，如果M、N分别为BD、BC上的动点，那么CM MN+的最小值是（）A．2.4B．3C．4D．4.815．如图，在ABC中，120BAC∠=︒，点D是BC上一点，BD的垂直平分线交AB于点E，将ACD沿AD 折叠，点C 恰好与点E 重合，则B ∠等于（） A ．19°B ．20°C ．24°D ．25°第15题第16题第18题16．如图，AP 是ABC ∆的角平分线，PM ，PN 分别是APB △，APC ∆的高，则下列结论错误的是（）A ．AM AN =B ．AB PC AC BP ⋅=⋅ C ．1()2ABCS AB AC MP =+⋅ D ．ABPACPAB S AC S⋅=⋅二、填空题（共12分）17．已知324122a b c a b c +++=+-+-，则a b c ++的值是_____________．18．如图，在Rt ABC △中，90ACB ∠=︒，BD 平分ABC ∠，E 是AB 上一点，且AE AD =，连接DE ，过E 作EF BD ⊥，垂足为F ，延长EF 交BC 于点G ．现给出以下结论：①EF FG =；①CD DE =；①BEG BDC ∠=∠；①45DEF ∠=︒．其中正确的是______．（写出所有正确结论的序号）19．将1、2、3、4……按如图方式排列．若规定（x ，y ）表示第x 排从左向右第y 个数，则：①（6，6）表示的数是______；①若2021在（x ，y ），则（2x ﹣y ）3的值为_______．三、解答题(共0分) 20（12分）．计算(1) ()113482112-+--+-； (2)312227-+；(2) ()()()23331222++--； (4)()24251228-⨯+---+⨯21．（8分）计算下列各题，(1)已知21b +的平方根为3±，321a b +-的算术平方根为4，求6a b +的立方根； (2)已知5a =，24b =，求2a b +．22．（6分）化简求值：221241442x x x x x x x -+⎛⎫⎛⎫-÷- ⎪ ⎪-+-⎝⎭⎝⎭，然后从55x -<<选一个合适的整数作为x 的值代入求值23．（8分）如图，点C 、F 在BE 上，BF CE =，AC DF ∥，A D ∠=∠，判断线段AB ，DE 的数量关系和位置关系，并说明理由．24．（10分）为落实“数字中国”的建设工作，市政府计划对全市中小学多媒体教室进行安装改造，现安排两个安装公司共同完成．已知甲公司安装工效是乙公司安装工效的1.5倍，乙公司安装36间教室比甲公司安装同样数量的教室多用3天． (1)求甲、乙两个公司每天各安装多少间教室？(2)已知甲公司安装费每天800元，乙公司安装费每天400元，现需安装教室120间，若想尽快完成安装工作且安装总费用不超过15000元，则最多安排甲公司工作多少天？25．（12分）已知：60AOB ∠=︒，小新在学习了角平分钱的知识后，做了一个夹角为120°（即120DPE ∠=︒）的角尺来作AOB ∠的角平分线．(1)如图1，他先在边OA 和OB 上分别取OD OE =，再移动角尺使PD PE =，然后他就说射线OP 是AOB ∠的角平分线．试根据小新的做法证明射线OP 是AOB ∠的角平分线；(2)如图2，将角尺绕点P 旋转了一定的角度后，OD OE ≠，但仍然出现了PD PE =，此时OP 是AOB ∠的角平分线吗？如果是，请说明理由．(3)如图3，在（2）的基础上，若角尺旋转后恰好使得DP OB ∥，请判断线段OD 与OE 的数量关系，并说明理由．1．A 2．C 3．B ． 4．C 5．B 6．D 7．C 8．A 9．B 10．D 11．B 12．A 13．B 14．A【详解】过点C 作CE AB ⊥于E ，交BD 于点M ，过点M 作MN BC ⊥于点N ， ①BD 平分ABC ∠， ①ME MN =，①CM MN CM ME CE +=+=，①Rt ABC △中，90ACB ∠=，3AC =，4BC =，5AB =，CE AB ⊥， ①1122ABC S AB CE AC BC =⋅=⋅△， ①534CE =⨯，① 2.4CE =，即CM MN +的最小值是2.4 15．B 16．D 17．9解：①3a b c +++=①114210a b c -+--+--=，①2221)2)1)0++=，10=20=10=，1=2=1，①1a =，5b =，3c =， ①1539a b c ++=++=， 18．①①① 【详解】①BD 平分ABC ∠， ①12∠=∠， ①EF BD ⊥，①349090EFD DFG ∠=∠=︒∠=∠=︒，，又①BF BF =， ①BEF BEG ≅， ①EF FG =,故①正确；过D 作DM ①AB ， ①90ACB ∠=︒， ①DC BC ⊥，又①BD 平分ABC ∠， ①DC DM =，在Rt EMD △中：ED>MD ， ①CD DE ≠，故①说法错误； ①BEF BEG ≅， ①56∠=∠，在四边形CDFG 中87180C DFG ∠+∠+∠+∠=︒，90C DFG ∠=∠=︒，①78180∠+∠=︒， ①76180∠+∠=︒， ①68∠=∠， ①38∠=∠，即BEG BDC ∠=∠，故①正确；设12x ∠=∠=，则902A x ∠=︒-， ①AE AD =，①45AED ADE x ∠=∠=︒+，在BED 中，145AED EDB x EDB x ∠=∠+∠=+∠=+︒， ①45EDB ∠=︒， ①90EFD ∠=︒，①45DEF ∠=︒，故①正确．故答案为：①①①． 19．31 125【详解】解：观察式子可得，第1排的个数为2111⨯-=，前1排的总数为211=，第2排的个数为2213⨯-=，前2排的总数为242=，从右到左依次增大排列，第3排的个数为2315⨯-=，前3排的总数为293=，从左到右依次增大排列，第4排的个数为2417⨯-=，前4排的总数为2164=，从右到左依次增大排列， ……第n 排的个数为(21)n -个，前n 排的总数为2n 个，奇数排是从左到右依次增大排列，偶数排是从右到左依次增大排列，（6，6）表示第6排从左向右第6个数前5排的总数为25，第6排的个数为11个，为偶数排，从右向左依次增大，第6排中，从左向右第6个数，也就是从右向左第6个数，所以（6，6）表示的数为25631+=；因为24419362021=<，24520252021=> 所以2021是在第45排，即45x = 第45排，为奇数排，从左向右依次增大，因为2021193685-=，所以85y =将45x =，85y =代入3(2)x y -得33(90852)5(2)1x y =-=- 20．(1)1 (2)53 (3)1243- (4)4 21．(1)3 (2)3或1 22．2144x x -+，当取1x =时，原式的值为1．23．解：AB DE =，AB DE ∥，理由：BF CE =，BF CF CE CF ∴+=+， BC EF ∴=， AC DF ∥，ACB DFE ∴∠=∠，在ABC 和DEC 中，A D ACB DFE BC EF ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()AAS ABC DEF ∴≌，AB DE ∴=，B E ∠=∠，AB DE ∴∥．24．（1）设乙公司每天安装x 间教室，则甲公司每天安装1.5x 间教室，根据题意得，363631.5x x-=，解得，4x =，经检验，4x =是所列方程的解，则1.5 1.546x =⨯=，答：甲公司每天安装6间教室，乙公司每天安装4间教室；（2）设安排甲公司工作y 天，则乙公司工作12064y-天，根据题意得：1206800400150004yy -+⨯≤，解这个不等式，得：15y ≤，答：最多安排甲公司工作15天． 25．（1）解：证明：如图1中，在OPD ∆和OPE ∆中， OD OE PD PE OP OP =⎧⎪=⎨⎪=⎩， ()OPD OPE SSS ∴∆≅∆，POD POE ∴∠=∠．（2）解：结论正确．理由：如图2中，过点P 作PH OA ⊥于H ，PK OB ⊥于K ．90PHO PKB ∠=∠=︒，60AOB ∠=︒， 120HPK ∴∠=︒，120DPE HPK ∠=∠=︒，DPH EPK ∴∠=∠，在OPH ∆和OPK ∆中， 90PHO PKB DPH EPKPD PE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ()DPH EPK AAS ∴∆≅∆，PH PK ∴=，则OP 是AOB ∠的角平分线；（3）解：结论：2OE OD =．理由：如图3中，在OB 上取一点T ，使得OT OD =，连接PT ．OP 平分AOB ∠，POD POT ∴∠=∠，在POD ∆和POT ∆中， OD OT POD POT OP OP =⎧⎪∠=∠⎨⎪=⎩， ()POD POT SAS ∴∆≅∆，ODP OTP ∴∠=∠， PD OB ∥，180PDO AOB ∴∠+∠=︒，180DPE PEO ∠+∠=︒，60AOB ∠=︒，120DPE ∠=︒，120ODP ∴∠=︒，60PEO ∠=︒，120OTP ODP ∴∠=∠=︒，60PTE ∴∠=︒， 60TPE PET ∴∠=∠=︒， TP TE ∴=，PTE TOP TPO ∠=∠+∠，30POT ∠=︒，30TOP TPO ∴∠=∠=︒，OT TP ∴=，OT TE ∴=，2OE OD ∴=．。

八年级数学上册周周练及答案全册

八年级数学上册周周练及答案全册一、简介八年级数学上册周周练及答案全册是为八年级学生编写的一套数学学习辅助材料。

本文档旨在为学生提供全册周周练习题及其答案，帮助学生巩固和提升数学知识和解题能力。

二、周周练习题第一周练习题1.求下列式子的值：a)$4 + 7 \\times 2 =$b)$\\frac{3}{4} \\times 2 + \\frac{2}{5} =$c)$\\frac{1}{3} + \\frac{1}{4} - \\frac{1}{6} =$2.简化下列代数表达式：a)x+2x+3x=b)2(x+x)−3x=c)$(2a + 3b) \\cdot 4 =$3.解下列方程：a)2x+5=15b)$\\frac{x}{4} = 6$c)3x+2=5x−3第二周练习题1.计算下列式子的值：a)$\\frac{3}{5} \\times \\frac{4}{9} +\\frac{2}{3} \\times \\frac{1}{2} =$b)$(\\frac{1}{2})^3 \\times (\\frac{1}{2})^{-2}=$c)$\\sqrt{16} + \\sqrt{25} =$2.求下列代数式的值：a)3x−2，当x=4时b)2x2+x−1，当x=−3时c)x3−3x2+2x，当x=1时3.解下列方程组：\\end{cases}$b)$\\begin{cases} 3x - 2y = 1 \\\\ x + y = 4\\end{cases}$c)$\\begin{cases} 2x - y = 3 \\\\ 3x + 4y = 8\\end{cases}$第三周练习题1.计算下列式子的值：a)$(\\frac{5}{8})^2 \\div (\\frac{7}{10})^3 =$b)$\\frac{3}{5} \\div (\\frac{2}{3} +\\frac{1}{4}) =$c)$\\sqrt{36} - \\sqrt{49} =$2.求下列代数式的值：a)2x2−3xx+5，当x=2,x=3时b)$\\frac{(a-b)^2}{a^2 - ab + b^2}$，当x=3,x=1时c)3x3+2x2−x，当x=−1时3.解下列方程组：\\end{cases}$b)$\\begin{cases} 2x - 3y = 1 \\\\ 4x + y = 5\\end{cases}$c)$\\begin{cases} x + 2y = -3 \\\\ 3x + 4y = 2\\end{cases}$三、答案第一周练习题答案1.求下列式子的值：a)$4 + 7 \\times 2 = 4 + 14 = 18$b)$\\frac{3}{4} \\times 2 + \\frac{2}{5} =\\frac{6}{4} + \\frac{2}{5} = \\frac{12}{8} +\\frac{2}{5} = \\frac{15}{10} + \\frac{4}{10} =\\frac{19}{10} = 1.9$c)$\\frac{1}{3} + \\frac{1}{4} - \\frac{1}{6} =\\frac{2}{6} + \\frac{3}{12} - \\frac{2}{12} =\\frac{4}{12} + \\frac{3}{12} - \\frac{2}{12} =\\frac{5}{12}$2.简化下列代数表达式：a)x+2x+3x=6xb)2(x+x)−3x=2x+2x−3x=2x−xc)$(2a + 3b) \\cdot 4 = 8a + 12b$3.解下列方程：a)2x+5=15解得x=5b)$\\frac{x}{4} = 6$解得x=24c)3x+2=5x−3解得 $x = \\frac{5}{2}$第二周练习题答案1.计算下列式子的值：a)$\\frac{3}{5} \\times \\frac{4}{9} +\\frac{2}{3} \\times \\frac{1}{2} = \\frac{12}{45} +\\frac{2}{6} = \\frac{12}{45} + \\frac{15}{45} =\\frac{27}{45} = \\frac{3}{5}$b)$(\\frac{1}{2})^3 \\times (\\frac{1}{2})^{-2}= \\frac{1}{8} \\times \\frac{1}{(\\frac{1}{2})^2} =\\frac{1}{8} \\times 4 = \\frac{4}{8} = \\frac{1}{2}$c)$\\sqrt{16} + \\sqrt{25} = 4 + 5 = 9$2.求下列代数式的值：a)3x−2，当x=4时解得 $3 \\times 4 - 2 = 12 - 2 = 10$b)2x2+x−1，当x=−3时解得 $2 \\times (-3)^2 + (-3) - 1 = 2 \\times 9 -3 - 1 = 18 - 3 - 1 = 14$c)x3−3x2+2x，当x=1时解得 $1^3 - 3 \\times 1^2 + 2 \\times 1 = 1 - 3 + 2 = 0$3.解下列方程组：a)$\\begin{cases} 2x + 3y = 7 \\\\ 4x - 5y = -2\\end{cases}$解得 $x = \\frac{19}{17}$, $y = \\frac{1}{17}$b)$\\begin{cases} 3x - 2y = 1 \\\\ x + y = 4\\end{cases}$解得 $x = \\frac{9}{5}$, $y = \\frac{11}{5}$c)$\\begin{cases} 2x - y = 3 \\\\ 3x + 4y = 8\\end{cases}$解得 $x = \\frac{20}{17}$, $y =\\frac{31}{17}$第三周练习题答案1.计算下列式子的值：a)$(\\frac{5}{8})^2 \\div (\\frac{7}{10})^3 =\\frac{25}{64} \\div \\frac{343}{1000} =\\frac{25}{64} \\times \\frac{1000}{343} =\\frac{25000}{21952}$b)$\\frac{3}{5} \\div (\\frac{2}{3} +\\frac{1}{4}) = \\frac{3}{5} \\div \\frac{8}{12} =\\frac{3}{5} \\times \\frac{12}{8} = \\frac{9}{10}$c)$\\sqrt{36} - \\sqrt{49} = 6 - 7 = -1$2.求下列代数式的值：a)2x2−3xx+5，当x=2,x=3时解得2(2)2−3(2)(3)+5=8−18+5=−5b)$\\frac{(a-b)^2}{a^2 - ab + b^2}$，当x=3,x=1时解得 $\\frac{(3-1)^2}{3^2 - 3(3)(1) + (1)^2} = \\frac{2^2}{9 - 9 + 1} = \\frac{4}{1} = 4$c)3x3+2x2−x，当x=−1时解得3(−1)3+2(−1)2−(−1)=−3+2+1= 03.解下列方程组：a)$\\begin{cases} 3x + 2y = 4 \\\\ 5x - 3y = 7\\end{cases}$解得 $x = \\frac{23}{19}$, $y = \\frac{2}{19}$b)$\\begin{cases} 2x - 3y = 1 \\\\ 4x + y = 5\\end{cases}$解得 $x = \\frac{17}{11}$, $y = \\frac{9}{11}$c)$\\begin{cases} x + 2y = -3 \\\\ 3x + 4y = 2\\end{cases}$解得 $x = -\\frac{14}{5}$, $y = \\frac{11}{5}$四、总结本文档提供了八年级数学上册周周练习题及其答案，涵盖了多个知识点和题型，并且给出了详细的解题步骤和答案，帮助学生巩固和提升数学知识和解题能力。

人教版八年级数学上册第十二章测试题

第十二章全等三角形周周测3一、选择题：1、如图，∠1=∠2，PD⊥OA，PE⊥OB，垂足分别为D、E，下列结论中错误的是（）A、PD=PEB、OD=OEC、∠DPO=∠EPOD、PD=OD2、如图，在△ABC中，AB=BC=AC，CE为∠ACB的平分线，CD为∠ACB外角的平分线，则∠BCE的余角是（）A、∠BCEB、∠ECAC、∠ACDD、∠ECD3、下列语句中正确的是（）A、三角形的一个外角等于两个内角的和B、有两边和一角对应相等的两个三角形一定全等C、有两边分别相等的两个直角三角形全等D、到角的两边距离相等的点在这个角的平分线上4、到三角形三边距离相等的点是（）A、三条角平分线的交点B、三条中线的交点C、三条高线的交点 D5、如图所示,MP⊥NP,MQ为△MNP的角平分线连结TQ,则下列结论不正确的是( ).A、TQ=PQB、∠MQT=∠MQPC、∠QTN=90°D、∠NQT=∠MQT6、如图,在△ABC中,AB=AC,AD是△ABC的内角平分线,DF⊥AB,DE⊥AC,垂足分别是E、F.则下面结论中正确的有（）①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点的距离相等;④图中共有3对全等三角形.A、1个B、2个C 、3个D 、4个二、填空题7、如图，△ABC 中，已知∠BAC ＝60°．按以下步骤作图．①以A 为圆心，以小于AC 长为半径画弧，分别交AC ，AB 于点E ，D ；两弧相交于点P ；②分别以D ，E 为圆心，以大于12DE 长为半径画弧，③连接AP 交BC 于点F ．则∠C AF ＝度． 8、如图，已知∠MON 的边OM 上有两点A 、B ，边ON 上有两点C 、D ，且AB ＝CD ，P 为∠MON 的平分线上一点△ABP 的面积是3，那么△PCD 是的面积等于 .9、如图所示,在△ABC 中,∠A=60°,∠B 和∠C 的平分线相交于点O,则∠BOC . 10、如图所示,CD 平分∠ACB,AE ∥DC 交BC 的延长线于点E,若∠ACE=80°,则∠CAE= 度.AB COABCD E11、如图，已知BQ 是∠ABC 的内角平分线，CQ 是∠ACB 外角的平分线，作点Q 到BC 、AC 和AB 的距离QM 、QN 和QK ，则QM 、QN 、QK的大小关系是 . 12、如图，在△ABC 中，∠B=30，∠C=90，AD 平分∠CAB 交CB 于D ，DE ⊥AB 于E ，且AC=4cm，则AB= .三、证明题13、如图,已知点D 、B 在∠A 的两边上，点C 是∠A 内一点，且AB=AD,BC=DC,CE ⊥AD 于E ，CF ⊥AB 于F.求证：CE=CF.FE D C BAN MKQCBA EDCBA14、如图,CE ⊥AB 于点E,BD ⊥AC 于点D,BD 、CE 交于点O,且AO 平分∠BAC.求证:OB=OC.15、如图，已知BD 平分∠ADE ，∠A=90°，AB=AC.ED ⊥BC 于点E ，△DEC 的周长为15cm ，求BC 的长.EDCBAAB CD EO16、已知OC 是∠AOB 的平分线，P 在OC 上，PD ⊥OA ，PE ⊥OB ，（1）求证：OD=OE ；（2）连结DE 交OP 于F ，求证：DF=FE.17、已知△ABC 中，D 是BC 中点，DE ⊥AB 于E ，DF ⊥AC 于F ，且DE=DF ，求证：AB=AC.FP E ODCBA18、如图，已知AB ∥DE ，AB=DE ，AF=CD ，BM 平分∠ABC ，EN 平分∠DEF ，求证：BM ∥EN.19、如图，已知AB=CD ，△PAB 的面积与△PCD 的面积相等，求证：OP 平分∠AOD.20、已知: 如图, AC 平分 ∠BAD, CE ⊥AB 于E,且 AD+AB =2AE.PO DC BA求证: ∠B +∠ADC = 180°.21．如图，AD⊥DC，BC⊥DC，E是DC上一点，AE平分∠DAB．（1）如果BE平分∠ABC，求证：点E是DC的中点；（2）如果E是DC的中点，求证：BE平分∠ABC．A DEB C22．如图，已知AD为等腰三角形ABC的底角的平分线，∠C＝90°，求证：AB＝AC＋CD．别浪费一分一秒——如何利用零散时间学人们常说,时间是公平的,每个人的一天只有24个小时,所以应该珍惜时间去充实自己。

人教版八年级数学上册第十三章轴对称测试题

第十三章轴对称周周测2一、选择题（每小题3分，共30分）1、下列图形中不是轴对称图形的是（）A B C D2、正方形的对称轴共有（）A．2条B．4条C．5条D．10条3、△ABC和△A’B’C’关于直线l对称，若△ABC的周长为12cm，则△A’B’C’的周长为（）A．24cm B．12cm C．6cm D．4cm4、点A(-2，3)关于x轴对称的点A’的坐标为（）A．（-2，-3）B．（2，3）C．（2，－3）D．（3，－2）5、已知点A（x,-4）与点B（3，y）关于y轴对称，那么x＋y的值为（）A．-1 B．-7 C．7 D．26、如图，△ABC与△A1B1C1关于直线l对称，则∠B的度数为（）A．30° B．50° C．90° D．100°第6题图第7题图第9题图第10题图7、如图，点D在AC的垂直平分线上，AB∥CD，若∠D＝130°，则∠BAC的度数为（）A．15° B．20° C．25° D．30°8、点（2，5）关于直线x=1的对称点的坐标为（）A．（－2，5）B．（-3，5）C．（4，5）D．（0，5）9、如图，△OBC的顶点O（0，0），B（-6，0），且∠OCB=90°，OC=BC，则点C关于x轴对称的点的坐标是（）A．（3，3）B．（－3，3）C．（－3，－3）D．（－6，6）1AB的长为半径画弧，两弧相交于点M、N，交BC于10、如图，在△ABC中，分别以点A和点B为圆心，大于2D,连接AD,若△ADC的周长为10，AB=7,则△ABC的周长为（）A．7 B．14 C．17 D．20二、填空题（每小题3分，共18分）11、如图,AB=4,AC=5,BC=3，△ABC与△A’B’C’关于直线l对称，则B’C’=____________第11题图第12题图第13题图12、如图，点A关于y轴对称的点的坐标是____________________13、如图，以正方形ABCD的中心为原点建立直角坐标系，若点A的坐标为（-1，1），则点B的坐标为____________ ，点C的坐标为_____________，点D的坐标为____________ .14、如图，∠AOB内一点P，P1、P2分别是点P关于OA、OB的对称点，P1、P2交OA于M,交OB于N，若P1P2=5cm，则△PMN的周长是__________ cmy OCBA第14题图第15题图第16题图15、如图，△ABC 的面积为2cm 2，AP 与∠B 的平分线垂直，垂足是点P ，则△PBC 的面积为__________ cm 2 16、如图，在平面直角坐标系中，AB=BC ，∠ABC=90°,A(0，3)，B(-1，0), 以AB 为直角边在AB 的右侧作等腰Rt △ABE ，则点E 的坐标是____________ 三、解答题（共8题，72分）17、（8分）如图，点A 在线段BD 的垂直平分线上，BF ⊥AD ，DE ⊥AB,垂足分别为F 、E. 求证：BF=DEDFE AB18、（8分）如图，将长方形ABCD 沿EF 折叠，使CD 落在GH 的位置，GH 交BC 于M ，若∠HMB=50°，求∠HEF的度数19、（8分）如图，分别作点A(-3,0)，B(-2,2)关于直线x=2的对称点A’、B’. （1）A’点坐标为_____________ , B’点坐标为____________.（2）四边形ABB’ A’的面积为___________20、（8分）已知A、B两点的坐标分别为（-2，1）和（2，3）（1）在图1中分别画出线段AB关于x轴和y轴的对称线段A1B1及A2B2，并写出相应端点的坐标；（2）在图2中分别画出线段AB关于直线ｘ＝－1和直线ｙ＝4的对称线段A3B3及A4B4，并写出相应端点的坐标。

八年级数学上册周周清9(检测内容 15.2.3-15.3)(新版)新人教版-(新版)新人教版初中八

得分________ 卷后分________ 评价________一、选择题(每小题4分，共32分)1．下列方程不是分式方程的是( B )A ．1x ＋x ＝1B ．x 3＋3x 4＝25C ．21＋x －11＋x ＝2D ．5x ＝7x －72．(2019·某某)某种计算机完成一次基本运算的时间约为1纳秒(ns)，已知1纳秒＝0.000 000 001秒，该计算机完成15次基本运算，所用时间用科学记数法表示为( C )×10－9秒 B ．15×10－9秒×10－8秒 D ．15×10－8秒3．在数(－12)－2，(－2)－2，(－12)－1，(－2)－1中，最大的数是( A ) A ．(－12 )－2 B ．(－2)－2 C ．(－12 )－1 D ．(－2)－1 4．解分式方程x 3＋x －22＋x＝1时，去分母后可得( C ) A ．x (2＋x )－2(3＋x )＝1B ．x (2＋x )－2＝2＋xC ．x (2＋x )－2(3＋x )＝(2＋x )(3＋x )D ．x －2(3＋x )＝3＋x5．(2019·株洲)关于x 的分式方程2x －5x －3＝0的解为( B ) A ．－3 B ．－2 C ．2 D ．36．(某某中考)已知关于x 的分式方程m －2x ＋1＝1的解是负数，则m 的取值X 围是( D ) A ．m ≤3 B ．m ≤3且m ≠2C ．m ＜3D ．m ＜3且m ≠27．如果m ＋n ＝1，那么代数式(3m ＋n m 2－mn ＋1m )·(m 2－n 2)的值为( D )A ．－4B ．－1C ．1D ．48．(2019·某某)世界文化遗产“三孔”景区已经完成5G 基站布设，“，在峰值速率下传输500兆数据，5G 网络比4G 网络快45秒，求这两种网络的峰值速率．设4G 网络的峰值速率为每秒传输x 兆数据，依题意，可列方程是( A )A ．500x －50010x ＝45B ．50010x －500x＝45 C ．5 000x －500x ＝45 D ．500x －5 000x＝45 二、填空题(每小题4分，共24分)9．将代数式2－1x －3y 2化为只含有正整数指数幂的形式：__y 22x __． 10．(2×10－6)×(3.2×103)＝__6.4×10－3__．11．(2019·某某)分式方程5y －2＝3y 的解为y ＝__－3__. 12．(2019·某某)甲、乙两地相距1 000 km ，如果乘高铁列车从甲地到乙地比乘特快列车少用3 h ，，设特快列车的平均速度为x km/h ，根据题意可列方程为__1 000x －1 000x＝3__． 13．(某某中考)某商店第一次用600元购进2B 铅笔若干支，第二次又用600元购进该款铅笔，但这次每支的进价是第一次进价的54倍，购进数量比第一次少了30支．则该商店第一次购进的铅笔每支的进价是__4__元．14．(达州中考)若关于x 的分式方程xx －3＋3a 3－x ＝2a 无解，则a 的值为__1或12__．三、解答题(共44分)15．(6分)计算下列各式：(1)(－14)－1＋(－2)2×2 0200－(13)－2；解：原式＝－9(2)(a 3b －1)－2·(a －3b 2)2. 解：原式＝a －6b 2·a －6b 4＝a －12b 6＝b 6a 1216．(6分)解下列方程：(1)(某某中考)x －3x －2＋1＝32－x；解：去分母，得x －3＋x －2＝－3，整理，得2x ＝2，解得x ，x ＝1是原方程的解(2)(2019·某某)x x －1－3（x －1）（x ＋2）＝1. 解：去分母，得x 2＋2x －3＝(x －1)(x ＋2)，解得x ＝1，经检验x ＝1不是原分式方程的解．∴原方程无解17．(10分)先阅读下面的材料，然后解答问题．通过计算，发现：方程x ＋1x ＝2＋12的解为x 1＝2，x 2＝12；方程x ＋1x ＝3＋13的解为x 1＝3，x 2＝13；方程x ＋1x ＝4＋14的解为x 1＝4，x 2＝14；… (1)观察猜想：关于x 的方程x ＋1x ＝n ＋1n 的解是__x 1＝n ，x 2＝1n__； (2)实践运用：对于关于x 的方程x －1x ＝m －1m的解，小明观察得“x 1＝m ”是该方程的一个解，请你猜想该方程的另一个解，并用方程的解的概念对该解进行验证；(3)拓展延伸：请利用上面的规律，求关于x 的方程x ＋1x －3＝a ＋1a －3的解．解：(1)x 1＝n ，x 2＝1n(2)另一个解是 x 2＝－1m，验证略 (3)x ＋1x －3＝a ＋1a －3，可得x －3＋1x －3＝a －3＋1a －3，类比(1)可得：x 1＝a ，x 2＝1a －3＋3＝3a －8a －318．(10分)(2019·某某)甲、乙两同学的家与某科技馆的距离均为4 000 m ．甲、乙两人同时从家出发去科技馆，甲同学先步行800 m ，然后乘公交车，乙同学骑自行车．已知乙骑自行车的速度是甲步行速度的4倍，公交车的速度是乙骑自行车速度的2倍，结果甲同学比乙同学晚到2.5 min.求乙到达科技馆时，甲离科技馆还有多远．解：设甲步行的速度为x 米/分，则乙骑自行车的速度为4x 米/分，公交车的速度是8x米/分钟，根据题意得4 0004x ＋2.5＝800x ＋4 000－8008x，解得x ，x ＝80是原分式方程的解．所以2.5×8×80＝1 600(m)，答：乙到达科技馆时，甲离科技馆还有1 600 m19．(12分)(某某中考)为落实“美丽某某”的工作部署，市政府计划对城区道路进行改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的32倍，甲队改造360米的道路比乙队改造同样长的道路少用3天．(1)甲、乙两工程队每天能改造道路的长度分别是多少米？(2)若甲队工作一天需付费用7万元，乙队工作一天需付费用5万元，如需改造的道路全长1 200米，改造总费用不超过145万元，至少安排甲队工作多少天？解：(1)设乙工程队每天能改造道路的长度为x 米，则甲工程队每天能改造道路的长度为32x 米，根据题意得360x －36032x ＝3，解得x ，x ＝40是原分式方程的解，且符合题意， ∴32x ＝32×40＝60. 答：乙工程队每天能改造道路的长度为40米，甲工程队每天能改造道路的长度为60米(2)设安排甲队工作m 天，则安排乙队工作1 200－60m 40天，根据题意，得7m ＋5×1 200－60m 40≤145，解得m ≥10.答：至少安排甲队工作10天。

八年级上册数学周练试卷1.doc

扬州市江都区国际学校初二数学周练试卷1班级学号姓名成绩2015.09. 02一、选择题（本大题共10小题，每小题3分，共30分.）1.下列运算正确的是（）A. o3 - a~=a6B. （a2）2=«4C. （— 3a）'= —9a，D. a4+a5=a g2.不等式:组上一2 2 -1,的解集在数轴上可表示为（）（3x-l > 8~ k A—‘.，__ L一,_」—■C. 0 1 2 3 4D. 2 3 43.下列各式中，不能用平方差公式计算的是（）A. （2x - y）（2x + y）B. （x - j）（ - y - x）C. （b - d）（b + a）D. （ - x + y）（x - y）4.下列各组线段能组成一个三•角形的是（）A. 4 cm, 6 cm, 11 cmB. 4 cm, 5 cm , 1 cmC. 3 cm, 4 cm, 5 cmD. 2cm, 3 cm, 6 cm5.若实数Q,b, c在数轴上对应点的位置如图所示，则.下列二一~b一~6―c不等式成立的是（）A. ac >bcB. ab>cbC. a + c>b + cD. a + b>c + b6.若m+n=3,贝ij 2m2 + 4mn + 2n2— 6 的值为（）A. 12B. 6C. 3D. 07.下列从左到右的变形，属于•分解因式的是（）A. （。

+ 3）（。

- 3）=疽-9B. x2 + x - 5=x（x - 1） - 5C. a + a=a（a +1）D. x y=x • x • y8.一个多边形的内.角和是1080°,这个多边形的边数是（）A. 6B. 7C. 8D. 99.如图所示，AB〃CD, ZE=37° , ZC=20°,则ZEAB的度数为（）A. 57° B. 60° C. 63° D. 123°10.如图，ZABC=ZACB, AD. BQ、CQ 分别平分ZXABC 的外角ZEAC,内角ZABC,外角ZACF.以下结论：①AD勿BC；②ZACB=2ZADB；③ZADC=9Q° -AABD-,④ZBDC=ZBAC.其中正确的结论有（）A. 1个B. 2个C. 3个D. 4个二、填空题本大题共10小题.每小题3分，共30分）11 5 ・ 311.X —X =.12.中东呼吸综合征冠状病毒属于冠状病毒科，病毒粒子呈球形，直径为0.用科学计数法表示m.13.已知m + n= 5, m n=3,则m2 n + m n2=.14.若三角形三条边长分别是1, a, 5（其中a为整数），则a的取值为15.如图，将三角尺的直角顶点放在直尺的一边上，Zl=25° , Z3= 20°贝以2的度数为° .16.已知0 > b, a b =2且/+》2=5,则a - b=.00000012m,17. 如图，点 B, C, E, F 在一直线上，AB 〃DC, DE 〃GF, ZB=Z（第17x- y = 9k 2x + y +z = 9,F=72° ,则 ZD=0 .18. 甲乙两队进行篮球对抗赛，比赛规则规定每队胜••场得3分，平一•场得1分，负一场得0分，两队一共比赛了 10场，甲队保持不败,得分不低于24分，甲队至少胜了场.19. 若关于工，y 的二元一次方程组>艾'的解也是二元一次方程攻 -----------------------2x + 3y = 6的解，则k 的值为20. 如图，将一张长方形纸片沿对角线AC 折叠后，点D 落在点E 处, 与BC 交于点F,图中全等三角形（包含△ AOC ）对数有对。

人教版八年级上册周周练(151～1521)有答案-(数学)

人教版八年级上册周周练(151～1521)有答案-（数学）周周练(15.1～15.2.1)(时间：45分钟满分：100分)一、选择题(每小题3分，共18分)某＋11．(温州中考)要使分式有意义，则某的取值应满足()某－2A．某≠2B．某≠－1C．某＝2D．某＝－12．下列等式正确的是()aaaabA.＝2B.＝bbba＋baa＋caabC.＝D.＝2bb＋cbb某＋y3．如果把分式的某和y都变为原来的相反数，分式的值()某－yA．变成原来的相反数B．不变C．分式的值为1D．无法确定某＋1b4．已知分式，当某取a时，该分式的值为0；当某取b时，分式无意义，则a的值等于()2－某1A．－2B.2C．1D．22a15．已知22÷M＝，则M等于()a－ba－b2aa＋bA.B.a＋b2a2aa－bC.D.a－b2a6．下列计算结果正确的是()y2y3m23mA．－()＝2B．()＝22某4某4n4n2a24aa3aC．()＝2)＝－32D．(－a－ba－b2b8b二、填空题(每小题4分，共16分)0.5某－17．不改变分式的值，把它的分子和分母中的各项系数都化为整数，则所得的结果为________．129．若|某－y＋1|＋(2某－3)＝0，则分式的值为________．4某－2y222239222某2某28410．若(2)÷(3)＝3，则某y＝________．yy三、解答题(共66分)11．(6分)求使下列分式有意义的某的取值范围：某＋12某－1某－32某－5－某某－912．(8分)当某取何值时，下列分式的值是零？|某|－1(1)2；某＋2某－3（某－2）（某－1）(2).|某|－113．(24分)计算：某－1某－某(1)(滨州中考)·2；某＋1某－2某＋1a－1a－1(2)(襄阳中考)2÷；a＋2aa22233ab8某y3某(3)3·(－2)÷；2某y9ab－4b2某＋6某－2某(4)2÷(某＋3)·；某＋2某2－某z3某z2－某4(5)(－2)÷()·(2)；某y－yya＋b3a－b212(6)(].2)÷(3)÷[2abab2（a－b）a－1a－41214．(8分)化简求值：·2÷2，其中a－a＝0.a＋2a－2a＋1a－12222215．(10分)某商场销售一批电视机，1月份每台电视机的毛利润是售价的20%，2月份该商场将每台的售价降低10%(进价不变)，结果销售量比1月份增加了120%，求2月份的毛利润总额与1月份毛利润总额的比是多少？21世纪教育网版权所有某yz2某＋y－z16．(10分)已知＝＝≠0，求分式的值．345某y－yz＋z某222参考答案5某－10某－4某＋21.A2.D3.B4.C5.A6.D7.8.29.110.93某＋20某－2某某511.(1)某≠.(2)某≠0.(3)某≠±3.212.(1)由题意可得|某|－1＝0，∴某＝±1.把某＝1代入某＋2某－3，得1＋2－3＝0.不合题意，舍去．把某＝－1代入某＋2某－3，得(－1)＋2某(－1)－3＝－4，|某|－1∴当某＝－1时，2的值为零．某＋2某－3（2）由题意得，某－2＝0或某－1＝0，∴某＝2或某＝1，∵|某|－1≠0.∴某≠±1，∴某的取值应为2.13.(1)原式＝某.a＋1(2)原式＝.a＋216b(3)原式＝3.9a某2(4)原式＝－.某＋2z(5)原式＝－49.某ya＋b(6)原式＝.2a14.原式＝a－a－2.当a－a＝0时，原式＝0－2＝－2.15.设1月份每台电视机的出售价是a元，销售量为b台，则1月份的毛利润总额是20元.2月份每台电视机的毛利润是(90%a－80%a)元，2月份的销售量为(1＋120%)b台，21教育网∴（90%a－80%a）·（1＋120%）b11＝.2022222222211∴2月份的毛利润总额与1月份毛利润总额的比是.10某yz16.设＝＝＝k，345∴某＝3k，y＝4k，z＝5k.2某＋y－z2（3k）＋（4k）－（5k）9k9∴＝＝2＝.某y－yz＋z某3k·4k－4k·5k＋5k·3k7k72222222。

数学名校课堂周测八年级上册安徽专版

数学名校课堂周测八年级上册安徽专版安徽省八年级数学名校课堂周测（一）一、选择题（每小题3分，共30分）1. 用现实生活中的例子说明“原点”的含义，可以说是（）A. 向左旋转45°B. 向右旋转90°C. 向上移动1米D. 向下移动50米2. 在给定点A（2,3）B（3,0）两点，若对直线AB上的点P，P坐标满足2x-3y=7，则P的坐标为（）A. (1, -2)B. (2, -1)C. (3, 1)D. (4, 2)3. 下列说法正确的是（）A. 全集（U）=交集（M∩N）B. 幂集（P）=补集（M′）C. 补集（M′）=联集（M∪N）D. 补集（M′）=全集（U）4. 下列图形中属于全等三角形的有（）A. B. C. D.二、填空题（每小题2分，共20分）5. 将几何中用于表示两个图形不相交的符号表示为方框中的符号：6. 已知点P（-2，-3），它相对原点的对称中心为：7. 用代数式表示：x的3次幂加1等于：8. 已知平面直角坐标系中的点A（3,2），它所在的直线的方程为：三、解答题（每小题5分，共50分）9. 已知平面直角坐标系中的点A（-1，-3），其对称中心在原点，求点A关于原点对称后的坐标。

解：关于原点对称可以用如下公式求解：横坐标x不变，纵坐标y取反，即新点A'（-1，3）。

10. 设平面内有一点A（2,3），若将这点关于坐标原点（0,0）进行旋转90°，求旋转后的点坐标解：若将点A（2,3）进行旋转90°，则可以用如下的公式求解：x取反，y不变，则旋转后的点坐标为A'（-3,2）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级数学测试
【时间：40分钟满分：120分】
班级_______姓名_________成绩________
一、填空题（每题5分，共50分）
1、Rt ABC 中，,5,3,90===∠b a B 则=c ________。

2、一个三角形的三边长分别为5，12，13，则这个三角形最长边上的高为________。

3、在Rt ABC 中，，，43==AC AB 则第三边=BC ________。

4、等腰三角形腰长为10cm, 底边长为16cm, 则底边上的高为________。

5、如果一个数的算术平方根是5，则这个数是，它的平方根是________。

6、16的算术平方根是______;平方根是______;立方根是________。

7、若942=x ，则x =________,若,32=x 则=x ______
8、=332-）（=________
_______ ；()24-=_______。

9、若x 的平方根中有一个为5，则x 的另一个平方根为_______。

10、王强同学动手制作了一个表面积为12的正方体礼盒，试问这个礼盒的棱长是________。

二、计算与解答题（共50分）
11、（12分）求出下列各数的算术平方根与平方根。

81， 0 ，
25
49， 1.21， 7， 4-6
12、（10分）求出下列各数的立方根。

64， 278-， 125， -1， 3
61-⎪⎭
⎫ ⎝⎛
∆∆
13、（10分）如果一个正数的平方根是1a +和27a -。

（1）求出a 的值。

（2）求出该正数的值。

14、（10分）如果
9-a +(b+27)2=0, 求3b a +的值。

15、（8分）如图，校园内有两棵树，相距12m ，一棵树高13m ，另一棵树高8m ，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞多少m ？
附加题(共20分) 16、（10分）如图，长方体的长为5，宽为4，高为3，一只蚂蚁如果要沿着长方体的表面从顶点A 爬到顶点B ，爬行的最短距离是多少？
17、（10分）计算：-22-121-⎪⎭
⎫ ⎝⎛-+()42--()06+83-
A 5 3 4
B · ·。