车辆调度方法ppt课件
合集下载
配送路线安排与车辆调度ppt课件

B0
表 6-2 节约量表 (单位:公里)
B1
5
B2
2
7
B3
3
8
18
B4
14 8
5
7
B5
9
10
10
13
17
B6
11 10 10 14 22 24
B7
17
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
4
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
二、VRP问题精确求解方法的局限性
1. VRP问题求解思路 VRP问题的求解方法一般相当复杂,通常 的做法是应用相关技术将问题分解或者转化 为一个或多个已经研究过的基本问题(如旅 行商问题、指派问题、运输问题、最短路问 题、最小费用流问题、中国邮递员问题等), 再使用相对比较成熟的基本理论和方法进行 求解。
1
第一节 常见心律失常心电图诊断的误区诺如病毒感染的防控知识介绍责任那些事浅谈用人单位承担的社会保险法律责任和案例分析现代农业示范工程设施红地球葡萄栽培培训材料
配送路线安排与车辆调度问题
及节约法原理
一、配送路线安排与车辆调度问题
配送路线安排与车辆优化调度问题常被分为车
辆路线安排问题(Vehicle Routing Problem,
7
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
表 6-2 节约量表 (单位:公里)
B1
5
B2
2
7
B3
3
8
18
B4
14 8
5
7
B5
9
10
10
13
17
B6
11 10 10 14 22 24
B7
17
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
4
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
二、VRP问题精确求解方法的局限性
1. VRP问题求解思路 VRP问题的求解方法一般相当复杂,通常 的做法是应用相关技术将问题分解或者转化 为一个或多个已经研究过的基本问题(如旅 行商问题、指派问题、运输问题、最短路问 题、最小费用流问题、中国邮递员问题等), 再使用相对比较成熟的基本理论和方法进行 求解。
1
第一节 常见心律失常心电图诊断的误区诺如病毒感染的防控知识介绍责任那些事浅谈用人单位承担的社会保险法律责任和案例分析现代农业示范工程设施红地球葡萄栽培培训材料
配送路线安排与车辆调度问题
及节约法原理
一、配送路线安排与车辆调度问题
配送路线安排与车辆优化调度问题常被分为车
辆路线安排问题(Vehicle Routing Problem,
7
常见心律失常心电图诊断的误区诺如 病毒感 染的防 控知识 介绍责 任那些 事浅谈 用人单 位承担 的社会 保险法 律责任 和案例 分析现 代农业 示范工 程设施 红地球 葡萄栽 培培训 材料
《调车作业计划》PPT课件

23
24
第三节 调车作业 计 划
(二)编组调车作业计划
由于解体广泛采用了解体照顾编组,按调车场 固定线路分解车辆的作业方法,所以除编组摘挂列 车外,其他列车的编组作业,一般只在一条线上或 几条线上连挂车辆和车列转线两项作业。例如,表 3-4解体30138次“坐编”30052次的调车作业计划 中,属于编组作业的只有最后两钩。
第三章 车站作业计划与指挥 第三节 调车作业计划
1
第三节 调车作业 计 划
班计划规定了一个班的总任务,阶段 计划规定了每台调车机车解编、取送等 各项作业顺序和起止时间;调车作业计 划规则是每台调车机的具体行动计划。
调车作业计划由调车领导人(车站调 度员、调车区长或车站值班员)负责编 制,并以调车作业通知单的形式下达给 调车指挥人及有关人员执行。
22
第三节 调车作业 计 划
要求分部解体30053次后,将30051次和30053次 到达乙站的20车送货217车、送货33车,并将货场往 丙站的10车取回10道。为此,应从乙2(货2)后开 口,以便利用机前集结,实现对口连挂,减少钩数 。同时,在解体第二批车列时,为了减少重复作业 ,照顾送车,应将乙3(货3)活用线路,分解到9道 ,调车作业计划如表3-5所示。
在毛玻璃板上画成与车场股道相同的格数,根据担当解 体任务的机车所在方向,统一规定上下端代表的方向。例 如,调车场两端为南北方向,担当解体任务的机车在南端 ,可规定上端为北,下端为南。此时,毛玻璃板上现车自 上而下的顺序,就是调车场现车从北到南的顺序。
8
什么是毛玻璃?
用金刚砂等磨过或以化学方法处理过﹐表面粗 糙的半透明玻璃。也就是磨砂玻璃的俗称。
10
第三节 调车作业 计 划
三、调车区现车的掌握 编组列车或送车时,根据调车作业通知
24
第三节 调车作业 计 划
(二)编组调车作业计划
由于解体广泛采用了解体照顾编组,按调车场 固定线路分解车辆的作业方法,所以除编组摘挂列 车外,其他列车的编组作业,一般只在一条线上或 几条线上连挂车辆和车列转线两项作业。例如,表 3-4解体30138次“坐编”30052次的调车作业计划 中,属于编组作业的只有最后两钩。
第三章 车站作业计划与指挥 第三节 调车作业计划
1
第三节 调车作业 计 划
班计划规定了一个班的总任务,阶段 计划规定了每台调车机车解编、取送等 各项作业顺序和起止时间;调车作业计 划规则是每台调车机的具体行动计划。
调车作业计划由调车领导人(车站调 度员、调车区长或车站值班员)负责编 制,并以调车作业通知单的形式下达给 调车指挥人及有关人员执行。
22
第三节 调车作业 计 划
要求分部解体30053次后,将30051次和30053次 到达乙站的20车送货217车、送货33车,并将货场往 丙站的10车取回10道。为此,应从乙2(货2)后开 口,以便利用机前集结,实现对口连挂,减少钩数 。同时,在解体第二批车列时,为了减少重复作业 ,照顾送车,应将乙3(货3)活用线路,分解到9道 ,调车作业计划如表3-5所示。
在毛玻璃板上画成与车场股道相同的格数,根据担当解 体任务的机车所在方向,统一规定上下端代表的方向。例 如,调车场两端为南北方向,担当解体任务的机车在南端 ,可规定上端为北,下端为南。此时,毛玻璃板上现车自 上而下的顺序,就是调车场现车从北到南的顺序。
8
什么是毛玻璃?
用金刚砂等磨过或以化学方法处理过﹐表面粗 糙的半透明玻璃。也就是磨砂玻璃的俗称。
10
第三节 调车作业 计 划
三、调车区现车的掌握 编组列车或送车时,根据调车作业通知
《车辆调度方法》PPT课件

最优化原理的应用:从最短路上的每一点到终点的部分道路,也一定是从该点到终点的最短路 。
18
第四阶段:两个始点D1和D2,终点只有一个;
表1
本阶段始点 (状态)
D1 D2
阶段4 本阶段各终点(决策)
E 10 6
到E的最短距离
10 6
本阶段最优终点 (最优决策)
E E
分析得知:从D1和D2到E的最短路径唯一。
表3 阶段2
本阶段始点
本阶段各终点(决策)
(状态)
C1
C2
B1
2+12=14
1+11=12
B2
4+12=16
7+11=18
B3
4+12=16
8+11=19
B4
7+12=19
5+11=16
分析得知:如果经过B1,则走B1-C2-D2-E;
如果经过B2,则走B2-C3-D1-E;
如果经过B3,则走B3-C3-D1-E;
乙圈: 半圈长=4+4+5+8/2=10.5公里 外圈长=8公里 里圈长=4+5=9公里
练习
最短路径问题
例1 多阶段决策法 下图表示从起点A到终点E之间各点的距离。求A到E的最短路径。
4
A
3
3 2
B1
2
1 6
4
B2
7
2
4
8
B3 3
75 1
4
C1
8 6
7
C2
5
1 6
C3
D1
10
E
D2
6
讨论:
1、以上求从A到E的最短路径问题,可以转化为四个性质完全相同,但规模较小的子问题,即分 别从Di 、Ci、Bi、A到E的最短路径问题。
18
第四阶段:两个始点D1和D2,终点只有一个;
表1
本阶段始点 (状态)
D1 D2
阶段4 本阶段各终点(决策)
E 10 6
到E的最短距离
10 6
本阶段最优终点 (最优决策)
E E
分析得知:从D1和D2到E的最短路径唯一。
表3 阶段2
本阶段始点
本阶段各终点(决策)
(状态)
C1
C2
B1
2+12=14
1+11=12
B2
4+12=16
7+11=18
B3
4+12=16
8+11=19
B4
7+12=19
5+11=16
分析得知:如果经过B1,则走B1-C2-D2-E;
如果经过B2,则走B2-C3-D1-E;
如果经过B3,则走B3-C3-D1-E;
乙圈: 半圈长=4+4+5+8/2=10.5公里 外圈长=8公里 里圈长=4+5=9公里
练习
最短路径问题
例1 多阶段决策法 下图表示从起点A到终点E之间各点的距离。求A到E的最短路径。
4
A
3
3 2
B1
2
1 6
4
B2
7
2
4
8
B3 3
75 1
4
C1
8 6
7
C2
5
1 6
C3
D1
10
E
D2
6
讨论:
1、以上求从A到E的最短路径问题,可以转化为四个性质完全相同,但规模较小的子问题,即分 别从Di 、Ci、Bi、A到E的最短路径问题。
车辆调度作用及特点介绍.ppt

任务布置
门店 A B
品名 龙井茶叶 光明牛奶 可口可乐
雪碧 喜多毛巾 可口可乐 光明牛奶
雪碧
需求商品情况
规格
数量
毛重
总重
500克/袋
5箱 11千克/箱 55千克
250克/袋
10箱 8.5千克/箱 85千克
1.25千克/瓶 50箱 8.5千克/箱 425千克
1.25千克/瓶 50箱 8.5千克/箱 425千克
各种问题,准确及时地发
布调度命令,保证运输计
划的完成。
及时性
4
调度工作的时间尤其重要,无论是
工时的利用、配送环节的衔接,还
是装卸效率的提高、运输时间的缩
短,无不体现了时间的观念。
4
辆、货物、驾驶员等资源,实现最
小的运力投入。
车辆调度特点
计划性
事先划分好配送区域,配送车
辆按照已经划分好的区域线路
1
执行每日的配送工作。
预防性。
2
运输过程中的影响因素多,情况变
化快,因此,调度人员应对生产中
可能产生的问题有预见。
车辆调度特点
机动性
机动性就是必须加强运输
信息的反馈,及时了解运
3
输状况,机动灵活地处理
统筹全局考虑接到的订单情况,
提前做好订单实施的准备
1
及时了解配送任务的执行情况
调度工作覆盖了接收订单、订单实
2
施等部分,覆盖了配送任务的整个
过程。
车辆调度作用
促进配送及相关作业的有序进行
做好工作计划,并不断监
督,这种情况下,配送等
3
有关作业可以按照调度的
计划按部就班地实施下去。
调车作业ppt课件

01
02
03
04
人员准备
指定作业负责人,明确人员分 工和岗位职责。
车辆准备
检查车辆状态,确保符合调车 作业要求。
设备准备
检查调车作业所需的各种设备 ,如信号灯、通讯设备等,确
保其正常可用。
安全准备
制定安全措施,确保作业过程 中的安全。
调车作业执行
信号指挥
按照调车作业计划,通 过信号灯或通讯设备指
挥车辆移动。
加强质量监督和检查
建立完善的质量监督和检查机制,对 调车作业进行定期或不定期的检查和 评估,发现问题及时整改。
鼓励创新和改进
鼓励调车人员在实践中进行创新和改 进,提出合理化建议和改进措施,不 断提高作业质量和服务水平。
05
调车作业发展趋势
智能化调车作业
总结词
随着科技的不断发展,智能化调车作业已成为未来的发展趋势。
定期进行安全培训
建立安全检查制度
定期组织调车作业人员进行安全培训,提 高他们的安全意识和操作技能。
建立定期和不定期的安全检查制度,对调 车作业场所、设备和安全防护用品进行检 查,确保其处于良好状态。
安全注意事项
遵守操作规程
调车作业人员应严格遵守安全操作规程,不 得违章作业。
保持稳定的心态
调车作业人员应保持稳定的心态,不得在疲 劳、情绪不稳定等情况下进行作业。
调车作业PPT课件
目录
• 调车作业概述 • 调车作业流程 • 调车作业安全 • 调车作业优化建议 • 调车作业发展趋势
01调车作业概述来自调车作业的定义总结词
调车作业是指在铁路运输过程中,根据列车运行计划和车辆 检修计划,对车辆进行编组、解体、摘挂、转场等作业。
行车调度概述课件

同时积极参与救援工作的指挥。 l (7)建立、健全运营生产、调度指挥等各项原始记录台账及统计,分析报表,并按规定向
上级主管部门报告。 l (8)密切关注客流动态,协同有关部门根据客流变化采取相应的组织方案。
1.2 行车调度指挥的原则
1.2 行车调度指挥的原则
1.安全生产原则
在列车调度指挥工作中,必须坚持安全生产的原则,正确指挥列车运行。不能发布 没有安全保障依据的命令和指示。当得到有关危及行车安全的信息时,要正确、及 时、妥善处理,以保证列车的安全为重点,组织列车安全运行。
车辆段等相关单位进行广播,具有人工和自动广播两种模式,并可指定区域广播。
谢谢观看
16
1.中央运营协调与应急指挥中心
释义
中央运营协调与应急指挥中心负责协调整个运营网络中 的各条线路运营控制中心和相关部门,对路网的运营状 态、设备运行情况进行实时监控。在遇到突发事件时, 根据影响程度及时发布预警指令,控制影响范围,减少 不利影响,根据公司信息传递的相关规定做好内外部信 息的传递工作。特别是发生影响两条及以上线路的紧急 情况时,实现运营资源的统筹、协调和联动,提升应急 突发事件的处置能力。
中央运营协调与应急指挥中心的基本任务如下:
l (1)管辖范围为试运营及运营载客的线路、车站、出入口、通道、停车场、车辆段等的列 车服务,客流变化、设施设备运转状态的处置与协调。
l (2) 实时监督运营状态,监督日常行车组织、客运组织、设备状态等各类生产活动。 l (3)协调运营生产,协调企业内部各单位和部门之间、各运营线路之间的日常运营生产。 l (4)实时诱导路网客流。 l (5)收集反映路网运营生产情况的基础数据, 汇总每日路网运营生产情况。 l (6)对外发布运营实时信息与信息控制。 l (7)指挥与协调社会影响较大的突发事件。
上级主管部门报告。 l (8)密切关注客流动态,协同有关部门根据客流变化采取相应的组织方案。
1.2 行车调度指挥的原则
1.2 行车调度指挥的原则
1.安全生产原则
在列车调度指挥工作中,必须坚持安全生产的原则,正确指挥列车运行。不能发布 没有安全保障依据的命令和指示。当得到有关危及行车安全的信息时,要正确、及 时、妥善处理,以保证列车的安全为重点,组织列车安全运行。
车辆段等相关单位进行广播,具有人工和自动广播两种模式,并可指定区域广播。
谢谢观看
16
1.中央运营协调与应急指挥中心
释义
中央运营协调与应急指挥中心负责协调整个运营网络中 的各条线路运营控制中心和相关部门,对路网的运营状 态、设备运行情况进行实时监控。在遇到突发事件时, 根据影响程度及时发布预警指令,控制影响范围,减少 不利影响,根据公司信息传递的相关规定做好内外部信 息的传递工作。特别是发生影响两条及以上线路的紧急 情况时,实现运营资源的统筹、协调和联动,提升应急 突发事件的处置能力。
中央运营协调与应急指挥中心的基本任务如下:
l (1)管辖范围为试运营及运营载客的线路、车站、出入口、通道、停车场、车辆段等的列 车服务,客流变化、设施设备运转状态的处置与协调。
l (2) 实时监督运营状态,监督日常行车组织、客运组织、设备状态等各类生产活动。 l (3)协调运营生产,协调企业内部各单位和部门之间、各运营线路之间的日常运营生产。 l (4)实时诱导路网客流。 l (5)收集反映路网运营生产情况的基础数据, 汇总每日路网运营生产情况。 l (6)对外发布运营实时信息与信息控制。 l (7)指挥与协调社会影响较大的突发事件。
车辆调度方法

)确定目标
(1)以效益最高为目标。 (2)以成本最低为目标。 (3)以路程最短为目标。 (4)以吨千米数最小为目标。 (5)以准确性最高为目标。 (二)确定配送路线的约束条件
(1)满足所有收货人对货物品种、规格、数量的要求; (2)满足收货人对货物送达时间范围的要求; (3)任允许通行的时间段内进行配送; (4)各配送路线的货物量不得超过率辆容积和载员量的
• 三、集装箱尺寸和重量
(一)集装箱尺寸
1、外部尺寸
2、内部尺寸
集装箱内部高度尺寸分为公称高度尺寸和净空高 度尺寸
公称尺寸是指不计公差,用近似整数表示的集装 箱的尺寸;
净空尺寸是指集装箱内部不考虑角件凸出部分的 尺寸。
3、集装箱箱门尺寸:箱门开口部分的宽度和高度的 尺寸
集装箱箱门最小开口尺寸
箱型
高度(mm) 宽度(mm)
1AA
2282以上
2290以上
1A、1B、1C、 1D
2130以上
2290以上
• (二)集装箱重量 自重(T),又称空箱重量 载重(P),又称载货重量 额定重量(R),最大工作总重量
P=R-T
• 四、集装箱的结构
(一)常用的干货集装箱的基本结构和构件 主要有:
框架、两个侧壁、两个端壁、箱顶、箱底、 箱门和角件
1.3
1.6
运输定额比派车
车辆种类 运水泥车 运盘条车 运玻璃车 车辆总数
辆数
辆数
辆数
大型车辆 5
6
9
20
中型车辆
20
20
小型车辆 30
30
货运量 580
402
126
(吨)
集装箱
一、集装箱的定义 具有一定强度、刚度和规格专供周转使用的大型装货容器。 国际标准化组织(ISO)对国际标准集装箱作如下定义: 集装箱是一种运输设备: (1)具有耐久性,其坚固程度足以反复使用 (2)便于为商品运送而专门设计的,在一种或多种运输方式 种运输时,无需中途换装 (3)装有便于装卸和搬运的装置,特别是从一种运输方式转 移到另一种运输方式时 (4)设计时注意到便于货物装满和卸空 (5)内容积1立方米或1立方米以上
(1)以效益最高为目标。 (2)以成本最低为目标。 (3)以路程最短为目标。 (4)以吨千米数最小为目标。 (5)以准确性最高为目标。 (二)确定配送路线的约束条件
(1)满足所有收货人对货物品种、规格、数量的要求; (2)满足收货人对货物送达时间范围的要求; (3)任允许通行的时间段内进行配送; (4)各配送路线的货物量不得超过率辆容积和载员量的
• 三、集装箱尺寸和重量
(一)集装箱尺寸
1、外部尺寸
2、内部尺寸
集装箱内部高度尺寸分为公称高度尺寸和净空高 度尺寸
公称尺寸是指不计公差,用近似整数表示的集装 箱的尺寸;
净空尺寸是指集装箱内部不考虑角件凸出部分的 尺寸。
3、集装箱箱门尺寸:箱门开口部分的宽度和高度的 尺寸
集装箱箱门最小开口尺寸
箱型
高度(mm) 宽度(mm)
1AA
2282以上
2290以上
1A、1B、1C、 1D
2130以上
2290以上
• (二)集装箱重量 自重(T),又称空箱重量 载重(P),又称载货重量 额定重量(R),最大工作总重量
P=R-T
• 四、集装箱的结构
(一)常用的干货集装箱的基本结构和构件 主要有:
框架、两个侧壁、两个端壁、箱顶、箱底、 箱门和角件
1.3
1.6
运输定额比派车
车辆种类 运水泥车 运盘条车 运玻璃车 车辆总数
辆数
辆数
辆数
大型车辆 5
6
9
20
中型车辆
20
20
小型车辆 30
30
货运量 580
402
126
(吨)
集装箱
一、集装箱的定义 具有一定强度、刚度和规格专供周转使用的大型装货容器。 国际标准化组织(ISO)对国际标准集装箱作如下定义: 集装箱是一种运输设备: (1)具有耐久性,其坚固程度足以反复使用 (2)便于为商品运送而专门设计的,在一种或多种运输方式 种运输时,无需中途换装 (3)装有便于装卸和搬运的装置,特别是从一种运输方式转 移到另一种运输方式时 (4)设计时注意到便于货物装满和卸空 (5)内容积1立方米或1立方米以上
铁路运输组织学-第七篇铁路运输调度工作PPT课件

根据列车运行情况,及时调整列车作业计划,确保列车安全、准时、高效地完成运 输任务。
列车运行信息的收集与传递
建立完善的列车运行信息管理 系统,实时收集列车运行数据, 如车次、时间、位置、速度等。
通过无线通信、数据传输等方 式,及时将列车运行信息传递 给相关人员,以便于调度指挥 和运输组织。
对列车运行信息进行统计分析, 为优化列车调度和运输组织提 供数据支持。
旅客列车调度指挥工
04
作
旅客列车运行计划的编制与调整
根据客流情况,合理安排旅客列 车车次、始发终到时间、经由路 线和停站时分,满足旅客出行需
求。
及时调整列车运行计划,应对突 发客流、天气等变化,确保列车
运行安全、正点。
优化列车开行方案,提高旅客出 行效率,降低运输成本。
旅客列车调度的基本方法
采用先进的调度指挥系统,实时监控旅客列车运行状态,实现科学调度。
调度指挥原则
02
预防为主,及时应对,确保安全。
调度指挥措施
03
加强与气象、防汛等部门的沟通协作,提前预警,及时采取应
对措施,降低自然灾害对铁路运输的影响。
THANKS.
调度工作的基本原则
01
02
03
04
安全第一
确保列车运行安全是调度工作 的首要任务。
集中领导
调度工作实行集中领导,统一 指挥。
按图行车
列车应按照列车运行图规定的 时刻和线路运行。
保障重点
优先保障重点列车和重要物资 的运输。
列车调度指挥工作
02
列车运行计划的编制与调整
根据客货流调查和预测,结合列 车编组计划、运输方案及运输能 力等因素,编制列车运行计划。
注意事项
列车运行信息的收集与传递
建立完善的列车运行信息管理 系统,实时收集列车运行数据, 如车次、时间、位置、速度等。
通过无线通信、数据传输等方 式,及时将列车运行信息传递 给相关人员,以便于调度指挥 和运输组织。
对列车运行信息进行统计分析, 为优化列车调度和运输组织提 供数据支持。
旅客列车调度指挥工
04
作
旅客列车运行计划的编制与调整
根据客流情况,合理安排旅客列 车车次、始发终到时间、经由路 线和停站时分,满足旅客出行需
求。
及时调整列车运行计划,应对突 发客流、天气等变化,确保列车
运行安全、正点。
优化列车开行方案,提高旅客出 行效率,降低运输成本。
旅客列车调度的基本方法
采用先进的调度指挥系统,实时监控旅客列车运行状态,实现科学调度。
调度指挥原则
02
预防为主,及时应对,确保安全。
调度指挥措施
03
加强与气象、防汛等部门的沟通协作,提前预警,及时采取应
对措施,降低自然灾害对铁路运输的影响。
THANKS.
调度工作的基本原则
01
02
03
04
安全第一
确保列车运行安全是调度工作 的首要任务。
集中领导
调度工作实行集中领导,统一 指挥。
按图行车
列车应按照列车运行图规定的 时刻和线路运行。
保障重点
优先保障重点列车和重要物资 的运输。
列车调度指挥工作
02
列车运行计划的编制与调整
根据客货流调查和预测,结合列 车编组计划、运输方案及运输能 力等因素,编制列车运行计划。
注意事项
装车配载与车辆调度作业ppt课件

触,承运人不得任意开封。 • 4.同一地点货物尽可能一次积载,根据车厢确定方法。 • 5.确定合理的堆码层次及方法,恰当积载方法使车厢
高度、长度、宽度充分利用 • 6.积载时不允许超过车辆所允许的最大载重量。 • 7.积载时车厢内货物重要应分布均匀 • 8.车厢内应分布均,防止碰撞、沾污。
5
6
二、车辆调度
15
2.车辆调度工作的特点 ⑴计划性 ⑵预防性 ⑶机动性
16
容量配装法
• 车厢容积V,车辆载重量W,现要装载质量 体积为R1、R2的两种货物,使得车辆的载 重量和车厢容积均被充分利用。
• 设两种货物的配装量为W1和W2
W1+W2=W
W1=V-WR2/R1-R2
• W1R1+W2R2=V
W2=V-WR1/R1-R2
50 80
120
100
B1 (140) B3 (60) A4(140) B4(100)
80
A3 (60)
20 B2 (20)
20
• 步骤: • 1.破圈:从距离最大的地方破。 • 2.配送:就近原则实施配送的初始方案 • 3.验证:无对流;内圈长与长均与外圈长均
小于相应总圈长的一半,即为合理方案 • 4.调整:若不合理,例如内圈长大于总圈长
装满载。
4
• 车辆积载的原则
• 安排好顺序,如:后送先装,还要考虑(怕震、怕压、 怕撞)、形状、体积、质量,选择恰当的装卸方式。
• 1.轻重搭配的原则,重货置底部,避免重货压轻货。 • 2.大小搭配,采取不同尺寸大小货物,在同一层或上
下层合理搭配,减少厢内的空间。 • 3.货物性质搭配,注意化学属性、物理属性,相互抵
(一)车辆调度工作的原则及程序 (二)车辆调度的要求 (三)车辆调度的技术设备 (四)车辆调度的工作特点 (五)车辆调度的方法
高度、长度、宽度充分利用 • 6.积载时不允许超过车辆所允许的最大载重量。 • 7.积载时车厢内货物重要应分布均匀 • 8.车厢内应分布均,防止碰撞、沾污。
5
6
二、车辆调度
15
2.车辆调度工作的特点 ⑴计划性 ⑵预防性 ⑶机动性
16
容量配装法
• 车厢容积V,车辆载重量W,现要装载质量 体积为R1、R2的两种货物,使得车辆的载 重量和车厢容积均被充分利用。
• 设两种货物的配装量为W1和W2
W1+W2=W
W1=V-WR2/R1-R2
• W1R1+W2R2=V
W2=V-WR1/R1-R2
50 80
120
100
B1 (140) B3 (60) A4(140) B4(100)
80
A3 (60)
20 B2 (20)
20
• 步骤: • 1.破圈:从距离最大的地方破。 • 2.配送:就近原则实施配送的初始方案 • 3.验证:无对流;内圈长与长均与外圈长均
小于相应总圈长的一半,即为合理方案 • 4.调整:若不合理,例如内圈长大于总圈长
装满载。
4
• 车辆积载的原则
• 安排好顺序,如:后送先装,还要考虑(怕震、怕压、 怕撞)、形状、体积、质量,选择恰当的装卸方式。
• 1.轻重搭配的原则,重货置底部,避免重货压轻货。 • 2.大小搭配,采取不同尺寸大小货物,在同一层或上
下层合理搭配,减少厢内的空间。 • 3.货物性质搭配,注意化学属性、物理属性,相互抵
(一)车辆调度工作的原则及程序 (二)车辆调度的要求 (三)车辆调度的技术设备 (四)车辆调度的工作特点 (五)车辆调度的方法
城市轨道交通系统的构成——行车调度 ppt课件

1)横坐标。 2)纵坐标。 3)垂直线。 4)水平线。 ① 按区间实际里程比率确定:即按照整个区段各个车站实际里程的 比例来确定站名线的位置。采用这种方法,列车运行图上的站间距 能完全反映实际情况,能明显表示出站间距的大小。但是由于各区 间线路和横纵断面的不同,列车运行的速度也不相同,列车在整个 区段的运行线是一条折线。这样画出来的列车运行图非常不美观, 并且不利于发现区间运行时分上的差错,所以一般不采用此种方法。
PPT课件
20
【理论知识】 10.2 列车运行图
图10-8 单双线运行图
PPT课件
21
【理论知识】 10.2 列车运行图
图10-9 平行运行图
PPT课件
22
【理论知识】 10.2 列车运行图
② 非平行运行图(见图10-10):列车运行图中铺画有不同速度和不同类 型的列车,因此运行图中的运行线相互不平行。在城市轨道交通系统 中,市郊铁路会采用此种类型的运。
下行的列车数量以及列车运行方式的不同,列车运行图可以分为不同
的类型。
1)按区间正线数目不同分类。
① 单线运行图(见图10-6):在单线区段上,上下行方向的列车都在同
一正线上运行,两个方向的列车必须在车站进行交会。单线运行图多
数在运量不大的市郊铁路运用。
② 双线运行图(见图10-4):在双线区段上,上下行方向的列车分别在
PPT课件
4
【理论知识】 10.1 城市轨道交通调度的工作内容
1.城市轨道交通调度工作的作用与任务
图10-1 控制中心调度机构PPT Nhomakorabea件5
【理论知识】 10.1 城市轨道交通调度的工作内容
2.城市轨道交通调度机构: 具体分工包括:运营控制中心(OCC)。 车辆段控制中心(DCC)。 车辆段信号控制室。 车站综控室。 行车调度员。 列车驾驶员 。 车站行车值班员 车辆段运转值班员。
PPT课件
20
【理论知识】 10.2 列车运行图
图10-8 单双线运行图
PPT课件
21
【理论知识】 10.2 列车运行图
图10-9 平行运行图
PPT课件
22
【理论知识】 10.2 列车运行图
② 非平行运行图(见图10-10):列车运行图中铺画有不同速度和不同类 型的列车,因此运行图中的运行线相互不平行。在城市轨道交通系统 中,市郊铁路会采用此种类型的运。
下行的列车数量以及列车运行方式的不同,列车运行图可以分为不同
的类型。
1)按区间正线数目不同分类。
① 单线运行图(见图10-6):在单线区段上,上下行方向的列车都在同
一正线上运行,两个方向的列车必须在车站进行交会。单线运行图多
数在运量不大的市郊铁路运用。
② 双线运行图(见图10-4):在双线区段上,上下行方向的列车分别在
PPT课件
4
【理论知识】 10.1 城市轨道交通调度的工作内容
1.城市轨道交通调度工作的作用与任务
图10-1 控制中心调度机构PPT Nhomakorabea件5
【理论知识】 10.1 城市轨道交通调度的工作内容
2.城市轨道交通调度机构: 具体分工包括:运营控制中心(OCC)。 车辆段控制中心(DCC)。 车辆段信号控制室。 车站综控室。 行车调度员。 列车驾驶员 。 车站行车值班员 车辆段运转值班员。
《调车作业规定》课件

调车过程中车辆可能受到 撞击或损坏,需要进行维 护和检修。
3 环境污染
调车作业涉及油料和化学 品的使用,需要正确处理 和回收,防止环境污染。
调车相关的法律法规和标准
安全标准
国家制定了一系列的安全标 准,以确保调车作业的安全 和合规。
法律法规
调车作业需要遵守相关的法 律法规,包括劳动法和安全 生产法等。
《调车作业规定》PPT课 件
作业规范的重要性。良好的作业规范能够确保调车作业的安全和高效进行, 减少人员伤亡和设备损坏的风险。
调车的定义和种类
调车的定义
调车是指将火车车辆按照一 定的计划进行编组、分离和 重新组合的操作。
调车的种类
调车可以分为进路调车、编 组调车、挂车和分离调车等 多种类型。
调车任务
技术规范
调车作业还需要按照相关的 技术规范进行操作,以确保 作业的顺利进行。
总结和建议
1 总结
调车作业规定为调车提供了明确的指导和标准,对保障调车作业的安全和高效至关重要。
2 建议
建议调车人员和管理者要认真学习和遵守作业规定,加强培训和安全意识。
调车方法和流程
1
计划调车
制定调车计划,确定调车的起始站和目
组织调车
2
的站,以及中间需要停靠的调车站。分配调车人员和资源Fra bibliotek确保调车的顺利
进行。
3
实施调车
按照计划和操作规程进行各项调车工作, 包括车辆编组和分离、挂车和分离等。
调车中可能出现的危险和应对措施
1 人员伤亡
2 车辆损坏
调车作业中可能发生碰撞、 坠落等事故,应加强安全 培训和使用防护设施。
调车任务包括运输、装卸货 物和车辆调度等多个方面。
调车作业ppt课件

总结词
调车作业流程改进
详细描述
该编组站对调车作业流程进行了全面优化,通过采用先进的编组技术,优化车辆编组结 构,提高编组效率;同时加强与货运部门的协作,实现信息共享和协同作业,提高运输
组织效率。此外,还加强了安全管理和监督,确保作业过程的安全可控。
REPORT
THANKS
感谢观看
CATALOG
DATE
制度进行责任追究和处理。
对于发生的调车作业安全事故, 应认真总结经验教训,加强安全 教育和培训,防止类似事故再次
发生。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
04
调车作业优化
作业时间优化
总结词
合理安排时间
详细描述
通过合理安排作业时间,减少等待和 空闲时间,提高调车作业的效率。
调车作业时应配备必要的安全防护用品,如安全帽、防护服、手套等,以降低作业 风险。
调车作业时应加强现场监控和应急救援措施,确保在出现紧急情况时能够及时处理 和应对。
安全事故处理
一旦发生调车作业安全事故,应 立即启动应急预案,进行事故处
置和调查。
对于发生的调车作业安全事故, 应严格按照相关法律法规和公司
02
调车作业流程
调车作业计划编制
计划内容确定
明确调车作业计划的具体内容, 包括作业车种、作业地点、作业 时间、作业方式等。
资料收集
收集相关资料,如车辆位置、货 物状态、线路使用情况等,为计 划编制提供依据。
调车作业准备
人员组织
根据调车作业计划,合理安排作业人 员,明确各自职责。
工具设备检查
对所需工具和设备进行检查,确保其 完好可用。
调车作业流程改进
详细描述
该编组站对调车作业流程进行了全面优化,通过采用先进的编组技术,优化车辆编组结 构,提高编组效率;同时加强与货运部门的协作,实现信息共享和协同作业,提高运输
组织效率。此外,还加强了安全管理和监督,确保作业过程的安全可控。
REPORT
THANKS
感谢观看
CATALOG
DATE
制度进行责任追究和处理。
对于发生的调车作业安全事故, 应认真总结经验教训,加强安全 教育和培训,防止类似事故再次
发生。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
04
调车作业优化
作业时间优化
总结词
合理安排时间
详细描述
通过合理安排作业时间,减少等待和 空闲时间,提高调车作业的效率。
调车作业时应配备必要的安全防护用品,如安全帽、防护服、手套等,以降低作业 风险。
调车作业时应加强现场监控和应急救援措施,确保在出现紧急情况时能够及时处理 和应对。
安全事故处理
一旦发生调车作业安全事故,应 立即启动应急预案,进行事故处
置和调查。
对于发生的调车作业安全事故, 应严格按照相关法律法规和公司
02
调车作业流程
调车作业计划编制
计划内容确定
明确调车作业计划的具体内容, 包括作业车种、作业地点、作业 时间、作业方式等。
资料收集
收集相关资料,如车辆位置、货 物状态、线路使用情况等,为计 划编制提供依据。
调车作业准备
人员组织
根据调车作业计划,合理安排作业人 员,明确各自职责。
工具设备检查
对所需工具和设备进行检查,确保其 完好可用。
列车运行调整PPT模板

隔过密等)佩和戴发工现紧作急牌事。件的情况下。 度较小的线路上反向运行,来恢
发生紧急事件需要扣车的情况主要有
复列车正点运行。另外,当某个
正线列车脱轨、正线断轨、正线列车
方向因列车故障救援而造成较大
冲突、恐怖袭击、运营列车失火、车
行车间隔时,也可采用列车反向
站火灾、地下站水淹等。
运行的方式来缩小行车间隔。
三、列车运行调整方法
(一)在始发站提前 或推迟发车
(二)改变列车区间运 行时间
(三)增加或缩短列 车停站时间
根据列车的速度和位置,可以预测
当列车因中途某区段需要限速运行,
列车到达下一站的到站时间,如果
而在到达终点站晚点时,行车调度员
预测的到站时间晚于计划时间,行
可向司机下达调观度察命乘客令的,入使站其情在况始,发发现携车带调违度禁员物可品通时过要修及改列车运行等级、
当某区段发生故障时,由于故障区 段列车运行速度低、办理作业时间 长 , 而 ATC 正 常 区 段 列 车 运 行 速 度 高、行车作业时间短,这样会造成 列车堵塞。此时,行车调度员可通 过减少线上列车数量(即抽线)的 方法实现均衡运输,从而达到列车 运行调整的目的。这种方法便于调 度指挥,方便客流组织。
2、快速及时原则 在进行列车运行调整时,调度相关人员 要做到反应快、报告快、处置快,首先 在保证线路安全的情况下第一时间恢复 通车,然后再处置突发事件带来的影响, 尽量把握事发初期的关键时间,将突发 事件对运营组织的影响降低到最小。
4、全面原则 在进行运行调整时,行车调度员要有 全局观,不能只调整个别列车的晚点, 应在ATC系统功能良好区段,适当缩 短两列车间的正常追踪时间,实现晚 点危害的“分散化”,让所有列车共 同承担晚点。
列车调度指挥PPT课件

❖ 为使行车调度命令格式规范化,借鉴国铁,以国内部分 城市轨道交通系统为例,常用的调度命令格式规定如下 (不用的字句划销)。
❖ 1.救援命令 ❖ (1)救援列车加开命令格式
XX站~XX站(车厂信号楼、派班室),
受
XX站(车厂)交XX次司机
令
处
所
日期 XXX
命令 行调代 发令时
号
号
间
码
XXX XXX XXX
❖ 4.按列车等级进行调整
❖ 在发生列车运行秩序混乱的情况下,列车调度员须进行列 车运行调整。对不能按列车运行图运行的列车,应按下列 等级顺序进行运行整理:专运列车、旅客列车、调试列车、 回空列车、其它列车。
❖ (二)列车运行调整方法
❖ 列车正点始发是保证列车正点运行和实现列车运行图的基 础。对始发列车,行调应在列车出库、列车折返交路和客 流情况等方面进行具体掌握和组织,保证正点发车。列车 运行晚点时,行调应根据列车运行的实际情况,按规定的 列车等级顺序进行调整,对同一等级的旅客列车可根据列 车的接续车次和乘客的多少等情况进行调整,尽可能在最 短时间内使列车恢复按图运行。
❖ 2.单一指挥
❖ 在列车运行调整中,行车各有关部门必须服从所在区段的 列车调度员的集中统一指挥,各级领导对列车运行的指示, 必须通过所在区段的列车调度员去实现,坚决禁止令出多 口或多头指挥,维护调度命令的严肃性和权威性。
❖ 3.安全生产
❖ 调度指挥必须坚持安全生产,正确及时地指挥列车运行, 防止因指挥不当造成事故隐患。遇突发紧急事件时,要冷 静、正确、及时处理,努力提高业务水平,提高应变能力。 发布调度命令要正确、完整、清新。
❖ 城市轨道交通运营的行车组织指挥工作原则为安全生 产,高度集中,统一指挥,逐级负责。本章以国内部分地 铁公司为例,各地铁公司规定略有不同,使用时应注意细 微差别。
❖ 1.救援命令 ❖ (1)救援列车加开命令格式
XX站~XX站(车厂信号楼、派班室),
受
XX站(车厂)交XX次司机
令
处
所
日期 XXX
命令 行调代 发令时
号
号
间
码
XXX XXX XXX
❖ 4.按列车等级进行调整
❖ 在发生列车运行秩序混乱的情况下,列车调度员须进行列 车运行调整。对不能按列车运行图运行的列车,应按下列 等级顺序进行运行整理:专运列车、旅客列车、调试列车、 回空列车、其它列车。
❖ (二)列车运行调整方法
❖ 列车正点始发是保证列车正点运行和实现列车运行图的基 础。对始发列车,行调应在列车出库、列车折返交路和客 流情况等方面进行具体掌握和组织,保证正点发车。列车 运行晚点时,行调应根据列车运行的实际情况,按规定的 列车等级顺序进行调整,对同一等级的旅客列车可根据列 车的接续车次和乘客的多少等情况进行调整,尽可能在最 短时间内使列车恢复按图运行。
❖ 2.单一指挥
❖ 在列车运行调整中,行车各有关部门必须服从所在区段的 列车调度员的集中统一指挥,各级领导对列车运行的指示, 必须通过所在区段的列车调度员去实现,坚决禁止令出多 口或多头指挥,维护调度命令的严肃性和权威性。
❖ 3.安全生产
❖ 调度指挥必须坚持安全生产,正确及时地指挥列车运行, 防止因指挥不当造成事故隐患。遇突发紧急事件时,要冷 静、正确、及时处理,努力提高业务水平,提高应变能力。 发布调度命令要正确、完整、清新。
❖ 城市轨道交通运营的行车组织指挥工作原则为安全生 产,高度集中,统一指挥,逐级负责。本章以国内部分地 铁公司为例,各地铁公司规定略有不同,使用时应注意细 微差别。
公交运营调度基本方法PPT70页
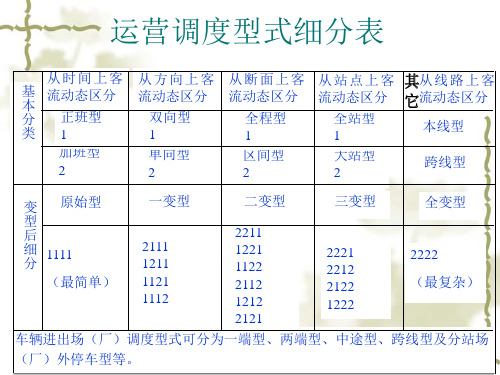
运营调度型式细分表
车辆进出场(厂)调度型式可分为一端型、两端型、中途型、跨线型及分站场(厂)外停车型等。
2222 (最复杂)
2211 1221 1122 2112 1212 2121
1111 (最简单)
原始型
变型后细分
区间型 2
单向型 2
加班型 2
大站型 2
跨线型
双向型 1
全程型 1
全站型 1
本线型
单位直达班车调度方法示意图
四、平峰时间的调度方法
在执行行车作业计划的过程中,往往由于社会活动,天气因素等影响正常客流规律,出现乘客人次增减悬殊的情况,作为公共交通企业的调度工作人员,必须随时采取相应的措施,适应变化以后的客流需要。为切实做到:“人多车密,人少车稀,定而不死,活而不乱”,可采取以下几种方法:
[例] 某线路高峰小时的各站客流集散量
(五)直达车的调度方法
线路乘客交替系数较小或线路较短,乘座全程的乘客又较多,适合采用这种直达车运送乘客的方法。在采用这种方法时,必须进行乘客流向量的调查,同时还要考虑以下因素: A.直达车的乘客密度要等于或大于正班车的乘客密度。 B.能够比发正班车多发车次。 C.不破坏中途站的服务。 具体调度方法有以下几种:
[例] 某线路由甲站到乙站,上班时间去乙站方向的客流大。早晨出库后,线路上共计行驶10部车,间隔5分,按标准每车在甲乙两个终点站各停3分。为解决甲站去乙站方向的客流高峰,可在甲站停8分(存点5分)早高峰到来后,甲站可发4分间隔的车5个,待停站时间回到3分时,仍按对方站发来的5分间隔发车。乙站见到4分间隔的车到站后,正值由乙站去甲站的客流高峰尖,也可以按4分间隔送回甲站。这样甲乙两个方向的客流高峰都能得到解决。
总之,区间调度方法在实际运用中是多种多样的,它随着客流量的变化而变化。虽然,区间车是一种解决区段客流需要,平衡客流的好方法,但是区间在运能的利用方面则存在很多不利因素。如区间车在两端站的调头环境问题,交通管理问题等。所以,在设计线路时,必须考虑各区段客流的平衡,一条线路不宜过多的设区间车。
车辆进出场(厂)调度型式可分为一端型、两端型、中途型、跨线型及分站场(厂)外停车型等。
2222 (最复杂)
2211 1221 1122 2112 1212 2121
1111 (最简单)
原始型
变型后细分
区间型 2
单向型 2
加班型 2
大站型 2
跨线型
双向型 1
全程型 1
全站型 1
本线型
单位直达班车调度方法示意图
四、平峰时间的调度方法
在执行行车作业计划的过程中,往往由于社会活动,天气因素等影响正常客流规律,出现乘客人次增减悬殊的情况,作为公共交通企业的调度工作人员,必须随时采取相应的措施,适应变化以后的客流需要。为切实做到:“人多车密,人少车稀,定而不死,活而不乱”,可采取以下几种方法:
[例] 某线路高峰小时的各站客流集散量
(五)直达车的调度方法
线路乘客交替系数较小或线路较短,乘座全程的乘客又较多,适合采用这种直达车运送乘客的方法。在采用这种方法时,必须进行乘客流向量的调查,同时还要考虑以下因素: A.直达车的乘客密度要等于或大于正班车的乘客密度。 B.能够比发正班车多发车次。 C.不破坏中途站的服务。 具体调度方法有以下几种:
[例] 某线路由甲站到乙站,上班时间去乙站方向的客流大。早晨出库后,线路上共计行驶10部车,间隔5分,按标准每车在甲乙两个终点站各停3分。为解决甲站去乙站方向的客流高峰,可在甲站停8分(存点5分)早高峰到来后,甲站可发4分间隔的车5个,待停站时间回到3分时,仍按对方站发来的5分间隔发车。乙站见到4分间隔的车到站后,正值由乙站去甲站的客流高峰尖,也可以按4分间隔送回甲站。这样甲乙两个方向的客流高峰都能得到解决。
总之,区间调度方法在实际运用中是多种多样的,它随着客流量的变化而变化。虽然,区间车是一种解决区段客流需要,平衡客流的好方法,但是区间在运能的利用方面则存在很多不利因素。如区间车在两端站的调头环境问题,交通管理问题等。所以,在设计线路时,必须考虑各区段客流的平衡,一条线路不宜过多的设区间车。
车辆调度方法

• 二、集装箱的标准与规格
(一)现行的国际集装箱标准与规格 目前,国际标准集装箱的宽度均为8ft,高度有 8.6ft和小于8ft三种,长度有40ft、30ft、20ft和 10ft四种。 40ft集装箱=2TEU 30ft集装箱=1.5TEU 20ft集装箱=1TEU 10ft集装箱=0.5TEU
• 九、集装装箱拆箱作业 • (一)装箱业务 1、办理货物交接 2、领取空箱 3、装箱、制作装箱单 4、将拼箱的集装箱运至堆场 • (二)拆箱业务 1、做好交货准备工作 2、发出交货通知 3、从堆场领取载货的集装箱 4、拆箱交货及还箱
配送路线优化
• 一、配送路线优化的意义 配送路线是指各送货车辆向各个用户送货时 所要经过的线路。配送运输由于配送方法的 不同其运输过程也不尽相同。影响配送运输 的因素有:车流量的变化、道路状况、客户 的分布状况和配送中心的选址、车辆定额载 重量以及车辆运行限制,等等。 配送线路优化就是综合分析了配送运输的各 因素后,及时、安全、方便、经济地将客户 所需的不同物资准确送达客户手中,以便提 供优良的物流配送服务。
车辆调度方法
1、经验调度法
依据长期的车辆调度经验对运输车 辆调配做出决定。在能够保证满载的 情况下,应优先使用大型车辆,且先 载运大批量的货物
• 2、运输定额比法 运用理论方法做出决定,计算每种车 辆运输不同货物的定额比(小于1的定 额比忽略不计),根据定额比的大小 优先考虑安排车辆。
• 例如 某建材配送中心某日需要运输水泥580 吨、盘条400吨和不定量的平板玻璃。 该中心有大型车辆20辆、中型车辆20 辆、小型车辆30辆,各种车每日只运 输一种货物。三种车辆的运输定额如 图所示:
车辆运输定额
车辆种类
单位:吨/(日.辆)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析得知:如果经过C1,则最短路为C1-D2-E; 如果经过C2,则最短路为C2-D2-E; 如果经过C3,则最短路为C3-D1-E。
19
第二阶段:有 4个始点 B1,B2,B3,B4,终点有 C1,C2,C3。对始点和终点进行 分析和讨论分别求B1,B2,B3,B4到C1,C2,C3 的最短路径问题:
在超过全圈总长1/2 的里(外)圈各段流向线上减去最小运 量,然后在相反方向的外(里)圈流向线上和原来没有流向线 的各段上,加上减去的最小运量,这样可以得到一个新的线路 流向图,然后转到第二步检查有无迂回现象。如此反复,直到 得到最优线路流向图为止。 如果全圈存在两个及两个以上的圈,则需分别对各圈进行是 否存在迂回线路的检查,如果各圈的里、外圈都不超过全圈总 线长的1/2 ,则不存在迂回现象,此方案为最优运输方案。
18
分析得知:从D1和D2到E的最短路径唯一。
第三阶段:有三个始点C1,C2,C3,终点有D1,D2,对始点和终点进行分析和 讨论分别求C1,C2,C3到D1,D2 的最短路径问题: 表2 阶段3 本阶段始点 (状态) C1 C2 C3 本阶段各终点(决策) D1 8+10=18 7+10=17 1+10=11 D2 6+6=12 5+6=11 6+6=12 本阶段最优终点 到E的最短距离 (最优决策) 12 11 11 D2 D2 D1
20
D +20 E F +100 -20
60
H 50 G 80
10
+60 -30 外圈长=45+25+18+23=111公里 里圈长=23公里
-70
全圈长=45+23+25+18+23+36=170公里 半圈长=170/2=85公里
调整流向
A +20 20 B -30 10 C -50 20 D +20 E F +100 -20
乙圈: 半圈长=4+4+5+8/2=10.5公里 外圈长=0公里 里圈长=4+4+5=13公里
调整方案
1 4
பைடு நூலகம்
3
甲圈 2
乙圈
2
6 7
甲圈: 半圈长=7+2+3+6+4+3/2=12.5公里 外圈长=4+7=11公里 里圈长=2+3+3=8公里
乙圈: 半圈长=4+4+5+8/2=10.5公里 外圈长=8公里 里圈长=4+5=9公里
表3 阶段2 本阶段始点 (状态) B1 B2 B3 B4 本阶段各终点(决策) 到E的最 短距离 12 13 14 12 本阶段最优终 点(最优决策) C2 C3 C3 C3
C1
2+12=14 4+12=16 4+12=16 7+12=19
C2
1+11=12 7+11=18 8+11=19 5+11=16
规模较小的子问题,即分别从Di 、Ci、Bi、A到E的最短路径问题。 最优化原理的应用:从最短路上的每一点到终点的部分道路,也一定是
从该点到终点的最短路。
第四阶段:两个始点D1和D2,终点只有一个;
表1 阶段4 本阶段始点 (状态) D1 D2 本阶段各终点(决策) E 10 6 10 6 到E的最短距离 本阶段最优终点 (最优决策) E E
40
H 30 G 80
I
30
+60 -30 外圈长=25+18+23=66公里 里圈长=23+36=59公里
-70
全圈长=45+23+25+18+23+36=170公里 半圈长=170/2=85公里
3.运输线路成两圈的图上作业法
初始方案
5 2
4
甲圈 3
乙圈
8 8 1
甲圈: 半圈长=7+2+3+6+4+3/2=12.5公里 外圈长=4公里 里圈长=2+3+6+3=14公里
车辆调度方法
图上作业法
——物资调拨
图上作业法
图上作业法的原则可以归纳为:
流向划右方,对流不应当;
里圈、外圈分别算,要求不能过半圈长;
如若超过半圈长,应去运量最小段;
反复运算可得最优方案。
1.运输线路不成圈的图上作业法
对于运输线路不成圈的流向图,只要不出现对流现象, 就是最优调运方案。
练习
最短路径问题
例1 多阶段决策法 下图表示从起点 A到终点E之间各点的距离。求A到 E 的最短路径。
B 2 1 1 6 4 A 3 2 3 B2 7 2 C2
C1
6
8
4
D1 7 5
10 E
4
B3 7 3
8 C3 1
1 6
D 2
6
5
4
讨论:
1、以上求从 A到E的最短路径问题,可以转化为四个性质完全相同,但
重新去段 破圈,调 整流向
2.运输线路成圈的图上作业法
第一步 作出初始方案
A +20 (36) B -30 (23) C -50 (13) (18) H (25) G -70 (29) F +100 D +20 E -20
(45)
I -30 (23)
+60
A +20 20 I
B -30
30
C -50
详 述
去段破圈 确定初始 运输方案
就是在成圈的线路中,先假设某两点间的线路“不通”, 去掉这段线路,把成圈线路转化为不成圈的线路,即破圈;按 照运输线路不成圈的图上作业法,即可得到初始运输方案。
检查有无 迂回现象
因为流向箭头都统一画在线路右边,所以圈内圈外都画有 一些流向。分别检查每个小圈,如果圈内和圈外流向的总长度 都不超过全圈总长度的1/2 ,那么,全圈就没有迂回现象了,这 个线路流向图就是最优的,对应的就是最优运输方案。否则转 向第三步。
运输线路不成圈的图上作业法较简单。就是从各端点开
始,按“各站供需就近调拨”的原则进行调配。
1.运输线路不成圈的图上作业法
A D B -2 C +3 F E -11 +9
+10
G
-4
-5
1.运输线路不成圈的图上作业法
A D 10 B -2 8 C 3 +3 F 6 E -11 4
+10
G
-4
-5
5
+9
2.运输线路成圈的图上作业法
运输线路成圈,就是形成闭合回路的“环”形路线,包 括一个圈(有三角形、四边形、多边形)和多个圈。成圈的线
路流向图要同时达到既无对流现象、又无迂回现象的要求才是
最优流向图。
对于成圈运输线路的图上作业法,可按下述三个步骤寻 求最优方案,如表所示。
表
步骤
成圈运输线路的图上作业法的步骤
C3
6+11=17 2+11=13 3+11=14 1+11=12
分析得知:如果经过B1,则走B1-C2-D2-E; 如果经过B2,则走B2-C3-D1-E; 如果经过B3,则走B3-C3-D1-E; 如果经过B4,则走B4-C3-D1-E。
