含电容器电路的分析与计算201501
含容电路和电路故障分析

含容电路和电路故障分析一、含电容电器的分析与计算方法在直流电路中,当电容器充、放电时,电路里有充、放电电流.一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电的情况)的元件,在电容器处电路可看作是断路,简化电路时可去掉它.简化后若要求电容器所带电量时,可接在相应的位置上.分析和计算含有电容器的直流电路时,需注意以下几点:(1)电路稳定后,由于电容器所在支路无电流通过,所以在此支路中的电阻上无电压降,因此电容器两极间的电压就等于该支路两端的电压.(2)当电容器和电阻并联后接入电路时,电容器两极间的电压与其并联电阻两端的电压相等.(3)电路的电流、电压变化时,将会引起电容器的充(放)电.如果电容器两端电压升高,电容器将充电;如果电压降低,电容器将通过与它连接的电路放电.【例1】如图所示,电源电动势E =12V ,内阻r =1Ω,电阻R 1=3Ω,R 2=2Ω,R 3=5Ω,电容器的电容C 1=4μF ,C 2=1μF 。
求:(1)当S 闭合时间足够长时,C 1和C 2所带的电量各是多少?(2)然后把S 断开,S 断开后通过R 2的电量是多少?解:(1)当S 闭合时间足够长时,C 1两端的电压等于R 2两端的电压;C 2两端的电压等于路端电压 回路电流122E I A r R R ==++ C 1两端的电压U C1=U 2=IR 2=4VC 1的带电量为:Q 1=C 1U C1=4×10-6×4C =1.6×10-5CC 2两端的电压U C2=U =I (R 1+R 2)=10VC 2的带电量为:Q 2=C 2U C2=1×10-6×10C =1.0×10-5C(2)断开S 后,电容器C 1通过电阻R 2、R 3放电;电容器C 2通过电阻R 1、R 2、R 3放电,放电电流均流过R 2,且方向相同。
因此,通过R 2的电量为:Q =Q 1+Q 2=1.6×10-5C +1.0×10-5C =2.6×10-5C【例2】如图,已知源电动势E =12V ,内电阻不计。
含电容器电路的分析与计算

含电容器电路的分析与计算电容器是一个储存电能的元件.在直流电路中,当电容器充放电时,电路里有充放电电流,一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电的情况)的元件,在电容器处电路看作是断路,简化电路时可去掉它.简化后若要求电容器所带电荷量时,可在相应的位置补上.分析和计算含有电容器的直流电路时,需注意以下几点:(1)电路稳定后,由于电容器所在支路无电流通过.所以在此支路中的电阻上无电压降,因此电容器两极间的电压就等于该支路两端的电压.(2)当电容器和用电器并联后接入电路时,电容器两极间的电压与其并联用电器两端的电压相等.(3)电路的电流、电压变化时,将会引起电容器的充(放)电.如果电容器两端电压升高,电容器将充电,如果电压降低,电容器将通过与它并联的电路放电.电容器两根引线上的电流方向总是相同的,所以要根据正极板电荷变化情况来判断电流方向。
⑷如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始末状态电容器电荷量的差;如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始末状态电容器电荷量之和。
含有电容器的电路解题方法(1)先将含电容器的支路去掉(包括与它串在同一支路上的电阻),计算各部分的电流、电压值。
(2)电容器两极扳的电压,等于它所在支路两端点的电压。
(3)通过电容器的电压和电容可求出电容器充电电量。
(4)通过电容器的电压和平行板间距离可求出两扳间电场强度,再分析电场中带电粒子的运动。
例1:如图所示的电路,水平放置的平行板电容器中有一个带电液滴正好处于静止状态,现将滑动变阻器的滑片P向左移动,则()A.电容器中的电场强度将增大B.电容器上的电荷量将减少C.电容器的电容将减小D.液滴将向上运动由题意可知,电容器与R2并联,根据闭合电路欧姆定律可确定随着滑片左移,电阻的变化,导致电压的变化,从而判定电阻R2的电压变化,再根据可得,电容器的电量及由E=知两极间的电场强度如何变化.【解析】A、电容器两板间电压等于R2两端电压.当滑片P向左移动时,R2两端电压U减小,由E=知电容器中场强变小,A错误;B、根据可得,电容器放电,电荷量减少,B项正确;C、电容器的电容与U的变化无关,保持不变,C项错误.D、带电液滴所受电场力变小,使液滴向下运动,D项错误;故选:B例2:在如图所示的电路中,电源两端A、B 间的电压恒定不变,开始时S断开,电容器上充有电荷.闭合S后,以下判断正确的是()A.C1所带电量增大,C2所带电量减小B.C1所带电量减小,C2所带电量增大C.C1、C2所带电量均减小D.C1、C2所带电量均增大S断开时,外电路中没有电流,两电容器的电压都等于电源的电动势,S闭合后,两电容器的电压都小于电源的电动势,根据Q=CU分析电容器电量的变化.【解析】S断开时,外电路中没有电流,两电容器的电压都等于电源的电动势.S闭合后,两电阻串联,电容器C1的电压等于R1的电压,电容器C2的电压等于R2的电压,可知两电容器的电压都小于电源的电动势,根据Q=CU分析可知两电容器电量均减小.故C正确,ABD错误.故选C例3:如图所示的电路中,R1、R2、R3是固定电阻,R4是光敏电阻,其阻值随光照的强度增强而减小.当开关S闭合且没有光照射时,电容器C 不带电.当用强光照射R4且电路稳定时,则与无光照射时比较()A.电容器C的上极板带正电B.电容器C的下极板带正电C.通过R4的电流变小,电源的路端电压增大D.通过R4的电流变大,电源提供的总功率变小电容在电路稳定时可看作开路,故由图可知,R1、R2串联后与R3、R4并联,当有光照射时,光敏电阻的阻值减小,由闭合电路欧姆定律可得出电路中总电流的变化及路端电压的变化,再分析外电路即可得出C两端电势的变化,从而得出电容器极板带电情况;同理也可得出各电阻上电流的变化.【解析】因有光照射时,光敏电阻的阻值减小,故总电阻减小;由闭合电路的欧姆定律可知,干路电路中电流增大,由E=U+Ir可知路端电压减小;R1与R2支路中电阻不变,故该支路中的电流减小;则由并联电路的电流规律可知,另一支路中电流增大,即通过R2的电流减小,而通过R4的电流增大,故C、D错误;当没有光照时,C不带电说明C所接两点电势相等,以电源正极为参考点,R1上的分压减小,而R3上的分压增大,故上极板所接处的电势低于下极板的电势,故下极板带正电;故A错误,B正确;故选B.例4:如图所示的电路中,两平行金属板A、B水平放置,极板长L=80cm,两板间的距离d=40cm.电源电动势E=40V,内电阻r=1Ω,电阻R=15Ω,闭合开关S,待电路稳定后,将一带负电的小球从B板左端且非常靠近B 板的位置以初速度v=4m/s水平向右射入两板间,该小球可视为质点.若小球带电量q=1×10-2C,质量为m=2×10-2kg,不考虑空气阻力,电路中电压表、电流表均是理想电表.若小球恰好从A板右边缘射出(g取10m/s2).求:(1)滑动变阻器接入电路的阻值为多少?(2)此时电流表、电压表的示数分别为多少?(3)此时电源的输出功率是多少?(1)小球进入电场中做类平抛运动,小球恰好从A板右边缘射出时,水平位移为L,竖直位移为d,根据运动学和牛顿第二定律结合可求出板间电压,再根据串联电路分压特点,求解滑动变阻器接入电路的阻值.(2)根据闭合电路欧姆定律求解电路中电流,由欧姆定律求解路端电压,即可求得两电表的读数.(3)电源的输出功率P=UI,U是路端电压,I是总电流.【解析】(1)小球进入电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速运动,则有:水平方向:L=vt竖直方向:d=由上两式得:a===20m/s2又根据牛顿第二定律得:a=联立得:U==V=24V根据串联电路的特点有:=代入得:=解得,滑动变阻器接入电路的阻值为 R′=24Ω(2)根据闭合电路欧姆定律得电流表的示数为:I==A=1A电压表的示数为:U=E-Ir=(40-1×1)V=39V(3)此时电源的输出功率是 P=UI=39×1W=39W.答:(1)滑动变阻器接入电路的阻值为24Ω.(2)此时电流表、电压表的示数分别为1A和39V.(3)此时电源的输出功率是39W.每日一练解析C为板间距离固定的电容器,电路连接如图所示,当滑动触头P向右缓慢滑动的过程中,下列说法中正确的是()A.电容器C充电B.电容器C放电C.流过电流计G的电流方向为a→G→bD.流过电流计G的电流方向为b→G→a首先明确含电容器的支路等效为断路,且两端的电压为并联部分的电压相等;当滑动触头P向右缓慢滑动的过程中,该电路的总电阻不变,但与电容器并联部分的电阻减少,即电容器两端的电压减少,根据C=可知,电容器极板电量减少,即放电;电容器右极板与电源负极相连,所以自由电子从a移动到b,故流过电流计G的电流方向为b→G→a.【解析】AB、含电容器的支路等效为断路,且两端的电压为并联部分的电压相等;当滑动触头P向右缓慢滑动的过程中,该电路的总电阻不变,但与电容器并联部分的电阻减少,即电容器两端的电压减少,根据C=可知,电容器极板电量减少,即放电,故A错误,B正确.CD、以上分析可知,电容器放电,且电容器右极板与电源负极相连,所以自由电子从a移动到b,电流的方向与电子的方向相反,故流过电流计G的电流方向为b→G→a,故C错误,D正确.故选:BD.。
高中物理:含电容器电路的分析方法

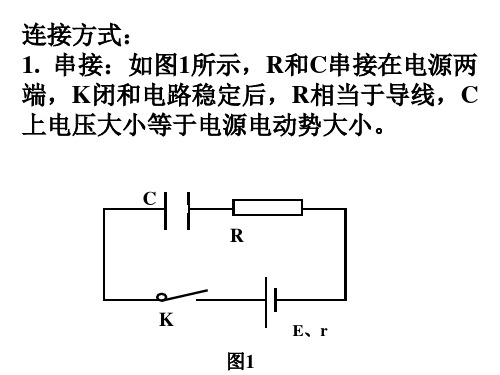
高中物理:含电容器电路的分析方法一、电容器在电路中的连接方式1、串接:如图1所示,R和C串接在电源两端,K闭合,电路稳定后,R相当于导线,C上的电压大小等于电源电动势大小.2、并接:如图2所示,R和C并接,C上电压永远等于R上的电压.3、跨接:如图3所示,K闭合,电路稳定后,两支路中有恒定电流,电容器两极板间电压等于跨接的两点间的电势差,即二、静态分析稳定状态下,电容器在直流电路中起阻断电流作用,电容器两极间存在电势差,电容器容纳一定的电量,并满足Q=CU.三、动态分析当直流电路中的电流和电势分布发生变化影响到电容器支路两端时,电容器的带电量将随之改变(在耐压范围内),即电容器发生充、放电现象,并满足△O=C△U.例1、如图4电路中电源E=12V,r=1Ω,定值电阻R1=3Ω,R2=2Ω,R3=5Ω,C1=4μF,C2=1μF,当电路闭合且稳定后各电容器的带电量为多少?当K断开时,通过R1、R2的电量各为多少?解析:静态分析:R3相当于导线,C2与R1、R2串联起来的部分并联,C1和R2并联.,且C1的下极板,C2的右极板带正电.动态分析:断开K后,C1通过R3、R2放电,C2通过R3、R2和R1放电,最后电压都为0,电容上电量也都为0.故通过R2的电量为Q=Q1+Q2=2.6x10-5C,通过R1的电量为Q2=.例2、如图5所示的电路中,电源电动势为E,内阻不计,电容器的电容为C,R2=R3=R4=R5=R,R1为滑动变阻器,其阻值可在0~2R 范围内变化,则当滑动头从最左端向最右端滑动的过程中,通过R5的电量是多少?解析:动态分析:本题电容器的接法为跨接,且电阻R1连续变化,C上电压为连续变化,不妨设电源负极为零电势点.则有当P置于R1的最左端时当P置于R1中间某位置时当P置于R1的最右端时当滑动头P从最左端向最右端滑动的过程中,电容器上下极板电势差改变为则通过R5的电量。
含电容器电路的分析与计算方法

含电容器电路的剖析与计算方法1、电路稳固后,因为电容器所在支路无电流经过,因此在此支路中的电阻上无电压降,因此电容器两极板间的电压就等于该支路两头的电压。
2、当电容器和电阻并联接入电路时,电容器两极板间的电压与其并联电阻两头的电压相等。
3、电路的电流、电压变化时,将会惹起电容器的充(放)电。
假如电容器两头的电压高升,电容器将充电,反之则放电。
1、如下图,电源两头电压为U=10 V保持不变, R1=Ω, R2=Ω, C= C=30μF.先闭合开关S,待电路稳固后,再将S 断1 2开,则 S 断开后,经过R1的电荷量为( )A.× 10 - 4 CB.× 10 - 4 CC.× 10 - 4 CD.× 10 - 4 C2、如图 16 所示,两个同样的平行板电容器C1、 C2用导线相连,开始都不带电.现将开关S 闭合给两个电容器充电,待充电均衡后,电容器C1两板间有一带电微粒恰巧处于均衡状态.再将开关S 断开,把电容器C2两板稍错开一些( 两板间距离保持不变) ,从头均衡后,以下判断正确的选项是A.电容器C1两板间电压减小B.电容器C2两板间电压增大C.带电微粒将加快上涨D.电容器C1所带电荷量增大3、在如下图,c1=6μ F,c2=3 μ F,R1=3Ω ,R2=6Ω,电源电动势E=18V,内阻不计,以下说法正确的选项是:A. 开关 s 断开时, a、 b 两点电势相等B. 开关 s 闭合后, a, b 两点间的电流时2AC.开关 s 断开时 C1带的电荷量比开关s 闭合后 C1 带的电荷量大D.无论开关s 断开仍是闭合,C1 带的电荷量总比C2 带的电荷量大。
原创1:含容电路的分析与计算

由欧姆定律得通过R1的电流
E
10
I
A 1A
R1 R2 4 6
(2)S断开前,C两端电压U1=IR2=6 V C所带电量Q1=CU1=30×10-6×6 C=1.8×10-4 C 开关S断开稳定后,总电流为零, 电容器两端电压为E, 所带电量Q2=CE=30×10-6×10 C=3×10-4 C 通过R1的电量,即为电容器增加的电量 ΔQ=Q2-Q1=1.2×10-4 C. 答案:(1)1 A (2)1.2×10-4 C 规律总结:处于稳定状态时,电容器相当于断路,与之串联的电阻不
例1.如图所示,电路中E=10 V,R1=4 Ω,R2=6 Ω,C=30 μF.电 池内阻可忽略. (1)闭合开关S,求稳定后通过R1的电流. (2)然后将开关S断开,求这以后通过R1的总电量.
解析:(1)电路稳定后,电容器所在的支路上无电流通过,
因此R1与R2串联,C两端的电压即为R2两端的电压.
R0为定值电阻,R1、R2为可调电阻,用绝缘细线 将质量为m、带正电的小球悬于电容器内部.闭合 电键S,小球静止时受到悬线的拉力为F,下列关 于F的大小变化的判断正确的是( ) A.保持R2不变,缓慢增大R1时,F将变大 B.保持R1不变,缓慢增大R2时,F将变小 C.保持R1、R2不变,减小平行板MN的间距,F将变大 D.保持R1、R2不变,减小平行板MN的间距,F将变小
·R2=3 V.
Q=CU2=12×10-6 C,且a板带正电,b板带负电.
SQ闭′=合C,U1C=两7端.2×电1压0-即6 RC1.两且端a电板压带,负由电电,路b分板析带:正U电1=.R1
R1 R2
·r
E R外
·R外=1.8 V.
据此通过电流表电量ΔQ=Q+Q′=1.92×10-5 C. 答案:1.92×10-5 C
含电容器直流电路的分析与计算问题

【 应用拓展】 如 图 3所 示 , 电源 电 动 势 E 一6 . 0 0 V, 内阻 忽 略 不 计 。电 阻 R 1 =2 . 4 KD, R 2 =4 . 8 K1 2 , 电容 器 C - -4 . 7 F 。 闭合 开 关 S , 待 电流稳定后 , 用 电压 表 测 R1 两端 电压 , 其 稳 定值为 1 . 5 0 V, ( 1 ) 该 电压 表 的 内阻 为 多 大 ? ( 2 ) 由于 电压 表 的 接 入 , 电容 器 所带 电荷 量 变 化 了多 少 ?
3 . 2 V,
故 电 容器 电 荷 量 Q— C U c: 3 0X 1 0 ×3 . 2 =9 . 6×
1 O一 C
( 3 ) 断开电源 , R - 与R z 并联 , 与R a 、 C构成 放 电 回路 , 故
通过 R 的 电荷 量 Q。 = =
‘
=4 . 8 ×1 0 一 s c
路, 然后 利 用 欧姆 定 律 及 串联 的 特 点 建 立 方程 。 学生 的 问 题 大 多 不是 出在 电路 分 析 阶段 , 而 是 建 立 方程 阶 段 。 关键词 : 含 电容 器 , 直 流 电路 ; 分析 , 计 算
中 图分 类 号 : G6 3 3 . 7 文献标识码 : E 文章 编 号 : 1 0 0 6 —5 9 6 2 ( 2 0 1 3 ) O 1 一O 1 9 4 一O 1
考试
EXAM l N题
赵 建 刚 王均 英
( 山东 省莱 阳 市第 一 中学 山东 莱 阳 2 6 5 2 0 0 )
摘要 : 初 次接 触 电路 问 题 的 中学 生在 利 用 欧姆 定 律 和 串、 并 联 电路 的特 点进 行 定 性 分 析 和 定 量 计 算 时 , 往 往 觉得 很 ” 繁” 、 很” 乱” 、 很” 难” 。其 实 , 解 决 电路 问题 的 关键 在 于 掌握 思 路 和 方 法 : 一 般 是 先 对 电路 进 行 变 形 、 整 理, 组 成 简单的 串、 并联 电
含电容器电路的分析与计算

含电容器电路的分析与计算电容器是一种重要的电子元件,广泛应用于电路中。
在电容器电路的分析与计算中,我们需要了解电容器的基本原理、参数和特性,以及如何计算电容器电路中的电压、电流和时间常数等。
首先,电容器是一种能够储存电荷的电子元件,由两个导体板和介质组成。
常用的电容器有金属箔电容器、陶瓷电容器和电解电容器等,其容值单位是法拉(F)。
电容器的容量取决于其两个导体板之间的面积、板间的距离和介质的电容常数。
在电容器电路中,电容器的两个导体板分别连接到电路的两个节点,形成一个开回路。
当电容器充电时,电容器两个板之间的电荷会积累,并且在两个板之间形成一个电势差。
根据库仑定律,电容器的电压与其所储存的电荷量成正比。
电容器的电压-电荷关系可以表示为V=Q/C,其中V 是电容器的电压,Q是电容器所储存的电荷量,C是电容器的容值。
在电容器电路中,常用于分析和计算的是RC电路和RLC电路。
1.RC电路:RC电路由电阻和电容器组成,常用于滤波和积分电路。
在RC电路中,电容器会充电和放电,形成一个充放电过程。
当电容器充电时,电流通过电阻,电压逐渐上升。
当电容器放电时,电流从电容器流向电阻,电压逐渐下降。
在RC电路中,电容器的充放电过程遵循指数衰减的规律,其电压变化可以用指数函数来描述。
2.RLC电路:RLC电路由电感、电阻和电容器组成,常用于振荡、滤波和谐振电路。
在RLC电路中,电容器和电感可以形成共振回路,当外部输入信号频率等于回路共振频率时,电流最大。
RLC电路的分析和计算可利用电压-电流关系和频率响应等进行求解。
在电容器电路分析和计算时,我们可以通过以下步骤进行:1.确定电容器电路的拓扑结构:确定电容器的连接方式、电阻和电感的位置等。
2.建立电容器电路的数学模型:通过电压和电流的关系、电容器的电压-电荷关系等,建立电容器电路的数学方程。
3.求解电容器电路的初始条件:根据电路的初始状态,确定初始电荷量、电压和电流。
含容电路的分析与计算

D.不论开关 S 断开还是闭合,C1 带的电荷量总比 C2 带的电荷量 大
3、含容电路上的电阻
稳定时,与电容器串联的定 值电阻对电路有没有影响?
第二章 恒定电流
含容电路的分析与计算
稳定时,电容器中有“电流”流过吗?
Hale Waihona Puke R1 E,r CR3 R2 bP a
一、含容电路处理方法
1、含容电路的简化
直流电路中,稳定后电容器可视为断路,简化
电路时可先去掉.
R1 E,r C
R2 bP a
如图所示,R 是光敏电阻,当它受到的光照强度增大 时( )
考
向
互
动
探
究
A.灯泡 L 变暗
B.光敏电阻 R 上的电压增大
C.电压表 V 的读数减小
D.电容器 C 的带电荷量减小
2、含容电路的电压 电容器两端电压等于什么?
R1 E,r C
R2 bP a
2、电容器两端的电压:与其并联支路两端的电压相等 可将其当作一理想电压表
(多选)如图所示,C1=6 μF,C2=3 μF,R1=3 Ω,R2=6 Ω, 电源电动势 E=18 V,内阻不计.下列说法正确的是( )
A.增大R1
B.增大R4
C.减小R2
D.减小R3
R4
C2
C1
R2
R3
R1
E,r
3.如图所示的电路中,电源电动势E=3V,内阻忽略不
计,R1=5Ω, R2=4Ω, C=50μF ,先闭后开关S,当电 路稳定后,断开开关,求开关断开后流过电阻R1的电 量?
新授课——含电容器的电路分析
Q Q1 Q2 2.6 10 C
5
Q2 1.0 10 C
5
例 2 . 如 图 5 所 示 的 电 路 中 , 电 源 电 动 势 为 E, 内阻不计,电容器的电容为C,R1为滑动变阻器, R2 R3 R4 R5 R , 其阻值可在0—2R范围内变化, 则当滑动头从最左端向右端滑动的过程中,通过 R5的电量是多少?
E I 2A R1 R2 r
U C1 IR2 4V
U C 2 I ( R1 R2 ) 10V
Q1 C1U C1 1.6 105 C
Q2 C2U C 2 1.0 10 C
5
且C1的下极板,C2的右极板带正电。
动态分析:断开 K 后, C1 通过 R3、R2 放电, C2 通 过 R3、R2 和 R1 放电,最后电压都为 0 ,电容上电 量也都为0。 故通过R2的电量为 通过R1的电量为
U U M U N
M
Nቤተ መጻሕፍቲ ባይዱ
图3
[典型例题] 1.静态分析:稳定状态下,电容器在直流电路 中起阻断电流作用,电容器两极间存在电势差, 电容器容纳一定的电量,并满足
Q CU
2.动态分析:当直流电路中的电流和电势分布 发生变化影响到电容器支路两端时,电容器的 带电量将随之改变(在耐压范围内),即电容 器发生充、放电现象,并满足
如图所示的电路中,电源的电动势恒定,要想 使灯泡变暗,可以 (A)增大R1 (B)减小R1 (C)增大R2 (D)减小R2
(1997年全国)
图示的电路图中, C2=2C1,R2=2R1 下列说法正确的是 ( ) ①开关处于断开状态,电容C2的电量大于C1的电量 ②开关处于断开状态,电容C1的电量大于C2的电量
含容电路分析计算技巧和实例

含容电路分析计算技巧和实例电容器是一个储存电能的元件.在直流电路中,当电容器充放电时,电路里有充放电电流,一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电的情况)的元件,在电容器处电路看作是断路,简化电路时可去掉它。
简化后若要求电容器所带电荷量时,可在相应的位置补上。
分析和计算含有电容器的直流电路时,需注意以下几点:(1)电路稳定后,由于电容器所在支路无电流通过.所以在此支路中的电阻上无电压降,因此电容器两极间的电压就等于该支路两端的电压.(2)当电容器和用电器并联后接入电路时,电容器两极间的电压与其并联用电器两端的电压相等.(3)电路的电流、电压变化时,将会引起电容器的充(放)电.如果电容器两端电压升高,电容器将充电,如果电压降低,电容器将通过与它并联的电路放电.电容器两根引线上的电流方向总是相同的,所以要根据正极板电荷变化情况来判断电流方向。
⑷如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始末状态电容器电荷量的差;如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始末状态电容器电荷量之和。
含有电容器的电路解题方法(1)先将含电容器的支路去掉(包括与它串在同一支路上的电阻),计算各部分的电流、电压值。
(2)电容器两极扳的电压,等于它所在支路两端点的电压。
(3)通过电容器的电压和电容可求出电容器充电电量。
(4)通过电容器的电压和平行板间距离可求出两扳间电场强度,再分析电场中带电粒子的运动。
例1:如图所示的电路,水平放置的平行板电容器中有一个带电液滴正好处于静止状态,现将滑动变阻器的滑片P向左移动,则()A.电容器中的电场强度将增大B.电容器上的电荷量将减少C.电容器的电容将减小D.液滴将向上运动由题意可知,电容器与R2并联,根据闭合电路欧姆定律可确定随着滑片左移,电阻的变化,导致电压的变化,从而判定电阻R2的电压变化,再根据可得,电容器的电量及由E=知两极间的电场强度如何变化.【解析】A、电容器两板间电压等于R2两端电压.当滑片P向左移动时,R2两端电压U 减小,由E=知电容器中场强变小,A错误;B、根据可得,电容器放电,电荷量减少,B项正确;C、电容器的电容与U的变化无关,保持不变,C项错误.D、带电液滴所受电场力变小,使液滴向下运动,D项错误;故选:B例2:在如图所示的电路中,电源两端A、B 间的电压恒定不变,开始时S断开,电容器上充有电荷.闭合S后,以下判断正确的是()A.C1所带电量增大,C2所带电量减小B.C1所带电量减小,C2所带电量增大C.C1、C2所带电量均减小D.C1、C2所带电量均增大S断开时,外电路中没有电流,两电容器的电压都等于电源的电动势,S闭合后,两电容器的电压都小于电源的电动势,根据Q=CU分析电容器电量的变化.【解析】S断开时,外电路中没有电流,两电容器的电压都等于电源的电动势.S闭合后,两电阻串联,电容器C1的电压等于R1的电压,电容器C2的电压等于R2的电压,可知两电容器的电压都小于电源的电动势,根据Q=CU分析可知两电容器电量均减小.故C正确,ABD错误.故选C例3:如图所示的电路中,R1、R2、R3是固定电阻,R4是光敏电阻,其阻值随光照的强度增强而减小.当开关S闭合且没有光照射时,电容器C不带电.当用强光照射R4且电路稳定时,则与无光照射时比较()A.电容器C的上极板带正电B.电容器C的下极板带正电C.通过R4的电流变小,电源的路端电压增大D.通过R4的电流变大,电源提供的总功率变小电容在电路稳定时可看作开路,故由图可知,R1、R2串联后与R3、R4并联,当有光照射时,光敏电阻的阻值减小,由闭合电路欧姆定律可得出电路中总电流的变化及路端电压的变化,再分析外电路即可得出C两端电势的变化,从而得出电容器极板带电情况;同理也可得出各电阻上电流的变化.【解析】因有光照射时,光敏电阻的阻值减小,故总电阻减小;由闭合电路的欧姆定律可知,干路电路中电流增大,由E=U+Ir可知路端电压减小;R1与R2支路中电阻不变,故该支路中的电流减小;则由并联电路的电流规律可知,另一支路中电流增大,即通过R2的电流减小,而通过R4的电流增大,故C、D错误;当没有光照时,C不带电说明C所接两点电势相等,以电源正极为参考点,R1上的分压减小,而R3上的分压增大,故上极板所接处的电势低于下极板的电势,故下极板带正电;故A错误,B正确;故选B.例4:如图所示的电路中,两平行金属板A、B水平放置,极板长L=80cm,两板间的距离d=40cm.电源电动势E=40V,内电阻r=1Ω,电阻R=15Ω,闭合开关S,待电路稳定后,将一带负电的小球从B板左端且非常靠近B板的位置以初速度v=4m/s水平向右射入两板高效课堂—实验微专题间,该小球可视为质点.若小球带电量q=1×10-2C,质量为m=2×10-2kg,不考虑空气阻力,电路中电压表、电流表均是理想电表.若小球恰好从A板右边缘射出(g取10m/s2).求:(1)滑动变阻器接入电路的阻值为多少?(2)此时电流表、电压表的示数分别为多少?(3)此时电源的输出功率是多少?(1)小球进入电场中做类平抛运动,小球恰好从A板右边缘射出时,水平位移为L,竖直位移为d,根据运动学和牛顿第二定律结合可求出板间电压,再根据串联电路分压特点,求解滑动变阻器接入电路的阻值.(2)根据闭合电路欧姆定律求解电路中电流,由欧姆定律求解路端电压,即可求得两电表的读数.(3)电源的输出功率P=UI,U是路端电压,I是总电流.【解析】(1)小球进入电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速运动,则有:水平方向:L=vt竖直方向:d=由上两式得:a===20m/s2又根据牛顿第二定律得:a=联立得:U==V=24V根据串联电路的特点有:=代入得:=解得,滑动变阻器接入电路的阻值为R′=24Ω(2)根据闭合电路欧姆定律得电流表的示数为:I==A=1A电压表的示数为:U=E-Ir=(40-1×1)V=39V(3)此时电源的输出功率是P=UI=39×1W=39W.答:(1)滑动变阻器接入电路的阻值为24Ω.(2)此时电流表、电压表的示数分别为1A和39V.(3)此时电源的输出功率是39W.每日一练解析C为板间距离固定的电容器,电路连接如图所示,当滑动触头P向右缓慢滑动的过程中,下列说法中正确的是()A.电容器C充电B.电容器C放电C.流过电流计G的电流方向为a→G→bD.流过电流计G的电流方向为b→G→a首先明确含电容器的支路等效为断路,且两端的电压为并联部分的电压相等;当滑动触头P向右缓慢滑动的过程中,该电路的总电阻不变,但与电容器并联部分的电阻减少,即电容器两端的电压减少,根据C=可知,电容器极板电量减少,即放电;电容器右极板与电源负极相连,所以自由电子从a移动到b,故流过电流计G的电流方向为b→G→a.【解析】AB、含电容器的支路等效为断路,且两端的电压为并联部分的电压相等;当滑动触头P向右缓慢滑动的过程中,该电路的总电阻不变,但与电容器并联部分的电阻减少,即电容器两端的电压减少,根据C=可知,电容器极板电量减少,即放电,故A错误,B正确.CD、以上分析可知,电容器放电,且电容器右极板与电源负极相连,所以自由电子从a移动到b,电流的方向与电子的方向相反,故流过电流计G的电流方向为b→G→a,故C错误,D正确.。
电磁感应与含电容器电路的综合分析

电磁感应与含电容器电路的综合分析
如图所示,图中M、N分别表示相距L的两根光滑而平 直的金属导轨 ,ab 是电阻为 Ro 的金属棒 , 此棒可紧贴平行 导轨滑动 . 相距为 d水平放置的金属板 A 、 C 与导轨相连 (d 较小 ,A 、C 两板的面积较大 ) 定值电阻阻值为 R, 其它电阻 忽略不计.整个装置处于垂直纸面向里,磁感应强度为B的 匀强磁场中 . 当 ab以某一速率向右运动时 , 一带电微粒恰 好也在 A、 C 两极间做半径为 r 的匀速圆周运动 , 圆周运动 的速率与 ab 向右运动的速率相同 . 求在此情况下 ,ab 向右 a 的力的大小? M电磁感应与含电容器电 Nhomakorabea的综合分析
如图所示 , 一定滑轮由四根长度均为 L, 电阻均为 R 的 相互垂直的辐条支撑着无电阻导体轮缘,滑轮被直置于磁 感应强度为B的匀强磁场中.在滑轮边缘绕着很长的(许多 匝)细线,线下悬挂着质量为m的砝码,右侧电路 (R1=R/4,R2=R, 电容器电容为 C) 通过电刷与滑轮中心和轮 缘相接触 . 现将砝码无初速释放 ,且 S处于闭合状态 ,不计 其它电阻及一切摩擦.求: (1)当砝码下落速度稳定时,流过R2的电流大小和方向 (2)当断开S后,流过R2的电量
4 2 Q BL C 3 4 Q BL2C 9
a c b C o
电磁感应与含电容器电路的综合分析
如图所示,平行导轨置于磁感应强度为B的匀强磁 场中(方向向里),间距为 L,左端电阻为 R,其 余电阻不计,导轨右端接一电容为C的电容器。现 有一长2L的金属棒ab放在导轨上,ab以a为轴顺时 针转过90°的过程中,通过R的电量为多少?
电磁感应与含电容器电路的综合分析 如图所示,线圈面积S=1X10-6m2,匝数N=100,两 端点连接一电容器,其电容C=20μF.线圈中磁场的 磁感应强度按ΔB/Δt=0.1T/s增加,磁场方向垂直 线圈平面向里 ,那么电容器所带电荷量为多少 ?电 容器的极板a带什么种类的电荷?
(完整版)含电容器电路的归类分析.docx

含电容器电路的归类分析山东潍坊寒亭一中 张启光 李瑞芳(邮编 261100)电容器是一个储能元件, 在直流电路中, 当电路稳定后, 电容器相当于一个阻值无限大 的元件,含有电容器的支路看作断路,关于电路中电容器的考查常见以下几方面:一、考查电容器所带电荷量例 1如图 1 所示电路中, 已知电容器的电容C=2F ,电源电动势 E=12V ,内阻不计,R 1 : R 2 : R 3 : R 4 =1:2:6:3 ,则 S 闭合时电容器 a 板所带电荷量为 ()A .- 8×106CB . 4× 10 6C1a2RRC .-4×10 6CD . 8×10 6 CR 3b R 4解析 :电源内阻不计则路端电压为12V ,电路稳定后电容器相当于断路,由串联正比分压有U 1 R 11 ,则U 2=8V ,同理SU 2 R 2 2图 1U 3 R 3 2,则U 4 =4V ,取电源的负极电势为零,则a 板电势为 8V ,b 板电势为 4V ,U 4R 41故电容器两极板间电势差U = 4V , a 板带正电荷 qCU =8×10 6C ,正确答案为D .二、考查电路变化后流过用电器的电荷量例 2如图 2 所示电路中 R 1= R 2= R 3 =8,电容器电容 C=5F ,1R 3电源电动势 E=6V ,内阻不计, 求电键 S 由稳定的闭合状态断开后流过R 3 的Ra b电荷量.解析 :电键闭合时电路结构为R 1 和 R 2 串联后与 R 3 并联,电容器并在R 2SR 2 两端,电源内阻不计,由串联正比分压得U 2 = 3V , b 板带正电,电荷量Q =CU = 15× 10 6R和 R 串联,电容器通过图 2C ;电键断开后电路结构为122R 并在 R 两端,则电容器两端电压为U 1 = 3V ,b 板带负电,电荷量 QCU 1=15×106 C ,31所以电键断开后电容器通过 R 3 先放电后反向充电, 流过 R 3 的电荷量为两情况下电容器所带电荷量之和 Q Q Q = 3× 10-5C .注意 :求电路变化后流过用电器的电荷量的问题, 一定要注意同一极板上所带电荷的电性是否变化, 不变则流过用电器的电荷量为初、 末状态电容器所带电荷量之差, 变化则为二者之和.三、以电容器为背景考查力电综合问题例 3如图 3 所示, R 1 = R 2 = R 3 = R 4 = R ,电键 S 闭合时, 间距为 d 的平行板电容器C 的正中间有一质量为m 、电荷量为 q 的小球恰好处于静止状态;R 1R 2电键 S 断开时,小球向电容器的一个极板运动并发生碰撞,碰后小R 3S·球带上与极板同性质的电荷.设碰撞过程中没有机械能的损失,小4R球反弹后恰好能运动到电容器的另一极板,不计电源内阻,求电源的电动势和碰后小球所带的电荷量.图 3解析 :电键 S 闭合时 R 1 、 R 3 并联后与 R 4 串联( R 2 中没有电流通过) ,电容器并在 R 42E ,对带电小球有 mg U C,解得 E3mgd上,U C = U 4 =q.电键 S 断开时, 仅 R 1 、3d2qR 4 串联,电容器仍并在R 4上,U CE,故小球向下运动,设小球与下极板碰撞后带电荷2量 为 q ,从小球开始运动到小球恰好运动到上极板的全过程由动能定理得mgdqU Cq U C =0,综合解得 q7q 22.6点评 :分析和计算含有电容器的直流电路问题, 关键是准确地判断和求出电容器两端的电压,具体方法是:( 1)明确电路结构,确定电容器和哪部分电路并联,该电路两端电压就是电容器两端电压.(2)当电容器与某一电阻串联后接入电路时,此支路中没有电流,所以与电容器串联的电阻看成导线,电路两端的电压就是电容器两极板间电压.(3)对于较复杂电路,需要将电容器两端的电势与基准点的电势比较后才能确定电容器两端的电压.。
含容电路的分析与计算

由两个相互靠近的导体组成,能 够储存电能,具有“隔直通交” 的特性。
电容器作用与特性
储存电能
01
电容器能够储存电能,其储存的电能与电容器的电容量和电压
的平方成正比。
隔直通交
02
电容器对直流电具有隔断作用,而对交流电则具有导通作用,
其导通程度取决于电容器的电容量和交流电的频率。
充放电过程
03
电容器在充电过程中储存电能,而在放电过程中释放电能。
电容器将电场能释放,转换为其他形式的能量(如热能、机械能等)。
效率计算方法及优化措施
效率定义
计算方法
选择高性能元器件
优化电路设计
控制策略优化
在含容电路中,效率通 常定义为有用功率与输 入功率之比,用于衡量 能量转换的有效程度。
效率计算涉及对输入功 率、输出功率以及损耗 功率的测量与计算。通 常使用功率计或相关仪 表进行测量,并结合电 路参数进行分析。
报告范围
01
02
03
04
含容电路基本概念
介绍含容电路的定义、特点以 及常见类型等基本概念。
分析方法
详细介绍含容电路的分析方法 ,包括等效电路法、相量法、
复频域分析法等。
计算实例
通过具体的计算实例,展示含 容电路分析方法的实际应用和
计算过程。
结论与展望
总结报告的主要内容和成果, 并展望含容电路未来的发展趋
复杂含容电路稳态分析
含多个电容器的复杂电路 稳态分析
对于含有多个电容器的复杂电路,可以采用 节点电压法或网孔电流法进行分析。首先, 根据电路的连接方式确定各电容器之间的电 压或电流关系;然后,利用基尔霍夫定律建 立电路的方程组;最后,通过求解方程组得 到各电容器上的电压或电流值。
含容电路分析

(1)当 K 闭合时间足够长时, C1 和 C2 所带的电量各是多少?
(2)然后把 K 打开, K 打开后通过 R2 的电量是多少?
R1
C2
R2
C1
R3
U
K
小专题 含容电路的分析
1.电路简化 把电容器所在的支路视为断路,简化电路时可以去掉,求电荷量时再在 相应位置补上. 2.电容器的电压 (1)电容器所在的支路中没有电流,与之串联的电阻两端无电压,相当于 导线. (2)电容器两端的电压等于与之并联的电阻两端的电压.
3.电容器的电荷量及变化 (1)电路中电流、电压的变化可能会引起电容器的充、放电.若电容器两 端电压升高,电容器将充电;若电压降低,电容器将通过与它连接的电 路放电. (2)如果变化前后极板带电的电性相同,通过所连导线的电荷量为|Q1-Q2|; (3)如果变化前后极板带电的电性相反,通过所连导线的电荷量为Q1+Q2.
3.(含容电路的动态分析)(多选)(2020·福建师大附中期末)如图11所示,电源电动势为E,内阻为r.电路中的R2、R3 均为总阻值一定的滑动变阻器,R0为定值电阻,R1为光敏电阻(其电阻随光照强度增大而减小).当电键S闭合时, 电容器中一带电微粒恰好处于静止状态.有关下列说法中正确的是
√A.只逐渐增大R1的光照强度,电阻R0消耗的电功率变大,电 阻R3中有向上的电流
1.如图6所示,电路中R1、R2均为可变电阻,电源内阻不能忽略,平行 板电容器C的极板水平放置.闭合电键S,电路达到稳定时,带电油滴悬
浮在两板之间静止不动.如果仅改变下列某一条件,油滴仍能静止不动
的是
A.增大R1的阻值
√B.增大R2的阻值
C.增大两板间的距离
D.断开电键S
图6
含电容器电路的分析与计算201501

含电容器电路的分析与计算1、关键是准确地判断并求出电容器的两端的电压,其具体方法是:(1)确定电容器和哪个电阻并联,该电阻两端电压即为电容器两端电压.(2)当电容器和某一电阻串联后接在某一电路两端时,此电路两端电压即为电容器两端电压.(3)对于较复杂电路,需要将电容器两端的电势与基准点的电势比较后才能确定电容器两端的电压.2、分析和计算含有电容器的直流电路时,注意以下几个方面:(1)电路稳定时电容器在电路中就相当于一个阻值无限大的元件,在电容器处电路看做是断路,画等效电路时,可以先把它去掉.(2)若要求电容器所带电荷量时,可在相应的位置补上,求出电容器两端的电压,根据Q =CU计算.(3)电路稳定时电容器所在支路上电阻两端无电压,该电阻相当于导线.(4)当电容器与电阻并联后接入电路时,电容器两端的电压与并联电阻两端的电压相等.(5)电路中的电流、电压变化时,将会引起电容器的充放电,如果电容器两端的电压升高,电容器将充电,反之电容器放电.通过与电容器串联的电阻的电量等于电容器带电量的变化量.3、含电容器电路问题的分析方法(1)应用电路的有关规律分析出电容器两极板间的电压及其变化情况.(2)根据平行板电容器的相关知识进行分析求解.练习1.如图所示电路中,开关S闭合一段时间后,下列说法中正确的是A.将滑片N向右滑动时,电容器放电B.将滑片N向右滑动时,电容器继续充电C.将滑片M向上滑动时,电容器放电D.将滑片M向上滑动时,电容器继续充电2.如图所示,M、N是平行板电容器的两个极板,R0为定值电阻,R1、R2为可调电阻,用绝缘细线将质量为m、带正电的小球悬于电容器内部.闭合开关S,小球静止时受到悬线的拉力为F.调节R1、R2,关于F的大小判断正确的是A.保持R1不变,缓慢增大R2时,F将变大B.保持R1不变,缓慢增大R2时,F将变小C.保持R2不变,缓慢增大R1时,F将变大D.保持R2不变,缓慢增大R1时,F将变小3.如图所示,电源电动势为E,内阻为r,平行板电容器两金属板水平放置,开关S是闭合的,两板间一质量为m、电荷量为q的油滴恰好处于静止状态,G为灵敏电流计.则以下说法正确的是A.在将滑动变阻器滑片P向上移动的过程中,油滴向上加速运动,G 中有从b到a的电流B.在将滑动变阻器滑片P向下移动的过程中,油滴向下加速运动,G中有从b到a的电流C.在将滑动变阻器滑片P向上移动的过程中,油滴仍然静止,G中有从a到b的电流D.在将S断开后,油滴仍保持静止状态,G中无电流通过4.如图所示的电路中,电源电动势E=6 V,内阻r=1 Ω,电阻R1=6 Ω、R2=5 Ω、R3=3 Ω,电容器的电容C=2×10-5 F,若将开关S闭合,电路稳定时通过R2的电流为I;断开开关S后,通过R1的电荷量为q。
电容与电路的分析与计算

混合串联并联:复杂电路中,电容器可能既有串联又有并联
实际应用:根据电路需求选择合适的电容器联接方式
电容与电路的分析方法
04
基尔霍夫定律
基尔霍夫电流定律:在任意时刻,通过电路中任意节点的电流之和等于零
基尔霍夫电压定律:在任意时刻,沿电路中任意闭合路径的电压降之和等于零
基尔霍夫定律的应用:用于分析电路中的电流和电压关系,以及电路的稳定性和性能
基尔霍夫定律的局限性:只适用于线性电路,不适用于非线性电路和时变电路
叠加原理
叠加原理的优点:简化电路分析过程,提高计算效率
叠加原理的定义:将多个电源或电阻等元件组合在一起,使其效果等同于一个电源或电阻的效果
叠加原理的应用:在电路分析中,可以将复杂的电路分解为简单的电路,便于分析和计算
电容的大小与极板面积、极板间距和电介质的性质有关
电容的符号是C,单位是法拉(F)
电容在电路中起到滤波、耦合、谐振等作用
电容器的种类和特性
02
固定电容器
特点:容量固定,不易受温度、湿度等环境因素影响
结构:由两个相互绝缘的电极和夹在中间的电介质组成
材料:电极通常由金属、石墨、陶瓷等导电材料制成,电介质通常由塑料、橡胶、云母等绝缘材料制成
频率特性:电容器的电容量随频率变化的特性
温度特性:电容器的电容量随温度变化的特性
电容器的联接
03
电容器的串联
串联电容器的总电容等于各个电容器的电容值之和
串联电容器的等效电容等于各个电容器的电容值之和除以电容器的个数
串联电容器的电压分配与电容器的电容值成反比
串联电容器的电流分配与电容器的电容值成正比
叠加原理的局限性:只适用于线性电路,不适用于非线性电路
电容器典型习题及含容电路计算

在含容电路计算中,移相作用是电容器的基本特性之一,通过计算电容器容量和电压的变化, 可以推导出电路中电流和功率的变化规律。
移相作用的应用非常广泛,例如在电力系统中用于提高电力系统的稳定性,在电子设备中用于 实现信号处理和传输等功能。
电容器分类
按照结构分类:固定电容器、可变电容器、半可变电容器 按照介质分类:纸介电容器、油浸电容器、聚合物电容器、陶瓷电容器等 按照用途分类:滤波电容器、耦合电容器、旁路电容器、调谐电容器等 按照容量分类:小容量电容器、大容量电容器
电容器参数
耐压值:电容器能够承受的 最大电压
电容值:表示电容器容纳电 荷的能力
THANK YOU
汇报人:XX
并联:总电容等于各电容 倒数之和
串并联电路的分析方法: 利用串并联关系求解
注意事项:考虑电容器之 间的耦合和影响
含容电路的阻抗
定义:含容电路 的阻抗是指电路 中电容产生的电 抗,用符号Xc表 示。
计算公式: Xc=1/(2πfC), 其中f为交流电的 频率,C为电容 器的电容。
单位:含容电路 的阻抗的单位是 法拉(F),常用单 位还有微法拉 (μF)和皮法拉 (pF)。
电容器可以用于低通滤波器,阻止高频噪声的干扰,同时允许直流或低频信号通过。
在电源电路中,电容器可以起到平滑直流电压的作用,消除纹波,提高电源的稳定性。 电容器还可以用于有源滤波器通过与电阻、电感等元件的配合,实现特定频率范围的滤波功 能。
移相作用
电容器在电路中起到移相作用,通过改变电容器容量,可以改变电路中的相位差。
电容器典型习题解析
电容器串并联习题解析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
含电容器电路的分析与计算1、关键是准确地判断并求出电容器的两端的电压,其具体方法是:(1)确定电容器和哪个电阻并联,该电阻两端电压即为电容器两端电压.(2)当电容器和某一电阻串联后接在某一电路两端时,此电路两端电压即为电容器两端电压.(3)对于较复杂电路,需要将电容器两端的电势与基准点的电势比较后才能确定电容器两端的电压.2、分析和计算含有电容器的直流电路时,注意以下几个方面:(1)电路稳定时电容器在电路中就相当于一个阻值无限大的元件,在电容器处电路看做是断路,画等效电路时,可以先把它去掉.(2)若要求电容器所带电荷量时,可在相应的位置补上,求出电容器两端的电压,根据Q =CU计算.(3)电路稳定时电容器所在支路上电阻两端无电压,该电阻相当于导线.(4)当电容器与电阻并联后接入电路时,电容器两端的电压与并联电阻两端的电压相等.(5)电路中的电流、电压变化时,将会引起电容器的充放电,如果电容器两端的电压升高,电容器将充电,反之电容器放电.通过与电容器串联的电阻的电量等于电容器带电量的变化量.3、含电容器电路问题的分析方法(1)应用电路的有关规律分析出电容器两极板间的电压及其变化情况.(2)根据平行板电容器的相关知识进行分析求解.练习1.如图所示电路中,开关S闭合一段时间后,下列说法中正确的是A.将滑片N向右滑动时,电容器放电B.将滑片N向右滑动时,电容器继续充电C.将滑片M向上滑动时,电容器放电D.将滑片M向上滑动时,电容器继续充电2.如图所示,M、N是平行板电容器的两个极板,R0为定值电阻,R1、R2为可调电阻,用绝缘细线将质量为m、带正电的小球悬于电容器内部.闭合开关S,小球静止时受到悬线的拉力为F.调节R1、R2,关于F的大小判断正确的是A.保持R1不变,缓慢增大R2时,F将变大B.保持R1不变,缓慢增大R2时,F将变小C.保持R2不变,缓慢增大R1时,F将变大D.保持R2不变,缓慢增大R1时,F将变小3.如图所示,电源电动势为E,内阻为r,平行板电容器两金属板水平放置,开关S是闭合的,两板间一质量为m、电荷量为q的油滴恰好处于静止状态,G为灵敏电流计.则以下说法正确的是A.在将滑动变阻器滑片P向上移动的过程中,油滴向上加速运动,G 中有从b到a的电流B.在将滑动变阻器滑片P向下移动的过程中,油滴向下加速运动,G中有从b到a的电流C.在将滑动变阻器滑片P向上移动的过程中,油滴仍然静止,G中有从a到b的电流D.在将S断开后,油滴仍保持静止状态,G中无电流通过4.如图所示的电路中,电源电动势E=6 V,内阻r=1 Ω,电阻R1=6 Ω、R2=5 Ω、R3=3 Ω,电容器的电容C=2×10-5 F,若将开关S闭合,电路稳定时通过R2的电流为I;断开开关S后,通过R1的电荷量为q。
则A.I=0.75 A B.I=0.5 AC.q=2×10-5 C D.q=1×10-5 C5.在如图电路中,开关S1、S2、S3、S4均闭合,C是极板水平放置的平行板电容器,板悬浮着一油滴P,断开哪一个开关后P会向下运动A.S1B.S2C.S3D.S46.如图所示的电路中,电源的电动势恒定,要想使灯泡变暗,可以A.增大R1B.减小R1C.增大R2D.减小R27.一平行板电容器C,极板是水平放置的,它和三个可变电阻及电源联接成如图所示的电路.今有一质量为m的带电油滴悬浮在两极板之间静止不动.要使油滴上升,可采用的办法是A.增大R1 B.增大R2C.增大R3 D.减小R28.如图所示的电路,已知电池电动势E=90 V,内阻r=5 Ω,R1=10 Ω,R2=20 Ω,板面水平放置的平行板电容器的两极板M、N相距d=3 cm,在两板间的正中央有一带电液滴,其电荷量q=-2×10-7 C,其质量m=4.5×10-5kg,取g=10 m/s2,问(1)若液滴恰好能静止平衡时,滑动变阻器R的滑动头C正好在正中点,那么滑动变阻器的最大阻值R m是多大?(2)将滑动片C迅速滑到A端后,液滴将向哪个极板做什么运动?到达极板时的速度是多大?9.如图所示的电路中,4个电阻的阻值均为R,E为直流电源,其内阻可以不计,没有标明哪一极是正极.平行板电容器两极板间的距离为d。
在平行极板电容器的两个平行极板之间有一个质量为m,电荷量为q的带电小球。
当开关K闭合时,带电小球静止在两极板间的中点O上.现把开关打开,带电小球便往平行极板电容器的某个极板运动,并与此极板碰撞,设在碰撞时没有机械能损失,但带电小球的电荷量发生变化,碰后小球带有与该极板相同性质的电荷,而且所带的电荷量恰好刚能使它运动到平行极板电容器的另一极板.求小球与电容器某个极板碰撞后所带的电荷量。
10.如图所示.两根相距为L 的竖直金属导轨MN 和PQ 的上端接有一个电容为C 的电容器,质量为m 的金属棒ab 可紧贴竖直导轨无摩擦滑动,且滑动中ab 始终保持水平,整个装置处于磁感应强度为B 的磁场中,不计电阻,求最后通过C 的充电电流.11.图所示,金属棒ab 质量m =5 g ,放在相距L =1 m 的光滑金属导轨MN 、PQ 上,磁感应强度B =0.5 T ,方向竖直向上,电容器的电容C =2μF ,电源电动势E =16 V ,导轨距地面高度h =0.8 m.当单刀双掷开关先掷向1后,再掷向2,金属棒被抛到水平距离s =6.4 cm 的地面上,问电容器两端的电压还有多大?12.如图1,若轨道左端接一电容器,电容器的电容为C ,导体棒在水平拉力的作用下从静止开始向右运动。
电容器两极板电势差随时间变化的图象如图2所示,已知t 1时刻电容器两极板间的电势差为U 1。
求导体棒运动过程中受到的水平拉力大小。
tUt O图2UBM Pb a图1C含电容器电路的分析与计算练习参考答案8.(1)滑片C 在AB 中央时,对带电液滴由平衡条件得mg =qdU MN所以UMN =q mgd =7241021031045---⨯⨯⨯⨯ V =67.5(V ) 由题意知U MN =UBC =67.5 V 由欧姆定律得21mR R r E ++=UBC即21590mR +2m R ⨯=67.5 所以R m =90 Ω (2)滑片滑到A 时UMN ′=m 1m R R r ER ++15909090+⨯V =77V >67.5 V所以液滴向M 板运动,设达M 板时速度为v 由动能定理得q ·mg U MN -'2·2d =21mv 2所以v =0.2 m/s9.由电路图可以看出,因R 4支路上无电流,电容器两极板间电压,无论K 是否闭合始终等于电阻R 3上的电压U 3,当K 闭合时,设此两极板间电压为U ,电源的电动势为E ,由分压关系可得U =U 3=32E ①小球处于静止,由平衡条件得dqU=mg②当K 断开,由R 1和R 3串联可得电容两极板间电压U ′为U ′=2E ③由①③得U ′=43U ④U ′<U 表明K 断开后小球将向下极板运动,重力对小球做正功,电场力对小球做负功,表明小球所带电荷与下极板的极性相同,由功能关系mg2d -q 212='U mv 2-0⑤因小球与下极板碰撞时无机械能损失,设小球碰后电荷量变为q ′,由功能关系得 q ′U ′-mgd =0-21mv 2⑥联立上述各式解得 q ′=67q 即小球与下极板碰后电荷符号未变,电荷量变为原来的67.10.经分析知最终ab 棒做匀加速下滑,设最终充电电流为I ,在Δt 内电荷量、速率、电动势的变化量分别为ΔQ 、Δv 和ΔE则有I =t Q ∆∆=C ·t E∆∆=CBL ·t v ∆∆=CBLa 由牛顿第二定律有mg -BIL =ma 解得I =CL B m mgCBL22+11.电容器充电后电荷量为Q =CE .开关掷向位置2时,电容器通过ab 放电,其放电电荷量为ΔQ ,则通过棒中电流为I =tQ∆∆ 金属棒受安培力F =BIL =BL tQ∆∆①据F = m (v -0) /Δt② 由平抛运动可知v =s/hgsg h 22=③由式①、②、③得BLtQ∆∆·Δt =m sh g 2所以ΔQ =hg BL ms2=1.6×10-5C 电容器所余电荷量Q ′=Q -ΔQ =CE -ΔQ =1.6×10-5 C 所以电容器两端电压为U′=CQ '=8V12. 感应电动势与电容器两极板间的电势差相等U BLv =由电容器的U -t 图可知t t U U 11=导体棒的速度随时间变化的关系为t BLt U v 11=可知导体棒做匀加速直线运动,其加速度11BLt U a =由 U QC = tQ I = 则 11t CU t CU I ==由牛顿第二定律ma BIL F =-可得1111BLt mU t BLCU F +=。
