离散数学期末考试试题及答案
离散数学期末考试题及详细答案

离散数学期末考试题及详细答案一、选择题(每题5分,共20分)1. 在离散数学中,下列哪个概念用来描述元素与集合之间的关系?A. 并集B. 交集C. 子集D. 元素答案:D2. 布尔代数中,下列哪个运算符表示逻辑“与”?A. ∨B. ∧C. ¬D. →答案:B3. 下列哪个命题的否定是正确的?A. 如果今天是周一,则明天是周二。
B. 如果今天是周一,则明天不是周二。
答案:B4. 在图论中,一个图的顶点数为n,边数为m,下列哪个条件可以保证该图是连通的?A. m > nB. m ≥ nC. m = nD. m > n-1答案:D二、填空题(每题5分,共20分)1. 在集合论中,一个集合的幂集包含该集合的所有______。
答案:子集2. 如果一个函数f: A → B是单射的,那么对于任意的a1, a2 ∈ A,如果a1 ≠ a2,则f(a1) ≠ f(a2)。
这种性质称为函数的______。
答案:单射性3. 在图论中,一个图的直径是指图中任意两个顶点之间的最短路径的最大值。
如果一个图的直径为1,则该图被称为______。
答案:完全图4. 一个布尔表达式可以表示为一系列逻辑运算符和变量的组合。
布尔表达式(A ∧ B) ∨ (¬ A ∧ C)的真值表中,当A为真,B为假,C为真时,整个表达式的值为______。
答案:真三、简答题(每题10分,共30分)1. 请简述什么是图的哈密顿回路,并给出一个例子。
答案:哈密顿回路是图中的一个回路,它恰好访问每个顶点一次。
例如,在一个完全图中,任意一个顶点出发,依次访问其他顶点,最后回到出发点的路径就是一个哈密顿回路。
2. 请解释什么是二元关系,并给出一个二元关系的例子。
答案:二元关系是定义在两个集合上的一个关系,它关联了第一个集合中的元素和第二个集合中的元素。
例如,小于关系是实数集合上的一个二元关系,它关联了每一对实数,如果第一个数小于第二个数。
离散数学期末试题及答案完整版

离散数学期末试题及答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】326《离散数学》期末考试题(B )一、填空题(每小题3分,共15分)1.设,,},,{{b a b a A =?},则-A ? = ( ),-A {?} = ( ),)(A P 中的元素个数=|)(|A P ( ).2.设集合A 中有3个元素,则A 上的二元关系有( )个,其中有( )个是A 到A 的函数.3.谓词公式))()(())()((y P y Q y x Q x P x ⌝∧∃∧→∀中量词x ∀的辖域为( ), 量词y ∃的辖域为( ).4.设}24,12,8,6,4,3,2,1{24=D ,对于其上的整除关系“|”,元素( )不存在补元.5.当n ( )时,n 阶完全无向图n K 是平面图,当当n 为( )时,n K 是欧拉图. 二.1. 若n B m A ==||,||,则=⨯||B A ( ),A 到B 的2元关系共有( )个,A 上的2元关系共有( )个.2. 设A = {1, 2, 3}, f = {(1,1), (2,1), (3, 1)}, g = {(1, 1), (2, 3), (3, 2)}和h = {(1, 3), (2, 1), (3, 1)},则( )是单射,( )是满射,( )是双射.3. 下列5个命题公式中,是永真式的有( )(选择正确答案的番号). (1)q q p p →→∧)(; (2))(q p p ∨→; (3))(q p p ∧→; (4)q q p p →∨∧⌝)(; (5)q q p →→)(.4. 设D 24是24的所有正因数组成的集合,“|”是其上的整除关系,则3的补元( ),4的补元( ),6的补元( ).5. 设G 是(7, 15)简单平面图,则G 一定是( )图,且其每个面恰由( )条边围成,G 的面数为( ).三.1.设}}{},,{{c b a A =,}}{},,{},{{c c b a B =,则)(=⋃B A ,)(=⋂B A ,)()(=A P .2.集合},,{c b a A =,其上可定义( )个封闭的1元运算,( )个封闭的2元运算,( )个封闭的3元运算.3.命题公式1)(↑∧q p 的对偶式为( ).4.所有6的因数组成的集合为( ).5.不同构的5阶根树有( )棵.四、(10分)设B A f →:且C B g →:,若g f 是单射,证明f 是单射,并举例说明g 不一定是单射.五、(15分)设},,,{d c b a A =,A 上的关系)},(),,(),,(),,(),,(),,(),,(),,(),,{(c d b d a d c c b c a c c a b a a a R =,1.画出R 的关系图R G .2.判断R 所具有的性质.3.求出R 的关系矩阵R M .六、(10分)利用真值表求命题公式))(())((p q r r q p A →→↔→→=的主析取范式和主合取范式.七、(10分) 边数30<m 的简单平面图G ,必存在节点v 使得4)deg(≤v . 八、(10分) 有六个数字,其中三个1,两个2,一个3,求能组成四位数的个数.《离散数学》期末考试题(B)参考答案一、1. {{a , b }, a , b , ?}, {{a , b }, a , b },16.2.92, 27.3.)()(x Q x P →, )()(y P y Q ⌝∧.4. 2, 4, 6, 12.5.4≤,奇数.二、1.22,2,m mn mn ., g , g . ,2,4.,不存在,不存在. 5.连通,3,10.三、1. }}{},,{},,{},{{c c b b a a B A =⋃,}}{{c B A =⋂,{)(=A P ?, {{a , b }}, {{c }}, {{a , b }, {c }}}.2.27933,3,3. 3.0)(↓∨q p .4.{-1,-2,-3,-6,1,2,3,6}. .四、证 对于任意A y x ∈,,若)()(y f x f =,则))(())((y f g x f g =,即))(())((y g f x g f =. 由于g f 是单射,因此y x =,于是f 是单射.例如取},,{},3,2,1(},,{γβα===C B b a A ,令)}2,(),1,{(b a f =,)},3(),,2(),,1{(ββα=g ,这时)},(),,{(βαb a g f = 是单射,而g 不是单射.五、解 1. R 的关系图R G 如下:2.(1)由于R b b ∉),(,所以R 不是自反的. (2)由于R a a ∈),(,所以R 不是反自反的.(3)因为R b d ∈),(,而R d b ∉),(,因此R 不是对称的. (4)因R a c c a ∈),(),,(,于是R 不是反对称的.(5)经计算知R c d a d c c b c a c c a b a a a R R ⊆=)},(),,(),,(),,(),,(),,(),,(),,{( ,进而R 是传递的.综上所述,所给R 是传递的.3.R 的关系矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=0111011100000111R M .六、解 命题公式))(())((p q r r q p A →→↔→→=的真值表如下:由表可知,))(())((p q r r q p A →→↔→→=的主析取范式为A 的主合取范式为)()(r q p r q p A ⌝∨⌝∨∧∨⌝∨⌝=.七、证 不妨设G 的阶数3≥n ,否则结论是显然的. 根据推论1知,63-≤n m . 若G 的任意节点v 的度数均有5)deg(≥v ,由握手定理知n v m v5)deg(2≥=∑.于是m n 52≤,进而652363-⋅≤-≤m n m . 因此30≥m ,与已知矛盾. 所以必存在节点v 使得4)deg(≤v .八、解 设满足要求的r 位数的个数有a r 种,r = 0,1,2,…,则排列计数生成函数65432121211219619431x x x x x x ++++++=,因而38!412194=⋅=a .。
离散数学期末试卷及答案

一.判断题(共10小题,每题1分,共10分)在各题末尾的括号内画 表示正确,画 表示错误:1.设p、q为任意命题公式,则(p∧q)∨p ⇔ p ( )2.∀x(F(y)→G(x)) ⇔ F(y)→∃xG(x)。
( )3.初级回路一定是简单回路。
( )4.自然映射是双射。
( )5.对于给定的集合及其上的二元运算,可逆元素的逆元是唯一的。
( )6.群的运算是可交换的。
( )7.自然数集关于数的加法和乘法<N,+, >构成环。
( )8.若无向连通图G中有桥,则G的点连通度和边连通度皆为1。
( )9.设A={a,b,c},则A上的关系R={<a,b>,<a,c>}是传递的。
( )10.设A、B、C为任意集合,则A⨯(B⨯C)=(A⨯B)⨯C。
( )二、填空题(共10题,每题3分,共30分)11.设p:天气热。
q:他去游泳。
则命题“只有天气热,他才去游泳”可符号化为。
12.设M(x):x是人。
S(x):x到过月球。
则命题“有人到过月球”可符号化为。
13.p↔q的主合取范式是。
14.完全二部图K r,s(r < s)的边连通度等于。
15.设A={a,b},,则A上共有个不同的偏序关系。
16.模6加群<Z6,⊕>中,4是阶元。
17.设A={1,2,3,4,5}上的关系R={<1,3>,<1,5>,<2,5>,<3,3>,<4,5>},则R的传递闭包t(R) = 。
.18.已知有向图D的度数列为(2,3,2,3),出度列为(1,2,1,1),则有向图D的入度列为。
19.n阶无向简单连通图G的生成树有条边。
20.7阶圈的点色数是。
三、运算题(共5小题,每小题8分,共40分)21.求∃xF(x)→∃yG(x,y)的前束范式。
22.已知无向图G有11条边,2度和3度顶点各两个,其余为4度顶点,求G 的顶点数。
离散数学期末试卷(4套附答案)

一、单项选择题(每小题3分,共30分)1.下列为两个命题变元p,q的最小项的是( ) A .p∧q∧⎤ pB .⎤ p∨qC .⎤ p∧qD .⎤ p∨p∨q 2.下列句子不是命题的是( ) A .中华人民共和国的首都是北京 B .张三是学生 C .雪是黑色的D .太好了!3.对于公式(∀x ) (∃y )(P (x )∧Q (y ))→(∃x )R (x ,y ),下列说法正确的是( ) A .y 是自由变元 B .y 是约束变元C .(∃x )的辖域是R(x , y )D .(∀x )的辖域是(∃y )(P (x )∧Q (y ))→(∃x )R (x ,y )4.7.集合A={1,2,…,10}上的关系R={(x ,y )|x +y =10,x ∈A ,y ∈A},则R 的性质是( )A .自反的B .对称的C .传递的、对称的D .反自反的、传递的 5.设论域为{l ,2},与公式)(x xA ∃等价的是( ) A.A (1)∨A (2)B. A (1)→A (2)C.A (1)D. A (2)→A (1)6. 下列关系矩阵所对应的关系具有反自反性的是( ) A .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001110101B .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101100001 C .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001100100D .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0010101017. 下列运算不满足...交换律的是( ) A .a *b =a+2bB .a *b =min(a ,b )C .a *b =|a -b |D .a *b =2ab8..设A 是奇数集合,下列构成独异点的是( ) A.<A ,+> B.<A ,-> C.<A ,×> D.<A ,÷> 9. 右图的最大入度是( ) A .0 B .1 C .2D .3第9题图拟题学院(系): 高密校区 适用专业: 学年 2学期 离散数学 (B卷) 试题标准答案10. 设有向图D 的节点数大于1,D=(V ,E )是强连通图,当且仅当( ) A. D 中至少有一条通路 B. D 中至少有一条回路C. D 中有通过每个结点至少一次的通路D. D 中有通过每个结点至少一次的回路 二、填空题(每空3分,共30分)1.设A ={1,2,3,4},B ={2,4,6},则A -B =________,A ⊕B =________。
离散数学期末练习题 (带答案)

离散数学复习注意事项:1、第一遍复习一定要认真按考试大纲要求将本学期所学习内容系统复习一遍。
2、第二遍复习按照考试大纲的要求对第一遍复习进行总结。
把大纲中指定的例题及书后习题认真做一做。
检验一下主要内容的掌握情况。
3、第三遍复习把随后发去的练习题认真做一做,检验一下第一遍与第二遍复习情况,要认真理解,注意做题思路与方法。
离散数学综合练习题一、选择题1.下列句子中,()是命题。
A.2是常数。
B.这朵花多好看呀!C.请把门关上!D.下午有会吗?2.令p: 今天下雪了,q:路滑,r:他迟到了。
则命题“下雪路滑,他迟到了”可符号化为()。
A. p q r∨→∧→ B. p q rC. p q r∨↔∧∧ D. p q r3.令:p今天下雪了,:q路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为()。
A.p q∧∧⌝ B.p qC.p q→⌝∨⌝ D. p q4.设()Q x:x会飞,命题“有的鸟不会飞”可符号化为()。
P x:x是鸟,()A. ()(()())Q x⌝∀∧())x P x Q x⌝∀→ B. ()(()x P xC. ()(()())Q x⌝∃∧())x P x Q x⌝∃→ D. ()(()x P x5.设()L x y:x大于等于y;命题“所有整数f x:x的绝对值,(,)P x:x是整数,()的绝对值大于等于0”可符号化为()。
A. (()((),0))∀→x P x L f x∀∧B. (()((),0))x P x L f xC. ()((),0)∀→xP x L f x∀∧ D. ()((),0)xP x L f x6.设()F x:x是人,()G x:x犯错误,命题“没有不犯错误的人”符号化为()。
A.(()())⌝∃→⌝x F x G x∀∧B.(()())x F x G xC.(()())⌝∃∧⌝x F x G x⌝∃∧D.(()())x F x G x7.下列命题公式不是永真式的是()。
离散数学期末考试试题(配答案)

离散数学期末考试试题(配答案)1. 谓词公式)()(x xQ x xP ∃→∀的前束范式是___________。
2. 设全集{}{}{},5,2,3,2,1,5,4,3,2,1===B A E 则A ∩B =____;=A _____;=B A Y __ _____3. 设{}{}b a B c b a A ,,,,==;则=-)()(B A ρρ__ __________;=-)()(A B ρρ_____ ______。
二.选择题(每小题2分;共10分)1. 与命题公式)(R Q P →→等价的公式是( )(A )R Q P →∨)( (B )R Q P →∧)( (C ))(R Q P ∧→ (D ))(R Q P ∨→ 2. 设集合{}c b a A ,,=;A 上的二元关系{}><><=b b a a R ,,,不具备关系( )性质 (A ) (A)传递性 (B)反对称性 (C)对称性 (D)自反性 三.计算题(共43分)1. 求命题公式r q p ∨∧的主合取范式与主析取范式。
(6分)2. 设集合{}d c b a A ,,,=上的二元关系R 的关系矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛=1000000011010001R M ;求)(),(),(R t R s R r 的关系矩阵;并画出R ;)(),(),(R t R s R r 的关系图。
(10分)5. 试判断),(≤z 是否为格?说明理由。
(5分)(注:什么是格?Z 是整数;格:任两个元素;有最小上界和最大下界的偏序)四.证明题(共37分)1. 用推理规则证明D D A C C B B A ⌝⇒∧⌝⌝⌝∧∨⌝→)(,)(,。
(10分)2. 设R 是实数集;b a b a f R R R f +=→⨯),(,:;ab b a g R R R g =→⨯),(,:。
求证:g f 和都是满射;但不是单射。
(10分)一;1; _ ∃x ∃y¬P(x)∨Q(y)2; {2} {4;5} {1;3;4;5}3; {{c};{a ;c};{b ;c};{a ;b ;c}} Φ_ 二;B D三;解:主合取方式:p ∧q ∨r ⇔(p ∨q ∨r)∧(p ∨¬q ∨r)∧(¬p ∨q ∨r)= ∏0.2.4主析取范式:p ∧q ∨r ⇔(p ∧q ∧r) ∨(p ∧q ∧¬r) ∨(¬p ∧q ∧r) ∨(¬p ∧¬q ∧r) ∨(p ∧¬q ∧r)= ∑1.3.5.6.7 四;1;证明:编号 公式 依据 (1) (¬B∨C )∧¬C 前提 (2) ¬B∨C ;¬C (1) (3) ¬B (2) (4) A →B (3) (5) ¬A (3)(4) (6) ¬(¬A∧D ) 前提 (7) A ∨¬D (6) (8)¬D (5)(6)2;证明:要证f 是满射;即∀y ∈R ;都存在(x1;x2)∈R ×R ;使f (x1;x2)=y ;而f (x1;x2)=x1+x2;可取x1=0;x2=y ;即证得;再证g 是满射;即∀y ∈R ;;都存在(x1;x2)∈R ×R ;使g (x1;x2)=y ;而g (x1;x2)=x1x2;可取x1=1;x2=y ;即证得;最后证f 不是单射;f (x1;x2)=f (x2;x1)取x1≠x2;即证得;同理:g (x1;x2)=g (x2;x1);取x1≠x2;即证得。
离散数学期末考试题(附答案和含解析)

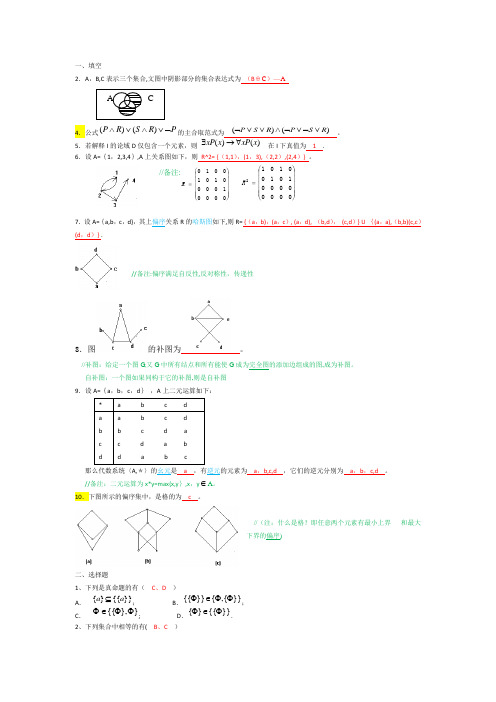
一、填空2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 (B ⊕C)-A4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 )()(R S P R S P ∨⌝∨⌝∧∨∨⌝ 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 1 。
6.设A={1,2,3,4},A 上关系图如下,则 R^2= {(1,1),(1,3),(2,2),(2,4)} 。
//备注:⎪⎪⎪⎪⎪⎭⎫⎝⎛=0000100001010010R⎪⎪⎪⎪⎪⎭⎫⎝⎛=00000000101001012R7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图如下,则R= {(a,b),(a,c), (a,d), (b,d), (c,d)} U {(a,a),(b,b)(c,c)(d,d)} 。
//备注:偏序满足自反性,反对称性,传递性8.图的补图为 。
//补图:给定一个图G ,又G 中所有结点和所有能使G 成为完全图的添加边组成的图,成为补图. 自补图:一个图如果同构于它的补图,则是自补图 9.设A={a ,b ,c ,d} ,A 上二元运算如下:* a b c d a b c da b c d b c d a c d a b d a b c那么代数系统<A ,*>的幺元是 a ,有逆元的元素为 a,b,c,d ,它们的逆元分别为 a,b,c,d 。
//备注:二元运算为x*y=max{x,y},x,y ∈A 。
10.下图所示的偏序集中,是格的为 c 。
//(注:什么是格?即任意两个元素有最小上界 和最大下界的偏序)二、选择题1、下列是真命题的有( C 、D )A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C .}},{{ΦΦ∈Φ; D .}}{{}{Φ∈Φ。
2、下列集合中相等的有( B 、C )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
离散数学期末考试试题及答案

离散数学试题(B卷答案1)一、证明题(10分)1)(P∧(Q∧R))∨(Q∧R)∨(P∧R)R证明: 左端(P∧Q∧R)∨((Q∨P)∧R)((P∧Q)∧R))∨((Q∨P)∧R)((P∨Q)∧R)∨((Q∨P)∧R)((P∨Q)∨(Q∨P))∧R((P∨Q)∨(P∨Q))∧RT∧R(置换)R2) x (A(x)B(x))xA(x)xB(x)证明:x(A(x)B(x))x(A(x)∨B(x))x A(x)∨xB(x)xA(x)∨xB(x)xA(x)xB(x)二、求命题公式(P∨(Q∧R))(P∧Q∧R)的主析取范式和主合取范式(10分)。
证明:(P∨(Q∧R))(P∧Q∧R)(P∨(Q∧R))∨(P∧Q∧R))(P∧(Q∨R))∨(P∧Q∧R)(P∧Q)∨(P∧R))∨(P∧Q∧R)(P∧Q∧R)∨(P∧Q∧R)∨(P∧Q∧R))∨(P∧Q∧R))∨(P∧Q∧R)m0∨m1∨m2∨m7M3∨M4∨M5∨M6三、推理证明题(10分)1)C∨D,(C∨D)E,E(A∧B),(A∧B)(R∨S)R∨S 证明:(1) (C∨D) E P(2) E(A∧B) P(3) (C∨D)(A∧B) T(1)(2),I(4) (A∧B)(R∨S) P(5) (C∨D)(R∨S) T(3)(4),I(6) C∨D P(7) R∨S T(5),I2) x(P(x)Q(y)∧R(x)),xP(x)Q(y)∧x(P(x)∧R(x))证明(1)xP(x) P(2)P(a) T(1),ES(3)x(P(x)Q(y)∧R(x)) P(4)P(a)Q(y)∧R(a) T(3),US(5)Q(y)∧R(a) T(2)(4),I(6)Q(y) T(5),I(7)R(a) T(5),I(8)P(a)∧R(a) T(2)(7),I(9)x(P(x)∧R(x)) T(8),EG(10)Q(y)∧x(P(x)∧R(x)) T(6)(9),I四、某班有25名学生,其中14人会打篮球,12人会打排球,6人会打篮球和排球,5人会打篮球和网球,还有2人会打这三种球。
离散数学期末考试试题及答案

离散数学期末考试试题及答案离散数学试题(B卷答案1)一、证明题(10分)1)(P∧(Q∧R))∨(Q∧R)∨(P∧R)R证明: 左端(P∧Q∧R)∨((Q∨P)∧R)((P∧Q)∧R))∨((Q∨P)∧R)((P∨Q)∧R)∨((Q∨P)∧R)((P∨Q)∨(Q∨P))∧R((P∨Q)∨(P∨Q))∧RT∧R(置换)R2) x (A(x)B(x))xA(x)xB(x)证明:x(A(x)B(x))x(A(x)∨B(x))x A(x)∨xB(x)xA(x)∨xB(x)xA(x)xB(x)二、求命题公式(P∨(Q∧R))(P∧Q∧R)的主析取范式和主合取范式(10分)。
证明:(P∨(Q∧R))(P∧Q∧R)(P∨(Q∧R))∨(P∧Q∧R))(P∧(Q∨R))∨(P∧Q∧R)(P∧Q)∨(P∧R))∨(P∧Q∧R)(P∧Q∧R)∨(P∧Q∧R)∨(P∧Q∧R))∨(P∧Q∧R))∨(P∧Q∧R)m0∨m1∨m2∨m7M3∨M4∨M5∨M6三、推理证明题(10分)1)C∨D,(C∨D)E, E(A∧B),(A∧B)(R∨S)R∨S证明:(1)(C∨D) E ?P(2) E(A∧B) ??P(3) (C∨D)(A∧B) T(1)(2),I(4) (A∧B)(R∨S)??P(5) (C∨D)(R∨S) ? T(3)(4),I(6)C∨D P(7) R∨S T(5),I2) x(P(x)Q(y)∧R(x)),xP(x)Q(y)∧x(P(x)∧R(x))证明(1)xP(x) P(2)P(a) T(1),ES(3)x(P(x)Q(y)∧R(x)) P(4)P(a)Q(y)∧R(a) T(3),US(5)Q(y)∧R(a) T(2)(4),I(6)Q(y) T(5),I(7)R(a) T(5),I(8)P(a)∧R(a) T(2)(7),I(9)x(P(x)∧R(x)) T(8),EG(10)Q(y)∧x(P(x)∧R(x)) T(6)(9),I四、某班有25名学生,其中14人会打篮球,12人会打排球,6人会打篮球和排球,5人会打篮球和网球,还有2人会打这三种球。
大学离散数学期末考试题库和答案

大学离散数学期末考试题库和答案一、单项选择题(每题2分,共20分)1. 在集合论中,以下哪个符号表示“属于”?A. ∈B. ∉C. ⊆D. ⊂答案:A2. 如果A和B是两个集合,那么A∪B表示什么?A. A和B的交集B. A和B的并集C. A和B的差集D. A和B的补集答案:B3. 以下哪个命题是真命题?A. ∀x∈N, x^2 > xB. ∃x∈N, x^2 = x + 1C. ∀x∈N, x^2 ≥ xD. ∃x∈N, x^2 < x答案:C4. 在图论中,一个无向图的边数为E,顶点数为V,那么这个图的生成树的边数是多少?A. EB. V-1C. VD. E-1答案:B5. 以下哪个算法是用于解决旅行商问题(TSP)的?A. 动态规划B. 贪心算法C. 分支限界法D. 回溯法答案:D6. 在逻辑中,以下哪个符号表示“蕴含”?A. ∧B. ∨C. →D. ↔答案:C7. 以下哪个是二进制数?A. 1010B. 2A3C. 12BD. ZYX答案:A8. 在关系数据库中,以下哪个操作用于删除表中的行?A. SELECTB. INSERTC. UPDATED. DELETE答案:D9. 以下哪个是布尔代数的基本运算?A. 并集B. 交集C. 差集D. 所有以上答案:D10. 在离散数学中,以下哪个概念用于描述两个集合之间的关系?A. 函数B. 映射C. 序列D. 所有以上答案:D二、多项选择题(每题3分,共15分)11. 以下哪些是集合的基本运算?A. 并集B. 交集C. 差集D. 补集答案:ABCD12. 在图论中,以下哪些是图的基本类型?A. 无向图B. 有向图C. 完全图D. 二分图答案:ABCD13. 在逻辑中,以下哪些是命题逻辑的基本连接词?A. 与(∧)B. 或(∨)C. 非(¬)D. 蕴含(→)答案:ABCD14. 在关系数据库中,以下哪些是SQL的基本操作?A. SELECTB. INSERTC. UPDATED. DELETE答案:ABCD15. 在离散数学中,以下哪些是组合数学的基本概念?A. 排列B. 组合C. 二项式系数D. 图论答案:ABC三、填空题(每题3分,共30分)16. 如果集合A={1, 2, 3},集合B={2, 3, 4},那么A∩B=______。
大学《离散数学》期末考试试卷及答案(1)

大学《离散数学》期末考试试卷及答案(1)一、选择题1. 离散数学的主要研究对象是()。
A. 连续的数学结构B. 有限的数学结构C. 数学的综合应用D. 数学的哲学思考2. 命题逻辑是离散数学的一个重要组成部分,它主要研究()。
A. 命题之间的真假关系B. 变量之间的关系C. 函数之间的关系D. 集合之间的关系3. 集合的基本运算包括()。
A. 并、交、差、补B. 加、减、乘、除C. 包含、相等、不等、自反D. 大于、小于、等于、不等于二、填空题1. 若集合A={m|2m-1>3},则A中的元素为______。
2. 有一个集合A={1,2,3},则集合A的幂集为______。
3. 若命题p为真,命题q为假,则复合命题“p∧q”的真值为______。
三、解答题1. 请写出离散数学中常用的数学符号及其含义。
2. 请解释命题逻辑中的充分必要条件及其符号表示,并给出一个例子。
3. 请定义集合的笛卡尔积,并给出两个集合进行笛卡尔积运算的例子。
四、问答题1. 离散数学在计算机科学中有着重要的应用,请列举三个与计算机科学相关的离散数学应用领域并简要介绍。
2. 请简要解释归纳法在离散数学中的作用,并给出一个使用归纳法证明的例子。
3. 什么是有向图?请给出一个有向图的例子,并解释该图中的关系。
参考答案:一、选择题1. B2. A3. A二、填空题1. A={m|2m-1>3}2. {{}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}3. 假三、解答题1. 常用数学符号及含义:- ∪:并,表示集合的合并操作。
- ∩:交,表示集合的交集操作。
- ∖:差,表示减去一个集合中的元素。
- ⊆:包含,表示一个集合包含于另一个集合。
- =:相等,表示两个集合具有相同的元素。
2. 充分必要条件是指一个命题的成立与另一个命题的成立互为必要条件,若A是B的充分必要条件,那么当A成立时B一定成立,且当A不成立时B也一定不成立。
离散数学期末考试题(附答案和含解析1)
一、填空2.A ,B,C 表示三个集合,文图中阴影部分的集合表达式为 (B ⊕C )—A4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 )()(R S P R S P ∨⌝∨⌝∧∨∨⌝ 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 1 . 6.设A={1,2,3,4},A 上关系图如下,则 R^2= {(1,1),(1,3),(2,2),(2,4)} 。
//备注:⎪⎪⎪⎪⎪⎭⎫⎝⎛=0000100001010010R⎪⎪⎪⎪⎪⎭⎫⎝⎛=00000000101001012R7.设A={a,b ,c ,d},其上偏序关系R 的哈斯图如下,则R= {(a ,b),(a ,c ), (a ,d), (b,d ), (c,d )} U {(a ,a),(b,b)(c,c )(d ,d )} .//备注:偏序满足自反性,反对称性,传递性8.图的补图为 。
//补图:给定一个图G ,又G 中所有结点和所有能使G 成为完全图的添加边组成的图,成为补图。
自补图:一个图如果同构于它的补图,则是自补图 9.设A={a ,b ,c ,d } ,A 上二元运算如下:* a b c d a b c da b c d b c d a c d a b d a b c那么代数系统〈A,*〉的幺元是 a ,有逆元的元素为 a ,b,c,d ,它们的逆元分别为 a ,b ,c,d 。
//备注:二元运算为x*y=max{x,y },x ,y ∈A 。
10.下图所示的偏序集中,是格的为 c 。
//(注:什么是格?即任意两个元素有最小上界 和最大下界的偏序)二、选择题1、下列是真命题的有( C 、D )A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C .}},{{ΦΦ∈Φ; D .}}{{}{Φ∈Φ.2、下列集合中相等的有( B 、C )A CA .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
《离散数学》期末练习题考试卷和答案

a , b, c , d , e, f , g,那么 所对应的 19. 设集合 A a , b , c , d , e , f , g , A 上有一个划分
等价关系 R 应有( )个序偶。 )。
20. 在有理数集合 Q 上定义二元运算*: a * b a b ab ,则 Q , * 的幺元是(
等价关系 R 应有( )个序偶。 )。
25. 在有理数集合 Q 上定义二元运算*: a * b a b ab ,则 Q , * 的幺元是(
26. 一个(
)称为布尔代数。
27.P Q P Q 的主析取范式是
。(写出一般
5
表示形式即可) 28.设集合 A a , b , c , d , R 是 A 上的二元关系,且 R a , b , b , a , b , c , c , d , a , c , 则 R 的传递闭包 t R 。
C. x x是正整数, x 5
D. x x是有理数, x 5
。
6.下面有关集合之间的包含和属于关系的说法,正确的是 Ⅰ. Ⅲ.
Ⅱ. , ,
Ⅳ.
a, b a, b, a, b
B.Ⅰ和Ⅲ
a, b a, b, a, b, c
二、填空题 1.设 A 为非空集合,且 A n ,则 A 上不同的二元关系的个数为 为 。 时, P Q 的真值为 1。 , A 上不同的映射的个数
2.设 P 、 Q 为两个命题,当且仅当
3. 在运算表中的空白处填入适当符号,使 a , b , c, * 成为群。 *
a a
a b c
4. 当 n 为 数时, K n n 3 必为欧拉图。
离散数学期末考试题及答案

离散数学期末考试题及答案一、单项选择题(每题2分,共20分)1. 集合A={1,2,3},B={2,3,4},则A∩B=()。
A. {1,2,3}B. {2,3}C. {2,4}D. {1,4}答案:B2. 命题“若x>0,则x>1”的逆否命题是()。
A. 若x≤0,则x≤1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤1,则x≤0答案:B3. 函数f: A→B的定义域是集合A,值域是集合B,则()。
A. A⊆BB. A⊂BC. A⊇BD. A⊃B答案:A4. 集合{1,2,3}与集合{3,2,1}是否相等?()。
A. 是B. 否C. 无法确定D. 以上都不对答案:A5. 命题p:“x>0”,则¬p为()。
A. x≤0B. x<0C. x=0D. x<0或x=0答案:A6. 命题“若x>0,则x>1”的逆命题是()。
A. 若x>0,则x>1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤0,则x≤1答案:C7. 函数f: A→B的定义域是集合A,值域是集合B,则()。
A. A⊆BB. A⊂BC. A⊇BD. A⊃B答案:A8. 集合{1,2,3}与集合{3,2,1}是否相等?()。
A. 是B. 否C. 无法确定D. 以上都不对答案:A9. 命题p:“x>0”,则¬p为()。
A. x≤0B. x<0C. x=0D. x<0或x=0答案:A10. 命题“若x>0,则x>1”的逆命题是()。
A. 若x>0,则x>1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤0,则x≤1答案:C二、填空题(每题2分,共20分)1. 集合A={1,2,3},B={2,3,4},则A∪B=______。
答案:{1,2,3,4}2. 命题“若x>0,则x>1”的逆否命题是:若x≤1,则x≤0。
(完整word版)离散数学期末考试试题及答案

离散数学试题(B卷答案1)一、证明题(10分)1)(⌝P∧(⌝Q∧R))∨(Q∧R)∨(P∧R)⇔R证明: 左端⇔(⌝P∧⌝Q∧R)∨((Q∨P)∧R)⇔((⌝P∧⌝Q)∧R))∨((Q∨P)∧R)⇔(⌝(P∨Q)∧R)∨((Q∨P)∧R)⇔(⌝(P∨Q)∨(Q∨P))∧R⇔(⌝(P∨Q)∨(P∨Q))∧R⇔T∧R(置换)⇔R2) ∃x (A(x)→B(x))⇔∀xA(x)→∃xB(x)证明:∃x(A(x)→B(x))⇔∃x(⌝A(x)∨B(x))⇔∃x⌝A(x)∨∃xB(x)⇔⌝∀xA(x)∨∃xB(x)⇔∀xA(x)→∃xB(x)二、求命题公式(P∨(Q∧R))→(P∧Q∧R)的主析取范式和主合取范式(10分)。
证明:(P∨(Q∧R))→(P∧Q∧R)⇔⌝(P∨(Q∧R))∨(P∧Q∧R))⇔(⌝P∧(⌝Q∨⌝R))∨(P∧Q∧R)⇔(⌝P∧⌝Q)∨(⌝P∧⌝R))∨(P∧Q∧R)⇔(⌝P∧⌝Q∧R)∨(⌝P∧⌝Q∧⌝R)∨(⌝P∧Q∧⌝R))∨(⌝P∧⌝Q∧⌝R))∨(P∧Q∧R)⇔m0∨m1∨m2∨m7⇔M3∨M4∨M5∨M6三、推理证明题(10分)1)C∨D, (C∨D)→⌝E,⌝E→(A∧⌝B), (A∧⌝B)→(R∨S)⇒R∨S 证明:(1) (C∨D)→⌝E P(2) ⌝E→(A∧⌝B) P(3) (C∨D)→(A∧⌝B) T(1)(2),I(4) (A∧⌝B)→(R∨S) P(5) (C∨D)→(R∨S) T(3)(4), I(6) C∨D P(7) R∨S T(5),I2) ∀x(P(x)→Q(y)∧R(x)),∃xP(x)⇒Q(y)∧∃x(P(x)∧R(x))证明(1)∃xP(x) P(2)P(a) T(1),ES(3)∀x(P(x)→Q(y)∧R(x)) P(4)P(a)→Q(y)∧R(a) T(3),US(5)Q(y)∧R(a) T(2)(4),I(6)Q(y) T(5),I(7)R(a) T(5),I(8)P(a)∧R(a) T(2)(7),I(9)∃x(P(x)∧R(x)) T(8),EG(10)Q(y)∧∃x(P(x)∧R(x)) T(6)(9),I四、某班有25名学生,其中14人会打篮球,12人会打排球,6人会打篮球和排球,5人会打篮球和网球,还有2人会打这三种球。
离散数学期末考试题及答案

离散数学期末考试题及答案1. 题目描述:以下是离散数学期末考试的题目。
请仔细阅读每个问题,并在题后给出相应的答案。
请注意,答案应尽量详细和准确,以确保得分。
1.1 命题与谓词逻辑(20分)1.1.1 什么是命题逻辑?它可以用于解决哪些问题?1.1.2 简要解释谓词逻辑的概念和其在离散数学中的应用。
1.2 集合和图论(30分)1.2.1 定义两个集合的并、交和差的概念。
1.2.2 解释有向图和无向图的区别,并给出一个实际应用中的例子。
1.3 关系和函数(40分)1.3.1 什么是关系?请给出一个实际应用中关系的例子。
1.3.2 定义函数的概念,并解释函数与关系的区别。
1.4 计数原理(20分)1.4.1 简要阐述乘法原理和加法原理的概念,并给出一个应用实例。
1.4.2 什么是排列和组合?请说明它们的应用场景,并给出一个例子。
2. 答案解析:2.1 命题与谓词逻辑1.1.1 命题逻辑是一种数学分支,用于研究命题之间的关系和推理规则。
其应用范围广泛,包括数学、计算机科学、哲学等领域。
1.1.2 谓词逻辑是一种扩展了命题逻辑的逻辑体系,它考虑了命题中的变量、谓词和量词等元素。
在离散数学中,谓词逻辑常用于描述集合、函数和关系等概念。
2.2 集合和图论1.2.1 集合的并(∪)是指将两个或多个集合中的所有元素取出形成一个新的集合;交(∩)指仅包含两个或多个集合中共有的元素;差(-)是指从一个集合中去除另一个集合中的元素。
1.2.2 有向图中,边是具有方向性的;而在无向图中,边是没有方向性的。
例如,在社交网络中,有向图可以表示人与人之间的关注关系,而无向图可以表示人与人之间的好友关系。
2.3 关系和函数1.3.1 关系是集合之间的一种特殊的子集,它描述了元素之间的某种联系。
例如,家族中的血亲关系可以看作是一个关系。
关系可以用图、矩阵等方式表示。
1.3.2 函数是一种特殊的关系,它将一个集合中的每个元素映射到另一个集合中的唯一元素。
离散数学考试试题及答案

离散数学考试试题及答案一、单项选择题(每题5分,共20分)1. 在离散数学中,以下哪个概念不是布尔代数的基本元素?A. 逻辑与B. 逻辑或C. 逻辑非D. 逻辑异或答案:D2. 下列哪个命题不是命题逻辑中的命题?A. 所有学生都是勤奋的B. 有些学生是勤奋的C. 学生是勤奋的D. 勤奋的学生答案:D3. 在集合论中,以下哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 以下哪个图不是无向图?A. 简单图B. 完全图C. 有向图D. 多重图答案:C二、填空题(每题5分,共20分)1. 如果一个命题的逆否命题为真,则原命题的________为真。
答案:逆命题2. 在图论中,如果一个图的任意两个顶点都由一条边连接,则称这个图为________图。
答案:完全3. 一个集合的幂集是指包含该集合的所有________的集合。
答案:子集4. 如果一个函数的定义域和值域都是有限集合,那么这个函数被称为________函数。
答案:有限三、简答题(每题10分,共30分)1. 请简述什么是图的欧拉路径。
答案:欧拉路径是一条通过图中每条边恰好一次的路径。
2. 解释什么是二元关系,并给出一个例子。
答案:二元关系是指定义在两个集合之间的关系,它将第一个集合中的元素与第二个集合中的元素联系起来。
例如,小于关系就是一个二元关系。
3. 请说明什么是递归函数,并给出一个简单的例子。
答案:递归函数是一种通过自身定义来计算函数值的函数。
例如,阶乘函数就是一个递归函数,定义为:n! = n * (n-1)!,其中n! = 1当n=0时。
四、计算题(每题10分,共30分)1. 计算以下逻辑表达式:(P ∧ Q) ∨ ¬R答案:首先计算P ∧ Q,然后计算¬R,最后计算两者的逻辑或。
2. 给定集合A = {1, 2, 3},B = {2, 3, 4},求A ∪ B。
答案:A ∪ B = {1, 2, 3, 4}3. 已知函数f(x) = 2x + 3,求f(5)。
离散数学期末练习题 (带答案)

离散数学复习注意事项:1、第一遍复习一定要认真按考试大纲要求将本学期所学习内容系统复习一遍。
2、第二遍复习按照考试大纲的要求对第一遍复习进行总结。
把大纲中指定的例题及书后习题认真做一做。
检验一下主要内容的掌握情况。
3、第三遍复习把随后发去的练习题认真做一做,检验一下第一遍与第二遍复习情况,要认真理解,注意做题思路与方法。
离散数学综合练习题一、选择题1.下列句子中,()是命题。
A.2是常数。
B.这朵花多好看呀!C.请把门关上!D.下午有会吗?2.令p: 今天下雪了,q:路滑,r:他迟到了。
则命题“下雪路滑,他迟到了”可符号化为()。
A. p q r∨→∧→ B. p q rC. p q r∧∧ D. p q r∨↔3.令:p今天下雪了,:q路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为()。
A.p q∧∧⌝ B.p qC.p q∨⌝ D. p q→⌝4.设()Q x:x会飞,命题“有的鸟不会飞”可符号化为()。
P x:x是鸟,()A. ()(()())⌝∀∧())x P xQ xx P x Q x⌝∀→ B. ()(()C. ()(()())Q x⌝∃∧())x P x Q x⌝∃→ D. ()(()x P x5.设()L x y:x大于等于y;命题“所有整数f x:x的绝对值,(,)P x:x是整数,()的绝对值大于等于0”可符号化为()。
A. (()((),0))∀→x P x L f x∀∧B. (()((),0))x P x L f xC. ()((),0)∀→xP x L f x∀∧ D. ()((),0)xP x L f x6.设()G x:x犯错误,命题“没有不犯错误的人”符号化为()。
F x:x是人,()A.(()())⌝∃→⌝x F x G xx F x G x∀∧B.(()()) C.(()())x F x G x⌝∃∧⌝⌝∃∧D.(()())x F x G x7.下列命题公式不是永真式的是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学期末考试试题及答案
一、(单项选择题)
本大题共15小题,每小题3分,共45分在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在答题卷相应题号处。
1、在由3个元素组成的集合上,可以有种不同的关系。
[A] 3 [B] 8 [C]9 [D]27
2、设A1,2,3,5,8,B1,2,5,7,则AB 。
[A] 3,8 [B]3 [C]8 [D]3,8
3、若X是Y的子集,则一定有。
[A]X不属于Y [B]X∈Y
[C]X真包含于Y [D]X∩Y=X
4、下列关系中是等价关系的是。
[A]不等关系 [B]空关系
[C]全关系 [D]偏序关系
5、对于一个从集合A到集合B的映射,下列表述中错误的是。
[A]对A的每个元素都要有象 [B] 对A的每个元素都只有一个象
[C]对B的每个元素都有原象 [D] 对B的元素可以有不止一个原象
6、设p:小李努力学习,q:小李取得好成绩,命题“除非小李努力学习,否则他不能取得好成绩”的符号化形式为。
[A]p→q [B]q→p [C]┐q→┐p [D]┐p→q
7、设A={a,b,c},则A到A的双射共有。
[A]3个 [B]6个 [C]8个 [D]9个
8、一个连通G具有以下何种条件时,能一笔画出:即从某结点出发,经过中每边仅一次回到该结点。
[A] G没有奇数度结点 [B] G有1个奇数度结点
[C] G有2个奇数度结点 [D] G没有或有2个奇数度结点
9、设〈G,*〉是群,且|G|>1,则下列命题不成立的’是。
[A] G中有幺元 [B] G中么元是唯一的
[C] G中任一元素有逆元 [D] G中除了幺元外无其他幂等元
10、令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为
[A] p→┐q [B] p∨┐q
[C] p∧q [D] p∧┐q
11、设G=的结点集为V={v1,v2,v3},边集为E={,}.则G的割点集是。
[A]{v1} [B]{v2} [C]{v3} [D]{v2,v3}
12、下面4个推理定律中,不正确的为。
[A]A=>A∨B 附加律[B]A∨B∧┐A=>B 析取三段论
[C]A→B∧A=>B 假言推理[D]A→B∧┐B=>A 拒取式
13、在右边中过v1,v2的初级回路有多少条
[A] 1 [B] 2 [C] 3 [D] 4
14、若R,,是环,且R中乘法适合消去律,则R是。
[A]无零因子环
[C]整环 [B]除环 [D]域
15、无向G中有16条边,且每个结点的度数均为2,则结点数是。
[A]8 [B]16 [C]4 [D]32
二、(判断题)
本大题共8小题,每小题3分,共24分正确的填T,错误的填F,填在答题卷相应题号处。
16、是空集。
17、设S,T为任意集合,如果S—T=,则S=T。
18、在命题逻辑中,任何命题公式的主合取范式都是存在的,并且是唯一的。
19、关系的复合运算满足交换律。
20、集合A上任一运算对A是封闭的。
21、0,1,2,3,4,max,min是格。
22、强连通有向一定是单向连通的。
23、设都是命题公式,则PQQP。
三、(解答题)
本大题共3小题,24、25每小题10分,26小题11分,共31分请将答案填写在答题
卷相应题号处。
24、设集合A={a, b, c},B={b, d, e},求
1BA; 2AB; 3A-B; 4BA.
25、设非空集合A,验证PA,,,~,,A是布尔代数
26、如果他是计算机系本科生或者是计算机系研究生,那么他一定学过DELPHI语言
而且学过C++语言。
只要他学过DELPHI语言或者C++语言,那么他就会编程序。
因此如果
他是计算机系本科生,那么他就会编程序。
请用命题逻辑推理方法,证明该推理的有效结论。
离散数学试题答案
一、(单项选择题)本大题共15小题,每小题3分,共45分
BDDCCCBABDADCBB
二、(判断题)本大题共8小题,每小题3分,共24分
FFTFTTTF
三、(解答题)本大题共3小题,24、25每小题10分,26小题11分,共31分 24、设集合A={a, b, c},B={b, d, e},求 1BA; 2AB; 3A-B; 4BA. 标准答案:1BA={a, b, c}{b, d, e}={ b }
2AB={a, b, c}{b, d, e}={a, b, c, d, e }
3A-B={a, b, c}-{b, d, e}={a, c}
4BA= AB-BA={a, b, c, d, e }-{ b }={a, c, d, e }
复习范围或考核目标:考察集合的基本运算,包括交集,并集,见课件第一章第
二节,集合的运算。
25、设非空集合A,验证PA,,,~,,A是布尔代数
标准答案:证明因为集合A非空,故PA至少有两个元素,显然,是PA上的二元运算. 由定理10 ,任给B,C,DPA, H1 BD=DC CD=DC
H2 BCD=BCBD BCD=BCBD
H3 PA存在和A,BPA, 有B=B, BA=B
H4,BPA, BA,存在A~B,有
BA~B= A BA~B=
所以PA,,,~,,A是布尔代数.
复习范围或考核目标:考察布尔代数的基本概念,集合的运算,见课件代数系统中布尔代数小节。
26、如果他是计算机系本科生或者是计算机系研究生,那么他一定学过DELPHI语言而且学过C++语言。
只要他学过DELPHI语言或者C++语言,那么他就会编程序。
因此如果他是计算机系本科生,那么他就会编程序。
请用命题逻辑推理方法,证明该推理的有效结论。
标准答案:令p:他是计算机系本科生
q:他是计算机系研究生 r:他学过DELPHI语言
s:他学过C++语言
t:他会编程序
前提:p∨q→r∧s,r∨s→t
结论:p→t
证①p P附加前提
②p∨q T①I
③p∨q→r∧s P前提引入
④r∧s T②③I
⑤r T④I
⑥r∨s T⑤I
⑦r∨s→t P前提引入
⑧t T⑤⑥I
感谢您的阅读,祝您生活愉快。
