affinity propagation算法Matlab代码实现
遗传算法及Matlab说明

其MATLAB实现者:老牛网友评论17 条浏览次数602(1)遗传算法简介(2)遗传算法的MA TLAB实现(3)应用举例(4)遗传算法优化神经网络方向在工业工程中,许多最优化问题性质十分复杂,很难用传统的优化方法来求解.自1960年以来,人们对求解这类难解问题日益增加.一种模仿生物自然进化过程的、被称为“进化算法(evolutionary algorithm)”的随机优化技术在解这类优化难题中显示了优于传统优化算法的性能。
目前,进化算法主要包括三个研究领域:遗传算法、进化规划和进化策略。
其中遗传算法是迄今为止进化算法中应用最多、比较成熟、广为人知的算法。
一、遗传算法简介遗传算法(Genetic Algorithm, GA)最先是由美国Mic-hgan大学的John Holland于1975年提出的。
遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型。
它的思想源于生物遗传学和适者生存的自然规律,是具有“生存+检测”的迭代过程的搜索算法。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。
其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定等5个要素组成了遗传算法的核心内容。
遗传算法的基本步骤:遗传算法是一种基于生物自然选择与遗传机理的随机搜索算法,与传统搜索算法不同,遗传算法从一组随机产生的称为“种群(Population)”的初始解开始搜索过程。
种群中的每个个体是问题的一个解,称为“染色体(chromosome)”。
染色体是一串符号,比如一个二进制字符串。
这些染色体在后续迭代中不断进化,称为遗传。
在每一代中用“适值(fitness)”来测量染色体的好坏,生成的下一代染色体称为后代(offspring)。
后代是由前一代染色体通过交叉(crossover)或者变异(mutation)运算形成的。
基于Matlab的动态规划算法的实现及应用

基于Matlab的动态规划算法的实现及应用动态规划是一种常用的优化算法,可以在给定的约束条件下,求解具有最优解的问题。
它通过将原问题拆分成若干子问题,并保存子问题的解,从而避免重复计算,减少运算量,提高算法的效率。
在Matlab中,可以通过使用递归或迭代的方式来实现动态规划算法。
下面将介绍一种基于Matlab的动态规划算法的实现及应用。
我们需要确定问题的状态,即在求解过程中需要保存的信息。
然后,定义状态转移方程,即问题的解与其子问题的解之间的关系。
确定边界条件,即问题的基本解。
以求解斐波那契数列为例,斐波那契数列的定义如下:F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2) (n>=2)我们可以使用动态规划算法来求解斐波那契数列。
定义一个数组dp,用来保存每个子问题的解。
然后,通过迭代的方式,计算从小到大的每个子问题的解,直到得到问题的最优解。
在Matlab中,可以使用以下代码实现动态规划算法求解斐波那契数列:```matlabfunction [result] = Fibonacci(n)% 初始化数组dpdp = zeros(1, n+1);% 定义边界条件dp(1) = 0;dp(2) = 1;% 迭代计算每个子问题的解for i = 3:n+1dp(i) = dp(i-1) + dp(i-2);end% 返回问题的最优解result = dp(n+1);end```运行以上代码,输入一个整数n,即可求解斐波那契数列的第n项。
除了求解斐波那契数列,动态规划算法还可以应用于其他许多领域,如路径规划、背包问题等。
在路径规划中,我们可以使用动态规划算法来求解最短路径或最优路径;在背包问题中,我们可以使用动态规划算法来求解能够装入背包的最大价值。
动态规划算法是一种强大的优化算法,在Matlab中的实现也相对简单。
通过定义问题的状态、状态转移方程和边界条件,我们可以使用动态规划算法来求解各种不同类型的问题。
遗传算法优化的matlab案例

遗传算法优化的matlab案例以下是一个简单的遗传算法优化的Matlab 案例:假设我们想找到一个函数f(x) 的最大值,其中x 的取值范围为[0,10]。
我们可以使用遗传算法来找到最大值。
步骤如下:1. 定义适应度函数我们可以使用f(x) 来定义适应度函数。
在这个例子中,我们使用函数f(x) = x^2。
在Matlab 中,我们可以这样定义适应度函数:function y = fitness(x)y = x.^2;end2. 定义遗传算法参数我们需要定义一些遗传算法的参数,如种群大小、交叉概率、变异概率等。
在这个例子中,我们定义种群大小为50,交叉概率为0.8,变异概率为0.1。
pop_size = 50; % 种群大小crossover_rate = 0.8; % 交叉概率mutation_rate = 0.1; % 变异概率3. 执行遗传算法优化我们可以使用Matlab 自带的ga 函数来执行遗传算法优化。
我们需要传入适应度函数、变量的取值范围等参数。
lb = 0; % 变量下限ub = 10; % 变量上限nvars = 1; % 变量个数options =gaoptimset('Display','iter','PopulationSize',pop_size,'CrossoverFraction',c rossover_rate,'MutationFcn',@mutationadaptfeasible,'MutationRate',mut ation_rate,'StallGenLimit',50); % 遗传算法参数[x,fval] = ga(@fitness,nvars,[],[],[],[],lb,ub,[],options); % 执行遗传算法优化disp(['Optimal value: ',num2str(fval)]);disp(['Optimal solution: [',num2str(x),']']);在上面的代码中,我们使用了mutationadaptfeasible 函数来保证变异产生的新个体也满足变量取值范围。
AP近邻传播聚类算法原理及Matlab实现

AP近邻传播聚类算法原理及Matlab实现Affinity Propagation (AP)聚类是2007年在Science杂志上提出的一种新的聚类算法。
它根据N个数据点之间的相似度进行聚类,这些相似度可以是对称的,即两个数据点互相之间的相似度一样(如欧氏距离);也可以是不对称的,即两个数据点互相之间的相似度不等。
这些相似度组成N×N的相似度矩阵S(其中N为有N个数据点)。
AP算法不需要事先指定聚类数目,相反它将所有的数据点都作为潜在的聚类中心,称之为exemplar。
以S矩阵的对角线上的数值s(k, k)作为k点能否成为聚类中心的评判标准,这意味着该值越大,这个点成为聚类中心的可能性也就越大,这个值又称作参考度p( preference)。
聚类的数量受到参考度p的影响,如果认为每个数据点都有可能作为聚类中心,那么p就应取相同的值。
如果取输入的相似度的均值作为p的值,得到聚类数量是中等的。
如果取最小值,得到类数较少的聚类。
AP算法中传递两种类型的消息,(responsiility)和(availability)。
r(i,k)表示从点i发送到候选聚类中心k的数值消息,反映k点是否适合作为i点的聚类中心。
a(i,k)则从候选聚类中心k发送到i的数值消息,反映i点是否选择k作为其聚类中心。
r(i, k)与a (i, k)越强,则k点作为聚类中心的可能性就越大,并且i点隶属于以k点为聚类中心的聚类的可能性也越大。
AP算法通过迭代过程不断更新每一个点的吸引度和归属度值,直到产生m个高质量的exemplar,同时将其余的数据点分配到相应的聚类中。
在这里介绍几个文中常出现的名词:exemplar:指的是聚类中心。
similarity:数据点i和点j的相似度记为S(i,j)。
是指点j作为点i的聚类中心的相似度。
preference:数据点i的参考度称为P(i)或S(i,i)。
是指点i作为聚类中心的参考度。
matlab如何做傅里叶变换

matlab如何做傅里叶变换Matlab是一款高级的计算机可视化程序,具有强大的图形和数据处理功能。
它可以帮助你快速处理大量数据,并进行准确的分析。
Matlab中的傅里叶变换(FFT)是用于分析数字信号(如声音或图像)的有用工具,它将时域信号转换为频域信号。
FFT可以显示出信号中每一段的频率、幅度和相位,从而可以反映出信号的构成成分。
在Matlab中,可以使用fft()函数来计算信号的傅里叶变换。
假设要对一段持续时间为T的实信号X(t)做FFT变换,首先要定义变换的采样频率fs,然后构造一个长度为N(N>T*fs)的数组x,填充X(t)的采样点,其中x[k] = X(k/fs)。
在Matlab中,可以使用linspace()函数快速生成x。
之后使用fft()来计算X(t)的FFT:y = fft(x);在此调用后,y数组就会保存有X(t)的FFT结果,它的长度为N,其中y[k]表示X(t)在频率为k/T的Fourier系数。
对于对称的实信号,Matlab还提供了一种快速的FFT实现——fftshift()函数,它可以快速计算一维实信号的FFT,省去了上述步骤所需的构造数组和调用fft()函数的时间。
要使用fftshift(),只需要调用函数fftshift(X)即可,其中X是X(t)的采样点。
总之,Matlab中的FFT工具可用于快速分析信号,方法简单便捷。
可以通过fft()和fftshift()函数快速获得信号的频谱,其结果可以反映出信号的频率、幅度和相位。
Matlab中的FFT功能可以为你的信号处理工作带来很大的方便。
蝙蝠算法matlab程序

蝙蝠算法matlab程序蝙蝠算法(Bat Algorithm)是一种启发式算法,用于解决优化问题。
它模拟了蝙蝠捕食时的行为,通过调整蝙蝠位置和频率来寻找最优解。
在Matlab中,可以实现蝙蝠算法的程序来解决各种优化问题。
以下是一个简单的蝙蝠算法的Matlab程序示例:matlab.function [best, fmin]=bat_algorithm()。
% 初始化参数。
N=40; % 蝙蝠个数。
n=2; % 优化问题的维度。
A=0.5; % 蝙蝠的响度。
r=0.5; % 蝙蝠的脉冲发射率。
Qmin=0; % 最小频率。
Qmax=2; % 最大频率。
% 随机生成初始种群。
if isvector(Lb)。
Lb=Lb'; Ub=Ub';end.% 随机生成初始种群。
Q=zeros(N,1); v=zeros(N,n); Sol=zeros(N,n);for i=1:N.Sol(i,:)=Lb+(Ub-Lb).rand(1,n); end.% 初始化适应度值。
fitness=zeros(N,1);% 最优解。
best=zeros(1,n);fmin=inf;% 开始迭代。
for t=1:Max_iteration.% 随机选择频率。
for i=1:N.Q(i)=Qmin+(Qmin-Qmax)rand;v(i,:)=v(i,:)+(Sol(i,:)-best)Q(i); S=Sol(i,:)+v(i,:);% 边界处理。
for j=1:n.if S(j)<Lb(j)。
S(j)=Lb(j);elseif S(j)>Ub(j)。
S(j)=Ub(j);end.end.if rand<A.S=best+0.001randn(1,n);end.% 评估新解。
Fnew=benchmark_func(S);% 判断是否更新最优解。
if (Fnew<=fitness(i)) && (rand<r)。
用MATLAB演示互相关算法的应用例子

用MATLAB演示互相关算法的应用例子互相关是一种在信号处理和图像处理领域常用的算法,其可以用于找到两个信号之间的相互关系。
MATLAB是一个功能强大的数值计算和科学编程语言,提供了丰富的工具和函数用于实现互相关算法。
下面将介绍两个互相关算法的应用例子,并用MATLAB进行演示。
例子一:音频信号的相似性匹配
假设我们有两段音频信号,分别是原始音频和目标音频。
我们希望找到原始音频中与目标音频最相似的部分。
通过互相关算法可以实现这个目标。
首先,我们需要将音频信号读入MATLAB中。
可以使用MATLAB的audioread函数实现:
```matlab
[inputSignal, Fs] = audioread('input.wav');
[targetSignal, Fs] = audioread('target.wav');
```
读入后的原始音频保存在`inputSignal`变量中,目标音频保存在
`targetSignal`变量中。
用Matlab实现快速傅立叶变换

用Matlab实现快速傅立叶变换FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在就根据实际经验来说说FFT结果的具体物理意义。
一个模拟信号,经过ADC采样之后,就变成了数字信号。
采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此啰嗦了。
采样得到的数字信号,就可以做FFT变换了。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。
为了方便进行FFT运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。
那么FFT之后结果就是一个为N点的复数。
每一个点就对应着一个频率点。
这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。
而第一个点就是直流分量,它的模值就是直流分量的N倍。
而每个点的相位呢,就是在该频率下的信号的相位。
第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。
Matlab中的多目标优化算法实现指南

Matlab中的多目标优化算法实现指南简介:多目标优化是在现实问题中常见的一种情况,例如在工程设计、金融投资和决策支持等领域。
Matlab作为一种强大的数值计算和工程仿真软件,提供了多种多目标优化算法的工具箱,如NSGA-II、MOGA等。
本文将介绍如何使用Matlab实现多目标优化算法,并给出一些应用示例。
一、多目标优化问题多目标优化问题是指在存在多个冲突的目标函数的情况下,找到一组最优解,使得这些目标函数能够达到最优。
在现实问题中,通常会涉及到多个目标,例如在工程设计中同时考虑成本和性能,或者在金融投资中同时考虑风险和收益等。
二、Matlab的多目标优化工具箱Matlab提供了多种多目标优化算法的工具箱,如Global Optimization Toolbox、Optimization Toolbox等。
这些工具箱可以帮助用户快速实现多目标优化算法,并且提供了丰富的优化函数和评价指标。
三、NSGA-II算法实现NSGA-II(Non-dominated Sorting Genetic Algorithm II)是一种常用的多目标优化算法,它通过遗传算法的方式来搜索最优解。
在Matlab中,我们可以使用NSGA-II工具箱来实现该算法。
1. 确定目标函数首先,我们需要确定待优化的问题中具体的目标函数,例如最小化成本和最大化性能等。
在Matlab中,我们可以使用函数句柄来定义这些目标函数。
2. 设定决策变量决策变量是影响目标函数的参数,我们需要确定这些变量的取值范围。
在Matlab中,可以使用函数句柄或者向量来定义这些变量。
3. 设定其他参数除了目标函数和决策变量,NSGA-II算法还需要其他一些参数,例如种群大小、迭代次数等。
在Matlab中,我们可以使用结构体来存储这些参数。
4. 运行算法将目标函数、决策变量和其他参数传递给NSGA-II工具箱,然后运行算法。
Matlab会自动进行优化计算,并给出一组最优解。
霍夫曼编码matlab

霍夫曼编码matlab在Matlab中实现霍夫曼编码可以通过以下步骤完成:1. 构建霍夫曼树,首先,你需要根据输入的数据统计每个符号出现的频率。
然后,使用这些频率构建霍夫曼树。
你可以使用Matlab中的数据结构来表示霍夫曼树,比如使用结构体或者类来表示节点。
2. 生成霍夫曼编码,一旦构建了霍夫曼树,你可以通过遍历树的方式生成每个符号对应的霍夫曼编码。
这可以通过递归或者迭代的方式实现。
3. 对数据进行编码和解码,使用生成的霍夫曼编码对输入的数据进行编码,然后再对编码后的数据进行解码。
这可以帮助你验证霍夫曼编码的正确性。
以下是一个简单的示例代码,用于在Matlab中实现霍夫曼编码: matlab.% 假设有一个包含符号频率的向量 freq 和对应符号的向量symbols.% 构建霍夫曼树。
huffTree = hufftree(freq);% 生成霍夫曼编码。
huffCodes = huffenco(symbols, huffTree);% 对数据进行编码。
data = [1 0 1 1 0 1 1 1]; % 你的输入数据。
encodedData = huffenco(data, huffCodes);% 对数据进行解码。
decodedData = huffmandeco(encodedData, huffTree);需要注意的是,以上代码仅为简单示例,实际应用中可能需要根据具体情况进行调整和完善。
同时,对于大规模数据的处理,也需要考虑到内存和性能方面的优化。
希望这个简单的示例能够帮助你在Matlab中实现霍夫曼编码。
共轭梯度法matlab程序

共轭梯度法matlab程序共轭梯度法是一种用于求解无约束优化问题的迭代算法。
以下是一个简单的MATLAB 程序示例,用于实现共轭梯度法:matlab复制代码function[x, fval, iter] = conjugate_gradient(A, b, x0, tol,max_iter)% A: 矩阵% b: 向量% x0: 初始解% tol: 容忍度% max_iter: 最大迭代次数r = b - A*x0;p = r;x = x0;fval = A*x - b;iter = 0;while (norm(r) > tol) && (iter < max_iter)Ap = A*p;alpha = dot(p, r) / dot(p, Ap);x = x + alpha*p;r = r - alpha*Ap;if iter == 0fval_new = dot(r, r);elsebeta = dot(r, r) / dot(p, Ap);p = r + beta*p;fval_new = dot(r, r);endif fval_new < fvalfval = fval_new;enditer = iter + 1;endend该程序接受一个矩阵A、一个向量b、一个初始解x0、一个容忍度tol和一个最大迭代次数max_iter作为输入,并返回最终解x、目标函数值fval和迭代次数iter。
使用该函数时,您需要将要优化的目标函数转换为矩阵形式,并调用该函数来找到最优解。
例如,假设您要最小化一个函数f(x),可以将该函数转换为矩阵形式A*x - b,其中A是目标函数的雅可比矩阵,b是目标函数的常数项向量。
然后,您可以调用该函数来找到最优解,例如:matlab复制代码A = jacobian(f); % 计算目标函数的雅可比矩阵b = [1, 2, 3]; % 目标函数的常数项向量x0 = [0, 0, 0]; % 初始解向量tol = 1e-6; % 容忍度max_iter = 1000; % 最大迭代次数[x, fval, iter] = conjugate_gradient(A, b, x0, tol, max_iter); % 调用共轭梯度法函数求解最优解。
matlab迭代函数程序

matlab迭代函数程序Matlab是一种高级的数学软件,其内置了许多迭代函数,可以帮助用户更方便地进行数值计算和数据分析。
本文将介绍一些常用的Matlab迭代函数及其应用,希望能够对读者有所帮助。
一、for循环for循环是Matlab中最基本的迭代函数之一,其语法格式为: for 循环变量=初始值:步长:终止值循环体end其中,循环变量是一个标量或向量,初始值、步长和终止值都是数值。
循环体中的语句将会被重复执行,直到循环变量达到终止值为止。
下面是一个简单的例子,计算1到10的累加和:sum = 0;for i = 1:10sum = sum + i;enddisp(sum);输出结果为55,即1+2+3+...+10的和。
二、while循环while循环是另一种常用的迭代函数,其语法格式为:while 条件循环体end其中,条件可以是任何能够返回逻辑值的表达式,循环体中的语句将会被重复执行,直到条件为假为止。
下面是一个简单的例子,计算1到10的累加和:sum = 0;i = 1;while i <= 10sum = sum + i;i = i + 1;enddisp(sum);输出结果为55,与for循环的结果相同。
三、递归函数递归函数是一种特殊的函数,其定义中包含对自身的调用。
在Matlab中,递归函数的语法与普通函数相同,但需要注意避免死循环。
下面是一个递归函数的例子,计算n的阶乘:function f = factorial(n)if n == 0f = 1;elsef = n * factorial(n-1);endend该函数首先判断n是否为0,若是则返回1;否则返回n乘以n-1的阶乘。
例如,计算5的阶乘可以使用以下语句:disp(factorial(5));输出结果为120。
四、向量化运算向量化运算是Matlab的一大特色,可以大大提高计算效率。
其基本思想是将循环语句转化为矩阵运算,避免了循环带来的额外开销。
MATLAB实现快速傅里叶变换的原理和基本代码
MATLAB实现快速傅里叶变换的原理和基本代码
作者:头铁的小甘
快速傅里叶变换原理
在分析和处理信号时,一般需要将信号时域转换到频域空间表示,这样可以清楚知道信号的频率成分分布,也便于对其进行信息提取,滤波、去噪等操作。
由于计算复杂和繁琐,一般采取计算机进行计算和处理,为了提高计算速率,快速傅里叶变换应运而生,大大减少计算机的乘法操作,因此大幅度减少计算时间。
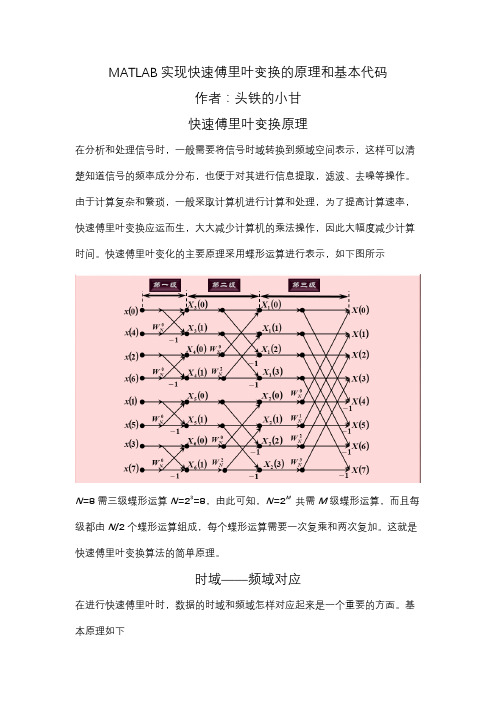
快速傅里叶变化的主要原理采用蝶形运算进行表示,如下图所示
N=8需三级蝶形运算N=23=8,由此可知,N=2M共需M级蝶形运算,而且每级都由N/2个蝶形运算组成,每个蝶形运算需要一次复乘和两次复加。
这就是快速傅里叶变换算法的简单原理。
时域——频域对应
在进行快速傅里叶时,数据的时域和频域怎样对应起来是一个重要的方面。
基本原理如下
模拟数据进行采样成离散时间,便于计算机操作,采样满足奈奎斯特定理,所以采样间隔就是1/fs,fs是采样频率。
对于频域来说:总长应该是采样频率,步长应该为fs/n,n是数据样本的数据长度。
对应原理图如下所示
Matlab快速傅里叶变换基本代码
结果显示
按照三角函数的傅里叶变换,图中可以看到幅频特性应该是在f=100Hz是呈现狄拉克函数(冲激函数),数据点越多越满足结果。
信赖域方法 matlab 代码

信赖域方法是一种在优化问题中常用的数值方法。
它是一种迭代算法,通常用于解决无约束非线性优化问题。
信赖域方法以牛顿方法为基础,通过限制每次迭代中自变量的变化范围来保证收敛性和稳定性。
在matlab中,可以使用信赖域方法来解决各种实际问题,例如最小二乘拟合、参数估计和非线性方程组求解等。
在使用matlab实现信赖域方法时,需注意以下几点:1. 定义优化目标函数。
在使用信赖域方法优化问题时,首先需要定义一个目标函数。
该函数应该是一个关于自变量的非线性函数,可以是一个标量函数,也可以是一个向量函数。
2. 定义目标函数的梯度和海森矩阵。
由于信赖域方法是基于牛顿方法的改进算法,因此需要定义目标函数的梯度和海森矩阵。
这两个定义通常是问题的难点,需要根据实际问题进行推导和计算。
3. 设置算法参数。
信赖域方法有许多参数可以调整,如信赖域半径、收敛容许度等。
在matlab中,需要根据实际问题设置这些参数,以保证算法能够顺利收敛。
4. 编写优化函数。
在matlab中,可以使用内置的`fminunc`函数来实现信赖域方法。
这个函数可以接受目标函数及其梯度和海森矩阵作为输入,然后自动进行优化计算。
以下是一个使用matlab实现信赖域方法的示例代码:```matlab定义目标函数function f = myfun(x)f = (x(1)-1)^2 + (x(2)-2.5)^2;end定义目标函数的梯度function g = mygrad(x)g = [2*(x(1)-1); 2*(x(2)-2.5)];end设置算法参数options = optimoptions('fminunc','Algorithm','trust-region','SpecifyObjectiveGradient',true);编写优化函数x0 = [0,0];[x,fval,exitflag,output,grad,hessian] = fminunc(myfun,x0,options); ```在这个示例代码中,首先定义了一个简单的目标函数`myfun`,然后定义了该函数的梯度`mygrad`。
matlab智能算法代码

matlab智能算法代码MATLAB是一种功能强大的数值计算和科学编程软件,它提供了许多智能算法的实现。
下面是一些常见的智能算法及其在MATLAB中的代码示例:1. 遗传算法(Genetic Algorithm):MATLAB中有一个专门的工具箱,称为Global Optimization Toolbox,其中包含了遗传算法的实现。
以下是一个简单的遗传算法示例代码:matlab.% 定义目标函数。
fitness = @(x) x^2;% 设置遗传算法参数。
options = gaoptimset('Display', 'iter','PopulationSize', 50);% 运行遗传算法。
[x, fval] = ga(fitness, 1, options);2. 粒子群优化算法(Particle Swarm Optimization):MATLAB中也有一个工具箱,称为Global Optimization Toolbox,其中包含了粒子群优化算法的实现。
以下是一个简单的粒子群优化算法示例代码:matlab.% 定义目标函数。
fitness = @(x) x^2;% 设置粒子群优化算法参数。
options = optimoptions('particleswarm', 'Display','iter', 'SwarmSize', 50);% 运行粒子群优化算法。
[x, fval] = particleswarm(fitness, 1, [], [], options);3. 支持向量机(Support Vector Machine):MATLAB中有一个机器学习工具箱,称为Statistics and Machine Learning Toolbox,其中包含了支持向量机的实现。
matlab法诺拟合

matlab法诺拟合在MATLAB中进行法诺(Fano)拟合通常涉及对实验数据进行处理和分析,以提取有关共振或散射过程的信息。
法诺共振是一种在物理系统中观察到的现象,其中离散态和连续态之间的相互作用导致了一个不对称的线型。
要在MATLAB中进行法诺拟合,你可以遵循以下步骤:1.导入数据:首先,你需要将实验数据导入MATLAB。
这通常涉及读取包含频谱数据的文件。
2.定义法诺公式:法诺共振的线型可以用一个特定的公式来描述,该公式通常包括一个洛伦兹项和一个干扰项。
在MATLAB中,你可以定义一个函数来表示这个公式。
3.拟合数据:使用MATLAB的拟合工具箱(例如fit函数或lsqcurvefit函数)来拟合你的数据。
你需要提供实验数据和法诺公式作为输入,并调整公式中的参数以获得最佳拟合。
4.评估拟合质量:通过计算拟合残差、R-square值等指标来评估拟合的质量。
5.可视化结果:使用MATLAB的绘图功能来显示原始数据和拟合曲线,以便直观地检查拟合效果。
以下是一个简化的示例代码,展示了如何在MATLAB中进行基本的法诺拟合:matlab复制代码% 导入数据% 假设你已经有了两个向量:frequency(频率)和 amplitude (幅度)% 定义法诺公式fano_formula = @(B, f) (B(1).*(f-B(2)).^2) ./ ((f-B(2)).^2 + B(3).^2) + B(4);% 初始参数估计initial_params = [1, 0, 1, 0]; % 这些值需要根据你的数据进行调整% 使用lsqcurvefit进行拟合fitted_params = lsqcurvefit(fano_formula,initial_params, frequency, amplitude);% 可视化结果figure;plot(frequency, amplitude, 'b.'); % 原始数据hold on;f = linspace(min(frequency), max(frequency), 1000); plot(f, fano_formula(fitted_params, f), 'r-'); % 拟合曲线xlabel('Frequency');ylabel('Amplitude');legend('Data', 'Fano Fit');title('Fano Resonance Fit');请注意,这个示例是一个基本的指导,你可能需要根据你的具体数据和需求进行调整。
Affinity Propagation聚类算法的研究及应用的开题报告

Affinity Propagation聚类算法的研究及应用的开题报告一、选题背景随着互联网和移动互联网的快速发展,数据量不断增加,如何从大数据中寻找到有价值的信息并且能够有效地对其进行处理和分析,成为了数据科学家们需要解决的实际问题。
而聚类算法作为数据分析的一种重要手段,能够发现数据中的不同类别,为数据处理提供基础。
目前,聚类算法在生物信息学、图像处理、文本挖掘和金融等领域得到了广泛的应用。
Affinity Propagation(AP)算法是Clustering Research Group在2007年提出的一种聚类算法。
与传统的聚类算法相比,AP算法无需预先设定聚类的个数,并且不需要训练数据,可以自动对数据进行聚类,并且能够有效的处理高维数据。
二、研究目的本文的研究目的是深入研究Affinity Propagation聚类算法的理论基础和实现方法,并且探究算法在数据挖掘领域中的具体应用。
通过对算法进行分析和优化,提高算法的执行效率和准确性,并且通过实验验证算法的实用性和可行性。
三、研究内容1. Affinity Propagation聚类算法的理论基础2. Affinity Propagation聚类算法的算法流程和实现方法3. Affinity Propagation聚类算法的主要优缺点及适用范围4. Affinity Propagation聚类算法在图像处理、文本挖掘和生物信息学等领域中的应用5. 通过实验验证Affinity Propagation聚类算法的效果,并且优化算法四、研究方法本文采用文献调研和实验验证相结合的方法,对Affinity Propagation聚类算法进行深入的研究和探讨。
在理论分析的基础上,通过编写程序实现算法,验证算法的正确性和实用性,并且通过实验对算法进行优化。
五、预期结果1. 深入了解Affinity Propagation聚类算法的理论基础和实现方法2. 探究算法在不同领域的实际应用3. 验证算法的准确性和可行性4. 对算法进行优化,提高算法的执行效率六、研究意义Affinity Propagation聚类算法是一种新型的聚类算法,在数据挖掘和机器学习领域受到越来越多的关注。
affinity propagation算法Matlab代码实现

%APCLUSTER Affinity Propagation Clustering (Frey/Dueck, Science 2007) % [idx,netsim,dpsim,expref]=APCLUSTER(s,p) clusters data, using a set% of real-valued pairwise data point similarities as input. Clusters% are each represented by a cluster center data point (the "exemplar"). % The method is iterative and searches for clusters so as to maximize% an objective function, called net similarity.%% For N data points, there are potentially N^2-N pairwise similarities;% this can be input as an N-by-N matrix 's', where s(i,k) is the% similarity of point i to point k (s(i,k) needn抰equal s(k,i)). In% fact, only a smaller number of relevant similarities are needed; if% only M similarity values are known (M < N^2-N) they can be input as % an M-by-3 matrix with each row being an (i,j,s(i,j)) triple.%% APCLUSTER automatically determines the number of clusters based on % the input preference 'p', a real-valued N-vector. p(i) indicates the% preference that data point i be chosen as an exemplar. Often a good% choice is to set all preferences to median(s); the number of clusters% identified can be adjusted by changing this value accordingly. If 'p'% is a scalar, APCLUSTER assumes all preferences are that shared value. %% The clustering solution is returned in idx. idx(j) is the index of% the exemplar for data point j; idx(j)==j indicates data point j% is itself an exemplar. The sum of the similarities of the data points to % their exemplars is returned as dpsim, the sum of the preferences of% the identified exemplars is returned in expref and the net similarity% objective function returned is their sum, i.e. netsim=dpsim+expref.%% [ ... ]=apcluster(s,p,'NAME',VALUE,...) allows you to specify% optional parameter name/value pairs as follows:%% 'maxits' maximum number of iterations (default: 1000)% 'convits' if the estimated exemplars stay fixed for convits% iterations, APCLUSTER terminates early (default: 100)% 'dampfact' update equation damping level in [0.5, 1). Higher % values correspond to heavy damping, which may be needed % if oscillations occur. (default: 0.9)% 'plot' (no value needed) Plots netsim after each iteration% 'details' (no value needed) Outputs iteration-by-iteration% details (greater memory requirements)% 'nonoise' (no value needed) APCLUSTER adds a small amount of % noise to 's' to prevent degenerate cases; this disables that.%% Copyright (c) B.J. Frey & D. Dueck (2006). This software may be% freely used and distributed for non-commercial purposes.% (RUN APCLUSTER WITHOUT ARGUMENTS FOR DEMO CODE)function [idx,netsim,dpsim,expref]=apcluster(s,p,varargin);if nargin==0, % display demofprintf('Affinity Propagation (APCLUSTER) sample/demo code\n\n');fprintf('N=100; x=rand(N,2); % Create N, 2-D data points\n');fprintf('M=N*N-N; s=zeros(M,3); % Make ALL N^2-N similarities\n');fprintf('j=1;\n');fprintf('for i=1:N\n');fprintf(' for k=[1:i-1,i+1:N]\n');fprintf(' s(j,1)=i; s(j,2)=k; s(j,3)=-sum((x(i,:)-x(k,:)).^2);\n');fprintf(' j=j+1;\n');fprintf(' end;\n');fprintf('end;\n');fprintf('p=median(s(:,3)); % Set preference to median similarity\n');fprintf('[idx,netsim,dpsim,expref]=apcluster(s,p,''plot'');\n');fprintf('fprintf(''Number of clusters: %%d\\n'',length(unique(idx)));\n');fprintf('fprintf(''Fitness (net similarity): %%g\\n'',netsim);\n');fprintf('figure; % Make a figures showing the data and the clusters\n');fprintf('for i=unique(idx)''\n');fprintf(' ii=find(idx==i); h=plot(x(ii,1),x(ii,2),''o''); hold on;\n');fprintf(' col=rand(1,3); set(h,''Color'',col,''MarkerFaceColor'',col);\n');fprintf(' xi1=x(i,1)*ones(size(ii)); xi2=x(i,2)*ones(size(ii)); \n');fprintf(' line([x(ii,1),xi1]'',[x(ii,2),xi2]'',''Color'',col);\n');fprintf('end;\n');fprintf('axis equal tight;\n\n');return;end;start = clock;% Handle arguments to functionif nargin<2 error('Too few input arguments');elsemaxits=1000; convits=100; lam=0.9; plt=0; details=0; nonoise=0;i=1;while i<=length(varargin)if strcmp(varargin{i},'plot')plt=1; i=i+1;elseif strcmp(varargin{i},'details')details=1; i=i+1;elseif strcmp(varargin{i},'sparse')% [idx,netsim,dpsim,expref]=apcluster_sparse(s,p,varargin{:});fprintf('''sparse'' argument no longer supported; see website for additional software\n\n');return;elseif strcmp(varargin{i},'nonoise')nonoise=1; i=i+1;elseif strcmp(varargin{i},'maxits')maxits=varargin{i+1};i=i+2;if maxits<=0 error('maxits must be a positive integer'); end;elseif strcmp(varargin{i},'convits')convits=varargin{i+1};i=i+2;if convits<=0 error('convits must be a positive integer'); end;elseif strcmp(varargin{i},'dampfact')lam=varargin{i+1};i=i+2;if (lam<0.5)||(lam>=1)error('dampfact must be >= 0.5 and < 1');end;else i=i+1;end;end;end;if lam>0.9fprintf('\n*** Warning: Large damping factor in use. Turn on plotting\n');fprintf(' to monitor the net similarity. The algorithm will\n');fprintf(' change decisions slowly, so consider using a larger value\n');fprintf(' of convits.\n\n');end;% Check that standard arguments are consistent in sizeif length(size(s))~=2 error('s should be a 2D matrix');elseif length(size(p))>2 error('p should be a vector or a scalar');elseif size(s,2)==3tmp=max(max(s(:,1)),max(s(:,2)));if length(p)==1 N=tmp; else N=length(p); end;if tmp>Nerror('data point index exceeds number of data points');elseif min(min(s(:,1)),min(s(:,2)))<=0error('data point indices must be >= 1');end;elseif size(s,1)==size(s,2)N=size(s,1);if (length(p)~=N)&&(length(p)~=1)error('p should be scalar or a vector of size N');end;else error('s must have 3 columns or be square'); end;% Construct similarity matrixif N>3000fprintf('\n*** Warning: Large memory request. Consider activating\n');fprintf(' the sparse version of APCLUSTER.\n\n');end;if size(s,2)==3 && size(s,1)~=3,S=-Inf*ones(N,N,class(s));for j=1:size(s,1), S(s(j,1),s(j,2))=s(j,3); end;else S=s;end;if S==S', symmetric=true; else symmetric=false; end;realmin_=realmin(class(s)); realmax_=realmax(class(s));% In case user did not remove degeneracies from the input similarities,% avoid degenerate solutions by adding a small amount of noise to the% input similaritiesif ~nonoiserns=randn('state'); randn('state',0);S=S+(eps*S+realmin_*100).*rand(N,N);randn('state',rns);end;% Place preferences on the diagonal of Sif length(p)==1 for i=1:N S(i,i)=p; end;else for i=1:N S(i,i)=p(i); end;end;% Numerical stability -- replace -INF with -realmaxn=find(S<-realmax_); if ~isempty(n), warning('-INF similarities detected; changing to -REALMAX to ensure numerical stability'); S(n)=-realmax_; end; clear('n');if ~isempty(find(S>realmax_,1)), error('+INF similarities detected; change to a large positive value (but smaller than +REALMAX)'); end;% Allocate space for messages, etcdS=diag(S); A=zeros(N,N,class(s)); R=zeros(N,N,class(s)); t=1;if plt, netsim=zeros(1,maxits+1); end;if detailsidx=zeros(N,maxits+1);netsim=zeros(1,maxits+1);dpsim=zeros(1,maxits+1);expref=zeros(1,maxits+1);end;% Execute parallel affinity propagation updatese=zeros(N,convits); dn=0; i=0;if symmetric, ST=S; else ST=S'; end; % saves memory if it's symmetricwhile ~dni=i+1;% Compute responsibilitiesA=A'; R=R';for ii=1:N,old = R(:,ii);AS = A(:,ii) + ST(:,ii); [Y,I]=max(AS); AS(I)=-Inf;[Y2,I2]=max(AS);R(:,ii)=ST(:,ii)-Y;R(I,ii)=ST(I,ii)-Y2;R(:,ii)=(1-lam)*R(:,ii)+lam*old; % DampingR(R(:,ii)>realmax_,ii)=realmax_;end;A=A'; R=R';% Compute availabilitiesfor jj=1:N,old = A(:,jj);Rp = max(R(:,jj),0); Rp(jj)=R(jj,jj);A(:,jj) = sum(Rp)-Rp;dA = A(jj,jj); A(:,jj) = min(A(:,jj),0); A(jj,jj) = dA;A(:,jj) = (1-lam)*A(:,jj) + lam*old; % Dampingend;% Check for convergenceE=((diag(A)+diag(R))>0); e(:,mod(i-1,convits)+1)=E; K=sum(E);if i>=convits || i>=maxits,se=sum(e,2);unconverged=(sum((se==convits)+(se==0))~=N);if (~unconverged&&(K>0))||(i==maxits) dn=1; end;end;% Handle plotting and storage of details, if requestedif plt||detailsif K==0tmpnetsim=nan; tmpdpsim=nan; tmpexpref=nan; tmpidx=nan;elseI=find(E); notI=find(~E); [tmp c]=max(S(:,I),[],2); c(I)=1:K; tmpidx=I(c);tmpdpsim=sum(S(sub2ind([N N],notI,tmpidx(notI))));tmpexpref=sum(dS(I));tmpnetsim=tmpdpsim+tmpexpref;end;end;if detailsnetsim(i)=tmpnetsim; dpsim(i)=tmpdpsim; expref(i)=tmpexpref;idx(:,i)=tmpidx;end;if plt,netsim(i)=tmpnetsim;figure(234);plot(((netsim(1:i)/10)*100)/10,'r-'); xlim([0 i]); % plot barely-finite stuff as infinitexlabel('# Iterations');ylabel('Fitness (net similarity) of quantized intermediate solution');% drawnow;end;end; % iterationsI=find((diag(A)+diag(R))>0); K=length(I); % Identify exemplarsif K>0[tmp c]=max(S(:,I),[],2); c(I)=1:K; % Identify clusters% Refine the final set of exemplars and clusters and return resultsfor k=1:K ii=find(c==k); [y j]=max(sum(S(ii,ii),1)); I(k)=ii(j(1)); end; notI=reshape(setdiff(1:N,I),[],1);[tmp c]=max(S(:,I),[],2); c(I)=1:K; tmpidx=I(c);tmpdpsim=sum(S(sub2ind([N N],notI,tmpidx(notI))));tmpexpref=sum(dS(I));tmpnetsim=tmpdpsim+tmpexpref;elsetmpidx=nan*ones(N,1); tmpnetsim=nan; tmpexpref=nan;end;if detailsnetsim(i+1)=tmpnetsim; netsim=netsim(1:i+1);dpsim(i+1)=tmpdpsim; dpsim=dpsim(1:i+1);expref(i+1)=tmpexpref; expref=expref(1:i+1);idx(:,i+1)=tmpidx; idx=idx(:,1:i+1);elsenetsim=tmpnetsim; dpsim=tmpdpsim; expref=tmpexpref; idx=tmpidx;end;if plt||detailsfprintf('\nNumber of exemplars identified: %d (for %d data points)\n',K,N);fprintf('Net similarity: %g\n',tmpnetsim);fprintf(' Similarities of data points to exemplars: %g\n',dpsim(end));fprintf(' Preferences of selected exemplars: %g\n',tmpexpref);fprintf('Number of iterations: %d\n\n',i);fprintf('Elapsed time: %g sec\n',etime(clock,start));end;if unconvergedfprintf('\n*** Warning: Algorithm did not converge. Activate plotting\n');fprintf(' so that you can monitor the net similarity. Consider\n');fprintf(' increasing maxits and convits, and, if oscillations occur\n');fprintf(' also increasing dampfact.\n\n');end;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%APCLUSTER Affinity Propagation Clustering (Frey/Dueck, Science 2007) % [idx,netsim,dpsim,expref]=APCLUSTER(s,p) clusters data, using a set% of real-valued pairwise data point similarities as input. Clusters% are each represented by a cluster center data point (the "exemplar"). % The method is iterative and searches for clusters so as to maximize% an objective function, called net similarity.%% For N data points, there are potentially N^2-N pairwise similarities;% this can be input as an N-by-N matrix 's', where s(i,k) is the% similarity of point i to point k (s(i,k) needn抰equal s(k,i)). In% fact, only a smaller number of relevant similarities are needed; if% only M similarity values are known (M < N^2-N) they can be input as % an M-by-3 matrix with each row being an (i,j,s(i,j)) triple.%% APCLUSTER automatically determines the number of clusters based on % the input preference 'p', a real-valued N-vector. p(i) indicates the% preference that data point i be chosen as an exemplar. Often a good% choice is to set all preferences to median(s); the number of clusters% identified can be adjusted by changing this value accordingly. If 'p'% is a scalar, APCLUSTER assumes all preferences are that shared value. %% The clustering solution is returned in idx. idx(j) is the index of% the exemplar for data point j; idx(j)==j indicates data point j% is itself an exemplar. The sum of the similarities of the data points to % their exemplars is returned as dpsim, the sum of the preferences of% the identified exemplars is returned in expref and the net similarity% objective function returned is their sum, i.e. netsim=dpsim+expref.%% [ ... ]=apcluster(s,p,'NAME',VALUE,...) allows you to specify% optional parameter name/value pairs as follows:%% 'maxits' maximum number of iterations (default: 1000)% 'convits' if the estimated exemplars stay fixed for convits% iterations, APCLUSTER terminates early (default: 100)% 'dampfact' update equation damping level in [0.5, 1). Higher % values correspond to heavy damping, which may be needed % if oscillations occur. (default: 0.9)% 'plot' (no value needed) Plots netsim after each iteration% 'details' (no value needed) Outputs iteration-by-iteration% details (greater memory requirements)% 'nonoise' (no value needed) APCLUSTER adds a small amount of % noise to 's' to prevent degenerate cases; this disables that.%% Copyright (c) B.J. Frey & D. Dueck (2006). This software may be% freely used and distributed for non-commercial purposes.% (RUN APCLUSTER WITHOUT ARGUMENTS FOR DEMO CODE)function [idx,netsim,dpsim,expref]=apcluster(s,p,varargin);if nargin==0, % display demofprintf('Affinity Propagation (APCLUSTER) sample/demo code\n\n');fprintf('N=100; x=rand(N,2); % Create N, 2-D data points\n');fprintf('M=N*N-N; s=zeros(M,3); % Make ALL N^2-N similarities\n');fprintf('j=1;\n');fprintf('for i=1:N\n');fprintf(' for k=[1:i-1,i+1:N]\n');fprintf(' s(j,1)=i; s(j,2)=k; s(j,3)=-sum((x(i,:)-x(k,:)).^2);\n');fprintf(' j=j+1;\n');fprintf(' end;\n');fprintf('end;\n');fprintf('p=median(s(:,3)); % Set preference to median similarity\n');fprintf('[idx,netsim,dpsim,expref]=apcluster(s,p,''plot'');\n');fprintf('fprintf(''Number of clusters: %%d\\n'',length(unique(idx)));\n');fprintf('fprintf(''Fitness (net similarity): %%g\\n'',netsim);\n');fprintf('figure; % Make a figures showing the data and the clusters\n');fprintf('for i=unique(idx)''\n');fprintf(' ii=find(idx==i); h=plot(x(ii,1),x(ii,2),''o''); hold on;\n');fprintf(' col=rand(1,3); set(h,''Color'',col,''MarkerFaceColor'',col);\n');fprintf(' xi1=x(i,1)*ones(size(ii)); xi2=x(i,2)*ones(size(ii)); \n');fprintf(' line([x(ii,1),xi1]'',[x(ii,2),xi2]'',''Color'',col);\n');fprintf('end;\n');fprintf('axis equal tight;\n\n');return;end;start = clock;% Handle arguments to functionif nargin<2 error('Too few input arguments');elsemaxits=1000; convits=100; lam=0.9; plt=0; details=0; nonoise=0;i=1;while i<=length(varargin)if strcmp(varargin{i},'plot')plt=1; i=i+1;elseif strcmp(varargin{i},'details')details=1; i=i+1;elseif strcmp(varargin{i},'sparse')% [idx,netsim,dpsim,expref]=apcluster_sparse(s,p,varargin{:});fprintf('''sparse'' argument no longer supported; see website for additional software\n\n');return;elseif strcmp(varargin{i},'nonoise')nonoise=1; i=i+1;elseif strcmp(varargin{i},'maxits')maxits=varargin{i+1};i=i+2;if maxits<=0 error('maxits must be a positive integer'); end;elseif strcmp(varargin{i},'convits')convits=varargin{i+1};i=i+2;if convits<=0 error('convits must be a positive integer'); end;elseif strcmp(varargin{i},'dampfact')lam=varargin{i+1};i=i+2;if (lam<0.5)||(lam>=1)error('dampfact must be >= 0.5 and < 1');end;else i=i+1;end;end;end;if lam>0.9fprintf('\n*** Warning: Large damping factor in use. Turn on plotting\n');fprintf(' to monitor the net similarity. The algorithm will\n');fprintf(' change decisions slowly, so consider using a larger value\n');fprintf(' of convits.\n\n');end;% Check that standard arguments are consistent in sizeif length(size(s))~=2 error('s should be a 2D matrix');elseif length(size(p))>2 error('p should be a vector or a scalar');elseif size(s,2)==3tmp=max(max(s(:,1)),max(s(:,2)));if length(p)==1 N=tmp; else N=length(p); end;if tmp>Nerror('data point index exceeds number of data points');elseif min(min(s(:,1)),min(s(:,2)))<=0error('data point indices must be >= 1');end;elseif size(s,1)==size(s,2)N=size(s,1);if (length(p)~=N)&&(length(p)~=1)error('p should be scalar or a vector of size N');end;else error('s must have 3 columns or be square'); end;% Construct similarity matrixif N>3000fprintf('\n*** Warning: Large memory request. Consider activating\n');fprintf(' the sparse version of APCLUSTER.\n\n');end;if size(s,2)==3 && size(s,1)~=3,S=-Inf*ones(N,N,class(s));for j=1:size(s,1), S(s(j,1),s(j,2))=s(j,3); end;else S=s;end;if S==S', symmetric=true; else symmetric=false; end;realmin_=realmin(class(s)); realmax_=realmax(class(s));% In case user did not remove degeneracies from the input similarities,% avoid degenerate solutions by adding a small amount of noise to the% input similaritiesif ~nonoiserns=randn('state'); randn('state',0);S=S+(eps*S+realmin_*100).*rand(N,N);randn('state',rns);end;% Place preferences on the diagonal of Sif length(p)==1 for i=1:N S(i,i)=p; end;else for i=1:N S(i,i)=p(i); end;end;% Numerical stability -- replace -INF with -realmaxn=find(S<-realmax_); if ~isempty(n), warning('-INF similarities detected; changing to -REALMAX to ensure numerical stability'); S(n)=-realmax_; end; clear('n');if ~isempty(find(S>realmax_,1)), error('+INF similarities detected; change to a large positive value (but smaller than +REALMAX)'); end;% Allocate space for messages, etcdS=diag(S); A=zeros(N,N,class(s)); R=zeros(N,N,class(s)); t=1;if plt, netsim=zeros(1,maxits+1); end;if detailsidx=zeros(N,maxits+1);netsim=zeros(1,maxits+1);dpsim=zeros(1,maxits+1);expref=zeros(1,maxits+1);end;% Execute parallel affinity propagation updatese=zeros(N,convits); dn=0; i=0;if symmetric, ST=S; else ST=S'; end; % saves memory if it's symmetricwhile ~dni=i+1;% Compute responsibilitiesA=A'; R=R';for ii=1:N,old = R(:,ii);AS = A(:,ii) + ST(:,ii); [Y,I]=max(AS); AS(I)=-Inf;[Y2,I2]=max(AS);R(:,ii)=ST(:,ii)-Y;R(I,ii)=ST(I,ii)-Y2;R(:,ii)=(1-lam)*R(:,ii)+lam*old; % DampingR(R(:,ii)>realmax_,ii)=realmax_;end;A=A'; R=R';% Compute availabilitiesfor jj=1:N,old = A(:,jj);Rp = max(R(:,jj),0); Rp(jj)=R(jj,jj);A(:,jj) = sum(Rp)-Rp;dA = A(jj,jj); A(:,jj) = min(A(:,jj),0); A(jj,jj) = dA;A(:,jj) = (1-lam)*A(:,jj) + lam*old; % Dampingend;% Check for convergenceE=((diag(A)+diag(R))>0); e(:,mod(i-1,convits)+1)=E; K=sum(E);if i>=convits || i>=maxits,se=sum(e,2);unconverged=(sum((se==convits)+(se==0))~=N);if (~unconverged&&(K>0))||(i==maxits) dn=1; end;end;% Handle plotting and storage of details, if requestedif plt||detailsif K==0tmpnetsim=nan; tmpdpsim=nan; tmpexpref=nan; tmpidx=nan;elseI=find(E); notI=find(~E); [tmp c]=max(S(:,I),[],2); c(I)=1:K; tmpidx=I(c);tmpdpsim=sum(S(sub2ind([N N],notI,tmpidx(notI))));tmpexpref=sum(dS(I));tmpnetsim=tmpdpsim+tmpexpref;end;end;if detailsnetsim(i)=tmpnetsim; dpsim(i)=tmpdpsim; expref(i)=tmpexpref;idx(:,i)=tmpidx;end;if plt,netsim(i)=tmpnetsim;figure(234);plot(((netsim(1:i)/10)*100)/10,'r-'); xlim([0 i]); % plot barely-finite stuff as infinitexlabel('# Iterations');ylabel('Fitness (net similarity) of quantized intermediate solution');% drawnow;end;end; % iterationsI=find((diag(A)+diag(R))>0); K=length(I); % Identify exemplarsif K>0[tmp c]=max(S(:,I),[],2); c(I)=1:K; % Identify clusters% Refine the final set of exemplars and clusters and return resultsfor k=1:K ii=find(c==k); [y j]=max(sum(S(ii,ii),1)); I(k)=ii(j(1)); end; notI=reshape(setdiff(1:N,I),[],1);[tmp c]=max(S(:,I),[],2); c(I)=1:K; tmpidx=I(c);tmpdpsim=sum(S(sub2ind([N N],notI,tmpidx(notI))));tmpexpref=sum(dS(I));tmpnetsim=tmpdpsim+tmpexpref;elsetmpidx=nan*ones(N,1); tmpnetsim=nan; tmpexpref=nan;end;if detailsnetsim(i+1)=tmpnetsim; netsim=netsim(1:i+1);dpsim(i+1)=tmpdpsim; dpsim=dpsim(1:i+1);expref(i+1)=tmpexpref; expref=expref(1:i+1);idx(:,i+1)=tmpidx; idx=idx(:,1:i+1);elsenetsim=tmpnetsim; dpsim=tmpdpsim; expref=tmpexpref; idx=tmpidx;end;if plt||detailsfprintf('\nNumber of exemplars identified: %d (for %d data points)\n',K,N);fprintf('Net similarity: %g\n',tmpnetsim);fprintf(' Similarities of data points to exemplars: %g\n',dpsim(end));fprintf(' Preferences of selected exemplars: %g\n',tmpexpref);fprintf('Number of iterations: %d\n\n',i);fprintf('Elapsed time: %g sec\n',etime(clock,start));end;if unconvergedfprintf('\n*** Warning: Algorithm did not converge. Activate plotting\n');fprintf(' so that you can monitor the net similarity. Consider\n');fprintf(' increasing maxits and convits, and, if oscillations occur\n');fprintf(' also increasing dampfact.\n\n');end;。
