综合训练(二)相似
2021年高考语文二轮复习 专题综合训练2

2021年高考语文二轮复习专题综合训练21.下面这首小诗借“梅”表达了作者对“生命”的思考,请选择另一事物表达你对另一话题的思考。
梅一片玉瓣,是一滴生命;剥落了生命,你召来了燕语和莺啼。
【解析】本题要注意三个方面:(1)根据“一片玉瓣,是一滴生命”,要描绘出形象特点;(2)根据“剥落了生命,你召来了燕语和莺啼”,要准确描写内在品质;(3)要符合逻辑,有一定哲理性。
【答案】书:一页历史,是一面镜子;擦亮了镜子,你呼唤着理性与良知。
船:一片归帆,是一缕乡情;倾注着乡情,你满载着沧桑和希望。
2.仿照下面诗歌的修辞手法,选取新的事物,另写一组意思完整、句式相近的句子。
(不要求与原诗各句字数相同)眼睛很宽容_________能装下整个世界_________它又很苛刻_________容不得一粒沙尘_________【解析】在内容上,可仿照原诗歌内容,抓住例句中关键性词语,充分展开联想和想象。
从选取新事物的正反两方面的特点来写。
在句式上,采用“……很……,……,它又很……不得……”的结构。
【答案】嘴巴很豁达,吞得下所有辛酸;它又很狭隘,说不得一点是非。
3.仿照下面的示例,话题不变,另写一组句子,要求修辞、句式与示例相同。
命运如一壶翻腾的沸水,我们是一撮生命的清茶。
没有水的浸泡,茶只能蜷伏一隅;没有命运的冲刷,人生只会索然无味。
_________________________________________________________________ _________________________________________________________________ _________________________________________________________________【解析】所写的句子应以“命运”为话题,由两句构成,第一句要用比喻,第二句要从反面展开,并且要先承接喻体展开,再承本体展开,两个分句构成并列关系。
2020年九年级中考数学复习专题训练:《相似综合 》(含答案)

2020年九年级中考数学复习专题训练:《相似综合》1.如图1,点P从菱形ABCD的顶点B出发,沿B→D→A匀速运动到点A,BD的长是;图2是点P运动时,△PBC的面积y(cm2)随时间x(s)变化的函数图象.(1)点P的运动速度是cm/s;(2)求a的值;(3)如图3,在矩形EFGH中,EF=2a,FG﹣EF=1,若点P、M、N分别从点E、F、G三点同时出发,沿矩形的边按逆时针方向匀速运动,当点M到达点G(即点M与点G重合)时,三个点随之停止运动;若点P不改变运动速度,且点P、M、N的运动速度的比为2:6:3,在运动过程中,△PFM关于直线PM的对称图形是△PF'M,设点P、M、N的运动时间为t(单位:s).①当t=s时,四边形PFMF'为正方形;②是否存在t,使△PFM与△MGN相似,若存在,求t的值;若不存在,请说明理由.2.如图1,四边形ABCD中,AD∥BC,∠A=90°,AD=3,AB=4,BC=6,动点P从点A出发以1个单位/秒的速度沿AB运动,动点Q同时从点C出发以2个单位/秒的速度沿CB 运动,过点P作EP⊥AB,交BD于E,连接EQ.当点Q与点B重合时,两动点均停止运动,设运动的时间为t秒.(1)当t=1时,求线段EP的长;(2)运动过程中是否存在某一时刻,使△BEQ与△ABD相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由;(3)如图2,连接CE,求运动过程中△CEQ的面积S的最大值.3.如图1,在△ABC中,AB=AC=10,,点D为BC边上的动点(点D不与点B,C 重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.(1)求证:△ABD∽△DCE;(2)当DE∥AB时(如图2),求AE的长;(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.4.如图(1),在矩形ABCD中,AD=nAB,点M,P分别在边AB,AD上(均不与端点重合),且AP=nAM,以AP和AM为邻边作矩形AMNP,连接AN,CN.【问题发现】(1)如图(2),当n=1时,BM与PD的数量关系为,CN与PD的数量关系为.【类比探究】(2)如图(3),当n=2时,矩形AMNP绕点A顺时针旋转,连接PD,则CN与PD之间的数量关系是否发生变化?若不变,请就图(3)给出证明;若变化,请写出数量关系,并就图(3)说明理由.【拓展延伸】(3)在(2)的条件下,已知AD=4,AP=2,当矩形AMNP旋转至C,N,M三点共线时,请直接写出线段CN的长.5.如图,在△ABC中,∠C=90°,AB=10,AC=8,D、E分别是AB、BC的中点.连接DE.动点P从点A出发,以每秒5个单位长度的速度沿AB向终点B运动.同时,动点Q从点C 出发,沿折线CE﹣ED向终点D运动,在CE、ED上的速度分别是每秒3个单位长度和4个单位长度,连接PQ,以PQ、PD为边作▱DPQM.设▱DPQM与四边形ACED重叠部分图形的面积是S(平方单位),点P的运动时间为t(s).(1)当点P在AD上运动时,PQ的长为(用含t的代数式表示);(2)当▱DPQM是菱形时,求t的值;(3)当0<t<2时,求S与t之间的函数关系式;(4)当△DPQ与△BDE相似时,直接写出t的值.6.如图,在平行四边形ABCD中,AC为对角线,过点D作DE⊥DC交直线AB于点E,过点E 作EH⊥AD于点H,过点B作BF⊥AD于点F.(1)如图1,若∠BAD=60°,AF=3,AH=2,求AC的长;(2)如图2,若BF=DH,在AC上取一点G,连接DG、GE,若∠DGE=75°,∠CDG=45°﹣∠CAB,求证:DG=CG.7.(1)问题引入:如图1所示,正方形ABCD和正方形AEFG,则BE与DG的数量关系是,=;(2)类比探究:如图2所示,O为AD、HG的中点,正方形EFGH和正方形ABCD中,判断BE和CF的数量关系,并求出的值;(3)解决问题:①若把(1)中的正方形都改成矩形,且==,则(1)中的结论还成立吗?若不能成立,请写出BE与GD的关系,并求出值;②若把(2)中的正方形也都改成矩形,且==2n,请直接写出BE和CF的关系以及的8.在正方形ABCD中,点E是直线AB上动点,以DE为边作正方形DEFG,DF所在直线与BC 所在直线交于点H,连接EH.(1)如图1,当点E在AB边上时,延长EH交GF于点M,EF与CB交于点N,连接CG,①求证:CD⊥CG;②若tan∠HEN=,求的值;(2)当正方形ABCD的边长为4,AE=1时,请直接写出EH的长.9.如图a,在正方形ABCD中,E、F分别为边AB、BC的中点,连接AF、DE交于点G.(1)求证:AF⊥DE;(2)如图b,连接BG,BD,BD交AF于点H.①求证:GB2=GA•GD;②若AB=10,求三角形GBH的面积.10.如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP 翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.(1)求证:AD2=DP•PC;(2)请判断四边形PMBN的形状,并说明理由;(3)如图2,连接AC分别交PM、PB于点E、F.若AD=3DP,探究EF与AE之间的的数量关系.11.△ABC中,∠C=90°,∠A=60°,AC=2cm.长为1cm的线段MN在△ABC的边AB上沿AB方向以1cm/s的速度向点B运动(运动前点M与点A重合).过M,N分别作AB的垂线交直角边于P,Q两点,线段MN运动的时间为ts.(1)当0≤t≤1时,PM=,QN=(用t的代数式表示);(2)线段MN运动过程中,四边形MNQP有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;(3)t为何值时,以C,P,Q为顶点的三角形与△ABC相似?12.如图,四边形ABCD是矩形,AB=6,BC=4,点E在边AB上(不与点A、B重合),过点D作DF⊥DE,交边BC的延长线于点F.(1)求证:△DAE∽△DCF.(2)设线段AE的长为x,线段BF的长为y,求y与x之间的函数关系式.(3)当四边形EBFD为轴对称图形时,则cos∠AED的值为.13.如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N 在直线AD上,MN交CD于点E.(1)求证:△AMN是等腰三角形;(2)求证:AM2=2BM•AN;(3)当M为BC中点时,求ME的长.14.如图,在平面直角坐标系中,过原点O及A(8,0)、C(0,6)作矩形OABC,连接AC,一块直角三角形PDE的直角顶点P始终在对角线AC上运动(不与A、C重合),且保持一边PD始终经过矩形点B,PE交x轴于点Q(1)=;(2)在点P从点C运动到点A的过程中,的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;(3)若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为.15.如图,在矩形OABC中,点A,B的坐标分别为A(4,0),B(4,3),动点N,P分别从点B,A同时出发,点N以1单位/秒的速度向终点C运动,点P以5/4单位/秒的速度向终点C运动,连结NP,设运动时间为t秒(0<t<4)(1)直接写出OA,AB,AC的长度;(2)求证:△CPN∽△CAB;(3)在两点的运动过程中,若点M同时以1单位/秒的速度从点O向终点A运动,求△MPN的面积S与运动的时间t的函数关系式(三角形的面积不能为0),并直接写出当S =时,运动时间t的值.16.如图,在正方形ABCD中,点E在边CD上(不与点C,D重合),连结AE,BD交于点F.(1)若点E为CD中点,AB=2,求AF的长.(2)若tan∠AFB=2,求的值.,(3)若点G在线段BF上,且GF=2BG,连结AG,CG,=x,四边形AGCE的面积为S1,求的最大值.△ABG的面积为S217.如图1,在△ABC中,AB=AC,点D,E分别是边BC,AC上的点,且∠ADE=∠B.(1)求证:AB•CE=BD•CD;(2)若AB=5,BC=6,求AE的最小值;(3)如图2,若△ABC为等边三角形,AD⊥DE,BE⊥DE,点C在线段DE上,AD=3,BE =4,求DE的长.18.如图,△ABC中,AB=AC,点P为BC边上一动点(不与B,C重合),以AP为边作∠APD=∠ABC,与BC的平行线AD交于点D,与AC交于点E,连结CD.(1)求证:△ABP∽△DAE.(2)已知AB=AC=5,BC=6.设BP=x,CE=y.①求y关于x的函数表达式及自变量x的取值范围;=时,求CE的值.②当S△ACD19.如图,在矩形ABCD的边AB上取一点E,连接CE并延长和DA的延长线交于点G,过点E作CG的垂线与CD的延长线交于点H,与DG交于点F,连接GH.(1)当tan∠BEC=2且BC=4时,求CH的长;(2)求证:DF•FG=HF•EF;(3)连接DE,求证:∠CDE=∠CGH.20.定义:若一个四边形能被其中一条对角线分割成两个相似三角形,则称这个四边形为“友好四边形”.(1)如图1,在4×4的正方形网格中,有一个网格Rt△ABC和两个网格四边形ABCD与ABCE,其中是被AC分割成的“友好四边形”的是;(2)如图2,将△ABC绕点C逆时针旋转得到△A'B'C,点B'落在边AC,过点A作AD∥A'B'交CA'的延长线于点D,求证:四边形ABCD是“友好四边形”;(3)如图3,在△ABC中,AB≠BC,∠ABC=60°,△ABC的面积为6,点D是∠ABC 的平分线上一点,连接AD,CD.若四边形ABCD是被BD分割成的“友好四边形”,求BD 的长.参考答案1.解:(1)由图2可知,s点P从点B运动到点D,∵BD=,∴点P的运动速度=÷=1(cm/s),故答案为:1;(2)如图1,作DQ⊥BC于点Q,当点P在BD上时,a=×BC×DP,∵四边形ABCD为菱形,点P的运动速度为1,∴AD=BC=1×a=a,∴a=×a×DP,解得,DQ=2,在Rt△BDQ中,BQ==1,∴CQ=a﹣1,在Rt△CDQ中,CD2=CQ2+DQ2,即a2=(a﹣1)2+22,解得,a=;(3)①∵点P的运动速度1cm/s,点P、M的运动速度的比为2:6 ∴点M的运动速度3cm/s,由题意得,EF=2a=5,∵FG﹣EF=1,∴FG=6,∴PF=5﹣t,FM=3t,由翻转变换的性质可知,PF=PF′,FM=FM′,当PF=FM时,PF=PF′=FM=FM′,∴四边形PFMF'为菱形,又∠F=90°,∴四边形PFMF'为正方形,∴5﹣t=3t,即t=1.25时,四边形PFMF'为正方形,故答案为:1.25;②存在,∵点P的运动速度1cm/s,点P、M、N的运动速度的比为2:6:3,∴点M的运动速度3cm/s,点N的运动速度1.5cm/s,∴PF=5﹣t,FM=3t,GN=1.5t,∵点M的运动速度3cm/s,FG=6,∴0≤t≤2,当△PFM∽△MGN时,=,即=,解得,t=,当△PFM∽△NGM时,=,即=,解得,t1=﹣7﹣(舍去),t2=﹣7+,综上所述,当t=或﹣7+时,△PFM与△MGN相似.2.解:(1)当t=1时,则AP=1,∴BP=AB﹣AP=3,∵EP⊥AB,∴∠EPB=∠A=90°,∴EP∥AD,∴△BPE∽△BAD,∴,∴,∴EP=;(2)∵∠A=90°,AD=3,AB=4,∴BD===5,∵EP⊥AB,∴∠EPB=∠A=90°,∴EP∥AD,∴△BPE∽△BAD,∴,∴,∴BE=5﹣t,∵AD∥BC,∴∠ADB=∠EBQ,若∠BEQ=∠A=90°,∴△BAD∽△QEB,∴,∴=,∴t=28(不合题意舍去),若∠BQE=∠A=90°,∴△BAD∽△EQB,∴,∴t=,(3)∵S=×CQ×PB=×2t×(4﹣t)=﹣(t﹣2)2+4,∴当t=2时,S最大值为4,∴△CEQ的面积S的最大值为4.3.证明:(1)∵AB=AC,∴∠B=∠ACB,∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,∴∠BAD=∠CDE,∴△BAD∽△DCE;(2)如图2中,作AM⊥BC于M.在Rt△ABM中,设BM=4k,∵=,∴,由勾股定理,得到AB2=AM2+BM2,∴102=(3k)2+(4k)2,∴k=2或﹣2(舍弃),∴AM=6,BM=8,∵AB=AC,AM⊥BC,∴BC=2BM=2×2k=16,∵DE∥AB,∴∠BAD=∠ADE,∵∠ADE=∠B,∠B=∠ACB,∴∠BAD=∠ACB,∵∠ABD=∠CBA,∴△ABD∽△CBA,∴,∴=,∵DE∥AB,∴,∴=.(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.理由:作FH⊥BC于H,AM⊥BC于M,AN⊥FH于N.则∠NHM=∠AMH=∠ANH=90°,∴四边形AMHN为矩形,∴∠MAN=90°,MH=AN,∵AB=AC,AM⊥BC,∵AB=10,∴BM=CM=8,∴BC=16,在Rt△ABM中,由勾股定理,得AM=6,∵AN⊥FH,AM⊥BC,∴∠ANF=90°=∠AMD,∵∠DAF=90°=∠MAN,∴∠NAF=∠MAD,∴△AFN∽△ADM,∴,∴,∴CH=CM﹣MH=CM﹣AN=8﹣=,当DF=CF时,由点D不与点C重合,可知△DFC为等腰三角形,∵FH⊥DC,∴CD=2CH=7,∴BD=BC﹣CD=16﹣7=9,∴点D在BC边上运动的过程中,存在某个位置,使得DF=CF,此时BD=9.4.解:(1)BM=PD,,理由如下:当n=1,则AD=AB,AP=AM,∴AD﹣AP=AB﹣AM,∴DP=BM,∵四边形ABCD是矩形,四边形AMNP是矩形,∴AD=CD=AB,AP=AM=NP,∠ADC=∠APN=90°,∴AC=AD,AN=AP,∴AC﹣AN=(AD﹣AP),∴CN=PD,故答案为:BM=PD,;(2)CN与PD之间的数量关系发生变化,,理由如下:如图(1)在矩形ABCD和矩形AMNP中,∵当n=2.AD=2AB,AP=2AM,∴,,∴.,如图(3)连接AC,∵矩形AMNP绕点A顺时针旋转,∴∠NAC=∠PAD,∴△ANC∽△APD,∴,∴;(3)如图,当点N在线段CM上时,∵AD=4,AD=2AB,∴AB=CD=2,∴AC===,∵AP=2,AP=2AM,∴AM=1,∴CM===,∴CN=CM﹣MN=﹣2;如图,当点M在线段CN上时,同理可求CM=,∴CN=CM+MN=+2;综上所述:线段CN的长为或.5.解:(1)∵∠C=90°,AB=10,AC=8,∴BC===6,∵D、E分别是AB、BC的中点.∴DE∥AC,DE=AC=4,BD=AD=5,BE=CE=3,∵动点P从点A出发,以每秒5个单位长度的速度沿AB向终点B运动,∴AP=5t,∴BP=10﹣5t,∵DE∥AC,∴△BPQ∽△BAC,∴,∴∴PQ=8﹣4t,故答案为:8﹣4t;(2)当点P在AD上运动时,∵四边形DPQM是菱形,∴PD=PQ,∴5﹣5t=8﹣4t,∴t=﹣3(不合题意舍去),当点P在BD上运动时,过点P作PH⊥DQ于H,∵四边形DPQM是菱形,∴PD=PQ,且PH⊥DQ,∴DH=HQ=DQ=[4﹣4(t﹣1)]=4﹣2t,∵DE∥AC,∴∠DEB=∠ACB=90°=∠PHD,∴PH∥BE,∴△PDH∽△BDE,∴,∴,∴t=,PH=3t﹣3,综上所述:当t=时,▱DPQM是菱形;(3)当0<t<1时,S=×(8﹣4t+4)×(3﹣3t)=6t2﹣24t+18,当t=1时,不能作出▱DPQM,当1<t<2时,S=×(8﹣4t)×(3t﹣3)=﹣6t2+18t﹣12;(4)当点P在AD上时,不存在△DPQ与△BDE相似,当点P在BD上时,则∠PDQ=∠BDE,若∠PQD=∠DEB=90°时,∴△PDQ∽△BDE,∴,∴∴t=,若∠DPQ=∠DEB=90°时,∴△QPD∽△BED,∴,∴∴t=综上所述:当t=或时,△DPQ与△BDE相似.6.解:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,CD=AB,CD∥AB,∵BF⊥AD于F,∴∠AFB=90°,∵∠BAD=60°,∴AB=2AF=6,BF=AF=3,∵EH⊥AD于H,∴AE=2AH=4,EH=AH=2,∵DE⊥DC交AB于E,∴∠DEA=90°,∴AD=2AE=8,∴CB=AD=8,如图1,作AM⊥CB于M,则∠ABM=∠BAD=60°,∴BM=(1/2)AB=3,AM=BM=3,∴CM=CB+BM=11,在Rt△ACM中:AC===2.(2)如图2,作EN⊥AC于N,连接DN、CE,则∠CNE=90°.∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,CD=AB,CD∥AB,∵DE⊥DC交AB于E,∴∠CDE=∠DEA=90°,∵EH⊥AD于H,∴∠DHD=∠EHA=90°,∵BF⊥AD于F,∴∠DFB=∠AFB=90°,∴∠DHE=∠BFA,∵∠DEH+∠HEA=∠HEA+∠BAF=90°,∴∠DEH=∠BAF,∵DH=BF,∴△DEH≌△BAF(AAS),∴DE=BA=CD,∴△CDE是等腰直角三角形,∠DCE=∠DEC=45°,∵∠CDE=∠CNE=90°,∴C、D、N、E四点共圆,∴∠DNC=∠DEC=45°,∵∠CDG=45°﹣∠CAB,∴∠CDG+∠CAB=45°,∵CD∥AB,∴∠CAB=∠DCG,∴∠DGN=∠DCG+∠CDG=45°=∠DNC,∴△DGN是等腰直角三角形,∠GDN=90°,DG=DN,∵∠CDG+∠GDE=∠GDE+∠EDN=90°,∴∠CDG=∠EDN,∴△CDG≌△EDN(SAS),∴EN=CG,∵∠CGD=75°,∴∠CGN=∠CGD﹣∠DGN=30°,∴GN=EN=CG,∴DG=GN=CG7.解:(1)如图1中,连接AC,AF.∵四边形ABCD,四边形AEFG都是正方形,∴AB=AD,AE=AG,∠BAD=∠EAG=90°,AC=AB,AF=AE,∠BAC=45°,∠EAF=45°,∴∠BAE=∠DAG,∴△BAE≌△DAG(SAS),∴BE=DG,∵AC=AB,AF=AE,∴=,∵∠BAC=∠EAF=45°,∴∠BAE=∠CAF,∴△BAE∽△CAF,∴==,∵DG=BE,∴=.故答案为:BE=DG,.(2)如图2中,连接OB,OE,OF,OC.∵四边形ABCD是正方形,OA=OD,∴∠A=∠CDO=90°,AB=CD,∴△AOB≌△DOC(SAS),∴OB=OC,同法可证OE=OF,∴∠OBC=∠OCB,∠OEF=∠OFE,∵BC∥AD,∴∠CBO=∠AOB,∴tan∠CBO=tan∠AOB=2,同法可证:tan∠FEO=2,∴tan∠CBO=tan∠FEO,∴∠CBO=∠FEO,∴∠OBC=∠OCB=∠OEF=∠OFE,∴∠BOC=∠EOF,∴∠EOB=∠FOC,∵OE=OF,OB=OC,∴△OEB≌△OFC(SAS),∴BE=FC,∵tan∠COD=tan∠COD=2,∴∠FOG=∠COD,∴∠FOC=∠GOD,∵==,∴△FOG∽△GOD,∴==.(3)①如图3中,结论不成立,BE=3DG.连接BE,AC,AF,CF.∵四边形ABCD,四边形AEFG都是矩形,∴∠BAD=∠EAG=90°,∴∠BAE=∠DAG,∵AB=3AD,AE=3AG,∴△BAE∽△DAG,∴==3,∴BE=3DG,由题意:=,=,∴=,∴=,∵tan∠BAC=tan∠EAF=,∴∠BAC=∠EAF,∴∠BAE=∠CAF,∴△BAE∽△CAF,∴==,∴=.②如图4中,连接OE,OB,OF,OC.由(2)可知,∠BOC=∠EOF,OE=OF,OB=OC,∴∠EOB=∠FOC,∴△EOB≌△FOC(SAS),∴BE=CF.同法可证△FOC∽△GOD,∴=,设EH=k,则GH=2nk,∴OG=nk,∴OF==•k,∵BE=CF,∴==.8.证明:(1)①∵四边形ABCD和四边形DEFG是正方形,∴∠A=∠ADC=∠EDG=90°,AD=CD,DE=DG,∴∠ADE=∠CDG,在△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴∠A=∠DCG=90°,∴CD⊥CG;②如图1,过点N作NP∥DE,∵四边形DEFG是正方形,∴EF=GF,∠EFH=∠GFH=45°,且HF=HF,∴△EFH≌△GFH(SAS),∴EH=GH,∠HEF=∠HGF,∵∠HEF=∠HGF,EF=GF,∠EFM=∠GFN,∴△EFM≌△GFN(ASA),∴FM=NF,EM=GN,∵tan∠HEN==,∴EF=4MF=4NF=GF,∴GM=3MF=EN=3NF,∴NP∥DE,∴△PNE∽△MFE,∴,∴PN=MF,∵NP∥DE,∴=,∴;(2)如图1,∵AD=4,AE=1,∴DE===,∴EF=GF=,∴NF=EF=,∵GN2=GF2+NF2,∴GN=,∵∴GH=GN=,∴EH=GH=若点E在点A左侧,如图2,设AB与DH于点O,过点F作FN⊥AB,∵∠DEA+∠FEB=90°,∠DEA+∠ADE=90°,∴∠ADE=∠FEB,且∠DAE=∠FNE=90°,DE=EF,∴△ADE≌△NEF(AAS)∴AE=NF=1,DA=EN=4,∴AN=3,BN=1,∵DA∥NF,∴,∴ON=,∴BO=,∴AO=∵DA∥BH,∴,∴BH=,∴EH===9.证明:(1)∵正方形ABCD,E、F分别为边AB、BC的中点,∴AD=BC=DC=AB,AE=BE=AB,BF=CF=BC,∴AE=BF,∵在△ADE和△BAF中,∴△ADE≌△BAF(SAS)∴∠BAF=∠ADE,∵∠BAF+∠DAF=90°∴∠ADE+∠DAF=90°=∠AGD,∴AF⊥DE;(2)①如图b,过点B作BN⊥AF于N,∵∠BAF=∠ADE,∠AGD=∠ANB=90°,AB=AD,∴△ABN≌△ADG(AAS)∴AG=BN,DG=GN,∵∠AGE=∠ANB=90°,∴EG∥BN,∴,且AE=BE,∴AG=GN,∴AN=2AG=DG,∵BG2=BN2+GN2=AG2+AG2,∴BG2=2AG2=2AG•AG=GA•DG;②∵AB=10,∴AE=BF=5,∴DE===5,∵×AD×AE=×DE×AG,∴AG=2,∴GN=BN=2,∴AN=DG=4,∴△DGH∽△BNH,∴==2,∴GH=2HN,且GH+HN=GN=2,∴GH=,=×GH×BN=××2=.∴S△GHB10.(1)证明:过点P作PG⊥AB于点G,如图1所示:则四边形DPGA和四边形PCBG是矩形,∴AD=PG,DP=AG,BG=PC,∵∠APB=90°,∴∠APG+∠GPB=∠GPB+∠PBG=90°,∴∠APG=∠PBG,∴△APG∽△PBG,∴=,∴PG2=AG•BG,即AD2=DP•PC;(2)解:四边形PMBN是菱形;理由如下:∵四边形ABCD是矩形,∴AB∥CD,∵BM∥PN,BN∥MP,∴四边形PMBN是平行四边形,∵DP∥AB,∴∠DPA=∠PAM,由题意可知:∠DPA=∠APM,∴∠PAM=∠APM,∵∠APB﹣∠PAM=∠APB﹣∠APM,即∠ABP=∠MPB∴AM=PM,PM=MB,∴四边形PMBN是菱形;(3)解:∵AD=3DP,∴设DP=1,则AD=3,由(1)可知:AG=DP=1,PG=AD=3,∵PG2=AG•BG,∴32=1•BG,∴BG=PC=9,AB=AG+BG=10,∵CP∥AB,∴△PCF∽△BAF,∴==,∴=,∵PM=MB,∴∠MPB=∠MBP,∵∠APB=90°,∴∠MPB+∠APM=∠MBP+∠MAP=90°,∴∠APM=∠MAP,∴PM=MA=MB,∴AM=AB=5,∵AB∥CD,∴△PCE∽△MAE,∴==,∴=,∴EF=AF﹣AE=AC﹣AC=AC,∴==.11.解:(1)由题意得:AM=t,∵PM⊥AB,∴∠PMA=90°,∵∠A=60°,∴∠APM=30°,∴PM=AM=t.∵∠C=90°,∴∠B=90°﹣∠A=30°,∴AB=2AC=4,BC=AC=2,∵MN=1,∴BN=AM﹣AM﹣1=3﹣t,∵QN⊥AB,∴QN=BN=(3﹣t);故答案为:tcm,(3﹣t)cm.(2)四边形MNQP有可能成为矩形,理由如下:由(1)得:QN=(3﹣t).由条件知,若四边形MNQP为矩形,则需PM=QN,即t=(3﹣t),∴t=.∴当t=s时,四边形MNQP为矩形;(3)由(2)知,当t=s时,四边形MNQP为矩形,此时PQ∥AB,∴△PQC∽△ABC.除此之外,当∠CPQ=∠B=30°时,△QPC∽△ABC,此时=tan30°=.∵=cos60°=,∴AP=2AM=2t.∴CP=2﹣2t.∵=cos30°=,∴BQ=(3﹣t).又∵BC=2,∴CQ=2 .∴.综上所述,当s或s时,以C,P,Q为顶点的三角形与△ABC相似.12.证明:(1)∵四边形ABCD是矩形,∴AD∥BC,∠A=∠BCD=∠ADC=90°,AD=BC=4,AB=CD=6,∴∠ADE+∠EDC=90°,∵DF⊥DE,∴∠EDC+∠CDF=90°,∴∠ADE=∠CDF,且∠A=∠DCF=90°,∴△DAE∽△DCF;(2)∵△DAE∽△DCF,∴,∴∴y=x+4;(3)∵四边形EBFD为轴对称图形,∴DE=BE,∵AD2+AE2=DE2,∴16+AE2=(6﹣AE)2,∴AE=,∴DE=BE=,∴cos∠AED==,故答案为:.13.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠NAM=∠BMA,∵∠AMN=∠AMB,∴∠AMN=∠NAM,∴AN=MN,即△AMN是等腰三角形;(2)证明:∵四边形ABCD是矩形,∴AD∥BC,AD=BC=2,AB=CD=3,∴∠NAM=∠BMA,作NH⊥AM于H,如图所示:∵AN=MN,NH⊥AM,∴AH=AM,∵∠NHA=∠ABM=90°,∠NAM=∠BMA,∴△NAH∽△AMB,∴=,∴AN•BM=AH•AM=AM2,∴AM2=2BM•AN;(3)解:∵M为BC中点,∴BM=CM=BC=×2=1,由(2)得:AM2=2BM•AN,即:AM2=2AN,∵AM2=AB2+BM2=32+12=10,∴10=2AN,∴AN=5,∴DN=AN﹣AD=5﹣2=3,设DE=x,则CE=3﹣x,∵AN∥BC,∴△DNE∽△CME∴=,即=,解得:x=,即DE=,∴CE=DC﹣DE=3﹣=,∴ME===.14.解:(1)∵A(8,0)、C(0,6),∴OA=8,OC=6,∵四边形OABC是矩形,∴∠ABC=∠OAB=90°,BC=OA=8,AB=OC=6,∴==,故答案为:;(2)的值不发生变化,=,理由如下:∵∠OAB=∠BPQ=90°,∴∠AOB+∠BPQ=180°,∴A、B、P、Q四点共圆,∴∠PQB=∠PAB,∵∠ABC=∠BPQ=90°,∴△PBQ∽△BCA,∴==;(3)设BQ交AP于M,如图所示:在Rt△ABC中,由勾股定理得:AC===10,由折叠的性质得:BQ⊥AP,PM=AM,∴∠AMB=90°=∠ABC,∵∠BAM=∠CAB,∴△ABM∽△ACB,∴=,即=,解得:AM=3.6,∴PA=2AM=7.2,∴PC=AC﹣PA=10﹣7.2=2.8;故答案为:2.8.15.(1)证明:∵四边形OABC是矩形,A(4,0),B(4,3),∴OA=BC=4,AB=OC=3,∠AOC=90°,∴AC===5;(2)解:由题意得:BN=t,AP=t,∵=,==,∴=,∴PN∥AB,∴△CPN∽△CAB;(3)解:分两种情况:①当0<t<2时,延长NP交OA于D,如图1所示:由(2)得:PD∥AB,∴△APD∽△ACO,∴==,即==,解得:PD=t,AD=t,∴PN=3﹣t,DM=4﹣t﹣t=4﹣2t,∴△MPN的面积S=PN×DM=×(3﹣t)×(4﹣2t)=t2﹣t+6,即S=t2﹣t+6(0<t<2);②当2<t<4时,延长NP交OA于D,如图2所示:由(2)得:PD∥AB,∴△APD∽△ACO,∴==,即==,解得:PD=t,AD=t,∴PN=3﹣t,DM=t+﹣4t=2t﹣4,∴△MPN的面积S=PN×DM=×(3﹣t)×(2t﹣4)=﹣t2+t﹣6,即S=﹣t2+t﹣6(2<t<4);当S=,0<t<2时,则t2﹣t+6=,整理得:t2﹣6t+6=0,解得:t=3﹣,或t=3+(不合题意舍去),∴t=3﹣;当S=,2<t<4时,则﹣t2+t﹣6=,整理得:t2﹣6t+10=0,∵△=36﹣40<0,∴此方程无解;综上所述,当S=时,运动时间t的值为(3﹣)秒.16.解:(1)∵点E为CD中点,AB=AD=CD=2,∴DE=,∴AE===5,∵AB∥CD,∴△ABF∽△EDF,∴,∴AF=2EF,且AF+EF=5,∴AF=;(2)如图1,连接AC,∵四边形ABCD是正方形,∴AB=BC=CD=AD,BD=AB,AO⊥BD,AO=BO=CO=DO,∴AO=DO=BO=AB,∵tan∠AFB==2,∴OF=AO=AB,∴DF=OD﹣OF=AB,BF=OB+OF=AB,∴;(3)如图2,设AB=CD=AD=a,则BD=a,∵=x,∴DE=xa,∴S△ADE=×AD×DE=xa2,∵△ABF∽△EDF,∴=x,∴DF=x•BF,∴S△ABF=a2,∵GF=2BG,∴S2=S△ABG=S△ABF=,∵AB=CB,∠ABG=∠CBG,BG=BG,∴△ABG≌△CBG(SAS)∴S△ABG =S△CBG,∴S1=四边形AGCE的面积=a2﹣xa2﹣2×∴=﹣3x2+3x+4=﹣3(x﹣)2+∴当x=时,的最大值为.17.(1)证明:∵AB=AC,∴∠B=∠C,∵∠ADC为△ABD的外角,∴∠ADE+∠EDC=∠B+∠DAB,∵∠ADE=∠B,∴∠BAD=∠CDE,又∠B=∠C,∴△ABD∽△DCE,∴=,∴AB•CE=BD•CD;(2)解:设BD=x,AE=y,由(1)得,5×(5﹣y)=x×(6﹣x),整理得,y=x2﹣x+5=(x﹣3)2+,∴AE的最小值为;(3)解:作AF⊥BE于F,则四边形ADEF为矩形,∴EF=AD=3,AF=DE,∴BF=BE﹣EF=1,设CD=x,CE=y,则AF=DE=x+y,由勾股定理得,AD2+CD2=AC2,CE2+BE2=BC2,AF2+BF2=AB2,∵△ABC为等边三角形,∴AB=AC=BC,∴32+x2=AC2,y2+42=BC2,(x+y)2+12=AC2,∴x2﹣y2=7,y2+2xy=8,解得,x=,y=,∴DE=x+y=.18.(1)证明:∵AB=AC,∴∠ABC=∠ACB,∵∠APC=∠ABC+∠BAP,∠APC=∠APD+∠EPC,∠APD=∠ABC,∴∠BAP=∠EPC,∴△ABP∽△PCE,∵BC∥AD,∴△PCE∽△DAE,∴△ABP∽△DAE;(2)解:①∵△ABP∽△PCE,∴=,即=,∴y=﹣x2+x(0<x<6);②∵△ABP∽△DAE,∴=,即=,∴AD=,∵AD∥BC,∴,∵,∴,∴,即13x2+24x﹣100=0,∴x=2,(舍去)1∴.19.(1)解:在Rt△BCE中,当tan∠BEC=2,∴=2,即=2,解得,BE=2,由勾股定理得,CE===2,∵四边形ABCD为矩形,∴AB∥CD,∴∠ECH=∠BEC,∴tan∠ECH==2,即=2,∴EH=4,∴CH==10;(2)证明:∵∠FEG=∠FDH=90°,∠EFG=∠DFH,∴△EFG∽△DFH,∴=,∴DF•FG=HF•EF;(3)证明:∵△EFG∽△DFH,∴∠CGD=∠CHE,又∠GCD=∠HCE,∴△GCD∽△HCE,∴=,又∠GCD=∠HCE,∴△CDE∽△CGH,∴∠CDE=∠CGH.20.解:(1)AB=2,BC=1,AD=4,由勾股定理得,AC==,CD==,AE==2,CE==5,===,∴△ABC∽△EAC,∴四边形ABCE是“友好四边形”,≠,∴△ABC与△ACD不相似,∴四边形ABCD不是“友好四边形”,故答案为:四边形ABCE;(2)证明:根据旋转的性质得,∠A'CB'=∠ACB,∠CA'B'=∠CAB,∵AD∥A'B',∴∠CA'B'=∠D,∴∠CAB=∠D,又∠A'CB'=∠ACB,∴△ABC∽△DAC,∴四边形ABCD是“友好四边形”;(3)如图3,过点A作AM⊥BC于M,在Rt△ABM中,AM=AB•sin∠ABC=AB,∵△ABC的面积为6,∴BC×AB=6,∴BC×AB=24,∵四边形ABCD是被BD分割成的“友好四边形”,且AB≠BC,∴△ABD∽△DBC∴,∴BD2=AB×BC=24,∴BD==2.。
高三生物综合训练(二)

高中学生学科素质训练高三生物综合训练(二)本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分第I卷(每题只有一个选项符合题目要求,本题共52分)1.下列哪类生物肯定具有细胞结构()A.原始生命B.原核生物C.烟草花叶病毒D.大肠杆菌T4噬菌体2.单位质量的脂肪与糖类相比,其所含元素与有耗氧量的特点是,前者()A.含C、H原子多,氧化时耗氧多B.含C、H原子多,氧化时耗氧少C.含C、H原子少,氧化时耗氧多D.含C、H原子少,氧化时耗氧少3.小孩能合成与母亲相似的脂肪酶,这主要与母体内含有哪类物质有关()A.脂类B.蛋白质C.糖类D.核酸4.通常情况下,分子式为C63H103O45N17S2的多肽化合物中最多含有肽键()A.62个B.2个C.17个D.16个5.在细胞周期中每个染色体只含有一个双链DNA分子的时期是()A.间期和前期B.前期和中期C.中期和后期D.后期和末期6.把青蛙和小白鼠从25℃的室温中移至5℃的环境中,这两种动物的需氧量的变化是()A.两种动物的耗氧量都减少B.两种动物的耗氧量都增加C.青蛙的耗氧量减少,小白鼠耗氧量增加D.青蛙的耗氧量增加,小白鼠耗氧量减少7.一分子CO2从叶肉细胞的线粒体基质中扩散出来,进入一相邻细胞的叶绿体基质内,共穿越过的生物膜层数是()A.5 B.6 C.7 D.88.下列各类生物在细胞代谢过程中,能产生相应化合物的一项是()A.乳酸菌产生CO2B.人体产生酒精C.酵母菌产生乳酸D.甘薯产生丙酮酸9.通过某些微生物的作用,可能把空气中游离的氮素固定转变为含氮化合物,这一过程就是一种生物固氮作用。
为确定固氮的最终产物,做了如下两个实验:(1)把固氮菌培养在含15N2的空气中,细胞迅速固定氮素,短期内细菌的谷氨酸中出现大量的15N。
(2)如果把细菌培养在含有15NH3的培养基中,固氮能力立刻停止,但吸入氨态氮迅速转入谷氨酸中。
由此可以推断,该微生物固氮最终产物是()A.NH3B.NO2C.NO3D.谷氨酸10.人体在下列哪一活动过程中ADP含量会增加()A.K+被吸收进入肾小管壁的上皮细胞的过程B.葡萄糖进入红细胞的过程C.线粒体中的氢与氧结合生成水的过程D.甘油吸收进入消化道上皮细胞的过程11.对于育种来说,有性生殖的主要优点是能产生()A.更多的后代B.更多各种各样的后代C.健康的后代D.发育更快的后代12.每个四分体(2N生物)含有染色体、着丝点、染色单体的数目分别是()A.2、2、4 B.4、4、4 C.2、4、4 D.2、4、213.用生长素处理的方法培育无籽番茄,其无籽的原因是()A.发生了染色体变异B.不能进行正常的减数分裂C.不能形成纺缍体D.没有经过受精作用14.蛙胚发育至原肠胚时,说法不正确的是()A.胚体已经形成胚孔B.胚体已形成中胚层C.胚体的原肠腔由内胚层细胞围成D.胚体具有囊胚腔和原肠腔15.将4株长势相同,具有顶芽的健壮植株分别进行如下处理,其中哪一处理办法最有利于侧芽发育成枝条()A.去顶芽后,在断口上放一块琼脂小块B.去顶芽后,在断口上放一块富含生长素的琼脂小块C.不去顶芽,在侧芽涂以含低浓度生长素的琼脂D.不去顶芽,在侧芽上涂以琼脂16.把二龄猎蝽若虫的某腺体切除后,该若虫发育加快,这种腺体分泌的激素是()A.保幼激素B.脑激素C.性外激素D.蜕皮激素17.某生物有3对等位基因AaBbCc分别位于3对同源染色体上,在精巢内,若有4万个初级精母细胞,经减数分裂后能形成abc的精子个数约有()A.1万个B.2万个C.4万个D.8万个18.在双链DNA分子中,有腺嘌呤P个,占全部碱基的比例为N/M(M>2N),则该DNA 分子中鸟嘌呤的个数为()A.(PM/N)-P B.(PM/2N)-P C.PM/2N D.N-2P/2M19.根据下表中的内容,指出下列哪一项是色氨酸的密码子20.采用A、B、C、D中的哪一套方法,可以依次解决①~④的遗传学问题()①鉴定一只白羊是否纯种②在一对相对性状中区分显隐性③不断提高小麦抗病品种的纯合度④检验杂种F1的基因型A.杂交、自交、测交、测交B.测交、杂交、自交、测交C.测交、测交、杂交、自交D.杂交、杂交、杂交、测交21.基因型分别为aaBbCCDd和AABbCCdd的两种豌豆杂交,其子代中纯合体的比例为()A.1/4 B.1/8 C.1/16 D.022.在某一生态系统内,蛇和猫头鹰捕食鼹鼠和田鼠,如果鹰在这一生态系统内出现,就要成为另一种捕食动物。
八(下)期末综合训练二

八(下)期末综合训练二一、选择题 1、不等式组⎩⎨⎧+xx x 2132 的解集是( )A .2331 x B .23 x C .1 x D .231 x 2、若分式方程231x x -=1m x -有增根,则m 的值为( )A .1B .-1C .3D .-33、如图,平行四边形ABCD 中,AE ∶EB =1∶2,若2AE F 6S cm =△,则=CDF S △( )A .542cm B . 182cm C .12 2cm D .242cm4、已知()0332=++++m y x x 中,y 为负数,则m 的取值范围是( )A .9 mB .9 mC .9- mD .9- m5、如图,把△ABC 沿AB 边平移到△C B A '''的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC 的面积的一半,若2=AB ,则此时三角形移动的距离A A '是( ) A .12- B .22C .1D .216、如图所示,在△ABC 中,︒=∠90BAC ,AD ⊥BC 于D ,若AB=2,BC =3,则DC 的长是( )A .38B .32C .34D .35 7、a 、b 两数在数轴上的位置如图所示,设b a M +=,b a N +-=,b a H -=,b a G --=,则下列各式中正确的是( )A .G H N MB .N G M HC .G N M HD .N M H G8、若分式()()112-+-x x x 的值为零,则x 的取值应为( )A .2=x 或1-=xB .1-=xC .1±=xD .2=x 9、已知)0(12≠=++a a y ax ,用含x 的代数式表示y 为( )A .a a x y +=B .a a x y 3+=C .a a x y +=D .1-=ax y 10、若分式方程()()5812-=-+x a a x 的解是51-=x ,则a 等于( )A .65 B .5 C .65- D .5- 11、一件工作,甲单独做a 天完成,乙单独做b 天完成,两天合作完成共需的天数为( ) A .b a + B .b a 11+ C .b a +1 D .ba ab+ 12、已知下列命题:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两直线平行;⑤邻补角的平分线互相垂直.其中,正确命题的个数为( ) A 、0 B 、1个 C 、2个 D 、3个13、△ABC 中,BP 平分∠B ,CP 平分∠C ,若∠A=60º,则∠BPC= 14、6把下列命题“对顶角相等”改写成:如果 ,那么.15、当=k 时,方程1131=-+-xx k 会产生增根。
2021-2022学年浙教版九年级数学上册《第4章相似三角形》期末综合复习训练2(附答案)

2021-2022学年浙教版九年级数学上册《第4章相似三角形》期末综合复习训练2(附答案)1.已知,那么下列等式中,不成立的是()A.B.C.(y≠﹣4a)D.4x=3y2.下列线段中,能成比例的是()A.3cm,6cm,8cm,9cm B.3cm,5cm,6cm,9cmC.3cm,6cm,7cm,9cm D.3cm,6cm,9cm,18cm3.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是()A.B.C.D.4.如图,AB与CD相交于点E,AD∥BC,,CD=16,则DE的长为()A.3B.6C.D.105.若将一个正方形的各边长扩大为原来的4倍,则这个正方形的面积扩大为原来的()A.16倍B.8倍C.4 倍D.2 倍6.如图,在△ABC中,AB=9,BC=18,AC=12,点D在边AC上,且CD=4,过点D 作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是()A.12B.16C.12或16D.以上都不对7.附加题:若x=,则x=.8.已知线段a=4,b=1,如果线段c是线段a、b的比例中项,那么c=.9.如图,△ABC中,D在AC上,且AD:DC=1:n,E为BD的中点,AE的延长线交BC 于F,那么的值为(用n表示).10.利用复印机的缩放功能放大一个三角形,将原图中边长为3,5,6的三角形的最长边放大到8,那么放大后的那个三角形的周长为.11.如图,一个矩形广场的长为90m,宽为60m,广场内有两横,两纵四条小路,且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2m,那么每条纵向小路的宽为m.12.两个相似三角形周长的差是4cm,面积的比是16:25,那么这两个三角形的周长分别是cm和cm13.如图,在▱ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD 于点F,已知S△AEF=4,则下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF ∽△ACD,其中一定正确的是.(填序号)14.如图,在直线m上摆放着三个等边三角形:△ABC、△HFG、△DCE,已知BC=CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=12,则S2=.15.如图,数学兴趣小组测量校园内旗杆的高度,小华拿一支刻有厘米分划的小尺,站在距旗杆30米的地方,手臂向前伸直,小尺竖直,看到尺上约12个分划恰好遮住旗杆,已知臂长60cm,则旗杆高为米.16.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA =2.OC=1,则矩形AOCB的对称中心的坐标是;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是.17.如图,四边形ABCD与四边形ABFE都是矩形,AB=3,AD=6.5,BF=2.(1)求下列各线段的比:,,;(2)指出AB,BC,CF,CD,EF,FB这六条线段中的成比例线段(写一组即可)18.如图,D在AB上,且DE∥BC交AC于E,F在AD上,且AD2=AF•AB.求证:EF∥CD.19.如图,BC,AD相交于点C,△ABC∽△DEC,AC=4.8,CD=1.6,BC=9.3.(1)求CE的长;(2)求证:BC⊥AD.20.如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:(1)当t=2时,判断△BPQ的形状,并说明理由;(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;(3)作QR∥BA交AC于点R,连接PR,当t为何值时,△APR∽△PRQ.21.如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.①求证:△DAE≌△DCF;②求证:△ABG∽△CFG.22.已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.(1)如图1,当OA=OB,且D为OA中点时,求的值;(2)如图2,当OA=OB,且时,求tan∠BPC的值.(3)如图3,当AD:AO:OB=1:n:时,直接写出tan∠BPC的值.参考答案1.解:A、∵,∴=,此选项正确,不合题意;B、∵,∴=﹣,此选项错误,符合题意;C、∵,∴=,此选项正确,不合题意;D、∵,∴4x=3y,此选项正确,不合题意;故选:B.2.解:A、∵3×9≠6×8,故此选项错误;B、∵3×9≠5×6,故此选项错误;C、∵3×9≠6×7,故此选项错误;D、∵3×18=6×9,故此选项正确;故选:D.3.解:∵DE∥BC,∴,∴当时,,∴EF∥CD,故C选项符合题意;而A,B,D选项不能得出EF∥CD,故选:C.4.解:∵AD∥BC,∴△CBE∽△AED,∴BE:AE=CE:ED=3:5,∵CD=16.CE+ED=CD,∴DE=,故选:D.5.解:根据正方形面积的计算方法和积的变化规律,如果一个正方形的边长扩大为原来的4倍,那么正方形的面积是原来正方形面积的4×4=16倍.故选:A.6.解:∵∠A=∠A,分为两种情况:①DE∥BC(即∠ADE=∠C),∴△ADE∽△ACB,∴=,∴,∴DE=12,②∠ADE′=∠B,∵∠A=∠A,∴△ADE∽△ABC,∴=,∴=,∴AE=>AB,不合题意,故选:A.7.解:①a+b+c=0时,b+c=﹣a,c+a=﹣b,a+b=﹣c,∴x===﹣1;②a+b+c≠0时,x===.综上所述,x=或﹣1.故答案为:或﹣1.8.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.则c2=4×1,c=±2,(线段是正数,负值舍去),故c=2;故答案为2.9.证明:∵AD:DC=1:n,∴AD:AC=1:(n+1).作DG平行于AF交BC于G,则=,根据比例的性质知,==,又E是BD的中点,∴EF是△BGD的中位线,∴BF=FG.∴=.故答案为:.10.解:因为原图中边长为3,5,6的三角形的最长边放大到8,所以放大前后的两个三角形的周长比为6:8=14:,故答案为:11.解:设每条纵向小路的宽为xm.∵小路内外边缘所围成的两个矩形相似,∴,解得,x=1.8,或,解得x=25.8(不符合实际意义)故答案为:1.8.12.解:由题意,相似比=4:5,两个相似三角形周长的比是4:5,可得:5x﹣4x=4,解得:x=4,所以这两个三角形的周长分别是16cm,20cm;故答案为:16;2013.解:∵在▱ABCD中,AO=AC,∵点E是OA的中点,∴AE=CE,∵AD∥BC,∴△AFE∽△CBE,∴==,∵AD=BC,∴AF=AD,∴=;故①正确;∵S△AEF=4,=()2=,∴S△BCE=36;故②正确;∵==,∴=,∴S△ABE=12,故③正确;∵BF不平行于CD,∴△AEF与△ADC只有一个角相等,∴△AEF与△ACD不一定相似,故④错误,故答案为:①②③.14.解:设AC与FH交于P,CD与HG交于Q,∵F、G分别是BC、CE的中点,AB∥HF∥DC∥GN,∴MF=AC=BC,PF=AB=BC,又∵BC=CE=CG=GE,∴CP=MF,CQ=BC,QG=GC=CQ=AB,∴S1=S,S3=2S,∵S1+S3=12,∴S+2S=12,∴S=4.8,故答案为:4.8.15.解:由题意可知△ABC是等腰三角形,AG为高,∴BG=BC,DF=DE=×12cm=0.06m,AF为臂长,即60cm=0.6m.AG=30m,由题意可知△AFD∽△AGB,即=,即=,解得BG=3m,∴BC=2BG=2×3=6m.16.解:∵OA=2.OC=1,∴B(﹣2,1),∴矩形AOCB的对称中心的坐标为(﹣1,),∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,∴B1(﹣3,),同理可得B2(﹣,),B3(﹣,),B4(﹣,),∴矩形A4OC4B4的对称中心的坐标是(﹣,).故答案为(﹣1,),(﹣,).17.解:(1)∵四边形ABCD与四边形ABFE都是矩形,AB=3,AD=6.5,BF=2,∴CD=EF=AB=3,BC=AD=6.5,CF=BC﹣BF=4.5,∴==,==,=;(2)成比例线段有=.18.证明:∵DE∥BC,∴,∵AD2=AF•AB,∴,∴,∴EF∥DC.19.解:(1)∵△ABC∽△DEC,∴又∵AC=4.8,CD=1.6,BC=9.3∴EC=3.1;(2)∵△ABC∽△DEC,∴∠ACB=∠DCE,∵∠ACB+∠DCE=180°,∴∠ACB=∠DCE=90°,∴BC⊥AD.20.解:(1)△BPQ是等边三角形当t=2时AP=2×1=2,BQ=2×2=4∴BP=AB﹣AP=6﹣2=4∴BQ=BP又∵∠B=60°∴△BPQ是等边三角形;(2)过Q作QE⊥AB,垂足为E在Rt△BEQ中,∠BQE=90°﹣∠B=30°,QB=2t,∴BE=t,QE=t由AP=t,得PB=6﹣t∴S△BPQ=×BP×QE=(6﹣t)×t=﹣t ∴S=﹣t;(3)∵QR∥BA∴∠QRC=∠A=60°,∠RQC=∠B=60°∴△QRC是等边三角形∴QR=RC=QC=6﹣2t∵BE=BQ•cos60°=×2t=t∴EP=AB﹣AP﹣BE=6﹣t﹣t=6﹣2t∴EP∥QR,EP=QR∴四边形EPRQ是平行四边形∴PR=EQ=t又∵∠PEQ=90°,∴∠APR=∠PRQ=90°∵△APR∽△PRQ,∴,∴解得t=∴当t=时,△APR∽△PRQ.21.证明:①∵正方形ABCD,等腰直角三角形EDF,∴∠ADC=∠EDF=90°,AD=CD,DE=DF,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF,在△ADE和△CDF中,,∴△ADE≌△CDF;②延长BA到M,交ED于点M,∵△ADE≌△CDF,∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,∵∠MAD=∠BCD=90°,∴∠EAM=∠BCF,∵∠EAM=∠BAG,∴∠BAG=∠BCF,∵∠AGB=∠CGF,∴△ABG∽△CFG.22.解:(1)过D作DE∥CO交AC于E,∵D为OA中点,∴AE=CE=,,∵点C为OB中点,∴BC=CO,,∴,∴PC==,∴=2;(2)过点D作DE∥BO交AC于E,∵,∴==,∵点C为OB中点,∴,∴,∴PC==,过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,∵OA=OB,点C为OB中点,∴CO=2a,在Rt△ACO中,AC===2a,又∵Rt△ADF∽Rt△ACO,∴,∴AF=,DF=,PF=AC﹣AF﹣PC=2a﹣﹣=,tan∠BPC=tan∠FPD==.(3)与(2)的方法相同,设AD=a,求出DF=a,PF=a,所以tan∠BPC=.。
地生中考复习—地理综合训练 (2)

地生中考复习—地理综合训练编号:022 班级:姓名:相信你能成功!请认真阅读以下几点注意事项:1.本场测试包括地理和生物两门学科,分值各100分,时间共90分钟。
2.请按要求填涂答题卡。
1~40题填涂地理答案,41~80题填涂生物答案。
一、本大题共20小题,每小题2分,共40分。
每小题给出的三个选项中只有一项是符合题目要求的。
1. 下列有关亚洲的世界之最说法正确的是A.有世界上最高大的山脉落基由脉B.亚洲东部和北部是世界面积最大、最典型的季风区C.亚洲有世界最高的高原青藏高原2. 欧洲的荷兰是世界著名的“低地国”,国土的1/3是依靠围海大坝保护的,这说明A.人类活动能影响海陆变迁B.现代人改造自然能力很强,想怎么改造就怎么改造,无需顺应自然规律C.荷兰害怕地壳运动引起海水的入侵3. 日本城市中因为建筑风格与长安、洛阳相似,有“洛都”之称的是A.东京B.大阪C.京都4. 同为金砖国家,俄罗斯和印度有很多相似之处,下列描述正确的是①都与我国陆上接壤②都邻太平洋,位于北温带③都是亚洲国家④都有较发达的航天工业A.③④B. ②③C.①④5. 读右图,人们因地制宜,随山势修筑层层叠叠的梯田,主要种植水稻等作物。
这种景观最典型的地区是A.黄土高原地区B.云南省元阳县山区梯田C.青藏高原地区6. 淮安计划修建有关南北方分界“主题公园”,目的是让游客在“一脚横跨”中国南北的同时,直接感受南北方在自然环境、农业生产及民俗等方面的差异。
下列关于“主题公园”的规划,你认为合理的是A.河流南岸种小麦,北岸种水稻B.河流南岸选栽常绿树种,北岸选栽落叶树种C.河流南岸建坡度较小的泥土房,北岸建坡度较大的砖瓦房7. 要将5000吨哈密瓜从乌鲁木齐运到广州,考虑运费因素应选择的运输方式是A.铁路运输B.水路运输C.公路运输8. 上海市郊农业主要种植花卉、蔬菜,发展肉、乳、禽、蛋生产,其主要影响因素是A.自然条件B.市场需求C.政策要求9. 三峡大坝高程185米,蓄水高程l75米,水库长600多公里,总库容393亿立方米,也是世界上最大的水库之一。
最新九年级数学中考专题训练:二次函数综合压轴题(相似三角形问题)

2023年九年级数学中考专题训练:二次函数综合压轴题(相似三角形问题)1.已知,二次函数23y ax bx =+-的图象与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于C 点,点A 的坐标为()1,0-,且OB OC =.(1)求二次函数的解析式;(2)当04x ≤≤时,求二次函数的最大值和最小值分别为多少?(3)设点C '与点C 关于该抛物线的对称轴对称.在y 轴上是否存在点P ,使PCC '△与POB 相似,且PC 与PO 是对应边?若存在,求出点P 的坐标;若不存在,请说明理由.2.如图1,抛物线234y x x =-++与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C ,连接,AC BC .(1)求ABC 的面积;(2)如图2,点P 为直线上方抛物线上的动点,过点P 作PD AC ∥交直线BC 于点D ,过点P 作直线PE x ∥轴交直线BC 于点E ,求PD PE +的最大值及此时P 的坐标;(3)在(2)的条件下,将原抛物线234y x x =-++沿射线AC 方向平移M 是新抛物线与原抛物线的交点,N 是平面内任意一点,若以P 、B 、M 、N 为顶点的四边形是平行四边形,请直接写出点N 的坐标.3.已知抛物线2y x bx c =++与x 轴交于()()1030A B ,、,两点,且与y 轴的公共点为点C ,设该抛物线的顶点为D .(1)求抛物线的表达式,并求出顶点D 的坐标;(2)若点P 为抛物线上一点,且满足PB PC =,求点P 的横坐标;(3)连接CD BC ,,点E 为线段BC 上一点,过点E 作EF CD ⊥交CD 于点F ,若12=DF CF ,求点E 的坐标.4.如图1,在平面直角坐标系中,点O 为坐标原点,抛物线24y ax bx =++与x 轴交于点A 、B (点A 在点B 左侧),与y 轴交于点C ,直线4y x =-+经过B 、C 两点,4OB OA =.(1)求抛物线的解析式;(2)如图2,点P 为第四象限抛物线上一点,过点P 作PD x ⊥轴交BC 于点D ,垂足为N ,连接PC 交x 轴于点E ,设点P 的横坐标为t ,PCD 的面积为S ,求S 与t 的函数关系式;(3)在(2)的条件下,如图3,过点P 作PF PC ⊥交y 轴于点F ,PF PE =.点G 在抛物线上,连接PG ,45CPG ∠=︒,连接BG ,求直线BG 的解析式.5.如图1,已知二次函数2y ax bx c =++的图象的顶点为()0,1D ,且经过点()2,2A .(1)求二次函数的解析式;(2)过点A 的直线与二次函数图象的另一交点为B ,与y 轴交于点C ,若BDC 的面积是ADC △的两倍,求直线AB 的解析式;(3)如图2,已知(),0E m ,是x 轴上一动点(E ,O 不重合),过E 的两条直线1l ,2l 与二次函数均只有一个交点,且直线1l ,2l 与y 轴分别交于点M 、N .对于任意的点E ,在y 轴上(点M 、N 上方)是否存在一点()0,F t ,使N FEM F E △∽△恒成立.若存在,求出t 的值;若不存在,请说明理由.6.如图,抛物线y 2b c x ++与x 轴交于点A 、B ,点A 、B 分别位于原点的左、右两侧,BO =3AO =3,过点B 的直线与y 轴正半轴和抛物线的交点分别为C 、D ,BC.(1)求b、c的值;(2)求直线BD的直线解析式;(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.7.如图1,抛物线与坐标轴分别交于A(-1,0),B(3,0),C(0,3).(1)求抛物线解析式;(2)抛物线上是否存在点P,使得△CBP=△ACO,若存在,求出点P的坐标,若不存在,说明理由;(3)如图2,Q是△ABC内任意一点,求DQ EQ QFAD BE CF++的值.8.如图所示,平面直角坐标系中,二次函数y=a(x+2k)(x﹣k)图象与x轴交于A、B两点,抛物线对称轴为直线x=﹣2;(1)求k 的值;(2)点C 为抛物线上一点,连接BC 、AC ,作CD △x 轴于D ,当△BCA =90°时,设CD 长度为d ,求d 与a 的函数关系式;(3)抛物线顶点为S ,作S T 垂直AB 于T ,点Q 为第一象限抛物线上一点,连接AQ 交S T 于点P ,过B 作x 轴的垂线交AQ 延长线于点E ,连接OE 交BQ 于点G ,过O 作OE 的垂线交AQ 于点F ,若OF =OG ,tan△ABQ =2时,连接S Q ,求证:S Q =S P .9.已知抛物线23y x bx =-++的图象与x 轴相交于点A 和点B ,与y 轴交于点C ,图象的对称轴为直线=1x -.连接AC ,有一动点D 在线段AC 上运动,过点D 作x 轴的垂线,交抛物线于点E ,交x 轴于点F .设点D 的横坐标为m .(1)求AB 的长度;(2)连接AE CE 、,当ACE △的面积最大时,求点D 的坐标; (3)当m 为何值时,ADF △与CDE 相似.10.如图,抛物线28y ax bx =++与x 轴交于()2,0A -和点()8,0B ,与y 轴交于点C ,顶点为D ,连接AC ,BC ,BC 与抛物线的对称轴l 交于点E .(1)求该抛物线的函数表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,设四边形PBOC 和AOC 的面积分别为PBOC S 四边形和AOCS,记AOC PBOC S S S =-△四边形,求S 最大值点P 的坐标及S 的最大值;(3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与BOC 相似?若存在,求点M 的坐标;若不存在,请说明理由.11.如图,抛物线24y ax bx =+-经过点()1,0C -,点()4,0B ,交y 轴于点A ,点H 是该抛物线上第四象限内的一个动点,HE △x 轴于点E ,交线段AB 于点D ,HQ △y 轴,交y 轴于点Q .(1)求抛物线的函数解析式.(2)若四边形HQOE 是正方形,求该正方形的面积.(3)连接OD 、AC ,抛物线上是否存在点H ,使得以点O 、A 、D 为顶点的三角形与△ABC 相似,若存在,请直接写出点H 的坐标,若不存在,请说明理由.12.如图,已知抛物线2y ax x c =-+的对称轴为直线x =1,与x 轴的一个交点为()10A -,,顶点为B .点()5C m ,在抛物线上,直线BC 交x 轴于点E .(1)求抛物线的表达式及点E 的坐标; (2)连接AB ,求△B 的余切值;(3)点G 为线段AC 上一点,过点G 作CB 的垂线交x 轴于点M (位于点E 右侧),当△CGM 与△ABE 相似时,求点M 的坐标.13.如图所示,抛物线2=23y x x --与x 轴相交于A 、B 两点,与y 轴相交于点C ,点M 为抛物线的顶点.(1)求点C 及顶点M 的坐标.(2)若点N 是第四象限内抛物线上的一个动点,连接BN 、CN ,求BCN △面积的最大值. (3)直线CM 交x 轴于点E ,若点P 是线段EM 上的一个动点,是否存在以点P 、E 、O 为顶点的三角形与ABC 相似.若存在,求出点P 的坐标;若不存在,请说明理由.14.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.15.综合与探究如图,抛物线212y x bx c =-++与x 轴交于A ,B 两点,与y 轴交于点C ,点B ,C 的坐标分别为(2,0),(0,3),点D 与点C 关于x 轴对称,P 是直线AC 上方抛物线上一动点,连接PD 、交AC 于点Q .(1)求抛物线的函数表达式及点A 的坐标; (2)在点P 运动的过程中,求PQ :DQ 的最大值;(3)在y 轴上是不存在点M ,使45AMB ∠=︒?若存在,请直接写出点M 的坐标;若不存在,请说明理由.16.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得△CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.17.如图(1),直线y =-x +3与x 轴、y 轴分别交于点B (3,0)、点C (0,3),经过B 、C 两点的抛物线2y x bx c =++与x 轴的另一个交点为A ,顶点为P .(1)求该抛物线的解析式与点P 的坐标;(2)当0<x <3时,在抛物线上求一点E ,使△CBE 的面积有最大值; (3)连接AC ,点N 在x 轴上,点M 在对称轴上,△是否存在使以B 、P 、N 为顶点的三角形与△ABC 相似?若存在,请求出所有符合条件的点N 的坐标;若不存在,请说明理由;△是否存在点M ,N ,使以C 、P 、M 、N 为顶点的四边形是平行四边形?若存在,请直接写出点M 的坐标;若不存在,请说明理由. (图(2)、图(3)供画图探究)18.如图,已知抛物线213222y x x =-++与x 轴交于点A 、B ,与y 轴交于点C .(1)则点A 的坐标为_________,点B 的坐标为_________,点C 的坐标为_________;(2)设点11(,)P x y ,22(,)Q x y (其中12x x >)都在抛物线213222y x x =-++上,若121x x =+,请证明:12y y >;(3)已知点M 是线段BC 上的动点,点N 是线段BC 上方抛物线上的动点,若90CNM ∠=︒,且CMN 与OBC △相似,试求此时点N 的坐标.参考答案:1.(1)2=23y x x --(2)函数的最大值为5,最小值为4-(3)存在,(0,9)P -或9(0,)5P -2.(1)10;(2)最大值为4,()2,6P ; (3)N 点坐标为113,24⎛⎫ ⎪⎝⎭或345,24⎛⎫- ⎪⎝⎭或53,24⎛⎫- ⎪⎝⎭.3.(1)243y x x =-+,()21-,(2)⎝⎭或⎝⎭(3)207,99⎛⎫ ⎪⎝⎭4.(1)254y x x =-+ (2)32122S t t =-+ (3)416y x =-5.(1)2114y x =+ (2)312y x =-或132y x =-+ (3)存在,=2t6.(1)132b c ⎧=-⎪⎪⎨⎪=-⎪⎩(2)y=+(3)Q 1(,0)、Q 2(0)、Q 3,0)、Q 4(,0) 7.(1)223y x x =-++(2)存在,1217(,),(1,4)24P P - (3)DQ EQ QF AD BE CF ++的值为18.(1)k =4 (2)1d a=-9.(1)4(2)(32-,32-) (3)当2m =-或1m =-时ADF △与CDE 相似10.(1)21382y x x =-++ (2)()4,12P ,最大值为56(3)存在,()3,8,(3,5,()3,1111.(1)234y x x =--(2)6+(3)存在,点H 的坐标为1684,525⎛⎫- ⎪⎝⎭或521,24⎛⎫- ⎪⎝⎭12.(1)21322y x x =--;E (2,0) (2)3(3)M 点的坐标为(5,0)或(7,0)13.(1)C 点坐标为(0,-3),顶点M 的坐标为(1,-4);(2)278(3)P 点的坐标为39(,)44--或(-1,-2).14.(1)抛物线L 1:2=23y x x --,抛物线L 2:223y x x =-++; (2)435(,)39M 或(4,5)M -.15.(1)211322y x x =--+,A (-3,0); (2)316; (3)存在,M (0,6)或(0,-6)16.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)17.(1)243y x x =-+,顶点坐标为P (2,-1) (2)33,24E ⎛⎫- ⎪⎝⎭(3)△存在,()10,0N 或27,03N ⎛⎫ ⎪⎝⎭;△存在,点M 的坐标为(2,2);(2,-4);(2,4)18.(1)(-1,0),(4,0),(0,2);(3)点N 的坐标为(32,258)或(3,2).。
综合训练(二)试题解析答案

综合训练(二)一、选择题(本题共20小题;每小题2.5分,满分50分)1.已知西瓜红瓤(R)对黄瓤(r)为显性。
黄瓤西瓜自交产生的种子萌发后用秋水仙素处理,以得到的四倍体为母本,纯合二倍体红瓤西瓜为父本,杂交获得三倍体。
该三倍体开花后授以纯合二倍体红瓤西瓜花粉,则所结无子西瓜瓜瓤的颜色和基因型分别为()A.红瓤,Rrr B.红瓤,RRrC.红瓤,RRR D.黄瓤,rrr解析:选A。
考查三倍体无子西瓜的培育。
四倍体的母本基因型是rrrr,与RR杂交后其三倍体的后代基因型为Rrr,该三倍体作母本,所结果实的果皮基因型和表现型均和亲本相同。
2.在美国《国家科学院院刊》2009年7月15日发表的一项研究中,来自美国北卡罗来纳州立大学和杜克大学的科学家发现,有性生殖的月见草比同科无性生殖的植株能更好的抵御食草昆虫的侵害,科学家认为,有性生殖会使基因混合,这样个体植株就可以去掉一些不好的基因,保留好的基因,这有助于他们不断发展新的方法以抵御虫害,下列有关叙述中错误的是()A.有性生殖可增加遗传物质重组的机会B.进行有性生殖的后代个体具有双亲的遗传性,有更大的变异性和生活力C.在有性生殖过程中可能会发生交叉互换现象D.有性生殖可保持亲、子代遗传性状的一致解析:选D。
由“有性生殖会使基因混合,这样个体植株就可以去掉一些不好的基因,保留好的基因,这有助于他们不断发展新的方法以抵御虫害”可知选项A、B正确;在有性生殖形成配子过程中,减数第一次分裂前期同源染色体会出现联会现象,可能会发生同源染色体的交叉互换,所以C选项正确;有性生殖继承了双亲的遗传物质,但非同源染色体发生了自由组合,所以亲子代之间既有相似性也有差别,故选项D错误。
3.下图表示某正常基因及指导合成的多肽中的氨基酸顺序。
A~D位点发生的突变导致肽链延长停止的是[除图中密码子外,已知GAC(天冬氨酸)、GGU(甘氨酸)、GGG(甘氨酸)、AUG(甲硫氨酸)、UAG(终止)]()A.G/C→A/T B.T/A→G/CC.T/A→C/G D.丢失T/A解析:选A。
年人教版小学英语六年级下期末综合训练试卷及答案(2).doc

天门市2013年春季学期小学英语六年级综合训练(二)Listening Part 听力部分(共四大题,计40分)一、听录音,给下列图片排序。
每小题读两遍。
(共5小题,计10分)()A. ()B. ()C.()D. ()E.二、听录音,选出正确的图片,每小题读两遍。
(共5小题,计10分)()1、A. B. C.()2、A. B. C.()3、A. B. C.()4、A. B. C.()5、A. B. C.三、听录音,选择你所听到的答语,每小题读两遍。
(共5小题,计10分)()1、A、You can go there by subway.B、You can go there by the No.5 bus.()2、A、I’m going to the shoe store next week.B、I’m going to the shoe store tomorrow.()3、A、She is a cleaner. She works in a factory.B、She is an accountant. She works in a bank..()4、A、It comes from the rain.B、It comes from the vapour.()5、A、Water it and wait for it to grow.B、Water it and put it in the sun.四、听录音,判断下列句子正(T)误(F)。
每小题读两遍。
(共5小题,计10分)()1、Li Wei is going to see a film with his father.()2、Fang Lin is going to visit her grandpa.()3、Fang Lin’s father is an accountant.()4、Fang Lin’s father works in a factory.()5、Fang Lin and her father are going to the movie theatre by bike.Writing Part(共八大题,计60分)五、读单词,选出每组单词中不同类的一项。
2.几何综合提高专题(相似、圆) 优录选拔综合训练(二)

ED CBANMEDCBAEDCBAE DCBAl3l2l1C/B/A/CBAl3l2l1C/B/A/CBA基础知识归纳1、相似三角形中几个的基本图形2、由相似三角形得到的几个常用定理定理1 平行于三角形一边的直线截得的三角形与原三角形形似.如图,若DE∥BC,则AD AE DEAB AC BC==,或AD BDAE CE=.定理2 平行切割定理如图,,D E分别是ABCD的边,AB AC上的点,过点A的直线交,DE BC于,M N,若DE∥MN,则DM BNME NC=定理3 (平行线分线段成比例定理)两条直线被一组平行线截得的对应线段成比例.如图,若1l∥2l∥3l,则AB BC ACA B B C A C==ⅱⅱⅱ,定理4(角平分线性质定理)如图,,AD AE分别是ABCD的内角平分线与外角平分线,则DB EB ABDC EC AC==.定理5 射影定理直角三角形斜边上的高分原三角形成两个直角三角形,这两个三角形与原三角形相似.定理6 相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。
即:在⊙O 中,∵弦AB 、CD 相交于点P ,∴PA PB PC PD ⋅=⋅定理7 推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
即:在⊙O 中,∵直径AB CD ⊥, ∴2CE AE BE =⋅定理8 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
即:在⊙O 中,∵PA 是切线,PB 是割线 ∴ 2PA PC PB =⋅定理9 割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如上图)。
即:在⊙O 中,∵PB 、PE 是割线 ∴PC PB PD PE ⋅=⋅基础能力检测1. 如图,点D 为△ABC 的外心,DE 平分ADB ∠,DE=DA ,CE 交DB 于点F ,∠ADB=120°,∠DBC=50°,则∠DFC 的度数为( ) A .50° B .70° C .80° D .100°考点:本题考查了三角形的外心;等腰三角形的性质;构造辅助圆;圆的垂径定理;圆周角定理。
人教版小学英语六年级下期末综合训练试卷及答案(2)

天门市春季学期小学英语六年级天门市春季学期小学英语六年级综合训练(二)综合训练(二)Listening Part Listening Part 听力部分(共四大题,计听力部分(共四大题,计40分)一、听录音,给下列图片排序。
每小题读两遍。
(共5小题,计10分)( )A.( )B.( )C.( )D.( )E.二、听录音,选出正确的图片,每小题读两遍。
(共5小题,计10分)( )1、A.B.C.( )2、A.B.C.( )3、A.B. C.( )4、A.B. C.( )5、A. B. C.三、听录音,选择你所听到的答语,每小题读两遍。
(共5小题,计10分)( )1、A 、You can go there by subway. B 、You can go there by the No.5 bus. ( )2、A 、I ’m going to the shoe store next week. B 、I ’m going to the shoe store tomorrow. ( )3、A 、She is a cleaner. She works in a factory. B 、She is an accountant. She works in a bank.. ( )4、A 、It es from the rain. B 、It es from the vapour. ( )5、A 、ater it and wait for it to grow. B 、ater it and put it in the sun.四、听录音,判断下列句子正(四、听录音,判断下列句子正(T T )误()误(F F )。
每小题读两遍。
(共5小题,计10分) ( )1、Li ei is going to see a film with his father.( )2、Fang Lin is going to visit her grandpa. ( )3、Fang Lin’s father is an accountant. ( )4、Fang Lin ’s father works in a factory.( )5、Fang Lin and her father are going to the movie theatre by bike.riting Part riting Part(共八大题,计(共八大题,计60分)分)五、读单词,选出每组单词中不同类的一项。
2020年浙教版科学中考综合提升专题19解答题综合训练2含答案解析

(2)样品中CaCO3的质量分数是多少?______
(3)反应结束时溶液中MgCl2的质量分数是多少_______?(精确到0.1%)
14.风是永不枯竭的能源。自古以来风能就受到人们的青睐,帆船、风车都是对风能的利用。现在,由于电能的广泛利用,风力发电得到世界各国的高度重视。
(3)传统的火力发电不仅会释放各种大气污染物,而且效率不高,每生产1千瓦时的电能需要消耗标准煤约0.4千克。若功率为30000千瓦的风力发电机组工作24小时,相当于替代标准煤多少吨________?
15.自动上水电热水壶因其方便取水越来越受到人们的喜欢。取水时,只要闭合取水开关,水泵在电动机的带动下,就能将水抽到壶内,如图甲。
(2)温度控制器接通电路的工作过程是,当感温剂气体温度上升时,________,动触点和固定触点接通,压缩机开始工作。
(3)某同学模拟冰箱温控制冷电路,制作了一个恒温箱,如图丙。恒温箱中温度控制器的轻质硬杆OA长为5厘米,OB长为12厘米,注射器的最大刻度为30毫升,刻度部分长为10厘米。
查阅资料得知,在弹性限度内,弹簧的长度l与所挂钩码质量m的关系遵循函数l=km+b(k和b为常数)。为了确定该弹簧k和b的值,在弹簧上挂钩码测得三组数据如上表。
(2)图丙是小敏设计的可以手动调节高、中、低三档加热的电热眼罩原理图。电源电压U恒为4.8伏,已知电热丝R1阻值为4欧,电热丝Ra阻值为6欧,开关S3只接a或b。
①丙图电路中S1闭合,S2断开,S3接a时,加热电路为________(选填“高”、“中”或“低”)温档。
②中温档功率为多少瓦?_______
③高温档工作20分钟,眼罩消耗的电能为多少焦?_______
语言文字运用综合训练(二)(原卷版)2023高考语文一轮复习语言文字运用(全国通用)

【2022高考一轮复习考点专题精练】第一部分语言文字运用(2022新题型)语言文字运用综合训练(二)第一组(一)语言文字运用Ⅰ(9分)阅读下面的文字,完成1~3题。
江南河港交流,且又地滨大海,湖沼特多,故空气里时含水分;到得冬天,不时也会下着微雨,而这微雨寒村里的冬霖景象,又是一种说不出的悠闲境界。
你试想想,秋收过后,河流边三五人家会聚在一个小村子里,门对长桥,窗临远阜,这中间又多是树枝槎桠的杂木树林;在这一幅冬日农村的图上,再洒上一层细得同粉也似的白雨,加上一层淡得几不成墨的背景,你说还够不够悠闲?若再要点些景致进去,则门前可以泊一只乌篷小船,茅屋里可以添几个喧哗的酒客;天垂暮了,还可以加一味红黄,在茅屋窗中画上一圈暗示着灯光的月晕。
人到了这一个境界,自然会胸襟洒脱起来,终至于得失俱亡,死生不问了。
我们总该还记得唐朝那位诗人做的“暮雨潇潇江上村”的一首绝句罢?诗人到此,连对绿林豪客都客气起来了,这不是江南冬景的迷人又是什么?一提到雨,也就必然地要想到雪。
“__①__”自然是江南日暮的雪景。
“__②__”,则雪月梅的冬宵三友,会合在一道,在调戏酒姑娘了。
“__③__”,是江南雪夜,更深人静后的景况。
“__④__”,又到了第二天的早晨,和狗一样喜欢弄雪的村童来报告村景了。
诗人的诗句,也许不尽是江南所写,而做这几句诗的诗人,也许不尽是江南人,但这几句诗来描写江南的雪景,岂不直截了当,比我这一枝愚劣的笔所写的散文更美丽得多?1.下列各项中,和文中画波浪线的句子使用的修辞手法相同的一项是()(3分)A.春色满园关不住,一枝红杏出墙来。
B.山河破碎风飘絮,身世浮沉雨打萍。
C.落红不是无情物,化作春泥更护花。
D.想当年,金戈铁马,气吞万里如虎。
2.给文中画横线的部分填上恰当的诗句,符合原文意境的一项是()(3分)A.①寒沙梅影路,微雪酒香村②晚来天欲雪,能饮一杯无?③柴门闻犬吠,风雪夜归人④前村深雪里,昨夜一枝开B.①晚来天欲雪,能饮一杯无?②寒沙梅影路,微雪酒香村③柴门闻犬吠,风雪夜归人④前村深雪里,昨夜一枝开C.①晚来天欲雪,能饮一杯无?②柴门闻犬吠,风雪夜归人③寒沙梅影路,微雪酒香村④前村深雪里,昨夜一枝开D.①前村深雪里,昨夜一枝开②晚来天欲雪,能饮一杯无?③寒沙梅影路,微雪酒香村④柴门闻犬吠,风雪夜归人3.文中画横线的语句有语病,请修改。
三角形相似综合训练-2023年中考数学拉分专题(教师版含解析)
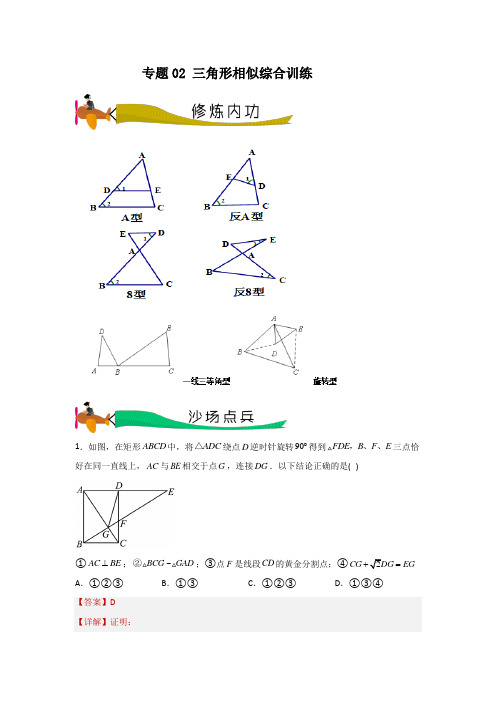
专题02 三角形相似综合训练1.如图,在矩形ABCD 中,将ADC △绕点D 逆时针旋转90︒得到FDE B F E ,、、三点恰好在同一直线上,AC 与BE 相交于点G ,连接DG .以下结论正确的是( )①AC BE ⊥;BCG GAD ~②;③点F 是线段CD 的黄金分割点;④CG EG = A .①②③ B .①③C .①②③D .①③④【答案】D 【详解】证明:FDE ADC ≌,∴AD DF DC DE ==,又∴四边形ABCD 是矩形,∴90ADC ∠=︒, ∴90DAC DCA ∠+∠=即DAG DEF ∠+∠=即BGC 是直角三角形,而AGD 不是直角三角形,∴②错误;Rt FCB 和Rt 中, BFC EFC ∠=∠Rt FCB Rt FDE ∽, FC BCDF DE=, BC AD DF DE DC ===,FC DFDF DC=, F 是线段CD 的黄金分割点,和DEG '中,∴SAS DCG DEG '≌(DG DG CDG ='∠=,90CDG GDA ∠+∠=︒90EDG GDA ∠'+∠=90GDG ∠'=︒,∴GDG '是等腰直角三角形,2GG DG '=EG CG '=EG EG ='故选:D .【我思故我在】2.如图,在ABC 中,D 、E 分别在AB 边和AC 边上,//DE BC ,M 为BC 边上一点(不与B 、C 重合),连结AM 交DE 于点N ,则( )A .ADANANAEB .BD MNMN CEC .DN NEBM MCD .DN NEMC BM,AN ANNE DN NEAM AMMCBMMC,故选相似三角形的判定和性质,解题的关键是熟练掌握3.如图,在ABC ∆中,2AC =,4BC =,D 为BC 边上的一点,且CAD B ∠=∠.若ADC ∆的面积为a ,则ABD ∆的面积为( )A .2aB .52aC .3aD .72aACD BCA ∆,再由相似三角形的性质得到答案ACD BCA ∆,2AC BC ⎛⎫= ⎪⎝⎭,即BCA ∆的面积为的面积为:.4.如图,在矩形ABCD 中,E,F分别为边BC 、CD 中点,线段AE ,AF 与对角线BD 分别交于点G ,H .设矩形ABCD 的面积为S ,则以下4个结论中:①AG :GE =2:1 ②BG :GH :HD =1:1:1;③12325S S S S ++=;④ 246124S S S =::::正确的结论有( )A .1个B .2个C .3个D .4个【答案】C∴,BGE DGA ∽ 2,AG AD BGGE BE DG===②∴AG AD BGGE BE DG==13BG BD =,1所以本题的3个结论符合题意; 故选:C .【我思故我在】本题考查了矩形的性质,三角形相似的性质和判定,三角形面积等知识,解题的关键是理解题意,等底同高三角形面积相等,相似三角形面积的比等于相似比的平方. 5.如图,在正方形ABCD 中,BPC △是等边三角形,BP 、CP 的延长线分别交AD 于E 、F ,连接BD 、DP ,BD 与CF 相交于点H .给出以下结论:①3BE AE =;②DFP BPH ;③2DP PH PC =⋅;④若2AB =,则1BPD S △.其中正确结论的是( )A .①②③④B .②③④C .①②④D .①③④从而证明DFP BPH ,正确;利用DPH CPD ~,得DP PC ,将ΔBPD S 转化为S 四边形解:BPC ∆是等边三角形,BC ,60PBC PCB BPC ∠=∠=∠=ABCD 中,AB BC CD =,A ∠30ABE DCF ∴∠==︒2BE AE ∴=故①错误PC CD =PDC ∴∠=FDP ∴∠=DBA =∠DFP ∠=DFP BPH ∴~,故②正确;30PDH PCD ∠=∠=︒DPH CPD ∴~,∴DP PHPC DP=, 2DP PH PC ∴=⋅,故③正确;如图,过点P 作PM正方形的边长6.如图, 在平行四边形ABCD 中, 点,M N 分别是AD BC 、上的点, 且22AM DM BN CN ==,, 点O 是CM , DN 的交点, 直线AB 分别与CM DN ,的延长线交于点,P Q . 若平行四边形ABCD 的面积为144 , 则POQ △的面积为( )A .72B .216C .268D .300∴AMP DMC ∽, AP AMDC DM=, 2AM DM = 2AP AMDC DM==, 2AP CD =, ∴COD POQ ∽, 1215h CD h PQ ==, ∴∴POQ 的高为56h ,144ABCDS CD h =⋅=151POQS=故选:D 【我思故我在】的性质及平行四边形的性质是解题的关键.7.如图,在正方形ABCD 中,点G 是BC 上一点,且12GC BG =,连接DG 交对角线AC 于F 点,过D 点作DE DG ⊥交CA 的延长线于点E ,若5AE =,则DF 的长为( )A .BC .92D ,证明DEH DGC ∽,推出,求出5EH HA ==延长线于H ,DE DG ⊥EDG ∠∴21∴∠+∠1∠∠∴=DEH DGC ∴∽,∴EH DHGC DC =, 12GC BG =, ∴设GC x =,则BG =∴3EH DHGC x=, AC 是正方形DAC ∴∠EAH ∠=HEA ∴∠=EH HA ∴=2EH HA ∴+EH HA ∴=在正方形8.已知,如图,平行四边形ABCD 中,:1:3=CE BE ,且1EFC S =△,那么ABCS=_____.ACD ABC SS =,证明1:4AD =,则CE AD =. 9.P 是ABC 边上的任一点(P 不与A 、B 、C 重合),过点P 的一条直线截ABC ,如果截得的三角形与ABC 相似,我们称这条直线为过点P 的∴ABC 的“相似线”.Rt ABC △中,90C ∠=︒,30B ∠=︒,当点P 是边BC 上一个三等分点时(PB PC >),过点P 的ABC 的“相似线”最多有___________条.【答案】4【分析】根据相似线的定义,可知截得的三角形与ABC 有一个公共角,分①公共角为A ∠时;②公共角为B ∠时;③公共角为C ∠时;三种情况进行讨论,即可得出答案.【详解】解:①当公共角为A ∠时,不存在;②公共角为B ∠时,过点P 作PD BC ⊥,交AB 于点D ,如图所示:∴90DPB C ∠=∠=︒,B B ∠=∠,∴BPD BCA ∽;过点P 作PD AB ⊥于点D ,如图所示:∴90PDB C ∠=∠=︒,B B ∠=∠,∴BPD BAC ∽△△;③公共角为C ∠时,连接AP ,如图所示:∴30B ∠=︒,∴2AB AC =,设AC a =,则2AB a =,∴ACP BCA∽;过点P作PD AB∥,交∴CDP CAB∽;综上分析可知,过点的ABC的“相似线故答案为:4.【我思故我在】本题主要考查了相似三角形的判定,平行线的性质,勾股定理,解题的关键是熟练掌握三角形相似的判定方法.10.如图,在ABC中,6BC=,AE AFEB FC=,动点P在射线EF上,BP交CE于点D,CBP∠的平分线交CE于点Q,当14CQ CE=时,EP BP+的值为______.【答案】18【分析】如图,延长EF交BQ的延长线于G.首先证明PB PG=,EP PB EG+=,由EG BC∥,11.如图,在矩形ABCD中,点E,F分别是,==∠=︒∠=︒,则BC的长度是___________.3,6,30,45BE CD FED FDE【答案】3##3+【分析】作FN DE ⊥于点N ,延长DE 交CB 的延长线于点M ,先证FND ∆是等腰直角三角形,设FN x =,利用勾股定理、含30度角的直角三角形的性质求出DN ,EF ,NE 的长度,FDE ∠=DFN ∴∠FND ∴∆是等腰直角三角形.由题意得:设FN x =FED ∠=2EF FN ∴=NE ∴=DE DN ∴=3BE =,AE BE ∴=又EAD ∠=EAD ∴∆∆≌AD BM ∴=EBM ∠=EBM ∴∆∽BM BE MN NF ∴=解得:BM 12.如图,在ABC 中,146AB AC ==,,在AC 上取一点D ,使2AD =,如果在AB 上取点E ,使ADE 和ABC 相似,则AE =___________.①ABC AED ;②ABC ADE ;可根据各四条线段的比例关系式求出AE 的长.此时ADE ACB ,::AC AE AD =,146AC AD ==,,此时ADE ABC ,::AC AD AE =,146AC AD ==,,67=, 故答案为:143或67.13.如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M 在旋转中心O 的正下方,某一时刻,太阳光线恰好垂直照射叶片OA 、OB ,此时各叶片影子在点M 右侧成线段CD .测得8.5m MC =,13m CD =,垂直于地面的木棒EF 与影子FG 的比为23:.则点O 、M 之间的距离等于___________m ;【答案】10【分析】连接OM 交AC 于点H ,过点C 作CN BD ⊥,通过证明HMC EFG HAO ∽∽△△△,通过相似三角形对应边成比例即可解答.【详解】解:连接OM 交AC 于点H ,过点C 作CN BD ⊥,14.如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE 并延长,交对角线BD 于点F 、DC 的延长线于点G .如果23CE BE =,求FE EG的值.15.矩形ABCD 中,AC BD ,为对角线,6cm 8cm AB BC ==,,E 为DC 中点,动点P 从点A 出发沿AB 方向,向点B 运动,动点Q 同时以相同速度,从点B 出发沿BC 方向向点C 运动,P 、Q 的速度都是1cm/秒,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为x 秒.()06t <<(1)PQ AC ∥时,求运动时间t ;(2)PQ BD ⊥时,求运动时间t ;(3)当t 为何值时,以点P ,B ,Q 为顶点的三角形与QCE 相似?(4)连接PE PQE ,△的面积能否达到矩形ABCD 面积的三分之一,若能求出t 的值;若不能,说明理由.7BP BQBP BQ为顶点的三角形与QCE相似216.解答题=;(1)如图1,ABC和ADE都是等边三角形,连接BD、CE,求证,BD CE[类比探究](2)如图2,ABC 和ADE 都是等腰直角三角形,90ABC ADE ∠=∠=︒,连接BD CE ,.求BD CE的值.[拓展提升](3)如图3,ABC 和ADE 都是直角三角形,90ABC ADE ∠=∠=︒,2AC AE AB AD==.连接BD CE 、,延长CE 交BD 于点F ,连接AF .若AFC ∠恰好等于90︒,请直接写出此时AF BF CF ,,之间的数量关系.证明BAD CAE ∽,从而得出结果;B 作BH CF ⊥,垂足为点AOF BOH ∆∽,根据对应边成比例,【详解】(1)解:∴ABC 和ADE 都是等边三角形,AC ,AD AE =,∠∠DAE BAC =BAC BAE ∠-∠,即:在BAD 和CAE 中,AB AC DAB EAC AD AE =∠=∠=,(SAS BAD CAE ≌△△BD CE =.∴ABC 和ADE 都是等腰直角三角形,45BAC =∠=︒,ADE ∠ADE △∽,AE AC ,则AD AB AE AC=,BAE BAC -∠=∠-∠在BAD 和CAE 中,DAB EAC =∠,AD AE ∴BAD CAE ∽,BD AB CE AC =, 令AB x =,根据勾股定理可得:2BD AB x CE AC x===(3)∴BAD CAE ∽,ACE ABD ∠=∠,在FOB ∆和AOC ∆中,ACE ABD ∠=∠,∠60OFB OAC ∠=∠=设FH x =,OH y =,则17.在△ABC 中,90ACB ∠=,BE 是AC 边上的中线,点D 在射线BC 上.(1)如图1,点D 在BC 边上,:1:2CD BD =,AD 与BE 相交于点P ,过点A 作AF BC ,交BE 的延长线于点F ,易得AP PD的值为 ; (2)如图2,在△ABC 中,90ACB ∠=,点D 在BC 的延长线上,AD 与AC 边上的中线BE 的延长线交于点P ,:1:2DC BC =,求AP PD的值; (3)在(2)的条件下,若CD=2,AC=6,则BP= .18.在∴ABC 中,CA CB =,ACB α∠=,点P 在平面内不与点A ,C 重合,连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接,,AD BD CP .(1)如图①,当60α=︒,BD CP的值是 ,直线BD 与直线CP 相交所成的较小角的度数是 . (2)如图②,当90α=︒时,请写出BD CP的值及直线BD 与直线CP 相交所成的较小角的度数,并说明理由. (3)当90α=︒时,若点E ,F 分别是,CA CB 中点,点P 在直线EF 上,请直接写出当C ,P ,D 在同一直线上时,求AD CP 的值. ,ABC 是等腰直角三角形,根据等腰直角三角形的性质证明,利用相似的性质即可得解;上,和P 在线段解:如图,延长CP 交60︒,∴ABC 是等边三角形,由题意可知∴PAD 是等边三角形,PAD ∠=∠CAP ∠+∠在CAP 和BAD 中,CA BA CAP BAD AP AD =⎧⎪∠=∠⎨⎪=⎩,CAP BAD △≌△ (SAS),PC BD ACP =∠=∠在AOC 和△1BD PC=,直线BD ∴ABC 是等腰直角三角形,CAB ∠=∠∴ AB AC =AB AD AC AP∴=CAB ∠+∠AD是ABC的中位线,2219.如图,点E是矩形ABCD的边AB的中点,F是BC边上一动点(点F与点B,点C不重合),线段DE和:AF相交于点P,连接PC.(1)若在线段DP 上取一点Q ,使得2DP EQ =,连接AQ ,猜想PC 与AQ 的关系并证明;(2)若AF DE ⊥时,8,10AB AD ==,求BF 的长;(3)当点F 为BC 的中点时,求AP PF 的值. AEQCDP ∆,即可得出结论;,再判断出DAE ABF ,即可得出结论;,先判断出(AAS)ADE BGE ∆≅∆,再判断出2,2AD BF BG BF ==,进而判断出,即可得出结论.∴90BAF AED .90BAF AFB ∠+∠=︒,AED AFB ∠=∠,90DAE ABF ∠=∠=︒,∴DAEABF , AD AE AB BF =,即1083.2BF =;(3)解:如图,延长AD GC ,APD FPG ∆,23AD GF ==.【我思故我在】此题查了矩形的性质,构造出相似三角形是解本题的关键.。
2020年九年级数学典型中考压轴题训练《相似综合》含答案

2020年九年级数学典型中考压轴题训练《相似综合》1.如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG =,求线段AH长.2.如图1,在△ABC中,AB=AC,点D,E分别是边BC,AC上的点,且∠ADE=∠B.(1)求证:AB•CE=BD•CD;(2)若AB=5,BC=6,求AE的最小值;(3)如图2,若△ABC为等边三角形,AD⊥DE,BE⊥DE,点C在线段DE上,AD=3,BE =4,求DE的长.3.如图,AB是⊙O的直径,AB=10,延长弦CD至点E,CD=6,AB⊥CD于点F,点M在AB 上,AM=,连接EM,点N在半径OB上,ON=2,ND∥ME.(1)求tan∠E的值;(2)延长OB至点G,使BG=,连接GD并延长交ME于点H,判断GH与⊙O的位置关系,并求MH的长.4.在Rt△ACB中,∠ACB=90°,点D为AB上一点.(1)如图1,若CD⊥AB,求证:CD2=AD•DB;(2)如图2,若AC=BC,EF⊥CD于H,EF与BC交于E,与AC交于F,且=,求的值;(3)如图3,若AC=BC,点H在CD上,且∠AHD=45°,CH=3DH,直接写出tan∠ACH 的值为.5.定义:连结菱形的一边中点与对边的两端点的线段把它分成三个三角形,如果其中有两个三角形相似,那么称这样的菱形为自相似菱形.(1)判断下列命题是真命题,还是假命题?①正方形是自相似菱形;②有一个内角为60°的菱形是自相似菱形.③如图1,若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED.(2)如图2,菱形ABCD是自相似菱形,∠ABC是锐角,边长为4,E为BC中点.①求AE,DE的长;②AC,BD交于点O,求tan∠DBC的值.6.如图,在矩形ABCD中,AB=3,BC=4,点E是线段AC上的一个动点且=k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.(1)求证:△MED∽△NFE;(2)当EF=FC时,求k的值.(3)当矩形EFHD的面积最小时,求k的值,并求出矩形EFHD面积的最小值.7.如图1,△ABC中,∠ACB的平分线CE交AB于点E.(1)求证:=;(2)如图2,AD⊥BC交CE于F,BD=2AD,∠AEC=45°.①求证:BE=2AE;②直接写出sin∠ACE的值.8.如图1,在△ABC中,点D在AC边上,连接BD,∠ABD=∠C.(1)求证:△ADB∽△ABC;(2)点E在AB边上,连接DE,BE=DE.①如图2,若∠C=30°,求证:3AE•BE=AD•CD;②如图3,△ABC为锐角三角形,AB=6,AC=9,tan C=,请直接写出AE的长.9.在四边形ABCD中,E、F分别是BD、BC上的点,∠BAE=∠BDA.(1)如图1,求证:AB2=BE•BD;(2)如图2,若四边形ABCD是平行四边形,A、E、F三点在同一条直线上,,∠ABC=60°,求的值;(3)如图3,若A、E、F不在同一条直线,∠DEF=∠C,AB=2,BD=4,,,则CD=(直接写出结果).10.矩形ABCD 中,点P 在对角线BD 上(点P 不与点B 重合),连接AP ,过点P 作PE ⊥AP 交直线BC 于点E .(1)如图1,当AB =BC 时,猜想线段PA 和PE 的数量关系: ; (2)如图2,当AB ≠BC 时.求证:(3)若AB =8,BC =10,以AP ,PE 为边作矩形APEF ,连接BF ,当PE =时,直接写出线段BF 的长.11.已知矩形ABCD 中,E 是BC 的中点,DF ⊥AE 于点F . (1)如图1,若BE =,求AE •AF 的值;(2)如图2,连接AC 交DF 于点G ,若=,求cos ∠FCE 的值;(3)如图3,延长DF 交AB 于点G ,若G 点恰好为AB 的中点,连接PC ,过A 作AK ∥FC 交FD 于K ,设△ADK 的面积为S 1,△CDF 的面积为S 2,则的值为 .12.如图1,AB⊥BC,分别过点A,C作BM的垂线,垂足分别为M,N.(1)求证:BM•BC=AB•CN;(2)若AC=BC.①如图2,若BM=MN,过点A作AD∥BC交CM的延长线于点D,求DN:CN的值;②如图3,若BM>MN,延长BN至点E,使BM=ME,过点A作AF∥BC交CE的延长线于点F,若E是CF的中点,且CN=1,直接写出线段AF的长.13.请阅读下列材料,并完成相应的任务.梅涅劳斯(Menelaus)是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,三角形各边(或其延长线)被一条不过任何一个顶点也不与任何一条边平行的直线所截,这条直线可能与三角形的两条边相交(一定还会与一条边的延长线相交),也可能与三条边都不相交(与三条边的延长线都相交).他进行了深入研究并证明了著名的梅涅劳斯定理(简称梅氏定理):设D,E,F依次是OABC的三边AB,BC,CA或其延长线上的点,且这三点共线,则满足.这个定理的证明步骤如下:情况①:如图1,直线DE交△ABC的边AB于点D,交边AC于点F,交边BC的延长线与点E.过点C作CM∥DE交AB于点M,则,(依据)∴=∴BE•AD•FC=BD•AF•EC,即.情况②:如图2,直线DE分别交△ABC的边BA,BC,CA的延长线于点D,E,F.…(1)情况①中的依据指:(2)请你根据情况①的证明思路完成情况②的证明.(3)如图3,D,F分别是△ABC的边AB,AC.上的点,且AD:DB=CF:FA=2:3,连接DF并延长,交BC的延长线于点E,那么BE:CE=.14.如图a,在正方形ABCD中,E、F分别为边AB、BC的中点,连接AF、DE交于点G.(1)求证:AF⊥DE;(2)如图b,连接BG,BD,BD交AF于点H.①求证:GB2=GA•GD;②若AB=10,求三角形GBH的面积.15.问题发现:(1)如图1,在Rt△ABC中,∠A=90°,AB=k•AC(k>1),D是AB上一点,DE∥BC,则BD,EC的数量关系为.类比探究(2)如图2,将△AED绕着点A顺时针旋转,旋转角为a(0°<a<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由拓展延伸:(3)如图3,在(2)的条件下,将△AED绕点A继续旋转,旋转角为a(a>90°).直线BD,CE交于F点,若AC=1,AB=,则当∠ACE=15°时,BF•CF的值为.参考答案1.证明:(1)过点E作EI⊥EF交CF于点I,如图①所示:∵CF⊥AB,∴∠AFG=90°,又∵EF平分∠AFG,∴∠EFA=∠EFI=45°,又∵EF⊥EI,∴∠FEI=90°,又∵∠EFI+∠EIF=90°,∴∠EIF=45°,∴EF=EI,又∵∠EAF+∠AFG+∠FGE+∠GEA=360°,∠AFG=∠AEG=90°,∴∠EGF+∠FAE=180°,又∵∠EGF+∠EGI=180°,∴∠EGI=∠FAE,又∵∠AEB=∠AEF+∠FEG,∠FEI=∠GEI+∠FEG,∴∠AEF=∠GEI,在△AEF和△GEI中,,∴△AEF≌△GEI(AAS),∴AE=GE;(2)连接DO并延长,交⊙O于点P,连接AP,如图②甲所示:∵∠ABD与∠P是⊙O上弧AD所对的圆周角,∴∠ABD=∠P,又∵DP为⊙O的直径,∴∠PAD=90°,又∵tan∠FBG=,∴tan∠P==,又∵AD=3,∴AP=4,PD=5,∴OD=,过点H作HJ⊥AC于点J,过点O作OK⊥AC于点K,设AJ=3t,CF=x,如图②乙所示,∵HJ⊥AC,BD⊥AC,∴HJ∥BD,∴∠ABD=∠AHJ,又∵tan∠ABD=∴tan∠AHJ=,又∵AJ=3t,∴HJ=4t,在Rt△AHJK由勾股定理得:AH===5t,又∵CH是∠ACF的平分线,且HF⊥CF,HJ⊥AC,∴HF=HJ=4t,∴AF=AH+HF=9t,又∵CF=x,∴CJ=x,又∵∠BFG=∠GEC,∠FGB=∠EGC,∴△FBG∽△ECG,∴∠FBG=∠ECG,∴tan∠FCJ===,解得:x=12t,∴CF=CJ=12t,∴AC=15t,∴CK=t,又∵OK∥HJ,∴=,∴OK===t,∴在Rt△OCK中,由勾股定理得:OK2+KC2=OC2,即(t)2+(t)2=()2,解得:t=,或t=﹣(舍去),∴AH=5t=.2.(1)证明:∵AB=AC,∴∠B=∠C,∵∠ADC为△ABD的外角,∴∠ADE+∠EDC=∠B+∠DAB,∵∠ADE=∠B,∴∠BAD=∠CDE,又∠B=∠C,∴△ABD∽△DCE,∴=,∴AB•CE=BD•CD;(2)解:设BD=x,AE=y,由(1)得,5×(5﹣y)=x×(6﹣x),整理得,y=x2﹣x+5=(x﹣3)2+,∴AE的最小值为;(3)解:作AF⊥BE于F,则四边形ADEF为矩形,∴EF=AD=3,AF=DE,∴BF=BE﹣EF=1,设CD=x,CE=y,则AF=DE=x+y,由勾股定理得,AD2+CD2=AC2,CE2+BE2=BC2,AF2+BF2=AB2,∵△ABC为等边三角形,∴AB=AC=BC,∴32+x2=AC2,y2+42=BC2,(x+y)2+12=AC2,∴x2﹣y2=7,y2+2xy=8,解得,x=,y=,∴DE=x+y=.3.解:(1)如图,连接OD,∵AB=10,∴OA=OB=5,∵AB⊥CD,∴CF=DF=CD=3,∴OF===4,∴NF=OF﹣ON=2,∵DN∥ME,∴∠E=∠NDF,∴tan∠E=tan∠NDF==;(2)∵FB=OB﹣OF=1,∴FG=+1=,∵,∴,且∠DFG=∠DFO=90°,∴△DFO∽△GFD,∴∠G=∠ODF,∵∠FOD+∠ODF=90°=∠FOD+∠G,∴∠ODG=90°,∴OD⊥DG,且OD是半径,∴GH是⊙O的切线,∵AM=,∴GM=10﹣+=,在Rt△DFN中,DN===,∵DN∥ME,∴∴∴MH=2.4.(1)证明:∵CD⊥AB,∴∠ADC=∠CDB=90°,∵∠ACB=90°,∴∠B+∠BCD=∠ACD+∠BCD=90°,∴∠B=∠ACD,∴△CBD∽△ACD,∴CD:AD=BD:CD,∴CD2=AD•DB;(2)解:∵=,∴设FH=4a,则HE=9a(a>0),∵∠ACB=90°,EF⊥CD,∴同(1)得:CH2=HE•FH=9a×4a=36a2,∴CH=6a,在Rt△CHF中,tan∠ACD===,过D作DP⊥AC于P,如图2所示:则DP∥BC,在Rt△DPC中,tan∠ACD==,∵AC=BC,∠ACB=90°,∴∠A=45°,∴△ADP是等腰直角三角形,∴AP=DP,∴==,∵DP∥BC,∴==;(3)解:过点D作DM⊥AH于M,如图3所示:∵CH=3DH,∴设DH=2x,则CH=6x(x>0),∴CD=DH+CH=8x,∵AC=BC,∠ACB=90°,∴∠BAC=45°=∠AHD,又∵∠ADH=∠CDA,∴△ADH∽△CDA,∴∠DAH=∠ACH,AD:CD=DH:AD,∴AD2=DH•CD=16x2,∴AD=4x,∵DM⊥AH,∠AHD=45°,∴△ADM是等腰直角三角形,∴DM=HM=DH=x,∴AM===x,∴tan∠ACH=tan∠DAH===;故答案为:.5.解:(1)①正方形是自相似菱形,是真命题;理由如下:如图3所示:∵四边形ABCD是正方形,点E是BC的中点,∴AB=CD,BE=CE,∠ABE=∠DCE=90°,在△ABE和△DCE中,,∴△ABE≌△DCE(SAS),∴△ABE∽△DCE,∴正方形是自相似菱形;②有一个内角为60°的菱形是自相似菱形,是假命题;理由如下:如图4所示:连接AC,∵四边形ABCD是菱形,∴AB=BC=CD,AD∥BC,AB∥CD,∵∠B=60°,∴△ABC是等边三角形,∠DCE=120°,∵点E是BC的中点,∴AE⊥BC,∴∠AEB=∠DAE=90°,∴只能△AEB与△DAE相似,∵AB∥CD,∴只能∠B=∠AED,若∠AED=∠B=60°,则∠CED=180°﹣90°﹣60°=30°,∴∠CDE=180°﹣120°﹣30°=30°,∴∠CED=∠CDE,∴CD=CE,不成立,∴有一个内角为60°的菱形不是自相似菱形;③若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED,是真命题;理由如下:∵∠ABC=α(0°<α<90°),∴∠C>90°,且∠ABC+∠C=180°,△ABE与△EDC不能相似,同理△AED与△EDC也不能相似,∵四边形ABCD是菱形,∴AD∥BC,∴∠AEB=∠DAE,当∠AED=∠B时,△ABE∽△DEA,∴若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED;(2)①∵菱形ABCD是自相似菱形,∠ABC是锐角,边长为4,E为BC中点,∴BE=2,AB=AD=4,由(1)③得:△ABE∽△DEA,∴==,∴AE2=BE•AD=2×4=8,∴AE=2,DE===4,②过E作EM⊥AD于M,过D作DN⊥BC于N,如图2所示:则四边形DMEN是矩形,∴DN=EM,DM=EN,∠M=∠N=90°,设AM=x,则EN=DM=x+4,由勾股定理得:EM2=DE2﹣DM2=AE2﹣AM2,即(4)2﹣(x+4)2=(2)2﹣x2,解得:x=1,∴AM=1,EN=DM=5,∴DN=EM===,在Rt△BDN中,∵BN=BE+EN=2+5=7,∴tan∠DBC==.6.(1)证明:∵四边形ABCD是矩形,∴∠B=90°,AD=BC=4,DC=AB=3,AD∥BC,∵MN⊥BC,∴MN⊥AD,∴∠EMD=∠FNE=90°,∵四边形DEFH是矩形,∴∠MED+∠NEF=90°,∴∠NEF=∠MDE,∴△MED∽△NFE;(2)解:设AM=x,则MD=NC=4﹣x,∵tan∠DAC=tan∠MAE===,∴ME=x,∴NE=3﹣x,∵△MED∽△NFE,∴=,即=,解得:NF=x,∴FC=4﹣x﹣x=4﹣x,EF==,当EF=FC时,4﹣x=,解得:x=4或x=,由题意可知x=4不合题意,当x=时,AE=,∵AC===5,∴k==;(3)解:由(1)可知:△MED∽△NFE,∴==,∴DE=EF,∴矩形EFHD的面积=DE×EF=EF2=[(3﹣x)2+(x)2]=[(x﹣)2+],∴当x﹣=0时,即x=时,矩形EFHD的面积最小,最小值为:×=,∵cos∠MAE===,∴AE=AM=×=,此时k==.7.(1)证明:过B作BG∥AC交CE的延长线于G,如图1所示:则∠G=∠ACE,∵CE平分∠ACB,∴∠ACE=∠BCE,∴∠G=∠BCE,∴BG=BC,∵BG∥AC,∴△ACE∽△BGE,∴,∴;(2)①证明:过E作EM⊥AB交BC于M,如图2所示:则∠AEM=90°,∵∠AEC=45°,∴∠MEC=45°=∠AEC,在△AEC和△MEC中,,∴△AEC≌△MEC(ASA),∴ME=AE,∵AD⊥BC,EM⊥AB,∴∠MEB=∠ADB=90°,∵∠B=∠B,∴△BME∽△BAD,∴,∴BE=2EM,∴BE=2AE;②解:由(1)得:=,∵BE=2AE,∴,设AC=x,BC=2x,AD=1,BD=2,则CD=2x﹣2,又AC2=AD2+CD2,∴x2=12+(2x﹣2)2,=1,,∴x1又2x﹣2>0,∴x=,∴AC=,CD=,作FG⊥AC于G,如图3所示:∵CE平分∠ACB,AD⊥BC,∴FD=FG,∴===,∴,∴DF=AD=×1=,∴CF===,∴sin∠DCF=,∴sin∠ACE=sin∠DCF=.8.(1)证明:∵∠ABD=∠C,∠A=∠A,∴△ADB∽△ABC(2)①证明:过点A作AF∥DE交BD的延长线于点F,过E作EG⊥BD于点G,如图2所示:∵BE=DE,∴∠ABD=∠BDE,∵AF∥DE,∴∠F=∠BDE,∵∠ABD=∠C=30°,∴∠ABD=∠BDE=∠F=∠C=30°,∵∠ADF=∠BDC,∴△ADF∽△BDC,∴DF:CD=AD:BD,∴BD•DF=AD•CD,∵BE=DE,EG⊥BD,∴BG=DG,EG=BE,∴BG=EG=BE,∴BD=2BG=BE,∵AF∥DE,∴DF:AE=BD:BE,∴DF=AE,∴BE•AE=AD•CD,∴3AE•BE=AD•CD;②解:AE=,理由如下:由(1)得:△ADB∽△ABC,∴AB:AC=AD:AB,∴AB2=AD•AC,即62=9AD,∴AD=4,∴CD=AC﹣AD=5,过点A作AF∥DE交BD的延长线于点F,过E作EG⊥BD于点G,如图3所示:∵BE=DE,∴∠ABD=∠BDE,∵AF∥DE,∴∠F=∠BDE,∵∠ABD=∠C,∴∠ABD=∠BDE=∠F=∠C,∵∠ADF=∠BDC,∴△ADF∽△BDC,∴DF:CD=AD:BD,∴BD•DF=AD•CD,∵BE=DE,EG⊥BD,∴BG=DG,tan∠ABD==tan C=,∴BG=EG=BE,∴BD=2BG=BE,∵AF∥DE,∴DF:AE=BD:BE=8:5,∴DF=AE,∴BE•AE=AD•CD,∴64AE•BE=25AD•CD;设AE=x,则BE=6﹣x,∴64x(6﹣x)=25×4×5,解得:x=,或x=,∵AE=>4=AD,∴∠ADE>∠AED=2∠C,∵AF∥DE,∴∠DAF=∠ADE>2∠C,∵△ADF∽△BDC,∴∠DBC=∠DAF>2∠C,∴∠ABC>3∠C>90°,∴x=不合题意舍去,∴AE═.9.(1)证明:∵∠BAE=∠BDA,∠ABE=∠DBA,∴△BAE~△BDA,∴AB:BD=BE:AB,∴AB2=BE•BD;(2)解:作BG⊥AD于G,如图2所示:∵,∴设BF=x,则FC=2x,∵四边形ABCD是平行四边形,∴AD=BC=BF+CF=3x,AD∥BC,∴∠BAG=∠ABC=60°,△BEF∽△DEA,∴==,∴DE=3BE,设BE=y,DE=3y,则BD=BE+DE=4y,由(1)得:AB2=BE•BD=y×4y=4y2,∴AB=2y,∵BG⊥AD,∠BAG=60°,∴∠ABG=30°,∴AG=AB=y,BG=AG=y,∴DG=AG+AD=y+3x,在Rt△BDG中,由勾股定理得:BG2+DG2=BD2,即(y)2+(y+3x)2=(4y)2,解得:x=,∴=,∴===;(3)解:作FH⊥BD于H,在BC的延长线上截取DT=DC,连接DT,如图3所示:则∠DCT=∠T,由(1)得:AB2=BE•BD,即22=BE×4,解得:BE=1,∵=,∴EH=2FH,设FH=a,则EH=2a,BH=1﹣2a,在Rt△BFH中,由勾股定理得:a2+(1﹣2a)2=()2,解得:a=,或a=(不合题意舍去),∴FH=,EH=,∴EF===,∵∠DEF=∠BCD,∠DEF+∠BEF=180°,∠BCD+∠DCT=180°,∴∠BEF=∠DCT=∠T,∵∠EBF=∠TBD,∴△BEF∽△BTD,∴=,即=,∴DT=,∴CD=;故答案为:.10.(1)解:线段PA和PE的数量关系为:PA=PE,理由如下:过点P作PM⊥AB于M,PN⊥BC于N,如图1所示:∵四边形ABCD是矩形,AB=BC,∴四边形ABCD是正方形,∴∠ABC=90°,BD平分∠ABC,∴PM=PN,∴四边形MBNP是正方形,∴∠MPN=90°,∵PE⊥AP,∴∠APE=90°,∴∠APM+∠MPE=90°,∠EPN+∠MPE=90°,∴∠APM=∠EPN,在△APM和△EPN中,,∴△APM≌△EPN(ASA),∴PA=PE,故答案为:PA=PE;(2)证明:过点P作PM⊥AB于M,PN⊥BC于N,如图2所示:∵四边形ABCD是矩形,∴AD=BC,CD=AB,AD⊥AB,CD⊥BC,∠ABC=90°,∴四边形MBNP是矩形,∴∠MPN=90°,∵PE⊥AP,∴∠APE=90°,∴∠APM+∠MPE=90°,∠EPN+∠MPE=90°,∴∠APM=∠EPN,∵∠AMP=∠ENP=90°,∴△APM∽△EPN,∴=,∵PM⊥AB,PN⊥BC,AD⊥AB,CD⊥BC,∴PM∥AD,PN∥CD,∴△BPM∽△BDA,△BPN∽△BDC,∴=,=,∴=,∴==,∴;(3)解:连接AE、PF交于Q,连接QB,过点A作AO⊥BD于O,①当P在O的右上方时,如图3所示:由(2)得:==,∴PA=PE=×=,∵四边形ABCD是矩形,∴AD=BC=10,∠BAD=90°,∴BD===2,∵AO⊥BD,∵△ABD的面积=BD×AO=AB×AD,∴AO===,∵tan∠ABD==,∴=,解得:BO=,由勾股定理得:OP===,∴BP=BO+OP=,∵四边形APEF是矩形,∴∠AEP=90°,AE=PE,QA=QE=QP=QF,∴PF=AE===,∵∠ABE=90°,∴QB=AE=QE,∴QA=QE=QP=QF=QB,∴点A、P、E、B、F五点共圆,AE、PF为圆的直径,∴∠PBF=90°,∴BF===;②当P在O的左下方时,如图4所示:同理可得:AO=,BO=,OP=,PF=,则BP=BO﹣OP=,同理可得:点A、P、E、B、F五点共圆,AE、PF为圆的直径,∴BF===;综上所述,当PE=时,线段BF的长为或.11.解:(1)∵E是BC的中点,∴BC=2BE=2,∵四边形ABCD是矩形,∴AD=BC=2,∠B=90°,AD∥BC,∵DF⊥AE,∴∠AFD=90°=∠B,∴△ABE∽△DFA,∴=,∴AE•AF=AD•BE=2×=4;(2)延长DE交CB的延长线于H,连接DE、AH,如图2所示:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∠BCD=90°,∴△ADG∽△CHG,∴==,∴BH=BC,∵E是BC的中点,∴BE=CE=BH,∴EH=BC=AD,∴四边形ADEH是平行四边形,∵DF⊥AE,∴四边形ADEH是菱形,∴DF=HF,∠AEH=∠AED,DE=AD=EH=BC,∴CE=DE,∴∠CDE=30°,∴∠CED=90°﹣30°=60°,∴∠AEH=∠AED=60°,∵DF⊥AE,∴∠FDE=30°=∠CDE,∴FE=CE,∴∠FCE=∠CFE=∠AEH=30°,∴cos∠FCE=;(3)过F作PQ⊥AB于P,交CD于Q,作KH⊥AD于H,如图3所示:则PQ=AD,AP=DQ,PQ∥BC∥AD,∵G是AB的中点,E是BC的中点,∴AB=2AG,BC=2BE,∵四边形ABCD是矩形,∴AD=BC,AB=CD,∠B=∠DAG=90°,∵DF⊥AE,∴∠ADF+∠DAF=∠BAE+∠DAF=90°,∴∠BAE=∠ADF,∴△ABE∽△DAG,∴=,∴AB•AG=AD•BE,即AB2=AD2,∴AB=AD,∴四边形ABCD是正方形,∴AB=BC=CD=AD=PQ,设AB=BC=CD=AD=PQ=4a,则BE=AG=2a,∴tan∠ADG=tan∠BAE==,AE=DG==2a,∵DF⊥AE,∴AF===a,∵PQ∥BC,∴△APF∽△ABE,∴==,即==,解得:AP=a,PF=a,∴CQ=PB=AB﹣AP=4a﹣a=a,FQ =PQ ﹣PF =4a ﹣a =a ,∵KH ⊥AD ,∴tan ∠ADG ==, 设KH =x ,则DH =2x ,∵PQ ∥AD ,AK ∥FC ,∴∠DAF =∠QFE ,∠KAF =∠CFE ,∴∠DAK =∠QFC ,又∵∠AHK =∠FQC =90°,∴△AHK ∽△FQC , ∴=,即=,解得:AH =x ,∵AH +DH =AD , ∴x +2x =4a ,解得:x =a ,∴KH =a ,∵△ADK 的面积为S 1=AD ×KH ,△CDF 的面积为S 2=CD ×FQ , ∴===; 故答案为:.12.(1)证明:如图1中,∵AM⊥BN,CN⊥BN,AB⊥BC,∴∠AMB=∠N=∠ABC=90°,∴∠A+∠ABM=90°,∠ABM+∠CBN=90°,∴∠A+∠CBN=90°,∴△ABM∽△BCN,∴=,∴BM•BC=AB•CN.(2)解:如图2中,连接AN,延长AN交BC的延长线于H,作BK⊥AN于K.由(1)可知:△ABM∽△BCN,∴=∵AB=BC,∴AM=BN,BM=CN,设CN=m,∵BM=MN,∴BM=CN=MN=m,BN=AM=2m,∵AM⊥BN,BM=MN,∵S=•BN•AM=•AN•BK.△ABN∴BK==m,∴AK===m,∵∠BAK=∠BAH,∠ABH=∠AKB=90°,∴△ABK∽△AHB,∴=,∴=,∴AH=m,∴HN=AH﹣AN=m﹣m=m,∵AD∥CH,∴===.(3)解:如图3中,连接AE,延长AE交BC的延长线于H.∵AF∥CH,∴∠F=∠ECH,∵∠AEF=∠CEH,EF=CF,∴△AFE≌△HCE(ASA),∴AE=EH,AF=CH,∵AM⊥BE,BM=ME,∴AB=AE,∵∠ABH=90°,∵CN=BM=ME=1,∴BE=AE=EH=2,∴AB=BC=AE=2,∴BH==2,∴CH=BH﹣BC=2﹣2,∴AF=2﹣2.13.解:(1)情况①中的依据是:两条直线被一组平行线所截,所得的对应线段成比例.故答案为两条直线被一组平行线所截,所得的对应线段成比例.(2)如图2中,作CN∥DE交BD于N.则有=,=,=,∴•=•,∴BE•AD•FC=BD•AF•EC,∴••=1.(3)如图3中,∵••=1,AD:DB=CF:FA=2:3,∴=.故答案为.14.证明:(1)∵正方形ABCD,E、F分别为边AB、BC的中点,∴AD=BC=DC=AB,AE=BE=AB,BF=CF=BC,∴AE=BF,∵在△ADE和△BAF中,∴△ADE≌△BAF(SAS)∴∠BAF=∠ADE,∵∠BAF+∠DAF=90°∴∠ADE+∠DAF=90°=∠AGD,∴AF⊥DE;(2)①如图b,过点B作BN⊥AF于N,∵∠BAF=∠ADE,∠AGD=∠ANB=90°,AB=AD,∴△ABN≌△ADG(AAS)∴AG=BN,DG=GN,∵∠AGE=∠ANB=90°,∴EG∥BN,∴,且AE=BE,∴AG=GN,∴AN=2AG=DG,∵BG2=BN2+GN2=AG2+AG2,∴BG2=2AG2=2AG•AG=GA•DG;②∵AB=10,∴AE=BF=5,∴DE===5,∵×AD×AE=×DE×AG,∴AG=2,∴GN=BN=2,∴AN=DG=4,∵GE∥BN,∴△DGH∽△BNH,∴==2,∴GH=2HN,且GH+HN=GN=2,∴GH=,=×GH×BN=××2=.∴S△GHB15.解:问题发现:(1)∵DE∥BC,∴,∵AB=k•AC,∴BD=k•EC,故答案为:BD=k•EC;类比探究:(2)成立,理由如下:连接BD由旋转的性质可知,∠BAD=∠CAE∵=,∴△ABD∽△ACE,∴==k,故BD=k•EC;拓展延伸:(3)BF•CF的值为2或1;由旋转的性质可知∠BAD=∠CAE∵=,∴△ABD∽△ACE∴∠ACE=15°=∠ABD∵∠ABC+∠ACB=90°∴∠FBC+∠FCB=90°∴∠BFC=90°∵∠BAC=90°,AC=1,AB=,∴tan∠ABC=,∴∠ABC=30°∴∠ACB=60°分两种情况分析:①如图2,∴在Rt△BAC中,∠ABC=30°,AC=1,∴BC=2AC=2,∵在Rt△BFC中,∠CBF=30°+15°=45°,BC=2 ∴BF=CF=∴BF•CF=()2=2②如图3,设CF=a,在BF上取点G,使∠BCG=15°∵∠BCF=60°+15°=75°,∠CBF=∠ABC﹣∠ABD=30°﹣15°=15°,∴∠CFB=90°∴∠GCF=60°∴CG=BG=2a,GF=a.∵CF2+BF2=BC2∴a2+(2a+a2=22,解得a2=2﹣,∴BF•CF=(2+)a•a=(2+)•a2=1,即:BF•CF=1或2.故答案为:1或2.。
九年级中考复习数学考点训练——几何专题:《相似综合》(二)(word版,带答案)

九年级中考复习数学考点训练——几何专题:《相似的综合》(二)1.已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),当t为何值时,以A、P、Q为顶点的三角形与△ABC相似?2.如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)求证:∠GDA=∠GCB;(2)连接FE,求证:∠GDA=∠GFE;(3)如图2,若AD、BC所在直线互相垂直,试判断是否为定值,若为定值请求出;若不存在定值请说明理由.3.如图,在△ABC中,点D,E分别在边AB,BC上,AE与CD相交于点F,过点E作EG ∥CD交AC的延长线于点G.若AE平分∠BAC,CE=CF.(1)①求证:∠ABC=∠ACD;②求证:△EGC∽△CBD(2)如图2,若∠BAC=90°,AD=2,BD=6,求CG的长.4.如图,点A(10,0),B(0,20),连接AB,动点M、N分别同时从点A,O出发,以1单位长度/秒和2单位长度/秒的速度向终点O、B移动,当其中一点到达终点时停止运动,移动时间为t秒.(1)用含t的代数式表示点M的坐标为(,),点N的坐标为(,);(2)当四边形AMNB的面积恰好为76时,求此时t的值;(3)当t为何值时,△MON与△AOB相似.5.如图,在▱ABCD中,对角线AC、BD交于点O,M为AD中点,连接OM、CM,且CM 交BD于点N,ND=1.(1)证明:△MNO~△CND;(2)求BD的长.6.如图,已知锐角△ABC,AD、CE分别是BC、AB边上的高.(1)证明:△ABD∽△CBE;(2)若△ABC和△BDE的面积分别是24和6,DE=2,求点B到直线AC的距离.7.如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.(1)求证:△GBE∽△ECF;(2)设BG=x,CF=y,求y关于x的函数表达式,并写出自变量的取值范围;(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.8.我们做如下的规定:如果一个三角形在运动变化时保持形状和大小不变,则把这样的三角形称为三角形板.把两块边长为4的等边三角形板ABC和DEF叠放在一起,使三角形板DEF的顶点D与三角形板ABC的AC边中点O重合,把三角形板ABC固定不动,让三角形板DEF绕点O旋转,设边DE与边AB相交于点M,边DF与边BC相交于点N.(1)如图1,当边DF经过点B,即点N与点B重合时,易证△ADM∽△CND.此时,AMCN=.(2)将三角形板DEF绕点O沿逆时针方向旋转得到图2,问AMCN的值是否改变?说明你的理由.(3)在(2)的条件下,设AM=x,两块三角形板重叠面积为y,则y与x的函数关系式为.9.如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,点P从点A出发,以每秒2个单位长度的速度沿AB向点B运动,过点P作PD⊥AB交边AC或边BC于点D,点E是射线PB上的一点,且PE=2PD,以PD、PE为邻边作矩形PEFD.设矩形PEFD与△ABC重叠部分图形的面积为S,点P的运动时间为t(秒).(1)用含t的代数式表示线段PE的长.(2)当点F落在BC上时,求t的值.(3)当矩形PEFD与△ABC重叠部分图形为四边形时,求S与t之间的函数关系式.(4)若△ABC重心为G,矩形DPEF中心为O,当点O与点G到直线AB距离相同时,请直接写出t的值.10.在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,点E为AC边上一点,连接BE交CD于点F,过点E作EG⊥BE交AB于点G,(1)如图1,当点E为AC中点时,线段EF与EG的数量关系是;(2)如图2,当,求的值;(3)如图3,当,不需要求解过程,直接写出的值.参考答案1.解:∵∠C=90°,AC=4cm,BC=3cm,∴AB==5,则BP=t,AQ=2t,AP=5﹣t,∵∠P AQ=∠BAC,当=时,△APQ∽△ABC,即=,解得t=;当=时,△APQ∽△ACB,即=,解得t=;答:t为s或s时,以A、P、Q为顶点的三角形与△ABC相似.2.(1)证明:∵点E是AB的中点,GE⊥AB,∴GE是AB的垂直平分线,∴GA=GB,同理:GD=GC,在△AGD和△BGC中,,∴△AGD≌△BGC(SAS),∴∠GDA=∠GCB;(2)证明:∵∠AGD=∠BGC,∴∠AGB=∠DGC,∵=,∴△AGB∽△DGC,∴=,∵∠AGE=∠DGF,∴∠AGD=∠EGF,∴△AGD∽△EGF,∴∠GDA=∠GFE;(3)解:如图1,延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH,∵△AGD≌△BGC,∴∠GAD=∠GBC,在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,∴∠AGB=∠AHB=90°,∴∠AGE=∠AGB=45°,∴=,∵△AGD∽△EGF,∴==.3.解:(1)①证明:∵CE=CF,∴∠CEF=∠CFE.∵AE平分∠BAC,∴∠BAE=∠CAE,又∵∠CEF=∠ABC+∠BAE,∠CFE=∠ACD+∠CAE,∴∠ABC=∠ACD;②证明:∵EG∥CD,∴∠CEG=∠DCB,∠ACD=∠G,∵∠ABC=∠ACD,∴∠ABC=∠G,∴△EGC∽△CBD;(2)在△AEB和△AEG中,∴△AEB≌△AEG(AAS),∴AG=AB.∠ABC=∠G,∵AD=2,BD=6,∴AB=AD+BD=2+6=8,∴AG=8.∵∠ABC=∠ACD,∠BAC=∠CAD,∴△ABC∽△ACD,∴AB:AC=AC:AD,∴AC2=ABAD=8×2=16,∴AC=4(舍负),∴CG=AG﹣AC=8﹣4=4.4.解:(1)∵ON=2tcm,OM=(10﹣t)cm,∴N(0,2t),M(10﹣t,0);故答案为:0,2t,10﹣t,0;(2)∵S四边形AMNB=S△ABO﹣S△MON,∴76=×10×20﹣×2t×(10﹣t),∴t=4或6,∴当t=4或6时,四边形AMNB的面积为76cm2.(3)∵△MON与△AOB相似,∠MON=∠AOB=90°,∴=或∴或,解得:t=5或2,∴当t=5或2时,△MON与△AOB相似.5.∵OM是△ACD的中位线,∴OM=CD.∵由(1)知,△MNO~△CND,ND=1,∴==,∴ON=,∴OD=ON+ND=,∴BD=2OD=3.6.解:(1)证明:∵AD、CE分别是BC、AB边上的高,∴∠ADB=∠CEB=90°,又∵∠B=∠B,∴△ABD∽△CBE;(2)∵△ABD∽△CBE,∴=,又∵∠B=∠B,∴△BED∽△BCA,∴=.∵△ABC和△BDE的面积分别是24和6,DE=2,∴=,∴AC=4,∴点B到直线AC的距离为:==6.7.解:如图1,延长FE交AB的延长线于F',∵点E是BC的中点,∴BE=CE=2,∵四边形ABCD是正方形,∴AB∥CD,∴∠F'=∠CFE,在△BEF'和△CEF中,,∴△BEF'≌△CEF(SSA),∴BF'=CF,EF'=EF,∵∠GEF=90°,∴GF'=GF,∴∠BGE=∠EGF,∵∠GBE=∠GEF=90°,∴△GBE∽△GEF;(2)∵∠FEG=90°,∴∠BEG+∠CEF=90°,∵∠BEG+∠BGE=90°,∴∠BGE=∠CEF,∵∠EBG=∠C=90°,∴△BEG∽△CFE,∴,由(1)知,BE=CE=2,∵BG=x,CF=y,∴=,∴y=(0≤x≤4);(3)∵AC是正方形ABCD的对角线,∴∠BAC=∠BCA=45°,∵△AGQ与△CEP相似,∴①△AGQ∽△CEP,∴∠AGQ=∠CEP,由(2)知,∠CEP=∠BGE,∴∠AGQ=∠BGE,由(1)知,∠BGE=∠FGE,∴∠AGQ=∠BGQ=∠FGE,∴∠AGQ+∠BGQ+∠FGE=180°,∴∠BGE=60°,∴∠BEG=30°,在Rt△BEG中,BE=2,∴BG=,∴AG=AB﹣BG=4﹣,②△AGQ∽△CPE,∴∠AQG=∠CEP,∵∠CEP=∠BGE=∠FGE,∴∠AQG=∠FGE,∴EG∥AC,∴△BEG∽△BCA,∴=,∴,∴BG=2,∴AG=AB﹣BG=2,即:当△AGQ与△CEP相似,线段AG的长为2或4﹣.8.解:(1)∵∠A=∠C=∠EDB=60°,∴∠ADM+∠CDN=120°,∠ADM+∠AMD=120°,∴∠CDN=∠AMD,∴△ADM∽△CND,∴,∴AMCN=ADCD,∵顶点D与三角形板ABC的AC边中点O重合,∴AD=CD=2,∴AMCN=ADCD=2×2=4,故答案为:4;(2)AMCN的值不会改变.在△ADM与△CND中,∵∠A=∠C=60°,∠DNC=∠DBN+∠BDN=30°+α,∠ADM=30°+α,∴∠ADM=∠CND,∴△ADM∽△CND∴,∴AMCN=ADCD=2×2=4,∴AMCN的值不会改变;(3)情形1,当0°<α<60°时,1<AM<4,即1<x<4,此时两三角形板重叠部分为四边形DMBN,如图2,过D作DQ⊥AB于Q,DG⊥BC于G,∴DQ=DG=,由(2)知,AMCN=4,得CN=,于是y=AB2﹣AMDQ﹣CNDQ=4﹣x﹣(1<x<4);情形2,当60°≤α<90°时,AM≥4时,即x≥4,此时两三角形板重叠部分为△DPN,如图3,过点D作DH∥BC交AM于H,易证△MBP∽△MHD,∴,又∵MB=x﹣4,MH=x﹣2,DH=2,∴BP=,∴PN=4﹣﹣,于是y=PNDG=(4﹣﹣)=﹣,综上所述,y=.故答案为:y=.9.解:(1)∵∠C=90°,AC=8,BC=4,∴AB=,如图2,当D与C重合时,CP⊥AB,cos∠A=,即,AP=,tan∠A=,即,∴PD=t,∴当0<t≤时,如图1,PE=2PD=2×t=2t,如图3,AP=2t,∴PB=4﹣2t,tan∠DBP=,即,PD=8﹣4t,当<t≤4时,如图3,PE=2PD=2(8﹣4t)=16﹣8t;(2)当点F落在BC上时,如图4,BE=4﹣4t,EF=PD=t,∵EF=2BE,∴t=2×(4﹣4t),t=(秒);(3)当0<t≤时,如图1,矩形PEFD与△ABC重叠部分图形是矩形PEFD,S=PDPE=t2t=10t2;如图5,当E与B重合时,PB=2PD,则4﹣2t=2×,t=1,当1<t≤时,如图6,cos∠A=,即,AD=5t,∴CD=8﹣5t,∵DM∥AB,∴∠CDM=∠A,∴cos∠A=cos∠CDM=,即,DM=4﹣t,S=(4﹣t+4﹣2t)t=﹣t2+20t;综上,S与t之间的函数关系式是:S=.(4)∵AQ=QB,G是△ABC的重心,∴QG:GC=1:2,∵AC=8,BC=4,∴AB=,∴CK=,∵GJ∥CK,∴△QGJ∽△QCK,∴,∴,∴GJ=,当点O与点G到直线AB距离相同时,当0<t≤时,PD=,解得:t=,当<t≤4时,PD=,解得:t=,综上所述,当点O与点G到直线AB距离相同时,t的值为或.10.解:如图1,过E作EM⊥AB于M,EN⊥CD于N,∵CD⊥AB,∴四边形EMDN为矩形,∴∠MEN=90°,∵∠ACB=90°,AC=BC,∴∠A=∠ABC=45°,∴AD=CD,∵点E为AC的中点,CD⊥AB,EN⊥DC,∴EN=AD,同理可知,EM=CD,∴EN=EM,∵∠GEB=90°,∠MEN=90°,∴∠NEF=∠GEM,在△EFN和△EGM中,,∴△EFN≌△EGM(ASA),∴EF=EG,故答案为:EF=EG;(2)如图2,过点E作EP⊥AB于点P,作EQ⊥CD于点Q,则△CEQ和△APE均为等腰直角三角形,∴==,由(1)可知,∠QEF=∠PEG,∵∠EQF=∠EPG=90°,∴△EQF∽△EPG,∴==;(3)如图3,过点E作EH⊥AB于点H,作ER⊥CD于点R,则==,由(2)可知,△ERF∽△EHG,∴==.。
2024中考备考重难点重难点相似三角形模型及其综合题综合训练(11大题型+满分技巧+限时分层检测)

重难点02 相似三角形模型及其综合题综合训练中考数学中《相似三角形模型及其综合题综合训练》部分主要考向分为五类:一、K型相似二、8字图相似三、A字图相似四、母子型相似五、手拉手相似相似三角形的综合题中各种相似模型的掌握是解决对应压轴题的便捷方法,所以本专题是专门针对相似三角形模型压轴题的,对提高类型的学生可以自主训练。
考向一:K型相似1.(2023•锡山区校级四模)如图,矩形ABCD中,AB=10,BC=8.点P在AD上运动(点P不与点A、D重合)将△ABP沿直线翻折,使得点A落在矩形内的点M处(包括矩形边界),则AP的取值范围是,连接DM并延长交矩形ABCD的AB边于点G,当∠ABM=2∠ADG时,AP的长是.2.(2023•福田区模拟)综合与探究在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上的点F处.(1)如图①,若BC=2BA,求∠CBE的度数;(2)如图②,当AB=5,且AF•FD=10时,求EF的长;(3)如图③,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF=AN+FD时,请直接写出的值.3.(2023•桐柏县一模)【初步探究】(1)把矩形纸片ABCD如图①折叠,当点B的对应点B'在MN的中点时,填空:△EB'M△B'AN (“≌”或“∽”).【类比探究】(2)如图②,当点B的对应点B'为MN上的任意一点时,请判断(1)中结论是否成立?如果成立,请写出证明过程;如果不成立,请说明理由.【问题解决】(3)在矩形ABCD中,AB=4,BC=6,点E为BC中点,点P为线段AB上一个动点,连接EP,将△BPE沿PE折叠得到△B'PE,连接DE,DB',当△EB'D为直角三角形时,BP的长为.考向二:8字图相似1.(2023•海州区校级二模)“关联”是解决数学问题的重要思维方式.角平分线的有关联想就有很多……【问题提出】(1)如图①,PC是△P AB的角平分线,求证:.小明思路:关联“平行线、等腰三角形”,过点B作BD∥P A,交PC的延长线于点D,利用“三角形相似”.小红思路:关联“角平分线上的点到角的两边的距离相等”,过点C分别作CD⊥P A交P A于点D,作CE⊥PB交PB于点E,利用“等面积法”.请根据小明或小红的思路,选择一种并完成证明.【理解应用】(2)如图②,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将△ACD沿AD所在直线折叠,使点C恰好落在边AB上的E点处,落AC=1,AB=2,则DE的长为.【深度思考】(3)如图③,△ABC中,AB=6,AC=4,AD为∠BAC的角平分线.AD的垂直平分线EF交BC延长线于点F,连接AF,当BD=3时,AF的长为.【拓展升华】(4)如图④,PC是△P AB的角平分线,若AC=3,BC=1,则△P AB的面积最大值是.2.(2023•衢州二模)如图1,在正方形ABCD中,点E在线段BC上,连接AE,将△ABE沿着AE折叠得到△AFE,延长EF交CD于点G.(1)求证:DG=FG;(2)如图2,当点E是BC中点时,求tan∠CGE的值;(3)如图3,当时,连接CF并延长交AB于点H,求的值.考向三:A字图相似1.(2023•宿城区一模)如图,在矩形ABCD中,AB=5,AD=3,先将△ABC沿AC翻折到△AB′C处,再将△AB'C沿翻折到△AB'C'处,延长CD交AC′于点M,则DM的长为.2.(2023•沙坪坝区校级模拟)如图,△ABC中,D在AB上,E在BC上,∠AED=∠ABC,F在AE上,EF=DE.(1)如图1,若CE=BD,求证:BE=CF;(2)如图2,若CE=AD,G在DE上,∠EFG=∠EFC,求证:CF=2GF;(3)如图3,若CE=AD,EF=2,∠ABC=30°,当△CEF周长最小时,请直接写出△BCF的面积.3.(2023•中山区模拟)如图,在平面直角坐标系中,直线y=﹣x+4与x轴,y轴分别交于点A、B,点P为射线AO上的一个动点,过点P作PQ⊥AB于点Q,将沿PQ翻折得到R.设△PQR与△AOB重合部分的面积为S,点P的坐标为(m,0).(1)求AR的长.(用含m的代数式表示)(2)求S关于m的函数解析式,并直接写出自变量m的取值范围.考向四:母子型相似1.(2023•樊城区模拟)【基础巩固】(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.【尝试应用】(2)如图2,在▱ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF =6,AD=9,求CE的长.【拓展提高】(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,连接DE、DF分别交AC于M,N,∠EDF=∠BAD,DF=AE,若MN=18,求EF的值.2.(2023•润州区二模)如图1,在△ABC中,点D在边AB上,点P在边AC上,若满足∠BPD=∠BAC,则称点P是点D的“和谐点”.(1)如图2,∠BDP+∠BPC=180°.①求证:点P是点D的“和谐点”;②在边AC上还存在某一点Q(不与点P重合),使得点Q也是点D的“和谐点”,请在图2中仅用圆规作图,找出点Q的位置,并写出证明过程.(保留作图痕迹)(2)如图3,以点A为原点,AB为x轴正方向建立平面直角坐标系,已知点B(6,0),C(2,4),点P在线段AC上,且点P是点D的“和谐点”.①若AD=1,求出点P的坐标;②若满足条件的点P恰有2个,直接写出AD长的取值范围是.考向五:手拉手相似1.(2023•宝安区校级三模)【问题背景】已知D、E分别是△ABC的AB边和AC边上的点,且DE∥BC,则△ABC∽△ADE,把△ADE绕着A逆时针方向旋转,连接BD和CE.①如图2,找出图中的另外一组相似三角形;②若AB=4,AC=3,BD=2,则CE=;【迁移应用】在Rt△ACB中,∠BAC=90°,∠C=60°,D、E,M分别是AB、AC、BC中点,连接DE和CM.①如图3,写出CE和BD的数量关系;②如图4,把Rt△ADE绕着点A逆时针方向旋转,当D落在AM上时,连接CD和CE,取CD中点N,连接MN,若,求MN的长.【创新应用】如图5:,BC=4,△ADE是直角三角形,∠DAE=90°,tan∠ADE=2,将△ADE绕着点A旋转,连接BE,F是BE上一点,,连接CF,请直接写出CF的取值范围.2.(2023•东港市二模)(1)问题发现:如图1,已知正方形ABCD,点E为对角线AC上一动点,将BE绕点B顺时针旋转90°到BF处,得到△BEF,连接CF.填空:①=;②∠ACF的度数为;(2)类比探究:如图2,在矩形ABCD和Rt△BEF中,∠EBF=90°,∠ACB=∠EFB=60°,连接CF,请分别求出的值及∠ACF的度数;(3)拓展延伸:如图3,在(2)的条件下,将点E改为直线AC上一动点,其余条件不变,取线段EF 的中点M,连接BM,CM,若,则当△CBM是直角三角形时,请直接写出线段CF的长.3.(2023•晋中模拟)综合与实践问题情境:(1)如图1,在△ABC和△ADE中,AB=AC,AD=AE.如图2,将△ABC绕顶点A按逆时针方向旋转15°得到△AB'C',连接B′D,C′E,求证:B′D=C′E.深入研究:(2)①如图3,在正方形ABCD和正方形CEFG中,已知点B,C,E在同一直线上,连接DE,AF,交于点P,求AF:DE的值;②如图4,若将正方形CEFG绕点C按顺时针方向旋转一定角度,AF:DE的值变化吗?请说明理由.拓展应用:(3)如图5,若把正方形ABCD和正方形CEFG分别换成矩形ABCD和矩形CEFG,且AD:AB=CG:CE=k,请直接写出此时AF:DE的值.(建议用时:150分钟)1.(2023•菏泽)(1)如图1,在矩形ABCD中,点E,F分别在边DC,BC上,AE⊥DF,垂足为点G.求证:△ADE∽△DCF.【问题解决】(2)如图2,在正方形ABCD中,点E,F分别在边DC,BC上,AE=DF,延长BC到点H,使CH=DE,连接DH.求证:∠ADF=∠H.【类比迁移】(3)如图3,在菱形ABCD中,点E,F分别在边DC,BC上,AE=DF=11,DE=8,∠AED=60°,求CF的长.2.(2023•济南)在矩形ABCD中,AB=2,AD=2,点E在边BC上,将射线AE绕点A逆时针旋转90°,交CD延长线于点G,以线段AE,AG为邻边作矩形AEFG.(1)如图1,连接BD,求∠BDC的度数和的值;(2)如图2,当点F在射线BD上时,求线段BE的长;(3)如图3,当EA=EC时,在平面内有一动点P,满足PE=EF,连接P A,PC,求P A+PC的最小值.3.(2023•武汉)问题提出如图(1),E是菱形ABCD边BC上一点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°),AF交CD于点G,探究∠GCF与α的数量关系.问题探究(1)先将问题特殊化,如图(2),当α=90°时,直接写出∠GCF的大小;(2)再探究一般情形,如图(1),求∠GCF与α的数量关系.问题拓展将图(1)特殊化,如图(3),当α=120°时,若,求的值.4.(2023•内蒙古)已知正方形ABCD,E是对角线AC上一点.(1)如图1,连接BE,DE.求证:△ABE≌△ADE;(2)如图2,F是DE延长线上一点,DF交AB于点G,BF⊥BE.判断△FBG的形状并说明理由;(3)在第(2)题的条件下,BE=BF=2.求的值.5.(2023•湖州)【特例感知】(1)如图1,在正方形ABCD中,点P在边AB的延长线上,连结PD,过点D作DM⊥PD,交BC的延长线于点M.求证:△DAP≌△DCM.【变式求异】(2)如图2,在Rt△ABC中,∠ABC=90°,点D在边AB上,过点D作DQ⊥AB,交AC于点Q,点P在边AB的延长线上,连结PQ,过点Q作QM⊥PQ,交射线BC于点M.已知BC=8,AC=10,AD =2DB,求的值.【拓展应用】(3)如图3,在Rt△ABC中,∠BAC=90°,点P在边AB的延长线上,点Q在边AC上(不与点A,C重合),连结PQ,以Q为顶点作∠PQM=∠PBC,∠PQM的边QM交射线BC于点M.若AC=mAB,CQ=nAC(m,n是常数),求的值(用含m,n的代数式表示).6.(2023•鞍山)如图,在△ABC中,AB=AC,∠BAC=α,点D是射线BC上的动点(不与点B,C重合),连接AD,过点D在AD左侧作DE⊥AD,使AD=kDE,连接AE,点F,G分别是AE,BD的中点,连接DF,FG,BE.(1)如图1,点D在线段BC上,且点D不是BC的中点,当α=90°,k=1时,AB与BE的位置关系是,=.(2)如图2,点D在线段BC上,当α=60°,k=时,求证:BC+CD=2FG.(3)当α=60°,k=时,直线CE与直线AB交于点N,若BC=6,CD=5,请直接写出线段CN的长.7.(2023•益阳)如图,在Rt△ABC中,∠ACB=90°,AC>BC,点D在边AC上,将线段DA绕点D按顺时针方向旋转90°得到DA′,线段DA′交AB于点E,作A′F⊥AB于点F,与线段AC交于点G,连接FC,GB.(1)求证:△ADE≌△A′DG;(2)求证:AF•GB=AG•FC;(3)若AC=8,tan A=,当A′G平分四边形DCBE的面积时,求AD的长.8.(2023•福建)如图1,在△ABC中,∠BAC=90°,AB=AC,D是AB边上不与A,B重合的一个定点.AO ⊥BC于点O,交CD于点E.DF是由线段DC绕点D顺时针旋转90°得到的,FD,CA的延长线相交于点M.(1)求证:△ADE∽△FMC;(2)求∠ABF的度数;(3)若N是AF的中点,如图2,求证:ND=NO.9.(2022•湖北)问题背景:一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图1,已知AD是△ABC的角平分线,可证=.小慧的证明思路是:如图2,过点C作CE∥AB,交AD的延长线于点E,构造相似三角形来证明=.尝试证明:(1)请参照小慧提供的思路,利用图2证明:=;应用拓展:(2)如图3,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB上的E点处.①若AC=1,AB=2,求DE的长;②若BC=m,∠AED=α,求DE的长(用含m,α的式子表示).10.(2022•宁波)【基础巩固】(1)如图1,在△ABC中,D,E,F分别为AB,AC,BC上的点,DE∥BC,BF=CF,AF交DE于点G,求证:DG=EG.【尝试应用】(2)如图2,在(1)的条件下,连结CD,CG.若CG⊥DE,CD=6,AE=3,求的值.【拓展提高】(3)如图3,在▱ABCD中,∠ADC=45°,AC与BD交于点O,E为AO上一点,EG∥BD交AD于点G,EF⊥EG交BC于点F.若∠EGF=40°,FG平分∠EFC,FG=10,求BF的长.11.(2023•广州)如图,AC是菱形ABCD的对角线.(1)尺规作图:将△ABC绕点A逆时针旋转得到△ADE,点B旋转后的对应点为D(保留作图痕迹,不写作法);(2)在(1)所作的图中,连接BD,CE.①求证:△ABD~△ACE;②若tan∠BAC=,求cos∠DCE的值.。
