2016-2017年度美国“数学大联盟杯赛”(中国赛区)初赛(五年级)
美国“数学大联盟杯赛” 中国赛区 初赛五年级试卷

2017-2018年度美国“数学大联盟杯赛”(中国赛区)初赛(五年级)(初赛时间:2017年11月26日,考试时间90分钟,总分200分)学生诚信协议:考试期间,我确定没有就所涉及的问题或结论,与任何人、用任何方式交流或讨论, 我确定我所填写的答案均为我个人独立完成的成果,否则愿接受本次成绩无效的处罚。
请在装订线内签名表示你同意遵守以上规定。
考前注意事项:1. 本试卷是五年级试卷,请确保和你的参赛年级一致;2. 本试卷共4页(正反面都有试题),请检查是否有空白页,页数是否齐全;3. 请确保你已经拿到以下材料:本试卷(共4页,正反面都有试题)、答题卡、答题卡使用说明、英文词汇手册、 草稿纸。
考试完毕,请务必将英文词汇手册带回家,上面有如何查询初赛成绩、 及如何参加复赛的说明。
其他材料均不能带走,请留在原地。
选择题:每小题5分,答对加5分,答错不扣分,共200分,答案请填涂在答题卡上。
1. The smallest possible sum of two different prime numbers isA) 3B) 4C) 5D) 62. The greatest common factor of two numbers is3. The product of these two numbers mustbe divisible byA) 6 B) 9 C) 12 D) 18 3. The sum of 5 consecutive one-digit integers is at most A) 15 B) 25 C) 35 D) 45 4. How many two-digit multiples of 10 are also multiples of 12?A) 4B) 3C) 2D) 15. I have read exactly13of the total number of chapters in my 120-page book. If each chapter has the same whole number of pages, then the total number of chapters I have left could beA) 16 B) 24 C) 32 D) 50 6. What is the greatest odd factor of 44 × 55 × 66?A) 36 B) 55 C) 35 × 55 D) 36 × 55 7. What is the sum of the factors of the prime number 2017? A) 2016B) 2017C) 2018D) 20198. Lynn ran in 6 times as many races as the number of racesshe won. How many of her 126 races did Lynn not win?A) 21B) 90C) 96D) 1059. The least common multiple of 8 and 12 is the greatest common factor of 120 andA) 80B) 124C) 144D) 18010. January has the greatest possible number of Saturdays when January 1 occurs on any ofthe following days of the week exceptA) Thursday B) Friday C) Saturday D) Sunday 11. The number that is 10% of 1000 is 10 more than 10% ofA) 90B) 100C) 900D) 99012. The sum of 16 fours has the same value as the product of ? fours.A) 2 B) 3 C) 4 D) 16 13. Of the following, which is the sum of two consecutive integers?A) 111 111B) 222 222C) 444 444D) 888 88814. Abe drove for 2 hours at 30 km/hr. and for 3 hours at 50 km/hr. What was Abe’s averagespeed over the 5 hours?A) 35 km/hr.B) 40 km/hr.C) 42 km/hr.D) 45 km/hr.15. My broken watch runs twice as fast as it should. If my watch first broke at 6:15 P.M.,what time was displayed on my watch 65 minutes later?A) 7:20 P.M. B) 7:25 P.M.C) 8:20 P.M. D) 8:25 P.M.16. (2018 × 2017) + (2018 × 1) =A) 20172 B) 20182 C) 20183D) (2018 + 2017)217. A prized bird lays 2, 3, or 4 eggs each day. If the bird laid 17 eggs in 1 week,on at most how many days that week did the bird lay exactly 2 eggs?A) 2B) 3C) 4D) 518. Of the following, which could be the perimeter of a rectangle whoseside-lengths, in cm, are prime numbers?A) 10 cmB) 22 cmC) 34 cmD) 58 cm19. The average of all possible total values of a 4-coin stack of nickels and dimes (containingat least one of each coin) isA) 20¢B) 30¢C) 40¢D) 60¢20. The diameter of Ann’s drum i s 40 cm more than the radius. What is half the circumference of the drum?A) 120π cmB) 80π cmC) 60π cmD) 40π cm21. Of the following, which expression has the greatest number offactors that are multiples of 2018?A) 2018 × 12B) 20182C) 20192D) 20192019第1页,共4页 第2页,共4页22. When the sum of the factors of a prime number is divided by that prime number, theremainder isA) 0 B) 1 C) 2 D) 3 23. What is the sum of the digits of the greatest integer that has a square root less than 100? A) 18B) 36C) 99D) 10024. My favorite number has 6 different factors. If the product of all 6 factors is 123, what isthe sum of the factors of my favorite number?A) 24B) 28C) 32D) 3625. For how many different pairs of unequal positive integers less than 10 is the least commonmultiple of the numbers less than their product?A) 6B) 7C) 8D) 926. Exactly 12 of the students in my class have at least one brother, and 12 have at least onesister. If 13have no siblings, what fraction of the students in my class have at least onebrother and at least one sister?A) 16 B) 15 C) 14 D) 1327. Each day, Sal swims a lap 1 second faster than on the daybefore. If Sal swims a lap in 60 minutes on the 1st day, on what day does he swim a lap in 10% less time than the 1st day?A) 359th B) 360th C) 361st D) 362nd 28. 20172018 × 20172019 = 2017 ? × 20171009A) 1010B) 2010C) 3028D) 403829. Both arcs AB and AD are quarter circles of radius 5, figure on the right.Arc BCD is a semi-circle of radius 5. What is the area of the region ABCD ?A) 25 B) 10 + 5π C) 50D) 50 + 5π30. For every $5 I earn from my job, I save $2. For every $4 I save from my job, I am givenan additional $1 from my parents to add to my savings. How much must I earn in order to have $40 in savings?A) $160B) $120C) $100D) $8031. In the figure on the right, the side-length of the smaller squareis 4. The four arcs are four semi-circles. Each side of square ABCD is tangent to one of the semi-circles. The area of ABCD isA) 32B) 36C) 48D) 6432. A million is a large number, a “1” follo wed by 6 zeros. A googol is a large number, a “1”followed by one hundred zeros. A googolplex is a large number, a “1” followed by a googol of zeros. A googolplexian is a large number, a “1” fo llowed by a googolplex of zeros. A googolplexian isA) 10100 B) 1001010C) 100101010D) None of the above33. An integral triangle is a triangle with positive integral side-lengths and a positive area.Such a triangle can have a perimeter as small as 3. What is the next smallest possible perimeter of an integral triangle?A) 4B) 5C) 6D) 734. 2 liter of 2% fat milk + 3 liter of 3% fat milk = 5 liter of ? fat milkA) 2.5%B) 2.6%C) 5%D) 6%35. One day, a motorist came to a hill that was ten-mile drive up one side and a ten-mile drivedown the other. He drove up the hill at an average speed of 30 miles per hour. How fast will he have to drive down the other side to average 60 miles per hour for the entire 20-mile distance?A) 30 miles per hour B) 60 miles per hour C) 90 miles per hour D) None of the above 36. What is the weight of a fish if it weighs ten pounds plus half its weight?A) 10B) 15C) 20D) 2537. Without using pennies, how many different combinations of coins (nickels, dimes,quarters) will make 30 cents?A) 3B) 4C) 5D) 638. A man once bought a fine suit for which he paid $30 more than14of its price. How much did he pay for the suit? A) $30B) $35C) $40D) $4539. A father is five times as old as his son. In fifteen years he will be only twice as old. Howold is the father at present?A) 40B) 35C) 30D) 2540. It takes 30 minutes to completely fill a tank. If, however, a hole allows13of the water that is entering the tank to escape, how long will it then take to fill the tank?A) 40 B) 45 C) 60 D) 90第3页,共4页第4页,共4页。
2017年世界青少年奥林匹克数学竞赛(中国区)选拔赛五年级数学决赛试卷

第1页 共四页 第2页 共四页秘密★启用前世界青少年奥林匹克数学竞赛(中国区)选拔赛全国总决赛试卷注意事项: 1、考生按要求用黑色、蓝色圆珠笔或钢笔在密封线内填好考生的相关信息。
2、考试时间120分钟。
3、本试卷共4页,满分100分。
4、不得在答卷或答题卡上做任何标记。
5、考生超出答题区域答题将不得分。
6、考生在考试期间不得作弊,否则试卷记零分处理。
小学五年级试题一、计算题(每题3分,共12分) 1. 7.1×35+39×3.5-352. (5.6×4.5×8.1)÷(2.8×1.5×2.7)3. 0.7777×0.7+0.1111×2.14. 987654321×123456789-987654320×123456788二、填空题(每空3分,共24分)1. 把一根木头锯成4段需要12分钟,如果锯成8段需要( )分钟。
2. 有三个好朋友,他们的年龄一个比一个大3岁,他们3人年龄数的乘积是3240。
其中最小的年龄是( )岁。
3. 三个不同的自然数的和为2001,它们分别除以19,23,31所得的商相同,所得的余数也相同,这三个数中最大的是( )。
4. 一本书的中间被撕掉了一张,余下的页码数之和正好是907,这本书有( )页。
5. 下列格点中,相邻两个点之间的距离是1cm ,图中三角形的面积是( )平方厘米。
6. 一个最简分数,若分母加上1,分数值是21,若分子加上1,分数值是32,这个分数是( )。
7. 数列1,1,2,3,5,8,13,21…的排列规律是:从第三个数开始,每一个数都是它前面两个数的和,这样的数列叫做斐波拉契数列。
斐波拉契数列的前2017个数中,有( )个偶数。
8. 2008个2008相乘的末位数字是( )。
三、解决问题(每题8分,共64分)1. 图中三角形ABC 的面积是52平方厘米,三角形ABD 与三角形ADC 的面积相等。
美国数学大联盟杯赛五年级试卷(2020新教材)

——教学资料参考参考范本——美国数学大联盟杯赛五年级试卷(2020新教材)______年______月______日____________________部门(初赛时间:2018年11月14日,考试时间90分钟,总分200分)学生诚信协议:考试期间,我确定没有就所涉及的问题或结论,与任何人、用任何方式交流或讨论,我确定以下的答案均为我个人独立完成的成果,否则愿接受本次成绩无效的处罚。
如果您同意遵守以上协议请在装订线内签名选择题:每小题5分,答对加5分,答错不扣分,共200分,答案请填涂在答题卡上。
1. A 6 by 6 square has the same area as a 4 by ? rectangle.A) 3 B) 6 C) 8 D) 92.Every prime has exactly ? positive divisors.A) 1 B) 2 C) 3 D) 4 or more3.If I answered 34 out of 40 questions on my math testcorrectly, I answered ? % of the questions correctly.A) 75 B) 80 C) 85 D) 904.120 ÷ 3 ÷ 4 × 12 =A) 1 B) 10 C) 12 D) 1205.10 × 20 × 30 × 40 = 24 × ?A) 1000 B) 10 000 C) 100 000 D) 1000 0006.One of my boxes contains 1 pencil and the others each contain 5 pencils. If there are101 pencils in my boxes, how many boxes do I have?A) 19 B) 20 C) 21 D) 227.of those are damaged. How many light bulbs are not damaged?A) 25 B) 504 C) 1512 D) 20xx8.50 × (16 + 24) is the square ofA) -40 B) -4 C) 4 D) 809.Which of the following numbers has exactly 3 positive divisors?A) 49 B) 56 C) 69 D) 10010.Ten people stand in a line. Counting from the left, Jerrystands at the 5th position. Counting from the right, which position is he at?A) 4 B) 5 C) 6 D) 711.On a teamwork project, Jack contributed 2/7 of the totalamount of work, Jill contributed 1/4 of the work, Patcontributed 1/5 of the work, and Matt contributed the rest.第1页,共4页Who contributed the most toward this project?A) Jack B) Jill C) Pat D) Matt12.Which of the following numbers is a factor of 20xx?A) 5 B) 11 C) 48 D) 9913.2 × 4 × 8 × 16 × 32 × 64 =A) 210B) 215C) 221D) 212014.On a game show, Al won four times as much as Bob, and Bobwon four times as much as Cy. If Al won $1536, how much did Al, Bob, and Cy win together?A) $96 B) $384 C) $1920 D) $20xx15. cannot beA) odd B) even C) 11 D) 1716.If a and b are positive integers such that a/b = 5/7, thena +b isA) 12 B) 24 C) 36 D) not able to be determined17.What is the greatest odd factor of the number of hours in all the days of the year 20xx?A) 3 B) 365 C) 1095 D) 328518. If the current month is February, what month will it be 1199 999 months from now?A) January B) February C) March D) April 19. ° less than the other. What is the measure of the larger angle?A) 36°B) 54°C) 63°D) 72°20. (The square root of 16) + (the cube root of 64) + (the 4throot of 256) =A) 12B) 24C) 32D) 6421. In ∆ABC, m ∠A – m ∠B = m ∠B – m ∠C. What is the degreemeasure of ∠B?A) 30B) 60C) 90D) 12022. For every 3 math books I bought, I bought 2 biology books. I bought 55 books in all. How many of those are math books?A) 11 B) 22C) 33D) 4423. ? 1s.A) 17B) 19C) 29D) 3224. Weird Town uses three types of currencies: Cons, Flegs, and Sels. If 3 Sels = 9 Cons and 2 Cons = 4 Flegs, then 5 Sels = ? Flegs.A) 12B) 24 C) 30 D) 3625. If the length of a rectangular prism with volume V isdoubled while the width and the height are halved, the volume of the new prism will beA) 4VB) V /2C) VD) 2V26. Rick and Roy each stands at different ends of a straight road that is 64 m long. They run toward each other. Rick ’s speed is 3 m/s and Roy ’s speed is 5 m/s. They will meet in? seconds.……………线…………………………………………………………… ……………答…………………题………………………………………。
【2020】最新美国数学大联盟杯赛五年级试卷

(初赛时间:2018年11月14日,考试时间90分钟,总分200分)学生诚信协议:考试期间,我确定没有就所涉及的问题或结论,与任何人、用任何方式交流或讨论,我确定以下的答案均为我个人独立完成的成果,否则愿接受本次成绩无效的处罚。
如果您同意遵守以上协议请在装订线内签名选择题:每小题5分,答对加5分,答错不扣分,共200分,答案请填涂在答题卡上。
1. A 6 by 6 square has the same area as a 4 by ? rectangle.A) 3 B) 6 C) 8 D) 92.Every prime has exactly ? positive divisors.A) 1 B) 2 C) 3 D) 4 or more3.If I answered 34 out of 40 questions on my math test correctly, I answered ? % of the questionscorrectly.A) 75 B) 80 C) 85 D) 904.120 ÷ 3 ÷ 4 × 12 =A) 1 B) 10 C) 12 D) 1205.10 × 20 × 30 × 40 = 24 × ?A) 1000 B) 10 000 C) 100 000 D) 1000 0006.One of my boxes contains 1 pencil and the others each contain 5 pencils. If there are 101 pencils inmy boxes, how many boxes do I have?A) 19 B) 20 C) 21 D) 227.of those are damaged. How many light bulbs are not damaged?A) 25 B) 504 C) 1512 D) 20xx8.50 × (16 + 24) is the square ofA) -40 B) -4 C) 4 D) 809.Which of the following numbers has exactly 3 positive divisors?A) 49 B) 56 C) 69 D) 10010.Ten people stand in a line. Counting from the left, Jerry stands at the 5th position. Counting fromthe right, which position is he at?A) 4 B) 5 C) 6 D) 72 / 4第1页,共4页23. ? 1s.4 Flegs, then5 Sels = ? Flegs.。
上海走美5年级初赛,如果没学过奥数能得多少分

啰里啰嗦写了这么多,只是个人看法,欢迎拍砖。
【上海】沙漏
37+1
19
3
73+1
37
2
145+1
73
1
289+1
145
不成功尝试之一,再尝试把猴王不摘桃的次序上下移,不能得到题目规定的范围值, 因此 385 是唯一答案
第 10 题:长方形内有 2017 个点,连同长方形 4 个顶点,一共 2021 个点,这些点任意 3 个点都不在同一条直线上,以这些点中某 3 个点为顶点,可作出多少个互不重叠的三角 形
第 9 题: 一堆桃子,奇数个且数量大于 360 小于 400。猴王分桃规则是:若桃子偶数个,分桃猴子 分走 1 半,若奇数个,猴王从树上摘一个桃子放入桃堆让分桃猴子分一半,当桃子剩下一 个后停止分桃。第 9 个猴子分桃后剩下一个桃子,猴王一共摘了 7 个桃子放入桃堆,问原 来有多少个桃 个人以为跟高大上的二进制没啥大关系,不用二进制,照样做出来,规则还是找规律。 从最后剩下 1 个桃来看,第 9 个猴子分桃前只能剩下 2 个桃子,如果剩 3 个,则分好后必 然剩下 2 个桃子,进而推出第 8 个猴子分桃前剩下的桃子数可能为 3 或 4,然后列表倒推
第 7 题:从 1、2、3、4、5、6、7、8、9 这 9 个数选出 6 个不同的数,分别写在一个正方 体的 6 个面上,使任意相邻的面所写 2 个数的差不小于 2,这 6 个数之和最小多少?
找规律,1 和 2 对面后不能选 3,45 对面后不能选 6,选 78,得 27
2017年第十五届“走美杯”小数数学竞赛初赛试卷(五年级B卷答案及解析)

2017年第十五届“走美杯”小数数学竞赛初赛试卷(五年级B卷)-学生用卷一、填空题共15题,共120 分1、计算:(写成小数的形式,精确到小数点后三位)。
2、两个标准骰子一起投掷次,点数之和第一次为,第二次为的可能性(概率)为/(先填分子,再填分母)。
3、大于的自然数,如果满足所有因数之和等于它自身的倍,则这样的数称为完美数或完全数。
比如,的所有因数为,,,,,是最小的完美数。
是否有无限多个完美数的问题至今仍然是困扰人类的难题之一。
研究完美数可以从计算自然数的所有因数之和开始,的所有因数之和为。
4、昊宇写好了五封信和五个不同地址的信封,要将每封信放入相应的信封中,一个信封只放入一封信。
只有一封信装对,其余全部被装错的情形有种。
5、“点游戏”是很多人熟悉的数学游戏,游戏过程如下:任意从张扑克牌(不包括大小王)中抽取张,用这张扑克牌上的数字(,,,)通过加减乘除四则运算得出,最先找到算法者获胜。
游戏规定张扑克牌都要用到,而且每张牌只能用次,比如,,,,则可以由算法得到,海亮在一次游戏中抽到了,,,,经过思考,他发现,我们将满足的牌组称为“海亮牌组”,请再写出组不同的“海亮牌组”。
6、在中国古代的历法中,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫作“十二地支,;十天干和十二地支进行循环组合:甲子、乙丑、丙寅。
一直到癸亥,共得到个组合,称为六十甲子。
如此周而复始用来纪年的方法,称为甲子纪年法。
在甲子纪年中,以“丑”结尾的年份除了“乙丑”外,还有。
7、现有个抽屉,每个抽屉中都放置个玻璃球(形状大小相同),分别为蓝色、红色与黄色。
如果分别从这个抽屉中各取出一个玻璃球放在一个布袋中,则布袋中的个玻璃球共有种不同情况。
8、古希腊的数学家们将自然数按照以下方式与多边形联系起来,定义了多边形数:比如,根据图示,三边形数:,,,,四边形数:,,,,五边形数:,,,,六边形数:,,,,那么,第个三边形数,四边形数,五边形数,六边形数分别为。
第15届走美杯决赛五年级自测卷(解析版) -

B P 【解析】将 BP 反向延长如下图所示构造弦图,
C
A E B F H G
D
C
P 以 BP 为底,△PAB 的高是 AF,于是有:S△PAB=PB×AF÷2=90,即 AF=15 厘米, 同理有 CG=8 厘米.因此 S□ABCD=152+82=289 平方厘米.
10、有一堆石头,第一次取走一个,第二次取走两个,每次比前一次多一个,如果最后一次 不够则全取。结果发现每次取完后剩余的石头数目都不是质数。当一开始的石头数目在 1000-1100 之间时只有一个值符合,这个值是 。 【考点】质数合数、构造 【答案】1081 【解析】本题考查的是构造的思想,题目中说开始的石头数目在 1000-1100 之间只有一个值 符合,意思就是说只要找到一个符合题意的数其它的数肯定就不符合,也不需要证明。我们 知道连续 n(n≥3)个自然数的和一定是合数(奇数项,中间项是平均数。偶数项,刚好配 对) 。构造 1+2+3+4+……+45+46=1081,检验 1081-1 即为 2+3+4+……+45+46 其结果必为合数,1081-1-2 即为 3+4+5+……+45+46 其结果必为合数,……,1081 -1-2-……-43 即为 44+45+46 其结果必为合数,再减 44 最后的结果为 45+46=91 也 是合数(注:剩最后两数时必须检验,因为 n<3 时不一定是合数) ,所以符合条件的值为 1081。 填空题Ⅲ(每题 12 分,共 60 分) 11、将四个不同的数字排在一起,可以组成 24 个不同的四位数(4×3×2×1=24) 。将这 24 个四位数按从小到大排列顺序排列,第二个是 5 的倍数;按从大到小排列,第二个是不 能被 4 整除的偶数; 按从小到大排列的第五个与第二十个的差在 3000~4000 之间。 请求出这 24 个四位数中最大的一个数是 。 【考点】数的整除 【答案】7543 【解析】设这个四个不同的数字从小到大依次为 A、B、C、D;因为这个四个互不相同的数 字可以组成 4× 3× 2× 1=24 个不同的四位数;所以这个四个数字均不为 0。因为这 24 个四位 数按从小到大排列顺序排列,第二个 ABDC 是 5 的倍数;所以 5|C,C=5; 因为这 24 个四位数按从大到小排列顺序排列,第二个 DCAB 是不能被 4 整除的偶数;所 以 AB 是不能被 4 整除的偶数,因为 A<B<C=5;所以 AB =14 或 34,即 B=4,A=1 或 3; 因为这 24 个四位数按从小到大排列顺序排列,第五个与第二十个的差 DACB ADBC 在 3000~4000 之间;比较百位数字可知 A<D,需从千位借位相减;所以 D-A-1=3,D-A =4;当 A=1 时, D=5,而 C=5,不符合题意;所以 A=3,D=7,这 24 个四位数中 最大的一个 DCBA =7543。
117度—数学科校外比赛奖项
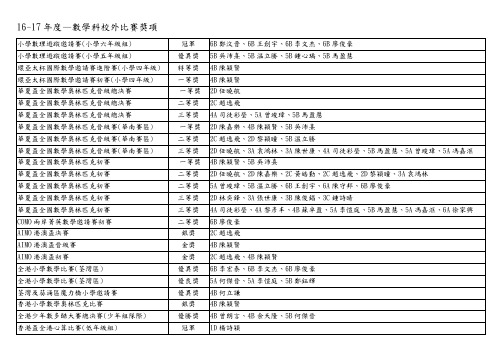
小學數理遊蹤邀請賽(小學六年級組) 小學數理遊蹤邀請賽(小學五年級組) 環亞太杯國際數學邀請賽進階賽(小學四年級) 環亞太杯國際數學邀請賽初賽(小學四年級) 華夏盃全國數學奧林匹克晉級總決賽 華夏盃全國數學奧林匹克晉級總決賽 華夏盃全國數學奧林匹克晉級總決賽 華夏盃全國數學奧林匹克晉級賽(華南賽區) 華夏盃全國數學奧林匹克晉級賽(華南賽區) 華夏盃全國數學奧林匹克晉級賽(華南賽區) 華夏盃全國數學奧林匹克初賽 華夏盃全國數學奧林匹克初賽 華夏盃全國數學奧林匹克初賽 華夏盃全國數學奧林匹克初賽 華夏盃全國數學奧林匹克初賽 COMO 兩岸菁英數學邀請賽初賽 AIMO 港澳盃決賽 AIMO 港澳盃晉級賽 AIMO 港澳盃初賽 全港小學數學比賽(荃灣區) 全港小學數學比賽(荃灣區) 荃灣及葵涌區魔力橋小學邀請賽 香港小學數學奧林匹克比賽 全港少年數多酷大賽總決賽(少年組隊際) 香港盃全港心算比賽(低年級組) 冠軍 優異獎 特等獎 一等獎 一等獎 二等獎 三等獎 一等獎 二等獎 三等獎 一等獎 二等獎 二等獎 三等獎 三等獎 二等獎 銀獎 金獎 金獎 優異獎 優良獎 優異獎 銀獎 優勝獎 冠軍 6B 鄭汶晋、6B 王創宇、6B 李文杰、6B 廖俊豪 5B 吳沛熹、5B 温立勝、5B 鍾心瑀、5B 馬盈慧 4B 陳穎賢 4B 陳穎賢 2D 任曉航 2C 趙逸飛 4A 司徒彩瑩、5A 曾竣瑋、5B 馬盈慧 2D 陳嘉樂、4B 陳穎賢、5B 吳沛熹 2C 趙逸飛、2D 黎穎瞳、5B 溫立勝 2D 任曉航、3A 袁鴻林、3A 陳世康、4A 司徒彩瑩、5B 馬盈慧、5A 曾竣瑋、5A 馮嘉洭 4B 陳穎賢、5B 吳沛熹 2D 任曉航、2D 陳嘉樂、2C 黃皓勤、2C 趙逸飛、2D 黎穎瞳、3A 袁鴻林 5A 曾竣瑋、5B 溫立勝、6B 王創宇、6A 陳守邦、6B 廖俊豪
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017年度美国“数学大联盟杯赛”(中国赛区)初赛(五年级)1.Which of the has the greatest value?A) 2017 B) 2017C) 20 × 17 D) 20 + 172.Which of the leaves a remainder of 2 when divided by 4?A) 2014 B) 2015 C) 2016 D) 20173.Which of the is a product of two consecutive primes?A) 30 B) 72 C) 77 D) 1874.A Bizz-Number is a integer that either contains the 3 or is a multiple of 3. What is the of the 10th Bizz-Number?A) 24 B) 27 C) 30 D) 315.The of an isosceles triangle with side-lengths 1 and 1008 isA) 1010 B) 1012 C) 2017 D) 20186.How integers less than 2017 are divisible by 16 but not by 4?A) 0 B) 126 C) 378 D) 5047.Jon has a number of pens. If he distributed them evenly among 4 students, he have 3 left. If he distributed them evenly among 5 students, he have4 left. The minimum number of pens that Jon have isA) 14 B) 17 C) 19 D) 248.Which of the numbers is not divisible by 8?A) 123168 B) 234236 C) 345424 D) 4566249.Which of the is both a square and a cube?A) 36 × 58B) 36 × 59C) 36 × 512D) 39 × 51210.The of two prime numbers cannot beA) odd B) even C) prime D) composite11.At the end of day, the amount of water in a cup is twice what it was at the beginning of the day. If the cup is at the end of 2017th day, then it was1/4 at the end of the ? day.A) 504th B) 505th C) 2015th D) 2016th12.The grades on an exam are 5, 4, 3, 2, or 1. In a class of 200 students,1/10 of got 5’s, 1/5 of got 4’s, 25% of got 3’s, and 15%of got 2’s. How many students got 1’s?A) 40 B) 60 C) 80 D) 10013.22000 × 52017 = 102000 × ?A) 517B) 51000C) 52000D) 5201714.1% of 1/10 of 10000 is ? percent than 10A) 0 B) 9 C) 90 D) 90015.What is the of the of Circle C to the of Square S if the ofa diameter of C and a of S are equal?A) π:1 B) π:2 C) π:3 D) π:416.Which of the is not a prime?A) 2003 B) 2011 C) 2017 D) 201917.If the sum of prime numbers is 30, what is the possible value of any of the primes?A) 19 B) 23 C) 27 D) 2918.For $3 I spend on books, I spend $4 on and $5 on toys. If I spent $20 on food, how much, in dollars, did I spend in total?A) 60 B) 90 C) 120 D) 15019.How positive odd factors does 25 × 35 × 55 have?A) 25 B) 36 C) 125 D) 21620.The of scalene triangles with perimeter 15 and side-lengths isA) 3 B) 5 C) 6 D) 721.Which of the when rounding to the nearest thousands, hundreds, and tens, 3000, 3500, and 3460, respectively?A) 3210 B) 3333 C) 3456 D) 351722.Which of the below has exactly 5 positive divisors?A) 16 B) 49 C) 64 D) 10023.Each after the 1st in the sequence 1, 5, 9, … is 4 than the previous term. The greatest in sequence that is < 1000 and that leavesa of 1 when divided by 6 isA) 991 B) 995 C) 997 D) 99924.For integer from 100 to 999 I the of the integer’s digits. How many of the products I are prime?A) 4 B) 8 C) 12 D) 1625.If a machine paints at a of 1 m2/sec, its is alsoA) 600 cm2/min B) 6000 cm2/minC) 60000 cm2/min D) 600000 cm2/min26.The of Square A is 1. The of Square B is times ofSquare A. The of Square C is times of Square B. The of Square C is ? times of Square A.A) 3 B) 6 C) 36 D) 8127.If the 17 minutes ago was 19:43, what will be the 17 minutes from now?A) 20:00 B) 20:17 C) 20:34 D) 20:1528.Pick any greater than 100 and subtract the sum of its from the integer. The largest that must the result isA) 1 B) 3 C) 9 D) 2729.The number of needed in a room so there are always at least five in the room born in the same month isA) 48 B) 49 C) 60 D) 6130.If M, A, T, and H are digits such that MATH + HTAM = 12221, is the value of M + A + T + H?A) 8 B) 20 C) 22 D) 2431.If 10 forks, 20 knives, and 30 $360, and 30 forks, 20 knives, and10 $240, what is the of 5 forks, 5 knives, and 5 spoons?A) 15 B) 75 C) 150 D) 22532.Write, in reduced form, the value ofA) 0.5 B) 1 C) 1.5 D) 233.Al, Barb, Cal, Di, Ed, Fred, and participated in a chess tournament. Each player play each of his six opponents exactly once. So far, Al has 1 match. Barb has 2 matches. Cal has 3 matches. Di has 4 matches. Ed has 5 matches, and has 6 matches. How manymatches has at this point?A) 1 B) 3 C) 5 D) 734.What is the number of different integers I can choose from the 100 positive integers so that no of these integers could be the of the sides of the same triangle?A) 8 B) 9 C) 10 D) 1135.What is the value of change that you can have in US (pennies, nickels, dimes, and quarters) without being able to someone exact change for a one-dollar bill?A) $0.90 B) $0.99 C) $1.19 D) $1.2936.小罗星期一工作了2个小时。
