CONVECTIONCURRENTSamp;THEMANTLEVancouver…地幔对流电流amp
巨正蒙特卡罗方法原理

巨正蒙特卡罗方法原理第一部分:引言蒙特卡罗方法,顾名思义,源自著名的赌场之城——蒙特卡罗。
但这个方法远不仅仅用于赌博,它在科学、金融、工程和许多其他领域都有广泛的应用。
巨正蒙特卡罗方法则是一种基于统计学原理的蒙特卡罗方法,它在众多领域中都有着深刻的应用。
在本文中,我们将深入探讨巨正蒙特卡罗方法的原理,了解它如何工作以及为什么它如此强大。
第二部分:蒙特卡罗方法的基础蒙特卡罗方法是一种基于随机采样的数值模拟技术,用于解决复杂的数学和物理问题。
它的基本原理是通过生成大量的随机样本来估计问题的答案。
这些样本是根据已知的概率分布或随机过程生成的,然后根据这些样本的统计特性来得出问题的解。
巨正蒙特卡罗方法是蒙特卡罗方法的一种变种,它特别适用于高维空间中的数值积分和概率问题。
它的核心思想是利用大量的随机样本来逼近问题的解,通过这种方式来减小误差,尤其在高维情况下更加有效。
第三部分:随机采样和积分在巨正蒙特卡罗方法中,首要的步骤是进行随机采样。
这意味着从问题的输入空间中生成随机的采样点。
这些采样点通常根据某种已知的概率分布生成,如均匀分布或正态分布。
一旦有了足够的随机采样点,就可以利用这些点进行数值积分。
数值积分的目的是估计函数的期望值或概率。
对于一个一维函数,积分可以表示为:I=∫fba (x)dx≈1N∑fNi=1(x i)其中,N是采样点的数量,f(x)是要积分的函数,x i是从概率分布中生成的随机采样点。
通过大量的采样和求和,我们可以得到函数的期望值的估计。
第四部分:高维空间中的挑战在高维空间中,传统的数值积分方法往往变得低效或不可行。
这是因为随着维度的增加,采样点的数量呈指数增长,导致计算成本急剧上升。
这就是巨正蒙特卡罗方法的优势所在,它可以更好地应对高维空间中的挑战。
第五部分:巨正蒙特卡罗方法的原理巨正蒙特卡罗方法的核心思想是通过分解高维积分问题为一系列一维积分问题来降低计算复杂度。
这个方法的名称中的“巨正”源自正交分解(Orthogonal Decomposition ),它是该方法的关键步骤。
混杂边界轴向运动Timoshenko梁固有频率数值解

混杂边界轴向运动Timoshenko梁固有频率数值解胡超荣;丁虎;陈立群【摘要】The differential quadrature method was developed to solve natural frequencies of an axially moving asymmetric hybrid supported Timoshenko beams with randomly varying spring coefficients at both sides. The weighted coefficient matrices were modified for dealing with the hybrid boundary. The axially moving speed, the stiffness of the beam and the spring coefficients were numerically investigated for clarifying their influences on the first two natural frequencies, and the results were compared with the semi-analytical and semi-numerical solutions. It was shown that both of them are basically consistent.%运用微分求积方法求解两端带有扭转弹簧且弹簧系数均可任意变化的非对称下的轴向运动Timoshenko 梁的固有频率.以权系数修改法处理轴向运动Timoshenko梁的混杂边界.研究系统的前两阶固有频率随轴向速度、刚度系数以及弹簧弹性系数变化的情况,并将数值计算结果与半解析半数值的研究结果进行比较,结果表明,数值计算结果与半解析半数值结果基本吻合.【期刊名称】《振动与冲击》【年(卷),期】2011(030)007【总页数】5页(P245-249)【关键词】轴向运动梁;Timoshenko模型;固有频率;微分求积法【作者】胡超荣;丁虎;陈立群【作者单位】上海大学上海市应用数学和力学研究所,上海200444;上海大学力学系,上海200072;上海大学上海市应用数学和力学研究所,上海200444,上海大学力学系,上海200072【正文语种】中文【中图分类】O32军事、航空航天以及机械电子工程等研究、制造及生产领域的多种工程元件都可简化为轴向运动连续体模型,比如空中缆车索道、传输带、升降机缆绳等。
第五讲VNM(冯诺伊曼效用函数与风险升水培训资料.ppt

E(Y ) E(g( X )) g(x) f (x)dx
.,
12
2、预期(期望)效用函数
• V-N-M期望效用函数
n
E(u(x)) p1u(x1) L p1u(x1) piu(xi ) i1 b
E(u(x)) a u(x) f (x)dx
.,
13
如果有一个单赌,g=(p,A,B)=pA+(1-p)B,那么,
• 不确定选择公理主要有: • (1)次序完全公理 • 对于两个不同的结果A和B,消费者的偏好序或者是 A B
• 或者是 B A 或者是 A : B 。并且,如 A B 并且B C 那么, • 必有A C
• 次序完全公理是完备性与传递性公理的汇合。 • (2)连续性公理:这个假定意味着代表偏好关系的效用函数的存
令L 1
( P1 ,
A, B)
P1 A (1
P1 ) B,
令L 2
(
P2
,
L ,L 3
4
),L3
( P3 , A, B),
L 4
( P4 , A, B),是一个复赌,如果
P1 P2 P3 (1 P2 ) P4 , 则L2 :
L。 1
这是可以推导出来,因为
L 3
( P3 , A, B)
P3 A (1 P3 ) B...(4.4)
对应的效用函数记为:
u(g)=pu(A)+(1-p)u(B)...(4.6)
如果有两个单赌g 1
(
p1,
A1,
A2 )与g2
(
p2 ,
A3 ,
A4 )
则我们说消费者在g 与g 之间更偏好g ,当且仅当
第五讲 VNM(冯.诺伊曼-摩
用朗之万方程估算黎曼流形随机波动率的方法

用朗之万方程估算黎曼流形随机波动率的方法2015年7月20日摘要在本文中,我们采用贝叶斯方程估计重尾分布的随机波动性模型,并使用朗之万方程调整黎曼流形图的随机波动率。
我们使用这两种方法解析波动率的表达式,并利用两个金融时间的序列数集作为模拟数据来验证这两种方法的可靠性。
1.介绍泰勒在1986年提出随机波动率模型,这个模型的推广,使其成功的应用在了随时间波动的金融序列数集上。
在文献中有几种关于这个模型的估算方法,例如哈维1994年提出的“准度—最大值”估算方法,安德森和索伦森在1996年提出的广义矩量算法,马尔可夫和蒙特卡罗1994年提出的估算方法,拉普拉在2010年提出的集成嵌套估值方法。
以及布鲁和鲁伊斯正在研究的账户模型估算方法。
但值得注意的是,特密度方法被认为是一种最有效的估值方法,分别由杰克和蒂姆在1994年和1998年提出。
最近,格罗曼妮和库德森提出了一个基于郎之万方程和蒙特卡洛抽样的方法,这种方法利用黎曼几何和统计数据之间的关系来克服现有的蒙特卡罗算法的一些不足,他们提供的证据表明这种算法可以大程度的改变估值的空间,从而解决了之前的这个问题。
值得注意的是,这些作者讨论了正常的SV模型的波动。
因为这个模型会导致之后较高的相关性,所以对估值十分有用。
近期,努格鲁和森本司(2014)就提出了一个基于蒙特卡罗方程的算法实现了随机波动模型的估值。
在本文中,我们用郎之万方程来修改SV模型的估值,并给出了表达式,评估了性能并说明有两个真实的数据集。
因为随机波动模型的计算时间是至关重要的,我们实现了利用参数和玛拉方程估值黎曼流形的计划。
特别的,本文中所有的计算都是开源的软件环境(R 核心开发团队,2006)本文的文章安排如下,第二节和第三节讨论估值的方法,利用蒙特卡罗方法做的估值实验在第四节,第五节分享了经验以及数据,并作总结。
2.方法我们利用以下随机波动模型:y t = βexp(h t/2)εt, (1)h t = φh t−1 + ηt, (2)在{εT }是一个序列的独立同分布(IID)随机变量具有零均值和方差分布单元,{ηt}是随机变量独立同分布的序列,ηT∼N(0,2,σ)ηT和T是独立ε之外的所有T。
交通流

Network impacts of a road capacity reduction:Empirical analysisand model predictionsDavid Watling a ,⇑,David Milne a ,Stephen Clark baInstitute for Transport Studies,University of Leeds,Woodhouse Lane,Leeds LS29JT,UK b Leeds City Council,Leonardo Building,2Rossington Street,Leeds LS28HD,UKa r t i c l e i n f o Article history:Received 24May 2010Received in revised form 15July 2011Accepted 7September 2011Keywords:Traffic assignment Network models Equilibrium Route choice Day-to-day variabilitya b s t r a c tIn spite of their widespread use in policy design and evaluation,relatively little evidencehas been reported on how well traffic equilibrium models predict real network impacts.Here we present what we believe to be the first paper that together analyses the explicitimpacts on observed route choice of an actual network intervention and compares thiswith the before-and-after predictions of a network equilibrium model.The analysis isbased on the findings of an empirical study of the travel time and route choice impactsof a road capacity reduction.Time-stamped,partial licence plates were recorded across aseries of locations,over a period of days both with and without the capacity reduction,and the data were ‘matched’between locations using special-purpose statistical methods.Hypothesis tests were used to identify statistically significant changes in travel times androute choice,between the periods of days with and without the capacity reduction.A trafficnetwork equilibrium model was then independently applied to the same scenarios,and itspredictions compared with the empirical findings.From a comparison of route choice pat-terns,a particularly influential spatial effect was revealed of the parameter specifying therelative values of distance and travel time assumed in the generalised cost equations.When this parameter was ‘fitted’to the data without the capacity reduction,the networkmodel broadly predicted the route choice impacts of the capacity reduction,but with othervalues it was seen to perform poorly.The paper concludes by discussing the wider practicaland research implications of the study’s findings.Ó2011Elsevier Ltd.All rights reserved.1.IntroductionIt is well known that altering the localised characteristics of a road network,such as a planned change in road capacity,will tend to have both direct and indirect effects.The direct effects are imparted on the road itself,in terms of how it can deal with a given demand flow entering the link,with an impact on travel times to traverse the link at a given demand flow level.The indirect effects arise due to drivers changing their travel decisions,such as choice of route,in response to the altered travel times.There are many practical circumstances in which it is desirable to forecast these direct and indirect impacts in the context of a systematic change in road capacity.For example,in the case of proposed road widening or junction improvements,there is typically a need to justify econom-ically the required investment in terms of the benefits that will likely accrue.There are also several examples in which it is relevant to examine the impacts of road capacity reduction .For example,if one proposes to reallocate road space between alternative modes,such as increased bus and cycle lane provision or a pedestrianisation scheme,then typically a range of alternative designs exist which may differ in their ability to accommodate efficiently the new traffic and routing patterns.0965-8564/$-see front matter Ó2011Elsevier Ltd.All rights reserved.doi:10.1016/j.tra.2011.09.010⇑Corresponding author.Tel.:+441133436612;fax:+441133435334.E-mail address:d.p.watling@ (D.Watling).168 D.Watling et al./Transportation Research Part A46(2012)167–189Through mathematical modelling,the alternative designs may be tested in a simulated environment and the most efficient selected for implementation.Even after a particular design is selected,mathematical models may be used to adjust signal timings to optimise the use of the transport system.Road capacity may also be affected periodically by maintenance to essential services(e.g.water,electricity)or to the road itself,and often this can lead to restricted access over a period of days and weeks.In such cases,planning authorities may use modelling to devise suitable diversionary advice for drivers,and to plan any temporary changes to traffic signals or priorities.Berdica(2002)and Taylor et al.(2006)suggest more of a pro-ac-tive approach,proposing that models should be used to test networks for potential vulnerability,before any reduction mate-rialises,identifying links which if reduced in capacity over an extended period1would have a substantial impact on system performance.There are therefore practical requirements for a suitable network model of travel time and route choice impacts of capac-ity changes.The dominant method that has emerged for this purpose over the last decades is clearly the network equilibrium approach,as proposed by Beckmann et al.(1956)and developed in several directions since.The basis of using this approach is the proposition of what are believed to be‘rational’models of behaviour and other system components(e.g.link perfor-mance functions),with site-specific data used to tailor such models to particular case studies.Cross-sectional forecasts of network performance at specific road capacity states may then be made,such that at the time of any‘snapshot’forecast, drivers’route choices are in some kind of individually-optimum state.In this state,drivers cannot improve their route selec-tion by a unilateral change of route,at the snapshot travel time levels.The accepted practice is to‘validate’such models on a case-by-case basis,by ensuring that the model—when supplied with a particular set of parameters,input network data and input origin–destination demand data—reproduces current mea-sured mean link trafficflows and mean journey times,on a sample of links,to some degree of accuracy(see for example,the practical guidelines in TMIP(1997)and Highways Agency(2002)).This kind of aggregate level,cross-sectional validation to existing conditions persists across a range of network modelling paradigms,ranging from static and dynamic equilibrium (Florian and Nguyen,1976;Leonard and Tough,1979;Stephenson and Teply,1984;Matzoros et al.,1987;Janson et al., 1986;Janson,1991)to micro-simulation approaches(Laird et al.,1999;Ben-Akiva et al.,2000;Keenan,2005).While such an approach is plausible,it leaves many questions unanswered,and we would particularly highlight two: 1.The process of calibration and validation of a network equilibrium model may typically occur in a cycle.That is to say,having initially calibrated a model using the base data sources,if the subsequent validation reveals substantial discrep-ancies in some part of the network,it is then natural to adjust the model parameters(including perhaps even the OD matrix elements)until the model outputs better reflect the validation data.2In this process,then,we allow the adjustment of potentially a large number of network parameters and input data in order to replicate the validation data,yet these data themselves are highly aggregate,existing only at the link level.To be clear here,we are talking about a level of coarseness even greater than that in aggregate choice models,since we cannot even infer from link-level data the aggregate shares on alternative routes or OD movements.The question that arises is then:how many different combinations of parameters and input data values might lead to a similar link-level validation,and even if we knew the answer to this question,how might we choose between these alternative combinations?In practice,this issue is typically neglected,meaning that the‘valida-tion’is a rather weak test of the model.2.Since the data are cross-sectional in time(i.e.the aim is to reproduce current base conditions in equilibrium),then in spiteof the large efforts required in data collection,no empirical evidence is routinely collected regarding the model’s main purpose,namely its ability to predict changes in behaviour and network performance under changes to the network/ demand.This issue is exacerbated by the aggregation concerns in point1:the‘ambiguity’in choosing appropriate param-eter values to satisfy the aggregate,link-level,base validation strengthens the need to independently verify that,with the selected parameter values,the model responds reliably to changes.Although such problems–offitting equilibrium models to cross-sectional data–have long been recognised by practitioners and academics(see,e.g.,Goodwin,1998), the approach described above remains the state-of-practice.Having identified these two problems,how might we go about addressing them?One approach to thefirst problem would be to return to the underlying formulation of the network model,and instead require a model definition that permits analysis by statistical inference techniques(see for example,Nakayama et al.,2009).In this way,we may potentially exploit more information in the variability of the link-level data,with well-defined notions(such as maximum likelihood)allowing a systematic basis for selection between alternative parameter value combinations.However,this approach is still using rather limited data and it is natural not just to question the model but also the data that we use to calibrate and validate it.Yet this is not altogether straightforward to resolve.As Mahmassani and Jou(2000) remarked:‘A major difficulty...is obtaining observations of actual trip-maker behaviour,at the desired level of richness, simultaneously with measurements of prevailing conditions’.For this reason,several authors have turned to simulated gaming environments and/or stated preference techniques to elicit information on drivers’route choice behaviour(e.g. 1Clearly,more sporadic and less predictable reductions in capacity may also occur,such as in the case of breakdowns and accidents,and environmental factors such as severe weather,floods or landslides(see for example,Iida,1999),but the responses to such cases are outside the scope of the present paper. 2Some authors have suggested more systematic,bi-level type optimization processes for thisfitting process(e.g.Xu et al.,2004),but this has no material effect on the essential points above.D.Watling et al./Transportation Research Part A46(2012)167–189169 Mahmassani and Herman,1990;Iida et al.,1992;Khattak et al.,1993;Vaughn et al.,1995;Wardman et al.,1997;Jou,2001; Chen et al.,2001).This provides potentially rich information for calibrating complex behavioural models,but has the obvious limitation that it is based on imagined rather than real route choice situations.Aside from its common focus on hypothetical decision situations,this latter body of work also signifies a subtle change of emphasis in the treatment of the overall network calibration problem.Rather than viewing the network equilibrium calibra-tion process as a whole,the focus is on particular components of the model;in the cases above,the focus is on that compo-nent concerned with how drivers make route decisions.If we are prepared to make such a component-wise analysis,then certainly there exists abundant empirical evidence in the literature,with a history across a number of decades of research into issues such as the factors affecting drivers’route choice(e.g.Wachs,1967;Huchingson et al.,1977;Abu-Eisheh and Mannering,1987;Duffell and Kalombaris,1988;Antonisse et al.,1989;Bekhor et al.,2002;Liu et al.,2004),the nature of travel time variability(e.g.Smeed and Jeffcoate,1971;Montgomery and May,1987;May et al.,1989;McLeod et al., 1993),and the factors affecting trafficflow variability(Bonsall et al.,1984;Huff and Hanson,1986;Ribeiro,1994;Rakha and Van Aerde,1995;Fox et al.,1998).While these works provide useful evidence for the network equilibrium calibration problem,they do not provide a frame-work in which we can judge the overall‘fit’of a particular network model in the light of uncertainty,ambient variation and systematic changes in network attributes,be they related to the OD demand,the route choice process,travel times or the network data.Moreover,such data does nothing to address the second point made above,namely the question of how to validate the model forecasts under systematic changes to its inputs.The studies of Mannering et al.(1994)and Emmerink et al.(1996)are distinctive in this context in that they address some of the empirical concerns expressed in the context of travel information impacts,but their work stops at the stage of the empirical analysis,without a link being made to net-work prediction models.The focus of the present paper therefore is both to present thefindings of an empirical study and to link this empirical evidence to network forecasting models.More recently,Zhu et al.(2010)analysed several sources of data for evidence of the traffic and behavioural impacts of the I-35W bridge collapse in Minneapolis.Most pertinent to the present paper is their location-specific analysis of linkflows at 24locations;by computing the root mean square difference inflows between successive weeks,and comparing the trend for 2006with that for2007(the latter with the bridge collapse),they observed an apparent transient impact of the bridge col-lapse.They also showed there was no statistically-significant evidence of a difference in the pattern offlows in the period September–November2007(a period starting6weeks after the bridge collapse),when compared with the corresponding period in2006.They suggested that this was indicative of the length of a‘re-equilibration process’in a conceptual sense, though did not explicitly compare their empiricalfindings with those of a network equilibrium model.The structure of the remainder of the paper is as follows.In Section2we describe the process of selecting the real-life problem to analyse,together with the details and rationale behind the survey design.Following this,Section3describes the statistical techniques used to extract information on travel times and routing patterns from the survey data.Statistical inference is then considered in Section4,with the aim of detecting statistically significant explanatory factors.In Section5 comparisons are made between the observed network data and those predicted by a network equilibrium model.Finally,in Section6the conclusions of the study are highlighted,and recommendations made for both practice and future research.2.Experimental designThe ultimate objective of the study was to compare actual data with the output of a traffic network equilibrium model, specifically in terms of how well the equilibrium model was able to correctly forecast the impact of a systematic change ap-plied to the network.While a wealth of surveillance data on linkflows and travel times is routinely collected by many local and national agencies,we did not believe that such data would be sufficiently informative for our purposes.The reason is that while such data can often be disaggregated down to small time step resolutions,the data remains aggregate in terms of what it informs about driver response,since it does not provide the opportunity to explicitly trace vehicles(even in aggre-gate form)across more than one location.This has the effect that observed differences in linkflows might be attributed to many potential causes:it is especially difficult to separate out,say,ambient daily variation in the trip demand matrix from systematic changes in route choice,since both may give rise to similar impacts on observed linkflow patterns across re-corded sites.While methods do exist for reconstructing OD and network route patterns from observed link data(e.g.Yang et al.,1994),these are typically based on the premise of a valid network equilibrium model:in this case then,the data would not be able to give independent information on the validity of the network equilibrium approach.For these reasons it was decided to design and implement a purpose-built survey.However,it would not be efficient to extensively monitor a network in order to wait for something to happen,and therefore we required advance notification of some planned intervention.For this reason we chose to study the impact of urban maintenance work affecting the roads,which UK local government authorities organise on an annual basis as part of their‘Local Transport Plan’.The city council of York,a historic city in the north of England,agreed to inform us of their plans and to assist in the subsequent data collection exercise.Based on the interventions planned by York CC,the list of candidate studies was narrowed by considering factors such as its propensity to induce significant re-routing and its impact on the peak periods.Effectively the motivation here was to identify interventions that were likely to have a large impact on delays,since route choice impacts would then likely be more significant and more easily distinguished from ambient variability.This was notably at odds with the objectives of York CC,170 D.Watling et al./Transportation Research Part A46(2012)167–189in that they wished to minimise disruption,and so where possible York CC planned interventions to take place at times of day and of the year where impacts were minimised;therefore our own requirement greatly reduced the candidate set of studies to monitor.A further consideration in study selection was its timing in the year for scheduling before/after surveys so to avoid confounding effects of known significant‘seasonal’demand changes,e.g.the impact of the change between school semesters and holidays.A further consideration was York’s role as a major tourist attraction,which is also known to have a seasonal trend.However,the impact on car traffic is relatively small due to the strong promotion of public trans-port and restrictions on car travel and parking in the historic centre.We felt that we further mitigated such impacts by sub-sequently choosing to survey in the morning peak,at a time before most tourist attractions are open.Aside from the question of which intervention to survey was the issue of what data to collect.Within the resources of the project,we considered several options.We rejected stated preference survey methods as,although they provide a link to personal/socio-economic drivers,we wanted to compare actual behaviour with a network model;if the stated preference data conflicted with the network model,it would not be clear which we should question most.For revealed preference data, options considered included(i)self-completion diaries(Mahmassani and Jou,2000),(ii)automatic tracking through GPS(Jan et al.,2000;Quiroga et al.,2000;Taylor et al.,2000),and(iii)licence plate surveys(Schaefer,1988).Regarding self-comple-tion surveys,from our own interview experiments with self-completion questionnaires it was evident that travellersfind it relatively difficult to recall and describe complex choice options such as a route through an urban network,giving the po-tential for significant errors to be introduced.The automatic tracking option was believed to be the most attractive in this respect,in its potential to accurately map a given individual’s journey,but the negative side would be the potential sample size,as we would need to purchase/hire and distribute the devices;even with a large budget,it is not straightforward to identify in advance the target users,nor to guarantee their cooperation.Licence plate surveys,it was believed,offered the potential for compromise between sample size and data resolution: while we could not track routes to the same resolution as GPS,by judicious location of surveyors we had the opportunity to track vehicles across more than one location,thus providing route-like information.With time-stamped licence plates, the matched data would also provide journey time information.The negative side of this approach is the well-known poten-tial for significant recording errors if large sample rates are required.Our aim was to avoid this by recording only partial licence plates,and employing statistical methods to remove the impact of‘spurious matches’,i.e.where two different vehi-cles with the same partial licence plate occur at different locations.Moreover,extensive simulation experiments(Watling,1994)had previously shown that these latter statistical methods were effective in recovering the underlying movements and travel times,even if only a relatively small part of the licence plate were recorded,in spite of giving a large potential for spurious matching.We believed that such an approach reduced the opportunity for recorder error to such a level to suggest that a100%sample rate of vehicles passing may be feasible.This was tested in a pilot study conducted by the project team,with dictaphones used to record a100%sample of time-stamped, partial licence plates.Independent,duplicate observers were employed at the same location to compare error rates;the same study was also conducted with full licence plates.The study indicated that100%surveys with dictaphones would be feasible in moderate trafficflow,but only if partial licence plate data were used in order to control observation errors; for higherflow rates or to obtain full number plate data,video surveys should be considered.Other important practical les-sons learned from the pilot included the need for clarity in terms of vehicle types to survey(e.g.whether to include motor-cycles and taxis),and of the phonetic alphabet used by surveyors to avoid transcription ambiguities.Based on the twin considerations above of planned interventions and survey approach,several candidate studies were identified.For a candidate study,detailed design issues involved identifying:likely affected movements and alternative routes(using local knowledge of York CC,together with an existing network model of the city),in order to determine the number and location of survey sites;feasible viewpoints,based on site visits;the timing of surveys,e.g.visibility issues in the dark,winter evening peak period;the peak duration from automatic trafficflow data;and specific survey days,in view of public/school holidays.Our budget led us to survey the majority of licence plate sites manually(partial plates by audio-tape or,in lowflows,pen and paper),with video surveys limited to a small number of high-flow sites.From this combination of techniques,100%sampling rate was feasible at each site.Surveys took place in the morning peak due both to visibility considerations and to minimise conflicts with tourist/special event traffic.From automatic traffic count data it was decided to survey the period7:45–9:15as the main morning peak period.This design process led to the identification of two studies:2.1.Lendal Bridge study(Fig.1)Lendal Bridge,a critical part of York’s inner ring road,was scheduled to be closed for maintenance from September2000 for a duration of several weeks.To avoid school holidays,the‘before’surveys were scheduled for June and early September.It was decided to focus on investigating a significant southwest-to-northeast movement of traffic,the river providing a natural barrier which suggested surveying the six river crossing points(C,J,H,K,L,M in Fig.1).In total,13locations were identified for survey,in an attempt to capture traffic on both sides of the river as well as a crossing.2.2.Fishergate study(Fig.2)The partial closure(capacity reduction)of the street known as Fishergate,again part of York’s inner ring road,was scheduled for July2001to allow repairs to a collapsed sewer.Survey locations were chosen in order to intercept clockwiseFig.1.Intervention and survey locations for Lendal Bridge study.around the inner ring road,this being the direction of the partial closure.A particular aim wasFulford Road(site E in Fig.2),the main radial affected,with F and K monitoring local diversion I,J to capture wider-area diversion.studies,the plan was to survey the selected locations in the morning peak over a period of approximately covering the three periods before,during and after the intervention,with the days selected so holidays or special events.Fig.2.Intervention and survey locations for Fishergate study.In the Lendal Bridge study,while the‘before’surveys proceeded as planned,the bridge’s actualfirst day of closure on Sep-tember11th2000also marked the beginning of the UK fuel protests(BBC,2000a;Lyons and Chaterjee,2002).Trafficflows were considerably affected by the scarcity of fuel,with congestion extremely low in thefirst week of closure,to the extent that any changes could not be attributed to the bridge closure;neither had our design anticipated how to survey the impacts of the fuel shortages.We thus re-arranged our surveys to monitor more closely the planned re-opening of the bridge.Unfor-tunately these surveys were hampered by a second unanticipated event,namely the wettest autumn in the UK for270years and the highest level offlooding in York since records began(BBC,2000b).Theflooding closed much of the centre of York to road traffic,including our study area,as the roads were impassable,and therefore we abandoned the planned‘after’surveys. As a result of these events,the useable data we had(not affected by the fuel protests orflooding)consisted offive‘before’days and one‘during’day.In the Fishergate study,fortunately no extreme events occurred,allowing six‘before’and seven‘during’days to be sur-veyed,together with one additional day in the‘during’period when the works were temporarily removed.However,the works over-ran into the long summer school holidays,when it is well-known that there is a substantial seasonal effect of much lowerflows and congestion levels.We did not believe it possible to meaningfully isolate the impact of the link fully re-opening while controlling for such an effect,and so our plans for‘after re-opening’surveys were abandoned.3.Estimation of vehicle movements and travel timesThe data resulting from the surveys described in Section2is in the form of(for each day and each study)a set of time-stamped,partial licence plates,observed at a number of locations across the network.Since the data include only partial plates,they cannot simply be matched across observation points to yield reliable estimates of vehicle movements,since there is ambiguity in whether the same partial plate observed at different locations was truly caused by the same vehicle. Indeed,since the observed system is‘open’—in the sense that not all points of entry,exit,generation and attraction are mon-itored—the question is not just which of several potential matches to accept,but also whether there is any match at all.That is to say,an apparent match between data at two observation points could be caused by two separate vehicles that passed no other observation point.Thefirst stage of analysis therefore applied a series of specially-designed statistical techniques to reconstruct the vehicle movements and point-to-point travel time distributions from the observed data,allowing for all such ambiguities in the data.Although the detailed derivations of each method are not given here,since they may be found in the references provided,it is necessary to understand some of the characteristics of each method in order to interpret the results subsequently provided.Furthermore,since some of the basic techniques required modification relative to the published descriptions,then in order to explain these adaptations it is necessary to understand some of the theoretical basis.3.1.Graphical method for estimating point-to-point travel time distributionsThe preliminary technique applied to each data set was the graphical method described in Watling and Maher(1988).This method is derived for analysing partial registration plate data for unidirectional movement between a pair of observation stations(referred to as an‘origin’and a‘destination’).Thus in the data study here,it must be independently applied to given pairs of observation stations,without regard for the interdependencies between observation station pairs.On the other hand, it makes no assumption that the system is‘closed’;there may be vehicles that pass the origin that do not pass the destina-tion,and vice versa.While limited in considering only two-point surveys,the attraction of the graphical technique is that it is a non-parametric method,with no assumptions made about the arrival time distributions at the observation points(they may be non-uniform in particular),and no assumptions made about the journey time probability density.It is therefore very suitable as afirst means of investigative analysis for such data.The method begins by forming all pairs of possible matches in the data,of which some will be genuine matches(the pair of observations were due to a single vehicle)and the remainder spurious matches.Thus, for example,if there are three origin observations and two destination observations of a particular partial registration num-ber,then six possible matches may be formed,of which clearly no more than two can be genuine(and possibly only one or zero are genuine).A scatter plot may then be drawn for each possible match of the observation time at the origin versus that at the destination.The characteristic pattern of such a plot is as that shown in Fig.4a,with a dense‘line’of points(which will primarily be the genuine matches)superimposed upon a scatter of points over the whole region(which will primarily be the spurious matches).If we were to assume uniform arrival rates at the observation stations,then the spurious matches would be uniformly distributed over this plot;however,we shall avoid making such a restrictive assumption.The method begins by making a coarse estimate of the total number of genuine matches across the whole of this plot.As part of this analysis we then assume knowledge of,for any randomly selected vehicle,the probabilities:h k¼Prðvehicle is of the k th type of partial registration plateÞðk¼1;2;...;mÞwhereX m k¼1h k¼1172 D.Watling et al./Transportation Research Part A46(2012)167–189。
Experimental and quasi-experimental designs for research

AND EXPERIMENTAL QUASI-EXPERIMENTAL FORGENERALIZED DESIGNS CAUSALINFERENCE
William R. Shadish
Trru UNIvERSITYop MEvPrrts
.jr-*", '"+.'-, iLli"
**
Thomas D. Cook
NonrrrwpsrERN UNrvPnslrY
fr
Donald T. Campbell
COMPANY MIFFLIN HOUGHTON
Boston New York
and Experiments Causal Generalized lnference
Ex.per'i'ment (ik-spEr'e-mant):[Middle English from Old French from Latin experime; seeper- in Indo-European Roots.] n. Abbr. exp., expt, 1. a. A test under controlled conditions that is made to demonstratea known truth, examine the validity of a hypothesis, or determine the efficacyof something previously untried' b. The processof conducting such a test; experimentation. 2' An innovative "Democracy is only an experiment in gouernment" act or procedure: (.V{illiam Ralph lnge). Cause (k6z): [Middle English from Old French from Latin causa' teason, purpose.] n. 1. a. The producer of an effect, result, or consequence. b. The one, such as a person, an event' or a condition, that is responsible for an action or a result. v. 1. To be the causeof or reason for; result in. 2. To bring about or compel by authority or force.
(完整版)威科夫理论名词汇总,推荐文档

OKR关键位置反转K线HH HL更高的高点更高的低点overbought对超买线,或者反向趋势线的穿越Smart Money——庄家,主力Herd——群体,散户,羊群(与Smart Money相对的一个概念)Up bar——上涨竹线,上涨棒线(收盘价高于前一条竹线的收盘价)Down bar——下跌竹线,下跌棒线(收盘价低于前一条竹线的收盘价)Ultra High volume——超高成交量,成交量异常放大Ultra Low volume——越低成交量,成交量异常萎缩sign of strength——强势征兆(缩写为SOS)sign of weakness——弱势征兆(缩写为SOW)Shakeout——洗盘Stopping V olume——停止成交量(在某个点使市场停止运动)No Supply——无供给No Demand——无需求Test(s)——测试(庄家操纵市场靠近某个价位,看市场中是否还有供给或需求)Upthrust——上冲,射击线Supply Coming In——供给进入UTAD(Upthrust after distribution)派发之后的上冲Absorption 浮筹消化吸收Accumulation吸筹Across 穿过Re-accumulation 再吸筹,发生在一个相当大的上升趋势中AR(Automatic Rally)自然反弹AR(Automatic Reaction)自然下跌AR (Automatic rally or reaction)自动反弹or自动回调BC(Buying Climax)抢购高潮/超买高潮,买入密集区焦急的大众在顶部附近买入,专业人士则在卖出ICE(Critical resistance)冰面,比喻,指连接回调的最低点的曲线,也就是支撑线Break 打破/突变Breakdown 跳水Breakout 突破Break ICE 打破冰面BOI(Backing up to ice)BTI(Breaking the ice)破冰BUEC(Backup to edge of creek)cause vs effect原因与结果COB(change of behavior)背景转换Creek 回测小溪(Critical Support)关键位/颈线/边界CM(Composite Man/Composite Operator)大资金、作手、主力机构、一群掌握大资金的人或联盟机构Demand 初步支撑/最后支撑点demand vs supply 供应与需求Distribution 派发effort vs result 努力与效果Ending action 结束动作Final Shakeout 终极震仓FTI(First time over ice)第一时间结束冰点Ice 冰Lines 横线JAC(Jumping across the creek)(or JOC)跳过小河JOC(Jump over the creek)突破边界,这是一个SOS信号,价格强烈上涨突破了前期的关键阻力位置或者突破了交易区间的上边界Lower Creek 下边界LPS(Last point of Support)最后支撑点,回调确认LPSY (Last point of Supply)最后的供应点MU(Mark up)上涨MD(Mark down)下跌Ordinary Shakeout 普通震仓Over sold 超卖Over bought 超买Price and volume 价格与数量PS (Preliminary support)初次支撑/初次需求PSY(Preliminary supply)初始供应Rally 反弹Resistance 阻力Resistance Line 阻力线SC(Selling Climax)恐慌抛售/超卖高潮,卖出密集区,大众恐慌性的卖盘Setup 计划Shake out 震仓/晃出Short covering 平掉空仓SOS(Sign of strength)强势信号,强势上涨行为,显示需求控制市场的信号或者上升趋势中需求良好的表现SOT(Shortening of thrust)停止行为/突破递减,冲击减弱,幅度递减,价速递减SOW (Sign of weakness)弱势信号,显示供应控制市场,急速下跌/大幅下挫Speed 速度Spring 下冲反弹,弹簧效应,价格突破先前的支撑区域,测试底部供应强度,功效等同震仓,震仓相当于CM制造的人为的第二次恐慌抛售,目的在于震出之前没有消除的供应ST (Secondary test)二次测试,跟随在自然回调之后和超卖高潮之后Support 支撑Supply 供应Supply and Demand 供需关系/供应与需求Test 测试/回踩/返回Test of breakout:突破区域回踩Test of breakdown:跳水区域回踩Test of spring:弹簧区域回踩TR(Trading Range)交易区间/盘整区间,震荡区TSO(Terminal shake out(Spring))TUT(Terminal thrust)UT(Up thrust)上冲失败/上冲回落,价格快速上涨但随后立刻回到阻力之下的现象UTAD(Upthrust after distribution)派发之后的上冲,长钉现象Upthrust Entry 做多入场Upper Creek 上边界Vertical demand 垂直上升VDB(vertical demand bar)垂直需求柱VSB(vertical supply bar)垂直供应柱,放量阴线。
托福阅读tpo27R-2原文+译文+题目+答案+背景知识

托福阅读tpo27R-2原文+译文+题目+答案+背景知识原文 (1)译文 (4)题目 (6)答案 (16)背景知识 (17)原文The Formation of Volcanic Islands①Earth’s surface is not made up of a single sheet of rock that forms a crust but rather a number of “tectonic plates” that fit closely, like the pieces of a giant jigsaw puzzle. Some plates carry islands or continents, others form the seafloor. All are slowly moving because the plates float on a denser semi-liquid mantle, the layer between the crust and Earth’s core. The plates have edges that are spreading ridges (where two plates are moving apart and new seafloor is being created), subduction zones (where two plates collide and one plunges beneath the other), or transform faults (where two plates neither converge nor diverge but merely move past one another). It is at the boundaries between plates that most of Earth’s volcanism and earthquake activity occur.②Generally speaking, the interiors of plates are geologically uneventful. However, there are exceptions. A glance at a map of the Pacific Ocean reveals that there are many islands far out at sea that are actually volcanoes----many no longer active, some overgrown with coral----that originated from activity at points in the interior of the Pacific Plate that forms the Pacific seafloor.③How can volcanic activity occur so far from a plate boundary? The Hawaiian islands provide a very instructive answer. Like many other island groups, they form a chain. The Hawaiian Islands Chain extends northwest from the island of Hawaii. In the 1840s American geologist James Daly observed that the different Hawaii islands seem to share a similar geologic evolution but are progressively more eroded, and therefore probable older, toward the northwest. Then in 1963, in the early days of the development of the theory of plate tectonics. Canadian geophysicist Tuzo Wilson realized that this age progression could result if the islands were formed on a surface plate moving over a fixed volcanic source in the interior. Wilson suggested that the long chain of volcanoes stretching northwest from Hawaii is simply the surface expression of a long-lived volcanic source located beneath the tectonic plate in the mantle. Today’s most northwest island would have been the first to form. They as the plate moved slowly northwest, new volcanic islands would have forms as the plate moved over the volcanic source. The most recentisland, Hawaii, would be at the end of the chain and is now over the volcanic source.④Although this idea was not immediately accepted, the dating of lavas in the Hawaii (and other) chains showed that their ages increase away from the presently active volcano, just as Daly had suggested. Wilson’s analysis of these data is now a central part of plate tectonics. Most volcanoes that occur in the interiors of plates are believed to be produced by mantle plumes, columns of molten rock that rise from deep within the mantle. A volcano remains an active “hot spot” as long as it is over the plume. The plumes apparently originate at great depths, perhaps as deep as the boundary between the core and the mantle, and many have been active for a very long time. The oldest volcanoes in the Hawaii hot-spot trail have ages close to 80 million years. Other islands, including Tahiti and Easter Islands in the pacific, Reunion and Mauritius in the India Ocean, and indeed most of the large islands in the world’s oceans, owe their existence to mantle plumes.⑤The oceanic volcanic islands and their hot-spot trails are thus especially useful for geologist because they record the past locations of the plate over a fixed source. They therefore permit the reconstruction of the process of seafloor spreading, and consequently of the geography of continents and of ocean basins in the past. For example, given thecurrent position of the Pacific Plate, Hawaii is above the Pacific Ocean hot spot. So the position of The Pacific Plate 50 million years ago can be determined by moving it such that a 50-million-year-old volcano in the hot-spot trail sits at the location of Hawaii today. However because the ocean basins really are short-lived features on geologic times scale, reconstruction the world’s geography by backtracking along the hot-spot trail works only for the last 5 percent or so of geologic time.译文火山岛的形成①地球的外壳并不是由单块岩石形成的,而是许多的"构造板块"严密的组合在一起的,就像是一个巨大的拼图。
LTC3787_datasheet

ORDER INFORMATION
LEAD FREE FINISH
TAPE AND REEL
PART MARKING*
PACKAGE DESCRIPTION
TEMPERATURE RANGE
LTC3787EUFD#PBF
LTC3787EUFD#TRPBF 3787
28-Lead (4mm × 5mm) Plastic QFN
100pF 0.1μF
4mΩ
47μF
3.3μH
VOUT 24V AT 10A
220μF
3787 TA01a
EFFICIENCY (%)
POWER LOSS (mW)
Efficiency and Power Loss vs Output Current
100
10000
90
80
1000
70
60
100
50
3787fc
1
LTC3787
ABSOLUTE MAXIMUM RATINGS (Notes 1, 3)
VBIAS ........................................................ –0.3V to 40V BOOST1 and BOOST2 ................................ –0.3V to 76V SW1 and SW2............................................ –0.3V to 70V RUN ............................................................. –0.3V to 8V
β-Hermite 随机矩阵最大特征值精确渐近性的一般形式

β-Hermite 随机矩阵最大特征值精确渐近性的一般形式刘银萍【摘要】For a fairly wide range of boundary function and quasi weight function,the author obtained a general form of precise asymptotics in complete moment convergence for the largest eigenvalue by using the weak convergence theorem and the small deviation conclusion for largest eigenvalue ofβ-Hermite random matrix and tail probability inequality of the generalβ Tracy-Wisdom distribution.%对于相当广泛的边界函数和拟权函数,利用β-Hermite 随机矩阵最大特征值的弱收敛定理、小偏差结论及广义β Tracy-Wisdom 分布的尾概率不等式,得到了其最大特征值的矩完全收敛性的精确渐近性的一般形式。
【期刊名称】《吉林大学学报(理学版)》【年(卷),期】2016(054)006【总页数】5页(P1328-1332)【关键词】最大特征值;广义βTracy-Wisdom 分布;矩完全收敛性;精确渐近性;一般形式【作者】刘银萍【作者单位】吉林师范大学数学学院,吉林四平 136000【正文语种】中文【中图分类】O211.4β-Hermite随机矩阵[1]在格子气理论与统计力学中应用广泛,最早的研究成果主要集中在β=1,2,4的特殊情形下,其最大特征值收敛到经典的Tracy-Wisdom分布[2-4]; 文献[5-6]得到了对于任意β>0情形下的结果,此时最大特征值λmax(Hβ)的极限分布为广义β Tracy-Wisdom分布,其中Hβ表示β-Hermite总体下的随机矩阵.目前,关于随机变量序列精确渐近性质的研究已有很多结果,对于拟权函数φ(x)和边界函数g(x),精确渐近性主要研究级数φ的收敛速度以及当ε↓a(a≥0)时的极限值,其中Sn为随机变量的部分和[7-14]. 而对于随机矩阵最大特征值精确渐近性的研究报道较少,基于此,本文对β-Hermite随机矩阵最大特征值的矩完全收敛的精确渐近性进行研究.假设条件:(H1) g(x)为[n0,∞)上具有非负导数g′(x)的正值可导函数,且g(x)↑∞,x→∞;(H2) g′(x)在[n0,∞)上单调非降或单调非增,且当g′(x)单调非降时,满足在[n0,∞)上单调非降或单调非增,且当φ(x)单调非降时,满足(H4) φ在[n0,∞)上单调非降或单调非增,且当φ(x)单调非降时,满足其中在[n0,∞)上单调非降或单调非增,且当ρ(x)单调非降时,满足其中s>0,p>0.本文主要结果如下.定理1 若假设条件(H1),(H2),(H4)成立,则对于有其中TWβ为广义β Tracy-Wisdom分布.定理2 若假设条件(H1),(H3),(H5)成立,则对于p≥0,β≥1,有其中TWβ为广义β Tracy-Wisdom分布.注1 满足假设条件(H1)~(H5)的g(x)有很多,如g(x)=xα,(log x)β,(log log x)γ,其中α>0,β>0,γ>0为某些适当的参数.注2 广义β Tracy-Wisdom分布的任意阶矩存在.注3 在定理1中,分别令p=1,,g(n)=n及则可分别得到文献[10]中的定理1.1和定理1.2; 在定理1中,令其中t>0,则可得到文献[11]中的定理1.1; 在定理2中,令p=1,则可得到文献[11]中的定理1.2. 因此本文推广了目前已有的结果.本文C表示正常数,不同之处可表示不同的值.引理1[6] 对于任意的β>0,有令Fβ(·)为TWβ的分布函数,则对于充分大的a,有引理2[15] 对任意的n≥1,0<ε≤1,β≥1,有令a(ε)=[g-1(Mε-1/s)],其中: g-1(x)为g(x)的反函数; M≥1.命题1 在定理1的假设条件下,有证明: 利用引理1和引理2,类似文献[11]中定理1.1的证明,可知该命题成立.命题2 在定理1的假设条件下,对于p>0,有证明: 类似文献[11]中命题2.1的证明.命题3 在定理1的假设条件下,对于p>0,有证明: 显然其中:根据引理1,当n→∞时,Δn→0. 首先估计Δn1. 由于n≤A(ε)表明εgs(n)≤Ms,从而有其次估计Δn3. 由引理1,有最后估计Δn2. 由引理2,注意到p>0,有从而由式(5)~(7),可得又由式(8)、φ(x)的单调性以及Toeplitz引理[16]可知式(3)成立. 证毕.命题4 在定理1的条件下,对于p>0,有证明: 由1/s>p>0及引理2,有命题5 在定理1的条件下,对于p>0,有证明: 利用引理1,类似命题4的证明可证.2.1 定理1的证明当p=0时,由于则由命题1可知定理1成立. 当1/s>p>0时,注意到故要证明式(1),只需证明下列两式成立即可:由命题1可知式(9)成立. 由命题2~命题5及三角不等式可知式(10)成立,从而式(1)成立.2.2 定理2的证明定理2的证明与定理1的证明类似,故略.【相关文献】[1] Baker T H,Forrester P J. The Calogero-Sutherland Model and Generalized Classical Polynomials [J]. Comm Math Phys,1997,188(1): 175-216.[2] Tracy C A,Widom H. Level-Spacing Distributions and the Airy Kernel [J]. Phys LettB,1993,305(1/2): 115-118.[3] Tracy C A,Widom H. Level-Spacing Distributions and the Airy Kernel [J]. Comm Math Phys,1994,159(1): 151-174.[4] Tracy C A,Widom H. On Orthogonal and Symplectic Matrix Ensembles [J]. Comm Math Phys,1996,177(3): 727-754.[5] Dumitriu I,Edelman A. Matrix Models for Beta Ensembles [J]. J Math Phys,2002,43(11): 5830-5847.[6] Ramírez J A,Rider B,Virg B. Beta Ensembles,Stochastic Airy Spectrum,and a Diffusion [J]. J Amer Math Soc,2011,24(4): 919-944.[7] Gut A,Spătaru A. Precise Asymptotics in the Baum-Katz and Davis Law of Large Numbers [J]. J Math Anal Appl,2000,248(1): 233-246.[8] SU Zhonggen. Precise Asymptotics for Random Matrices and Random Growth Models [J]. Acta Math Sin (Engl Ser),2008,24(6): 971-982.[9] 孙晓祥,杨丽娟. 独立情形下一阶矩收敛的精确渐近性的注记 [J]. 吉林大学学报(理学版),2013,51(5): 871-875. (SUN Xiaoxiang,YANG Lijuan. A Note on the Precise Asymptotics for the First Moment Convergence of i.i.d. Random Variables [J]. Journal of Jilin University(Science Edition),2013,51(5): 871-875.)[10] XIE Junshan. The Moment Conve rgence Rates for Largest Eigenvalues of β Ensembles [J]. Acta Math Sin (Engl Ser),2013,29(3): 477-488.[11] XIE Junshan,ZHAO Jing. A Result on Precise Asymptotics for Largest Eigenvalues of β Ensembles [J/OL]. J Inequal Appl,2014-10-16. doi: 10.1186/1029-242X-2014-408.[12] JIANG Hui,YU Lei. Precise Asymptotics in Complete Moment Convergence of Parameter Estimator in the Gaussian Autoregressive Process [J]. Comm Statist Theory Methods,2015,44(7): 1483-1496.[13] 邹广玉,吕阳阳. NA序列部分和之和的大数定律及重对数律的精确渐近性 [J]. 吉林大学学报(理学版),2015,53(1): 54-58. (ZOU Guangyu,LÜ Yangyang. Precise Asymptotics in the Law of Large Numbers and Iterated Logarithm for the Sum of Partial Sums of NA Sequences [J]. Journal of Jilin University (Science Edition),2015,53(1): 54-58.)[14] Spătaru A. Co nvergence and Precise Asymptotics for Series Involving Self-normalized Sums [J]. J Theoret Probab,2016,29(1): 267-276.[15] Ledoux M,Rider B. Small Deviations for Beta Ensembles [J]. Electron JProbab,2010,15(41): 1319-1343.[16] Hall P,Heyde C C. Martingale Limit Theory and Its Application [M]. New York: Academic Press,1980.。
非线性最小二乘法Levenberg-Marquardt-method

Levenberg-Marquardt Method(麦夸尔特法)Levenberg-Marquardt is a popular alternative to the Gauss-Newton method of finding the minimum of afunction that is a sum of squares of nonlinear functions,Let the Jacobian of be denoted , then the Levenberg-Marquardt method searches in thedirection given by the solution to the equationswhere are nonnegative scalars and is the identity matrix. The method has the nice property that, forsome scalar related to , the vector is the solution of the constrained subproblem of minimizingsubject to (Gill et al. 1981, p. 136).The method is used by the command FindMinimum[f, x, x0] when given the Method -> Levenberg Marquardt option.SEE A LSO:Minimum, OptimizationREFERENCES:Bates, D. M. and Watts, D. G. N onlinear Regr ession and Its Applications. New York: Wiley, 1988.Gill, P. R.; Murray, W.; and Wright, M. H. "The Levenberg-Marquardt Method." §4.7.3 in Practical Optim ization. London: Academic Press, pp. 136-137, 1981.Levenberg, K. "A Method for the Solution of Certain Problems in Least Squares." Quart. Appl. Math.2, 164-168, 1944. Marquardt, D. "An Algor ithm for Least-Squares Estimation of Nonlinear Parameters." SIAM J. Appl. Math.11, 431-441, 1963.Levenberg–Marquardt algorithmFrom Wikipedia, the free encyclopediaJump to: navigation, searchIn mathematics and computing, the Levenberg–Marquardt algorithm (LMA)[1] provides a numerical solution to the problem of minimizing a function, generally nonlinear, over a space of parameters of the function. These minimization problems arise especially in least squares curve fitting and nonlinear programming.The LMA interpolates between the Gauss–Newton algorithm (GNA) and the method of gradient descent. The LMA is more robust than the GNA, which means that in many cases it finds a solution even if it starts very far off the final minimum. For well-behaved functions and reasonable starting parameters, the LMA tends to be a bit slower than the GNA. LMA can also be viewed as Gauss–Newton using a trust region approach.The LMA is a very popular curve-fitting algorithm used in many software applications for solving generic curve-fitting problems. However, the LMA finds only a local minimum, not a global minimum.Contents[hide]∙ 1 Caveat Emptor∙ 2 The problem∙ 3 The solutiono 3.1 Choice of damping parameter∙ 4 Example∙ 5 Notes∙ 6 See also∙7 References∙8 External linkso8.1 Descriptionso8.2 Implementations[edit] Caveat EmptorOne important limitation that is very often over-looked is that it only optimises for residual errors in the dependant variable (y). It thereby implicitly assumes that any errors in the independent variable are zero or at least ratio of the two is so small as to be negligible. This is not a defect, it is intentional, but it must be taken into account when deciding whether to use this technique to do a fit. While this may be suitable in context of a controlled experiment there are many situations where this assumption cannot be made. In such situations either non-least squares methods should be used or the least-squares fit should be done in proportion to the relative errors in the two variables, not simply the vertical "y" error. Failing to recognise this can lead to a fit which is significantly incorrect and fundamentally wrong. It will usually underestimate the slope. This may or may not be obvious to the eye.MicroSoft Excel's chart offers a trend fit that has this limitation that is undocumented. Users often fall into this trap assuming the fit is correctly calculated for all situations. OpenOffice spreadsheet copied this feature and presents the same problem.[edit] The problemThe primary application of the Levenberg–Marquardt algorithm is in the least squares curve fitting problem: given a set of m empirical datum pairs of independent and dependent variables, (x i, y i), optimize the parameters β of the model curve f(x,β) so that the sum of the squares of the deviationsbecomes minimal.[edit] The solutionLike other numeric minimization algorithms, the Levenberg–Marquardt algorithm is an iterative procedure. To start a minimization, the user has to provide an initial guess for the parameter vector, β. In many cases, an uninformed standard guess like βT=(1,1,...,1) will work fine;in other cases, the algorithm converges only if the initial guess is already somewhat close to the final solution.In each iteration step, the parameter vector, β, is replaced by a new estimate, β + δ. To determine δ, the functions are approximated by their linearizationswhereis the gradient(row-vector in this case) of f with respect to β.At its minimum, the sum of squares, S(β), the gradient of S with respect to δwill be zero. The above first-order approximation of gives.Or in vector notation,.Taking the derivative with respect to δand setting theresult to zero gives:where is the Jacobian matrix whose i th row equals J i,and where and are vectors with i th componentand y i, respectively. This is a set of linear equations which can be solved for δ.Levenberg's contribution is to replace this equation by a "damped version",where I is the identity matrix, giving as the increment, δ, to the estimated parameter vector, β.The (non-negative) damping factor, λ, isadjusted at each iteration. If reduction of S is rapid, a smaller value can be used, bringing the algorithm closer to the Gauss–Newton algorithm, whereas if an iteration gives insufficientreduction in the residual, λ can be increased, giving a step closer to the gradient descentdirection. Note that the gradient of S withrespect to β equals .Therefore, for large values of λ, the step will be taken approximately in the direction of the gradient. If either the length of the calculated step, δ, or the reduction of sum of squares from the latest parameter vector, β + δ, fall below predefined limits, iteration stops and the last parameter vector, β, is considered to be the solution.Levenberg's algorithm has the disadvantage that if the value of damping factor, λ, is large, inverting J T J + λI is not used at all. Marquardt provided the insight that we can scale eachcomponent of the gradient according to thecurvature so that there is larger movement along the directions where the gradient is smaller. This avoids slow convergence in the direction of small gradient. Therefore, Marquardt replaced theidentity matrix, I, with the diagonal matrixconsisting of the diagonal elements of J T J,resulting in the Levenberg–Marquardt algorithm:.A similar damping factor appears in Tikhonov regularization, which is used to solve linear ill-posed problems, as well as in ridge regression, an estimation technique in statistics.[edit] Choice of damping parameterVarious more-or-less heuristic arguments have been put forward for the best choice for the damping parameter λ. Theoretical arguments exist showing why some of these choices guaranteed local convergence of the algorithm; however these choices can make the global convergence of the algorithm suffer from the undesirable properties of steepest-descent, in particular very slow convergence close to the optimum.The absolute values of any choice depends on how well-scaled the initial problem is. Marquardt recommended starting with a value λ0 and a factor ν>1. Initially setting λ=λ0and computing the residual sum of squares S(β) after one step from the starting point with the damping factor of λ=λ0 and secondly withλ0/ν. If both of these are worse than the initial point then the damping is increased by successive multiplication by νuntil a better point is found with a new damping factor of λ0νk for some k.If use of the damping factor λ/ν results in a reduction in squared residual then this is taken as the new value of λ (and the new optimum location is taken as that obtained with this damping factor) and the process continues; if using λ/ν resulted in a worse residual, but using λresulted in a better residual then λ is left unchanged and the new optimum is taken as the value obtained with λas damping factor.[edit] ExamplePoor FitBetter FitBest FitIn this example we try to fit the function y = a cos(bX) + b sin(aX) using theLevenberg–Marquardt algorithm implemented in GNU Octave as the leasqr function. The 3 graphs Fig 1,2,3 show progressively better fitting for the parameters a=100, b=102 used in the initial curve. Only when the parameters in Fig 3 are chosen closest to the original, are thecurves fitting exactly. This equation is an example of very sensitive initial conditions for the Levenberg–Marquardt algorithm. One reason for this sensitivity is the existenceof multiple minima —the function cos(βx)has minima at parameter value and[edit] Notes1.^ The algorithm was first published byKenneth Levenberg, while working at theFrankford Army Arsenal. It was rediscoveredby Donald Marquardt who worked as astatistician at DuPont and independently byGirard, Wynn and Morrison.[edit] See also∙Trust region[edit] References∙Kenneth Levenberg(1944). "A Method for the Solution of Certain Non-Linear Problems in Least Squares". The Quarterly of Applied Mathematics2: 164–168.∙ A. Girard (1958). Rev. Opt37: 225, 397. ∙ C.G. Wynne (1959). "Lens Designing by Electronic Digital Computer: I". Proc.Phys. Soc. London73 (5): 777.doi:10.1088/0370-1328/73/5/310.∙Jorje J. Moré and Daniel C. Sorensen (1983)."Computing a Trust-Region Step". SIAM J.Sci. Stat. Comput. (4): 553–572.∙ D.D. Morrison (1960). Jet Propulsion Laboratory Seminar proceedings.∙Donald Marquardt (1963). "An Algorithm for Least-Squares Estimation of NonlinearParameters". SIAM Journal on AppliedMathematics11 (2): 431–441.doi:10.1137/0111030.∙Philip E. Gill and Walter Murray (1978)."Algorithms for the solution of thenonlinear least-squares problem". SIAMJournal on Numerical Analysis15 (5):977–992. doi:10.1137/0715063.∙Nocedal, Jorge; Wright, Stephen J. (2006).Numerical Optimization, 2nd Edition.Springer. ISBN0-387-30303-0.[edit] External links[edit] Descriptions∙Detailed description of the algorithm can be found in Numerical Recipes in C, Chapter15.5: Nonlinear models∙ C. T. Kelley, Iterative Methods for Optimization, SIAM Frontiers in AppliedMathematics, no 18, 1999, ISBN0-89871-433-8. Online copy∙History of the algorithm in SIAM news∙ A tutorial by Ananth Ranganathan∙Methods for Non-Linear Least Squares Problems by K. Madsen, H.B. Nielsen, O.Tingleff is a tutorial discussingnon-linear least-squares in general andthe Levenberg-Marquardt method inparticular∙T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). Vieweg+Teubner, ISBN 978-3-8348-1022-9.[edit] Implementations∙Levenberg-Marquardt is a built-in algorithm with Mathematica∙Levenberg-Marquardt is a built-in algorithm with Matlab∙The oldest implementation still in use is lmdif, from MINPACK, in Fortran, in thepublic domain. See also:o lmfit, a translation of lmdif into C/C++ with an easy-to-use wrapper for curvefitting, public domain.o The GNU Scientific Library library hasa C interface to MINPACK.o C/C++ Minpack includes theLevenberg–Marquardt algorithm.o Several high-level languages andmathematical packages have wrappers forthe MINPACK routines, among them:▪Python library scipy, modulescipy.optimize.leastsq,▪IDL, add-on MPFIT.▪R (programming language) has theminpack.lm package.∙levmar is an implementation in C/C++ with support for constraints, distributed under the GNU General Public License.o levmar includes a MEX file interface for MATLABo Perl (PDL), python and Haskellinterfaces to levmar are available: seePDL::Fit::Levmar, PyLevmar andHackageDB levmar.∙sparseLM is a C implementation aimed at minimizing functions with large,arbitrarily sparse Jacobians. Includes a MATLAB MEX interface.∙ALGLIB has implementations of improved LMA in C# / C++ / Delphi / Visual Basic.Improved algorithm takes less time toconverge and can use either Jacobian orexact Hessian.∙NMath has an implementation for the .NET Framework.∙gnuplot uses its own implementation .∙Java programming language implementations:1) Javanumerics, 2) LMA-package (a small,user friendly and well documentedimplementation with examples and support),3) Apache Commons Math∙OOoConv implements the L-M algorithm as an Calc spreadsheet.∙SAS, there are multiple ways to access SAS's implementation of the Levenberg-Marquardt algorithm: it can be accessed via NLPLMCall in PROC IML and it can also be accessed through the LSQ statement in PROC NLP, and the METHOD=MARQUARDT option in PROC NLIN.。
HYDRUS Model Use, Calibration, and Validation

Submitted for review in September 2011 as manuscript number SW 9401; approved for publication by the Soil & Water Division of ASABE in April 2012. The authors are Jiří Šimůnek, Professor and Hydrologist, Department of Environmental Sciences, University of California, Riverside, California; Martinus Th. van Genuchten, Professor, Department of Mechanical Engineering, Federal University of Rio de Janeiro, Brazil; and Miroslav Šejna, Director, PC-Progress s.r.o., Prague, Czech Republic. Corresponding author: Jiří Šimůnek, Department of Environmental Sciences, University of California-Riverside, Riverside, CA 92521; phone: 951-8277854; e-mail: Jiri.Simunek@.
HYDRUS: MODEL USE, CALIBRATION, AND VALIDATION
J. n, M. Šejna
ABSTRACT. The HYDRUS numerical models are widely used for simulating water flow and solute transport in variably saturated soils and groundwater. Applications involve a broad range of steady-state or transient water flow, solute transport, and/or heat transfer problems. They include both short-term, one-dimensional laboratory column flow or transport simulations, as well as more complex, long-duration, multi-dimensional field studies. The HYDRUS models can be used for both direct problems when the initial and boundary conditions for all involved processes and corresponding model parameters are known, as well as inverse problems when some of the parameters need to be calibrated or estimated from observed data. The approach to model calibration and validation may vary widely depending upon the complexity of the application. Model calibration and inverse parameter estimation can be carried out using a relatively simple, gradient-based, local optimization approach based on the Marquardt-Levenberg method, which is directly implemented into the HYDRUS codes, or more complex global optimization methods, including genetic algorithms, which need to be run separately from HYDRUS. In this article, we provide a brief overview of the HYDRUS codes, discuss which HYDRUS parameters can be estimated using internally built optimization routines and which type of experimental data can be used for this, and review various calibration approaches that have been used in the literature in combination with the HYDRUS codes. Keywords. Calibration, HYDRUS-1D, HYDRUS (2D/3D), Numerical model, Optimization methods, Parameter estimation, Solute transport, Unsaturated soils, Validation, Water flow.
用于治疗化疗抗性癌症起始细胞的方法[发明专利]
![用于治疗化疗抗性癌症起始细胞的方法[发明专利]](https://img.taocdn.com/s3/m/5b1a2ec6dd36a32d72758188.png)
专利名称:用于治疗化疗抗性癌症起始细胞的方法
专利类型:发明专利
发明人:R·卡斯,L·李,路秀玲,J·M·佩里,G·S·斯塔姆帕拉姆,A·罗伊,X·C·何
申请号:CN201680043900.1
申请日:20160728
公开号:CN109310767A
公开日:
20190205
专利内容由知识产权出版社提供
摘要:本公开提供了通过选择性抑制p‑S‑β‑链蛋白,p‑T‑β‑链蛋白,p‑T‑β‑链蛋白和/或
p‑S‑β‑链蛋白的产生和/或活性而治疗癌症的方法。
这样的方法还减少和/或限制癌症起始细胞。
申请人:康涅狄格大学,美国斯托瓦斯医学研究所,堪萨斯大学
地址:美国康涅狄格州
国籍:US
代理机构:北京市中伦律师事务所
更多信息请下载全文后查看。
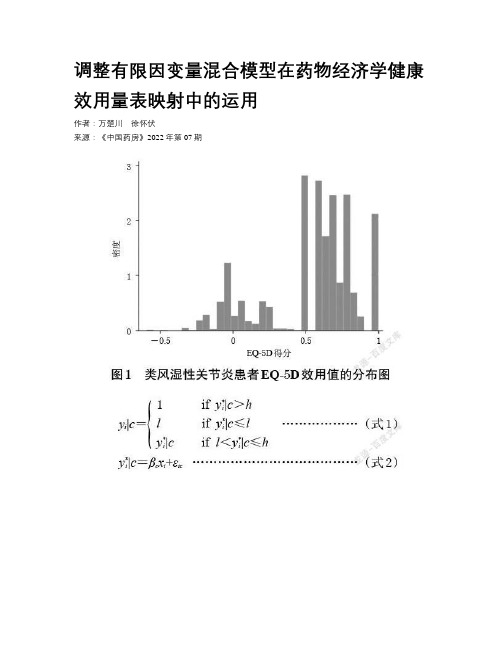
调整有限因变量混合模型在药物经济学健康效用量表映射中的运用
调整有限因变量混合模型在药物经济学健康效用量表映射中的运用作者:万楚川徐怀伏来源:《中国药房》2022年第07期中图分类号 R956 文献标志码 A 文章编号 1001-0408(2022)07-0867-06DOI 10.6039/j.issn.1001-0408.2022.07.17摘要目的介绍调整有限因变量混合模型(ALDVMM)及其在映射研究中的运用情况,为需要通过映射获取健康效用值的药物经济学评价提供参考。
方法采用文献研究的方法,分别从ALDVMM的开发背景、模型原理、模型确定与检验、模型优势以及目前该模型在实证研究中的運用现状等方面进行介绍。
结果与结论 ALDVMM是国外学者针对欧洲五维健康量表(EQ-5D)在健康效用值1处截断不连续且存在多峰现象而开发的混合模型。
相较于传统模型,ALDVMM可行且更具有优势,能更有效、灵活地捕捉EQ-5D的实际分布情况并处理好边界值问题,有助于更准确、有效地获取健康效用值并开展更高质量的药物经济学评价。
关键词调整有限因变量混合模型;健康效用值;映射;欧洲五维健康量表;药物经济学ABSTRACT OBJECTIVE To introduce adjusted limited dependent variable mixed model (ALDVMM) and study its application in mapping research, so as to provide reference for pharmacoeconomic evaluation that needs to obtain health utility value through mapping. METHODS Using the method of literature research, ALDVMM was introduced from the aspects of development background, model principle, model determination and test, model advantages and the current application of the model in empirical research. RESULTS & CONCLUSIONS ALDVMM is a mixed model developed by foreign scholars for the truncation and multimodality phenomenon of EuroQoL group’s 5D (EQ-5D) at the health utility value 1. Compared with the traditional model,ALDVMM is feasible and has more advantages, and can more effectively and flexibly capture the actual distribution of EQ-5D and deal with the boundary value problem, which is helpful to obtain the health utility value more accurately and efficiently and carry out high-quality pharmacoeconomic evaluation.KEYWORDS adjusted limited dependent variable mixed model; health utility value; mapping; EuroQoL group’s 5D; pharmacoeconomics随着人们对健康越来越重视,卫生需求急剧增长。
欧洲药典7.5版

INDEX
To aid users the index includes a reference to the supplement in which the latest version of a text can be found. For example : Amikacin sulfate...............................................7.5-4579 means the monograph Amikacin sulfate can be found on page 4579 of Supplement 7.5. Note that where no reference to a supplement is made, the text can be found in the principal volume.
English index ........................................................................ 4707
Latin index ................................................................................. 4739
EUROPEAN PHARMACOPபைடு நூலகம்EIA 7.5
Index
Numerics 1. General notices ................................................................... 7.5-4453 2.1.1. Droppers...................
肯特纳通道

肯特纳通道(KC)是一个移动平均通道,由叁条线组合而成(上通道、中通道及下通道)。
若股价於边界出现不沉常的波动,即表示买卖机会。
肯特纳通道是基于平均真实波幅原理而形成的指标,对价格波动反应灵敏,它可以取代布林线或百分比通道作为判市的新工具。
肯特纳通道是由两根围绕线性加权移动平均线波动的环带组成的,其中线性加权均线的参数通道是20。
价格突破带状的上轨和下轨时,通常会产生做多或做空的交易信号,指标的发明人是Chester Keltner,由Linda Raschke再度优化改进,她采用10单位的线性加权均线来计算平均真实波段(ATR)。
类同于所有的包络线或环带状系统,价格倾向于在环带内运动,当价格突破环带时,通常意味着会产生做多或做空的机会。
当价格报收在顶部环带之上时,通常意味着向上动能的突破,其后价格会继续走高。
当价格报收在底部环带之下时,则预期价格会走低。
在一个上升的市道里,中线或20单位线性加权均线,对价格能够产生支撑作用,相反,下降的市道里,中线会压制价格上行。
和所有的跟随趋势系统一样,肯特纳通道在上升和下降趋势里表现出色,在盘整市内则有所逊色,原因很简单,跟随趋势系统不会致力于寻底猜头。
肯特纳通道应当和其他指标混合应用,比如说相对强弱指标(RSI)和平滑异同移动平均线(MACD),这样可以对市场的强度进行确认。
与趋势线和其他指标配合的出场策略十分重要,从上图的案例中,我们会明白这一点,等待价格收在底部环带之下,意味着一个良好趋势中的许多利润会被侵蚀掉。
基于平均真实波幅的肯特纳通道运算公式如下:对于顶部环带来讲,在10单位周期基础上计算出平均真实波幅,乘以双倍,然后把这个数值与20单位周期的线性加均线数值相加,就会得出新的顶部环带数值。
对于底部环带来讲,在10单位周期基础上计算出平均真实波幅,乘以双倍,把这个数值从20单位周期线性加权均线数值扣除,就会得出新的底部环带数值。
1、当价格报收在顶部环带之上时,意味着价格呈强势,后市看涨。
对弗里德曼-萨维奇之谜的解释:兼论修正的vnm效用函数

作者: 张晖;孙杰
作者机构: [1]天津科技大学金融研究所,天津,300222
出版物刊名: 浙江金融
年卷期: 2012年 第2期
主题词: 弗里德曼-萨维奇之谜;vnm效用函数;理性交易者
摘要:本文研究的主要问题是弗里德曼-萨维奇之谜,即为什么交易者在参与保险的同时,也参与赌博.本文在考察行为金融学对此问题解释的基础上,提出了修正的vnm效用函数;通过数学推导,得出了理性交易者既参加保险又购买彩票的结论,对科学地解释主流市场交易者的行为模式具有重要的理论启示.。
