武汉大学文科高等数学-2003真题
2023成人高考《高数二》真题及答案_高等数学二

2023成人高考《高数二》真题及答案_高等数学二2023成人高考《高数二》真题及答案(回忆版)成人高考高数备考技巧有哪些?成人高考高数备考技巧有以下几点:重视新版《考试大纲》,全面进行复习;掌握学习方法,注意知识的系统性;多做题,加强练习,注意试题要少而精;学会在练习中总结类型与解题规律,培养解题能力;归纳总结,把知识条理化、网络化。
成人高考有几门考试成人高考高起专考试科目一共三门,文科考语文、数学(文)、英语;理科考语文、数学(理)、英语。
成人高考高起专考试科目一共四门,文科考语文、数学(文)、英语、史地;理科考语文、数学(理)、英语、理化。
成人高考专升本考试科目一共三科,政治、外语、一门专业基础课,专业基础课根据具体专业的不同而不同:文史类考大学语文;艺术类考艺术概论;理工类考高等数学(一);经管类考高等数学(二);法学类考民法;教育学类考教育理论;农学类考生态学基础;医学类考医学综合。
成人高考该如何备考1.熟读教材、掌握大纲:成人高考教材是成人高考复习的根本,考试所考的知识点在教材中都有体现。
成人高考考试大纲是对成人高考教材各章节知识点的梳理,考试命题也不会超出成人高考考试大纲。
2.适量做题:做题是对学习的一种检测,只有在做题中了解自己是否掌握了教材中的知识点,尤其是历年成人高考的考试内容,考生可以反复琢磨,看历年的考点都是什么。
所以适量的做一些成人高考练习题,对大家掌握知识点是很有作用的。
成考专升本数学如何提高分数1、熟悉考试题型,合理安排做题时间其实,不仅仅是成考数学考试,在参加任何一门考试之前,你都要弄清楚或明确几个问题:考试一共有多长时间,总分多少,选择、填空和其他主观题各占多少。
2.详细分析出题方式选择题:打破常规的按照顺序答题的方式,有选择性的先答会做的题目,不会做的题目就放弃了,不要浪费太多时间。
对于完全不会的题目,也必须要答,想一个答案填上去,切记不要留空。
大题:就算不会也要把解字写上也会得到一分,把知道的公式写上也会得分。
武汉理工大学-历年真题清单

武汉理工大学研招办经济学院西方经济学(含微观、宏观经济学)2007——2009经济学(含微观、宏观经济学)1997——2000,2002——2006(2002——2004,2006有答案)宏观经济学2004——2006(2004有答案)货币银行学2004——2007(2004有答案)国际贸易概论1998——2000,2002——2009(2002——2004有答案)国际金融学2002,2004——2009(2002,2004有答案)国际市场营销2002财政学2007产业经济学2002,2006——2009(2002有答案)电子商务概论2008——2009运输经济学2002——2009区域经济学2007人力资源管理2007管理学概论2004——2007(2004有答案)管理学原理1997——2000,2002——2009(2002——2004有答案)微机原理及应用1997——2000,2002——2007概率论与数理统计2001——2009复试科目:国际贸易学2003加试科目:国际金融学2003;国际市场营销学2003复试科目:产业经济学2003复试科目:数量经济学专业复试2003文法学院伦理学基础综合2007——2009伦理学原理2007——2009伦理学2002——2005民法学2007民商法学2008——2009民商法学综合2007——2009经济法学2002,2004——2009经济法综合2007——2009法学综合2002——2006知识产权2007知识产权法2002——2005法理学与知识产权法2004——2005社会心理学2002心理学2002思想政治教育学原理与方法2002——2009中国化的马克思主义2007——2009马克思主义基本原理及其发展2007——2009马克思主义基本原理2007马克思主义哲学原理2002——2009新闻传播专业综合考试(含广告学、编辑出版学)2004——2005出版发行综合2006——2009广告学综合2006——2009传播学原理2004——2009专业综合(教育学、运动训练学)2007体育教育综合(运动生理学、运动训练学)2008——2009运动生理学2007复试科目:综合复试2003;复试(科技法方向)2003加试科目:专业加试2003;加试(科技法方向)2003高等教育研究所教育学2002——2006,2008——2009教育管理学2002——2006,2008——2009复试科目:综合复试2003加试科目:教育学2003;教育心理学2003外国语学院二外日语2002——2009二外法语2002——2009二外德语2002——2009二外俄语2003——2009基础英语2001——2009(注:其中2002,2003,2005年的试卷名称为“综合英语”)英语语言学2001——2003,2006——2009(2001有答案)语言学及英美文学2004——2005英美文学2007——2009英语写作2002复试科目:外国语言学及应用语言学专业复试2003艺术与设计学院设计艺术学专业综合(含设计艺术史论、工业设计及其理论、环境艺术设计及其理论、视觉传播艺术设计、动画艺术设计及其理论、数字艺术设计及其理论)2008——2009美术学专业综合2008——2009艺术学专业综合2008——2009设计艺术学专业史论2003——2006,2008——2009 美术学专业史论2008——2009艺术学专业史论2008——2009音乐艺术研究专业综合(报考艺术管理方向)2009 视觉传播艺术设计基础2007速写与焦墨山水画2005速写与花卉白描2005——2006速写与人物写生画2005——2006速写与色彩人物写生2005,2007速写与泥塑人物写生2007速写与素描人物写生2005速写与水彩或水粉画创作2005速写与装饰画创作2005——2006中外美术史2002,2005,2007中国美术史专题2006中国画创作基础2007艺术美术专业基础2007美术史论2005——2007美术理论2004艺术学概论2007艺术设计史基础2004——2005,2007艺术史论基础2007艺术设计史论基础2003,2006艺术设计理论2002艺术设计史2002专业史论2007艺术设计学“专业设计基础”2002专业设计2002信息设计基础2004——2005动画创作基础2004——2006艺术管理专业基础2004——2005,2007艺术教育专业基础2007民艺专业基础2004 ——2005民间美术2007民间艺术设计及其原理2006设计基础理论与设计基础表达2002环境艺术设计基础2006——2007环境艺术设计与公共艺术创作专业基础2002动画与数字化设计艺术基础2007动画设计与数码设计基础2002系统设计及传播艺术基础2002系统设计及传播艺术理论2002工业设计理论2002工业设计基础2004——2007数码设计理论2002数码艺术设计基础2003中外建筑史2002动画创作理论2002动画创作基础2003环境艺术设计2002环境艺术设计基础2004——2005公共艺术创作与设计2002公共艺术设计基础2006卡通画创作2002专业设计(计算机艺术设计)2002专业设计(系统设计及传播艺术设计)2002环境艺术设计专业方向(环境艺术设计基础)2003设计艺术学专业工业设计方向设计基础2003平面设计基础2003——2005平面艺术设计基础2006现代美术与公共艺术设计基础2003设计管理2006设计基础(展示设计及理论方向)2006信息设计基础2006影视艺术设计基础2006音乐艺术研究2007复试科目:艺术与设计学院复试2003加试科目:艺术与设计学院加试2003理工学院材料力学1997——2000,2002——2009弹性力学2002——2004,2007理论力学2002——2009工程力学2004微机原理及应用1997——2000,2002——2007微机原理(即:微型计算机原理)1997——2000,2002——2004 岩石力学1997——2000,2002岩体力学2003——2007(注:2003年有两种)结构力学2002——2009量子力学2004——2009物理光学2002,2004——2009电磁场与电磁波2004电磁场理论2005——2009概率论与数理统计2001——2009数值分析2002,2004——2007高等代数2001——2009数学分析2002——2009常微分方程2002——2007线性代数2002普通物理2002——2009运筹学2002——2008(注:2002年试卷有两种)物理化学2002——2009有机化学2002——2007无机化学2002——2009化学原理2008——2009基础无机化学2007物理化学原理2007高等数学2007,2009高等数学(工)2002——2006,2008高等数学(二)2004高等数学(文)2003——2005复试科目:应用化学专业复试2003复试科目:应用数学专业复试2003复试科目:固体力学专业复试2003资源与环境工程学院物理化学2002——2009材料力学1997——2000,2002——2009岩石力学1997——2000,2002岩体力学2003——2007(注:2003年有两种)岩石力学与工程2004——2009矿山岩石力学2002无机化学2002——2009浮选2002固体废物处理工程2002水污染控制工程2002大气污染控制工程2002化工基础2002——2007化工原理2002——2009(注:2002年称“环境化工原理”)采矿学2002安全工程学2007——2009爆破工程2002——2009(注:2003年称“凿岩爆破”)流体力学2002——2004胶体化学2003——2009结晶矿物学2003——2006环境学概论2004——2009环境化学2004——2007环境流体力学2002,2005——2007环境工程微生物学2005——2006环境生物学2005——2007矿物加工工程专业复试科目:综合复试2003采矿工程专业复试科目:专业复试2003环境工程专业复试科目:环境工程专业复试2003;加试科目:环境工程专业加试2003材料科学与工程学院材料科学基础2002——2009普通物理2002——2009材料力学1997——2000,2002——2009医学综合一(含生物化学、无机化学)2008——2009医学综合二(含生物化学、高分子化学)2008医学综合三(含生物化学、组织学)2008——2009医学综合2002,2004细胞生物学2002——2007组织学2002——2007物理光学2002,2004——2009计算机在材料科学中的应用2007计算机在材料中的应用2004——2005工程材料2002——2007生物化学2002——2007物理化学2002——2009有机化学2002——2007无机化学2002——2009陶瓷工艺原理2002玻璃工艺原理2002复合材料工艺2002铸造合金及其熔炼2002塑性成型原理2002材料成型原理2003——2009焊接冶金2002金属热处理2002金属材料学2007固体物理2002——2009聚合物加工原理与工艺2002胶凝材料学2002无机非金属材料工学2002,2004——2009金属学及热处理2002硅酸盐物理化学2002高分子化学及物理2002高分子化学2003——2009金属学原理2002——2007材料物理与化学专业复试科目:综合复试2003;加试科目:物理化学2003;材料学院同等学历加试2003材料学专业复试科目:综合复试2003;加试科目:物理化学2003;材料学院同等学历加试2003材料加工工程专业复试科目:综合复试2003;加试科目:物理化学2003;材料学院同等学历加试2003生物医学工程专业复试科目:生物医学工程专业复试2003;加试科目:生物化学2003;组织学2003机电工程学院材料力学1997——2000,2002——2009机械原理1997——2000,2002——2009机械设计1997——2000,2002——2009控制工程基础2002——2009统计质量管理2005——2009传感器原理2003——2009传感检测技术2002——2003传感技术1997——2000传感与检测技术2002电子技术基础2002——2009微机原理及应用1997——2000,2002——2007人机工程学2002——2006机电工程学院2003年同等学历考研加试题(测试技术)机电工程学院2003年同等学历考研加试题(机械原理)机电工程学院2003年同等学力考研加试题(机械设计)机电工程学院2003级硕士研究生复试试题汽车工程学院材料力学1997——2000,2002——2009理论力学2002——2009汽车理论基础2002——2009发动机原理2002——2009摩托车理论与结构设计2002汽车运用工程2002——2009汽车运输工程2002——2003工程热力学2002——2008汽车运输学2003——2005,2007交通运输学2006汽车营销与策划2009汽车市场学2004——2008动力机械及工程专业复试科目:动力机械及工程复试2003;加试科目:发动机构造2003;发动机原理2003车辆工程专业复试科目:综合复试2003;加试科目:汽车构造2003;汽车理论2003载运工具运用工程专业复试科目:综合复试2003自动化学院电路1997——2000,2002——2009电工技术基础2002电工原理2003——2006控制理论基础2002自动控制原理1997——2000,2002——2009信号处理技术2002——2005(注:2002——2003年称“信号分析与处理”)传感技术1997——2000传感与检测技术2002传感检测技术2002——2003传感器原理2003——2009电机及拖动基础2001电力电子技术(一)2007电力电子技术2002——2006,2008——2009微机原理及接口技术2002——2009数字电路2003——2009逻辑设计2004——2006电力电子与电力传动专业复试科目:电力电子与电力传动专业复试2003检测技术与自动化装置专业复试科目:检测技术与自动化装置专业复试2003 控制理论与控制工程专业复试科目:控制理论与控制工程专业复试2003;加试科目:自动控制原理2003;微机原理及接口技术2003计算机科学与技术学院数据结构1997——2000,2002——2008操作系统1998——2000,2002——2008计算机组成原理2002——2007微机原理及应用1997——2000,2002——2007C语言2007微机原理(即:微型计算机原理)1997——2000,2002——2004离散数学2002——2006计算机网络1999——2000,2002软件工程2002——2006数据库原理2002编译原理2002计算机原理2002计算方法2003——2005复试科目:计算机应用技术、计算机软件与理论专业2003加试科目:微机原理及应用2003;数据库应用2003信息工程学院数据结构1997——2000,2002——2008信号与系统1999——2000,2002——2009信号与线性系统2002——2006物理光学2002,2004——2008光纤光学2007现代光学2006高频电路2002微机原理及应用1997——2000,2002——2007微机原理(即:微型计算机原理)1997——2000,2002——2004 脉冲与数字电路1999——2000,2002电子技术基础2002——2009高频电子线路1999——2000,2002微机原理及其通信接口2003——2009信号分析与处理2002——2008传感技术1997——2000电路1997——2000,2002——2009数字信号处理1999——2000,2002,2009土木工程与建筑学院材料力学1997——2000,2002——2009传热学2002——2007中外建筑史2002——2009建筑历史2004——2007建筑设计2002——2004,2008——2009建筑设计(1)2005——2007建筑设计(2)2005——2007规划设计2007——2008城市规划原理2003——2009建筑结构抗震设计2007抗震结构设计2004结构力学2002——2009工程项目管理2008——2009建筑施工与工程项目管理2003——2007建筑施工技术2002建筑工程经济与企业管理2002工程热力学2002——2009土质学与土力学2002——2007水分析化学2002——2005水分析与物理化学2006——2007水力学与水泵2002——2007水力学与水分析化学2008——2009土力学2002——2009建筑构造2002岩石力学1997——2000,2002岩体力学2003——2007(注:其中2003年有两种)钢筋混凝土结构2002,2006——2009混凝土结构原理2003钢筋砼结构2005土力学与基础工程2002结构动力学2002结构设计原理2002(第1种),2002(第2种),2005——2007桥梁工程2002给水工程2002排水工程2002路基路面工程2002,2005——2007工程地质学2004——2006美学2004建筑设计及其理论专业复试科目:建筑设计2003;建筑设计知识2003;加试科目:中外建筑史2003结构工程专业复试科目:结构工程2003;综合复试(建筑工程施工技术、建设工程项目管理方向)2003;加试科目:施工组织学2003;建筑经济与企业管理2003;结构力学2003;混凝土结构2003桥梁与隧道工程专业复试科目:桥梁与隧道工程专业复试2003;加试科目:桥梁与隧道工程专业加试Ⅰ2003;桥梁与隧道工程专业加试Ⅱ2003岩土工程专业复试科目:综合复试2003市政工程专业复试科目:专业复试2003交通学院高等数学2007,2009高等数学(工)2002——2006,2008高等数学(二)2004交通运输装备2005——2007桥梁设计与施工2005,2007第三方物流理论与实践2007现代物流与运输2005——2006物流学2006现代物流学2002,2007——2009运输经济学2002——2009路基路面工程2002,2005——2007工程热力学2002——2009结构分析2008——2009理论力学2002——2009土质学与土力学2002——2006材料力学1997——2000,2002——2009施工组织及概预算2004土工原理与计算2008——2009公路工程施工组织及概预算2003信号与系统1999——2000,2002——2009微机原理及应用1997——2000,2002——2007运筹学2002——2009(注:2002年试卷有两种)船舶结构力学2002,2004——2009船舶原理2002——2009船舶设计原理2002——2009流体力学2002——2004,2006——2008环境学导论2002国际航运经济与政策2002——2004计算机辅助船体建造2002船舶技术经济学2002传热学2002——2007国际集装箱运输与多式联运2002——2004港口管理(运输企业管理学)2002——2005港口企业管理学2007运输企业管理学2006道路勘测设计2002船舶强度与结构设计2002——2007环境质量评价2002交通环境工程地质与应用2002声学基础2002,2006航运管理2002——2006(注:2002年有两种)结构设计原理2002(第1种),2002(第2种),2005——2007计算机辅助船舶设计2002船舶营运管理2007船舶建造工艺学2003——2007船机制造工艺学2002结构力学计算2008——2009结构力学与结构电算2003——2007运动生物力学2004划船运动概论2004船体振动学2006液压原理与控制2002机械制造工艺学2002流体力学专业复试科目:流体力学2003;加试科目:流体力学2003,工程热力学和传热学、水力学2003工程力学专业复试科目:理论力学2003道路与铁道工程专业复试科目:道路与铁道工程2003,桥梁工程2003;加试科目:土力学2003交通运输规划与管理专业复试科目:综合复试2003;加试科目:交通运输设备概论2003船舶与海洋结构物设计制造专业复试科目:综合复试2003;加试科目:船舶与海洋工程学2003结构工程专业复试科目:结构综合2003;加试科目:钢结构2003航运学院船舶管理2002——2009航运管理2002——2006(注:2002年有两种)航海学2002船舶操纵与避碰2002——2006航海气象学与海洋学2004,2006——2007(注:2007年试卷共3页,缺第2页)物理海洋数字计算2008信号与系统1999——2000,2002——2009能源与动力学院电力电子技术2008——2009电力电子技术(二)2006——2007测试技术2007A卷,2007B卷工程热力学与传热学2006——2009机械振动学2006热能与动力机械制造工艺学2006——2007轮机自动化2007——2009智能运输系统概论2006——2009专业综合(含工程热力学、传热学、内燃机原理)2005专业综合(含工程热力学、传热学、机械设计)2005专业综合(含自动控制理论、测试技术、计算机技术)2005专业综合(含自动控制理论、电工电子技术、计算机控制技术)2005专业综合(含机械设计、测试技术、自动控制理论)2005工程热力学2002——2009机械设计1997——2000,2002——2009船舶柴油机2009内燃机原理2007A卷,2007B卷内燃机原理2002——2004,2006传热学2002——2007自动控制理论2003——2004,2006——2007自动控制原理1997——2000,2002——2009动力机械制造与维修2009船舶动力装置原理与设计2002船舶建造工艺学2003——2007船机制造工艺学2002船舶机械制造与修理2003——2004船舶管理2002——2009机械制造工艺学2002轮机工程专业复试科目:轮机工程2003;加试科目:内燃机学2003;轮机概论2003;工程热力学和传热学2003载运工具运用工程专业复试科目:载运工具运用工程2003管理学院管理学原理1997——2000,2002——2009(2002——2004有答案)管理经济学基础2005——2007管理信息系统2002——2007(2002——2004部分有答案)概率论与数理统计2001——2009线性代数2002线性代数与概率统计2003——2009会计学原理1997——2000,2002——2009(2002——2004有答案)(注:1998年共3页,缺P3)技术经济学2002——2009(2002——2004部分有答案)运筹学2002——2009(注:2002年试卷有两种)现代工业管理2003——2004(2003——2004部分有答案)公司理财原理2002——2009(2002——2004有答案)(注:2002年称“财务管理学”,2003——2004称“公司财务管理”)项目管理2005——2007企业管理学2002(2002有答案)生产管理学2002(2002部分有答案)市场营销学2001(2001有答案)技术创新管理2003(2003部分有答案)工商管理硕士(MBA)专业复试科目:MBA专业综合课2003;加试科目:市场学2003;投资学2003会计学专业复试科目:财务会计与管理会计2003;加试科目:财务管理2003;会计学2003管理科学与工程专业复试科目:企业管理概论2003;加试科目:管理经济学2003;企业管理学2003技术经济及管理专业复试科目:投资分析2003;加试科目:产业经济学2003;投资学2003企业管理专业复试科目:市场营销与生产管理2003;加试科目:市场学2003;管理学原理2003系统工程专业复试科目:系统工程概论与线性规划2003;加试科目:概率统计2003;线性代数2003政治与行政学院邓小平理论和“三个代表”重要思想2007——2009邓小平理论2002——2006马克思主义哲学原理2002——2009政治学原理2007——2009西方哲学史2007——2009西方政治思想史2008——2009中外政治思想2007高等数学(文)2003——2004思想政治教育理论与方法2002——2005,2007科学技术史2002——2007中共党史2002——2009自然辩证法2002——2009中国近代史2002科学技术哲学专业复试科目:综合复试2003;加试科目:马克思主义哲学原理2003;现代科技导论2003中共党史专业复试科目:综合复试2003;加试科目:政治学原理2003;中国近代史2003物流工程学院机械设计基础2005——2009机械工程基础2004机械CAD基础2006起重运输机械2005——2009起重机械2002物流信息技术2005——2009物流学2006现代物流学2002,2007管理学基础2005——2009画法几何2002——2003,2005——2007材料力学1997——2000,2002——2009理论力学2002——2009机械原理1997——2000,2002——2009机械设计1997——2000,2002——2009电子技术基础2002——2009微机原理及应用1997——2000,2002——2007工程材料2002——2007工程力学2004运筹学2002——2009(注:2002年试卷有两种)运筹学与系统工程2004计算机应用基础与计算机技术基础2004仓储技术与设备2006——2007自动识别技术2007CAD/CAM技术2002液压原理与控制2002机械制造工艺学2002机电一体化技术2002液压技术2002机械制造及自动化专业复试科目:机械制造及自动化专业复试2003;面试科目:机械制造专业2003机械电子工程专业复试科目:机械电子工程专业复试2003;面试科目:机械一体化技术(机电专业)2003机械设计及理论专业复试科目:机械设计及理论专业复试2003化学工程学院制药化学2005——2009化工原理2005——2009药物分析2005——2007物理化学2006——2007。
中国地质大学(武汉)高等数学期末考试试卷(含答案)

中国地质大学(武汉)高等数学期末考试试卷(含答案) 一、高等数学选择题
1.微分方程的通解是().
A、
B、
C、
D、
【答案】B
2.设函数,则.
A、正确
B、不正确
【答案】A
3.设函数,,则函数.
A、正确
B、不正确
【答案】A
4.设函数,则().
A、
B、
C、
D、
【答案】A
5.不定积分().
A、
B、
C、
D、
【答案】D
6.定积分.
A、正确
B、不正确
【答案】B
7.不定积分.
A、正确
B、不正确
【答案】B
8.设,则微分.
A、正确
B、不正确
【答案】B
二、二选择题
9.().
A、
B、
C、
D、
【答案】C
10.不定积分.
A、正确
B、不正确
【答案】A
11. ( ).
A、
B、
C、
D、
【答案】B
12.函数的图形如图示,则是函数的
( ).
A、最大值点
B、极大值点
C、极小值点也是最小值点
D、极小值点但非最小值点
【答案】C
13.是偶函数.
A、正确
B、不正确
【答案】A
14.函数的导数.
A、正确
B、不正确
【答案】B
15.设,则.
A、正确
B、不正确
【答案】B。
文科高等数学介绍

不含功利色彩;有所思有所想
教学内容、学时分配
模块 模块 顺序 内容
模块 具体内容
学时 大致安排
1
数学文化 数学推理、数学思维、
数学悖论、数学危机等
6 (2次)
2
一元微积分 集合、函数、极限、连续 12 (4次)
一元微分方法
6安排
《文科高等数学十讲》
第一讲 漫话数学(1)——数学思维、数学精神、数学与人文各学科的关系 第二讲 漫话数学(2)——数学悖论、数学危机、数学发现及解决的启示 第三讲 集合与函数——具体问题符号化、结构化、抽象化 第四讲 极限及其哲学思想(1)——有限与无限,以不变应万变 第五讲 极限及其应用分析(2)——有限与无限,以不变应万变 第六讲 连续与间断——居安思危,危机中孕育希望 第七讲 函数导数——变化率问题 第八讲 一元微分方法——由复杂化简约 第九讲 泰勒中值定理——联结局部与整体的纽带 第十讲 一元不定积分方法——矛盾转化与逆向思维 第十讲 一元定积分方法——总量问题
《文科高等数学》
刘淑环
科学技术教学部数学教研室
第一周,2010年2月21日
课程性质及定位
1.《文科高等数学》为我校政法人文等专业自然 科学类的通识主干选修课程之一(2门核心课 程,13门通识主干选修课程,一般通识课程)
2. 课程定位:一方面注重培养学生以理性的 方 式认识自然世界,思考人类与自然之间的关系, 另一方面培养具有科学素养的公民,使学生可以 参与社会性科学议题的讨论,并能够以日常科学 思考的方式解决生活中的问题。
中国政法大学大学生素质教育网
/cn/。
点击“博学近思”,点击“文科高等数学”即可进入 可以通过留言版、论坛、发送邮件等多种方式交流, 大家可通过网络环节交流学习心得,上传资料共享,并与 老师进行网上讨论,提高学习的主动性及学习的实效性。
武汉大学强军计划专业课考研真题、笔记、参考书、大纲、录取分数线、报录比

武汉大学强军计划专业课考研真题、笔记、参考书、大纲、
录取分数线、报录比
武汉大学强军计划专业课考研大纲
一、政治理论题型:
1、单选题10分(10小题)
2、多选题30分(15小题)
3、判断题20分(4小题)
4、简述题20分(4小题)
5、论述题20分(2小题)
考试内容:1.马克思主义基本原理;2.毛泽东思想和中国特色社会主义理论体系概论;3.思想道德修养与法律基础;4.中国近现代史纲要;5.时事。
二、英语题型:
1、词汇20分(40小题)
2、完形填空30分(30小题)
3、阅读理解50分(25小题)
三、俄语题型:
1、词汇语法30分(30题)
2、完型填空20分(20题)
3、阅读50分(25小题)
四、日语题型:
1、文字和词语30分(30题)
2、语法构句20分(20题)
3、阅读理解50分(25题)
五、数学题型:
1、填空题25分(5小题)
2、单选题25分(5小题)
3、计算题100分(10小题)
考试内容:高等数学:1、函数与极限;2、导数与微分;3、中值定理与导数应用;4、不定积分;5、定积分;6、定积分应用;7、空间解析几何;8、多元函数微分法及其应用;
9、重积分;10、曲线积分与曲面积分;11、无穷级数;12、常微分方程。
六、专业课考试科目
专业课考试科目与统考研究生专业课考试科目相同,请参考《哈尔滨工程大学2015年硕士研究生招生专业目录》和《哈尔滨工程大学2015年硕士研究生入学考试专业课考试大纲》。
大学文科数学-张国楚-定积分

.
10
1.3求定积分过程中的辨证思维
无论是求曲边梯形的面积,还是求变力作 功,初等数学都无法解决,而高等数学可迎 刃而解. 定积分中的极限方法可以使有关常量与 变量、变与不变等矛盾的对立双方相互 转化,从而化未知为已知,体现了对立 统一法则。同时也体现了否定之否定法 则。
.
11
1.4可积条件
定理1 (可积的必要条件) 若函数f(x)在[a,b] 上可积,则 f
根据定理1,
也是f(x)的一个原函数,而这两个
原函数之差为某个常数,所以
F(x) x f(t)dt C a
若令x = a,则因
a f(t)dt 0 a
得 C = F(a).于是
在上式中令x = b,就得到所要证明的公式
b f(x)dt F(b) F(a) a
.
18
例1 计算 2 sin xdx 0
原型Ⅰ和Ⅱ的问题可以简洁地表述为:
⑴ 连续曲线y=f(x) ≥0 在[a,b] 上构成的曲边梯形的 面积为函数 y=f(x) 在[a,b] 上的定积分,即
s b f(x)dx a
⑵在连续变力F (x) 作用下,质点m 沿x 轴从点 a 位移 到点b 所作的功为F (x) 在[a,b] 上的定积分,即
第六章 定积分
求总量的问题
.
1
(一)教学目标
教学目标:要求学生掌握定积分的概念、 微积分基本定理、非正常积分、定积分 的应用;要求理解定积分的概念,会求 定积分与非正常,能利用定积分解决一 些几何问题;理解李善兰对我国近代数 学发展所起的作用。
.
2
(二)教学重点
教学重点:定积分的概念和性质、微积 分基本定理、定积分的换元积分法和分 部积分法、定积分在几何学中的应用。
2002—2003年第一学期A卷

2002-2003年第一学期※※※※※※高等数学(180学时)试题A 卷※※※※※※一.填空题(每小题4分,共20分)1.若()()1--=x x ae xf x 有无穷间断点0=x 及可去间断点1=x ,则.______=a解:由于0=x 为无穷型间断点,故()()∞=--=→1lim 0x x ae xf x x ,所以().101lim 0≠⇒≠-=-→a a a e x x又1=x 为可去型间断点,故()()A x x ae xf x x x =--=→→1lim lim 11存在,所以()()()0.01lim .1lim lim 111==---=-=-→→→A x x ae x x a e a e x x x xx ,即.e a =2.函数x ln 在2=x 处的泰勒公式为.________________________ 解:记()x x f ln =,则()11-=='x xx f ;()()2.1--=''x x f ;()()()3.21---='''x x f ; ……一般地,()()()n n x n x f ----='''.!111.由公式:()()()()()()()()()()()n n n x x o x x n x f x x x f x x x f x f x f 000200000!!2!-+-++-''+-'+= 得:()()()()()()()()n n n n x o x n n x x x 22!.21!112!2.2112212ln ln 122-+---++--+-+=- ()()()()()()()nn nn x o x n x x 22.21122.2112212ln 122-+--++--+-+=- ()()()()nnk k kk x o x k22.2112ln 11-+--+=∑=- 3.若()⎪⎩⎪⎨⎧≤->=.0,cos 7,0,tan 3sin x x e x ax xx f x在0=x 处连续,则.______=a解:()=+→x f x 0lim =+→ax x x tan 3sin lim 0(等价)aax x x 33lim 0=+→; ()=-→x f x 0lim ()=--→x e xx cos 7lim 0.617=- 令63=a ,得.21=a 4.曲线x xe y 2=的拐点是.__________解:()x e y x 212+=';()().142212222x e e x e y x x x +=++=''令 0=''y ,得.1-=x又因为当1-<x 时,0<''y ,曲线x xe y 2=是上凸的;而当1->x 时,0>''y ,曲线x xe y 2=是下凸的,所以()2,1---e 是曲线x xe y 2=的拐点.5.设0>a 为常数,则级数()⎪⎭⎫ ⎝⎛--∑∞=n a n n cos 111的敛散性为.__________解:记 ()⎪⎭⎫ ⎝⎛--=n a u n n cos 11,则.2sin 2cos 12n a n a u n =-= 因为 n a n n u n n n 2sin .lim 21lim 222∞→∞→=(等价)22.lim 2222a n a n n =⎪⎭⎫ ⎝⎛=∞→且∑∞=121n n 收敛,故∑∞=1n n u 收敛,所以=∑∞=1n n u ()⎪⎭⎫ ⎝⎛--∑∞=n a n n cos 111绝对收敛. 二.计算下列各题(每小题5分,共20分) 1.求极限:.45215lim22-+--→x x x x 解:45215lim22-+--→x x x x ()()()5215423lim 22++---=→x x x x x()().81521523lim2=++-+=→x x x x2.求极限:.sin lim cos 110xx x x -→⎪⎭⎫⎝⎛+解:xx x x cos 110sin lim -→⎪⎭⎫⎝⎛+xx x x x cos 110sin 1lim -→⎪⎭⎫ ⎝⎛-+=+().sin 1lim 31cos 1sin sin 0----→=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+=+e x x x x x x x xx xx其中 ()x x xx x cos 1sin lim 0--+→(等价)2.sin lim 20xx x x x -=+→(洛必达) 20231cos limxx x -=+→(等价).31232lim 220-=-=+→x x x 3.设,1sin 2xx x y +=求.dx dy解:()()()22212.sin 1cos sin x x x x x x x x dx dy +-++=()()()22221sin 1cos 1xxx x x x +-++=. 4.设()()()⎩⎨⎧'+-='+-=.3,3sin 2t f t t f y t f x 求,dx dy ,22dx yd 其中f 具有二阶导数且().0≠''t f 解: (一)()()()[]()t f t t f t t f t f dtdy ''=''+'+'-=;().t f dt dx ''=.t dtdx dt dy dx dy == (二)()()().1.22t f dx dt dt t d t dx d dx dy dx d dx y d ''===⎪⎭⎫ ⎝⎛=三.计算下列各题(每小题6分,共18分) 1.求().11003dx x x ⎰-解:()dx x x ⎰-10031()()()dx x x ⎰--+=1003111 ()dx x ⎰-=10011()dx x x ⎰--+100113()()dx x x ⎰--+1002113()()dx x x ⎰--+100311 ()()111100--=⎰x d x ()()1113100---+⎰x d x x ()()()11131002---+⎰x d x x()()()1111003---+⎰x d x x ()991991---=x ()981983---x ()971973---x ().196196c x +--- 2.求.2sin tan 136θθθππd ⎰+ 解:θθθππd ⎰+362sin tan 1θθππd ⎰=362sin 1θθθππd ⎰+362sin tan()θθππ22csc 2136d ⎰=θθππd ⎰+362sec 21|362cot 2csc ln 21ππθθ-=θtan 21+|36ππ3ln 21=.31+ 3.求().112⎰+∞+x x dx解:()⎰+∞+121x x dx dx x x x ⎰∞+⎥⎦⎤⎢⎣⎡-++=12111dx x x ⎰∞+⎥⎦⎤⎢⎣⎡++=1111dx x ⎰+∞-11 []d x x x ⎰+∞++=1ln 1ln dx x ⎰+∞-121||1111ln∞+∞+-+=x x x .2ln 111lim 2ln 1ln lim -=⎪⎭⎫ ⎝⎛---+=+∞→+∞→x x x x x 四.(8分)设可微函数()x y y =由方程23333=-++x y y x 确定,试讨论并求出()x f 的极大值和极小值.解: (一) 方程23333=-++x y y x ① 两边对x 求导,得.033.3322=-'+'+y y y x ② 令 ()0='x y ,代入②,则有.0332=-x ③由③解得 ,1-=x 或.1=x将1-=x 代入①,得 ()()104104323=⇒=++-⇒=-+y y y y y y (注意到04721422>+⎪⎭⎫ ⎝⎛+=++y y y ); 将1=x 代入①,得 ().0030323=⇒=+⇒=+y y y y y 所以函数()x y y =有两个驻点,11-=x .12=x (二) ②式两边关于x 再求导,得.033.6622=''+''+'+y y y y y x ④将1=x ,()11=y ,()01='y 代入④,有()011<-=''y ,故()11=y 为函数()x y y =的极大值;将1-=x ,()01=-y ,()01=-'y 代入④,有()011>=-''y ,故()01=-y 为函数()x y y =的极小值. 五.(8分)判别级数()()()[]∑∞=+---11253222222n n 的敛散性.解:记()()()1253222222+---=n n u ),2,1( =n则因为 ==+∞→nn n u u 1limρ()11222lim 32<-=-+∞→n n ,故 ()()()[]∑∞=+---11253222222n n 是收敛的.六.(10分)曲线()03≥=x x y 与直线()0>=λλx y 相交于原点O 和P 点,PA 垂直于x 轴且垂足为A .(1)曲线3x y =分OAP ∆为两部分21,A A ,证明:1A 与2A 的面积相等. (2)图形21,A A 分别绕x 轴旋转的旋转体的体积比是多少?解:(1)联立⎩⎨⎧==.,3x y x y λ解得⎩⎨⎧==.0,0y x 或⎩⎨⎧==.,λλλy x 故().,λλλP()4231λλλ=-=⎰dx x x A ;.4232λλ==⎰dx x A所以.21A A =(2)()32317λλπλ==⎰dx x V ; ().21473.3333122λλπλλπλλπλλλπ=-=-=V V 所以 .4:3:21=V V七.(10分)设函数()x f 在()+∞∞-,上连续且大于0,()()()⎪⎪⎩⎪⎪⎨⎧=≠=⎰⎰.0,0,0,00x x dtt f dtt tf x g x x (1) 求().x g '(2) 证明:()x g '在()+∞∞-,上连续. 解:(1)当0≠x 时, ()()()()()()2000..⎥⎦⎤⎢⎣⎡-='⎰⎰⎰xxxdt t f dt t tf x f dt t f x xf x g ;当0=x 时,()()()00lim 00--='→x g x g g x ()()⎰⎰→=x xx dtt f x dt t tf 000lim (洛必达法则)()()()⎰+=→xx x xf dt t f x xf 0lim()()()x f xdt t f x f xx +=⎰→0lim其中 ()xdt t f x x ⎰→0lim (洛必达法则)()();01limf x f x ==→ ()().0lim 0f x f x =→所以()='0g ()()()()()().21000lim lim lim 000=+=+→→→⎰f f f x f xdt t f x f x xx x综上()()()()()(),0,.0,21.2000≠⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡-='⎰⎰⎰x x dt t f dtt tf x f dt t f x xf x g x xx(2)八.(6分)设()x f 在[]1,0上连续,在()1,0内可导,且()00=f ,对任意()1,0∈x ,有()0≠x f ,证明:存在()1,0∈c ,使()()()()c f c f c f c f n --'='11(n 是自然数).证明:令()()()x f x f x F n -=1..则()()()()()().1.1.1x f x f x f x f x nf x F n n ---'='- ()x F 在[]1,0上连续,在()1,0内可导,且()()()().011.00===F f nf F 故()x F 在[]1,0上满足罗尔定理的条件.由罗尔定理知,存在()1,0∈c ,使()0='c F ,即()()()()()01.1.1=---'-c f c f c f c f c nf n n 亦即()()()().11c f c f c f c f n --'='。
高等教育出版社样书目录(数学类)
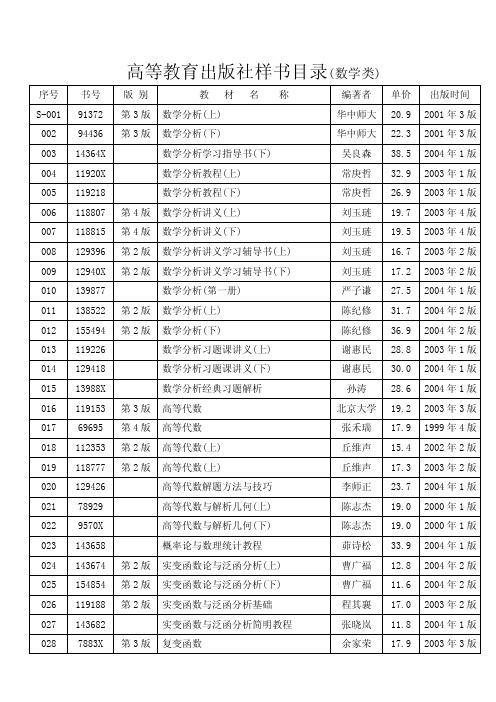
同济大学 10.1 2001 年 2 版
重温微积分
齐民生 39.6 2004 年 1 版
第 2 版 微积分(上)
同济大学 24.9 2003 年 2 版
第 2 版 微积分(下)
同济大学 23.1 2003 年 2 版
微积分学习辅导与习题选解
同济大学 28.4 2004 年 1 版
第 2 版 微积分学简明教程(上)
余家荣 17.9
出版时间 2001 年 3 版 2001 年 3 版 2004 年 1 版 2003 年 1 版 2003 年 1 版 2003 年 4 版 2003 年 4 版 2003 年 2 版 2003 年 2 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 1 版 2004 年 1 版 2004 年 1 版 2003 年 3 版 1999 年 4 版 2002 年 2 版 2003 年 2 版 2004 年 1 版 2000 年 1 版 2000 年 1 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 2 版 2004 年 1 版 2003 年 3 版
高等教育出版社样书目录(数学类)
版别
教材名 称
编著者 单价 出版时间
第4版 第3版
概率论与数理统计教程 概率论与数理统计教程学习辅导与习题 选解
概率论与数理统计
沈恒范 沈恒范 盛骤
20.6 2003 年 4 版 17.6 2003 年 1 版 19.3 2001 年 3 版
概率论与数理统计习题全解指南
第 2 版 数学史概论
李文林 21.0 2002 年 2 版
大学文科高等数学(第一册)
姚孟臣 11.9 1997 年 1 版
2003—2004年第一学期A卷

2003-2004年第一学期※※※※※※高等数学(180学时)试题A 卷※※※※※※一.填空题(每小题4分,共20分)1.()⎪⎩⎪⎨⎧≥+-<=.0,23,0,2sin 2x k x x x xxx f 在0=x 处连续,则常数.______=k 解:()x f x -→0lim xx x 2sin lim0-→=(等价替换)22lim0==-→xx x ;()x f x +→0lim ()k k x x x =+-=+→23lim 20.令()x f x -→0lim ().2lim 0=⇒=+→k x f x2.()[]x x x x ln 1ln lim -++∞→ .________________________解:()[]x x x x ln 1ln lim -++∞→xx x x +=+∞→1lnlim ⎪⎭⎫ ⎝⎛+=+∞→x x x 11ln lim (等价替换) .11.lim ==+∞→xx x3.()x f 的一个原函数为x x ln ,则().______='x f解:()()x x x x f ln 1ln +='=;()().1ln 1xx x f ='+='4.()=-+⎰-22241dx x x __________.解:()=-+⎰-22241dx x x +-⎰-2224dx x ⎰--2224dx x x[].202212ππ=+=5.使级数()()∑∞=+++1222111n nnx x 收敛的实数x 的取值范围是.__________解:记()()()nnnx x x u 222111+++=,...)2,1(=n(一)当0=x 时,由于()021lim ≠=∞→x u nn ,故()()∑∞=+++1222111n nnx x 发散;(二)当0≠x 时,令 ()()()()()[]()[]()nn nn n nn n x x x x x u x u x 222222121111111lim lim++++++==++∞→+∞→ρ ()()()()22222222111111111lim x x x x x nn n +=⎥⎥⎦⎤⎢⎢⎣⎡+++⎥⎥⎦⎤⎢⎢⎣⎡+++=∞→ 因为对于0≠∀x ,都有 ()1<x ρ ,故()()∑∞=+++1222111n nnx x 收敛.所以使级数()()∑∞=+++1222111n nnx x 收敛的实数x 的取值范围是()().,00,+∞⋃∞-二.选择题(每小题4分,共20分) 1.()()()11sin ln 22-+=x x x x xx f 的可去间断点的个数是( D )0.A 1.B 2.C 3.D2.已知()21='f ,则()()=+--→xx f x f x 11lim(D )2.A 2.-B 4.C 4.-D3.设dx xx I ⎰=41tan π,dx xx I ⎰=42tan π,则(B )1.21>>I I A 21.1.I I B >> 1.12>>I I C .1.12I I D >>4.级数∑+∞=⎪⎭⎫ ⎝⎛-k n n 1cos 1(k 为正整数)的敛散性是(A ).A 绝对收敛 .B 条件收敛 .C 发散 .D 与k 无关5.已知()x f 二阶导数连续,且()00=f 以及()1lim 2=→xx f x ,则曲线()x f y =在0=x 处的曲率k 为(C )0.A 1.B 2.C .D 不存在三.计算下列各题(每小题6分,共30分)1.求极限xx x x cos 110sin lim -→⎪⎭⎫ ⎝⎛ 解:x x x x cos 110sin lim -→⎪⎭⎫ ⎝⎛x x x x x cos 110.sin 1lim -→⎪⎭⎫ ⎝⎛-+= ()x x xx x x xx x x x cos 1sin sin 0sin 1lim ---→⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+=().lim 31cos 1sin 0---→==e e x x x x x 其中 ()x x xx x cos 1sin lim0--→(等价)2021.sin limx x xx x -=→(洛必达)2031cos lim 2x x x -=→ (等价).31321lim 2220-=-=→xx x 2.x y 2sin =,求().2004y解:x x x y 2sin cos .sin 2=='; x y 2cos .2='';()x y 2sin .212-='''; ()()x y 2cos .2134-=; ()x y 2sin .245=;………归纳可得 ().212sin .21⎪⎭⎫⎝⎛-+=-πn x y n n 特别地()⎪⎭⎫⎝⎛+=π220032sin .220032004x y .2cos .22003x -=3.求不定积分.cos 2sin cos dx xx x ⎰+解:令t x =2tan,即t x arctan 2=,.122dt tdx +=dx x x x⎰+cos 2sin cos dt t t t t t t t 22222212.11.21211++-+++-=⎰()()dt t t tt ⎰+++--=222111dt t t t t t ⎰⎪⎭⎫ ⎝⎛+--++-+-=22142.51112.51dt t t t ⎰++-+-=112512dt t t ⎰+-21251dt t ⎰++21154()c t t t t +++-++-=arctan 541ln 511ln 5122.2tan arctan 542tan 1ln 5112tan2tan ln 5122c x x x x +⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+-++-=另解:令 dx xx x I ⎰+=cos 2sin cos ① dx xx xJ ⎰+=cos 2sin sin ②则⎪⎩⎪⎨⎧+=+-=-=++=+⎰⎰,cos 2sin ln cos 2sin sin 2cos 2,cos 2sin cos 2sin 2x x dx x x xx J I x dx x x x x J I解得:.2cos 2sin ln 5152c x x x I +++=4.求广义积分()().1101512⎰+∞--++dx x x解:设()()⎰+∞--++=0151211dx x x I ()()⎰+∞++=52111dx x x ①则I ()()⎰+∞++=052111dx x x (令t x 1=,则dt tdx 21-=)⎰∞+⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=0252111111dt t t t ()()⎰∞+++=052511dt t t t()()⎰∞+++=525.11dx x x x ②①+ ②,得: ()()⎰∞++++=5251112dx x x x I .2arctan 11|2π==+=+∞+∞⎰x dx x所以 .4π=I5.设()1ln ,ln 12122>⎪⎩⎪⎨⎧==⎰⎰t uu y udu u x t t ,求.22dx y d解:(一)()t t t t t dtdy ln 42.ln .5222-=-=;.ln 42.ln .322t t t t t dtdx ==2t dtdx dtdy dxdy -==.(二)()().ln 121ln 41.2.232222t t tt t dx dt dt t d t dx d dx dy dx d dx y d -=-=-=-=⎪⎭⎫ ⎝⎛= 四.(8分)曲线()x f y =由方程2516922=+y x 给出. (1)求所给的曲线上点()b a P ,处的切线方程.(2)在所给的曲线位于第一象限的那部分上求一点,使其切线与坐标轴所围的面积最小.解:(一)方程2516922=+y x ① 两边关于x 求导,得 .0.3218=+dxdy y x故.169yx dx dy -= 所以曲线上点()b a P ,处的切线方程为().169a x ba b y --=-即 22169916b a ax by +=+ 亦即 .25916=+ax by (因为 ① ) ② (二)由②式,令0=y ,得.925a x =令0=x ,得.1625by =故()b a P ,处的切线与坐标轴所围的面积为 ().925.21,a b a S =b 1625.ab1.288625= ③ 由于 ()()254322=+b a 所以()()()()[].252414321.1214.3121.22⨯=+≤=b a b a b a ④④式当且仅当b a 43=,即285,265==b a 时成立.所以().1225252411.288625,=⨯≥b a S即最小面积为.1225五.(7分)平面图形D 由曲线y x xy ==,1以及2=x 围成,求D 绕x 轴旋转所成的立体的体积.解一:在⎥⎦⎤⎢⎣⎡1,21上取代表区间[]y y y ∆+,,对应[]y y y ∆+,部分立体的体积y y y V ∆⎪⎪⎭⎫⎝⎛-≈∆1221π 所以,取dy y y dV ⎪⎪⎭⎫⎝⎛-=1221π 故⎰⎪⎪⎭⎫⎝⎛-=1211122dy y y V π[]22|1212ππ=-=y y .在[]2,1上取代表区间[]y y y ∆+,,对应[]y y y ∆+,部分立体的体积 ()y y y V ∆-≈∆222π 所以,取()dy y y dV -=222π 故()⎰-=21222dy y y V π.3432|2132ππ=⎥⎦⎤⎢⎣⎡-=y y . 所以 .61134221πππ=+=+=V V V解二:dx x dx x V V V ⎰⎰⎪⎭⎫⎝⎛-=-=212122211ππ .61113||21213πππ=+=xx六.(8分)证明:方程dx x e x x ⎰--=π2cos 1ln 在()+∞,0内有且仅有两个根.证明:(一)令()dx x ex x x f ⎰-+-=π2cos 1ln ,().,0+∞∈x则()0222cos 10>=-=⎰dx x e f π;()-∞=+→x f x 0lim ;().lim +∞=+∞→x f x故由零点定理知,方程()0=x f 在()+∞,0内至少有两个不相等的实根. (二)又令()011=-=-='xex e e x x f ,得唯一驻点.e x =当e x <<0时,()0>'x f ;而当e x >时,().0<'x f 故方程()0=x f 在()+∞,0内至多有两个实根综合(一)、(二)知方程dx x e x x ⎰--=π2cos 1ln 在()+∞,0内有且仅有两个根.七.(7分)()x f 具有三阶连续导数,且().0≠'''a f ()x f 在a x =处的一阶泰勒公式为 ()()()()().1022<<+''+'+=+θθh a f h a f h a f h a f ①试证:当0→h 时,.31→θ证明:由①式,可知()()()()h a f h a f h a f h a f θ+''='--+22 ②由②式,得()()()()h a f ha f h a f h a f θ+''='--+2222 ③由③式,进一步可得()()()()()()ha f h a f h a f h a f h a f h a f ''-+''=''-'--+θ32222 ④④两边令0→h ,取极限,得:()()()()()()⎥⎦⎤⎢⎣⎡''-+''=''-'--+→→h a f h a f h a f h a f h a f h a f h h θθθ0320.lim 222lim⑤ 又⑤左()()()()320222lim h a f h a f h a f h a f h ''-'--+=→()()()23222lim ha f h a f h a f h ''-'-+'=→()()ha f h a f h 622lim''-+''=→()()()a f ha f h a f h '''=''-+''=→31lim310;⑤右()()⎥⎦⎤⎢⎣⎡''-+''=→→h a f h a f h h θθθ00lim .lim ()..lim 0a f h '''=→θ所以,有()='''a f 31()..lim 0a f h '''=→θ于是,得到.31.lim 0=→h θ。
武汉理工大学高等数学练习册答案

武汉理工大学高等数学练习册答案一、选择题1.下列八个关系式①{0}= ② =0 ③ { } ④ { } ⑤{0} ⑥0 ⑦ {0} ⑧ { }其中正确的个数( )(A)4 (B)5 (C)6 (D)72.集合{1,2,3}的真子集共有( )(A)5个 (B)6个 (C)7个 (D)8个3.集合A={x } B={ } C={ }又则有( )(A)(a+b) A (B) (a+b) B (C)(a+b) C (D) (a+b) A、B、C任一个4.设A、B是全集U的两个子集,且A B,则下列式子成立的是( )(A)CUA CUB (B)CUA CUB=U(C)A CUB= (D)CUA B=5.未知子集A={ } B={ }则A =( )(A)R (B){ }(C){ } (D){ }6.下列语句:(1)0与{0}表示同一个集合;(2)由1,2,3组成的集合可表示为{1,2,3}或{3,2,1};(3)方程(x-1)2(x-2)2=0的所有解的集合可表示为{1,1,2};(4)集合{ }是有限集,正确的是( )(A)只有(1)和(4) (B)只有(2)和(3)(C)只有(2) (D)以上语句都不对7.未知A={1,2,a2-3a-1},B={1,3},A {3,1}则a等同于( )(A)-4或1 (B)-1或4 (C)-1 (D)48.设U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(CUA) (CUB)=( )(A){0} (B){0,1}(C){0,1,4} (D){0,1,2,3,4}9.设S、T是两个非空集合,且S T,T S,令X=S 那么S X=( )(A)X (B)T (C) (D)S10.设A={x },B={x },若A B={2,3,5},A、B分别为( )(A){3,5}、{2,3} (B){2,3}、{3,5}(C){2,5}、{3,5} (D){3,5}、{2,5}11.设一元二次方程ax2+bx+c=0(a<0)的根的判别式,则不等式ax2+bx+c 0的边值问题为( )(A)R (B)(C){ } (D){ }(A)P Q(B)Q P(C)P=Q (D)P Q=12.未知P={ },Q={ ,对于一切 R设立},则以下关系式中设立的就是( )13.若M={ },N={ Z},则M N等于( )(A) (B){ } (C){0} (D)Z14.下列各式中,正确的是( )(A)2(B){ }(C){ }(D){ }={ }15.设U={1,2,3,4,5},A,B为U的子集,若A B={2},(CUA) B={4},(CUA) (CUB)={1,5},则以下结论恰当的就是( )(A)3 (B)3(C)3 (D)316.若U、分别表示全集和空集,且(CUA) A,则集合A与B必须满足( )(A) (B)(C)B= (D)A=U且A B17.未知U=N,A={ },则CUA等同于( )(A){0,1,2,3,4,5,6} (B){1,2,3,4,5,6}(C){0,1,2,3,4,5} (D){1,2,3,4,5}18.二次函数y=-3x2+mx+m+1的图像与x轴没有交点,则m的取值范围是( )(A){ } (B){ }(C){ } (D){ }19.设全集U={(x,y) },子集M={(x,y) },N={(x,y) },那么(CUM) (CUN)等同于( )(A){(2,-2)} (B){(-2,2)}(C) (D)(CUN)20.不等式(A){x } (B){x }(C){ x } (D){ x }二、填空题1. 在直角坐标系中,坐标轴上的点的集合可表示为2. 若A={1,4,x},B={1,x2}且A B=B,则x=3. 若A={x } B={x },全集U=R,则A =4. 若方程8x2+(k+1)x+k-7=0存有两个负根,则k的值域范围就是5. 集合{a,b,c}的所有子集是真子集是 ;非空真子集是6. 方程x2-5x+6=0的边值问题可以则表示为方程组7.设子集A={ },B={x },且A B,则实数k的值域范围就是。
文科高等数学教材简介

26
数学概论 西南交大出版社 2001
我们认为这是很切合文科类学生需要的,为此, 我们于2001年西南交通大学出版社出版了《数 学概论》一书,也是本着这个精神编写的。介 绍了数学简史、实数的势与连续、函数的极限 与连续、导数与微分、积分及应用、矩阵与方 程组、概率与模糊、运筹学简介、数学建模与 数学实验简介,这些章节也属专题介绍性质, 在内容上有一定的独立性,在教学上有一定的 灵活性,通过三年的教学实践,我们认为这个 思路是正确的,也受到学生的欢迎。
张华安 1992.12
33
美国的文科数学 教材
30
化学工业出版社
高等数学(文科类)· 上下册 / 罗定军,盛立人
主编. - 北京: 化学工业出版社, 2001
(罗定军:南京师范大学数科院教授,博士生导师,)
本书分上、下两册。上册包括微积分与微分方程,下册 包括线性代数、概率统计与实用规划。
31
高等数学(文科) 作 者:王升瑞,张晓宁,朱开永编
23
科学出版社
2001 首都师范大学 张饴慈
24
大学文科数学 / 张饴慈等编著.
- 北京: 科学出版社, 2001
张饴慈:首都师范大学数学系张饴慈教授
本书是专为文、史、哲、政治、语言等专业本科生编写 的数学教材,内容包括微积分大意、随机数学的基本思想、 线性代数初步、几何、无穷的比较、应用举例等。
属于本科的文科十 五国家级规划的教 材
文科数 学基础
出版 社:
高等教育电子 音像出版社
作者: 陈吉象
19
天津大学出版社(1999.9)
大学文科数学(网络课程)
研制单位:南开大学
主编:陈吉象
(陈吉象 天津市大学数学教学研究会副理事长、南开大教授)
中国地质大学武汉远程与继续教育学院入学考试复习题高等数学

★标准答案:D
54.曲线 ( )
A.既有水平渐近线,又有垂直渐近线 B.只有水平渐近线
C.有垂直渐近线 D.没有渐近线
高等数学
一单选题(共100题)
1.函数 的反函数是()
A. B. ,
C. , D.不存在
★标准答案:C
2.若 , 为常数,则 。
A. ; B. ; C. ; D.
★标准答案:A
3.曲线 在对应 的点处的法平面方程是.
A. B. C. D.
★标准答案:C
4.设空间三点的坐标分别为M(1,1,1)、A(2,2,1)、B(2,1,2)。则 =
★标准答案:A
49. =( )
A.0 B.1 C.2
★标准答案:D
50.设 ,则 ( )
2 B.
C.2 2
★标准答案:D
51.微分方程 是( )
A.六阶微分方程 B.三阶微分方程
C.一阶微分方程 D.二阶微分方程
★标准答案:C
52.设 ,则 ( )
A. B. C. D.
★标准答案:B
53.当 时,函数 取得极值,则 =( )
C. 是比 高阶的无穷小量 D. 是比 低阶的无穷小量
★标准答案:B
22.设函数(x)可导,且 ,则当 时,该函数在x0处的微分是( ).
A.Δx的等阶无穷小 B.Δx的同阶无穷小 C.Δx的高阶无穷小 D.Δx的低阶无穷小
★标准答案:B
23.设偶函数 有连续二阶导数,且 ,则 ( ).
A.不是 的驻点 B.一定是 的极值点
C.在 的某个小区间上有 ; D.在 内至少有一点使 .
★标准答案:D
11.函数 单调增的区间是( )
2002—2003年第一学期B卷

2002-2003年第一学期※※※※※※高等数学(180学时)试题B 卷※※※※※※一.填空题(每小题4分,共20分)1.若()⎪⎪⎩⎪⎪⎨⎧<--≥+=.0,,0,2cos x x x a a x x x x f 有跳跃间断点0=x ,则.______=a解:()=-→x f x 0lim x xa a x ---→0lim a x a a x 211lim 0=++=-→; ()=+→x f x 0lim =++→2cos lim 0x x x .212cos lim 0=++→x x x 若0=x 是()x f 的跳跃间断点,则2121≠a,故.1≠a 2.级数()∑∞=+02!1n n n 的和为.________________________解:()∑∞=+02!1n n n ∑∞==02!n n n ∑∞=+0!2n n n ∑∞=+0!1n n 其中∑∞=02!n n n ∑∞==12!n n n ()∑∞=-=1!1n n n ()()∑∞=-+-=1!111n n n ()()∑∞=--=1!11n n n ()∑∞=-+1!11n n ()()∑∞=--=2!11n n n ∑∞=+0!1n n()∑∞=-=2!21n n ∑∞=+0!1n n ∑∞==0!1n n ∑∞=+0!1n n e n n 2!120==∑∞=;∑∞=0!2n n n ∑∞==1!2n n n ()∑∞=-=1!112n n e n n 2!120==∑∞=;.!1e n n =∑∞= 故 ().5!102e n n n =+∑∞=3.若()⎪⎩⎪⎨⎧=≠-+=.0,,0,12sin 2x a x x e x x f ax 在()+∞∞-,上连续,则.______=a解:()=→x f x 0lim x e x ax x 12sin lim 20-+→+=→x x x 2sin lim 0xe ax x 1lim 20-→(等价替换)+=→x x x 2lim0.222lim 0a xaxx +=→ 令 ()().2220lim 0-=⇒=+⇒=→a a a f x f x4.曲线()x y y =由参数方程⎩⎨⎧-=+=.2,923t t y t t x 确定,则曲线()x y y =在区间__________是下凸的.解: 22-=t dt dy ;.932+=t dtdx .31.32.932222+-=+-==='t t t t dt dx dt dy dx dy y dx dtdx dy dt d dx dy dx d dty d y .22⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛==''=⎪⎭⎫ ⎝⎛+-=dtdx t t dt d 1.31.322()()()931.32.13.322222++--+t t t t t ().323.92322++-=t tt 令()().0314.92322>+--=''t t y 则得:()31412<<-⇒<-t t又因为0932>+=t dtdx,故t t x 93+=在[]3,1-上单增,所以当31<<-t 时,有 5410<<-x ,故曲线()x y y =在区间()54,10-是下凸的.5.级数()()n n n n-+-∑∞=111的敛散性为.__________解:记()()()nn n n nn++-=-+-11111,原级数即为 ()nn n n++-∑∞=1111.记 () ,2,111=++=n nn u n则显然{}n u 单减,且0lim =∞→n n u ,故由莱布尼兹审敛法知,()()n n n n-+-∑∞=111收敛;又()nn nn ++-∑∞=1111nn n ++=∑∞=111∑∞==1n n u 发散(因为21lim=∞→nu n n ) ,所以()()n n n n-+-∑∞=111是条件收敛的.二.计算下列各题(每小题5分,共20分)1.求极限:.111lim 0⎪⎭⎫ ⎝⎛--+-→x e xx x 解:⎪⎭⎫ ⎝⎛--+-→x e x x x 111lim 0()x x x e x e x x --→-+-+=11lim 20(等价)x x e x x x x .1lim 20-→+-+= (洛必达法则)x e x x x 221lim 0-→-+=(洛必达法则).2322lim0=+=-→x x e 2.求极限:()()33ln 3ln cos lim e e x x x x --+→ 解:()()33ln 3ln cos lim e e x x x x --+→()()33ln 3ln lim 3cos ee x x x --=+→(洛必达法则) 3331lim 3cos e e ex x x x --=+→3lim 3cos 333--=+→x e e e x x ()31lim 3cos 3333--=-→+x e e e x x (等价替换) ()33lim 3cos 333--=+→x x e ex .3cos .3cos 33==e e 3.求函数设xx x x y -++--+=1111ln的导函数.解:xx xx y -++--+=1111ln()xx x 211ln2-++=xx 211ln--= ().ln 11ln 2x x ---=()x x x y 11111122-'----='()x x x x 111210111222-⎪⎪⎭⎫⎝⎛'-----=x x x x x 1111222-⎪⎪⎭⎫ ⎝⎛--+=x x x x 111122---+=.112x x -= 4.设()x y y =由⎩⎨⎧=+-++=.01sin ,3232y t e t t x y 所确定,求.|022=t dx yd解:将y x ,均视为参数t 的函数,对所给方程两边关于t 求导,得()⎪⎩⎪⎨⎧=-++=+=)2(.0cos sin )1(,31226dt dy t e t dtdy e t t dt dxy y由(2)知t e t e dt dy y y sin 1cos .-=.2cos .yt e y -= (3) 联立(1)、(3)得()().2312cos y t te dt dx dt dy dx dy y y -+===' (4)由(4)式,得().312cos 2t ty ey y+='- (5) 对(5)式两端关于x 求导,得()()()dx dtt t t t y e y y e y y e e y y y y y .31cos 331.sin .212222+-+-=''-+'-'-'- 即()().31cos 331.sin .412332t tt t y e y y e y y y +++-=''-+'--(6) 又0=t 时,1=y ,由(4)知.2ey ='将它们代入(6)式,得.4312|0-=''+-=t y e e故 ==|022t dx y d ().324432|0-=⎪⎭⎫ ⎝⎛-=''=e ee e y t三.计算下列各题(每小题6分,共18分) 1.求.sin 5dx x ⎰解:dx x ⎰5sin ()()x d x cos cos 122⎰--=()x d x x cos )cos cos 21(42⎰+--= .cos 51cos 32cos 53c x x x +-+-= 2.求.ln 1dx x ee⎰解:1111111111ln ln ln ln ln ||e ee ee eee x dx xdx xdx x x dx x x dx ----⎡⎤⎡⎤=-+=--+-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰⎰⎰()1111111ln ln 21||||e ee e x x x x x x e ---⎡⎤⎡⎤=--+-=-⎢⎥⎢⎥⎣⎦⎣⎦ 3.求.arctan 13⎰+∞dx xx解:⎰+∞13arctan dx x x ⎰∞+⎪⎭⎫⎝⎛-=121arctan 21x xd ()⎰+∞+∞++-=122121121arctan 21|dx x x x xdx x x x x x ⎰∞++∞→⎪⎭⎫⎝⎛+-+⎥⎦⎤⎢⎣⎡--=1222111214arctan .1lim 21π|1arctan 1214021∞+⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛--=x x π⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-=+∞→41arctan 2lim 218ππx x x ⎪⎭⎫ ⎝⎛---=412218πππ.21= 四.(8分)求函数()3252x x y -=在区间[]2,1-上最大值与最小值.解:令()0131032.52233132=-=-+='-x x x x x y ,得驻点1=x ;又显然()3252x x y -=在0=x 处不可导.比较()71-=-y 、()00=y 、()31-=y 及()342-=y ,得 最小值为()71-=-y ;最大值为()00=y .五.(8分)设函数()x ϕ在()+∞∞-,上连续,周期为1,且()⎰=10dx x ϕ,函数()x f 在[]1,0上有连续的导数.设()()⎰=1dx nx x f a n ϕ,证明:级数∑∞=12n n a 收敛.证明:由于函数()x ϕ在()+∞∞-,周期为1,且()⎰=10dx x ϕ,故()⎰=1du u ϕ()==⎰ 21du u ϕ()01⎰-=nn du u ϕ ①令 ()()⎰=x du u x F 0ϕ ② 因为 ()()⎰+=+11x du u x F ϕ()+=⎰1du u ϕ()⎰+xdu u 11ϕ()().00x F du u x=+=⎰ϕ故()x F 也是周期为1的连续函数,且()()00==F n F ,()().x x F ϕ=' ③ 因此有()()⎰'=10dx nx F x f a n ()()[]⎰=11nx F d x f n ()()()()dx nx F x f n nx F x f n ⎰'-=101011|()()dx nx F x f n ⎰'-=11 ④故()x F 有界,即存在01>M ,使得()1M x F ≤().,+∞∞-∈x ⑤又由于函数()x f 在[]1,0上有连续的导数,则存在在01>M ,使得().2M x f ≤' []1,0∈x ⑥从而可得()().1.12110M M ndx nx F x f n a n ≤'≤⎰所以 ()221221M M n a n≤,且∑∞=121n n 收敛,故由比较判别法知级数∑∞=12n n a 收敛.六.(10分)假设()x f 在[]1,0上连续,在()1,0内二阶可导,过点()()0,0f A 与()()1,1f B 的直线与曲线()x f y =相交于点()()c f c C ,,其中10<<c ,证明:在()1,0内至少存在一点ξ,使得().0=''ξf 证明:由题意,知CB AC k k =,即()()00--c f c f ()()cc f f --=11 ① 又由拉格朗日中值定理,分别存在()c ,01∈ξ及()b c ,2∈ξ,使得()()()100ξf c f c f '=-- ,()()().112ξf cc f f '=-- 故由①式可得到()().21ξξf f '='因为()x f '在[]21,ξξ上连续,在()21,ξξ内可导,所以由罗尔定理知,至少存在一点()()1,0,21⊂∈ξξξ,使得().0=''ξf七.(10分)曲线2xx e e y -+=与直线()0,0>==t t x x 及0=y 围成一曲边梯形,该曲边梯形绕x 轴旋转一周得一旋转体,其体积为()t V ,侧面积为()t S ,在t x =处的底面积为().t F (1) 求()()t V t S 的值. (2) 计算极限()().lim t F t S t +∞→ 解:(1)()dx y y t S t⎰'+=0212π()dx e e e e t S txx x x ⎰⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫⎝⎛+=--022122π dx e e t xx ⎰⎪⎪⎭⎫⎝⎛+=-0222π ① ()dx e e t V txx 202⎰⎪⎪⎭⎫⎝⎛+=-π ② 故()().12=t V t S (2) ().22⎪⎪⎭⎫ ⎝⎛+=-tt e e t F π()()t F t S t +∞→lim 202222lim⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛+=--+∞→⎰t t tx x t e e dx e e ππ(洛必达法则) ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛+=---+∞→22222lim2tt t t t t t e e e e e e ππt t t t t e e e e --+∞→-+=lim .111lim 22=-+=--+∞→t tt e e 八.(6分)证明:()23x e x x f -=为有界函数.证明:因为()==∞→-∞→23limlim x x x ex x f =∞→223lim2x x xex .023lim2=∞→x x xe故由函数极限的定义知,对01>=ε,存在0>X ,使得当X x >时,有 ().1=<εx f ① 又由于()23x e x x f -=为初等函数,它在[]X X ,-上必连续,因此由闭区间上连续函数的性质,知()23x e x x f -=在[]X X ,-上必有界,即存在常数01>M ,使得对[]X X x ,-∈∀,都有().1M x f < ② 取 {}0,1max 1>=M M ,则由①、 ②式得到 ()+∞∞-∈∀,x ,都有().M x f < 即证明了()23x e x x f -=为有界函数.。
武汉纺织大学高等数学期末考试试卷(含答案)

武汉纺织大学高等数学期末考试试卷(含答案)一、高等数学选择题1.设函数,则().A、B、C、D、【答案】A2.设函数,则().A、B、C、D、【答案】C3.设曲线如图示,则在内( ).A、没有极大值点B、有一个极大值点C、有两个极大值点D、有三个极大值点【答案】B4.设,不定积分(1)(2)(3)则上述解法中().A、第(1)步开始出错B、第(2)步开始出错C、第(3)步出错D、全部正确【答案】A5.定积分.A、正确B、不正确【答案】B6.是偶函数.A、正确B、不正确【答案】B7.设,则.A、正确B、不正确【答案】A8. ( ).A、B、C、D、【答案】D9.是微分方程.A、正确B、不正确【答案】B10.设函数,则().A、B、C、D、【答案】C11.不定积分 ( ).A、B、C、D、【答案】A12.微分方程的通解是().A、B、C、D、【答案】A一、一选择题13.函数的图形如图示,则函数 ( ).A、有四个极大值B、有两个极大值C、有一个极大值D、没有极大值【答案】C14.微分方程的通解是().A、B、C、D、【答案】C15.函数的定义域为.A、正确B、不正确【答案】B。
2017年武汉大学各专业初试真题汇总
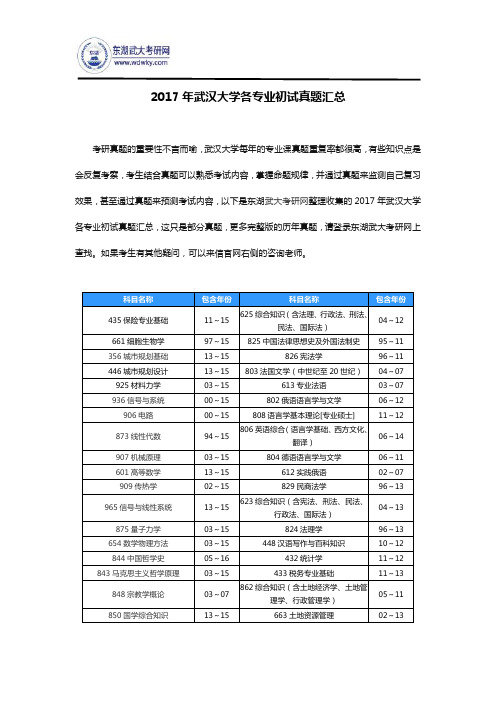
2017年武汉大学各专业初试真题汇总考研真题的重要性不言而喻,武汉大学每年的专业课真题重复率都很高,有些知识点是会反复考察,考生结合真题可以熟悉考试内容,掌握命题规律,并通过真题来监测自己复习效果,甚至通过真题来预测考试内容,以下是东湖武大考研网整理收集的2017年武汉大学各专业初试真题汇总,这只是部分真题,更多完整版的历年真题,请登录东湖武大考研网上查找。
如果考生有其他疑问,可以来信官网右侧的咨询老师。
科目名称包含年份科目名称包含年份435保险专业基础11~15625综合知识(含法理、行政法、刑法、民法、国际法)04~12661细胞生物学97~15825中国法律思想史及外国法制史95~11 356城市规划基础13~15826宪法学96~11 446城市规划设计13~15803法国文学(中世纪至20世纪)04~07 925材料力学03~15613专业法语03~07 936信号与系统00~15802俄语语言学与文学06~12 906电路00~15808语言学基本理论[专业硕士]11~12873线性代数94~15806英语综合(语言学基础、西方文化、翻译)06~14907机械原理03~15804德语语言学与文学06~11 601高等数学13~15612实践俄语02~07 909传热学02~15829民商法学96~13965信号与线性系统13~15623综合知识(含宪法、刑法、民法、行政法、国际法)04~13875量子力学03~15824法理学96~13 654数学物理方法03~15448汉语写作与百科知识10~12 844中国哲学史05~16432统计学11~12 843马克思主义哲学原理03~15433税务专业基础11~13848宗教学概论03~07862综合知识(含土地经济学、土地管理学、行政管理学)05~11850国学综合知识13~15663土地资源管理02~13348文博综合13~15859综合知识(含西方行政学理论、国家公务员制度、政策科学)03~13900水力学07~14政治与公共管理学院863西方经济学01~13 846伦理学概论03~07615专业日语与翻译04~11 640西方哲学问题06~07653数学分析03~15 894环境工程学03~15926结构力学03~13 931计算机原理00~15849科学技术哲学05~07 893地图学03~15845西方哲学史与现代西方哲学05~13 673生物化学97~15933计算机基础05~14 885分子生物学01~15837国际经济法90~13 676生物化学01~15835国际法90~13638哲学基础05~15法学院627综合知识(含法理、宪法、行政法、民法、国际法)05~13658普通生态学13~15法学院830刑事诉讼法学93~13886生态学02~15外国语言文学学院243二外俄语04~12 887普通生物学02~15805日本概况与写作04~11 833经济法学(含劳动与社会保障法学、公司证券法学)03~12335出版综合素质与能力[专业硕士]11~13 651马克思主义基本原理03~10611基础英语13~14 856近现代中外政治制度02~11文学院354汉语基础[专业硕士]10~14 963有机化学99~14434国际商务专业基础[专业硕士]11~15861社会保障02~14211翻译硕士英语10~15 897无机及分析化学96~09644公共管理学05~13 659微生物学01~15357英语翻译基础10~15 937误差理论与数据处理02~11811广播电视理论与实务12 440新闻与传播专业基础11~15437社会工作实务[专业硕士]10~13 334新闻与传播专业综合能力11~15外国语言文学学院242二外英语99~11 643政治学原理04~13621出版发行学02~13 637考古学通论03~07801英语综合(语言学、文学)06~14 655分析化学和物理化学95~13820运筹学与技术经济学03~13 883化工原理03~13331社会工作原理10~13 652思想政治教育原理与方法01~14246二外德语03~15 871比较德育学02~14614基础德语06~11 865社会学方法03~13245二外法语04~14 647社会学理论03~13441出版专业基础[专业硕士]11~13 834环境资源法96~09840汉语基础11~14836国际私法03~13817图书营销与管理02~13法学院综合知识(含628综合知04~13603高等数学(理学)13~15识、629综合知识等)831行政诉讼法学98~13244二外日语99~11828刑事法学(含刑法学、刑事诉96~11638哲学基础05~15讼法学)827行政法学98~12436资产评估专业基础[专业硕士]11~13法学院626综合知识(含法理、04~12635语言学理论10~13宪法、民法、刑法、国际法)法学院624综合知识(含法理、04~13宪法、刑法、民法、行政法)【专业课不再难】专业课自主命题,信息少,没教材,真题难,怎么办?武汉大学考研初试成绩占到总评成绩的50%~70%的成绩,其中专业课成绩占分比重最大,也是考生之间拉开差距的关键,东湖武大考研网推出专业课一对一通关班,一个对策解决初试专业课遇到的所有问题,你离武大只有一个通关班的距离!文章摘自东湖武大考研网!。
