专题10等差数列与等比数列—三年高考(2015-2017)数学(文)真题汇编
等差数列与等比数列专题辅导(小编推荐)

等差数列与等比数列专题辅导(小编推荐)第一篇:等差数列与等比数列专题辅导(小编推荐)等差数列与等比数列专题辅导(1)在等差数列{an}中, a7=9, a13=-2, 则a25=()A-22B-24C60D64(2)在等比数列{an}中, 存在正整数m, 有am=3,am+5=24, 则am+15=()A864B1176C1440D1536(3)已知等差数列{an}的公差为2,若a1,a3,a4成等比数列, 则a2=()A–4B–6C–8D–10(4)设数列{an}是等差数列,且a2=-6,a8=6,Sn是数列{an}的前n 项和,则()AS4>S3BS4=S2CS6(5)已知由正数组成的等比数列{an}中,公比q=2, a1·a2·a3·…·a30=245, 则a1·a4·a7·…·a28=5101520A 2B2C2D2(6)若{an}是等差数列,首项a1>0,a2003+a2004>0,a2003.a2004<0,则使前n项和Sn>0成立的最大自然数n是:()A.4005B.4006C.4007D.4008(7)在等比数列{an}中, a1<0, 若对正整数n都有anAq>1B0a1(3n-1)(8)设数列{an}的前n项和为Sn,Sn=(对于所有n≥1),且a4=54,则a1=__________.2(9)等差数列{an}的前m项和为30, 前2m项和为100, 则它的前3m项和为_________.(10)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列{an}是等和数列, 且a1=2, 公和为5,那么a18的值为_______,这个数列的前21项和S21的值为.(11)已知等差数列{an}共2n+1项, 其中奇数项之和为290, 偶数项之和为261,求第n+1项及项数2n+1的值.(12)设{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110且a1,a2,a4成等比数列.(Ⅰ)证明a1=d;(Ⅱ)求公差d的值和数列{an}的通项公式.(13)已知等比数列{an}的各项都是正数, Sn=80, S2n=6560, 且在前n项中, 最大的项为54, 求n的值.(14)ΔOBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2), 设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n, Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn), an=(Ⅰ)求a1,a2,a3及an;(Ⅱ)证明yn+4=1-(Ⅲ)若记bn=y4n+41yn+yn+1+yn+2.2yn,n∈N*;4-y4n,n∈N*,证明{bn}是等比数列.答案:1-7 BDBDA BB8.29.21010.3, 5211.29, 1912.(2)d=2 an=2n13.n=414.(1)an=2(2)(3)证明略第二篇:等差数列与等比数列等差数列与等比数列⎧>0,递增数列⎪一、等差数列的定义:an+1-an=d(d:公差)(常数)⎨=0,常数列,⎪<0,递减数列⎩1.证明数列{an}为等差数列:(1)定义:an+1-an=d(常数)(2)等差中项:2an+1=an+an+2注:(1)不可用a2-a1=a3-a2=a4-a3=Λ=“常数”证(2)a1=⎨例1.(1)已知数列{an}为等差数列,求证:数列{an+an+1}为等差数列;变式:①已知数列{an}为等差数列,求证:数列{an+t}(t为常数)为等差数列;②已知数列{an}为等差数列,求证:数列{tan}(t为常数)为等差数列;③已知数列{an}、{bn}均为等差数列,求证:数列{an+bn}为等差数列(2)已知数列{an}的前n项和为Sn,且Sn=n2,求证:数列{an}为等差数列;变式:①已知数列{an}的前n项和为Sn,且Sn=n2+1,求:an②已知数列{an}的前n项和为Sn,且Sn=an2+bn,求:an ③已知数列{an}的前n项和为Sn,且Sn=an2+bn+c,求:an(3)已知数列{an}满足:a1=1,an+1=数列;(4)已知数列{an},a1=1,an+1=为等差数列(5)设数列{an}的前n项和为Sn,求证:数列{an}为等差数列的充要条件是{an}为等差数列⎧S1,n=1⎩Sn-Sn-1,n≥2an1,且bn=,求证:数列{bn}为等差an+1ann1an+,且bn=nan,求证:数列{bn}n+1n+1Sn=n(a1+an)22.证明数列{an}为单调数列:an+1-an=f(n)⎨⎧>0,递增数列递减数列⎩<0,注:(1)求数列{an}中an的极值也可采用此方法(2)已知数列{an}为等差数列ⅰ.若a1<0,d>0,则Sn有最小值;解法:①令an≤0{bn}②Snⅱ.若a1>0,d<0,则Sn有最大值;解法:①令an≥0②Sn例2.已知an=(11-2n)2n,求数列{an}的最大项例3.(1)已知等差数列{an}的前n项和为Sn,且an=10-2n,求Sn的最大值;(2)已知等差数列{an}的前n项和为Sn,且an=2n-13,求Sn的最小值;3.叠加法:已知a1=a,an+1-an=f(n),求an例4.(1)已知数列{an}为等差数列,首项为a1,公差为d,求an;(2)已知数列{an},a1=1,an+1=4.通项公式:an=a1+(n-1)d(1)an=am+(n-m)d(2)an是关于n的一次函数,且n的系数为公差d.例5.已知数列{an}为等差数列,a5=-3,a9=13,求an5.等差中项:若a、b、c成等差数列,则b=(1)若数列{an}为等差数列,则2an+1n+11an+,求an nna+c称为a、c的等差中项2=an+an+2;(2)若已知三个数成等差数列,且其和为定值,则可设这三个数为a-d、a、a+d;(3)若数列{an}为等差数列,且公差d≠0,则am+an=ap+aq⇔m+n=p+q(4)在有穷等差数列{an}中,与首尾两项距离相等的两项的和等于首尾两项的和.即:a1+an=a2+an-1=a3+an-2=Λ=ak+an-k+1例6.(1)已知:等差数列中连续三项的和为21,平方和为179,求这三项(2)在3与19之间插入3个数后成等差数列,求这三个数(3)已知:a、b、c成等差数列求证:①b+c、a+c、a+b成等差数列;②a(b+c)、b(a+c)、c(a+b)成等差数列;③a-bc、b-ac、c-ab 成等差数列(4)已知:a、b、c成等差数列,求证:2222111成等差数列 b+ca+ca+blg(a-c)、lg(a+c-2b)成等差(5)已知:成等差数列,求证:lg(a+c)、数列(6)若方程a(b-c)xb(c-a)x+c(a-b)=0有相等实根,求证:成等差111abc111abc数列例7.在等差数列{an}中,(1)若a5+a10=12,求S14;(2)若a8=m,求S15;(3)若a4+a6+a15+a17=50,求S20;(4)若a2+a4=18,a3+a5=32,求S6;(5)若a2+a5+a12+a15=36,求S16;(6)若a3+a4+a5+a6+a7=450,求a2+a8(7)若等差数列{an}的各项都是负数,且a32+a82+2a3⋅a8=9,则其前10项和S10= ____________(8)在等差数列{an}中,若a3+a15=a5+an,则n=_______6.数列{an}的前n项和Sn=注:(1)倒序法求和;(2)等差数列{an}的前n项和Sn是关于自然数n的二次函数,且n的系数为n(a1+an)n(n-1)n(n-1)=na1+d=nan-d 222d,2常数项为零,即:Sn=An2+Bn(当A=0时数列{an}为常数列);(3)①S2n-1=(2n-1)an(可以将项与和之间进行相互转化)。
近三年数列全国卷高考真题

2015-2017年全国卷数列真题1、(2015全国1卷17题)n S 为数列{n a }的前n 项和.已知n a >0,2n n a a +=43n S +.(Ⅰ)求{n a }的通项公式; (Ⅱ)设11n n n b a a +=,求数列{n b }的前n 项和。
2、(2015全国2卷4题)已知等比数列{}n a 满足a 1=3,135a a a ++ =21,则357a a a ++= ( )A .21B .42C .63D .843、(2015全国2卷16题)设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则n S =________.4、(2016全国1卷3题)已知等差数列{}n a 前9项的和为27,108a =,则100a = ( ) (A)100 (B )99 (C )98 (D)975、(2016全国2卷15题)设等比数列{}n a 满足a 1+a 3=10,a 2+a 4=5,则a 1a 2 …a n 的最大值为 .6、(2016全国2卷17题)n S 为等差数列{}n a 的前n 项和,且11a =,728S =.记[]lg n n b a =,其中[]x 表示不超过x 的最大整数,如[]0.90=,[]lg991=.(Ⅰ)求1b ,11b ,101b ;(Ⅱ)求数列{}n b 的前1000项和. 7、(2016全国3卷17题)已知数列{}n a 的前n 项和1n nS a λ=+,其中0λ≠.(I )证明{}n a 是等比数列,并求其通项公式;(II )若53132S =,求λ.8、(2017年国1卷4题)记n S 为等差数列{}n a 的前n 项和,若4562448a a S +==,,则{}n a 的公差为()A .1B .2C .4D .8 9、(2017年国1卷12题)几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是02,接下来的两项是02,12,在接下来的三项式62,12,22,依次类推,求满足如下条件的最小整数N :100N >且该数列的前N 项和为2的整数幂.那么该款软件的激活码是( )A .440B .330C .220D .110 10、(2017全国2卷3题)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( ) A .1盏 B .3盏 C .5盏 D .9盏 11、(2017全国2卷15题)等差数列{}n a 的前n 项和为n S ,33a =,410S =,则11nk kS ==∑ . 12、(2017全国3卷9题)等差数列{}na 的首项为1,公差不为0.若2a ,3a ,6a 成等比数列,则{}n a 前6项的和为() A .24- B .3- C .3 D .813、(2017全国3卷14题)设等比数列{}n a 满足121a a +=-,133a a -=-,则4a =________.。
高考文科数学数列专题复习(附答案及解析)

高考文科数学数列专题复习数列常用公式数列的通项公式与前n 项的和的关系a n s , n 11s s ,n 2n n 1( 数列{a n} 的前n 项的和为s n a1 a2 a n ).等差数列的通项公式*a a1 (n 1)d dn a1 d(n N ) ;n等差数列其前n 项和公式为n(a a ) n(n 1)1 ns na1 d n2 2 d 12n (a d)n .12 2等比数列的通项公式an 1 1 n *a a1q q (n N )nq;等比数列前n 项的和公式为na (1 q )1s 1 qn , q 1或sna a q1 n1 q,q 1na ,q 1 1 na ,q 1 1一、选择题1.( 广东卷) 已知等比数列{a n} 的公比为正数,且a3 ·a9 =2 2a ,a2 =1,则a1 =5A. 12B.22C. 2D.22.(安徽卷)已知为等差数列,,则等于A. -1B. 1C. 3D.7 3(. 江西卷)公差不为零的等差数列{a n} 的前n项和为S n .若a4 是a3与a7 的等比中项, S8 32, 则S等于10A. 18B. 24C. 60D. 904(湖南卷)设S n 是等差数列a n 的前n 项和,已知a2 3,a6 11,则S7 等于【】第1页/ 共8页A .13 B.35 C.49 D.633.(辽宁卷)已知a为等差数列,且a7 -2 a4 =-1, a3 =0, 则公差d=n(A)-2 (B)-12 (C)12(D)24.(四川卷)等差数列{a n }的公差不为零,首项a1 =1,a2 是a1 和a5 的等比中项,则数列的前10 项之和是A. 90B. 100C. 145D. 1905.(湖北卷)设x R, 记不超过x 的最大整数为[ x ], 令{x }= x -[ x ],则{ 52 1} ,[ 521],521A.是等差数列但不是等比数列B.是等比数列但不是等差数列C.既是等差数列又是等比数列D.既不是等差数列也不是等比数列6.(湖北卷)古希腊人常用小石子在沙滩上摆成各种性状来研究数,例如:他们研究过图1 中的1,3,6,10,⋯,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16⋯这样的数成为正方形数。
2015《数列》高考真题总结及答案

2015《数列》高考真题总结1.(2015·新课标I 卷13)在数列{a n }中,a 1=2,a n +1=2a n ,S n 为{a n }得前n 项与.若S n =126,则n =________、2.(2015·浙江卷10)已知{a n }就是等差数列,公差d 不为零.若a 2,a 3,a 7成等比数列,且2a 1+a 2=1,则a 1=__________________,d =__________________、3.(2015·安徽卷13)已知数列{a n }中,a 1=1,a n =a n -1+12(n ≥2),则数列{a n }得前9项与等于________.4.(2015·新课标I 卷7)已知{a n }就是公差为1得等差数列,S n 为{a n }得前n 项与,若S 8=4S 4,则a 10=( ) A 、172 B 、192 C .10 D .125.(2015·新课标Ⅱ卷5)设S n 就是等差数列{a n }得前n 项与,若a 1+a 3+a 5=3,则S 5=( )A .5B .7C .9D .116、(2015·北京卷16)已知等差数列{a n }满足a 1+a 2=10,a 4-a 3=2、(1)求{a n }得通项公式;(2)设等比数列{b n }满足b 2=a 3,b 3=a 7,问:b 6与数列{a n }得第几项相等?7.(2015四川文科16)设数列{a n }得前n 项与S n 满足S n =2a n -a 1,且a 1,a 2+1,a 3成等差数列.(1)求数列{a n }得通项公式、(2)设数列⎩⎨⎧⎭⎬⎫1a n 得前n 项与为T n ,求T n 、8、(2015·重庆卷16)已知等差数列{a n }满足a 3=2,前3项与S 3=92、(2)设等比数列{b n }满足b 1=a 1,b 4=a 15,求{b n }得前n 项与T n 、 9、(2015·浙江卷17)已知数列{a n }与{b n }满足a 1=2,b 1=1,a n +1=2a n (n∈N *),b 1+12b 2+13b 3+…+1n b n =b n +1-1(n ∈N *).(1)求a n 与b n ;(2)记数列{a n b n }得前n 项与为T n ,求T n 、10.(2015·福建卷17)等差数列{a n }中,a 2=4,a 4+a 7=15、(1)求数列{a n }得通项公式;(2)设b n =2a n -2+n ,求b 1+b 2+b 3+…+b 10得值.11、(2015·安徽卷18)已知数列{a n }就是递增得等比数列,且a 1+a 4=9,a 2a 3=8、(1)求数列{a n }得通项公式;(2)设S n 为数列{a n }得前n 项与,b n =a n +1S n S n +1,求数列{b n }得前n项与T n 、12、(2015·天津卷18)已知{a n }就是各项均为正数得等比数列,{b n }就是等差数列,且a 1=b 1=1,b 2+b 3=2a 3,a 5-3b 2=7、(1)求{a n }与{b n }得通项公式;(2)设c n =a n b n ,n ∈N *,求数列{c n }得前n 项与.13、(2015·广东卷19)设数列{a n }得前n 项与为S n ,n ∈N *、已知a 1=1,a 2=32,a 3=54,且当n ≥2时,4S n +2+5S n =8S n +1+S n -1、(1)求a 4得值;(2)证明:⎩⎨⎧⎭⎬⎫a n +1-12a n 为等比数列;14、(2015·湖北卷19)设等差数列{a n }得公差为d ,前n 项与为S n ,等比数列{b n }得公比为q 、已知b 1=a 1,b 2=2,q =d ,S 10=100、(1)求数列{a n },{b n }得通项公式;(2)当d >1时,记c n =a nb n,求数列{c n }得前n 项与T n 、15、(2015·湖南卷19)设数列{a n }得前n 项与为S n 、已知a 1=1,a 2=2,且a n +2=3S n -S n +1+3,n ∈N *、(1)证明:a n +2=3a n ; (2)求S n 、16、(2015·山东卷19)已知数列{a n }就是首项为正数得等差数列,数列{1a n ·a n +1}得前n 项与为n 2n +1、 (1)求数列{a n }得通项公式;(2)设b n =(a n +1)·2a n ,求数列{b n }得前n 项与T n 、17.(2015·新课标Ⅱ卷9)已知等比数列{a n }满足a 1=14,a 3a 5=4(a 4-1),则a 2=( )A .2B .1C 、12D 、182015《数列》高考真题答案1、【答案】6【解析】∵112,2n n a a a +==,∴数列{}n a 就是首项为2,公比为2得等比数列,∴2(12)12612n n S -==-,∴264n=,∴n=6、2、【答案】2,13-【解析】由题可得,2111(2)()(6)a d a d a d +=++,故有1320a d +=,又因为1221a a +=,即131a d +=,所以121,3d a =-=、3、【答案】27【解析】∵2≥n 时,21,21121+=+=-a a a a n n 且 ∵{}1a a n是以为首项,21为公差得等差数列 ∵2718921289199=+=⨯⨯+⨯=S4.【答案】B 【解析】∵公差1d =,844S S =,∴11118874(443)22a a +⨯⨯=+⨯⨯,解得1a =12,∴1011199922a a d =+=+=,故选B 、5.【答案】A6、【答案】(I )22n a n =+;(II )6b 与数列{}n a 得第63项相等、试题解析:(Ⅰ)设等差数列{}n a 得公差为d 、因为432a a -=,所以2d =、又因为1210a a +=,所以1210a d +=,故14a =、所以42(1)22n a n n =+-=+(1,2,)n =、(Ⅱ)设等比数列{}n b 得公比为q 、因为238b a ==,3716b a ==,所以2q =,14b =、所以61642128b -=⨯=、由12822n =+,得63n =、所以6b 与数列{}n a 得第63项相等、7、【解析】(Ⅰ) 由已知S n =2a n -a 1,有a n =S n -S n-1=2a n -2a n -1(n ≥2)即a n =2a n -1(n ≥2),从而a 2=2a 1,a 3=2a 2=4a 1,又因为a 1,a 2+1,a 3成等差数列 即a 1+a 3=2(a 2+1),所以a 1+4a 1=2(2a 1+1),解得a 1=2 所以,数列{a n }就是首项为2,公比为2得等比数列。
三年高考(2015-2017)高考数学试题解析13数列小题理

专题13数列小题1。
【2017课标1,理4】记nS 为等差数列{}na 的前项和.若4524a a +=,648S =,则{}na 的公差为A .1B .2C .4D .8 【答案】C 【解析】试题分析:设公差为d ,45111342724a a a d a d a d +=+++=+=,611656615482S ad a d ⨯=+=+=,联立112724,61548a d a d +=⎧⎨+=⎩解得4d =,故选C.秒杀解析:因为166346()3()482a a S a a +==+=,即3416aa +=,则4534()()24168a a a a +-+=-=,即5328a a d -==,解得4d =,故选C 。
【考点】等差数列的基本量求解【名师点睛】求解等差数列基本量问题时,要多多使用等差数列的性质,如{}na 为等差数列,若m np q +=+,则mnpqa a a a +=+。
2。
【2017课标3,理9】等差数列{}na 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}na 前6项的和为A .24-B .3-C .3D .8 【答案】A 【解析】故选A 。
【考点】等差数列求和公式;等差数列基本量的计算【名师点睛】(1)等差数列的通项公式及前n 项和公式,共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,体现了用方程的思想解决问题.(2)数列的通项公式和前n 项和公式在解题中起到变量代换作用,而a1和d是等差数列的两个基本量,用它们表示已知和未知是常用方法.3。
【2017课标II,理3】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏B.3盏C.5盏D.9盏【答案】B【解析】试题分析:设塔的顶层共有灯x盏,则各层的灯数构成一个首项为x,公比为2的等比数列,结合等比数列的求和公式有:()712381 12x⨯-=-,解得3x=,即塔的顶层共有灯3盏,故选B。
专题02 函数—三年高考(2015-2017数学(文)真题分项版解析(原卷版)(批量下载)
精品“正版”资料系列,由本公司独创。
旨在将“人教版”、”苏教版“、”北师大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友。
本资源创作于2020年8月,是当前最新版本的教材资源。
包含本课对应内容,是您备课、上课、课后练习以及寒暑假预习的最佳选择。
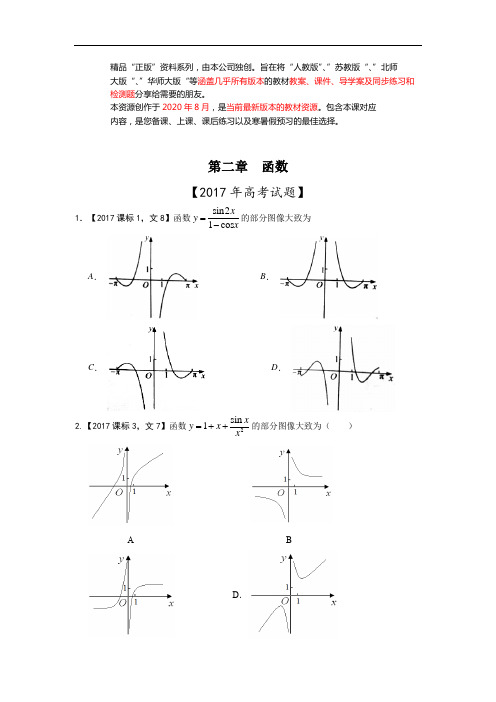
第二章 函数【2017年高考试题】1.【2017课标1,文8】函数sin21cos x y x=-的部分图像大致为 A . B .C .D .2.【2017课标3,文7】函数2sin 1x y x x =++的部分图像大致为( )A BD .C D3.【2017浙江,5】若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M – mA .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关4.【2017北京,文5】已知函数1()3()3x x f x =-,则()f x (A )是偶函数,且在R 上是增函数(B )是奇函数,且在R 上是增函数(C )是偶函数,且在R 上是减函数(D )是奇函数,且在R 上是增函数5.【2017北京,文8】根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N最接近的是 (参考数据:lg3≈0.48)(A )1033 (B )1053(C )1073 (D )10936.【2017山东,文9】设()()121,1x f x x x <<=-≥⎪⎩,若()()1f a f a =+,则1f a ⎛⎫= ⎪⎝⎭ A. 2 B. 4 C. 6 D. 87.【2017天津,文6】已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==,则,,a b c 的大小关系为 (A )a b c <<(B )b a c <<(C )c b a <<(D )c a b <<8.【2017课标II ,文8】函数2()ln(28)f x x x =-- 的单调递增区间是A.(,2)-∞-B. (,1)-∞-C. (1,)+∞D. (4,)+∞9.【2017课标1,文9】已知函数()ln ln(2)f x x x =+-,则A .()f x 在(0,2)单调递增B .()f x 在(0,2)单调递减C .y =()f x 的图像关于直线x =1对称D .y =()f x 的图像关于点(1,0)对称 10.【2017山东,文10】若函数()e x f x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是A . ()2x f x -= B. ()2f x x = C. ()3xf x -= D. ()cos f x x = 11.【2017天津,文8】已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+≥⎪⎩设a ∈R ,若关于x 的不等式()||2x f x a ≥+在R 上恒成立,则a 的取值范围是 (A )[2,2]-(B)[2]-(C)[2,-(D)[-12.【2017课标II ,文14】已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+,则(2)f = ________.13.【2017北京,文11】已知0x ≥,0y ≥,且x +y =1,则22x y +的取值范围是__________.14.【2017课标3,文16】设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是__________.15【2017山东,文14】已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当[3,0]x ∈- 时,()6x f x -=,则f (919)= .16.【2017江苏,11】已知函数31()2e ex x f x x x =-+-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,则实数a 的取值范围是 .17.【2017江苏,14】设()f x 是定义在R 且周期为1的函数,在区间[0,1)上,2,,(),,x x D f x x x D ⎧∈⎪=⎨∉⎪⎩其中集合1,*n D x x n n -⎧⎫==∈⎨⎬⎩⎭N ,则方程()lg 0f x x -=的解的个数是 . 【2016,2015,2014高考题】1. 【2016高考新课标1文数】若0a b >>,01c <<,则( )(A )log a c <log b c (B )log c a <log c b (C )a c <b c (D )c a >c b2. 【2014高考北京文第2题】下列函数中,定义域是R 且为增函数的是( )A.x y e -=B.3y x = C.ln y x = D.y x =3. 【2014高考北京文第8题】加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p 与加工时间t (单位:分钟)满足的函数关系2p at bt c =++(a 、b 、c 是常数),下图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为( )A.3.50分钟B.3.75分钟C.4.00分钟D.4.25分钟4. 【2014高考北京文第6题】已知函数()26log f x x x =-,在下列区间中,包含()f x 零点的区间是( )A.()0,1B.()1,2C.()2,4D.()4,+∞5. 【2015高考北京,文3】下列函数中为偶函数的是( )A .2sin y x x =B .2cos y x x =C .ln y x =D .2x y -=6. 【2014高考广东卷.文.5】下列函数为奇函数的是( )A .122x x - B .3sin x x C .2cos 1x + D .22x x +7. 【2016高考新课标1文数】函数22x y x e =-在[]2,2-的图像大致为( ) (A )(B )(C )(D )8. 【2015高考广东,文3】下列函数中,既不是奇函数,也不是偶函数的是( )A .2sin y x x =+B .2cos y x x =-C .122x xy =+D .sin 2y x x =+9. 【 2014湖南文4】下列函数中,既是偶函数又在区间(,0)-∞上单调递增的是( ) 21.()A f x x= 2.()1B f x x =+ 3.()C f x x = .()2x D f x -= 10. 【2016高考新课标2文数】下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是( )(A )y =x (B )y =lg x (C )y =2x (D )y= 11. 【2016高考新课标2文数】已知函数f (x )(x ∈R )满足f (x )=f (2-x ),若函数y =|x 2-2x -3| 与y =f (x ) 图像的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则1=mii x =∑( ) (A)0 (B)m (C) 2m (D) 4m12. 【2014山东.文3】 函数1log 1)(2-=x x f 的定义域为( )A. (0,2)B. (0,2]C. ),2(+∞D. [2,)+∞13. 【2014山东.文6】已知函数log ()(,a y x c a c =+为常数,其中0,1)a a >≠的图象如右图,则下列结论成立的是( )A.1,1a c >>B.1,01a c ><<C.01,1a c <<>D.01,01a c <<<<14. [2016高考新课标Ⅲ文数]已知4213332,3,25a b c ===,则( )(A) b a c << (B)a b c << (C) b c a << (D) c a b << 15. 【2016高考浙江文数】函数y =sin x 2的图象是( )16. 【2015高考山东,文2】设0.6 1.50.60.60.6 1.5a b c ===,,,则a b c ,,的大小关系是( )(A )a b c << (B )a cb << (C )b ac << (D )b c a << 17. 【2014山东.文5】 已知实数,x y 满足(01)x y aa a <<<,则下列关系式恒成立的是( )A.33x y >B.sin sin x y >C.22ln(1)ln(1)x y +>+D.221111x y >++ 18. 【2016高考浙江文数】已知a ,b >0,且a ≠1,b ≠1,若log >1a b ,则( )A.(1)(1)0a b --<B. (1)()0a a b -->C. (1)()0b b a --<D. (1)()0b b a -->19. 【2015高考山东,文8】若函数21()2x x f x a+=-是奇函数,则使3f x >()成立的x 的取值范围为( )(A )( ) (B)() (C )0,1() (D )1,+∞()20. 【2015高考山东,文10】设函数3,1()2,1x x b x f x x -<⎧=⎨≥⎩,若5(())46f f =,则b = ( ) (A )1 (B )78 (C )34 (D)1221. 【2016高考浙江文数】已知函数f (x )=x 2+bx ,则“b <0”是“f (f (x ))的最小值与f (x )的最小值相等”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件22. 【2015高考陕西,文4】设10()2,0x x f x x ⎧≥⎪=⎨<⎪⎩,则((2))f f -=( ) A .1- B .14 C .12 D .3223. 【2016高考浙江文数】已知函数()f x 满足:()f x x ≥且()2,x f x x ≥∈R .( )A.若()f a b ≤,则a b ≤B.若()2bf a ≤,则a b ≤C.若()f a b ≥,则a b ≥D.若()2b f a ≥,则a b ≥24. 【2014高考陕西版文第7题】下了函数中,满足“()()()f x y f x f y +=”的单调递增函数是( ) (A )()3f x x = (B )()3x f x = (C )()23f x x = (D )()12xf x ⎛⎫= ⎪⎝⎭ 25. 【2015高考陕西,文9】 设()sin f x x x =-,则()f x =( )A .既是奇函数又是减函数B .既是奇函数又是增函数C .是有零点的减函数D .是没有零点的奇函数26. 【2015高考陕西,文10】设()ln ,0f x x a b =<<,若p f =,()2a b q f +=,1(()())2r f a f b =+,则下列关系式中正确的是( ) A .q r p =< B .q r p => C .p r q =< D .p r q =>27. 【2016高考北京文数】已知(2,5)A ,(4,1)B ,若点(,)P x y 在线段AB 上,则2x y -的最大值为( )A.−1B.3C.7D.828. 【2016高考北京文数】下列函数中,在区间(1,1)- 上为减函数的是( ) A.11y x=- B.cos y x = C.ln(1)y x =+ D.2x y -= 29. 【2014四川,文7】已知,,,,则下列等式一定成立的是( )A 、B 、C 、D 、 0b >5log b a =lg b c =510d =d ac =a cd =c ad =d a c =+30. 【2015高考四川,文5】下列函数中,最小正周期为π的奇函数是( )(A )y =sin (2x +2π) (B )y =cos (2x +2π) (C )y =sin 2x +cos 2x (D )y =sinx +cosx31.【2016高考上海文科】设()f x 、()g x 、()h x 是定义域为R 的三个函数,对于命题:①若()()f x g x +、()()f x h x +、()()g x h x +均为增函数,则()f x 、()g x 、()h x 中至少有一个增函数;②若()()f x g x +、()()f x h x +、()()g x h x +均是以T 为周期的函数,则()f x 、()g x 、()h x 均是以T 为周期的函数,下列判断正确的是( )A 、①和②均为真命题B 、①和②均为假命题C 、①为真命题,②为假命题D 、①为假命题,②为真命题32. 【2015高考四川,文8】某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系kx b y e +=( 2.718...e =为自然对数的底数,,k b 为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是( )(A )16小时 (B )20小时 (C )24小时 (D )21小时33. 【2014全国1,文5】设函数)(),(x g x f 的定义域为R ,且)(x f 是奇函数,)(x g 是偶函数,则下列结论中正确的是( )A.)()(x g x f 是偶函数B. )(|)(|x g x f 是奇函数C. |)(|)(x g x f 是奇函数D. |)()(|x g x f 是奇函数34.【2015高考新课标1,文10】已知函数1222,1()log (1),1x x f x x x -⎧-≤=⎨-+>⎩ ,且()3f a =-,则(6)f a -=( )(A )74- (B )54- (C )34- (D )14- 35. 【2016高考山东文数】若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是( )(A )sin y x = (B )ln y x = (C )e x y = (D )3y x =36. 【2015高考新课标1,文12】设函数()y f x =的图像与2x a y +=的图像关于直线y x=-对称,且(2)(4)1f f -+-=,则a =( )(A ) 1- (B )1 (C )2 (D )437. 【2014年.浙江卷.文7】已知函数c bx ax x x f +++=23)(,且3)3()2()1(0≤-=-=-<f f f ,则( )A.3≤cB.63≤<cC. 96≤<cD.9>c38. 【2016高考山东文数】已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x —12).则f(6)= ( ) (A )-2 (B )-1(C )0 (D )239. 【2015高考浙江,文5】函数()1cos f x x x x ⎛⎫=-⎪⎝⎭(x ππ-≤≤且0x ≠)的图象可能为( )A .B .C .D .40. 【2014年.浙江卷.文8】在同一坐标系中,函数)0()(>=x x x f a ,x x g a log )(=的图象可能是( )41. 【2016高考四川文科】某公司为激励创新,计划逐年加大研发奖金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( )(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30)(A)2018年 (B) 2019年 (C)2020年 (D)2021年42. 【2014高考重庆文第4题】下列函数为偶函数的是( ).()1A f x x =- 2.()B f x x x =+ .()22x x C f x -=-.()22x x D f x -=+43. 【2014高考重庆文第10题】已知函数13,(1,0](),()()1,1]1,(0,1]x f x g x f x mx m x x x ⎧-∈-⎪==---+⎨⎪∈⎩且在(内有且仅有两个不同的零点,则实数m 的取值范围是( ) A.91(,2](0,]42-- B.111(,2](0,]42-- C.92(,2](0,]43-- D.112(,2](0,]43-- 44. 【2015高考重庆,文3】函数22(x)log (x 2x 3)f 的定义域是( )(A) [3,1] (B) (3,1)(C) (,3][1,)-∞-+∞ (D) (,3)(1,)-∞-+∞ 45. 【2014,安徽文5】设 1.1 3.13log 7,2,0.8a b c ===则( )A .c a b <<B .b a c <<C .a bc << D .b c a <<46. 【2015高考安徽,文4】下列函数中,既是偶函数又存在零点的是( ) (A )y =lnx (B )21y x =+ (C )y =sinx (D )y =cosx47. 【2015高考安徽,文10】函数()32f x ax bx cx d =+++的图像如图所示,则下列结论成立的是( )(A )a >0,b <0,c >0,d >0 (B )a >0,b <0,c <0,d >0 (C )a <0,b <0,c <0,d >0 (D )a >0,b >0,c >0,d <048. 【2014,安徽文9】若函数()12f x x x a =+++的最小值3,则实数a 的值为 ( )A .5或8B .1-或5C . 1-或4-D .4-或849.【2014天津,文4】设,,log ,log 2212-===πππc b a 则( )A.c b a >>B.c a b >>C.b c a >>D.a b c >> 50. 【2015高考天津,文8】已知函数22||,2()(2),2x xf x x x ,函数()3(2)g x f x ,则函数y()()f x g x 的零点的个数为( )(A) 2 (B) 3 (C)4 (D)551. 【2015高考天津,文7】 已知定义在R 上的函数||()21()xm f x m 为实数为偶函数,记0.5(log 3),af 2b (log 5),c(2)f f m ,则,,a b c ,的大小关系为( )(A) b c a(B) b c a (C) b a c (D) b c a52.【2014年普通高等学校招生全国统一考试湖北卷9】已知)(x f 是定义在R 上的奇函数,当0≥x 时,x x x f 3)(2-=,则函数3)()(+-=x x f x g 的零点的集合为( )A.{1,3}B.{3,1,1,3}--C.{2D.{2-53. 【2015高考湖北,文6】函数256()lg 3x x f x x -+=-的定义域为( )A .(2,3)B .(2,4]C .(2,3)(3,4]D .(1,3)(3,6]-54. 【2015高考湖北,文7】设x ∈R ,定义符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩则( ) A .|||sgn |x x x = B .||sgn ||x x x = C .||||sgn x x x =D .||sgn x x x =55. 【2014福建,文8】若函数()log 0,1a y x a a =>≠且的图象如右图所示,则下列函数正确的是 (56. 【2014福建,文9】要制作一个容积为34m ,高为1m 的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是 ( ).80.120.160.240A B C D 元元元元57. 【2015高考福建,文3】下列函数为奇函数的是( )A.y = B .x y e = C .cos y x = D .x x y e e -=-58. 【2014辽宁文3】已知132a -=,21211log ,log 33b c ==,则( ) A .a b c >> B .a c b >> C .c a b >> D .c b a >>59. (2014课标全国Ⅰ,文5)设函数f (x ),g (x )的定义域都为R ,且f (x )是奇函数,g (x )是偶函数,则下列结论中正确的是( ).A .f (x )g (x )是偶函数B .|f (x )|g (x )是奇函数C .f (x )|g (x )|是奇函数D .|f (x )g (x )|是奇函数60. 【2015新课标2文11】如图,长方形的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠= ,将动点P 到A ,B 两点距离之和表示为x 的函数()f x ,则的图像大致为( )A .B .C .D .61. 【2015新课标2文12】设函数21()ln(1||)1f x x x=+-+,则使得()(21)f x f x >-成立的x 的取值范围是( ) A .1,13⎛⎫ ⎪⎝⎭ B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C .11,33⎛⎫-⎪⎝⎭ D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭62. 【2014辽宁文10】已知()f x 为偶函数,当0x ≥时,1cos ,[0,]2()121,(,)2x x f x x x π⎧∈⎪⎪=⎨⎪-∈+∞⎪⎩,则不等式1(1)2f x -≤的解集为( ) A .1247[,][,]4334 B .3112[,][,]4343-- C .1347[,][,]3434 D .3113[,][,]4334--63. 【2014辽宁文11】 将函数3sin(2)3y x π=+的图象向右平移2π个单位长度,所得图象对应的函数( ) A .在区间7[,]1212ππ上单调递减B .在区间7[,]1212ππ上单调递增C .在区间[,]63ππ-上单调递减 D .在区间[,]63ππ-上单调递增 二、填空题1. 【2016高考四川文科】已知函数()f x 是定义在R 上的周期为2的奇函数,当0<x <1时,()4xf x =,则5()(1)2f f -+= .2. 【2015高考北京,文10】32-,123,2log 5三个数中最大数的是 . 3. 【2015高考湖南,文14】若函数()|22|xf x b =--有两个零点,则实数b 的取值范围是_____.4. 【 2014湖南文15】若()()ax ex f x++=1ln 3是偶函数,则=a ____________.5. 【2014高考陕西版文第12题】已知42a=,lg x a =,则x =________. 6. 【2014高考陕西版文第14题】已知0,1)(≥+=x xxx f ,若++∈==N n x f f x f x f x f n n )),(()(),()(11,则)(2014x f 的表达式为________.7. 【2014全国2,文15】偶函数)(x f y =的图像关于直线2=x 对称,3)3(=f ,则)1(-f =________.8. 【2016高考上海文科】已知点(3,9)在函数xa x f +=1)(的图像上,则________)()(1=-x f x f 的反函数.9. 【2014四川,文13】设是定义在R 上的周期为2的函数,当时,()f x [1,1)x ∈-,则 . 10. 【2015高考四川,文12】lg 0.01+log 216=_____________.11. 【2015高考四川,文15】已知函数f (x )=2x ,g (x )=x 2+ax (其中a ∈R ).对于不相等的实数x 1,x 2,设m =1212()()f x f x x x --,n =1212()()g x g x x x --,现有如下命题:①对于任意不相等的实数x 1,x 2,都有m >0;②对于任意的a 及任意不相等的实数x 1,x 2,都有n >0; ③对于任意的a ,存在不相等的实数x 1,x 2,使得m =n ; ④对于任意的a ,存在不相等的实数x 1,x 2,使得m =-n . 其中真命题有___________________(写出所有真命题的序号).12. 【2014年.浙江卷.文15】设函数⎪⎩⎪⎨⎧>-≤++=0,0,22)(22x x x x x x f ,若2))((=a f f ,则=a .13. 【2016高考浙江文数】设函数f (x )=x 3+3x 2+1.已知a ≠0,且f (x )–f (a )=(x –b )(x –a )2,x ∈R ,则实数a =_____,b =______.14. 【2015高考浙江,文9】计算:2log 2= ,24log 3log 32+= . 15. 【2015高考浙江,文12】已知函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩,则()2f f -=⎡⎤⎣⎦ ,()f x 的最小值是 .16. 【2014,安徽文11】34331654+log log 8145-⎛⎫+=⎪⎝⎭________. 17. 【2016高考山东文数】已知函数2||,()24,x x m f x x mx m x m ≤⎧=⎨-+>⎩其中0m >,若存在实数b ,使得关于x 的方程f (x )=b 有三个不同的根,则m 的取值范围是________________. 18. 【2014,安徽文14】若函数()()R x x f ∈是周期为4的奇函数,且在[]2,0上的解析式为()⎩⎨⎧≤<≤≤-=21,sin 10),1(x x x x x x f π,则_______641429=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛f f .242,10,(),01,x x f x x x ⎧-+-≤<=⎨≤<⎩3()2f =19. 【2016高考北京文数】函数()(2)1xf x x x =≥-的最大值为_________. 20. 【2015高考安徽,文14】在平面直角坐标系xOy 中,若直线a y 2=与函数1||--=a x y 的图像只有一个交点,则a 的值为 . 21. 【2015高考安徽,文11】=-+-1)21(2lg 225lg. 22. 【2014天津,文12】函数2()lg f x x =的单调递减区间是________.23. 【2014天津,文14】已知函数()⎪⎩⎪⎨⎧>-≤++=0,220,452x x x x x x f 若函数x a x f y -=)(恰有4个零点,则实数a 的取值范围为_______24. 【2014年普通高等学校招生全国统一考试湖北卷15】如图所示,函数)(x f y =的图象由两条射线和三条线段组成.若R ∈∀x ,)1()(->x f x f ,则正实数a 的取值范围是 .25. 【2015高考湖北,文13】函数2π()2sin sin()2f x x x x =+-的零点个数为_________.26. 【2014上海,文3】设常数a R ∈,函数2()1f x x x a =-+-,若(2)1f =,则(1)f = .27. 【2014上海,文9】设,0,()1,0,x a x f x x x x -+≤⎧⎪=⎨+>⎪⎩若(0)f 是()f x 的最小值,则a 的取值范围是 .28. 【2014上海,文11】若2132)(x x x f -=,则满足0)(<x f 的x 取值范围是 .29. 【2016高考天津文数】已知函数2(43)3,0()(01)log (1)1,0a x a x a x f x a a x x ⎧+-+<⎪=>≠⎨++≥⎪⎩且在R上单调递减,且关于x 的方程|()|23xf x =-恰有两个不相等的实数解,则a 的取值范围是_________.30. 【2014福建,文15】(函数()⎩⎨⎧>+-≤-=0,ln 620,22x x x x x x f 的零点个数是__________.31. 【2015高考福建,文15】若函数()2()x af x a R -=∈满足(1)(1)f x f x +=-,且()f x 在[,)m +∞单调递增,则实数m 的最小值等于_______.32. 【2015新课标2文13】已知函数()32f x ax x =-的图像过点(-1,4),则a = .33. (2014课标全国Ⅰ,文15)设函数()113e ,1,,1,x x f x x x -⎧<⎪=⎨⎪≥⎩则使得f (x )≤2成立的x 的取值范围是__________.34. 【2014辽宁文16】对于0c >,当非零实数a ,b 满足22420a ab b c -+-=,且使|2|a b +最大时,124a b c++的最小值为 .三、解答题1.【2015高考湖北,文17】a 为实数,函数2()||f x x ax =-在区间[0,1]上的最大值记为()g a . 当a =_________时,()g a 的值最小.2. 【2014上海,文20】(本题满分14分)本题有2个小题,第一小题满分6分,第二小题满分1分.设常数0≥a ,函数aa x f x x -+=22)((1)若a =4,求函数)(x f y =的反函数)(1x fy -=;(2)根据a 的不同取值,讨论函数)(x f y =的奇偶性,并说明理由.3. 【2016高考上海文科】(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分. 已知a ∈R ,函数()f x =21log ()a x+.(1)当 1a =时,解不等式()f x >1;(2)若关于x 的方程()f x +22log ()x =0的解集中恰有一个元素,求a 的值;(3)设a >0,若对任意t ∈1[,1]2,函数()f x 在区间[,1]t t +上的最大值与最小值的差不超过1,求a 的取值范围.专题3 导数的几何意义与运算1.【2015高考北京,文8】某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.注:“累计里程“指汽车从出厂开始累计行驶的路程在这段时间内,该车每100千米平均耗油量为( )A .6升B .8升C .10升D .12升 2.【2014高考陕西版文第10题】如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连续(相切),已知环湖弯曲路段为某三次函数图像的一部分,则该函数的解析式为( )(A )321122y x x x =-- (B )3211322y x x x =+- (C )314y x x =- (D )3211242y x x x =+-3.【2016高考四川文科】设直线l 1,l 2分别是函数f (x )= ln ,01,ln ,1,x x x x -<<⎧⎨>⎩图象上点P 1,P 2处的切线,l 1与l 2垂直相交于点P ,且l 1,l 2分别与y 轴相交于点A ,B ,则△P AB 的面积的取值范围是( )(A)(0,1) (B) (0,2) (C) (0,+∞) (D) (1,+ ∞)4.【2017课标1,文14】曲线21y x x=+在点(1,2)处的切线方程为______________. 5.【2017天津,文10】已知a ∈R ,设函数()ln f x ax x =-的图象在点(1,(1)f )处的切线为l ,则l 在y 轴上的截距为 .6.【2014高考广东卷.文.11】曲线53xy e =-+在点()0,2-处的切线方程为________.7. [2016高考新课标Ⅲ文数]已知()f x 为偶函数,当0x ≤ 时,1()x f x ex --=-,则曲线()y f x =在(1,2)处的切线方程式_____________________________.9.【2015高考新课标1,文14】已知函数()31f x ax x =++的图像在点()()1,1f 的处的切线过点()2,7,则 a = .10. 【2014,安徽文15】若直线l 与曲线C 满足下列两个条件:)(i 直线l 在点()00,y x P 处与曲线C 相切;)(ii 曲线C 在P 附近位于直线l 的两侧,则称直线l 在点P 处“切过”曲线C ,下列命题正确的是_________(写出所有正确命题的编号) ①直线0:=y l 在点()0,0P 处“切过”曲线C :3yx =②直线1:-=x l 在点()0,1-P 处“切过”曲线C :2)1(+=x y ③直线x y l =:在点()0,0P 处“切过”曲线C :x y sin = ④直线x y l =:在点()0,0P 处“切过”曲线C :x y tan = ⑤直线1:-=x y l 在点()0,1P 处“切过”曲线C :x y ln =11. 【2015高考天津,文11】已知函数()()ln ,0,f x ax x x =∈+∞ ,其中a 为实数,()f x '为()f x 的导函数,若()13f '= ,则a 的值为 .12. 【2015新课标2文16】已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a = .13.【2017山东,文20】(本小题满分13分)已知函数()3211,32f x x ax a =-∈R ., (I)当a =2时,求曲线()y f x =在点()()3,3f 处的切线方程;(II)设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值.14.【2017北京,文20】已知函数()e cos xf x x x =-. (Ⅰ)求曲线()y f x =在点(0,(0))f 处的切线方程; (Ⅱ)求函数()f x 在区间π[0,]2上的最大值和最小值.15.【2016高考新课标2文数】已知函数()(1)ln (1)f x x x a x =+--.(I )当4a =时,求曲线()y f x =在()1,(1)f 处的切线方程; (Ⅱ)若当()1,x ∈+∞时,()0f x >,求a 的取值范围.16.【2015高考山东,文20】设函数. 已知曲线 在点(1,(1))f 处的切线与直线平行.(Ⅰ)求a 的值;(Ⅱ)是否存在自然数k ,使得方程()()f x g x =在(,1)k k +内存在唯一的根?如果存在,求出k ;如果不存在,请说明理由;(Ⅲ)设函数()min{(),()}m x f x g x =({},min p q 表示,,p q 中的较小值),求()m x 的最大值.17.【2014全国2,文21】(本小题满分12分) 已知函数32()32f x x x ax =-++,曲线()y f x =在点(0,2)处的切线与x 轴交点的横坐标为2-. (Ⅰ)求a ; (Ⅱ)证明:当1k<时,曲线()y f x =与直线2y kx =-只有一个交点.18.【2016高考北京文数】(本小题13分) 设函数()32.f x x ax bx c =+++(I )求曲线().y f x =在点()()0,0f 处的切线方程;(II )设4a b ==,若函数()f x 有三个不同零点,求c 的取值范围; (III )求证:230a b ->是().f x 有三个不同零点的必要而不充分条件.19.【2014高考重庆文第19题】(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分) 已知函数23ln 4)(--+=x x a x x f ,其中R a ∈,且曲线)(x f y =在点))1(,1(f 处的切线垂直于x y 21=. (Ⅰ)求a 的值;(Ⅱ)求函数)(x f 的单调区间与极值.20.【2015高考天津,文20】(本小题满分14分)已知函数4()4,,f x x x x R (I )求()f x 的单调区间;(II )设曲线()y f x 与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为()yg x ,求证:对于任意的正实数x ,都有()()f x g x ; (III )若方程()=()f x a a 为实数有两个正实数根12x x ,,且12x x ,求证:1321-43a x x。
等差数列和等比数列-2017年高考数学(文)母题题源系列(新课标2专版)含解析

【母题原题1】【2017全国Ⅱ,文17】已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,11221,1,2a b a b =-=+=.(1)若335a b +=,求{}n b 的通项公式;(2)若321T=,求3S .【答案】(1)b n =2n−1;(2)当q =−5 时,S 3=21.当q =4时,S 3=−6.试题解析:设{a n }的公差为d ,{b n }的公比为q ,则a n =−1+(n −1)d ,b n =q n−1.由a 2+b 2=2得d +q =3.①(1)由a 3+b 3=5得2d +q 2=6.②联立①和②解得{d =3,q =0(舍去),{d =1,q =2.因此{b n }的通项公式为b n =2n−1. (2)由b 1=1,T 3=21得q 2+q −20=0. 解得q =−5,q =4.当q =−5时,由①得d =8,则S 3=21. 当q =4时,由①得d =−1,则S 3=−6.【考点】等差、等比数列通项与求和【名师点睛】在解决等差、等比数列的运算问题时,有两种处理思路:一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法. 【母题原题2】【2016全国Ⅱ,文17】等差数列{na }中,34574,6aa a a +=+=.(Ⅰ)求{na }的通项公式;(Ⅱ) 设[]nn ba =,求数列{}nb 的前10项和,其中[]x 表示不超过x的最大整数,如=0,=2. 【答案】(Ⅰ)235n n a +=;(Ⅱ)24. 【解析】试题分析:(Ⅰ) 根据等差数列的通项公式及已知条件求1a ,d,从而求得na ;(Ⅱ)由(Ⅰ)求nb ,再求数列{}n b 的前10项和.(Ⅱ)由(Ⅰ)知235nn b +⎡⎤=⎢⎥⎣⎦. 当n =1,2,3时,2312,15n n b +≤<=; 当n =4,5时,2323,25n n b +≤<=; 当n =6,7,8时,2334,35n n b +≤<=;当n=9,10时,2345,45n n b +≤<=. 所以数列{}n b 的前10项和为1322334224⨯+⨯+⨯+⨯=. 【考点】等差数列的通项公式,数列的求和【名师点睛】求解本题时常出现以下错误:对“[]x 表示不超过x 的最大整数”理解出错.【母题原题3】【2015全国Ⅱ,文5】设nS 是等差数列{}na 的前n项和,若1353a aa ++=,则5S =( )A .B .C .D .11 【答案】A【考点定位】本题主要考查等差数列的性质及前n 项和公式的应用.【名师点睛】本题解答过程中用到了的等差数列的一个基本性质即等差中项的性质,利用此性质可得1532.a aa +=高考中数列客观题大多具有小、巧、活的特点,在解答时要注意数列相关性质的应用,尽量避免小题大做.【2015全国Ⅱ,文9】已知等比数列{}na 满足114a=,()35441a a a =-,则2a =( )A.2B.11C.21D.8【答案】C 【解析】试题分析:由题意可得()235444412a a a a a ==-⇒=,所以34182a q q a ==⇒= ,故2112a a q ==,选C .【考点定位】本题主要考查等比数列性质及基本运算. 【名师点睛】解决本题的关键是利用等比数列性质211n n n aaa -+=得到一个关于4a 的一元二次方程,再通过解方程求4a 的值,我们知道,等差、等比数列各有五个基本量,两组基本公式,而这两组公式可看作多元方程,利用这些方程可将等差、等比数列中的运算问题转化解关于基本量的方程(组),因此可以说数列中的绝大部分运算题可看作方程应用题,所以用方程思想解决数列问题是一种行之有效的方法.【命题意图】考查特殊数列的通项及前n 项和或通项与前n 项和nS 间的递推关系,通过转化为等差数列或等比数列,考查数列运算及转化能力.【命题规律】由递推关系求数列通项公式或特定项问题,有时以小题形式来考,主要以考查,nna S 间的关系为主,通过转化为特殊数列求解;以解答题形式考查,会多步设问,通过提示或其他方式构造特殊数列求解.【答题模板】作答数列问题,一般四个步骤:1、判断所求解数列问题是否为等差等比数列问题;2、利用等差、等比数列通项公式及前n 项和公式列出等式或方程;3、利用等差、等比定义将非等差、等比数列经过变形、构造等方法转化为等差、等比数列问题;4、运用特殊方法求数列的前n 项和,如错位相减法,分组求和或裂项求和法等. 【方法总结】关于通项公式与前n 项和nS 间的递推关系问题,可以转化为项na 与1n a 的递推式,进而求na ;或者转化为nS 与1n S 的递推式,先求nS ,再求na ,其中转化关键为11,1,, 2.nn n S n aS S n -=⎧=⎨-≥⎩,通过转化为特殊数列或易求通项公式的递推式求解. (一)主要知识:有关等差、等比数列的结论 1.(1)等差数列证明方法:1nn a a d 或112n n n a a a ;(2)等比数列的证明方法:)0(1≠=-q q a a n n 或112+-=n n n a a a . 2. 等差数列的通项公式:d n a an)1(1-+=,d m n a a m n )(-+=)1(11≠--=n n a a d n 或mn a a d m n --=.3. 等差数列的前项和公式(由倒序相加法推得):2)(1n n a a n s +=,d n n na sn2)1(1-+=. 4.数列n a 是等差数列na pn q (,p q 为常数)3.数列na 是等差数列2nS an bn (,a b 为常数)6.等差数列{}na 的任意连续m项的和构成的数列232,,,m m m m m S S S S S --仍为等差数列.7.等差数列{}na 中,若m n p q +=+,则q p n ma a a a +=+8.等比数列的通项公式:11-=n nq a am n m n q a a -=(m n >). 9.当1≠q 时:qq a s n n --=1)1(1或qqa a s n n --=11当1=q 时:1na sn=(有关等比数列的求和问题,当不能确定“1≠q ”时,应分1,1≠=q q 来讨论). 10.等比数列{}na 中,若m n p q +=+,则mn p q aa a a ⋅=⋅11.等比数列{a n }的任意连续m 项的和构成的数列232,,,m m m m m S S S S S --仍为等比数列.12.两个等差数列{}na 与{}nb 的和差的数列{}nn a b ±仍为等差数列.13.两个等比数列{}na 与{}nb 的积、商、倒数的数列{}n nab ⋅、⎭⎬⎫⎩⎨⎧n n b a 、⎭⎬⎫⎩⎨⎧n b 1仍为等比数列. (二)主要方法:1.解决等差数列和等比数列的问题时,通常考虑两类方法:①基本量法:即运用条件转化为关于1a 和()d q 的方程;②巧妙运用等差数列和等比数列的性质,一般地运用性质可以化繁为简,减少运算量.2.深刻领会两类数列的性质,弄清通项和前n 项和公式的内在联系是解题的关键.1.【2017安徽阜阳二模】等比数列{}n a 中, 132410,30a a a a +=+=,则数列{}n a 前项和5S = ( )A . 81B . 90C . 100D . 121【答案】D2.【2017江西九江三模】已知数列{}n a 为等比数列,若2102,8a a ==,则6a =()A . 4±B . 4-C .D .【答案】C【解析】由题意可得:844106284,2,224a q q a a q a ==∴===⨯=.本题选择C 选项.3.【2017广西5月考前联考】已知等差数列{}n a 的前项和为nS ,8430S S =-≠,则412S S 的值为( )A .13-B . 112- C .112D .13【答案】B 【解析】因为844444216S S S d S d =++⨯=+,即4441632165d S S d S -=+⇒=-,所以12844192483485d S S S d S d =++⨯=+=,则4121651519212Sd S d =-⨯=-,应选答案B .4.【2017江西九江三模】已知数列{}n a 的前项和为n S ,且满足111,2n n n a a a S +=⋅=,设213nn n a a b -=,则数列{}n b 的前项和为__________. 【答案】113nn +-数列{}n b 的前n 项和为:0112112231113333333n n n n nn n T -++⎛⎫⎛⎫⎛⎫=-+-++-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.点睛:使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源与目的.5.【2017河北唐山三模】{}n a 是公差不为0的等差数列, {}n b 是公比为正数的等比数列, 111a b ==, 43a b =,84a b =,则数列{}n n a b 的前项和等于__________.【答案】()121n n -+所以12212nn n S n --=-⋅-,整理得: ()121n n S n =-⋅-. 方法点睛:用错位相减法求和时,要注意以下几个问题:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“nS ”与“nqS ”的表达式时应特别注意将两式“错项对齐”,以便下一步准确写出“nn SqS -”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.6.【2017广东佛山二模】已知{}n a 是等差数列, {}n b 是各项均为正数的等比数列,且111b a==, 34b a =, 12334b b b a a ++=+.(Ⅰ)求数列{}n a , {}n b 的通项公式; (Ⅱ)设nn n ca b =,求数列{}n c 的前项和n T .【答案】(Ⅰ)nan =, 12n n b -=;(Ⅱ)()121n n T n =-⋅+.【解析】试题分析:(1)根据条件列出关于公差与公比的方程组,解方程组可得1d =, 2q =,再代入等差与等比数列通项公式,(2)利用错位相减法求和,注意相减时项的符号变化,中间部分利用等比数列求和时注意项数,最后要除以1q - 试题解析:(Ⅰ)设数列{}n a 的公差为d , {}n b 的公比为,依题意得2213{125d q q q d+=++=+解得1d =, 2q =,所以()11n a n n =+-=,11122n n n b --=⨯=点睛:用错位相减法求和应注意的问题(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“nS ”与“nqS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“nn SqS -”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.7.【2017重庆二诊】已知等差数列{}n a 的前项和为nS ,49a =,315S =.(1)求nS ;(2)设数列1n S ⎧⎫⎨⎬⎩⎭的前项和为nT ,证明:34n T <. 【答案】(Ⅰ)()2n S n n =+; (Ⅱ)见解析.【解析】(1)由已知,根据等差数列的通项公式()11n a a n d =+-、前项公式()112nn n Sna d-=+,建立关于,a d 的方程,进行求解即可;(2)由(1)求出数列1n S ⎧⎫⎨⎬⎩⎭的通项公式,根据其表达式的特点,利用裂项求和的方法求出nT ,由数列极限,从而不等式可得证.试题解析:(Ⅰ)3223155S a a ==⇒=, 4222a a d -∴==, 21n a n ∴=+, ()32122n n S n n n ++=⋅=+; (Ⅱ)()111111111111132422324352nTn n n n ⎛⎫=+++=-+-+-++- ⎪⨯⨯++⎝⎭11113122+124n n ⎛⎫=+--< ⎪+⎝⎭.8.【2017安徽马鞍山二模】已知数列{}n a 是公差不为0的等差数列, 23a =,且3a , 5a , 8a 成等比数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设cos2nnn a ba π=,求数列{}nb 的前2017项和.【答案】(Ⅰ)1n a n =+(Ⅱ)1010.-【解析】试题分析:(Ⅰ)等差数列{}n a 的公差为d ,根据提议列出关于首项1a 和公差d 的方程组,解方程组即可得到结果;(Ⅱ) 根据数列{}n b 每相邻四项的和为常数,可得数列{}n b 的前2017项和.9.【2017河北唐山二模】数列{}n a 的前项和为nS ,()21n n n S a =-,且11a=.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)若nn bna =,求数列{}n b 的前项和n T .【答案】(Ⅰ)112n n a -⎛⎫= ⎪⎝⎭;(Ⅱ)1242nn n T-+=-. 【解析】试题分析:(Ⅰ)对已知等式()21nnn S a =-利用1n n nS S a --=化简整理得()1122n n a n a -=≥,进而可推断出数列{}n a 是一个以1为首项, 12为公比的等比数列,根据等比数列的通项公式求得答案;(Ⅱ)利用错位相减法求结果. 试题解析:(Ⅰ)由()21nnn S a =-,可得()11121n n n S a ---=-(2n ≥),两式相减,得()()1112121n n nn n n SS a a ----=---,()()112221nn n n a a ---=-,即()1122n n a n a -=≥, 故{}n a 是一个以1为首项, 12为公比的等比数列,所以112n n a -⎛⎫= ⎪⎝⎭.点睛:本题主要考查了等比数列的概念,以及数列的求和,属于高考中常考知识点,难度不大;常见的数列求和的方法有公式法即等差等比数列求和公式,分组求和类似于n n n c a b =+,其中{}n a 和{}nb 分别为特殊数列,裂项相消法类似于()11n a n n =+,错位相减法类似于n n n c a b =⋅,其中{}na 为等差数列,{}n b 为等比数列等.10.【2017福建三明5月质检】已知数列{}n a 的前项和为nS ,且22nn Sa =-.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设1nnn ba +=,求数列{}n b 前项和n T . 【答案】(I )2n n a =;(II )()1332nn T n ⎛⎫=-+ ⎪⎝⎭.试题解析:(Ⅰ) 22n n S a =-,当1n =时, 1122a a =-,则12a =, 当2n ≥时,22n n S a =-, 1122n n S a --=-,两式相减,得122nn n a a a -=-,所以12n n a a -=.所以{}n a 是以首项为2,公比为2的等比数列,所以2n na=.(Ⅱ)因为()11122nn n n b n +⎛⎫==+ ⎪⎝⎭,()23111123412222nn T n ⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+++⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,()234111111234122222n n T n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+++⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,两式相减,即得()123111111121222222n n n T n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⨯++++-+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,11211112222n T ⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()311111222nn n +⎛⎫⎛⎫⎛⎫++-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,()1111221111122212nn n T n +⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=+-+ ⎪⎝⎭-,()11111112222nn n T n +⎛⎫⎛⎫=+--+ ⎪ ⎪⎝⎭⎝⎭,所以()1332nn T n ⎛⎫=-+ ⎪⎝⎭.。
三年高考2015_2017高考数学试题分项版解析专题13数列小题理20171102342

专题13数列小题1.【2017课标1,理4】记S为等差数列{a}的前项和.若a4a524,n n S648,则{a}n的公差为A.1 B.2 C.4 D.8【答案】C【解析】试题分析:设公差为d,a4a5a13d a14d 2a1 7d 24,2a 7d 2465S6a d6a15d48,,联立161126a15d481解得d 4,故选C.6(a a)秒杀解析:因为S 163(a a)48,即6342a a ,则3416(a a)(a a)24168,即5328a a d ,解得d 4,故选C. 4534【考点】等差数列的基本量求解【名师点睛】求解等差数列基本量问题时,要多多使用等差数列的性质,如{a}为等差数列,n若m n p q,则a a a a.m n p q2.【2017课标3,理9】等差数列a的首项为1,公差不为0.若a2,a3,a6成等比数列,n则a前6项的和为nA.24B.3C.3 D.8【答案】A【解析】故选A.【考点】等差数列求和公式;等差数列基本量的计算【名师点睛】(1)等差数列的通项公式及前n项和公式,共涉及五个量a1,a n,d,n,S n,知其中三个就能求另外两个,体现了用方程的思想解决问题.(2)数列的通项公式和前n项和公式1在解题中起到变量代换作用,而a1和d是等差数列的两个基本量,用它们表示已知和未知是常用方法.3.【2017课标II,理3】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏B.3盏C.5盏D.9盏【答案】B【解析】试题分析:设塔的顶层共有灯x盏,则各层的灯数构成一个首项为x,公比为2的等比数列,结合等比数列的求和公式有:x 12712381,解得x 3,即塔的顶层共有灯3盏,故选B。
2015《数列》高考真题总结及答案

2015《数列》高考真题总结1.(2015·新课标I 卷13)在数列{a n }中,a 1=2,a n +1=2a n ,S n 为{a n }的前n 项和.若S n =126,则n =________.2.(2015·浙江卷10)已知{a n }是等差数列,公差d 不为零.若a 2,a 3,a 7成等比数列,且2a 1+a 2=1,则a 1=__________________,d =__________________.3.(2015·安徽卷13)已知数列{a n }中,a 1=1,a n =a n -1+12(n ≥2),则数列{a n }的前9项和等于________.4.(2015·新课标I 卷7)已知{a n }是公差为1的等差数列,S n 为{a n }的前n 项和,若S 8=4S 4,则a 10=( ) A.172 B.192C .10 D .12 5.(2015·新课标Ⅱ卷5)设S n 是等差数列{a n }的前n 项和,若a 1+a 3+a 5=3,则S 5=( )A .5B .7C .9D .116.(2015·北京卷16)已知等差数列{a n }满足a 1+a 2=10,a 4-a 3=2.(1)求{a n }的通项公式;(2)设等比数列{b n }满足b 2=a 3,b 3=a 7,问:b 6与数列{a n }的第几项相等?7.(2015四川文科16)设数列{a n }的前n 项和S n 满足S n =2a n -a 1,且a 1,a 2+1,a 3成等差数列.(1)求数列{a n }的通项公式.(2)设数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为T n ,求T n .8.(2015·重庆卷16)已知等差数列{a n }满足a 3=2,前3项和S 3=92.(1)求{a n }的通项公式;(2)设等比数列{b n }满足b 1=a 1,b 4=a 15,求{b n }的前n 项和T n .9.(2015·浙江卷17)已知数列{a n }和{b n }满足a 1=2,b 1=1,a n +1=2a n (n∈N *),b 1+12b 2+13b 3+…+1n b n =b n +1-1(n ∈N *).(1)求a n 与b n ;(2)记数列{a n b n }的前n 项和为T n ,求T n .10.(2015·福建卷17)等差数列{a n }中,a 2=4,a 4+a 7=15.(1)求数列{a n }的通项公式;(2)设b n =2a n -2+n ,求b 1+b 2+b 3+…+b 10的值.11.(2015·安徽卷18)已知数列{a n }是递增的等比数列,且a 1+a 4=9,a 2a 3=8.(1)求数列{a n }的通项公式;(2)设S n 为数列{a n }的前n 项和,b n =a n +1S n S n +1,求数列{b n }的前n 项和T n .12.(2015·天津卷18)已知{a n }是各项均为正数的等比数列,{b n }是等差数列,且a 1=b 1=1,b 2+b 3=2a 3,a 5-3b 2=7.(1)求{a n }和{b n }的通项公式;(2)设c n =a n b n ,n ∈N *,求数列{c n }的前n 项和.13.(2015·广东卷19)设数列{a n }的前n 项和为S n ,n ∈N *.已知a 1=1,a 2=32,a 3=54,且当n ≥2时,4S n +2+5S n =8S n +1+S n -1.(1)求a 4的值;(2)证明:⎩⎨⎧⎭⎬⎫a n +1-12a n 为等比数列;(3)求数列{a n }的通项公式. 14.(2015·湖北卷19)设等差数列{a n }的公差为d ,前n 项和为S n ,等比数列{b n }的公比为q .已知b 1=a 1,b 2=2,q =d ,S 10=100.(1)求数列{a n },{b n }的通项公式;(2)当d >1时,记c n =a nb n,求数列{c n }的前n 项和T n .15.(2015·湖南卷19)设数列{a n }的前n 项和为S n .已知a 1=1,a 2=2,且a n +2=3S n -S n +1+3,n ∈N *.(1)证明:a n +2=3a n ; (2)求S n .16.(2015·山东卷19)已知数列{a n }是首项为正数的等差数列,数列{1a n ·a n +1}的前n 项和为n 2n +1. (1)求数列{a n }的通项公式; (2)设b n =(a n +1)·2a n ,求数列{b n }的前n 项和T n .17.(2015·新课标Ⅱ卷9)已知等比数列{a n }满足a 1=14,a 3a 5=4(a 4-1),则a 2=( )A .2B .1C.12D.182015《数列》高考真题答案1.【答案】6【解析】∵112,2n n a a a +==,∴数列{}n a是首项为2,公比为2的等比数列, ∴2(12)12612n n S -==-,∴264n=,∴n=6.2.【答案】2,13-【解析】由题可得,2111(2)()(6)a d a d a d +=++,故有1320a d +=,又因为1221a a +=,即131a d +=,所以121,3d a =-=.3.【答案】27【解析】∵2≥n 时,21,21121+=+=-a a a a n n 且 ∴{}1a a n是以为首项,21为公差的等差数列 ∴2718921289199=+=⨯⨯+⨯=S4.【答案】B 【解析】∵公差1d =,844S S =,∴11118874(443)22a a +⨯⨯=+⨯⨯,解得1a =12,∴1011199922a a d =+=+=,故选B.5.【答案】A6.【答案】(I )22n a n =+;(II )6b 与数列{}n a 的第63项相等.试题解析:(Ⅰ)设等差数列{}n a 的公差为d .因为432a a -=,所以2d =.又因为1210a a +=,所以1210a d +=,故14a =.所以42(1)22n a n n =+-=+(1,2,)n = .(Ⅱ)设等比数列{}n b 的公比为q .因为238b a ==,3716b a ==,所以2q =,14b =.所以61642128b -=⨯=.由12822n =+,得63n =.所以6b 与数列{}n a 的第63项相等.7.【解析】(Ⅰ) 由已知S n =2a n -a 1,有a n =S n -S n-1=2a n -2a n -1(n ≥2)即a n =2a n -1(n ≥2),从而a 2=2a 1,a 3=2a 2=4a 1,又因为a 1,a 2+1,a 3成等差数列 即a 1+a 3=2(a 2+1),所以a 1+4a 1=2(2a 1+1),解得a 1=2 所以,数列{a n }是首项为2,公比为2的等比数列。
专题10 等差数列与等比数列—三年高考(2015-2017)数学(文)真题分项版解析(原卷版)(打包下载)

专题10 等差数列与等比数列1.【2017浙江,6】已知等差数列{a n }的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6>2S 5”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件2.【2015高考新课标1,文7】已知{}n a 是公差为1的等差数列,n S 为{}n a 的前n 项和,若844S S =,则10a =( ) (A )172 (B )192(C )10 (D )12 3.【2014高考重庆文第2题】在等差数列{}n a 中,1352,10a a a =+=,则7a =( ) .5A .8B .10C .14D 4. 【2014天津,文5】设{}n a 是首项为1a ,公差为1-的等差数列,n S 为其前n 项和,若,,,421S S S 成等比数列,则1a =( )A.2B.-2C.21 D .12- 5. 【2014辽宁文9】设等差数列{}n a 的公差为d ,若数列1{2}n a a为递减数列,则( ) A .0d < B .0d > C .10a d < D .10a d >6. 【2015新课标2文5】设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =( ) A .5 B .7 C .9 D .117. 【2015新课标2文9】已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =( )A.2B.11C.2 1D.88.【2014全国2,文5】等差数列{}n a 的公差是2,若248,,a a a 成等比数列,则{}n a 的前n 项和n S =( )A. (1)n n +B. (1)n n -C.(1)2n n + D. (1)2n n -9.【2015高考广东,文13】若三个正数a ,b ,c 成等比数列,其中5a =+5c =-,则b = .10. 【2014高考广东卷.文.13】等比数列{}n a 的各项均为正数,且154a a =, 则2122232425log log log log log a a a a a ++++= .11.【2015高考新课标1,文13】数列{}n a 中112,2,n n n a a a S +==为{}n a 的前n 项和,若126n S =,则n = .12.【2015高考浙江,文10】已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a = ,d = .13. 【2015高考陕西,文13】中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为________14.【2017江苏,9】等比数列{}n a 的各项均为实数,其前n 项的和为n S ,已知3676344S S ==,,则8a = .15.【2017课标1,文17】记S n 为等比数列{}n a 的前n 项和,已知S 2=2,S 3=-6.(1)求{}n a 的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列.16.【2017课标II ,文17】已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,11221,1,2a b a b =-=+= (1)若335a b += ,求{}n b 的通项公式; (2)若321T =,求3S .17.【2015高考北京,文16】(本小题满分13分)已知等差数列{}n a 满足1210a a +=,432a a -=.(I )求{}n a 的通项公式;(II )设等比数列{}n b 满足23b a =,37b a =,问:6b 与数列{}n a 的第几项相等? 18. 【2015高考广东,文19】(本小题满分14分)设数列{}n a 的前n 项和为n S ,n *∈N .已知11a =,232a =,354a =,且当2n ≥ 时,211458n n n n S S S S ++-+=+. (1)求4a 的值; (2)证明:112n n a a +⎧⎫-⎨⎬⎩⎭为等比数列; (3)求数列{}n a 的通项公式.19.【2016高考新课标2文数】等差数列{n a }中,34574,6a a a a +=+=.(Ⅰ)求{n a }的通项公式;(Ⅱ) 设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]=0,[2.6]=220.【2016高考北京文数】(本小题13分)已知}{n a 是等差数列,}{n b 是等差数列,且32=b ,93=b ,11b a =,414b a =. (1)求}{n a 的通项公式;(2)设n n n b a c +=,求数列}{n c 的前n 项和.21.【2015高考四川,文16】设数列{a n }(n =1,2,3…)的前n 项和S n 满足S n =2a n -a 3,且a 1,a 2+1,a 3成等差数列. (Ⅰ)求数列的通项公式; (Ⅱ)设数列1{}na 的前n 项和为T n ,求T n . 22.【2016高考四川文科】(本小题满分12分)已知数列{n a }的首项为1,n S 为数列{}n a 的前n 项和,11n n S qS +=+ ,其中q >0,*n N ∈ .(Ⅰ)若2323,,a a a a + 成等差数列,求{}n a 的通项公式;(Ⅱ)设双曲线2221n y x a -= 的离心率为n e ,且22e = ,求22212n e e e ++⋅⋅⋅+.23.【2015高考重庆,文16】已知等差数列{}n a 满足3a =2,前3项和3S =92. (Ⅰ)求{}n a 的通项公式,(Ⅱ)设等比数列{}n b 满足1b =1a ,4b =15a ,求{}n b 前n 项和n T .专题11 数列通项公式与求和1.【2016高考浙江文数】如图,点列{}{},n n A B 分别在某锐角的两边上,且*1122,,n n n n n n A A A A A A n ++++=≠∈N ,*1122,,n n n n n n B B B B B B n ++++=≠∈N .(P ≠Q 表示点P 与Q 不重合)若n n n d A B =,n S 为1n n n A B B +△的面积,则( )A.{}n S 是等差数列B.{}2n S 是等差数列 C.{}n d 是等差数列 D.{}2nd 是等差数列2.【2016高考上海文科】无穷数列{}n a 由k 个不同的数组成,n S 为{}n a 的前n 项和.若对任意*∈N n ,{}3,2∈n S ,则k 的最大值为________.3.【2014全国2,文16】数列}{n a 满足2,1181=-=+a a a nn ,则=1a ________.4. 【2014,安徽文12】如图,在等腰直角三角形ABC 中,斜边BC =过点A 作BC 的垂线,垂足为1A ;过点1A 作AC 的垂线,垂足为2A ;过点2A 作1AC 的垂线,垂足为3A ;…,以此类推,设1BA a =,12AA a =,123A A a =,…,567A A a =,则7a =________.5. 【2015高考安徽,文13】已知数列}{n a 中,11=a ,211+=-n n a a (2≥n ),则数列}{n a 的前9项和等于 .6. 【2015高考福建,文16】若,a b 是函数()()20,0f x x px q p q =-+>> 的两个不同的零点,且,,2a b - 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p q + 的值等于________.7.【2017课标3,文17】设数列{}n a 满足123(21)2n a a n a n +++-=.(1)求{}n a 的通项公式; (2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和.8.【2017山东,文19】(本小题满分12分)已知{a n }是各项均为正数的等比数列,且121236,a a a a a +==.(I)求数列{a n }通项公式;(II){b n }为各项非零的等差数列,其前n 项和S n ,已知211n n n S b b ++=,求数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和n T .9.【2017天津,文18】已知{}n a 为等差数列,前n 项和为*()n S n ∈N ,{}n b 是首项为2的等比数列,且公比大于0,2334111412,2,11b b b a a S b +==-=.(Ⅰ)求{}n a 和{}n b 的通项公式; (Ⅱ)求数列2{}n n a b 的前n 项和*()n ∈N .10.【2017北京,文15】已知等差数列{}n a 和等比数列{}n b 满足a 1=b 1=1,a 2+a 4=10,b 2b 4=a 5. (Ⅰ)求{}n a 的通项公式;(Ⅱ)求和:13521n b b b b -++++.11.【2017江苏,19】 对于给定的正整数k ,若数列{}n a 满足1111n k n knnn kn ka aa a aa--+-++-++++++++ 2n ka =对任意正整数()n n k >总成立,则称数列{}n a 是“()P k 数列”. (1)证明:等差数列{}n a 是“(3)P 数列”;(2)若数列{}n a 既是“(2)P 数列”,又是“(3)P 数列”,证明:{}n a 是等差数列.12【2016高考新课标1文数】(本题满分12分)已知{}n a 是公差为3的等差数列,数列{}n b 满足12111==3n n n n b b a b b nb +++=1,,,. (I )求{}n a 的通项公式; (II )求{}n b 的前n 项和.13.【2014高考广东卷.文.19】(本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,且n S 满足()223n n S n n S -+--()230n n +=,n N *∈. (1)求1a 的值;(2)求数列{}n a 的通项公式;(3)证明:对一切正整数n ,有()()()112211111113n n a a a a a a +++<+++.14. [2016高考新课标Ⅲ文数]已知各项都为正数的数列{}n a 满足11a =,211(21)20n n n n a a a a ++---=.(I )求23,a a ;(II )求{}n a 的通项公式.15. 【2015高考湖南,文19】(本小题满分13分)设数列{}n a 的前n 项和为n S ,已知121,2a a ==,且13n n a S +=*13,()n S n N +-+∈,(I)证明:23n na a +=;(II )求n S 。
等差数列等比数列高考历年真题

温馨提示:高考题库为Word 版,请按住Ctrl ,滑动鼠标滚轴,调节合适的观看比例,点击右上角的关闭按钮可返回目录。
【考点16】等差数列、等比数列2009年考题1.(2009安徽高考)已知{}n a 为等差数列,1a +3a +5a =105,246a a a ++=99,以n S 表示{}n a 的前n 项和,则使得n S 达到最大值的n 是( )(A )21 (B )20 (C )19 (D ) 18 【解析】选B.由1a +3a +5a =105得33105,a =即335a =,由246a a a ++=99得4399a =即433a = ,∴2d =-,4(4)(2)412n a a n n =+-⨯-=-,由得20n =. 2.(2009安徽高考)已知为等差数列,,则等于( )A. -1B. 1C. 3D.7【解析】选B.∵135105a a a ++=即33105a =∴335a =同理可得433a =∴公差432d a a =-=-. 3.(2009福建高考)等差数列{}n a 的前n 项和为n S ,且3S =6,1a =4, 则公差d 等于( ) A .1 B53C.- 2 D 3 【解析】选C.∵且3112 =4 d=-2a a d a =+∴.4.(2009海南宁夏高考)等差数列{}n a 的前n 项和为n S ,已知2110m m ma a a -++-=,2138m S -=,则m =( )(A )38 (B )20 (C )10 (D )9【解析】选C.因为{}n a 是等差数列,所以,112m m m a a a -++=,由2110m m ma a a -++-=,得:2m a -2m a =0,所以,m a =2,又2138m S -=,即=38,即(2m -1)×2=38,解得m =10.5.(2009广东高考)已知等比数列{}n a 满足0,1,2,n a n >=,且25252(3)n n a a n -⋅=≥,则当1n ≥时,2123221log log log n a a a -+++=( )A. (21)n n -B. 2(1)n +C. 2nD. 2(1)n -【解析】选C.由25252(3)n n a a n -⋅=≥得n n a 222=,0>n a ,则n n a 2=, +⋅⋅⋅++3212log log a a 2122)12(31log n n a n =-+⋅⋅⋅++=-.6.(2009广东高考)已知等比数列}{n a 的公比为正数,且3a ·9a =225a ,2a =1,则1a = ( )A.21B. 22C.2 D.2【解析】选B.设公比为q ,由已知得()22824111a q a q q a q ⋅=,即22q =,因为等比数列}{n a 的公比为正数,所以2q =,故.7.(2009辽宁高考)设等比数列{ n a }的前n 项和为n S ,若 63S S =3 ,则 69SS =( )(A ) 2 (B )73(C ) 83 (D )3【解析】选B.设公比为q ,则=1+q 3=3q 3=2于是63693112471123S q q S q ++++===++.8.(2009辽宁高考)已知{}n a 为等差数列,且7a -24a =-1, 3a =0,则公差d =( )(A )-2 (B )-12(C )12(D )2【解析】选B. a 7-2a 4=a 3+4d -2(a 3+d)=2d =-1d =-12.9.(2009湖南高考)设n S 是等差数列{}n a 的前n 项和,已知23a =,611a =,则7S 等于( ).A .13B .35C .49D . 63 【解析】选C.172677()7()7(311)49.222a a a a S +++====故选C. 或由21161315112a a d a a a d d =+==⎧⎧⇒⎨⎨=+==⎩⎩, 716213.a =+⨯=所以1777()7(113)49.22a a S ++=== 10.(2009四川高考)等差数列{n a }的公差不为零,首项1a =1,2a 是1a 和5a 的等比中项,则数列的前10项之和是( )A. 90B. 100C. 145D. 190 【解析】选B.设公差为d ,则)41(1)1(2d d +⋅=+.∵d ≠0,解得d =2,∴10S =100.11.(2009辽宁高考)等差数列{}n a 的前n 项和为n S ,且53655,S S -=则4a = 【解析】∵S n =na 1+12n(n -1)d ∴S 5=5a 1+10d,S 3=3a 1+3d∴6S 5-5S 3=30a 1+60d -(15a 1+15d)=15a 1+45d =15(a 1+3d)=15a 4 答案:3112.(2009山东高考)在等差数列}{n a 中,6,7253+==a a a ,则____________6=a . 【解析】设等差数列}{n a 的公差为d ,则由已知得解得,所以61513a a d =+=. 答案:13.13.(2009海南宁夏高考)等比数列{n a }的公比0q >, 已知2a =1,216n n n a a a +++=,则{n a }的前4项和4S =【解析】由216n n n a a a +++=得:116-+=+n n n q q q ,即062=-+q q ,0q >,解得q =2,又2a =1,所以,,=152。
高三理科数学高考真题三年(2015-2017年)考点分类汇编:专题13数列小题

专题13数列小题一、选择题1.【等差数列及其运算】【2016,新课标1卷】已知等差数列{}n a 前9项的和为27,108a =,则100a =( ) A.100 B.99 C.98 D.97【答案】C2. 【等差数列的定义】【2016,浙江理数】如图,点列{A n },{B n }分别在某锐角的两边上,且1122,,n n n n n n A A A A A A n ++++=≠∈*N ,1122,,n n n n n n B B B B B B n ++++=≠∈*N ,(P Q P Q ≠表示点与不重合).若1n n n n n n n d A B S A B B +=,为△的面积,则( )A .{}n S 是等差数列B .2{}n S 是等差数列 C .{}n d 是等差数列D .2{}n d 是等差数列【答案】A3. 【等比数列的应用】【2016,四川理数】某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( )(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg2≈0.30) A.2018年B.2019年C.2020年D.2021年【答案】B4. 【等差数列及作差比较法】【2015,北京,理6】设{}n a 是等差数列. 下列结论中正确的是( ) A .若120a a +>,则230a a +> B .若130a a +<,则120a a +<C .若120a a <<,则2a >D .若10a <,则()()21230a a a a -->【答案】C5. 【等差数列的通项公式及其前n 项和,等比数列的概念】【2015,浙江,理3】已知{}n a 是等差数列,公差d 不为零,前n 项和是n S ,若3a ,4a ,8a 成等比数列,则( )A.140,0a d dS >>B.140,0a d dS <<C.140,0a d dS ><D.140,0a d dS <>【答案】B.6. 【等差数列的通项公式与等差数列的性质】【2015,重庆,理2】在等差数列{}n a 中,若2a =4,4a =2,则6a =( )A.-1B.0C.1D.6【答案】B7. 【等差中项和等比中项】【2015,福建,理8】若,a b 是函数()()20,0f x x px q p q =-+>>的两个不同的零点,且,,2a b -这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p q +的值等于( )A .6B .7C .8D .9【答案】D8. 【等比数列通项公式和性质】【2015,课标2理4】已知等比数列{}n a 满足a 1=3,135a a a ++ =21,则357a a a ++= ( )A .21B .42C .63D .84【答案】B 二、非选择题9. 【等比数列的定义,等比数列的前n 项和】【2016,浙江理数】设数列{a n }的前n 项和为S n .若S 2=4,a n +1=2S n +1,n ∈N *,则a 1=_______,S 5=____________.【答案】112110. 【等比数列及其应用】【2016,新课标1卷】设等比数列{}n a 满足a 1+a 3=10,a 2+a 4=5,则a 1a 2 …a n 的最大值为____________.【答案】6411. 【等差数列性质】【2016,江苏卷】已知{}n a 是等差数列,{S }n 是其前n 项和.若21253,S =10a a +=-,则9a 的值是 .【答案】2012. 【等差数列和递推关系】【2015,新课标2,理16】设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则n S =________.【答案】1n-13.【数列通项,裂项求和】【2015,江苏,11】数列}{n a 满足11=a ,且11+=-+n a a n n (*N n ∈),则数列}1{na 的前10项和为__________.【答案】201114. 【等差中项】【2015,陕西,理13】中位数1010的一组数构成等差数列,其末项为2015,则该数列的首项为______.【答案】515. 【等比数列的性质,等比数列的前n 项和公式】【2015,安徽,理14】已知数列{}n a 是递增的等比数列,14239,8a a a a +==,则数列{}n a 的前n 项和等于_________.【答案】21n-16. 【等差数列与等比数列的性质】【2015,湖南理14】设n S 为等比数列{}n a 的前n 项和,若11a =,且13S ,22S ,3S 成等差数列,则n a =________________.【答案】13-n .1. 【等差数列的基本量求解】【2017,课标1,理4】记n S 为等差数列{}n a 的前n 项和.若4524a a +=,648S =,则{}n a 的公差为( )A .1B .2C .4D .8【答案】C 【解析】秒杀解析:因为166346()3()482a a S a a +==+=,即3416a a +=,则4534()()24168a a a a +-+=-=,即5328a a d -==,解得4d =,故选C.【名师点睛】求解等差数列基本量问题时,要多多使用等差数列的性质,如{}n a 为等差数列,若m n p q +=+,则m n p q a a a a +=+.2. 【等差数列求和公式,等差数列基本量的计算】【2017,课标3,理9】等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为( ) A .24-B .3-C .3D . 8【答案】A 【解析】故选A.【名师点睛】(1)等差数列的通项公式及前n项和公式,共涉及五个量a1,a n,d,n,S n,知其中三个就能求另外两个,体现了用方程的思想解决问题.(2)数列的通项公式和前n项和公式在解题中起到变量代换作用,而a1和d是等差数列的两个基本量,用它们表示已知和未知是常用方法.3.【等比数列的应用,等比数列的求和公式】【2017,课标II,理3】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏 B.3盏 C.5盏 D.9盏【答案】B【解析】试题分析:设塔的顶层共有灯x盏,则各层的灯数构成一个首项为x,公比为2的等比数列,结合等比数列的求和公式有:()71238112x⨯-=-,解得3x=,即塔的顶层共有灯3盏,故选B。
专题10 数列-三年(2022–2024)高考数学真题分类汇编(全国通用)(原卷版)

专题10数列考点三年考情(2022-2024)命题趋势考点1:等差数列基本量运算2023年全国Ⅰ卷、2024年全国Ⅱ卷2023年新课标全国Ⅰ卷数学真题2022年高考全国乙卷数学(文)真题2023年高考全国甲卷数学(文)真题2023年高考全国乙卷数学(理)真题2024年高考全国甲卷数学(文)真题2024年高考全国甲卷数学(理)真题2023年高考全国乙卷数学(文)真题高考对数列的考查相对稳定,考查内容、频率、题型、难度均变化不大.等差数列、等比数列以选填题的形式为主,数列通项问题与求和问题以解答题的形式为主,偶尔出现在选择填空题当中,常结合函数、不等式综合考查.考点2:等比数列基本量运算2023年全国Ⅱ卷、2023年天津卷2023年高考全国甲卷数学(理)真题2022年高考全国乙卷数学(理)真题2023年高考全国甲卷数学(文)真题2023年高考全国乙卷数学(理)真题考点3:数列的实际应用2024年北京高考数学真题2023年北京高考数学真题2022年新高考全国II卷数学真题2022年高考全国乙卷数学(理)真题考点4:数列的最值问题2022年高考全国甲卷数学(理)真题2022年新高考北京数学高考真题考点5:数列的递推问题(蛛网图问题)2024年高考全国甲卷数学(文)真题2024年新课标全国Ⅱ卷数学真题2022年新高考浙江数学高考真题2023年北京高考数学真题考点6:等差数列与等比数列的综合应用2022年新高考浙江数学高考真题2022年新高考全国II卷数学真题2024年北京高考数学真题考点7:数列新定义问题2022年新高考北京数学高考真题2024年上海夏季高考数学真题2023年北京卷、2024年北京卷考点8:数列通项与求和问题2024年高考全国甲卷数学(理)真题2024年天津高考数学真题2023年高考全国甲卷数学(理)真题2022年新高考天津数学高考真题考点9:数列不等式2023年天津高考数学真题2023年全国Ⅱ卷、2022年全国I卷考点1:等差数列基本量运算1.(2023年新课标全国Ⅰ卷数学真题)设等差数列{}n a 的公差为d ,且1d >.令2n nn nb a +=,记,n n S T 分别为数列{}{},n n a b 的前n 项和.(1)若2133333,21a a a S T =++=,求{}n a 的通项公式;(2)若{}n b 为等差数列,且999999S T -=,求d .2.(2022年高考全国乙卷数学(文)真题)记n S 为等差数列{}n a 的前n 项和.若32236S S =+,则公差d =.3.(2023年高考全国甲卷数学(文)真题)记n S 为等差数列{}n a 的前n 项和.若264810,45a a a a +==,则5S =()A .25B .22C .20D .154.(2023年高考全国乙卷数学(理)真题)已知等差数列{}n a 的公差为23π,集合{}*cos N n S a n =∈,若{},S a b =,则ab =()A .-1B .12-C .0D .125.(2024年高考全国甲卷数学(文)真题)已知等差数列{}n a 的前n 项和为n S ,若91S =,则37a a +=()A .2-B .73C .1D .296.(2024年高考全国甲卷数学(理)真题)记n S 为等差数列{}n a 的前n 项和,已知510S S =,51a =,则1a =()A .72B .73C .13-D .711-7.(2023年高考全国乙卷数学(文)真题)记n S 为等差数列{}n a 的前n 项和,已知21011,40a S ==.(1)求{}n a 的通项公式;(2)求数列{}n a 的前n 项和n T .8.(2024年新课标全国Ⅱ卷数学真题)记n S 为等差数列{}n a 的前n 项和,若347a a +=,2535a a +=,则10S =.9.(2023年新课标全国Ⅰ卷数学真题)记n S 为数列{}n a 的前n 项和,设甲:{}n a 为等差数列;乙:{}nS n为等差数列,则()A .甲是乙的充分条件但不是必要条件B .甲是乙的必要条件但不是充分条件C .甲是乙的充要条件D .甲既不是乙的充分条件也不是乙的必要条件考点2:等比数列基本量运算10.(2023年新课标全国Ⅱ卷数学真题)记n S 为等比数列{}n a 的前n 项和,若45S =-,6221S S =,则8S =().A .120B .85C .85-D .120-11.(2023年高考全国甲卷数学(理)真题)设等比数列{}n a 的各项均为正数,前n 项和n S ,若11a =,5354S S =-,则4S =()A .158B .658C .15D .4012.(2023年天津高考数学真题)已知数列{}n a 的前n 项和为n S ,若()112,22N n n a a S n *+==+∈,则4a =()A .16B .32C .54D .16213.(2022年高考全国乙卷数学(理)真题)已知等比数列{}n a 的前3项和为168,2542a a -=,则6a =()A .14B .12C .6D .314.(2023年高考全国甲卷数学(文)真题)记n S 为等比数列{}n a 的前n 项和.若6387S S =,则{}n a 的公比为.15.(2023年高考全国乙卷数学(理)真题)已知{}n a 为等比数列,24536a a a a a =,9108a a =-,则7a =.考点3:数列的实际应用16.(2024年北京高考数学真题)汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器,其中升量器、斗量器、斛量器的形状均可视为圆柱.若升、斗、斛量器的容积成公比为10的等比数列,底面直径依次为65mm,325mm,325mm ,且斛量器的高为230mm ,则斗量器的高为mm ,升量器的高为mm .17.(2023年北京高考数学真题)我国度量衡的发展有着悠久的历史,战国时期就已经出现了类似于砝码的、用来测量物体质量的“环权”.已知9枚环权的质量(单位:铢)从小到大构成项数为9的数列{}n a ,该数列的前3项成等差数列,后7项成等比数列,且1591,12,192a a a ===,则7a =;数列{}n a 所有项的和为.18.(2022年新高考全国II 卷数学真题)图1是中国古代建筑中的举架结构,,,,AA BB CC DD ''''是桁,相邻桁的水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中1111,,,DD CC BB AA 是举,1111,,,OD DC CB BA 是相等的步,相邻桁的举步之比分别为11111231111,0.5,,DD CC BB AAk k k OD DC CB BA ====.已知123,,k k k 成公差为0.1的等差数列,且直线OA 的斜率为0.725,则3k =()A .0.75B .0.8C .0.85D .0.919.(2022年高考全国乙卷数学(理)真题)嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星,为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{}n b :1111b α=+,212111b αα=++,31231111b ααα=+++,…,依此类推,其中(1,2,)k k α*∈=N .则()A .15b b <B .38b b <C .62b b <D .47b b <考点4:数列的最值问题20.(2022年高考全国甲卷数学(理)真题)记n S 为数列{}n a 的前n 项和.已知221nn S n a n+=+.(1)证明:{}n a 是等差数列;(2)若479,,a a a 成等比数列,求n S 的最小值.21.(2022年新高考北京数学高考真题)设{}n a 是公差不为0的无穷等差数列,则“{}n a 为递增数列”是“存在正整数0N ,当0n N >时,0n a >”的()A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件考点5:数列的递推问题(蛛网图问题)22.(2024年高考全国甲卷数学(文)真题)已知等比数列{}n a 的前n 项和为n S ,且1233n n S a +=-.(1)求{}n a 的通项公式;(2)求数列{}n S 的前n 项和.23.(2024年新课标全国Ⅱ卷数学真题)已知双曲线()22:0C x y m m -=>,点()15,4P 在C 上,k 为常数,01k <<.按照如下方式依次构造点()2,3,...n P n =:过1n P -作斜率为k 的直线与C 的左支交于点1n Q -,令n P 为1n Q -关于y 轴的对称点,记n P 的坐标为(),n n x y .(1)若12k =,求22,x y ;(2)证明:数列{}n n x y -是公比为11kk+-的等比数列;(3)设n S 为12n n n P P P ++ 的面积,证明:对任意正整数n ,1n n S S +=.24.(2022年新高考浙江数学高考真题)已知数列{}n a 满足()21111,3n n n a a a a n *+==-∈N ,则()A .100521002a <<B .100510032a <<C .100731002a <<D .100710042a <<25.(2023年北京高考数学真题)已知数列{}n a 满足()31166(1,2,3,)4n n a a n +=-+= ,则()A .当13a =时,{}n a 为递减数列,且存在常数0M ≤,使得n a M >恒成立B .当15a =时,{}n a 为递增数列,且存在常数6M ≤,使得n a M <恒成立C .当17a =时,{}n a 为递减数列,且存在常数6M >,使得n a M >恒成立D .当19a =时,{}n a 为递增数列,且存在常数0M >,使得n a M <恒成立考点6:等差数列与等比数列的综合应用26.(2022年新高考浙江数学高考真题)已知等差数列{}n a 的首项11a =-,公差1d >.记{}n a 的前n 项和为()n S n *∈N .(1)若423260S a a -+=,求n S ;(2)若对于每个n *∈N ,存在实数n c ,使12,4,15n n n n n n a c a c a c +++++成等比数列,求d 的取值范围.27.(2022年新高考全国II 卷数学真题)已知{}n a 为等差数列,{}n b 是公比为2的等比数列,且223344a b a b b a -=-=-.(1)证明:11a b =;(2)求集合{}1,1500k m k b a a m =+≤≤中元素个数.28.(2024年北京高考数学真题)设{}n a 与{}n b 是两个不同的无穷数列,且都不是常数列.记集合{}*|,N k k M k a b k ==∈,给出下列4个结论:①若{}n a 与{}n b 均为等差数列,则M 中最多有1个元素;②若{}n a 与{}n b 均为等比数列,则M 中最多有2个元素;③若{}n a 为等差数列,{}n b 为等比数列,则M 中最多有3个元素;④若{}n a 为递增数列,{}n b 为递减数列,则M 中最多有1个元素.其中正确结论的序号是.考点7:数列新定义问题29.(2022年新高考北京数学高考真题)已知12:,,,k Q a a a 为有穷整数数列.给定正整数m ,若对任意的{1,2,,}n m ∈ ,在Q 中存在12,,,,(0)i i i i j a a a a j +++≥ ,使得12i i i i j a a a a n +++++++= ,则称Q 为m -连续可表数列.(1)判断:2,1,4Q 是否为5-连续可表数列?是否为6-连续可表数列?说明理由;(2)若12:,,,k Q a a a 为8-连续可表数列,求证:k 的最小值为4;(3)若12:,,,k Q a a a 为20-连续可表数列,且1220k a a a +++< ,求证:7k ≥.30.(2024年上海夏季高考数学真题)无穷等比数列{}n a 满足首项10,1a q >>,记[][]{}121,,,n n n I x y x y a a a a +=-∈⋃,若对任意正整数n 集合n I 是闭区间,则q 的取值范围是.31.(2024年新课标全国Ⅰ卷数学真题)设m 为正整数,数列1242,,...,m a a a +是公差不为0的等差数列,若从中删去两项i a 和()j a i j <后剩余的4m 项可被平均分为m 组,且每组的4个数都能构成等差数列,则称数列1242,,...,m a a a +是(),i j -可分数列.(1)写出所有的(),i j ,16i j ≤<≤,使数列126,,...,a a a 是(),i j -可分数列;(2)当3m ≥时,证明:数列1242,,...,m a a a +是()2,13-可分数列;(3)从1,2,...,42m +中一次任取两个数i 和()j i j <,记数列1242,,...,m a a a +是(),i j -可分数列的概率为m P ,证明:18m P >.32.(2023年北京高考数学真题)已知数列{}{},n n a b 的项数均为m (2)m >,且,{1,2,,},n n a b m ∈ {}{},n n a b 的前n 项和分别为,n n A B ,并规定000A B ==.对于{}0,1,2,,k m ∈ ,定义{}max ,{0,1,2,,}k i k r iB A i m =≤∈∣ ,其中,max M 表示数集M 中最大的数.(1)若1231232,1,3,1,3,3a a a b b b ======,求0123,,,r r r r 的值;(2)若11a b ≥,且112,1,2,,1,j j j r r r j m +-≤+=- ,求n r ;(3)证明:存在{},,,0,1,2,,p q s t m ∈ ,满足,,p q s t >>使得t p s q A B A B +=+.33.(2024年北京高考数学真题)已知集合(){}{}{}{}{},,,1,2,3,4,5,6,7,8,M i j k w i j k w i j k w =∈∈∈∈+++且为偶数.给定数列128:,,,A a a a ,和序列12:,,s T T T Ω ,其中()(),,,1,2,,t t t t t T i j k w M t s =∈= ,对数列A 进行如下变换:将A 的第1111,,,i j k w 项均加1,其余项不变,得到的数列记作()1T A ;将()1T A 的第2222,,,i j k w 项均加1,其余项不变,得到数列记作()21T T A ;……;以此类推,得到()21s T T T A ,简记为()A Ω.(1)给定数列:1,3,2,4,6,3,1,9A 和序列()()():1,3,5,7,2,4,6,8,1,3,5,7Ω,写出()A Ω;(2)是否存在序列Ω,使得()A Ω为123456782,6,4,2,8,2,4,4a a a a a a a a ++++++++,若存在,写出一个符合条件的Ω;若不存在,请说明理由;(3)若数列A 的各项均为正整数,且1357a a a a +++为偶数,求证:“存在序列Ω,使得()A Ω的各项都相等”的充要条件为“12345678a a a a a a a a +=+=+=+”.考点8:数列通项与求和问题34.(2024年高考全国甲卷数学(理)真题)记n S 为数列{}n a 的前n 项和,已知434n n S a =+.(1)求{}n a 的通项公式;(2)设1(1)n n n b na -=-,求数列{}n b 的前n 项和n T .35.(2024年天津高考数学真题)已知数列{}n a 是公比大于0的等比数列.其前n 项和为n S .若1231,1a S a ==-.(1)求数列{}n a 前n 项和n S ;(2)设11,2,kn n k k k n a b b k a n a -+=⎧=⎨+<<⎩,*k ∈N .(ⅰ)当12,k k n a +≥=时,求证:1n k n b a b -≥⋅;(ⅱ)求1nS i i b =∑.36.(2023年高考全国甲卷数学(理)真题)设n S 为数列{}n a 的前n 项和,已知21,2n n a S na ==.(1)求{}n a 的通项公式;(2)求数列12n n a +⎧⎫⎨⎬⎩⎭的前n 项和n T .37.(2022年新高考天津数学高考真题)设{}n a 是等差数列,{}n b 是等比数列,且1122331a b a b a b ==-=-=.(1)求{}n a 与{}n b 的通项公式;(2)设{}n a 的前n 项和为n S ,求证:()1111n n n n n n n S a b S b S b +++++=-;(3)求211(1)nk k k k k a a b +=⎡⎤--⎣⎦∑.考点9:数列不等式38.(2023年天津高考数学真题)已知{}n a 是等差数列,255316,4a a a a +=-=.(1)求{}n a 的通项公式和()1212N n n ii a n --*=∈∑.(2)设{}n b 是等比数列,且对任意的*N k ∈,当1221k k n -≤≤-时,则1k n k b a b +<<,(Ⅰ)当2k ≥时,求证:2121kk k b -<<+;(Ⅱ)求{}n b 的通项公式及前n 项和.39.(2023年新课标全国Ⅱ卷数学真题)已知{}n a 为等差数列,6,2,n n na nb a n -⎧=⎨⎩为奇数为偶数,记n S ,n T 分别为数列{}n a ,{}n b 的前n 项和,432S =,316T =.(1)求{}n a 的通项公式;(2)证明:当5n >时,n n T S >.40.(2022年新高考全国I 卷数学真题)记n S 为数列{}n a 的前n 项和,已知11,n n S a a ⎧⎫=⎨⎬⎩⎭是公差为13的等差数列.(1)求{}n a 的通项公式;(2)证明:121112na a a +++< .。
数列-三年(2017-2019)高考真题数学(文)专题

数列专题1.【2019年高考全国III 卷文数】已知各项均为正数的等比数列{}n a 的前4项和为15,且53134a a a =+,则3a = A .16 B .8C .4D .22.【2019年高考浙江卷】设a ,b ∈R ,数列{a n }满足a 1=a ,a n +1=a n 2+b ,n *∈N ,则 A . 当101,102b a => B . 当101,104b a => C . 当102,10b a =-> D . 当104,10b a =->3.【2018年高考浙江卷】已知1234,,,a a a a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则 A .1324,a a a a << B .1324,a a a a >< C .1324,a a a a <>D .1324,a a a a >>4.【2018年高考北京卷文数】设a,b,c,d 是非零实数,则“ad=bc ”是“a,b,c,d 成等比数列”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件5.【2018年高考北京卷文数】“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于若第一个单音的频率为f ,则第八个单音的频率为A BC .D .6.【2017年高考浙江卷】已知等差数列{a n }的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6>2S 5”的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件7.【2019年高考全国I 卷文数】记S n 为等比数列{a n }的前n 项和.若13314a S ==,,则S 4=___________.8.【2019年高考全国III 卷文数】记n S 为等差数列{}n a 的前n 项和,若375,13a a ==,则10S =___________.9.【2019年高考江苏卷】已知数列*{}()n a n ∈N 是等差数列,n S 是其前n 项和.若25890,27a a a S +==,则8S 的值是__________.10.【2018年高考江苏卷】已知集合*{|21,}A x x n n ==-∈N ,*{|2,}nB x x n ==∈N .将AB 的所有元素从小到大依次排列构成一个数列{}n a .记n S 为数列{}n a 的前n 项和,则使得112n n S a +>成立的n 的最小值为___________.11.【2017年高考江苏卷】等比数列{}n a 的各项均为实数,其前n 项和为n S ,已知3676344S S ==,,则8a =___________.12.【2019年高考全国I 卷文数】记S n 为等差数列{a n }的前n 项和,已知S 9=-a 5.(1)若a 3=4,求{a n }的通项公式;(2)若a 1>0,求使得S n ≥a n 的n 的取值范围.13.【2019年高考全国II 卷文数】已知{}n a 是各项均为正数的等比数列,1322,216a a a ==+.(1)求{}n a 的通项公式;(2)设2log n n b a =,求数列{}n b 的前n 项和.14.【2019年高考北京卷文数】设{a n }是等差数列,a 1=–10,且a 2+10,a 3+8,a 4+6成等比数列.(1)求{a n }的通项公式;(2)记{a n }的前n 项和为S n ,求S n 的最小值.15.【2019年高考天津卷文数】设{}n a 是等差数列,{}n b 是等比数列,公比大于0,已知1123323,,43a b b a b a ====+.(1)求{}n a 和{}n b 的通项公式;(2)设数列{}n c 满足21n n n c b n ⎧⎪=⎨⎪⎩,为奇数,,为偶数.求*112222()n n a c a c a c n +++∈N .16.【2019年高考江苏卷】定义首项为1且公比为正数的等比数列为“M-数列”.(1)已知等比数列{a n }()n *∈N 满足:245132,440a a a a a a =-+=,求证:数列{a n }为“M-数列”;(2)已知数列{b n }()n *∈N 满足:111221,n n n b S b b +==-,其中S n 为数列{b n }的前n 项和. ①求数列{b n }的通项公式;②设m 为正整数,若存在“M-数列”{c n }()n *∈N ,对任意正整数k ,当k ≤m 时,都有1k k k c b c +成立,求m 的最大值.17.【2019年高考浙江卷】设等差数列{}n a 的前n 项和为n S ,34a =,43a S =,数列{}n b 满足:对每个12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.(1)求数列{},{}n n a b 的通项公式; (2)记,n c n *=∈N证明:12+.n c c c n *++<∈N18.【2018年高考全国I 卷文数】已知数列{}n a 满足11a =,()121n n na n a +=+,设nn a b n=. (1)求123b b b ,,; (2)判断数列{}n b 是否为等比数列,并说明理由; (3)求{}n a 的通项公式.19.【2018年高考全国III 卷文数】等比数列{}n a 中,15314a a a ==,. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .20.【2018年高考全国II 卷文数】记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-. (1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.21.【2018年高考北京卷文数】设{}n a 是等差数列,且123ln2,5ln2a a a =+=. (1)求{}n a 的通项公式; (2)求12e e e n a aa+++.22.【2018年高考天津卷文数】设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (1)求S n 和T n ;(2)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值.23.【2018年高考浙江卷】已知等比数列{a n }的公比q >1,且a 3+a 4+a 5=28,a 4+2是a 3,a 5的等差中项.数列{b n }满足b 1=1,数列{(b n +1−b n )a n }的前n 项和为2n 2+n . (1)求q 的值;(2)求数列{b n }的通项公式.24.【2018年高考江苏卷】设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项为1b ,公比为q 的等比数列.(1)设110,1,2a b q ===,若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围;(2)若*110,,a b m q =>∈∈N ,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,,1n m =+均成立,并求d 的取值范围(用1,,b m q 表示).25.【2017年高考全国I 卷文数】记S n 为等比数列{}n a 的前n 项和,已知S 2=2,S 3=−6.(1)求{}n a 的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列.26.【2017年高考全国II 卷文数】已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,11221,1,2a b a b =-=+=.(1)若335a b +=,求{}n b 的通项公式; (2)若321T =,求3S .27.【2017年高考全国III 卷文数】设数列{}n a 满足123(21)2n a a n a n +++-=.(1)求{}n a 的通项公式; (2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和.28.【2017年高考北京卷文数】已知等差数列{}n a 和等比数列{}n b 满足a 1=b 1=1,a 2+a 4=10,b 2b 4=a 5.(1)求{}n a 的通项公式; (2)求和:13521n b b b b -++++.29.【2017年高考山东卷文数】已知{}n a 是各项均为正数的等比数列,且121236,a a a a a +==. (1)求数列{}n a 的通项公式;(2){}n b 为各项非零的等差数列,其前n 项和S n ,已知211n n n S b b ++=,求数列{}nnb a 的前n 项和n T .30.【2017年高考天津卷文数】已知{}n a 为等差数列,前n 项和为*()n S n ∈N ,{}n b 是首项为2的等比数列,且公比大于0,2334111412,2,11b b b a a S b +==-=.(1)求{}n a 和{}n b 的通项公式;(2)求数列2{}n n a b 的前n 项和*()n ∈N .31.【2017年高考江苏卷】对于给定的正整数k ,若数列{}n a 满足:1111n k n k n n n k n k a a a a a a --+-++-++++++++2n ka =对任意正整数()n n k >总成立,则称数列{}n a 是“()P k 数列”.(1)证明:等差数列{}n a 是“(3)P 数列”;(2)若数列{}n a 既是“(2)P 数列”,又是“(3)P 数列”,证明:{}n a 是等差数列.32.【2017年高考浙江卷】已知数列{x n }满足:x 1=1,x n =x n +1+ln(1+x n +1)(n *∈N ).证明:当n *∈N 时, (1)0<x n +1<x n ;(2)2x n +1− x n ≤12n n x x +; (3)112n -≤x n ≤212n -.数列答案1.【2019年高考全国III 卷文数】已知各项均为正数的等比数列{}n a 的前4项和为15,且53134a a a =+,则3a = A .16 B .8C .4D .2【答案】C【解析】设正数的等比数列{a n }的公比为q ,则231111421111534a a q a q a q a q a q a ⎧+++=⎨=+⎩, 解得11,2a q =⎧⎨=⎩,2314a a q ∴==,故选C .【名师点睛】本题利用方程思想求解数列的基本量,熟练应用公式是解题的关键. 2.【2019年高考浙江卷】设a ,b ∈R ,数列{a n }满足a 1=a ,a n +1=a n 2+b ,n *∈N ,则 A . 当101,102b a => B . 当101,104b a => C . 当102,10b a =-> D . 当104,10b a =->【答案】A【解析】①当b =0时,取a =0,则0,n a n *=∈N .②当<0b 时,令2x x b =+,即20x x b -+=.则该方程140b ∆=->,即必存在0x ,使得2000x x b -+=, 则一定存在10 ==a a x ,使得21n n n a a b a +=+=对任意n *∈N 成立,解方程20a a b -+=,得a =,10≤时,即90b -时,总存在a =,使得121010a a a ==⋯=≤, 故C 、D 两项均不正确.③当0b >时,221a a b b =+≥,则2232a a b b b =+≥+,()22243a a bbb b =+++.(ⅰ)当12b =时,22451111711,1222162a a ⎡⎤⎛⎫++=>>+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦≥,则26111112224a ⎛⎫>++=> ⎪⎝⎭,2719222a >+=, 28918310224a ⎛⎫>+=> ⎪⎝⎭ ,则2981102a a =+>, 21091102a a =+> , 故A 项正确.(ⅱ)当14b =时,令1==0a a ,则2231111,4442a a ⎛⎫==+< ⎪⎝⎭,所以224311114242a a ⎛⎫=+<+= ⎪⎝⎭,以此类推,所以2210911114242a a ⎛⎫=+<+= ⎪⎝⎭,故B 项不正确. 故本题正确答案为A.【名师点睛】遇到此类问题,不少考生会一筹莫展.利用函数方程思想,通过研究函数的不动点,进一步讨论a 的可能取值,利用“排除法”求解.3.【2018年高考浙江卷】已知1234,,,a a a a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则 A .1324,a a a a << B .1324,a a a a >< C .1324,a a a a <>D .1324,a a a a >>【答案】B【解析】令()ln 1,f x x x =--则()11f x x'=-,令()0,f x '=得1x =,所以当1x >时,()0f x '>,当01x <<时,()0f x '<,因此()()10,ln 1f x f x x ≥=∴≥+.若公比0q >,则()1234123123ln a a a a a a a a a a +++>++>++,不合题意; 若公比1q ≤-,则()()212341110,a a a a a q q +++=++≤但()()212311ln ln 1ln 0a a a a q q a ⎡⎤++=++>>⎣⎦,即()12341230ln a a a a a a a +++≤<++,不合题意; 因此()210,0,1q q -<<∈,22113224,0a a q a a a q a ∴>=<=<,故选B.【名师点睛】构造函数对不等式进行放缩,进而限制参数取值范围,是一个有效方法.如()2ln 1,e 1,e 10.x x x x x x x ≥+≥+≥+≥4.【2018年高考北京卷文数】设a,b,c,d 是非零实数,则“ad=bc ”是“a,b,c,d 成等比数列”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件【答案】B【解析】当14,1,1,4a b c d ====时,,,,a b c d 不成等比数列,所以不是充分条件;当,,,a b c d 成等比数列时,则ad bc =,所以是必要条件.综上所述,“ad bc =”是“,,,a b c d 成等比数列”的必要不充分条件,故选B.【名师点睛】证明“ad bc =”⇒“,,,a b c d 成等比数列”只需举出反例即可,论证“,,,a b c d 成等比数列”⇒“ad bc =”可利用等比数列的性质.5.【2018年高考北京卷文数】“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于若第一个单音的频率为f ,则第八个单音的频率为A BC .D .【答案】D【解析】因为每一个单音的频率与前一个单音的频率的比都为,所以()*12,n n a n n -=≥∈N,又1a f =,则7781a a q f ===,故选D.【名师点睛】此题考查等比数列的实际应用,解决本题的关键是能够判断单音成等比数列.等比数列的判断方法主要有如下两种:(1)定义法,若1n n a q a +=(*0,q n ≠∈N )或1nn a q a -=(*0,2,q n n ≠≥∈N ),数列{}n a 是等比数列;(2)等比中项公式法,若数列{}n a 中,0n a ≠且212n n n a a a --=⋅(*3,n n ≥∈N ),则数列{}n a 是等比数列.6.【2017年高考浙江卷】已知等差数列{a n }的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6>2S 5”的 A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C【解析】由46511210212(510)S S S a d a d d +-=+-+=,可知当0d >时,有46520S S S +->,即4652S S S +>,反之,若4652S S S +>,则0d >,所以“d >0”是“S 4 + S 6>2S 5”的充要条件,选C .【名师点睛】本题考查等差数列的前n 项和公式,通过套入公式与简单运算,可知4652S S S d +-=, 结合充分必要性的判断,若p q ⇒,则p 是q 的充分条件,若p q ⇐,则p 是q 的必要条件,该题“0d >”⇔“46520S S S +->”,故互为充要条件.7.【2019年高考全国I 卷文数】记S n 为等比数列{a n }的前n 项和.若13314a S ==,,则S 4=___________. 【答案】58【解析】设等比数列的公比为q ,由已知223111314S a a q a q q q =++=++=,即2104q q ++=. 解得12q =-,所以441411()(1)521181()2a q S q ---===---. 【名师点睛】准确计算,是解答此类问题的基本要求.本题由于涉及幂的乘方运算、繁分式的计算,部分考生易出现运算错误.一题多解:本题在求得数列的公比后,可利用已知计算3343431315()428S S a S a q =+=+=+-=,避免繁分式计算.8.【2019年高考全国III 卷文数】记n S 为等差数列{}n a 的前n 项和,若375,13a a ==,则10S =___________.【答案】100【解析】设等差数列{}n a 的公差为d ,根据题意可得317125,613a a d a a d =+=⎧⎨=+=⎩得11,2a d =⎧⎨=⎩ 101109109101012100.22S a d ⨯⨯∴=+=⨯+⨯= 【名师点睛】本题考点为等差数列的求和,为基础题目,利用基本量思想解题即可,充分记牢等差数列的求和公式是解题的关键.9.【2019年高考江苏卷】已知数列*{}()n a n ∈N 是等差数列,n S 是其前n 项和.若25890,27a a a S +==,则8S 的值是__________. 【答案】16【解析】由题意可得:()()()25811191470989272a a a a d a d a d S a d ⎧+=++++=⎪⎨⨯=+=⎪⎩, 解得:152a d =-⎧⎨=⎩,则8187840282162S a d ⨯=+=-+⨯=. 【名师点睛】等差数列、等比数列的基本计算问题,是高考必考内容,解题过程中要注意应用函数方程思想,灵活应用通项公式、求和公式等,构建方程(组),如本题,从已知出发,构建1a d ,的方程组. 10.【2018年高考江苏卷】已知集合*{|21,}A x x n n ==-∈N ,*{|2,}nB x x n ==∈N .将AB 的所有元素从小到大依次排列构成一个数列{}n a .记n S 为数列{}n a 的前n 项和,则使得112n n S a +>成立的n 的最小值为___________. 【答案】27【解析】所有的正奇数和()2n n *∈N 按照从小到大的顺序排列构成{}n a ,在数列|{}n a 中,25前面有16个正奇数,即5621382,2a a ==.当n =1时,1211224S a =<=,不符合题意;当n =2时,2331236S a =<=,不符合题意;当n =3时,3461248S a =<=,不符合题意;当n =4时,4510<12=60S a =,不符合题意;……;当n =26时,()2752621221(141)441625032121=2516S a ⨯-⨯+=+=+=<-,不符合题意;当n =27时,()8527221222(143)21484+62=546>12=5420S a⨯-⨯+=+=-,符合题意.故使得+1>12n n S a 成立的n 的最小值为27.【名师点睛】本题主要考查等差数列、等比数列的前n 项和,考查考生的运算求解能力,考查的核心素养是数学运算.11.【2017年高考江苏卷】等比数列{}n a 的各项均为实数,其前n 项和为n S ,已知3676344S S ==,,则8a =___________. 【答案】32【解析】当1q =时,显然不符合题意;当1q ≠时,3161(1)714(1)6314a q q a q q ⎧-=⎪-⎪⎨-⎪=⎪-⎩,解得1142a q ⎧=⎪⎨⎪=⎩,则7812324a =⨯=. 【名师点睛】在解决等差、等比数列的运算问题时,有两个处理思路:①利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;②利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质成立的前提条件,有时需要进行适当变形.在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.12.【2019年高考全国I 卷文数】记S n 为等差数列{a n }的前n 项和,已知S 9=-a 5.(1)若a 3=4,求{a n }的通项公式;(2)若a 1>0,求使得S n ≥a n 的n 的取值范围.【答案】(1)210n a n =-+;(2)110()n n *≤≤∈N .【解析】(1)设{}n a 的公差为d . 由95S a =-得140a d +=. 由a 3=4得124a d +=. 于是18,2a d ==-.因此{}n a 的通项公式为102n a n =-.(2)由(1)得14a d =-,故(9)(5),2n n n n da n d S -=-=. 由10a >知0d <,故n n S a ≥等价于211100n n -+,解得1≤n ≤10. 所以n 的取值范围是{|110,}n n n *≤≤∈N .【名师点睛】该题考查的是有关数列的问题,涉及到的知识点有等差数列的通项公式,等差数列的求和公式,在解题的过程中,需要认真分析题意,熟练掌握基础知识是正确解题的关键.13.【2019年高考全国II 卷文数】已知{}n a 是各项均为正数的等比数列,1322,216a a a ==+.(1)求{}n a 的通项公式;(2)设2log n n b a =,求数列{}n b 的前n 项和.【答案】(1)212n n a -=;(2)2n S n =.【解析】(1)设{}n a 的公比为q ,由题设得22416q q =+,即2280q q --=.解得2q =-(舍去)或q =4.因此{}n a 的通项公式为121242n n n a --=⨯=.(2)由(1)得2(21)log 221n b n n =-=-, 因此数列{}n b 的前n 项和为21321n n +++-=.【名师点睛】本题考查数列的相关性质,主要考查等差数列以及等比数列的通项公式的求法,考查等差数列求和公式的使用,考查化归与转化思想,考查计算能力,是简单题.14.【2019年高考北京卷文数】设{a n }是等差数列,a 1=–10,且a 2+10,a 3+8,a 4+6成等比数列.(1)求{a n }的通项公式;(2)记{a n }的前n 项和为S n ,求S n 的最小值.【答案】(1)212n a n =-;(2)当5n =或者6n =时,n S 取到最小值30-.【解析】(1)设{}n a 的公差为d . 因为110a =-,所以23410,102,103a d a d a d =-+=-+=-+. 因为23410,8,6a a a +++成等比数列, 所以()()()23248106a a a +=++. 所以2(22)(43)d d d -+=-+. 解得2d =.所以1(1) 212n a a n d n =+-=-. (2)由(1)知,212n a n =-.所以,当7n ≥时,0n a >;当6n ≤时,0n a ≤. 所以,n S 的最小值为630S =-.【名师点睛】等差数列基本量的求解是等差数列中的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用.15.【2019年高考天津卷文数】设{}n a 是等差数列,{}n b 是等比数列,公比大于0,已知1123323,,43a b b a b a ====+.(1)求{}n a 和{}n b 的通项公式;(2)设数列{}n c 满足21n n n c b n ⎧⎪=⎨⎪⎩,为奇数,,为偶数.求*112222()n n a c a c a c n +++∈N .【答案】(1)3n a n =,3nn b =;(2)22(21)369()2n n n n +*-++∈N【解析】(1)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q .依题意,得2332,3154,q d q d =+⎧⎨=+⎩解得3,3,d q =⎧⎨=⎩故133(1)3,333n n n n a n n b -=+-==⨯=.所以,{}n a 的通项公式为3n a n =,{}n b 的通项公式为3nn b =.(2)112222n n a c a c a c +++()()135212142632n n n a a a a a b a b a b a b -=+++++++++123(1)36(6312318363)2n n n n n -⎡⎤=⨯+⨯+⨯+⨯+⨯++⨯⎢⎥⎣⎦()2123613233n n n =+⨯+⨯++⨯.记1213233n n T n =⨯+⨯++⨯,① 则231313233n n T n +=⨯+⨯++⨯,②②−①得,()12311313(21)332333331332n n n n nn n T n n +++--+=---⨯=-+⨯=--+-. 所以,122112222(21)3336332n n n n n a c a c a c n T n +-++++=+=+⨯()22(21)3692n n n n +*-++=∈N . 【名师点睛】本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识,考查数列求和的基本方法和运算求解能力,属于中档题目.16.【2019年高考江苏卷】定义首项为1且公比为正数的等比数列为“M -数列”.(1)已知等比数列{a n }()n *∈N 满足:245132,440a a a a a a =-+=,求证:数列{a n }为“M -数列”;(2)已知数列{b n }()n *∈N 满足:111221,n n n b S b b +==-,其中S n 为数列{b n }的前n 项和. ①求数列{b n }的通项公式;②设m 为正整数,若存在“M -数列”{c n }()n *∈N ,对任意正整数k ,当k ≤m 时,都有1k k k c b c +成立,求m 的最大值.【答案】(1)见解析;(2)①b n =n ()*n ∈N ;②5.【解析】(1)设等比数列{a n }的公比为q ,所以a 1≠0,q ≠0.由245321440a a a a a a =⎧⎨-+=⎩,得244112111440a q a q a q a q a ⎧=⎨-+=⎩,解得112a q =⎧⎨=⎩.因此数列{}n a 为“M—数列”.(2)①因为1122n n n S b b +=-,所以0n b ≠. 由1111,b S b ==,得212211b =-,则22b =. 由1122n n n S b b +=-,得112()n n n n n b b S b b ++=-, 当2n ≥时,由1n n n b S S -=-,得()()111122n n n nn n n n n b b b b b b b b b +-+-=---,整理得112n n n b b b +-+=.所以数列{b n }是首项和公差均为1的等差数列. 因此,数列{b n }的通项公式为b n =n ()*n ∈N .②由①知,b k =k ,*k ∈N .因为数列{c n }为“M–数列”,设公比为q ,所以c 1=1,q >0. 因为c k ≤b k ≤c k +1,所以1k k q k q -≤≤,其中k =1,2,3,…,m .当k =1时,有q ≥1; 当k =2,3,…,m 时,有ln ln ln 1k kq k k ≤≤-. 设f (x )=ln (1)x x x >,则21ln ()xf 'x x-=. 令()0f 'x =,得x =e.列表如下:因为ln 2ln8ln 9ln 32663=<=,所以max ln 3()(3)3f k f ==. 取q =k =1,2,3,4,5时,ln ln kq k,即k k q ≤,经检验知1k qk -≤也成立.因此所求m 的最大值不小于5.若m ≥6,分别取k =3,6,得3≤q 3,且q 5≤6,从而q 15≥243,且q 15≤216, 所以q 不存在.因此所求m 的最大值小于6. 综上,所求m 的最大值为5.【名师点睛】本题主要考查等差和等比数列的定义、通项公式、性质等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力.17.【2019年高考浙江卷】设等差数列{}n a 的前n 项和为n S ,34a =,43a S =,数列{}n b 满足:对每个12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.(1)求数列{},{}n n a b 的通项公式; (2)记,n c n *=∈N证明:12+.n c c c n *++<∈N【答案】(1)()21n a n =-,()1n b n n =+;(2)证明见解析. 【解析】(1)设数列{}n a 的公差为d ,由题意得11124,333a d a d a d +=+=+,解得10,2a d ==.从而*22,n a n n =-∈N . 所以2*n S n n n =-∈N ,,由12,,n n n n n n S b S b S b +++++成等比数列得()()()212n n n n n n S b S b S b +++=++.解得()2121n n n n b S S S d++=-. 所以2*,n b n n n =+∈N .(2)*n c n ===∈N . 我们用数学归纳法证明.(i )当n =1时,c 1=0<2,不等式成立;(ii )假设()*n k k =∈N 时不等式成立,即12k c c c +++<.那么,当1n k =+时,121k k c c c c +++++<<<==.即当1n k =+时不等式也成立.根据(i )和(ii ),不等式12n c c c +++<对任意*n ∈N 成立.【名师点睛】本题主要考查等差数列、等比数列、数列求和、数学归纳法等基础知识,同时考查运算求解能力和综合应用能力.18.【2018年高考全国I 卷文数】已知数列{}n a 满足11a =,()121n n na n a +=+,设nn a b n=. (1)求123b b b ,,; (2)判断数列{}n b 是否为等比数列,并说明理由; (3)求{}n a 的通项公式.【答案】(1)b 1=1,b 2=2,b 3=4;(2)见解析;(3)a n =n ·2n -1. 【解析】(1)由条件可得a n +1=2(1)n n a n+. 将n =1代入得,a 2=4a 1,而a 1=1,所以,a 2=4. 将n =2代入得,a 3=3a 2,所以,a 3=12. 从而b 1=1,b 2=2,b 3=4.(2){b n }是首项为1,公比为2的等比数列. 由条件可得121n na a n n+=+,即b n +1=2b n , 又b 1=1,所以{b n }是首项为1,公比为2的等比数列. (3)由(2)可得12n na n-=, 所以a n =n ·2n -1. 【名师点睛】该题考查的是有关数列的问题,涉及到的知识点有根据数列的递推公式确定数列的项,根据不同数列的项之间的关系,确定新数列的项,利用递推关系整理得到相邻两项之间的关系确定数列是等比数列,根据等比数列通项公式求得数列{b n }的通项公式,借助于{b n }的通项公式求得数列{a n }的通项公式,从而求得最后的结果.19.【2018年高考全国III 卷文数】等比数列{}n a 中,15314a a a ==,. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m . 【答案】(1)1(2)n n a -=-或12n n a -=;(2)6m =. 【解析】(1)设{}n a 的公比为q ,由题设得1n n a q -=. 由已知得424q q =,解得0q =(舍去),2q =-或2q =. 故1(2)n n a -=-或12n n a -=. (2)若1(2)n n a -=-,则1(2)3nn S --=.由63m S =得(2)188m -=-,此方程没有正整数解. 若12n n a -=,则21n n S =-. 由63m S =得264m =,解得6m =. 综上,6m =.【名师点睛】等差、等比数列中的基本量的求解,可利用通项公式及前n 项和公式建立1, a d (或q ),, ,n n n a S 五个基本量间的关系式,即“知三求二”.非等差、等比数列的求和常用三种方法:一是分组求和法,特征是原数列可以拆成几个等差或等比数列的和;二是裂项相消求和法,特征是通项是分式形式,如等差数列{}n a 的的公差是d ,则111111n n n n n b a a d a a ++⎛⎫==- ⎪⎝⎭;三是错位(项)相减求和法,特征是通项可以看成一个等差数列与一个等比数列对应项的积(或商).20.【2018年高考全国II 卷文数】记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-. (1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.【答案】(1)a n =2n –9;(2)S n =n 2–8n ,最小值为–16. 【解析】(1)设{a n }的公差为d ,由题意得3a 1+3d =–15. 由a 1=–7得d =2.所以{a n }的通项公式为a n =2n –9. (2)由(1)得S n =n 2–8n =(n –4)2–16. 所以当n =4时,S n 取得最小值,最小值为–16.【名师点睛】数列是特殊的函数,研究数列最值问题,可利用函数性质,但要注意其定义域为正整数集这一限制条件.(1)根据等差数列前n 项和公式,求出公差,再代入等差数列通项公式得结果;(2)根据等差数列前n 项和公式得n S 关于n 的二次函数关系式,根据二次函数对称轴以及自变量为正整数求函数最值.21.【2018年高考北京卷文数】设{}n a 是等差数列,且123ln2,5ln2a a a =+=. (1)求{}n a 的通项公式; (2)求12e e e n a aa+++.【答案】(1)ln 2n a n =;(2)122n +-. 【解析】(1)设等差数列{}n a 的公差为d , ∵235ln2a a +=, ∴1235ln2a d +=, 又1ln2a =, ∴ln2d =.∴()11ln 2n a a n d n =+-=. (2)由(1)知ln2n a n =, ∵ln 2ln2e e e =2nn a n n ==, ∴{}ena 是以2为首项,2为公比的等比数列.∴212ln2ln2ln221e e e e e e =222=22nn a a a n n ++++=++++++-.∴12e e e n a a a +++1=22n +-.【名师点睛】等差数列的通项公式及前n 项和共涉及五个基本量1,,,,n n a a d n S ,知道其中三个可求另外两个,体现了用方程组解决问题的思想.(1)设公差为d ,根据题意可列关于1,a d 的方程组,求解1,a d ,代入通项公式可得;(2)由(1)可得e 2n a n =,进而可利用等比数列求和公式进行求解.22.【2018年高考天津卷文数】设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (1)求S n 和T n ;(2)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值. 【答案】(1)(1)2n n n S +=,21nn T =-;(2)4. 【解析】(1)设等比数列{}n b 的公比为q ,由b 1=1,b 3=b 2+2,可得220q q --=.因为0q >,可得2q =,故12n n b -=.所以,122112nn n T -==--. 设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d +=从而11,1a d ==,故n a n =, 所以,(1)2n n n S +=. (2)由(1),有131122(12)(222)=2 2.12n nn n T T T n n n +⨯-+++=+++--=---由12()4n n n n S T T T a b ++++=+可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --=解得1n =-(舍),或4n =. 所以n 的值为4.【名师点睛】本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.23.【2018年高考浙江卷】已知等比数列{a n }的公比q >1,且a 3+a 4+a 5=28,a 4+2是a 3,a 5的等差中项.数列{b n }满足b 1=1,数列{(b n +1−b n )a n }的前n 项和为2n 2+n . (1)求q 的值;(2)求数列{b n }的通项公式.【答案】(1)2q =;(2)2115(43)()2n n b n -=-+⋅.【解析】本题主要考查等差数列、等比数列、数列求和等基础知识,同时考查运算求解能力和综合应用能力.(1)由42a +是35,a a 的等差中项得35424a a a +=+, 所以34543428a a a a ++=+=, 解得48a =.由3520a a +=得18()20q q+=, 因为1q >,所以2q =.(2)设1()n n n n c b b a +=-,数列{}n c 前n 项和为n S .由11,1,, 2.n n n S n c S S n -=⎧=⎨-≥⎩解得41n c n =-.由(1)可知12n n a -=,所以111(41)()2n n n b b n -+-=-⋅,故211(45)(),22n n n b b n n ---=-⋅≥,11123221()()()()n n n n n b b b b b b b b b b ----=-+-++-+-23111(45)()(49)()73222n n n n --=-⋅+-⋅++⋅+.设221113711()(45)(),2222n n T n n -=+⋅+⋅++-⋅≥,2211111137()(49)()(45)()22222n n n T n n --=⋅+⋅++-⋅+-⋅ 所以22111111344()4()(45)()22222n n n T n --=+⋅+⋅++⋅--⋅,因此2114(43)(),22n n T n n -=-+⋅≥,又11b =,所以2115(43)()2n n b n -=-+⋅.【名师点睛】用错位相减法求和应注意的问题:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n −qS n ”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.24.【2018年高考江苏卷】设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项为1b ,公比为q 的等比数列.(1)设110,1,2a b q ===,若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围; (2)若*110,,a b m q =>∈∈N ,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,,1n m =+均成立,并求d 的取值范围(用1,,b m q 表示). 【答案】(1);(2)见解析.【解析】本小题主要考查等差和等比数列的定义、通项公式、性质等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力.满分16分.(1)由条件知:.因为1||n n a b b -≤对n =1,2,3,4均成立, 即对n =1,2,3,4均成立,即11,1d 3,32d 5,73d 9,得. 因此,d 的取值范围为.(2)由条件知:.若存在d ,使得1||n n a b b -≤(n =2,3,···,m +1)成立,即,即当时,d 满足. 因为,则,从而,,对均成立.因此,取d =0时,1||n n a b b -≤对均成立.下面讨论数列的最大值和数列的最小值().75[,]32112(,)n n n a n d b -=-=112|()1|n n d ---≤≤≤≤≤≤≤≤7532d ≤≤75[,]32111(1),n n n a b n d b b q -=+-=1111 |1|2,3,,(1())n b n d b q b n m -+--≤=+2,3,,1n m =+1111211n n q q b d b n n ---≤≤--q ∈112n m q q -<≤≤11201n q b n --≤-1101n q b n ->-2,3,,1n m =+2,3,,1n m =+12{}1n q n ---1{}1n q n --2,3,,1n m =+①当时,, 当时,有,从而.因此,当时,数列单调递增, 故数列的最大值为. ②设,当x >0时,,所以单调递减,从而<f (0)=1.当时,, 因此,当时,数列单调递减, 故数列的最小值为. 因此,d 的取值范围为.25.【2017年高考全国I 卷文数】记S n 为等比数列{}n a 的前n 项和,已知S 2=2,S 3=−6.(1)求{}n a 的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列.【答案】(1)(2)nn a =-;(2)122(1)33n n n S +=-+-⋅,证明见解析. 【解析】(1)设{}n a 的公比为q .由题设可得121(1)2,(1) 6.a q a q q +=⎧⎨++=-⎩解得2q =-,12a =-. 故{}n a 的通项公式为(2)nn a =-.(2)由(1)可得11(1)22()1331n n n n a q S q +-==--+-. 2n m ≤≤111 2222111()()()n n n n n n n n q q nq q nq n q q q n n n n n n -------+--+-==---112mq <≤2n m q q ≤≤1() 20n n nn q q q ---+>21n m ≤≤+12{}1n q n ---12{}1n q n ---2m q m-()()21xf x x =-ln 21(0(n )l 22)xf x x '=--<()f x ()f x 2n m ≤≤111112111()()()nn n q q n n f q n n n n --=≤-=<-21n m ≤≤+1{}1n q n --1{}1n q n --mq m11(2)[,]m mb q b q m m-。
等差数列、等比数列的性质-2017年高考数学三轮讲练测核心热点总动员含解析

2016年学易高考三轮复习系列:讲练测之核心热点 【全国通用版】热点八 等差数列,等比数列的性质【名师精讲指南篇】 【高考真题再现】1.【2015全国卷1文】已知{}na 是公差为1的等差数列,nS为{}na 的前项和,若844SS =,则10a =()。
A 。
172B 。
192C 。
10D.12【答案】B2。
【2015全国卷1文】在数列{}n a 中,112,2n n a a a +==,n S 为{}n a 的前n 项和。
若126nS =,则n =。
【答案】6【解析】由12n n a a +=,得12n na a +=,即数列{}n a 是公比为2的等比数列。
()()11212126112n n n a q S q--===--,得6n =。
故填6。
3。
【2015全国卷2文】已知等比数列{}na 满足411=a ,()35441a a a =-,则=2a ( ).A. B. C 。
21 D 。
81【答案】C【解析】由等比数列的性质得2354a aa =,即()24441a a =-,则42a =.所以有3418a qa ==,所以2q =.故2112a a q == 。
故选C.4.【2015全国卷2文】 设nS 是等差数列}{na 的前项和,若3531=++a a a ,则=5S ().A. B 。
C 。
D 。
11【答案】A【解析】由已知1353a aa ++=,则333a =,31a =.又因为()15353552=5=522a a a Sa +⨯== 。
故选A 。
5。
【2015全国卷2理】设nS 是数列{}n a 的前项和,且1111,n n n a a S S ++=-=,则n S =____________________.【答案】1nSn=-6。
【2016全国卷1理】已知等差数列{}na 前项的和为27,10=8a ,则100=a ( )。
A. 100B.99 C 。
98 D.97【答案】C【解析】设等差数列{}n a 的公差为d ,由95279Sa ==,得53a =。
专题10 等差数列与等比数列—三年高考(2015-2017)数学(文)真题分项版解析(原卷版)

专题10 等差数列与等比数列1.【2017浙江,6】已知等差数列{a n }的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6>2S 5”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件2.【2015高考新课标1,文7】已知{}n a 是公差为1的等差数列,n S 为{}n a 的前n 项和,若844S S =,则10a =( ) (A )172 (B )192(C )10 (D )12 3.【2014高考重庆文第2题】在等差数列{}n a 中,1352,10a a a =+=,则7a =( ).5A .8B .10C .14D4. 【2014天津,文5】设{}n a 是首项为1a ,公差为1-的等差数列,n S 为其前n 项和,若,,,421S S S 成等比数列,则1a =( )A.2B.-2C.21D .12- 5. 【2014辽宁文9】设等差数列{}n a 的公差为d ,若数列1{2}n a a为递减数列,则( ) A .0d < B .0d > C .10a d < D .10a d >6. 【2015新课标2文5】设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =( ) A .5 B .7 C .9 D .117. 【2015新课标2文9】已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =( )A.2B.1 1C.2 1D.88.【2014全国2,文5】等差数列{}n a 的公差是2,若248,,a a a 成等比数列,则{}n a 的前n 项和n S =( )A. (1)n n +B. (1)n n -C.(1)2n n + D. (1)2n n -9.【2015高考广东,文13】若三个正数a ,b ,c 成等比数列,其中5a =+5c =-则b = .10. 【2014高考广东卷.文.13】等比数列{}n a 的各项均为正数,且154a a =, 则2122232425log log log log log a a a a a ++++= .11.【2015高考新课标1,文13】数列{}n a 中112,2,n n n a a a S +==为{}n a 的前n 项和,若126n S =,则n = .12.【2015高考浙江,文10】已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a = ,d = .13. 【2015高考陕西,文13】中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为________14.【2017江苏,9】等比数列{}n a 的各项均为实数,其前n 项的和为n S ,已知3676344S S ==,,则8a = .15.【2017课标1,文17】记S n 为等比数列{}n a 的前n 项和,已知S 2=2,S 3=-6.(1)求{}n a 的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列.16.【2017课标II ,文17】已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,11221,1,2a b a b =-=+= (1)若335a b += ,求{}n b 的通项公式; (2)若321T =,求3S .17.【2015高考北京,文16】(本小题满分13分)已知等差数列{}n a 满足1210a a +=,432a a -=.(I )求{}n a 的通项公式;(II )设等比数列{}n b 满足23b a =,37b a =,问:6b 与数列{}n a 的第几项相等? 18. 【2015高考广东,文19】(本小题满分14分)设数列{}n a 的前n 项和为n S ,n *∈N .已知11a =,232a =,354a =,且当2n ≥ 时,211458n n n n S S S S ++-+=+. (1)求4a 的值; (2)证明:112n n a a +⎧⎫-⎨⎬⎩⎭为等比数列; (3)求数列{}n a 的通项公式.19.【2016高考新课标2文数】等差数列{n a }中,34574,6a a a a +=+=.(Ⅰ)求{n a }的通项公式;(Ⅱ) 设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]=0,[2.6]=220.【2016高考北京文数】(本小题13分)已知}{n a 是等差数列,}{n b 是等差数列,且32=b ,93=b ,11b a =,414b a =. (1)求}{n a 的通项公式;(2)设n n n b a c +=,求数列}{n c 的前n 项和.21.【2015高考四川,文16】设数列{a n }(n =1,2,3…)的前n 项和S n 满足S n =2a n -a 3,且a 1,a 2+1,a 3成等差数列. (Ⅰ)求数列的通项公式; (Ⅱ)设数列1{}na 的前n 项和为T n ,求T n . 22.【2016高考四川文科】(本小题满分12分)已知数列{n a }的首项为1,n S 为数列{}n a 的前n 项和,11n n S qS +=+ ,其中q >0,*n N ∈ .(Ⅰ)若2323,,a a a a + 成等差数列,求{}n a 的通项公式;(Ⅱ)设双曲线2221n y x a -= 的离心率为n e ,且22e = ,求22212n e e e ++⋅⋅⋅+.23.【2015高考重庆,文16】已知等差数列{}n a满足3a=2,前3项和3S=9 2 .(Ⅰ)求{}n a的通项公式,(Ⅱ)设等比数列{}n b满足1b=1a,4b=15a,求{}n b前n项和n T.。
高考真题与模拟训练 专题10 等差数列(解析版)

专题10 等差数列第一部分 真题部分一、选择题1.(2021·北京高考真题){}n a 和{}n b 是两个等差数列,其中()15kka kb ≤≤为常值,1288a =,596=a ,1192b =,则3b =( )A .64B .128C .256D .512【答案】B【解析】由已知条件可得5115a a b b =,则51519619264288a b b a ⨯===,因此,1531926412822b b b ++===. 故选:B.2.(2021·北京高考真题)数列{}n a 是递增的整数数列,且13a ≥,12100n a a a ++⋅⋅⋅+=,则n 的最大值为( ) A .9 B .10C .11D .12【答案】C【解析】若要使n 尽可能的大,则1a ,递增幅度要尽可能小,不妨设数列{}n a 是首项为3,公差为1的等差数列,其前n 项和为n S , 则2n a n =+,1131311881002S +=⨯=<,12314121021002S +=⨯=>, 所以n 的最大值为11. 故选:C.3.(2020·浙江高考真题)已知等差数列{a n }的前n 项和S n ,公差d ≠0,11a d≤.记b 1=S 2,b n+1=S 2n+2–S 2n ,n *∈N ,下列等式不可能...成立的是( ) A .2a 4=a 2+a 6 B .2b 4=b 2+b 6C .2428a a a = D .2428b b b =【答案】D【解析】对于A ,因为数列{}n a 为等差数列,所以根据等差数列的下标和性质,由4426+=+可得,4262a a a =+,A 正确;对于B ,由题意可知,21212222n n n n n b S a a S ++++=+=-,1212b S a a ==+, ∴234b a a =+,478b a a =+,61112b a a =+,81516b a a =+. ∴()47822b a a =+,26341112b b a a a a +=+++.根据等差数列的下标和性质,由31177,41288+=++=+可得()26341112784=2=2b b a a a a a a b +=++++,B 正确;对于C ,()()()()2224281111137222a a a a d a d a d d a d d d a -=+-++=-=-,当1a d =时,2428a a a =,C 正确; 对于D ,()()22222478111213452169b a a a d a a d d =+=+=++,()()()()2228341516111125229468145b b a a a a a d a d a a d d =++=++=++,()22428112416832b b b d a d d d a -=-=-.当0d >时,1a d ≤,∴()113220d a d d a -=+->即24280b b b ->;当0d <时,1a d ≥,∴()113220d a d d a -=+-<即24280b b b ->,所以24280b b b ->,D 不正确.故选:D.4.(2019·全国高考真题(理))记n S 为等差数列{}n a 的前n 项和.已知4505S a ==,,则 A .25n a n =- B . 310n a n =- C .228n S n n =-D .2122n S n n =- 【答案】A【解析】由题知,41514430245d S a a a d ⎧=+⨯⨯=⎪⎨⎪=+=⎩,解得132a d =-⎧⎨=⎩,∴25n a n =-,故选A . 二、填空题5.(2021·江苏高考真题)已知等比数列{}n a 的公比为q ,且116a ,24a ,3a 成等差数列,则q 的值是___________. 【答案】4【解析】因为{}n a 为等比数列,且公比为q , 所以21a a q =⋅,231a a q =⋅且10a ≠,0q ≠. 因为116a ,24a ,3a 成等差数列, 所以1321624a a a +=⨯,有21111624a a q a q +⋅=⨯⋅,28160q q -+=, 解得4q =. 故答案为:4.6.(2020·海南高考真题)将数列{2n –1}与{3n –2}的公共项从小到大排列得到数列{a n },则{a n }的前n 项和为________. 【答案】232n n -【解析】因为数列{}21n -是以1为首项,以2为公差的等差数列, 数列{}32n -是以1首项,以3为公差的等差数列,所以这两个数列的公共项所构成的新数列{}n a 是以1为首项,以6为公差的等差数列, 所以{}n a 的前n 项和为2(1)16322n n n n n -⋅+⋅=-, 故答案为:232n n -.7.(2020·全国高考真题(文))记n S 为等差数列{}n a 的前n 项和.若1262,2a a a =-+=,则10S =__________.【答案】25 【解析】{}n a 是等差数列,且12a =-,262a a +=设{}n a 等差数列的公差d根据等差数列通项公式:()11n a a n d +-= 可得1152a d a d +++= 即:()2252d d -++-+= 整理可得:66d =解得:1d =根据等差数列前n 项和公式:*1(1),2n n n S na d n N -=+∈ 可得:()1010(101)1022045252S ⨯-=-+=-+=∴1025S =.故答案为:25.8.(2019·江苏高考真题)已知数列*{}()n a n ∈N 是等差数列,n S 是其前n 项和.若25890,27a a a S +==,则8S 的值是_____. 【答案】16.【解析】由题意可得:()()()25811191470989272a a a a d a d a d S a d ⎧+=++++=⎪⎨⨯=+=⎪⎩, 解得:152a d =-⎧⎨=⎩,则8187840282162S a d ⨯=+=-+⨯=. 9.(2019·全国高考真题(理))记S n 为等差数列{a n }的前n 项和,12103a a a =≠,,则105S S =___________. 【答案】4.【解析】因213a a =,所以113a d a +=,即12a d =,所以105S S =11111091010024542552a d a a a d⨯+==⨯+. 三、解答题10.(2021·天津高考真题)已知{}n a 是公差为2的等差数列,其前8项和为64.{}n b 是公比大于0的等比数列,1324,48b b b =-=. (I )求{}n a 和{}n b 的通项公式; (II )记2*1,n n nc b b n N =+∈, (i )证明{}22n n c c -是等比数列;(ii)证明)*nk n N =∈【答案】(I )21,n a n n N *=-∈,4,n n N b n *=∈;(II )(i )证明见解析;(ii )证明见解析.【解析】(I )因为{}n a 是公差为2的等差数列,其前8项和为64. 所以12818782642a a a a ⨯++⋅⋅⋅+=+⨯=,所以11a =, 所以()12121,n n n n N a a *=+-=-∈; 设等比数列{}n b 的公比为(),0q q >,所以()221321484q b b b q q b q ==-=--,解得4q =(负值舍去),所以114,n n n b q n N b -*==∈; (II )(i )由题意,221441n n n n n b c b =++=, 所以22224211442444n n nn nnn c c ⎛⎫⎛⎫=+-+=⋅ ⎪ ⎪⎝⎭⎝⎭-, 所以220nn c c ≠-,且212222124424n n n n nn c c c c +++⋅==⋅--, 所以数列{}22n n c c -是等比数列;(ii )由题意知,()()22122222121414242222n n n n n n n n n a n n c c a +-+-==<-⋅⋅⋅,12n n-==,所以112nn k k k k-==<, 设10121112322222nn k n k k nT --===+++⋅⋅⋅+∑, 则123112322222n n nT =+++⋅⋅⋅+, 两式相减得21111111122121222222212nn n n nn n n n T -⎛⎫⋅- ⎪+⎝⎭=+++⋅⋅⋅+-=-=--, 所以1242n n n T -+=-,所以1112422n nk nk kk n--==+⎫=-<⎪⎭11.(2021·全国高考真题)记n S是公差不为0的等差数列{}n a的前n项和,若35244,a S a a S==.(1)求数列{}n a的通项公式n a;(2)求使n nS a>成立的n的最小值.【答案】(1)26na n=-;(2)7.【解析】(1)由等差数列的性质可得:535S a=,则:3335,0a a a=∴=,设等差数列的公差为d,从而有:()()22433a a a d a d d=-+=-,()()()41234333322S a a a a a d a d a a d d=+++=-+-++-=-,从而:22d d-=-,由于公差不为零,故:2d=,数列的通项公式为:()3326na a n d n=+-=-.(2)由数列的通项公式可得:1264a=-=-,则:()()214252nn nS n n n-=⨯-+⨯=-,则不等式n nS a>即:2526n n n->-,整理可得:()()160n n-->,解得:1n<或6n>,又n为正整数,故n的最小值为7.12.(2021·全国高考真题)已知数列{}n a满足11a=,11,,2,.nnna naa n++⎧=⎨+⎩为奇数为偶数(1)记2n nb a=,写出1b,2b,并求数列{}n b的通项公式;(2)求{}n a的前20项和.【答案】(1)122,5b b==;(2)300.【解析】(1)由题设可得121243212,1215b a a b a a a==+===+=++=又22211k ka a++=+,2122k ka a+=+,*()k N∈故2223k ka a+=+,即13n nb b+=+,即13n nb b+-=所以{}n b为等差数列,故()21331nb n n=+-⨯=-.(2)设{}n a 的前20项和为20S ,则2012320S a a a a =++++,因为123419201,1,,1a a a a a a =-=-=-,所以()20241820210S a a a a =++++-()1291091021021023103002b b b b ⨯⎛⎫=++++-=⨯⨯+⨯-= ⎪⎝⎭.13.(2021·全国高考真题(理))已知数列{}n a 的各项均为正数,记n S 为{}n a 的前n 项和,从下面①②③中选取两个作为条件,证明另外一个成立.①数列{}n a 是等差数列:②数列是等差数列;③213aa =.注:若选择不同的组合分别解答,则按第一个解答计分. 【答案】答案见解析【解析】选①②作条件证明③:(0)an b a =+>,则()2n S an b =+, 当1n =时,()211a S a b ==+;当2n ≥时,()()221n n n a S S an b an a b -=-=+--+()22a an a b =-+;因为{}n a 也是等差数列,所以()()222a b a a a b +=-+,解得0b =;所以()221n aa n =-,所以213a a =.选①③作条件证明②:因为213a a =,{}n a 是等差数列, 所以公差2112d a a a =-=,所以()21112n n n S na d n a -=+==,)1n =+=,所以是等差数列.选②③作条件证明①:(0)an b a =+>,则()2n S an b =+, 当1n =时,()211a S a b ==+;当2n ≥时,()()221n n n a S S an b an a b -=-=+--+()22a an a b =-+;因为213a a =,所以()()2323a a b a b +=+,解得0b =或43a b =-; 当0b =时,()221,21n a a a a n ==-,当2n ≥时,2-1-2n n a a a =满足等差数列的定义,此时{}n a 为等差数列; 当43a b =-4=3an b an a =+-03a=-<不合题意,舍去.综上可知{}n a 为等差数列.14.(2021·全国高考真题(理))记n S 为数列{}n a 的前n 项和,n b 为数列{}n S 的前n 项积,已知212n nS b +=. (1)证明:数列{}n b 是等差数列; (2)求{}n a 的通项公式.【答案】(1)证明见解析;(2)()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.【解析】(1)由已知212n n S b +=得221n n n b S b =-,且0n b ≠,12n b ≠, 取1n =,由11S b =得132b =, 由于n b 为数列{}n S 的前n 项积,所以1212222212121n n n b b b b b b b ⋅⋅⋅⋅=---, 所以1121121222212121n n n b b b b b b b +++⋅⋅⋅⋅=---,所以111221n n n nb bb b +++=-,由于10n b +≠所以12121n n b b +=-,即112n n b b +-=,其中*n N ∈ 所以数列{}n b 是以132b =为首项,以12d =为公差等差数列; (2)由(1)可得,数列{}n b 是以132b =为首项,以12d =为公差的等差数列,()3111222n nb n ∴=+-⨯=+, 22211n n n b nS b n+==-+,当n =1时,1132a S ==, 当n ≥2时,()121111n n n n n a S S n n n n -++=-=-=-++,显然对于n =1不成立, ∴()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.15.(2019·江苏高考真题)定义首项为1且公比为正数的等比数列为“M -数列”. (1)已知等比数列{a n }满足:245132,440a a a a a a =-+=,求证:数列{a n }为“M -数列”; (2)已知数列{b n }满足:111221,n n n b S b b +==-,其中S n 为数列{b n }的前n 项和. ①求数列{b n }的通项公式;②设m 为正整数,若存在“M -数列”{c n },对任意正整数k ,当k ≤m 时,都有1k k k c b c +成立,求m 的最大值.【答案】(1)见解析;(2)①b n =n ()*n ∈N ;②5.【解析】(1)设等比数列{a n }的公比为q ,所以a 1≠0,q ≠0.由245321440a a a a a a =⎧⎨-+=⎩,得244112111440a q a q a q a q a ⎧=⎨-+=⎩,解得112a q =⎧⎨=⎩.因此数列{}n a 为“M —数列”.(2)①因为1122n n n S b b +=-,所以0n b ≠. 由1111,b S b ==得212211b =-,则22b =. 由1122n n n S b b +=-,得112()n n n n n b b S b b ++=-,当2n ≥时,由1n n n b S S -=-,得()()111122n n n nn n n n n b b b b b b b b b +-+-=---,整理得112n n n b b b +-+=.所以数列{b n }是首项和公差均为1的等差数列. 因此,数列{b n }的通项公式为b n =n ()*n N ∈.②由①知,b k =k ,*k N ∈.因为数列{c n }为“M –数列”,设公比为q ,所以c 1=1,q >0. 因为c k ≤b k ≤c k +1,所以1k k q k q -≤≤,其中k =1,2,3,…,m .当k =1时,有q ≥1;当k =2,3,…,m 时,有ln ln ln 1k kq k k ≤≤-. 设f (x )=ln (1)x x x >,则21ln ()xf 'x x-=. 令()0f 'x =,得x =e .列表如下:x(1,e)e(e ,+∞) ()f 'x+0 –f (x )极大值因为2663=<=,所以max ()(3)3f k f ==.取q =k =1,2,3,4,5时,ln ln k q k,即k k q ≤,经检验知1k q k -≤也成立.因此所求m 的最大值不小于5.若m ≥6,分别取k =3,6,得3≤q 3,且q 5≤6,从而q 15≥243,且q 15≤216, 所以q 不存在.因此所求m 的最大值小于6. 综上,所求m 的最大值为5.16.(2019·北京高考真题(文))设{a n }是等差数列,a 1=–10,且a 2+10,a 3+8,a 4+6成等比数列. (Ⅰ)求{a n }的通项公式;(Ⅱ)记{a n }的前n 项和为S n ,求S n 的最小值. 【答案】(Ⅰ)212n a n =-;(Ⅱ)30-. 【解析】(Ⅰ)设等差数列{}n a 的公差为d ,因为234+10+8+6a a a ,,成等比数列,所以2324(+8)(+10)(+6)a a a =,即2(22)(34)d d d -=-,解得2d =,所以102(1)212n a n n =-+-=-.(Ⅱ)由(Ⅰ)知212n a n =-, 所以22102121112111()224n n S n n n n -+-=⨯=-=--;当5n =或者6n =时,n S 取到最小值30-.第二部分 模拟训练1.若数列{}n a 为等差数列,且16a π=,32a π=,则20cos a =( )A .12B C .12-D . 【答案】C 【解析】3126a a d π-== 201101963a a ππ=+⋅=201041cos coscos cos 3332a ππππ⎛⎫===+=- ⎪⎝⎭ 故选:C2.记n S 为数列{}n a 的前项和,已知点(,)n n a 在直线102y x =-上,若有且只有两个正整数n 满足n S k ≥,则实数k 的取值范围是( ) A .(8,14] B .(14,18] C .(18,20] D .81(18,]4【答案】C【解析】解:由已知可得102n a n =-,由12n n a a --=-,所以数列{}n a 为等差数列,首项为8,公差为-2, 所以2(1)8(2)92n n n S n n n -=+⨯-=-+, 当n =4或5时, n S 取得最大值为20, 因为有且只有两个正整数n 满足n S k ≥, 所以满足条件的4n =和5n =, 因为3618S S ==,所以实数k 的取值范围是(]18,20. 故选:C .3.已知n S 为等差数列{}n a 的前n 项和,3518a S +=-,63a a =-,则下列数值中最大的是( )A .416S B .525S C .636SD .749S【答案】D【解析】设等差数列{}n a 的公差为d,3518a S +=-,63a a =-,()111154+2+5+182+5+2a d a d a d a d ⨯⎧=-⎪∴⎨⎪=-⎩,解得17a =-,2d =,()217282n n n S n n n -=-+⨯=-,281n S n n ∴=-,可得2n S n ⎧⎫⎨⎬⎩⎭是单调递增数列, 所以在416S ,525S ,536S ,749S 中,最大的为749S . 故选:D.4.在正项等比数列{}n a 中.24a =.416a =.满足123m a a a a =21ma +.则m =( ) A .4 B .3C .5D .8【答案】A【解析】由题意得公比2q ===, 首项21422a a q ===, ∴111222n n nn a a q --==⨯=,由21231m m a a a a a +=,()(1)12212331 (2)2222222m m m m m++++++===可得(1)2(1)222m m m ++=,解得4m =,故选:A.5.已知数列{}n a 的前n 项和为n S ,且21122n S n n =+,若()1211n n n n n b a a ++=-⋅,则数列{}n b 的前n 项和n T =______.【答案】,12,1n nn n T n n n ⎧-⎪⎪+=⎨+⎪-⎪+⎩为偶数为奇数【解析】21122n S n n =+, 当1n =时,111a S ==,当2n ≥时,()()2211111112222n n n a S S n n n n n -⎡⎤=-=+--+-=⎢⎥⎣⎦,满足11a =, n a n ∴=,()()()()12111++121111+1nn n n n n n n b a n n a n n +++=-⋅=-⋅=⎛⎫∴⋅ ⎪⎝⎭-, 当n 为偶数时,111111111+122334111n n T n n n n ⎛⎫⎛⎫⎛⎫⎛⎫=-++-++++=-+=- ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭, 当n 为奇数时,1111111121+122334111n n T n n n n +⎛⎫⎛⎫⎛⎫⎛⎫=-++-++-+=--=- ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭, ,12,1n n n n T n n n ⎧-⎪⎪+∴=⎨+⎪-⎪+⎩为偶数为奇数.故答案为:,12,1n nn n T n n n ⎧-⎪⎪+=⎨+⎪-⎪+⎩为偶数为奇数6.数列{}n a 的前n 项和为n S ,23nn n a S +=,数列{}n b 满足()()211332n bn n a a n N *++=-∈,则数列{}n b 的前10项和为______. 【答案】65【解析】由23nn n a S +=知:11123n n n a S ++++=,则1112233n n n n n n a S a S ++++--=-,得1323n n n a a +-=⨯,∴121323n n n a a +++-=⨯,而()()211332n bn n a a n N *++=-∈, ∴1n b n =+,故数列{}n b 的前10项和为1010(211)652T ⨯+==, 故答案为:65.7.设公差不为0的等差数列{}n a 的前n 项和为n S .若数列{}n a 满足:存在三个不同的正整数,,r s t ,使得,,r s t a a a 成等比数列,222,,r s t a a a 也成等比数列,则1990nnS S a +的最小值为___________.【答案】45【解析】设1(1)n a a n d =+-,0d ≠, 由题意,,r s t a a a 成等比数列,s t r s a a a a =,所以s t s t r s r s a a a a s t a a a a r s--===--, 222,,r s t a a a 也成等比数列,2222s t r s a a a a =,所以222222222222s t s t r s r s a a a a s t s t a a a a r s r s---====---, 所以s t r s a a a a =2222s t r s a a a a ==,所以s t r s a a a a =2222s t r s a a a a ==2222s s r r a a s s sa a r r r--===--, 1111(1)(1)s r a a s d a d sd s a a r d a d rd r+--+===+--+,所以10a d -=,1d a =. 1111(1)99099099012(1)22nnn n a na dS S n a a n d n -+++==+++-,4445<<,设9901()22n f n n =++,由勾形函数性质知()f n在上递减,在)+∞上递增,又*n N ∈, (45)45f =,990441(44)454422f =++=,所以()f n 的最小值为45.即1990nnS S a +的最小值为45.故答案为:45.8.已知定义在[0,)+∞上的函数()f x 满足()()151,0222,2x x f x f x x ⎧--≤<⎪=⎨--≥⎪⎩.设()f x 在[)()*22,2n n n -∈N上的最大值记作n a ,n S 为数列{}n a 的前n 项和,则n S 的最大值为___________. 【答案】64【解析】由题意,函数()()151,0222,2x x f x f x x ⎧--≤<⎪=⎨--≥⎪⎩,当1n =时,[0,2)x ∈,此时()151f x x =--,此时函数()f x 在[0,2)上的最大值为()1151115f =--=,所以115a =,当2n =时,[2,4)x ∈,此时()()22f x f x =--,此时2[0,2)x -∈, 所以()()2215212133f x f x x x =--=----=--,此时函数()f x 在[2,4)[0,2)上的最大值为()3133313f =--=,所以213a =,当[22,2)x n n ∈-时,()15[(22)]2(1)15(22)12(1)f x f x n n x n n =-----=------, 此时函数()f x 的最大值为()172f n n =-,所以172n a n =-,当18,n n N +≤≤∈时,0n a >,当9,n n N +≥∈时,0n a <,所以n S 的最大值为8818()8(151)6422a S a +⨯+===. 故答案为:64.9.设等差数列{}n a 的前n 项和为n S ,首项11a =,且41412S S -=.数列{}n b 的前n 项和为n T ,且满足111,21n n b b T +==+.(1)求数列{}n a 和{}n b 的通项公式;(2)求数列n n a b ⎧⎫⎨⎬⎩⎭的前n 项和.【答案】(1)21n a n =-,13n n b -=;(2)1133n n n T -+=-. 【解析】解:(1)设数列{}n a 的公差为d ,且11a =, 又41412S S -=,则()12341412312a a a a a d +++-=++=, 所以2d =,则1(1)221n a n n =+-⋅=-;由121n n b T +=+可得121(2)n n b T n -=+≥, 两式相减得12n n n b b b +-=,13(2)n n b b n +=≥,又21213b T =+=, 所以213b b =,故{}n b 是首项为1,公比为3的等比数列,所以13n n b -=.(2)设1213n n n n a n c b --==, 记{}n c 的前n 项和为n T .则0121135213333n n n T --=++++, 12311352133333n n n T -=++++, 两式相减得:121222221133333n n n n T --=++++-,11112212233122133313n n n n n n T -⎛⎫⨯- ⎪-+⎝⎭=+⨯-=--,所以1133n n n T -+=-.10.已知数列{}n a 满足31212311212121212n n n a a a a ++++=-++++,n *∈N .(1)求数列{}n a 的通项公式;(2)设等差数列{}n b 的前n 项和为n S ,且21122n S n n k =-+,令2n n n c b a kn =-+,求数列{}n c 的前n 项和n T .【答案】(1)112n n a =--;(2)()11122n n n n T +=+- . 【解析】(1)当1n =时,11132a =-,132a ∴=-;当2n ≥时,由31212311212121212n n n a a a a ++++=-++++,①得31121231111212121212nn n a a a a ---++++=-++++,② ①-②得,111121222n n n n n a -=-=-+,112n n a ∴=--,132=-a 也符合,因此,数列{}n a 的通项公式为112n n a =--; (2)由题意,设等差数列{}n b 的公差为d , 则()221111122222n n n d d d S nb n b n n n k -⎛⎫=+=+-=-+ ⎪⎝⎭, 11221220d d b k ⎧=⎪⎪⎪∴-=-⎨⎪=⎪⎪⎩,解得,1010b d k =⎧⎪=⎨⎪=⎩,()111n b b n d n ∴=+-=-;由(1)知,212n n n nc b a kn n =-+=+, 故123231*********2n n nT c c c c n ⎛⎫=++++=+++++++++ ⎪⎝⎭()()111111*********n n n n n n ⎛⎫- ⎪++⎝⎭=+=+--. 11.已知数列{}n a 满足0n a ≠恒成立.(1)若221n n n a a ka ++=且0n a >,当{}lg n a 成等差数列时,求k 的值;(2)若2212n n n a a a ++=且0n a >,当11a =、4a =2a 以及n a 的通项公式;(3)若21312n n n n a a a a +++=-,11a =-,3[4,8]a ∈,20200a <,设n S 是{}n a 的前n 项之和,求2020S 的最大值.【答案】(1)1 ;(2)2a ,()21n n a -=;(3)505143-【解析】(1)若221n n n a a ka ++=且0n a >,所以221lg lg n n n a a ka ++=,即21lg lg 2lg lg n n n a a k a ++=++,当{}lg n a 成等差数列时,21lg lg 2lg n n n a a a ++=+, 所以lg 0k =,解得:1k = ;(2)2212n n n a a a ++=,令1n =可得21322a a a =,即2322a a =,令2n =可得22432a a a =,即2232a =所以42224a =⨯,因为0n a >,所以32a =,解得2a =, 由2212n n n a a a ++=可得2112n n n na aa a +++=, 所以1n n a a +⎧⎫⎨⎬⎩⎭是首项为21a a =2的等比数列,所以112n n na a -+=,所以0212a a =,1322a a =,2432a a =,212n nn a a --=, 以上式子累乘得:()()()()()()21211112101222122n n n n n n n n n na a --------++++-=⨯=⨯=⨯=,所以()21n n a -=,(3)由21312n n n n a a a a +++=-可得132412n n n n a a a a ++++=-, 所以22424111224n n n n n n a a a a a a +++++⎛⎫=-- ⎪=⎝⎭⨯, 因为0n a ≠,所以414n n a a +=,即44n n a a +=, 所以2505504202020162012444444k k a a a a a -=====,因为20200a <,所以504440a <,所以40a <,因为213412a a a a =-,所以341220a a a a =+即2432a a a =, ()()()202015920172610201837112019S a a a a a a a a a a a a =++++++++++++++()48122020a a a a +++++()()250425041214441444a a =+++++++++()250431444a +++++()250441444a +++++()()250412341444a a a a =+++++++,因为2432a a a =,3[4,8]a ∈,所以240a a >,因为40a <,所以20a <,所以()24a a +-≥=-24a a +≤-所以123431a a a a a +++≤-+-,令31y a =-+-2,t ⎡=⎣,21y t =--,对称轴为t =,是开口向上的抛物线,在2,t ⎡∈⎣单调递增,所以t =时取得最大值,故1234a a a a +++最大值为(211-=-,所以()()2504202012341444S a a a a =+++++++最大值为50550514141143---⨯=-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.【2017浙江,6】已知等差数列{a n }的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6>2S 5”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C【考点】 等差数列、充分必要性【名师点睛】本题考查等差数列的前n 项和公式,通过公式的套入与简单运算,可知4652S S S d +-=, 结合充分必要性的判断,若q p ⇒,则p 是q 的充分条件,若q p ⇐,则p 是q 的必要条件,该题“0>d ”⇔“02564>-+S S S ”,故为充要条件.2.【2015高考新课标1,文7】已知{}n a 是公差为1的等差数列,n S 为{}n a 的前n 项和,若844S S =,则10a =( )(A )172 (B )192(C )10 (D )12 【答案】B【解析】∵公差1d =,844S S =,∴11118874(443)22a a +⨯⨯=+⨯⨯,解得1a =12,∴1011199922a a d =+=+=,故选B. 【考点定位】等差数列通项公式及前n 项和公式【名师点睛】解等差数列问题关键在于熟记等差数列定义、性质、通项公式、前n 项和公式,利用方程思想和公式列出关于首项与公差的方程,解出首项与公差,利用等差数列性质可以简化计算.3.【2014高考重庆文第2题】在等差数列{}n a 中,1352,10a a a =+=,则7a =( ).5A .8B .10C .14D【答案】B【解析】试题分析:设等差数列{}n a 的公差为d ,由题设知,12610a d +=,所以,110216ad -==所以,716268a a d =+=+=.故选B.考点:等差数列通项公式.【名师点睛】本题考查了等差数列的概念与通项公式,本题属于基础题,利用下标和相等的两项的和相等更能快速作答. 4. 【2014天津,文5】设{}n a 是首项为1a ,公差为1-的等差数列,n S 为其前n 项和,若,,,421S S S 成等比数列,则1a =( ) A.2 B.-2 C.21 D .12-【答案】D考点:等比数列【名师点睛】本题考查等差数列的通项公式和前n 项和公式,本题属于基础题,利用等差数列的前n 项和公式表示出,,,421S S S 然后依据,,,421S S S 成等比数列,列出方程求出首项.这类问题考查等差数列和等比数列的基本知识,大多利用通项公式和前n 项和公式通过列方程或方程组就可以解出.5. 【2014辽宁文9】设等差数列{}n a 的公差为d ,若数列1{2}na a 为递减数列,则( )A .0d <B .0d >C .10a d <D .10a d >【答案】C 【解析】试题分析:由已知得,11122n n a a a a -<,即111212nn a a a a -<,1n1(a)21n a a --<,又n 1a n a d --=,故121a d <,从而10a d<,选C .【考点定位】1、等差数列的定义;2、数列的单调性.【名师点睛】本题考查等差数列的通项公式、数列的性质等,解答本题的关键,是写出等差数列的通项,利用1{2}na a 是递减数列,确定得到111212nn a a a a -<,得到结论.本题是一道基础题.在考查等差数列等基础知识的同时,考查考生的计算能力. 6. 【2015新课标2文5】设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =( )A .5B .7C .9D .11 【答案】A【考点定位】本题主要考查等差数列的性质及前n 项和公式的应用.【名师点睛】本题解答过程中用到了的等差数列的一个基本性质即等差中项的性质,利用此性质可得1532.a a a +=高考中数列客观题大多具有小、巧、活的特点,在解答时要注意数列相关性质的应用,尽量避免小题大做.7. 【2015新课标2文9】已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =( )A.2B.1 1C.2 1D.8【答案】C 【解析】试题分析:由题意可得()235444412a a a a a ==-⇒=,所以34182a q q a ==⇒= ,故2112a a q ==,选C.【考点定位】本题主要考查等比数列性质及基本运算.【名师点睛】解决本题的关键是利用等比数列性质211n n n a a a -+= 得到一个关于4a 的一元二次方程,再通过解方程求4a 的值,我们知道,等差、等比数列各有五个基本量,两组基本公式,而这两组公式可看作多元方程,利用这些方程可将等差、等比数列中的运算问题转化解关于基本量的方程(组),因此可以说数列中的绝大部分运算题可看作方程应用题,所以用方程思想解决数列问题是一种行之有效的方法.8.【2014全国2,文5】等差数列{}n a 的公差是2,若248,,a a a 成等比数列,则{}n a 的前n项和nS =( )A. (1)n n +B. (1)n n -C. (1)2n n +D. (1)2n n - 【答案】A【解析】由已知得,2428a a a =⋅,又因为{}n a 是公差为2的等差数列,故2222(2)(6)a d a a d +=⋅+,22(4)a +22(12)a a =⋅+,解得24a =,所以2(2)n a a n d =+-2n =,故1()(n 1)2n n n a a S n +==+.【考点定位】1.等差数列;2.等比数列.【名师点睛】本题主要考查了等差数列的通项公式,等比中项的概念,等差数列的前n 项和公式,本题属于基础题,解决本题的关健在于熟练掌握相应的公式.9.【2015高考广东,文13】若三个正数a ,b ,c 成等比数列,其中5a =+5c =-则b = . 【答案】1【考点定位】等比中项.【名师点晴】本题主要考查的是等比中项,属于容易题.解题时要抓住关键字眼“正数”,否则很容易出现错误.解本题需要掌握的知识点是等比中项的概念,即若a ,G ,b 成等比数列,则G 称为a 与b 的等比中项,即2G ab =. 10. 【2014高考广东卷.文.13】等比数列{}n a 的各项均为正数,且154a a =,则2122232425log log log log log a a a a a ++++= .【答案】5.【解析】由题意知21534a a a ==,且数列{}n a 的各项均为正数,所以32a =,()()()223512345152433352a a a a a a a a a a a a a ∴=⋅⋅=⋅==,()521222324252123452log log log log log log log 25a a a a a a a a a a ∴++++===.【考点定位】本题考查等比数列的基本性质与对数的基本运算,属于中等偏难题.【名师点晴】本题主要考查的是等比数列的性质和对数的基本运算,属于中等偏难题.解题时要抓住关键字眼“正数”,否则很容易出现错误.解本题需要掌握的知识点是等比数列的性质和对数的基本运算,即等比数列{}n a 中,若m n p q +=+(m 、n 、p 、q *∈N ),则m np q a a a a =,()log log log a a a MN =M +N (0a >,1a ≠,0M >,0N >).11.【2015高考新课标1,文13】数列{}n a 中112,2,n n n a a a S +==为{}n a 的前n 项和,若126n S =,则n = .【答案】6考点:等比数列定义与前n 项和公式【名师点睛】解等差数列问题关键在于熟记等比数列定义、性质、通项公式、前n 项和公式,利用方程思想和公式列出关于首项与公比的方程,解出首项与公比,利用等比数列性质可以简化计算.12.【2015高考浙江,文10】已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a = , d = .【答案】2,13- 【解析】由题可得,2111(2)()(6)a d a d a d +=++,故有1320a d +=,又因为1221a a +=,即131a d+=,所以121,3d a =-=.【考点定位】1.等差数列的定义和通项公式;2.等比中项.【名师点睛】本题主要考查等差数列的定义和通项公式.主要考查学生利用等差数列的定义以及等比中项的性质,建立方程组求解数列的首项与公差.本题属于容易题,主要考查学生正确运算的能力.13. 【2015高考陕西,文13】中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为________ 【答案】5【解析】若这组数有21n +个,则11010n a +=,212015n a +=,又12112n n a a a +++=,所以15a =;若这组数有2n 个,则1101022020n n a a ++=⨯=,22015n a =,又121n n n a a a a ++=+,所以15a =;故答案为5【考点定位】等差数列的性质.【名师点睛】1.本题考查等差数列的性质,这组数字有可能是偶数个,也有可能是奇数个.然后利用等差数列性质m n p q m n p q a a a a +=+⇒+=+.2.本题属于基础题,注意运算的准确性.14.【2017江苏,9】等比数列{}n a 的各项均为实数,其前n 项的和为n S ,已知3676344S S ==,,则8a = ▲ .【答案】32【考点】等比数列通项【名师点睛】在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.15.【2017课标1,文17】记S n 为等比数列{}n a 的前n 项和,已知S 2=2,S 3=-6.(1)求{}n a 的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列.【答案】(1)(2)nn a =-;(2)32)1(321+⋅-+=n n n S ,证明见解析.【解析】试题分析:(1)由等比数列通项公式解得2q =-,12a =-;(2)利用等差中项证明S n +1,S n ,S n +2成等差数列.试题解析:(1)设{}n a 的公比为q .由题设可得121(1)2(1)6a q a q q +=⎧⎨++=-⎩ ,解得2q =-,12a =-.故{}n a 的通项公式为(2)n na =-.(2)由(1)可得11(1)22()1331n n n n a q S q +-==--+-. 由于3212142222()2[()]2313313n n n n n n n n S S S +++++-+=--++=-=-, 故1n S +,n S ,2n S +成等差数列. 【考点】等比数列【名师点睛】等差、等比数列的性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.16.【2017课标II ,文17】已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,11221,1,2a b a b =-=+= (1)若335a b += ,求{}n b 的通项公式;(2)若321T =,求3S .【答案】(Ⅰ);(Ⅱ)当时,.当时,.试题解析:(1)设的公差为d ,的公比为q ,则,.由得d+q=3. ①(1) 由得 ②联立①和②解得(舍去),因此的通项公式(2) 由得.解得当时,由①得,则. 当时,由①得,则.【考点】等差、等比数列通项与求和【名师点睛】在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法. 17.【2015高考北京,文16】(本小题满分13分)已知等差数列{}n a 满足1210a a +=,432a a -=.(I )求{}n a 的通项公式;(II )设等比数列{}n b 满足23b a =,37b a =,问:6b 与数列{}n a 的第几项相等?【答案】(I )22na n =+;(II )6b 与数列{}n a 的第63项相等.试题解析:(Ⅰ)设等差数列{}n a 的公差为d .因为432a a -=,所以2d =.又因为1210a a +=,所以1210a d +=,故14a =.所以42(1)22na n n =+-=+ (1,2,)n =L .(Ⅱ)设等比数列{}n b 的公比为q .因为238b a ==,3716b a ==, 所以2q =,14b =. 所以61642128b -=⨯=.由12822n =+,得63n =. 所以6b 与数列{}n a 的第63项相等. 考点:等差数列、等比数列的通项公式.【名师点晴】本题主要考查的是等差数列的通项公式和等比数列的通项公式,属于中档题.本题通过求等差数列和等比数列的基本量,利用通项公式求解.解本题需要掌握的知识点是等差数列的通项公式和等比数列的通项公式,即等差数列的通项公式:()11n a a n d =+-,等比数列的通项公式:11n n a a q-=.18. 【2015高考广东,文19】(本小题满分14分)设数列{}n a 的前n 项和为n S ,n *∈N .已知11a =,232a =,354a =,且当2n ≥ 时,211458n n n n S S S S ++-+=+.(1)求4a 的值; (2)证明:112n n a a +⎧⎫-⎨⎬⎩⎭为等比数列; (3)求数列{}n a 的通项公式.【答案】(1)78;(2)证明见解析;(3)()11212n n a n -⎛⎫=-⨯ ⎪⎝⎭.再将数列112n n a a +⎧⎫-⎨⎬⎩⎭的通项公式转化为数列12n n a ⎧⎫⎪⎪⎪⎪⎨⎬⎛⎫⎪⎪⎪⎪⎪⎝⎭⎩⎭是等差数列,进而可得数列{}n a 的通项公式. 试题解析:(1)当2n =时,4231458S S S S +=+,即435335415181124224a ⎛⎫⎛⎫⎛⎫+++++=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得:478a =(2)因为211458n n n n S S S S ++-+=+(2n ≥),所以21114444n n n n n n S S S S S S ++-+-+-=-(2n ≥),即2144n n n a a a +++=(2n ≥),因为3125441644a a a +=⨯+==,所以2144n n n a a a +++=,因为()2121111111114242212142422222n n n n n n n n n n n n n n n n n a a a a a a a a a a a a a a a a a +++++++++++-----====----,所以数列112n n a a +⎧⎫-⎨⎬⎩⎭是以21112a a -=为首项,公比为12的等比数列(3)由(2)知:数列112n n a a +⎧⎫-⎨⎬⎩⎭是以21112a a -=为首项,公比为12的等比数列,所以111122n n n a a -+⎛⎫-= ⎪⎝⎭即1141122n n n na a ++-=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,所以数列12n n a ⎧⎫⎪⎪⎪⎪⎨⎬⎛⎫⎪⎪⎪⎪⎪⎝⎭⎩⎭是以1212a =为首项,公差为4的等差数列,所以()2144212nna n n =+-⨯=-⎛⎫⎪⎝⎭,即()()111422122nn n a n n -⎛⎫⎛⎫=-⨯=-⨯ ⎪ ⎪⎝⎭⎝⎭,所以数列{}n a 的通项公式是()11212n n a n -⎛⎫=-⨯ ⎪⎝⎭考点:1、等比数列的定义;2、等比数列的通项公式;3、等差数列的通项公式.【名师点晴】本题主要考查的是等比数列的定义、等比数列的通项公式和等差数列的通项公式,属于难题.本题通过将n S 的递推关系式转化为n a 的递推关系式,利用等比数列的定义进行证明,进而可得通项公式,根据通项公式的特点构造成等差数列进行求解.解题时一定要注意关键条件“2n ≥”,否则很容易出现错误.解本题需要掌握的知识点是等比数列的定义、等比数列的通项公式和等差数列的通项公式,即等比数列的定义:1n na q a +=(常数),等比数列的通项公式:11n n a a q-=,等差数列的通项公式:()11n a a n d =+-.19.【2016高考新课标2文数】等差数列{n a }中,34574,6a a a a +=+=.(Ⅰ)求{n a }的通项公式;(Ⅱ) 设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]=0,[2.6]=2. 【答案】(Ⅰ)235n n a +=;(Ⅱ)24. 【解析】试题分析:(Ⅰ) 题目已知数列{n a }是等差数列,根据通项公式列出关于1a ,d 的方程,解方程求得1a ,d ,从而求得n a ;(Ⅱ)根据条件[]x 表示不超过x 的最大整数,求n b ,需要对n =分类讨论,再求数列{}n b 的前10项和.当n =1,2,3时,2312,15n n b +≤<=; 当n =4,5时,2323,25n n b +≤<=;当n =6,7,8时,2334,35n n b +≤<=;当n =9,10时,2345,45n n b +≤<=,所以数列{}n b 的前10项和为1322334224⨯+⨯+⨯+⨯=. 考点:等差数列的性质 ,数列的求和. 【名师点睛】求解本题会出现以下错误:①对“[]x 表示不超过x 的最大整数”理解出错;20.【2016高考北京文数】(本小题13分)已知}{n a 是等差数列,}{n b 是等差数列,且32=b ,93=b ,11b a =,414b a =. (1)求}{n a 的通项公式;(2)设n n n b a c +=,求数列}{n c 的前n 项和.【答案】(1)21n a n =-(1n =,2,3,⋅⋅⋅);(2)2312-+n n【解析】试题分析:(Ⅰ)求出等比数列{}n b 的公比,求出11b a =,414b a =的值,根据等差数列的通项公式求解;(Ⅰ)根据等差数列和等比数列的前n 项和公式求数列}{n c 的前n 项和. 试题解析:(I )等比数列{}n b 的公比32933b q b ===,所以211b b q==,4327b b q ==. 设等差数列{}n a 的公差为d . 因为111a b ==,14427a b ==, 所以11327d +=,即2d =.所以21n a n =-(1n =,2,3,⋅⋅⋅).()11321133n n S n -=++⋅⋅⋅+-+++⋅⋅⋅+ ()12113213n n n +--=+-2312n n -=+.考点:等差、等比数列的通项公式和前n 项和公式,考查运算能力.【名师点睛】1.数列的通项公式及前n 项和公式都可以看作项数n 的函数,是函数思想在数列中的应用.数列以通项为纲,数列的问题,最终归结为对数列通项的研究,而数列的前n 项和S n 可视为数列{S n }的通项.通项及求和是数列中最基本也是最重要的问题之一;2.数列的综合问题涉及到的数学思想:函数与方程思想(如:求最值或基本量)、转化与化归思想(如:求和或应用)、特殊到一般思想(如:求通项公式)、分类讨论思想(如:等比数列求和,1=q 或1≠q )等.21.【2015高考四川,文16】设数列{a n }(n =1,2,3…)的前n 项和S n 满足S n =2a n -a 3,且a 1,a 2+1,a 3成等差数列. (Ⅰ)求数列的通项公式; (Ⅱ)设数列1{}na 的前n 项和为T n ,求T n . 【解析】(Ⅰ) 由已知S n =2a n -a 1,有a n =S n -S n -1=2a n -2a n -1(n ≥2)(Ⅱ)由(Ⅰ)得112n n a =所以T n =211[1()]111122 (11222212)n n n-+++==-- 【考点定位】本题考查等差数列与等比数列的概念、等比数列通项公式与前n 项和等基础知识,考查运算求解能力.【名师点睛】数列问题放在解答题第一题,通常就考查基本概念和基本运算,对于已知条件是S n 与a n 关系式的问题,基本处理方法是“变更序号作差”,这种方法中一定要注意首项a 1是否满足一般规律(代入检验即可,或者根据变换过程中n 的范围和递推关系中的表达式判断).数列求和时,一定要注意首项、公比和项数都不能出错.同时注意,对于较为简单的试题,解析步骤一定要详细具体,不可随意跳步.属于简单题. 22.【2016高考四川文科】(本小题满分12分)已知数列{n a }的首项为1,n S 为数列{}n a 的前n 项和,11n n S qS +=+ ,其中q >0,*n N ∈ .(Ⅰ)若2323,,a a a a + 成等差数列,求{}n a 的通项公式;(Ⅱ)设双曲线2221n y x a -= 的离心率为n e ,且22e = ,求22212n e e e ++⋅⋅⋅+.【答案】(Ⅰ)1=n n a q -;(Ⅱ)1(31)2n n +-.【解析】试题分析:(Ⅰ)已知n S 的递推式11n n S qS +=+,一般是写出当2n ≥时,11n n S qS -=+,两式相减,利用1n n n a S S -=-,得出数列{}n a 的递推式,从而证明{}n a为等比数列,利用等比数列的通项公式得到结论;(Ⅱ)先利用双曲线的离心率定义得到n e 的表达式,再由22e =解出q 的值,最后利用等比数列的求和公式求解计算.由2323+a a a a ,,成等差数列,可得32232=a a a a ++,所以32=2,a a ,故=2q . 所以1*2()n n a n -=?N .(Ⅱ)由(Ⅰ)可知,1n n a q -=. 所以双曲线2221ny x a -=的离心率n e =.由22e =解得q =所以,22222(1)12222(1)2(11)(1+)[1]1[1]11(31).2n n n n ne e e q q q n q q n q n --++鬃?=+++鬃?+-=+++鬃?=+-=+-,考点:数列的通项公式、双曲线的离心率、等比数列的求和公式 23.【2015高考重庆,文16】已知等差数列{}n a 满足3a =2,前3项和3S =92. (Ⅰ)求{}n a 的通项公式,(Ⅱ)设等比数列{}n b 满足1b =1a ,4b =15a ,求{}n b 前n 项和n T . 【答案】(Ⅰ)+1=2n n a ,(Ⅱ)21nn T =-. 【解析】试题分析:(Ⅰ)由已知及等差数列的通项公式和前n 项和公式可得关于数列的首项a 1和公式d 的二元一次方程组,解此方程组可求得首项及公差的值,从而可写出此数列的通项公式, (Ⅱ)由(Ⅰ)的结果可求出b 1和b 4的值,进而就可求出等比数列的公比,再由等比数列的前n 项和公式1(1)1n n b q T q-=-即可求得数列{}n b 前n 项和n T .试题解析: (1)设{}n a 的公差为d ,则由已知条件得(2)由(1)得141515+1=1==82b b a =,. 设{}n b 的公比为q,则341q 8b b ==,从而2q =. 故{}n b 的前n 项和1(1)1(12)21112n n n n b q T q -?===---.【考点定位】1. 等差数列,2. 等比数列.【名师点睛】本题考查等差数列及等比数列的概念、通项公式及前n 项的求和公式,利用方程组思想求解.本题属于基础题,注意运算的准确性.。
