钢结构基本原理课后作业答案第二章和第四章
(0763)《钢结构基本原理》网上作业题及答案

(0763)《钢结构基本原理》网上作业题及答案1:第四章轴心受力构件2:第五章受弯构件3:第三章钢结构的连接4:第一章绪论5:第六章拉弯与压弯构件6:第二章钢结构的材料1:[论述题]11-17题:11、选择钢材屈服强度作为静力强度标准值以及将钢材看作是理想弹性―塑性材料的依据是什么?12、请问钢材的强度常常用哪两个指标来表示?设计中如何考虑或使用这两个指标?13、钢结构是用钢板、热轧型钢或冷加工成型的薄壁型钢制造而成的结构。
钢结构与其它材料的结构相比,钢结构具有哪些特点?14、钢材塑性性能可用哪两个指标表示?这两个指标有什么特点?15、引起钢材变脆的因素有哪些?16、钢材塑性性能伸长率δ5和δ10各表示什么含义?数值的大小关系如何?17、选择结构用钢材时要考虑哪些材料性能?参考答案:11、答:依据:他是①钢材弹性及塑性工作的分界点,且钢材屈服后,塑性变形很大(2%―3%)。
极易为人们察觉,可以及时处理,避免突然破坏;②从屈服开始到断裂,塑性工作区域很大,比弹性工作区域约大200倍,是钢材极大的后备强度,且抗拉强度和屈服强度的比例又较大,这二点一起赋予构件屈服强度作为强度极限的可靠安全储备。
弹塑性材料的依据:①对于没有缺陷和残余应力影响的试件,比例极限和屈服强度是比较接近,又因为钢材开始屈服时应变很小,因此近似认为在屈服点以前钢材为完全弹性的,即将屈服点以前的应力应变图简化为一条斜线;②因为钢材流幅相当长,而强化阶段的强度在计算中又不用,从而将屈服点后的应力应变图简化为一条水平线。
12、答:钢材的强度指标常常用屈服强度和抗拉强度来表示。
依据屈服强度确定构件截面尺寸,抗拉强度体现了构件或结构的安全储备。
13、答:优点:⑴钢结构强度高,强重比大、塑性好、韧性好;⑵材质均匀,几乎完全符合我们学过的力学假定;⑶制作简便,施工工期短。
缺点:⑴耐热但不耐火;⑵钢结构易腐蚀,维护费用大。
14、答:伸长率和断面收缩率;伸长率测量方便;断面收缩率能更好地衡量材料的塑性性能。
钢结构基本原理课后习题答案
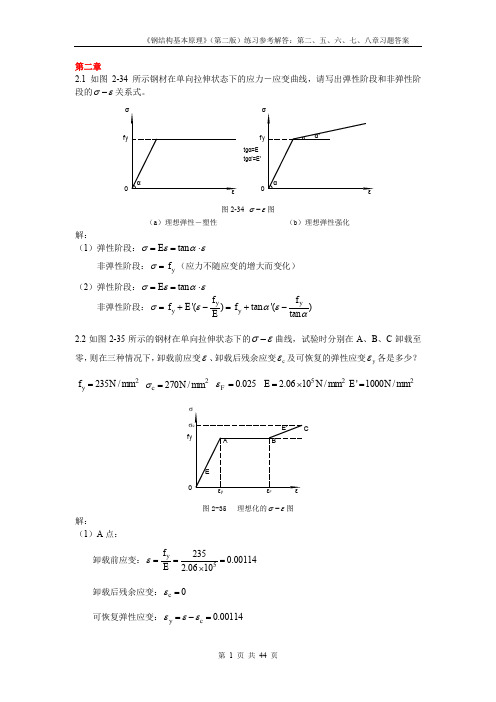
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基础第四章课后习题答案
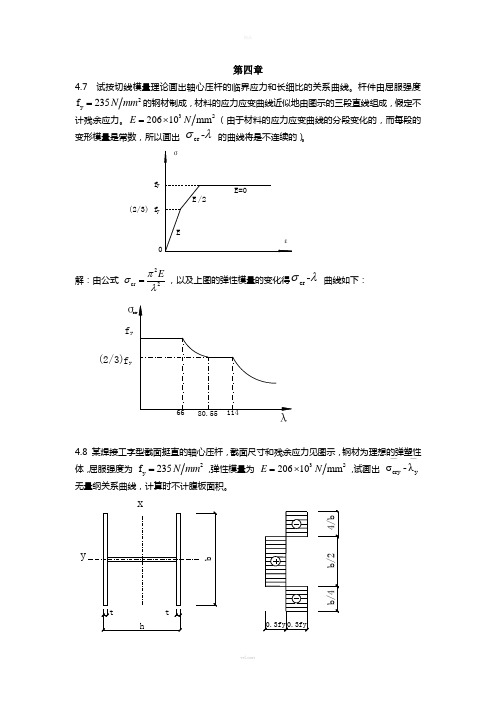
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cry y σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为0.6f yfyλσ0.20.40.60.81.0cryN=1500KN 。
解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
钢结构基础(第二版)课后习题第四章答案
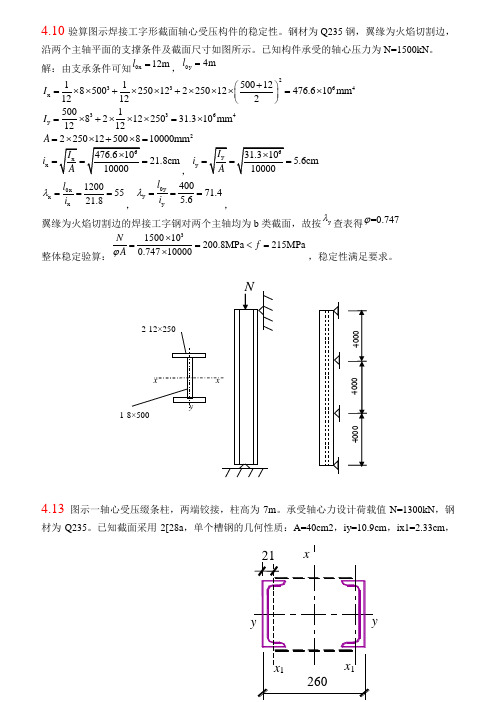
4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500kN 。
解:由支承条件可知0x 12m l =,0y 4ml =23364x 1150012850025012225012476.610mm12122I +⎛⎫=⨯⨯+⨯⨯+⨯⨯⨯=⨯ ⎪⎝⎭ 3364y 5001821225031.310mm 1212I =⨯+⨯⨯⨯=⨯2225012*********mm A =⨯⨯+⨯=x 21.8cm i ===,y 5.6cmi ===0x x x 12005521.8l i λ===,0y y y 40071.45.6l i λ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b 类截面,故按y λ查表得=0.747ϕ整体稳定验算:3150010200.8MPa 215MPa0.74710000N f A ϕ⨯==<=⨯,稳定性满足要求。
4.13图示一轴心受压缀条柱,两端铰接,柱高为7m 。
承受轴心力设计荷载值N=1300kN ,钢材为Q235。
已知截面采用2[28a ,单个槽钢的几何性质:A=40cm2,iy=10.9cm ,ix1=2.33cm ,Ix1=218cm4,y0=2.1cm ,缀条采用∟45×5,每个角钢的截面积:A1=4.29cm2。
试验算该柱的整体稳定性是否满足?解:柱为两端铰接,因此柱绕x 、y 轴的计算长度为:0x 0y 7ml l ==224x x10262221840 2.19940.8cm 22b I I A y ⎡⎤⎡⎤⎛⎫⎛⎫=+-=+-=⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦x 11.1cm i === 0x xx 70063.111.1l i λ=== 0y y y 70064.210.9l i λ===0x 65.1λ===格构柱截面对两轴均为b 类截面,按长细比较大者验算整体稳定既可。
钢结构基本原理-同济第二版沈祖炎重点习题课后答案
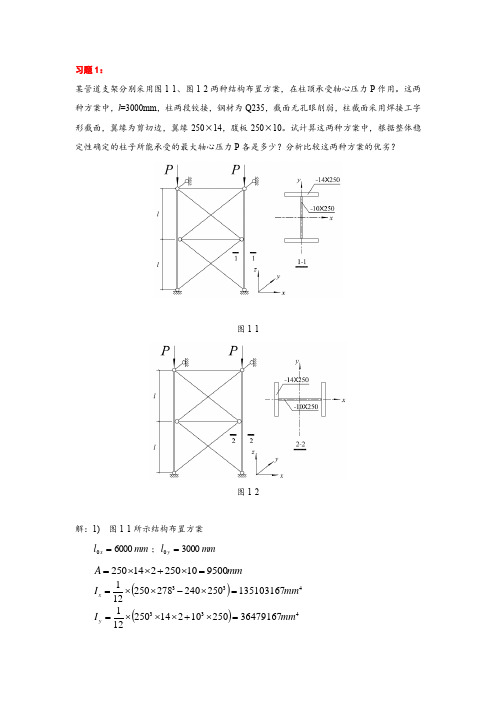
习题1:某管道支架分别采用图1-1、图1-2两种结构布置方案,在柱顶承受轴心压力P 作用。
这两种方案中,l =3000mm ,柱两段铰接,钢材为Q235,截面无孔眼削弱,柱截面采用焊接工字形截面,翼缘为剪切边,翼缘-250×14,腹板-250×10。
试计算这两种方案中,根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少?分析比较这两种方案的优劣?图1-1图1-2解:1) 图1-1所示结构布置方案mm l x 60000=;mm l y 30000=mm A 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=mm A I i x x 3.1199500135103167===;mm AI i y y 0.62950036479167===3.503.11960000===x x x i l λ;4.480.6230000===y y y i l λ此截面对x 轴为b 类,对y 轴为c 类,查表得855.0=x ϕ(附表4-4);785.0=y ϕ(附表4-5)应根据y ϕ确定柱子整体稳定的承载力kN Af P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案mm l x 60000=;mm l y 30000=mm A 9500=;mm i x 0.62=;mm i y 3.119= 8.960.6260000===x x x i l λ;1.253.11930000===y y y i l λ此截面对x 轴为c 类,对y 轴为b 类,查表得478.0=x ϕ(附表4-5);953.0=y ϕ(附表4-4)应根据x ϕ确定柱子整体稳定的承载力kN Af P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同,但是图1-1所示方案(为下文表述的方便,以后简称方案A )的承载力为1603kN ,而图1-2所示方案(为下文表述的方便,以后简称方案B )的承载力仅为976kN 。
钢结构第四章答案

习题参考答案题:欧拉临界荷载的推证(一端固定,一端自由);解:由构件x 处截面的力矩平衡,得到方程)()(''y P x h P EIy -+-=δα,可进行数学推导,求得欧拉临界荷载值。
EIP Ph x EI P -EI P ''δαα++=+y ,令EI Pk 2=,则δαα2222k h k x k -k ''++=+y ;显然平衡方程即为二阶常系数非齐次线性方程的求解。
齐次方程求解:0k ''2=+y ,令rx e y =,便可解得ki r ±=,故通解为sinkx A coskx A y 21+=。
方程的特解求解:有0x 222e )x (k h k x k -ϕδαα=++,其中)x (ϕ为一次多项式,由于0不是特征方程的根,可令21B B y +=x ,代入方程得δαα222212)(k h k x k B x B k ++-=+,则α-=1B ,δα+=h B 2。
于是可得方程的全解为:δαα++-+=h x sinkx A coskx A y 21。
边界条件:⎩⎨⎧=+-=⇒⎩⎨⎧=-=++⇒==k A h A kA h A y y /)(000)0(')0(2121αδααδα;所以:22sinkh coskh )(y(h)δαααδαδ++-++-==h h kh ,将方程进行变换便可得到h kααδ-=tankh 2,即得证P84中的式(4-4b )。
当2kh π=时,自由端位移2δ趋近于无穷大,即构件失稳,则欧拉临界荷载为2222E 4h)2h (k EI P ππ===,即22E 4h EI P π=。
4.9题:要求按照等稳定条件确定焊接工字型截面轴心压杆腹板的高厚比。
钢材为Q235,杆件长细比为100=λ,翼缘有火焰切割和轧制边两种。
计算结果请与规范规定作对比。
解: 轴心压杆的弹性模量修正系数为,.18287.0)10206/(235))10206/(2351000248.01(1001013.0/)/0248.011013.0332222≤=⨯⨯⨯⨯⨯-⨯⨯=-=Ef E f y y λλη(由表4-4,翼缘为火焰切割边的焊接工字型截面的强弱轴均为b 类截面,而翼缘为轧制边的焊接工字型截面的弱轴为c 类截面,故由杆件长细比查附表17-2和17-3得轴心受压构件的稳定系数分别为0.555和0.463。
《钢结构基本原理》作业解答

《钢结构基本原理》作业解答[判断题]18、在格构式柱中,缀条可能受拉,也可能受压,但设计时缀条应按拉杆来进行设计。
参考答案:错误[论述题]14、工字形截面绕强轴的塑性发展系数与绕弱轴的塑性发展系数哪个大?为什么?15、对于轴压构件,有时也常采用格构式截面(1)请说明什么情况下比较适合采用格构式截面?(2)采用格构式截面时,为什么采用换算长细比来计算虚轴的稳定承载力?(3)在已知双肢格构柱截面形式的条件下,如何计算换算长细比和验算绕虚轴的稳定性?(4)对于双肢缀条柱,除了上一问的验算外还需验算哪些内容?答:14、答:绕弱轴的塑性发展系数大;绕强轴受弯,翼?发生屈服以后截面继续发生塑性发展的潜力不大。
16、答:(1)A 、柱的计算长度较大 B 、柱所承受的轴向荷载较大 C 、对柱的刚度要求较严格,这样情况下截面强度富余,由稳定控制做实腹式浪费材料,所以采用格构式。
(2)构件在微弯的临界平衡状态外,将在截面上产生剪力,从而产生剪切变形。
对于实腹式构件而言,剪力由腹板承担,而腹板的剪切刚度又很大,所以剪切变形小可以忽略不计,但是对于由缀材组成的格构式截面,剪力由缀材承担变形较大不能忽略。
考虑剪切变形的影响,构件的临界承载力降低了,规范用增大长细比的方法考虑这种影响,所以绕虚轴失稳时,采用换算长细比。
1227A A x ox +=λλ(3)缀条柱 (4)还需验算:A 、格构柱的净截面强度;B 、格构柱绕实轴的稳定性 C 、格构柱绕两个轴的长细比是否需要满足刚度要求 D 、单肢的稳定 E 、缀条的稳定 F 、缀条与柱肢连接的强度验算.论述题]13、某焊接工字形截面柱,截面几何尺寸如图所示。
柱的上、下端均为铰接,柱高4。
2m,承受的轴心压力设计值为1000kN ,钢材为Q235,翼缘为火焰切割边,焊条为E43系列,手工焊。
试验算该柱的整体稳定性。
参考资料: f=215N/mm 2【论述题]12、分析图示实腹轴心受压柱头的传力路线,写出焊缝①、②的计算表达式。
钢结构基础第四章课后习题答案
b不计残余应力。
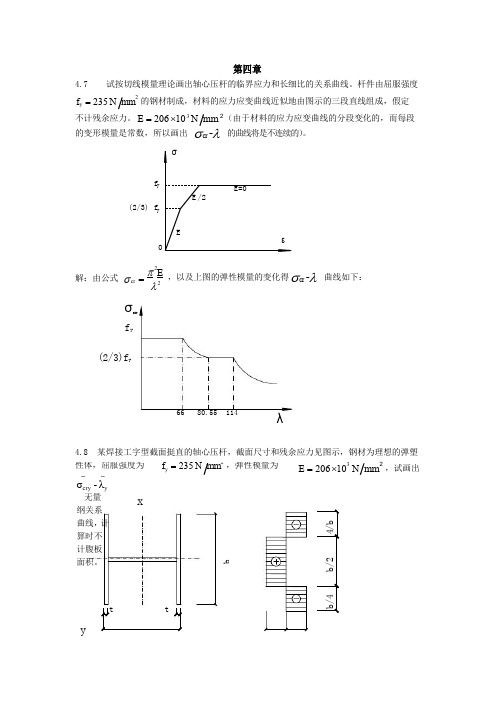
E=206⨯10N mm(由于材料的应力应变曲线的分段变化的,而每段yycr性体,屈服强度为f y=235N mm2,弹性模量为第四章4.7试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度f y=235N mm2的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定32的变形模量是常数,所以画出σcr-λ的曲线将是不连续的)。
f(2/3)f解:由公式σcr=σf y(2/3)f yπ2Eλ2,以及上图的弹性模量的变化得σcr-λ曲线如下:6680.55114λ4.8某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑——σcry-λy无量纲关系曲线,计算时不计腹板面积。
yxE=206⨯103N mm2,试画出h0.3fy0.3fyf y0.6f y全截面对y 轴的惯性矩 I y = 2tb 12 ,弹性区面积的惯性矩 I ey = 2t (kb ) 12π 2E π 2E I ey λ y 2 λ y 2 π 2E 3 λ y 2σ c r = = (1- 0.3k 2 ) f y3y 2解:当 σ cr ≤ f y - 0.3 f y = 0.7 f y , 构件在弹性状态屈曲;当 σ cr > f y - 0.3 f y = 0.7 f y 时, 构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图3 3 σ cry = ⨯ = = I y 2tb 3 12k截面的平均应力2btf y - 2kbt ⨯ 0.5⨯ 0.6kf y 2bt——二者合并得 σcry - λy 的关系式σ cry+ (0.027λ4 - 3)σ cry + 3σcry -1 = 0 画图如下σ1.00.8 0.6 0.4 0.2λ4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为 Q235 钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
钢结构-第四章课后答案

P1084.1解: 示意图要画焊缝承受的剪力V=F=270kN ;弯矩M=Fe=270300=81kN.mI x =[0.8(38-20.8)3]/12+[(15-2)119.52]2=13102cm 4=腹板A e =0.8(38-20.8)=29.12 cm 2截面最大正应力max M/W= 81106200/13102104=123.65 N/mm 2f t w =185N/mm 2剪力全部由腹板承担=V/A w =270103/2912=92.72 N/mm 2 =f v w =125N/mm 2腹板边缘处”1”的应力 1(M/W)(190/200) =123.65(190/200)=210.19=117.47腹板边缘处的折算应力应满足 2213 1.1w zs t f σστ=+≤22117.47392.72=+⨯=198..97N/mm 2 1.1f t w =203.5N/mm 2焊缝连接部位满足要求4.2解:(1) 角钢与节点板的连接焊缝“A ”承受轴力N=420kN连接为不等边角钢长肢相连 题意是两侧焊肢背分配的力N 1=0.65 420=273 kN肢背分配的力N 2=0.35 420=147 kNh fmin =1.5(t max )1/2=1.5(10)1/2=4.74mmh fmax =1.2(t min )=1.2(6)=7.2mm取h f =6mm 肢背需要的焊缝长度l w1=273103/(20.76160)+26=203.12+12=215.13mm 肢尖需要的焊缝长度l w2=147103/(20.76160)+26=109.38+12=121.38mm 端部绕角焊2h f 时,应加h f (书中未加)取肢背的焊缝长度l w1=220mm ;肢尖的焊缝长度l w2=125mm 。
l wmax =60h f =360mm ;l wmin =8h f =48mm ;焊缝“A ”满足要求4.3解:节点板与端板间的连接焊缝“B ”承受拉力N 对焊缝“B ”有偏心,焊缝“B ”承受拉力N=(1.5/1.8) 420=350kN ;剪力V=(1/1.8) 420=233.33 kN ;弯矩M=35050=17.5 kN.mh fmin =1.5(t max )1/2=1.5(20)1/2=6.71mm h fmax =1.2(t min )=1.2(10)=12mm焊缝“B ”h f =7mm焊缝“B ”A 点的力最大焊缝“B ”承受的剪应力=233.33103/(20.77386)=61.68 N/mm 2焊缝“B ”承受的最大正应力 =N/Ae+M/W=350103/(20.77386)+17.5106200/(20.773863/12) =92.52+71.91 =164.43 N/mm 2验算焊缝“B ”的强度=148.19 N/mm 2<f f w 焊缝“B ”满足要求。
钢结构基本原理(第二版)习题参考解答第二章

钢结构基本原理(第二版)习题参考解答第二章第二章钢结构的基本材料和构件习题参考解答1. 钢材的基本性能指标有哪些?请简要描述各项性能指标的含义。
答:钢材的基本性能指标包括强度、韧性、可塑性和耐腐蚀性。
- 强度:钢材的强度是指钢材抵抗外力的能力,通常以屈服强度、抗拉强度和抗压强度来表示。
屈服强度是指钢材在受到外力作用时,开始产生塑性变形的应力值;抗拉强度是指钢材在拉伸状态下最大的抵抗外力的应力值;抗压强度是指钢材在受到压缩状态下最大的抵抗外力的应力值。
强度的高低决定了钢材的承载能力。
- 韧性:钢材的韧性是指钢材在受到外力作用时,能够发生塑性变形而不断延展的能力。
韧性的好坏决定了钢结构在受到冲击或震动时的抵抗能力。
- 可塑性:钢材的可塑性是指钢材在受到外力作用时,能够发生塑性变形而不断延展的能力。
可塑性的好坏决定了钢材的加工性能和成型性能。
- 耐腐蚀性:钢材的耐腐蚀性是指钢材在受到各种腐蚀介质(如大气、水、酸等)的侵蚀时,能够保持其力学性能和表面的完整性。
耐腐蚀性的好坏决定了钢结构的使用寿命。
2. 钢材的分类方法有哪些?请简要描述各种分类方法。
答:钢材的分类方法有按化学成分分类、按用途分类和按加工方法分类。
- 按化学成分分类:钢材按化学成分可分为碳素钢、合金钢和不锈钢。
碳素钢的主要成分是碳和铁,其含碳量通常在0.08%~2.11%之间;合金钢是在碳素钢中添加其他合金元素(如铬、钼、锰等)来改善钢材的性能;不锈钢是指含有至少12%的铬元素,在大气或酸性介质中形成一层致密的氧化铬膜,起到防腐蚀的作用。
- 按用途分类:钢材按用途可分为结构钢、机械钢、特种钢和工具钢等。
结构钢是用于制造各种钢结构的钢材,如建筑、桥梁、船舶等;机械钢是用于制造机械零部件的钢材,如轴承、齿轮、轴等;特种钢是用于特殊工作条件下的钢材,如高温、低温、高压等环境下的钢材;工具钢是用于制造各种切削工具和模具的钢材,如刀具、冲压模具等。
- 按加工方法分类:钢材按加工方法可分为热轧钢材、冷轧钢材和锻制钢材。
钢结构第二版课后习题答案

钢结构第二版课后习题答案【篇一:钢结构基础(第二版)课后习题第四章答案】q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为n=1500kn。
l?4m解:由支承条件可知l0x?12m,0y11?500?12?64ix??8?5003??250?123?2?250?12476.6?10 mm12122?? 50031iy??8?2??12?2503?31.3?106mm412122a?2?250?12?500?8?10000mmix??21.8cmiy5.6cm,l0y400l0x120071.4?x?55?y?i5.6ix21.8y,,2翼缘为火焰切割边的焊接工字钢对两个主轴均为b类截面,故按y查表得?=0.747n1500?103200.8mpa?f?215mpa整体稳定验算:?a0.747?10000,稳定性满足要求。
4.13图示一轴心受压缀条柱,两端铰接,柱高为7m。
承受轴心力设计荷载值n=1300kn,钢材为q235。
已知截面采用2[28a,单个槽钢的几何性质:a=40cm2,iy=10.9cm,ix1=2.33cm,解:柱为两端铰接,因此柱绕x、y轴的计算长度为:l0x?l0y?7m22b26??ix?2?ix1?a??y02?218?40??2.19940.8cm422l0y700l0x70064.263.1ix???11.1cmyxiy10.9ix11.10x格构柱截面对两轴均为b类截面,按长细比较大者验算整体稳定既可。
由?0x?65.1,b类截面,查附表得??0.779,65.1n1300?103208.6mpa?f?215mpa2整体稳定验算:?a0.779?2?40?10 所以该轴心受压的格构柱整体稳定性满足要求。
4.17焊接简支工字形梁如图所示,跨度为12m,跨中6m处梁上翼缘有简支侧向支撑,材料为q345钢。
集中荷载设计值为p=330kn,间接动力荷载,验算该梁的整体稳定是否满足要求。
钢结构基础第四章课后习题答案汇编
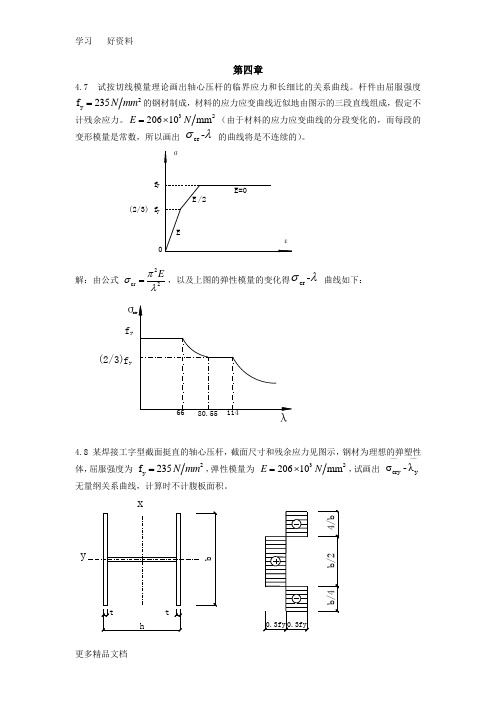
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cryy σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500KN 。
0.6f yfyλσ0.20.40.60.81.0cry解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
(完整版)钢结构设计原理习题集及答案

式中N——轴心拉力或轴心压力
An——构件的净截面面积
n——在节点或拼接处,构件一端连接的高强度螺栓数目;
n1——所计算截面上高强度螺栓数目;
f——钢材的抗拉或抗压强度设计值。
上式括号内数值小于1,这表明所计算截面上的轴心力N已有一定程度的减少。对比普通螺栓受剪连接构件开孔截面的净截面强度的计算公式:
钢结构设计原理习题集及答案(2011-09-28 10:53:54)
标签:a格极限状态焊缝构件承载力教育分类:试卷题库
钢结构设计原理习题集及答案
第一章绪论
练习题
一、简答题
1.简述钢结构的特点和应用范围。
答:特点:(1)承载能力大;(2)稳妥可靠;(3)便于工业化生产,施工周期短;(4)密闭性好;耐热但不耐火;(5)耐腐蚀性差;(6)容易产生噪音
综上所述,无论是从焊条等焊接材料的消耗和焊接速度、焊接残余应力,或是从焊缝的相对强度,角焊缝都以选用小焊脚尺寸为宜。因此,当焊件的焊接长度较富余,在满足最大焊缝长度的要求下,采用小而长比大强度螺栓的较普通螺栓的小?
答:摩擦型高强度螺栓的受剪连接传力特点不同于普通螺栓。后者是靠螺栓自身受剪和孔壁承压传力,而前者则是靠被连接板叠间的摩擦力传力。一般可认为摩擦力均匀分布于螺栓孔四周,故孔前传力约为0.5。因此,构件开孔截面的净截面强度的计算公式为:
应用范围:(1)承受荷载很大或跨度大,高度大的结构;(2)承受动力荷载作用或经常移动的结构;(3)经常拆装的拼装式结构;(4)对密闭性要求高的结构;(5)高温车间或需承受一定高温的结构;(6)轻型结构
钢结构基础第二章习题答案

第二章1.钢结构和其他材料的结构相比具有哪些特点?答(1)强度高,塑性和韧性好(2)钢结构的重量轻(3)材质均匀,和力学计算的假定比较符合(4)钢结构制作简便,施工工期短(5)钢结构密闭性较好(6)钢结构耐腐蚀性差(7)钢材耐热但不耐火(8)钢结构在低温和其他条件下,可能发生脆性断裂,还有厚板的层状撕裂,应引起设计者的特别注意。
2.《钢结构设计规范》(GB500l7—2003)(以下简称《规范》)采用什么设计方法?答:《规范》除疲劳计算外,均采用以概率理论为基础的极限状态设计方法,用分项系数的设计表达式进行计算。
3.什么是极限状态?钢结构的极限状态可分为哪两种?各包括哪些内容?答:当结构或其组成部分超过某一特定状态就不能满足设计规定的某一功能要求时,此特定状态就称为该功能的极限状态。
4.钢结构的极限状态可分为:承载能力极限状态与正常使用极限状态。
(1)承载能力极限状态:包括构件和连接的强度破坏、疲劳破坏和因过度变形而不适于继续承载,结构和构件丧失稳定,结构转变为机动体系和结构倾覆。
(2)正常使用极限状态:包括影响结构、构件和非结构构件正常使用或外观的变形,影响正常使用的振动,影响正常使用或耐久性能的局部损坏(包括混凝土裂缝)。
5.结构的可靠性与结构的安全性有何区别?建筑结构的可靠性包括安全性、适用性和耐久性三项要求。
结构可靠度是结构可靠性的概率度量,其定义是:结构在规定的时间内,在规定的条件下,完成预定功能的概率,称为结构可靠度6.钢结构设计的基准期是多少?当结构使用超过基淮期后是否可继续使用?规定时间:一般指结构设计基准期,一般结构的设计基准期为 50年,桥梁工程的设计基准期为100年。
设计基准期(design reference period):为了确定可变作用及与时间有关的材料性能等取值而选用的时间参数。
※设计使用期与设计使用寿命的关系:当结构的设计使用年限超过设计基准期时,表明它的失效概率可能会增大,但并不等于结构丧失所要求的功能甚至报废。
钢结构基本原理课后习题集答案解析(第二版)

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =σf yCσF图2-35 理想化的σε-图 解: (1)A 点: 卸载前应变:52350.001142.0610y f E ε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点: 卸载前应变:0.025Fεε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构第四章答案

习题参考答案题:欧拉临界荷载的推证(一端固定,一端自由);解:由构件x 处截面的力矩平衡,得到方程)()(''y P x h P EIy -+-=δα,可进行数学推导,求得欧拉临界荷载值。
EIP Ph x EI P -EI P ''δαα++=+y ,令EI Pk 2=,则δαα2222k h k x k -k ''++=+y ;显然平衡方程即为二阶常系数非齐次线性方程的求解。
齐次方程求解:0k ''2=+y ,令rx e y =,便可解得ki r ±=,故通解为sinkx A coskx A y 21+=。
方程的特解求解:有0x 222e )x (k h k x k -ϕδαα=++,其中)x (ϕ为一次多项式,由于0不是特征方程的根,可令21B B y +=x ,代入方程得δαα222212)(k h k x k B x B k ++-=+,则α-=1B ,δα+=h B 2。
于是可得方程的全解为:δαα++-+=h x sinkx A coskx A y 21。
边界条件:⎩⎨⎧=+-=⇒⎩⎨⎧=-=++⇒==k A h A kA h A y y /)(000)0(')0(2121αδααδα;所以:22sinkh coskh )(y(h)δαααδαδ++-++-==h h kh ,将方程进行变换便可得到h kααδ-=tankh 2,即得证P84中的式(4-4b )。
当2kh π=时,自由端位移2δ趋近于无穷大,即构件失稳,则欧拉临界荷载为2222E 4h)2h (k EI P ππ===,即22E 4h EI P π=。
4.9题:要求按照等稳定条件确定焊接工字型截面轴心压杆腹板的高厚比。
钢材为Q235,杆件长细比为100=λ,翼缘有火焰切割和轧制边两种。
计算结果请与规范规定作对比。
解: 轴心压杆的弹性模量修正系数为,.18287.0)10206/(235))10206/(2351000248.01(1001013.0/)/0248.011013.0332222≤=⨯⨯⨯⨯⨯-⨯⨯=-=Ef E f y y λλη(由表4-4,翼缘为火焰切割边的焊接工字型截面的强弱轴均为b 类截面,而翼缘为轧制边的焊接工字型截面的弱轴为c 类截面,故由杆件长细比查附表17-2和17-3得轴心受压构件的稳定系数分别为0.555和0.463。
钢结构基本原理课后作业答案第二章和第四章

σ=E ε (ε≤f y /E )σ=f y (ε>f yE ) σ=E ε (ε≤fy /E )σ=f y +E ′(ε−f yE ) (ε>f yE )2.2A: 卸载前 ε=f y E=2352.06∗105=1.14∗10−3卸载后ε=0弹性εy =ε=1.14∗10−3 B: 卸载前ε=εF =0.025卸载后εc =εF −f yE =0.025−2352.06∗105=0.02386 弹性εy =f y E=1.14∗10−3C: 卸载前ε=εF +σc −f y E ′=0.025+270−2351000=0.06卸载后εc =ε−σc E=0.06−2702.06∗105=0.05869弹性εy =σc E=2702.06∗105=1.31∗10−32.6A 点:σmax =120Nmm 2 σmin =−80Nmm 2 ρ=−80120=−0.0667 ∆σ=200 Nmm 2B 点:ρ=−20−120=0.167 ∆σ=100N mm 2改为 σ1=20Nmm 2σ2=−120N mm 2ρ=20−120=−0.167 ∆σ=140N mm 22.7Q235AF f y =235Nmm 2 A 级沸腾钢 Q390E f y =390N mm 2 E 级特殊镇静钢 Q345D f y =345N mm 2 D 级特殊镇静钢 Q235D f y =235N mm 2 D 级特殊镇静钢A n=2∗24∗2+96∗0.8=172.8cm2I x=24∗100312+2.4−0.8∗96312=2.895∗105cm4W nx=I xx/2=2.895∗10550=5790cm3W pnx=2∗24∗2∗962+22+962∗0.8∗964=6547cm3N=1500kN M x=ql28=8∗104q公式(4-13)NA n +M xW nx≤f d1500 172.8+8∗104q5790≤21.5 q≤0.927kNcm=92.7kN/m(4-18)NA n f d =1500172.8∗21.5=0.4037>0.13N A n +11.15M xW pnx≤f d1500 172.8+11.158∗104q6547≤21.5q≤1.206kNcm=120.6kN/m(4-17)NN p =NAf y=1500172.8∗23.5=0.369>0.13N N p +11.15M xM px=1 1500172.8∗23.5+11.158∗104q6547∗23.5=1q≤1.395kNcm=139.5kN/m(4-18)NA n +M xr x W nx≤f d1500 172.8+8∗104q1.05∗5790≤21.5q≤0.974kNcm=97.4kN/m稳定考虑:NA −MW<0 1500172.8−8∗104q5790<0 q≤0.628kNcm=62.8kN/m时需考虑稳定问题下面是诗情画意的句子欣赏,不需要的朋友可以编辑删除!!谢谢1. 染火枫林,琼壶歌月,长歌倚楼。
钢结构—第四章课后答案

P108 4.1解:示意图要画焊缝承受的剪力V=F=270kN ;弯矩M=Fe=270´300=81kN.m I x =[0.8´(38-2´0.8)3]/12+[(15-2)´1´19.52]´2=13102cm 4= 腹板A e =0.8´(38-2´0.8)=29.12 cm2截面最大正应力s max =M/W= 81´106´200/13102´104=123.65 N/mm 2£f t w =185N/mm2剪力全部由腹板承担t =V/A w =270´103/2912£=92.72 N/mm2 =f v w =125N/mm 2 腹板边缘处”1”的应力s 1=(M/W)(190/200) =123.65(190/200)=210.19 =117.47 腹板边缘处的折算应力应满足2213 1.1w zs tf s s t =+£22117.47392.72=+´=198..97N/mm 2£1.1f t w =203.5N/mm 2 焊缝连接部位满足要求4.2解:(1) 角钢与节点板的连接焊缝“A ”承受轴力N=420kN 连接为不等边角钢长肢相连题意是两侧焊肢背分配的力N 1=0.65 ´420=273 kN 肢背分配的力N 2=0.35 ´420=147 kN h fmin =1.5(t max )1/2=1.5(10)1/2=4.74mm h fmax =1.2(t min )=1.2(6)=7.2mm 取h f =6mm 肢背需要的焊缝长度l w1=273´103/(2´0.7´6´160)+2´6=203.12+12=215.13mm 肢尖需要的焊缝长度l w2=147´103/(2´0.7´6´160)+2´6=109.38+12=121.38mm 端部绕角焊2h f 时,应加h f (书中未加)取肢背的焊缝长度l w1=220mm ;肢尖的焊缝长度l w2=125mm 。
