南京理工大学本科电路笔记dxja7_1
南京理工大学本科电路笔记dxja8_2

§8-2 含有耦合电感的电路的计算一、一对耦合电感的串联:1、顺接: 电流从同名端流入的串联。
1212i i i u u u ===+121111di diu R i L M dt dt =++ 212222di diu R i L M dt dt=++1212()(2)di diu R R i L L M Ri L dt dt=++++=+顺2、反接:电流异名端流入的串联。
12(2)di di u L L M L dt dt=+-=反 122L L L M =+-反二、一对耦合电感的并联:1、同侧并联:同名端在同一侧时的并联。
R R R =+ 122L L L M =++2j L ω.2.j L ω同1L2RLM+ _+_ u1u 2uu12...1112...2221...122...12122121222U j L I j M I U j L I j M I I I I L L M U j I j L IL L M L L M L L L Mωωωωωω=+=+=+-==+--=+-同同2、异侧并联:同名端不在同一侧时的并联。
212121212122212121212............220............20.......20............0.......22L L M L L L L L ML L L L L M L L L M M L L M L L M L L M L L M L L M-=>+++=++>=+-><--=>=><+-++同异顺反同反异 三、耦合系数k :反映耦合松紧程度。
kM M ω==四、一对耦合电感的三端联接 1、同名端相接2j L ω.2j L ω异121312123212di di u L M dt dt di diu L M dt dti i i =+=+=+在u 13表达式中消去i 2;在u 23表达式中消去i 1,经整理后,得3121131132122322()()di di di diu L M L M M dt dt dt dtdi di di diu L M L M M dt dt dt dt =+=-+=+=-+ 由此式画出去耦等效电路,如下图。
南京理工考研电路笔记

1. 1电路和电路模型
一、电路:
1.电路:构成电流通路的一切设备的总和。
2.作用:进行能量的转换和传输(强电)
进行信号的处理和传递(弱电)
进行信息的存储
二、电路模型
可以表征或近似地表示一个实际器件(或电路)中所有的主要物理现象。
电路模型可以通过理想的电路元件相互联接而成。
三、理想电路元件 1.无源元件:电阻元件R
消耗电能
电感元件 L
存储磁场能量
电容元件 C
存储电场能量
2.有源元件: 独立电源⎪⎩⎪⎨⎧电流源电压源
四、“集中假设”及集中电路
元件及电路各方向的尺寸远远小于电路周围的电磁波波长
例电感线圈 直流
低频
高频
s
s s ) C。
南理工模电课件7-1

7.1 反馈的基本概念和分类
1. 反馈的基本概念 2. 反馈的分类 3. 负反馈的组态(类型)
第七章 反馈放大电路
7.1 反馈的基本概念和分类 1. 反馈的基本概念 (1) 反馈概念的引出 对于电子系统,在输入信号一定时,要求输 出信号是稳定的,但由于各种因素的影响, 输出信号会发生不应有的变化。因此,需要 设法将输出信号的变化送回到输入回路,让 输入信号根据输出量的变化作调整,以保持 输出量的稳定,这一过程就是“反馈”。
Rf1、Rf2: 直流反馈
Re1: 交流反馈
Re2: 交流反馈
(5) 电压反馈和电流反馈
从需要稳定的输出量和输出端的采样方式 来划分,反馈分为以下两种: 电压反馈:反馈信号和输出电压成正比。 电流反馈:反馈信号和输出电流成正比。
X f kVo
X f kIo
判断电压和电流反馈的方法
将输出端短路(即令vo=0): 如果原来的反馈是电压反馈,则反馈 消失;如果反馈仍存在,则原来的反 馈一定是电流反馈。
R1、Re2:直流负反馈
例题1
Rf、Re11、Ce : 交流负反馈 电压串联
若要实现电 压串联负反 馈,Rf应接 何处?并标 示出运放的 同相和反相 输入端。
例题2
作业
314页:7.1.1
314页:7.1.2 315页:7.1.7 注意:为了便于7.1.7题答案统一,指 定i接输出端,j接输入端。作业中不 必画出电路连接图,直接给出各个端 点如何对接即可。
IRCe::R需实b1 要现稳反IB 定馈的的T1量元IC R器c 件 V(C采C 样R电b2 阻),对输IE 出电VCC 流进行采样 Re
ReIE ReIC:反馈信号 (采样量)
温度 IC IE Re IE VBE ( VB Re IE ) IB IC
南京理工大学电工电子实验1

南京理⼯⼤学电⼯电⼦实验1电⼯电⼦综合实验论⽂班级:学号:姓名:⾮线性电阻电路的应⽤---混沌电路⼀、摘要:蔡式电路是美国贝莱克⼤学的蔡少堂教授设计的能产⽣混沌⾏为的最为简洁的⼀种⾃治电路,该型电路并不唯⼀,在⾮线性系统及混沌研究中,占有极为重要的地位。
该电路结构简单,但却出现双涡卷奇怪引⼦和及其丰富的混沌动⼒学⾏为。
本实验研究⾮线性电阻的特性和混沌电路。
试验中利⽤两个运算放⼤器模拟⾮线性电阻,并⽤列表法测量做出其伏安特性曲线,并利⽤⽰波器观察其伏安特性曲线。
同样利⽤两个运算放⼤器,实现混沌现象,并研究其图像的规律。
⼆、关键词:⾮线性负电阻,混沌电路,三、引⾔:混沌(Chaos)是20世纪物理学的重⼤事件。
混沌研究最先起源于洛伦兹研究天⽓预报时⽤到的三个动⼒学⽅程。
后来的研究表明,⽆论时复杂的系统,如⽓象系统、太阳系,还是简单系统,如滴⽔龙头等,皆因存在着内在随机性⽽出现类似⽆轨,但实际是⾮周期有序运动,即混沌现象。
现在混沌研究涉及的领域包括数学、物理学、⽣物学、化学、天⽂学、经济学及⼯程技术的众多学科,并对这些学科的发展产⽣了重要影响,混沌包含的物理内容⾮常⼴泛,研究这些内容更需要⽐较深⼊的数学理论,如微分动⼒学⽅程、拓补学、分形⼏何学等。
⽬前混沌的研究重点已转向多维动⼒学系统中的混沌、量⼦及时空混沌、混沌的同步及控制等⽅⾯。
本实验借助⾮线性电阻电路,从实验上对这⼀现象进⾏了探索。
四、正⽂:1.实验材料与设备装置。
⽰波器,可变电阻,定值电阻,直流电源,电流表,TL082CD运算放⼤器,线性电感,电容。
2.实验过程。
(1)实验电路图。
这是由两个线性电容C1、C2,⼀个线性电感L,和⼀个可变性电阻R0,⼀个⾮线性电阻R构成。
电感和C2并联构成振荡电路,线性电阻R0的作⽤是分相,⾮线性电阻R的伏安特性I R=g(u R),是⼀个分段线性负电阻,整体呈现对称但⾮线性的趋势。
由于g 总体是⾮线性函数,所以三元⾮线性⽅程组没有解析解。
南京理工大学电工电子综合实验

电工电子综合实验实验报告数字计时器设计姓名:学号:学院:自动化学院专业:自动化2013-9-6一、实验目的:1、掌握常见集成电路实现单元电路的设计过程。
2、了解各单元再次组合新单元的方法。
二、实验要求:实现0分0秒到59分59秒的可整点报时的数字计时器。
三、实验内容:1、设计实现信号源的单元电路。
2、设计实现0分0秒到59分59秒的计时单元电路。
3、设计实现快速校分单元电路,含防抖动电路。
4、加入任意时刻复位单元电路。
5、设计实现整点报时的单元电路。
四、实验所用元件及功能介绍元件型号数量NE555 1片CD4040 1片CD4518 2片CD4511 2片74LS00 3片74LS20 1片74LS21 3片74LS74 1片电容0.047uf 1个电阻1504个电阻1k1个电阻3k1个单字屏共阴极数码管2块蜂鸣器1个开关2个2、主要芯片引脚图及功能表2.2.1、CD4511译码器图2.2.1 CD4511译码器引脚图表2.2.1 CD4511译码器功能表输入输出LT BI LE D4 D3 D2 D1 g f e d c b a 字符测灯0 ×××××× 1 1 1 1 1 1 1 8 灭零 1 0 ×0 0 0 0 0 0 0 0 0 0 0 消隐锁存 1 1 1 ××××显示LE=0→1时数据译码1 1 0 0 0 0 0 0 1 1 1 1 1 1 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 2 1 1 0 0 0 1 1 1 0 0 1 1 1 1 3 1 1 0 0 1 0 0 1 1 0 0 1 1 0 4 1 1 0 0 1 0 1 1 1 0 1 1 0 1 5 1 1 0 0 1 1 0 1 1 1 1 1 0 0 6 1 1 0 0 1 1 1 0 0 0 0 1 1 1 7 1 1 0 1 0 0 0 1 1 1 1 1 1 1 8 1 1 0 1 0 0 1 1 1 0 0 1 1 1 92.2.2、CD4518计数器图2.2.2 CD4518BCD码计数器引脚图表2.2.2 CD4518BCD码计数器功能表:输入输出CR CP EN Q3 Q2 Q1 Q0 清零 1 ××0 0 0 0 计数0 ↑ 1 BCD码加法计数保持0 ×0 保持计数0 0 ↓BCD码加法计数保持0 1 ×保持2.2.3、CD4040分频器图2.2.3 CD4040分频器引脚图2.2.4、NE555定时器图2.2.2 NE555定时器引脚图表2.2.2 NE555定时器功能表Vi1(引脚6) Vi2(引脚2) VO(引脚3) (引脚4 )0 ××01 >2/3Vcc >1/3Vcc 01 <2/3 Vcc <1/3Vcc 11 <2/3 Vcc >1/3Vcc 不变2.2.5、74LS74 D触发器图2.2.5 74LS74D触发器引脚图表2.2.5 74LS74D触发器功能表输入输出CP D清零×0 1 ×0 1 置“1”× 1 0 × 1 0 送“0”↑ 1 1 0 0 1 送“1”↑ 1 1 1 1 0 保持0 1 1 ×保持不允许×0 0 ×不确定2.2.6、74LS00 双四与非门图2.2.6 74LS00双四与非门引脚图2.2.7、74LS20 四入双与非门图2.2.7 74LS20 四入双与非门引脚图2.2.8、74LS21四入双与门图2.2.8 74LS21四入双与门引脚图3、电子计时器设计原理3.1、各部分电路解析3. 1.1、脉冲发生电路脉冲发生电路即为电子计时器产生脉冲的电路,本文采用NE555振荡器和CD4040分频器产生实验所需要的脉冲信号频率其中:f0=1.44/[(R1+2R2)C]=4.38kHz R1=1KΩ,R2=3KΩ,C=0,047uF。
南京理工大学 数字电路课件

P
A
X B C Q 高位
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7
≥1
F(Q,X,P)
F(Q,X,P)=m0+m1+m4+m6+m7
P
A
X B C Q 高位
&
F(Q,X,P)
F(Q,X,P)=m0m1m4m6m7
③ 利用高电平输出有效的译码器和或非门。 F(Q,X,P)=m2+m3+m5
74148为8线—3线优先编码器, 输入为低电平有效,输出 为3位二进制反码,HPRI是最高位优先编码器的说明.图 中: ST端为输入控制端,当ST=0时,电路处于正常工作状 态; 当ST=1时,电路禁止工作, Y2Y1Y0=111 .
YS:选通输出端.
YS=ST I0I1I2I3I4I5I6I7
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
F 0 0 0 1 0 1 1 1
(2) 化简、求最简函数表达式 BC 00 A 0 1
01
11
1
10
1
1
1
F=AB+AC+BC =AB· BC AC·
(3) 画电路图
F
&
&
&
&
A
B
C
例
设计一个两位二进制数比较器。
设计一个具有互相排斥输入条件的编码器. 输入: X0 、X1、X2 、X3 对应关系:
输入 X0 X1 X2 X3
输出:A1、A0
A1 A0 0 0 0 1 1 0 1 1
南京理工大学本科电路笔记dxja5_1

第五章 一阶电路和二阶电路§5-1 动态电路的方程及其初始条件一阶电路:用一阶微分方程描述的电路。
一.换路:指电路中开关的突然接通或断开,元件参数的变化,激励形式的改变等。
换路时刻0t (通常取0t =0),换路前一瞬间:0_t ,换路后一瞬间:0t +。
二.换路定则 c 0c 0()()u t u t +-= L 0L 0()()i t i t +-= C 0C 0()()i t i t +-≠, L 0L 0()()u t u t +-≠, R 0R 0()()i t i t +-≠, R 0R 0()()u t u t +-≠三.初始值的计算: 1. 求C 0L 0(),()u t i t --: ①给定C 0L 0(),()u t i t --;②0t t <时,原电路为直流稳态 : C —断路 L —短路③0t t -=时,电路未进入稳态 : 0C 0C ()()|t t u t u t --==, 0L 0L ()()|t t i t i t --== 2. 画0t +时的等效电路:C 00()()u t u t +-=,L 0L 0()()i t i t +-= 换路前后电压(流)不变的为电压(流)源C —电压源 L —电流源C 0()0u t -=, L 0()0i t -=C —短路 L —断路3. 利用直流电阻电路的计算方法求初始值。
例1已知:0t <时,原电路已稳定,0t =时,打开开关S 。
求:0t +=时,各物理量的初始值。
解: 1. 求C L (0),(0)u i --:0t -=时,C L (0)7.5V,(0)0.25A u i --==2. 画0t +=时的等效电路:3. 0t +=时:R1(0)0.2510u +=⨯= R27.5(0)0.5A 15i +== L R1C (0)(0)10(0)0u u u +++=-+-=2C L R (0)(0)(0)0.25i i i A +-+=-=-例2:已知:0t <时,原电路已稳定,0t =时,打开开关S 。
南京理工大学本科电路笔记dxja10

第10章 非正弦周期电流电路按照傅里叶级数展开法,任何一个满足狄里赫利(Dirichlet)条件的非正弦周期信号(函数)都可以分解为一个恒定分量与无穷多个频率为非正弦周期信号频率的整数倍、不同幅值的正弦分量的和。
01()cos()()2S km k S k u t U U k t u t Tωϕπωω∞==++=---∑为非正弦周期函数基波频率k ---k 次谐波频率§10-1 不同频率正弦量作用下线性电路的稳态分析一、分析方法-------谐波分析法1. 根据线性电路的叠加原理,非正弦周期信号作用下的线性电路稳态响应可以视为一个恒定分量和上述无穷多个正弦分置单独作用下各稳态响应分虽之叠加。
因此,非正弦周期信号作用下的线性电路稳态响应分析可以转化成直流电路和正弦电路的稳态分析。
2. 应用电阻电路计算方法计算出恒定分量作用于线性电路时的稳态响应分量。
利用直流稳态方法:C -断路 L -短路3. 应用相量法计算出不同频率正弦分量作用于线性电路时的稳态响应分量。
各次谐波单独作用,利用相量法1Lk Ck X X k Ck Lωω==。
4. 对各分量在时间域进行叠加。
即可得到线性电路在非正弦周期信号作用下的稳态响应。
二、举例:例1:已知12R L Cωω===Ω,()10100cos 40cos3V u t t t ωω=++ (),(),()C L i t i t i t 求:。
(u t ()t解:⑴10V 分量作用:00005A C L I I I ===⑵100cos V t ω分量作用:11111.....100045A 2j2100045A 2j2500ALm Cm m Lm Cm I I I I I ∠==-+∠==-=+=∠⑶40cos3V t ω分量作用:33333.....40071.6A 2j640018.4A 22j3200.81ALm Cm m Lm Cm I I I I I ∠==-+∠==-=+=∠(4).在时间域进行叠加。
南理工 电路 第10章 三相电路

南京理工大学自动化学院
10.2 负载星形联结的三相电路
(不对称三相电路)星形联结
通过分析,在三相四线制配电系统中,保险丝不能
装在中线上
A
FU
g
IA
+g
. g
UC
_U A _N
_
+ C
g
UB
+
B FU
C’
g
IB
A’
Z
.N’ Z
Z
B’
FU
g
IC
电路
南京理工大学自动化学院
10.2 负载星形联结的三相电路
以uA为参考正弦量,它们的瞬时值表达式为: uA Um cost uB Um cos(t 120o) uC Um cos(t 120o)
式中ω为正弦电压变化的角频率,Um为相电压幅值
电路
南京理工大学自动化学院
10.1 三相电源
三相电压
有效值相量表示为:
g
UA U 0
g
UB U 120
g
g
UB
电路
南京理工大学自动化学院
10.2 负载星形联结的三相电路
线电压与相电压的关系
相电压对称,线电压也对称
Ul 3UP
线电压超前对应相电压 30
g
U BC
g
U CA
g
UC g UA
g
UB
g
U AB
电路
南京理工大学自动化学院
10.2 负载星形联结的三相电路
线电流与相电流的关系
g
g
Il IP
电路
0
ZA ZB ZC
上式表明:负载中性点N’与电源中性点N之间有电位差, 使得负载的相电压不再对称
南理工电路大纲

南京理工大学电路2011年考研大纲 《电路》课程考试大纲 电路》 教材“电路”邱关源主编有关内容 参考书:“电路分析基础” 注:打“*”内容电路考试满分为75分时,不作要求。
一、电路模型和电路定律 电路和电路模型,电流和电压的参考方向,功率,电阻、电感、电容元件、电压源和电 流源、受控源、基尔霍夫定律. 二、电阻电路 电阻的串联、并联和串并联,电源的等效变换,回路法,节点法,叠加原理,替代定理, 戴维南定理和诺顿定理。
三、一阶电路和二阶电路 一阶电路的零输入响应,一阶电路的零状态响应,一阶电路的完全响应,一阶电路的三 要素法,一阶电路的阶跃响应,*一阶电路的冲激响应,*二阶电路的零输入响应。
四、正弦电流电路和相量法 正弦量,相量法的基本概念,R、L、 C 中的正弦电流,复阻抗,复导纳,正弦电流电 路的功率,复功率,正弦电流电路的稳态计算,最大功率传输。
五、具有互感的电路 互感,具有互感电路的计算,空心变压器,理想变压器。
六、电路中的谐振 串联电路的谐振,并联电路的谐振。
七、三相电路 三相电路,对称三相电路的计算,不对称三相电路的计算,三相电路的功率。
八、非正弦周期电流电路 非正弦周期电流,有效值、平均值和平均功率,非正弦周期电流电路的计算。
*九、拉普拉斯变换(拉氏变换) 拉氏变换, 拉氏反交换, 电路定律的运算形式, 利用拉氏变换分析线性电路, 网络函数, 复频率平面、极点和零点。
*十、网络图论和网络方程 网络图论的基本概念,节点电压方程的矩阵形式,状态方程,特勒根定理。
*十—、二端口网络 二端口网络的方程和参数,二端口网络的转移函数,二端口网络的联接。
*十二、多端元件 多端元件,运算放大器,含理想运算放大器电路的计算,回转器。
*十三、非线性电阻电路 非线性电阻电路的分析,小信号分析法。
2011年硕士研究生入学考试大纲(初试) (控制理论基础,占75分) 一、总要求以胡寿松编著的教材《自动控制原理》 (第五版)的第 1、2、3、4、5、6 章内容为主要命题 范围,全面考查考生对经典控制理论的基本概念、基本方法掌握的程度,以及灵活运用基本概念和原理分析问题、解决问题的能力。
南京理工大学本科电路笔记dxja3_1
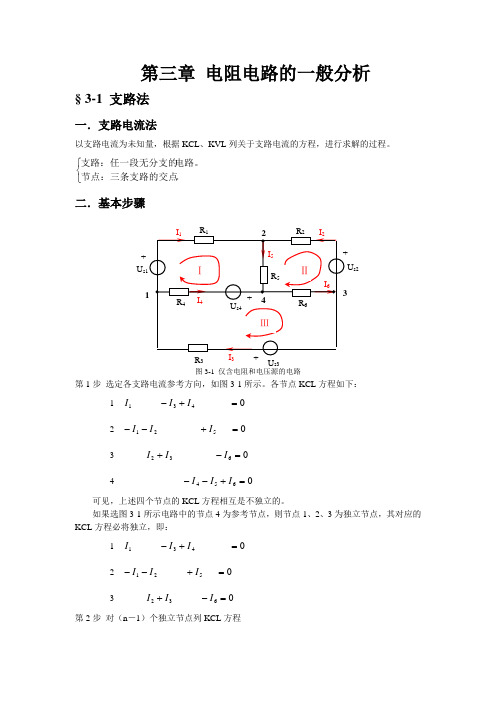
第三章 电阻电路的一般分析
§ 3-1 支路法
一.支路电流法
以支路电流为未知量,根据KCL 、KVL 列关于支路电流的方程,进行求解的过程。
⎩⎨
⎧。
节点:三条支路的交点
电路。
支路:任一段无分支的
二.基本步骤
图3-1 仅含电阻和电压源的电路
第1步 选定各支路电流参考方向,如图3-1所示。
各节点KCL 方程如下:
1 04
31
=+-I I I 2 05
21=+--I I I 3 0632=-+I I I
4
0654=+--I I I
可见,上述四个节点的KCL 方程相互是不独立的。
如果选图3-1所示电路中的节点4为参考节点,则节点1、2、3为独立节点,其对应的KCL 方程必将独立,即:
1 04
31
=+-I I I 2 05
21=+--I I I
3 063
2=-+I I I
第2步 对(n -1)个独立节点列KCL 方程
U s3
3 3
第3步.对)1(--n b 个独立回路列关于支路电流的KVL 方程 Ⅰ:014445511=--++s s U I R U I R I R Ⅱ:05566222=--+-I R I R U I R s Ⅲ:033366444=+-+-I R U I R U I R s s 第4步.求解。
南京理工大学电路课件

电路
1.5 电压源和电流源
为了得到各种实际电源的电路模型,定义两种理想的 电路元件——理想电压源和理想电流源.
电压源
理想电压源 若一个二端元件输出电压恒定则称为理想电压源. 电路符号:
.
电路
Us
.
.
us(t) _ +
.
南京理工大学电光学院
1.5 电压源和电流源
理想电压源
基本性质: I + + Us _ 输出电压恒定,和外电路无关.
第1章 电路模型和电路定律
1.1 电路和电路模型 1.2 电流和电压的参考方向 1.3 功率和能量 1.4 电阻元件 1.5 电压源和电流源 1.6 受控源 1.7 基尔霍夫定律
电路 南京理工大学电光学院
1.1 电路和电路模型
电路的概念
电路是由用电设备或元器件(称为负载)与供电设备 (称为电源)通过导线连接而构成的提供给电荷流动 的通路.
dt
量纲:安培(A) 1安培 = 1库仑/秒 1kA=103A ;1mA=10-3A;1μA=10-6A
电路 南京理工大学电光学院
1.2 电流和电压的参考方向
一些常用的十进制倍数的表示方法:
符号 T 中文 太 G 吉 M k c m 毫 μ 微 n 纳 p 皮
兆 千 厘
数量 1012 109 106 103 10-2 10-3 10-6 10-9 10-12
电压
电路中a、b两点之间的电压uab:将单位正电荷从a点移
到b点所需的能量或功.
Wa
q
+
Wb
失去能量 Wa-Wb
a
.
b
.
Wa Wb dW uab q dq
南京理工大学 数字电路课件

F1(A,B,C)=Σm(1,5,6,7)
F2(A,B,C)=Σm(0,1,3,6,7)
F3(A,B,C)=Σm(3,4,5,6,7)
A B C
1
1
1
& & & & & & & &
m0
m1 m2 m3
m4
m
5
m6 m7
≥1 ≥1 ≥1
F1 F2 F3
2) 存放数据表和函数表:例如三角函数、对数、乘法等表 格。 3)存放调试好的程序。 * 2)、3)是PROM的主要用途。
③ 将地址输入和Fi之间的关系填入真值表得: 地址 A1 A0 0 0 0 1 1 0 1 1
F0 0 1 0 0
数据 F1 F2 1 0 0 0 1 1 0 1
F3 0 1 0 0
F0=A1A0 F1=A1A0+ A1A0 F2=A1A0+ A1A0 F3=A1A0
ROM实际是一种组合电路结构。
6.2.1 可编程阵列逻辑(PAL)
PAL的基本结构 A0
1 1 1
& & & & ≥1 ≥1
A1
A2
实际产品中,构成输出的 乘积项可达8个.
F0 F1
1. PLA的输出结构 PAL的与阵列结构类同.但输出结构有多种: 1) 组合输出型(这种结构适用于实现组合逻辑电路)
输入项
① 专用输出结构 共有三种形式: 高输出有效; 低输出有效; 互补输出. 本例为低 输出有效 I
ASIC分类: ASIC属用户定制电路。(Custom Design IC).包括全定制和半定制两种。 全定制(Full custom design IC):半导体生产厂家根据用户 的特定要求专门设计并制造。 特点:生产周期长,费用高,风险大。在大批量定型产品 中使用。 半定制(Semi- custom design IC):半导体生产厂家设计并 制造出的标准的半成品芯片。 半定制电路分类: ㈠ 门阵列 (Gate Array)
南京理工大学本科电路笔记dxja8_1

第8章 含耦合电感的电路耦合电感:耦合元件,储能元件,记忆元件。
理想变压器:多端元件,既不储能又不耗能,非记忆元件。
§8-1 互感一、耦合电感:为互感线圈的理想化电路模型自感:对于线性非时变电感元件,当电流的参考方向与磁通的参考方向符合右螺旋定则时,磁链Ψ电流i 成正比,即Ψ=Li ,式中L 为与时间无关的正实常数。
根据电磁感应定律和线圈的绕向,如果电压的参考正极性指向参考负极性的方向与产生它的磁通的参考方向符合右螺旋定则时,也就是在电压和电流关联参考方向下,则dtdi L dt d u =ψ= 在此电感元件中,磁链Ψ和感应电压u 均由流经本电感元件的电流所产生,此磁链感应电压分别称为自感磁链和自感电压。
互感:如图所示表示两个有磁耦合的线圈(简称耦合电感),电流i 1在线圈1和2中产生的磁通分别为Φ11和Φ21,则Φ21≤Φ11。
这种一个线圈的磁通交链于另一线圈的现象,称为磁耦合。
电流i 1称为施感电流。
Φ11称为线圈1的自感磁通,Φ21称为耦合磁通或互感磁通。
如果线圈2的匝数为N 2,并假设互感磁通Φ21与线圈2的每一匝都交链,则互感磁链为Ψ21=N 2Φ21。
同理,电流i 2在线圈2和l 中产生的磁通分别为Φ22和Φ12,且Φ12≤Φ22。
Φ22称为线圈2的自感磁通,Φ12称为耦合磁通或互感磁通。
如果线圈1的匝数为N 1,并假设互感磁通Φ12与线圈1的每一匝都交链,则互感磁链为Ψ12=N 1Φ12。
i 1 Ψi ψ=1 1'2 2' φ21如图所示,当两个有磁耦合的线圈,都通以电流i 1 、i 2,在线圈l 中产生的磁通分别为Φ11和Φ12。
在线圈2中产生的磁通分别为Φ21和Φ22。
于是,线圈1的总磁链为自感磁链与互感磁链的叠加Ψ1=Ψ11+Ψ12=N 1Φ11+N 1Φ12线圈2的总磁链为自感磁链与互感磁链的叠加Ψ1=Ψ21+Ψ22=N 2Φ21+N 2Φ22二、互感电压与互感系数:根据电磁感应定律,自感磁通Φ11将在线圈1中产生自感电压 1111d i u Ldt= ; 互感磁通Φ21将在线圈2中产生互感电压u 21:1 1'2 2' φ1 1'2 2' φφ21 22 i 1 ψ21211i i 2 Ψ12 12122M i ψ 0211212121 , d di u u M dt dtψ== 在正弦电流电路中,互感电压也可以用相量表示...21211m 1 j U j M I X I ω= L X L ω=--自感抗 M X M ω=--互感抗同理根据电磁感应定律,自感磁通Φ22将在线圈2中产生自感电压 2222d i u L dt= ; 互感磁通Φ12将在线圈1中产生互感电压u 12:...12212121212122m 2 , , j d di u u M U j M I X I dt dt ψω=== 可以证明: 1221M M M =三、同名端标记约定:一对互感线圈中,一个线圈的电流发生变化时,在本线圈中产生的自感电压与在相邻线圈中所产生的互感电压极性相同的端点称为同名端,以“*”,“·”,“Δ”等符号表示。
南京理工大学-电工电子综合实验一-非线性电阻电路及应用的研究

南京理工大学电工电子综合实验论文非线性电阻电路2012-5-14运用串联分解法和并联分解法,设计两个非线性电阻电路,分别满足所要求的两个伏安特性曲线。
使用Multisim7.0软件仿真,并在仿真试验后对电路进行修正。
得到所需要的伏安特性的电路连接、元件参数,非线性电阻串并联对电路的影响。
非线性电阻电路及应用的研究——非线性电阻电路一.摘要运用串联分解法和并联分解法,设计两个非线性电阻电路,分别满足所要求的两个伏安特性曲线。
使用Multisim7.0软件仿真,并在仿真试验后对电路进行修正。
得到所需要的伏安特性的电路连接、元件参数,非线性电阻串并联对电路的影响。
二.关键词伏安特性非线性电阻电路Multisim7.0仿真凹电阻凸电阻串联分解并联分解三.引言非线性系统的研究是当今科学研究领域的一个前沿课题,其涉及面广,应用前景非常广阔。
非线性电阻电路也是研究混沌现象的基础。
通过对非线性电阻电路的研究,熟练掌握各二端电阻元件的伏安特性,及用他们组合成非线性电阻电路的方法,初步了解非线性电阻电路的应用。
四.正文1.设计要求(1)用二极管、稳压管、稳流管、等元器件设计如图1,2所示伏安特性的非线性电阻电路。
图1 伏安特性(一)(2)测量所设计的电路的伏安特性并作曲线,与图1,2对比。
2.设计参考(1)非线形电阻电路的伏安特性①对于一个一端口网络,不管内部组成,其端口电压与电流的关系可以用u—i 平面的一条曲线表示。
则是将其看成一个二端电阻元件。
u—i平面的曲线称为伏安特性。
常见的二端电阻元件有二极管、稳压管、稳流管、电压源、电流源和线形电阻。
伏安特性如图3所示。
运用这些元件串、并联或混联就可得到各种分段单调的伏安特性曲线。
图3②凹电阻当两个或两个以上元件串联时,电路的伏安特性图上的电压是各元件电压之和。
如下图所示,是将图9.10中的a、c、d三个元件串联组成的,其伏安特性曲线如图9.11所示。
它是由a、c、d三个元件的伏安特性在I相等的情况下相加而成的。
简单电阻电路分析(南京理工大学)

若两个三端网络的电压u13、u23与电流i1、i2之间的 关系完全相同时,则称这两个三端网络对外互为等效。
1
i1 +
R1
R2 .
u13 R3 _
2 i2 +
u23
_3
R12
i2 .
2 i2 +
1
. i1 +
R31 u13
._
R23 u23
_3
2.3 电阻的Y-Δ等效变换
1
i1 +
R1
.
R2
u13 R3 _
b
R ab75 ,R cd21
2.2 电阻的串联、并联和混联
字母标注法
aR a
a Rc
1、在各节点处标上节点字母,短路线联接的点或
c 等位点用同一字母标注;
R R
R
R
2、将接在同一对字母间的电阻用并联后的等效电 阻替代;
b
c
b b 0.5R
d
3、整理并简化电路,求出总的等效电阻。
a
0.5R c
a
RR
Y △变换:R31R1R2RR 2R 23R3R1
分子为Y形电阻的两两乘积之和
分母为Y形与之对应两节点无关的电阻
分母为Y形中三个电导之和 分子为Y形中与之对应节点相联的电导之积
例: 求I
6
2.3 电阻的Y-Δ等效变换
R 1 2R 1R 2R R 1R 32,R 1R 1 2 R 1 R 22 R 33 1R 3 1
R 1 R 1 2 R 1 R 2 2 R 3 3 1 R 3 1 ;R 2 R 1 2 R 1 R 2 2 R 3 2 3 R 3 1 ;R 3 R 1 2 R 2 R 3 2 R 3 3 1 R 3 1
南京理工大学数字电路课内实验数字电路4

数字逻辑电路实验实验报告学院:电子工程与光电技术学院班号:9171040G06姓名:徐延宾学号:9171040G0633实验编号:0259指导教师:花汉兵2019年5月14日目录1实验目的3 2实验要求3 3实验内容3 4实验原理45实验步骤55.174LS194四位双向移位寄存器逻辑功能测试 (5)5.274LS194设计实现左,右循环计数 (5)5.374LS194设计实现扭环计数 (8)5.4模15计数器设计 (8)5.574LS194设计实现五分频电路 (9)6实验思考与总结11参考文献11实验4移位寄存器及应用1实验目的掌握移位寄存器的逻辑功能及应用。
2实验要求用移位寄存器实现循环工作和分频器工作。
并绘制分频器工作波形。
3实验内容1.按表测试74LS194四位双向移位寄存器逻辑功能。
2.用74LS194设计实现(自启动)左,右循环计数,状态如图1。
图1:左,右循环计数状态转换图3.用74LS194设计实现(无自启动)扭环计数,状态如图2。
图2:扭环计数状态转换图4.用74LS194实现M=2n−1最大长度计数,反馈表达式为D SR=Q3⊕Q2观察并记录计数器循环状态(无自启动)。
5.用74LS194设计实现五分频电路,状态如图3。
通过示波器绘制工作波形。
图3:五分频电路状态图4实验原理74LS194四位双向移位寄存器•74LS194四位双向移位寄存器逻辑图图4:74LS194四位双向移位寄存器逻辑图•74LS194四位双向移位寄存器引脚部局图图5:74LS194四位双向移位寄存器引脚部局图•74LS194四位双向移位寄存器结构为四个主从RS触发器(已经转换成D触发器)与一些门电路组成。
1.C r:为异步清零端,低电平有效。
2.CP:为时钟脉冲输入端,上升沿有效。
3.D SR:为右移串行数据输入端。
4.D SL:为左移串行数据输入端。
5.M A,M B:为移位寄存器工作状态控制端,有四种状态可使用。
电工技术基础第1章

熔断涂覆电阻器
FUSIBLE FILM RESISTOR
线绕涂覆电阻器
WIRE WOUND RESISTOR(KNP TYPE)
绕涂覆电阻器
WIRE WOUND RESISTOR(KNH TYPE)
电工技术基础
南京理工大学
电工技术基础
南京理工大学
1.1 电路及电路模型 3. 理想的电路元件
有源元件: 独立源
是一种任意选定的方向
约定:
i>0时,实际方向与参考方向一致 i<0时,实际方向与参考方向相反
电流正负仅对参考方向而言
电流参考方向也可用双下标表示iAB
南京理工大学
注意事项
电工技术基础
1.2 电路的基本物理量及其参考方向
2.电压(voltage) 电压:
dW ( t ) 定义: u( t ) dq( t )
A +
. .
I
U
B _
. .
P UI
I
U
A _
B +
P UI
电工技术基础
南京理工大学
1.2 电路的基本物理量及其参考方向 能量
电路从0到t时刻所吸收的电能为:
W p(t )dt
0t单位:焦耳 (J)来自. 1度 = 1千瓦 小时
电工技术基础
南京理工大学
1.2 电路的基本物理量及其参考方向
实际电流源
U I IS Ro + U
-
U=RoISRoI
0
Is
I
Ro越大越好
电工技术基础
南京理工大学
1.4 独立电源(independent source)
实际电流源
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 正弦稳态电路分析
§7-1 阻抗和导纳
一.阻抗
1. 定义:在正弦稳态无源二端网络端钮处的电压相量与电流相量之比定义为该二端网络
的阻抗,记为Z ,
注意:此时电压相量U g
与电流相量I g
的参考方向向内部关联。
u
i
U U Z I I
ψψ∠=
∠
(复数)阻抗()Ω
z j Z R X ψ=∠=+
其中 ()U
Z I
=
Ω —阻抗Z 的模,即阻抗的值。
Z u i ϕψψ=- —阻抗Z 的阻抗角
z cos ()R Z ϕ=Ω —阻抗Z 的电阻分量 z sin ()X Z ϕ=Ω —阻抗Z 的电抗分量
电阻元件的阻抗: 在电压和电流关联参考方向下电阻的伏安关系的相量形式为
R R U R I =
则 R R R
U Z R I ==
电感元件的阻抗: 在电压和电流关联参考方向下电感的伏安关系的相量形式为
g
U U Z I
=-
g
g
g
R
X
|Z |
Z ϕ
g
R
U g
R I 与R U 共线
阻抗三角形
L L j U L I ω=
则 L L L L
j j U Z L X I ω==
电容的阻抗: 在电压和电流关联参考方向下电容的伏安关系的相量形式为
C C
C C
C j 11j j I C U U I I C C
ωωω===-
则 C
C C C
1j
j U Z X C I ω=-=
C 1X C ω=- —容抗 2. 欧姆定律的相量形式 U Z I =
j g
g
1j
- C U
g
g
C
电阻、电感、电容的串联阻抗:
在电压和电流关联参考方向下,电阻、电感、电容的串联,得到等效阻抗eq Z
R L C eq R L C
1
L C Z
Z I Z I Z I
U Z Z Z Z I
I R j L R jX jX R jX j C Z ωωϕ++=
=
=++=++=++=+=∠
其中:阻抗Z 的模为
||Z =
阻抗角分别为 1/L
C
Z
X L C arctg arctg
arctg
R
R
R
X
X
ωωϕ+-===。
可见,电抗X 是角频率ω的函数。
当电抗X >0(ωL >1/ωC )时,阻抗角φZ >0,阻抗Z 呈感性; 当电抗X <0(ωL <1/ωC =时,阻抗角φZ <0,阻抗Z 呈容性; 当电抗X =0(ωL =1/ωC )时,阻抗角φZ =0,阻抗Z 呈阻性。
3. 串联阻抗分压公式:
引入阻抗概念以后,根据上述关系,并与电阻电路的有关公式作对比,不难得知,若一端口正弦稳态电路的各元件为串联的,则其阻抗为
∑==n
k k Z Z 1
串联阻抗分压公式
eq
k k Z U U Z =
二.导纳
1.定义:正弦稳态无源二端网络端钮的电流相量与电压相量之比定义为该二端网络的
C
g
导纳,记为Y ,即
i u
1I I
Y Z U U ψψ∠==
∠
复导纳(S ) Y j Y G B ψ=∠=+
其中 I
Y U
=—导纳Y 的模(S )
Y i u Z ϕψψϕ=-=- —导纳Y 的导纳角。
Y cos (s)G Y ϕ= —导纳Y 的电导分量 Y sin (s)B Y ϕ= —导纳Y 的电纳分量
可见,同一二端网络的Z 与Y 互为倒数 特例:
电阻的导纳 R R 1Y G R
Z =
= 电容的 C C j j C Y C Z B ω== B C 电容的电纳,简称容纳。
电感的 L L 1j
j L Y B Z L
ω=-= B L 称为电感的电纳,简称感纳;
2. 欧姆定律的另一种相量形式
I Y U =
若一端口正弦稳态电路的各元件为并联的,则其导纳为
g
G
B
|Y |
Y ϕ
导纳三角形
∑==
n
k k
Y Y 1
并联导纳的分流公式:
eq
k k Y I I Y =
RLC 并联正弦稳态电路中,根据导纳并联公式,得到等效导纳Y
Y C L R Y jB G L
C j R C j L
j R Y Y Y Y ϕωωωω/||)1
(111=+=-+=
++=++=
可见,等效导纳Y 的实部是等效电导G (=1/R )=|Y |cos φY ;
等效导纳Y 的虚部是等效电纳B =|Y |sin φY =B C +B L =ωC -1/ωL ,是角频率ω
的函数。
导纳的模为:||Y =
导纳角分别为: 1/C
L Y
B C L arctg arctg
arctg
G
G
G
B
B ωωϕ+-===
由于电纳B 是角频率ω的函数,
当电纳B >0(ωC >1/ωL )时,导纳角φY >o ,导纳Y 呈容性; 当电纳B <0(ωC <1/ωL )时,导纳角φY <o ,导纳Y 呈感性; 当电纳B =0(ωC =1/ωL )时,导纳角φY =0导纳Y 呈阻性。
注意:两个电阻的并联与两个阻抗的并联对应
12121212
R R Z Z
R Z R R Z Z =
⇒=++
22Z1R11212
R Z I I I I R R Z Z =⇒=++
三.对同一二端网络:
1
U I
Z Y Y Z
I
U
=
=
=
其中:22()()()()R G R X ωωωω=
+ , 22
()
()()()
X B R X ωωωω-=+, Y Z ϕϕ=- 一般情况下,一个由电阻、电感、电容所组成的不含独立源的一端口正弦稳态电路的等效阻抗Z (j ω)是外施正弦激励角频率ω的函数,即
Z (j ω)=R (ω)+jX (ω)
式中R (ω)=Re[Z (j ω)]称为Z (j ω)的电阻分量,X (ω)=Im[Z (j ω)]称为Z (j ω)的电抗分量。
式中电阻分量和电抗分量都是角频率ω的函数。
所以,要注意到电路结构和R 、L 、C 的值相同的不含独立源的正弦稳态电路,对于角频率ω不同的外施正弦激励而言,其等效阻抗是不同的。
如下图电路的等效阻抗
eq 22j 1j (j )1
()(j )j ()R L R L R L Z j R L C R L C
ωωωωωωω⋅⋅-=
+-=+-++
222222()1j ()()R L R L R L R L C ωωωωω⎡⎤=+-⎢⎥++⎣⎦
()j ()R X ωω=+
同理,一个由电阻、电感、电容所组成的不含独立源的一端口正弦稳态电路的等效导纳Y (j ω)也是外施正弦激励角频率ω的函数,即
Y (j ω)=G (ω)+jB (ω)
式中G (ω)=Re[Y (j ω)]称为Y (j ω)的电导分量,B (ω)=Im[Y (j ω)]称为Y (j ω)的电纳分量。
电导分量和电纳分量也都是角频率ω的函数。
所以要注意到电路结构和R 、L 、C 的值相同下的不含独立源的一端口正弦稳态电路,对于角频率ω不同的外施正弦激励言,其等效导纳是不同的。
四.电路的计算 完全与电阻电路一样
可变,找不到适于任何场合下的等效电路
j ω L
1
j
-
例:求如图所示电路等效阻抗。
22222112
2
222
1m 2m 22
2
111
(j )j j j eq 1
1j (j )j C U U U C C C R R C g C g U C U U R R U Z I
ωωωωωωω+++
+++++=
=
=
R 2
g
1
R2
Z eq。
