安徽大学matlab第三次试验
(最新版)MATLAB实验报告

(最新版)MATLAB实验报告实验一典型环节的MATLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB软件,在命令窗口栏“>>”提示符下键入simulink命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个simulink 仿真环境常规模板。
3.在simulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击simulink下的“Continuous”,再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在simulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink 的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
5)选择输出方式。
用鼠标点击simulink下的“Sinks”,就进入输出方式模块库,通常选用“Scope”的示波器图标,将其用左键拖至新建的“untitled”窗口。
matlab 模拟 实验报告

matlab 模拟实验报告Matlab模拟实验报告引言:Matlab作为一种功能强大的数学软件,广泛应用于科学研究和工程领域。
本文将通过模拟实验的方式,探讨Matlab在信号处理和控制系统中的应用。
一、信号处理实验在信号处理领域,Matlab提供了丰富的工具和函数,可以对各种类型的信号进行处理和分析。
我们选择了音频信号作为实验对象,通过Matlab模拟实验,探索不同的信号处理技术。
1.1 信号生成与显示首先,我们使用Matlab生成一个正弦信号,并通过plot函数将其显示出来。
代码如下:```matlabt = 0:0.001:1; % 时间范围为0到1秒,采样率为1000Hzf = 10; % 信号频率为10Hzx = sin(2*pi*f*t); % 生成正弦信号plot(t, x); % 显示信号```通过运行以上代码,我们可以在Matlab的图形界面中看到一个频率为10Hz的正弦信号波形。
1.2 信号滤波接下来,我们将对生成的正弦信号进行滤波处理,以去除其中的高频噪声。
我们使用Matlab中的滤波函数fir1来实现。
代码如下:```matlabfs = 1000; % 采样率为1000Hzfc = 100; % 截止频率为100HzN = 50; % 滤波器阶数b = fir1(N, fc/(fs/2)); % 生成滤波器系数y = filter(b, 1, x); % 对信号进行滤波plot(t, y); % 显示滤波后的信号```通过运行以上代码,我们可以观察到滤波后信号中高频成分的减弱。
二、控制系统实验在控制系统领域,Matlab提供了丰富的工具和函数,可以进行系统建模、控制器设计和系统仿真等操作。
我们选择了一个简单的控制系统作为实验对象,通过Matlab模拟实验,探索不同的控制策略。
2.1 系统建模首先,我们需要对控制系统进行建模。
假设我们的控制系统是一个带有传感器、控制器和执行器的闭环系统。
matlab实验心得总结

matlab实验心得总结在通过完成一系列的Matlab实验后,我对这个强大的数学计算软件有了更深入的认识。
通过这些实验,我不仅学到了如何使用Matlab进行数据处理和分析,还体会到了它在科学研究和工程应用中的广泛使用。
实验一:Matlab基础操作在第一次接触Matlab时,我首先学习了它的基本操作。
Matlab提供了友好的用户界面和丰富的命令工具,使得数据处理变得简单且高效。
在实验中,我学会了如何定义变量、进行基本的数学运算和使用矩阵操作等。
这些基础操作为后续的实验打下了坚实的基础。
实验二:数据可视化数据可视化在科学研究和工程领域中起着重要的作用。
在这个实验中,我学会了如何利用Matlab绘制各种图形,如折线图、散点图和柱状图等。
通过调整图形的样式和颜色,使得数据更加直观和易于理解。
同时,我还学会了如何添加标题、坐标轴标签和图例,使得图形具有更好的可读性。
实验三:模拟与仿真Matlab不仅可以进行数据处理和图形绘制,还可以进行模拟和仿真。
在这个实验中,我学会了如何使用Matlab进行数学模型的建立和仿真。
通过设定合适的参数和方程,我可以模拟出各种现实世界中的物理、生物和工程现象。
这对于科学研究和工程设计具有重要的意义。
实验四:信号处理信号处理是Matlab的一个重要应用领域。
在这个实验中,我学会了如何使用Matlab对信号进行分析和处理。
通过应用不同的滤波器,我可以去除信号中的噪声和干扰,提取出感兴趣的信息。
同时,我还学会了如何进行频域分析,通过傅里叶变换将信号转换到频率域,进一步分析信号的频谱特性。
实验五:数值计算Matlab还提供了强大的数值计算功能。
在这个实验中,我学会了如何使用Matlab进行数值计算和优化。
通过使用不同的数值求解方法,我可以解决复杂的数学方程和优化问题,得到精确的计算结果。
这对于科学研究和工程计算具有重要的价值。
总结起来,通过这些实验,我对Matlab的应用能力有了明显的提升。
电子科大matlab与数值分析第三次上机实践报告

Matlab上机实践报告实践内容:线性方程组求解和函数的数值逼近学院:姓名:学号:指导老师:实践日期:题目(一)1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
题目分析:本题目的是演示方程解和扰动变量ε的关系,又题目显然可以看出多项式的解,所以可以先画出多项式的真解。
然后生成若干组扰动多项式,求解扰动多项式,分别用不同颜色绘图,比较它们与真解的差距。
题目程序: x=1:20;y=zeros(1,20);rao=zeros(1,21); %创建扰动控制矩阵scatter(x,y,'m') %绘出真解,以‘o ’型显示 ,洋红颜色标出 title('方程真根及扰动后的根') hold on; %保持真解 pause; %暂停for x=1:5 %产生五组扰动 rao(2)=10^(-x); %在十九次方项产生扰动e=roots(poly(1:20)+rao); %求解添加扰动后的根 plot(e,'.') %绘出添加扰动后的根,用实点标出 e %显示扰动后的根 hold on ; %保持 pause; %暂停 end 演示结果:0510152025303540-20-15-10-505101520方程真根及扰动后的根备注:扰动后根的数据太多,我只把图形结果呈现出来了。
实验结论:实验产生一个不大的干扰就能产生一个挺大的误差,而且扰动量越大,结果差距就越大。
题目(二)2. 对n=2~20,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
题目分析:这个题目考察的是求解矩阵的条件数,以及求解矩阵的根,并且能够分析出方程组是否为病态。
matlab数字信号部分上机实验解读

0n3 4n7 other
x6 (n) cos8t cos16t cos 20t
(2) 令x(n)=x4(n)+x5(n), 用FFT计算 8 点和 16 点离散傅里 叶变换,
X(k)=DFT[x(n)] (3) 令x(n)=x4(n)+jx5(n), 重复(2)。
4. 思考题 (1) 在N=8时, x2(n)和x3(n)的幅频特性会相同吗? 为 什么? N=16呢? (2) 如果周期信号的周期预先不知道, 如何用FFT进 行谱分析? 5. 实验报告要求 (1) 简述实验原理及目的。 (2) 结合实验中所得给定典型序列幅频特性曲线, 与理论结果比较, 并分析说明误差产生的原因以及用 FFT作谱分析时有关参数的选择方法。 (3) 总结实验所得主要结论。 (4) 简要回答思考题。
} K = LH; while(J>=K) { J=J-K; K=(int)(K/2+0.5); } J=J+K;
} }
实验三: 用双线性变换法设计 IIR数字滤波器
1. 实验目的 (1) 熟悉用双线性变换法设计IIR数字滤波器的原理 与方法。 (2) 掌握数字滤波器的计算机仿真方法。 (3) 通过观察对实际心电图信号的滤波作用, 获得 数字滤波的感性知识。
0n3 4n7
其它n
4 n 0 n 3
x3(n) n 3 4 n 7
0
x4 (n)
cos
4
n
其它n
x5
(n)
sin
8
n
x6(n) cos8 t cos16 t cos 20 t
(4) 编写主程序。 图 1 给出了主程序框图, 供参考。 本实验提供 FFT子程序和通用绘图子程序。 (5) 按实验内容要求, 上机实验, 并写出实验 报告。
matlab实验三级数word精品文档6页

实验三 级数【实验目的】1.了解级数的有关理论。
2.了解函数的Taylor 展开式。
3.学习,掌握MATLAB 软件中有关命令。
【实验内容】1.求函数sin y x =的级数,并考察其Taylor 展开式的前几项构成的多项式函数的图形向sin y x =的图形的逼近情况。
2.计算级数211n n ∞=∑的值。
3.验证Euler 公式111lim(1ln )0.577123x C n n→∞=++++-=。
【实验准备】 1.级数的基本概念。
数项级数;Taylor 级数。
2.级数的MATLIB 命令。
主要用symsum,taylor 求级数的和及进行Taylor 展开式。
【实验重点】1、级数的计算【实验难点】1、无穷级数的计算【实验方法与步骤】练习1 先用Taylor 命令观察函数sin y x =Maclaurin 展开式的前几项,若观察前6项,相应的MATLIB 代码为>>clear;syms x;>>taylor(sin(x),0,2) >>taylor(sin(x),0,3) >>taylor(sin(x),0,4) >>taylor(sin(x),0,5) >>taylor(sin(x),0,6) 运行结果为>> taylor(sin(x),0,1) ans =>> taylor(sin(x),0,2) ans =x>> taylor(sin(x),0,3) ans =x>> taylor(sin(x),0,4) ans =x-1/6*x^3>> taylor(sin(x),0,5) ans =x-1/6*x^3ans =x-1/6*x^3+1/120*x^5然后在同一坐标系里作出函数siny x=和其Taylor展开式的前几项构成的多项式函数,y x=33!xy x=-,35,,3!5!x xy x=-+的图形,观察这些多项式函数的图形向siny x=的图形逼近的情况。
matlab实验内容答案

m a t l a b实验内容答案(总16页) -本页仅作为预览文档封面,使用时请删除本页-实验报告说明:matlab 课程实验需撰写8个实验报告,每个实验报告内容写每次实验内容中标号呈黑体大号字显示的题目。
第一次实验内容:实验一 MATLAB 运算基础一、实验目的1.熟悉启动和退出MATLAB 的方法。
2.熟悉MATLAB 命令窗口的组成。
3.掌握建立矩阵的方法。
4.掌握MATLAB 各种表达式的书写规则以及常用函数的使用。
二、实验内容1.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1)22sin8511z e ︒=+ (2)12ln(2z x =,其中2120.455i +⎡⎤=⎢⎥-⎣⎦(3)0.30.33sin(0.3), 3.0, 2.9, 2.8,,2.8,2.9,3.02a ae e z a a --=+=--- 提示:利用冒号表达式生成a 向量,求各点的函数值时用点乘运算。
(4)2220141122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪--≤<⎩,其中t =0::提示:用逻辑表达式求分段函数值。
2.已知12344347873657A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,131203327B -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦求下列表达式的值:(1) A+6=B 和A-B+I(其中I 为单位矩阵)。
(2) A*B 和A.*B 。
(3) A^3和A^.3 。
(4) A/B 和B\A 。
(5)[A ,B]和[A([1,3],;);B^2] 。
3.设有矩阵A 和B12345678910111213141516171819202122232425A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 30161769023497041311B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D(3) 查看MATLAB 工作空间使用情况。
Matlab数字信号处理实验报告

数字信号处理实验报告基础实验篇实验一离散时间系统及离散卷积一、实验原理利用Matlab软件计算出系统函数的零极点分布、单位脉冲响应和系统频率响应等的图像并于笔算结果进行比较,找出异同。
编译合适程序能计算取值范围不同的离散卷积。
二、实验目的(1)熟悉MATLAB软件的使用方法。
(2)熟悉系统函数的零极点分布、单位脉冲响应和系统频率响应等概念。
(3)利用MATLAB绘制系统函数的零极点分布图、系统频率响应和单位脉冲响应。
三、实验步骤(1)自编并调试实验程序,并且,给实验程序加注释;(2)按照实验内容完成笔算结果;(3)验证计算程序的正确性,记录实验结果。
(4)至少要求一个除参考实例以外的实验结果,在实验报告中,要描述清楚实验结果对应的系统,并对实验结果进行解释说明。
四、实验源程序及实验结果a=[1,-1,0.9];b=1;x=chongji(-20,120);n=-20:120;h=filter(b,a,x);figure(1)stem(n,h);title('冲击响应');实验1-2运行结果b=[0.0181,0.0543,0.0543,0.0181];a=[1.000,-1.76,1.1829,-0.2781];w=pi*freqspace(500);H=freqz(b,a,w);MH=abs(H);AH=angle(H);subplot(2,1,1);plot(w/pi,MH);grid;axis([0,1,0,1]);xlabel('w(pi)');ylabel('|H|');title('幅度、相位响应');subplot(2,1,2);plot(w/pi,AH);grid;xlabel('w(pi)');ylabel('angle(H)');实验1-3运行结果n=0:30;%输入x(n)和冲激响应h(n) x=zeros(1,length(n)); h=zeros(1,length(n)); x([find((n>=0)&(n<=4))])=1; h([find((n>=0)&(n<=8))])=0.5;figure(1) subplot(3,1,1); stem(n,x);axis([0,30,0,2]); title('输入序列'); xlabel('n'); ylabel('x(n)');subplot(3,1,2); stem(n,h);axis([0,30,0,2]); title('冲激响应序列'); xlabel('n'); ylabel('h(n)');%输出响应y=conv(x,h); subplot(3,1,3); n=0:length(y)-1; stem(n,y);title('输出响应'); xlabel('n'); ylabel('y(n)');实验二 离散傅立叶变换与快速傅立叶变换一、 实验原理对有限长序列使用离散Fouier 变换(DFT)可以很好的反映序列的频谱特性,而且易于用快速算法在计算机上实现,当序列x(n)的长度为N 时,它的DFT 定义为()()[]()∑==-=1N n nk N W n x n x DFT k X 10-≤≤N k反变换为()()[]()∑==-=-101N n nkN W k X N k X IDFT n x 10-≤≤N n 有限长序列的DFT 是其Z 变换在单位圆上的等距采样,或者说是序列Fourier 变换的等距采样,因此可以用于序列的谱分析。
数字信号处理matlab实验报告材料-数字信号处理实验3

alpha=(N-1)/2; %求滤波器的相位延迟
xlabel(频率/Hz);ylabel(相位/^o);grid on;
m=n-alpha+eps; %eps 为 MATLAB 系统的精度
figure(2)
hd=sin(wc*m)./(pi*m); %求理想滤波器脉冲响应
f1=8;f2=21;%输入信号含有的频率
主函数(picture.m)
function d = mid_filter(x)
J=imread( C:\Users\yangk\Desktop\666\SaltPapperNoise.tif);%
[height, width]=size(x); %输入图像是 hight x width
读取图片
x1=double(x);
win=hanning(Nw); %接受汉宁窗
N=100;%数据点数
h=hd.*win; %在时间域乘积对应于频率域的卷积
dt=T;n=0:N-1;t=n*dt; %时间序列
b=h;
x=sin(2*pi*f1*t)+0.5*cos(2*pi*f2*t);%输入信号
figure(1)
subplot(2,1,1),plot(t,x),title(输入信号)
[height, width]=size(picture); %输入图像是 hight x width
图 1 Building.tif
图 2 Cups.tif
x1=double(picture);
实现函数(sharpen_filter.m)
x2=x1;
%3*3 锐化实现函数
for i=1:height-2%最终一列不用计算
end
matlab实验报告3

matlab实验报告3课程名称:学生学号:所属院部:实验报告实验四、LTI系统的响应MATLAB应用技术专业班级:通信1422***-*****31 学生姓名:周妍智电子信息工程系指导教师:徐树梅2015 ―― 2016 学年第二学期实验项目名称:LTI系统的响应实验学时:16 学生姓名:周妍智实验地点:微机11 实验日期:2016.4.17 实验成绩:批改教师:徐树梅批改时间:一、实验目的1. 熟悉连续时间系统的单位冲激响应、阶跃响应的意义及求解方法2. 熟悉连续(离散)时间系统在任意信号激励下响应的求解方法3. 熟悉应用MATLAB实现求解系统响应的方法二、实验原理1.连续时间系统对于连续的LTI系统,当系统输入为f(t),输出为y(t),则输入与输出之间满足如下的线性常系数微分方程:?ayii?0n(i)(t)??bjf(j)(t),当系统输入为单位冲激信号δ(t)时产生j?0m的零状态响应称为系统的单位冲激响应,用h(t)表示。
若输入为单位阶跃信号ε(t)时,系统产生的零状态响应则称为系统的单位阶跃响应,记为g(t),如下图所示。
系统的单位冲激响应h(t)包含了系统的固有特性,它是由系统本身的结构及参数所决定的,与系统的输入无关。
我们只要知道了系统的冲激响应,即可求得系统在不同激励下产生的响应。
因此,求解系统的冲激响应h(t)对我们进行连续系统的分析具有非常重要的意义。
在MATLAB中有专门用于求解连续系统冲激响应和阶跃响应,并绘制其时域波形的函数impulse( ) 和step( )。
如果系统输入为f(t),冲激响应为h(t),系统的零状态响应为y(t),则有:y(t)?h(t)?f(t)。
若已知系统的输入信号及初始状态,我们便可以用微分方程的经典时域求解方法,求出系统的响应。
但是对于高阶系统,手工计算这一问题的过程非常困难和繁琐。
在MATLAB中,应用lsim( )函数很容易就能对上述微分方程所描述的系统的响应进行仿真,求出系统在任意激励信号作用下的响应。
matlab信号处理实验报告

matlab信号处理实验报告Matlab信号处理实验报告引言信号处理是一门研究如何获取、分析、变换和解释信号的学科。
在现代科技的发展中,信号处理在许多领域都扮演着重要的角色。
本文将以Matlab为工具,进行信号处理实验,并对实验结果进行分析和讨论。
实验一:信号的采样和重构在信号处理中,采样是指将连续时间的信号转化为离散时间的信号。
重构则是将离散时间的信号恢复为连续时间的信号。
我们选取了一个正弦信号进行实验。
首先,我们生成一个频率为10Hz的正弦信号,并对其进行采样。
使用Matlab的函数进行采样,可以得到离散时间的信号。
接下来,我们对采样后的信号进行重构。
使用Matlab的函数进行重构,可以得到连续时间的信号。
通过实验,我们可以观察到采样和重构过程中的信号失真情况。
信号的采样频率越高,重构后的信号越接近原始信号。
这是因为高采样频率可以提供更多的采样点,从而更好地还原原始信号。
实验二:信号的频谱分析频谱分析是信号处理中常用的一种方法,用于分析信号的频率成分。
我们选取了一个复杂的信号进行频谱分析。
首先,我们生成一个由多个正弦信号叠加而成的复杂信号。
使用Matlab的函数进行信号合成,可以得到复杂信号。
接下来,我们对复杂信号进行频谱分析。
使用Matlab的函数进行频谱分析,可以得到信号的频谱图。
通过实验,我们可以观察到复杂信号的频谱图中的不同频率成分。
频谱图上的峰值表示信号中的主要频率成分,而峰值的高度表示该频率成分的强度。
通过频谱分析,我们可以了解信号的频率特性,进而对信号进行进一步处理和分析。
实验三:信号的滤波处理滤波是信号处理中常用的一种方法,用于去除信号中的噪声或不需要的频率成分。
我们选取了一个包含噪声的信号进行滤波处理。
首先,我们生成一个包含噪声的信号。
使用Matlab的函数生成噪声信号,并将其与原始信号叠加,可以得到包含噪声的信号。
接下来,我们对包含噪声的信号进行滤波处理。
使用Matlab的函数进行滤波处理,可以得到去除噪声后的信号。
MATLAB实验报告3
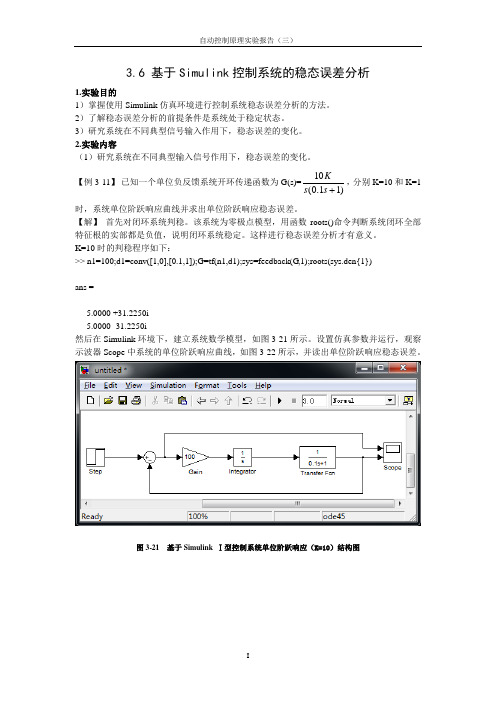
3.6 基于Simulink 控制系统的稳态误差分析1.实验目的1)掌握使用Simulink 仿真环境进行控制系统稳态误差分析的方法。
2)了解稳态误差分析的前提条件是系统处于稳定状态。
3)研究系统在不同典型信号输入作用下,稳态误差的变化。
2.实验内容(1)研究系统在不同典型输入信号作用下,稳态误差的变化。
【例3-11】 已知一个单位负反馈系统开环传递函数为G(s)=)11.0(10 s s K ,分别K=10和K=1时,系统单位阶跃响应曲线并求出单位阶跃响应稳态误差。
【解】 首先对闭环系统判稳。
该系统为零极点模型,用函数roots()命令判断系统闭环全部特征根的实部都是负值,说明闭环系统稳定。
这样进行稳态误差分析才有意义。
K=10时的判稳程序如下:>> n1=100;d1=conv([1,0],[0.1,1]);G=tf(n1,d1);sys=feedback(G ,1);roots(sys.den{1})ans =-5.0000 +31.2250i-5.0000 -31.2250i然后在Simulink 环境下,建立系统数学模型,如图3-21所示。
设置仿真参数并运行,观察示波器Scope 中系统的单位阶跃响应曲线,如图3-22所示,并读出单位阶跃响应稳态误差。
图3-21 基于Simulink Ⅰ型控制系统单位阶跃响应(K=10)结构图图3-22 基于Simulink Ⅰ型控制系统单位阶跃响应稳态误差曲线【分析】实验曲线表明,Ⅰ型单位反馈系统在单位阶跃输入作用下,稳态误差e ssr=0,即Ⅰ型单位反馈系统稳态时能完全跟踪阶跃输入,是一阶无静差系统。
K=1时的判稳程序如下:>> n1=10;d1=conv([1,0],[0.1,1]);G=tf(n1,d1);sys=feedback(G,1);roots(sys.den{1})ans =-5.0000 + 8.6603i-5.0000 - 8.6603i在Simulink环境下建立的数学模型及仿真参数运行后示波器Scope中系统的单位阶跃响应曲线如下图所示。
MATLAB信号与系统实验报告.doc

MATLAB信号与系统实验报告.doc实验目的:通过对MATLAB信号与系统工具箱中的函数学习和使用,掌握信号离散化、信号离散时间傅里叶变换、数字滤波器等信号处理方法并在MATLAB环境下实现,加深对信号与系统基础知识的理解。
实验原理:1.信号离散化:连续信号在计算机中只能被离散表示,因此需要对信号进行离散化处理。
MATLAB中有许多函数用于将连续信号离散化,包括‘sampling’和‘downsampling’函数。
2.离散时间傅里叶变换:离散时间傅里叶变换(DTFT)是信号处理中常用的方法,用于分析信号的频域特性。
使用MATLAB中的‘fft’(快速傅里叶变换)函数计算DTFT,其结果为复数。
3.数字滤波器:数字滤波器是在数字信号中进行滤波的一种方法。
MATLAB中提供了各种数字滤波器的函数,如‘designfilt’,‘filtfilt’,‘filter’等。
实验过程:1.信号离散化使用sinc函数生成一个连续信号,通过将其与离散时间通过平均取样的方法进行离散化,编写MATLAB代码将连续信号进行离散化,具体过程如下:Fs = 200; % sampling frequencyTs = 1/Fs; % sampling periodt = 0:Ts:1; % time vectorf1 = 5; % frequency of continuous signalsignal = sin(2*pi*f1*t); % continuous signalsampled = downsample(signal, 4); % downsample the signal by a factor of 4figure;plot(t, signal, 'b--', 'LineWidth', 1);hold on;stem(0:Ts*4:1, sampled, 'ro', 'LineWidth', 1.5);xlabel('Time (s)'); ylabel('Amplitude'); legend('Continuous', 'Sampled');其中,Fs表示采样频率,Ts为采样周期,t是时间向量,f1为连续信号的频率,signal为生成的连续信号。
信号与系统matlab实验报告

信号与系统matlab实验报告信号与系统MATLAB实验报告引言信号与系统是电子工程、通信工程和控制工程等领域中的重要基础课程。
通过实验,我们可以更好地理解信号与系统的概念和基本原理,并掌握使用MATLAB进行信号与系统分析的方法。
本报告将介绍我们在信号与系统实验中的实验过程、结果和分析。
实验一:连续时间信号的采样与重构在这个实验中,我们研究了连续时间信号的采样与重构。
首先,我们通过MATLAB生成了一个连续时间信号,并使用采样定理确定了采样频率。
然后,我们对连续时间信号进行采样,并通过重构方法将采样信号还原为连续时间信号。
最后,我们通过观察重构信号与原始信号的相似性来评估重构的效果。
实验二:线性时不变系统的频率响应在这个实验中,我们研究了线性时不变系统的频率响应。
首先,我们通过MATLAB生成了一个输入信号,并设计了一个线性时不变系统。
然后,我们通过将输入信号输入到系统中,并记录输出信号的幅度和相位,从而得到系统的频率响应。
最后,我们绘制了系统的幅频特性和相频特性曲线,并对其进行了分析和讨论。
实验三:离散时间信号的采样与重构在这个实验中,我们研究了离散时间信号的采样与重构。
首先,我们通过MATLAB生成了一个离散时间信号,并使用采样定理确定了采样周期。
然后,我们对离散时间信号进行采样,并通过重构方法将采样信号还原为离散时间信号。
最后,我们通过观察重构信号与原始信号的相似性来评估重构的效果,并讨论了离散时间信号的采样与重构的特点。
实验四:离散时间系统的差分方程在这个实验中,我们研究了离散时间系统的差分方程。
首先,我们通过MATLAB生成了一个输入信号,并设计了一个离散时间系统。
然后,我们通过将输入信号输入到系统中,并根据系统的差分方程计算输出信号。
最后,我们对输入信号和输出信号进行了分析和比较,并讨论了离散时间系统的差分方程的特点和应用。
实验五:连续时间信号的傅里叶变换在这个实验中,我们研究了连续时间信号的傅里叶变换。
MATLAB上机实验实验报告

MATLAB上机实验实验报告实验名称:用MATLAB实现多项式拟合及插值一、实验目的:通过使用MATLAB实现多项式拟合及插值的方法,掌握MATLAB软件的基本操作和函数应用,进一步了解多项式拟合及插值的原理和实现过程。
二、实验原理:多项式拟合及插值是一种常见的数值分析方法,通过对已知数据点集合的拟合或插值,构造出一个多项式函数,用于近似表示原始数据。
1.多项式拟合:通过最小二乘法原理,选择一个合适的多项式函数,使得拟合出的多项式与已知数据点之间的误差最小。
拟合函数可以是一次、二次或高阶多项式。
2.多项式插值:通过已知数据点的横纵坐标值,构造一个满足这些点的多项式函数。
插值函数可以是一次、二次或高阶多项式。
插值函数经过每个已知数据点。
三、实验步骤:1.数据准备:选择一组已知数据,包含横纵坐标值。
数据点的个数可以根据具体情况自行确定。
2.多项式拟合:使用MATLAB中的polyfit函数,根据已知数据点进行多项式拟合。
根据拟合结果,获取拟合的多项式系数。
3.多项式插值:使用MATLAB中的polyfit函数,根据已知数据点进行多项式插值。
通过plot函数绘制原始数据点的散点图和插值多项式的曲线图。
可以尝试不同阶数的多项式插值。
4.结果分析:根据实验结果,分析拟合与插值的效果。
对比拟合结果与原始数据的误差大小,评估拟合的准确性。
对比插值结果与原始数据的差异,评估插值的精确度。
五、实验总结:通过这次实验,我熟练掌握了使用MATLAB实现多项式拟合及插值的方法。
在实验中,我了解了多项式拟合的原理,以及如何利用最小二乘法求取多项式拟合的系数。
同时,我也学会了如何使用MATLAB中的polyfit函数实现多项式拟合和插值。
通过实验结果的分析,我对拟合和插值的实际应用和效果有了更加深入的认识。
[1]MATLAB官方文档[2]高等数值分析教程以上为MATLAB上机实验实验报告,共计1200字。
安徽大学matlab第三次试验

Matlab 第三次实验作业-----------2015年11月17日星期二班级:软件工程学号: E21314003 姓名:李世1. 设计一个程序对“北京、上海、广州、深圳、南京、武汉、天津、重庆、成都、沈阳、杭州、合肥”12个城市进行随机排序。
代码:>>clear>> a={'南京','武汉','天津','重庆','成都','沈阳','北京','上海','广州','深圳', '杭州','合肥'}; a(randperm(numel(a)))ans =Columns 1 through 11'合肥' '广州' '天津' '深圳' '重庆' '北京' '武汉' '杭州' '上海' '沈阳' '南京'Column 12'成都'2. 根据下面函数表达式编写M 函数,分别计算x 在1,0,31,1--处的函数值,并画出函数曲线图⎪⎪⎪⎩⎪⎪⎪⎨⎧-<<≤-+≥=-21002121021)(2x x x x ex f x>>clear>> x=input('请输入变量值:');if x>=0f=0.5*exp((-0.5).*x)else if -1/2<=x&&x<0f=x+0.5elsef=0endend请输入变量值:-1f =>> 0ans =>> 1ans =1>> -1/3ans =-0.3333a=-3:0.01:-1/2;b=0;c=-1/2:0.01:0;d=c+1/2;e=0:0.01:3;f=1/2*exp(-e/2); plot(a,b,c,d,e,f)3.求[100,200]之间第一个能被13整除的整数。
MATABLE_3.0

实验内容:
N=101; n=0:N-1; x=[5+3*cos(0.2*pi*n)+4*sin(0.6*pi*n)];
a=[1 2 1]; b=[1 -0.5 0.25]; ;
subplot(2,2,1); zplane(b,a);
y=filter(b,a,x);
实验结果分析思考题解答1我们观察次信号与林零极限的比值比值越小就代表其越稳定
实验报告格式
院系:专业:班级:
实验名称:
课程名称:
数字信号处理
实验室:
实验C楼201
成绩
实验人:
学号:
指导教师:赵发勇
实验目的:
1、熟悉离散时间系统的时域和频域分析方法。
2、掌握利用MATLAB求解差分方程和频率响应的方法。
实验结果分析
思考题解答
1、我们观察次信号与林零极限的比值,比值越小就代表其越稳定。
2、
subplot(2,2,2 );stem(n,y) ;
[H,w]=freqz(b,a) ;
PhaseH=angle(H);
Z = filtic( b, a, y, x )
Subplot(2,abs(H));
Subplot(2,2,4);plot(w/pi,MagH);
实验三 matable插值法

end
h=sym(0);
for (i=1:n)
l=sym(yห้องสมุดไป่ตู้i));
for(j=1:i-1)
l=l*(t-x(j))/(x(i)-x(j));
end;
for(j=i+1:n)
l=l*(t-x(j))/(x(i)-x(j));
end;
h=h+l;
end
simplify(h);
if(nargin == 3)
10 11 12
求满足插值条件
的拉格朗日插值多项式在x=115处的值,并估计误差(要求小数点后6位)。进一步研究
1)求出插值多项式
2)写成函数形式
一实验目的
1.进一步熟悉matlab环境。
2.掌握用拉格朗日插值法对方程组求解。
3.进一步掌握用函数形式编写程序。
二实验内容
1.用拉格朗日插值法对方程组求解的算法:
(1)求变量之间的差值向量
(2)用循环求出各个基函数中数组的内积。
(3)求出各个基函数。
(4)利用基函数与各函数值求出插值公式。
(5)利用插值公式求出所要求的值。
(6)按照求余项的公式计算余项(公式为:R2(x)=f3(ξ)*(x-100)*(x-121)*(x-144)/3!,其中ξ的值为100)。
石家庄经济学院
实验报告
(学院)系:信息工程学院
专业:计算机科学与技术
姓名:李鑫
班级:4091090302
学号:409109070220
任课教师:罗毅老师
《数值分析》实验报告
姓名
李鑫
学号
409109070220
日期
2011年11月15日
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab 第三次实验作业
-----------2015年11月17日星期二
班级:软件工程学号: E21314003 姓名:李世
1. 设计一个程序对“北京、上海、广州、深圳、南京、武汉、天津、重庆、成都、沈阳、杭州、合肥”12个城市进行随机排序。
代码:>>clear
>> a={'南京','武汉','天津','重庆','成都','沈阳','北京','上海','广州','深圳', '杭州','合肥'}; a(randperm(numel(a)))
ans =
Columns 1 through 11
'合肥' '广州' '天津' '深圳' '重庆' '北京' '武汉' '杭州' '上海' '沈阳' '南京'
Column 12
'成都
'
2. 根据下面函数表达式编写M 函数,分别计算x 在1,0,3
1
,1--处的函数值,并画出函数曲线图
⎪⎪⎪⎩⎪⎪⎪⎨⎧-<<≤-+
≥=-210
0212
102
1)(2x x x x e
x f x
>>clear
>> x=input('请输入变量值:');
if x>=0
f=0.5*exp((-0.5).*x)
else if -1/2<=x&&x<0
f=x+0.5
else
f=0
end
end
请输入变量值:-1
f =
>> 0
ans =
>> 1
ans =
1
>> -1/3
ans =
-0.3333
a=-3:0.01:-1/2;
b=0;
c=-1/2:0.01:0;
d=c+1/2;
e=0:0.01:3;
f=1/2*exp(-e/2); plot(a,b,c,d,e,f)
3.求[100,200]之间第一个能被13整除的整数。
>>clear
>> A=100:200;
i=find(mod(A,13)==0);
x=input('请输入你想查找的第n个能被13整除的数:');
if x>8
input('输入有误!')
else
A(i(x))
end
请输入你想查找的第n个能被13整除的数:4
ans =
143
4.求出斐波那契数列中第一个大于10000的元素及序号
A=[];
A(1)=1;
A(2)=1;
i=2;
while(A(i)<=10000)
i=i+1;
A(i)=A(i-1)+A(i-2);
end;
i
A(i)
i =
21
ans =
10946
5. 判断向量组]7,1,3,1[],9,8,2,5[],2,3,1,1[],2,3,1,1[4321-=-=--==a a a a 是否线性相关,如不相关,找
出其中最大线性无关组。
>> a1=[1,1,3,2];
a2=[-1,1,-3,2];
a3=[5,-2,8,9];
a4=[-1,3,1,7];
A=[a1;a2;a3;a4]
det(A)
B=transpose(A)
A =
1 1 3 2
-1 1 -3 2
5 -2 8 9
-1 3 1 7
ans =
-118
B =
1 -1 5 -1
1 1 -
2 3
3 -3 8 1 2 2 9 7。
