中考二次函数压轴题专题分类训练
中考数学总复习《二次函数压轴题(面积问题)》专题训练-附含答案

中考数学总复习《二次函数压轴题(面积问题)》专题训练-附含答案学校:___________班级:___________姓名:___________考号:___________1.如图,在平面直角坐标系中,抛物线2y ax x c =-+与y 轴交于点()0,4A -,与x 轴交于点()4,0B ,连接AB .(1)求抛物线的解析式.(2)P 是AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点C ,过点P 作PD x ⊥轴于点D .①求PC PD +的最大值.①连接PA ,PB ,是否存在点P ,使得线段PC 把PAB 的面积分成3:5两部分?若存在,请直接写出点P 的坐标;若不存在,请说明理由.2.综合与探究如图1,抛物线212y x bx c =-++经过点(4,0)B 和(0,2)C ,与x 轴的另一个交点为A ,连接AC ,BC .(1)求该抛物线的解析式及点A 的坐标;(2)如图1,点D 是线段AC 的中点,连接BD .点E 是抛物线上一点,若ABE BCD S S =△△,设点E 的横坐标为x ,请求出x 的值;(3)试探究在抛物线上是否存在一点P ,使得45PBO OBC ∠+∠=︒?若存在,请直接写出点P 的坐标;若不存在,请说明理由.3.如图抛物线2y ax bx c =++经过点()1,0A -,点()0,3C ,且OB OC =.(1)求抛物线的解析式及其对称轴;(2)点D 、E 是直线1x =上的两个动点,且1DE =,点D 在点E 的上方,求四边形ACDE 的周长的最小值.(3)点P 为抛物线上一点,连接CP ,直线CP 把四边形CBPA 的面积分为3:5两部分,求点P 的坐标.4.已知二次函数23y ax bx a =+-经过点()1,0A -和()0,3C ,与x 轴交于另一点B ,抛物线的顶点为D .(1)求此二次函数解析式;(2)连接DC 、BC 和DB ,判断BCD △的形状并说明理由;(3)在对称轴右侧抛物线上找一点P ,使得P 、D 、C 构成以PC 为底边的等腰三角形,求出点P 的坐标及此时四边形PBCD 的面积.5.如图,抛物线214y x bx c =-++与x 轴交于点,A B 两点(点A 在点B 的右侧),点()()8,02,0A B -、,与y 轴交于点C .(1)求抛物线的解析式; (2)点D 为抛物线的顶点,过点D 作DE AC ∥交抛物线于点E ,点P 为抛物线上点,D E 之间的一动点,连接,,,,AC AE AP CE CP ,线段,AP CE 交于点G ,记CPG △的面积为1,S AEG △的面积为2S ,且12S S S =-,求S 的最大值及此时点P 的坐标;(3)在(2)的条件下,将拋物线沿射线AC 方向平移5个单位长度后得到新抛物线,点Q 是新拋物线对称轴上一动点,在平面内确定一点R ,使得以点P Q B R 、、、为顶点的四边形是矩形.直接写出所有符合条件的点R 的坐标.6.如图,有一个长为30米的篱笆,一面利用墙(墙的最大可用长度18a =米)围成的中间隔有一道篱笆的长方形花圃设花圃的宽AB 为x 米,面积为y 平方米.(1)求y 与x 的函数关系式,并直接写出自变量x 的取值范围;(2)如何设计才能使长方形花圃面积最大;并求其最大面积.7.如图,过原点的抛物线212y x bx c =-++与x 轴的另一个交点为A ,且抛物线的对称轴为直线2x =,点B 为顶点(1)求抛物线的解析式(2)如图(1),点C 为直线OB 上方抛物线上一动点,连接AB,BC 和AC ,线段AC 交直线OB 于点E ,若CBE △的面积为1S ,ABE 的面积为2S ,求12S S 的最大值 (3)如图(2),设直线()20y kx k k =-≠与抛物线交于D ,F 两点,点D 关于直线2x =的对称点为D ,直线D F '与直线2x =交于点P ,求证:BP 的长是定值.8.抛物线2y x bx c =-++经过点A ,B ,C ,已知()1,0A -和()0,3C .(1)求抛物线的解析式及顶点E 的坐标;(2)点D 在BC 上方的抛物线上.①如图1,若CAB ABD ∠=∠,求点D 的坐标;①如图2,直线BD 交y 轴于点N ,过点B 作AD 的平行线交y 轴于点M ,当点D 运动时,求CBD AMNS S △△的最大值及此时点D 的坐标. 9.在平面直角坐标系中,O 为坐标原点,抛物线244y ax ax =-+交x 轴于点A 、B (A 左B右),交y 轴于点C ,直线123y x =-+,经过B 点,交y 轴于点D .(1)如图1,求a 的值;(2)如图2,点P 在第一象限内的抛物线上,过点A 、B 作x 轴的垂线,分别交直线PD 于点E 和F ,若PF DE =,求点P 的坐标;(3)如图3,在(2)的条件下,点Q 在第一象限内的抛物线上,过点Q 作QH DP ⊥于点H ,交直线BD 于点R ,连接EQ 和ER ,当QE ER =时,求ERQ △的面积.10.已知抛物线213222y x x =-++与x 轴交于B 、C 两点(点B 在点C 的左侧),与y 轴交于点A .(1)判断ABC 的形状,并说明理由.(2)设点(,)P m n 是抛物线在第一象限部分上的点,过点P 作PH x ⊥轴于H ,交AC 于点Q ,设四边形OAPC 的面积为S ,求S 关于m 的函数关系式,并求使S 最大时点P 的坐标和QHC △的面积;(3)在(2)的条件下,点N 是坐标平面内一点,抛物线的对称轴上是否存在点M ,使得以P 、C 和M 、N 为顶点的四边形是菱形,若存在,写出点M 的坐标,并选择一个点写出过程,若不存在,请说明理由.11.已知,如图,在平面直角坐标系中,点O 为坐标原点,直线6y x =+与x 轴相交于点B ,与y 轴交于点C ,点A 是x 轴正半轴上一点,且满足2tan 3ACO ∠=.(1)若抛物线2y ax bx c =++经过A 、B 和C 三点,求抛物线的解析式;(2)若点M 是第二象限内抛物线上的一个动点,过点M 作MP y ∥轴,交BC 于点P ,连接OP ,在第一象限内找一点Q ,过点Q 作⊥OQ OP 且OQ OP =,连接PQ ,MQ ,设MPQ 的面积为S ,点P 的横坐标为t ,求S 与t 的函数关系式,并直接写出自变量的取值范围;(3)在(2)的条件下,设PQ 与y 轴相交于点R ,若53=PR PC 时,求点P 的坐标. 12.已知抛物线22y ax ax c =-+过点()10A -,和()03C ,,与x 轴交于另一点B .(1)求抛物线的解析式;(2)若抛物线的顶点为D ,在直线BC 上方抛物线上有一点P (与D 不重合),BCP 面积与BCD △面积相等,求点P 的坐标;(3)若点E 为抛物线对称轴上一点,在平面内是否存在点F ,使得以E 、F 和B 、C 为顶点的四边形是菱形,若存在,请直接写出F 点的坐标;若不存在,请说明理由.13.如图,抛物线过点()08D ,,与x 轴交于()20A -,,()40B ,两点.(1)求抛物线的解析式;(2)若点C 为二次函数的顶点,求BCD S △.14.如图,O 为平面直角坐标系坐标原点,抛物线22y ax ax c =-+经过点()6,0B ,点()0,6C 与x 轴交于另一点A .(1)求抛物线的解析式;(2)D 点为第一象限抛物线上一点,连接AD 和BD ,设点D 的横坐标为t ,ABD △的面积为S ,求S 关于t 的函数解析式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,P 为第四象限抛物线上一点,连接PA 交y 轴于点E ,点F 在线段BC 上,点G 在直线AD 上,若1tan 2DAO ∠=,四边形BEFG 为菱形,求点P 的坐标. 15.已知抛物线2()20y ax x c a =++≠与x 轴交于点(1,0)A -和点B ,与直线3y x =-+交于点B 和点C ,M 为抛物线的顶点,直线ME 是抛物线的对称轴.(1)求抛物线的解析式及点M 的坐标;(2)点P 为直线BC 上方抛物线上一点,连接PB ,PC ,当PBC 的面积取最大值时,求点P 的坐标.参考答案:1.(1)2142y x x =-- (2)① PC PD +取得最大值254 ① 53,2⎛⎫- ⎪⎝⎭或 316,2⎛⎫+- ⎪⎝⎭2.(1)213222y x x =-++ (1,0)-; (2)3172+或3172-或3332+或3332- (3)存在,517(,)39--或113(,)39-3.(1)故抛物线的表达式为:223y x x =-++,函数的对称轴为:1x =;(2)10113++(3)()4,5-或()8,45-4.(1)223y x x =-++(2)BCD △为直角三角形(3)点P 的坐标为()2,3,四边形PBCD 的面积为45.(1)213442y x x =-++ (2)S 的最大值为1,()4,6P(3)()7,3或()5,3-6.(1)2330S x x =-+ 410x ≤<;(2)当宽AB 为5米,长15BC =米时,长方形花圃的最大面积为75平方米.7.(1)2122y x x =-+ (2)188.(1)()1,4(2)①()2,3D ;①CBD AMN S S △△的最大值为916,此时315,24D ⎛⎫ ⎪⎝⎭9.(1)13a =- (2)()4,4P(3)1010.(1)直角三角形(2)244S m m =-++ (2,3)P 1QHC S =(3)存在,点M 坐标为3651(,)22+或3651(,)22-或333(,)22或333(,)22-或31(,)22,理由见解析11.(1)211642=--+y x x (2)()2396042S t t t =---<< (3)()()124,2,2,4P P --12.(1)223y x x =-++(2)()23P ,(3)存在,点F 的坐标为()417,或()417-,或()2314-+,或()2314--,13.(1)228y x x =-++(2)614.(1)211642y x x =-++ (2)2553042S t t =-++ (3)()8,6P -15.(1)抛物线的解析式为223y x x =-++,点M 的坐标为(1,4)(2)315,24P ⎛⎫ ⎪⎝⎭。
2024年中考数学高频压轴题训练——二次函数压轴题(特殊四边形)及参考答案

2024年中考数学高频压轴题训练——二次函数压轴题(特殊四边形)()1求该抛物线的表达式;()2点P在该抛物线上,点Q在y轴上,要使以点形,求所有满足条件的点P的坐标.2.如图,已知抛物线223=--+y x x的左侧),与y轴交于点C.点E为抛物线对称轴上的一个动点:(1)当点E 在x 轴上方且CE BD ∥时,求sin DEC ∠(2)若点P 在抛物线上,是否存在以点B ,E ,C ,P 求出点P 的坐标;(3)若抛物线对称轴上有点E ,使得55AE DE +取得最小值,连接限抛物线为点M ,从请直接写出AM 的长度.3.如图,抛物线23y ax bx =+-与x 轴交于(1,0A -(1)求抛物线的解析式;(2)若点D 是抛物线上的一点,当ABD △的面积为(3)点P 是抛物线对称轴上的一点,在抛物线上是否存在一点为顶点的四边形是平行四边形?若存在,求出点Q(1)求出抛物线与直线的解析式;(2)已知点K为线段AD上一动点,过点K作AH,求AHD的最大面积;(3)若点M是x轴上的一动点,点N是抛物线上一动点,当以点顶点的四边形是平行四边形时,请你直接写出符合条件的点(1)求抛物线的解析式;(2)若点P 是抛物线第四象限上的一个动点,过点P 作PQ AC ∥交BC 于点Q .①如图1,记APQ △面积为1,S BPQ 面积为2S ,求12S S +的面积最大值及此时点P 的坐标.②如图2,若将QP 沿直线BC 翻折得到QE ,且点E 落在线段AC 上,求此时点P 的坐标.6.如图,抛物线y =﹣54x 2+bx +c 与直线y =12x +c 相交于A (0,1),B (3,52)两点,过点B 作BC ⊥x 轴,垂足为点C ,在线段AB 上方的抛物线上取一点D ,过D 作DF 轴,垂足为点F ,交AB 于点E .(1)求该抛物线的表达式;(2)求△ABD面积的最大值;(3)连接BD、CE,四边形BDEC能否成为平行四边形?若能,求出点D的坐标;若不能,请说明理由.7.在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(2,'''.1).将此矩形绕点O逆时针旋转90°,得到矩形OA B C(1)求过点A、A'、C'的抛物线的解析式;(2)将矩形OABC沿x轴正方向平移,使点C落在抛物线上,求平移的距离.12.如图,在平面直角坐标系中,点()3,4A -、()5,10B -在抛物线2y x bx c =++上,点P 为该抛物线上一点,其横坐标为m .(1)求该抛物线的解析式;(2)当点P 与点A 关于该抛物线的对称轴对称时,求PAB 的面积;(3)当该抛物线在点B 与点P 之间部分(含点B 和点P )的最高点与最低点的纵坐标之差为3时,求m 的值;(4)点Q 为该抛物线的对称轴上任意一点,当以点A 、B 、P 、Q 为顶点的四边形是平行四边形时,直接写出点P 的坐标.13.如图,抛物线2y x bx c =-++交x 轴于点A B ,,交y 轴于点C ,点B 的坐标为()3,0,点C 的坐标为()0,3,点C 与点D 关于抛物线的对称轴对称.(1)求抛物线的解析式;(2)若点P 为抛物线对称轴上一点,连接BD ,以PD PB 、为边作平行四边形PDNB ,是否存在这样的点P ,使得PDNB 是矩形?若存在,请求出tan BDN ∠的值;若不存在,请说明理由;(3)点Q 在y 轴右侧抛物线上运动,当ACQ 的面积与ABQ 的面积相等时,请直接写出点Q 的坐标.14.如图,在平面直角坐标系中,抛物线2y x bx c =-++与x 轴交于点()1,0A -,与y 轴交于点()0,3B .P 是该抛物线上一点,其横坐标为m ,作点P 关于原点O 的对称点Q .当线段PQ 不与坐标轴垂直时,以PQ 为对角线构造矩形PMQN ,该矩形的边均与某条坐标轴垂直.(1)求该抛物线对应的函数解析式;(2)当点P 是该抛物线的顶点时,求点Q 的坐标;(3)当点B 在矩形PMQN 的边上时,求m 的值;(4)当0m >,且矩形PMQN 与该抛物线有三个交点时,直接写出m 的取值范围.(1)试求抛物线的解析式;(2)直线()10y kx k =+>与y 轴交于点D ,与抛物线在第一象限交于点于点M ,记CPM CDMS m S =△△,试求m 的最大值及此时点P 的坐标;(3)在(2)的条件下,m 取最大值时,点Q 是x 轴上的一个动点,点参考答案:t。
中考数学压轴题之二次函数(中考题型整理,突破提升)附详细答案
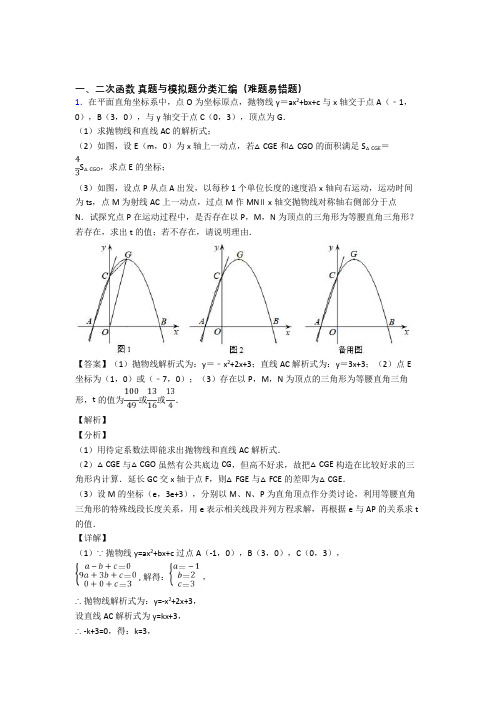
一、二次函数真题与模拟题分类汇编(难题易错题)1.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,3),顶点为G.(1)求抛物线和直线AC的解析式;(2)如图,设E(m,0)为x轴上一动点,若△CGE和△CGO的面积满足S△CGE=S△CGO,求点E的坐标;(3)如图,设点P从点A出发,以每秒1个单位长度的速度沿x轴向右运动,运动时间为ts,点M为射线AC上一动点,过点M作MN∥x轴交抛物线对称轴右侧部分于点N.试探究点P在运动过程中,是否存在以P,M,N为顶点的三角形为等腰直角三角形?若存在,求出t的值;若不存在,请说明理由.【答案】(1)抛物线解析式为:y=﹣x2+2x+3;直线AC解析式为:y=3x+3;(2)点E 坐标为(1,0)或(﹣7,0);(3)存在以P,M,N为顶点的三角形为等腰直角三角形,t的值为或或.【解析】【分析】(1)用待定系数法即能求出抛物线和直线AC解析式.(2)△CGE与△CGO虽然有公共底边CG,但高不好求,故把△CGE构造在比较好求的三角形内计算.延长GC交x轴于点F,则△FGE与△FCE的差即为△CGE.(3)设M的坐标(e,3e+3),分别以M、N、P为直角顶点作分类讨论,利用等腰直角三角形的特殊线段长度关系,用e表示相关线段并列方程求解,再根据e与AP的关系求t 的值.【详解】(1)∵抛物线y=ax2+bx+c过点A(-1,0),B(3,0),C(0,3),, 解得:,∴抛物线解析式为:y=-x2+2x+3,设直线AC解析式为y=kx+3,∴-k+3=0,得:k=3,∴直线AC解析式为:y=3x+3.(2)延长GC交x轴于点F,过G作GH⊥x轴于点H,∵y=-x2+2x+3=-(x-1)2+4,∴G(1,4),GH=4,∴S△CGO=OC•x G=×3×1=,∴S△CGE=S△CGO=×=2,①若点E在x轴正半轴上,设直线CG:y=k1x+3,∴k1+3=4 得:k1=1,∴直线CG解析式:y=x+3,∴F(-3,0),∵E(m,0),∴EF=m-(-3)=m+3,∴S△CGE=S△FGE-S△FCE=EF•GH-EF•OC=EF•(GH-OC)=(m+3)•(4-3)=,∴=2,解得:m=1,∴E的坐标为(1,0).②若点E在x轴负半轴上,则点E到直线CG的距离与点(1,0)到直线CG距离相等,即点E到F的距离等于点(1,0)到F的距离,∴EF=-3-m=1-(-3)=4,解得:m=-7 即E(-7,0),综上所述,点E坐标为(1,0)或(-7,0).(3)存在以P,M,N为顶点的三角形为等腰直角三角形,设M(e,3e+3),则y N=y M=3e+3,①若∠MPN=90°,PM=PN,如图2,过点M作MQ⊥x轴于点Q,过点N作NR⊥x轴于点R,∵MN∥x轴,∴MQ=NR=3e+3,∴Rt△MQP≌Rt△NRP(HL),∴PQ=PR,∠MPQ=∠NPR=45°,∴MQ=PQ=PR=NR=3e+3,∴x N=x M+3e+3+3e+3=7e+6,即N(7e+6,3e+3),∵N在抛物线上,∴-(7e+6)2+2(7e+6)+3=3e+3,解得:e1=-1(舍去),e2=−,∵AP=t,OP=t-1,OP+OQ=PQ,∴t-1-e=3e+3,∴t=4e+4=,②若∠PMN=90°,PM=MN,如图3,∴MN=PM=3e+3,∴x N=x M+3e+3=4e+3,即N(4e+3,3e+3),∴-(4e+3)2+2(4e+3)+3=3e+3,解得:e1=-1(舍去),e2=−,∴t=AP=e-(-1)=−+1=,③若∠PNM=90°,PN=MN,如图4,∴MN=PN=3e+3,N (4e+3,3e+3), 解得:e=−,∴t=AP=OA+OP=1+4e+3=,综上所述,存在以P ,M ,N 为顶点的三角形为等腰直角三角形,t 的值为或或.【点睛】本题考查了待定系数法求函数解析式,坐标系中三角形面积计算,等腰直角三角形的性质,解一元二次方程,考查了分类讨论和方程思想.第(3)题根据等腰直角三角形的性质找到相关线段长的关系是解题关键,灵活运用因式分解法解一元二次方程能简便运算.2.(2017南宁,第26题,10分)如图,已知抛物线2239y ax ax a =--与坐标轴交于A ,B ,C 三点,其中C (0,3),∠BAC 的平分线AE 交y 轴于点D ,交BC 于点E ,过点D 的直线l 与射线AC ,AB 分别交于点M ,N .(1)直接写出a 的值、点A 的坐标及抛物线的对称轴;(2)点P 为抛物线的对称轴上一动点,若△PAD 为等腰三角形,求出点P 的坐标; (3)证明:当直线l 绕点D 旋转时,11AM AN+均为定值,并求出该定值.【答案】(1)a =13-,A 30),抛物线的对称轴为x 32)点P 的坐标为3034);(3)32. 【解析】试题分析:(1)由点C 的坐标为(0,3),可知﹣9a =3,故此可求得a 的值,然后令y =0得到关于x 的方程,解关于x 的方程可得到点A 和点B 的坐标,最后利用抛物线的对称性可确定出抛物线的对称轴;(2)利用特殊锐角三角函数值可求得∠CAO =60°,依据AE 为∠BAC 的角平分线可求得∠DAO =30°,然后利用特殊锐角三角函数值可求得OD =1,则可得到点D 的坐标.设点P 的,a ).依据两点的距离公式可求得AD 、AP 、DP 的长,然后分为AD =PA 、AD =DP 、AP =DP 三种情况列方程求解即可;(3)设直线MN 的解析式为y =kx +1,接下来求得点M 和点N 的横坐标,于是可得到AN 的长,然后利用特殊锐角三角函数值可求得AM 的长,最后将AM 和AN 的长代入化简即可.试题解析:(1)∵C (0,3),∴﹣9a =3,解得:a =13-.令y =0得:290ax a --=,∵a ≠0,∴290x --=,解得:x =x =∴点A 0),B (0),∴抛物线的对称轴为x(2)∵OA OC =3,∴tan ∠CAO ∴∠CAO =60°.∵AE 为∠BAC 的平分线,∴∠DAO =30°,∴DO =1,∴点D 的坐标为(0,1).设点P a ).依据两点间的距离公式可知:AD 2=4,AP 2=12+a 2,DP 2=3+(a ﹣1)2. 当AD =PA 时,4=12+a 2,方程无解.当AD =DP 时,4=3+(a ﹣1)2,解得a =0或a =2(舍去),∴点P 0).当AP =DP 时,12+a 2=3+(a ﹣1)2,解得a =﹣4,∴点P ,﹣4).综上所述,点P 04).(3)设直线AC 的解析式为y =mx +3,将点A 的坐标代入得:30+=,解得:m ∴直线AC 的解析式为3y =+. 设直线MN 的解析式为y =kx +1.把y =0代入y =kx +1得:kx +1=0,解得:x =1k -,∴点N 的坐标为(1k-,0),∴AN =1k-.将3y =+与y =kx +1联立解得:x,∴点M .过点M 作MG ⊥x 轴,垂足为G .则AG∵∠MAG =60°,∠AGM =90°,∴AM =2AG =4233k +-=2323k k --,∴11AM AN +=323231k k k k -+-- =33232k k --=3(31)2(31)k k -- =32. 点睛:本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,分类讨论是解答问题(2)的关键,求得点M 的坐标和点N 的坐标是解答问题(3)的关键.3.如图,某足球运动员站在点O 处练习射门,将足球从离地面0.5m 的A 处正对球门踢出(点A 在y 轴上),足球的飞行高度y(单位:m )与飞行时间t(单位:s )之间满足函数关系y =at 2+5t +c ,已知足球飞行0.8s 时,离地面的高度为3.5m . (1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)若足球飞行的水平距离x(单位:m )与飞行时间t(单位:s )之间具有函数关系x =10t ,已知球门的高度为2.44m ,如果该运动员正对球门射门时,离球门的水平距离为28m ,他能否将球直接射入球门?【答案】(1)足球飞行的时间是85s 时,足球离地面最高,最大高度是4.5m ;(2)能. 【解析】试题分析:(1)由题意得:函数y=at 2+5t+c 的图象经过(0,0.5)(0.8,3.5),于是得到,求得抛物线的解析式为:y=﹣t 2+5t+,当t=时,y 最大=4.5;(2)把x=28代入x=10t 得t=2.8,当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,于是得到他能将球直接射入球门.解:(1)由题意得:函数y=at 2+5t+c 的图象经过(0,0.5)(0.8,3.5), ∴,解得:,∴抛物线的解析式为:y=﹣t2+5t+,∴当t=时,y最大=4.5;(2)把x=28代入x=10t得t=2.8,∴当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,∴他能将球直接射入球门.考点:二次函数的应用.4.如图,抛物线y=ax2+bx(a≠0)过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)直接写出点C的坐标,并求出△ABC的面积;(3)点P是抛物线上一动点,且位于第四象限,是否存在这样的点P,使得△ABP的面积为△ABC面积的2倍?若存在,求出点P的坐标,若不存在,请说明理由;(4)若点M在直线BH上运动,点N在x轴正半轴上运动,当以点C,M,N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.【答案】(1)y=-x2+4x;(2)C(3,3),面积为3;(3)P的坐标为(5,-5);(4)52或5.【解析】试题分析:(1)利用待定系数法进行求解即可;(2)先求出抛物线的对称轴,利用对称性即可写出点C的坐标,利用三角形面积公式即可求面积;(3)利用三角形的面积以及点P所处象限的特点即可求;(4)分情况进行讨论,确定点M、N,然后三角形的面积公式即可求.试题解析:(1)将A(4,0),B(1,3)代入到y=ax2+bx中,得16403a ba b+=⎧⎨+=⎩,解得14ab=-⎧⎨=⎩,∴抛物线的表达式为y=-x2+4x.(2)∵抛物线的表达式为y=-x2+4x,∴抛物线的对称轴为直线x=2.又C,B关于对称轴对称,∴C(3,3).∴BC=2,∴S△ABC=12×2×3=3.(3)存在点P.作PQ⊥BH于点Q,设P(m,-m2+4m).∵S△ABP=2S△ABC,S△ABC=3,∴S△ABP=6.∵S△ABP+S△BPQ=S△ABH+S梯形AHQP∴6+12×(m-1)×(3+m2-4m)=12×3×3+12×(3+m-1)(m2-4m)整理得m2-5m=0,解得m1=0(舍),m2=5,∴点P的坐标为(5,-5).(4)52或5.提示:①当以M为直角顶点,则S△CMN=52;②当以N为直角顶点,S△CMN=5;③当以C为直角顶点时,此种情况不存在.【点睛】本题是二次函数的综合题,主要考查待定系数法求解析式,三角形面积、直角三角形的判定等,能正确地根据题意确定图形,分情况进行讨论是解题的关键.5.在平面直角坐标系xOy中(如图).已知抛物线y=﹣12x2+bx+c经过点A(﹣1,0)和点B(0,52),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.(1)求这条抛物线的表达式;(2)求线段CD 的长;(3)将抛物线平移,使其顶点C 移到原点O 的位置,这时点P 落在点E 的位置,如果点M 在y 轴上,且以O 、D 、E 、M 为顶点的四边形面积为8,求点M 的坐标.【答案】(1)抛物线解析式为y=﹣12x 2+2x+52;(2)线段CD 的长为2;(3)M 点的坐标为(0,72)或(0,﹣72). 【解析】【分析】(1)利用待定系数法求抛物线解析式;(2)利用配方法得到y=﹣12(x ﹣2)2+92,则根据二次函数的性质得到C 点坐标和抛物线的对称轴为直线x=2,如图,设CD=t ,则D (2,92﹣t ),根据旋转性质得∠PDC=90°,DP=DC=t ,则P (2+t ,92﹣t ),然后把P (2+t ,92﹣t )代入y=﹣12x 2+2x+52得到关于t 的方程,从而解方程可得到CD 的长;(3)P 点坐标为(4,92),D 点坐标为(2,52),利用抛物线的平移规律确定E 点坐标为(2,﹣2),设M (0,m ),当m >0时,利用梯形面积公式得到12•(m+52+2)•2=8当m <0时,利用梯形面积公式得到12•(﹣m+52+2)•2=8,然后分别解方程求出m 即可得到对应的M 点坐标.【详解】(1)把A (﹣1,0)和点B (0,52)代入y=﹣12x 2+bx+c 得 10252b c c ⎧--+=⎪⎪⎨⎪=⎪⎩,解得252b c =⎧⎪⎨=⎪⎩,∴抛物线解析式为y=﹣12x 2+2x+52; (2)∵y=﹣12(x ﹣2)2+92,∴C(2,92),抛物线的对称轴为直线x=2,如图,设CD=t,则D(2,92﹣t),∵线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处,∴∠PDC=90°,DP=DC=t,∴P(2+t,92﹣t),把P(2+t,92﹣t)代入y=﹣12x2+2x+52得﹣12(2+t)2+2(2+t)+52=92﹣t,整理得t2﹣2t=0,解得t1=0(舍去),t2=2,∴线段CD的长为2;(3)P点坐标为(4,92),D点坐标为(2,52),∵抛物线平移,使其顶点C(2,92)移到原点O的位置,∴抛物线向左平移2个单位,向下平移92个单位,而P点(4,92)向左平移2个单位,向下平移92个单位得到点E,∴E点坐标为(2,﹣2),设M(0,m),当m>0时,12•(m+52+2)•2=8,解得m=72,此时M点坐标为(0,72);当m<0时,12•(﹣m+52+2)•2=8,解得m=﹣72,此时M点坐标为(0,﹣72);综上所述,M点的坐标为(0,72)或(0,﹣72).【点睛】本题考查了二次函数的综合题,涉及到待定系数法、抛物线上点的坐标、旋转的性质、抛物线的平移等知识,综合性较强,正确添加辅助线、运用数形结合思想熟练相关知识是解题的关键.6.在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=14x与抛物线交于A、B两点,直线l为y=﹣1.(1)求抛物线的解析式;(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.【答案】(1)抛物线的解析式为y=14x2﹣x+1.(2)点P的坐标为(2813,﹣1).(3)定点F的坐标为(2,1).【解析】分析:(1)由抛物线的顶点坐标为(2,0),可设抛物线的解析式为y=a(x-2)2,由抛物线过点(4,1),利用待定系数法即可求出抛物线的解析式;(2)联立直线AB与抛物线解析式成方程组,通过解方程组可求出点A、B的坐标,作点B关于直线l的对称点B′,连接AB′交直线l于点P,此时PA+PB取得最小值,根据点B的坐标可得出点B′的坐标,根据点A、B′的坐标利用待定系数法可求出直线AB′的解析式,再利用一次函数图象上点的坐标特征即可求出点P的坐标;(3)由点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征,即可得出(1-12-12y0)m2+(2-2x0+2y0)m+x02+y02-2y0-3=0,由m的任意性可得出关于x0、y0的方程组,解之即可求出顶点F的坐标.详解:(1)∵抛物线的顶点坐标为(2,0),设抛物线的解析式为y=a(x-2)2.∵该抛物线经过点(4,1),∴1=4a,解得:a=14,∴抛物线的解析式为y=14(x-2)2=14x2-x+1.(2)联立直线AB与抛物线解析式成方程组,得:214114y x y x x ⎧⎪⎪⎨⎪-+⎪⎩==,解得:11114x y ⎧⎪⎨⎪⎩==,2241x y ⎧⎨⎩==, ∴点A 的坐标为(1,14),点B 的坐标为(4,1). 作点B 关于直线l 的对称点B′,连接AB′交直线l 于点P ,此时PA+PB 取得最小值(如图1所示).∵点B (4,1),直线l 为y=-1, ∴点B′的坐标为(4,-3).设直线AB′的解析式为y=kx+b (k≠0), 将A (1,14)、B′(4,-3)代入y=kx+b ,得: 1443k b k b ⎧+⎪⎨⎪+-⎩==,解得:131243k b ⎧-⎪⎪⎨⎪⎪⎩==, ∴直线AB′的解析式为y=-1312x+43, 当y=-1时,有-1312x+43=-1, 解得:x=2813, ∴点P 的坐标为(2813,-1). (3)∵点M 到直线l 的距离与点M 到点F 的距离总是相等, ∴(m-x 0)2+(n-y 0)2=(n+1)2, ∴m 2-2x 0m+x 02-2y 0n+y 02=2n+1. ∵M (m ,n )为抛物线上一动点,∴n=14m2-m+1,∴m2-2x0m+x02-2y0(14m2-m+1)+y02=2(14m2-m+1)+1,整理得:(1-12-12y0)m2+(2-2x0+2y0)m+x02+y02-2y0-3=0.∵m为任意值,∴00220001110222220230yx yx y y⎧--⎪⎪-+⎨⎪+--⎪⎩===,∴021xy⎧⎨⎩==,∴定点F的坐标为(2,1).点睛:本题考查了待定系数法求二次(一次)函数解析式、二次(一次)函数图象上点的坐标特征、轴对称中的最短路径问题以及解方程组,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数解析式;(2)利用两点之间线段最短找出点P的位置;(3)根据点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征,找出关于x0、y0的方程组.7.如图,已知抛物线2y ax bx c=++的顶点为()4,3A,与y轴相交于点()0,5B-,对称轴为直线l,点M是线段AB的中点.(1)求抛物线的表达式;(2)写出点M的坐标并求直线AB的表达式;(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.【答案】(1)21452=-+-y x x;(2)()2,1-M,25y x=-;(3)点P、Q的坐标分别为()6,1或()2,1、()4,3-或()4,1.【解析】【分析】(1)函数表达式为:()243y a x ==+,将点B 坐标代入上式,即可求解; (2)()4,3A 、()0,5B -,则点()2,1-M ,设直线AB 的表达式为:5y kx =-,将点A 坐标代入上式,即可求解;(3)分当AM 是平行四边形的一条边、AM 是平行四边形的对角线两种情况,分别求解即可. 【详解】解:(1)函数表达式为:()243y a x ==+, 将点B 坐标代入上式并解得:12a =-, 故抛物线的表达式为:21452=-+-y x x ; (2)()4,3A 、()0,5B -,则点()2,1-M , 设直线AB 的表达式为:5y kx =-,将点A 坐标代入上式得:345k =-,解得:2k =, 故直线AB 的表达式为:25y x =-; (3)设点()4,Q s 、点21,452P m m m ⎛⎫-+- ⎪⎝⎭, ①当AM 是平行四边形的一条边时,点A 向左平移2个单位、向下平移4个单位得到M ,同样点21,452P m m m ⎛⎫-+-⎪⎝⎭向左平移2个单位、向下平移4个单位得到()4,Q s , 即:24m -=,214542m m s -+--=, 解得:6m =,3s =-,故点P 、Q 的坐标分别为()6,1、()4,3-; ②当AM 是平行四边形的对角线时, 由中点定理得:424m +=+,2131452m m s -=-+-+, 解得:2m =,1s =,故点P 、Q 的坐标分别为()2,1、()4,1;故点P 、Q 的坐标分别为()6,1,()4,3-或()2,1、()4,3-,()2,1或()4,1. 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图象的面积计算等,其中(3),要主要分类求解,避免遗漏.8.抛物线与x轴交于A,B两点(OA<OB),与y轴交于点C.(1)求点A,B,C的坐标;(2)点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<2).①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时,的值最小,求出这个最小值并写出此时点E,P的坐标;②在满足①的条件下,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请直接写出点F的坐标;若不存在,请说明理由.【答案】(1)A(2,0),B(4,0),C(0,2);(2)①t=1时,有最小值1,此时OP=2,OE=1,∴E(0,1),P(2,0);②F(3,2),(3,7).【解析】试题分析:(1)在抛物线的解析式中,令y=0,令x=0,解方程即可得到结果;(2)①由题意得:OP=2t,OE=t,通过△CDE∽△CBO得到,即,求得有最小值1,即可求得结果;②存在,求得抛物线的对称方程为x=3,设F(3,m),当△EFP为直角三角形时,①当∠EPF=90°时,②当∠EFP=90°时,③当∠PEF=90°时,根据勾股定理列方程即可求得结果.试题解析:(1)在抛物线的解析式中,令y=0,即,解得:,,∵OA<OB,∴A(2,0),B(4,0),在抛物线的解析式中,令x=0,得y=2,∴C(0,2);(2)①由题意得:OP=2t,OE=t,∵DE∥OB,∴△CDE∽△CBO,∴,即,∴DE=4﹣2t,∴===,∵0<t<2,始终为正数,且t=1时,有最大值1,∴t=1时,有最小值1,即t=1时,有最小值1,此时OP=2,OE=1,∴E(0,1),P(2,0);②存在,∵抛物线的对称轴方程为x=3,设F(3,m),∴,=,=,当△EFP为直角三角形时,①当∠EPF=90°时,,即,解得:m=2,②当∠EFP=90°时,,即,解得;m=0或m=1,不合题意舍去,∴当∠EFP=90°时,这种情况不存在,③当∠PEF=90°时,,即,解得:m=7,综上所述,F(3,2),(3,7).考点:1.二次函数综合题;2.动点型;3.最值问题;4.二次函数的最值;5.分类讨论;6.压轴题.9.如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C.(1)求这个二次函数的表达式;(2)点P是直线BC下方抛物线上的一动点,求△BCP面积的最大值;(3)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m的值.【答案】(1)这个二次函数的表达式是y=x2﹣4x+3;(2)S△BCP最大=278;(3)当△BMN是等腰三角形时,m22,1,2.【解析】分析:(1)根据待定系数法,可得函数解析式;(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PE的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;(3)根据等腰三角形的定义,可得关于m的方程,根据解方程,可得答案.详解:(1)将A (1,0),B (3,0)代入函数解析式,得309330a b a b ++⎧⎨++⎩==, 解得14a b ⎧⎨-⎩==,这个二次函数的表达式是y=x 2-4x+3; (2)当x=0时,y=3,即点C (0,3),设BC 的表达式为y=kx+b ,将点B (3,0)点C (0,3)代入函数解析式,得30k b b +⎧⎨⎩==, 解这个方程组,得13k b -⎧⎨⎩== 直线BC 的解析是为y=-x+3, 过点P 作PE ∥y 轴,交直线BC 于点E (t ,-t+3), PE=-t+3-(t 2-4t+3)=-t 2+3t , ∴S △BCP =S △BPE +S CPE =12(-t 2+3t )×3=-32(t-32)2+278,∵-32<0,∴当t=32时,S △BCP 最大=278. (3)M (m ,-m+3),N (m ,m 2-4m+3) MN=m 2-3m ,2|m-3|,当MN=BM 时,①m 22(m-3),解得2, ②m 22m-3),解得2 当BN=MN 时,∠NBM=∠BMN=45°, m 2-4m+3=0,解得m=1或m=3(舍) 当BM=BN 时,∠BMN=∠BNM=45°,-(m 2-4m+3)=-m+3,解得m=2或m=3(舍), 当△BMN 是等腰三角形时,m 的值为2,-2,1,2.点睛:本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用面积的和差得出二次函数,又利用了二次函数的性质,解(3)的关键是利用等腰三角形的定义得出关于m 的方程,要分类讨论,以防遗漏.10.如图,△ABC 的顶点坐标分别为A (﹣6,0),B (4,0),C (0,8),把△ABC 沿直线BC 翻折,点A 的对应点为D ,抛物线y=ax 2﹣10ax+c 经过点C ,顶点M 在直线BC 上.(1)证明四边形ABCD 是菱形,并求点D 的坐标; (2)求抛物线的对称轴和函数表达式;(3)在抛物线上是否存在点P ,使得△PBD 与△PCD 的面积相等?若存在,直接写出点P 的坐标;若不存在,请说明理由. 【答案】(1)详见解析(2)22y x 4x 85=-+ (3)详见解析 【解析】 【分析】(1)根据勾股定理,翻折的性质可得AB=BD=CD=AC ,根据菱形的判定和性质可得点D 的坐标.(2)根据对称轴公式可得抛物线的对称轴,设M 的坐标为(5,n ),直线BC 的解析式为y=kx+b ,根据待定系数法可求M 的坐标,再根据待定系数法求出抛物线的函数表达式. (3)分点P 在CD 的上面下方和点P 在CD 的上方两种情况,根据等底等高的三角形面积相等可求点P 的坐标: 设P 22x,x 4x 85⎛⎫-+ ⎪⎝⎭,当点P 在CD 的上面下方,根据菱形的性质,知点P 是AD 与抛物线22y x 4x 85=-+的交点,由A,D 的坐标可由待定系数法求出AD 的函数表达式:1y x 32=+,二者联立可得P 1(529,48); 当点P 在CD 的上面上方,易知点P 是∠D 的外角平分线与抛物线22y x 4x 85=-+的交点,此时,∠D 的外角平分线与直线AD 垂直,由相似可知∠D 的外角平分线PD 的斜率等于-2,可设其为y 2x m =-+,将D (10,8)代入可得PD 的函数表达式:y 2x 28=-+,与抛物线22y x 4x 85=-+联立可得P 2(﹣5,38). 【详解】(1)证明:∵A (﹣6,0),B (4,0),C (0,8), ∴AB=6+4=10,AC 10==.∴AB=AC .由翻折可得,AB=BD ,AC=CD .∴AB=BD=CD=AC .∴四边形ABCD 是菱形. ∴CD ∥AB .∵C (0,8),∴点D 的坐标是(10,8).(2)∵y=ax 2﹣10ax+c ,∴对称轴为直线10ax 52a-=-=. 设M 的坐标为(5,n ),直线BC 的解析式为y=kx+b ,∴4k b 0b 8+=⎧⎨=⎩,解得k 2b 8=-⎧⎨=⎩.∴直线BC 的解析式为y=﹣2x+8.∵点M 在直线y=﹣2x+8上,∴n=﹣2×5+8=﹣2. ∴M (5,,-2).又∵抛物线y=ax 2﹣10ax+c 经过点C 和M ,∴25a 50a c 2c 8-+=-⎧⎨=⎩,解得2a 5c 8⎧=⎪⎨⎪=⎩.∴抛物线的函数表达式为22y x 4x 85=-+. (3)存在.点P 的坐标为P 1(529,48),P 2(﹣5,38)。
中考数学二次函数综合压轴题型归类

中考二次函数综合压轴题型归类一、常考点汇总1、两点间的距离公式:()()22B A B A x x y y AB -+-=2、中点坐标:线段AB 的中点C 的坐标为:⎪⎭⎫⎝⎛++22B A B A y y x x ,直线11b x k y +=(01≠k )与22b x k y +=(02≠k )的位置关系:(1)两直线平行⇔21k k =且21b b ≠ (2)两直线相交⇔21k k ≠ (3)两直线重合⇔21k k =且21b b = (4)两直线垂直⇔121-=k k3、一元二次方程有整数根问题,解题步骤如下:① 用∆和参数的其他要求确定参数的取值范围;② 解方程,求出方程的根;(两种形式:分式、二次根式)③ 分析求解:若是分式,分母是分子的因数;若是二次根式,被开方式是完全平方式。
例:关于的一元二次方程()01222=-m x m x ++有两个整数根,5<m 且m 为整数,求m 的值。
4、二次函数与x 轴的交点为整数点问题。
(方法同上)例:若抛物线()3132+++=x m mx y 与x 轴交于两个不同的整数点,且m 为正整数,试确定此抛物线的解析式。
5、方程总有固定根问题,可以通过解方程的方法求出该固定根。
举例如下:已知关于x 的方程23(1)230mx m x m --+-=(m 为实数),求证:无论m 为何值,方程总有一个固定的根。
解:当0=m 时,1=x ;当0≠m 时,()032≥-=∆m ,()m m x 213∆±-=,mx 321-=、12=x ;综上所述:无论m 为何值,方程总有一个固定的根是1。
6、函数过固定点问题,举例如下:已知抛物线22-+-=m mx x y (m 是常数),求证:不论m 为何值,该抛物线总经过一个x解:把原解析式变形为关于m 的方程()x m x y -=+-122;∴ ⎩⎨⎧=-=+-01 02 2x x y ,解得:⎩⎨⎧=-=1 1 x y ;∴ 抛物线总经过一个固定的点(1,-1)。
2023年数学《二次函数》在中考高频压轴题中的分类特训

二次函数在中考高频压轴题中的分类训练基础知识:如图,已知抛物线y=- 14x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴;(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;(3)证明:△ABC为直角三角形(5)在BC上求一个点D,使得OD将△ABC的面积平分(一)最值问题:(6) 在抛物线的对称轴上求一点P,使PA+PC的值最小值?若P1是∠ABC角平分线上的一点,P2是射线BC上的一点,求CP1+P1P2最小值(7)M为BC上方抛物线上的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;(8)M为BC上方抛物线上的一点,求△BCM面积的最大值;变式练习:1若点E 是抛物线顶点,点D (4,m )在抛物线上,在X 轴和Y 轴上找两个点M,N 使四边形DEMN 的周长最小,求M 和N 点的坐标2.若点Q 是线段AB 上的动点,过点Q 作QE\\BC,交AC 于点E ,连接CQ ,当△CQE 面积最大时,求点Q 坐标3.若点Q 是抛物线上的动点,过点Q 作QE\\X 轴,交线段AC 于点E ,交线段BC 于点F,分别过E,F 两点向X 轴作垂线,垂足分别为M,N ,当矩形EMNF 面积最大时,求点Q 坐标4.若M 为BC 上方抛物线上的一点,N 为线段BC 上的一点,且MN 垂直于BC,垂足为N ,求MN 的最大值;5.若M 为BC 上方抛物线上的一点,连接OM 交BC 于点N ,求ONMN的最大值;6.若M为BC上方抛物线上的一点,N为线段BC上的一点,且MN平行于AC,交点为N,求MN的最大值;(二)面积问题:(9)在抛物线上找一个点P,使△ABC与△PBC的面积相等变式练习:1若点F是抛物线上的一个动点,是否存在点F使△BCF的面积为8,若存在,求出点F的坐标;若不存在,请说明理由(三)等腰三角形问题:(10)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.变式练习:1.若点N在X轴上运动,当△BCN是等腰三角形时,求N点的坐标。
二次函数多结论压轴小题精选30道(必考点分类集训)(原卷版)—2024-2025学年九年级数学上册

二次函数多结论压轴小题精选30道1.(2024春•岳麓区校级期末)已知抛物线y =ax 2+bx +c 的图象如图所示,则下列结论中,正确的有( )①abc >0;②b 2>4ac ;③a ﹣b +c <0;④2a ﹣b >0;⑤a +c <1.A .1个B .2个C .3个D .4个2.(2024•宝安区校级模拟)已知抛物线y =ax 2+bx +c (a ≠0)的图象如图所示,则下列结论①abc <0,②a +b +c =2,③a >12④0<b <1中正确的有( )A .①②B .①②③C .①②④D .①②③④3.(2024•凤凰县模拟)已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,在下列5个结论:①abc <0;②b <a +c ;③4a +2b +c >0;④2c <3b ;⑤a +b <m (am +b )(m ≠1的实数).其中正确结论个数有( )A .4个B .3个C .2个D .1个4.(2024•汝阳县一模)图形结合法既可以由数解决形的问题,也可以由形解决数的问题.如图所示,已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①ab>0;②4a﹣2b+c<0;③2a﹣b<0;④|a+c|<|b|.其中正确的个数有( )A.1B.2C.3D.45.(2024•斗门区校级模拟)二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②3a+c>0;③(a+c)2﹣b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的为( )A.①④B.②③④C.①②④D.①②③④6.(2024•岚山区二模)已知二次函数y=ax2+bx+c(a≠0)与x轴的一个交点为(4,0),其对称轴为直线x=1,其部分图象如图所示,有下列5个结论:①abc<0;②b2﹣4ac<0;③8a+c=0;④若关于x 的方程ax2+bx+c=﹣1有两个实数根x1x2,且满足x1<x2,则x1<﹣2,x2>4;⑤直线y=kx﹣4k(k≠0)经过点(0,c),则关于x的不等式ax2+(b﹣k)x+c+4k>0的解集是0<x<4.其中正确结论的个数为( )A.5B.4C.3D.27.(2024•旺苍县三模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b2<4ac;③2c<3b;④a+b>m(am+b)(m≠1);⑤若方程|ax2+bx+c|=1有四个根,则这四个根的和为2.其中正确的结论有( )A.2个B.3个C.4个D.5个8.(2023秋•龙港区期中)函数y=ax2+bx+c与y=kx的图象如图所示,下列结论:①b2﹣4ac>0;②a+b+c=0;③x=﹣2时,函数y=﹣ax2+(k﹣b)x﹣c有最大值;④关于x的方程ax2+(b﹣k)x+c=0的根是x1=﹣1,x2=﹣3,其中正确的个数是( )A.1B.2C.3D.49.(2023•石城县模拟)二次函数y=ax2+bx+c(a≠0)的图象如图所示.下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax21+bx1=ax22+bx2且x1≠x2,则x1+x2=2.其中正确的有( )A.①④B.③④C.②⑤D.②③⑤10.(2024•苍溪县模拟)如图,已知二次函数y=ax2+bx+c(a,b,c是常数)的图象关于直线x=﹣1对称,则下列五个结论:①abc>0;②2a﹣b=0;③9a﹣3b+c<0;④a(m2﹣1)+b(m+1)≤0(m为任意实数);⑤3a+c<0.其中结论正确的个数为( )A.2个B.3个C.4个D.5个11.(2024•高青县校级一模)小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0;②abc>0;③a﹣b+c>0;④2a﹣3b=0;⑤c﹣4b>0,你认为其中正确信息的个数有( )A.2个B.3个C.4个D.5个12.(2024•沂源县一模)已知二次函数y=ax2+bx+c(a≠0)的图象的一部分如图所示,其中对称轴为:x =1,下列结论:①abc>0;②a+c>0;③2a+3b>0;④a+b>am2+bm(m≠1);上述结论中正确结论的个数为( )A.1个B.2个C.3个D.4个13.(2024•桃江县一模)抛物线y =ax 2+bx +c 的顶点坐标为(2,﹣a )(如图所示),则下列说法:①abc <0;②(a +b )2≥c ;③关于x 的方程ax 2+bx =0有两个不相等的实数根;④﹣1≤a ≤0.则正确的结论有( )A .1个B .2个C .3个D .4个14.(2023秋•中山市校级期末)二次函数y =ax 2+bx +c (a ≠0)的图象如图所示.下列结论:①2a +b =0;②3a +c >0;③m 为任意实数,则a +b >am 2+bm ;④若A (x 1,0),B (x 2,0),则x 1+x 2=2,其中正确的有( )A .①②B .①③C .①④D .②④15.(2023秋•西城区校级月考)已知二次函数y =ax 2+bx +c 的图象如图所示,则下列结论:①a <0;②9a +3b +c >0;③c >0;④﹣3<―b 2a<0其中正确的有( )A .4个B .3个C .2个D .1个16.(2023•东港区校级三模)函数y =x 2+bx +c 与y =x 的图象如图所示,有以下结论:①b 2﹣4c >0;②b +c =0;③2b +c +3=0;④当1<x <3时,x 2+(b ﹣1)x +c <0其中正确的有( )个.A .4B .3C .2D .117.(2023•双台子区校级一模)二次函数y =ax 2+bx +c 的图象如图所示,给出四个结论:①abc >0;②4a ﹣2b +c >0;③对于任意实数m ,有am 2+bm +c <a ﹣b +c ;④c a >―3,其中正确的有( )A .①②B .①④C .②③D .③④18.(2023•遂溪县模拟)如图是二次函数y =ax 2+bx +c 的图象,对称轴是直线l ,则以下说法:①a ﹣b +c =0;②4a +b =0;③ab c>0;④16a +5b +2c >0,其中正确的个数是( )A .1B .2C .3D .419.(2023秋•义乌市期中)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc >0;②b2>4ac;③a(m2﹣1)+b(m﹣1)<0(m≠1);④关于x的方程|ax2+bx+c|=1有四个根,且这四个根的和为4.其中正确的结论有( )A.①②③B.②③④C.①④D.②③20.(2023秋•铜梁区校级期中)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②2a+b<0;③若﹣1<m<n<1,则m+n<―b a ;④3|a|+|c|<2|b|.其中正确的结论有( )A.1个B.2个C.3个D.4个21.(2023•仁怀市模拟)如图,根据二次函数y=ax2+bx+c的图象得到如下结论:①abc>0 ②2a﹣b=0 ③a+b+c=0 ④3a+c<0 ⑤当x>﹣2时,y随x的增大而增大⑥一定存在实数x0,使得ax20+bx0>a﹣b 成立.上述结论,正确的是( )A.①②⑤B.②③④C.②③⑥D.③④⑤22.(2023•广东模拟)二次函数y =ax 2+bx +c 的图象如图所示,有如下结论:①abc <0;②2a ﹣b +c ≤0;③3b ﹣2c <0;④对任意实数m ,都有2am 2+2bm ﹣b ≥0.其中正确的有( )A .①②B .②③C .②④D .③④23.(2023•凤凰县模拟)已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列结论①abc <0;②3a +b >―13c ;③2c <3b ;④(k +1)(ak +a +b )≤a +b ,其中正确的是( )A .①③④B .C .①④D .②③④24.(2024•黄石模拟)已知抛物线y =ax 2+bx +c (a <0)与x 轴交于点(x 1,0),(2,0),其中﹣1<x 1<0.下列四个结论:①abc <0;②a ﹣b +c >0;③2b ﹣c <0;④不等式ax 2+bx +c >―c 2x +c 的解集为0<x <2.其中正确结论的序号为( )A .①②B .①③C .②③D .①④25.(2024•殷都区模拟)如图,在平面直角坐标系中,直线y 1=mx +n 与抛物线y 2=ax 2+bx ―3相交于点A ,B .结合图象,判断下列结论:①当﹣3<x <2时,y 1>y 2;②x =﹣3是方程ax 2+bx ﹣3=0的一个解;③若(﹣4,t 1),(1,t 2)是抛物线上的两点,则t 1>t 2;④对于抛物线y 2=ax 2+bx ―3,当﹣3<x <2时,y 2的取值范围是0<y 2<5.其中正确结论的个数是( )A .4个B .3个C .2个D .1个26.(2024•东港区校级一模)如图,抛物线 y =ax 2+bx +c (a ≠0)与x 轴交于点A (﹣1,0),顶点坐标为(1,n ),与y 轴的交点在(0,2)和(0,3)两点之间(包含端点).下列结论中正确的是( )①不等式ax 2+c <﹣bx 的解集为x <﹣1或x >3;②9a 2﹣b 2<0;③一元二次方程cx 2+bx +a =0的两个根分别为x 1=13,x 2=﹣1;④6≤3n ﹣2≤10.A .①②③B .①②④C .②③④D .①③④二.填空题(共4小题)27.(2024•射洪市一模)二次函数y =ax 2+bx +c (a ≠0)的大致图象如图所示(1<x =h <2,0<x A <1).下列结论:①abc <0;②2a +b >0;③若OC =2OA ,则2b ﹣ac =4;④3a ﹣c <0.其中正确的有 .(只填写序号)28.(2023秋•太康县期末)已知二次函数y =ax 2+bx +c (a ≠0,a 、b 、c 为常数)的图象如图所示.下列4个结论:①b >0;②b <a +c ;③c <4b ;④a +b <k 2a +kb (k 为常数,且k ≠1).其中正确的结论序号是 .29.(2023秋•青山区期末)已知抛物线y =ax 2+bx +c 经过点(2,c ),且满足a ﹣b +c =0.下列四个结论:①抛物线的对称轴是直线x =1;②b 与c 同号;③若a +2b +4c >0,则不等式ax 2+bx +c <﹣2ax ﹣a ﹣b 的解集﹣2<x <2;④抛物线上的两个点M (m ﹣1,y 1),N (m +2,y 2),当c <0,且y 1>y 2时,m <12.其中一定正确的是 .(填写序号)30.(2023秋•城厢区校级月考)如图,是抛物线y 1=ax 2+bx +c (a ≠0)图象的一部分,抛物线的顶点坐标为A (1,3),与x 轴的一个交点为B (4,0),点A 和点B 均在直线y 2=mx +n (m ≠0)上.①2a +b =0;②abc >0;③抛物线与x 轴的另一个交点是(﹣4,0);④方程ax 2+bx +c =﹣3有两个不相等的实数根;⑤a ﹣b +c <4m +n ;⑥不等式mx +n >ax 2+bx +c 的解集为1<x <4.其中正确的是 .。
二次函数(压轴精选40题)(解析版)-2023-2024学年九年级数学上《重难点题型高分突破》人教版

第2单元二次函数压轴精选40题一.选择题(共3小题)1.对于二次函数y=ax2+bx+c,规定函数y=是它的相关函数.已知点M,N的坐标分别为(﹣,1),(,1),连接MN,若线段MN与二次函数y=﹣x2+4x+n的相关函数的图象有两个公共点,则n的取值范围为()A.﹣3<n≤﹣1或B.﹣3<n<﹣1或C.n≤﹣1或D.﹣3<n<﹣1或n≥1【答案】A【解答】解:如图1所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有1个公共点.所以当x=2时,y=1,即﹣4+8+n=1,解得n=﹣3.如图2所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有3个公共点.∵抛物线y=x2﹣4x﹣n与y轴交点纵坐标为1,∴﹣n=1,解得:n=﹣1.∴当﹣3<n≤﹣1时,线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.如图3所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有3个公共点.∵抛物线y=﹣x2+4x+n经过点(0,1),∴n=1.如图4所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.∵抛物线y=x2﹣4x﹣n经过点M(﹣,1),∴+2﹣n=1,解得:n=.∴1<n≤时,线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.综上所述,n的取值范围是﹣3<n≤﹣1或1<n≤,故选:A.2.如图,函数y=ax2+bx+c的图象过点(﹣1,0)和(m,0),请思考下列判断:①abc<0;②4a+c<2b;③=1﹣;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=正确的是()A.①③⑤B.①②③④⑤C.①③④D.①②③⑤【答案】B【解答】解:∵抛物线开口向下,∴a<0,∵抛物线交y轴于正半轴,∴c>0,∵﹣>0,∴b>0,∴abc<0,故①正确,∵x=﹣2时,y<0,∴4a﹣2b+c<0,即4a+c<2b,故②正确,∵y=ax2+bx+c的图象过点(﹣1,0)和(m,0),∴﹣1×m=,am2+bm+c=0,∴++=0,∴=1﹣,故③正确,∵﹣1+m=﹣,∴﹣a+am=﹣b,∴am=a﹣b,∵am2+(2a+b)m+a+b+c=am2+bm+c+2am+a+b=2a﹣2b+a+b=3a﹣b<0,故④正确,∵m+1=|﹣|,∴m+1=||,∴|am+a|=,故⑤正确,故选:B.3.定义符号min{a,b}含义为:当a>b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,2)=﹣4.则min{﹣x2+1,﹣x}的最大值是()A.B.C.1D.0【答案】A【解答】解:在同一坐标系xOy中,画出二次函数y=﹣x2+1与正比例函数y =﹣x的图象,如图所示.设它们交于点A、B.令﹣x2+1=﹣x,即x2﹣x﹣1=0,解得:x=或,∴A(,),B(,).观察图象可知:①当x≤时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而增大,其最大值为;②当<x<时,min{﹣x2+1,﹣x}=﹣x,函数值随x的增大而减小,其最大值为小于;③当x≥时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而减小,最大值为.综上所述,min{﹣x2+1,﹣x}的最大值是.故选:A.二.填空题(共2小题)4.设O为坐标原点,点A、B为抛物线y=2x2上的两个动点,且OA⊥OB.连接点A、B,过O作OC⊥AB于点C,则点C到y轴距离的最大值为.【答案】.【解答】解:如图,分别作AE、BF垂直于x轴于点E、F,设OE=a,OF=b,由抛物线解析式为y=2x2,则AE=2a2,BF=2b2,作AH⊥BF于H,交y轴于点G,连接AB交y轴于点D,设点D(0,m),∵DG∥BH,∴△ADG∽△ABH,∴,即.化简得:m=2ab.∵∠AOB=90°,∴∠AOE+∠BOF=90°,又∠AOE+∠EAO=90°,∴∠BOF=∠EAO,又∠AEO=∠BFO=90°,∴△AEO∽△OFB.∴,即,化简得4ab=1.则,说明直线AB过定点D,D点坐标为.∵,∴点C是在以DO为直径的圆上运动,∴当点C到y轴距离为时,点C到y轴的距离最大.故答案为:.5.二次函数y=x2的图象如图.点A0位于坐标原点,点A1,A2,A3,…,A n在y轴的正半轴上,点B1,B2,B3,…,B n在二次函数位于第一象限的图象上,点C1,C2,C3,…,∁n在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3,…,四边形A n﹣1B n A n∁n都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3=…=∠A n﹣1B n A n=60°,则△A0B1A1的边长为B n A n∁n的周长为.,菱形A n﹣1【答案】,.【解答】解:过点B1作B1D1垂直x轴于点D1,过点B2作B2D2垂直x轴于点D2,过点B3作B3D3垂直x轴于点D3,过点A1E1⊥B2D2于点E1,过点A2E2⊥B3D3于点E2,∵四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3,…,四边形.A n﹣1B n A n∁n 都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3=⋅⋅⋅=∠A n﹣1B n A n=60°,∴△A0B1A1是等边三角形,设点B1坐标为(x,y),则:y=x2,∵∠A0B1A1=60°,∴∠B1A0D1=30°,在Rt△B1D1A0中,,∴,解得:(舍去)或,∴,∴,∴△A0B1A1的边长为,∴菱形A0B1A1C1的周长=;设点B2坐标为(x,y),在Rt△B2E1A1中,,且y=x2,∴,解得,或(舍去),∴,∵,∴,∴,∴菱形A1B2A2C2的周长=;同法可得:菱形A2B3A3C3的周长=;B n A n∁n的周长为:;∴菱形A n﹣1故答案为:,.三.解答题(共35小题)6.在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)如图甲,在y轴上找一点D,使△ACD为等腰三角形,请直接写出点D 的坐标;(3)如图乙,点P为抛物线对称轴上一点,是否存在P、Q两点使以点A,C,P,Q为顶点的四边形是菱形?若存在,求出P、Q两点的坐标,若不存在,请说明理由.【答案】(1)y=﹣x2﹣2x+3;(2)(0,0)或(0,﹣3)或(0,3﹣3)或(0,3+3);(3)存在,P(﹣1,3﹣),Q(﹣4,﹣)或P(﹣1,3+),Q(﹣4,)或P(﹣1,1),Q(﹣2,2)或P(﹣1,),Q(2,3+)或P(﹣1,﹣),Q(2,3﹣).【解答】解:(1)∵A(﹣3,0),B(1,0)两点在抛物线上,∴,解得:,∴抛物线的解析式为:y=﹣x2﹣2x+3;(2)令x=0,y=3,∴C(0,3),等腰△ACD,如图甲,当以点D为顶点时,DA=DC,点D与原点O重合,∴D(0,0);当以点A为顶点时,AC=AD,AO是等腰△ACD中线,∴OC=OD,∴D(0,﹣3);当以点C为顶点时,AC=CD===3,∴点D的纵坐标为3﹣3或3+3,∴D(0,3﹣3)或(0,3+3);综上所述,点D的坐标为(0,0)或(0,﹣3)或(0,3﹣3)或(0,3+3);(3)存在,理由如下:抛物线y=﹣x2﹣2x+3的对称轴为:x=﹣1,设P(﹣1,t),Q(m,n),∵A(﹣3,0),C(0,3),则AC2=(﹣3)2+32=18,AP2=(﹣1+3)2+t2=t2+4,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,∵四边形ACPQ是菱形,∴分三种情况:以AP为对角线或以AC为对角线或以CP为对角线,①当以AP为对角线时,则CP=CA,如图1,∴t2﹣6t+10=18,解得:t=3±,∴P1(﹣1,3﹣),P2(﹣1,3+),∵四边形ACPQ是菱形,∴AP与CQ互相垂直平分,即AP与CQ的中点重合,当P1(﹣1,3﹣)时,∴=,=,解得:m=﹣4,n=﹣,∴Q1(﹣4,﹣),当P2(﹣1,3+)时,∴=,=,解得:m=﹣4,n=,∴Q2(﹣4,);②以AC为对角线时,则PC=AP,如图2,∴t2﹣6t+10=t2+4,解得:t=1,∴P3(﹣1,1),∵四边形APCQ是菱形,∴AC与PQ互相垂直平分,即AC与CQ中点重合,∴=,=,解得:m=﹣2,n=2,∴Q3(﹣2,2);③当以CP为对角线时,则AP=AC,如图3,∴t2+4=18,解得:t=±,∴P4(﹣1,),P5(﹣1,﹣),∵四边形ACQP是菱形,∴AQ与CP互相垂直平分,即AQ与CP的中点重合,∴=,=,解得:m=2,n=3±,∴Q4(2,3+),Q5(2,3﹣);综上所述,符合条件的点P、Q的坐标为:P(﹣1,3﹣),Q(﹣4,﹣)或P(﹣1,3+),Q(﹣4,)或P(﹣1,1),Q(﹣2,2)或P(﹣1,),Q(2,3+)或P(﹣1,﹣),Q(2,3﹣).7.已知函数y=﹣x2+(m﹣3)x+2m(m为常数).(1)试判断该函数的图象与x轴的公共点的个数;(2)求证:不论m为何值,该函数的图象的顶点都在函数y=x2+4x+6的图象上;(3)若直线y=x与二次函数图象交于A、B两点,当﹣4≤m≤2时,求线段AB的取值范围.【答案】(1)2个;(2)证明见解答过程;(3)4≤|AB|≤8.【解答】(1)解:∵Δ=(m﹣3)2+8m=(m+1)2+8>0,∴该函数图象与x轴的公共点的个数2个;(2)证明:∵y=﹣x2+(m﹣3)x+2m=﹣(x﹣)2+,把x=代入y=x2+4x+6=(x+2)2+2得:y=(+2)2+2=+2=,∴不论m为何值,该函数的图象的顶点都在函数y=x2+4x+6的图象上.(3)解:过A作AC∥x轴,过B作BC∥y轴,如图,则△ACB是等腰直角三角形,设直线y=x与y=﹣x2+(m﹣3)x+2m的交点为A(x1,y1)B(x2,y2),联立方程得:,化简得:x2﹣(m﹣4)x﹣2m=0,∴x1+x2=m﹣4,x1x2=﹣2m,∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=(m﹣4)2﹣4(﹣2m)=m2+16,∴|AB|=,∵﹣4≤m≤2,∴当m=0时,|AB|有最小值为4,当m=﹣4时,|AB|有最大值为8,∴4≤|AB|≤8.8.如图,已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,点P为直线BC上方抛物线上一点.(1)求抛物线的解析式;(2)当点P的坐标为(1,4)时,求△PBC的面积;(3)当∠BCP=∠CAB时,求点P的坐标;(4)若点P的坐标为(2,3),连接PA,交直线BC于点E,交y轴于点F,点H在抛物线上,过H作HK∥y轴,交直线AP于点K.点Q是平面内一点,当以点E,H,K,Q为顶点的四边形是正方形时,请直接写出点Q的坐标.【答案】(1)y=﹣x2+2x+3;(2)3;(3);(4)点Q的坐标为(5,2)或或.【解答】解:(1)把A(﹣1,0)、B(3,0)、C(0,3)三点代入y=ax2+bx+c,得:,解得:,∴抛物线的解析式为:y=﹣x2+2x+3;(2)由(1)可知:y=﹣x2+2x+3,∴y=﹣(x﹣1)2+4,∵点P的坐标为(1,4),∴点P即为抛物线的顶点,过点P作PM∥y轴,交BC于点M,∵B(3,0)、C(0,3),设直线BC的解析式为:y=k1x+b1,∴,解得:,∴直线BC的解析式为:y=﹣x+3,∵PM∥y轴,P(1,4),M(1,2),∴PM=2,=S△PCM+S△BPM=,=∴S△PBC=3;(3)过B点作BD⊥x轴交射线CP于D,如图所示:∵A(﹣1,0)、B(3,0)、C(0,3),∴AB=4,OB=OC=3,∴,∠ABC=∠DBC=45°,∵∠BCP=∠CAB,∴△ABC~△CBD,∴,∴,∴,∴,设直线CD的解析式为:y=k2x+3,将代入得,,∴,∴直线CD的解析式为:,∴,解得:或,∴(4)∵P(2,3),A(﹣1,0)设直线CD的解析式为:y=mx+n,∴,解得:,∴直线AP的解析式为:y=x+1,∴F(0,1),∴OF=OA=1,∴∠EAB=45°,∵∠EBA=45°,∴∠AEB=90°,∴AP⊥BC,由(1)可知:直线BC的解析式为:y=﹣x+3,∴,解得:,∴E(1,2),∵以点E,H,K,Q为顶点的四边形是正方形,∴分两种情况讨论,:①当EH⊥EK时,H点在BC上,K点在AP上,如图所示:∵点H在抛物线上,∴点H为直线BC与抛物线的交点,∴,∴或,H(0,3)或H(3,0),当H(0,3)时,,∴,∴K(0,1),∴HK的中点为(0,2),则EQ的中点也为(0,2),∴Q(﹣1,2),但此时HK与y轴重合,不符合与y轴平行,∴Q(﹣1,2)不符合题意;当H(3,0)时,,∴,∴K(3,4),∴HK的中点为(3,2),则EQ的中点也为(3,2),∴Q(5,2),②当EH⊥HK时,此时EH⊥y轴,如图所示:∵y=﹣x2+2x+3,令y=2,则﹣x2+2x+3=2,解得:,∴或,当时,,∴,∴;当时,,∴,∴;综上所述:当以点E,H,K,Q为顶点的四边形是正方形,点Q的坐标为(5,2)或或.9.如图,在平面直角坐标系中,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)求线段AC的长度;(2)点P为直线AC下方抛物线上的一动点,且点P在抛物线对称轴左侧,过点P作PD∥y轴,交AC于点D,作PE∥x轴,交抛物线于点E.求3PD+PE 的最大值及此时点P的坐标;(3)在(2)中3PD+PE取得最大值的条件下,将该抛物线沿着射线CA方向平移个单位长度,得到一条新抛物线y′,M为射线CA上的动点,过点M作MF∥x轴交新抛物线y′的对称轴于点F,点N为直角坐标系内一点,请直接写出所有使得以点P,F,M,N为顶点的四边形是菱形的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.【答案】(1)线段AC的长度为;(2)3PD+PE取最大值6,P的坐标为(﹣2,﹣2);(3)N的坐标为(,﹣2)或(﹣6,)或(,﹣2)或(,﹣2).【解答】解:(1)在y=x2+x﹣2中,令x=0得y=﹣2;∴C(0,﹣2);令y=0得:0=x2+x﹣2,解得x=1或x=﹣3,∴A(﹣3,0),B(1,0),∴AC==,∴线段AC的长度为;(2)∵y=x2+x﹣2=(x+1)2﹣,∴抛物线y=x2+x﹣2的对称轴是直线x=﹣1,设P(m,m2+m﹣2),由A(﹣3,0),C(0,﹣2)得直线AC的解析式为y=﹣x﹣2,∴D(m,﹣m﹣2),∴PD=﹣m﹣2﹣(m2+m﹣2)=﹣m2﹣2m,∵PE关于直线x=﹣1对称,∴PE=2(﹣1﹣m)=﹣2﹣2m,∴3PD+PE=3(﹣m2﹣2m)﹣2﹣2m=﹣2m2﹣8m﹣2=﹣2(m+2)2+6,∵﹣2<0,∴当m=﹣2时,3PD+PE取最大值6,此时P的坐标为(﹣2,﹣2);(3)∵A(﹣3,0),C(0,﹣2),∴将抛物线y=(x+1)2﹣沿着射线CA方向平移个单位长度相当于先向左平移3个单位,再向上平移2个单位,∴新抛物线解析式为y'=(x+1+3)2﹣+2=(x+4)2﹣,∴新抛物线的对称轴为直线x=﹣4;设M(t,﹣t﹣2),N(p,q),则F(﹣4,﹣t﹣2),而P(﹣2,﹣2),①若MN,FP为对角线,则MN,FP的中点重合,且PM=PN,∴,解得:或(此时M不在射线CA上,舍去);∴N(,﹣2);②若MF,NP为对角线,则MF,NP的中点重合,且PM=PF,∴,解得:(此时N,P重合,舍去)或,∴N(﹣6,);③若MP,NF为对角线,则MP,NF的中点重合,且MF=PF,∴,解得:或,∴N(,﹣2)或(,﹣2);综上所述,N的坐标为(,﹣2)或(﹣6,)或(,﹣2)或(,﹣2).10.如图所示,抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C.点M为抛物线的顶点.(1)求抛物线的表达式及顶点M的坐标;(2)若点N是第四象限内抛物线上的一个动点,连接BN、CN,求△BCN面积的最大值及此时点N的坐标;(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,请直接写出点G的坐标;若不存在,试说明理由.【答案】(1)y=x2﹣2x﹣3,顶点坐标为:(1,﹣4);(2)N的坐标为();(3)G点坐标存在,为(2,﹣3)或(4,5)或(﹣2,5).【解答】解:(1)将A(﹣1,0)、B(3,0)代入y=ax2+bx﹣3,∴,解得,∴y=x2﹣2x﹣3=(x﹣1)2﹣4;顶点坐标为:(1,﹣4).(2)过N点作x轴的垂线交直线BC于Q点,如图:在y=x2﹣2x﹣3中,令x=0得y=﹣3,∴C(0,﹣3),设直线BC解析式为y=kx+m,∴,解得,∴直线BC的解析式为:y=x﹣3,设N点坐标为(n,n2﹣2n﹣3),则Q点坐标为(n,n﹣3),其中0<n<3,∴NQ=n﹣3﹣(n2﹣2n﹣3)=﹣n2+3n,=NQ•|x B﹣x C|=(﹣n2+3n)×3=﹣n2+n=﹣(n﹣)2+,∴S△BCN∵﹣<0,有最大值为,∴当n=时,S△BCN此时n2﹣2n﹣3=()2﹣2×﹣3=﹣,∴N的坐标为();(3)设D点坐标为(1,t),G点坐标为(m,m2﹣2m﹣3),且B(3,0),C(0,﹣3).分情况讨论:①当DG为对角线时,则另一对角线是BC,由对角线互相平分及中点坐标公式可知,解得,经检验此时四边形DCGB为平行四边形,此时点G的坐标为(2,﹣3).②当DB为对角线时,则另一对角线是GC,由对角线互相平分及中点坐标公式可知,,解得,经检验此时四边形DCBG为平行四边形,此时点G的坐标为(4,5).③当DC为对角线时,则另一对角线是GB,由对角线互相平分及中点坐标公式可知,,解得,经检验此时四边形DGCB为平行四边形,此时点G的坐标为(﹣2,5).综上所述,G点坐标存在,为(2,﹣3)或(4,5)或(﹣2,5).11.已知抛物线y=x2+bx﹣3与x轴交于A、B两点,与y轴交于点C,其中点A 在x轴的负半轴上,点B在x轴的正半轴上,且tan∠ACO=.(1)求抛物线的解析式.(2)如图1,在第一象限内的抛物线上是否存在点D,满足条件∠DCB=∠ACO?若存在,请求出点D的坐标;若不存在,请说明理由.(3)如图2,设P是y轴上的一个动点,连接AP并延长交抛物线于另一点M,连接BP并延长交抛物线于另一点N,若M、N的横坐标分别为m、n.试探究m、n之间的数量关系.【答案】(1)y=x2﹣2x﹣3;(2)存在;D(4,5);(3)m+3n=0.【解答】解:(1)由题意可得点C(0,﹣3),∴OC=3,∴OA=OC•tan∠ACO=1,∴点A的坐标为:(﹣1,0),′代入y=x2+bx﹣3,得0=1﹣b﹣3,∴b=﹣2,∴抛物线解析式为:y=x2﹣2x﹣3;(2)存在.设CD交x轴于点E,由(1)可得:B(3,0),C(0,﹣3),∴OB=OC=3,∠OBC=∠OCB=45°,∵∠DCB=∠ACO,∴∠AEC=∠DCB+45°=∠ACO+45°,又∵∠ACB=∠ACO+45°,∴∠AEC=∠ACB,而∠CAB=∠BAC,∴△ACE∽△ABC,∴.其中AB=4,AC=,∴AE=,∴OE=AE﹣OA=,即点E(,0).设CD:y=kx+a,把C、E的坐标代入,得:,解得:,∴CD:y=2x﹣3,联立方程组得:,解得:或(舍去),∴D(4,5);(3)设点P的坐标为(0,t),由A(﹣1,0),P(0,t)可得:AP:y=tx+t.把y=tx+t代入y=x2﹣2x﹣3,消去y,并化简得:x2﹣(t+2)x﹣t﹣3=0,∵x A=﹣1,x M=m是上面方程的两个根,∴x A•x M=﹣t﹣3,∴m=t+3①;同理可得BP:y=﹣x+t.把y=x+t代入y=x2﹣2x﹣3,消去y,并化简得:x﹣t﹣3=0,∵x B=3,x N=n是上面方程的两个根,∴x B•x N=﹣t﹣3,∴3n=﹣t﹣3②,由①+②得:m+3n=0.12.如图,在平面直角坐标系中,二次函数y=﹣+bx+c的图象与y轴交于点A(0,8),与x轴交于B、C两点,其中点B的坐标是(﹣8,0),点P (m,n)为该二次函数在第二象限内图象上的动点,点D为(0,4),连接BD.(1)求该二次函数的表达式;(2)依题补图1:连接OP,过点P作PQ⊥x轴于点Q;当△OPQ和△OBD 相似时,求m的值;(3)如图2,过点P作直线PQ∥BD,和x轴交点为Q,在点P沿着抛物线从点A到点B运动过程中,当PQ与抛物线只有一个交点时,求点Q的坐标.【答案】(1);(2)m的值为﹣4或;(3).【解答】解:(1)把A(0,8),B(﹣8,0)代入得,,解得,∴该二次函数的表达为;(2)如图:设,由∠OQP=∠BOD=90°,分两种情况:当△POQ∽△BDO时,,∴,∴PQ=2OQ,即,解得m=﹣4,或m=8(舍去);当△POQ∽△DBO时,,∴OQ=2PQ,即,解或(舍去),综上所述,m的值为﹣4或;(3)如图,设直线BD解析式为y=kx+n,∴,解得,∴直线BD解析式为,∵PQ∥BD,∴设直线PQ的解析式为,当直线PQ与的图象只有一个交点时,联立,整理得x2+6x﹣32+4n2=0,∴Δ=62﹣4×(﹣32+4n2)=0,解得,∴当时,直线PQ的解析式为,此时直线PQ与的图象只有一个交点,令y=0,则,解得,此时.13.如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A 在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高.球第一次落地点后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1)求足球开始飞出到第一次落地时,该抛物线的表达式.(2)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取,)【答案】见试题解答内容【解答】解:(1)如图,设第一次落地时,抛物线的表达式为y=a(x﹣6)2+4.由已知:当x=0时y=1.即1=36a+4,∴a=﹣.∴表达式为y=﹣(x﹣6)2+4;(2)由题意得:0=﹣(x﹣6)2+4解得:x1=4+6≈13,x2=﹣4+6<0(舍去),∴点C坐标为(13,0).设第二次落地的抛物线为y=﹣(x﹣k)2+2.将C点坐标代入得:0=﹣(13﹣k)2+2.解得:k1=13﹣2<13(舍去),k2=13+2≈18.∴y=﹣(x﹣18)2+2.0=﹣(x﹣18)2+2.x 1=18﹣2(舍去),x2=18+2≈23,∴BD=23﹣6=17(米).答:运动员乙要抢到第二个落点D,他应再向前跑17米.14.如图1,在平面直角坐标系中,二次函数y=ax2+bx﹣3(a≠0)的图象与x 轴于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是直线BC下方抛物线上一动点.(1)求这个二次函数的解析式;(2)当动点P运动到什么位置时,使四边形ACPB的面积最大,求出此时四边形ACPB的面积最大值和P的坐标;(3)如图2,点M在抛物线对称轴上,点N是平面内一点,是否存在这样的点M、N,使得以点M、N、A、C为顶点的四边形是菱形?若存在,请直接写出所有M点的坐标;若不存在,请说明理由.【答案】(1)y2=x2﹣2x﹣3;(2)当时,四边形ABCP的最大值是,此时点P的坐标为;(3)存在,、;M 3(1,0);M5(1,﹣1).【解答】解:(1)∵二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,∴,解得:,∴这个二次函数的表达式为:y=x2﹣2x﹣3;(2)设点P的坐标为(m,m2﹣2m﹣3),S四边形ACPB=S△AOC+S△COP+S△BOP,===,∵,∴当时,四边形ABCP的最大值是,此时点P的坐标为,(3)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴为直线x=1,当x=0时,y=﹣3,∴C(0,﹣3),设点M的坐标为(1,t),则:AM2=(﹣1﹣1)2+(0﹣t)2,AC2=(﹣1﹣0)2+[0﹣(﹣3)]2,CM2=(0﹣1)2+(﹣3﹣t)2,设AC的中点为Q,则点Q的坐标为,即,∴,,当AM=AC时,则AM2=AC2,∴(﹣1﹣1)2+(0﹣t)2=(﹣1﹣0)2+[0﹣(﹣3)]2,解得,,∴、,;当CM=CA时,则CM2=CA2,∴(0﹣1)2+(﹣3﹣t)2=(﹣1﹣0)2+[0﹣(﹣3)]2,解得,t1=0,t2=﹣6,∴M3(1,0)、M4(1,﹣6)(舍去,此时M、A、C三点共线,无法构成菱形);当AC为对角线时则有:AQ2+QM2=AM2,∴=(﹣1﹣1)2+(0﹣t)2,解得,t=﹣1,∴M5(1,﹣1),∴存在这样的点M、N能够使得以点M、N、A、C为顶点的四边形是菱形,此时点M的坐标为:、、M 3(1,0)、M5(1,﹣1).15.如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交点C,抛物线y=﹣2x2+bx+c过A,C两点,与x轴交于另一点B.(1)求抛物线的解析式;(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当时,求E点坐标;(3)在(2)的条件下,若点E位于对称轴左侧,点M是抛物线对称轴上一点,点N是抛物线上一点,当以M,N,E,B为顶点的四边形是菱形时,直接写出点M的坐标.【答案】(1)y=﹣2x2﹣4x+6;(2)E点坐标为(﹣2,6)或(﹣1,8);(3)M的坐标为(﹣1,)或(﹣1,﹣)或(﹣1,)或(﹣1,﹣2+6)或(﹣1,2+6).【解答】解:(1)在y=2x+6中,当x=0时y=6,当y=0时x=﹣3,∴C(0,6),A(﹣3,0),∵抛物线y=﹣2x2+bx+c的图象经过A、C两点,∴,解得,∴抛物线的解析式为y=﹣2x2﹣4x+6;(2)方法一:令﹣2x2﹣4x+6=0,解得x1=﹣3,x2=1,∴B(1,0),设E(t,﹣2t2﹣4t+6),如图,过点E作EH⊥x轴于点H,过点F作FG⊥x轴于点G,则EH∥FG,∵EF=BF,∴===,∵BH=1﹣t,∴BG=BH=﹣t,∴点F的横坐标为+t,∵点F在直线y=2x+6上,∴y=2(+t)+6=+t,∴F(+t,+t),∴﹣2t2﹣4t+6=(+t),∴t2+3t+2=0,解得t1=﹣2,t2=﹣1,当t=﹣2时,﹣2t2﹣4t+6=6,当t=﹣1时,﹣2t2﹣4t+6=8,∴E1(﹣2,6),E2(﹣1,8),综上所述:E点坐标为(﹣2,6)或(﹣1,8);方法二:过点E作EH⊥x轴交AC于点H,过点B作BM⊥x轴交AC于点M,∴EH∥BM,设E(m,﹣2m2﹣4m+6),∵直线AC解析式为y=2x+6,∴H(m,2m+6),M(1,8),∴EH=﹣2m2﹣4m+6﹣2m﹣6=﹣2m2﹣6m,MB=8,∵EH∥BM,∴△EHF∽△BMF,∴==,∴=,∴m1=﹣2,m2=﹣1,∴E1(﹣2,6),E2(﹣1,8),综上所述:E点坐标为(﹣2,6)或(﹣1,8);(3)∵抛物线的解析式为y=﹣2x2﹣4x+6=﹣2(x+1)2+8,∴抛物线顶点坐标为(﹣1,8),对称轴方程为x=﹣1,在(2)的条件下,∵点E位于对称轴左侧,∴E(﹣2,6),∵点M是抛物线对称轴上一点,∴设M(﹣1,m),∵B(1,0),E(﹣2,6),∴BM2=(1+1)2+(0﹣m)2=m2+4,BE2=(1+2)2+(0﹣6)2=45,ME2=(﹣1+2)2+(m﹣6)2=m2﹣12m+37,①当EB为菱形的边时,BM=BE,即BM2=BE2,∴m2+4=45,∴m=±,∴M(﹣1,)或(﹣1,﹣);②当EB为菱形的对角线时,BM=ME,即BM2=ME2,∴m2+4=m2﹣12m+37,∴m=,∴M(﹣1,),③当BE=ME时,即BE2=ME2,∴45=m2﹣12m+37,∴m=﹣3+6或m=3+6,∴M(﹣1,﹣2+6)或(﹣1,2+6);综上所述,M的坐标为(﹣1,)或(﹣1,﹣)或(﹣1,)或(﹣1,﹣2+6)或(﹣1,2+6).16.如图1,直线y=﹣2x+2交x轴于点A,交y轴于点C,过A、C两点的抛物线与x轴的另一交点为B.(1)请直接写出该抛物线的函数解析式;(2)点D是第二象限抛物线上一点,设D点横坐标为m.①如图2,连接BD,CD,BC,求△BDC面积的最大值;②如图3,连接OD,将线段OD绕O点顺时针旋转90°,得到线段OE,过点E作EF∥x轴交直线AC于F.求线段EF的最大值及此时点D的坐标.【答案】(1)y=﹣x+2;(2)①4;②(﹣2,3).【解答】解:(1)由题意可得,当x=0时,y=﹣2×0+2=2,当y=0时,﹣2x+2=0,解得x=1,∴A(1,0),B(0,2),代入y=﹣+bx+c得,y=﹣x+2;(2)①连接OD,,令y=0,则﹣x+2=0,解得x1=﹣4,x2=1,∴B(﹣4,0)D在第二象限,∴﹣4<m<0,=S△BOD+S△COD﹣S△BOC∴S△BCD=×4×2=﹣m2﹣4m=﹣(m+2)2+4,当m=﹣2时,△BCD的面积最大为4,②过D作DM⊥x轴于M,EF交y轴于N,在△ODM和△OEN中,,∴△ODM≌△OEN(AAS),∴DM=EN=﹣m+2OM=ON=﹣m,∴,令y=﹣m,则﹣m=﹣2x+2x=m+1EF=﹣m﹣1=﹣﹣2m+1=﹣(m+2)2+3,∴当m=﹣2时EF最大为3,D点的坐标(﹣2,3).17.如图1,抛物线y=ax2+x+c与x轴交于A(﹣2,0),B(4,0)两点,与y轴交于C.(1)求抛物线的解析式;(2)点P是直线BC上方抛物线上的—个动点,使△PBC的面积等于△ABC面积的,求点P的坐标;(3)过点C作直线l∥x轴,将抛物线在y轴左侧的部分沿直线l翻折,抛物线的其余部分保持不变,得到一个新图象(如图2),请你结合新图象解答:当直线y=﹣x+d与新图象只有一个公共点Q(m,n),且n≥﹣8时,求d 的取值范围.【答案】(1)抛物线的解析式为y=﹣x2+x+4;(2)点P的坐标为(1,)或(3,);(3)d的取值范围是﹣5≤d<4或d>.【解答】解:(1)把A(﹣2,0),B(4,0)代入y=ax2+x+c得:,解得:,∴抛物线的解析式为y=﹣x2+x+4;(2)过P作PK∥y轴交BC于K,如图:在y=﹣x2+x+4中,令x=0得y=4,∴C(0,4),∵A(﹣2,0),B(4,0),∴AB=6,=×6×4=12,∴S△ABC由B(4,0),C(0,4)得直线BC函数表达式为y=﹣x+4,设P(m,﹣m2+m+4),则K(m,﹣m+4),∴PK=﹣m2+m+4﹣(﹣m+4)=﹣m2+2m,∵△PBC的面积等于△ABC面积的,∴×(﹣m2+2m)×4=12×,解得m=1或m=3,∴点P的坐标为(1,)或(3,);(3)①当公共点Q(m,n)在C(0,4)下方时,在y=﹣x2+x+4中,令y=﹣8得:﹣8=﹣x2+x+4,解得x=6或x=﹣4,∵将抛物线在y轴左侧的部分沿直线l翻折,抛物线的其余部分保持不变,得到一个新图象,∴新图象过点(6,﹣8),当直线y=﹣x+d与新图象公共点为(6,﹣8)时,﹣8=﹣×6+d,解得d=﹣5,如图:∵C(0,4),当﹣5≤d<4时,观察图象可知直线y=﹣x+d与翻折后的抛物线无交点,∴当﹣5≤d<4时,直线y=﹣x+d与新图象只有一个公共点;②当公共点Q(m,n)在C(0,4)上方时,如图:若有两个相等的实数解,即﹣x2+x+4﹣d=0的Δ=0,则()2﹣4×(﹣)(4﹣d)=0,解得d=;由图可知,当d>时,直线y=﹣x+d与新图象只有一个公共点;综上所述,d的取值范围是﹣5≤d<4或d>.18.如图,已知抛物线y=﹣x2+bx+c经过B(﹣3,0),C(0,3)两点,与x 轴的另一个交点为A.(1)求抛物线的解析式;(2)若直线y=mx+n经过B,C两点,则m=1;n=3;(3)在抛物线对称轴上找一点E,使得AE+CE的值最小,直接写出点E的坐标;(4)设点P为x轴上的一个动点,是否存在使△BPC为等腰三角形的点P,若存在,直接写出点P的坐标;若不存在,说明理由.【答案】(1)y=﹣x2﹣2x+3;(2)1,3;(3)E的坐标为(﹣1,2);(4)点P的坐标为(﹣3﹣3,0)或(3﹣3,0)或(0,0)或(3,0).【解答】解:(1)把点B(﹣3,0),C(0,3)代入y=﹣x2+bx+c得:,解得:,∴抛物线的解析式是y=﹣x2﹣2x+3;(2)把B(﹣3,0),C(0,3)代入y=mx+n中得:,解得:;故答案为:1,3;(3)如图1,由(2)知:直线BC的解析式为y=x+3,抛物线的对称轴为直线x=﹣=﹣1,直线BC与直线x=﹣1相交于点E,则EB=EA,此时AE+CE最小,此时点E的坐标为(﹣1,2);(4)∵B(﹣3,0),C(0,3),∴OB=OC=3,∴BC=3,分三种情况:①BC=BP,如图2,此时点P的坐标为(﹣3﹣3,0)或(3﹣3,0);②当P与O重合时,△BPC也是等腰三角形,此时P(0,0);③BC=CP,如图3,此时点P的坐标为(3,0);综上所述,点P的坐标为(﹣3﹣3,0)或(3﹣3,0)或(0,0)或(3,0).19.在平面直角坐标系xOy中,已知抛物线y=ax2﹣2(a+1)x+a+2(a≠0).(1)当a=﹣时,求抛物线的对称轴及顶点坐标;(2)请直接写出二次函数图象的对称轴(用含a的代数式表示)及二次函数图象经过的定点坐标是(1,0).(3)若当1≤x≤5时,函数值有最大值为8,求二次函数的解析式;(4)已知点A(0,﹣3)、B(5,﹣3),若抛物线与线段AB只有一个公共点,请直接写出a的取值范围.【答案】(1)直线x=﹣7,(﹣7,8);(2)(1,0);(3)y=x2﹣4x+3;(4)a的取值范围是:a=或0<a<或﹣5<a<0.【解答】解:(1)a=﹣时,y=﹣x2﹣x+∴对称轴为直线x=﹣=﹣7,把x=﹣7代入y=﹣x2﹣x+得,y=8,∴顶点坐标为(﹣7,8);(2)∵y=ax2﹣2(a+1)x+a+2(a≠0).∴对称轴为直线x=﹣=1+,∵y=ax2﹣2(a+1)x+a+2=a(x﹣1)2﹣2(x﹣1)=(x﹣1)[a(x﹣1)﹣2],∴二次函数经过的定点坐标为(1,0);故答案为:(1,0);(3)由(2)知:二次函数图象的对称轴为直线x=1+,分两种情况:①当a<0时,1+<1,在自变量x的值满足1≤x≤5的情况下,y随x的增大而减小,∴当x=1时,y=0,而当1≤x≤5时,函数值有最大值为8,所以此种情况不成立;②当a>0时,1+>1,i)当1<1+≤3时,即a≥,当x=5时,二次函数的最大值为y=25a﹣10(a+1)+a+2=8,∴a=1,此时二次函数的解析式为y=x2﹣4x+3;ii)当1+>3时,在自变量x的值满足1≤x≤5的情况下,y随x的增大而减小,即x=1有最大值,所以此种情况不成立;综上所述:此时二次函数的解析式为:y=x2﹣4x+3;(4)分三种情况:①当抛物线的顶点在线段AB上时,抛物线与线段AB只有一个公共点,即当y=﹣3时,ax2﹣2(a+1)x+a+2=﹣3,ax2﹣2(a+1)x+a+5=0,Δ=4(a+1)2﹣4a(a+5)=0,∴a=,当a=时,x2﹣x+=0,解得:x1=x2=4(符合题意,如图1),②当a>0时,如图2,当x=0时,y>﹣3;当x=5时,y<﹣3,∴,解得:﹣5<a<,∴0<a<;③当a<0时,如图3,当x=0时,y>﹣3;当x=5时,y<﹣3,∴,解得:﹣5<a<,∴﹣5<a<0;综上所述,a的取值范围是:a=或0<a<或﹣5<a<0.20.如图1,在平面直角坐标系中,抛物线与x轴交于A、B两点,与y轴交于C点,其中A(﹣3,0),∠ACB=90°.(1)求该抛物线的函数解析式;(2)点P是直线AC上方抛物线上的一动点,过P作PM⊥AC于M点,在射线MA上取一点N,使得2MN=AC,连接PN,求△PMN面积的最大值及此时点P的坐标;(3)如图2,在(2)中△PMN面积取得最大值的条件下,将抛物线向左平移,当平移后的抛物线过点P时停止平移,平移后点C的对应点为C',D为原抛物线上一点,E为直线AC上一点,若以O、C′、D、E为顶点的四边形为平行四边形,求符合条件的D点横坐标.【答案】(1)抛物线的解析式为y=﹣x2﹣x+;最大值为×=,点P的坐标为(﹣,);(2)S△PMN(3)满足条件的点D坐标为(,)或(,)或(1,0)或(﹣4,﹣).【解答】解:(1)当x=0时,y=,则C(0,),OC=,∵A(﹣3,0),∴OA=3,则tan∠OAC==,∴∠OAC=30°,又∠ACB=90°,∴∠ABC=90°﹣30°=60°,∴OB==1,则B(1,0),设抛物线的解析式为y=a(x+3)(x﹣1),将C(0,)代入,得﹣3a=,解得a=﹣,∴抛物线的解析式为y=﹣(x+3)(x﹣1)=﹣x2﹣x+;(2)如图1,过P作PH∥y轴交AC于H,则∠PHM=∠ACO=90°﹣∠OAC =60°,∵PM⊥AC,∴PM=PH•sin∠PHM=PH,∵AC=2OC=2,2MN=AC,∴MN=,=•MN•PM=PM=PH,当PH最大时,S△PMN最大;∴S△PMN设直线AC解析式为y=kx+b′,将A(﹣3,0)、C(0,)代入,得,解得,∴直线AC的解析式为y=x+,由题意,设P(p,﹣p2﹣p+),则H(p,p+),∴PH=﹣p2﹣p+﹣(p+)=﹣p2﹣p=﹣(p+)2+,∵﹣<0,﹣3<p<0,∴当p=﹣时,PH有最大值,最大值为,最大,最大值为×=,此时,点P的坐标为(﹣,);即S△PMN(3)y=﹣x2﹣x+=﹣(x+1)2+,设抛物线向左平移a个单位,则新的抛物线解析式为y=﹣(x+1+a)2+,将点P(﹣,)代入,得=﹣(﹣+1+a)2+,解得a=1或a=0(不合题意,舍去),∴抛物线向左平移1个单位,∵C(0,),∴平移后点C的对应点C′的坐标为(﹣1,),由题意,设D(m,﹣m2﹣m+),E(n,n+),若以O、C′、D、E为顶点的四边形为平行四边形,则分三种情况:当OC′、DE为对角线时,则,消去n,得m2+3m﹣2=0,解得:m=,则点D坐标为(,)或(,);当OD、C′E为对角线时,则,消去n,得m2+3m+4=0,∵Δ=32﹣4×1×4=﹣7<0,∴方程无实数根,即点D不存在;当OE、C′D为对角线时,则,消去n,得m2+3m﹣4=0,解得:m=1或m=﹣4,∴点D的坐标为(1,0)或(﹣4,﹣),综上,满足条件的点D坐标为(,)或(,)或(1,0)或(﹣4,﹣).21.如图1,抛物线y=ax2+bx+3与x轴交于点A(﹣1,0)、点B,与y轴交于点C,顶点D的横坐标为1,对称轴交x轴于点E,交BC于点F.(1)求顶点D的坐标;(2)如图2所示,过点C的直线交线段BD于点M,交抛物线于点N.①若直线CM将△BCD分成的两部分面积之比为2:1,求点M的坐标;②若∠NCB=∠DBC,求点N的坐标.(3)如图1,若点P为线段OC上的一动点,请直接写出2AP+CP的最小值.【答案】(1)(1,4);(2)①或者;②;(3).【解答】解:(1)将A(﹣1,0)代入y=ax2+bx+3得:0=a﹣b+3①,∵顶点D的横坐标为1,∴,即b=﹣2a②,联立①②解得a=﹣1,b=2,∴y=﹣x2+2x+3,当x=1时,y=4,∴D(1,4);(2)①由(1)得y=﹣x2+2x+3,当y=0时,x1=﹣1,x2=3,∴B(3,0),即BO=3,如图,取DB的三等分点M1,M2,过点M1,M2分别作x轴,y轴的平行线分别交DE、x轴于点G、H、P、Q,∴△DGM1∽△DHM2∽△DEB,△BQM2∽△BPM1∽△BED,且相似比为1:2:3,∴,,∴,同理可得:,∴点M的坐标为:,;②∵∠NCB=∠DBC,∴CM=MB,取线段BC的中点G,作直线GM,。
二次函数60道压轴题型专项训练(12大题型)(原卷版)—2024-2025学年九年级数学上册(浙教)

二次函数60道压轴题型专项训练(12大题型)【题型目录】压轴题型一 二次函数的图象与性质压轴题压轴题型二 二次函数与各项系数符号压轴题压轴题型三 根据二次函数的对称性求值压轴题型四 二次函数的平移压轴题压轴题型五 二次函数与坐标轴交点压轴题压轴题型六 二次函数的应用(销售、增长率等问题)压轴题型七 二次函数的应用(图形运动、拱桥、投球等问题)压轴题型八 二次函数中的存在性问题压轴题型九 二次函数与一次函数压轴题压轴题型十 二次函数的翻折问题压轴题型十一 二次函数最值问题压轴题型十二 二次函数的综合【压轴题型一 二次函数的图象与性质压轴题】1.(2024·浙江嘉兴·二模)已知直线3y x =--与抛物线2()4=--y x m 对称轴左侧部分的图象有且只有一个交点,则m 的取值范围是( )A .54m £B .54m £或74m =C .1m £D .1m £或54m =2.(2024·浙江宁波·二模)已知二次函数2y x bx c =++的图象与x 轴只有一个公共点,且当x a =和x a n =+时函数值都为m ,则m 与n 的等量关系为 .3.(2024·浙江杭州·一模)已知二次函数()()13y a x x =--的图像过点()4,m ,(),p n (1)当1m =时,求a 的值;(2)若>>0m n ,求p 的取值范围;(3)求证:0>am an +.4.(2024·浙江杭州·一模)已知二次函数2(2)3(0)y m x m =-->的图象与x 轴交于点(,0),(,0)A a B b .(1)当3a =-时,求b 的值.(2)当0a b <<时,求m 的取值范围.(3)若(1,),(1,)P a p Q b q ++两点也都在此函数图象上,求证:0p q +>.5.(2024·浙江杭州·一模)在平面直角坐标系中,点(1,)m 和(3,)n 都在二次函数2y ax bx =+(0,,¹a a b 是常数)的图象上.(1)若6==-m n ,求该二次函数的表达式和函数图象的对称轴.(2)若1a =-,m n <,求b 的取值范围.(3)已知点()()()1231,,2,,4,y y y -也都在该二次函数图象上,若0mn <且a<0,试比较123y y y ,,的大小,并说明理由.【压轴题型二 二次函数与各项系数符号压轴题】1.(23-24九年级上·浙江杭州·阶段练习)抛物线()20y ax bx c a =++¹的顶点为(12)D -,,与x 轴的一个交点A 在点(30)-,和(20)-,之间,其部分图象如图,则以下结论:①0abc <;②若方程20ax bx c m ++-=没有实数根,则2m >;③320b c +<;④图象上有两点()11,P x y 和()22,Q x y ,若12x x <且122x x +<-,则一定有12y y >;正确的是( )A .4个B .3个C .2个D .1个2.(20-21九年级上·浙江·期末)抛物线2y ax bx c =++(a ,b ,c 为常数,且0a ¹)经过点()1,0-和()0m ,;且12m <<,当1x <-时,y 随着x 的增大而减小.下列结论:①0abc >;②0a b +>③若点()13,A y -,点()23,B y 都在抛物线上,则12y y <;④()10a m b -+=;⑤若1c £-,则244b ac a -£.其中结论正确的是.3.(23-24九年级上·浙江杭州·期中)在二次函数223(0)y x tx t =-+>中.(1)若函数图象的顶点在x 轴上,求t 的值.(2)若点(,)t s 在抛物线上,令q t s =+,求证:134q £.(3)如果(2,)A m a -,()4,B b ,(,)C m a 都在这个二次函数图象上,且3a b <<,求m 的取值范围.4.(2024·云南昆明·二模)在平面直角坐标系中,抛物线()24430y mx mx m m =-+->与x 轴的交点为A ,B .(1)求抛物线的对称轴及顶点坐标;(2)若 1,m =当 3t x t +≤≤时,函数最小值为 2-,求t 的值;(3)横、纵坐标都是整数的点叫做整点.若抛物线在点 A ,B 之间的部分与线段 AB 所围成的区域内(包括边界)恰有10个整点,求m 的取值范围.5.(23-24九年级下·北京·阶段练习)已知抛物线()20y ax bx c a =++>,(1)若抛物线过点()()35m m -,,,,求抛物线的对称轴;(2)已知点()()()()0112042y x y y n -,,,,,,,在抛物线上,其中121x -<<-,若存在1x 使1y n >,试比较012y y y ,,的大小关系.【压轴题型三 根据二次函数的对称性求值】1.(2024·山东淄博·二模)二次函数2y ax bx c =++(a ,b ,c 是常数,0a ¹)的自变量x 与函数值y 的部分对应值如下表:x…2-1-012…2y ax bx c=++…tm2-2-n…且当12x =-时,与其对应的函数值0y >,有下列结论:①函数图象的顶点在第四象限内;②2-和3是关于x 的方程2ax bx c t ++=的两个根;③36m n +<-,其中正确的结论个数是( )A .0个B .1个C .2个D .3个2.(23-24九年级上·安徽芜湖·期中)已知二次函数2y ax bx c =++的图像过点(1,0)A -和(0,1)C .(1)若此抛物线的对称轴是直线12x =,点C 与点P 关于直线12x =对称,则点P 的坐标是 .(2)若此抛物线的顶点在第一象限,设t a b c =++,则t 的取值范围是 .3.(2024·云南曲靖·二模)已知抛物线²y ax bx c =++(a ,b ,c 为常数,0a ¹)(1)若20a b -=,4-+=a b c ,求此抛物线的顶点坐标;(2)在(1)的条件下,抛物线经过点()0,2,将抛物线²y ax bx c =++的图象0x <的部分向下平移h (h 为正整数)个单位长度,平移后的图象恰好与x 轴有2个交点,若点1(,)S m n y -与点2(,)Q m y 在平移后的抛物线上(点S ,Q 不重合),且点S 与点 Q 关于对称轴对称,求代数式22281244m mn n n h -+-+的值.4.(23-24九年级上·北京朝阳·期中)在平面直角坐标系xOy 中,点()1,m ,()4,n 在抛物线()20y ax bx c a =++>上.设抛物线的对称轴为直线x t =.(1)若30a b +=.比较,,m n c 的大小关系,并说明理由;(2)点()00),1(x m x ¹在抛物线上,若m c n <<,求t 及0x 的取值范围.5.(23-24九年级上·北京西城·期中)已知点()11,M x y ,()22,N x y 在抛物线()220y ax bx a =++>的图象上,设抛物线的对称轴为x t =.(1)若()2,1M -,()8,1N -,则t =_______;(2)当12x =-,223x <<时,都有122y y >>,求t 的取值范围.【压轴题型四 二次函数的平移压轴题】1.(2024·河北邯郸·二模)我们把横、纵坐标都是整数的点称为整点,如图,抛物线1C :224y x x =-++与()22:C y x m =-(m 是常数)围成的封闭区域(边界除外)内整点的个数不能是( )A .1个B .2个C .3个D .4个2.(2024·福建·模拟预测)定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC 中,点()02A ,,点()20C ,,则互异二次函数()2y x m m =--与正方形OABC 有交点时m 的最大值和最小值的差为3.(2024·广东广州·二模)在平面直角坐标系中,将过点()2,1-的抛物线211:4C y x bx =-+(b 为常数)向右平移m 个单位(0m >),再向上平移n 个单位(0n ³)得到新的抛物线2C ,其顶点为E .(1)求点E 的坐标;(用含m ,n 的式子表示)(2)若抛物线2C 与坐标轴有且只有两个公共点,求满足条件的点E 的纵坐标;(3)当1n =时,抛物线2C 与x 轴交于A 、B 两点,与y 轴交于点D ,且当02x ££时,对抛物线1C 上的任意一点P ,在抛物线2C 上总存在一点Q ,使得点P ,Q 的纵坐标相等,探究下列问题:①求m 的取值范围;②若存在一点F ,满足DF AF BF ==,求点F 的纵坐标的取值范围.4.(2024·内蒙古赤峰·二模)小爱同学学习二次函数后,对函数()21y x =--进行了探究.在经历列表、描点、连线步骤后,得到如图的函数图象.请根据函数图象,回答下列问题:(1)观察探究:①至少写出该函数的两条性质;②直接写出方程()211x --=-的解;③直接写出方程()21x a --=有四个实数根时a 的取值范围.(2)延伸思考:将函数()21y x =--的图象经过怎样的平移可得到函数()21213y x =---+的图象?写出平移过程,并直接写出当123y <£时,自变量x 的取值范围.5.(2024·山东济南·二模)已知抛物线1C :26y x mx m =--+交x 轴于点A ,B ,交y 轴于点C .(1)如图1,当点A 坐标为()30-,时,求抛物线的解析式;(2)在(1)的条件下,点D 是第二象限内抛物线上的一点,连接BD ,若BD 将四边形ABCD 平分成面积相等的两部分,求点D 的横坐标;(3)如图2,EFH V 为等边三角形,点F ,H 在x 轴上,且点E 的坐标为()06,,将抛物线1C :26y x mx m =--+向右平移m 个单位,再向下平移6m 个单位后得到新的抛物线2C ,若2C 与等边EFH V 三边恰有四个交点,求m 的取值范围.【压轴题型五 二次函数与坐标轴交点压轴题】1.(2024·浙江杭州·一模)已知抛物线2y ax bx =+与2y bx ax =+的交点为A ,与x 轴的交点分别为B ,C ,点A ,B ,C 的横坐标分别为1x ,2x ,3x ,且1230x x x ¹.若0a b +<,20a b +>,则下列说法正确的是( )A .231x x x <<B .321x x x <<C .213x x x <<D .312x x x <<2.(2023·浙江绍兴·中考真题)在平面直角坐标系xOy 中,一个图形上的点都在一边平行于x 轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图,函数()2(2)03y x x =-££的图象(抛物线中的实线部分),它的关联矩形为矩形OABC .若二次函数()21034y x bx c x =++££图象的关联矩形恰好也是矩形OABC ,则b =.3.(23-24九年级上·浙江杭州·期中)已知抛物线()230y ax ax c a =++¹与y 轴交于点A .(1)当1a =,2c =,求该抛物线与x 轴交点坐标;(2)若1a =,点(),P m n 在二次函数抛物线23y ax ax c =++的图象上,且0n c ->,试求m 的值;(3)若点A 的坐标是()0,1,当2c c -<时,抛物线与x 轴只有一个公共点,求a 的取值范围.4.(22-23九年级上·浙江湖州·期末)在书本阅读材料中提到利用几何画板可以探索函数2y ax bx c =++的系数a ,b ,c 与图像的关系.如图1,在几何画板软件中绘制一个二次函数的图像的具体步骤如下:步骤一:在直角坐标系内的x 轴上取任意三个点A (A 不在原点),B ,C ,度量三个点的横坐标,分别记为a ,b ,c ;步骤二:绘制函数2y ax bx c =++;步骤三:任意移动A ,B ,C 三点的位置,发现抛物线的开口方向、大小、位置会发生变化.问题:如图2,将点A 移动到点()1,0-的位置.(1)若点B 移动到点()4,0-,请求出此时抛物线的对称轴;(2)在点B ,C 移动的过程中,且满足AB AC =,是否存在某一位置使得抛物线与x 轴只有一个交点,若存在,请求出此时点B 的坐标,若不存在,请说明理由.5.(22-23九年级上·浙江杭州·期末)已知二次函数2(0)y ax bx c a =++>的图象经过点(1,1)A -和(2,4)B .(1)求a ,b 满足的关系式;(2)当自变量x 的值满足12x -££时,y 随x 的增大而增大,求a 的取值范围;(3)若函数图象与x 轴无交点,求2a b +的取值范围.【压轴题型六 二次函数的应用(销售、增长率等问题)】1.(2024·天津红桥·三模)某服装店试销一种成本为每件60元的服装,规定试销期间每件服装的销售单价不低于成本,且获得的利润不得高于成本的45%.经试销发现,销售量y (件)与销售单价x (元)符合一次函数关系120y x =-+.有下列结论:①销售单价可以是90元;②该服装店销售这种服装可获得的最大利润为891元;③销售单价有两个不同的值满足该服装店销售这种服装获得的利润为500元,其中,正确结论的个数是( )A .0B .1C .2D .32.(2021·江苏连云港·中考真题)某快餐店销售A 、B 两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A 种快餐的利润,同时提高每份B 种快餐的利润.售卖时发现,在一定范围内,每份A 种快餐利润每降1元可多卖2份,每份B 种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.3.(2024·四川德阳·三模)“端午节”吃粽子是中国传统习俗,在端午节来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒定价为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x 元,日销售量为P 盒.(1)当60x =时,P 等于______;(2)当每盒售价定为多少元时,日销售利润W (元)最大?最大利润是多少?(3)小强说:“当日销售利润最大时,日销售额不是最大.”小红说:“当日销售利润不低于8000元时,每盒售价x 的范围为6080x ££.”你认为他们的说法正确吗?4.(22-23八年级下·浙江杭州·期中)某商店进购一商品,第一天每件盈利(毛利润)10元,销售500件.(1)第二、三天该商品十分畅销.销售量持续走高.在售价不变的基础上,第二、三天的销售量达到605件,求第二、三天的日平均增长率;(2)经市场调查发现,在进货价不变的情况下,若每件涨价1元,日销量将减少20件.①现要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每件应张价多少元?②现需按毛利润的10%交纳各种税费,人工费每日按销售量每件支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每件涨价应为多少?5.(2023·湖北省直辖县级单位·一模)某销售卖场对一品牌商品的销售情况进行了调查,已知该商品的进价为每件3元,每周的销售量y (件)与售价x (元/件)(x 为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:x (元/件)456y (件)1000095009000(1)求y 关于x 的函数关系式(不求自变量的取值范围);(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)抗疫期间,该商场这种商品的售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠整数m 元()15m ££,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出整数m 的值.【压轴题型七 二次函数的应用(图形运动、拱桥、投球等问题)】1.(22-23九年级上·浙江台州·期末)以初速度v (单位:m/s )从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h (单位:m )与小球的运动时间t (单位:s )之间的关系是24.9h vt t =-.现将某弹性小球从地面竖直向上抛出,初速度为9.8m/s ,经过a 秒后,将第二个相同材质的小球从地面以初速度4.9m/s 竖直上抛.若两球能在空中相遇,则a 的取值范围为( )A .34a <<B .12a <<C .324a <<D 2a <<2.(23-24九年级上·浙江湖州·期末)如图,乒乓球桌桌面是长 2.7m AB =,宽 1.5m AD =的矩形,E F ,分别是AB 和CD 的中点,在E ,F 处设置高0.15m HE =的拦网.一次运动员在AD 端发球,在P 点击打乒乓球后经过桌面O 点反弹后的运行路径近似二次项系数427a =-的抛物线的一部分.已知本次发球反弹点O 在到桌面底边AD 的距离为0.1m ,到桌面侧边AB 的距离为0.1m 处.若乒乓球沿着正前方飞行(垂直于BC ),此时球在越过拦网时正好比拦网上端GH 高0.1m ,则乒乓球落在对面的落点Q 到拦网EF 的距离为 m ;若乒乓球运行轨迹不变,飞行方向从O 点反弹后飞向对方桌面,落点Q 在距离BC 为0.2m 的Q 点处,此时QC 的长度为 m .3.(2023·浙江杭州·模拟预测)已知点(2,2)A -和点(4,)B n -在抛物线2(0)y ax a =¹上.(1)求a 的值及点B 的坐标;(2)点P 在y 轴上,且ABP V 是以AB 为直角边的三角形,求点P 的坐标;(3)将抛物线2(0)y ax a =¹向右并向下平移,记平移后点A 的对应点为A ¢,点B 的对应点为B ¢,若四边形ABB A ¢¢为正方形,求此时抛物线的表达式.4.(22-23九年级上·天津河西·期末)如图所示,在ABC V 中,90B Ð=°,5cm AB =,7cm BC =,点P 从点A 开始沿AB 边向点B 以1cm /s 的速度运动,点Q 从点B 开始沿BC 边向点C 以2cm /s 的速度运动.P 、Q 分别从A 、B 同时出发,当P 、Q 两点中有一点停止运动时,则另一点也停止运动.设运动的时间为s t .(0)t ≥(1)当t 为何值时,PQ 的长度等于5cm ;(2)求出V BPQ S 关于t 的函数解析式,计算P 、Q 出发几秒时,V BPQ S 有最大值,并求出这个最大面积?5.(23-24九年级上·浙江温州·期中)如图,抛物线2y x bx c =-++与x 轴交于点()3,0A -、()1,0B ,与y 轴交于点C .(1)求抛物线的表达式.(2)已知点D 为y 轴上一点,点D 关于直线AC 的对称点为1D .①当点1D 刚好落在第二象限的抛物线上时,求出点D 的坐标.②点P 在抛物线上(点P 不与点A 、点C 重合),连接PD ,1PD ,1DD ,是否存在点P ,使1PDD △为等腰直角三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.【压轴题型八 二次函数中的存在性问题】1.(2024·浙江宁波·一模)新定义:若一个点的横纵坐标之和为6,则称这个点为“和谐点”.若二次函数22y x x c =-+(c 为常数)在13-<<的图象上存在两个“和谐点”,则c 的取值范围是( )A .2574c <<B .2544c <<C .11c -<<D .2504c <<2.(23-24九年级上·浙江温州·期中)图1是洞头深门大桥,其桥底呈抛物线,以O 为原点,OA 所在直线为x 轴建立平面直角坐标系(如图2所示),桥面CB ∥OA ,其抛物线解析式为()218020320y x =--+,抛物线上点A 离桥面距离22AB =米,若存在一点E 使得38CE CB =,则点E 到抛物线的距离ED = 米.3.(2024·浙江宁波·模拟预测)如图,一次函数y =的图象与坐标轴交于点A 、B ,抛物线2y x bx c =++的图象经过A 、B 两点.(1)求二次函数的表达式;(2)若点P 为抛物线上一动点,在直线AB 上方是否存在点P 使PAB V 的面积最大?若存在,请求出PAB V 面积的最大值及点P 的坐标,请说明理由.4.(23-24九年级上·黑龙江伊春·期末)如图,已知抛物线22y ax x c =-+与直线y kx b =+都经过(0,3)A -、(3,0)B 两点,该抛物线的顶点为.(1)求此抛物线和直线AB 的表达式;(2)设直线AB 与该抛物线的对称轴交于点E ,在射线EB 上是否存在一点M ,过M 作x 轴的垂线交抛物线于点N ,使点M ,N ,C ,E 是平行四边形的四个顶点?若存在,直接写出点M 的坐标;若不存在,说明理由;5.(22-23九年级上·浙江温州·期中)如图,直线212y x =-+与x 轴交于点C ,与y 轴交于点B ,抛物线23103y ax x c =++经过B C ,两点,与x 轴交于另一点A ,点E 是直线BC 上方抛物线上的一动点,过E 作EF y ∥轴交x 轴于点F ,交直线BC 于点M .(1)求抛物线的解析式;(2)求线段EM 的最大值;(3)在(2)的条件下,连接AM ,点Q 是抛物线对称轴上的动点,在抛物线上是否存在点P ,使得以P Q A M ,,,为顶点的四边形为平行四边形?如果存在,请直接写出P 点坐标;如果不存在,请说明理由.【压轴题型九 二次函数与一次函数压轴题】1.(2024·浙江杭州·一模)二次函数21y x bx c =++(b ,c 是常数)过()2,0-,()0m ,两个不重合的点,一次函数2y x d =+过()0m ,和二次函数的顶点,则m 的值为( )A .﹣1B .0C .1D .22.(23-24九年级上·浙江绍兴·期末)二次函数2(,,y ax bx c a b c =++为常数,且0)ab ¹经过()()11,0,,0x ,一次函数y a x c =+经过()2,0x ,一次函数y b x c =+经过()3,0x .已知1254,1x m x m -<<-<<+,31n x n <<+,其中,m n 为整数,则m n +的值为 .3.(2024·浙江舟山·三模)已知一次函数5y x =-的图象与x 轴,y 轴分别交于点A ,B ,将点A 向左平移4个单位,得到点A ¢,且点A ¢恰好在二次函数23y ax bx =+-(a 、b 是常数,0a ¹)图象的对称轴上.(1)用含a 的代数式表示b .(2)求证:二次函数与一次函数图象交于一个定点,并求出该点的坐标.(3)若二次函数图象与线段AB 恰有一个公共点,结合函数图象,求a 的取值范围.4.(23-24九年级上·浙江宁波·期末)如图,在平面直角坐标系xOy 中,一次函数121y x =+的图象与二次函数22y x ax b =++的图象相交于A ,B 两点,点A 坐标为()1m -,,点B 坐标为()25,.(1)求m 的值以及二次函数的解析式.(2)根据图象,直接写出当1y >2y 时x 的取值范围.(3)若将二次函数向上平移t 个单位长度后,得到的图象与x 轴没有交点,求t 的取值范围.5.(2023·浙江金华·三模)如图,一次函数()00b y x b a b a=-+>>,与坐标轴交于A ,B 两点,以A 为顶点的抛物线过点B ,过点B 作y 轴的垂线交该抛物线另一点于点D ,以AB ,AD 为边构造ABCD Y ,延长BC 交抛物线于点E .(1)若2a b ==,如图1.①求该抛物线的表达式.②求点E 的坐标.(2)如图2,请问BE AB 是否为定值,若是,请求出该定值;若不是,请说明理由.【压轴题型十 二次函数的翻折问题】1.(22-23九年级上·浙江湖州·期末)抛物线223y x x =-++与y 轴交于点C ,过点C 作直线l 垂直于y 轴,将抛物线在y 轴右侧的部分沿直线l 翻折,其余部分保持不变,组成图形G ,点()1,M m y ,()21,N m y +为图形G 上两点,若12y y >,则m 的取值范围是( )A .102m £<B 1m <<C m <<D 12m <<2.(2023江苏南通·模拟预测)如图,将二次函数2y x m =-(其中0m >)的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,形成新的图象记为1y ,另有一次函数2y x =+的图象记为2y ,若1y 与2y 恰有两个交点时,则m 的范围是 .3.(2024·浙江·模拟预测)如图,抛物线22(0)y x x m m =-++>与y 轴交于A 点,其顶点为D .直线122y x m =--分别与x 轴、y 轴交于B 、C 两点,与直线AD 相交于E 点.(1)求A 、D 的坐标(用m 的代数式表示);(2)将ACE V 沿着y 轴翻折,若点E 的对称点P 恰好落在抛物线上,求m 的值;(3)抛物线22(0)y x x m m =-++>上是否存在一点P ,使得以P 、A 、C 、E 为顶点的四边形是平行四边形?若存在,求此抛物线的解析式;若不存在,请说明理由.4.(23-24九年级上·浙江绍兴·期中)如图,在平面直角坐标系中,将二次函数223y x x =--在x 轴上方的图象沿x 轴翻折到x 轴下方,图象的其余部分不变,将这个组合的图象记为M .(1)若直线12y x n =+与图象M 恰好有3个交点.求n 的值.(2)若直线12y x n =+与图象M 恰好有2个交点.求n 的取值范围.5.(2023·浙江杭州·二模)已知二次函数2420y mx mx m m =-+-¹(),且与x 轴交于不同点M 、N .(1)若二次函数图象经过点30A (,),①求二次函数的表达式和顶点坐标;②将抛物线在05x ££之间的那部分函数图象沿直线5x =翻折,将抛物线翻折前后的这两部分合记为图象F ,若直线y kx n =+过点151C (,),且与图象F 恰有两个交点,求n 的取值范围;(2)若0m <,当4MN £时,求实数m 的取值范围.【压轴题型十一 二次函数最值问题】1.(2024·浙江温州·二模)已知二次函数222y x x -=+, 当0x t ££时,函数最大值为M ,最小值为N .若5M N =,则t 的值为 ( )A .0.5B .1.5C .3D .42.(2023·浙江杭州·模拟预测)已知二次函数()2211y ax b x =--+(a ,b 为常数且0a >),当21x -££-时,y 随x 的增大而增大,则ab 的最大值为 .3.(2024·浙江嘉兴·三模)已知二次函数 23y x bx =++的图象经过点()()()12,,,43A x n B x t C -,,.(1)求二次函数的函数表达式;(2)当 212x x -=时,①若 0nt £,求 t n -的取值范围;②设直线AB 的函数表达式为y kx m =+,求m 的最大值.4.(2024·浙江宁波·模拟预测)已知二次函数214y x bx c =-++的图象经过原点O 和点()8,0A t +,其中0t ³.(1)当0=t 时.①求y 关于x 的函数解析式;求出当x 为何值时,y 有最大值?最大值为多少?②当x a =和x b =时()a b ¹,函数值相等,求a 的值.(2)当0t >时,在08x ££范围内,y 有最大值18,求相应的t 和x 的值.5.(23-24九年级上·浙江湖州·期末)设二次函数2y ax bx c =++(a b c ,,均为常数,且0a ¹).已知函数值y 和自变量x 的部分对应取值如下表所示:x L3-2-1-01L y L n 5a -n a-4a L (1)若1a =.①求二次函数的表达式,并写出顶点坐标;②已知点()1,m y 与()23,m y -都在该二次函数图象上,且12y y ³,请求出1y 的最小值.(2)将该二次函数图象向右平移k (02k <<)个单位,若平移后的二次函数图象在20x -££的范围内有最小值为3116a -,求k 的值.【压轴题型十二 二次函数的综合】1.(22-23九年级上·浙江宁波·阶段练习)如图,抛物线218333y x x =+-与x 轴交于点A 和点B 两点,与y 轴交于点C ,D 点为抛物线上第三象限内一动点,当2180ACD ABC Ð+Ð=°时,点D 的坐标为( )A .(8,3)--B .(,)--1673C .(6,7)--D .(5,8)--2.(23-24九年级上·浙江金华·期末)定义:若x ,y 满足:24x y k =+,24y x k =+(k 为常数)且x y ¹,则称点(),M x y 为“好点”.(1)若()5,P m 是“好点”,则m .(2)在32x -<<的范围内,若二次函数23y x x c =-+的图象上至少存在一个“好点”,则c 的取值范围为 .3(2024·浙江温州·二模)在平面直角坐标系中,已知抛物线()2233y mx m x m =--+-(m 是常数,且0m ¹)经过点()2,4,且与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求出二次函数的表达式.(2)垂直于y 轴的直线l 与抛物线交于点(),P a p 和(),Q b q ,与直线AB 交于点(),c n ,若a c b <<,直接写出a b c ++的取值范围.(3)当13x t =-,2x t =,33x t =+时,对应的函数值分别为1y ,2y ,3y .求证:123454y y y ++³.4.(23-24九年级下·浙江宁波·期中)如图,已知抛物线21:4C y x =,()01F ,,点()11,A x y ,()22,B x y 为抛物线上第一象限内的两点,且满足FA FB ^,以FA FB 、为边向右作矩形FAPB ,若P 点纵坐标为5.(1)求12y y +的值;(2)求12x x 的值;(3)求矩形FAPB 的面积.5.(21-22九年级上·浙江·周测)如图,在平面直角坐标系中,抛物线24y ax bx =++交y 轴于点A ,交x 轴于点()6,0B -和点()2,0C ,连接AB 、AQ 、BQ ,BQ 与y 轴交于点N .(1)求抛物线表达式;(2)点713Q æöç÷èø,,点M 在x 轴上,点E 在平面内,若BME AOM V V ≌,且四边形ANEM 是平行四边形.①求点E 的坐标;②设射线AM 与BN 相交于点P ,交BE 于点H ,将BPH V 绕点B 旋转一周,旋转后的三角形记为11BPH △,求11BP 的最小值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考二次函数压轴题专题分类训练题型一:面积问题【例1】(2009湖南益阳)如图2,抛物线顶点坐标为点C (1,4),交x轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式; (2)求△CAB 的铅垂高CD 及S △CAB ;(3)设点P是抛物线(在第一象限内)上的一个动点,是否存在一点P ,使S△PAB =89S △C AB,若存在,求出P 点的坐标;若不存在,请说明理由.【变式练习】1.(2009广东省深圳市)如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段O A绕原点O顺时针旋转120°,得到线段OB . (1)求点B 的坐标;(2)求经过A 、O 、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△B OC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.图22.(2010绵阳)如图,抛物线y = a x2+ bx + 4与x 轴的两个交点分别为A (-4,0)、B(2,0),与y 轴交于点C,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x轴、y轴分别交于F 、G .(1)求抛物线的函数解析式,并写出顶点D的坐标;(2)在直线EF 上求一点H,使△CDH 的周长最小,并求出最小周长; (3)若点K 在x轴上方的抛物线上运动,当K 运动到什么位置时, △EFK 的面积最大?并求出最大面积.3.(2012铜仁)如图,已知:直线3+-=x y 交x 轴于点A,交y 轴于点B,抛物线y=ax 2+b x+c经过A、B 、C (1,0)三点.(1)求抛物线的解析式;(2)若点D 的坐标为(-1,0),在直线3+-=x y 上有一点P,使ΔABO 与ΔADP 相似,求出点P 的坐标;(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE 的面积等于四边形APC E的面积?如果存在,请求出点E 的坐标;如果不存在,请说明理由.C ED GAxy OB F题型二:构造直角三角形【例2】(2010山东聊城)如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求此时点M的坐标;(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90º的点P的坐标.【变式练习】1.(2012广州)如图,抛物线y =与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式. E2.(2009成都)在平面直角坐标系xOy 中,已知抛物线y =2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为M,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N,且C OS∠BCO=10。
(1)求此抛物线的函数表达式;(2)在此抛物线上是否存在异于点C 的点P ,使以N 、P 、C 为顶点的三角形是以NC 为一条直角边的直角三角形?若存在,求出点P 的坐标:若不存在,请说明理由;(3)过点A 作x 轴的垂线,交直线MC 于点Q.若将抛物线沿其对称轴上下平移,使抛物线与线段NQ 总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?3.(2012杭州) 在平面直角坐标系内,反比例函数和二次函数y=k (x 2+x ﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k ).(1)当k=﹣2时,求反比例函数的解析式;(2)要使反比例函数和二次函数都是y 随着x 的增大而增大,求k应满足的条件以及x 的取值范围;(3)设二次函数的图象的顶点为Q ,当△ABQ 是以AB 为斜边的直角三角形时,求k 的值4.如图(1),抛物线42y x x =+-与y 轴交于点A ,E (0,b )为y轴上一动点,过点E 的直线y x b =+与抛物线交于点B 、C.(1)求点A的坐标;4>-时,上述关,求出b;若不存题型三:构造等腰三角形【例3】如图,已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A(1,0)和点B (-3,0),与y 轴交于点C .(1)求抛物线的解析式;(2)在x 轴上是否存在一点Q 使得△A CQ 为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由;(3)设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.【变式练习】1.如图,在平面直角坐标系中,点A 的坐标为(m ,m),点B 的坐标为(n ,﹣n),抛物线经过A 、O 、B 三点,连接OA、OB 、AB ,线段AB 交y 轴于点C .已知实数m 、n(m<n)分别是方程x2﹣2x﹣3=0的两根. (1)求抛物线的解析式;(2)若点P 为线段OB 上的一个动点(不与点O 、B重合),直线PC 与抛物线交于D 、E 两点(点D 在y 轴右侧),连接OD 、BD. ①当△OPC 为等腰三角形时,求点P的坐标; ②求△BOD 面积的最大值,并写出此时点D 的坐标.2.如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC =BC .(1)写出A,B,C三点的坐标并求抛物线的解析式;(2)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.3.(2010黄冈)已知抛物线2(0)y ax bx c a =++≠顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线54y =作垂线,垂足为M,连FM (如图). (1)求字母a,b,c的值;(2)在直线x=1上有一点3(1,)4F ,求以PM 为底边的等腰三角形PFM 的P 点的坐标,并证明此时△PFM 为正三角形;(3)对抛物线上任意一点P,是否总存在一点N(1,t),使P M=PN 恒成立,若存在请求出t 值,若不存在请说明理由.AC By x0 11题型四:构造相似三角形【例4】(2011临沂)如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求抛物线的解析式;(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.【变式练习】1.(2012天水)如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.(1)求该抛物线的解析式;(2)在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.ﻫ(3)P是直线x=1右侧的该抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.7),且顶点C的横坐标为4,该图象在x 轴上截2. 如图,二次函数的图象经过点D(0,39得的线段AB的长为6.(1)求二次函数的解析式;(2)在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;(3)在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.【例5】(2012苏州)如图,已知抛物线y=x2 - (b+1)x+(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.ﻫ(1)点B的坐标为 ,点C的坐标为(用含b的代数式表示);ﻫ(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;ﻫ(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.ﻬ【变式练习】1.(2012上海宝山)如图,平面直角坐标系xOy中,已知点A(2,3),线段AB垂直于y轴,垂足为B ,将线段AB 绕点A 逆时针方向旋转90°,点B 落在点C 处,直线BC 与x 轴的交于点D .(1)试求出点D的坐标;(2)试求经过A 、B 、D 三点的抛物线的表达式,并写出其顶点E 的坐标;(3)在(2)中所求抛物线的对称轴上找点F ,使得以点A 、E 、F 为顶点的三角形与△ACD 相似.2.(2012上海杨浦区)已知直线112y x =+与x 轴交于点A ,与y 轴交于点B ,将△AOB 绕点O 顺时针旋转90︒,使点A 落在点C ,点B 落在点D ,抛物线2y ax bx c =++过点A 、D 、C ,其对称轴与直线AB 交于点P , (1)求抛物线的表达式; (2)求∠POC 的正切值; (3)点M 在x 轴上,且△ABM 与△APD 相似,求点M的坐标。
3.(2012宁波)如图,二次函数y =ax 2+bx +c 的图象交x 轴于A (﹣1,0),B(2,0),交y 轴于C (0,﹣2),过A,C 画直线.(1)求二次函数的解析式;(2)点P在x轴正半轴上,且PA=PC,求OP的长;(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;②若⊙M的半径为,求点M的坐标.题型五:构造梯形【例6】已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 32-=与边BC 相交于点D . (1)求点D的坐标;(2)抛物线c bx ax y ++=2经过点A 、D 、O ,求此抛物线的表达式;(3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.【变式练习】1.已知平面直角坐标系xOy 中, 抛物线y =ax2-(a +1)x与直线y =kx 的一个公共点为A(4,8).(1)求此抛物线和直线的解析式;(2)若点P 在线段OA 上,过点P作y 轴的平行线交(1)中抛物线于点Q ,求线段P Q长度的最大值;(3)记(1)中抛物线的顶点为M ,点N 在此抛物线上,若四边形AOMN 恰好是梯形,求点N的坐标及梯形AOMN 的面积.2.(2011义乌)已知二次函数的图象经过A (2,0)、C (0,12) 两点,且对称轴为直线x =4,设顶点为点P ,与x 轴的另一交点为点B . (1)求二次函数的解析式及顶点P 的坐标;(2)如图1,在直线 y =2x 上是否存在点D ,使四边形OPBD 为等腰梯形?若存在,求出点D 的坐标;若不存在,请说明理由;(3)如图2,点M 是线段OP 上的一个动点(O、P 两点除外),以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN//x 轴,交P B于点N. 将△PMN 沿直线MN 对折,得到△P 1MN . 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒,求S 关于t 的函数关系式.3.如图1,二次函数)0(2<++=p q px x y 的图象与x 轴交于A、B 两点,与y 轴交于点C (0,-1),△ABC 的面积为45. (1)求该二次函数的关系式;(2)过y 轴上的一点M(0,m )作y轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D,使以A 、B、C 、D 为顶点的四边形为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由.题型六:构造平行四边形【例7】(2010陕西)如图,在平面直角坐标系中,抛物线经过A(—1,0),B(3,0),C(0,—1)三点。
