3 螺栓最小破坏扭矩的计算与分析
螺栓破坏扭矩试验

螺栓破坏扭矩试验螺栓破坏扭矩试验是用来测试螺栓材料的力学性质以及其在实际使用中承受的载荷能力的试验方法。
螺栓是一种常用的连接元件,广泛应用于工程、机械、建筑等领域。
螺栓破坏扭矩试验对于确保螺栓连接的可靠性和安全性至关重要。
螺栓破坏扭矩试验主要通过在试验机上施加逐渐增大的扭矩力矩来进行。
在试验过程中,首先将螺栓安装在试验机上,然后通过旋转试验机的驱动装置施加扭矩力矩。
在施加的力矩逐渐增大的同时,对螺栓进行监测和观察,直到螺栓发生破坏为止。
试验结束后,将螺栓的破坏扭矩值记录下来,以作为评估其质量和性能的依据。
螺栓破坏扭矩试验的目的是确定螺栓在扭矩加载下的破坏性能。
通过测试螺栓的扭矩破坏值,可以评估其在实际工作环境中承受扭矩载荷的能力。
这对于确保螺栓连接的稳定性和可靠性非常重要。
螺栓破坏扭矩试验的结果主要有两个方面的意义。
首先,它可以用于评估螺栓的性能和质量。
通过对螺栓破坏扭矩值的测量,可以判断螺栓的材料强度和连接性能是否符合设计要求。
其次,它还可以用于优化螺栓的设计和选择。
通过研究不同规格和材料的螺栓在破坏扭矩试验中的表现,可以为螺栓的设计和选择提供参考依据。
螺栓破坏扭矩试验需要注意的一些因素是温度和湿度等环境因素对试验结果的影响。
温度和湿度的变化可能会导致材料的力学性质发生变化,从而影响试验结果的准确性。
因此,在进行试验前应对试验环境进行严格控制,并对试验结果进行相应的修正。
综上所述,螺栓破坏扭矩试验是一种用于评估螺栓材料性能和连接质量的试验方法。
它通过施加逐渐增大的扭矩力矩来测试螺栓的破坏扭矩值,并以此为依据评估其在实际工作环境中的扭矩载荷能力。
螺栓破坏扭矩试验结果对于确保螺栓连接的稳定性和可靠性非常重要,可以用于评估螺栓性能、优化设计和选择螺栓。
同时,在进行试验时需注意环境因素对试验结果的影响,并进行相应的修正,以确保试验结果的准确性。
螺栓破坏扭矩试验是一种重要的测试方法,用于评估螺栓在扭矩载荷下的耐力和可靠性。
螺栓拧紧残余扭矩测量方法盘点

螺栓拧紧残余扭矩测量方法盘点1 前言紧固件拧紧的本质是为了获取夹紧力,通过夹紧力,可以抵抗各种比如横向和轴向外载荷。
但由于夹紧力无法直接监控,最终拧紧的可靠性是通过扭矩监控的,所以通过有效的监控方法,检测紧固件拧紧后的残余扭矩,是判断紧固件拧紧可靠性的重要方法。
如下图所示,紧固件扭矩衰减一般是在瞬间就完成了60-70%的衰减。
对于任何连接,随着时间的推移,都会有一定程度的扭矩衰减,一般有以下两种情况中:粗糙的表面配合时造成的衰减和软连接中的扭矩衰减。
总之发生扭矩衰减的原因是多种多样,可以通过人、机、料、法、环等各角度去分析,目前螺丝君里该类资料很多,在此不多多说,但如何去有效监测拧紧后的残余扭矩呢?目前方法也很多,小编一一带各位了解下。
图1 扭矩衰减过程2 残余扭矩测试方法(1)再拧紧扭矩法具体做法:再拧紧扭矩法是在拧紧的螺栓上进一步拧紧较小的角度获得的静态扭矩到动态扭矩装化点的扭矩,拧紧的角度一般为10-15°。
优缺点:无需破坏连接副、操作便利、工具价格适中,可靠性强,目前该种方法在主机厂使用较为广泛。
如下图所示,为再拧紧扭矩法的测试方法和测试工具,常用的表盘扳手和数显扳手就可以满足,当然测试人员一般是需要经过专门培训的。
图2 再拧紧扭矩法测试过程如果对再拧紧扭矩不是太清楚,下图是通过记录扭矩和转角的曲线,先拧紧15°,再反松90°,下图中圈出的拐点位置即为对应点的再拧紧扭矩。
图3 再拧紧扭矩测试曲线那如何评判拧紧点的再拧紧扭矩是否合格呢?下面为经验数值:将拧紧点根据重要性分为A,B,C三种等级,A是涉及安全的拧紧点,B 是涉及是否会出现故障的拧紧点,C是一般普通的拧紧点。
测试推荐完成拧紧后的15-30min,对于A类和B类拧紧点,0.8*预拧紧扭矩≤再拧紧扭矩≤1.2*预拧紧扭矩对于C类拧紧点,0.7*预拧紧扭矩≤再拧紧扭矩≤1.2*预拧紧扭矩对于软连接点,0.5*预拧紧扭矩≤再拧紧扭矩≤1.2*预拧紧扭矩那何为软连接点,即拧紧副中含有塑料等较软,拧紧角度较大的连接点。
8.8级以下螺栓的最小破坏扭矩

8.8级以下螺栓的最小破坏扭矩随着工程技术的不断发展,各种螺栓在建筑结构和机械设备中扮演着重要的角色。
而螺栓的质量和性能直接影响着工程项目和设备的安全性和稳定性。
对于螺栓的性能指标需严格要求,其中最小破坏扭矩是一个重要的指标之一。
本文将围绕8.8级以下螺栓的最小破坏扭矩进行探讨。
一、螺栓的概念和作用螺栓是一种常用的连接零件,通常由头、螺杆和螺纹部分组成。
它的作用是利用螺纹的摩擦来连接和固定零部件,传递和承受机械载荷。
螺栓主要用于连接结构,承受静力和动力负荷,而螺栓的性能指标包括拉伸强度、抗剪强度、抗扭强度等。
二、8.8级以下螺栓的性能要求根据国家标准GB/T 5782-2000《六角头螺栓》和GB/T 5783-2000《六角头螺母》的规定,8.8级以下螺栓的性能要求包括拉伸强度、抗剪强度等。
在应用中,螺栓需要承受一定的扭矩,因此其最小破坏扭矩也是一个重要的技术指标。
三、螺栓的最小破坏扭矩计算方法螺栓的最小破坏扭矩是指在受到外力作用下,螺栓发生破坏前所能承受的最小扭矩。
计算其数值的方法通常有两种,一种是通过公式计算,另一种是通过实验测试。
公式计算方法一般是根据螺栓的材料、直径和螺纹尺寸等参数,经过一定的计算得出最小破坏扭矩的数值;而实验测试方法则是将螺栓安装到测试设备上,通过施加外力和扭矩,观察螺栓开始滑动或者破坏的情况,从而确定最小破坏扭矩。
四、螺栓的最小破坏扭矩的意义螺栓的最小破坏扭矩是螺栓的重要性能参数之一,它直接关系到螺栓在实际工程中的使用安全性和可靠性。
如果螺栓的最小破坏扭矩过小,就会出现扭矩不足而导致螺栓松动甚至螺断的问题;反之,如果最小破坏扭矩过大,就会使得螺栓在安装和拆卸时难以操作,增加了工作的难度和成本。
螺栓的最小破坏扭矩是一个关乎工程安全和质量的重要指标,企业和制造商应该严格控制螺栓的生产和质量,确保其达到相关标准要求,并在实际使用中做好检测和保养工作,以确保螺栓的可靠性和安全性。
螺丝破坏扭力计算方法

螺丝破坏扭力计算方法在螺纹紧固件的使用中应用的较广泛的是螺栓-螺母连接副的形式,应用的较多的是有预紧力的连接方式,预紧力的连接可以提高螺栓连接的可靠性、防松能力及螺栓的疲劳强度,并且能增强螺纹连接体的紧密性和刚度。
在螺纹紧固件的连接使用中,没有预紧力或预紧力不够时,起不到真正的连接作用,一般称之为欠拧;但过高的预紧力或者不可避免的超拧也会导致螺纹连接的失败。
众所周知,螺纹连接的可靠性是由预紧力来设计和判断的,但是,除在实验室可以测量外,在装配现场一般是不易直观的测量。
螺纹紧固件的预紧力则多是采用力矩或转角的手段来达到的。
因此,当设计确定了预紧力之后,安装时采用何种控制方法?如何规定拧紧力矩的指标?则成为关键重要问题,这就提出来了螺纹紧固件(如塑料螺丝)扭(矩)-拉(力)关系的研究课题。
螺纹紧固件扭-拉关系,不仅涉及到扭矩系数、摩擦系数(含螺纹摩擦系数和支撑面摩擦系数)、屈服紧固轴力、屈服紧固扭矩和极限紧固轴力等以一系列螺纹连接副的紧固特性的测试及计算方法,还涉及到螺纹紧固件的应力截面积和承载面积的计算方法等基础的术语、符号的规定。
并且也还必须给出螺纹紧固件紧固的基本规则、主要关系式以及典型的拧紧方法。
目前,这些内容ISO/TC2尚无相应的标准,德国工程师协会早在七十年代就发表了DVI2230《高强度螺栓连接的系统计算》技术准则。
日本也于1987和1990年发布了三项国家标准,尚未查到其他国家的标准。
国内尚未发现相应的行业标准,仅少数企业制定了企业标准。
尤其是随着引进技术的国产化不断的拓展和螺纹紧固件技术发展的需要,这一需求日趋迫切。
这也就是制定此项标准的初衷。
日本国家标准JIS B1082-1987《螺纹紧固件应力截面积和承载面积》、JIS B 1083-1990《螺纹紧固件紧固通则》及JIS B1084-1990《螺纹紧固件拧紧试验方法》三个标准,概括了国际上有关螺纹紧固件扭-拉关系的研究成果和应用经验,根据标准验证,对我国也是适用的。
螺栓破坏扭矩试验

螺栓破坏扭矩试验螺栓破坏扭矩试验是一种常用的力学试验方法,用于评估螺栓的强度和耐久性。
本文将介绍螺栓破坏扭矩试验的原理、步骤和意义。
螺栓是一种常见的紧固件,广泛应用于各行各业。
为了确保螺栓能够承受正常工作条件下的载荷,必须对其进行严格的测试。
螺栓破坏扭矩试验是其中一种重要的试验方法,通过施加扭矩来模拟螺栓在使用过程中受到的力。
螺栓破坏扭矩试验的原理是基于材料力学的基本原理。
在受到扭矩作用下,螺栓会发生变形和应变,当扭矩达到一定数值时,螺栓将失去其原有的强度,出现破坏。
通过测定破坏前的扭矩数值,可以评估螺栓的强度和耐久性。
螺栓破坏扭矩试验的步骤如下:1. 准备试样:选择符合标准规范的螺栓作为试样,并对其进行清洁和处理,确保试样表面无杂质和缺陷。
2. 安装试样:将试样安装在扭矩测试设备上,确保试样与设备之间的连接牢固。
3. 施加扭矩:逐渐增加扭矩,直到试样发生破坏。
在施加扭矩的过程中,需要记录下扭矩-角度曲线,以便后续分析。
4. 分析结果:根据记录的扭矩-角度曲线,确定螺栓的破坏扭矩。
破坏扭矩是指试样发生破坏时所施加的最大扭矩。
螺栓破坏扭矩试验的意义在于评估螺栓的强度和耐久性。
通过该试验可以确定螺栓在工作条件下所能承受的最大扭矩,从而确保螺栓在实际使用中不会发生破坏。
此外,该试验还可以用于比较不同材料和不同规格的螺栓的性能差异,为螺栓的设计和选型提供参考依据。
螺栓破坏扭矩试验是一种重要的力学试验方法,用于评估螺栓的强度和耐久性。
通过施加扭矩来模拟螺栓在使用过程中受到的力,可以确定螺栓的破坏扭矩,并为螺栓的设计和选型提供参考依据。
这一试验对于确保螺栓的可靠性和安全性具有重要意义。
汽轮机检修中螺栓损坏原因分析及对策

汽轮机检修中螺栓损坏原因分析及对策摘要:汽轮机组中存在着大量的螺栓,如果在维修中没有得到正确的处理,不仅会导致螺栓的损坏,而且还会导致维修周期的加长,从而增加维修费用,还会对设备造成不同程度的损伤,影响到蒸汽机组的安全和效率。
鉴于此,本文从汽轮机中螺栓检修的基本流程出发,对螺栓损伤的成因进行了分析,并提出了有针对性的对策,从而保证了机组的安全稳定运行。
关键词:汽轮机;检修;螺栓损坏;原因及对策一般来说,我们所说的螺栓指的是高压、高温螺栓,它不仅包括主汽门、连通管、调节气门、高压导气管和汽缸法兰螺栓,还包括各个轴承紧固螺栓。
因为在正常的情况下,汽轮机需要承受很大的压力,而且在机组的工作中,螺栓的工作状态是不断的做功,所以,在这样的工作条件下,螺栓会因为承受了很大的应力而产生疲劳,从而造成设备的破坏。
根据某电厂的一次检修,对造成螺栓损坏的因素作了详细的剖析,并根据工作实践,提出了相应的解决措施,从而提高了机组的安全性和稳定性。
1 汽轮机中螺栓检修基本流程分析为了提高汽轮机螺栓维修工作的效率和质量,需要对螺栓的维修基本过程进行合理的设定,并结合科学的维修工艺,对存在的问题进行及时妥善的处理。
汽轮机螺栓检修的基本程序是这样的。
首先,正确而有效的拆除螺栓。
在高效地拆除涡轮螺栓时,需要将金属表面的温度降到80℃以下,才能保证以后工作的正常进行。
拆除完毕后,应将螺栓保存好,并对其进行编号,这样才能保证检修的顺利进行。
其次是对螺栓的检查和维护。
检修前要做好准备工作,即一一拆开清理螺扣、螺帽等,去除氧化皮,保证零件的清洁。
如果螺母安装顺利,松开螺母,那就说明螺母没有问题,如果有问题,那就需要检查。
同时,要正确地选用维护方式,保证螺栓的良好状态和螺栓的表面光洁。
最终,在检修结束后,及时返回安装。
做完螺栓检修工作后,要立即回装。
在回位时,需要在合理的次序支撑下,对螺栓进行冷紧,热紧作业。
在实际工作中,需要对力矩进行有效的控制,并严格执行密封处理,从而保证螺栓的安全使用,避免出现漏气的情况。
级粗牙螺栓最小破坏扭矩探讨

4.8级粗牙螺栓最小破坏扭矩探讨1. 引言:国标和机械设计手册只规定了8.8级及以上螺栓的抗最小破坏扭矩,而实际上目前使用最广泛的确实4.8级的螺栓,经常会碰到螺栓在紧固过程中别扭断的情况,却无法判断是螺栓质量的原因还是操作不当的原因,此文希望抛砖引玉,探讨解决常用4.8级螺栓的最小破坏扭矩问题。
2. 分析:方法一:计算法根据GB 3098.13,最小破坏扭矩的计算公式如下所示:d1min的数值见如下所示(摘自机械设计手册,此处只列举部分的值,其他的值可以查询化学工业出版社的机械设计手册第五版第二卷表5-1-5):图1τ为抗剪强度,又称剪切强度,材料产生剪断时的极限强度。
抗剪强度是指外力与材料轴线垂直,并对材料呈剪切作用时的强度极限,反映材料抵抗剪切滑动的能力,在数值上等于剪切面上的切向应力值,即剪切面上形成的剪切力与破坏面积之比。
分单剪和双剪两种形式,在双剪的情况下,破坏面积是试件横截面积的两倍。
螺栓等效于轴,在工程上要求圆轴扭转时的最大切应力不得超过材料的许用切应力,〔τ〕即τmax=(T/W P)max≦ 〔τ〕上式成为圆轴扭转强度条件。
抗扭截面系数为:W P=I P/(D/2)= (πD4/32)/(D/2)= πD3/16这个跟前面讲的GB 3098.13中的公式是一致的。
试验证明,许用剪应力与许用拉应力的关系如下:对于塑性材料 [τ]=0.6~0.8[σ] ;对于脆性材料 [τ]=0.8~1.0[σ]4.8级的螺栓材料一般是Q235钢,钢材是塑性材料,其许用拉伸应力[σ]与抗拉强度极限、屈服强度极限的关系如下:对于塑性材料[σ]=σs / n ;对于脆性材料[σ]=σb / n,其中 σs—屈服强度极限,σb—抗拉强度极限,n—安全系数。
钢材螺纹链接的安全系数一般是1.2-1.7,n取1.2,按机械设计手册,查询4.8级螺栓的屈服强度σs为340Mpa,抗拉强度σb为420Mpa,如下表所示,(摘自化学工业出版社的机械设计手册第五版第二卷表5-1-69):因此, [τ]的值如下:[τ]=0.7x[σ]=0.8x(340/1.2)=226.7Mpa=2.267x108PaX= [τ]/ σb=226.7/420=0.54按照上面的公式,为方便计算和验证,我们下面以4.8级的M8的螺栓为例,根据图1右边的表中,查得M8的小径d1为6.647mm,M8螺栓的最小极限扭矩M Bmin的值如下:M Bmin= τBmin x W Pmin =τ x (π/16 x d1min3)=2.267 x108x [ 3.142/16 x(6.647x10-3)]3=13.07N.m 上面的计算看,4.8级的M8螺栓的最小紧固扭矩是13N.m,而实际上,M8的螺栓在做扭矩破坏试验时,其破坏扭矩在22~26N.m之间,所以上述的计算太过于保守,跟实际差距很大,因此方式不合理。
螺栓与螺钉的扭矩试验和破坏扭矩

螺栓与螺钉的扭矩试验和破坏扭矩小规格螺栓或螺钉或者长度很短的螺栓或螺钉,除了仲裁维氏硬度以外,还应该怎么检测它们的物理性能呢?有没有相关的标准要求?本期对破坏扭矩试验进行解读。
一、破坏扭矩试验的执行标准破环扭矩实验的国家标准G B/T3098.13,等同采用国际标准I S O898-7。
标准中规定了公称直径为1-10m m、性能等级8.8级-12.9级的螺栓与螺钉的扭矩实验方法和最小破坏扭矩值。
破坏扭矩试验适用于螺纹规格小于M3,在GB/T 3098.1中未规定最小拉力载荷与保证载荷的螺栓与螺钉;以及公称直径3—10mm,由于长度过短而不能实施拉力试验的螺栓与螺钉。
破坏扭矩试验不适用于内六角紧定螺钉。
二、破坏扭矩试验的要求及流程试验原理-将试验的螺栓或螺钉夹紧在实验装置中,测定其破坏扭矩。
试验条件-试验时,螺栓或螺钉应只承受扭力。
在达到最小破坏扭矩之前,试件不得断裂。
试验时,螺栓或螺钉头部和螺纹部分不应有摩擦而影响试验结果。
上图为破坏扭矩实验示例,所使用的扭力计(扭力扳手)示值不应超过对试件规定的最小破环扭矩的5倍,扭力计(扭力扳手)的最大误差为试件最小的破坏扭矩±7%。
三、最小破坏扭矩值的要求下表给出了M1-M10,8.8级-12.9级符合破坏扭矩试验要求的螺栓与螺钉的最小破坏扭矩值。
四、关于破坏扭矩试验的注释在螺栓和螺钉规格较小的情况下,因受螺纹精度和试验装置精度的影响,准确的判定断裂载荷和保证载荷是很难实现的;规格大于M3到M10的螺栓和螺钉,经常由于长度过短而无法实施拉力或保证载荷试验。
因此,对M1-M10(包括M8×1、M10x1、M10x1.25细牙螺纹)的螺栓和螺钉规定最小破坏扭矩,为评定其使用性能提供了依据。
目前,仅对8.8级-12.9级规定了最小破坏扭矩。
由于低性能等级的螺栓和螺钉的破坏扭矩试验结果十分分散,无法形成有效统计,因此低性能等级的螺栓与螺钉的破坏扭矩试验还需要更多的研究。
螺栓最小破坏扭矩国家标准

螺栓最小破坏扭矩国家标准螺栓作为一种常见的紧固件,在工业生产中扮演着重要的角色。
螺栓在连接件和机械装置中起到了至关重要的作用,而螺栓的质量和性能直接关系到设备的安全性和稳定性。
为了确保螺栓的使用安全和可靠性,国家颁布了《螺栓最小破坏扭矩国家标准》,规定了螺栓的最小破坏扭矩标准,以下是相关内容介绍:1. 标准概述螺栓最小破坏扭矩是指在螺栓材料内部发生塑性变形之前,其松动所需扭矩的最小允许值。
该数值反映了螺栓与螺母之间的紧固力矩大小,是保证紧固件在使用中不产生松动的重要参数。
《螺栓最小破坏扭矩国家标准》规范了各类螺栓的最小破坏扭矩数值,并确保生产和使用过程中的一致性和规范性。
2. 标准内容该国家标准根据螺栓的用途和材料等不同因素,将螺栓分为多个等级,每个等级都有相应的最小破坏扭矩标准。
标准规定了螺栓的等级划分、最小破坏扭矩测试方法、试验条件、记录要求等内容,确保螺栓生产厂家和使用单位在质量控制和实际使用中具有可操作性和指导性。
3. 标准实施《螺栓最小破坏扭矩国家标准》是国家对螺栓生产和使用过程中的质量监督和管理的依据之一。
生产企业在生产过程中必须按照国家标准的要求进行产品质量控制和检测,确保所生产的螺栓符合标准要求。
而使用单位在使用螺栓时,也应按照国家标准规定的最小破坏扭矩数值进行紧固操作,以确保设备在使用过程中的安全和稳定性。
4. 标准的重要性螺栓最小破坏扭矩国家标准的制定和实施,对于提高螺栓产品的质量和可靠性具有重要意义。
通过规范螺栓的生产、检测和使用过程,可以有效避免因螺栓失效导致的事故和损失,保障设备和人员的安全。
遵守国家标准不仅是企业的法定责任,也是保障生产和使用安全的基本保障措施。
结语《螺栓最小破坏扭矩国家标准》的实施对螺栓质量和使用安全产生了积极的推动作用。
生产企业和使用单位应加强对标准内容的理解和执行,不断提升螺栓产品的质量和可靠性水平,共同维护生产安全和人员健康。
愿《螺栓最小破坏扭矩国家标准》能够在螺栓产业中发挥更大的作用,为我国工业生产的蓬勃发展提供良好保障。
3螺栓最小破坏扭矩的计算与分析
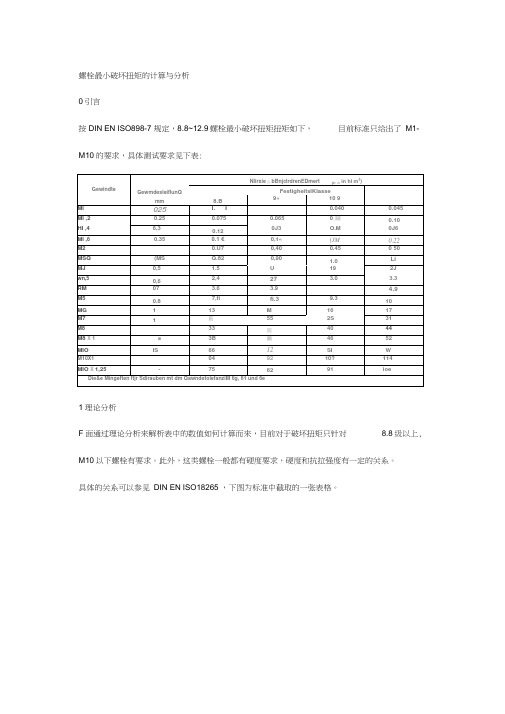
螺栓最小破坏扭矩的计算与分析0引言按DIN EN ISO898-7 规定,8.8~12.9螺栓最小破坏扭矩扭矩如下,目前标准只给出了M1- M10的要求,具体测试要求见下表:1理论分析F面通过理论分析来解析表中的数值如何计算而来,目前对于破坏扭矩只针对8.8级以上, M10以下螺栓有要求。
此外,这类螺栓一般都有硬度要求,硬度和抗拉强度有一定的关系。
具体的关系可以参见DIN EN ISO18265 ,下图为标准中截取的一张表格。
下面来分析最小破坏扭矩如何计算获得,计算公式如下(来自材料力学,材料力学有详细推导关系);MBmin= T Bmin WPmin其中,WPmin=冗/16 d3lmin (抗扭截面系数,具体推导可参见材料力学)iBmi n=X • bminMBmi n —最小破坏扭矩T B—扭转强度ob —抗拉强度X —强度比T / O bdlmi n=d-1.0825P其中,dlmin为断裂最小直径P为螺纹螺距强度比X由上表,随着材料强度越高,材料的扭转强度与抗拉强度的比越来越低,以10.9级M10螺栓螺距P=1为例:obmi n=1000MPaiBmi n= X • bmi n=0.79 1000MPa=790MPa螺距P=1,则其小径为dlmin=d-1.0825P=10-1.0825=8.9175mm故MBmin= T3min WPmin=790MPa • /16 (180.34mm)3=109.942NmWPmin= TI/16 d3lmin= 冗/16 (8.9175mm)3而标准中的M10x1,10.9 级的最小破坏扭矩为102Nm,和计算数值相差7Nm,这里小编猜测制定标准的人可能考虑到材料性能的分散和测试数据的分散性,并根据经验制定的测试数值,各位读者也可以在留言区留言来讨论计算数值和标准数值的差异原因。
按照这个逻辑计算,我们可以计算出更大的螺栓对应的破坏扭矩,计算数值可以作为测试数值的参考。
螺栓拧紧力矩国家标准

螺栓的拧紧力矩标准本篇文章将列出各类螺丝的拧紧力矩标准,当用户未注明拧紧力矩要求时,我们所参考的参考的标准。
需要强调的是:拧紧力矩和破坏扭力是两个概念,拧紧力(矩)是指螺丝拧入工件的建议值;破坏扭力(即破坏扭矩)指将螺丝拧断的最小值(详见紧固件的破坏扭矩标准GB3098.13),很显然,拧紧力矩是少于破坏扭矩的。
这是普通螺栓拧紧力矩:公制螺栓扭紧力矩Q/STB 12.521.5-2000范围:本标准适用于机械性能10.9级,规格从M6-M39的螺栓的扭紧力矩,对于使用尼龙垫圈、密封垫圈、其它非金属垫圈的螺栓,本标准不适用。
注:对于设计图纸有明确力矩要求的,应按图纸要求执行。
谈螺栓预紧力的选用和螺栓强度校核螺栓作为连接件,使用十分广泛, 其在机车车辆、航太航空、风电机组上的使用环境大多是高强度高应力, 而在乘用车主要部件的使用环境大多是低应力卨周期,但仍然存在著极大的隐患。
从安全角度来说,螺栓所联接的部件都是很昂贵的。
所以,螺栓失效时,损坏的不仅仅是它们本身,而是整个产品。
螺栓连接作为汽车装配上的重要应用,据有关资料介绍,根据发动机上的螺纹紧固件通常在1500?2000 颗左右,品种更是高达100个以上,规格也是从M6?M30不等,而其中大约100颗是与车辆的安全性能有密切联系的。
而做为在装配过程中最重要的螺栓规格及预紧力的选用,存在理论上的不足和认识的误区。
不论螺纹紧件作为连接或密封作用,还是需要装配的子零件,都有一定的屈服极限。
在装配过程中,如果预紧力过大,使零件的变形量超过零件的屈服强度,零件就会损环。
故装配件要长时间稳定有效工作,设计人员必须对螺栓预紧力进行规范设计。
1.螺栓预紧力的选用螺栓作为重要的连接件,在总成件安装时必须拧紧,在连接承受工作载荷之前,预先受到力的作用,这个预加的力就是预紧力;预紧的目得到是为了增强连接的可靠性和紧密性,防止总成安装件在工作时候,受到力的作用,各连接件之间出现缝隙或相对滑移,所以在总成件的设计中,必须对预紧力的大小进行规范设计。
螺栓的机械性能解读

螺栓的机械性能解读“ 碳钢以及合金钢制造的螺栓,其性能等级可分为3.6、4.8、5.6、5.8、6.8、8.8、10.9、12.9级等多个级别。
由不锈钢制造的螺栓,其性能等级根据其材质钢类和组别有50、70、80等多个级别。
在不同的工况环境中选择合适的性能等级螺栓也是至关重要的,此刻小万将与您一起解读关于螺栓性能等级的基础知识。
”一、性能等级标记制度螺栓的性能等级是如何标记的?不同材质其标记是否存在区别?由碳钢、合金钢制造的螺栓其性能标记是由点隔开的两部分数字组成➢点左边的数字表示公称抗拉强度的1/100,公称抗拉强度用Rm表示。
➢点右边的数字表示公称屈服强度(下屈服强度ReL)或规定非比例延伸为0.2%的公称应力(RP0.2,公称)或规定非比例延伸0.004 8d的公称应力(RPf,公称)与公差抗拉强度(Rm,公称)比值的10倍。
以下一张图让您明白,碳钢螺栓螺钉各性能等级的由来。
若材料性能与8.8级相同,但实际承载能力有低于8.8级的紧固件,其性能等级应标记“08.8”由不锈钢材质制造的螺栓性能标记是由钢的组别和性能等级两部分组成➢第一部分:不锈钢的组别,由字母和数字组成。
字母:A-奥氏体钢C-马氏体钢F-铁素体钢数字:表示该类钢的化学成分范围。
➢第二部分:不锈钢的性能等级标记,由2-3个数字组成。
该数字表示紧固件抗拉强度的1/10。
举例:A2-70“A2”表示奥氏体不锈钢的A2组别。
“70”表示产品的性能等级,其最小抗拉强度为700MPa.关于不锈钢(奥氏体、马氏体、铁素体)螺栓机械性能可参考下表:注:含碳量低于0.03%的低碳奥氏体不锈钢可增加标记“L” ,如:A4-80L。
进行表面钝化处理,可增加标记:“P” ,如:A4-80P。
关于不锈钢螺栓更多机械性能数据请查阅相关标准且以标准为准。
二、材质与化学成分不同性能等级的螺栓其钢的化学成分、热处理工艺、回火温度在标准中做了相应的规定。
相关标准对于各个性能等级材料的化学成分做了极限规定,具体可参考以下列表。
抗震支吊架用螺栓扭矩

抗震支吊架用螺栓扭矩
摘要:
一、抗震支吊架的作用
二、抗震支吊架用螺栓扭矩的重要性
三、螺栓扭矩的计算方法
四、如何正确地施加螺栓扭矩
五、结论
正文:
抗震支吊架是一种用于支撑和固定建筑物的结构组件,其主要作用是在地震发生时,缓解建筑物的震动,降低破坏程度。
抗震支吊架的稳定性与螺栓扭矩的施加密切相关,因此,掌握抗震支吊架用螺栓扭矩的计算和施加方法至关重要。
首先,我们需要了解抗震支吊架用螺栓扭矩的重要性。
螺栓扭矩是保证抗震支吊架安全性能的关键因素,适当的螺栓扭矩可以确保支吊架与建筑物结构之间的紧密连接,防止在地震发生时支吊架出现松动、脱落等现象。
其次,我们需要掌握螺栓扭矩的计算方法。
根据国家相关标准和建筑物的实际情况,可以采用以下公式计算螺栓扭矩:
扭矩= 摩擦系数× 螺栓预紧力
其中,摩擦系数是螺栓与螺母之间的摩擦系数,螺栓预紧力可以根据建筑物的荷载情况计算得出。
在计算出螺栓扭矩后,我们需要正确地施加螺栓扭矩。
具体操作步骤如
下:
1.使用扭矩扳手,将螺栓拧紧至计算出的扭矩值。
2.保持一段时间,以确保螺栓与螺母之间的摩擦力达到稳定。
3.再次使用扭矩扳手,对螺栓进行复查,确保扭矩值符合设计要求。
总之,抗震支吊架用螺栓扭矩在地震防治中具有重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
螺栓最小破坏扭矩的计算与分析
0引言
按DIN EN ISO898-7规定,8.8~12.9螺栓最小破坏扭矩扭矩如下,目前标准只给出了M1-M10的要求,具体测试要求见下表:
1 理论分析
下面通过理论分析来解析表中的数值如何计算而来,目前对于破坏扭矩只针对8.8级以上,M10以下螺栓有要求。
此外,这类螺栓一般都有硬度要求,硬度和抗拉强度有一定的关系。
具体的关系可以参见DIN EN ISO18265,下图为标准中截取的一张表格。
下面来分析最小破坏扭矩如何计算获得,计算公式如下(来自材料力学,材料力学有详细推导关系);
MBmin=τBmin·WPmin
其中,WPmin=π/16·d3lmin(抗扭截面系数,具体推导可参见材料力学)
τBmin=X·σbmin
MBmin—最小破坏扭矩
τB—扭转强度
σb—抗拉强度
X—强度比τ/σb
dlmin=d-1.0825P
其中,dlmin为断裂最小直径
P为螺纹螺距
强度比X
由上表,随着材料强度越高,材料的扭转强度与抗拉强度的比越来越低,
以10.9级M10 螺栓螺距P=1为例:
σbmin=1000MPa
τBmin= X·σbmin=0.79·1000MPa=790MPa
螺距P=1,则其小径为dlmin=d-1.0825P=10-1.0825=8.9175mm
WPmin=π/16·d3lmin=π/16·(8.9175mm)3
故MBmin=τBmin·WPmin=790MPa·π/16·(180.34mm)3=109.942Nm
而标准中的M10x1,10.9级的最小破坏扭矩为102Nm,和计算数值相差7Nm,这里小编猜测制定标准的人可能考虑到材料性能的分散和测试数据的分散性,并根据经验制定的测试数值,各位读者也可以在留言区留言来讨论计算数值和标准数值的差异原因。
按照这个逻辑计算,我们可以计算出更大的螺栓对应的破坏扭矩,计算数值可以作为测试数值的参考。
以10.9级M30螺栓为例,其中P=3.5
σbmin=1000MPa
τBmin= X·σbmin=0.75·1000MPa=750MPa
螺距P=3.5,则其小径为dlmin=d-1.0825P=30-1.0825·3.5=26.21125mm
WPmin=π/16·d3lmin=π/16·(26.21125mm)3
故MBmin=τBmin·WPmin=750MPa·π/16·(26.21125mm)3=2650Nm
2破坏扭矩的测试台架和注意事项
测试台架
图1 破坏扭矩测试台架
注意事项:
(1)、如无特殊要求,台虎钳夹持长度应大于1d 的有效长度以上;
(2)、如需工装辅助,工装与样件有效配合长度也应为1d 以上,且头部不得受力;
(3)、拧断后测量最大扭矩,应符合标准要求;
(4)、查看断裂处,样件不得断裂在头部R 角及装夹位置,如是断裂在R 角处即为问题零
件,断裂在装夹处则是装夹力度过大,螺纹可能已被破坏。
3测试曲线
某M6x45,8.8级螺栓的破坏扭矩测试曲线,标准要求≥13Nm,测试数值为14Nm,满足标准要求,从测试曲线来看,螺栓12 Nm就已经开始屈服,随后转动约150°断裂,螺栓在纯拧的状态,断裂角度一般都较小,如图2所示;而螺栓在实际使用过程中,是拉拧组合,主要以拉伸为主,该螺栓实际装配的屈服扭矩为13Nm,而实际装配的拧断扭矩为16 Nm,螺栓的从屈服到拧断的角度约800°,远高于拧断的角度,如图3所示。
图2 纯拧状态的螺栓(破坏扭矩)
图3 拉拧状态的螺栓(模拟装配曲线)
4 结论
1 螺栓的最小破坏扭矩可采用MBmin=τBmin·WPmin进行计算,计算的数值可作为参考。
2 硬度和抗拉强度关系参见DIN EN ISO18265。
3 破坏扭矩测试的螺栓为纯拧状态,受剪切力,正常装配的零件为拉拧组合,屈服至断裂角度一般远高于纯拧状态的零件,具体差异和螺栓长度有一定关系,装配的断裂扭矩也高于纯扭转的断裂扭矩。
