共轭梯度法

合集下载

共轭梯度法公式

共轭梯度法公式
共轭梯度法是一种用于求解线性方程组的迭代算法。

其主要思想是通过利用前一次迭代的信息来加速当前迭代的速度，从而减少迭代次数和计算量。

共轭梯度法公式包括以下几个步骤：
1. 初始化：设初始解为x0，残量b0为Ax0-b，共轭方向d0=b0。

2. 迭代求解：对于第k次迭代，计算步长αk，使得xk+1=xk+αkd，其中d是共轭方向，满足dTkAd=0，即d是A的共轭向量。

3. 更新残量：计算新的残量bk+1=Axk+1-b，如果bk+1小于预设精度，则停止迭代。

4. 更新共轭方向：计算新的共轭方向dk+1=bk+1+βkdk，其中βk=(bk+1)Tbk+1/(bk)Tbk，保证dk+1与之前的共轭方向都是A的共轭向量。

5. 重复迭代，直到满足收敛条件，返回最终解xk+1。

共轭梯度法是一种高效的求解大型线性方程组的方法，尤其适用于稀疏矩阵和对称正定矩阵。

公式简单易懂，容易实现，且具有较快的收敛速度。

- 1 -。

共轭梯度法

Hesteness和Stiefel于1952年为解线性方程组而提出
•基本思想:把共轭性与最速下降法相结合,利用已知点处的梯度构造一组共轭方向,并沿着这组方向进行搜索,求出目标函数的极小点
4.4共轭梯度法
先讨论对于二次凸函数的共轭梯度法,考虑问题
min f (x) 1 xT Ax bT x c
3, giT d (i) giT gi (蕴涵d (i) 0)
证明: 显然m1,下用归纳法(对i)证之.
当i 1时,由于d (1) g1,从而3)成立,对i 2时, 关系1)和2)成立,从而3)也成立.
4.4共轭梯度法
设对某个i<m,这些关系均成立,我们证明对于i+1
也成立.先证2),
因此
2 / 3 1 5/ 9
d (2)

1/ 1
3

1 9

2 0

5/9 1

从x(2)出发,沿方向d (2)进行搜索,求步长2,使满足 :
f
( x (1)

2d (1) )

min
0
f
(x(2)

d (2))

2 0

4.4共轭梯度法
显然, d (1)不是目标函数在x(1)处的最速下降方向.
下面,我们用FR法构造两个搜索方向.
从x(1)出发,沿方向d (1)进行搜索,求步长1,使满足 :
f
( x (1)
1d (1) )

min
0
f
( x (1)

d (1) )
得1 2 3
A正定,故x是f(x)的极小值点.

共轭梯度法

最速下降法1.最速下降方向函数f(x)在点x处沿方向d的变化率可用方向导数来表示。

对于可微函数，方向导数等于梯度与方向的内积，即：Df(x;d) = ▽f(x)T d,因此，求函数f(x)在点x处的下降最快的方向，可归结为求解下列非线性规划：min ▽f(x)T ds.t. ||d|| ≤ 1当 d = -▽f(x) / ||▽f(x)||时等号成立。

因此，在点x处沿上式所定义的方向变化率最小，即负梯度方向为最速下降方向。

2.最速下降算法最速下降法的迭代公式是x(k+1) = x(k) + λk d(k) ,其中d(k)是从x(k)出发的搜索方向，这里取在x(k)处的最速下降方向，即d = -▽f(x(k)).λk是从x(k)出发沿方向d(k)进行一维搜索的步长，即λk满足f(x(k) + λk d(k)) = min f(x(k)+λd(k)) (λ≥0).计算步骤如下：(1)给定初点x(1) ∈ R n，允许误差ε> 0，置k = 1。

(2)计算搜索方向d = -▽f(x(k))。

(3)若||d(k)|| ≤ε，则停止计算；否则，从x(k)出发，沿d(k)进行一维搜索，求λk，使f(x(k) + λk d(k)) = min f(x(k)+λd(k)) (λ≥0).(4)令x(k+1) = x(k) + λk d(k)，置k = k + 1，转步骤(2)。

共轭梯度法1.共轭方向无约束问题最优化方法的核心问题是选择搜索方向。

以正定二次函数为例，来观察两个方向关于矩阵Ａ共轭的几何意义。

设有二次函数：f(x) = 1/2 (x - x*)T A(x - x*) ,其中A是n×n对称正定矩阵，x*是一个定点，函数f(x)的等值面1/2 (x - x*)T A(x - x*) = c是以x*为中心的椭球面，由于▽f(x*) = A(x - x*) = 0，A正定，因此x*是f(x)的极小点。

共轭梯度法

线性无关，由线性代数知识知
必有
p
T j
∇f
(X
n
)
=0(源自j=0,1,L,
n
− 1)
因为A正定，所以f (X ) 是凸函数，故 X n 是惟一的全局极小点。
从而
∇f (Xk ) = AXk + b
=
AX
j+1
+
λ* j+1
Apj+1
+L+
λ* k −2
Apk−2
+
λ* k −1
Apk
−1
+
b
=
∇f
(X
⎡6 ⎢⎣17
12⎤ 17⎥⎦
⎢⎣⎡−
90 289
−
210⎤ 289⎥⎦
T
−
210⎤⎡ 3 289⎥⎦⎢⎣−1
−11⎥⎦⎤⎢⎣⎡−
90 289
−
210⎤T 289⎥⎦
= 17 10
X2
=
X1
+
λ1 p1
=
⎡ 26 ⎢⎣17
38 ⎤ T 17 ⎥⎦
+ 17 10
⎢⎣⎡−
90 289
−
210 ⎤ T 289 ⎥⎦
= [1
1]T
∇f ( X 2 ) = [0 0]T
练习：试用共轭梯度法二次函数
min
f
(x)
=
x12
+
1 2
x22
+
1 2
x32
的极小点。取初始点为x( 0 ) = (1,1,1)T
3 、非二次函数的共轭梯度法
一般地，我们有：
⎧ X k+1 = X k + λk pk

共轭梯度法和梯度下降法

共轭梯度法和梯度下降法共轭梯度法和梯度下降法是两种常用的优化算法，它们在解决最小化目标函数的问题上具有重要作用。

本文将介绍这两种算法的原理、应用场景以及优缺点。

一、共轭梯度法共轭梯度法是一种迭代优化算法，用于求解线性方程组或非线性优化问题。

它的核心思想是通过迭代的方式寻找下降最快的搜索方向，并在每一次迭代中保证搜索方向互相正交，从而有效地加速优化过程。

共轭梯度法的优势在于对于大规模线性方程组或非线性优化问题，可以在有限的迭代次数内找到精确解。

这是由于它能够利用问题的特殊结构，充分利用历史信息，避免了重复计算。

因此，共轭梯度法在图像处理、机器学习、信号处理等领域得到广泛应用。

二、梯度下降法梯度下降法是一种基于负梯度方向进行搜索的优化算法。

它的核心思想是通过迭代的方式沿着目标函数梯度的反方向更新参数，从而逐步逼近最优解。

梯度下降法的优势在于简单易懂、易于实现，并且在许多优化问题中都能取得不错的效果。

它的应用范围非常广泛，包括线性回归、逻辑回归、神经网络等机器学习算法中的参数优化，以及函数逼近、图像处理等领域。

三、共轭梯度法与梯度下降法的区别和联系共轭梯度法和梯度下降法都是迭代优化算法，但它们之间存在一些重要的区别和联系。

1. 方向选择：共轭梯度法在每一次迭代中选择的搜索方向是互相正交的，这使得每一步的搜索方向都是全局最优的。

而梯度下降法只利用了当前位置的梯度信息，选择的搜索方向是当前位置的负梯度方向。

2. 收敛速度：共轭梯度法通常比梯度下降法收敛速度更快。

这是因为共轭梯度法充分利用了历史信息，避免了重复计算，从而加速了优化过程。

而梯度下降法通常需要更多的迭代次数才能达到相同的精度。

3. 适用场景：共轭梯度法适用于解决大规模线性方程组或非线性优化问题，特别是对于稀疏矩阵或具有特殊结构的问题效果更好。

而梯度下降法适用于一般的优化问题，特别是凸优化问题。

4. 存储需求：共轭梯度法只需要保存少量历史信息，因此在内存有限的情况下能够处理较大规模的问题。

共轭梯度法总结

共轭梯度法总结
共轭梯度法总结
一、什么是共轭梯度法
共轭梯度法（Conjugate Gradient Method），是一种用于求解线性方程组的迭代优化算法，它是一种搜索梯度的迭代算法。

共轭梯度法的基本思想是沿梯度的反方向搜索，并在每一步令搜索的方向接近更新的局部梯度。

它是一种非常有效的求解有约束的非线性优化问题的方法，是求解线性方程组的有效算法。

共轭梯度法可以看作是一种极小化函数的迭代方法，它最主要的思想是不断更新梯度的方向，从而寻找函数值最小的点。

二、共轭梯度法的原理
共轭梯度法是一种迭代优化算法，它以凸二次型函数为例，可以用来求解最小值问题。

它的基本思想是：
（1）首先求得函数的梯度，即每一步优化的搜索方向，使梯度变为最小；
（2）以梯度的反方向搜索，令搜索的方向接近更新的局部梯度，而不是与旧的梯度成正比的步长；
（3）逐步更新搜索的方向为新的梯度；
（4）重复这个过程，直到所有的自变量满足限制条件。

三、共轭梯度法的优缺点
共轭梯度法最大的优点是它具有收敛速度快，可以在有限的迭代步数内收敛到最优解；另外，它还具有计算量小，不需要计算精确的
Hessian矩阵的优点。

共轭梯度法的缺点是它不能用来求解非凸优化问题，因为它只能求解凸优化问题；另外，它也不能用于强不可约的优化问题。

共轭梯度法beamforming_理论说明

共轭梯度法beamforming 理论说明1. 引言1.1 概述共轭梯度法（Conjugate Gradient Method）是一种常用的优化算法，广泛应用于解决线性方程组和最优化问题。

Beamforming是一种利用信号处理技术来实现指向性传输和接收的方法，在通信、雷达等领域有着广泛的应用。

本篇长文将探讨共轭梯度法在Beamforming中的理论应用。

1.2 文章结构本文将按照以下结构进行论述：首先介绍共轭梯度法的原理和基本思想，包括线性方程求解的问题、共轭梯度法的基本思想以及迭代过程与收敛性分析；然后，将详细阐述Beamforming的基本概念，包括信号传输和接收的需求、Beamforming技术在通信中的应用以及技术实现原理和方法；接着，我们将探究共轭梯度法在Beamforming中的具体应用，涵盖了优化问题表述、目标函数定义及优化过程说明以及基于共轭梯度法的Beamforming实例分析与结果讨论；最后总结主要研究发现并展望取得成果和应用前景，并提出后续研究工作的建议。

1.3 目的本文的目标是通过理论说明共轭梯度法在Beamforming中的应用，以深入探讨这一优化算法在指向性传输和接收技术中的实际效果。

通过对共轭梯度法及其在Beamforming中的应用进行分析，旨在提供有关该算法与通信技术结合方面的研究参考，为相关领域的学者和工程师提供新思路和解决问题的方法。

2. 共轭梯度法的原理2.1 线性方程求解的问题在讨论共轭梯度法的原理之前，我们首先来了解一下线性方程求解的问题。

线性方程组是由多个线性等式组成的方程组，如Ax = b，其中A为已知矩阵，x为待求解向量，b为已知向量。

线性方程求解即为找到满足该方程组的解x。

2.2 共轭梯度法的基本思想共轭梯度法是一种用于求解对称正定线性方程组Ax = b的迭代方法。

它基于以下基本思想：通过选择合适的搜索方向，将目标函数在各个搜索方向上取得最小值，并以此逼近实际的最优解。

共轭梯度法

共轭梯度法对物质的一种分析方法，共轭梯度分析法是近几十年发展起来的无损检测技术。

共轭梯度技术是将多种物理效应相结合，并且具有较高的检出率、分辨率和灵敏度，这是一种具有很大发展潜力的分析技术。

共轭梯度法主要包括：共轭电子效应、共轭磁效应、共轭梯度效应。

共轭梯度分析技术是一种高效的新型无损检测技术。

其主要优点在于：①不需要使用电子源；②同时利用共轭电子效应和共轭磁效应，可以消除多种原子的外层电子对核磁矩的屏蔽作用，同时，也降低了铁磁性物质的饱和磁化强度的影响；③能够实现对缺陷浓度较低的金属或非金属材料的快速检测。

共轭梯度技术是20世纪70年代发展起来的无损检测技术，它是利用一些特殊的元素（如铝、铅、铋等）与一些有色金属的原子形成离子，或在两者之间形成过渡族的元素（如汞、铊、铟等），从而达到产生强共轭的效果，再利用超声场或磁场改变他们的相互作用，而不改变他们的化学性质。

共轭梯度的基本原理：①共轭电子效应。

就是利用一些电负性比较强的元素作为原子核，因此他们最外层的电子被核外其他电子吸引，由于距离原子核较远，受到核外电子的排斥，所以核外电子浓度较小。

其电子从价带跃迁到导带，然后再跃迁回价带，所以他们不显电性。

反之，价带中的电子被导带中的电子所吸引，从而降低了价带的电子密度，增加了导带的电子密度，使得原子的核外电子浓度减少，同样会使原子的磁矩减弱。

因此，与这些元素形成化合物的非金属元素的电子都会向原子核附近集聚，从而影响原子的磁矩。

但是当原子序数越高，因为核外电子对核磁矩的屏蔽作用越弱，元素形成的化合物的稳定性越高，原子序数越高的元素的电子就越容易向原子核靠拢。

②共轭磁矩效应。

与电子的共轭电子效应相反，铁磁性物质的原子的核外电子轨道对外磁矩的影响相对比较大。

当这些原子处于磁化状态时，内层电子只能自旋平行，但是这个平行的自旋磁矩，会使这些原子的自旋磁矩大小相等，互相抵消，因此这些原子呈顺磁性。

但当这些原子处于非磁化状态时，内层电子的自旋磁矩可以取向不同，所以，铁磁性物质又显示出反铁磁性。

共轭梯度方法

共轭梯度方法（Conjugate Gradient Method）是求解线性方程组的一种迭代算法。

该方法适用于求解大型稀疏的对称正定线性方程组，可以显著减少计算量和存储空间。

该方法的主要思想是利用共轭方向（Conjugate Directions）的性质，在有限次迭代中求解方程组的解。

共轭梯度方法的基本步骤如下：
选取一个初值$x_0$，并令$r_0=b-Ax_0$，其中$b$ 为方程组的右端向量，$A$ 为系数矩阵。

计算一个共轭方向$p_0=r_0$，即$p_0$ 与$r_0$ 正交，并满足$Ap_0 \neq 0$。

对于$k=0,1,2,\ldots$，执行以下操作：
a. 计算$\alpha_k=\frac{r_k^Tr_k}{p_k^TAp_k}$。

b. 更新解向量$x_{k+1}=x_k+\alpha_kp_k$。

c. 计算残差向量$r_{k+1}=r_k-\alpha_kAp_k$。

d. 计算$\beta_k=\frac{r_{k+1}^Tr_{k+1}}{r_k^Tr_k}$。

e. 更新共轭方向$p_{k+1}=r_{k+1}+\beta_kp_k$，即$p_{k+1}$ 与$p_k$ 具有共轭性。

如果残差向量$r_k$ 较小，则停止迭代，输出解向量$x_k$。

共轭梯度方法具有收敛速度快、存储空间小等优点，但对于非对称和非正定的线性方程组，该方法可能不收敛。

同时，该方法也有一些变体，如预处理共轭梯度法、共轭残差法等，可以更好地解决不同类型的线性方程组求解问题。

共轭梯度（ConjugateGradient，CG）算法

共轭梯度（ConjugateGradient，CG）算法
以下皆为从⽹络资料获取的感性认知
共轭定义
共轭在数学、物理、化学、地理等学科中都有出现。

本意：两头⽜背上的架⼦称为轭，轭使两头⽜同步⾏⾛。

共轭即为按⼀定的规律相配的⼀对。

通俗点说就是孪⽣。

在数学中有共轭复数、共轭根式、共轭双曲线、共轭矩阵等。

求解⽬标
共轭梯度法是数值分析⾥⾯⼀类⾮常重要的⽅法，是⽤来解决⽆约束凸⼆次规划问题的⼀种⽅法
⽅法的⽬的就是通过迭代求得多元⼆次函数 [公式] 的极值点
基本思想
每个⽅向上只找⼀次，对于 [公式] 维空间就进⾏ [公式] 次计算，也就是说，我每个⽅向上都能⾛到极致，这样我就不会⾛任何的回头路了，效率也就最⾼。

那么是如何实现的呢？如果每个⽅向上都是正交的，我肯定就是在这个⽅向上⾛到极致了，这样⽅向也就确定了，也就是每⼀次都⾛正交⽅向，然后再确定每次的步长就可以了。

抽象图。

共轭梯度法

共轭梯度法共轭梯度法(also known as Pearson-Newman gradient method)是电化学反应动力学中一种很有用的技术，主要应用于分析化学、环境工程、农药学、微生物学等领域。

用共轭梯度法时，以活性高的配体替代催化剂上的固定配体(一般为固定相)，使原来的催化剂仍能发挥作用，但具有选择性更好、灵敏度更高、应用范围更广的特点，同时能降低毒性和提高催化活性，还可改善催化剂的稳定性。

共轭梯度法(reaction-coordinate density technique，缩写为coAPD)，是由美国著名的电化学家S.C.R.（赫维斯特）于1976年提出的，最早是应用于考察水溶液中蛋白质在二级胺诱导下的变性行为。

后来，此方法被用于研究Cu(I)-Zn(II)氧化偶联反应，可用于测定其它一些金属离子。

它能够选择性地催化多种反应，并且操作简便，灵敏度高，催化效率高。

它与同样是基于电极过程机理的原位催化比较，在原理上具有优越性。

对于活性组分分子内部的小的不均匀结构，可以采用共轭梯度法实现更精确的测量。

在这个技术中，如果采用共轭体系，一般可以考虑将其作为一个三电子体系，而与电子得失的量子化运动相联系，即以共振状态作为激发条件。

因此，实验装置也称之为共振极限溶剂。

目前，已经开发了一些共轭体系，其中主要包括共轭二烯体系、共轭异戊二烯体系、共轭二炔体系等。

根据不同的选择性要求，又可将它们划分成几类：双齿配体系列、共轭乙炔体系列、共轭苯炔体系列、共轭乙烯体系列、共轭苯乙炔体系列、双烯类配体系列。

由于选择性较高，该技术广泛用于化学反应机理及反应产物分析。

特别是随着计算机技术的迅速发展，其应用更加广泛。

例如，在定量方面，可以在很短的时间内给出定量结果，可以很快地绘制出实验曲线或计算出数据。

在这个技术中，反应机理以原子轨道理论为基础。

根据反应机理，按照共振条件进行合理的实验设计，通过电化学反应测定反应的产物或催化剂的量，并绘制电位-时间图，即可达到定性、定量的目的。

线性方程组的共轭梯度法

迭代过程
计算方程组的雅可比矩阵A和右端项b，得到线性方程组Ax=b。计算初始残差r0=b-Ax0。进行迭代，对于k=0,1,2,...,max_iter，执行以下步骤
迭代过程
01
1. 计算搜索方向pk=-Ak^T。
02
2. 在搜索方向pk上进行线搜索，找到步长λk，使得 Axk+1=b-λk*r^k最小化。
感谢观看
THANKS
定义
线性方程组是由一组线性方程组成的数学模型，其中包含未知数和已知数。
分类
根据方程的系数矩阵和常数项矩阵，线性方程组可以分为多种类型，如超定方程组、欠定方程组和恰定方程组。
线性方程组的求解方法
直接法
通过消元或迭代等方法将方程组化为标准形式，然后求解。
迭代法
通过不断迭代更新解的近似值，逐步逼近方程的解。
在金融工程中的应用
投资组合优化
共轭梯度法可以用于求解投资组合优化问题，以最大化投资收益或最小化风险。
期权定价
在期权定价模型中，共轭梯度法可以用于求解 Black-Scholes方程，以得到期权的合理价格。
风险管理
在风险管理方面，共轭梯度法可以用于求解风险评估模型中的最优化问题，以评估和管理金融风险。
解效率。
02
常用的预处理方法包括对角占优预处理、不完全LU
分解预处理等。
03
预处理技术可以消除原始方程组中的病态条件，降低
数值误差的放大效应。
自适应步长调整策略
自适应步长调整策略可以根据上一步的搜索结果动态调整步长，提高算法的稳定性和收敛速度。
常见的自适应步长调整策略包括 Armijo线搜索、Goldstein线搜
科学计算

最优化课程练习-共轭梯度法

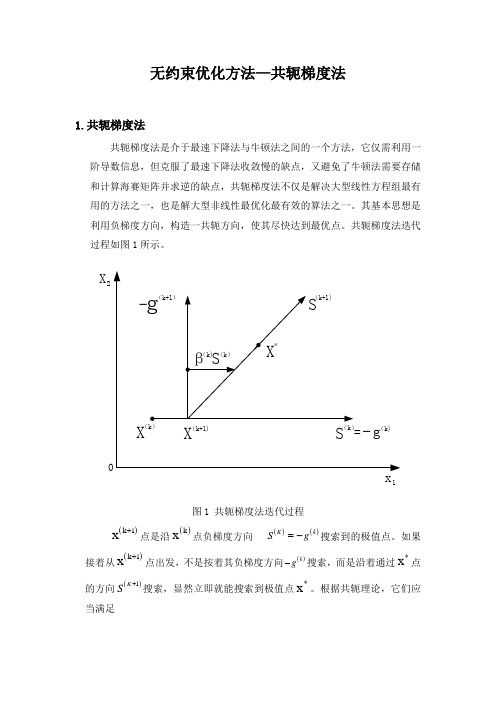
无约束优化方法—共轭梯度法1.共轭梯度法共轭梯度法是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算海赛矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。

其基本思想是利用负梯度方向，构造一共轭方向，使其尽快达到最优点。

共轭梯度法迭代过程如图1所示。

1X 2图1 共轭梯度法迭代过程()k 1x +点是沿()k x 点负梯度方向()()K k Sg =-搜索到的极值点。

如果接着从()k 1x +点出发，不是按着其负梯度方向()kg -搜索，而是沿着通过*x 点的方向()1K S +搜索，显然立即就能搜索到极值点*x 。

根据共轭理论，它们应当满足()()(1)1k Tk SAS+=即()KS 与()1K S +是互为共轭方向，新构造的共轭方向()1K S +，可由矢量合成，()(1)(1)()()2k k k k SgSβ++=-+()k β值可根据在极值点附近目标函数等值线近似为二次型函数的道理，推到出：()(1)(1)(1)2()()()()2||||3||||k T k k k k T k k gg g g g g β+++==利用两个点的梯度()k g和(1)k g+，就可以构造一个与梯度矢量为共轭的矢量()1K S +，沿着该方向搜索，即可求得极值点。

共轭梯度法程序框图如图2所示。

图2 共轭梯度法程序框图2. 共轭梯度法的应用用共轭梯度法计算22121212()52410f X x x x x x x =+---+ 的最优解，其中：初始点()0[1,1]T X =。

收敛精度ε=0.0001(1).共轭梯度法程序设计#include "stdio.h" #include "math.h"double fun1(double x1,double x2) {double y;y=x1*x1+x2*x2-5*x1*x2-2*x1-4*x2+10; return y; }double fun2(double g[],double d[]) {double buchang;buchang=-(g[0]*d[0]+g[1]*d[1])/(d[0]*(2*d[0]-5*d[1])+d[1]*(-5*d[0]+2*d[1])); return buchang; }main(){ double t, beta,x1=1,x2=1,d[2],g[4], y, m,e=0.0001; int k=1;g[0]=2*x1-5*x2-2; g[1]=2*x2-5*x1-4; m=(sqrt(g[0]*g[0]+g[1]*g[1]));while(m>e&&k<=200) { if (k==1) {d[0]=-g[0]; d[1]=-g[1];beta=0; } else {beta=(g[0]*g[0]+g[1]*g[1])/(g[2]*g[2]+g[3]*g[3]); d[0]=-g[0]+beta*d[0]; d[1]=-g[1]+beta*d[1]; }t=fun2(g,d); x1=x1+d[0]*t; x2=x2+d[1]*t; g[2]=g[0]; g[3]=g[1];g[0]= 2*x1-5*x2-2;g[1]= 2*x2-5*x1-4;m=sqrt(g[0]*g[0]+g[1]*g[1]); k++; }y=fun1(x1,x2);printf("迭代次数为k=%d\n",k);printf("分别输出x1=%f,x2=%f\n",x1,x2); printf("极小值y=%f",y); }(2).程序运行结果(3).结论用共轭梯度法计算22121212()52410f X x x x x x x =+---+的最优解为*( 1.142857,0.857143)X =-- ,*()12.857143F X = 。

共轭梯度法 c++

共轭梯度法c++一、共轭梯度法是一种优化算法，特别适用于解决对称正定矩阵的线性方程组。

它通过迭代的方式逐步逼近方程组的解，具有较快的收敛速度。

在C++中实现共轭梯度法可以为解决大规模线性系统提供高效的数值解。

二、共轭梯度法基本原理问题背景：考虑一个线性方程组Ax = b，其中A是对称正定矩阵，b是已知向量。

迭代过程：共轭梯度法通过迭代寻找一个逼近解x_k，使得残差r_k = b - Ax_k 最小。

迭代过程中，每一步都保证搜索方向共轭于前一步的搜索方向。

算法步骤：初始化：选择初始解x_0，计算残差r_0 = b - Ax_0，初始化搜索方向p_0 = r_0。

迭代：对于每一步k，计算步长alpha_k，更新解x_k+1 = x_k + alpha_k * p_k，计算新的残差r_k+1，更新搜索方向p_k+1。

收敛检测：当残差足够小时，停止迭代。

共轭方向的选择：在每一步中，选择共轭搜索方向可以通过Gram-Schmidt正交化方法得到。

这样能够确保搜索方向之间是线性无关的。

三、C++中的共轭梯度法实现在C++中实现共轭梯度法需要考虑以下关键步骤：矩阵和向量表示：使用C++中的数组或矩阵库表示矩阵A和向量b。

迭代过程：实现共轭梯度法的迭代过程，包括更新解、计算残差、计算步长等。

共轭方向选择：使用Gram-Schmidt正交化方法确保搜索方向共轭。

收敛检测：制定合适的收敛准则，如残差的阈值，判断是否停止迭代。

以下是一个简化的C++示例代码，演示了共轭梯度法的基本实现：#include <iostream>#include <cmath>#include <vector>using namespace std;// 定义矩阵和向量类型typedef vector<vector<double>> Matrix;typedef vector<double> Vector;// 共轭梯度法实现Vector conjugateGradient(const Matrix& A, const Vector& b, const Vector& x0, double tolerance, int maxIterations) {int n = A.size();Vector x = x0;Vector r = b - multiply(A, x);Vector p = r;for (int k = 0; k < maxIterations; ++k) {double alpha = dot(r, r) / dot(p, multiply(A, p));x = x + alpha * p;Vector newR = r - alpha * multiply(A, p);double beta = dot(newR, newR) / dot(r, r);p = newR + beta * p;r = newR;// 收敛检测if (sqrt(dot(r, r)) < tolerance) {cout << "Converged after " << k + 1 << " iterations." << endl;break;}}return x;}// 辅助函数：向量点积double dot(const Vector& a, const Vector& b) {double result = 0.0;for (size_t i = 0; i < a.size(); ++i) {result += a[i] * b[i];}return result;}// 辅助函数：矩阵与向量相乘Vector multiply(const Matrix& A, const Vector& x) {int n = A.size();Vector result(n, 0.0);for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {result[i] += A[i][j] * x[j];}}return result;}int main() {// 示例用例Matrix A = {{4, 1}, {1, 3}};Vector b = {1, 2};Vector x0 = {0, 0};double tolerance = 1e-6;int maxIterations = 1000;// 调用共轭梯度法Vector solution = conjugateGradient(A, b, x0, tolerance, maxIterations);// 输出结果cout << "Solution: ";for (double value : solution) {cout << value << " ";}cout << endl;return 0;}这个简单的示例演示了如何使用C++实现共轭梯度法。

共轭梯度法

一．介绍共轭梯度法（Conjugate Gradient ）是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse 矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。

在各种优化算法中，共轭梯度法是非常重要的一种。

其优点是所需存储量小，具有步收敛性，稳定性高，而且不需要任何外来参数。

共轭梯度法中最关键的两点是，搜索方向)(k d 和最佳步长k α。

其基本步骤是在点)(k X 处选取搜索方向)(k d , 使其与前一次的搜索方向)1(-k d 关于A 共轭，即(1)()(1),0k k k d d Ad --<>=然后从点)(k X 出发，沿方向)(k d 求得)(X f 的极小值点)1(+k X , 即)(min )()()(0)1(k dX f X f k k αλ+=>+如此下去, 得到序列{)(k X }。

不难求得0,)1()(>=<-k k Ad d 的解为)()()1(k k k k d X X α+=+其中，><><-=)()()()(,,k k k k kAd d Ad r α注意到)(k d 的选取不唯一，我们可取)1(1)()()(--+-∇=k k k k d X f d β由共轭的定义0,)1()(>=<-k k Ad d 可得：><><-=----)1()1()1()(1,,k k k k k Ad d Ad r β 共轭梯度法的计算公式如下：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+=><><-=+=><><-=-=-==+------(k)(k)1)(k )()()()()1(1(k))()1()1()1()(1(k)(k)(0)(0)d X X,,r ,,X r Xr d k k k k k k k k k k k k k k Ad d Ad r d d Ad d Ad r A b A b ααββ 二．程序框图定义矩阵A 和向量bAx=b定义x 的初值将x 代入计算公式误差到达精度要求Yes输出xNo 迭代出新的x 结束开始三．源码n=100;%矩阵阶数，可以按照题目需要更改syms x1 r1 d1A=zeros(n,n);b=zeros(n,1);b(1,1)=-1;b(n,1)=-1;for i=1:nA(i,i)=-2;endfor i=1:n-1A(i,i+1)=1;A(i+1,i)=1;endx1=zeros(n,1);for i=1:n*1000r1=b-A*x1;d1=r1;a=(r1'*d1)/(d1'*A*d1);x1=x1+a*d1;r2=b-A*x1;if(norm(x1)<=eps)breakendbb=-(r2'*A*d1)/(d1'*A*d1);d1=r2+bb*d1;enddisp([x1])四．结果矩阵A100阶的结果200阶的结果400阶的结果。

共轭梯度法

共轭梯度法对于任意形式的目标函数()f X ，在极值点*X 附近展开成泰勒级数，且取前三项，有()()()****2**1()...2TT f X f Xf X X X X X f X X X ⎡⎤⎡⎤⎡⎤⎡⎤≈+∇-+-∇-⎣⎦⎣⎦⎣⎦⎣⎦因在极值点*X 处()*0f X ∇=，而()2**()f X H X ∇=为()f X 在*X 的二阶偏导数矩阵，即Hessian 矩阵，故()****1().().2T f X f X X X H X X X ⎡⎤⎡⎤≈+--⎣⎦⎣⎦ 对于二次函数来说，若令()()()2*2*2*221122,,f X f X f X a b c x x x x ∂∂∂===∂∂∂∂则()**1(),a b H X f X d b c ⎡⎤==⎢⎥⎣⎦而—常数则，得到()()()()()()()()()()()()()()11221212121122*1**112*2**12**112**1222****11122-1()+--2---1=+--2--1-2---2x x a b f X d x x x x b c x x a x x b x x d x x x x b x x c x x d a x x b x x x x c x x ⎡⎤⎡⎤⎢⎥⎡⎤≈⎢⎥⎣⎦⎢⎥⎣⎦⎣⎦⎡⎤+⎢⎥⎡⎤⎣⎦⎢⎥+⎣⎦⎡⎤=+++⎢⎥⎣⎦由上式可知，当12*1**2x x X X x x ⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦时，得到目标函数的极小值()*1()f X f X d ==，当22(),,...f X d d =时，则有等值线族。

令2()f X d =，代入上式，则有()()()()112222****2111221()-2---2f X d d a x x b x x x x c x x ⎡⎤=≈+++⎢⎥⎣⎦所以目标函数()f X 在*X 点附近的等值线方程为()()()()112222****1122-2---0a x x b x x x x c x x d +++=式中，122()d d d =-=常数。

共轭梯度法

共轭梯度法简介共轭梯度法是一种迭代的最优化算法，用于求解线性方程组或求解非线性优化问题。

它在解决大规模线性方程组时表现出色，尤其适用于对称正定矩阵的问题。

共轭梯度法结合了最速下降法和共轭方向法的优点，能够在有限次数的迭代中快速收敛到最优解。

背景在数值计算和优化问题中，线性方程组的求解是一个常见且重要的问题。

例如，在图像处理、数据分析和机器学习等领域，我们经常需要求解一个大规模的线性方程组。

然而，传统的直接方法，如高斯消元法或LU分解，对于大规模问题往往计算量巨大，耗时较长。

因此，我们需要寻找一种高效的迭代方法来解决这些问题。

共轭梯度法的核心思想是通过一系列共轭的搜索方向来逼近最优解。

具体来说，对于一个对称正定的线性方程组Ax=b，共轭梯度法的步骤如下：1.初始化解向量x0和残差x0=x−xx0。

2.计算初始搜索方向x0=x0。

3.进行共轭梯度迭代：重复以下步骤n次或直到收敛为止。

a.计算步长$\\alpha_k=\\frac{r_k^Tr_k}{d_k^TAd_k}$。

b.更新解向量$x_{k+1}=x_k+\\alpha_kd_k$。

c.更新残差$r_{k+1}=r_k-\\alpha_kAd_k$。

d.计算新的搜索方向$d_{k+1}=r_{k+1}+\\frac{r_{k+1}^Tr_{k+1}}{r_k^Tr_k}d_k$。

共轭梯度法与其他迭代方法相比有以下特点：1.高效性：共轭梯度法能够在有限次数的迭代中收敛到最优解，尤其适用于对称正定矩阵。

相比于直接方法，其计算量较小，具有更高的计算效率。

2.无需存储完整矩阵：共轭梯度法只需知道矩阵A的乘法运算结果，不需要存储完整的矩阵。

这对于大规模问题是一个很大的优势。

3.不需要计算矩阵的特征值：相比于其他迭代方法，共轭梯度法不需要计算矩阵的特征值，因此在实际问题中更加实用。

算法应用共轭梯度法广泛应用于各个领域的优化问题和线性方程组求解问题，包括：1.图像处理：共轭梯度法用于图像恢复、图像去噪和图像分割等问题。

第四章共轭梯度法

n 设水平集 L x f ( x ) f ( x 0 ) 有界，f 是 R 上具有一阶连续
{ 偏导数的凸函数。 x k } 是由Fletcher-Reeves共轭梯度算法产生的迭代点列。则 { 1） f ( x k )} 为严格单调下降序列，且
lim f ( x k )
k
存在。
n
而
k 1
g k ( g k g k 1 )
T
d k 1 ( g k g k 1 )
T

gk gk g k 1 g k 1
T
T
共轭梯度法的迭代公式为：
x k 1 x k k d k （ d k 为共轭方向， k 为最佳步长因子）
对二次函数
k
gk dk dk Gdk
（4.7）
2)
k
g k 1 g k 1 gk gk
T
T
（Fletcher-Reeves公式）
（4.8）
3）
k
g k 1 ( g k 1 g k ) （Polak-Ribiere-Polyak 公式）
T
（4.9）
gk gk g k 1 g k 1 dk gk
T T
T
4）
m y
2 T 2 2
，使得
n
y f ( x ) y M y , y R , x L ,
其中 L x R n f ( x ) f ( x 0 ) 是有界水平集。
定理4.9 假定假设条件1和2满足，那么，每r步再开始的PRP和FR共轭梯度法产生的迭代点列 x k n步二阶收敛，即存在常数c>0，使得
设又设
fˆkr
0 表示应用到 fˆkr 上的共轭梯度法，并且令 d kr d kr g kr

共轭梯度法

共轭梯度法公式

共轭梯度法

共轭梯度法

共轭梯度法

共轭梯度法和梯度下降法

共轭梯度法总结

共轭梯度法beamforming_理论说明

共轭梯度法

共轭梯度方法

共轭梯度（ConjugateGradient，CG）算法

共轭梯度法

线性方程组的共轭梯度法

最优化课程练习-共轭梯度法

共轭梯度法 c++

共轭梯度法

共轭梯度法

共轭梯度法

第四章 共轭梯度法

第四章共轭梯度法