材料力学复习例题ppt课件
合集下载
材料力学习题(PPT)共17页文档
2 Pa 3
3E I
3
1
2l 1
Pll ) Pll l
2
3 GIp
fc
2Pl3 3EI
Pl3 GIp
T图
施加的单位力和P同位置、同方向, 所以M0c图、T0c图和M图、T图形 状一样
例7:图示开口刚架,EI=const。求沿P力作用线方向的相对 线位移 ΔAB 。
解:
AB2E Pa I38 11 322 12 1
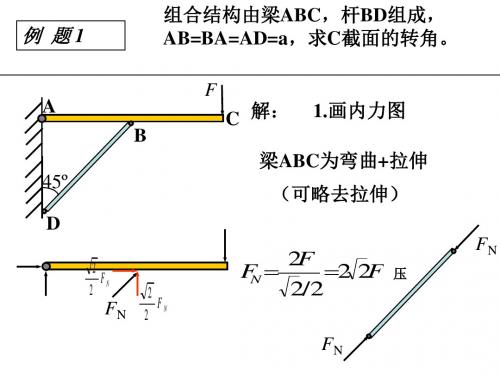
2F
压
画出AC的M图,DB 的轴力图。
F
FN
FN
2 2F
A
F C 2.加单位载荷m0=1,画内力图
B
FN a
1 2/2
2 a
压
45º
D
(M)
2 2
FN
FN
2 2 FN
m0=1
1
画出AC的 M 图,DB 的FN图。
FN
2
FN
a
3.图乘法
(M)
Fa
(FN)
M
2 2F
1
2 2F 2a 2
C
例3:图示梁的抗弯刚度为EI,试求D点的铅垂位移。
vC
3 EI
Pa2 2
2a
3
Pa 3 EI
例 题4
求C处的线位移。
解: 1.画内力图
BC段为弯曲(x 轴为 中性轴)
AB段为弯曲(z 轴为 中性轴)+扭转
y
x z
Al
ql 2 2
(MT)
ql 2
qC l
B
ql 2 2
2.求 cx ,应在C处沿x方向加单位力。
qa A 2
3E I
3
1
2l 1
Pll ) Pll l
2
3 GIp
fc
2Pl3 3EI
Pl3 GIp
T图
施加的单位力和P同位置、同方向, 所以M0c图、T0c图和M图、T图形 状一样
例7:图示开口刚架,EI=const。求沿P力作用线方向的相对 线位移 ΔAB 。
解:
AB2E Pa I38 11 322 12 1
2F
压
画出AC的M图,DB 的轴力图。
F
FN
FN
2 2F
A
F C 2.加单位载荷m0=1,画内力图
B
FN a
1 2/2
2 a
压
45º
D
(M)
2 2
FN
FN
2 2 FN
m0=1
1
画出AC的 M 图,DB 的FN图。
FN
2
FN
a
3.图乘法
(M)
Fa
(FN)
M
2 2F
1
2 2F 2a 2
C
例3:图示梁的抗弯刚度为EI,试求D点的铅垂位移。
vC
3 EI
Pa2 2
2a
3
Pa 3 EI
例 题4
求C处的线位移。
解: 1.画内力图
BC段为弯曲(x 轴为 中性轴)
AB段为弯曲(z 轴为 中性轴)+扭转
y
x z
Al
ql 2 2
(MT)
ql 2
qC l
B
ql 2 2
2.求 cx ,应在C处沿x方向加单位力。
qa A 2
材料力学复习PPTPPT课件

C 2
刚杆
D
F
a)
AB杆材料
CD杆材料
(%)
b)
23
例 结构受载荷作用如图a所示,已知杆AB 和杆BC 的抗拉 刚度为EA。试求节点B的水平及铅垂位移。
解 1)轴力计算
设两杆均受拉力,
由节点B(图b)的平衡
条件解得
2020年3月21日星期六
FN1 F , FN 2 2F
2)变形计算
l1
FN1l1 EA
E
0.57 s
cr
s
cr
s
1
c
2
中柔度杆
c
cr
2E 2
细长压杆
o
2020年3月21日星期六
c
l
i 16
临界力计算的步骤 确定长度系数 (yz
zl
iz
得出)
判断{确定临界力 (应力)计算公式}
p
Fcr
2EI ( l ) 2
cr
2E 2
2020年3月21日星期六
13 14
冲击
1、自由落体冲击 动荷系数——
2、水平冲击:
Kd 1
1 2h st
动荷系数——
v2
Kd g st
2020年3月21日星期六
18
截面法
基本变形
危险截面
内力计算
推导方法
变形计算
应力计算
强度、刚度计算
2020年3月21日星期六
危险点
19
第二章 轴向拉伸与压缩
基本要求: 1. 轴力计算,绘轴力图; 2. 横截面上的正应力计算,强度计算; 3. 绘变形与位移图,变形与位移计算; 4. 材料的力学性质; 5. 求解简单拉压超静定问题。 难点: 绘变形与位移图;求解简单拉压超静定问题。
材料力学复习习题(可打印版)ppt课件

r 4 1 2 3
两者均小于 []=170MPa 。可见,无论采用第三或是 第四强度理论进行强度校核,该结构都是安全的。
qL 2
L=3m
qL 2
+
x
M
qL 8
2
qL 3600 3 F 540 N S max 2 2
x
2 2 qL 3600 3 M 405 N max 8 8
+
q=3.6kN/m
求最大应力并校核强度
M M 6 4050 max 6 max max 2 2 W bh 0 . 12 0 . 18 z
件,[]=40MPa,试用第一强度理论校核杆的强度。 T P A T A A P
解:危险点A的应力状态如图:
P 4 50 3 10 6 . 37 MP 2 A 0 . 1
2
2
T 16 7000 35 . 7 MPa 3 W 0 . 1 n
sin 2 cos 2 xy
2、求主应力、主平面
主应力: m ax
m in
x y
2
(
x y2
2
) xy
2
80 . 7 ( MPa ), 0 ,3 60 . 7 ( MPa ) 1 2
主平面位置:
80 . 7 ( MP ) 40 60 40 60 2 2 ( ) ( 50 ) 60 . 7 ( MP ) 2 2
F 2 F A N 1 1 1
3、根据水平杆的强度,求许可载荷 查表得水平杆AB的面积为A2=2×12.74cm2
F F cos 3 F N 2 N 1
两者均小于 []=170MPa 。可见,无论采用第三或是 第四强度理论进行强度校核,该结构都是安全的。
qL 2
L=3m
qL 2
+
x
M
qL 8
2
qL 3600 3 F 540 N S max 2 2
x
2 2 qL 3600 3 M 405 N max 8 8
+
q=3.6kN/m
求最大应力并校核强度
M M 6 4050 max 6 max max 2 2 W bh 0 . 12 0 . 18 z
件,[]=40MPa,试用第一强度理论校核杆的强度。 T P A T A A P
解:危险点A的应力状态如图:
P 4 50 3 10 6 . 37 MP 2 A 0 . 1
2
2
T 16 7000 35 . 7 MPa 3 W 0 . 1 n
sin 2 cos 2 xy
2、求主应力、主平面
主应力: m ax
m in
x y
2
(
x y2
2
) xy
2
80 . 7 ( MPa ), 0 ,3 60 . 7 ( MPa ) 1 2
主平面位置:
80 . 7 ( MP ) 40 60 40 60 2 2 ( ) ( 50 ) 60 . 7 ( MP ) 2 2
F 2 F A N 1 1 1
3、根据水平杆的强度,求许可载荷 查表得水平杆AB的面积为A2=2×12.74cm2
F F cos 3 F N 2 N 1
材料力学复习_Microsoft_PowerPoint_演示文稿

除计算桡度时所需的公式给出外,其余所有公式必须 记住。
概念题为小题(25-30) 计算题未考到的内容均是出题范围:
连接件、平面弯曲的概念、弯曲切应力流与弯曲 中心;
桡曲线的大致形状、截面核心、交变应力和 疲劳破坏等等
考试时间:18周2(6月24日) 晚上6:30——8:30
地点:(由各院通知)
答疑时间:18周1、2上午、下午; 地点:高A-402室
Mx
(x)M
0 x
dx
l GI p
注意:方程中坐标一致;内力的符号要一致。
第13章 压杆稳定
一、压杆的临界力和临界应力
1、 p
——细长杆(大柔度杆)
cr
2E 2
Fcr
2 EI (l)2
l ,
i
P
2E P
2、 λP>λ >λ u
——中长杆(中柔度杆)
cr a b, Fcr cr A
或直接求内力 2、分别计算
3、叠加 4、强度计算
Fx—轴向力(拉或压) Fy、 Fz—剪力(忽略不计)
Mx—扭矩 My、 Mz——弯矩(圆截面:合成)
二、组合变形的应力分析和强度计算:
1、斜弯曲(双向弯曲)
A
F1
My
Fy
Mx
F2 MzFz B Fx
2、拉(压)与弯曲
3、偏心拉伸(压缩) 4、弯扭组合 5、拉弯扭组合
二.弯曲切应力和强度计算
FS
S
* z
Izb
——统一公式
1、各种截面切应力的分布
2、切应力的方向(切应力流)与弯曲中心的 概念
3、最大应力和强度校核
第6章 弯曲变形
概念题为小题(25-30) 计算题未考到的内容均是出题范围:
连接件、平面弯曲的概念、弯曲切应力流与弯曲 中心;
桡曲线的大致形状、截面核心、交变应力和 疲劳破坏等等
考试时间:18周2(6月24日) 晚上6:30——8:30
地点:(由各院通知)
答疑时间:18周1、2上午、下午; 地点:高A-402室
Mx
(x)M
0 x
dx
l GI p
注意:方程中坐标一致;内力的符号要一致。
第13章 压杆稳定
一、压杆的临界力和临界应力
1、 p
——细长杆(大柔度杆)
cr
2E 2
Fcr
2 EI (l)2
l ,
i
P
2E P
2、 λP>λ >λ u
——中长杆(中柔度杆)
cr a b, Fcr cr A
或直接求内力 2、分别计算
3、叠加 4、强度计算
Fx—轴向力(拉或压) Fy、 Fz—剪力(忽略不计)
Mx—扭矩 My、 Mz——弯矩(圆截面:合成)
二、组合变形的应力分析和强度计算:
1、斜弯曲(双向弯曲)
A
F1
My
Fy
Mx
F2 MzFz B Fx
2、拉(压)与弯曲
3、偏心拉伸(压缩) 4、弯扭组合 5、拉弯扭组合
二.弯曲切应力和强度计算
FS
S
* z
Izb
——统一公式
1、各种截面切应力的分布
2、切应力的方向(切应力流)与弯曲中心的 概念
3、最大应力和强度校核
第6章 弯曲变形
《材料力学总复习》PPT课件

M max [ ]
MmaxWz[]
刚 度
Tmax (rad/m)
GIp
w max
w
条 件
T G m Iax p180 (/m)
q q max
应
变 能
V
FN 2 (x)dx L 2EA
T 2(x)
V
dx 实L用2文G档 IP
M2(x)
V L
dx 2EI
一、剪切与挤压的实用计算
t FS t
y2
SZ a 7 2 5 145 2 0 325 1.6 5 1 0 4m 3
实S用Z文b档0m3
F
1
1000 1 1200
1000
3.64kN
Q:
40 a
150
b
75 10
4.36kN
a点应力:
M:
3.64kNm
4.36kNm
aM IZa y3.6 2 41.1 30 1 3 0 651 0 36.0M 4 P
2
r3M W 2T232 (0.2F )2 d 3(0.1F 8 )2[]
F实8 用文0 档16 00.03378N8
0.269 32
9-15、已知:W=40KN,nst=5。求:校核BD杆的稳定性。
A 32.8cm2 , I 144 cm4 , i 2.1cm
1 99.4, 2 57.1,
求:试校核轴的强度和刚度。
P1
P2
P3
分析:强度条件:tmax
T Wt
[t ]
d1
d2
A
C
D
0.5 0.3 1
刚度条件: T 180 []
B
GIP
M 19
材料力学复习 PPT课件
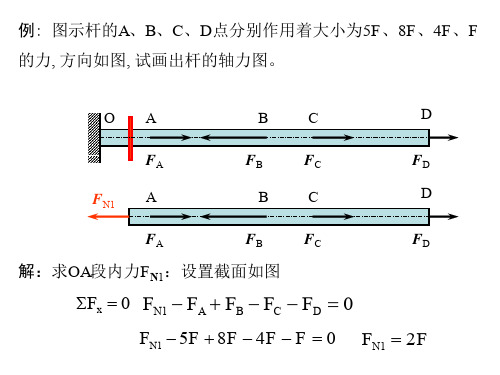
M c y1 Iz
[sc ]
y1 y2
[st ] [s c ]
20 y
20
F
q=F/b
A
CB
D
b
b
b
Fb/2
C截面的强度条件由最大的拉应
力控制。
Fb/4
s t max
MC y1 Iz
( F 2) 0.134 4 5493108
30 106
F 24.6 kN
B截面
s t max
T 0.2d 3
T
1930
d 3 0.2tmax 3 0.2 66.7 106 0.053 m 5.3 cm
A空 8.5 0.303 A实 28.2
可见, 采用钢管时, 其重量只有实心圆 轴的30%, 耗费的材料要少得多。
例: 作内力图。已知F1=F2=2 kN, Me=10 kN·m, q=1 kN/m。
s t max
My1 Iz
s cmax
My2 Iz
60 280
sc max
Oz
st max
s t max y1 [s t ] 1 s c max y2 [s c ] 3
y1 1 y2 3
d
60 280
y
y2
y1 y2 280 mm
由上两式确定出
Oz
y1
y
y y2 210 mm
80
120 20
y1
B截面
st
M B y1 Iz
4000 0.052 763108
27.2106 Pa 27.2 MPa [s t]
工学材料力学总复习PPT课件

B3 B B2 B3ctg
受力后B点移到 B其位移
B2B3 l2 cos l1
B B BB12 B1B 2
B1 B B1 B3 B3 B
第19页/共70页
例 求图所示等直杆AB上,下端的约束力,并求C截面 的位移。杆的拉压刚度为EA。
解: 1.平衡方程FA+FB-F=0
2.相容条件ΔBC+ΔAC=0
解: (1)绘扭矩图
2
A
B
2
TAB M 2 M1
C TAB 2kN.m
1 TBC m1 4kN.m
(2)计算IP:
T
4
IP
D4 (1 4 )
32
-2
x
I p 5.8106 m4
第30页/共70页
(3)算相对扭角
CA
BA
CB
TABl AB GI P
TBClBC GI P
CA
l GIP
y
2)如图三杆铰结,画A节点位移图, 列出变形相容条件。要注意所设的 变形性质必须和受力分析所中设定 的力的性质一致。由对称性知
1 2
1 3 cos
②
3)代入物理关系,建立补充方程
1
FN
1
1
E1 A1
FN1
E1 A1 cos
3
FN 3 3 E3 A3
FN 3 E3 A3
③
13
2
l
A
l2
向下的均布荷载
一段梁上的
q<0
外力情况
无荷载
向右下倾斜的直线
剪力图的特征
水平直线
集中力
F C
在C处有突变
集中力偶
m C
材料力学总复习(课堂PPT)

FQ 0.5F; (0.5l x l)
Mc1 0,
FA x F (x 0.5l) M 0, M 0.5F (l x) ; (0.5l x l) 11
例 已知:简支梁AB,跨度l ,F 作用在跨中 ,且垂直 于梁轴线,不计梁重。求梁内力方程并绘内力图 。
A
FA x
FQ
F
4、形心主惯性轴,形心主惯性矩。 ……
2
一、内力分析
1、截面法求内力(方程) 2、内力正负号规定 3、内力图 例2-2[1,3],例2-3[1,3],例2-7[2,3],例2-8[3,3], 习2-5(f)[2,3],习2-6(d、f)[2,3]。
3
内
变 力 分量
形
符号
正向图示
大小
轴向 轴力 拉力为“+”
拉压 FN
列
扭转 扭矩 矩矢指向截
平
Mx
面外法线为 “+”
衡 方
剪力 剪力之矩顺
程
平面 FQ 时针为 “+”
求
弯曲 弯矩 使梁上凹下
解
M 凸变形为
“+”
4
例 已知:如图所示,F1=18kN,F2=8kN,F3=4kN,试
绘制内力图。
解:研究AD杆,
FA
A1 B
F1
1
2C 2
3 D
F2
F3
3
Fx 0, F1 F2 F3 FA 0, FA F1 F2 F3 14kN;
C
0.5F
M
0.25Fl
B
FB
x 0.5F
解:1、求反力 易知, FA = FB = 0.5F ; 2、列剪力、弯矩方程 AC段,
FQ 0.5F; (0 x 0.5l) M 0.5F x ;(0 x 0.5l)
Mc1 0,
FA x F (x 0.5l) M 0, M 0.5F (l x) ; (0.5l x l) 11
例 已知:简支梁AB,跨度l ,F 作用在跨中 ,且垂直 于梁轴线,不计梁重。求梁内力方程并绘内力图 。
A
FA x
FQ
F
4、形心主惯性轴,形心主惯性矩。 ……
2
一、内力分析
1、截面法求内力(方程) 2、内力正负号规定 3、内力图 例2-2[1,3],例2-3[1,3],例2-7[2,3],例2-8[3,3], 习2-5(f)[2,3],习2-6(d、f)[2,3]。
3
内
变 力 分量
形
符号
正向图示
大小
轴向 轴力 拉力为“+”
拉压 FN
列
扭转 扭矩 矩矢指向截
平
Mx
面外法线为 “+”
衡 方
剪力 剪力之矩顺
程
平面 FQ 时针为 “+”
求
弯曲 弯矩 使梁上凹下
解
M 凸变形为
“+”
4
例 已知:如图所示,F1=18kN,F2=8kN,F3=4kN,试
绘制内力图。
解:研究AD杆,
FA
A1 B
F1
1
2C 2
3 D
F2
F3
3
Fx 0, F1 F2 F3 FA 0, FA F1 F2 F3 14kN;
C
0.5F
M
0.25Fl
B
FB
x 0.5F
解:1、求反力 易知, FA = FB = 0.5F ; 2、列剪力、弯矩方程 AC段,
FQ 0.5F; (0 x 0.5l) M 0.5F x ;(0 x 0.5l)
材料力学总复习-习题课4ppt课件

(a)桁架的承载能力强,因为(b) 桁架的压杆长度长,且压力大。
(a)
题4图
(b)
二、计算题
5. 作图示梁的剪力图和弯矩图,并写出
Q 和 M ,(15分)。 m ax m ax
解: FA = 7qa/6(↑), FD= qa/6(↓)
,
|Qmax|=7qa/6 |Mmax|=5qa2/6
6.已知电动机输出功率P=75kW,转速n=955rmp,输出轴直径D=50mm,输出轴 与外设轮毂采用键连接,已知键长度L=50mm,许用切应力和许用挤压应力分别 为 , ,试确定键的宽度b和高度h。(假设键各有一 60 MPa 100 MPa bs 半嵌入轴和轮毂内) (10分)
7.在xy平面内放置的直角折杆ABC,受力如图,已知F=120kN,q=8kN/m, a=2m;在yz平面内有 ,折杆ABC的直径d=150mm, =160MPa,试按第四 强度理论校核固定端A的强度。 (15分)
解:
轴力
弯矩
FN=F=120kN,
M 0 . 8 a q a 25 . 6 kN m
,
10.图示长、宽、高分别为l、b和h的矩形截面悬臂梁,在x-y平面和x-z平面内受到 两个垂直方向的力偶矩M1和M2的作用。已知该悬臂梁的弹性模量为E,泊松比为μ。 在某截面的前、后表面各粘贴了3个轴向应变片,其中应变片1和4位于前后表面的最 上端,应变片2和5位于前后表面的中间,应变片3和6位于前后表面的最下端。在不 提供额外温度补偿片的情况下,请选取若干个电阻应变片,组成两个惠斯通半桥, 分别直接测得外力偶矩M1和M2。要求:绘出惠斯通桥路接线图,并推导出外力偶矩 M1和M2和应变仪读数的显式关系式。 (15分) (1)用3,1应变片组成半桥测M1:
材料力学期末总复习资料PPT课件

F
F
解:受力分析如图
t b
t
Fs
Pbs
F 4
F
123
F
F
d
F/4
第17页/共87页
123
第18页/共87页
一、计算外力偶矩
已知 轴转速-n 转/分钟 输出功率-P 千瓦 求:力偶矩Me
Me
9549
Pk n
(牛顿米)
第19页/共87页
二、扭矩正负规定
右手螺旋法则
右手拇指指向外法线方向为 正(+),反之为 负(-)
应特别注意。
第14页/共87页
六、剪切和挤压的实用计算
切应力强度条件: Fs
A
挤压强度条件:
s bs
Fbs Abs
s bs
第15页/共87页
例 齿轮与轴由平键(b×h×L=20 ×12 ×100)连接,它传递的扭矩m=2KNm,轴的直 径d=70mm,键的许用切应力为[]= 60M Pa ,许用挤压应力为[sbs]= 100M Pa,试校 核键的强度。
第22页/共87页
五、剪切胡克定律
l 剪切胡克定律:当剪应力不超过材料的剪切比例极限时(τ ≤τp),剪应力与 剪应变成正比关系。
G
第23页/共87页
六、截面极惯性矩
a. 对于实心圆截面:
d
Ip
A 2dA
D4
32
O
D
b. 对于空心圆截面:
Ip
D4
32
(1- 4 )
d
O
D
第24页/共87页
第4页/共87页
二、变形固体的基本假设
一、连续性假设:物质密实地充满物体所在空间,毫无空隙。
材料力学培训资料PPT课件( 36页)

Vε
n i1
Ti 2li 2GI p
或
Vε
n i1
GIp 2li
ji2
M2 Ⅰ
M1
Ⅱ
M3
d
jAB B
lAB
A
lAC
jCA C
纯剪切应力状态下的应变能密度( p )
y
g d'
a
dy
p
O
b
' c
x
z
dx
O
g
dW1dydzgdx1gdxdydz
vε
1.5 210 3rad 32
jCA
T2l AC GIP
86031713 0M 3 0NPm πam 7500m m 04m m
1.6 9 1 3 0 rad 32
M2 Ⅰ
M1
Ⅱ
M3
d
jAB B
lAB
A
lAC
jCA C
3、 横截面C相对于B的扭转角:
d D 6.7 3 m 5 m
§3-6 等直圆杆扭转时的应变能
等直圆杆仅在两端受外力偶矩 Me 作用且 p 时
Me
Me j
Vε W12Mej
1 2
M e2l GI p
1 T 2l 2 GI p
或
Vε
1GIp 2l
j2
Me
Me
j M el GI p
j
j
当等直圆杆各段横截面上的扭矩不同时
对于精密机器的轴 [j]0 .1~ 5 0 .3/0 m
对于一般的传动轴 [j]2/m
例3-6 由45号钢制成的某空心圆截面轴,内、外直径
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FN1 FN2
FN1 cos FN2 cos FN3 F 0
B
DC
1
3 2
FN1
FN 3
EA E3 A3
cos2
A
FN3 1 2
F EA
cos2
1 3F 2
E3 A3
A
F
FN1
FN 2
1
2cos
E
E3 A3
A cos2
Δl3
Δl1
A'
11
第3章
1、扭矩图 2、扭转切应力计算及强度条件 3、扭转变形计算及强度条件
max
最大切应力发生在截面的周边上, 且垂直于半径.
M1
M2
B
C
l
l
T
max
15
3-2 图示阶梯圆轴,AB段的直径d1=120mm,BC 段的直径 d2=100mm.扭转力偶矩为MA = 22 kN·m, MB = 36 kN·m ,MC =14
kN·m. 已知材料的许用切应力[] = 80MPa,试校核该轴的强度.
l1
20
+
FN1 =20kN (+) FN2 =-15kN (-) FN3 =- 50kN (-)
5
Ⅲ
Ⅱ
Ⅰ
FRD
F3
F2
F1
DⅢ
C
Ⅱ
B
A Ⅰ
进行强度校核时一定要找出构件内
l3
l2 应力最大的截面l1,才是危险截面,
一般在横截面尺寸较小或内力最大
(2) 杆的最大正应力max
的位置上
AB段
AB
FN1 A1
176.8MPa
FN1 =20kN (+)
因 该((结σ)m构ax仍-[σ是])/安[σ全]=F的4N%2<=5-%15,因kN此 ( - )
BC段 BC
FN2 74.6MPa A2
()
DC段
DC
FN 3 A3
110.5MPa
()
FN3 =- 50kN ( - )
max = 176.8MPa>[σ]
解:(1)列静力平衡方程
Fx 0 FN1 FN2 Fy 0 FN1 cos
B
DC
y
1
3
2 FN1FN3
FN2
FN2 cos FN3 F 0 A
x A
这是一次超静定问题!
F
F
8
y
B
DC
1
3 2
A
F (2)变形几何方程
FN1FN3
FN2
x
A
F
B
DC
1
3
2
A
A'
由于问题在几何,物理及 受力方面都是对称,所以变形后A点将沿
发生在AB段.
6
Ⅲ
Ⅱ
Ⅰ
DⅢ l3
F3
C
Ⅱ
l2
F1 F2
B
A Ⅰ
l1
(3) B截面的位移及AD杆的变形
Δ3 10-4m
ΔlBC
FN 2 l2 EA2
1.42 10-4m
ΔlCD
FN 3 l3 EA3
1.58 10-4m
uB ΔlCD ΔlBC -0.3mm
32
得
D4
32Tmax 1800
G 2[]
0.0295m
取d=30mm
对于轴而言,其主控因素是刚度,因此由刚度条件算 出的轴直径会比强度大。该轴除受扭外还受弯曲的作 用,因此在机械设计中,一般按扭矩进行估算,设计 好轴的结构后再按弯扭进行校核。
解:作轴的扭矩图 分别校核两段轴的强度
MeA
MeB
MeC
1max
T1 Wt1
T1 πd13 /
16
22103 A π(0.123 ) / 16
22 kN·m
B
C
64.84MPa [ ]
+
2max
T2 Wt 2
T2
πd
3 2
/
16
14 103 π(0.13 ) / 16
_
14 kN·m
71.3MPa [ ] 因此,该轴满足强度要求. 16
AB段 T2+Me2-Me1=0
T2 =2kN·m (+)
最大扭矩发生在BC段
Tmax=4kN·m
2kN·m
+
2
1
Me1
Me2
A
B
C
l
l
T1 Me2
_
4kN·m
C
T2 Me1
Me2
B
C 14
(2)求轴的最大切应力, 并指出其位置
max
Tmax Wt
A
Tmax
πD3 (1 4 )
16
34.5MPa
第2章
1、轴力图 2、正应力计算及强度条件 3、拉压胡克定律及简单的静不定
1
例2-1 图示为一变截面圆杆ABCD.已知F1=20kN,F2=35kN F3=35kN. l1=l3=300mm,l2=400mm. d1=12mm,d2=16mm, d3=24mm,E=210GPa. 试求:
(1) Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III截面的轴力并作轴力图
ΔlAD ΔlAB ΔlBC ΔlCD -0.47 10-4mm
7
2-2 简单静不定问题
设 1,2,3 三杆用绞链连结如图所示,l1 = l2 = l,A1 = A2 = A, E1 = E2 = E,3杆的长度 l3 ,横截面积 A3 ,弹性模量E3 。试求在 沿铅垂方向的外力F作用下各杆的轴力.(P40-41)
例题3.4
解:求扭矩,画扭矩图 计算外力偶矩
由
Mx 0
17
得
作扭矩图,得到在轮Ⅲ和Ⅳ之间扭矩最大,且
由强度条件,
max
Tmax Wt
16Tmax
D3
[ ]
得
D 3 16Tmax 0.0272m
[ ] 18
由刚度条件,
m ax
Tmax GI p
1800
Tmax
G D4
1800
[]
FN1 20kN ()
Ⅰ
F2
F1
B
A Ⅰ
l1
FN1
F1
3
Ⅲ
FRD
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
FRD
FN3 FN2
Ⅰ
F2
F1
B
ⅠA
l1
F1 F2
FN3 FRD 0
F1 F2 FN2 0
FN3 50kN ()
FN2 15kN ()
4
Ⅲ
FRD
DⅢ l3
-
50
Ⅱ
F3
C
Ⅱ
l2
15
Ⅰ
F2
F1
B
ⅠA
(2) 杆的最大正应力max,如[σ]=170MPa,试校核其强度;
(3) B截面的位移及AD杆的变形
Ⅲ
Ⅱ
Ⅰ
DⅢ l3
F3
C
Ⅱ
l2
F1 F2
B
ⅠA
l1
2
Ⅲ
FRD
Ⅱ
F3
DⅢ l3
C
Ⅱ
l2
解:求支座反力 FRD = -50kN (1)Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III 截面的轴力并作轴力图
F1 FN1 0
12
3-1 图示空心圆轴外径D=100mm,内径d=80mm, M1=6kN·m, M2=4kN·m, 材料的切变模量 G=80GPa.
(1) 画轴的扭矩图;
(2) 求轴的最大切应力,并指出其位置.
M1
M2
A
B
C
l
l
13
解:(1)画轴的扭矩图
BC段 T1+Me2=0
T1 = -4kN·m (-)
铅垂方向下移.变形协调条件是变形后三杆仍绞结在一起﹗
9
B
DC
1
3
2
A
F 变形几何方程为
物理方程为
(3)补充方程
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
A'
Δl1 Δl3 cos
A'
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
FN1
FN 3
EA E3 A3
cos2
10
(4)联立平衡方程与补充方程求解
FN1 cos FN2 cos FN3 F 0
B
DC
1
3 2
FN1
FN 3
EA E3 A3
cos2
A
FN3 1 2
F EA
cos2
1 3F 2
E3 A3
A
F
FN1
FN 2
1
2cos
E
E3 A3
A cos2
Δl3
Δl1
A'
11
第3章
1、扭矩图 2、扭转切应力计算及强度条件 3、扭转变形计算及强度条件
max
最大切应力发生在截面的周边上, 且垂直于半径.
M1
M2
B
C
l
l
T
max
15
3-2 图示阶梯圆轴,AB段的直径d1=120mm,BC 段的直径 d2=100mm.扭转力偶矩为MA = 22 kN·m, MB = 36 kN·m ,MC =14
kN·m. 已知材料的许用切应力[] = 80MPa,试校核该轴的强度.
l1
20
+
FN1 =20kN (+) FN2 =-15kN (-) FN3 =- 50kN (-)
5
Ⅲ
Ⅱ
Ⅰ
FRD
F3
F2
F1
DⅢ
C
Ⅱ
B
A Ⅰ
进行强度校核时一定要找出构件内
l3
l2 应力最大的截面l1,才是危险截面,
一般在横截面尺寸较小或内力最大
(2) 杆的最大正应力max
的位置上
AB段
AB
FN1 A1
176.8MPa
FN1 =20kN (+)
因 该((结σ)m构ax仍-[σ是])/安[σ全]=F的4N%2<=5-%15,因kN此 ( - )
BC段 BC
FN2 74.6MPa A2
()
DC段
DC
FN 3 A3
110.5MPa
()
FN3 =- 50kN ( - )
max = 176.8MPa>[σ]
解:(1)列静力平衡方程
Fx 0 FN1 FN2 Fy 0 FN1 cos
B
DC
y
1
3
2 FN1FN3
FN2
FN2 cos FN3 F 0 A
x A
这是一次超静定问题!
F
F
8
y
B
DC
1
3 2
A
F (2)变形几何方程
FN1FN3
FN2
x
A
F
B
DC
1
3
2
A
A'
由于问题在几何,物理及 受力方面都是对称,所以变形后A点将沿
发生在AB段.
6
Ⅲ
Ⅱ
Ⅰ
DⅢ l3
F3
C
Ⅱ
l2
F1 F2
B
A Ⅰ
l1
(3) B截面的位移及AD杆的变形
Δ3 10-4m
ΔlBC
FN 2 l2 EA2
1.42 10-4m
ΔlCD
FN 3 l3 EA3
1.58 10-4m
uB ΔlCD ΔlBC -0.3mm
32
得
D4
32Tmax 1800
G 2[]
0.0295m
取d=30mm
对于轴而言,其主控因素是刚度,因此由刚度条件算 出的轴直径会比强度大。该轴除受扭外还受弯曲的作 用,因此在机械设计中,一般按扭矩进行估算,设计 好轴的结构后再按弯扭进行校核。
解:作轴的扭矩图 分别校核两段轴的强度
MeA
MeB
MeC
1max
T1 Wt1
T1 πd13 /
16
22103 A π(0.123 ) / 16
22 kN·m
B
C
64.84MPa [ ]
+
2max
T2 Wt 2
T2
πd
3 2
/
16
14 103 π(0.13 ) / 16
_
14 kN·m
71.3MPa [ ] 因此,该轴满足强度要求. 16
AB段 T2+Me2-Me1=0
T2 =2kN·m (+)
最大扭矩发生在BC段
Tmax=4kN·m
2kN·m
+
2
1
Me1
Me2
A
B
C
l
l
T1 Me2
_
4kN·m
C
T2 Me1
Me2
B
C 14
(2)求轴的最大切应力, 并指出其位置
max
Tmax Wt
A
Tmax
πD3 (1 4 )
16
34.5MPa
第2章
1、轴力图 2、正应力计算及强度条件 3、拉压胡克定律及简单的静不定
1
例2-1 图示为一变截面圆杆ABCD.已知F1=20kN,F2=35kN F3=35kN. l1=l3=300mm,l2=400mm. d1=12mm,d2=16mm, d3=24mm,E=210GPa. 试求:
(1) Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III截面的轴力并作轴力图
ΔlAD ΔlAB ΔlBC ΔlCD -0.47 10-4mm
7
2-2 简单静不定问题
设 1,2,3 三杆用绞链连结如图所示,l1 = l2 = l,A1 = A2 = A, E1 = E2 = E,3杆的长度 l3 ,横截面积 A3 ,弹性模量E3 。试求在 沿铅垂方向的外力F作用下各杆的轴力.(P40-41)
例题3.4
解:求扭矩,画扭矩图 计算外力偶矩
由
Mx 0
17
得
作扭矩图,得到在轮Ⅲ和Ⅳ之间扭矩最大,且
由强度条件,
max
Tmax Wt
16Tmax
D3
[ ]
得
D 3 16Tmax 0.0272m
[ ] 18
由刚度条件,
m ax
Tmax GI p
1800
Tmax
G D4
1800
[]
FN1 20kN ()
Ⅰ
F2
F1
B
A Ⅰ
l1
FN1
F1
3
Ⅲ
FRD
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
FRD
FN3 FN2
Ⅰ
F2
F1
B
ⅠA
l1
F1 F2
FN3 FRD 0
F1 F2 FN2 0
FN3 50kN ()
FN2 15kN ()
4
Ⅲ
FRD
DⅢ l3
-
50
Ⅱ
F3
C
Ⅱ
l2
15
Ⅰ
F2
F1
B
ⅠA
(2) 杆的最大正应力max,如[σ]=170MPa,试校核其强度;
(3) B截面的位移及AD杆的变形
Ⅲ
Ⅱ
Ⅰ
DⅢ l3
F3
C
Ⅱ
l2
F1 F2
B
ⅠA
l1
2
Ⅲ
FRD
Ⅱ
F3
DⅢ l3
C
Ⅱ
l2
解:求支座反力 FRD = -50kN (1)Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III 截面的轴力并作轴力图
F1 FN1 0
12
3-1 图示空心圆轴外径D=100mm,内径d=80mm, M1=6kN·m, M2=4kN·m, 材料的切变模量 G=80GPa.
(1) 画轴的扭矩图;
(2) 求轴的最大切应力,并指出其位置.
M1
M2
A
B
C
l
l
13
解:(1)画轴的扭矩图
BC段 T1+Me2=0
T1 = -4kN·m (-)
铅垂方向下移.变形协调条件是变形后三杆仍绞结在一起﹗
9
B
DC
1
3
2
A
F 变形几何方程为
物理方程为
(3)补充方程
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
A'
Δl1 Δl3 cos
A'
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
FN1
FN 3
EA E3 A3
cos2
10
(4)联立平衡方程与补充方程求解
