2018二次函数一题多问试卷
2018中考数学试题二次函数解答题试题汇编(含答案解析)

2018年全国各地中考数学试题《二次函数》解答题试题汇编(含答案解析)1.(2018•达州)如图,抛物线经过原点O(0,0),点A(1,1),点.(1)求抛物线解析式;(2)连接OA,过点A作AC⊥OA交抛物线于C,连接OC,求△AOC的面积;(3)点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N.问:是否存在点M,使以点O,M,N为顶点的三角形与(2)中的△AOC相似,若存在,求出点M的坐标;若不存在,说明理由.2.(2018•眉山)传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:y=(1)李明第几天生产的粽子数量为280只?(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价﹣成本)3.(2018•河南)如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.(1)求抛物线的解析式;(2)过点A的直线交直线BC于点M.①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M 的坐标.4.(2018•抚顺)俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y本,销售单价为x元.(1)请直接写出y与x之间的函数关系式和自变量x的取值范围;(2)当每本足球纪念册销售单价是多少元时,商店每天获利2400元?(3)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w 元最大?最大利润是多少元?5.(2018•张家界)如图,已知二次函数y=ax2+1(a≠0,a为实数)的图象过点A(﹣2,2),一次函数y=kx+b(k≠0,k,b为实数)的图象l经过点B(0,2).(1)求a值并写出二次函数表达式;(2)求b值;(3)设直线l与二次函数图象交于M,N两点,过M作MC垂直x轴于点C,试证明:MB=MC;(4)在(3)的条件下,请判断以线段MN为直径的圆与x轴的位置关系,并说明理由.6.(2018•资阳)已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值?(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.7.(2018•葫芦岛)某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.(1)请直接写出y与x之间的函数关系式;(2)如果每天获得160元的利润,销售单价为多少元?(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?8.(2018•新疆)如图,在平面直角坐标系中,抛物线y=x2﹣x﹣4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.(1)求点A,B,C的坐标;(2)点P从A点出发,在线段AB上以每秒2个单位长度的速度向B点运动,同时,点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t秒,求运动时间t为多少秒时,△PBQ的面积S最大,并求出其最大面积;(3)在(2)的条件下,当△PBQ面积最大时,在BC下方的抛物线上是否存在点M,使△BMC的面积是△PBQ面积的1.6倍?若存在,求点M的坐标;若不存在,请说明理由.9.(2018•山西)综合与探究如图,抛物线y=x﹣4与x轴交于A,B两点(点A在点B的左侧),与y 轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE ∥AC交x轴于点E,交BC于点F.(1)求A,B,C三点的坐标;(2)试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.10.(2018•青岛)某公司投入研发费用80万元(80万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为6元/件.此产品年销售量y(万件)与售价x(元/件)之间满足函数关系式y=﹣x+26.(1)求这种产品第一年的利润W1(万元)与售价x(元/件)满足的函数关系式;(2)该产品第一年的利润为20万元,那么该产品第一年的售价是多少?(3)第二年,该公司将第一年的利润20万元(20万元只计入第二年成本)再次投入研发,使产品的生产成本降为5元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件.请计算该公司第二年的利润W2至少为多少万元.11.(2018•福建)已知抛物线y=ax2+bx+c过点A(0,2).(1)若点(﹣,0)也在该抛物线上,求a,b满足的关系式;(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.①求抛物线的解析式;②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.12.(2018•乐山)已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).(1)求证:无论m为任何非零实数,此方程总有两个实数根;(2)若抛物线y=mx2+(1﹣5m)x﹣5=0与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.13.(2018•襄阳)襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为y=,且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成本是18元/千克,每天的利润是W 元(利润=销售收入﹣成本).(1)m=,n=;(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?14.(2018•荆门)随着龙虾节的火热举办,某龙虾养殖大户为了发挥技术优势,一次性收购了10000kg小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养10天的总成本为166000,放养30天的总成本为178000元.设这批小龙虾放养t天后的质量为akg,销售单价为y元/kg,根据往年的行情预测,a与t的函数关系为a=,y与t的函数关系如图所示.(1)设每天的养殖成本为m元,收购成本为n元,求m与n的值;(2)求y与t的函数关系式;(3)如果将这批小龙虾放养t天后一次性出售所得利润为W元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?(总成本=放养总费用+收购成本;利润=销售总额﹣总成本)15.(2018•贵阳)六盘水市梅花山国际滑雪自建成以来,吸引大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离y(单位:cm)与滑行时间x(单位:s)之间的关系可以近似的用二次函数来表示.(1)根据表中数据求出二次函数的表达式.现测量出滑雪者的出发点与终点的距离大约800m,他需要多少时间才能到达终点?(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向上平移5个单位,求平移后的函数表达式.16.(2018•盐城)如图①,在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且与y轴交于点C.(1)求抛物线的表达式;(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.(1)若点P的横坐标为﹣,求△DPQ面积的最大值,并求此时点D的坐标;(Ⅱ)直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.17.(2018•天津)在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx﹣2m(m是常数),顶点为P.(Ⅰ)当抛物线经过点A时,求顶点P的坐标;(Ⅱ)若点P在x轴下方,当∠AOP=45°时,求抛物线的解析式;(Ⅲ)无论m取何值,该抛物线都经过定点H.当∠AHP=45°时,求抛物线的解析式.18.(2018•邵阳)如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点B,和x轴的交点为点C,D(点D位于点C的左侧).(1)求函数y=ax2+bx+c的解析式;(2)从点A,C,D三个点中任取两个点和点B构造三角形,求构造的三角形是等腰三角形的概率;(3)若点M是线段BC上的动点,点N是△ABC三边上的动点,是否存在以AM 为斜边的Rt△AMN,使△AMN的面积为△ABC面积的?若存在,求tan∠MAN 的值;若不存在,请说明理由.19.(2018•济宁)如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).(1)求该抛物线的解析式;(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.20.(2018•杭州)设二次函数y=ax2+bx﹣(a+b)(a,b是常数,a≠0).(1)判断该二次函数图象与x轴的交点的个数,说明理由.(2)若该二次函数图象经过A(﹣1,4),B(0,﹣1),C(1,1)三个点中的其中两个点,求该二次函数的表达式.(3)若a+b<0,点P(2,m)(m>0)在该二次函数图象上,求证:a>0.21.(2018•温州)如图,抛物线y=ax2+bx(a≠0)交x轴正半轴于点A,直线y=2x 经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.(1)求a,b的值.(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m,△OBP的面积为S,记K=.求K关于m的函数表达式及K的范围.22.(2018•黔西南州)某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?23.(2018•黄冈)已知直线l:y=kx+1与抛物线y=x2﹣4x.(1)求证:直线l与该抛物线总有两个交点;(2)设直线l与该抛物线两交点为A,B,O为原点,当k=﹣2时,求△OAB的面积.24.(2018•河南)某公司推出一款产品,经市场调查发现,该产品的日销售量y (个)与销售单价x(元)之间满足一次函数关系关于销售单价,日销售量,日销售利润的几组对应值如表:(注:日销售利润=日销售量×(销售单价﹣成本单价))(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;(2)根据以上信息,填空:该产品的成本单价是元,当销售单价x=元时,日销售利润w最大,最大值是元;(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?25.(2018•黄冈)我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量y(万件)与月份x(月)的关系为:y=,每件产品的利润z(元)与月份x(月)的关系如下表:(1)请你根据表格求出每件产品利润z(元)与月份x(月)的关系式;(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;(3)当x为何值时,月利润w有最大值,最大值为多少?26.(2018•娄底)如图,抛物线y=ax2+bx+c与两坐标轴相交于点A(﹣1,0)、B (3,0)、C(0,3),D是抛物线的顶点,E是线段AB的中点.(1)求抛物线的解析式,并写出D点的坐标;(2)F(x,y)是抛物线上的动点:①当x>1,y>0时,求△BDF的面积的最大值;②当∠AEF=∠DBE时,求点F的坐标.27.(2018•黑龙江)如图,抛物线y=x2+bx+c与y轴交于点A(0,2),对称轴为直线x=﹣2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.(1)求此抛物线的解析式.(2)点P在x轴上,直线CP将△ABC面积分成2:3两部分,请直接写出P点坐标.28.(2018•北京)在平面直角坐标系xOy中,直线y=4x+4与x轴,y轴分别交于点A,B,抛物线y=ax2+bx﹣3a经过点A,将点B向右平移5个单位长度,得到点C.(1)求点C的坐标;(2)求抛物线的对称轴;(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.29.(2018•淄博)如图,抛物线y=ax2+bx经过△OAB的三个顶点,其中点A(1,),点B(3,﹣),O为坐标原点.(1)求这条抛物线所对应的函数表达式;(2)若P(4,m),Q(t,n)为该抛物线上的两点,且n<m,求t的取值范围;(3)若C为线段AB上的一个动点,当点A,点B到直线OC的距离之和最大时,求∠BOC的大小及点C的坐标.30.(2018•兰州)如图,抛物线y=ax2+bx﹣4经过A(﹣3,0),B(5,﹣4)两点,与y轴交于点C,连接AB,AC,BC.(1)求抛物线的表达式;(2)求证:AB平分∠CAO;(3)抛物线的对称轴上是否存在点M,使得△ABM是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.31.(2018•绍兴)学校拓展小组研制了绘图智能机器人(如图1),顺次输入点P1,P2,P3的坐标,机器人能根据图2,绘制图形.若图形是线段,求出线段的长度;若图形是抛物线,求出抛物线的函数关系式.请根据以下点的坐标,求出线段的长度或抛物线的函数关系式.(1)P1(4,0),P2(0,0),P3(6,6);(2)P1(0,0),P2(4,0),P3(6,6).32.(2018•巴中)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,﹣2),OB=4OA,tan∠BCO=2.(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)点M、N分别是线段BC、AB上的动点,点M从点B出发以每秒个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE 是等腰三角形?33.(2018•绵阳)如图,已知抛物线y=ax2+bx(a≠0)过点A(,﹣3)和点B(3,0).过点A作直线AC∥x轴,交y轴于点C.(1)求抛物线的解析式;(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D.连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;(3)抛物线上是否存在点Q,使得S=S△AOQ?若存在,求出点Q的坐标;△AOC若不存在,请说明理由.34.(2018•安徽)小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元).(1)用含x的代数式分别表示W1,W2;(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?35.(2018•遵义)在平面直角坐标系中,二次函数y=ax2+x+c的图象经过点C (0,2)和点D(4,﹣2).点E是直线y=﹣x+2与二次函数图象在第一象限内的交点.(1)求二次函数的解析式及点E的坐标.(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.36.(2018•随州)为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x 天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=设李师傅第x天创造的产品利润为W元.(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:(2)求李师傅第几天创造的利润最大?最大利润是多少元?(3)任务完成后,统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?37.(2018•广东)如图,已知顶点为C(0,﹣3)的抛物线y=ax2+b(a≠0)与x 轴交于A,B两点,直线y=x+m过顶点C和点B.(1)求m的值;(2)求函数y=ax2+b(a≠0)的解析式;(3)抛物线上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐标;若不存在,请说明理由.38.(2018•怀化)如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A (﹣1,0),B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.(1)求抛物线的解析式和直线AC的解析式;(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.39.(2018•黄石)已知抛物线y=a(x﹣1)2过点(3,1),D为抛物线的顶点.(1)求抛物线的解析式;(2)若点B、C均在抛物线上,其中点B(0,),且∠BDC=90°,求点C的坐标;(3)如图,直线y=kx+4﹣k与抛物线交于P、Q两点.①求证:∠PDQ=90°;②求△PDQ面积的最小值.40.(2018•达州)“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.(1)求该型号自行车的进价和标价分别是多少元?(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?41.(2018•遂宁)如图,已知抛物线y=ax2+x+4的对称轴是直线x=3,且与x 轴相交于A,B两点(B点在A点右侧)与y轴交于C点.(1)求抛物线的解折式和A、B两点的坐标;(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标.42.(2018•岳池县三模)如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P 的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.43.(2018•温州)温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元.设每天安排x人生产乙产品.(1)根据信息填表:(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.44.(2018•宜宾)在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=x与抛物线交于A、B两点,直线l为y=﹣1.(1)求抛物线的解析式;(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M 到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.45.(2018•深圳)已知顶点为A抛物线经过点,点.(1)求抛物线的解析式;(2)如图1,直线AB与x轴相交于点M,y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN ∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.46.(2018•湖州)已知抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),求a,b的值.47.(2018•岳阳)已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为(﹣,0).(1)求抛物线F的解析式;(2)如图1,直线l:y=x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);(3)在(2)中,若m=,设点A′是点A关于原点O的对称点,如图2.①判断△AA′B的形状,并说明理由;②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.48.(2018•无锡)已知:如图,一次函数y=kx﹣1的图象经过点A(3,m)(m >0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.(1)求这个一次函数的表达式;(2)已知一开口向下、以直线CD为对称轴的抛物线经过点A,它的顶点为P,若过点P且垂直于AP的直线与x轴的交点为Q(﹣,0),求这条抛物线的函数表达式.49.(2018•青海)如图,抛物线y=ax2+bx+c与坐标轴交点分别为A(﹣1,0),B (3,0),C(0,2),作直线BC.(1)求抛物线的解析式;(2)点P为抛物线上第一象限内一动点,过点P作PD⊥x轴于点D,设点P的横坐标为t(0<t<3),求△ABP的面积S与t的函数关系式;(3)条件同(2),若△ODP与△COB相似,求点P的坐标.50.(2018•日照)如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.51.(2018•湖北)绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?52.(2018•郴州)如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B (3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.(1)求抛物线的表达式;(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.(3)如图2,连接BC,PB,PC,设△PBC的面积为S.①求S关于t的函数表达式;②求P点到直线BC的距离的最大值,并求出此时点P的坐标.53.(2018•东营)如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B 两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.(1)求线段OC的长度;(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC 面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.54.(2018•扬州)“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,如图所示.(1)求y与x之间的函数关系式;(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?。
2018年中考数学真题分类汇编第二期专题13二次函数试题含解析

二次函数一.选择题1. (2018·湖北随州·3分)如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A.B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C.D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.其中正确的有()A.4个B.3个C.2个D.1个【分析】利用抛物线与y轴的交点位置得到c>0,利用对称轴方程得到b=﹣2a,则2a+b+c=c>0,于是可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点在点(﹣1,0)右侧,则当x=﹣1时,y <0,于是可对②进行判断;根据二次函数的性质得到x=1时,二次函数有最大值,则ax2+bx+c≤a+b+c,于是可对③进行判断;由于直线y=﹣x+c与抛物线y=ax2+bx+c交于C.D两点,D点在x轴下方且横坐标小于3,利用函数图象得x=3时,一次函数值比二次函数值大,即9a+3b+c<﹣3+c,然后把b=﹣2a代入解a的不等式,则可对④进行判断.【解答】解:∵抛物线与y轴的交点在x轴上方,∴c>0,∵抛物线的对称轴为直线x=﹣=1,∴b=﹣2a,∴2a+b+c=2a﹣2a+c=c>0,所以①正确;∵抛物线与x轴的一个交点在点(3,0)左侧,而抛物线的对称轴为直线x=1,∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,∴当x=﹣1时,y<0,∴a﹣b+c<0,所以②正确;∵x=1时,二次函数有最大值,∴ax2+bx+c≤a+b+c,∴ax2+bx≤a+b,所以③正确;∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C.D两点,D点在x轴下方且横坐标小于3,∴x=3时,一次函数值比二次函数值大,即9a+3b+c<﹣3+c,而b=﹣2a,∴9a﹣6a<﹣3,解得a<﹣1,所以④正确.故选:A.【点评】本题考查了二次函数与不等式(组):利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,可作图利用交点直观求解.也考查了二次函数图象与系数的关系.2. (2018·湖北襄阳·3分)已知二次函数y=x2﹣x+m﹣1的图象与x轴有交点,则m的取值范围是()A.m≤5 B.m≥2 C.m<5 D.m>2【分析】根据已知抛物线与x轴有交点得出不等式,求出不等式的解集即可.【解答】解:∵二次函数y=x2﹣x+m﹣1的图象与x轴有交点,∴△=(﹣1)2﹣4×1×(m﹣1)≥0,解得:m≤5,故选:A.【点评】本题考查了抛物线与x轴的交点,能根据题意得出关于m的不等式是解此题的关键.3.(2018•山东东营市•3分)如图所示,已知△ABC中,BC=12,BC边上的高h=6,D为BC上一点,EF∥BC,交AB于点E,交AC于点F,设点E到边BC的距离为x.则△DEF的面积y关于x的函数图象大致为()A.B.C.D.【分析】可过点A向BC作AH⊥BC于点H,所以根据相似三角形的性质可求出EF,进而求出函数关系式,由此即可求出答案.【解答】解:过点A向BC作AH⊥BC于点H,所以根据相似比可知:=,即EF=2(6﹣x)所以y=×2(6﹣x)x=﹣x2+6x.(0<x<6)该函数图象是抛物线的一部分,故选:D.【点评】此题考查根据几何图形的性质确定函数的图象和函数图象的读图能力.要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件,结合实际意义画出正确的图象.4.(2018•山东烟台市•3分)如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是()A.①③ B.②③ C.②④ D.③④【分析】根据二次函数图象与系数之间的关系即可求出答案.【解答】解:①图象与x轴交于点A(﹣1,0),B(3,0),∴二次函数的图象的对称轴为x==1∴=1∴2a+b=0,故①错误;②令x=﹣1,∴y=a﹣b+c=0,∴a+c=b,∴(a+c)2=b2,故②错误;③由图可知:当﹣1<x<3时,y<0,故③正确;④当a=1时,∴y=(x+1)(x﹣3)=(x﹣1)2﹣4将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣1﹣1)2﹣4+2=(x﹣2)2﹣2,故④正确;故选:D.【点评】本题考查二次函数图象的性质,解题的关键是熟知二次函数的图象与系数之间的关系,本题属于中等题型.5.(2018•上海•4分)下列对二次函数y=x2﹣x的图象的描述,正确的是()A.开口向下 B.对称轴是y轴C.经过原点 D.在对称轴右侧部分是下降的【分析】A.由a=1>0,可得出抛物线开口向上,选项A不正确;B.根据二次函数的性质可得出抛物线的对称轴为直线x=,选项B不正确;C.代入x=0求出y值,由此可得出抛物线经过原点,选项C正确;D.由a=1>0及抛物线对称轴为直线x=,利用二次函数的性质,可得出当x>时,y随x值的增大而增大,选项D不正确.综上即可得出结论.【解答】解:A.∵a=1>0,∴抛物线开口向上,选项A不正确;B.∵﹣=,∴抛物线的对称轴为直线x=,选项B不正确;C.当x=0时,y=x2﹣x=0,∴抛物线经过原点,选项C正确;D.∵a>0,抛物线的对称轴为直线x=,∴当x>时,y随x值的增大而增大,选项D不正确.故选:C.【点评】本题考查了二次函数的性质以及二次函数的图象,利用二次函数的性质逐一分析四个选项的正误是解题的关键.6.(2018•达州•3分)如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:①abc<0;②9a+3b+c>0;③若点M(,y1),点N(,y2)是函数图象上的两点,则y1<y2;④﹣<a<﹣.其中正确结论有()A.1个B.2个C.3个D.4个【分析】根据二次函数的图象与系数的关系即可求出答案.【解答】解:①由开口可知:a<0,∴对称轴x=>0,∴b>0,由抛物线与y轴的交点可知:c>0,∴abc<0,故①正确;②∵抛物线与x轴交于点A(﹣1,0),对称轴为x=2,∴抛物线与x轴的另外一个交点为(5,0),∴x=3时,y>0,∴9a+3b+c>0,故②正确;③由于<2,且(,y2)关于直线x=2的对称点的坐标为(,y2),∵,∴y1<y2,故③正确,④∵=2,∴b=﹣4a,∵x=﹣1,y=0,∴a﹣b+c=0,∴c=﹣5a,∵2<c<3,∴2<﹣5a<3,∴﹣<a<﹣,故④正确故选:D.【点评】本题考查二次函数的图象与性质,解题的关键是熟练运用图象与系数的关系,本题属于中等题型.7.(2018•遂宁•4分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是()A.B.C.D.【分析】利用抛物线开口方向得到a>0,利用抛物线的对称轴在直线x=1的右侧得到b<0,b<﹣2a,即b+2a <0,利用抛物线与y轴交点在x轴下方得到c<0,也可判断abc>0,利用抛物线与x轴有2个交点可判断b2﹣4ac>0,利用x=1可判断a+b+c<0,利用上述结论可对各选项进行判断.【解答】解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴在直线x=1的右侧,∴x=﹣>1,∴b<0,b<﹣2a,即b+2a<0,∵抛物线与y轴交点在x轴下方,∴c<0,∴abc>0,∵抛物线与x轴有2个交点,∴△=b2﹣4ac>0,∵x=1时,y<0,∴a+b+c<0.故选:C.【点评】本题考查了二次函数图象与系数的关系:二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a 与b同号时,对称轴在y轴左;当a与b异号时,对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由判别式确定:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.8. (2018•资阳•3分)已知二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有A.B.c三个字母的等式或不等式:①=﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是()A.4个B.3个C.2个D.1个【分析】此题可根据二次函数的性质,结合其图象可知:a>0,﹣1<c<0,b<0,再对各结论进行判断.【解答】解:①=﹣1,抛物线顶点纵坐标为﹣1,正确;②ac+b+1=0,设C(0,c),则OC=|c|,∵OA=OC=|c|,∴A(c,0)代入抛物线得ac2+bc+c=0,又c≠0,∴ac+b+1=0,故正确;③abc>0,从图象中易知a>0,b<0,c<0,故正确;④a﹣b+c>0,当x=﹣1时y=a﹣b+c,由图象知(﹣1,a﹣b+c)在第二象限,∴a﹣b+c>0,故正确.故选:A.【点评】本题考查了二次函数的性质,重点是学会由函数图象得到函数的性质.9. (2018•杭州•3分)四位同学在研究函数(b,c是常数)时,甲发现当时,函数有最小值;乙发现是方程的一个根;丙发现函数的最小值为3;丁发现当时,.已知这四位同学中只有一位发现的结论是错误的,则该同学是()A. 甲B.乙 C. 丙 D. 丁【答案】B【考点】二次函数图象与系数的关系,二次函数的最值【解析】【解答】解:根据题意得:抛物线的顶点坐标为:(1,3)且图像经过(2,4)设抛物线的解析式为:y=a(x-1)2+3∴a+3=4解之:a=1∴抛物线的解析式为:y=(x-1)2+3=x2-2x+4当x=-1时,y=7,∴乙说法错误故答案为:B【分析】根据甲和丙的说法,可知抛物线的顶点坐标,再根据丁的说法,可知抛物线经过点(2,4),因此设函数解析式为顶点式,就可求出函数解析式,再对乙的说法作出判断,即可得出答案。
2018年全国各地中考数学真题汇编:二次函数(含答案)-数学备课大师【全免费】

中考数学真题汇编:二次函数一、选择题1.给出下列函数:①y=﹣3x+2;②y= ;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是()A. ①③B. ③④C. ②④D. ②③【答案】B2.如图,函数和( 是常数,且)在同一平面直角坐标系的图象可能是()A. B. C. D.【答案】B3.关于二次函数,下列说法正确的是()A. 图像与轴的交点坐标为B. 图像的对称轴在轴的右侧C. 当时,的值随值的增大而减小D. 的最小值为-3【答案】D4.二次函数的图像如图所示,下列结论正确是( )A. B. C. D. 有两个不相等的实数根【答案】C5.若抛物线与轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )A. B. C. D.【答案】B6.若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线。
已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点()A. (-3,-6)B. (-3,0)C. (-3,-5)D. (-3,-1)【答案】B7.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是()A. 点火后9s和点火后13s的升空高度相同B. 点火后24s火箭落于地面C. 点火后10s的升空高度为139mD. 火箭升空的最大高度为145m【答案】D8.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是()A. 1B. 2C. 3D. 4【答案】B9.如图是二次函数(,,是常数,)图象的一部分,与轴的交点在点和之间,对称轴是.对于下列说法:①;②;③;④(为实数);⑤当时,,其中正确的是()A. ①②④B. ①②⑤C. ②③④D. ③④⑤【答案】A10.如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为-1,则一次函数y=(a-b)x+b的图象大致是()A. B. C. D.【答案】D11.四位同学在研究函数(b,c是常数)时,甲发现当时,函数有最小值;乙发现是方程的一个根;丙发现函数的最小值为3;丁发现当时,.已知这四位同学中只有一位发现的结论是错误的,则该同学是()A. 甲B. 乙C. 丙D. 丁【答案】B12.如图所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,则y与x之间的函数图象大致为()A. (B.C. D. (【答案】B二、填空题13.已知二次函数,当x>0时,y随x的增大而________(填“增大”或“减小”)【答案】增大14.右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加________m。
二次函数几何方面的应用(解析版)数学2018全国中考真题-3

2018年数学全国中考真题二次函数几何方面的应用(试题一)解析版一、选择题1.(2018广西省桂林市,12,3分)如图,在平面直角坐标系中,M、N、C三点的坐标分别为(12,1),(3,1),(3,0),点A为线段MN上的一个一动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A 从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )A.14-≤b≤1 B.54-≤b≤1 C.94-≤b≤12D.94-≤b≤1【答案】B.【思路分析】.如下图(1),连接CN,延长NM,交y轴于点D,设AN=x,则AD=3-x,DB=1b+,证明△BDA∽△ANC,可得b=23523124x x x-+-=--+⎛⎫⎪⎝⎭≤54,从而得到b的取值范围.【解题过程】解:如下图(1),连接CN,延长NM,交y轴于点D,设AN=x,则AD=3-x,∵点B的坐标为(0,b),∴DB=1b+,∵N、C两点的坐标分别为(3,1),(3,0),∴NC=1,AN⊥NC,∴∠ACN+∠CAN =90°,∵AB⊥AC,∴∠BAD+∠CAN=90°,∴∠ACN=∠CAN,又∵∠BDA=∠CNA=90°,∴△BDA∽△ANC,∴AD BDCN AN=,即131bxx+-=,213b x x+=-+,解得b=23523124x x x-+-=--+⎛⎫⎪⎝⎭≤54,又∵当点A与点N重合时,点B与点D重合,(如下图(2)),此时b=1,∴54-≤b≤1.,故选B.【知识点】二次函数;相似三角形的性质和判定;动点问题二、填空题1.(2018吉林长春,14,3分)如图,在平面直角坐标系中,抛物线y=x2 + mx 交x轴的负半轴于点A. 点B是y轴正半轴上一点,点A关于点B的对称点A' 恰好落在抛物线上. 过点A' 作x轴的平行线交抛物线于另一点C.若点A' 的横坐标为1,则A'C 的长为 .(第14题)【答案】3【思路分析】如下图,A'C 与y 轴交于点D. 因为点A 与点A' 关于点B 对称,则AB=A'B ;又因A'C// x 轴,则ΔABO ≌ ΔA'BD ,AO=A'D. 点A' 的横坐标为1,即A'D=AO=1.所以点A 坐标为(-1,0),把点A (-1,0)代入函数解析式可求得m 值,进而可知A' 坐标,由A'C// x 轴,可求出点C 横坐标,即可求出A'C 的长.【解题过程】解:如图,A'C 与y 轴交于点D. ∵点A 与点A' 关于点B 对称 ∴AB=A'B 又A'C// x 轴∴∠A'DB =∠AOB =90°,∠DA'B =∠OAB ∴ΔABO ≌ ΔA'BD ∴AO=A'D∵点A' 的横坐标为1 ∴A'D=AO=1∴A 坐标为(-1,0)把(-1,0) 代入抛物线解析式y =x 2 + mx 得m=1 ∴抛物线解析式为y =x 2 + x ∴ A' 坐标为(1,2) 令y =2得,x 1 = -2 , x 2=1 ∴A'C =1-(-2)=3.【知识点】待定系数法求抛物线解析式,对称的性质,平行线的性质,三角形全等,直角坐标系中求线段长度2. (2018广西贵港,12,3分)如图,抛物线y =14(x +2)(x -8)与x 轴交于A ,B 两点,与y 轴交于点C ,顶点为M ,以AB 为直径作⊙D ,下列结论:①抛物线的对称轴是直线x =3;②⊙D 的面积是16π;③抛物线上存在点E ,使四边形ACED 为平行四边形;④直线CM 与⊙D 相切.其中正确结论的个数是 A .1 B .2 C .3 D .4【答案】B【解析】抛物线y =14(x+2)(x-8)与x轴交于A,B两点,可知A(-2,0),B(8,0)所以D(3,0),所以抛物线的对称轴是直线x=3,即①正确;由于⊙D的半径为5,所以它的面积为25π,所以②不正确;过C作CF∥AD,则F(6,0),此时CF=6>5=AD,因此在抛物线上不可能存在点E,使四边形ACED为平行四边形,故③错误;当x=0时,y=-4,所以C点的坐标为(0,-4),因此DC=42+32=5,即C在⊙D上,又M(3,-254),所以DM=254,CM=32+⎝⎛⎭⎫254-42=154所以DC2+CM2=62516=DM2,所以DC⊥CM,所以直线CM与⊙D相切,故④正确;综上,有两项正确,故选B.3.(2018江苏苏州,18,3分)如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE 的中点.当点P在线段AB上移动时,点M,N之问的距离最短为(结果保留根号).【答案】23【解析】本题解答时要连接MP,PN,利用菱形的性质,得出△PMN为直角三角形,然后利用勾股定理,求出用PA的长来表示的MN的长,最后利用二次函数的性质求出MN的最小值.连接PM,PN,∵四边形APCD,PBFE是菱形,∴P A=PC,∵AM=MC,∴PM⊥AC,同理PN⊥BE.∴∠CPM+∠CPN=119022APC BPE∠+∠=゜,∵∠DAP=60゜,∴∠CAP==∠NPB=30゜,xyOACMBDE设AP =x ,则PB =8-x , ∴PM =12x ,PN)x -∴=∴当x =6时,MN有最小值,最小值为三、解答题1. (2018广西柳州市,26,10分)如图,抛物线y =ax 2+bx +c 与x 轴交于0),B 两点(点B 在点A 的左侧),与y 轴交于点C ,且OB =3OAOC ,∠OAC 的平分线AD 交y 轴于点D ,过点A 且垂直于AD 的直线l 交y 轴于点E ,点P 是x 轴下方抛物线的一个动点,过点P 作PF ⊥x 轴垂足为F ,交直线AD 于点H. (1)求抛物线的解析式;(2)设点P 的横坐标为m ,当FH =HP 时,求m 的值;(3)当直线PF 为抛物线的对称轴时,以点H 为圆心,12HC 为半径作⊙H ,点Q 为⊙H 上的一个动点,求14AQ +EQ 的最小值.【思路分析】(1)根据题意,先求出点B 、C 的坐标,运用待定系数求出抛物线的解析式; (2)用点m 表示出FH 和PF 的长,再由FH =HP 列关于m 的方程求解;FAP(3)连接AH ,以AH 为边构造相似三角形,将14AQ 转化为某一个固定点的线段,再由三点共线计算出14AQ +EQ 的最小值. 【解题过程】(1)∵OB =3OA =OC ,0),∴点B 、C 的坐标分别为(-,0),(-3,0).设抛物线的解析式为y =a (x +x ),代入点C 的坐标,得:-3=a ··(,解得:a =13.故该抛物线的解析式为y =13(x +)(x =13x 2x -3. ………………3分(2)在Rt △AOC 中,由tan ∠OAC =OCOA,∴∠OAC =60°.又∵AH 是∠FAC 的平分线,∴∠FAH =30°,则AF由点P 的横坐标为m ,则它的纵坐标为13m 2-3.∴AF m ,PF =3-13m 2.∴FH AF m ). ∵FH =HP ,则PF =2FH ,m )=13m 2-3.解得:m 舍去)或m故m ………………6分 (3)连接CH.∵AF =AC =,∠FAH =∠CAH ,AF =AF , ∴△AHF ≌△AHC(SAS), ∴FH =CH =2. 故⊙H 的半径为1.在HA 上截取HM =14,则AM =4-14=154. ∵HM HQ =14,HQ HA =14, ∴HM HQ =HQHA,且∠QHM =∠AHQ , ∴△QHM ∽△AHQ ,∴AQMQ=14,则14AQ=MQ,∴14AQ+QE=QM+QE. ………………9分∵点E、M是定点,故当点M、Q、E共线时,QM+QE的值最小,即最小值为线段ME的长.在Rt△AEM中,由勾股定理可知:ME………………10分2.(2018海南省,24,15分)如图12-1,抛物线32++=bxaxy交x轴于点A(﹣1,0)和点B(3,0).(1)求该抛物线所对应的函数解析式;(2)如图12-2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.①求四边形ACFD的面积;②点P是线段AB上的动点(点P不与点A,B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ,DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.【思路分析】将A(﹣1,0)和点B(3,0)代入32++=bxaxy,求解关于a,b的二元一次方程组即可;(2)①分别求出点C、F的坐标,S四边形ACFD=S△CDF+S△CDA;②当∠ADQ=90°时,如图24-2,设PQ交CD于点G,则PQ⊥CD,G点坐标为(t,3),作DH⊥x轴于H,则H(2,0),在Rt∠DHA中,DH=AH=3,∠DGQ为等腰三角形,GQ =GD ,()t t t -=-++-23322,求得t 的值并验证;当∠AQD =90°时,过点D 作DK ⊥PQ 于点K ,易证得∠PQA ∽△KDQ , KQ PA KD PQ =,()323123222++--+=-++-t t t t t t ,求得t 的值并验证. 【解题过程】(1)将A (﹣1,0)和点B (3,0)代入32++=bx ax y 得,⎩⎨⎧=++=+-033903b a b a ,解得⎩⎨⎧=-=21b a ,∴该抛物线的解析式为322++-=x x y .(2)①连接CD ,∵()413222+--=++-=x x x y ,F (1,4),当x =0时,y =3,∠C (0,3)又D (2,3),∠CD ∥x 轴,且CD =2,S 四边形ACFD =S △CDF +S △CDA =21CD ·(A F y y -)=44221=⨯⨯. ②设P (t ,0),则Q (t ,322++-t t ).Ⅰ:若∠DAQ =90°,如图24-1,此时点Q 必在第四象限,所对应的点P 在AB 的延长线上,此种情况不符合题意,故舍去.Ⅱ:若∠ADQ =90°,如图24-2,设PQ 交CD 于点G ,则PQ ⊥CD ,G 点坐标为(t ,3),作DH ⊥x 轴于H ,则H(2,0),∴在Rt∠DHA 中,DH =AH =3,∠∠DAH =45°,又CD ∥x 轴,∠∠ADC =∠DAH =45°,∠∠QDG =∠ADQ﹣∠ADC =45°,∠∠DGQ 为等腰三角形,∴GQ =GD ,()t t t -=-++-23322,整理得:0232=+-t t ,解得:11=t ,22=t ,当t=2时,D 与Q 重合,故舍去.当t =1时,4322=++-t t ,∠Q (1,4). Ⅲ:若∠AQD =90°,如图24-3过点D 作DK ⊥PQ 于点K ,∠∠APQ =∠QKD =90°,∠∠DQK +∠PQA =90°,又∠DQK +∠KDQ =90°,∴∠PQA =∠KDQ ,∠∠PQA ∽△KDQ ,∴KQ PA KD PQ =,∴()323123222++--+=-++-t t t t t t ,∴()()()21213-+=-+--t t t t t t ,∵1-≠t ,2≠t (即Q 不与A 、D 重合),∴()tt 13=--,整理得:0132=+-t t ,解得2531+=t ,2532-=t ,经验证,1t 、2t 均符合题意,其中:321<<t ,符合图24-3的情况,212<<-t ,符合图24-4的情况. 当2531+=t 时,255322-=++-t t ;当2532-=t 时,255322+=++-t t , ∴Q (253+,255-)或(253-,255+). 综上所述,当∠AQD 为直角三角形时,点Q 坐标为:(1,4)或(253+,255-)或(253-,255+). 【知识点】二次函数综合题,二次函数图象上点的存在性,相似三角形的性质与判定3. (2018黑龙江省龙东地区,23,6分) 如图,抛物线y =x 2+bx +c 与y 轴交于点A (0,2),对称轴为直线x =-2,平行于x 轴的直线与抛物线交于B 、C 两点,点B 在对称轴左侧,BC =6. (1)求此抛物线的解析式;(2)点P 在x 轴上,直线CP 将△ABC 面积分成2:3的两部分,请直接写出P 点坐标.【思路分析】对于(1),根据点A 坐标可求c 的值,根据对称轴直线可求b 的值;对于(2),先确定点C 和点B 的坐标,计算出△ABC 的面积,再根据直线CP 分△ABC 面积之比确定点P 存在的可能性有两种,结合两种情况,分别确定点P 的位置即可. 【解题过程】解:(1)∵点A (0,2)在抛物线y =x 2+bx +c 上,∴c =2,∵抛物线对称轴为直线x =-2,∴221b-=-⨯,∴b =4,∴抛物线的解析式为y =x 2+4x +2. (2)点P 的坐标为(-5,0)或(-13,0),理由如下:∵抛物线对称轴为直线x =-2,BC ∥x 轴,且BC =6,∴点C 的横坐标为6÷2-2=1,把x =1代入y =x 2+4x +2得y =7,∴C (1,7),∴△ABC 中BC 边上的高为7-2=5,∴S △ABC =12×6×5=15.令y =7,得x 2+4x +2=7,解得x 1=1,x 2=-5,∴B (-5,7),∴AB=CP 交AB 于点Q ,∵直线CP 将△ABC 面积分成2:3的两部分,∴符合题意的点P 有两个,对应的点Q 也有两个.①当AQ 1:BQ 1=2:3时,作Q 1M 1⊥y 轴,Q 1N 1⊥BC ,则AQ 1=Q 1M 1=2,BQ 1=Q 1N 1=3,Q 1(-2,4),∵C (1,7),∴直线CQ 1的解析式为y =x +5,令y =0,则x =-5,∴P 1(-5,0); ②当BQ 2:AQ 2=2:3时,作Q 2M 2⊥y 轴,Q 2N 2⊥BC ,则AQ 2=Q 2M 2=3,BQ 2=,Q 2N 2=2,Q 2(-3,5),∵C (1,7),∴直线CQ 2的解析式为y =12x +132,令y =0,则x =-13,∴P 2(-13,0) 综上,点P 的坐标为(-5,0)或(-13,0).【知识点】待定系数法;二次函数的性质;一次函数的性质;三角形的面积公式;平行线分线段成比例25.4. (2018山东省东营市,25,12分) 如图,抛物线13()()y a x x =--(0a >)与x 轴交于A 、B 两P 的坐解得:x 1=1,x 2=3则A (1,0),B (3,0)于是OA =1,OB =3∵△OCA ∽△OBC ∴OC ∶OB =OA ∶OC ∴OC 2=OA •OB =3即OC =(2)因为C 是BM 的中点 ∴OC =BC 从而点C 的横坐标为23又OC =,点C 在x 轴下方∴C ),(2323-设直线BM 的解析式为y =kx +b , 因其过点B (3,0),C ),(2323-,则有⎪⎩⎪⎨⎧-=+=+.232303b k b k ,∴, ∴ 又点C 在抛物线上,代入抛物线解析式,P 作PQ x 轴交直线BM 于点Q , 则Q (x ,),PQ = 当△BCP 面积最大时,四边形ABPC 的面积最大33=k 333-=x y ),(2323-32333-x 33333322-+-x x )()(△2321321-+-=x PQ x PQ S BCP )(23321-+-=x x PQ PQ 43=∴当时,有最大值,四边形ABPC 的面积最大, 此时点P 的坐标为(3)点P 存在. 设点P 坐标为(x ,),过点P 作PQ x 轴交直线BM 于点Q , 则Q (x ,),PQ = 当△BCP 面积最大时,四边形ABPC 的面积最大∴当时,有最大值,四边形ABPC 的面积最大, 此时点P 的坐标为43943923 2-+-=x x 492=-=a b x BCP S △)385-,49(323383322+-x x 333-x 33333322-+-x x )()(△2321321-+-=x PQ x PQ S BCP )(23321-+-=x x PQ PQ 43=43943923 2-+-=x x 492=-=a b x BCP S △)385-,49(【知识点】一元二次方程与二次函数的关系,中点坐标公式,相似三角形性质,待定系数法求直线与抛物线的解5. (2018四川乐山,1,3) 在平面直角坐标系中,抛物线2y ax bx c =++交x 轴于A 、B 两点,交y 轴于点C(0,43-),OA =1,OB =4,直线l 过点A ,交y 轴于点D ,交抛物线于点E ,且满足tan ∠OAD =34. (1)求抛物线的解析式;(2)动点P 从点B 出发,沿x 轴正方向以每秒2个单位长度的速度向点A 运动,动点Q 从点A 出发,沿射线AE 以每秒1个单位长度的速度向点E 运动,当点P 运动到点A 时,点Q 也停止运动,设运动为t 秒. ①在P 、Q 的运动过程中,是否存在某一时刻t ,使得△ADC 与△PQA 相似,若存在,求出t 的值;若不存在,请说明理由;②在P 、Q 的运动过程中,是否存在某一时刻t ,使得△APQ 与△CAQ 的面积之和最大?若存在,求出t 的值;若不存在,请说明理由.【思路分析】本题是代数几何综合题,以平面直角坐标系为背景,考查了求二次函数解析式,二次函数的性质,,方程组的解法,几何图形面积的表示,相似三角形的判定与性质,分类讨论思想,三角形的面积的最值问题,综合性强,难度大,解题的关键是需要学生有良好的运算能力及分析问题和解决问题的能力,还得富有耐心.(1)利用A 、B 、C 三点的坐标确定二次函数的解析式.(2)利用题目的已知条件表示出相关线段的长,①中利用三角函数值探索出∠P AQ =∠ACD ,再根据题目中的要求使得△ADC 与△PQA 相似,进行分类讨论得到对应线段成xyQ PEDCBAOyxQMC BA O P(第25题答案图2)比例,列出关于t 的方程求解即可;②直接利用三角形的面积公式列出△APQ 与△CAQ 的面积之和与时间t 之间的函数关系式,再将所得的二次函数的解析式配方确定最值即可得到答案. 【解题过程】解:(1)∵OA =1,OB =4,∴A (1,0),B (-4,0), -------------------- 1分 设所示抛物线的解析式为()()41y a x x =+-, ∵C (0,43-)在抛物线上, ∴()4413a -=⨯⨯-, 解得13a =, ∴抛物线的解析式为()()1413y x x =+-或21433y x x =+- ----------------------------- 3分 (2)存在t ,使得△ADC 与△PQA 相似,其理由如下: ①在Rt △AOC 中,OA =1,43OC =, 则3tan 4OA ACO OC ∠==, 又∵3tan 4OAD ∠=, ∴∠OAD =∠ACO , ------------------------------------------------------------------------------------- 4分 ∵直线l 的解析式为()314y x =- ,∴D (0,34-), 又∵C (0,43-), ∴CD =4373412-= 由AC 2=OC 2+OA 2,得53AC =. ---------------------------------------------------------------------- 5分 在△AQP 中,AP =AB -PB =5-2t ,AQ =t , 由∠P AQ =∠ACD ,要使△ADC 与△PQA 相似,只需AP CD AQ AC =或AP ACAQ CD=, ------------------------------------------------------------------- 6分 则有7521253t t -=或5523712t t -=, ----------------------------------------------------------------- 7分 解得110047t =,23534t =, ∵t 1<2.5,t 2<2.5, ∴存在10047t =或3534t =, 使得△APQ 与△PQA 相似 -------------------------------------- 9分 ②存在t ,使得△APQ 与△CAQ 的面积之和最大,其理由如下:作PF ⊥AQ 于点F ,CN ⊥AQ 于点N , 如图6所示,在△APF 中,()3sin 525PF AP PAF t =⋅∠=-, 在△AOD 中,由AD 2=OD 2+OA 2,得54AD =------------------------------------------------- 10分 在△ADC 中,由1122ADC S AD CN CD OA ∆=⋅=⋅, ∴717125154CD OA CN AD ⨯⋅=== ------------------------------------------------------------------- 11分∴()()11375222515APQ CAQS S AQ PF CN t t ∆∆⎡⎤+=+=-+⎢⎥⎣⎦231316959135t ⎛⎫=--+ ⎪⎝⎭ ∴当139t =时,△APQ 与△CAQ 的面积之和最大. ------------------------------------------- 12分图6【知识点】二次函数 ;勾股定理;三角形相似的判定与性质;三角形面积;待定系数法;转化思想;数形结合思想;分类讨论思想6.(2018甘肃省兰州市,28,12分)如图,抛物线42-+=bx ax y 经过A (-3,0),B (5,-4)两点,与y 轴交于点C ,连接AB ,AC ,BC .(1)求抛物线的表达式; (2)求证:AB 平分CAO ∠;(3)抛物线的对称轴上是否存在点M ,使得ABM ∆是以AB 为直角边的直角三角形.若存在,求出点M 的坐标;若不存在,说明理由.【思路分析】(1)根据A ,B 两点的坐标利用待定系数法求解即可.(2)通过证明点B 到直线AC 的距离等于点B 到x 轴的距离即可证明结论.(3)分AM 为该直角边的斜边和BM 为该直角三角形的斜边两种情况,分别计算即可.【解题过程】(1)将A ,B 两点的坐标分别代入42-+=bx ax y ,得⎩⎨⎧-=-+=--,44525,0439b a b a 解得⎪⎪⎩⎪⎪⎨⎧-==,65,61b a故抛物线的表达式为y =465612--=x x y . xyN F Q PED CBAOACBxyO第28题图(2)证明:设直线AB 的表达式为y =kx +b ′,则3'0,5'4,k b k b -+=⎧⎨+=-⎩解得⎪⎪⎩⎪⎪⎨⎧-=-=,23',21b k 故直线AB 的表达式为y =2321--x .设直线AB 与y 轴的交点为点D ,则点D 的坐标为(0,23-).易得点C 的坐标为(0,-4),则由勾股定理,可得AC =5)04(]30[22=--+--)(. 设点B 到直线AC 的距离为h , 则52132121⨯⨯+⨯⨯=⨯CD CD AC h , 解得h =4.易得点B 到x 轴的距离为4, 故AB 平分∠CAO . (3)存在.易得抛物线的对称轴为直线25=x , 设点M 的坐标为(m ,25).由勾股定理,得AB 2=[5-(-3)]2+(-4-0)2=80,AM 2=[25-(-3)]2+(m -0)2=4121+m 2,BM 2=(25-5)2+[m -(-4)]2=m 2+8m +489. 当AM 为该直角三角形的斜边时, 有AM 2=AB 2+BM 2,即4121+m 2=80+m 2+8m +489, 解得m =-9,故此时点M 的坐标为(25,-9).当BM 为该直角三角形的斜边时, 有BM 2=AB 2+AM 2,即m 2+8m +489=80+4121+m 2, 解得m =11,故此时点M 的坐标为(25,11). 综上所述,点M 的坐标为(25,-9)或(25,11). 【知识点】二次函数的图象和性质 角平分线的判定与性质 勾股定理 分类讨论7. (2018黑龙江省齐齐哈尔市,题号24,分值14)如图1所示,直线y=x+c 与x 轴交于点A (-4,0),与y 轴交于点C ,抛物线y=-x ²+bx+c 经过点A ,C. (1)求抛物线的解析式;(2)点E 在抛物线的对称轴上,求CE+OE 的最小值;(3)如图2所示,M 是线段OA 上的一个动点,过点M 垂直于x 轴的直线与直线AC 和抛物线分别交于点P 、N.①若以C ,P ,N 为顶点的三角形与△APM 相似,则△CPN 的面积为_________;②若点P 恰好是线段MN 的中点,点F 是直线AC 上一个动点,在坐标平面内是否存在点D ,使以点D ,F ,P ,M 为顶点的四边形是菱形?若存在,请直接写出点D 的坐标;若不存在,请说明理由.注:二次函数y=ax ²+bx+c (a ≠0)的顶点坐标为(24,24b ac b aa --)【思路分析】(1)根据一次函数求出c 的值,再将A (-4,0)和c 值代入抛物线解析式求得b 值,进而得出抛物线解析式;(2)先作对称确定最小值的情况,进而求出答案.(3)①根据直角与对顶角找出两种相似的情况,进而得出△CPN 的面积;②根据菱形的判定定理作出菱形,进而得出D 点坐标. 【解题过程】解:(1)将A (-4,0)代入y=x+c ,得c=4.将A (-4,0)和c=4代入y=-x²+bx+c,得b=-3. ∴抛物线的解析式为y=-x ²-3x+4.(2)如图所示,作点C 关于抛物线的对称轴直线l 的对称点C ’,连接OC 交直线l 于点E ,连接CE ,此时CE+OE 的值最小.∵抛物线额对称轴为x=332(1)2--=-⨯-,则C ’C=3,在Rt △C ’CO 中,由勾股定理,得OC ’22(')CC OC +∴CE+OE 的最小值为5.(3)①∵抛物线解析式为y=-x ²-3x+4,∴A (-4,0),B (1,0),C (0,4),△APM 为等腰直角三角形. 设M 为(a ,0),则N (a ,-a ²-3a+4),P(a ,a+4).当△AMP ∽△CNP 时,则AM MP CN NP=,得24434(4)a a a a a a ++=---+-+,解得a=-4(舍)或a=-3或a=0(舍). ∴CN=3,PN=3. ∴△CPN 的面积为12CN PN =92. 当△AMP∽△NCP时,则AM APNC NP=,得22222(4)34(4)(344)()a a a a a a a +=--+-+--+-+-,解得a=0(舍)或a=-2.∴.∴△CPN 的面积为12CN PC =4. 故答案为92或4.②存在. 1D (22-+,2),2D (22--,-2), 3D (-4,3),4D (12,32). 理由如下:当点P 是线段MN 的中点,则-a ²-3a+4=2(a+4), 解得a=-4(舍),或a=-1. ∴M (-1,0),P (-1,3),N (-1,6).设F(f ,f+4),过点M 作AC 的平行线,则此直线的解析式为 y=x+1.∵PM=3,当PM 为菱形的边时,作PF=PM ,过F 作FD 平行PM ,交AC 平行线于点D , ∴D (f ,f+1).∴3²=2(f+1)²,解得f=22-±.则1D 2D ). ∵PM=AM=3,∴当点F 与点A 重合时,过点F 在x 轴上方作DF ∥PM ,且DF=PM ,连接DP ,可得出四边形DPMF 为菱形.∴点D 的坐标为(-4,3).当PM 为菱形的对角线时,作PM 的垂直平分线,交直线AC 于点F ,作点F 关于PM 的对称点D ,连接MF,MD,PD,此时四边形DMFP 为菱形. ∴将32代入直线AC 的解析式可得,点F 的坐标为(-52,32). ∵直线PM 为x=-1, ∴点D 的坐标为(12,32).综上所述, 1D (22-+,2),2D (22--,-2), 3D (-4,3),4D (12,32).【知识点】待定系数法,二次函数图象的性质,两点之间线段最短,对称图形的性质,勾股定理.8. (2018湖北省江汉油田潜江天门仙桃市,26,12分)抛物线y =137322-+-x x 与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点C ,其顶点为D .将抛物线位于直线l :y =t (2524t <)上方的部分沿直线l 向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M ”形的新图象.(1)点A ,B ,D 的坐标分别为 , , ;(2)如图①,抛物线翻折后,点D 落在点E 处.当点E 在△ABC 内(含边界)时,求t 的取值范围;(3)如图②,当t =0时,若Q 是“M ”形新图象上一动点,是否存在以CQ 为直径的圆与x 轴相切于点P ?若存在,求出点P 的坐标;若不存在,请说明理由.【思路分析】(1)点A ,B 的坐标可以令y =0,解一元二次方程求出,点D 的坐标利用公式可求;(2)点E 可能在边界上也可能在边界内,∴要分情况讨论;(3)点Q 可能在原抛物线上也可能在翻折下来的部分抛物线上,∴要分情况讨论.要证明点Q 在圆上,只需证明QA 与QB 垂直即可. 【解题过程】(1)令y =137322-+-x x =0,解得x 1=21,x 1=3.∴A (21,0),B (3,0).根据抛物线顶点公式可得D (47,2425). 3分 (2)如图①,作直线DE ,交x 轴于点M ,交BC 于点N . ∵直线BC 经过B (3,0),C (0,-1)两点, ∴直线BC 的解析式为:y =31x -1. 又∵抛物线对称轴DE 为:x =47, ∴点N 的坐标为(47,-125). 4分 讨论:①当点D 与点M 重合时,此时点E 落在x 轴上的点M 处,图①lE yA B O D C· ·图②第25题图O ACBxy· D x∴t =21DM =21×2425=4825. 5分 ②当点D 与点N 重合时,此时点E 落在BC 边上的点N 处. ∵DN =DM +MN =丨2425丨+丨-125丨=2435. ∴21DN =4835>MN . ∴t =21DN -MN =4835-125=165. ∴t 的取值范围是:165≤t ≤4825. 7分(3)存在以CQ 为直径的圆与x 轴相切于点P .如图②,设以CQ 为直径的⊙G 与x 轴相切于点P ,连接PC ,PG ,PQ . 并作QH ⊥x 轴于点H ,则GC =GP =GQ ,且GP ⊥x 轴. ∴OC ∥PG ∥HQ .∴OP =PH . ∵CQ 为直径,∴∠CPQ =90°. ∴∠OPC =∠HQP . ∵tan ∠OPC =OPOC ,tan ∠HQP =HQ HP.∴OPOC =HQ HP. 即OC ·HQ =OP ·HP . 9分 讨论:①当点Q 在抛物线y =137322-+-x x 上时, 依题意有x ≤21或x >3. 设点Q 的坐标为(x ,137322-+-x x ). 第25题答图①lE yA B O DC· ·x则OH =|x |,HQ =|137322-+-x x |,OP =PH =21|x |.∵OC =1,∴|137322-+-x x |=21|x |·21|x |,即|137322-+-x x |=41x 2.∵点Q 位于x 轴下方,∴137322-+-x x ≤0.∴137322-+-x x =-41x 2.解得x 1=534214+,x 2=534214-. 10分 ②当点Q 在抛物线y =137322+-x x 上时,依题意有21<x ≤3.同理可得:|137322+-x x |=41x 2.∵点Q 位于x 轴下方,∴137322+-x x =-41x 2.解得x 3=116,x 4=2. 11分 ∴满足条件的x 的值有x 1=534214+,x 2=534214-,x 3=116,x 4=2. ∵OP =21OH =21|x |, ∴符合条件的点P 的坐标有4个,即: P 1(5347+,0),P 2(5347-,0),P 3(113,0),P 4(1,0). 12分【知识点】二次函数压轴题,存在性问题第25题答图②O ACBxy· D PQG9.(湖北省咸宁市,24,12)如图,直线343+-=x y 与x 轴交于点A ,与y 轴交于点B ,抛物线c bx x y ++-=283。
二次函数压轴题综合一题多练

压轴题专练如图,已知抛物线y=- 1/4x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴;(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;(3)证明:△ABC为直角三角形(一)最值问题:(4) 在抛物线的对称轴上求一点P,使PA+PC的值最小(5)M为BC上方抛物线上的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;(6)M为BC上方抛物线上的一点,求△BCM面积的最大值;(二)面积问题:(7)在抛物线上找一个点P,使△ABC与△PAB的面积相等变式练习:若点F是抛物线上的一个动点,是否存在点F使△BCF的面积为8,若存在,求出点F的坐标;若不存在,请说明理由(三)等腰三角形问题:(8)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.(四)相似问题:(9)在抛物线上找一点M,过M作MN垂直于X轴,垂足为N,使△ACO与△MAN相似变式练习:若D是C点关于对称轴的对称点,在抛物线上求一点P,使∠ACO=∠DCP(五)平行四边形问题:(10)若M是抛物线上的一个动点,N是X轴上的一个动点,如果以A,C,M,N为顶点的四边形为平行四边形,求M点坐标变式练习1:若点M在抛物线上,点N在其对称轴上,使得以A、C、N、M为顶点的四边形是平行四边形,且A C为其一边,求点M、N的坐标.变式练习2:在抛物线上找一点M,过M作MN垂直于X轴,交直线BC于点N,使O,C,M,N为顶点的四边形为平行四边形变式练习3:若点M在抛物线上,点N在直线BC上,使得以A、0、N、M为顶点的四边形是平行四边形,且以O A为一边,求点M、N的坐标.(六)直角三角形问题:(11)在对称轴上找一个点P,使△BCP为直角三角形(七)平移及交点问题:(12)若直线BC向上平移t个单位,当直线BC与抛物线有两个交点时,求t的取值范围?变式练习:将抛物线在x轴上方的图像记为c1,,将c1向右平移得c2,使A点和B点重合,若直线Y=2x+t 与c1, c2有三个交点,求t的取值范围?。
二次函数的一题多问含解析

,如图所示:
y
A
OB
E3
x
Q
E4
D
第(8)问图 3
求得
.
(9) 在 轴上是否存在一点 F,使 若不存在,请说明理由;
【解答】存在这样的点 F,
为等腰三角形,若存在,请求出 F 的坐标;
,
,
,
【解析】①以 A 为圆心 AD 长为半径作 , 与 轴有两个交点,分别为
,
即为所求,如下图所示:
y
F1
A
B
O
y
N2
N3
A
B
O
x
N1 D C
第(10)问图
令
,解得
(与点 C 重合,舍去),
;
令
,解得
,
综上所述
.
(11) 在抛物线上是否存在一点 H(不与点 A 重合),使
,若存在,求出
点 H 的坐标;若不存在,请说明理由;
【解答】存在点 H 使
【解析】过点 A 作 BC 的平行线,平行线与抛物线的交点即为 H,如图所示:
第(9)问图 3 是 AD 的中点,
即
,
且
,设
,将 M 坐标带入得到
,
当
时,
,所以
.
(10) 在抛物线上是否存在一点 N(N 不与点 C 重合),使
,若存在,求
出点 N 的坐标;若不存在,请说明理由;
【解答】
【解析】如图所示,利用三角形同底等高面积相等,两个三角形都以 AB 为底,只要高相 等即可.
,解得
,故
,
再次与二次函数解析式联立得
,
解得
,即
,
又因为
,设
北京市2018年度十八中分学校初三上学期二次函数单元考试试卷

二次函数单元测试卷一、选择题(共1小题)1.如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的解析式为()A.y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+2二、填空题(共2小题)2.已知二次函数y=x2+bx+c经过点(3,0)和(4,0),则这个二次函数的解析式是.3.抛物线y=ax2+bx+c(a≠0)经过点(1,2)和(﹣1,﹣6)两点,则a+c=.三、解答题(共13小题)4.已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.(1)求m、n的值;(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.5.如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x 轴、y轴的正半轴,抛物线y=﹣x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.(1)求此抛物线的解析式.(2)求此抛物线顶点D的坐标和四边形ABCD的面积.6.已知抛物线y=﹣x2+bx+c经过点A(3,0),B(﹣1,0).(1)求抛物线的解析式;(2)求抛物线的顶点坐标.7.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.(1)求此抛物线的解析式.(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.8.如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:(1)求抛物线的解析式.(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣.9.如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)(1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.10.如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.(1)求二次函数的解析式;(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.11.如图,抛物线y=a(x﹣1)2+4与x轴交于点A,B,与y轴交于点C,过点C 作CD∥x轴交抛物线的对称轴于点D,连接BD,已知点A的坐标为(﹣1,0)(1)求该抛物线的解析式;(2)求梯形COBD的面积.12.如图,抛物线y=x2﹣bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.(1)求抛物线的解析式;(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.13.在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,﹣2),B(3,4).(1)求抛物线的表达式及对称轴;(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,且点D纵坐标为t,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD 与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.14.如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:(1)求抛物线的解析式;(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣,).15.已知二次函数图象的顶点坐标为(1,﹣1),且经过原点(0,0),求该函数的解析式.16.如图①,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).(1)求抛物线的函数表达式;(2)求抛物线的顶点坐标和对称轴;(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).参考答案与试题解析一、选择题(共1小题)1.如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的解析式为()A.y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+2【分析】将A坐标代入反比例解析式求出m的值,确定出A的坐标,将A与B 坐标代入二次函数解析式求出b与c的值,即可确定出二次函数解析式.【解答】解:将A(m,4)代入反比例解析式得:4=﹣,即m=﹣2,∴A(﹣2,4),将A(﹣2,4),B(0,﹣2)代入二次函数解析式得:,解得:b=﹣1,c=﹣2,则二次函数解析式为y=x2﹣x﹣2.故选:A.【点评】此题考查了待定系数法求二次函数解析式,以及反比例函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.二、填空题(共2小题)2.已知二次函数y=x2+bx+c经过点(3,0)和(4,0),则这个二次函数的解析式是y=x2﹣7x+12.【分析】由于已知了二次函数与x轴的两交点坐标,则可设交点式易得其解析式.【解答】解:设二次函数的解析式为y=a(x﹣3)(x﹣4),而a=1,所以二次函数的解析式为y=(x﹣3)(x﹣4)=x2﹣7x+12.故答案为y=x2﹣7x+12.【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.3.抛物线y=ax2+bx+c(a≠0)经过点(1,2)和(﹣1,﹣6)两点,则a+c=﹣2.【分析】把两点的坐标代入二次函数的解析式,通过①+②,得出2a+2c=﹣4,即可得出a+c的值.【解答】解:把点(1,2)和(﹣1,﹣6)分别代入y=ax2+bx+c(a≠0)得:,①+②得:2a+2c=﹣4,则a+c=﹣2;故答案为:﹣2.【点评】此题考查了待定系数法求二次函数的解析式,解题的关键是通过①+②,得到2a+2c的值,再作为一个整体出现,不要单独去求a,c的值.三、解答题(共13小题)4.已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.(1)求m、n的值;(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.【分析】(1)利用对称轴公式求得m,把P(﹣3,1)代入二次函数y=x2+mx+n 得出n=3m﹣8,进而就可求得n;(2)根据(1)得出二次函数的解析式,根据已知条件,利用平行线分线段成比例定理求得B的纵坐标,代入二次函数的解析式中求得B的坐标,然后利用待定系数法就可求得一次函数的表达式.【解答】解:∵对称轴是经过(﹣1,0)且平行于y轴的直线,∴﹣=﹣1,∴m=2,∵二次函数y=x2+mx+n的图象经过点P(﹣3,1),∴9﹣3m+n=1,得出n=3m﹣8.∴n=3m﹣8=﹣2;(2)∵m=2,n=﹣2,∴二次函数为y=x2+2x﹣2,作PC⊥x轴于C,BD⊥x轴于D,则PC∥BD,∴=,∵P(﹣3,1),∴PC=1,∵PA:PB=1:5,∴=,∴BD=6,∴B的纵坐标为6,代入二次函数为y=x2+2x﹣2得,6=x2+2x﹣2,解得x1=2,x2=﹣4(舍去),∴B(2,6),∴,解得,∴一次函数的表达式为y=x+4.【点评】本题考查了待定系数法求二次函数的解析式和一次函数的解析式,根据已知条件求得B的坐标是解题的关键.5.如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x 轴、y轴的正半轴,抛物线y=﹣x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.(1)求此抛物线的解析式.(2)求此抛物线顶点D的坐标和四边形ABCD的面积.【分析】(1)根据题意确定出B与C的坐标,代入抛物线解析式求出b与c的值,即可确定出解析式;(2)把抛物线解析式化为顶点形式,找出顶点坐标,四边形ABDC面积=三角形ABC面积+三角形BCD面积,求出即可.【解答】解:(1)由已知得:C(0,4),B(4,4),把B与C坐标代入y=﹣x2+bx+c得:,解得:b=2,c=4,则解析式为y=﹣x2+2x+4;(2)∵y=﹣x2+2x+4=﹣(x﹣2)2+6,∴抛物线顶点坐标为(2,6),则S=S△ABC+S△BCD=×4×4+×4×2=8+4=12.四边形ABDC【点评】此题考查了待定系数法求二次函数解析式,以及二次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.6.已知抛物线y=﹣x2+bx+c经过点A(3,0),B(﹣1,0).(1)求抛物线的解析式;(2)求抛物线的顶点坐标.【分析】(1)根据抛物线y=﹣x2+bx+c经过点A(3,0),B(﹣1,0),直接得出抛物线的解析式为;y=﹣(x﹣3)(x+1),再整理即可,(2)根据抛物线的解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,即可得出答案.【解答】解:(1)∵抛物线y=﹣x2+bx+c经过点A(3,0),B(﹣1,0).∴抛物线的解析式为;y=﹣(x﹣3)(x+1),即y=﹣x2+2x+3,(2)∵抛物线的解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线的顶点坐标为:(1,4).【点评】此题考查了用待定系数法求函数的解析式,用到的知识点是二次函数的解析式的形式,关键是根据题意选择合适的解析式.7.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.(1)求此抛物线的解析式.(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.【分析】(1)利用待定系数法求二次函数解析式即可;(2)首先求出直线与二次函数的交点坐标进而得出E,F点坐标,即可得出△DEF 的面积.【解答】解:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,∴,解得:,故抛物线解析式为:y=x2﹣2x﹣3;(2)根据题意得:,解得:,,∴D(4,5),对于直线y=x+1,当x=0时,y=1,∴F(0,1),对于y=x2﹣2x﹣3,当x=0时,y=﹣3,∴E(0,﹣3),∴EF=4,过点D作DM⊥y轴于点M.=EF•DM=8.∴S△DEF【点评】此题主要考查了待定系数法求二次函数解析式以及三角形面积求法等知识,利用数形结合得出D,E,F点坐标是解题关键.8.如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:(1)求抛物线的解析式.(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣.【分析】(1)把点A(﹣4,﹣3)代入y=x2+bx+c得16﹣4b+c=﹣3,根据对称轴是x=﹣3,求出b=6,即可得出答案,(2)根据CD∥x轴,得出点C与点D关于x=﹣3对称,根据点C在对称轴左侧,且CD=8,求出点C的横坐标和纵坐标,再根据点B的坐标为(0,5),求出△BCD 中CD边上的高,即可求出△BCD的面积.【解答】解:(1)把点A(﹣4,﹣3)代入y=x2+bx+c得:16﹣4b+c=﹣3,c﹣4b=﹣19,∵对称轴是x=﹣3,∴﹣=﹣3,∴b=6,∴c=5,∴抛物线的解析式是y=x2+6x+5;(2)∵CD∥x轴,∴点C与点D关于x=﹣3对称,∵点C在对称轴左侧,且CD=8,∴点C的横坐标为﹣7,∴点C的纵坐标为(﹣7)2+6×(﹣7)+5=12,∵点B的坐标为(0,5),∴△BCD中CD边上的高为12﹣5=7,∴△BCD的面积=×8×7=28.【点评】此题考查了待定系数法求二次函数的解析式、二次函数的性质,用到的知识点是二次函数的图象和性质,此题难度适中,注意掌握数形结合思想与方程思想的应用.9.如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)(1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.【分析】(1)利用待定系数法把A(1,0),C(0,﹣3)代入二次函数y=x2+bx+c 中,即可算出b、c的值,进而得到函数解析式是y=x2+2x﹣3;(2)首先求出A、B两点坐标,再算出AB的长,再设P(m,n),根据△ABP 的面积为10可以计算出n的值,然后再利用二次函数解析式计算出m的值即可得到P点坐标.【解答】解:(1)∵二次函数y=x2+bx+c过点A(1,0),C(0,﹣3),∴,解得,∴二次函数的解析式为y=x2+2x﹣3;(2)∵当y=0时,x2+2x﹣3=0,解得:x1=﹣3,x2=1;∴A(1,0),B(﹣3,0),∴AB=4,设P(m,n),∵△ABP的面积为10,∴AB•|n|=10,解得:n=±5,当n=5时,m2+2m﹣3=5,解得:m=﹣4或2,∴P(﹣4,5)(2,5);当n=﹣5时,m2+2m﹣3=﹣5,方程无解,故P(﹣4,5)(2,5);【点评】此题主要考查了待定系数法求二次函数解析式,以及求点的坐标,关键是掌握凡是函数图象经过的点必能满足解析式.10.如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.(1)求二次函数的解析式;(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.【分析】(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;(3)画出图象,再根据图象直接得出答案.【解答】解:(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C (4,5)三点,∴,∴a=,b=﹣,c=﹣1,∴二次函数的解析式为y=x2﹣x﹣1;(2)当y=0时,得x2﹣x﹣1=0;解得x1=2,x2=﹣1,∴点D坐标为(﹣1,0);(3)图象如图,当一次函数的值大于二次函数的值时,x的取值范围是﹣1<x<4.【点评】本题考查了用待定系数法求二次函数的解析式以及一次函数的图象、抛物线与x轴的交点问题,是中档题,要熟练掌握.11.如图,抛物线y=a(x﹣1)2+4与x轴交于点A,B,与y轴交于点C,过点C 作CD∥x轴交抛物线的对称轴于点D,连接BD,已知点A的坐标为(﹣1,0)(1)求该抛物线的解析式;(2)求梯形COBD的面积.【分析】(1)将A坐标代入抛物线解析式,求出a的值,即可确定出解析式;(2)抛物线解析式令x=0求出y的值,求出OC的长,根据对称轴求出CD的长,令y=0求出x的值,确定出OB的长,利用梯形面积公式即可求出梯形COBD的面积.【解答】解:(1)将A(﹣1,0)代入y=a(x﹣1)2+4中,得:0=4a+4,解得:a=﹣1,则抛物线解析式为y=﹣(x﹣1)2+4;(2)对于抛物线解析式,令x=0,得到y=3,即OC=3,∵抛物线解析式为y=﹣(x﹣1)2+4的对称轴为直线x=1,∴CD=1,∵A(﹣1,0),∴B(3,0),即OB=3,则S==6.梯形COBD【点评】此题考查了利用待定系数法求二次函数解析式,二次函数的性质,以及二次函数与x轴的交点,熟练掌握待定系数法是解本题的关键.12.如图,抛物线y=x2﹣bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.(1)求抛物线的解析式;(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)根据抛物线经过点A(1,0),对称轴是x=2列出方程组,解方程组求出b、c的值即可;(2)因为点A与点C关于x=2对称,根据轴对称的性质,连接BC与x=2交于点P,则点P即为所求,求出直线BC与x=2的交点即可.【解答】解:(1)由题意得,,解得b=4,c=3,∴抛物线的解析式为.y=x2﹣4x+3;(2)∵点A与点C关于x=2对称,∴连接BC与x=2交于点P,则点P即为所求,根据抛物线的对称性可知,点C的坐标为(3,0),y=x2﹣4x+3与y轴的交点为(0,3),∴设直线BC的解析式为:y=kx+b,,解得,k=﹣1,b=3,∴直线BC的解析式为:y=﹣x+3,则直线BC与x=2的交点坐标为:(2,1)∴点P的坐标为:(2,1).【点评】本题考查的是待定系数法求二次函数的解析式和最短路径问题,掌握待定系数法求解析式的一般步骤和轴对称的性质是解题的关键.13.在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,﹣2),B(3,4).(1)求抛物线的表达式及对称轴;(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,且点D纵坐标为t,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD 与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.【分析】(1)将A与B坐标代入抛物线解析式求出m与n的值,确定出抛物线解析式,求出对称轴即可;(2)由题意确定出C坐标,以及二次函数的最小值,确定出D纵坐标的最小值,求出直线BC解析式,令x=1求出y的值,即可确定出t的范围.【解答】解:(1)∵抛物线y=2x2+mx+n经过点A(0,﹣2),B(3,4),代入得:,解得:,∴抛物线解析式为y=2x2﹣4x﹣2,对称轴为直线x=1;(2)由题意得:C(﹣3,﹣4),二次函数y=2x2﹣4x﹣2的最小值为﹣4,由函数图象得出D纵坐标最小值为﹣4,设直线BC解析式为y=kx+b,将B与C坐标代入得:,解得:k=,b=0,∴直线BC解析式为y=x,当x=1时,y=,则t的范围为﹣4≤t≤.【点评】此题考查了待定系数法求二次函数解析式,待定系数法求一次函数解析式,以及函数的最值,熟练掌握待定系数法是解本题的关键.14.如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:(1)求抛物线的解析式;(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣,).【分析】(1)将A与B代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;(2)利用顶点坐标公式表示出D点坐标,进而确定出E点坐标,得到DE与OE的长,根据B点坐标求出BO的长,进而求出BE的长,在直角三角形BED中,利用勾股定理求出BD的长.【解答】解:(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),∴将A与B坐标代入得:,解得:,则抛物线解析式为y=﹣x2+2x+3;(2)点D为抛物线顶点,由顶点坐标(﹣,)得,D(1,4),∵对称轴与x轴交于点E,∴DE=4,OE=1,∵B(﹣1,0),∴BO=1,∴BE=2,在Rt△BED中,根据勾股定理得:BD===2.【点评】此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.15.已知二次函数图象的顶点坐标为(1,﹣1),且经过原点(0,0),求该函数的解析式.【分析】设二次函数的解析式为y=a(x﹣1)2﹣1(a≠0),然后把原点坐标代入求解即可.【解答】解:设二次函数的解析式为y=a(x﹣1)2﹣1(a≠0),∵函数图象经过原点(0,0),∴a(0﹣1)2﹣1=0,解得a=1,∴该函数解析式为y=(x﹣1)2﹣1.【点评】本题考查了待定系数法求二次函数解析式,利用顶点式解析式求解更加简便.16.如图①,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).(1)求抛物线的函数表达式;(2)求抛物线的顶点坐标和对称轴;(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).【分析】(1)把点A、B、C代入抛物线解析式y=ax2+bx+c利用待定系数法求解即可;(2)把抛物线解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;(3)根据顶点坐标求出向上平移的距离,再根据阴影部分的面积等于平行四边形的面积,列式进行计算即可得解.【解答】解:(1)∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),∴,解得,所以抛物线的函数表达式为y=x2﹣4x+3;(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1),对称轴为直线x=2;(3)如图,∵抛物线的顶点坐标为(2,﹣1),∴PP′=1,阴影部分的面积等于平行四边形A′APP′的面积,平行四边形A′APP′的面积=1×2=2,∴阴影部分的面积=2.【点评】本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变换,(3)根据平移的性质,把阴影部分的面积转化为平行四边形的面积是解题的关键.。
二次函数题一题多问

一个18问的二次函数题姓名__________如图,对称轴x=﹣1的抛物线y=ax2+bx+c与x轴交于A(2,0),B两点,与y 轴交于点C(0,﹣2),(1)求抛物线的函数表达式;(2)若点P是直线BC下方的抛物线上的动点,求△BPC的面积的最大值及点P 的坐标。
(3)在对称轴上是否存在一点P,使△APC的周长最小.若存在,请求出P点的坐标和△APC周长的最小值;若不存在,请说明理由.(4)若点P在抛物线对称轴的左侧运动,过点P作PD⊥x轴于点D,交直线BC 于点E,且PE=OD,求点P的坐标;(5)点P为抛物线上的一个动点,过点P作x轴的垂线交直线BC于点D,交x轴于点E.若点P在第三象限内,当OE=2PE时,求点P的坐标及△POD的面积.(6)点P在x轴上,若△APC是等腰三角形,试直接写出点P的坐标。
(7)直线ED是抛物线的对称轴,抛物线顶点是D.点P是线段BD上一点,当PE=PC 时,求点P的坐标;(8)点P为抛物线上的一个动点,过点P作x轴的垂线交直线BC于点D,当以点O、C、D为顶点的三角形是等腰三角形时,请直接写出动点P的坐标.(9)点P在抛物线对称轴上,若△PBC是直角三角形,试求点P的坐标。
(10)点E在对称轴上,点P在抛物线上.若以B、C、E、P为顶点的四边形是平行四边形,试求点P的坐标。
(11)点M在对称轴上,点P在x轴上,以M、P、C、B为顶点的四边形是平行四边形.试求点P的坐标。
(12)点P在抛物线上,点N在x轴上,若以点A、C、P、N为顶点的四边形是平行四边形,试直接写出点P的坐标。
(13)在抛物线上有一点P,作PH垂直x轴,垂足为点H,若△APH相似于△BOC,试求点P的坐标。
(14)点P为抛物线上的一个动点,过点P作x轴的垂线交直线BC于点D,交x轴于点E.若△OBD∽△ABC,求点P的坐标.(15)点D与点C关于x轴对称,点Q在线段AB上运动,过点Q作x轴垂线交抛物线于点P,交直线BD于点M,是否存在点P,使B、P、M为顶点的三角形与△BOD相似?如果存在,试求点P的坐标;如果不存在请说明理由。
二次函数一课一题20问
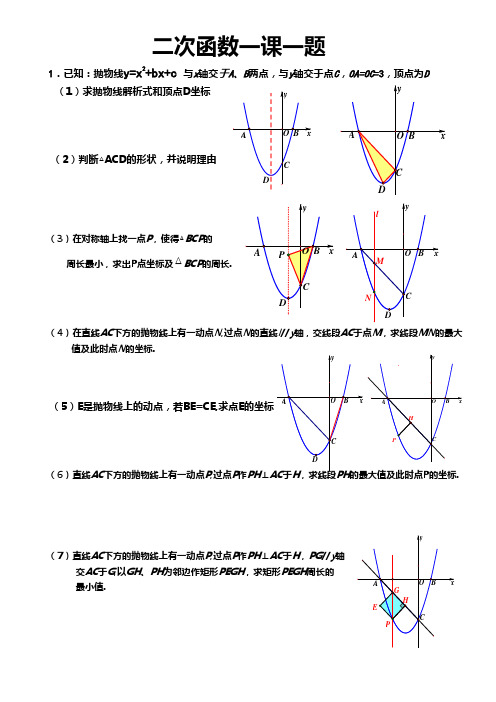
二次函数一课一题1.已知:抛物线y=x2+bx+c 与x 轴交于A 、B 两点,与y 轴交于点C ,OA=OC =3,顶点为D(1)求抛物线解析式和顶点D 坐标(2)判断△ACD的形状,并说明理由(3)在对称轴上找一点P ,使得△BCP 的周长最小,求出P 点坐标及△BCP 的周长.(4)在直线AC 下方的抛物线上有一动点N ,过点N 的直线l //y 轴,交线段AC 于点M ,求线段MN 的最大值及此时点N 的坐标.(5)E 是抛物线上的动点,若BE=CE,求点E 的坐标(6)直线AC 下方的抛物线上有一动点P ,过点P 作PH ⊥P 的坐标.(7)直线AC 下方的抛物线上有一动点P,过点P 作PH ⊥AC 于H ,PG //y 轴交AC 于G ,以GH 、PH 为邻边作矩形PEGH ,求矩形PEGH 周长的 最小值.(8)在AC 下方的抛物线上是否存在一点N ,使得△CAN 的面积最大?若存在,请求出△CAN 的最大面积及点N 的坐标(9)在AC 下方的抛物线上是否存在一点N ,使得四边形ABCN 的面积最大?若存在,请求出四边形ABCN 的最大面积(10)在抛物线上是否存在一点E ,使得△ADE 是以AD 为直角边的直角三角形?若存在,求出点E 的坐标;若不存在,请说明理由;(11)在抛物线上是否存在一点F ,使得△ADF 是以AD 为底边的等腰三角形?若存在,求出点F 的坐标;若不存在,请说明理由.ACOByxNACO B yxN S S(12)抛物线上是否存在一点N (不与点C 重合),使得 ?若存在,求出点N 的坐标;若不存在,请说明理由;(13)抛物线上是否存在一点H ,使得?若存在,求出 点H 的坐标;若不存在,请说明理由;(14)抛物线上是否存在一点Q ,得COQAOQ S S ∆∆=若存在,求出点Q 坐标;若不存在,请说明理由;ACO B xyACO B xy(15)抛物线上是否存在一点E ,使得BE 平分△ABC 的面积?若存在,求出点E 的坐标;若不存在,请说明理由.(16)抛物线上找一点P ,作PM ⊥x 轴,交线段AC 于 点N ,使AC 平分△APM 的面积.(17)在对称轴上有一点M ,在抛物线上有一点N ,若以A 、B 、M 、N BCH ABC S S ∆∆=NM ACOBxyP求M、N的坐标;(18)点E是抛物线上一动点,点F在抛物线的对称轴上,若以C、D、E、F为顶点的四边形是菱形,求点E的坐标.(19)在抛物线上能不能找到一点P,使得∠POC=∠PCO ?明理由.(2045°,所得直线与抛物线交于点M,求点M的坐标.。
二次函数与几何综合-一题多问---10.19
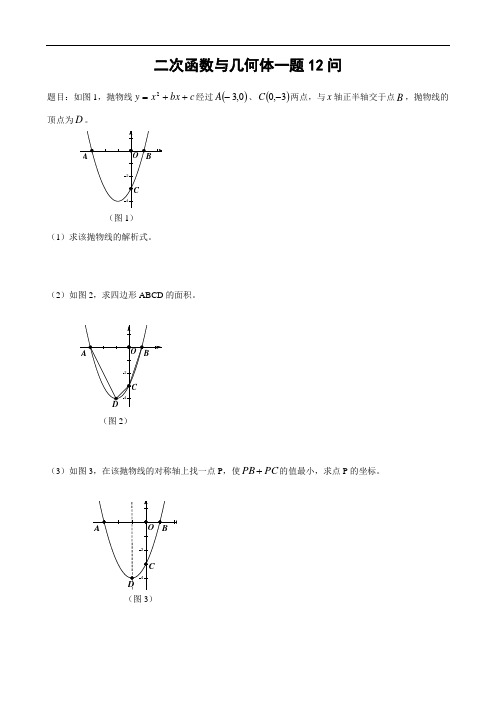
(12)如图12,抛物线的对称轴DG交AC于G,点F是(或添“直线AC下方的”)抛物线上一点,过F作EF⊥ 轴交直线AC于点E,以点E、F、D、G为顶点的四边形能否为平行四边形?若能,求点F的坐标;若不能,请说明理由。
二次函数与几何体一题12问
题目:如图1,抛物线 经过 、 两点,与 轴正半轴交于点 ,抛物线的顶点为 。
(1)求该抛物线的解析式。
(2)如图2,求四边形ABCD的面积。
(3)如图3,在该抛物线的对称轴上找一点P,使 的值最小,求点P的坐标。
(4)如图4,在该抛物线的对称轴上找一点Q,使 的值最大,求点Q的坐标。
(13)如图13,若点P是直线AC下方的抛物线上一动点,连接PC、PO,并把△POC沿OC翻折,得到四边形POP/C,是否存在点P,使四边形POP/C为菱形?若存在,求此时点P的坐标;若不存在,请说明理由。
(14)如图,点M是线段AB上任意一点(M与A、B不重合),过点M作 轴的垂线与直线AC交于E,交抛物线于P,过P作PQ∥AB交抛物线于Q,过Q作QN⊥ 轴于N,若点P在点Q的左边,当矩形PQNM的周长最大时,试求△AME的面积。
(5)如图5,在该抛物线的对称轴上找一点N,使 为直角三角形,求点N的坐标。
(6)如图6,在抛物线的对称轴上找一点M,使 为等腰三角形,求点M的坐标。
(7)如图7,在 轴上找一点R,使 为等腰三角形,求点R的坐标。
(8)如图8,在抛物线上找一点E,使 ,求点E的坐标。
(9)如图9,点N是直线AC下方的抛物线上一动点,过N作NM⊥ 轴交 轴于点M,若直线AC将△AMN分成面积相等的两部分,求点N的坐标。
2018年中考数学真题汇编 二次函数
中考数学真题汇编:二次函数一、选择题1.给出下列函数:①y=﹣3x+2;②y= ;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是()A. ①③B. ③④C. ②④D. ②③【答案】:B2.如图,函数和( 是常数,且)在同一平面直角坐标系的图象可能是()A. B. C.D.【答案】:B3.关于二次函数,下列说法正确的是()A. 图像与轴的交点坐标为B. 图像的对称轴在轴的右侧C. 当时,的值随值的增大而减小D. 的最小值为-3【答案】:D4.二次函数的图像如图所示,下列结论正确是( )A. B. C.D. 有两个不相等的实数根【答案】:C5.若抛物线与轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )A. B. C. D.【答案】:B6.若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线。
已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点()A. (-3,-6)B. (-3,0) C. (-3,-5) D. (-3,-1)【答案】:B7.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是()A. 点火后9s和点火后13s的升空高度相同B. 点火后24s火箭落于地面C. 点火后10s的升空高度为139mD. 火箭升空的最大高度为145m 【答案】:D8.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是()A. 1B. 2C. 3D. 4 【答案】:B9.如图是二次函数(,,是常数,)图象的一部分,与轴的交点在点和之间,对称轴是.对于下列说法:①;②;③;④(为实数);⑤当时,,其中正确的是()A. ①②④B. ①②⑤C. ②③④D. ③④⑤【答案】:A10.如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P 的横坐标为-1,则一次函数y=(a-b)x+b的图象大致是()A. B. C. D.【答案】:D11.四位同学在研究函数(b,c是常数)时,甲发现当时,函数有最小值;乙发现是方程的一个根;丙发现函数的最小值为3;丁发现当时,.已知这四位同学中只有一位发现的结论是错误的,则该同学是()A. 甲B. 乙C. 丙D. 丁【答案】:B12.如图所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜边DF上一动点,过B 作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,则y与x之间的函数图象大致为()A. (B.C. D. (【答案】:B二、填空题13.已知二次函数,当x>0时,y随x的增大而________(填“增大”或“减小”)【答案】:增大14.右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加________m。
(完整版)2018中考二次函数真题

二次函数参考答案与试题解析一.选择题(共22小题)1.(2018•泰安)一元二次方程(x+1)(x﹣3)=2x﹣5根的情况是()A.无实数根B.有一个正根,一个负根C.有两个正根,且都小于3 D.有两个正根,且有一根大于3【分析】直接整理原方程,进而解方程得出x的值.【解答】解:(x+1)(x﹣3)=2x﹣5整理得:x2﹣2x﹣3=2x﹣5,则x2﹣4x+2=0,(x﹣2)2=2,解得:x1=2+>3,x2=2﹣,故有两个正根,且有一根大于3.故选:D.2.(2018•杭州)四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是()A.甲B.乙C.丙D.丁【分析】假设两位同学的结论正确,用其去验证另外两个同学的结论,只要找出一个正确一个错误,即可得出结论(本题选择的甲和丙,利用顶点坐标求出b、c的值,然后利用二次函数图象上点的坐标特征验证乙和丁的结论).【解答】解:假设甲和丙的结论正确,则,解得:,∴抛物线的解析式为y=x2﹣2x+4.当x=﹣1时,y=x2﹣2x+4=7,∴乙的结论不正确;当x=2时,y=x2﹣2x+4=4,∴丁的结论正确.∵四位同学中只有一位发现的结论是错误的,∴假设成立.故选:B.3.(2018•潍坊)已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为()A.3或6 B.1或6 C.1或3 D.4或6【分析】分h<2、2≤h≤5和h>5三种情况考虑:当h<2时,根据二次函数的性质可得出关于h的一元二次方程,解之即可得出结论;当2≤h≤5时,由此时函数的最大值为0与题意不符,可得出该情况不存在;当h>5时,根据二次函数的性质可得出关于h的一元二次方程,解之即可得出结论.综上即可得出结论.【解答】解:当h<2时,有﹣(2﹣h)2=﹣1,解得:h1=1,h2=3(舍去);当2≤h≤5时,y=﹣(x﹣h)2的最大值为0,不符合题意;当h>5时,有﹣(5﹣h)2=﹣1,解得:h3=4(舍去),h4=6.综上所述:h的值为1或6.故选:B.4.(2018•泸州)已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且﹣2≤x≤1时,y的最大值为9,则a的值为()A.1或﹣2 B.或C.D.1【分析】先求出二次函数的对称轴,再根据二次函数的增减性得出抛物线开口向上a>0,然后由﹣2≤x≤1时,y的最大值为9,可得x=1时,y=9,即可求出a.【解答】解:∵二次函数y=ax2+2ax+3a2+3(其中x是自变量),∴对称轴是直线x=﹣=﹣1,∵当x≥2时,y随x的增大而增大,∴a>0,∵﹣2≤x≤1时,y的最大值为9,∴x=1时,y=a+2a+3a2+3=9,∴3a2+3a﹣6=0,∴a=1,或a=﹣2(不合题意舍去).故选:D.5.(2018•滨州)如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是()A.1 B.2 C.3 D.4【分析】直接利用二次函数的开口方向以及图象与x轴的交点,进而分别分析得出答案.【解答】解:①∵二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,且开口向下,∴x=1时,y=a+b+c,即二次函数的最大值为a+b+c,故①正确;②当x=﹣1时,a﹣b+c=0,故②错误;③图象与x轴有2个交点,故b2﹣4ac>0,故③错误;④∵图象的对称轴为x=1,与x轴交于点A、点B(﹣1,0),∴A(3,0),故当y>0时,﹣1<x<3,故④正确.故选:B.6.(2018•连云港)已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是()A.点火后9s和点火后13s的升空高度相同B.点火后24s火箭落于地面C.点火后10s的升空高度为139mD.火箭升空的最大高度为145m【分析】分别求出t=9、13、24、10时h的值可判断A、B、C三个选项,将解析式配方成顶点式可判断D选项.【解答】解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;C、当t=10时h=141m,此选项错误;D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;故选:D.7.(2018•成都)关于二次函数y=2x2+4x﹣1,下列说法正确的是()A.图象与y轴的交点坐标为(0,1)B.图象的对称轴在y轴的右侧C.当x<0时,y的值随x值的增大而减小D.y的最小值为﹣3【分析】根据题目中的函数解析式可以判断各个选项中的结论是否在成立,从而可以解答本题.【解答】解:∵y=2x2+4x﹣1=2(x+1)2﹣3,∴当x=0时,y=﹣1,故选项A错误,该函数的对称轴是直线x=﹣1,故选项B错误,当x<﹣1时,y随x的增大而减小,故选项C错误,当x=﹣1时,y取得最小值,此时y=﹣3,故选项D正确,故选:D.8.(2018•凉州区)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x 轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是()A.①②④B.①②⑤C.②③④D.③④⑤【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴判定b与0的关系以及2a+b=0;当x=﹣1时,y=a﹣b+c;然后由图象确定当x 取何值时,y>0.【解答】解:①∵对称轴在y轴右侧,∴a、b异号,∴ab<0,故正确;②∵对称轴x=﹣=1,∴2a+b=0;故正确;③∵2a+b=0,∴b=﹣2a,∵当x=﹣1时,y=a﹣b+c<0,∴a﹣(﹣2a)+c=3a+c<0,故错误;④根据图示知,当m=1时,有最大值;当m≠1时,有am2+bm+c≤a+b+c,所以a+b≥m(am+b)(m为实数).故正确.⑤如图,当﹣1<x<3时,y不只是大于0.故错误.故选:A.9.(2018•岳阳)抛物线y=3(x﹣2)2+5的顶点坐标是()A.(﹣2,5)B.(﹣2,﹣5)C.(2,5) D.(2,﹣5)【分析】根据二次函数的性质y=a(x+h)2+k的顶点坐标是(﹣h,k)即可求解.【解答】解:抛物线y=3(x﹣2)2+5的顶点坐标为(2,5),故选:C.10.(2018•宁波)如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P 的横坐标为﹣1,则一次函数y=(a﹣b)x+b的图象大致是()A.B.C.D.【分析】根据二次函数的图象可以判断a、b、a﹣b的正负情况,从而可以得到一次函数经过哪几个象限,本题得以解决.【解答】解:由二次函数的图象可知,a<0,b<0,当x=﹣1时,y=a﹣b<0,∴y=(a﹣b)x+b的图象在第二、三、四象限,故选:D.11.(2018•达州)如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:①abc<0;②9a+3b+c>0;③若点M(,y1),点N(,y2)是函数图象上的两点,则y1<y2;④﹣<a<﹣.其中正确结论有()A.1个 B.2个 C.3个 D.4个【分析】根据二次函数的图象与系数的关系即可求出答案.【解答】解:①由开口可知:a<0,∴对称轴x=>0,∴b>0,由抛物线与y轴的交点可知:c>0,∴abc<0,故①错误;②∵抛物线与x轴交于点A(﹣1,0),对称轴为x=2,∴抛物线与x轴的另外一个交点为(5,0),∴x=3时,y>0,∴9a+3b+c>0,故②正确;③由于<2,且(,y2)关于直线x=2的对称点的坐标为(,y2),∵,∴y1<y2,故③正确,④∵=2,∴b=﹣4a,∵x=﹣1,y=0,∴a﹣b+c=0,∴c=﹣5a,∵2<c<3,∴2<﹣5a<3,∴﹣<a<﹣,故④正确故选:C.12.(2018•青岛)已知一次函数y=x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是()A.B.C.D.【分析】根据反比例函数图象一次函数图象经过的象限,即可得出<0、c>0,由此即可得出:二次函数y=ax2+bx+c的图象对称轴x=﹣>0,与y轴的交点在y轴负正半轴,再对照四个选项中的图象即可得出结论.【解答】解:观察函数图象可知:<0、c>0,∴二次函数y=ax2+bx+c的图象对称轴x=﹣>0,与y轴的交点在y轴负正半轴.故选:A.13.(2018•天津)已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(﹣1,0),(0,3),其对称轴在y轴右侧.有下列结论:①抛物线经过点(1,0);②方程ax2+bx+c=2有两个不相等的实数根;③﹣3<a+b<3其中,正确结论的个数为()A.0 B.1 C.2 D.3【分析】①由抛物线过点(﹣1,0),对称轴在y轴右侧,即可得出当x=1时y>0,结论①错误;②过点(0,2)作x轴的平行线,由该直线与抛物线有两个交点,可得出方程ax2+bx+c=2有两个不相等的实数根,结论②正确;③由当x=1时y>0,可得出a+b>﹣c,由抛物线与y轴交于点(0,3)可得出c=3,进而即可得出a+b>﹣3,由抛物线过点(﹣1,0)可得出a+b=2a+c,结合a<0、c=3可得出a+b<3,综上可得出﹣3<a+b<3,结论③正确.此题得解.【解答】解:①∵抛物线过点(﹣1,0),对称轴在y轴右侧,∴当x=1时y>0,结论①错误;②过点(0,2)作x轴的平行线,如图所示.∵该直线与抛物线有两个交点,∴方程ax2+bx+c=2有两个不相等的实数根,结论②正确;③∵当x=1时y=a+b+c>0,∴a+b>﹣c.∵抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(0,3),∴c=3,∴a+b>﹣3.∵当a=﹣1时,y=0,即a﹣b+c=0,∴b=a+c,∴a+b=2a+c.∵抛物线开口向下,∴a<0,∴a+b<c=3,∴﹣3<a+b<3,结论③正确.故选:C.14.(2018•德州)如图,函数y=ax2﹣2x+1和y=ax﹣a(a是常数,且a≠0)在同一平面直角坐标系的图象可能是()A.B. C.D.【分析】可先根据一次函数的图象判断a的符号,再判断二次函数图象与实际是否相符,判断正误即可.【解答】解:A、由一次函数y=ax﹣a的图象可得:a<0,此时二次函数y=ax2﹣2x+1的图象应该开口向下,故选项错误;B、由一次函数y=ax﹣a的图象可得:a>0,此时二次函数y=ax2﹣2x+1的图象应该开口向上,对称轴x=﹣>0,故选项正确;C、由一次函数y=ax﹣a的图象可得:a>0,此时二次函数y=ax2﹣2x+1的图象应该开口向上,对称轴x=﹣>0,和x轴的正半轴相交,故选项错误;D、由一次函数y=ax﹣a的图象可得:a>0,此时二次函数y=ax2﹣2x+1的图象应该开口向上,故选项错误.故选:B.15.(2018•威海)抛物线y=ax2+bx+c(a≠0)图象如图所示,下列结论错误的是()A.abc<0 B.a+c<b C.b2+8a>4ac D.2a+b>0【分析】根据二次函数的图象与系数的关系即可求出答案.【解答】解:(A)由图象开口可知:a<0由对称轴可知:>0,∴b>0,∴由抛物线与y轴的交点可知:c>0,∴abc<0,故A正确;(B)由图象可知:x=﹣1,y<0,∴y=a﹣b+c<0,∴a+c<b,故B正确;(C)由图象可知:顶点的纵坐标大于2,∴>2,a<0,∴4ac﹣b2<8a,∴b2+8a>4ac,故C正确;(D)对称轴x=<1,a<0,∴2a+b<0,故D错误;故选:D.16.(2018•衡阳)如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为()A.1个 B.2个 C.3个 D.4个【分析】利用抛物线开口方向得到a<0,再由抛物线的对称轴方程得到b=﹣2a,则3a+b=a,于是可对①进行判断;利用2≤c≤3和c=﹣3a可对②进行判断;利用二次函数的性质可对③进行判断;根据抛物线y=ax2+bx+c与直线y=n﹣1有两个交点可对④进行判断.【解答】解:∵抛物线开口向下,∴a<0,而抛物线的对称轴为直线x=﹣=1,即b=﹣2a,∴3a+b=3a﹣2a=a<0,所以①正确;∵2≤c≤3,而c=﹣3a,∴2≤﹣3a≤3,∴﹣1≤a≤﹣,所以②正确;∵抛物线的顶点坐标(1,n),∴x=1时,二次函数值有最大值n,∴a+b+c≥am2+bm+c,即a+b≥am2+bm,所以③正确;∵抛物线的顶点坐标(1,n),∴抛物线y=ax2+bx+c与直线y=n﹣1有两个交点,∴关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.故选:D.17.(2018•枣庄)如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是()A.b2<4ac B.ac>0 C.2a﹣b=0 D.a﹣b+c=0【分析】根据抛物线与x轴有两个交点有b2﹣4ac>0可对A进行判断;由抛物线开口向上得a >0,由抛物线与y轴的交点在x轴下方得c<0,则可对B进行判断;根据抛物线的对称轴是x=1对C选项进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点为(﹣1,0),所以a﹣b+c=0,则可对D选项进行判断.【解答】解:∵抛物线与x轴有两个交点,∴b2﹣4ac>0,即b2>4ac,所以A选项错误;∵抛物线开口向上,∴a>0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴ac<0,所以B选项错误;∵二次函数图象的对称轴是直线x=1,∴﹣=1,∴2a+b=0,所以C选项错误;∵抛物线过点A(3,0),二次函数图象的对称轴是x=1,∴抛物线与x轴的另一个交点为(﹣1,0),∴a﹣b+c=0,所以D选项正确;故选:D.18.(2018•随州)如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.其中正确的有()A.4个 B.3个 C.2个 D.1个【分析】利用抛物线与y轴的交点位置得到c>0,利用对称轴方程得到b=﹣2a,则2a+b+c=c >0,于是可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点在点(﹣1,0)右侧,则当x=﹣1时,y<0,于是可对②进行判断;根据二次函数的性质得到x=1时,二次函数有最大值,则ax2+bx+c≤a+b+c,于是可对③进行判断;由于直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,利用函数图象得x=3时,一次函数值比二次函数值大,即9a+3b+c<﹣3+c,然后把b=﹣2a代入解a的不等式,则可对④进行判断.【解答】解:∵抛物线与y轴的交点在x轴上方,∴c>0,∵抛物线的对称轴为直线x=﹣=1,∴b=﹣2a,∴2a+b+c=2a﹣2a+c=c>0,所以①正确;∵抛物线与x轴的一个交点在点(3,0)左侧,而抛物线的对称轴为直线x=1,∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,∴当x=﹣1时,y<0,∴a﹣b+c<0,所以②正确;∵x=1时,二次函数有最大值,∴ax2+bx+c≤a+b+c,∴ax2+bx≤a+b,所以③正确;∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,∴x=3时,一次函数值比二次函数值大,即9a+3b+c<﹣3+c,而b=﹣2a,∴9a﹣6a<﹣3,解得a<﹣1,所以④正确.故选:A.19.(2018•襄阳)已知二次函数y=x2﹣x+m﹣1的图象与x轴有交点,则m的取值范围是()A.m≤5 B.m≥2 C.m<5 D.m>2【分析】根据已知抛物线与x轴有交点得出不等式,求出不等式的解集即可.【解答】解:∵二次函数y=x2﹣x+m﹣1的图象与x轴有交点,∴△=(﹣1)2﹣4×1×(m﹣1)≥0,解得:m≤5,故选:A.20.(2018•台湾)已知坐标平面上有一直线L,其方程式为y+2=0,且L与二次函数y=3x2+a 的图形相交于A,B两点:与二次函数y=﹣2x2+b的图形相交于C,D两点,其中a、b为整数.若AB=2,CD=4.则a+b之值为何?()A.1 B.9 C.16 D.24【分析】判断出A、C两点坐标,利用待定系数法求出a、b即可;【解答】解:如图,由题意A(1,﹣2),C(2,﹣2),分别代入y=3x2+a,y=﹣2x2+b可得a=﹣5,b=6,∴a+b=1,故选:A.21.(2018•绍兴)若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点()A.(﹣3,﹣6)B.(﹣3,0)C.(﹣3,﹣5)D.(﹣3,﹣1)【分析】根据定弦抛物线的定义结合其对称轴,即可找出该抛物线的解析式,利用平移的“左加右减,上加下减”找出平移后新抛物线的解析式,再利用二次函数图象上点的坐标特征即可找出结论.【解答】解:∵某定弦抛物线的对称轴为直线x=1,∴该定弦抛物线过点(0,0)、(2,0),∴该抛物线解析式为y=x(x﹣2)=x2﹣2x=(x﹣1)2﹣1.将此抛物线向左平移2个单位,再向下平移3个单位,得到新抛物线的解析式为y=(x﹣1+2)2﹣1﹣3=(x+1)2﹣4.当x=﹣3时,y=(x+1)2﹣4=0,∴得到的新抛物线过点(﹣3,0).故选:B.22.(2018•安顺)已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2,其中正确的结论有()A.1个 B.2个 C.3个 D.4个【分析】①由抛物线的开口方向,抛物线与y轴交点的位置、对称轴即可确定a、b、c的符号,即得abc的符号;②由抛物线与x轴有两个交点判断即可;③分别比较当x=﹣2时、x=1时,y的取值,然后解不等式组可得6a+3c<0,即2a+c<0;又因为a<0,所以3a+c<0.故错误;④将x=1代入抛物线解析式得到a+b+c<0,再将x=﹣1代入抛物线解析式得到a﹣b+c>0,两个不等式相乘,根据两数相乘异号得负的取符号法则及平方差公式变形后,得到(a+c)2<b2,【解答】解:①由开口向下,可得a<0,又由抛物线与y轴交于正半轴,可得c>0,然后由对称轴在y轴左侧,得到b与a同号,则可得b<0,abc>0,故①错误;②由抛物线与x轴有两个交点,可得b2﹣4ac>0,故②正确;③当x=﹣2时,y<0,即4a﹣2b+c<0 (1)当x=1时,y<0,即a+b+c<0 (2)(1)+(2)×2得:6a+3c<0,即2a+c<0又∵a<0,∴a+(2a+c)=3a+c<0.故③错误;④∵x=1时,y=a+b+c<0,x=﹣1时,y=a﹣b+c>0,∴(a+b+c)(a﹣b+c)<0,即[(a+c)+b][(a+c)﹣b]=(a+c)2﹣b2<0,∴(a+c)2<b2,故④正确.综上所述,正确的结论有2个.故选:B.。
2018年全国各地中考数学真题汇编:二次函数含答案

中考数学真题汇编:二次函数一、选择题1.给出下列函数:①y=﹣3x+2;②y= ;③y=2x2;④y=3x、上述函数中符合条作“当x>1时、函数值y随自变量x增大而增大“的是()A. ①③B. ③④C. ②④D. ②③【答案】B2.如图,函数和( 是常数,且)在同一平面直角坐标系的图象可能是()A. B. C. D.【答案】B3.关于二次函数、下列说法正确的是()A. 图像与轴的交点坐标为B. 图像的对称轴在轴的右侧C. 当时、的值随值的增大而减小D. 的最小值为-3【答案】D4.二次函数的图像如图所示、下列结论正确是( )A. B. C. D. 有两个不相等的实数根【答案】C5.若抛物线与轴两个交点间的距离为2、称此抛物线为定弦抛物线、已知某定弦抛物线的对称轴为直线、将此抛物线向左平移2个单位、再向下平移3个单位、得到的抛物线过点( ) A. B. C. D.【答案】B6.若抛物线y=x2+ax+b与x轴两个交点间的距离为2、称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线x=1、将此抛物线向左平移2个单位、再向下平移3个单位、得到的抛物线过点()A. (-3、-6)B. (-3、0)C. (-3、-5)D. (-3、-1)【答案】B7.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是()A. 点火后9s和点火后13s的升空高度相同B. 点火后24s火箭落于地面C. 点火后10s的升空高度为139mD. 火箭升空的最大高度为145m【答案】D8.如图、若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1、与y轴交于点C、与x轴交于点A、点B(﹣1、0)、则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时、﹣1<x<3、其中正确的个数是()A. 1B. 2C. 3D. 4【答案】B9.如图是二次函数(、、是常数、)图象的一部分、与轴的交点在点和之间、对称轴是.对于下列说法:①;②;③;④(为实数);⑤当时、、其中正确的是()A. ①②④B. ①②⑤C. ②③④D. ③④⑤【答案】A10.如图、二次函数y=ax2+bx的图象开口向下、且经过第三象限的点P.若点P的横坐标为-1、则一次函数y=(a-b)x+b的图象大致是()A. B. C. D.【答案】D11.四位同学在研究函数(b、c是常数)时、甲发现当时、函数有最小值;乙发现是方程的一个根;丙发现函数的最小值为3;丁发现当时、.已知这四位同学中只有一位发现的结论是错误的、则该同学是()A. 甲B. 乙C. 丙D. 丁【答案】B12.如图所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,则y与x之间的函数图象大致为()A. (B.C. D. (【答案】B二、填空题13.已知二次函数、当x>0时、y随x的增大而________(填“增大”或“减小”)【答案】增大14.右图是抛物线型拱桥、当拱顶离水面2m时、水面宽4m、水面下降2m、水面宽度增加________m.【答案】4 -4三、解答题15.学校拓展小组研制了绘图智能机器人(如图1)、顺次输入点P1、P2、P3的坐标、机器人能根据图2、绘制图形.若图形是线段、求出线段的长度;若图形是抛物线、求出抛物线的函数关系式.请根据以下点的坐标、求出线段的长度或抛物线的函数关系式.①P1(4、0)、P2(0、0)、P3(6、6).②P1(0、0)、P2(4、0)、P3(6、6).【答案】①∵P1(4、0)、P2(0、0)、4-0=4>0、∴绘制线段P1P2、P1P2=4.②∵P1(0、0)、P2(4、0)、P3(6、6)、0-0=0、∴绘制抛物线、设y=ax(x-4)、把点(6、6)坐标代入得a= 、∴、即.16.如图、抛物线(a≠0)过点E(10、0)、矩形ABCD的边AB在线段OE上(点A在点B 的左边)、点 C 、D在抛物线上.设A(t、0)、当t=2时、AD=4.(1)求抛物线的函数表达式.(2)当t为何值时、矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动、向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G 、H、且直线GH平分矩形的面积时、求抛物线平移的距离.【答案】(1)设抛物线的函数表达式为y=ax(x-10)∵当t=2时、AD=4∴点D的坐标是(2、4)∴4=a×2×(2-10)、解得a=∴抛物线的函数表达式为(2)由抛物线的对称性得BE=OA=t∴AB=10-2t当x=t时、AD=∴矩形ABCD的周长=2(AB+AD)=∵<0∴当t=1时、矩形ABCD的周长有最大值、最大值是多少(3)如图、当t=2时、点A、B、C、D的坐标分别为(2、0)、(8、0)、(8、4)、(2、4)∴矩形ABCD对角线的交点P的坐标为(5、2)当平移后的抛物线过点A时、点H的坐标为(4、4)、此时GH不能将矩形面积平分.当平移后的抛物线过点C时、点G的坐标为(6、0)、此时GH也不能将矩形面积平分.∴当G、H中有一点落在线段AD或BC上时、直线GH不可能将矩形面积平分.当点G、H分别落在线段AB、DC上时、直线GH过点P、必平分矩形ABCD的面积.∵AB∥CD∴线段OD平移后得到线段GH∴线段OD的中点Q平移后的对应点是P在△OBD中、PQ是中位线∴PQ= OB=4所以、抛物线向右平移的距离是4个单位.17.如图、一小球沿与地面成一定角度的方向飞出、小球的飞行路线是一条抛物线、如果不考虑空气阻力、小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x、请根据要求解答下列问题:(1)在飞行过程中、当小球的飞行高度为15m时、飞行时间是多少?(2)在飞行过程中、小球从飞出到落地所用时间是多少?(3)在飞行过程中、小球飞行高度何时最大?最大高度是多少?【答案】(1)解:当y=15时、15=﹣5x2+20x、解得、x1=1、x2=3、答:在飞行过程中、当小球的飞行高度为15m时、飞行时间是1s或3s(2)解:当y=0时、0═﹣5x2+20x、解得、x3=0、x2=4、∵4﹣0=4、∴在飞行过程中、小球从飞出到落地所用时间是4s(3)解:y=﹣5x2+20x=﹣5(x﹣2)2+20、∴当x=2时、y取得最大值、此时、y=20、答:在飞行过程中、小球飞行高度第2s时最大、最大高度是20m18.在平面直角坐标系中、点、点.已知抛物线(是常数)、定点为.(1)当抛物线经过点时、求定点的坐标;(2)若点在轴下方、当时、求抛物线的解析式;(3)无论取何值、该抛物线都经过定点.当时、求抛物线的解析式.【答案】(1)解:∵抛物线经过点、∴、解得.∴抛物线的解析式为.∵、∴顶点的坐标为.(2)解:如图1、抛物线的顶点的坐标为.由点在轴正半轴上、点在轴下方、、知点在第四象限.过点作轴于点、则.可知、即、解得、.当时、点不在第四象限、舍去.∴.∴抛物线解析式为.(3)解:如图2:由可知、当时、无论取何值、都等于 4.得点的坐标为.过点作、交射线于点、分别过点、作轴的垂线、垂足分别为、、则.∵、、∴.∴.∵、∴.∴.∴、.可得点的坐标为或.当点的坐标为时、可得直线的解析式为.∵点在直线上、∴.解得、.当时、点与点重合、不符合题意、∴.当点的坐标为时、可得直线的解析式为.∵点在直线上、∴.解得(舍)、.∴.综上、或.故抛物线解析式为或.19.如图、已知二次函数的图象经过点、与轴分别交于点、点.点是直线上方的抛物线上一动点.(1)求二次函数的表达式;(2)连接、、并把沿轴翻折、得到四边形.若四边形为菱形、请求出此时点的坐标;(3)当点运动到什么位置时、四边形的面积最大?求出此时点的坐标和四边形的最大面积.【答案】(1)解:将点B和点C的坐标代入,得、解得、.∴该二次函数的表达式为.(2)解:若四边形POP′C是菱形、则点P在线段CO的垂直平分线上;如图、连接PP′、则PE⊥CO、垂足为E、∵C(0、3)、∴E(0、),∴点P的纵坐标等于.∴,解得、(不合题意、舍去)、∴点P的坐标为(、).(3)解:过点P作y轴的平行线与BC交于点Q、与OB交于点F、设P(m、)、设直线BC的表达式为、则, 解得.∴直线BC的表达式为.∴Q点的坐标为(m、)、∴.当、解得、∴AO=1、AB=4、∴S四边形ABPC =S△ABC+S△CPQ+S△BPQ==当时、四边形ABPC的面积最大.此时P点的坐标为、四边形ABPC的面积的最大值为.20.如图1、四边形是矩形、点的坐标为、点的坐标为.点从点出发、沿以每秒1个单位长度的速度向点运动、同时点从点出发、沿以每秒2个单位长度的速度向点运动、当点与点重合时运动停止.设运动时间为秒.(1)当时、线段的中点坐标为________;(2)当与相似时、求的值;(3)当时、抛物线经过、两点、与轴交于点、抛物线的顶点为、如图2所示.问该抛物线上是否存在点、使、若存在、求出所有满足条件的点坐标;若不存在、说明理由.【答案】(1)(、2)(2)解:如图1、∵四边形OABC是矩形、∴∠B=∠PAQ=90°∴当△CBQ与△PAQ相似时、存在两种情况:①当△PAQ∽△QBC时、、∴、4t2-15t+9=0、(t-3)(t- )=0、t1=3(舍)、t2= 、②当△PAQ∽△CBQ时、、∴、t2-9t+9=0、t= 、、>7、∵0≤t≤6∴x= 不符合题意、舍去、综上所述、当△CBQ与△PAQ相似时、t的值是或(3)解:当t=1时、P(1、0)、Q(3、2)、把P(1、0)、Q(3、2)代入抛物线y=x2+bx+c中得:、解得:、∴抛物线:y=x2-3x+2=(x- )2- 、∴顶点k(、- )、∵Q(3、2)、M(0、2)、∴MQ∥x轴、作抛物线对称轴、交MQ于E、∴KM=KQ、KE⊥MQ、∴∠MKE=∠QKE= ∠MKQ、如图2、∠MQD= ∠MKQ=∠QKE、设DQ交y轴于H、∵∠HMQ=∠QEK=90°、∴△KEQ∽△QMH、∴、∴、∴MH=2、∴H(0、4)、易得HQ的解析式为:y=- x+4、则、x2-3x+2=- x+4、解得:x1=3(舍)、x2=- 、∴D(- 、);同理、在M的下方、y轴上存在点H、如图3、使∠HQM= ∠MKQ=∠QKE、由对称性得:H(0、0)、易得OQ的解析式:y= x、则、x2-3x+2= x、解得:x1=3(舍)、x2= 、∴D(、);综上所述、点D的坐标为:D(- 、)或(、)21.平面直角坐标系中、二次函数的图象与轴有两个交点. (1)当时、求二次函数的图象与轴交点的坐标;(2)过点作直线轴、二次函数的图象的顶点在直线与轴之间(不包含点在直线上)、求的范围;(3)在(2)的条件下、设二次函数图象的对称轴与直线相交于点、求的面积最大时的值.【答案】(1)解:当m=-2时、y=x2+4x+2当y=0时、则x2+4x+2=0解之:x1= 、x2=(2)解:∵=(x-m)2+2m+2∴顶点坐标为(m、2m+2)∵此抛物线的开口向上、且与x轴有两个交点、二次函数图像的顶点在直线l与x轴之间(不包括点A在直线l上)∴解之:m<-1、m>-3即-3<m<-1(3)解:根据(2)的条件可知-3<m<-1根据题意可知点B(m、m-1),A(m、2m+2)∴AB=2m+2-m+1=m+3S△ABO=∴m=-时、△ABO的面积最大.22.如图、已知抛物线与轴交于点和点、交轴于点.过点作轴、交抛物线于点.(1)求抛物线的解析式;(2)若直线与线段、分别交于、两点、过点作轴于点、过点作轴于点、求矩形的最大面积;(3)若直线将四边形分成左、右两个部分、面积分别为、、且、求的值.【答案】(1)解:根据题意得:9a-3b-3=0a+b-3=0解之:a=1、b=2∴抛物线的解析式为y-=x2+2x-3(2)解:解:∵x=0时、y=-3∴点C的坐标为(0、-3)∵CD∥X轴、∴点D(-2、-3)∵A(-3,0)、B(1,0)∴y AD=-3x-9、y BD=x-1∵直线与线段、分别交于、两点∴∴∴∴矩形的最大面积为 3(3)解:AB=1-(-3)=4、CD=0-(-2)=2,OC=3∵CD∥x轴∴S四边形ABCD=∵∴S1=4、S2=5∵若直线y=kx+1经过点D时、点D(-2、-3)-2k+1=-3解之:k=2∴y=2x+1当y=0时、x=∴点M的坐标为∴∴设直线y=kx+1与CD、AO分别交于点N、S∴∴解之:k=23.如图①、在平面直角坐标系中、圆心为P(x、y)的动圆经过点A(1、2)且与x轴相切于点B.(1)当x=2时、求⊙P的半径;(2)求y关于x的函数解析式、请判断此函数图象的形状、并在图②中画出此函数的图象;(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合)、给(2)中所得函数图象进行定义:此函数图象可以看成是到________的距离等于到________的距离的所有点的集合.(4)当⊙P的半径为1时、若⊙P与以上(2)中所得函数图象相交于点C、D、其中交点D(m、n)在点C的右侧、请利用图②、求cos∠APD的大小.【答案】(1)解:由x=2、得到P(2、y)、连接AP、PB、∵圆P与x轴相切、∴PB⊥x轴、即PB=y、由AP=PB、得到=y、解得:y= 、则圆P的半径为(2)解:同(1)、由AP=PB、得到(x﹣1)2+(y﹣2)2=y2、整理得:y= (x﹣1)2+1、即图象为开口向上的抛物线、画出函数图象、如图②所示;(3)点A;x轴(4)解:连接CD、连接AP并延长、交x轴于点F、设PE=a、则有EF=a+1、ED= 、∴D坐标为(1+ 、a+1)、代入抛物线解析式得:a+1= (1﹣a2)+1、解得:a=﹣2+ 或a=﹣2﹣(舍去)、即PE=﹣2+ 、在Rt△PED中、PE= ﹣2、PD=1、则cos∠APD= = ﹣2。
2018年中考数学真题分类汇编第一期专题13二次函数试题含解析

二次函数一、选择题1.(2018•山东枣庄•3分)如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是()A.b2<4ac B.ac>0 C.2a﹣b=0 D.a﹣b+c=0【分析】根据抛物线与x轴有两个交点有b2﹣4ac>0可对A进行判断;由抛物线开口向上得a>0,由抛物线与y轴的交点在x轴下方得c<0,则可对B进行判断;根据抛物线的对称轴是x=1对C选项进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点为(﹣1,0),所以a﹣b+c=0,则可对D选项进行判断.【解答】解:∵抛物线与x轴有两个交点,∴b2﹣4ac>0,即b2>4ac,所以A选项错误;∵抛物线开口向上,∴a>0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴ac<0,所以B选项错误;∵二次函数图象的对称轴是直线x=1,∴﹣=1,∴2a+b=0,所以C选项错误;∵抛物线过点A(3,0),二次函数图象的对称轴是x=1,∴抛物线与x轴的另一个交点为(﹣1,0),∴a﹣b+c=0,所以D选项正确;故选:D.【点评】本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=﹣;抛物线与y轴的交点坐标为(0,c);当b2﹣4ac>0,抛物线与x轴有两个交点;当b2﹣4ac=0,抛物线与x轴有一个交点;当b2﹣4ac<0,抛物线与x轴没有交点.2.(2018•四川成都•3分)关于二次函数,下列说法正确的是()A. 图像与轴的交点坐标为B. 图像的对称轴在轴的右侧C. 当时,的值随值的增大而减小D. 的最小值为-3【答案】D【考点】二次函数的性质,二次函数的最值【解析】【解答】解:A、当x=0时,y=-1,图像与轴的交点坐标为(0,-1),因此A不符合题意;B、对称轴为直线x=-1,对称轴再y轴的左侧,因此B不符合题意;C、当x<-1时y的值随值的增大而减小,当-1<x<0时,y随x的增大而增大,因此C不符合题意;D、 a=2>0,当x=-1时,y的最小值=2-4-1=-3,因此D符合题意;故答案为:D【分析】求出抛物线与y轴的交点坐标,可对A作出判断;求出抛物线的对称轴,可对B作出判断;根据二次函数的增减性,可对C作出判断;求出抛物线的顶点坐标,可对D作出判断;即可得出答案。
二次函数综合题(一题12问)

二次函数综合题(一题十问)如图,已知抛物线y=﹣x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).(1)求抛物线的解析式及它的顶点坐标和对称轴方程;(2)求点B、点C的坐标,连接AC、BC并求线段BC所在直线的解析式;(3)试判断△AOC与△COB是否相似?并说明理由;(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.(5)在抛物线的对称轴上是否存在点M,使△BCM为直角三角形?若存在,求出符合条件的M点坐标;若不存在,请说明理由.(6)在抛物线的对称轴上是否存在点P,使PA+PC最小?若存在,求出符合条件的P点坐标;若不存在,请说明理由.(7)在第一象限内的抛物线上是否存在点N,使得△BCN的面积最大?若存在,求出符合条件的N点坐标;若不存在,请说明理由.(8)若点D在抛物线上,点E在对称轴上,以点O、B、D、E为顶点的四边形是平行四边形,求点D的坐标。
(9)若点F在抛物线上,点H在对称轴上,以点A、B、F、H为顶点的四边形是平行四边形,求点F、H的坐标。
(10)若以点A、B、C、K为顶点的四边形是平行四边形,求点K的坐标。
(11)若点T在抛物线上,以点A、B、C、T为顶点的四边形是梯形,求点T的坐标。
(12)若点S在抛物线上,△BCS为直角三角形, 求点S的坐标。
解:(1)∵抛物线y=﹣x2+bx+4的图象经过点A(﹣2,0),∴﹣×(﹣2)2+b×(﹣2)+4=0,解得:b=,∴抛物线解析式为y=﹣x2+x+4,又∵y=﹣x2+x+4=﹣(x﹣3)2+,∴对称轴方程为:x=3.(2)在y=﹣x2+x+4中,令x=0,得y=4,∴C(0,4);令y=0,即﹣x2+x+4=0,整理得x2﹣6x﹣16=0,解得:x=8或x=﹣2,∴A(﹣2,0),B(8,0).设直线BC的解析式为y=kx+b,把B(8,0),C(0,4)的坐标分别代入解析式,得:,解得k=,b=4,∴直线BC的解析式为:y=x+4.(3)可判定△AOC∽△COB成立.理由如下:在△AOC与△COB中,∵OA=2,OC=4,OB=8,∴,又∵∠AOC=∠BOC=90°,∴△AOC∽△COB.(4)∵抛物线的对称轴方程为:x=3,可设点Q(3,t),则可求得:AC===,AQ==,CQ==.i)当AQ=CQ时,有=,25+t2=t2﹣8t+16+9,解得t=0,∴Q1(3,0);ii)当AC=AQ时,有=,t2=﹣5,此方程无实数根,∴此时△ACQ不能构成等腰三角形;iii)当AC=CQ时,有=,整理得:t2﹣8t+5=0,解得:t=4±,∴点Q坐标为:Q2(3,4+),Q3(3,4﹣).综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+),Q3(3,4﹣).(5)M(3,±10),M(3,2±)(6)P(3,2.5)(7)N(4,6)(8)D(11,-9.75),D(-5,-9.75)。
2018二次函数一题多问试卷

二次函数压轴题一题多问如图,在平面直角坐标系xoy 中,抛物线y=x 2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x-h)2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为D.(1)求h、k的值;及A、B、C、D坐标。
(2)判断△ACD的形状,并说明理由;(动点直角三角形)(3)在Y轴上是否存在一点E,使△ADE为直角三角形,若存在。
求出点E 的坐标;若不存在,说明理由。
(动点直角三角形)(4)在抛物线上是否存在一点E,使∠EAD=90°,△ADE为直角三角形,若存在。
求出点E的坐标;若不存在,说明理由。
(动点等腰三角形)(5)在Y轴上是否存在一点F,使△ADF为等腰三角形,若存在,求出点F 的坐标;若不存在,说明理由。
( 线段之和最小即饮水问题)(6)在对称轴上找一点P,使PB+PC最小,求出P点坐标。
(周长最小问题)(7)在对称轴上找一点P,使△BCP的周长最小,求出P点坐标及△BPC的周长。
(同侧线段之差最大)(8)在y轴上是否存在一点H,使CHAH 最大?(异侧线段之差最大)(9)在对称轴上是否存在一点H,使CHAH 最大?(截得线段最长)(10)在AC下方的抛物线上有一动点N,过点N作直线L∥y轴,交AC与点M,当点N坐标为多少时,线段MN最长。
(动点三角形面积最大)(11)在AC下方的抛物线上,是否存在一点N使△CAN面积最大。
且最大面积是多少?(动点三角形面积最大)(12)在AC下方的抛物线上,是否存在一点N使点N到直线AC的距离最大, 若存在,求出点N的坐标,并求出最大距离;若不存在,说明理由。
?(四边形面积最大)(13)在AC下方的抛物线上,是否存在一点N,使四边形ABCN面积最大,且最大面积是多少?(动点三角形面积最大)(14)若Q是线段AB是的一个动点(不与A,B重合),作QE∥BC,交AC于点E,当△QEC的面积最大时,求Q点的坐标.(15)在抛物线上是否存在一点N,使S△ABN=S△ABC,若存在,求出点N的坐标;若不存在,说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数压轴题一题多问
如图,在平面直角坐标系xoy 中,抛物线y=x 2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x-h)2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求h、k的值;及A、B、C、D坐标。
(2)判断△ACD的形状,并说明理由;
(动点直角三角形)(3)在Y轴上是否存在一点E,使△ADE为直角三角形,若存在。
求出点E 的坐标;若不存在,说明理由。
(动点直角三角形)(4)在抛物线上是否存在一点E,使∠EAD=90°,△ADE
为直角三角形,若存在。
求出点E的坐标;若不存在,说明理由。
(动点等腰三角形)(5)在Y轴上是否存在一点F,使△ADF为等腰三角形,若存在,求出点F 的坐标;若不存在,说明理由。
( 线段之和最小即饮水问题)(6)在对称轴上找一点P,使PB+PC最小,
求出P点坐标。
(周长最小问题)(7)在对称轴上找一点P,使△BCP的周长最小,求出P点坐标及△BPC的周长。
(同侧线段之差最大)(8)在y轴上是否存在一点H,使CH
AH 最大?
(异侧线段之差最大)(9)在对称轴上是否存在一点H,使CH
AH 最大?
(截得线段最长)(10)在AC下方的抛物线上有一动点N,过点N作直线L∥y轴,交AC与点M,当点N坐标为多少时,线段MN最长。
(动点三角形面积最大)(11)在AC下方的抛物线上,是否存在一点N使△CAN面积最大。
且最大面积是多少?
(动点三角形面积最大)(12)在AC下方的抛物线上,是否存在一点N使点N到直线AC的距离最大, 若存在,求出点N的坐标,并求出最大距离;若不存在,说明理由。
(四边形面积最大)(13)在AC下方的抛物线上,是否存在一点N,使四边形ABCN面积最大,且最大面积是多少?
(动点三角形面积最大)(14)若Q是线段AB是的一个动点(不与A,B重合),作QE∥BC,交AC于点E,当△QEC的面积最大时,求Q点的坐标.
(15)在抛物线上是否存在一点N,使S
△ABN
=S
△ABC
,若存在,求出点N的坐标;若不存在,说明理由。
(16)在抛物线上是否存在一点H,使S
△BCH
=S
△ABC
,若存在,求出点H的坐标;若不存在,说明理由。
(17) 在抛物线上是否存在一点P,使S
△PAC = S
△ABC
若存在,求出点P 的坐标;若不存在,说明理
由。
(18) 在抛物线上是否存在一点E,使BE平分△ABC的面积, 若存在,求出点E的坐标;若不存在,说明理由。
(19)在抛物线上找一点F,做FM⊥X轴,交AC与点H,使AC平分△AFM的面积?
(20)在抛物线上找一点P,使S
△PBC =2S
△ACD,
若存在,求出点P的坐标;
若不存在,说明理由。
(确定的相似三角形)(21)在线段AC上是否存在点M,使△AOM∽△ABC?若存在,
求出点M的坐标;若不存在,说明理由.
(不确定的相似三角形) (22)在线段AC上是否存在点M,使△AOM与△ABC相似?若存在,求出点M的坐标;若不存在,说明理由.
(动点平行四边形)(23)在对称轴上有一点K,在抛物线上有一点L,若使A,B,K,L为顶点形成平行四边形,求出K,L点的坐标。
(动点平行四边形)(24)作垂直于X轴的直线X=-1,交直线AC于点M,交抛物线于点N,以A,M,N,E 为顶点作平行四边形,求第四个顶点E的坐标。
