数据结构教材勘误表
数据结构（c语言版）清华大学出版社秦锋主编勘误（红色字体为修改后的内容）1.教材30页算法描述如下(假定顺序表A和B的存储空间足够)：void Inter_sec (PSeqList A, PSeqList B ){ /*求集合A和B的交集，入口参数：指向顺序表的指针，返回值：无，结果存放在顺序表A中*/ int i=0;while(i<A->length){if(!Location_Seqlist(B,A->data[i]))/*B中无A->data[i]*/Delete_SeqList(A,i+1);else i++;/*考察下一个元素*/}}2.教材43页算法如下：（考虑m＝1的特殊情况）int josephus_ LinkList (LinkList josephus_Link, int s, int m){ /*求约瑟夫问题的出列元素序列，入口参数：已经存放数据的链表头指针，起始位置s，从1报数到m,出口参数：1表示成功，0表示表中没有元素*/LinkList p,pre；/*p指向当前结点，pre指向其前驱结点*/int count；if ( ! josephus_Link){ printf(“表中无元素”)；return (0)；}/*找第s个元素*/p= josephus_Link；for(count=1；count<s；count++) /*查找第s个结点，用p作为第s个结点的指针*/ p=p->next；printf(“输出约瑟夫序列：”)；while ( p!=p->next) /*输出n-1个结点*/{ pre=p->next;while(pre->next!=p)pre=pre->next;/*pre指针初始化，pre是p的前驱指针*/ for(count=1；count<m；count++){ pre=p；p=p->next；} /*for*/printf(“%d\t”, p->data)；pre->next=p->next；free(p)；p=pre->next；}/*while*/printf(“%d\t”,p->data)； /*输出最后一个结点*/free(p)；return 1；}算法2.17该算法时间复杂度是O(n*m)。
3.教材45页算法如下：void Add_Polynomial(P_Polynomial P1, P_Polynomial P2){/*两个一元多项式P1，P2求和，求和的结果保存到P1中*/P_Polynomial Pre_Item,Cur_Item1, Cur_Item2;/*分别保存扫描过程中的P1的前一分量，当前分量及P2的当前分量*/Pre_Item=P1; Cur_Item1=P1->next; Cur_Item2=P2->next;while(Cur_Item1&&Cur_Item2) /*多项式P1,P2没有扫描完*/{if(Cur_Item1->e == Cur_Item2->e){Cur_Item1->p= Cur_Item1->p+ Cur_Item2->p;if(Cur_Item1->p == 0){Pre_Item->next= Cur_Item1->next;free(Cur_Item1);Cur_Item1=Pre_Item->next;/*合并后系数为零，释放当前分量*/Cur_Item2= Cur_Item1->next;}else{Pre_Item=Cur_Item1;Cur_Item1=Cur_Item1->next;Cur_Item2=Cur_Item2->next;/*同时扫描下一项*/}}/*第一种情形，P1和P2当前项的指数相等*/elseif(Cur_Item1->e < Cur_Item2->e){Pre_Item=Cur_Item1;Cur_Item1=Cur_Item1->next;} /*第二种情形，P1当前项的指数小于P2的当前项指数*/else /* 第三种情形:Cur_Item1->e > Cur_Item2->e 时将多项式P2的当前分量加入到P1中*/{P_Polynomial temp;if(! (temp=( P_Polynomial)malloc(sizeof(Polynomial)))){printf(“内存不足！\n”);exit(0);}temp->p=Cur_Item2->p;temp->e=Cur_Item2->e; /*复制P2当前分量*/temp->next=Cur_Item1;Pre_Item->next=temp;Pre_Item=Pre_Item->next; /*复制的当前分量插入P1中*/Cur_Item2=Cur_Item2->next;}/*end else*/} /*end while*/while(Cur_Item2) /*如果P2没有扫描完*/{P_Polynomial temp;if(!( temp=( P_Polynomial)malloc(sizeof(Polynomial)))) {printf(“内存不足！\n”);exit(0);}temp->p=Cur_Item2->p;temp->e=Cur_Item2->e;temp->next=NULL;Pre_Item->next=temp; /*将复制的当前分量加到P1的尾部*/Pre_Item=Pre_Item->next;Cur_Item2=Cur_Item2->next;}} /*end Add_Polynomial */算法2.184.教材197页算法如下：#define m 6 /* 迷宫的实际行 */#define n 8 /* 迷宫的实际列 */int path(int maze[m+2][m+2]，item *move){ /* maze 迷宫数组，move指向坐标增量数组的指针，item见【例3.2】(m,n)为迷宫出口点*/sqtype sq[NUM+1];int front,rear；int x,y,i,j,v;front=rear=0;sq[０].x=1; sq[０].y=1; sq[０].pre=-1; rear++; /*入口点入队*/maze[1][1]=-1; /*走过的位置做标记*/while (front<rear) /*队列不空*/{x=sq[front].x ; y=sq[front ].y ; /*取队头元素,但不出队列*/ for (v=0;v<4;v++) /*向四个方向探测*/{i=x+move[v].x;j=y+move[v].y;if (maze[i][j]==0) /*判断当前方向能走通?*/{ /*能走通,将新的点进队列*/sq[rear].x=i;sq[rear].y=j;sq[rear].pre=front;rear++;maze[i][j]= -1; /*走过的位置做标记*/}if (i==m&&j==n) /*到出口?*/{printpath(sq,rear); /*打印迷宫*/return 1;}} /*for v*/front++; /*当前点四个方向搜索完，取下一个点搜索*/} /*while*/return 0;} /*path*/算法 7.115.教材228页int BinSearch(Sqlist s , KeyType k){ /* 在表s中用折半查找法查找关键字k，若查找成功，则函数值为该元素在表中的位置，若查找失败，返回-1。
*/int low,mid,high；low=0；high=s.length-1；while(low<=high){ mid=(low+high)/2； /* 取区间中点 */if (s.r[mid].key==k) return(mid)； /* 查找成功 */else if (s.r[mid].key>k) high=mid-1； /* 在左区间中查找 */else low=mid+1； /* 在右区间中查找 */ }return(-1)； /* 查找失败 */}算法8.3 折半查找算法6.教材301页bool check3()/*检查第三题答案是否正确*/{bool ok=0；int i；i=question[2]；/*取第3题答案*/switch (i){case 1: if(i==question[0]) ok=true； break；/*第1题是A吗？*/case 2: if(i==question[1]) ok=true； break；/*第2题是B吗？*/case 3: if(i==question[3]) ok=true； break； /*第4题是C吗？*/case 4: if(i==question[6]) ok=true； break；/*第7题是D吗？*/case 5: if(i==question[5]) ok=true； break；/*第6题是E吗？*/}。
教材勘误表
勘误表1.P.13，倒第9行，将“左”字改这“右”字。
倒第10行，将“右”字改为“左”字，将“左字改为“右”字。
2.P.14，表1-1在Form1与Label1之间加横线。
3.P.15，第五行改为“Text2.Text=”””。
4.P.24，倒第14行，将“WindowsState”改为“WindowState”。
5.P.26，倒第10行，名尾加冒号。
6.P.36，倒第9行，句中一对全角双引号改成半角双引号。
7.P.41，将“图”字改为“表”字，在“所示”后加“，”。
8.P.43，第9行，将“WindowsState”改为“WindowState”。
9.P.55，倒第20行，改为“Area=3.14*Radius*Radius”10.P.56，倒第7行，将“-298.66”改为“-298.67”。
11.P.57，第1行，将（B）”女”后的小于号改成大于号。
12.P.68，倒第3行，除去语句中间的“Tab(40);”。
13.P.69，倒第13行，将句中的“10”改成“11”。
倒12行“全角字符”前加“为”字。
14.P.73，第4行，改成“Area=3.14*Radius_out*Radius_out-3.14* Radius_in* Radius_in”15.P.75，删除倒第11行至倒第16行。
16.P.76，第18行，第19行中的“；”改为半角的“;”。
17.P.78，倒第6行，答案改为“10+20=030.00”18.P.86，第19行，在“多个”和“变量”之间加“分离的”。
第27行删除“，同时Case X*Y>0也是错误的”。
19.P91，第4行，改成“If x+y>z And x+z>y And y+z>x Then”20.P.96，倒第10行。
改为“Sub Command2_Click()”21.P.100，第3行的句尾加冒号。
22.P.106，第12行的句尾加冒号。
数据结构(C语言版)(第2版)谌误表
数据结构（C语言版）（第2版）谌误表（ISBN 978-7-115-20703-6）(2010-1-10)黑色、蓝色字为书中原字；粉红字为更改注释；大红字为改正处。
P51图3.12中：（2）指针修改存在问题；第3章线性表的链式存储P45页11行语句pre->next=q->next; /*删除*/ 改为：if (p) {pre->next=q->next; /*删除*/P45页12行语句free(q); /*释放空间*/ 改为：free(q); } /*释放空间*/P58页第7行语句：（1）node *init_link_stack() 建立一个空链式栈改为：（1）node *init() 建立一个空链式栈P65页2行语句if (p->info==x) return p else return NULL; 改为：if (p->info==x) return p ; else return NULL;第4章字符串、数组和特殊矩阵P72页28行语句while (q->next) q=q->next; /*用q查找T中最后一个元素的位置*/ 改为：while (q&&q->next) q=q->next; /*用q查找T中最后一个元素的位置*/第8章图P188页11行，选择题第（5）题（5）已知一个有向图8.30所示，则从顶点a出发进行深度优先偏历，不可能得到的DFS序列为（）。
A．a d b e f c B．a d c e f b C．a d c b f e D．a d e f c b改为：（5）已知一个有向图8.30所示，则从顶点a出发进行深度优先遍历，不可能得到的DFS序列为（）。
A．a d b e f c B．a d c e f b C．adcebf D．adefbc第9章检索P206倒数第6行语句：空的二叉树的高度定义为-1。
数据结构勘误
5 月 22 号：
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------P56，倒数第 6 行，“因为数组下表不存在-1”，“下表”应为“下标”。 P61，注释的倒数第 8 行，“注意：字符型和整形的转换”，“整形”应为“整型”。 P64，“图 3.5 循环队列队空与对满的判断”，“对满”应为“队满”。: T& H5 n/ i. _% J% X, F c P66-P67，1-4 的序号应为 2-5。# r& w, ^/ r; i0 \5 i6 D
第一版最早的勘误
说明：下边红色字体处是必须要改的错
误，其他的错误属于明显的错字或者漏
子，不影响理解。PS:在 8 月 7 号之后的
发售的版本中下边的错误已经全部改正. f.
w; R3 }4 s- r9 m0 Z $ U" A7 k- j6 ?) X6 F) [. H; d8 h
前言，图中，1800 题的右边那个框里，“严办”应为“严版”，前言最后一行，多出一个逗号。
L1 u5 Q$ `% d, d
P46，第 20 题解释第二行，“输出地 i 个元素”，应为“第”。5 {% O K# U. X, y3 T
《数据结构及应用算法》勘误表
《数据结构及应用算法》第6章勘误表1.第158页图6.5中，数组BT[4]中漏了字母“D”；2.第165页算法6.5中，最后一行漏了右花括号“}”3.第169页第11行中，原文“data”应改为“val”4.第171页第3行中，原文“DBGEAHFIC”，应改为“DBGEACHFI”5.第173页算法6.12中，第3行原文“中序线索化二叉树p，设p中每个结点的…”，应改为“中序线索化二叉树T，设T中每个结点的…”6.第173页算法6.12中，倒数第4行原文“pre=p ;”，应改为“pre=T; ”7.第176页图6.14(b)中，原文“root=4”，应改为“root=3”8.第177页倒数第9行中，原文“下表”，应改为“下标”9.第189页图6.25(c)中，表格第5行第2列中原文“7”，应改为“0”，并去掉阴影；第6行第2列中原文“0”，应改为“7”，并填阴影。
10.P154 倒数11行原文“Dl，Dr”，应该是“R l，Rr”《数据结构及应用算法》第7章勘误表1.第196页，第4行，原文“G1＝（V1，E1）”重复，去掉2.第199页第5行原文“ID(A)=1，OD(A)=3”，应改为“ID(A)=2，OD(A)=2”3.第P202页倒数第8行的“Arctype”，应改为“EdgeType”4.第203页倒数第4行中的“arc[i][j]=0”，应改为“arc[i][j]=∞”5.第204页图7.10（b）中，邻接矩阵G.arcs的第0行第4列原文“13”，应改为“8”6.第204页算法7.1中第5、6行中的“arcnum”，应改为“vexnum”7.第207页第8行中，原文“图7.7(a)”，应改为“图7.8(a)”8.第208页第1行中，原文“无向图G”，应改为“有向图G”9.第215页倒数第6行“FirstArc”，应改为“FirstAdjV ex”10.第220页图7 .18(b)中，原文“第4步，k=2”，应改为“第4步，k=1”11.第220页图7.18（b）第一步第1列(0,7)，应改为(3,6)，相应P218图7.17（c）也要改，将虚线边（A,B,7）换成虚线边（D,B,6）12.第226页第3行中，原文“max{ve[j]} + 活动<v j, v k>的持续时间}”，应改为“max{ve[j] + 活动<v j, v k>的持续时间}”13.第226页第17行中，原文“（4）活动a i的最迟开始时间e[i]”，应改为“（4）活动a i的最迟开始时间l[i]”。
勘误表
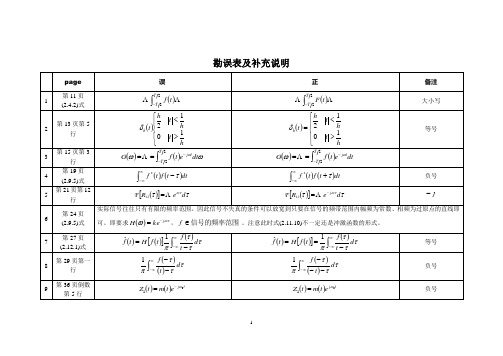
1. "线性调制"的一种定义是看它是否满足叠加原理(见[1],第 232 页) ,DSB 是线性调制:
m1 (t ) cos ωc t + m2 (t ) cos ωc t = [m1 (t ) + m2 (t )] cos ωc t
46 第 190 页倒 数第 3~5 行 在这个定义下,标准调幅 AM,SSB,2ASK,2PSK 都不是线性调制.但因为它门在实质上是 DSB,所以也可归类于线性调制. 注:对于 AM,用两个基带信号的和做 AM 调制结果虽然也是 AM 信号,但载波分量不是叠加关系 2.还有人将"线性调制"定义为: "调制后信号的频谱为调制信号频谱的平移及线性变换" (见[3],第 27 页) (见 3.因为"线性"一词有"成比例"的意思,故有人也把 FM 叫做线性调制,取 FM 的瞬时频偏同基带调制信号的电压成正比之意. [2],第 138 页)
V P(s1 ) p T s 1
+
∞
=∫
∞
[s1 (τ ) + nw (τ )]s1 (Tb t + τ )dτ
另外请注意其它各处 条件概率的记号
35
第 154 页 (5.3.45)式 第 158 页 (5.4.12)式
V p ( s2 ) p T s 2
P(s1 ) p(VT | s1 ) P(s2 ) p(VT | s2 )
4
33
page 第 147 页倒 数第 2 行
误 滤波器的三分贝单边带宽 B
正 滤波器的等效噪声带宽 B
备注
34 第 152 页 (5.3.27)式
∞ ∞ ∞
= ∫ r (τ )s1 (t Tb + τ )dτ =∫
教材勘误表
1、p5: 7.c语言难学可否改个标题？2、P15：第1行图2.5：改成：3、p21：倒数13行~20行整体改成：注意显示在屏幕上看到的结果与上述打印结果是不同的，显示的结果如图 2.10的所示。
在第一个printf()函数里，由于“\r”使当前位置回到本行开头，自此输出的字符（包括空格和跳格所经过的位置）将取代原来屏幕上该位置上显示的字符。
所以原有的“ ab c ”被新的字符“f g”代替，其后的“de”未被新字符取代。
在第二个printf()函数里，先输出“h i”，然后光标位置移到i右面一列处，再退两格后输出“j k”，j后面的空格符将原有的字符“i”取而代之。
因此屏幕上看不到“i”。
实际上，屏幕上完全按程序要求输出了全部的字符，只是因为在输出前面的字符后很快又输出后面的字符。
而打印机则是按顺序真实的打印了结果，实际上是“记录了”输出的过程。
4、p37: 顺数21行，②for( ) ～ (转向语句) 改成：②for( ) ～ (循环语句)5、p38：顺数18行，{ z=x+y；t=+z/100；printf("%f"，t)；}{ z=x+y；t+=z/100；printf("%f"，t)；}5、P39：倒数16行，“a=123,d=12345”改成“a=123,b=12345” ;6、P39：倒数11行，“指定数据的速出宽度”改成“指定数据的输出宽度”;7、P41：倒数第4 行，（如e+002,e+02）改成：（如e+002）8、p46：顺数第4行，getchar(字符)；改成：getchar()；9、P47: 最后一段倒数3行和4行：为什么会出现这样的结果？Turbo C 是把字符当成有符号数据处理，所以，能表示的数的范围只能是-128～127，所以，127再加1，就变成-128了； 改为：为什么会出现这样的结果？输出时把字符当成整型数据输出，所以，127再加1，就变成128了；10、P62:图3.4和图3.5替换成下图：图3.4 例3-7的流程图图3.5 例3-8的流程图11、P80：图3.43替换成下图：12、P89：图3.59替换成下图：图3.43 do ～while()流程图图3.59continue 进入下一轮循环13、P97：增加图3.7714、P98：图3.79替换为：15、p114：第四章【例4-11】中，倒数第8行 #include "c:\ex4_11_1.c" (此行去掉)若是写成project 文件不应该包含#include "c:\ex4_11_1.c"是是x j =0x j =0x j 能被x i 整除图3.77 F:是否x i =0？打印x i ，j++i++G:j%10=0 ?是否换行图3.79。
勘误表
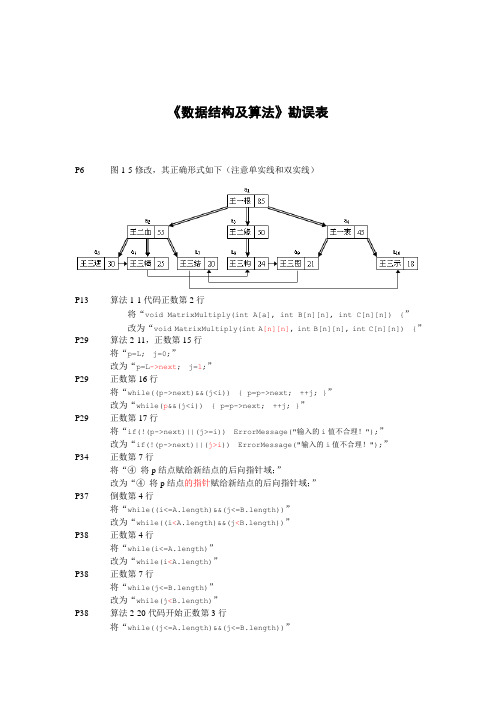
《数据结构及算法》勘误表P6 图1-5修改，其正确形式如下（注意单实线和双实线）P13 算法1-1代码正数第2行将“void MatrixMultiply(int A[a], int B[n][n], int C[n][n]) {”改为“void MatrixMultiply(int A[n][n], int B[n][n], int C[n][n]) {”P29 算法2-11，正数第15行将“p=L; j=0;”改为“p=L->next; j=1;”P29 正数第16行将“while((p->next)&&(j<i)) { p=p->next; ++j; }”改为“while(p&&(j<i)) { p=p->next; ++j; }”P29 正数第17行将“if(!(p->next)||(j>=i)) ErrorMessage("输入的i值不合理！");”改为“if(!(p->next)||(j>i)) ErrorMessage("输入的i值不合理！");”P34 正数第7行将“④将p结点赋给新结点的后向指针域；”改为“④将p结点的指针赋给新结点的后向指针域；”P37 倒数第4行将“while((i<=A.length)&&(j<=B.length))”改为“while((i<A.length)&&(j<B.length))”P38 正数第4行将“while(i<=A.length)”改为“while(i<A.length)”P38 正数第7行将“while(j<=B.length)”改为“while(j<B.length)”P38 算法2-20代码开始正数第3行将“while((j<=A.length)&&(j<=B.length))”改为“j=0;while((j<A.length)&&(j<B.length))”P52 算法3-7代码开始正数第3行将“S=new LNode;”改为“S=new S Node;”P53 算法3-10代码开始正数第3行将“if(S->next) EmptyMessage("链栈S空！");”改为“if(!(S->next)) EmptyMessage("链栈S空！");”P54 算法3-12代码开始正数第3行将“if(S->next) EmptyMessage("链栈S空！");”改为“if(!(S->next)) EmptyMessage("链栈S空！");”P61 算法3-22代码开始正数第3行将“if(Q.front->next) EmptyMessage("链队列Q空！");”改为“if(!(Q.front->next)) EmptyMessage("链队列Q空！");”P61 算法3-24代码开始正数第3行将“if(Q.front==Q.rear) EmptyMessage("链队列Q空！");”改为“if(!(Q.front->next)) EmptyMessage("链队列Q空！");”P63 算法3-26代码开始正数第16行将“if(k=1) return 1;”改为“if(k==1) return 1;”P76 正数22行将“(2) 确定两个串的最大相等前缀子串，"s1 s1 … s k "="t1 t1 … t k"（其中1≤k≤m，1≤k≤n）。
数据结构教材勘误表
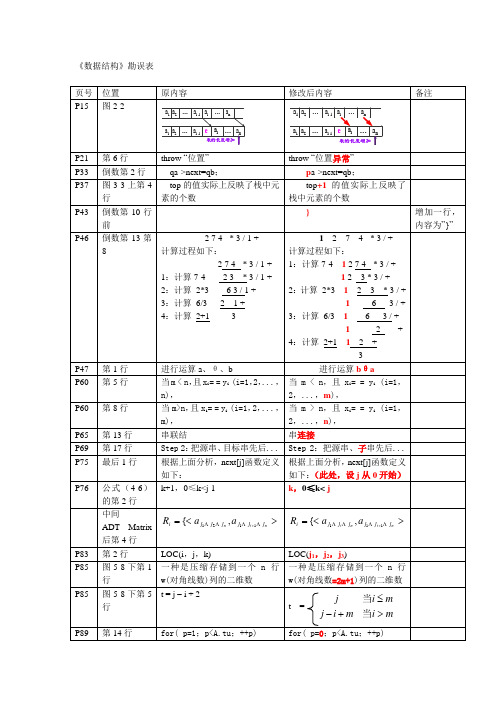
a1 a2 … ai-1 ai … an a1 a2 … ai-1 e ai … an
表的长度增加
修改后内容
a1 a2 … ai-1 ai … an a1 a2 … ai-1 e ai
备注
… an
表的长度增加
P21 P33 P37 P43 P46
for(col=0;col<A.nu ;++col) 0≤i<n，0≤j<m
p 1
A[i][k ] B[k ][ j ]
k 1
p
A[i][k ] B[k ][ j ]
k 0
108 108 108 117 119 123 132
15 18 倒数第 5 行 第一句 文字倒数第 4 行 图 6-13（c） 算法 6.6, 算法 6.13
……仍为 m 阶 B-树 //在 m 阶 B-树*t 上结点…… ……信息，以及指向…… ……解决以下两个问题： ……不同的符号在各位上…… ……位作为哈希地址。 ……稳定性：对任意…… ……进行排序，若相同…… ……将第 i 个记录后移： r[i+1]=r[i] 插入排序……的算法是简 单…… for(int j=i-1;j>=high+1;--j) 记录后移 L.key[j+1]=L.key[j]; L.key[high+1]=L.key[0]; 选择排序的思想是每一…… ……因此，它的空间复杂度为 O(1)。 Step1:……中的元素建大顶堆 不超过式（9-10） ： ……，即 //
（ki1,ki2,……，kid）<……
P243 P243 P244 P246 P247 P248 P257 P257 P258 P258 P261
统计学——教材勘误表
n n0 n 1 0 N
修改为
n
n0
1
n0 N
89 页
X i
1 r X ij ， （i＝1，2，„， r j 1
r） （5-13）
X i
1
s
1
X ij j
1
s
X j
1 X ij ， （j＝1，2，„， s i 1
去掉，表述有错误。
135 页 155 页
② 判定系数为 0.997
ˆ F bl Y T l t t
ቤተ መጻሕፍቲ ባይዱ
l 1,2,
Yˆ t l F t b tl
l 1,2,
另外，107 页最后一段关于单侧检验 p 值的结果没有错误。按照相关定义在这里计算 Z 值时必定取负值，由此给很多学生造成了一些困扰，提醒请各位老师注意。
s） （5-14）
s
X j
r
X ij i
1
r
91 页 第1行 94 页 第2行 105 页 倒 数 第6行 131 页 倒 数 第 2、 3 行 134 页
( )11 12 ( )ss 0
兴趣作为因子 根据表 6-3，计算出的 Dmax 统计量的值为 0.960（表中的 Kolmogorov-Smirnov Z）， 相应的 p 值（渐近显著性）为 0.315。 „„99.7%„„99.7%„„
( ) 11 12 ( ) rs 0
采伐状况作为因子 根据表 6-3，计算出的 Dmax 统计量的值 为 0.096，相应的 p 值（渐近显著性） 为 0.315。 „„99.4%„„99.4%„„
„„， “在 p 个自变量中，只要有一个自 变量同因变量的线性关系不显著，F 检验 就不能通过，因此 F 检验是对方程整体线 性关系的检验” 。 ② 修正自由度的判定系数为 0.997
《数据结构》勘误表(作者王祖俪)20170920
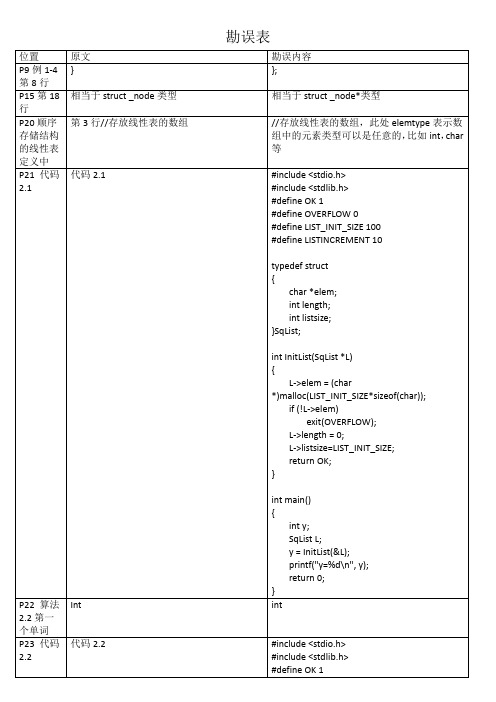
P64第27行
*S.top++=e;
删除此行
P73第1、2行
#include "stdio.h"
#include "malloc.h"
#include <stdio.h>
#include <malloc.h>
P73第二自然段第2行
为何不能“尾进头出”
为何不能“头进尾出”
P102倒数1行
如果同层的孩子结点左右互换
如果同层的兄弟结点左右互换
P103第1行
如果同层的孩子结点左右互换
如果同层的兄弟结点左右互换
P119图5-10(b)
第4行点2，30，点4，40
点3，30，点4，40
P123第11行
首先将光标停在代码5.6第5行任意位置
首先将光标停在代码5.6的main函数第5行（return 0;）任意位置
}
/*插入具体操作*/
q = &(L->elem[i-1]);
for (p = &(L->elem[L->length-1]); p >= q; p--)
{
*(p+1) = *p;
}
*q = e;
L->length++;
return OK;
}
int main()
{
int i, y;
SqList L;
Typedef struct Node
typedef struct Node
P48第23行
Struct Node *prior, *next;