惯性的经典效应_量子效应及起源的研究
10个神奇的物理现象

10个神奇的物理现象神奇的物理现象一直以来都是人们感到神秘和好奇的对象,下面将介绍十个神奇的物理现象。
1. 阿基米德原理阿基米德原理是人们在水中浮力的基础上发现的。
当一个物体浸入液体中时,它所受到的上浮力等于所排开的液体的重量。
这就是为什么我们可以看到一些物体在水中浮起来的原因,比如船只在水中浮起。
2. 光的折射光的折射是指光在不同介质中传播时发生的弯曲现象。
当光线从一种介质进入另一种介质时,由于介质的折射指数不同,光线会发生折射。
这就是为什么我们可以看到杯子里的水是弯的原因。
3. 声音的传播声音是通过介质的震动传播的,比如空气、水或固体。
声音传播的速度取决于介质的密度和弹性。
这就是为什么我们可以听到在空气中传播的声音,但在太空中无法听到声音的原因。
4. 磁悬浮磁悬浮是利用磁力使物体悬浮在空中的现象。
通过在物体和磁场之间产生相互作用的磁力,可以使物体浮起并保持悬浮状态。
这就是为什么磁悬浮列车可以在没有接触轨道的情况下高速运行的原因。
5. 电磁感应电磁感应是指磁场变化引起的电流的产生。
当磁场的强度或方向发生变化时,会在附近的导体中产生感应电流。
这就是为什么我们可以使用电磁感应原理制造发电机和变压器的原因。
6. 热膨胀热膨胀是物体在受热时膨胀,受冷时收缩的现象。
当物体受热时,其分子会加速运动,导致物体膨胀。
这就是为什么在冬天,水管会因为受冷而破裂的原因。
7. 光的干涉光的干涉是指两束或多束光线相遇并产生明暗条纹的现象。
当光线通过不同路径传播时,它们会相互干涉,形成交替出现的亮暗区域。
这就是为什么我们可以看到彩虹和油膜上的彩色条纹的原因。
8. 量子隧道效应量子隧道效应是指微观粒子在经典物理学中无法穿越的势垒时,却能以低于经典能量的方式通过的现象。
这就是为什么电子可以在禁带中传导,以及为什么核反应可以在太阳中发生的原因。
9. 引力透镜效应引力透镜效应是指质量较大的物体会扭曲其周围的时空,使光线弯曲的现象。
量子力学基本原理

量⼦⼒学基本原理量⼦⼒学是到现在为⽌⼈们能够给出的最好的理论,然⽽不应当认为它将永远的存在下去。
假如我们要重新引⼊决定论的观点,那就应当以某种⽅式付出代价,这种⽅式是什么,现在还⽆法推测。
——狄拉克狄拉克23岁成为量⼦⼒学创始⼈之⼀本⽂主要从量⼦论起源、能量⼦假设、光电效应、康普顿散射、玻尔量⼦论、德布罗意物质波、概率波函数、量⼦叠加态原理、不确定性原理、薛定谔⽅程等⼗⼤概念理解量⼦⼒学基本原理,见证⼆⼗世纪真正的神话。
量⼦⼒学其实描述的是物质的⾏为,特别是发⽣在原⼦尺度范围内的事件。
在极⼩尺度下事物的⾏为与我们有着直接经验的任何事物都不相同。
它们既不像波动,⼜不像粒⼦,也不像云雾,或悬挂在弹簧上的重物,总之不像我们曾经见过的任何东西。
费曼1、量⼦论起源量⼦论的起源来⾃⼀个⼤家熟悉的现象,这⼀现象并不属于原⼦物理学的核⼼部分。
任何⼀块物质在被加热时都会发光,并在⾼温度下达到红热和⽩热,发光的亮度与材料的表⾯关系不⼤,⽽对于⿊体,只与温度有关。
因此,⿊体在髙温下发出的辐射作为物理学研究的适当对象,被认为应该可以根据已知的辐射和热学定律找到⼀个简单的解释。
但是物理学家瑞利和⾦斯在⼗九世纪末的努⼒却以失败告终,揭⽰了⿊体辐射问题的严重性。
瑞利和⾦斯⼀切⼈类的直接经验和直觉都只适⽤于宏观物体。
——费曼2、能量⼦假设难以置信的是这个公式已经触动了我们描述⾃然的基础,我感到,我可能已经完成了⼀个第⼀流的发现,或许只有⽜顿的发现才能和它相⽐。
——普朗克普朗克⼤胆舍弃了“能量均分定理”,代之以“量⼦假设”——能量只能以分⽴的能量⼦的形式发射或吸收,这在概念上是⼀次⾰命性的突破,以致它不再适合于物理学的传统框架。
频率为v的电磁波和原⼦、分⼦等物质发⽣能量转换时候,能量不能连续变化,只能⼀份⼀份的跳变,且每份“能量⼦”为:ε=hv=ℏω,其中约化普朗克常数ℏ=h/(2π)普朗克普朗克公式普朗克根据能量的量⼦化,得出⾓频率为ω的电磁振动模式在温度T下的平均能量不再取“能量均分定理”给出的KT,⽽是:E(ω)=ℏω/(e^(ℏω/kT)-1)利⽤热⼒学和物理统计理论,导出了著名的(描述电磁波能量和⾓频率关系)的普朗克公式:ρ (ω)=(ℏω³/π²c³)/(e^(ℏω/kT)-1)3、光电效应年轻的爱因斯坦是物理学家中⼀个有⾰命性的天才,他不怕进⼀步背离旧的观念。
惯性定律的建立过程

惯性定律的建立过程惯性是指物体不受外力作用时,保持其原有运动状态的属性。
人们对于惯性这一认识有赖于惯性定律的建立,而它则依靠于对于力的认识以及区分运动状态和运动状态改变的认识,这一点在人类熟悉发展史上经历了漫长的岁月。
一、亚里士多德的学说和贡献在人类思想史上,两千多年前希腊的哲学家亚里士多德的学说无疑地起过广泛的影响,然而他关于物理学的论述,许多都是错误的。
他把物体的运动分为自然运动和强制运动。
他认为圆周是完善的几何图形,圆周运动对于所有星体都是天然的,因而是自然运动;另外,地球上的物体都具有其天然位置,重物趋于向下,轻物趋于向上,假如没有其他物体阻碍,物体力图回到天然位置的运动也是自然运动;其他所有形式的运动则都是强制运动。
他还进而指出,关于物体的强制运动,只有在外力的不断作用下才能发生;当外力的作用停止时,运动也立即停止。
从这里可以看出亚里士多德肯定了两点:一,自然运动不涉及曳力的问题,只有强制运动才存在力的问题;二、力是物体强制运动的原因。
从今天来看,这显然是错误的,然而它束缚了人们近两千年。
亚里士多德对运动和力的认识是:力是维持物体运动的原因,有力就有运动,没有力就没有运动。
虽然现在我们知道这是一个错误的观点,但亚里士多德在动力学方面给我们的最大贡献是:他第一次提出了力与运动间存在关系的论点。
不是有一句话吗?不怕做不到,就怕想不到。
亚里士多德想到了力与运动之间应该存在关系,这就是他对动力学的贡献。
二、伽利略的学说和贡献伽利略开创了实验和理性思维相结合的近代物理研究方法,并用于研究物体的运动。
他对于亚里士多德关于物体运动的粗糙的日常观察、抽象的猜测玄想和想当然的思辨推理十分不满,他通过科学实验和科学推理得到许多正确的结果,总结在他的著作《关于托勒密和哥白尼两大世界体系的对话》和《关于力学和运动两门新科学的对话》。
伽利略在研究物体在斜面上的运动时,发现当球从一个斜面上滑下来又滚上第二个斜面时,球在第二个斜面上所达到的高度与从第一个斜面上开始滑下来时的高度几乎相等。
最有名的六大科学热词有哪些

最有名的六大科学热词有哪些一、相对论(Relativity)相对论是指爱因斯坦的广义相对论和狭义相对论。
狭义相对论于1905年提出,它提出了相对物理学的概念,包括时空的相对性、物质和能量的等效性。
广义相对论于1915年提出,它建立了一种描述引力的全新理论,将时空视为弯曲的四维连续体。
相对论颠覆了牛顿力学的观念,对现代物理学的发展产生了深远的影响。
相对论是最有名的科学热词之一,因为它彻底改变了人们对时空和物质的看法。
它揭示了时间和空间的相对性,以及物质和能量之间的等效性。
相对论的公式E=mc^2被广泛引用,描述了质量和能量之间的关系,也成为了相对论的标志性公式。
二、量子力学(Quantum Mechanics)量子力学是描述微观粒子行为的理论,它于20世纪初由一系列科学家共同发展而成。
量子力学提出了一种全新的观点,即微观世界的粒子不以经典物理学的方式运动,而是以概率和波函数的形式描述。
量子力学是最有名的科学热词之一,因为它打破了经典物理学的框架,提供了对微观世界行为的全新理解。
量子力学的一些重要概念包括波粒二象性、不确定性原理和量子纠缠等。
量子力学的应用包括量子计算、量子通信和量子力学领域的各种技术。
三、基因组学(Genomics)基因组学是研究基因组的学科,包括基因的结构、功能、调控和进化等方面。
基因组学于20世纪末兴起,随着DNA测序技术的不断发展,人类基因组计划也于2001年完成了人类基因组的首次测序。
基因组学是最有名的科学热词之一,因为它成为了生物科学研究的重点领域之一。
基因组学的发展使得人们能够更好地理解基因在生物体中的作用,以及基因与环境的相互作用。
基因组学的应用包括基因治疗、人类起源研究和疾病研究等。
四、人工智能(Artificial Intelligence)人工智能是一门研究如何使计算机能够模拟和执行人类智能活动的学科。
人工智能于20世纪中叶开始兴起,随着计算机处理能力和算法的不断发展,人工智能的研究也取得了长足的进步。
量子霍尔效应

量子霍尔效应量子霍尔效应是一种在二维材料中观察到的量子输运现象,具有诸多重要的物理和应用意义。
本文将介绍量子霍尔效应的基本原理、实验观测以及相关应用领域。
一、量子霍尔效应的基本原理量子霍尔效应是指当在二维电子气体中施加一弱的磁场时,电子在垂直于磁场方向的平面内沿着边界形成准连续的态,而趋于不散射。
这种不散射的现象可以通过霍尔电阻测量,即电子在横向电场下的电流在垂直方向的电压降。
量子霍尔效应的本质是由于二维系统中的电子受到磁场的束缚,导致电子只能运动在垂直磁场方向的能级上,形成了称为“朗道能级”的能带结构。
在这个结构中,电子的态密度非常紧凑且高度定域,导致电子不易发生散射,从而实现了量子霍尔效应。
二、量子霍尔效应的实验观测量子霍尔效应最早由物理学家冯·克莱因在量子霍尔材料中实验观测到,并因此获得了诺贝尔物理学奖。
他们使用了非常低温以及超高纯度的半导体材料,以观察到这一现象。
实验观测量子霍尔效应的关键在于霍尔电阻的测量。
在二维电子气体中,施加横向电场后,由于电子发生霍尔效应,沿垂直方向会产生电压差。
通过测量这个电压差和施加电场的比值,即得到了霍尔电阻。
当温度趋近于绝对零度时,霍尔电阻呈现出量子化的特征,即呈现为离散的平台。
这种离散的霍尔电阻是量子霍尔效应的直接证据。
三、量子霍尔效应的应用领域量子霍尔效应在凝聚态物理学以及纳米电子学领域具有重要的应用。
其中最重要的应用之一是准粒子和拓扑能带的研究。
在量子霍尔系统中,由于存在较强的相互作用效应以及拓扑性质,准粒子如磁极子、准粒子夸克等得以在这个平面上实现。
这种拓扑态准粒子的研究对于理解凝聚态物理和发展新的量子计算技术具有重要的意义。
另外,量子霍尔效应还在纳米电子器件中有广泛的应用。
由于量子霍尔效应使得电子传输在边界上趋于无散射,因此可以用于构建更加稳定和可控的纳米电子器件。
例如,在量子霍尔体系中可以实现高精度的电流标准以及高灵敏度的传感器,这对于电子技术的发展具有重要的作用。
经典物理和量子物理的一些区别

高 中物理 的内容大 多是属于普通 物理 的范畴 , 为我 们的 日常生 活 所熟悉 , 学生学习起来 , 很容 易找 到对应物 , 有一个直观感受 , 理解接 受 起来 也 比较容 易。而近代 物理 的内容 , 对物理概 念 , 物理规 律的 阐述 , 以及对 一个 物理问题 的思考方式 , 与经典物理有很大的不 同, 而且 到现 在也 不是很成 熟。但它在 工业发展 中发挥着重要 的作用 , 也 代表着物 理发展 的方 向 , 因此 , 作 为高中生有 必要 对其有 一些了解。 1 . 经典物理量 内涵 的拓展和量子物理特有 的概念 在 高中物理力 学中 , 我们 学习 了接触 力 , 如人对 水箱 的推 力 , 摩擦 力, 弹力 ; 非接触 力 , 如万有 引力 , 库伦 力。在微观 物理领域 , 我们还会 接触一些有特别性 质的力 , 如核力与库伦力 , 库伦 力大小遵从平方反 比 定律 , 属于长程 力 ; 核力是 短程力 , 两个核子间 的有效作用距 离为费米 量级 , 超出此 范围 , 两个核 子之间就 没有核力 了, 而且核力 主要 是吸 引 力。高 中教 材所 涉及 的力的 问题 , 基 本上可 以用牛 顿定律 进行解 释 。 可 以说 , 牛顿定律 建造 了经典 力学这座宏 伟大厦 。牛顿定律适 用于惯 性系 中宏观物体低 速运动过程 , 对于高速运动过程 , 量 子力学得到 了实 验的很好验证 , 牛顿定律不再适用 。 我们所 学的 力, 电量 , 动量 等物理概念 在微观物理 中仍然使 J E f J , 但 也有些概 念是微观 物理所特有 的。 t h i n 原 子核的宇称 , 是量子 物理特 有的概 念, 它在经典物理 中找不到对应物。它描 写的是微观体系的一种 空间反演性 质。若一个体 系的波 函数满 足 , 】 f , ( ( 』) 一一( 0 、 ) p 训 ,
对惯性力起源问题的假说

第二十五届“冯如杯”学生创意大赛竞赛论文对惯性力起源问题的假说2015年 4 月摘要:本文以广义相对论为理论基础,探讨惯性力的起源问题,研究等效原理的内在机理,提出物质时空统一体这一猜想,分析引力和惯性力的本质及两者关系,并做了一些拓展。
笔者认为,物质、能量、时间和空间是一个统一体——物质时空,而引力和惯性力是物质时空本质属性的表现。
引力是物质时空的内部相互作用的体现,而惯性力是从外部观测时空产生的效应。
将引力和惯性力归结为时空属性,使等效原理具备了内在基础。
如有不当之处,希望指正。
关键字:惯性力,广义相对论,等效原理,物质时空Abstract:In this paper, based on the theory of general relativity, the author discusses the origin of the inertial force , research the inner mechanism of the equivalence principle, put forward the conjecturethe of the unity of space and time, analyze the relationship between the nature of gravity and inertia, and made some development.The author thinks that, material, energy, time and space is a continuum - unity of time and space,then,gravity and inertia force is essential attribute of time and space.Gravity is the embodiment of the internal interaction of the unityof time and space, and the inertial force from the external .Attributing gravity and inertia force to the essential attributes of space and time provides the equivalence principle with the internal foundation.If there are any wrong, please point out my mistakes.Keywords:inertial force,general relativity,equivalence principle, the unity of space and time目录第一章引言 (1)第二章惯性力起源问题假说 (2)(一)牛顿的水桶实验 (2)(二)马赫的反驳 (2)(三)笔者的假说 .............................................................................................. .31、水桶实验问题的本质和疑难 (3)2、笔者对惯性力的观点 (4)3、笔者观点的论证 (4)(1)广义相对论的基本内容 (4)(2)爱因斯坦对惯性力的解释是基于等效原理而并非马赫原理 (5)(3)笔者的进一步论证 (11)4、笔者假说的哲学基础 (12)5、笔者对该假说微观基础的猜想 (13)6、笔者假说在现实中的应用 (13)结论 (14)结束语......................................................... ................................................... . (14)参考文献 (14)第一章引言二十世纪初期的物理学革命尤其是相对论及量子力学给整个物理学带来了无限的生机与活力。
量子霍尔效应的研究与应用

量子霍尔效应的研究与应用量子霍尔效应(Quantum Hall Effect,QHE)是固体物理学中的一个重要现象,它在二维电子系统中展现出的非常特殊的电导行为引发了学术界的广泛兴趣。
本文将探讨量子霍尔效应的研究与应用,并着重介绍其在量子计算和拓扑绝缘体领域的应用。
1. 量子霍尔效应的发现量子霍尔效应最早由德国学者Klaus von Klitzing在1980年发现。
他发现当二维电子系统处于极低温和强磁场的条件下,电阻率沿垂直于磁场方向呈现定值,这个定值与电流与电压的比值之间存在着极为特殊的关系。
这个新发现引发了科学界的震惊,被誉为“到目前为止最精确的测量”。
2. 量子霍尔效应的理论基础量子霍尔效应的理论基础是基于量子力学的行为描述。
在强磁场下,能量的分布与电子的运动状态密切相关,而磁场的空间调制则会引起电子运动的特殊分布。
这种特殊分布会导致电子在晶格上的散射受到限制,使得电子无法通过传统方式散射,从而阻止了电子的电导行为。
量子霍尔效应通过量子力学力场的调制实现了这一限制。
3. 量子霍尔效应的实验观测随着量子霍尔效应的理论发展,科学家们开始尝试通过实验验证这一效应。
实验证明,当二维电子系统经过强磁场处理后,可以观察到电子在能带之间的分数量子霍尔效应(Fractional Quantum Hall Effect,FQHE),即电子在晶格上呈现出分数的电荷。
这一现象的发现被授予诺贝尔物理学奖,进一步验证了量子霍尔效应的存在和重要性。
4. 量子霍尔效应在量子计算中的应用由于量子霍尔效应在极低温和强磁场条件下出现,它为量子计算提供了理想的平台。
量子计算是一种利用量子力学规律来进行计算的新兴计算方式,相比传统计算机具有更高的运算速度和存储密度。
量子霍尔效应中的分数化电子能级可以用来构建量子比特(Qubit),成为实现量子计算的基础。
5. 量子霍尔效应在拓扑绝缘体研究中的应用拓扑绝缘体是一类独特的材料,具有在表面状态下呈现绝缘体特征但在体态下呈现导体特征的特殊现象。
量子霍尔效应
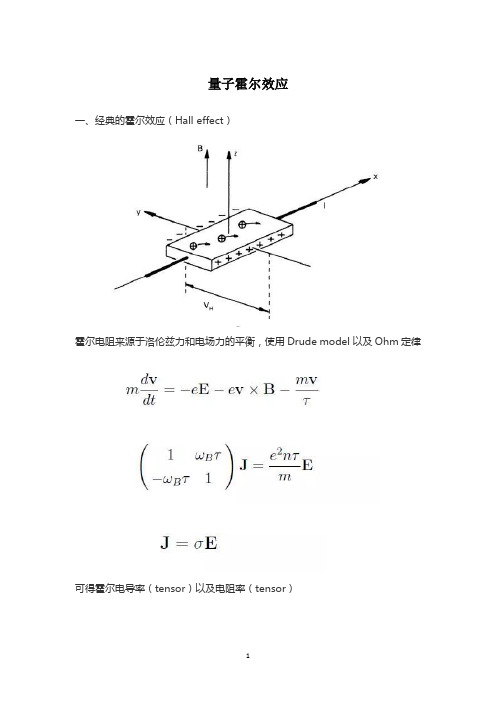
量子霍尔效应一、经典的霍尔效应(Hall effect)霍尔电阻来源于洛伦兹力和电场力的平衡,使用Drude model以及Ohm定律可得霍尔电导率(tensor)以及电阻率(tensor)二、(整数)量子霍尔效应弱磁场的情况下,非对角的霍尔电导和磁场强度满足经典的线性关系,强磁场作用下出现了很多量子化的平台量子化的起源-朗道能级这里使用Landau gauge,Hamiltonian可转化为谐振子模型从而求解其能级波函数代入current operator此时若在y方向加个电场ε,破坏其对称性得到的current依然是不变的(shift Gaussian wave packet center)。
对电流积分可得量子化的霍尔电导率,其中n对应了朗道能级的占据数目Laughlin’s gauge argument将IQHE解释为quantum pump,增加一个量子磁通的test flux的就对应着Gaussian wave packet移动一个单位。
Landauer's approach (Edge modes)Drift velocity 直接由化学电势差决定拓扑的引入(Kubo Formula,Chern number or TKNN number,Berry curvature...)Kubo Formula 是通过linear response得到的电导率上式红色部分是纯虚数,Berry curvature是纯实数所以第n个band的霍尔电导率是上式括号里面的积分是一个整数,即Chern number (first Chern number)=TKNN number。
证明略。
复旦大学物理学系教授修发贤课题组通过对量子霍尔效应的研究,实现了从二维迈向三维的新突破。
他们的科研成果于2018年12月18日在线发表于《自然》期刊上。
早在1879年,美国物理学家霍尔在研究金属的导电机制时发现,如果对通电的导体加上垂直于电流方向的磁场,电子的运动轨迹将发生偏转,在与导体纵向垂直的方向产生电压。
量子效应的概念

量子效应的概念全文共四篇示例,供读者参考第一篇示例:量子效应是指在微观尺度上,由于量子力学的规律所导致的一系列奇特现象。
量子力学是描述微观世界的理论,它揭示了物质在极小尺度上的行为,与我们日常生活中所熟知的经典力学有着根本的不同。
在量子力学的框架下,物质并不是像经典物理学所描述的那样具有确定的位置和速度,而是呈现出一种概率性的分布,可以同时存在于不同的状态中。
量子效应的概念来源于20世纪初量子力学的发展。
那时,科学家们发现了一些无法用经典力学解释的实验现象,例如双缝干涉实验和原子光谱的发现。
这些现象挑战了经典物理学的理论框架,促使科学家们提出了量子力学的新观念,其中包括波粒二象性、量子叠加原理和量子纠缠等。
波粒二象性是量子力学的一个基本概念,它认为微观粒子既可以表现为粒子,也可以表现为波。
这意味着微观粒子在某些实验中的行为既符合粒子的运动规律,又符合波的干涉现象。
在双缝干涉实验中,当一个粒子被发射到两个狭缝之间时,它并不只通过其中一个狭缝,而是以波的形式穿过两个狭缝,并在屏幕上形成干涉条纹,表现出波的特性。
量子叠加原理是另一个重要的量子效应,它指出微观粒子可以同时处于多种可能的状态之间。
换句话说,一个粒子既可以处于位置A,又可以处于位置B,直到被观察到时才确定其具体位置。
这种奇特的量子现象在实验中已被多次证实,例如量子隧穿效应和量子超导等。
量子纠缠是量子力学中最古怪的现象之一,它描述了两个粒子之间由于量子力学的作用而形成的一种非常特殊的关联。
当两个粒子发生纠缠后,它们之间的状态将会相互关联,不论它们之间有多远的距离。
这种现象曾被爱因斯坦称为“遥远的作用”,揭示了量子力学中的非局域性。
量子效应的发现不仅令科学家们对微观世界有了更深入的理解,也为现代科技的发展带来了许多突破性的应用。
量子力学在量子计算和量子通信领域的应用已经取得了一系列重大成就,为人类创造出了全新的技术前景。
量子效应是量子力学的基本特征之一,在微观世界中展现出反常的物理现象。
物理学中的经典力学与量子力学研究

物理学中的经典力学与量子力学研究物理学是研究自然界的运动和相互作用的科学。
其中,经典力学和量子力学是两个重要的分支。
经典力学主要研究宏观物体的运动规律,而量子力学则关注微观世界的奇妙行为。
这两个领域的研究为我们认识世界的不同层面提供了丰富的视角。
经典力学是牛顿力学的基础,也被称为牛顿力学,是自然科学的基石之一。
它将宏观物体视为质点,并以质点的质量和受力情况为基础,研究物体的运动规律。
经典力学的基本定律包括牛顿第一、第二和第三定律。
牛顿第一定律提出了惯性的概念,即物体在没有外力作用下将保持匀速直线运动或静止。
牛顿第二定律则给出了物体运动与受力之间的关系,表明物体的加速度与施加在其上的力成正比,与物体的质量成反比。
牛顿第三定律指出,任何两个物体之间都存在着相互作用力,且大小相等、方向相反。
经典力学的成功应用于诸多领域,如天体力学、航天工程和机械工程等。
然而,对于微观世界来说,经典力学的观点已无法解释一些奇特的现象,如波粒二象性和量子纠缠等。
在20世纪初,量子力学的诞生彻底颠覆了经典力学的观念,成为物理学的又一重要支柱。
量子力学以粒子的波动性为基础,引入了波函数和不确定性原理等概念。
波函数描述了粒子在空间中的分布和运动状态,它是一个复数函数,对应着粒子的概率幅。
量子力学的不确定性原理指出,无法同时准确测量粒子的位置和动量,这与经典力学中的确定性原理形成鲜明对比。
量子力学的发展产生了许多重要的理论和应用。
其中,量子力学描述了原子、分子和固体材料的结构和性质,为化学和材料科学的发展奠定了基础。
同时,量子力学也揭示了微观粒子的一些奇妙现象,如量子隧道效应和量子纠缠。
量子隧道效应指的是粒子能够穿过势垒的现象,即使在经典力学下是禁止的。
而量子纠缠则表明,在某些情况下,两个或多个粒子之间会发生一种奇特的相互关联,即使彼此之间相隔很远,它们也可以瞬间影响彼此的状态。
尽管经典力学和量子力学在理论模型和适用范围上有所不同,但它们并非完全独立。
量子霍尔效应

量子霍尔效应引言量子霍尔效应是一种独特的电学现象,被广泛应用于凝聚态物理领域。
它的发现不仅带来了重大的理论突破,也为今后的量子物理研究和技术应用提供了新的思路和可能性。
在本文中,我们将探讨量子霍尔效应的起源、原理和应用领域。
起源量子霍尔效应最早由德国物理学家冯·克利策提出,并于1980年由美国物理学家基斯·冯克勒斯和丹尼尔·范·温克尔发现。
他们发现当将电流通过处于低温和高磁场条件下的二维电子系统时,会出现电阻率的精确量子化。
这种量子化的电阻率极为稳定,且与外界条件几乎无关,这一现象就是量子霍尔效应。
原理量子霍尔效应来源于二维电子系统在强磁场下的量子行为。
当电子在给定的二维空间中移动时,其运动受到磁场的限制,促使电子形成能级的分立。
在这种情况下,电子会填充这些分立的能级,形成所谓的朗道能级,这导致电子在材料中的运动表现出一种独特的量子性质。
另一方面,磁场也会弯曲电子轨道,使其无法直接通过材料,从而增加了电子在材料中移动的阻抗,形成了稳定的电磁离子的输运状况。
应用领域量子霍尔效应在凝聚态物理领域有着广泛的应用。
首先,它被用于制造高精度的电阻标准器,在物理学和工程领域中具有非常重要的作用。
其次,量子霍尔效应还可以被用于制造高灵敏度的磁场传感器,用于检测微小磁场的变化。
此外,在量子计算和量子信息处理中,量子霍尔效应也扮演着不可或缺的角色,为开发未来的量子计算机和量子通信系统提供了理论基础。
结论综上所述,量子霍尔效应是一种重要的电学现象,具有极其优异的稳定性和精准性。
它的发现和研究对于深入理解凝聚态物理学,拓展新型电子器件的应用,以及推动未来量子技术的发展,具有重要的意义。
相信随着科学技术的不断进步,我们能够更好地利用量子霍尔效应为人类社会的进步和发展做出更多的贡献。
量子hall效应

量子hall效应量子Hall效应量子Hall效应是一种在强磁场下出现的电学现象,其具有高度的稳定性和精度。
该效应在许多领域中都有重要的应用,如材料科学、半导体技术、纳米电子学等。
本文将对量子Hall效应进行详细的介绍。
一、量子Hall效应的基本概念1.1 什么是量子Hall效应量子Hall效应是指在低温和强磁场下,二维电子气体中出现的一种电阻率为零而且霍尔电导σxy只有在一个精确值上非零的现象。
这个精确值就是普朗克常数h/e²的整数倍,即σxy=n(e²/h)。
1.2 量子Hall效应的发现历程1980年代初期,德国物理学家Klitzing等人在实验中发现了这个奇特的现象,并于1985年获得了诺贝尔物理学奖。
他们使用了一种被称为“分式量子霍尔效应”的方法来观察这个现象。
这种方法使用了一个特殊的二维电子气体结构,在低温和强磁场下可以产生非常稳定和精确的量子霍尔电导。
1.3 量子Hall效应的分类根据量子Hall效应的电导类型,可以将其分为整数量子霍尔效应和分数量子霍尔效应两种。
整数量子霍尔效应只在σxy=n(e²/h)时出现,而分数量子霍尔效应则在σxy=p/q(e²/h)时出现,其中p和q是互质的整数。
二、量子Hall效应的物理机制2.1 电荷输运理论在强磁场下,二维电子气体中的电荷输运受到约束。
由于磁场的作用,电子被限制在能级上移动,并且只能沿着轨道运动。
这些轨道被称为朗道能级。
当磁场足够强时,只有朗道能级最低的几个能级才会被占据。
因此,在低温下,只有这些占据态才对输运产生影响。
2.2 拓扑物理学理论拓扑物理学是一种新兴的物理学领域,它研究了材料中自旋、电荷等性质如何受到拓扑结构影响。
近年来,拓扑物理学已经成为了研究量子Hall效应的主要理论框架之一。
根据拓扑物理学的理论,量子Hall效应是由于电子在二维材料中运动时受到了拓扑结构的限制,从而导致霍尔电导只能在特定的值上出现。
量子霍尔效应的研究与应用

量子霍尔效应的研究与应用量子霍尔效应(Quantum Hall Effect)是指在低温、强磁场下,二维电子气体(或其他准二维系统)中出现的一种特殊的电子输运现象。
量子霍尔效应的发现和研究为凝聚态物理学和量子力学领域做出了重大贡献,并在实际应用中展现了巨大的潜力。
1. 量子霍尔效应的发现与背景量子霍尔效应最早于1980年由德国物理学家冯·克莱茵和美国物理学家罗伯特·拉夫利德共同发现。
他们在实验中观察到,在极低温下,二维电子气体在强磁场作用下产生了电阻的精确分数倍增量,这一现象引发了科学界的广泛关注。
2. 量子霍尔效应的理论解释量子霍尔效应的理论解释主要基于凝聚态物理学中的“陆标点拓扑不变量”理论。
这一理论认为,二维电子气体在强磁场下形成了一种特殊的电子能级结构,称为“朗道能级”。
在朗道能级填满的情况下,当系统的费米能级落在两个朗道能级之间时,将出现量子霍尔效应。
3. 量子霍尔效应的应用领域由于量子霍尔效应具有精确的电阻分数倍增特性和无视电流输运的形式,因此在实际应用中得到了广泛的研究和应用。
以下是几个典型的应用领域:3.1 量子电阻标准量子霍尔效应的精确电阻分数倍增特性为量子电阻标准的实现提供了重要基础。
研究人员通过精确测量量子霍尔效应所带来的电阻分数倍数,实现了新一代的电阻标准,不仅提高了电阻测量的精度,还为国际单位制的更新提供了重要参考依据。
3.2 量子霍尔效应晶体管量子霍尔效应晶体管是一种基于量子霍尔效应构建的新型电子器件。
由于量子霍尔效应具有无视电流输运的特性,量子霍尔效应晶体管在高频电子学和微弱信号探测领域具有巨大的潜力,可应用于放大器、频率混频器等器件的设计。
3.3 量子霍尔效应的拓扑电子学研究量子霍尔效应的研究为拓扑电子学领域带来了新的突破。
通过引入拓扑不变量的概念,研究人员成功构建了一类拓扑绝缘体,利用其特殊的边界态实现了量子计算和量子通信等领域的研究。
量子霍尔效应在拓扑电子学中的应用,为未来量子信息科学的发展做出了重要贡献。
惯性力不是力,可是为什么惯性力对物体有实实在在的作用?

导读:惯性力不是力,可是为什么惯性力对物体有实实在在的作用?这个问题值得深思,这是链接量子力学和相对论的一把钥匙。
铺垫文:惯性力,是指当物体有加速度时,物体具有的惯性会使物体有保持原有运动状态的倾向,而此时若以研究对象为参考系,并在该参考系上建立坐标系,看起来就仿佛有一股方向相反的力作用在研究对象上令研究对象在坐标系内发生位移。
在非惯性系中牛顿运动定律不成立,所以不能直接用牛顿运动定律处理力学问题。
若仍然希望能用牛顿运动定律处理这些问题,则必须引入一种作用于物体上的惯性力。
大统一理论(grand unified theories,GUTs),又称为万物之理,由于微观粒子之间仅存在四种相互作用力,万有引力、电磁力、强相互作用力、弱相互作用力。
理论上宇宙间所有现象都可以用这四种作用力来解释。
通过进一步研究四种作用力之间联系与统一,寻找能统一说明四种相互作用力的理论或模型称为大统一理论。
这一理论最初源于电磁的研究,麦克斯韦研究证明它们是电磁现象的同一种基本相互作用的两个方面,可以用同一组方程式加以描述。
到20世纪中叶前,这一描述又改进到包括了量子力学效应,并以量子电动力学(QED)形式出现。
正文:有人可能会问,为什么不把引力理解为类似惯性力这样的存在呢?其实很简单,理解为“惯性力”这样的存在,问题依然多,引力子,引力量子化,统一场论……都依然不能实现。
有的同学会提问,不能实现就不能,非要实现统一场论吗?当然,这不是必须要实现的。
但是从逻辑和哲学上来说,万物是有联系的,我们在相信这个哲学认识的前提下,自然而然的就能想到把基本力联系起来,可是现在联系不起来。
该怎么办呢?两个方向,其一是继续“深化改革”,从现有理论入手;而另一个方向是干脆放弃现有理论,另起炉灶,另辟蹊径来完成大统一理论。
于是弦论就应用而生,弦论中传递基本的力不再是各式各样的粒子了,而是一根根振动的“弦”。
同样,该理论带来惊喜的同时,也带来了问题,那就是高维度问题,而且不是一般地高。
惯性的经典效应、量子效应及起源的研究

一
^
^
其 中 ^一 ^ 一 :
其 逆 变 换
^ 一
( ) 2
对 坐 标 加 上 谐 和 条 件
一 0的 限 制 , 方 程 化 为 场
( ) 3
( ) 解 是 推 迟 势 3的
:
d 0
( ) 4
表 示 源 点 到 场 点 距 离 , 迟 势 推 12 弱 引 力 场 下 粒 子 的 运 动 方 程 .
1 惯 性 的经 典 效 应 是 惯 性 力 , 性 力 是 运 动 的 引 力 源所 产 生 的 变化 的 引 力 场 的 惯
一
种 表现
+h h , 是 一 级 小 量 , 认 为是 平 直 时 空 背 景 下 的 引 力 势 , 可 定
1 1 弱 引 力 场 下 的 推 迟 势 . 在弱 引力场下 度规 可表 示成 g 一
将 这 些 值 代 人 ( ) 可 得 弱 引 力 场 下 粒 子 的 运 动 方 程 为 5式
d xa 2
一
(d
s
ch , Z oo ,
一
ac ̄ (h ) q+
c
do : v
[ ^
一
‰ ]一
2
甜
() 6
13 考察粒 子在 半径 为 R、 . 静质量 为 M 、 以角速 度 相对 于其 内的观 察者旋 转的 中空球壳 内的运 动
是 光 速 传 播 的 .
收 稿 日期 : 0 1 1 1 20 1 2 第 1 作者 简 介 : 宋海 珍 ( 9 3 ) 女 . 南唐 伺 』 . 阳 师 范学 院讲 师 16~ . 河 、南
维普资讯
第 1 期
末海 珍 等 : 性 的经 典 效 应 、 子 垃 应 及起 源 的研 究 惯 量
惯性力的起源

惯性力的起源王云飞【摘要】在定义的复时空中,惯性力与万有引力本质相同,皆与时空有关.惯性力起源于非惯性系的时空形变,惯性质量和引力质量相等是自然内在统一性的必然反映.【期刊名称】《石家庄职业技术学院学报》【年(卷),期】2010(022)006【总页数】4页(P19-22)【关键词】复时空;惯性力;时空形变【作者】王云飞【作者单位】石家庄职业技术学院继续教育学院,河北,石家庄,050081【正文语种】中文【中图分类】O41牛顿定律成立的参考系被称为惯性系.物质成为惯性系的条件是相对静止或作匀速直线运动.非惯性系是指加速系或减速系.非惯性系中,牛顿定律不成立的原因是出现了一个来历不明、“处境尴尬”的力——惯性力,说其是力,是因为它有真实的力效应,能测量大小,并在生产、生活中得到了广泛的应用;说其不是力,是因为它不符合力的定义,它既不是物体之间的相互作用,也找不出它的施力物体与反作用力.惯性定律是牛顿力学的重要基石之一,从亚里士多德的自然哲学到牛顿的经典力学,最深刻的变化在于建立了惯性定律[1].费曼认为:惯性力是一种神秘的力,这个力用任何已知起源的力都解释不了[2].惯性力是一个见怪不怪的力,因为来源不明,无法深究,故认为是物质固有的.自然具有内在的统一性,物理学也同样,惯性力一定有来源,不过它隐藏在自然的最深处.马赫认为:一个孤立物体的惯性是没有意义的;惯性必须归结为物体的相互作用,惯性结构是由宇宙中质量的分布决定的;一个物体的惯性力是这个物体同远距离物质的相互作用.[3]马赫原理并没有得到实验的支持,而实验却发现在高精度上物体的引力质量等于惯性质量.在空间的局部区域,引力和适当的加速度是完全等价的.质量与引力的紧密联系强烈地向我们暗示,惯性质量最终将在所有相互作用中最明显的引力中找到它的来源.即使是错的,也值得去发现.当我们从这样的探索中走出来时,会带来一个深刻变革了的时空概念[3].惯性力的秘密是整个自然秘密的组成部分,发现惯性力的来源对于认识自然具有重要意义.绝对的、真实的和数学的时间,由其特性决定,自身均匀流逝,与一切外在事物无关.绝对空间的自身特性与一切外在事物无关,处处均匀,永不移动[4].当把在绝对时空观基础上建立起来的牛顿力学定律,应用到可与光速相比的高速运动领域和原子尺度的微观世界时,牛顿理论与实验不符.相对论否定了牛顿的绝对时空观,爱因斯坦认为:时空与物质密切相关,空间—时间未必能被看作是可以脱离物质世界的真实客体而独立存在的东西.并不是物体存在于空间中,而是这些物体具有空间广延性.这样看来,关于“一无所有的空间”的概念就失去了意义[5].相对论时空观无疑是人类物质观与时空观的一次飞跃.相对论时空又称为闵可夫斯基时空.其主要特点是:引入虚时间 it,,并用代替作为时间变量.x1=x,x2=y,x3=z,x4=ict.用“坐标”x1,x2, x3,x4描述的四维连续区,闵可夫斯基称之为“世界”,他把代表某一事件的点称作“世界点”.这样,三维空间里发生的“事件”按照物理学的说法就成为四维“世界”的一个“存在”.时空间隔s则是一个不变量.洛伦兹变换相当于坐标系在四维“世界”中转动[5].因此,式(1)可写成:四维时空间隔的不变性,是物理学中最重要的不变性之一,是狭义和广义相对论的基石.但是相对论时空也有其局限性,首先,在数学上,笼统地把时间和空间联系成四维空间并没有宽广的用途,因为空间的三个元素与时间有不同的数学物理性质.时间和空间在矢量运算法则上是无法联系在一起的.能把它们联系在一起的就是复空间[6].其次,相对论禁止大于光速的信息传输,而量子力学却允许相互耦合的微观粒子之间,存在某种被爱因斯坦称为“幽灵式的超距作用”[7].源于广义相对论的弯曲的几何形式总是与量子力学蕴含的狂乱的微观宇宙的行为不相容[8].由于现有时空观的局限性,要发现惯性力的起源,必须扩展时空的定义域.建立新的时空理论也许是找到惯性力来源的关键.对称是自然的根本属性.在最深层次上,我们所发现的一切就是各种对称性以及物质在这些对称变换下的反映.物质本身消融了,而宇宙自身则显得好像是自然的对称群的一个巨大的可约化的表示.这个尚未找到的、应该补充到量子力学中来的要素是某个或几个对称性原理[9].微观物理中已证实存在虚过程(如跃迁)和虚粒子(如虚光子、虚电子).真空中粒子的创生与湮灭,对应着粒子实、虚的转化.如果实时空存在有对称体虚时空,那么自然就可展现出最深刻和最广泛的对称性——复对称性,即实、虚对称性.现有的时空是实的空间和时间.按照对称性,提出一个虚时空,该时空的时间和空间都是虚的.实时空与虚时空构成复时空.在数学角度上,复时空就是复数意义上的时空,对复时空的研究可以转化为对相应复数的研究.用 X轴表示实时空,Y轴表示虚时空,XOY构成了一个复平面(图1).复时空中的物质状态可以用复数空间里的一个复数 z表示,该复数的代数式为z=x+iy,其中,;指数式为x=reiθ;三角式为z=r(cosθ+isinθ),式中.复数x与矢量 Z等价,把矢量 Z与 X轴正向的交角θ称为复数 z的辐角[10].复数的实部对应着物质状态在实时空的投影;虚部对应着物质状态在虚时空的投影.这种时空的分解与运动学中平抛运动可以分解为水平与垂直两种运动的叠加类似.实时空的时空坐标为实量,其在四维的时空间隔为式(2).对实时空的时空坐标进行虚实替换后,成为虚时空的时空坐标,虚时空的四维时空间隔为:式(3)运算后也得到式(2).虚时空同样满足四维时空间隔的不变性,因此,复时空具有虚实对称性.有充分理由认为,虚实对称性就是那个“尚未找到的、应该补充的”最根本的对称性.“发现一个对称性比发现一个特定的现象意义要大得多,如洛伦兹不变性这样的时空对称性统治着整个物理学.对称性是和统一的理念密切相关的,因为它有将表面看起来不相关的物理学的各个方面联系起来的威力.”[11]设有两个物质 k与,k为观测系,为运动系.光速不变性原理是整个物理学的根基,也是宇宙秩序性的根源.以光速为半径作一圆(见图2),圆上所有点都满足光速不变性.设为的一个矢量,当k和相对匀速运动速度为v时,矢量 Z与水平坐标轴的夹角为θ,见图2.矢量 Z由圆点出发并与光速圆相交于点A.由于既要保证光速的不变性,又要满足 k 和¯k之间相对匀速运动速度为v,并符合狭义相对论,故定义复数 z的辐角θ为复时空的时空偏转角(见图3),洛伦兹因子为时空偏转角的余弦.时空偏转角θ是考察物质运动的“观测角”.设有一个初速度为 v0的物质,分裂成3部分,分别以 v0继续运动、以加速度 a加速运动和以加速度a减速运动,根据式(4),其所对应的时空偏转角分别为:匀速直线运动的物质,θ0恒定,静止系中的观察者“认为”其时空是平直的,对应于欧几里德空间,曲率 k=0,三角形的内角和等于180°.变速运动的物质,θ随时间t变化,该观察者“认为”其时空是弯曲的(见图4).加速运动系(a>0)的时空对应于黎曼空间,曲率 k=1,三角形的内角和大于180°;减速运动系(a<0)的时空对应于罗巴切夫斯基空间,曲率 k=-1,三角形的内角和小于180°.如果将两坐标轴与时空偏转角θ随时间t变化的曲线所包围的面积定义为时空面积的话,3种不同运动所对应的时空面积见图5-8,阴影部分为时空面积.我们可以将时空面积变化形象化地视为时空形变的一种量度.变速运动系与匀速运动系相比,在相同时间内“扫过”的时空面积不同.匀速运动时空面积为一矩形 abdg;加速运动时空面积为 abeg,其相对于矩形 abdg时空面积增加deg;减速运动时空面积为abcg,其相对于矩形 abdg时空面积减少cgd.变速运动系或者说非惯性系相对于匀速系,即惯性系的这种时空形变正是惯性力的根源.处在这两种时空的静止物体或与该变速系加速度不相等的运动物体就会“感觉”到被向后拉和向前推的力.时空的“疏密”变化将产生力的效应,如,站在向前加速的汽车里的人,由于其时空相对于匀速运动汽车的时空更加“紧密”,人身体将向后仰;同理,站在减速汽车里的人,由于其时空相对于匀速运动时汽车的时空更加“稀疏”,身体向前倒.惯性力是时空的形变效应.相对于加速系加速度为零的物体,θ角不随时间改变,它感受不到时空的形变,因此,不产生时空力的效应,这是爱因斯坦建立广义相对论时所用的等效原理的物理本质. 爱因斯坦广义相对论将引力本质归结为时空弯曲[12].时空弯曲与时空形变是一个意思,只是语言表达的差异,引力与惯性力来源相同,都是时空效应,所以引力质量等于惯性质量.惯性质量和引力质量相等是广义相对性公理的一个论据[5].在复时空框架下,惯性力起源于非惯性系的时空形变,和广义相对论中引力的来源相同,本质上是同一个力.惯性质量和引力质量相等绝非偶然,而是自然内在统一性的必然反映.【相关文献】[1] 郭奕玲,沈慧君.物理学史:第2版 [M].北京:清华大学出版社,2005:9.[2] [美]理查德·费曼.物理学讲义[M].上海:上海科学技术出版社,1966:134.[3] [英]B·K·里德雷.时间、空间和万物[M].长沙:湖南科学技术出版社,2004:119.[4] 牛顿.自然哲学之数学原理 [M].西安:陕西人民出版社, 2005:10-11.[5] 爱因斯坦.狭义与广义相对论浅说 [M].北京:北京大学出版社,2006:1,96,52.[6] 宋文淼,阴和俊,张小娟.实物与暗物的数理逻辑 [M].北京:科学出版社,2006:82.[7] [英]戴维斯·布朗.原子中的幽灵[M].长沙:湖南科学技术出版社,2002:14.[8] [美]B·格林.宇宙的琴弦 [M].长沙:湖南科学技术出版社, 2005:6.[9] [美]理查·德费曼,S·温伯格.从反粒子到最终定律 [M].长沙:湖南科学技术出版社,2003:51.[10] 刘建亚.复变函数与积分变换 [M].北京:高等教育出版社, 2005:2.[11] [美]徐一鸿.可畏的对称[M].北京:清华大学出版社,2005: 69.[12] 赵展岳.相对论导引 [M].北京:清华大学出版社,2002:93.。
量子力学效应

量子力学效应
量子力学效应是指在微观量子物理领域中,粒子的行为和性质表现出来的奇特现象。
其中最著名的就是量子纠缠效应,即两个或多个粒子之间存在着互相影响的联系,即使它们之间相隔很远也是如此。
这种现象揭示了量子物理学的本质,即量子态的非局域性和相互依存性。
另一个重要的量子力学效应是量子隧穿效应。
在经典物理学中,粒子在遇到势垒时,只有能量高于势垒的部分才能穿过去,而低于势垒的部分会被反射回来。
但在量子力学中,粒子具有波粒二象性,即粒子同时表现为波和粒子的形式。
因此,即使粒子的能量低于势垒,也有一定的概率可以穿过去。
此外,量子力学效应还包括量子干涉效应、量子测量效应等等。
这些奇特的现象不仅为物理学家们提供了解释自然界的新思路,而且对于现代技术的发展也具有重要的应用价值。
例如,量子计算机、量子通信等领域都利用了这些效应,开辟出了新的前沿。
- 1 -。
量子芝诺效应

量子力学有一个基本点:观察会改变被观察的系统。
(量子芝诺效应quantum zeno effect)芝诺zeno悖论:一支在空中飞行的箭,其实是不动的。
为什么呢?因为在每一个瞬间,我们拍一张snapshot,那么这支箭在那一刻必定是不动的,所以一支飞行的箭,它等于千千万万个“不动”的组合。
问题是,每一个瞬间它都不动,连起来怎么可能变成“动”呢?所以飞行的箭必定是不动的!在我们的实验里也是一样,每一刻波函数(因为观察)都不发展,那么连在一起它怎么可能发展呢?所以它必定永不发展!从哲学角度来说我们可以对芝诺进行精彩的分析,比如恩格斯漂亮地反驳说,每一刻的箭都处在不动与动的矛盾中,而真实的运动恰好是这种矛盾本身!不过我们不在意哲学探讨,只在乎实验证据。
已经有相当多的实验证实,当观测频繁到一定程度时,量子体系的确表现出芝诺效应。
[量子物理史话]哲学早已经与科学结下了不解渊源,这里又是一个印证。
如果一个系统被连续不断地观测,那么它将是不变,不衰减的。
另外,还有一个量子反芝诺效应( anti zeno effect):如果观察的间隔大于特定时间(一个特征时间,称作zeno time),那么该系统将衰减的更快。
目前,主要的应用领域是量子计算。
在讲解芝诺悖论的时候,常常以"a watched pot never boils"来解释。
“一个被盯着看的水壶总也不开”,说起来像一个心理现象。
确实,许多物理规律,特别是量子物理,都似乎能在社会科学中找到对应,但是不严谨的。
量子力学就像是为一些神秘力量或主观逻辑想象的合理性而生的,但又有谁能否认也许那才是真正的世界呢?我google了一下,发现有blogger谈到了这个quantum zeno effect。
从comment里发现台湾的schee也曾对此非常感兴趣,虽然我不是很明白,他是如何把zeno effect和他所说的现象联系起来的。
但确实有许多现实生活中的问题与这个量子芝诺效应有相通之处,随便举个例子:某人想淡忘一些事情,淡忘需要时间,这就是zeno time,如果他总是受到刺激,间隔小于淡忘时间,那么他永远也忘不了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第30卷 第1期河南师范大学学报(自然科学版)Vol.30 No.1 2002年2月Journal o f Henan Normal Univer sity (Natural Science )Feb.2002 文章编号:1000-2367(2002)01-0050-05惯性的经典效应、量子效应及起源的研究①宋海珍,肖绍武(南阳师范学院物理系,河南南阳,473061)摘 要:惯性的经典效应是惯性力,量子效应是Unruh 效应,惯性起源于加速引起的真空变化.关键词:惯性;经典效应;量子效应中图分类号:O142 文献标识码:A对惯性溯本求源,可知惯性不是个别物体的性质,而是整个时空的性质.牛顿引力理论刻划的仅仅是静止源的引力场,两个静止源的相互作用是万有引力;广义相对论刻划的是一般的作任意运动的引力源所产生的变化引力场,作任意运动的引力源所产生的变化引力场对质点的作用在某种程度上表现为惯性力,惯性的经典效应是惯性力.考察引力场及惯性力场的量子效应时,发现引力场的量子效应是Hawking 效应,惯性力场的量子效应是Unruh 效应.进一步研究知道,Hawking 2Unruh 效应起源于真空能级的变化,惯性力与万有引力有着相同的本质和起源,它们起源于真空能级的变化.惯性效应的实质是一个起源于加速引起的真空“形变”的局域效应,惯性力是物体与“形变”的真空之间的相互作用,惯性力的反作用力作用在“形变”的真空上,惯性作用是以光速传播的.1 惯性的经典效应是惯性力,惯性力是运动的引力源所产生的变化的引力场的一种表现1.1 弱引力场下的推迟势在弱引力场下度规可表示成g μν=ημν+h μν,h μν是一级小量,可认为是平直时空背景ημν下的引力势,定义Φμν=h μν-12ημνh 其中h =h αα=ηαβh αβ(1)其逆变换 h μν=Φμν-12ημνΦ(2)对坐标加上谐和条件Φ′αμν=0的限制,场方程化为Φ′αμν ,α,=-16πG c4T μν(3)(3)的解是推迟势Φμν(γ→,t )=4Gc4∫T μν(γ′→,t -γc)γd 3x ′(4)γ表示源点γ′→到场点距离,推迟势Φμν是以光速传播的.1.2 弱引力场下粒子的运动方程①收稿日期:2001-11-12.第1作者简介:宋海珍(1963~),女,河南唐河人,南阳师范学院讲师.考虑带有空间指标的短程线方程,即-d 2x i d s 2=Γi 00(d x 0d s )2+2Гi j 0d x j d s d x 0d s +Гi jk νj νkc2(5)(5)式中v j ,v k 是粒子的通常速度,在弱引力场下,h μν精确到一级项,Christoffel 联络可写为Γi 00=-12h 00,i +h 0i ,0 Γi j 0=(h ij ,0+h i 0,j -h j 0,i ) Γijk =(h ij ,k +h ik ,j -h jk ,i )将这些值代入(5)式可得弱引力场下粒子的运动方程为c 2d 2x i d s 2=(d x 0d s )2[c 2h 00,i 2-5(ch 0i )5t ]+c 2d x 0d s d x jd s [h j 0,i -h i 0,j ]-c 2h ij ,o d x i d s d x 0d s -Γi jk v j v k(6)1.3 考察粒子在半径为R 、静质量为M 、以角速度ω相对于其内的观察者旋转的中空球壳内的运动设R s ,θ,φ为球壳元的球面坐标,a ,θ0,φ0为球壳内某点的球面坐标,该点的推迟势Φμν可有(4)式算出.设球壳机械应力很小,则能量-动量张量тμν近似等于ρm uμu ν,u μ,u ν表示球壳内的观察者所见的球壳元的四速度,精确到u2c2的Φμν值是:Ф00=4G Mc 2R s [1+ω2R 2s3c 2-2ω2a 215c 2+ω25c2a 2sin 2θ0 =4GMc 2R s [1+ω2R 2s 3c 2-2ω215c 2(x 2+y 2+z 2)+ω25c 2(x 2+y 2)],Ф11=4GM c 2R s [ω2R 2s 3c 2-ω2a 215c 2+ω25c2a 2sin 2θ0sin 2φ0]=4G M c 2R s [ω2R 2s 3c 2-ω215c 2(x 2+y 2+z 2)+ω25c 2y 2],(7)Ф22=4G M c 2R s [ω2R 2s 3c 2-ω2a 215c 2+ω25c2a 2sin 2θ0cos 2φ0]=4GM c 2R s [ω2R 2s 3c 2-ω215c 2(x 2+y 2+z 2)+ω25c2x 2],Ф33=Ф30=Ф23=0,Ф12=4GM ω25c 4R s -a 2sin 2θ0cos φ0sin φ0=-4G M ω25c 4R sxy ,Ф10=4G M ω3c 3R s a sin θ0cos φ0=4G Mω3c 3R s x ,Ф20=-4G M ω3c 3R s a sin θ0cos φ0=-4G Mω3c 3R sx ,Ф=Фμμ=-4G Mc 2R s [1-ω2R 2s3c2]. 由(2)、(7)可知,(6)式的最后两项是级数较v2c2为高的项,短程线方程取如下形式:c 2d 2x →d t 2= V -5A →t +v →× ×A→(8)其中V =c 22h 00=c 22(Φ00-12Φ),A i =ch 0i =cΦ0i ,把(7)代入,通过计算,最后得V =G Mω215R s c 2[4x i →+4y j →-8z k →],15第1期 宋海珍等:惯性的经典效应、量子效应及起源的研究-5A →t =-4G Mω3c 2R s d x d t i →+4G M ω3c 2R s d x d tj →,v →× ×A →=-4G M ω3c 2R s d y d t i →+4G M ω3c 2R s d x d tj→(8)式的分量形式即球壳内粒子的运动方程为:c 2d 2x d t 2=4G M 3c 2R s [15ω2x -ωd x d t -ωd yd t ],c 2d 2y d t 2=4G M 3c 2R s [15ω2y +2ωd xd t ],(9)c 2d 2z d t 2=8G Mω215R s c 2z. 由此可见:当粒子静止于旋转球壳内时,只观察到作用在该粒子上的离心力; V 包括了同相对转动相关联的离心力,v →× ×A →导致C oriolis 加速度,5A→5t代表由相对速度所引起的力;Einstein 引力理论刻划的是作任意运动的引力源所产生的变化引力场,惯性力是由于物质质量之间的相对加速运动引起的一个引力效应,是运动引力源产生的变化引力场的一种表现,惯性的经典效应是惯性力.2 惯性的量子效应是Unruh 效应2.1 任意变速参考系中的时空度规设参考系沿x 方向具有加速度a (t ),该系中的度规可表示为下面的形式:ds 2=ω(x ,t )-c 2d t 2-d x 2-d y 2-d z 2(10)Γτμν的不为零的分量是Γ000=121c 1ω(x ,t )5ω(x ,t )5t ,Γ001=Γ010=121ω(x ,t )5ω(x ,t )5x ,Γ100=125ω(x ,t )5x(11) 此参考系中,能量-动量张量T μν=0,场方程简化为R μν=0,将(11)代入场方程,在a (t )很小时,引力势可按牛顿力学计算,最后可得场方程的解:d s 2=[1+a (t )x c2]c 2d t 2-d x 2-d y 2-d z 2(12)2.2 惯性的量子效应是Unruh 效应当a (t )是常数时,可通过一个纯数学变换X =c 2a (ch at c -1)+x ch at c , T =c a sh at c +x c sh atc, Y =y , Z =z.(13)把惯性系的度规d s 2=c 2d T 2-d X 2-d Y 2-d Z 2(14)变换为匀加速直线运动系的度规d s 2=[1+ax/c 2]c 2d t 2-d x 2-d y 2-d z 2(15)(13)式的变换正是R 区的局域Rindler 变换X =(1a+ζ)ch (a η), T =(1a+ζ)sh (a η),(16)其中x =1a+ζ,t =aη 通过此Rindler 变换,R 区的时空线元由Minkowski 的时空线元(14)化为Rindler 时空线元d s 2=[1+a ζ]2d η2-d ζ2-d y 2-d z2(17) 可见,Minkowski 时空对应的是惯性系,Rindler 时空对应的是匀加速直线运动系.把(17)式代入零曲面方程25河南师范大学学报(自然科学版) 2002年gμν5f 5x μ5f 5xν=1(1+a ζ)2(5f 5η)2+(5f 5ζ)2+(5f 5y )2+(5f 5z )2=1(1+a ζ)2(5f 5η)2+(5f5ζ)2=0由此可知,ζ=-1a处存在事件视界.若用Rindler 时空的乌龟坐标表示,视界在ξ→-∞处.此坐标系中,静止观测者的固有加速度为b =a e -аξ,视界面上表面引力加速度为a ,在原点(ξ=0)加速度也等于a ,a 叫坐标加速度,原点附近的时空线元趋于Minkowski 的时空线元.把Rindler 时空中的K-G 方程和Dirac 方程在视界附近化成波动方程的标准形式,可以证明,有温度T =a2πK B 的热辐射从视界ζ=-1a 处射出,实测的固有温度T p =b 2πK B ,辐射谱为黑体谱N ω=1l ωK B T ±1.惯性系中的真空在匀加速直线运动的观测者看来是热态,温度正比于他的坐标加速度a ,而a 正是该加速系的惯性场强,这种效应叫Unruh 效应(或Rindler 效应),相应的辐射叫Rindler 辐射.Rindler 观察者感受到的热效应是一种量子效应,惯性系中的零点能在匀加速直线运动的参考系中看来,就是高于真空零点的能量,是真实可测的能量,这种能量以黑体谱热辐射的形态出现,因此,Rindler 观察者感到自己浸在热浴中,惯性的量子效应是Unruh 效应.3 惯性效应起源于加速引起的真空能级变化真空态被定义为没有任何粒子的状态,在闵氏时空中,可选u K =еi k →・x →-iωT 为模函数,把波函数Ψ展开Ψ=∑+∞K =-∞(aK u K +a +K u 3K ),式中T 为闵氏时间,a +为产生算符,a 为湮灭算符,对于闵氏时空的真空态有:a K |0>=0.a +K |0>=|1>. 在Rindler 时空中,R 区的模函数R u K 和L 区的模函数L u K 共同组成完备基. R u K =1(4π ω)1/2еiK ξ-i ωη L u K =1(4π ω)1/2еiKξ+i ωηK-G 方程中的波函数Ψ可展开为Ψ=∑+∞K =-∞(b (1)K L u k+bK(1)+Lu 3K +b K(2)Ru K +b (2)+KRu 3k )式中η是Rindler 时间,b (1)K,b (1)+K 为L 区的湮灭、产生算符,b (2)K ,b (2)+K 为R 区湮灭、产生算符,对于Rindler时空的真空态有b (1)K |0>=b (2)K |0>=0.利用Bog oliubov 变换,可以证明,对于Rindler 观察者,闵氏真空态中含有粒子,这些粒子的能谱为黑体谱 M <0|b (1)k +b (1)k |0>M =M <0|b (2)k +b (2)k |0>M =N ω=1l ωK B T ±1(18)其中 T =a2πK B.可见,对于Rindler 观察者,闵氏真空态存在热辐射,是温度为T 的热态.总之,不同的“时间坐标”对应不同的“真空”,惯性系中的真空是由Minkowski 时间T 来定义的,Minkowski 真空的虚粒子涨落形成零点能.Rindler 时间η也可以定义一个真空,Rindler 真空不是闵氏真空,它的能量零点比闵氏真空的能量零点低.闵氏真空的零点能在Rindler 观察者看来就是高于真空零点的能量,是真实可测的能量,这种能量以最简单的形态出现,呈现出具有黑体谱的热辐射能.原本一无所有的闵氏时空,所有惯性观察者均认为是真空,但是,在其中作匀加速直线运动的观察者会发现自己周围充满了热辐射,其辐射温度是T =a2πK B,这个温度取决于Rindler 系的坐标加速度a ,实测的温度是固有温35第1期 宋海珍等:惯性的经典效应、量子效应及起源的研究度T p=b2πK B,辐射谱为黑体谱Nω=1lωKBT±1.热辐射的出现源于真空能级的变化.闵氏时空对应于克鲁斯卡时空,Rindler时空对应于史瓦西时空.对于史瓦西时空,存在霍金辐射,辐射温度正比于视界的表面引力κ,而κ正是史瓦西时空的引力场强.对于Rindler时空,存在安鲁效应,辐射温度T正比于坐标加速度a,而a是加速系的惯性力场强.引力场的经典效应是万有引力、量子效应是霍金效应,惯性的经典效应是惯性力、量子效应是安鲁效应.由于霍金-安鲁效应起源于真空能级的升降,惯性力和万有引力也应起源于真空能级的变化,它们有着相同的本质和起源.惯性效应的实质是一个起源于加速引起的真空“形变”的局域效应,惯性力是物体与“形变”的真空之间的相互作用,是形变的“真空”造成的反作用力,惯性作用不是超距作用,而是以光速传播的.参 考 文 献1 赵 峥.黑洞与弯曲的时空[M].太原:山西科学技术出版社,20002 赵 峥.黑洞的热性质与时空奇异性[M].北京:北京师范大学出版社,19993 王永久.黑洞物理学[M].长沙:湖南师范大学出版社,20004 韦 伯.广义相对论与引力波[M].北京:科学出版社,1977The Study on the Classical E ffect,Q uantum E ffect and Origin of I nertiaS ONG Hai2zhen,XI AO Shao2wu(Department of Physics,Nanyang T eachers’C ollege,Henan Nanyang,473061,China)Abstract:Inertial classical effect is inertial force.Inertial quantum effect is Unruh effect.The inertia originates of the change of vacuum caused the acceleration.K ey w ords:inertia;classical effect;quantum effect45河南师范大学学报(自然科学版) 2002年。
