第二讲 电子衍射原理
电子衍射原理

h1u k1v l1 w 0 h2 u k 2 v l 2 w 0
得
u=k1l2-k2l1
v=l1h2-l2h1
w=h1k2-h2k1
简单易记法 h1 k1 l1 h1 k1 l1 h2 k2 l2 h2 k2
u
v
w
l2
六、电子衍射基本公式
电子衍射基本公式推导 TEM的电子衍射是把实际 晶体点阵转换为倒易点阵记 录下来,得到的图像叫做电 子衍射花样或叫电子衍射图。
电子束
光阑选区衍射(Le Pool方式)----用位于物镜象 平面上的选区光阑限制微区大小。先在明场象上找 到感兴趣的微区,将其移到荧光屏中心,再用选区 光阑套住微区而将其余部分挡掉。理论上,这种选 区的极限0.5m。 微束选区衍射 ----用微细的入射束直接在样品上 选择感兴趣部位获得该微区衍射像。电子束可聚焦 很细,所选微区可小于0.5m 。可用于研究微小析 出相和单个晶体缺陷等。目前已发展成为微束衍射 技术。
七、单晶电子衍射花样的标定
基本任务 确定花样中斑点的指数及其晶带轴方向[uvw]; 确定样品的点阵类型、物相和位向。 一般分析任务可分为两大类: 鉴定旧结构,这种结构的参数前人已作过测定,要求在这些
已知结构中找出符合的结构来。
测定新结构,这种结构的参数是完全未知的,在ASTM卡片中 和其它文献中都找不到;
OO*透射束,OG衍 射束,θ衍射角, G O*G=1/d
Θ
1/λ
o
O
1/λ
O*
**
五、晶带定律与零层倒易截面
1.晶带:晶体内同时平行于某一 方向[uvw] 的所有晶面组(hkl )构成一个晶带, [uvw]称为晶 带轴。
电子衍射原理

三、结构因子
结构因子F(hkl)是描述晶胞类型和衍射强度之间关系的一个函数。结构因子的数学表达
式为
N
F(hkl) f j exp[2i(hx j kyj lz j )]
j 1
fj 是单胞中位于(x j , y j , z j )的第j个原子对电子的散射振幅(或叫散射因子),它的大小与原 子序数有关。
c
c*
a
c*
b
0
a*
a
b*
b
c*
c
1
2、在倒易空间中,任意矢量的大小和方向可以用倒易矢量g来表示。
g
ha
*
kb *
lc*
1)ghkl垂直于(hkl)晶面。平行与(hkl)晶面的 法线N(hkl)。 2)倒易点阵中的一个点代表的是正点阵中的一组晶面。
微束选区衍射 ----用微细的入射束直接在样品上 选择感兴趣部位获得该微区衍射像。电子束可聚焦 很细,所选微区可小于0.5m 。可用于研究微小析 出相和单个晶体缺陷等。目前已发展成为微束衍射 技术。
一、电子衍射原理 透射电镜 单晶体
ቤተ መጻሕፍቲ ባይዱ多晶体
非晶体
二、布拉格定律 样品对入射电子的散射
• 晶体物质是由原子、离子或原子团在三维空间按一定 规律周期性排列构成的。当具有一定波长的单色平面 电子波射入晶体时,这些规则排列的质点将对入射电 子束中与其靠近的电子产生散射,由于散射强度较大 ,于是各个质点作为新波源发射次级波.
• 计算结构因子时要把晶胞中的所有原子考虑在内。
教学课件:第二章-电子衍射原理与分析

德布罗意假设
路易·德布罗意提出所有微观粒子都具 有波粒二象性。人们熟悉的电子、质 子、中子同样具有波粒二象性。
德布罗意波长
德布罗意波长的公式
λ=h/p,其中λ是德布罗意波长,h是普朗克常数,p是动量。
表面反应动力学研究
表面反应动力学是研究表面化学反应速率和反应机制的学科,电子衍射技术在表 面反应动力学研究中发挥着重要作用。
通过分析电子衍射数据,可以获得关于表面反应中间物、产物和反应路径的信息 ,有助于深入理解表面化学反应机理和动力学过程,为催化剂设计、环境保护和 能源转化等领域提供理论支持。
06 结论
电子衍射原理的重要性和应用价值
电子衍射原理是研究物质微观结构的 重要手段,通过分析电子衍射图样可 以获得物质内部的精细结构信息,对 于材料科学、物理学、化学等领域的 研究具有重要意义。
电子衍射原理的应用范围广泛,包括 材料结构表征、晶体缺陷分析、表面 形貌观察、纳米材料研究等方面,对 于推动科学技术进步和产业发展具有 重要作用。
表面电子态研究
表面电子态研究是电子衍射在表面科学中的另一个重要应 用。通过分析电子衍射数据,可以获得表面电子的能级结 构、占据情况和跃迁行为等信息,有助于深入理解表面物 理和化学性质以及电子传输和光学性能。
表面电子态的研究对于发展新型电子器件、光电器件和能 源材料等具有重要意义,有助于推动相关领域的技术进步 和创新。
对未来研究的展望
随着科学技术的发展,电子衍射原理 的应用前景将更加广阔。未来可以进 一步拓展其在新型材料、纳米科技、 生物医学等领域的应用,为解决人类 面临的能源、环境等问题提供更多有 效手段。
2_2.电子散射原理

7
夫朗和费(Fraunhofer)近似 和Fraunhofer衍射
Fraunhofer衍射是指当一个平面波与障碍物相 互作用时发生的衍射。由于从点光源反射的 波只有在很远的距离以外才能成为平面波, 所以这种衍射又称为远场衍射。 夫朗和费近似的实质是用平面波代替球面波。
( ) F ( K ) q(r ) exp[ 2iK r ]dr
第二讲 电子衍射原理
晶体学的预备知识 电子的散射与衍射 电子衍射谱的标定
1
电子的散射和衍射
电子衍射的发展过程
1912年,劳埃通过X-ray衍射实验
– 证实了晶体中原子的微观排列 – 开辟了用X-ray衍射研究晶体结构这一新领域
1926~1927年,实现了晶体的电子衍射
– 肯定了电子波动性 – 奠定了电子衍射学科
2me F Vhkl 2 h
Vhkl是(hkl )衍射方向的傅立叶系数
20
原子散射因子的推导——原子 对入射电子散射的波动理论*
在相对论下:
eV eV mc 2 m0 c 2 m m0 2 c m0 m v2 1 2 c
h 2 eV m m0
1 m 2c 2 2 2 2 0 2 m 2c 2 p2 eV m m0 mc m0 c m m0 m0 c 2 1 1 v 1 v 2 c c2
电子的散射和衍射
高速电子进入到固体中,与单个原子的原子核及核外电子间发生相 互作用,从而发生方向、能量的改变,称为散射。从能量损失的角 度分为弹性散射和非弹性散射
从粒子角度讲,为连续的粒子流与原子核及核外电子的相互作用 的库仑碰撞
从波的角度讲,为准单色电子波,受单个原子扰动而形成球面波 高速电子被固体中周期排列的原子散射后,其弹性散射部分是相干 的,能够在某些方位上相干加强,形成花样,是为衍射 电子的衍射为多原子相互作用的集体行为 衍射行为反映了固体原子排列的周期性 注意散射和衍射的本质和区别,在不同情况下,我们将根据习惯而 分别使用这两个术语。 5
电子衍射

❖
2、衍射斑点为倒易点的投影
可以证明,电子衍射标定(指标化),可得到 倒易点阵空间分布状态
16
17
例1
下图为某物质的电子衍射花样 ,试指标化并 求其晶胞参数和晶带方向。
RA=7.1mm, RB=10.0mm, RC=12.3mm, (rArB)90o, (rArC)55o , L=14.1mm Å.
人们能在高倍下选择微区进行晶体结构分析, 弄清微区的物相组成; 2)电子波长短,使单晶电子衍射斑点大都分布 在一二维倒易截面内,这对分析晶体结构和位 向关系带来很大方便; 3)电子衍射强度大,所需曝光时间短,摄取衍 射花样时仅需几秒钟。
2
2、单晶电子衍射 当一电子束照射在单晶体薄膜上时,透射束穿
8 Find [uvw]= g1 g2 =[110]
u k1l2 k2l1 v l1h2 l2h1 w h1k2 h2k1
112
A110
112C
002
000
112
110
B 002
112
24
例2 下图为某物质( CaO)的两个方向的电子衍射花 样 ,试指标化并求其晶胞参数和晶带方向。 L=800mm, V=100KV, R 列在下表。 解:K=Lλ=800*1.225/100,0001/2=2.961mm nm.
20
4检查夹角:
cosAB 0,AB 900,cosAC 1 3,AC 54.70
与测量值一致。
112
5对各衍射点指标化如下 。
6 a= 2dB=2.83 Å,
d a h2 k2 l2
002
7可得到 [uvw]=[220].
112
晶带轴为 [uvw]=[110]。
电子的衍射原理

电子的衍射原理电子的衍射原理是指当电子束通过一个尺寸与其波长接近的孔或经过晶体时,会发生衍射现象。
这个现象与光波的衍射原理非常相似,但是由于电子的特殊性质,使得电子的衍射具有一些独特的特点。
首先,我们知道根据德布罗意波动方程,物质粒子也具有波动性质。
对于电子来说,它的波长可以由德布罗意公式λ = h/p计算得出,其中h是普朗克常数,p为电子的动量。
电子的衍射主要是通过电子与晶体或孔的相互作用来产生的。
当电子束遇到晶格的时候,晶格的周期性结构会对电子束产生散射,这种散射就是电子的衍射。
晶格常数决定了衍射的微细结构,而晶体的平面则决定了衍射的方向性。
衍射的过程可以通过惠更斯-菲涅尔原理来描述。
根据该原理,每个点上的波前都可以看作是一系列波源发出的次级波的叠加,这些次级波形成了新的波前。
在电子的衍射过程中,散射的电子波可以视为次级波,而晶体或孔则形成了作为波前的电子波传播的界面。
电子的衍射表现出了一些有趣的现象。
首先是衍射图样的特点,类似于光的衍射,电子的衍射图样也会出现干涉条纹。
这些条纹的形状和分布可以提供关于晶体结构的有用信息,因此电子衍射技术在材料科学中有着重要的应用。
另一个有趣的现象是衍射的相对强度。
电子的散射过程中,不同方向的电子波会相互干涉,形成强度不均匀的衍射图样。
这些强度的变化可以通过使用衍射模型和计算方法来解释。
电子衍射原理在很多领域都有重要的应用,特别是在材料科学、凝聚态物理和电子显微镜技术中。
使用电子衍射技术,科学家们可以研究材料的晶体结构、晶格常数、晶格缺陷等重要的性质。
此外,电子衍射还可用于表征纳米材料、薄膜以及生物分子的结构,为相关研究提供了强有力的工具。
总之,电子的衍射原理是基于电子的波动性而实现的一种衍射现象。
通过电子与晶体或孔的相互作用,电子束会发生散射,形成干涉和衍射的图样。
电子衍射原理的理解和应用对于探索材料的微观结构、研究纳米领域以及发展电子显微镜技术都具有重要的意义。
电子衍射原理概述

测出正空间中各衍射晶面问的相对方位,这就是电子衍射分析要解
决的主要问题。
三、晶带定理与零层倒易截面
在正点阵中,同时平行于某一晶向 [uvw]的一组晶面构成一个晶带,而这 一晶向称为这一晶带的晶带轴。
图10-5为正空间中晶体的[uvw]晶带及 其相应的零层倒易截面(通过倒易原点) 。
特点:
1.晶面( h)1k1l1 (h2k2l2)、 、 ( h3k3l3) 的法向
的指数应是
1、 1 10 、 0 1 1 0 、 1 1、 2 0、 0 2 00 、 0 0、 2 0 2 0 0 。
再来看[011]晶带的标准零层倒易截面,
1. 1.满足晶带定理的条件是衍射晶面的k和l两个指数必须相等和
符号相反;
. 2.如果同时再考虑结构消光条件,则指数h必须是偶数。因此,
在中心点000周围的八个点应是
电子衍射原理概述
由于电子波与x射线相比具有下列不同之处:
透射电镜能在同一试样上把物相的形貌观察与结构分析结合起来 ,可借助显微图象,在放大几百万倍的情况下,将直径小到几个埃 的微晶挑选出来,进行晶体结构的研究,也可借助衍射花样,弄清 薄晶衍衬成象的衬度来源,对光怪陆离的现象加以确切解释。这些 ,对于材料科学工作这都是至关重要的。
2. 2.只有不产生消光的晶
面才能在零层倒易面上出
现倒易阵点。
图l0-7为体心立方晶体[001]和[011]晶带的标准零层倒易截面图。
对[001]晶带的零层例易截面来说, 1.要满足晶带定理的晶面指数必定是
hk型0的,
2.考虑体心立方晶体的消光条件是三指数之和应是奇数,因此,必
须使h、k 两个指数之和是偶数,此时在中心点000周围最近八个点
《电子衍射原理》课件

透射电子显微镜技术
透射电子显微镜技术是一种利用透射 电镜观察物质内部微细结构的方法, 具有高分辨率和高放大倍数的特点。 随着科技的不断进步,透射电子显微 镜技术的应用范围越来越广泛,在材 料科学、生物学、医学等领域得到广 泛应用。
VS
例如,在材料科学领域,透射电子显 微镜技术可用于研究材料的晶体结构 和相变行为,为新材料的开发和优化 提供有力支持。在生物学领域,透射 电子显微镜技术可用于研究细胞器和 生物大分子的结构和功能,为生命科 学和医学研究提供新的视角。
电子显微镜的放大倍数较高,能够观察到非常细微的结构细节,是研究物质结构和 形貌的重要工具之一。
电子源
电子源是电子显微镜中的核心部件之一,它能够产生用于观察和成像的 电子束。
电子源通常由加热阴极、栅极和加速电极等部分组成,通过加热阴极使 得电子逸出并经过栅极和加速电极的调制和加速,形成用于成像的电子
电子衍射可以揭示细胞内部的超微 结构,有助于理解细胞的生理和病 理过程。
在表面科学中的应用
表面晶体结构
电子衍射可以用于研究固体表面 的晶体结构和化学组成,对表面 改性和催化等应用具有指导意义
。
表面应力分析
通过电子衍射可以分析表面应力 状态,有助于理解表面行为的物
理机制。
表面吸附和反应
电子衍射可以研究表面吸附分子 的结构和反应活性,对表面化学 和工业催化等领域有重要意义。
05
电子衍射的发展前景
高能电子衍射技术
高能电子衍射技术是一种利用高能电子束进行物质结构分析的方法,具有高分辨 率和高灵敏度的特点。随着科技的不断进步,高能电子衍射技术的应用范围越来 越广泛,在材料科学、生物学、医学等领域发挥着重要作用。
例如,在材料科学领域,高能电子衍射技术可用于研究材料的微观结构和晶体取 向,为新材料的开发和优化提供有力支持。在生物学领域,高能电子衍射技术可 用于研究生物大分子的结构和功能,为药物设计和疾病治疗提供新的思路。
电子衍射原理

电子衍射原理电子衍射原理电子衍射electron diffraction当电子波(具有一定能量的电子)落到晶体上时,被晶体中原子散射,各散射电子波之间产生互相干涉现象。
晶体中每个原子均对电子进行散射,使电子改变其方向和波长。
在散射过程中部分电子与原子有能量交换作用,电子的波长发生变化,此时称非弹性散射;若无能量交换作用,电子的波长不变,则称弹性散射。
在弹性散射过程中,由于晶体中原子排列的周期性,各原子所散射的电子波在叠加时互相干涉,散射波的总强度在空间的分布并不连续,除在某一定方向外,散射波的总强度为零。
历史1927年,C.J.戴维孙和L.H.革末在观察镍单晶表面对能量为100电子伏的电子束进行散射时,发现了散射束强度随空间分布的不连续性,即晶体对电子的衍射现象。
几乎与此同时,G.P.汤姆孙和A.里德用能量为2万电子伏的电子束透过多晶薄膜做实验时,也观察到衍射图样。
电子衍射的发现证实了L.V.德布罗意提出的电子具有波动性的设想,构成了量子力学的实验基础。
装置最简单的电子衍射装置如图1所示。
从阴极K发出的电子被加速后经过阳极A的光阑孔和透镜L到达试样S上,被试样衍射后在荧光屏或照相底板P上形成电子衍射图样。
由于物质(包括空气)对电子的吸收很强,故上述各部分均置于真空中。
电子的加速电压一般为数万伏至十万伏左右,称高能电子衍射。
为了研究表面结构,电子加速电压也可低达数千甚至数十伏,这种装置称低能电子衍射装置。
模式电子衍射可用于研究厚度小于0.2微米的薄膜结构,或大块试样的表面结构。
前一种情况称透射电子衍射,后一种称反射电子衍射。
作反射电子衍射时,电子束与试样表面的夹角很小,一般在1゜~2゜以内,称掠射角。
自从60年代以来,商品透射电子显微镜都具有电子衍射功能(见电子显微镜),而且可以利用试样后面的透镜,选择小至1微米的区域进行衍射观察,称为选区电子衍射,而在试样之后不用任何透镜的情形称高分辨电子衍射。
电子衍射原理

电子衍射原理
电子衍射原理是一种利用电子束进行衍射的物理现象。
当电子束通过一系列定向的晶体或经过一定的物质时,会产生衍射效应,形成衍射图案。
这种图案可以用来研究物质的晶体结构和晶格常数,从而揭示物质的微观性质。
电子衍射原理的核心是电子波的波动性。
根据物质的粒子-波
二象性,电子也具有波动性。
当电子束通过晶体时,入射电子波会与晶体中的原子相互作用,发生散射。
这些散射的电子波会互相干涉形成衍射图案,通过测量衍射图案的特征,可以推导出晶体的结构信息。
根据布拉格衍射定律,电子束在晶格中的衍射图样由晶格常数、入射电子波长、衍射角等参数决定。
通过调节电子束的入射角度和晶体的取向,可以获得不同的衍射图案。
这些图案通常以点阵或环状的形式出现,其中点的位置和分布反映了晶体的结构参数。
电子衍射原理在材料科学、凝聚态物理、纳米科技等领域具有广泛的应用。
通过电子衍射技术,科学家可以研究材料的晶体结构、晶界和缺陷等微观性质,进一步揭示物质的物理化学特性。
同时,电子衍射还可以用于研究纳米材料、纳米颗粒和薄膜等微结构的形貌和晶态特征,对于材料设计和纳米器件的制备具有重要意义。
总之,电子衍射原理是一种基于电子束的衍射现象,可以用来研究物质的微观结构和性质。
它在材料科学和纳米技术等领域
的应用非常广泛,对于推动材料科学的发展和纳米技术的应用具有重要意义。
电子衍射原理与分析课件

05
电子衍射在生物学中的 应用
大分子结构分析
蛋白质晶体学
电子衍射技术在大分子结构分析中发挥 着重要作用,尤其在蛋白质晶体学领域 。通过电子衍射,可以解析蛋白质晶体 的空间结构,为理解蛋白质功能和设计 新药物提供关键信息。
当电子束以一定能量和方向入射 到晶体或非晶体材料上时,会发 生衍射,即电子的运动轨迹发生
弯曲。
衍射现象可以通过布拉格方程( nλ=2dsinθ)进行描述,其中λ 为入射电子波长,d为晶面间距
,θ为衍射角。
电子衍射与X射线衍射的区别
电子衍射的波长比X射线短, 因此具有更高的分辨率和灵敏 度,能够更准确地测定晶格常 数和晶体结构。
膜蛋白分析
电子衍射还可以用于分析生物膜上的 膜蛋白,如通道蛋白和转运蛋白。这 些蛋白在物质跨膜运输和信号转导过 程中发挥关键作用。
病毒形态与结构分析
病毒形态描述
通过电子衍射技术,可以详细描述病毒的形 态和大小,这对于病毒分类、鉴定和疫苗设 计具有重要意义。
病毒结构解析
病毒的结构通常由蛋白质外壳和内部的核酸 组成。电子衍射技术可以解析病毒的精细结 构,揭示其组装机制和感染机制,为抗病毒 药物的设计提供理论支持。
THANKS FOR WATCHING
感谢您的观看
扫描电子显微镜(SEM)
总结词
扫描电子显微镜是利用电子束扫描样品表面,通过收集和分析二次电子、反射电子等信号来观察样品 表面形貌和特征的实验方法。
详细描述
扫描电子显微镜具有较高的空间分辨率和放大倍数,能够观察样品表面的细微结构和形貌变化。在实 验过程中,需要对样品进行镀金或碳涂覆等处理,以增加导电性和二次电子信号的收集效率。
第二章电子衍射课件PPT课件

Bragg定律是必要条件,不充分, 如面心立方(100),(110), 体心立 方(100),(210)等
第13页/共56页
图2-9 相邻第两1原4页子/的共5散6页射波
r=xa+yb+zc d=r·(Kg-K0)
f=2p·d/=2p r·(Kg-K0) Fg=Σfnexp(ifn) =Σfnexp[2p r·(Kg-K0)] =Σfnexp[2p r·(hxn+kyn+lzn)] 利用欧拉公式改写 Fg2={[Σfn·cos2p (hxn+kyn+lzn)]2+[Σfn·sin2p (hxn+kyn+lzn)]2}
入射束
衍射束 倒易杆
厄瓦尔德球
强度(任意单位)
倒易空间原点
图2-14 薄晶的倒易点拉长为倒易杆产生衍射 的厄瓦尔德球构图
第22页/共56页
2.2. 实验方法
获取衍射花样的方法是光阑选区衍射和微束 选区衍射,前者多在5平方微米以上,后者可在 0.5平方微米以下,我们这里主要讲述前者。
光阑选区衍射是是通过物镜象平面上插入选 区光阑限制参加成象和衍射的区域来实现的。
正点阵基矢与倒易点阵基矢之间的 关系:
a·a*= b·b*= c·c*=1 a·b*= a·c*= b·a*= b·c*= c·a*= c·b*= 0 g=ha*+kb*+lb* 晶体点阵和倒易点阵实际是互为倒易的 r=ua+vb+wc r·g=hu+kv+lw=N
第4页/共56页
图2-5 与正点阵的关系
花样分析分为两类,一是结构已知, 确定晶体缺陷及有关数据或相关过程中 的取向关系;二是结构未知,利用它鉴 定物相。指数标定是基础。
电子衍射
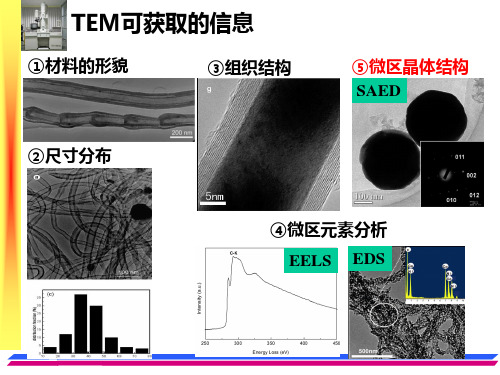
不同入射方向的C-ZrO2衍射斑点 单晶电子衍射成像原理 (a)[111]; (b)[011]; (c) [001]; (d) [112] 规则的二维网格形状
各种结构的衍射花样
• 2)多晶材料的电子衍射
a
多晶电子衍射成像原理
NiFe多晶纳米薄膜的电子衍射 (a)晶粒细小的薄膜 ; (b)晶粒较大的薄膜。
因此,许多问题可用与X射线衍射相类似的方法处理
概述
• 电子衍射与X射线衍射相比的优点
电子衍射能在同一试样上将形貌观察与结构分析 结合起来。 电子波长短,单晶的电子衍射花样如晶体的倒易 点阵的一个二维截面在底片上放大投影,从底片上 的电子衍射花样可以直观地辨认出一些晶体的结构 和有关取向关系,使晶体结构的研究比X射线简单。 物质对电子散射主要是核散射,因此散射强,约 为X射线一万倍,曝光时间短。
v+lw=0 已知某晶带中任意两个晶面(h1k1l1)和(h2k2l2),则可通过下 式求出该晶带的晶带轴方向[uvw]: u=k1l2—k2l1 v= l1h2—l2h1 w=h1k2—h2k1 例:立方晶胞以[001]作晶带轴时 ,(100)、(010)、(110)和 (210)等晶面均和[001]平行, 相应的零层倒易截面如图所示。
a=0.3966nm,b=1.3848nm,c=0.3696nm
当用蒸发法沉积在支撑膜上的MoO3晶 体,[010]方向总是接近和入射电子束 重合,当样品台保持水平时,得到电子 衍射花样的特征平行四边形为矩形,如 图所示。
第三节 电子显微镜中的电子衍射
三、磁转角
(2) 磁转角标定 当用蒸发法沉积在支撑膜上的MoO3晶体,[010]方向总是接 近和入射电子束重合,当样品台保持水平时,得到电子衍射花 样的特征平行四边形为矩形,如图所示。 六角形晶体的长边 总是[001]方向,g 是衍射花样上的 [001]方向,两者之 间的夹角就是磁转 角,表示图像相对 于衍射花样转过的 目前的电镜装有磁转角自动补正装臵,从 角度。 而使操作和结果分析简化。
第二章 电子衍射原理与分析

衍射波的合成 f合=Σj fj exp(iφi)
这里 exp(iφ)=cosφ+i sinφ
单胞内所有原子的衍射波的合成 n F=f合= f j exp[ 2i(G r j )] j 1
fj:单胞中第j 个原子的原子散射因子; rj=xja + yjb +zjc,单胞中第j个原子在正空间的位臵矢量; G = k-ko=ha* + kb* +lc*,是倒空间矢量,表示产生衍射束
3
§2.5 影响电子衍射的因素
Yuxi Chen Hunan Univ.
§2.1 电子衍射基础
§2.1.1 运动电子与物质的交互作用
入射高能电子 背散射电子 俄歇电子
二次电子 特征X射线 EDS
薄晶体样品
吸收电子
非弹性散射电子 衍射谱
透射电子
弹性散射电子 Z衬度像HAADF
4
衍衬像,EELS
Yuxi Chen Hunan Univ.
§2.2.3 正点阵和倒易点阵的指数互换
(1)立方晶系
*与(hkl)垂直的晶向(法线方向)为[hkl] *与[uvw]垂直的晶面为(uvw)
(2)六角晶系(密勒三指数)
*与[uvw]晶向垂直的晶面(hkl)
2 h a (u v / 2) k a 2 (v u / 2) 2 c w l
25
Yuxi Chen Hunan Univ.
本节重点
(1)倒易点阵的性质 (2)六角结构中(hkil)晶面的法线方向 如何计算?
26
Yuxi Chen Hunan Univ.
§2.3 电子衍射原理
§2.3.1 厄瓦尔德作图法
电子衍射原理

。倒易原点是入射电子束通过埃瓦尔德球心
和球面相交的那一点。
( )表示平面,*表示倒易, 0表示零 层倒易面。
这个倒易平面的法线即正空间晶带轴 [uvw]的方向,倒易平面上各个倒易点分别 0 代表着正空间的相应晶面。
四、晶带定律与零层倒易截面
r
g
r g 0
g
ha
*
kb *
1c
*
r ua vb wc
b* O*
a*
某一倒易基矢垂直于正点阵中和自 己异名的二基矢所成平面。
三、倒易点阵与爱瓦尔德球图解法 倒易点阵的性质
1、正倒点阵异名基矢点乘为零,同名基矢点乘为一。
a
*
b
a*
c
b*
a
b*
c
c*
a
c*
b
0
a*
a
b*
b
c*
c
1
2、在倒易空间中,任意g 矢h量a*的大kb小* 和l方c*向可以用倒易矢量g来表示。
G
2d hk l
透
衍
射
射衍射是把实际 晶体点阵转换为倒易点阵记 录下来,得到的图像叫做电 子衍射花样或叫电子衍射图。
1
:
L
1 d
:
R
Rd L
照相底板
七、电子衍射基本公式 电子衍射基本公式推导
电子衍射基本公式为
Rd L
单位: mm Å 或者 mm nm
mm Å mm nm
R:照相底板上中心斑点到衍射斑点的距离。 d:衍射晶面间距。 L:样品到底板的距离,通常叫相机长度。 λ: 入射电子波长 。
E mc2 h p mv
E mc2
hh
h h
电子衍射和中子衍射110315

众所周知,电子的波长可以用改变其速度的办法 来调节。当电子波长和晶体 dhkl 相当时,这样的电子 流照射晶体时也能发生衍射,所得的图像和 X 光衍射 是十分相似的。和 X 光衍射相比,电子衍射有如下不 同之处:
1)由于晶体强烈吸收电子波,它只能深 入到 20~25 个平面点阵,这也是电子衍射多数 用于表面结构分析的原因。
与X射线衍射相似,电子衍射也遵循布拉格方程,即 波长为λ的入射电子束与间距为d的点阵面之间的夹角θ满 足布拉格方程时,就会在与入射线成2θ角的方向上产生衍 射。晶体的各组衍射面产生的衍射斑构成了有一定规律的 衍射花样。单晶试样产生的衍射图样是按一定周期规则排 布的斑点,多晶试样则产生若干半径不等但同心的衍射环, 而非晶体物质的衍射花样只有一个漫散的中心斑点。
一、电子衍射基本原理
1、德布罗意波
1924年德布罗意提出:运动的实物粒子(如电子、质子等) 都有一种波与之对应,并认为粒子的特征波长与动量(p) 之间的关系应当与光子的相同,联系这种波的关系式是:
h h
(1)
p mv
式中是物质波的波长,h是普朗克常数,p是粒子的动量, m是运动粒子的质量,v是它的速度。(1)式称为德布罗意 波的关系式。
电子衍射有许多重要应用。通常将电子衍射分 为高能电子衍射和低能电子衍射。前者所需的电压 高达几十万、甚至几百万伏,后者所需加速电压则 低于1000 V。
单晶薄片的高能电子衍射图呈点状分布,分析 衍射图,可获得晶体的对称性、晶胞大小和形状、 单晶缺陷及相变等信息。多晶样品的高能电子衍射 图是一系列同心圆,根据实验条件&衍射图给出的 数据,利用有关公式,即可求得晶体的面间距。
• 2、将dEi与卡片上或d值表中查得的dTi比较,如吻合记下相应 的{hkl}i
2_2.电子散射原理

F ( )
f e i j 1
N
2 i K r j
19
晶胞结构因子
结构因子的积分形式——连续介质模型
即结构因子也可以表达为晶体势场的富氏变换
2ik r 2meVc F 2 V (r )e dr h Cell
单胞的散射因子与散射角有关,我们感兴趣于特定 Bragg衍射方向,故又写成某一Bragg衍射方向的形式
2
2
电子—原子核间相互作用,弹性为主, 电子—原子核散射截面为
Ze nucleus ( ) Rn V
2
2
为散射角,Rn, Re为瞄准距
12
成立条件:小角度散射近似, 非相对论近似
Rutherford散射
原子核对电子的散射类似于对粒子,符合 Rutherford散射的规律(Rutherford于1911年提出)
第二讲 电子衍射原理
晶体学的预备知识 电子的散射与衍射 电子衍射谱的标定
1
电子的散射和衍射
电子衍射的发展过程
1912年,劳埃通过X-ray衍射实验
– 证实了晶体中原子的微观排列 – 开辟了用X-ray衍射研究晶体结构这一新领域
1926~1927年,实现了晶体的电子衍射
– 肯定了电子波动性 – 奠定了电子衍射学科
电子的散射和衍射
高速电子进入到固体中,与单个原子的原子核及核外电子间发生相 互作用,从而发生方向、能量的改变,称为散射。从能量损失的角 度分为弹性散射和非弹性散射
从粒子角度讲,为连续的粒子流与原子核及核外电子的相互作用 的库仑碰撞
从波的角度讲,为准单色电子波,受单个原子扰动而形成球面波 高速电子被固体中周期排列的原子散射后,其弹性散射部分是相干 的,能够在某些方位上相干加强,形成花样,是为衍射 电子的衍射为多原子相互作用的集体行为 衍射行为反映了固体原子排列的周期性 注意散射和衍射的本质和区别,在不同情况下,我们将根据习惯而 分别使用这两个术语。 5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 晶体学的预备知识 2. 电子的散射与衍射 3. 电子衍射谱的标定提供什么?
电子衍射——揭示合金相的晶体结构 形貌特征——固体中的界面、位错形貌 晶体的原子结构——固体的原子结构
2
§1 晶体学的预备知识
掌握相当晶体学知识的重要性
晶体学是关于晶体结构及其表征的知识 晶体结构是电子显微分析的研究对象
例如,晶体的衍射特征 布拉格公式 衍射斑点的分布与倒易点阵平面对应
晶体学的必要知识
二维晶体学:
平面点阵(5)、平面点群(10)、平面群(17)
三位晶体学:
布拉菲点阵(17)及其相互间的变换关系、点群(32)、空间群(230)
晶体结构的表征:
晶面,晶面指数
倒易点阵的知识:
3
二维晶体学
* ac * bc cc ...
... ... 1 ... 18 ...
晶系 三斜
正点阵标量积矩阵
ab cos ac cos b a 2 ab cos bc cos a b 2 ac cos b bc cos a c
d uvw
*
1 ruvw
单胞体积
aa ab ac 1 2 V ba bb bc ca cb cc
V
*
1 V
* 1
1 2
V
* * a a * * b a * * c a
* * a b * * b b * * c b
(e)
六角点阵
六方形
a=b, =60 六方
3, 3m, 6, 6mm
4
二维晶体学
点对称性
点操作和点对称性:
保证某一点或某些点不变的操作称之为点操作;对晶体实施的 某些点操作后,晶体可以完全复原,这种特性称之为点对称性。
点对称性类型:
旋转对称性——旋转轴 N 1 a 360(0) 2 180 3 120 4 90 6 60
13
三维晶体学
菱面体单胞的六角坐标描述
变换关系
三个阵点的位置: (000), (1/3, 2/3, 1/3), (1/3, 2/3, 2/3)
aH cH
2 a 2 1 cos a 3a 2 1 cos a
1 a 3 cos a
3a H c H
2
2
2
2c H 2a H 2 c H 2a H
正交
2 a 0 0
0
b
0
2
0
0 0 2 c
1 2 a 0 0
0 1
2
b
0
0 0 1 2 c
四方
2 a 0 0
2 a 0 0
a
2
0
0
0 0 2 c
0 0 2 a
1 2 a 0 0
0 1
a
0
2
0 0 1 2 c
立方
a
2
0
1 2 a 0 0
0 1
2
a
0
0 0 1 2 a
20
倒易点阵
倒易关系
倒易关系的几何
2 2
2
14
三维晶体学
点群
新对称元素引入
1) 反演(反映)(x, y, z)(-x, -y, -z) 2) 倒反轴——旋转反演轴
中心对称
32种点群
空间群
新对称元素引入
1) 滑移反映——平移对称和反应对称的合成对称操 2) 螺旋对称轴
空间群 230种
15
倒易点阵
倒易点阵的概念
倒易点阵的定义
a aa ab ac ... b b a b b b c ... a b c ... c a b c c c ... c ... ... ... ... ...
0 1
2
b
0
cos b 2 ac sin b 0 1 2 2 b c sin
三角
2a a cos a 2 cos a a
2
a cos a a cos a a a cos a a cos a a
2 2 2 2 2 2
2 a cosa 1 cosa cosa 1 cosa 2 1 cos a 1 cos a a cos a 1 cos a a 2B 2 a cosa 1 cosa cosa 1 cosa
a
*
1
*
a sin b sin a sin b sin * 1 1 b* b sin * sin a b sin sin a * 1 1 c* c sin a * sin b c sin a sin b *
sin c
A = 1-cos2a-cos2b-cos2+2cos acosbcos
单斜
2 0 ac cos b
a
0
b
0
2
ac cos b 0 2
c
1 2 2 a sin b 0 cos b 2 ac sin b
2mm
正方p
4 4mm 3m 6
六角p
6mm
6
十种平面点群
1
2
3
4
6
m
2mm
3m
4mm
6mm
7
三维晶体学
平移对称性
r ut 1 vt 2 wt 3
8
三维晶体学
14种布拉菲点阵
晶系 三斜 单斜 点阵符号 P P C P C I F P I P I F R P 晶胞参数特征 abc ab abc a = 90, b 90 abc a = b = 90 a=bc a = b = 90 a=b=c a = b = 90 a=b=c a = b = 90 a=bc a= b = 90, 120 需注明的晶胞参数 a, b, c a , b, a, b, c b a, b, c 点对称性 1 2/m
* *
ca cb ca ab a 2bc(cos b cos cos a ) aa ab
a b* c* sin a * / V * ca sin b / V ab sin / V sin a * / V * V abc sin a * sin b sin abc sin a sin b * sin abc sin a sin b sin *
从几何上讲,每一个点阵(基矢为a,b,c)都对应一个倒易点阵:
* * * rhkl ha kb lc
其中基矢为:
* b c * c a * a b a ,b ,c V V V
倒易点阵的基矢与相应点阵的关系
1 , if i j a i b j b j a i ij 0 , if i j
正交
mmm
四方
a, c
4/mmm
立方
三角 六角
a
a a a, c
m3m
3m
6/mmm
9
三维晶体学
14种布拉菲点阵(I)
10
三维晶体学
14种布拉菲点阵(II)
11
三维晶体学
14种布拉菲点阵的推导
12
三维晶体学
菱面体单胞的六角坐标描述
优越性及注意事项
简单化:2个直角 多重胞:包含三个阵点 将三角和六角统一起来 出现消光
* *
16
倒易点阵
倒易点阵的概念
倒易点阵的意义
几何意义: 正点阵内的一组点阵平面对应于倒易点阵的一个 阵点 衍射物理: 正点阵与倒易点阵互为傅立叶变换 电子显微学的意义: 电子衍射图相当于一个二维倒易点阵平面的投影, 每一个衍射斑点对应于一个倒易点阵的阵点
17
倒易点阵
广义倒易点阵——正点阵标量积和倒易点阵标量积
sin
sin
sin
B = sin2a-2cos2a+2cos3a
19
六角
2 a 2 a 2 0
a
2
2
2
a
0
0 0 0
4 2 3a 2 2 3a 0
2
3a
4
2
3a
0
2
0 0 1 2 c
* b
* c
aa * * ba ... * ca ...
* ab * bb * cb ...
a * a * b b 1 * c c ... ...
表示一组平面族,其中每个平面 都是由三维点阵的阵点组成,它 们等间距排列,相互平行,法线 方向是r*,面间距为1/r. *
r r n
倒易点阵方向——密勒指数
晶面指数(hkl)构成了倒易点阵的 坐标分量。
倒易点阵长度
d hkl
1 rhkl
21
倒易点阵
互为倒易关系
倒易点阵的倒易面和正点阵的方向
反映对称(镜像对称)——镜线
平面点群:10种
平面群
微观对称操作——滑移反应 平面群:点对称操作与点阵的结合, 17种
