工程力学习题答案5廖明成教材
工程力学习题册第五章-答案

第五章拉伸和压缩一、填空题1•轴向拉伸或压缩的受力特点是作用于杆件两端的外力大小相等—和方向相反,作用线与—杆件轴线重合_。
其变形特点是杆件沿_轴线方向伸长或缩短—。
其构件特点是_等截面直杆_。
2•图5-1所示各杆件中受拉伸的杆件有AB、BC、AD、DC,受压缩的杆件有BE、BD 。
3•内力是外力作用引起的,不同的__外力—引起不同的内力,轴向拉、压变形时的内力称为_轴力__。
剪切变形时的内力称为剪力__,扭转变形时的内力称为—扭矩__,弯曲变形时的内力称为__剪力与弯矩。
4•构件在外力作用下,单位面积上的内力称为应力。
轴向拉、压时,由于应力与横截面垂直, 故称为—正应力___;计算公式彷=F N/A ;单位是_N/怦_或___ __。
1MPa= _106N/m2= _1__N/mm。
5•杆件受拉、压时的应力,在截面上是一均匀一分布的。
6•正应力的正负号规定与轴力相同, 拉伸时的应力为—拉应力__,符号为正。
压缩时的应力为__压应力-,符号位负。
7•为了消除杆件长度的影响,通常以绝对变形除以原长得到单位长度上的变形量,称为相对变形_,又称为线应变,用符号邑表示,其表达式是E= △ L/L。
8. 实验证明:在杆件轴力不超过某一限度时,杆的绝对变形与_轴力__和杆长__成正比,而与一横截面面积成反比。
9. 胡克定律的两种数学表达式为= E s 和△ L= F N L O/EA E称为材料的_弹性模量_。
它是衡量材料抵抗弹性变形能力的一个指标。
10. 实验时通常用低碳钢代表塑性材料,用灰铸铁代表脆性材料。
11. 应力变化不大,应变显着增大,从而产生明显的塑性变形—的现象,称为屈服_ 。
12. 衡量材料强度的两个重要指标是_屈服极限一和_抗拉强度_。
13. 采用—退火___的热处理方法可以消除冷作硬化现象。
14. 由于铸铁等脆性材料的—抗拉强度一很低,因此,不宜作为承拉零件的材料。
15. 工程上把材料丧失—工作能力—时的应力称为危险应力或—极限应力—,以符号仃°表示。
(建筑工程管理)工程力学习题廖明成

(建筑工程管理)工程力学习题廖明成*第十五章能量法简介习题15.1试计算图标结构的变形能。
略去剪切影响,为已知。
对于只受拉压变形的杆件,需要考虑拉压的变形能。
解:(a)如图a所示,因结构和载荷均对此,所以利用静力学平衡条件,可很容易地得到约束反力并且只取梁的一般进行计算。
AB段梁任一截面上的弯矩方程为梁的应变能为(b)如图b所示,利用静力学平衡条件,求的约束反力为梁各段的弯矩方程为BA段AC段应变能为(c)如图c所示,各杆段的弯矩方程为AB段BC段刚架的应变能为(d)如图d所示利用静力学平衡条件求得梁AC的支座反力和杆BD的轴力为(拉)梁各段的弯矩方程为CB段BA段结构的应变能为(e)如图e所示利用静力学平衡条件,得刚架的支座反力和轴力为,刚架各段的弯矩方程为AB段BC段结构的应变能为15.2试用卡氏定理计算习题15-1中各结构中截面A的铅垂位移以及B截面((e)图)的转角。
解:(a)受力分析如下图所示,有分析可得在x方向是不受力,只受y方向的力由于在A处并无垂直外力,为此,设想在A处加一垂直外力,这时求解共同作用下的支座反力,A受力分析如图所示,由平衡条件求得弯矩及对的偏导数为BA段AC段截面A的铅垂位移为(2)由于在A处并无垂直外力,为此,设想在A处加一垂直外力,这时求解共同作用下的支座反力,A受力分析如图所示,由平衡条件求得弯矩及对的偏导数为BA段AC段将以上结果代入得截面A的铅垂位移为(3)由于在A处并无垂直集中外力,为此,设想在A处加一垂直外力,这时求解共同作用下的支座反力,A受力分析如图所示,由平衡条件求得弯矩及对的偏导数为AB段BC段将以上结果代入得截面A的铅垂位移为(4)题中受力分析如图所示,由平衡条件求得弯矩及对的偏导数为AB段BC段同时求出BD轴力及偏导数为将以上结果代入得(5)1.题中受力分析如图所示,由平衡条件求得弯矩及对的偏导数为AB段BC段将以上结果代入得截面A的铅垂位移为2.由于在截面B处并无弯矩,设想在截面B处加一个弯矩,在杆件截面B上加了,如图所示,这时求共同作用下的支座反力,由平衡条件求得弯矩及对的偏导数为AB段BC段将以上结果代入得即15.3图示桁架,在节点B处承受铅垂载荷作用,试用卡氏定理计算点节B的水平位移。
《工程力学》课后习题答案全集

(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章 刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
解:如图示,车轮在A点打滑, m/s, =rad/s,车轮作平面运动,以O为基点。
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
解: 是四杆机构。速度分析如图。点P是AB杆和轮Ⅱ的速度瞬心,故:
杆 的角速度为: rad/s
两轮齿合点M的速度和轮Ⅰ的角速度分别为:
, rad/s
6.在图所示星齿轮结构中,齿轮半径均为 cm。试求当杆OA的角速度 rad/s、角加速度 时,齿轮Ⅰ上B和C两点的加速度。
解:(1)B为轮Ⅰ的速度瞬心,
即
以轮为研究对象列方程
⑦
;
将①和③代入②得
由于轮做纯滚动
8.如图所示两等长杆AB与BC在点B用铰链连接,又在杆的D、E两点连一弹簧。弹簧的刚度系数为k,当距离AC等于a时,弹簧内拉力为零,不计各构件自重与各处摩擦。如在点C作用一水平力F,杆系处于平衡,求距离AC之值。
解:(图)
弹簧力如图:为
各力作用点横向坐标及其变分为
解:火箭在空中飞行时,若只研究它的运行轨道问题,可将火箭作为质点处理。这时画出其受力和坐标轴 、 如下图所示,可列出平衡方程。
《工程力学》课后习题解答

解:(1) 取整体为研究对象,受力分析,A、B 处 x 方向和 y 方向的约束力分别组成力偶, 画 受力图。 (2) 列平衡方程:
M
FBz
x
0
FBz AB F2 2r 0
2rF2 2 20 5 2.5 N FAz FBz 2.5 N 80 AB M z 0 FBx AB F1 2r 0 FBx
W (c)
W
B
W A
FB
A FA
B
W A
(d)
(e)
1-2 试画出以下各题中 AB 杆的受力图。 A E C W D (a) B (b) W C D C B W (c) B A A
《工程力学》习题选解
A C
F A B (d) (e) A E C FA C W D B FB (a) A F C B (d) FB FA C W (e) (b) FD D B FB W (c) B FB C W B
10
《工程力学》习题选解
A FA
M1 M2 B
50
FB
解:(1) 取整体为研究对象,受力分析,A、B 的约束力组成一个力偶,画受力图; (2) 列平衡方程:
M 0
FB l M1 M 2 0
FB
M1 M 2 500 125 750 N l 50
FA FB 750 N
2-7 在四连杆机构 ABCD 的铰链 B 和 C 上分别作用有力 F1 和 F2,机构在图示位置平衡。 试 求平衡时力 F1 和 F2 的大小之间的关系。 C B
45o 90o F1 30o 60o
F2
A
D
解: (1)取铰链 B 为研究对象,AB、BC 均为二力杆,画受力图和封闭力三角形; FBC B FAB
工程力学习题 答案 廖明成

第四章 平面任意力系习 题4.1 重W ,半径为r 的均匀圆球,用长为L 的软绳AB 及半径为R 的固定光滑圆柱面支持如图,A 与圆柱面的距离为d 。
求绳子的拉力T F 及固定面对圆球的作用力N F 。
题4.1图F TyxOF N解:软绳AB 的延长线必过球的中心,力N F 在两个圆球圆心线连线上N F 和T F 的关系如图所示:AB 于y 轴夹角为θ 对小球的球心O 进行受力分析:0,sin cos TNX F F θθ==∑ 0,cos sin T NY F F W θθ=+=∑sin R rR d θ+=+ cos L rR dθ+=+ ()()()()22T R d L r F W R r L r ++=+++()()()()22NR d R r F W R r L r ++=+++4.2 吊桥AB 长L ,重1W ,重心在中心。
A 端由铰链支于地面,B 端由绳拉住,绳绕过小滑轮C 挂重物,重量2W 已知。
重力作用线沿铅垂线AC ,AC =AB 。
问吊桥与铅垂线的交角θ为多大方能平衡,并求此时铰链A 对吊桥的约束力A F 。
题4.2图A yF A xF解:对AB 杆件进行受力分析:120,sin cos 022A L M W W L θθ=-=∑ 解得:212arcsinW W θ= 对整体进行受力分析,由:20,cos02Ax X F W θ=-=∑2cos2Ax F W θ=210,sin02Ay Y F W W θ=+-=∑22121Ay W W F W +=4.3 试求图示各梁支座的约束力。
设力的单位为kN ,力偶矩的单位为kN ·m ,长度单位为m ,分布载荷集度为kN /m 。
(提示:计算非均布载荷的投影和与力矩和时需应用积分。
)题4.3图解:AyF AxF ByAxF AyF ByFBAxF AyF AyF Ax F AM(a )受力如图所示0,0.8cos300AxX F =-=∑ 0,0.110.80.150.20AByM F=⨯+⨯-=∑0,10.8sin300Ay By Y F F =+--=∑, 1.1,0.3Ax By Ay F F KN F KN ===(b )受力如图所示0,0.40AxX F =+=∑0,0.820.5 1.60.40.720A ByM F=⨯-⨯-⨯-=∑0,20.50Ay By Y F F =+-+=∑0.4,0.26,0.24Ax By Ay F KN F KN F KN =-==(c )受力如图所示0,sin300AxBX F F =-=∑ 0,383cos300ABM F =+-=∑ 0,cos3040AyBY F F =+-=∑2.12, 4.23,0.3Ax By Ay F KN F KN F KN ===(d )受力如图所示()()133q x x =- 0,0AxX F==∑()()33010,3 1.53Ay Y F q x dx x dx KN ===-=∑⎰⎰()30,0A A M M xq x dx =+=∑⎰()3013 1.53A M x x dx KN m =-=-•⎰4.4 露天厂房立柱的底部是杯形基础。
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
(完整版)工程力学习题解答(详解版)
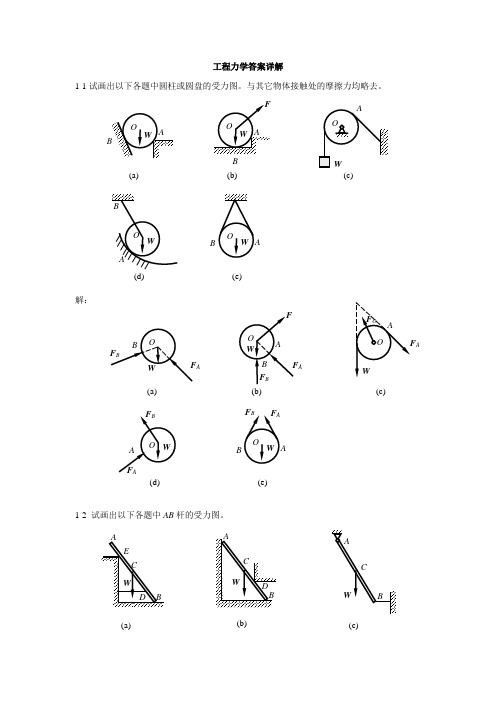
工程力学答案详解1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e) A(a)(b) A(c)A(d)A(e)(c)(a)(b)解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d) D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D BF1-5 试画出以下各题中指定物体的受力图。
(a) 结点A,结点B;(b) 圆柱A和B及整体;(c) 半拱AB,半拱BC及整体;(d) 杠杆AB,切刀CEF及整体;(e) 秤杆AB,秤盘架BCD及整体。
解:(a)(b)(c)(d)ATF BAF(b)(e)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。
工程力学课后题答案3 廖明成

第三章力偶系习题3.1 如图3.1A、B、C、D均为滑轮,绕过B、D两轮的绳子两端的拉力为400N,绕过A、C两轮的绳子两端的拉力F为300N,α=30°。
求这两力偶的合力偶的大小和转向。
滑轮大小忽略不计。
题3.1图解:两力偶的矩分别为1400sin60240400cos60200123138M N mm =•+•=•2300sin30480300cos30200123962M N mm =•+•=•合力偶矩为12247.1M M M N m=+=•(逆时针转向)3.2 已知粱AB上作用一力偶,力偶矩为M,粱长为L,粱重不计。
求在图3.2中a,b,c三种情况下,支座A和B的约束力。
题3.2图解:AB 梁受力如个图所示, 由0iM=∑,对图(a )(b)有0RA F l M -=得RA NB M F F l==对图(c )有cos 0RA F l M θ-=得cos RA NBMF F l θ==3.3 齿轮箱的两个轴上作用的力偶如图所示,它们的力偶矩的大小分别为M 1=500 N ·m ,M 2=125N ·m 。
求两螺栓处的铅垂约束力。
图中长度单位为cm 。
题3.3图FF 'NBF RAF RA F F 3l NBF RAF解:1200M Fd M M =+-=合, 750F N =-力的方向与假设方向相反3.4 汽锤在锻打工件时,由于工件偏置使锤头受力偏心而发生偏斜,它将在导轨DA 和BE 上产生很大的压力,从而加速导轨的磨损并影响锻件的精度。
已知锻打力F=1000kN ,偏心距e =20mm ,试求锻锤给两侧导轨的压力。
题3.4图N1F N2F解:锤头受力如图,这是个力偶系的平衡问题, 由10,0iN MF e F h =-=∑解得1220N N F F h==KN3.5四连杆机构在图示位置平衡,已知OA =60 m ,BC =40 cm , 作用在BC 上力偶的力偶矩大小M 1=1 N ·m ,试求作用在OA 上力偶的力偶矩大小M 1和AB 所受的力F AB 。
工程力学课后题答案廖明成
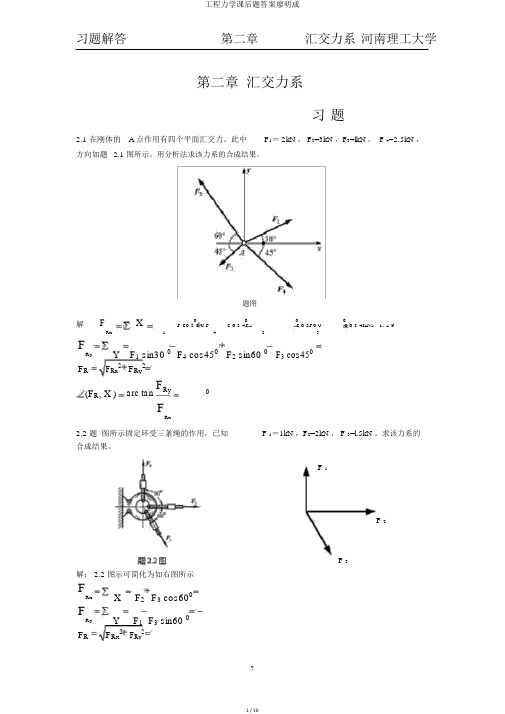
习题解答 第二章 汇交力系 河南理工大学第二章 汇交力系习 题2.1 在刚体的 A 点作用有四个平面汇交力。
此中 F 1= 2kN , F 2=3kN ,F 3=lkN , F 4=2.5kN ,方向如题 2.1 图所示。
用分析法求该力系的合成结果。
题图解FX0 0RxF co s 3 0 F4 c o s 4F52c o sF6 0c o s 4KN5 1. 2 913FRyY F 1 sin30 0 F 4 cos450 F 2 sin60 0 F 3 cos450F RF Rx 2 F Ry 2(F R , X ) arc tanF Ry 0FRx2.2 题 图所示固定环受三条绳的作用,已知 F 1=1kN ,F 2=2kN , F 3=l.5kN 。
求该力系的合成结果。
F 1F 2F 3解: 2.2 图示可简化为如右图所示F RxX F 2 F 3 cos600 FRyYF 1 F 3 sin60 0F RF Rx 2 F Ry 2(F R , X ) arc tanF RyF Rx2.3 力系如题 2.3 图所示。
已知: F 1= 100N ,F 2=50N , F 3=50N ,求力系的协力。
F 1F 2F 3解: 2.3 图示可简化为如右图所示BACarctan8053060F RxX F 3 F 2 cos 80KNFRyYF 1 F 2 sin 140KNF RF Rx 2 F Ry 2 161.25 KN(F R , X ) arc tanF Ry 0FRx2.4 球重为 W = 100N ,悬挂于绳上,并与圆滑墙相接触,如题 2.4 图所示。
已知 30 ,试求绳所受的拉力及墙所受的压力。
F 拉F 推OW题图解: 2.4 图示可简化为如右图所示X F 推 F 拉 sinY F 拉 cos WF拉,F推墙所受的压力2.5 均质杆AB重为W、长为l ,两头置于互相垂直的两圆滑斜面上,如题 2.5 图所示。
2021年工程力学第六章答案 梁的变形-工程力学梁的弯曲答案

第五章梁的变形欧阳光明(2021.03.07)测试练习1.判断改错题5-1-1梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角亦为零.()5-1-2两根几何尺寸、支承条件完全相同的静定梁,只要所受荷栽相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关。
()5-1-3悬臂梁受力如图所示,若A点上作用的集中力P在A B段上作等效平移,则A截面的转角及挠度都不变。
()5-1-4图示均质等直杆(总重量为W),放置在水平刚性平面上,若A端有一集中力P作用,使AC B部分仍与刚性平面贴剪力和)5-1-5挠曲线近似微分方程不能用于求截面直梁的位移。
()5-1-6等截面直梁在弯曲变形时,挠度曲线的曲率最大值发生在转角等于零的截面处。
()5-1-7两简支梁的抗刚度E I及跨长2a均相同,受力如图所示,则两梁跨中截面的挠度不等而转角是相等的。
题5-1-3图题5-1-4图( )5-1-8 简支梁在图示任意荷载作用下,截面C 产生挠度和转角,若在跨中截面C 又加上一个集中力偶M 0作用,则梁的截面C 的挠度要改变,而转角不变。
( )5-下别按放截面同。
( )5-1-10 图示变截面梁,当用积分法求挠曲线方程时,因弯矩方程有三个,则通常有6个积分常量。
( )5-2-1 挠曲线近似微分方程y "。
5-2-2 已知图示二梁的抗弯度E I 相同,若使二者自由端的挠度相等,则=21P P 5-2-3 应用叠加原理求梁的变形时应满足的条件是:。
5-2-4 在梁的变形中挠度和转角之间的关系是。
5-2-5 用积分法求图示的外伸梁(B D 为拉杆)的挠曲线方程时,求解积分常量所用到的边界条件是,连续条件是。
5-2-6 用积分法求图示外伸梁的挠曲线方程时,求解积分常量所用到边界条件是,连续条件是。
5-2-7 图示结构为次超静定梁。
题5-1-8图题5-1-7图题5-1-9图 题5-2-2图5-2-8形后曲线为5-2-9 两根E I 值相同、跨度之比为1:2的简支梁,当承受相同的均布荷载q 作用时,它们的挠度之比为。
工程力学习题-答案4-廖明成

第四章 平面任意力系习 题4.1 重W ,半径为r 的均匀圆球,用长为L 的软绳AB 及半径为R 的固定光滑圆柱面支持如图,A 与圆柱面的距离为d 。
求绳子的拉力T F 及固定面对圆球的作用力N F 。
题4.1图F TyxOF N解:软绳AB 的延长线必过球的中心,力N F 在两个圆球圆心线连线上N F 和T F 的关系如图所示:AB 于y 轴夹角为θ 对小球的球心O 进行受力分析:0,sin cos TNX F F θθ==∑ 0,cos sin T NY F F W θθ=+=∑sin R rR d θ+=+ cos L rR dθ+=+ ()()()()22T R d L r F W R r L r ++=+++()()()()22NR d R r F W R r L r ++=+++4.2 吊桥AB 长L ,重1W ,重心在中心。
A 端由铰链支于地面,B 端由绳拉住,绳绕过小滑轮C 挂重物,重量2W 已知。
重力作用线沿铅垂线AC ,AC =AB 。
问吊桥与铅垂线的交角θ为多大方能平衡,并求此时铰链A 对吊桥的约束力A F 。
题4.2图A yF A xF解:对AB 杆件进行受力分析:120,sin cos 022A L M W W L θθ=-=∑ 解得:212arcsinW W θ= 对整体进行受力分析,由:20,cos02Ax X F W θ=-=∑2cos2Ax F W θ=210,sin02Ay Y F W W θ=+-=∑22121Ay W W F W +=4.3 试求图示各梁支座的约束力。
设力的单位为kN ,力偶矩的单位为kN ·m ,长度单位为m ,分布载荷集度为kN /m 。
(提示:计算非均布载荷的投影和与力矩和时需应用积分。
)题4.3图解:AyF AxF ByAxF AyF ByFBAxF AyF AyF Ax F AM(a )受力如图所示0,0.8cos300AxX F =-=∑ 0,0.110.80.150.20AByM F=⨯+⨯-=∑0,10.8sin300Ay By Y F F =+--=∑0.43, 1.1,0.3Ax By Ay F KN F KN F KN ===(b )受力如图所示0,0.40AxX F =+=∑0,0.820.5 1.60.40.720AByM F=⨯-⨯-⨯-=∑0,20.50Ay By Y F F =+-+=∑0.4,0.26,0.24Ax By Ay F KN F KN F KN =-==(c )受力如图所示0,sin300AxBX F F =-=∑ 0,383cos300ABM F =+-=∑ 0,cos3040AyBY F F =+-=∑2.12, 4.23,0.3Ax By Ay F KN F KN F KN ===(d )受力如图所示()()133q x x =- 0,0AxX F==∑()()33010,3 1.53Ay Y F q x dx x dx KN ===-=∑⎰⎰()30,0A A M M xq x dx =+=∑⎰()3013 1.53A M x x dx KN m =-=-•⎰4.4 露天厂房立柱的底部是杯形基础。
参考资料(答案)-《工程力学(第五版)习题册》-A02-9111

F1y=F1 ·cos60°=20 N F2x=0 F2y= -F2= -40 N F3x= -F3= -40 N F3y=0 F4x=F4·cos135°= -28.28 N F4y=F4 ·cos45°=28.28 N 2. 解:F1x=F1=100N F1y=0 N F2x=0 N F2y=F2 =100 N F3x=F3 ·cos30°=129.9 N F3y=F3 ·cos60°=75 N F4x=F4 ·cos60°=50 N F4y=F4·cos150°= -86.6 N F5x=F5 ·cos60°=75 N F5y=F5·cos150°= -129.9 N F6x=F6·cos120°= -100 N
FDX =FD
FDY =0
FBX=FB·cos135°=-0.866FB FBY=FB·cos60°=0.5FB (3) 列 方 程
由 ∑Fix=0:FX +FDX +FBX =0 由 ∑Fiy=0:FY +FDY +FBY =0 (4) 解 方 程
解方程得到:FD=193.2 (N)(方向如图所示)
· 154 ·
F6y=F6·cos150°= -173.2 N 3. 解:MO(F1)=F1×1=F1
MA (F1)= -F1 ×1= -F1 MO (F2)= -F2 ×2= -2F2 MA (F2)= -F2 ×4= -4F2 MO(F3)=F3×0=0 MA(F3)=F3×1×sin45°=0.707F3 MO(F4)=F4×3=3F4 MA(F4)=F4×4=4F4 MO(F5)=F5×1.414=1.414F5 MA (F5)= -F5 ×1×sin45°= -0.707F5 4. 解: (a)MB(F)=F·la=50×0.6=30 N·m
工程力学课后题答案2廖明成

第二章 汇交力系习 题2.1 在刚体的A 点作用有四个平面汇交力。
其中F 1=2kN ,F 2=3kN ,F 3=lkN , F 4=2.5kN ,方向如题2.1图所示。
用解析法求该力系的合成结果。
题2.1图解 00001423cos30cos45cos60cos45 1.29Rx F X F F F F KN ==+--=∑ 00001423sin30cos45sin60cos45 2.54Ry F Y F F F F KN ==-+-=∑2.85R F KN ==0(,)tan63.07Ry R RxF F X arc F ∠==2.2 题2.2图所示固定环受三条绳的作用,已知F 1=1kN ,F 2=2kN ,F 3=l.5kN 。
求该力系的合成结果。
23解:2.2图示可简化为如右图所示023cos60 2.75Rx F X F F KN ==+=∑ 013sin600.3Ry F Y F F KN ==-=-∑2.77R F KN ==0(,)tan6.2Ry R RxF F X arc F ∠==-2.3 力系如题2.3图所示。
已知:F 1=100N ,F 2=50N ,F 3=50N ,求力系的合力。
32F 1解:2.3图示可简化为如右图所示080arctan5360BAC θ∠=== 32cos 80Rx F X F F KN θ==-=∑ 12sin 140Ry F Y F F KN θ==+=∑161.25R F KN ==0(,)tan60.25Ry R RxF F X arc F ∠==2.4 球重为W =100N ,悬挂于绳上,并与光滑墙相接触,如题2.4 图所示。
已知30α=,试求绳所受的拉力及墙所受的压力。
题2.4图解:2.4图示可简化为如右图所示sin 0X F F α=-=∑拉推 cos W 0Y Fα=-=∑拉115.47N 57.74N F F ∴==拉推,∴墙所受的压力F=57.74N2.5 均质杆AB 重为W 、长为 l ,两端置于相互垂直的两光滑斜面上,如题2.5图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 空间任意力系习 题托架A 套在转轴z 上,在点C 作用一力F = 2000 N 。
图中点C 在Oxy 平面内,尺寸如图所示,试求力F 对x ,y ,z 轴之矩。
题图解:cos 45sin 60 1.22x F F KN ==cos45cos600.7y F F KN ==sin 45 1.4z F F KN ==6084.85x z M F mm KN mm ==⋅5070.71y z M F mm KN mm ==⋅ 6050108.84z x y M F mm F mm KN mm =+=⋅正方体的边长为a ,在其顶角A 和B 处分别作用着力F 1和F 2,如图所示。
求此两力在轴x ,y ,z 上的投影和对轴x ,y ,z 的矩。
xyzOaaa ABF 1 F 2 αβα题图F F zF xyF yF x解:21sin cos sin x F F F αβα=-1cos cos y F F βα=-12sin cos z F F F βα=+12sin cos x z M F a aF aF βα==+ 1sin y M aF β=121cos cos sin cos sin z y x M F a F a aF aF aF βααβα=-=---如图所示正方体的表面ABFE 内作用一力偶,其矩M = 50 kN·m ,转向如图。
又沿GA 、BH 作用两力F 、F ′,F = F ′2kN ,a = 1 m 。
试求该力系向C 点的简化结果。
解:两力F 、F ′能形成力矩1M1502M Fa KN m ==⋅11cos 45x M M = 10y M =11sin 45z M M =1cos 4550x M M KN m ==⋅11sin 4550100z z M M M M KN m =+=+=⋅22505C z x M M M KN m =+=⋅Maa aF F ′ AB C D EFGHz题图y63.4α= 90β= 26.56γ=如图所示,置于水平面上的网格,每格边长a = 1m ,力系如图所示,选O 点为简化中心,坐标如图所示。
已知:F 1 = 5 N ,F 2 = 4 N ,F 3 = 3 N ;M 1 = 4 N·m ,M 2 = 2 N·m ,求力系向O 点简化所得的主矢'R F 和主矩M O 。
题图解:'1236R F F F F N =+-=方向为Z 轴正方向21232248x M M F F F N m =++-=⋅ 1123312y M M F F F N m =--+=-⋅2214.42O y x M M M N m =+=⋅56.63α= 33.9β=-90γ=如图所示圆柱重W =10kN ,用电机链条传动而匀速提升。
链条两边都和水平方向成300角。
已知鼓轮半径r =10cm ,链轮半径1r =20cm ,链条主动边(紧边)的拉力T 1大小是从动边(松边)拉力T 2大小的两倍。
若不计其余物体重量,求向心轴承A 和B 的约束力和链的拉力大小(图中长度单位cm )。
题图解:120,cos30cos300AxBx X F F T T =+++=∑210,sin30sin300AzBz Z F F T T W =+-+-=∑120,60cos3060cos301000zBx M T T F =---=∑ 120,3060sin3060sin301000xBz M W T T F =-+-+=∑ 21110,0yMWr T r T r =+-=∑20.78,13Ax Az F KN F KN =-= 7.79, 4.5Bx Bz F KN F KN == 1210,5T KN T KN ==如图所示均质矩形板ABCD 重为W = 200 N ,用球铰链A 和蝶形铰链B 固定在墙上,并用绳索CE 维持在水平位置。
试求绳索所受张力及支座A ,B 处的约束力。
解:取长方形板ABCD 为研究对象,受力如图所示重力W 作用于板的型心上。
选坐标系Axyz ,设AD 长题图2a ,AB 长为2b ,列出平衡方程并求解 F AxF AzF BxF BzWBzF=100AzF N=如图所示,水平轴上装有两个凸轮,凸轮上分别作用已知力F1=800N和未知力F。
如轴平衡,求力F和轴承约束力的大小。
xyzBAFF140cm60cm40cm2cm20cmBxFBzFAzFAxF题图解:10,0Ax BxX F F F=++=∑0,0Az BzZ F F F=++=∑10,1401000z BxM F F=--=∑10,20200yM F F =-=∑ 0,401000xBz MF F =+=∑320,480Ax Az F N F N ==- 1120,320Bx Bz F N F N =-=-800F N =扒杆如图所示,立柱 AB 用 BG 和 BH 两根缆风绳拉住,并在 A 点用球铰约束,A 、H 、G 三点位于Oxy 平面内,G 、H 两点的位置对称于y 轴,臂杆的D 端吊悬的重物重W = 20 kN ;求两绳的拉力和支座A 的约束反力。
题图解:G 、H 两点的位置对称于y 轴BG BH F F =0,sin 45cos60sin 45cos600BGBH Ax X F F F =-++=∑ 0,cos45cos60cos45cos600BGBH Ay Y F F F =--+=∑0,sin60sin600AzBG BH Z F F F W =---=∑0,5sin 45cos605sin 45cos6050xBG BH MF F W =+-=∑28.28,0,20,68.99BG BH Ax Ay Az F F KN F F KN F KN =====如图所示,一重量W = 1000N 的均质薄板用止推轴承A 、B 和绳索CE 支持在水平面上,可以绕水平轴AB 转动,今在板上作用一力偶,其力偶矩为M ,并设薄板平衡。
已知a = 3 m , b = 4 m ,h = 5 m ,M = 2000 N·m ,试求绳子的拉力和轴承A 、B 的约束力。
如图所示作用在踏板上的铅垂力F 1使得位于铅垂位置的连杆上产生的拉力F = 400 N ,o 30α=,a = 60 mm ,b = 100 mm ,c = 120 mm 。
求轴承A 、B 处的约束力和主动力F 1。
题图解:0,0ByAy Y F F =+=∑ 10,0AzBz Z FF F F =+--=∑10,2cos 0xM bF cF α=-=∑ 0,0yBz Az M aF bF bF =-+=∑ 0,0zBy Ay MbF bF =-=∑0Ay By F F ==,423.92Az F N =, 183.92Bz F N =1207.84F N =如图所示为一均质薄板,其尺寸单位为mm 并标示于图中,求该薄板的重心。
yxBAO6306204题 图解:三角形OAB 的中心为:()15,6.6721300A mm =小圆重心为:()6,6216A π=该薄板的重心:如图所示,从 R = 120 mm 的均质圆板中挖去一个等腰三角形。
求板的重心位置。
xyOR90 9090题5.12图解:圆重心:()0,0 11221216.8x A x A x A A -==-1122120.4y A y A y A A -==--2114400A mm π=三角形重心:()0,30228100A mm =板的重心位置:试求图所示均质板OABCD 的重心位置(图中尺寸的单位为mm )。
yxO90304060ⅢⅠ Ⅱ题5.13图ABCD题图解:I 部分重心:()45,20 212700A mm = ∏部分重心:()105,20 22900A mm =I∏部分重心:()60,20- 234800A mm =均质板OABCD 的重心:1122120x A x A x A A -==-1122126.54y A y A y A A -==--11223312360x A x A x A x mm A A A ++==++112233123 2.86y A y A y A y mmA A A ++==-++试求图所示均质等厚板的重心位置(图中尺寸的单位为mm )。
Oxy90ⅠⅢⅡ40202060解:I 部分重心:()2145,60,10800A mm =∏部分重心:()2273,60,800A mm π= I∏部分重心:()2345,20,2700A mm -=均质等厚板的重心:11223312349.4x A x A x A x mmA A A ++==++11223312346.5y A y A y A y mmA A A ++==++。
