历年高考立体几何大题试题汇编
十年高考真题分类汇编立体几何

十年高考真题分类汇编(2010—2019)数学专题10立体几何2.(2019·全国1·理T12)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )A.8√6πB.4√6πC.2√6πD.√6π【答案】D3.(2019·全国2·理T7文T7)设α,β为两个平面,则α∥β的充要条件是( )A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面【答案】B4.(2019·全国3·理T8文T8)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M 是线段ED的中点,则( )A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线【答案】B6.(2018·全国3·理T10文T12)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9√3,则三棱锥D-ABC体积的最大值为( )A.12√3B.18√3C.24√3D.54√3【答案】B7.(2018·全国1·理T7文T9)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )A.2√17B.2√5C.3D.2【答案】B10.(2018·上海·T15)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱,如图.若阳马以该正六棱柱的顶点为顶点,以AA1为底面矩形的一边,则这样的阳马的个数是( )A.4B.8C.12D.16【答案】D11.(2018·全国1·文T10)在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为( )A.8B.6√2C.8√2D.8√3【答案】C12.(2018·全国2·理T9)在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=√3,则异面直线AD1与DB1所成角的余弦值为( )A.15B.√56C.√55D.√22【答案】C13.(2018·全国2·文T9)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )A.√22B.√32C.√52D.√72【答案】C14.(2018·全国1·文T5)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A.12√2πB.12πC.8√2πD.10π【答案】B【解析】过直线O1O2的平面截该圆柱所得的截面为圆柱的轴截面,设底面半径为r,母线长为l,因为轴截面是面积为8的正方形,所以2r=l=2√2,r=√2,所以圆柱的表面积为2πrl+2πr2=8π+4π=12π.18.(2017·全国2·理T10)已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )A.√3B.√15C.√10D.√3【答案】C20.(2017·全国3·理T8文T9)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4C.π2D.π4【答案】B21.(2017·全国1·文T6)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )【答案】A4.(2016·浙江·理T2文T2)已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则( )A.m∥lB.m∥nC.n⊥lD.m⊥n【答案】C23.(2016·全国3·理T10文T11)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )A.4πB.9π2C.6π D.32π3【答案】B24.(2016·全国1·文T4)体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )A.12πB. πC.8πD.4π【答案】A25.(2016·全国1·理T11文T11)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )A.√32B.√22C.√33D.13【答案】A29.(2016·山东·理T5)一个由半球和四棱锥组成的几何体,其三视图如下图所示.则该几何体的体积为( )A.1+2πB.1+√2πC.1+√2πD.1+√2π【答案】C35.(2015·山东·理T7)在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3D.2π【答案】C40.(2015·浙江·理T8)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A'CD,所成二面角A'-CD-B的平面角为α,则( )A.∠A'DB≤αB.∠A'DB≥αC.∠A'CB≤αD.∠A'CB≥α【答案】B41.(2015·全国2·理T9文T10)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O-ABC体积的最大值为36,则球O的表面积为 ( )A.36πB.64πC.144πD.256π【答案】C42.(2015·安徽·理T5)已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行...与β平行的直线...,则在α内不存在D.若m,n不平行...垂直于同一平面...,则m与n不可能【答案】D43.(2015·浙江·文T4)设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β.( )A.若l⊥β,则α⊥βB.若α⊥β,则l⊥mC.若l∥β,则α∥βD.若α∥β,则l∥m【答案】A44.(2015·广东·文T6)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交【答案】D47.(2014·辽宁·理T4文T4)已知m,n表示两条不同直线,α表示平面.下列说法正确的是( )A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α【答案】B48.(2014·广东·理T7)在空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是( )A.l1⊥l4B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定【答案】D49.(2014·浙江·文T6)设m,n是两条不同的直线,α,β是两个不同的平面.( )A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m ⊥β,n ⊥β,n ⊥α,则m ⊥αD.若m ⊥n,n ⊥β,β⊥α,则m ⊥α 【答案】C50.(2014·陕西·理T5)已知底面边长为1,侧棱长为√2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( ) A.32π3B.4πC.2πD.4π3【答案】D51.(2014·大纲全国·理T8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A.81πB.16πC.9πD.27π【答案】A56.(2014·大纲全国·理T11)已知二面角α-l-β为60°,AB ⊂α,AB ⊥l,A 为垂足,CD ⊂β,C ∈l,∠ACD=135°,则异面直线AB 与CD 所成角的余弦值为( ) A.14 B.√24C.√34D.12【答案】B57.(2014·大纲全国·文T4)已知正四面体ABCD 中,E 是AB 的中点,则异面直线CE 与BD 所成角的余弦值为( ) A.16 B.√36C.13D.√33【答案】B66.(2013·辽宁·理T10)已知直三棱柱ABC-A 1B 1C 1的6个顶点都在球O 的球面上.若AB=3,AC=4,AB ⊥AC,AA 1=12,则球O 的半径为( ) A.3√172 B.2√10C.132D.3√10【答案】C【解析】过C 点作AB 的平行线,过B 点作AC 的平行线,交点为D,同理过C 1作A 1B 1的平行线,过B 1作A 1C 1的平行线,交点为D 1,连接DD 1,则ABCD-A 1B 1C 1D 1恰好成为球的一个内接长方体,故球的半径r=√32+42+1222=132.67.(2013·全国2·理T4)已知m,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m,l ⊥n,l ⊄α,l ⊄β,则( ) A.α∥β且l ∥α B.α⊥β且l ⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l 【答案】D【解析】因为m ⊥α,l ⊥m,l ⊄α,所以l ∥α.同理可得l ∥β.又因为m,n 为异面直线,所以α与β相交,且l 平行于它们的交线.故选D.68.(2013·广东·理T6)设m,n 是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是 ( ) A.若α⊥β,m ⊂α,n ⊂β,则m ⊥n B.若α∥β,m ⊂α,n ⊂β,则m ∥n C.若m ⊥n,m ⊂α,n ⊂β,则α⊥β D.若m ⊥α,m ∥n,n ∥β,则α⊥β 【答案】D【解析】选项A 中, m 与n 还可能平行或异面,故不正确; 选项B 中,m 与n 还可能异面,故不正确; 选项C 中,α与β还可能平行或相交,故不正确; 选项D 中,∵m ⊥α,m ∥n,∴n ⊥α. 又n ∥β,∴α⊥β.故选D.69.(2012·全国·理T11)已知三棱锥S-ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC=2,则此棱锥的体积为 ( ) A.√26 B.√36C.√23D.√22【答案】A【解析】∵SC 是球O 的直径,∴∠CAS=∠CBS=90°. ∵BA=BC=AC=1,SC=2,∴AS=BS=√3.取AB 的中点D,显然AB ⊥CD,AB ⊥SD,∴AB ⊥平面SCD. 在△CDS 中,CD=√32,DS=√112,SC=2,利用余弦定理可得cos ∠CDS=CD 2+SD 2-SC 22CD ·SD =-√33, ∴sin ∠√2√33∴S △CDS =12×√32×√112×√2√33=√22,∴V=V B-CDS +V A-CDS =13×S △CDS ×BD+13S △CDS ×AD=13S △CDS ×BA=13×√22×1=√26.70.(2012·全国·文T8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为√2,则此球的体积为( )A.√6πB.4√3πC.4√6πD.6√3π【答案】B【解析】设球O的半径为R,则R=√12+(√2)2=√3,故V球=43πR3=4√3π.71.(2012·全国·理T7文T7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A.6B.9C.12D.18【答案】B【解析】由三视图可推知,几何体的直观图如图所示,可知AB=6,CD=3,PC=3,CD垂直平分AB,且PC⊥平面ACB,故所求几何体的体积为13×(12×6×3)×3=9.72.(2012·大纲全国·理T4文T8)已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=2√2,E为CC1的中点,则直线AC1与平面BED的距离为( )A.2B.√3C.√2D.1【答案】D【解析】连接AC交BD于点O,连接OE,∵AB=2,∴AC=2√2.又CC1=2√2,则AC=CC1.作CH⊥AC1于点H,交OE于点M.由OE为△ACC1的中位线知,CM⊥OE,M为CH的中点.由BD⊥AC,EC⊥BD知,BD⊥面EOC,∴CM⊥BD.∴CM⊥面BDE.∴HM为直线AC1到平面BDE的距离.又△ACC 1为等腰直角三角形,∴CH=2.∴HM=1.73.(2011·陕西·文T5)某几何体的三视图如图所示,则它的体积为( ) A.8-2π3B.8-π3C.8-2πD.2π3【答案】A【解析】由几何体的三视图可知,原几何体是一个棱长为2的正方体且内部挖掉一个底面与正方体上底面内切,高等于正方体棱长的圆锥.正方体的体积为8,圆锥的体积为13πr 2h=2π3,所以所求几何体的体积为8-2π3. 74.(2011·全国·理T6文T8)在一个几何体的三视图中,正视图和俯视图如下图所示,则相应的侧视图可以为( )【答案】D【解析】由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示: 可知侧视图为等腰三角形,且轮廓线为实线,故选D.75.(2011·重庆·理T9)高为√24的四棱锥S-ABCD 的底面是边长为1的正方形,点S,A,B,C,D 均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为( )A.√24B.√22C.1D.√2【答案】C【解析】如图所示,过S点作SE⊥AC,交AC的延长线于E点,则SE⊥面ABCD,故SE=√24.设球心为O,A,B,C,D 所在圆的圆心为O 1,则O1为AC,BD的交点.在Rt△OAO1中,AO1=√22,AO=1,故OO1=√1-(√22)2=√22.故OO1=2SE.过S点作SO2⊥O1O于点O2,则O2为OO1的中点.故△OSO1为等腰三角形,则有O1S=SO=1.76.(2011·辽宁·理T8)如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )A.AC⊥SBB.AB∥平面SCDC.SA与平面SBD所成的角等于SC与平面SBD所成的角D.AB与SC所成的角等于DC与SA所成的角【答案】D【解析】∵SD⊥面ABCD,AC⊂面ABCD,∴SD⊥AC,又∵ABCD为正方形,∴AC⊥BD,又SD∩BD=D,∴AC⊥面SBD,AC⊥SB,故A对;∵AB∥CD,CD⊂面CDS,AB在面CDS外,∴AB∥平面SCD,故B对;设AC∩BD=O,由上面的分析知,∠ASO与∠CSO分别是SA与平面SBD,SC与平面SBD所成的角,易知∠ASO与∠CSO相等,故C对;∵CD⊥SD,CD⊥AD,AD∩SD=D,∴CD⊥平面SAD,∴DC⊥SA,DC与SA所成角为90°.又∵AB∥CD,∴AB与SC所成的角即为∠SCD,是锐角,故D错.77.(2010·浙江·理T6)设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )A.若l⊥m,m⊂α,则l⊥αB.若l⊥α,l∥m,则m⊥αC.若l∥α,m⊂α,则l∥mD.若l∥α,m∥α,则l∥m【答案】B【解析】对于A:若l⊥m,m⊂α,则l⊂α可能成立,l⊥α不一定成立,A错误;对于B:若l⊥α,l∥m,则m⊥α,B正确;对于C,若l∥α,m⊂α,l∥m或l与m异面,故C错误;对于D,若l∥α,m∥α,则l∥m或l与m 相交或l与m异面,故D错误.78.(2010·山东·文T4)在空间,下列命题正确的是( )A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行【答案】D【解析】对于A,平行直线的平行投影也可能平行或为两个点,故A错误;对于B,平行于同一直线的两个平面也可能相交,故B错误;对于C,垂直于同一平面的两个平面也可能相交,故C错误;由线面垂直的性质知D正确.故选D.79.(2010·全国·理T10)设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( )A.πa2B.7πa2C.11πa2D.5πa2【答案】B【解析】如图,O1,O分别为上、下底面的中心,D为O1O的中点,则DB为球的半径r,有r=DB=√OD2+OB2=√a2 4+a23=√7a212,∴S表=4πr2=4π×7a 212=73πa2.80.(2010·全国·文T7)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )A.3πa2B.6πa2C.12πa2D.24πa2【答案】B【解析】长方体体对角线长等于球的直径,2R=√a 2+a 2+(2a )2=√6a,R=√62a,S=4πR 2=4π·6a 24=6πa 2.81.(2010·大纲全国·理T12,难度)已知在半径为2的球面上有A,B,C,D 四点,若AB=CD=2,则四面体ABCD 的体积的最大值为( ) A.2√33 B.4√33 C.2√3 D.8√33【答案】B【解析】过CD 作平面PCD,使AB ⊥平面PCD,交AB 于P.设点P 到CD 的距离为h,则有 V 四面体ABCD =13×2×12×2×h=23h.当直径通过AB 与CD 的中点时,h max =2√22-12=2√3.故V max =4√33.82.(2019·全国3·理T16文T16)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD-A 1B 1C 1D 1挖去四棱锥O-EFGH 后所得的几何体,其中O 为长方体的中心,E,F,G,H 分别为所在棱的中点,AB=BC=6 cm,AA 1=4 cm.3D 打印所用原料密度为0.9 g/cm 3.不考虑打印损耗,制作该模型所需原料的质量为 g.【答案】118.8【解析】由题意得,四棱锥O-EFGH 的底面积为4×6-4×12×2×3=12(cm 2),点O 到平面BB 1C 1C 的距离为3 cm,则此四棱锥的体积为V 1=13×12×3=12(cm 3).又长方体ABCD-A 1B 1C 1D 1的体积为V 2=4×6×6=144(cm 3), 则该模型的体积为V=V 2-V 1=144-12=132(cm 3). 故其质量为0.9×132=118.8(g).83.(2019·天津·理T11文T12)已知四棱锥的底面是边长为√2的正方形,侧棱长均为√5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该 圆柱的体积为 . 【答案】π4【解析】由底面边长为√2,可得OC=1.设M 为VC 的中点,O 1M=12OC=12, O 1O=12VO,VO=√VC 2-OC 2=2, ∴O 1O=1.V 柱=π·O 1M 2·O 1O=π×122×1=π4.84.(2019·江苏·T9)如图,长方体ABCD-A 1B 1C 1D 1的体积是120,E 为CC 1的中点,则三棱锥E-BCD 的体积是 .【答案】10【解析】∵长方体ABCD-A 1B 1C 1D 1的体积为120, ∴AB ·BC ·CC 1=120.∵E 为CC 1的中点,CC 1⊥底面ABCD,∴CE 为三棱锥E-BCD 的底面BCD 上的高,CE=12CC 1, ∴V E-BCD =13×12AB ·BC ·CE =13×12AB ·BC ·12CC 1=112AB ·BC ·CC 1=112×120=10.85.(2019·全国2·理T16文T16)中国有悠久的金石文T 化,印信是金石文T 化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1,则该半正多面体共有 个面,其棱长为 .【答案】26 -1【解析】由题图2可知第一层与第三层各有9个面,共计18个面,第二层共有8个面,所以该半正多面体共有18+8=26个面.如图,设该半正多面体的棱长为x,则AB=BE=x,延长CB 与FE 的延长线交于点G,延长BC 交正方体的另一条棱于点H.由半正多面体的对称性可知,△BGE 为等腰直角三角形,所以BG=GE=CH=√2x,所以GH=2×√22x+x=(√2+1)x=1,解得x=√2+1=√2-1,即该半正多面体的棱长为√2-1.86.(2019·全国1·文T16)已知∠ACB=90°,P 为平面ABC 外一点,PC=2,点P 到∠ACB 两边AC,BC 的距离均为√3,那么P 到平面ABC 的距离为 . 【答案】√2【解析】作PD,PE 分别垂直于AC,BC,PO ⊥平面ABC.连接CO,OD,知CD ⊥PD,CD ⊥PO,PD ∩PO=P, ∴CD ⊥平面PDO,OD ⊂平面PDO,∴CD ⊥OD. ∵PD=PE=√3,PC=2,∴sin ∠PCE=sin ∠PCD=√32,∴∠PCB=∠PCA=60°.∴PO ⊥CO,CO 为∠ACB 平分线, ∴∠OCD=45°,∴OD=CD=1,OC=√2. 又PC=2,∴PO=√4-2=√2.87.(2018·全国2·文T16)已知圆锥的顶点为S,母线SA,SB 互相垂直,SA 与圆锥底面所成角为30°.若△SAB 的面积为8.则该圆锥的体积为 .【答案】8π 【解析】∵SA ⊥SB, ∴S △SAB =12·SA ·SB=8.∴SA=4.过点S 连接底面圆心O,则∠SAO=30°. ∴SO=2,OA=2√3.∴V=13πr 2h=13×π×(2√3)2×2=8π.88.(2018·天津·理T11)已知正方体ABCD-A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH 的体积为 . 【答案】112【解析】由题意可知,四棱锥M-EFGH 的底面EFGH 为正方形且边长为√22,其高为12, 所以V 四棱锥M-EFGH =1×(√2)2×1=1. 89.(2018·江苏·T10)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .【答案】43【解析】由题图可知,该多面体为两个全等的正四棱锥的组合体,且正四棱锥的高为1,底面正方形的边长为√2,所以该多面体的体积为2×13×1×(√2)2=43.90.(2018·全国2·理T16)已知圆锥的顶点为S,母线SA,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为5√15.则该圆锥的侧面积为_____________. 【答案】40√2π【解析】如图,设O 为底面圆圆心. ∵SA 与底面成45°角, ∴△SAO 为等腰直角三角形. 设OA=r,则SO=r,SA=SB=√2r. ∵在△SAB 中,cos ∠ASB=78, ∴sin ∠ASB=√158,∴S △SAB =12SA ·SB ·sin ∠ASB=12(√2r)2·√158=5√15, 解得r=2√10,∴SA=√2r=4√5,即母线长l=4√5, ∴S 圆锥侧=πrl=π×2√10×4√5=40√2π.91.(2017·全国1·理T16)如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC 的中心为O.D,E,F 为圆O 上的点,△DBC,△ECA,△FAB 分别是以BC,CA,AB 为底边的等腰三角形,沿虚线剪开后,分别以BC,CA,AB 为折痕折起△DBC,△ECA,△FAB,使得D,E,F 重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为 .【答案】4【解析】如图所示,连接OD,交BC 于点G. 由题意知OD ⊥BC,OG=√36BC. 设OG=x,则BC=2√3x,DG=5-x, 三棱锥的高h=√DG 2-OG 2= √25-10x +x 2-x 2=√25-10x .因为S △ABC =12×2√3x ×3x=3√3x 2,所以三棱锥的体积V=13S △ABC ·h=√3x 2·√25-10x =√3·√25x 4-10x 5.令f(x)=25x 4-10x 5,x ∈(0,52),则f'(x)=100x 3-50x 4.令f'(x)=0,可得x=2,则f(x)在(0,2)单调递增,在(2,52)单调递减, 所以f(x)max =f(2)=80.所以V≤√3×√80=4√15,所以三棱锥体积的最大值为4√15.92.(2017·全国2·文T15)长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 . 【答案】14π【解析】由题意可知长方体的体对角线长等于其外接球O 的直径2R,即2R=2+22+12=√14,所以球O 的表面积S=4πR 2=14π.93.(2017·全国1·文T16)已知三棱锥S-ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径,若平面SCA ⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC 的体积为9,则球O 的表面积为 . 【答案】36π【解析】取SC 的中点O,连接OA,OB. 因为SA=AC,SB=BC,所以OA ⊥SC,OB ⊥SC. 因为平面SAC ⊥平面SBC,且OA ⊂平面SAC,所以OA ⊥平面SBC.设OA=r,则V A-SBC =13×S △SBC ×OA=13×12×2r ×r ×r=13r 3, 所以13r 3=9,解得r=3.所以球O 的表面积为4πr 2=36π.94.(2017·天津·理T10文T11)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 . 【答案】9π2.【解析】 设正方体的棱长为a,外接球的半径为R,则2R=√3a.∵正方体的表面积为18,∴6a 2=18. ∴a=√3,R=32.∴该球的体积为V=43πR 3=4π3×278=9π2.95.(2017·江苏·T6)如图,在圆柱O 1O 2内有一个球O,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V1V 2的值是________________.【答案】32【解析】设球O的半径为r,则圆柱O1O2的高为2r,故V1V2=πr2·2r43πr3=32,答案为32.96.(2017·全国3·理T16)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60°角时,AB与b成30°角;②当直线AB与a成60°角时,AB与b成60°角;③直线AB与a所成角的最小值为45°;④直线AB与a所成角的最大值为60°.其中正确的是.(填写所有正确结论的编号)【答案】②③【解析】由题意,AB是以AC为轴,BC为底面半径的圆锥的母线,由AC⊥a,AC⊥b,得AC⊥圆锥底面,在底面内可以过点B,作BD∥a,交底面圆C于点D,如图所示,连接DE,则DE⊥BD,∴DE∥b.连接AD,在等腰三角形ABD 中,设AB=AD=√2,当直线AB与a成60°角时,∠ABD=60°,故BD=√2.又在Rt△BDE中,BE=2,∴DE=√2,过点B作BF∥DE,交圆C于点F,连接AF,由圆的对称性可知BF=DE=√2,∴△ABF为等边三角形,∴∠ABF=60°,即AB与b成60°角,②正确,①错误.由最小角定理可知③正确;很明显,可以满足直线a⊥平面ABC,直线AB与a所成的最大角为90°,④错误.故正确的说法为②③.97.(2016·全国2·理T14)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m ∥n,α∥β,那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 .(填写所有正确命题的编号) 【答案】②③④【解析】对于①,若m ⊥n,m ⊥α,n ∥β,则α,β的位置关系无法确定,故错误;对于②,因为n ∥α,所以过直线n 作平面γ与平面α相交于直线c,则n ∥c.因为m ⊥α,所以m ⊥c,所以m ⊥n,故②正确;对于③,由两个平面平行的性质可知正确;对于④,由线面所成角的定义和等角定理可知其正确,故正确命题的编号有②③④.98.(2016·天津·理T11)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则该四棱锥的体积为 m 3.【答案】2【解析】由三视图知四棱锥高为3,底面平行四边形的底为2,高为1,因此该四棱锥的体积为V=13×(2×1)×3=2.故答案为2.99.(2016·四川·理T13)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是 .【答案】√33【解析】由三棱锥的正视图知,三棱锥的高为1,底面边长分别为2√3,2,2,所以底面三角形的高为√22-(√3)2=1,所以,三棱锥的体积为V=13×12×2√3×1×1=√33.100.(2015·浙江·理T13)如图,在三棱锥A-BCD 中,AB=AC=BD=CD=3,AD=BC=2,点M,N 分别为AD,BC 的中点,则异面直线AN,CM 所成的角的余弦值是 .【答案】78【解析】连接DN,取DN 的中点P,连接PM,CP,因为M 是AD 的中点, 故PM ∥AN,则∠CMP 即为异面直线AN,CM 所成的角, 因为AB=AC=BD=CD=3,AD=BC=2,可得AN=CM=DN=2√2, 故MP=PN=√2. 在Rt △PCN中,CP=√PN 2+CN 2=√2+1=√3,由余弦定理,可得cos ∠CMP=CM 2+MP 2-CP 22·CM ·MP=2×22×2=78,故异面直线AN,CM 所成的角的余弦值为78.101.(2014·山东·理T13)三棱锥P-ABC 中,D,E 分别为PB,PC 的中点,记三棱锥D-ABE 的体积为V 1,P-ABC 的体积为V 2,则V 1V 2=________________. 【答案】1【解析】由题意,知V D-ABE =V A-BDE =V 1,V P-ABC =V A-PBC =V 2.因为D,E 分别为PB,PC 中点, 所以S△BDES △PBC=14.设点A 到平面PBC 的距离为d,则V 12=13S △BDE ·d 13S △PBC ·d=S△BDE△PBC=1. 102.(2014·山东·文T13)一个六棱锥的体积为2√3,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为 . 【答案】12【解析】根据题意知该六棱锥为正六棱锥,底面正六边形面积为6√3,设六棱锥的高为h,则V=13×6√3h=2√3,解得h=1.设侧面高为h',则h 2+(√3)2=h'2,∴h'=2.所以正六棱锥的侧面积为6×12×2×2=12.103.(2013·北京·理T14)如图,在棱长为2的正方体ABCD-A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,点P 到直线CC 1的距离的最小值为 .【答案】2√55【解析】如图,过E 点作EE 1垂直底面A 1B 1C 1D 1,交B 1C 1于点E 1,连接D 1E 1,过P 点作PH 垂直于底面A 1B 1C 1D 1,交D 1E 1于点H,P 点到直线CC 1的距离就是C 1H,故当C 1H 垂直于D 1E 1时,P 点到直线CC 1距离最小,此时,在Rt △D 1C 1E 1中,C 1H ⊥D 1E 1,D 1E 1·C 1H=C 1D 1·C 1E 1,∴C 1H=√5=2√55.104.(2013·全国2·文T15)已知正四棱锥O-ABCD 的体积为3√22,底面边长为√3,则以O 为球心,OA 为半径的球的表面积为 .【答案】24π【解析】如图所示,∵V O-ABCD =13×(√3)2×|OO 1|=3√22,∴|OO 1|=3√22, 在Rt △OO 1A 中,|AO 1|=√62,|OA|=√(3√22)2+(√62)2=√6, 即R=√6,∴S 球=4πR 2=24π.105.(2013·全国1·文T15)已知H 是球O 的直径AB 上一点,AH ∶HB=1∶2,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为 .【答案】9π2【解析】如图,设球O 的半径为R,则AH=2R 3,OH=R 3.又∵π·EH 2=π,∴EH=1.∵在Rt △OEH 中,R 2=(R 3)2+12,∴R 2=98.∴S 球=4πR 2=9π2.106.(2013·福建·理T12)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是 .【答案】12π【解析】由题意知该几何体是一个正方体内接于球构成的组合体,球的直径等于正方体体对角线长,即2r=√22+22+22=√12,所以r=√3,故该球的表面积为S 球=4πr 2=4π×3=12π. 107.(2012·辽宁·理T16)已知正三棱锥P-ABC,点P,A,B,C 都在半径为√3的球面上,若PA,PB,PC 两两相互垂直,则球心到截面ABC 的距离为 .【答案】√33 【解析】正三棱锥P-ABC 可看作由正方体PADC-BEFG 截得,如图所示,PF 为三棱锥P-ABC 的外接球的直径,且PF ⊥平面ABC.设正方体棱长为a,则3a 2=12,a=2,AB=AC=BC=2√2.S △ABC =1×2√2×2√2×√3=2√3.由V P-ABC =V B-PAC ,得1·h ·S △ABC =1×1×2×2×2,所以h=2√33,因此球心到平面ABC 的距离为√33. 108.(2012·安徽·理T12)某几何体的三视图如图所示,该几何体的表面积是 .【答案】92【解析】由三视图可知,该几何体为底面是直角梯形且侧棱垂直于底面的棱柱,该几何体的表面积为S=2×12×(2+5)×4+[2+5+4+√42+(5-2)2]×4=92. 109.(2011·全国·理T15)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且AB=6,BC=2√3,则棱锥O-ABCD 的体积为 .【答案】8【解析】如图所示,OO'垂直于矩形ABCD 所在的平面,垂足为O',连接O'B,OB,则在Rt △OO'B 中,由OB=4,O'B=2√3,可得OO'=2,故V O-ABCD =13S 矩形ABCD ·OO'=13×6×2√3×2=8√3.110.(2010·全国·理T14文T15)一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的 .(填入所有可能的几何体前的编号)①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥 ⑥圆柱【答案】①②③⑤【解析】只要判断正视图是不是正三角形就行了.111.(2011·全国·文T16)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的316,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为 .【答案】13【解析】设球面半径为R,圆锥底面半径为r.由题意知,πr 2=316×4πR 2,即r 2=34R 2.如图所示,设体积较小者的圆锥为A-CO 1D,其高为AO 1.体积较大的圆锥为B-CO 1D,其高为O 1B.在Rt △O 1CO中,CO 1=r,CO=R,则OO 1=√R 2-r 2=12R.又∵AO=R,∴AO 1=R 2.又∵O 1B=O 1O+OB=12R+R=32R,∴AO 1BO 1=R 232R =13. 112.(2019·全国1·文T19)如图,直四棱柱ABCD-A 1B 1C 1D 1的底面是菱形,AA 1=4,AB=2,∠BAD=60°,E,M,N 分别是BC,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE;(2)求点C 到平面C 1DE 的距离.【解析】(1)证明连接B 1C,ME.因为M,E 分别为BB 1,BC 的中点,所以ME ∥B 1C,且ME=12B 1C.又因为N 为A 1D 的中点,所以ND=12A 1D.由题设知A 1B 1 DC,可得B 1C A 1D,故ME ND,因此四边形MNDE 为平行四边形,MN ∥ED.又MN ⊄平面C 1DE,所以MN ∥平面C 1DE.(2)解过C 作C 1E 的垂线,垂足为H.由已知可得DE ⊥BC,DE ⊥C 1C,所以DE ⊥平面C 1CE,故DE ⊥CH.从而CH ⊥平面C 1DE,故CH 的长即为C 到平面C 1DE 的距离.由已知可得CE=1,C 1C=4,所以C 1E=√17,故CH=4√1717.从而点C 到平面C 1DE 的距离为4√1717.113.(2019·天津·文T17)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC ⊥平面PCD,PA⊥CD,CD=2,AD=3.(1)设G,H分别为PB,AC的中点,求证:GH∥平面PAD;(2)求证:PA⊥平面PCD;(3)求直线AD与平面PAC所成角的正弦值.【解析】(1)证明连接BD,易知AC∩BD=H,BH=DH.又由BG=PG,故GH∥PD.又因为GH⊄平面PAD,PD⊂平面PAD,所以GH∥平面PAD.(2)证明取棱PC的中点N,连接DN,依题意,得DN⊥PC,又因为平面PAC⊥平面PCD,平面PAC∩平面PCD=PC,所以DN⊥平面PAC,又PA⊂平面PAC,故DN⊥PA.又已知PA⊥CD,CD∩DN=D,所以PA⊥平面PCD.(3)解连接AN,由(2)中DN⊥平面PAC,可知∠DAN为直线AD与平面PAC所成的角.因为△PCD为等边三角形,CD=2且N为PC的中点,所以DN=√3,又DN⊥AN,在Rt△AND中,sin∠DAN=DNAD =√33.所以,直线AD与平面PAC所成角的正弦值为√33.114.(2019·全国2·文T17)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB 1C1;(2)若AE=A1E,AB=3,求四棱锥E-BB1C1C的体积.【解析】(1)证明由已知得B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.(2)解由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=∠A1EB1=45°,故AE=AB=3,AA1=2AE=6.作EF⊥BB1,垂足为F,则EF⊥平面BB1C1C,且EF=AB=3.所以,四棱锥E-BB1C1C的体积V=13×3×6×3=18.115.(2019·江苏·T16)如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:(1)A1B1∥平面DEC1;(2)BE⊥C1E.【解析】证明(1)因为D,E分别为BC,AC的中点,所以ED∥AB.在直三棱柱ABC-A1B1C1中,AB∥A1B1,所以A1B1∥ED.又因为ED⊂平面DEC1,A1B1⊄平面DEC1,所以A1B1∥平面DEC1.(2)因为AB=BC,E为AC的中点,所以BE⊥AC.因为三棱柱ABC-A1B1C1是直棱柱,所以C1C⊥平面ABC.又因为BE⊂平面ABC,所以C1C⊥BE.因为C1C⊂平面A1ACC1,AC⊂平面A1ACC1,C1C∩AC=C,所以BE⊥平面A1ACC1.因为C1E⊂平面A1ACC1,所以BE⊥C1E.116.(2019·全国3·文T19)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的四边形ACGD的面积.【解析】(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE.(2)解取CG的中点M,连接EM,DM.因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,故DE⊥CG.由已知,四边形BCGE是菱形,且∠EBC=60°得EM⊥CG,故CG⊥平面DEM.因此DM⊥CG.在Rt△DEM中,DE=1,EM=√3,故DM=2.所以四边形ACGD的面积为4.117.(2018·全国1·文T18)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=23DA,求三棱锥Q-ABP的体积.【解析】(1)由已知可得,∠BAC=90°,BA⊥AC.又BA⊥AD,所以AB⊥平面ACD.又AB⊂平面ABC,所以平面ACD⊥平面ABC.(2)由已知可得,DC=CM=AB=3,DA=3√2.又BP=DQ=23DA,所以BP=2√2.作QE⊥AC,垂足为E,则QE 13DC.由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC,QE=1.因此,三棱锥Q-APB的体积为V Q-ABP=13×QE×S△ABP=13×1×12×3×2√2sin 45°=1.118.(2018·全国3·文T19)如图,矩形ABCD所在平面与半⏜所在平面垂直,M是CD⏜上异于C,D的点.圆弧CD(1)证明:平面AMD⊥平面BMC;(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.【解析】(1)由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故⏜上异于C,D的点,且DC为直径,所以DM⊥CM.BC⊥DM.因为M为CD又BC∩CM=C,所以DM⊥平面BMC.而DM⊂平面AMD,故平面AMD⊥平面BMC.(2)当P为AM的中点时,MC∥平面PBD.证明如下:连接AC交BD于O.因为ABCD为矩形,所以O为AC中点.连接OP,因为P为AM中点,所以MC∥OP.MC⊄平面PBD,OP⊂平面PBD,所以MC∥平面PBD.119.(2018·北京·文T18)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.(1)求证:PE⊥BC;(2)求证:平面PAB⊥平面PCD;(3)求证:EF∥平面PCD.【解析】证明(1)∵PA=PD,且E为AD的中点,∴PE⊥AD.∵底面ABCD为矩形,∴BC∥AD,∴PE⊥BC.(2)∵底面ABCD为矩形,∴AB⊥AD.∵平面PAD⊥平面ABCD,∴AB⊥平面PAD.∴AB⊥PD.又PA⊥PD,PA∩AB=A,∴PD⊥平面PAB.∵PD⊂平面PCD,∴平面PAB⊥平面PCD.(3)如图,取PC的中点G,连接FG,GD.∵F,G分别为PB和PC的中点,。
历年高考立体几何真题+答案

历年高考真题1、2003(理科)(本题满分12分)已知平行六面体ABCD —A 1B 1C 1D 1中,A 1A ⊥平面ABCD ,AB=4,AD=2.若B 1D ⊥BC ,直线B 1D 与平面ABCD 所成的角等于30°,求平行六面体ABCD —A 1B 1C 1D 1的体积..[解]连结BD ,因为B 1B ⊥平面ABCD ,B 1D ⊥BC ,所以BC ⊥BD.在△BCD 中,BC=2,CD=4,所以BD=32.又因为直线B 1D 与平面ABCD 所成的角等于30°,所以 ∠B 1DB=30°,于是BB 1=31BD=2.故平行六面体ABCD —A 1B 1C 1D 1的体积为S ABCD ·BB 1=38. 2.2005(理科)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.已知正三棱锥ABC P -的体积为372,侧面与底面所成的二面角的大小为 60. (1)证明:BC PA ⊥;(2)求底面中心O 到侧面的距离.[证明](1)取BC 边的中点D ,连接AD 、PD ,则BC AD ⊥,BC PD ⊥,故⊥BC 平面APD . BCPA ⊥[解](2)如图, 由(1)可知平面⊥PBC 平面APD ,则PDA ∠面所成二面角的平面角.过点O 作E PD OE ,⊥为垂足,则OE 就是点O 到侧面的距离. 设OE 为h ,由题意可知点O 在AD 上,∴ 60=∠PDO ,h OP 2=.h BC h OD 4,32=∴=,∴ 2234)4(43h h S ABC ==∆, ∵ 3233823431372h h h =⋅⋅=,∴ 3=h . 即底面中心O 到侧面的距离为3.3、2006(理科)(本题满分 14分)本题共有 2个小题,第 1小题满分 5分,第 2小题满分满分 9分。
在三棱柱 ABC —A1B1C1 中,∠ABC=90°,AB=BC=1。
浙江省历年高考立体几何大题总汇(题目及答案)

1.(本题满分15分)如图,平面⊥平面,是以为斜边的等腰直角PAC ABC ABC ∆AC 三角形。
分别为的中点,。
,,E F O ,,PA PB PC 16,10AC PA PC ===(I ) 设是的中点,证明:平面;C OC //PC BOE (II )证明:在内存在一点,使⊥平面,并求点到,的距ABO ∆M FM BOE M OA OB 离。
2.如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,P 是侧棱CC 1上的一点,CP=m ,(Ⅰ)试确定m ,使得直线AP 与平面BDB 1D 1所成角的正切值为(Ⅱ)在线段A 1C 1上是否存在一个定点Q ,使得对任意的m ,D 1Q 在平面APD 1上的射影垂直于AP ,并证明你的结论。
3. 如图甲,△ABC 是边长为6的等边三角形,E ,D 分别为AB 、AC 靠近B 、C 的三等分点,点G 为BC 边的中点.线段AG 交线段ED 于F 点,将△AED 沿ED 翻折,使平面AED ⊥平面BCDE ,连接AB 、AC 、AG 形成如图乙所示的几何体。
(I )求证BC ⊥平面AFG ;(II )求二面角B -AE -D的余弦值..4在如图所示的几何体中,平面ABC ,平面ABC ,,EA ⊥DB ⊥AC BC ⊥,M 是AB 的中点.2AC BC BD AE ===(1)求证:;CM EM ⊥(2)求CM 与平面CDE 所成的角5.如图,矩形和梯形所在平面互相垂直,,ABCD BEFC BE CF ∥,,.90BCF CEF ∠=∠=o AD =2EF =(Ⅰ)求证:平面;AE ∥DCF (Ⅱ)当的长为何值时,二面角的大小为?AB A EF C --60o6. 如图,在矩形ABCD 中,点E ,F 分别在线段AB ,AD 上,AE=EB=AF=沿.432=FD 直线EF 将翻折成使平面平面BEF.AEF ∆,'EF A ∆⊥EF A ' (I )求二面角的余弦值;C FD A --' (II )点M ,N 分别在线段FD ,BC 上,若沿直线MN 将四边形MNCD 向上翻折,使C与重合,求线段FM 的长.'A EMACBD DABEFC(第18题)7. 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2(Ⅰ)证明:AP⊥BC;(Ⅱ)在线段AP上是否存在点M,使得二面角A-MC-B为直二面角?若存在,求出AM的长;若不存在,请说明理由。
《历年高考专题汇编》立体几何

《历年高考专题汇编》—>立体几何第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人 得分 一、选择题(题型注释)91.如图,l A B A B αβαβαβ⊥=∈∈I ,,,,,到l 的距离分别是a 和b ,AB 与αβ,所成的角分别是θ和ϕ,AB 在αβ,内的射影分别是m 和n ,若a b >,则( )A .m n θϕ>>,B .m n θϕ><,C .m n θϕ<<,D .m n θϕ<>,2.设,m n 是平面α内的两条不同直线;12,l l 是平面β内的两条相交直线,则//αβ的一个充分而不必要条件是( )A.1////m l βα且B.12////m l l 且nC.////m n ββ且D.2////m n l β且3.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是A 、球B 、三棱柱C 、正方形D 、圆柱4.一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为( )(A )48+122 (B )48+242 (C )36+122 (D )36+2425.已知某几何体的三视图如图所示,则该几何体的体积为A.8π3B.3πC .10π3D.6π6.某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a b的最大值为()A.22 B.23 C.4 D.257.将正三棱柱截去三个角(如图1所示A,B,C分别是△CHI三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为A、 B、 C、 D、8.正方体ABCD-1111A B C D中,B1B与平面AC1D所成角的余弦值为俯视图侧视图2正视图42 42(A )23 (B )3 (C )23 (D )6 9.已知正四棱柱ABCD- A 1B 1C 1D 1中 ,AB=2,CC 1=22 E 为CC 1的中点,则直线AC 1与平面BED 的距离为A 、2B 、3C 、2D 、110.已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( )A .13B .23C .33D .2311.已知正四棱锥S ABCD -中,23SA =,那么当该棱锥的体积最大时,它的高为A. 1B. 3C. 2D. 312.已知正四棱锥S ABCD -的侧棱长与底面边长都相等,E 是SB 的中点,则AE SD ,所成的角的余弦值为( )A .13B .2C .3D .2313.已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为( )A.2B.3C. 2D.214.半径为1的球面上的四点D C B A ,,,是正四面体的顶点,则A 与B 两点间的球面距离为(A ))33arccos(- (B ))36arccos(- (C ))31arccos(-(D ))41arccos(- 15.如图,体积为V 的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.V 1为小球相交部分(图中阴影部分)的体积,V 2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是A 、V 1=2VB 、 V 2=2VC 、V 1> V 2D 、V 1< V 216.如图,半径为R 的半球O 的底面圆O 在平面α内,过点O 作平面α的垂线交半球面于点A ,过圆O 的直径CD 作平面α成45o 角的平面与半球面相交,所得交线上到平面α的距离最大的点为B ,该交线上的一点P 满足60BOP ∠=o ,则A 、P 两点间的球面距离为( )A、R B 、4R π C、R 、3R π第II 卷(非选择题)请点击修改第II 卷的文字说明评卷人得分 二、填空题(题型注释)17.一个几何体的三视图如图所示,则该几何体的表面积为______________。
高三精选立体几何大题30题(含详细解答)
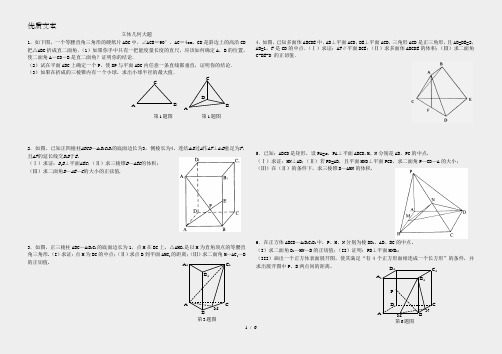
A BC第1题图ABCD第1题图立体几何大题1.如下图,一个等腰直角三角形的硬纸片ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高沿CD 把△ABC折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A,B的位置,使二面角A-CD-B是直二面角?证明你的结论.(2)试在平面ABC上确定一个P,使DP与平面ABC内任意一条直线都垂直,证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的大小的正弦值.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B 的正切值. 4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积.6.在正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点。
(I)求二面角B1—MN—B的正切值;(II)证明:PB⊥平面MNB1;(III)画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离。
高考数学立体几何试题汇编

高考数学立体几何试题汇编一、选择题1.(全国Ⅰ•理•7题)如图;正四棱柱1111D C B A ABCD -中;AB AA 21=;则异面直线11AD B A 与所成角的余弦值为( D )A .51 B .52 C .53 D .542.(全国Ⅱ•理•7题)已知正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等;则AB 1与侧面ACC 1A 1所成角的正弦等于( A )A .6 B .10C .22D .33.(北京•理•3题)平面α∥平面β的一个充分条件是( D )A .存在一条直线a a ααβ,∥,∥B .存在一条直线a a a αβ⊂,,∥C .存在两条平行直线a b a b a b αββα⊂⊂,,,,∥,∥D .存在两条异面直线a b a a b αβα⊂,,,∥,∥4.(安徽•理•2题)设l ;m ;n 均为直线;其中m ;n 在平面α内;“l α⊥”是l m⊥且“l n ⊥”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.(安徽•理•8题)半径为1的球面上的四点D C B A ,,,是正四面体的顶点;则A 与B 两点间的球面距离为( )A .)33arccos(-B .)36arccos(- C .)31arccos(-D .)41arccos(- 6.(福建•理•8题)已知m ;n 为两条不同的直线;α;β为两个不同的平面;则下列命题中正确的是( D )A .,,//,////m n m n ααββαβ⊂⊂⇒B . //,,//m n m n αβαβ⊂⊂⇒C .,//m m n n αα⊥⊥⇒D . //,m n n m αα⊥⇒⊥7.(福建•理•10题)顶点在同一球面上的正四棱柱ABCD -A 1B 1C 1D 1中;AB =1;AA 1=;则A 、C 两点间的球面距离为( B )A .4π B . 2πC .24πD . 22π8.(湖北•理•4题)平面α外有两条直线m 和n ;如果m 和n 在平面α内的射影分别是1m 和1n ;给出下列四个命题;①1m ⊥1n ⇒m ⊥n ; ②m ⊥n ⇒1m ⊥1n ;③1m 与1n 相交⇒m 与n 相交或重合; ④1m 与1n 平行⇒m 与n 平行或重合; 其中不正确的命题个数是( D )9.(湖南•理•8题)棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上;E F ,分别是棱1AA ;1DD 的中点;则直线EF 被球O 截得的线段长为( D )A .22B .1C .212+D .210.(江苏•理•4题)已知两条直线,m n ;两个平面,αβ;给出下面四个命题; ①//,m n m n αα⊥⇒⊥ ②//,,//m n m n αβαβ⊂⊂⇒ ③//,////m n m n αα⇒ ④//,//,m n m n αβαβ⊥⇒⊥ 其中正确命题的序号是( C )A .①③B .②④C .①④D .②③ 11.(江西•理•7题)如图;正方体AC 1的棱长为1;过点A 作平面A 1BD 的垂线;垂足为点H .则以下命题中;错误..的命题是( D ) A .点H 是△A 1BD 的垂心 B .AH 垂直平面CB 1D 1C .AH 的延长线经过点C 1D .直线AH 和BB 1所成角为45° 12.(辽宁•理•7题)若m n ,是两条不同的直线;αβγ,,是三个不同的平面;则下列命题中的真命题是( )A .若m βαβ⊂⊥,;则m α⊥B .若m αγ=n βγ=;m n ∥;则αβ∥C .若m β⊥;m α∥;则αβ⊥D .若αγ⊥;αβ⊥;则βγ⊥13.(陕西•理•6题)一个正三棱锥的四个顶点都在半径为1的球面上;其中底面的三个顶点在该球的一个大圆上;则该正三棱锥的体积是( B )A .433 B .33 C . 43 D .12314.(四川•理•4题)如图;ABCD -A 1B 1C 1D 1为正方体;下面结论错误..的是( D )A .BD ∥平面CB 1D 1 B .AC 1⊥BDC .AC 1⊥平面CB 1D 1 D .异面直线AD 与CB 1角为60°15.(宁夏•理•8题) 已知某个几何体的三视图如下;根据图中标出的尺寸(单位;cm );可得这个几何体的体积是( B )A.34000cm 3 B.38000cm 3C.32000cmD.34000cm16.(四川•理•6题)设球O 的半径是1;A 、B 、C 是球面上三点;已知A 到B 、C 两点的球面距离都是2π;且三面角B -OA -C 的大小为3π;则从A 点沿球面经B 、C 两点再回到A 点的最短距离是( C )A .67πB .45πC .34πD .23π17.(天津•理•6题)设a b ,为两条直线;αβ,为两个平面;下列四个命题中;正确的命题是( D )A.若a b ,与α所成的角相等;则a b ∥ B.若a b αβ,∥∥;αβ∥;则a b ∥C.若a b a b αβ⊂⊂,,∥;则αβ∥ D.若a b αβ⊥⊥,;αβ⊥;则a b ⊥18.(浙江•理•6题)若P 是两条异面直线,l m 外的任意一点;则( B )A .过点P 有且仅有一条直线与,l m 都平行B .过点P 有且仅有一条直线与,l m都垂直C .过点P 有且仅有一条直线与,l m 都相交D .过点P 有且仅有一条直线与,l m2020正视图20侧视图101020俯视图都异面二、填空题19.(全国Ⅰ•理•16题)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上。
2016年-2019年立体几何大题全国卷高考真题及答案

1、(2015年1卷18题)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.试题解析:(Ⅰ)连接BD ,设BD∩AC=G,连接EG ,FG ,EF ,在菱形ABCD 中,不妨设GB=1,由∠ABC=120°,可得AG=GC=3. 由BE ⊥平面ABCD ,AB=BC 可知,AE=EC , 又∵AE ⊥EC ,∴EG=3,EG ⊥AC ,在Rt △EBG 中,可得BE=2,故DF=22. 在Rt △FDG 中,可得FG=62. 在直角梯形BDFE 中,由BD=2,BE=2,DF=22可得EF=322, ∴222EG FG EF +=,∴EG ⊥FG , ∵AC∩FG=G,∴EG ⊥平面AFC ,∵EG ⊂面AEC ,∴平面AFC ⊥平面AEC.(Ⅱ)如图,以G 为坐标原点,分别以,GB GC 的方向为x 轴,y 轴正方向,||GB 为单位长度,建立空间直角坐标系G-xyz ,由(Ⅰ)可得A (030),E (2),F (-1,0,22),C (030),∴AE =(132),CF =(-1,3,22).…10分故cos ,3||||AE CF AE CF AE CF ⋅<>==-. 所以直线AE 与CF 所成的角的余弦值为3. 2、(2016年1卷18题)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60.(I )证明:平面ABEF ⊥平面EFDC ; (II )求二面角E -BC -A 的余弦值.试题解析:(I )由已知可得F DF A ⊥,F F A ⊥E ,所以F A ⊥平面FDC E . 又F A ⊂平面F ABE ,故平面F ABE ⊥平面FDC E .(II )过D 作DG F ⊥E ,垂足为G ,由(I )知DG ⊥平面F ABE .以G 为坐标原点,GF 的方向为x 轴正方向,GF 为单位长度,建立如图所示的空间直角坐标系G xyz -.由(I )知DF ∠E 为二面角D F -A -E 的平面角,故DF 60∠E =,则DF 2=,DG 3=,可得()1,4,0A ,()3,4,0B -,()3,0,0E -,(D . 由已知,//F AB E ,所以//AB 平面FDC E . 又平面CDAB 平面FDC DC E =,故//CD AB ,CD//F E .由//F BE A ,可得BE ⊥平面FDC E ,所以C F ∠E 为二面角C F -BE -的平面角,C F 60∠E =.从而可得(C -.所以(C E =,()0,4,0EB =,(C 3,A =--,()4,0,0AB =-. 设(),,n x y z =是平面C B E 的法向量,则C 00n n⎧⋅E =⎪⎨⋅EB =⎪⎩,即40x y ⎧+=⎪⎨=⎪⎩, 所以可取(3,0,n =.CABDEF设m 是平面CD AB 的法向量,则C 00m m ⎧⋅A =⎪⎨⋅AB =⎪⎩,同理可取()0,3,4m =.则219cos ,19n m n m n m ⋅==-. 故二面角C E -B -A 的余弦值为21919-.3(2016年2卷19题)(本小题满分12分)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将△DEF 沿EF 折到△D EF '的位置10OD '=.(I )证明:D H '⊥平面ABCD ; (II )求二面角B D A C '--的正弦值.【解析】⑴证明:∵54AE CF ==,∴AE CF AD CD=,∴EF AC ∥. ∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥,∴EF DH ⊥,∴EF DH'⊥.∵6AC =,∴3AO =;又5AB =,AO OB ⊥, ∴4OB =,∴1AE OH OD AO=⋅=,∴3DH D H '==,∴222'OD OH D H '=+, ∴'D H OH ⊥.又∵OH EF H =,∴'D H ⊥面ABCD .⑵建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,, ()430AB =,,,()'133AD =-,,,()060AC =,,,设面'ABD 法向量()1n x y z =,,,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩,取345x y z =⎧⎪=-⎨⎪=⎩, ∴()1345n =-,,.同理可得面'AD C 的法向量()2301n =,,, ∴12129575cos 255210n n n n θ⋅+===⋅,∴295sin 25θ=4、(2017年1卷18题)如图,在四棱锥P ABCD -中,AB CD ∥中,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,求二面角A PB C --的余弦值. 【解析】(1)证明:∵90BAP CDP ∠=∠=︒∴PA AB ⊥,PD CD ⊥又∵AB CD ∥,∴PD AB ⊥又∵PD PA P =,PD 、PA ⊂平面PAD ∴AB ⊥平面PAD ,又AB ⊂平面PAB ∴平面PAB ⊥平面PAD(2)取AD 中点O ,BC 中点E ,连接PO ,OE ∵AB CD∴四边形ABCD 为平行四边形 ∴OE AB由(1)知,AB ⊥平面PAD∴OE ⊥平面PAD ,又PO 、AD ⊂平面PAD ∴OE PO ⊥,OE AD ⊥ 又∵PA PD =,∴PO AD ⊥ ∴PO 、OE 、AD 两两垂直∴以O 为坐标原点,建立如图所示的空间直角坐标系O xyz - 设2PA =,∴()002D -,,、()220B ,,、()002P ,,、()202C -,,, ∴()022PD =--,,、()222PB =-,,、()2200BC =-,,设()n x y z =,,为平面PBC 的法向量由00n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩,得2220220x y z x ⎧+-=⎪⎨-=⎪⎩令1y =,则2z =,0x =,可得平面PBC 的一个法向量()012n =,, ∵90APD ∠=︒,∴PD PA ⊥又知AB ⊥平面PAD ,PD ⊂平面PAD ∴PD AB ⊥,又PA AB A = ∴PD ⊥平面PAB即PD 是平面PAB 的一个法向量,()022PD =--,, ∴23cos 323PD n PD n PD n⋅-===-⋅, 由图知二面角A PB C --为钝角,所以它的余弦值为33-5.(2018年1卷18题)如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥. ⑴证明:平面PEF ⊥平面ABFD ; ⑵求DP 与平面ABFD 所成角的正弦值.解答:(1),E F 分别为,AD BC 的中点,则//EF AB ,∴EF BF ⊥,又PF BF ⊥,EF PF F ⋂=,∴BF ⊥平面PEF , BE ⊂平面ABFD ,∴平面PEF ⊥平面ABFD . (2)PF BF ⊥,//BF ED ,∴PF ED ⊥,又PF PD ⊥,ED DP D ⋂=,∴PF ⊥平面PED ,∴PF PE ⊥, 设4AB =,则4EF =,2PF =,∴23PE =, 过P 作PH EF ⊥交EF 于H 点, 由平面PEF ⊥平面ABFD ,∴PH ⊥平面ABFD ,连结DH ,则PDH ∠即为直线DP 与平面ABFD 所成的角, 由PE PF EF PH ⋅=⋅,∴23234PH ⋅==, 而4PD =,∴3sin 4PH PDH PD ∠==, ∴DP 与平面ABFD 所成角的正弦值34. 6.(2018年新课标Ⅱ理)如图,在三棱锥P -ABC 中,AB =BC =22,P A =PB =PC =AC =4,O 为AC 的中点.(1)求证:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M -P A -C 为30°,求PC 与平面P AM 所成角的正弦值.【解析】(1)证明:∵AB =BC =22,AC =4,∴AB 2+BC 2=AC 2,即△ABC 是直角三角形. 又O 为AC 的中点,∴OA =OB =OC . ∵P A =PB =PC ,∴△POA ≌△POB ≌△POC . ∴∠POA =∠POB =∠POC =90°.∴PO ⊥AC ,PO ⊥OB ,OB ∩AC =0,∴PO ⊥平面ABC .(2)以O 坐标原点,OB ,OC ,OP 所在直线分别为x ,y ,z 轴建立空间直角坐标系如图所示.易知A (0,-2,0),P (0,0,23),C (0,2,0),B (2,0,0),BC →=(-2,2,0). 设BM →=λBC →=(-2λ,2λ,0),0<λ<1,则AM →=BM →-BA →=(-2λ,2λ,0)-(-2,-2,0)=(2-2λ,2λ+2,0), 则平面P AC 的一个法向量为m =(1,0,0).设平面MP A 的法向量为n =(x ,y ,z ),则PA →=(0,-2,23), 则n ·PA →=-2y -23z =0,n ·AM →=(2-2λ)x +(2λ+2)y =0. 令z =1,则y =-3,x =(λ+1)31-λ,即n =⎝ ⎛⎭⎪⎫(λ+1)31-λ,-3,1.∵二面角M -P A -C 为30°,∴cos 30°=m ·n |m ||n |=32,即(λ+1)3λ-1⎝ ⎛⎭⎪⎫(λ+1)31-λ2+1+3×1=32,解得λ=13或λ=3(舍去). ∴n =(23,-3,1),PC →=(0,2,-23).PC 与平面P AM 所成角的正弦值sin θ=|cos 〈PC →,n 〉|=⎪⎪⎪⎪⎪⎪-23-2316·16=4316=34.18.(2019年1卷18题)(12分)如图,直四棱柱ABCD ﹣A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ; (2)求二面角A ﹣MA 1﹣N 的正弦值.解答】(1)证明:如图,过N作NH⊥AD,则NH∥AA1,且,又MB∥AA1,MB=,∴四边形NMBH为平行四边形,则NM∥BH,由NH∥AA1,N为A1D中点,得H为AD中点,而E为BC中点,∴BE∥DH,BE=DH,则四边形BEDH为平行四边形,则BH∥DE,∴NM∥DE,∵NM⊄平面C1DE,DE⊂平面C1DE,∴MN∥平面C1DE;(2)解:以D为坐标原点,以垂直于DC得直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立空间直角坐标系,则N(,,2),M(,1,2),A1(,﹣1,4),,,设平面A1MN的一个法向量为,由,取x=,得,又平面MAA1的一个法向量为,∴cos<>===.∴二面角A﹣MA1﹣N的正弦值为.8.(12分)(2019年新课标Ⅱ理)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1. (1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,求二面角B –EC –C 1的正弦值.解:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BEEC ⊥,所以BE ⊥平面11EB C .(2)由(1)知190BEB ∠=︒.由题设知11Rt Rt ABE A B E ≅△△,所以45AEB ∠=︒,故AE AB =,12AA AB =.以D 为坐标原点,DA 的方向为x 轴正方向,||DA 为单位长,建立如图所示的空间直角坐标系D -xyz ,则C (0,1,0),B (1,1,0),1C (0,1,2),E (1,0,1),(1,1,1)CE =-,1(0,0,2)CC =.设平面EBC 的法向量为n =(x ,y ,x ),则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x x y z =⎧⎨-+=⎩ 所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =(x ,y ,z ),则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩m m 即20,0.z x y z =⎧⎨-+=⎩ 所以可取m =(1,1,0). 于是1cos ,||||2⋅<>==-n m n m n m .所以,二面角1B EC C --3.。
全国各地市历年高考立体几何题汇编(含参考答案)

全国各地市历年高考立体几何题汇编(含参考答案)(一)2018年高考立体几何题1.(北京理16)如图,在三棱柱ABC -111A B C 中,1CC 平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11AC ,1BB 的中点,AB=BC AC =1AA =2.(Ⅰ)求证:AC ⊥平面BEF ; (Ⅱ)求二面角B-CD -C 1的余弦值; (Ⅲ)证明:直线FG 与平面BCD 相交.2.(浙江-19)如图,已知多面体ABCA 1B 1C 1,A 1A ,B 1B ,C 1C 均垂直于平面ABC ,∠ABC =120°,A 1A =4,C 1C =1,AB =BC =B 1B =2. (Ⅰ)证明:AB 1⊥平面A 1B 1C 1;(Ⅱ)求直线AC 1与平面ABB 1所成的角的正弦值.3.(课标III 理-19)如图,边长为2的正方形所在的平面与半圆弧所在平面垂直,是上异于,的点.(1)证明:平面平面; (2)当三棱锥体积最大时, 求面与面所成二面角的正弦值.4.(课标II 理-20)如图,在三棱锥P ABC -中,AB BC ==4PA PB PC AC ====,O 为AC 的中点. (1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M PA C --为30︒,求PC 与平面PAM 所成角的正弦值.ABCD CD M CD C D AM D ⊥BMC M ABC -MABMCD5.(课标I理-18)如图,四边形ABCD为正方形,,E F分别为,AD BC的中点,以DF为折痕把DFC△折起,使点C到达点P的位置,且PF BF⊥.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.(二)2017年高考立体几何题1.(课标III理-19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.2.(课标II 理-19)如图,四棱锥P -ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD 的中点.(1)证明:直线CE ∥平面PAB ;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为o 45,求二面角M AB D --的余弦值.3.(课标I 理-18)如图,在四棱锥P −ABCD 中,AB//CD ,且90BAP CDP ∠=∠=. (1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=,求二面角A −PB −C 的余弦值.(三)2016年高考立体几何题 1.(课标III 理-19)如图,四棱锥中,地面,,,,为线段上一点,,为的中点.(I )证明平面;(II )求直线与平面所成角的正弦值.2.(课标II 理-19)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD上,54AE CF ==,EF 交BD 于点H .将△DEF 沿EF 折到△D EF'的位置OD '=(I )证明:DH'⊥平面ABCD ; (II )求二面角B D A C '--的正弦值. P ABC -PA ⊥ABCD AD BC 3AB AD AC ===4PA BC ==M AD 2AM MD =N PC MN PAB ANPMN3.(课标I 理-19)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD , 90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60. (Ⅰ)证明:平面ABEF ⊥平面EFDC ; (Ⅱ)求二面角E -BC -A 的余弦值.(四)2015年高考立体几何题 1.(课标II 理-19)如图,长方体1111ABCD A BC D -中,=16AB ,=10BC ,18AA =,点E ,F 分别在11A B ,11C D 上,114A E D F ==.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形. (Ⅰ)在图中画出这个正方形(不必说出画法和理由); (Ⅱ)求直线AF 与平面α所成角的正弦值.DD 1 C 1A 1EF ABCB 1参考答案(一)2018年高考立体几何题1.(北京理16)如图,在三棱柱ABC -111A B C 中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11AC ,1BB 的中点,AB=BCAC =1AA =2.(Ⅰ)求证:AC ⊥平面BEF ; (Ⅱ)求二面角B-CD -C 1的余弦值; (Ⅲ)证明:直线FG 与平面BCD 相交. 1.解析:(Ⅰ)在三棱柱ABC -A 1B 1C 1中,∵CC 1⊥平面ABC ,∴四边形A 1ACC 1为矩形. 又E ,F 分别为AC ,A 1C 1的中点,∴AC ⊥EF . ∵AB =BC ,∴AC ⊥BE ,∴AC ⊥平面BEF . (Ⅱ)由(I )知AC ⊥EF ,AC ⊥BE ,EF ∥CC 1. 又CC 1⊥平面ABC ,∴EF ⊥平面ABC . ∵BE ⊂平面ABC ,∴EF ⊥BE . 如图建立空间直角坐称系E -xyz .由题意得B (0,2,0),C (-1,0,0),D (1,0,1),F (0,0,2),G (0,2,1).∴=(201)=(120)CD CB u u u r u u r,,,,,, 设平面BCD 的法向量为()a b c =,,n , ∴00CD CB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uur n n ,∴2020a c a b +=⎧⎨+=⎩,令a =2,则b =-1,c =-4,∴平面BCD 的法向量(214)=--,,n , 又∵平面CDC 1的法向量为=(020)EB u u r ,,,∴cos =||||EB EB EB ⋅<⋅>=uu ruu r uu r n n n . 由图可得二面角B -CD -C 为钝角,所以二面角B -CD -C的余弦值为.(Ⅲ)平面BCD 的法向量为(214)=--,,n ,∵G (0,2,1),F (0,0,2),∴=(021)GF -u u u r ,,,∴2GF ⋅=-uu u r n ,∴n 与GF uuu r不垂直,∴GF 与平面BCD 不平行且不在平面BCD 内,∴GF 与平面BCD 相交.2.(浙江-19)如图,已知多面体ABCA 1B 1C 1,A 1A ,B 1B ,C 1C 均垂直于平面ABC ,∠ABC =120°,A 1A =4,C 1C =1,AB =BC =B 1B =2. (Ⅰ)证明:AB 1⊥平面A 1B 1C 1;(Ⅱ)求直线AC 1与平面ABB 1所成的角的正弦值. 2.解析:方法一:(Ⅰ)由得,所以.故.由,得, 由得由,得,故. 因此平面.(Ⅱ)如图,过点作,交直线于点,连结.由平面得平面平面, 由得平面, 所以是与平面所成的角. 由, 所以,故. 因此,直线与平面. 方法二:(Ⅰ)如图,以AC的中点O 为原点,分别以射线OB ,11112,4,2,,AB AA BB AA AB BB AB ===⊥⊥111AB AB ==2221111A B AB AA +=111AB A B ⊥2BC =112,1,BB CC ==11,BB BC CC BC ⊥⊥11B C =2,120AB BC ABC ==∠=︒AC =1CC AC ⊥1AC 2221111AB BC AC +=111ABB C ⊥1AB ⊥111A B C 1C 111C D A B ⊥11A B D AD 1AB ⊥111A B C 111A B C ⊥1ABB 111C D A B ⊥1C D ⊥1ABB 1C AD ∠1AC 1ABB 111111BC AB AC ==111111cos C A B C A B ∠=∠=1C D 111sin C D C AD AC ∠==1AC 1ABBOC 为x ,y 轴的正半轴,建立空间直角坐标系O -xyz . 由题意知各点坐标如下:因此 由得.由得. 所以平面. (Ⅱ)设直线与平面所成的角为.由(Ⅰ)可知 设平面的法向量.由即可取.所以. 因此,直线与平面. 3.(课标III 理-19)如图,边长为2的正方形所在的平面与半圆弧所在平面垂直,是上异于,的点.(1)证明:平面平面;(2)当三棱锥体积最大时, 求面与面所成二面角的正弦值.3.解析:(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC 平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为上异于C ,D 的点,且DC 为直径,所以 DM ⊥CM .又 BC CM =C ,所以DM ⊥平面BMC . 而DM 平面AMD ,故平面AMD ⊥平面BMC .(2)以D 为坐标原点,的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz .111(0,(1,0,0),(0,(1,0,2),),A B A B C 111112),3),AB A B AC ==-=-uuu r uuu u r uuu u r 1110AB A B ⋅=uuu r uuu u r 111AB A B ⊥1110AB AC ⋅=uuu r uuu u r111AB AC ⊥1AB ⊥111A B C 1AC 1ABB θ11(0,0,2),AC AB BB ===uuu r uu u r uuu r1ABB (,,)x y z =n 10,0,AB BB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uuu r n n 0,20,x z ⎧=⎪⎨=⎪⎩(,0)=n 111|sin |cos ,||||AC AC AC θ⋅===⋅uuu r uuu r uuu r n |n n |1AC 1ABB ABCD CD M CD C D AM D ⊥BMC M ABC -MAB MCD ⊂CD ⊂DA当三棱锥M −ABC 体积最大时,M 为的中点.由题设得,设是平面MAB 的法向量,则即可取.是平面MCD 的法向量,因此,,所以面MAB 与面MCD 所成二面角的正弦值是. 4.(课标II 理-20)如图,在三棱锥P ABC -中,AB BC ==4PA PB PC AC ====,O 为AC的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M PA C --为30︒,求PC 与平面PAM 所成角的正弦值.4.解:(1)因为4AP CP AC ===,O 为AC 的中点,所以OP AC ⊥,且OP =连结OB .因为2AB BC AC ==,所以ABC △为等腰直角三角形,且OB AC ⊥,122OB AC ==. 由222OP OB PB +=知PO OB ⊥. 由,OP OB OP AC ⊥⊥知PO ⊥平面ABC .(2)如图,以O 为坐标原点,OB uu u r的方向为x 轴正方向,建立空间直角坐标系O xyz -.由已知得(0,0,0),(2,0,0),(0,2,0),(0,2,0),23),(0,2,O B A C P AP -=u u u r取平面PAC 的法向量(2,0,0)OB =u u u r.设(,2,0)(02)M a a a -<≤,则(,4,0)AM a a =-u u u r. CD (0,0,0),(2,0,0),(2,2,0),(0,2,0),(0,1,1)D A B C M (2,1,1),(0,2,0),(2,0,0)AM AB DA =-==(,,)x y z =n 0,0.AM AB ⎧⋅=⎪⎨⋅=⎪⎩n n 20,20.x y z y -++=⎧⎨=⎩(1,0,2)=n DA 5cos ,5||||DA DA DA ⋅==n nn 2sin ,DA =n5由0,0AP AM ⋅=⋅=u u u r u u u r n n得20(4)0y ax a y ⎧+=⎪⎨+-=⎪⎩,可取,)a a =--n ,所以cos ,OB =uu u rn由已知得|cos ,|OB =uu u r n .解得4a =-(舍去),43a =.所以4()3=-n .又(0,2,PC =-u u u r,所以cos ,PC =uu u r n 所以PC 与平面PAM5.(课标I 理-18)如图,四边形ABCD 为正方形,,E F 分别为,AD BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥. (1)证明:平面PEF ⊥平面ABFD ; (2)求DP 与平面ABFD 所成角的正弦值.5.解:(1)由已知可得,BF ⊥PF ,BF ⊥EF ,所以BF ⊥平面PEF .又BF ⊂平面ABFD ,所以平面PEF ⊥平面ABFD . (2)作PH ⊥EF ,垂足为H .由(1)得,PH ⊥平面ABFD .以H 为坐标原点,HF 的方向为y 轴正方向,||BF 为单位长,建立如图所示的空间直角坐标系H −xyz . 由(1)可得,DE ⊥PE .又DP =2,DE =1, 所以PE=.又PF =1,EF =2,故PE ⊥PF . 可得32PH EH ==.则33(0,0,0),(1,,0),(1,22H P D DP --=HP =为平面ABFD 的法向量. 设DP 与平面ABFD 所成角为θ,则34sin ||||||3HP DP HP DP θ⋅===⋅所以DP 与平面ABFD所成角的正弦值为(二)2017年高考立体几何题 1.(课标III 理-19)如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD =∠CBD ,AB =BD . (1)证明:平面ACD ⊥平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角D –AE –C 的余弦值.1.【解析】(1)由题设可得,ABD CBD △≌△,从而AD DC =. 又ACD △是直角三角形,所以=90ADC ∠︒. 取AC 的中点O ,连接DO ,BO ,则DO ⊥AC ,DO =AO . 又由于ABC △是正三角形,故BO AC ⊥. 所以DOB ∠为二面角D AC B --的平面角. 在Rt AOB △中,222BO AO AB +=.又AB BD =,所以2222BO DO BO AO AB BD 22+=+==,故90DOB ∠=. 所以平面ACD ⊥平面ABC .(2)由题设及(1)知,,,OA OB OD 两两垂直,以O 为坐标原点,OA 的方向为x 轴正方向,OA 为单位长,建立如图所示的空间直角坐标系O x y z -.则()()()()1,0,0,,1,0,0,0,0,1A B C D -.由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12, 从而E 到平面ABC 的距离为D 到平面ABC 的距离的12, 即E 为DB的中点,得12E ⎛⎫ ⎪ ⎪⎝⎭. 故()()11,0,1,2,0,0,2AD AC AE ⎛⎫=-=-=- ⎪ ⎪⎝⎭.设()=x,y,z n 是平面DAE 的法向量,则00AD AE ⎧⋅=⎪⎨⋅=⎪⎩,,n n即0,10.2x z x y z -+=⎧⎪⎨-+=⎪⎩ 可取⎛⎫= ⎪ ⎪⎝⎭n .设m 是平面AEC 的法向量,则00AC AE ⎧⋅=⎪⎨⋅=⎪⎩,,m m同理可取(0,=-m .则cos ,⋅==n m n m n m .所以二面角D -AE -C. 2.(课标II 理-19)如图,四棱锥P -ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD 的中点. (1)证明:直线CE ∥平面PAB ;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为o 45,求二面角M AB D --的余弦值.2.解析:(1)取PA 中点F ,连结EF ,BF . 因为E 为PD 的中点,所以EF AD , 12EF AD =,由90BAD ABC ∠=∠=︒得//BC AD , 又12BC AD =所以//EF BC .四边形BCEF 为平行四边形, //CE BF . 又BF PAB ⊂平面, CE PAB ⊄平面,故//CE PAB 平面(2)由已知得BA AD ⊥,以A 为坐标原点, AB 的方向为x 轴正方向, AB 为单位长,建立如图所示的空间直角坐标系A-xyz ,则则()000A ,,, ()100B ,,, ()110C ,,,(01P ,(10PC =,,()100AB =,,,则 ()(1,1BM x y z PM x y z =-=-,,,,因为BM 与底面ABCD 所成的角为45°,而()001n =,,是底面ABCD 的法向量,所以0cos , sin45BM n =,=即(x-1)²+y ²-z ²=0又M 在棱PC 上,学|科网设,PM PC λ=则x ,1,y z λ==由①,②得()y=1 y=1 z z ⎧⎧⎪⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪==⎪⎪⎩⎩舍去,所以M ⎛ ⎝⎭,从而AM ⎛= ⎝⎭设()000x ,y ,z m =是平面ABM的法向量,则(0000x 2y 0·AM 0 ·AB 0x 0m m ⎧+=⎧=⎪⎨⎨==⎩⎪⎩即所以可取m =(0,2).于是·10,5m n cosm n m n == 因此二面角M-AB-D的余弦值为3.(课标I 理-18)如图,在四棱锥P −ABCD 中,AB//CD ,且90BAP CDP ∠=∠=. (1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=,求二面角A −PB −C 的余弦值.3.【解析】(1)由已知90BAP CDP ∠=∠=︒,得AB ⊥AP ,CD ⊥PD .由于AB//CD ,故AB ⊥PD ,从而AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD . (2)在平面PAD 内作PF AD ⊥,垂足为F ,由(1)可知,AB ⊥平面PAD ,故AB PF ⊥,可得PF ⊥平面ABCD .以F 为坐标原点,FA 的方向为x 轴正方向,||AB 为单位长,建立如图所示的空间直角坐标系F xyz -.由(1)及已知可得(2A,(0,0,2P,(2B,(2C -.所以(PC =-,(2,0,0)CB =,2(PA =,(0,1,0)AB =.设(,,)x y z =n 是平面PCB 的法向量,则0,0,PC CB ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0,y z ⎧+=⎪⎨=可取(0,1,=-n . 设(,,)x y z =m 是平面PAB 的法向量,则0,0,PA AB ⎧⋅=⎪⎨⋅=⎪⎩m m即0,220.x z y -=⎪⎨⎪=⎩可取(1,0,1)=m . 则cos ,||||⋅==<>n m n m n m ,所以二面角A PBC --的余弦值为(三)2016年高考立体几何题1.(课标III 理-19)如图,四棱锥中,地面,,,,为线段上一点,,为的中点.(I )证明//MN 平面;(II )求直线与平面所成角的正弦值. 1.解析:(Ⅰ)由已知得223AM AD ==. 取BP 的中点T ,连接,AT TN ,由N 为PC 中点知//TN BC ,122TN BC ==. 又//AD BC ,故,//TN AM TN AM =,四边形AMNT 为平行四边形,于是//MN AT . 因为AT ⊂平面PAB ,MN ⊄平面PAB ,所以//MN 平面.(Ⅱ)取BC 的中点E ,连结AE .由AB BC =得AE BC ⊥,从而AE AD ⊥,且.以A 为坐标原点, AE 的方向为轴正方向,建立如图所示的空间直角坐标系A xyz -.由题意知,P ABC -PA ⊥ABCD AD BC 3AB AD AC ===4PA BC ==M AD 2AMMD =N PC PAB AN PMN PAB,,,5(,1,2)N,()0,2,4PM =-, 52PN ⎛⎫=- ⎪⎪⎝⎭, 52AN ⎛⎫= ⎪⎪⎝⎭.设(),,n x y z =为平面PMN 的一个法向量,则0, 0,n PM n PN ⎧⋅=⎪⎨⋅=⎪⎩即240, 20,y z x y z -=⎧+-=可取()0,2,1n =. 于是85cos ,25n AN n AN n AN⋅〈〉==. 2.(课标II 理-19)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD上,54AE CF ==,EF 交BD 于点H .将△DEF 沿EF 折到△D EF'的位置OD '=(I )证明:DH'⊥平面ABCD ; (II )求二面角B D A C '--的正弦值. 2.【解析】⑴证明:∵54AE CF ==,∴A E C FA D C D=,∴E F A C ∥.∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥,∴EF D H ⊥,∴EF DH'⊥. ∵6AC =,∴3AO =;又5AB =,AO OB ⊥, ∴4OB =,∴1AEOH OD AO=⋅=, ∴3DH D H '==,∴222'OD OH D H '=+,∴'D H OH ⊥.又∵OH EF H =I ,∴'D H ⊥面ABCD .⑵建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,,()430AB =u u u r ,,,()'133AD =-u u u r ,,,()060AC =u u u r,,, 设面'ABD 法向量()1n x y z =,,u r,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩,取345x y z =⎧⎪=-⎨⎪=⎩,∴()1345n =-u r ,,.同理可得面'AD C 的法向量()2301n =u u r ,,,∴1212cos n n n n θ⋅=u r u u ru r u u r∴sin θ= 3.(课标I 理-19)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD , 90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60. (Ⅰ)证明:平面ABEF ⊥平面EFDC ; (Ⅱ)求二面角E -BC -A 的余弦值.3.【解析】试题分析:(Ⅰ)证明AF ⊥平面FDC E ,结合AF ⊂平面ABEF ,可得平面ABEF ⊥平面EFDC .(Ⅱ)建立空间坐标系,利用向量求解. 试题解析:(Ⅰ)由已知可得AF DF ⊥, AF FE ⊥,所以AF ⊥平面EFDC . 又AF ⊂平面ABEF ,故平面ABEF ⊥平面EFDC .(Ⅱ)过D 作DG EF ⊥,垂足为G ,由(Ⅰ)知DG ⊥平面ABEF .以G 为坐标原点, GF 的方向为x 轴正方向, GF 为单位长,建立如图所示的空间直角坐标系G xyz -.由(Ⅰ)知DFE ∠为二面角D AF E --的平面角,故60DFE ∠=,则2DF =, 3DG =,可得()1,4,0A , ()3,4,0B -, ()3,0,0E -,(D . 由已知, //AB EF ,所以//AB 平面EFDC .又平面ABCD ⋂平面EFDC DC =,故//AB CD , //CD EF .由//BE AF ,可得BE ⊥平面EFDC ,所以CEF ∠为二面角C BE F --的平面角,60CEF ∠=.从而可得(C -.所以(EC =, ()0,4,0EB =,(3,AC =--, ()4,0,0AB =-. 设(),,n x y z =是平面BCE 的法向量,则n EC n EB ⎧⋅=⎪⎨⋅=⎪⎩,即0 40x y ⎧+=⎪⎨=⎪⎩,所以可取(3,0,n =.设m 是平面ABCD 的法向量,则0m C m ⎧⋅A =⎪⎨⋅AB =⎪⎩,同理可取()0,3,4m =.则219cos ,n m n m n m ⋅〈〉==-. 故二面角E BC A --的余弦值为. (四)2015年高考立体几何题1.(课标II 理-19)如图,长方体1111ABCD A BC D -中,=16AB ,=10BC ,18AA =,点E ,F 分别在11A B ,11C D 上,114A E D F ==.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形. (Ⅰ)在图中画出这个正方形(不必说出画法和理由); (Ⅱ)求直线AF 与平面α所成角的正弦值. 1.【解析】(Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作EM AB ⊥,垂足为M ,则14A M A E ==,18EM AA ==,因为EHGF 为正方形,所以10EH EF BC ===.于是6MH =,所以10AH =.以D 为坐标原点,DA 的方向为x 轴的正方向,建立如图所示的空间直角坐标系D xyz -,则(10,0,0)A ,(10,10,0)H ,(10,4,8)E ,(0,4,8)F ,(10,0,0)FE =,(0,6,8)HE =-.设(,,)n x y z =是平面EHGF 的法向量,则0,0,n FE n HE ⎧⋅=⎪⎨⋅=⎪⎩即100,680,x y z =⎧⎨-+=⎩所以可取(0,4,3)n =.又(10,4,8)AF =-,故45cos ,15n AF n AF n AF⋅<>==⋅.所以直线AF 与平面α所成角的正弦值为15. 考点:1、直线和平面平行的性质;2、直线和平面所成的角.DD 1C 1A 1EFABCB 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015 年高考立体几何大题试卷
1. 【 2015 高考新课标 2,理 19】
如图,长方体 ABCD A 1B 1C 1D 1中, AB=16 , BC =10, AA 1 8,点E ,F 分别在 A 1B 1,
C 1
D 1上, A 1
E D 1
F 4.过点 E ,F 的平面 与此长方体的面相交,交线围成一个正方
形.
( 1 题图)
Ⅰ)在图中画出这个正方形(不必说出画法和理由) Ⅱ)求直线 AF 与平面 所成角的正弦值.
2. 【 2015江苏高考, 16】 如图,在直三棱柱 ABC A 1B 1C 1中,已知 AC BC ,
BC CC 1,设 AB 1的中点为 D , B 1C BC 1 E .求证:(1) DE //平面AA 1C 1C ;
2) BC 1 AB 1 .
3 题图)
3. 【2015 高考安徽,理 19】如图所示,在多面体 A 1B 1D 1DCBA ,四边形
2 题图)
A B
C
AA1B1B ,
ADD1 A1 , ABCD均为正方形,E为B1D1的中点,过A1,D, E的平面交CD1于 F.
4. 【2015 江苏高考, 22】如图,在四棱锥 P ABCD 中,已知 PA 平面 ABCD ,且
四边形 ABCD 为直角梯 形, ABC BAD ,PA AD 2, AB BC 1 2 1)求平面 PAB 与平面 PCD 所成二面角的余弦值;
2)点 Q 是线段 BP 上的动点,当直线 CQ 与 DP 所成角最小时,求线段 BQ 的长
面 BEC ,BE ^ EC ,AB=BE=EC=2 ,G ,F 分别是线
段
( Ⅰ ) 求证: GF // 平面 ADE ;
( Ⅱ)求平面 AEF 与平面 BEC 所成锐二面角的余弦值.
6.【2015 高考浙江,理 17】如图,在三棱柱 ABC A 1B 1C 1 -中, BAC 90 , AB
AC 2,A 1A 4 , A 1在底面 ABC 的射影为 BC 的中点, D 为B 1C 1的中点.
(1)证明: A 1D 平面 A 1B C ;
(2)求二面角 A 1 -BD- B 1的平面角的余弦值 .
Ⅰ)证明: EF //B 1C ; Ⅱ)求二面角 E A 1D B 1余弦值 .
4 题图)
5 题图)
5 .【 2015 高考福建, 理 17】如图, 在几何体 ABCDE 中, 四边形 ABCD 是矩形, AB ^ 平
BE , DC 的中点 .
B C
D
B
7. 【 2015高考山东,理 17】如图,在三棱台 DEF ABC 中, AB 2DE,G,H 分别为
AC,BC 的中点. (Ⅰ)求证: BD//平面 FGH ;
(Ⅱ)若 CF 平面 ABC , AB BC,CF DE , BAC 45 , 求平面 FGH 与 平面
ACFD 所成的角(锐角)的大小 .
8 . 【2015 高考天津,理 17】 如图,在四棱柱 ABCD - A 1B 1C 1D 1 中,侧棱
A 1 A 底面 ABCD , A
B A
C , AB=1,
AC = AA 1 = 2, AD = CD = 5,且点 M 和N 分别为 B 1C 和D 1D 的中点.
(I
)
MN //平面
(II ) 求二面角 D 1 - AC - B 1 的正弦值;
1
(III ) 设 E 为棱 A 1B 1上的点,若直线 NE 和平面 ABCD 所成角的正弦值为 ,求线段
3
A 1E 的长
6 题图)
7 题图)
B
9 题图)
9.【 2015 高考重庆,理 19】如题( 19)图,三棱锥P ABC 中,PC 平面
ABC, PC 3, ACB .D,E 分别为线段AB, BC上的点,且
2
CD DE 2,CE 2EB 2.
1)证明:DE 平面PCD (2)求二面角A PD C 的余弦值
10. 【2015 高考四川,理 18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设BC的中点为M ,GH 的中点为N
(1)请将字母F,G,H 标记在正方体相应的顶点处(不需说明理由)
(2)证明:直线MN / / 平面BDH
(3)求二面角A EG M 的余弦值 .
(10 题图)
11. 【2015 高考湖北,理 19】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ABCD 中,侧棱 PD 底面ABCD ,且PD CD ,过棱PC 的中点 E ,作 EF PB 交 PB于点 F ,连接DE, DF, BD,BE.
Ⅰ)证明:PB 平面 DEF .试判断四面体 DBEF 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
Ⅱ)若面 DEF与面ABCD所成二面角的大小为3π,求B D C C的值.
11 题图)
12. 【 2015高考陕西,理 18】如图1,在直角梯形CD中,D// C, D ,
2
C 1,
D 2,是D 的中点,是C与的交点.将沿折起到 1 的位置,如图2 .
I)证明:CD 平面 1 C ;
II )若平面 1 平面CD ,求平面 1 C 与平面1CD 夹角的余弦值.
13.【2015高考新课标 1,理 18】如图,,四边形ABCD为菱形,
∠ABC=120°,E,F 是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2 DF,AE⊥EC.
Ⅰ )证明:平面AEC⊥平面AFC;
Ⅱ )求直线AE与直线CF所成角的余弦值
A
C
E
B
14 题图)
14.【2015高考北京,理 17】如图,在四棱锥 A EFCB中,△AEF 为等边三角形,平面AEF 平面 EFCB ,EF ∥ BC ,BC 4,EF 2a, EBC FCB 60 ,O为EF 的中点.
(Ⅰ) 求证: AO BE ;(Ⅱ)求二面角 F AE B 的余弦值;
(Ⅲ)若BE 平面 AOC,求a的值.
15.【 2015 高考广东,理 18】如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直, PD = PC = 4 ,AB = 6 ,BC =3 .点E是CD边的中点,点F 、G分别在线段AB、BC上,且AF =2FB,CG=2GB.
1)证明: PE FG ;2)求二面角 P - AD - C 的正切值;
3)求直线PA与直线FG 所成角的余弦值.
15 题图)
( 16 题图)
16。
2015 高考湖南,理 19】如图,已知四棱台ABCD A1B1C1D1 上、下底面分别是边长为 3 和 6 的正方形,AA1 6,且AA1 底面ABCD ,点P,Q 分别在棱DD1,
BC上. (1)若P是DD1的中点,证明:AB1 PQ;(2)若PQ//平面ABB1
A1 ,3
二面角P QD A 的余弦值为,求四面体ADPQ 的体积
7
17.【2015 高考上海,理 19 】如图,在长方体CD 1 1C1D1中, 1 1 ,
D 2,、F分别是、C的中点.证明1、C1、F、四点共面,并
求直线CD1 与平面1C1F 所成的角的正弦值 .
17 题图)。
