求圆的切线方程的几种方法
求切线方程的三种方法

求切线方程的三种方法宝子们,今天咱们来唠唠求切线方程的那些事儿。
这切线方程啊,就像是给曲线找到一个最亲密接触的直线小伙伴,可有意思啦。
一、利用导数求切线方程。
咱先说说这个用导数的方法。
导数这玩意儿啊,其实就是曲线在某一点的斜率。
比如说有个函数y = f(x),咱们先求出它的导数f'(x)。
那在某一点x = a处的切线斜率k呢,就等于f'(a)。
这时候啊,我们已经知道了斜率,再知道这个点(a, f(a))在切线上,就可以用点斜式y - y₁ = k(x - x₁)来求出切线方程啦。
就像你知道一个朋友的走路速度(斜率),又知道他从哪个地方(点)出发,就能算出他走的路线(切线方程)啦。
二、设切点法。
再来说说设切点法。
有时候啊,题目没有直接告诉你切点是啥。
这时候咱就可以聪明点,设切点为(x₀, y₀)。
那这个点既在曲线上又在切线上哦。
如果曲线方程是y = f(x),那y₀ = f(x₀)。
然后呢,求出函数在x₀处的导数f'(x₀),这就是切线的斜率啦。
再根据点斜式写出切线方程y - y₀ = f'(x₀)(x - x₀)。
这就像是在玩一个猜谜游戏,我们先假设一个神秘的点(切点),然后通过各种线索(曲线方程和导数)来找出这个切线方程这个宝藏呢。
三、利用已知切线方程的形式来求。
还有一种方法呢,就是利用已知切线方程的形式。
比如说对于圆的方程(x - a)²+(y - b)² = r²,在点(x₁, y₁)处的切线方程是(x₁ - a)(x - a)+(y₁ - b)(y - b)= r²。
对于椭圆、双曲线等一些特殊的曲线也有类似的固定形式的切线方程哦。
这就像是有个小秘籍一样,直接套用这个形式就能求出切线方程啦。
就好比你有一把万能钥匙,遇到特定的锁(特殊曲线在某点的切线),直接一插就能打开(求出切线方程)啦。
宝子们,这三种求切线方程的方法是不是很有趣呀?只要多练练,你就能在求切线方程这个小天地里畅游无阻啦。
专题 证明圆的切线的常用方法(六大题型)(解析版)
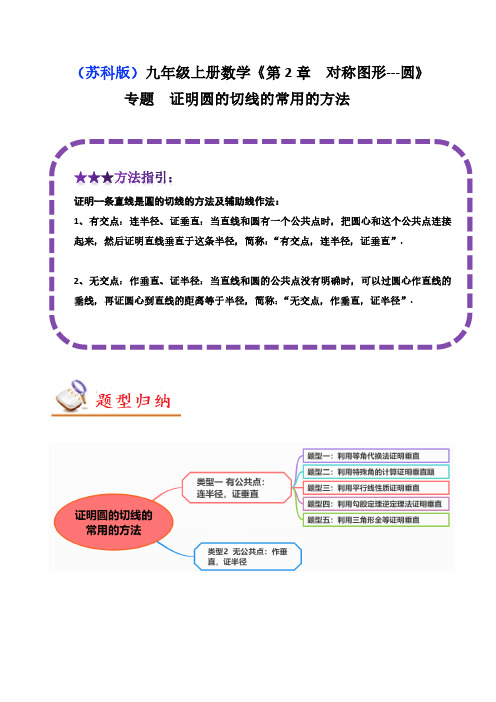
(苏科版)九年级上册数学《第2章对称图形---圆》专题证明圆的切线的常用的方法★★★方法指引:证明一条直线是圆的切线的方法及辅助线作法:1、有交点:连半径、证垂直:当直线和圆有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称:“有交点,连半径,证垂直”.2、无交点:作垂直、证半径:当直线和圆的公共点没有明确时,可以过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称:“无交点,作垂直,证半径”.类型一:有公共点:连半径,证垂直●●【典例一】(2022•雁塔区校级模拟)如图,AB 是⊙O 的直径,点D 在直径AB 上(D 与A ,B 不重合),CD ⊥AB ,且CD =AB ,连接CB ,与⊙O 交于点F ,在CD 上取一点E ,使得EF =EC .求证:EF 是⊙O 的切线;【分析】连接OF ,根据垂直定义可得∠CDB =90°,从而可得∠B +∠C =90°,然后利用等腰三角形的性质可得∠B =∠OFB ,∠C =∠EFC ,从而可得∠OFB +∠EFC =90°,最后利用平角定义可得∠OFE =90°,即可解答;【解答】证明:连接OF ,∵CD ⊥AB ,∴∠CDB =90°,∴∠B +∠C =90°,∵OB =OF ,EF =EC ,∴∠B =∠OFB ,∠C =∠EFC,∴∠OFB+∠EFC=90°,∴∠OFE=180°﹣(∠OFB+∠EFC)=90°,∵OF是⊙O的半径,∴EF是⊙O的切线:【点评】本题考查了切线的判定与性质,勾股定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【变式1-1】(2022•澄城县三模)如图,AB是△ABC外接圆⊙O的直径,过⊙O外一点D作BC的平行线分别交AC,AB于点G,E,交⊙O于点F,连接DB,CF,∠BAC=∠D.求证:BD是⊙O的切线;【分析】证明∠ABD=90°,根据切线的判定可得BD与⊙O相切;【解答】证明:∵AB是⊙O的直径,∴∠ACB=90°,∵DG∥BC,∴∠AGE=∠ACB=90°,∴∠A+∠AEG=90°,又∵∠A=∠D,∠AEG=∠DEB,∴∠D+∠DEB=90°,∴∠DBE=90°,∴AB⊥BD,∵AB为直径,∴BD与⊙O相切;【点评】此题考查了切线的判定,垂径定理,解答本题需要我们熟练掌握切线的判定.【变式1-2】如图,AB是⊙O的直径,点C是圆上一点,CD⊥AB于点D,点E是圆外一点,CA平分∠ECD.求证:CE是⊙O的切线.【分析】利用切线的判定定理证明∠OCE=90°即可得出结论.【解答】证明:∵CA平分∠ECD,∴∠ECA=∠DCA.∵CD⊥AB,∴∠CAD+∠DCA=90°,∴∠ECA+∠CAD=90°.∵OA=OC,∴∠CAD=∠ACO,∴∠ECA+∠ACO=90°,即∠OCE=90°,∴OC⊥EC,∵OC是⊙O的半径,∴CE是⊙O的切线.【点评】本题主要考查了圆的切线的判定,熟练应用圆的切线的判定定理是解题的关键.【变式1-3】(2022秋•阳谷县校级期末)如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.(1)求证:MN是半圆的切线.(2)求证:FD=FG.【分析】(1)欲证明MN是半圆的切线,只需证得∠MAB=90°,即MA⊥AB即可;(2)根据圆周角定理推论得到∠ACB=90°,由DE⊥AB得到∠DEB=90°,则∠1+∠5=90°,∠3+∠4=90°,又D是弧AC的中点,即弧CD=弧DA,得到∠3=∠5,于是∠1=∠4,利用对顶角相等易得∠1=∠2,则有FD=FG.【解答】证明:(1)如图,∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°.又∵∠MAC=∠ABC,∴∠MAC+∠CAB=90°,即∠MAB=90°,∴MA⊥AB.∴MN是半圆的切线.(2)∵AB为直径,∴∠ACB=90°,而DE⊥AB,∴∠DEB=90°,∴∠1+∠5=90°,∠3+∠4=90°,∵D是弧AC的中点,即弧CD=弧DA,∴∠3=∠5,∴∠1=∠4,而∠2=∠4,∴∠1=∠2,∴FD=FG.【点评】本题考查了切线的判定:经过半径的外端点,并且与半径垂直的直线是圆的切线.也考查了圆周角定理及其推论、三角形外角的性质以及等腰三角形的判定.【变式1-4】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接OC,PB,已知PB=6,DB=8,∠EDB=∠EPB.(1)求证:PB是⊙O的切线;(2)求⊙O的半径.(3)连接BE,求BE的长.【分析】(1)由已知角相等及直角三角形的性质得到∠OBP为直角,即可得证;(2)在直角三角形PBD中,由PB与DB的长,利用勾股定理求出PD的长,由切线长定理得到PC=PB =6,由PD﹣PC求出CD的长,在直角三角形OCD中,设OC=r,则有OD=8﹣r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,即为圆的半径.(3)延长PB、DE相交于点F,证明△PED≌△PEF(ASA),由全等三角形的性质得出PD=PF=10,DE =EF,求出DF的长,则可得出答案.【解答】(1)证明:∵DE⊥PE,∴∠DEO=90°,∵∠EDB=∠EPB,∠BOE=∠EDB+∠DEO,∠BOE=∠EPB+∠OBP,∴∠OBP=∠DEO=90°,∴OB⊥PB,∴PB为⊙O的切线;(2)解:在Rt△PBD中,PB=6,DB=8,根据勾股定理得:PD=10,∵PD与PB都为⊙O的切线,∴PC=PB=6,∴DC=PD﹣PC=10﹣6=4;在Rt△CDO中,设OC=r,则有OD=8﹣r,根据勾股定理得:(8﹣r)2=r2+42,解得:r=3,则圆的半径为3.(3)延长PB、DE相交于点F,∵PD与PB都为⊙O的切线,∴OP平分∠CPB,∴∠DPE=∠FPE,∵PE⊥DF,∴∠PED=∠PEF=90°,又∵PE=PE,∴△PED ≌△PEF (ASA ),∴PD =PF =10,DE =EF ,∴BF =PF ﹣PB =10﹣6=4,在Rt △DBF 中,DF==∴BE =12DF =【点评】本题考查了切线的判定和性质,勾股定理,平行线的性质,全等三角形的判定和性质,熟练掌握性质定理是解题的关键.●●【典例二】 如图,△ABC 是直角三角形,点O 是线段AC 上的一点,以点O 为圆心,OA 为半径作圆.O 交线段AB 于点D ,作线段BD 的垂直平分线EF ,EF 交线段BC 于点.(1)若∠B =30°,求∠COD 的度数;(2)证明:ED 是⊙O 的切线.【分析】(1)根据三角形的内角和定理得到∠A =60°,根据等腰三角形的性质得到∠ODA =∠A =60°,于是得到∠COD =∠ODA +∠A =120°;(2)根据线段垂直平分线的性质得到∠EDB =∠B =30°,求得ED ⊥DO ,根据切线的判定定理即可得到结论.【解答】(1)解:∵∠C =90°,∠B =30°,∴∠A =60°,∵OD =OA,∴∠COD=∠ODA+∠A=120°;(2)证明:∵EF垂直平分BD,∴∠EDB=∠B=30°,∴∠EDO=180°﹣∠EDB﹣∠ODA=180°﹣30°﹣60°=90°,∴ED⊥DO,∵OD是⊙O的半径,∴ED是⊙O的切线.【点评】本题考查了切线的判定,等腰三角形的性质,线段垂直平分线的性质,熟练掌握切线的判定定理是解题的关键.【变式2-1】如图,AB为⊙O的直径,点C,D在⊙O上,AC=CD=DB,DE⊥AC.求证:DE是⊙O的切线.【分析】连接OD,根据已知条件得到∠BOD=13×180°=60°,求得∠EAD=∠DAB=12∠BOD=30°,根据等腰三角形的性质得到∠ADO=∠DAB=30°,求得∠EDA=60°,根据切线的判定定理即可得到结论.【解答】证明:连接OD,∵AC=CD=DB,∴∠BOD=13×180°=60°,∵CD=DB,∴∠EAD=∠DAB=12∠BOD=30°,∵OA=OD,∴∠ADO=∠DAB=30°,∵DE⊥AC,∴∠E=90°,∴∠EDA=60°,∴∠EDO=∠EDA+∠ADO=90°,∴OD⊥DE,∵OD是⊙O的半径,∴DE是⊙O的切线.【点评】本题考查了切线的判定,等腰三角形的性质,正确的作出辅助线是解题的关键.【变式2-2】如图,AC是⊙O的直径,B在⊙O上,BD平分∠ABC交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.求证:DE是⊙O的切线.【分析】连接OD,根据圆周角定理的推论得到∠ABC=90°,根据角平分线的性质求出∠DBE=45°,根据圆周角定理得到∠DOC,根据平行线的性质求出∠ODE=90°,根据切线的判定定理证明结论;【解答】证明:连接OD,∵AC是⊙O的直径,∴∠ABC=90°,∵BD平分∠ABC,∴∠DBE=45°,∴∠DOC=2∠DBE=90°,∵DE∥AC,∴∠ODE=∠DOC=90°,∴DE是⊙O的切线;【点评】本题考查的是切线的判定定理、圆周角定理以及正方形的判定和性质,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.【变式2-3】(2023•鼓楼区校级模拟)如图,在⊙O中,AB为⊙O的直径,AC为弦,OC=4,∠OAC=60°.(1)求∠AOC的度数;(2)在图(1)中,P为直径BA的延长线上一点,且S△PAC=PC为⊙O的切线;【分析】(1)根据等腰三角形中有一角为60度时是等边三角形得到△ACO是等边三角形,则∠AOC=60°;(2)由等边三角形的性质以及勾股定理得出CD的长,再利用三角形外角的性质以及等腰三角形的性质得出∠PCA=30°,进而得出答案;【解答】(1)解:在△OAC中,∵OA=OC=4,∠OAC=60°,∴△OAC是等边三角形,∴∠AOC=60°;(2)证明:过点C作CD⊥AO于点D,∵△AOC是等边三角形,CD⊥AO,∴AD=DO=12OA=2,∠ACO=60°,∴CD∵S △PAC =∴12PA •CD =∴PA =4,∴PA =AC ,∴∠P =∠PCA =12∠OAC =30°,∴∠PCO =∠PCA +∠ACO =30°+60°=90°,∴OC ⊥PC ,∵OC 是⊙O 的半径,∴PC 为⊙O 的切线.【点评】本题考查了等边三角形的判定和性质,切线的判定,熟练掌握相关的性质和判定是解决问题的关键.【变式2-4】(2023•门头沟区二模)如图,AB 是⊙O 直径,弦CD ⊥AB 于E ,点F 在CD 上,且AF =DF ,连接AD ,BC .(1)求证:∠FAD =∠B(2)延长FA 到P ,使FP =FC ,作直线CP .如果AF ∥BC .求证:直线CP 为⊙O 的切线.【分析】(1)根据垂径定理、圆周角定理可得∠ACD =∠ACD =∠B ,根据等腰三角形的性质可得∠FAD=∠FDA,进而可得∠FAD=∠B;(2)根据平行线的性质以及三角形内角和定理可得∠FAB=∠FAD=∠FDA=30°,进而得到∠CFP=60°,再利用等边三角形的性质可得∠PCO=60°+30°=90°,由切线的判定方法可得结论.【解答】证明:(1)如图,连接AC,∵AB是⊙O直径,弦CD⊥AB,∴AC=AD,∴∠ACD=∠ACD=∠B,∵AF=FD,∴∠FAD=∠FDA,∴∠FAD=∠B;(2)如图,连接OC,∵AF∥BC,∴∠FAB=∠B,∴∠FAB=∠FAD=∠FDA,∵∠AED=90°,∴∠FAB=∠FAD=∠FDA=30°,∴∠CFP=60°,∵FP=FC,∴△CFP是等边三角形,∴∠PCF=60°,∵OB=OC,∴∠B=∠OCB=30°,∴∠OCD=30°,∴∠PCO=60°+30°=90°,即OC⊥PC,∵OC是半径,∴PC是⊙O的切线.【点评】本题考查切线的判定,圆周角定理、平行线的性质以及三角形内角和定理,掌握切线的判定方法,圆周角定理是正确解答的前提.●●【典例三】如图,四边形ABCD 内接于⊙O ,AB 为⊙O 的直径,过点C 作CE ⊥AD 交AD 的延长线于点E ,延长EC ,AB 交于点F ,∠ECD =∠BCF .求证:CE 为⊙O 的切线;【分析】连接OC ,BD ,可推出EF ∥BD ,进而可证CD =BC ,进而得出CE 为⊙O 的切线;【解答】证明:如图1,连接OC ,BD ,∵AB 是⊙O 的直径,∴∠ADB =90°,∵CE ⊥AE,∴∠E=∠ADB,∴EF∥BD,∴∠ECD=∠CDB,∠BCF=∠CBD,∵∠ECD=∠BCF,∴∠CDB=∠CBD,∴CD=BC,∴半径OC⊥EF,∴CE为⊙O的切线;【点评】本题考查了圆周角定理及其推论,圆的切线判定,解决问题的关键是作合适的辅助线.【变式3-1】(2022秋•阿瓦提县校级期末)已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连结AC,过点D作DE⊥AC,垂足为E.求证:DE为⊙O的切线.【分析】连接OD,根据OA=OB,CD=BD,得出OD∥AC,∠ODE=∠CED,再根据DE⊥AC,即可证出OD⊥DE,从而得出答案.【解答】证明:如图,连接OD.∵AB是⊙O的直径,∴∠ADB=90°,∴CD=BD,∵OA=OB,∴OD∥AC.∴∠ODE=∠CED.∵DE⊥AC,∴∠CED=90°.∴∠ODE=90°,∴OD⊥DE,∵OD是⊙O的半径,∴DE是⊙O的切线.【点评】本题考查了切线的判定与性质,解决本题的关键是掌握圆周角定理的推论、线段垂直平分线的性质以及等边三角形的判定,是一道常考题型.【变式3-2】已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.(1)求证:点D是AB的中点;(2)判断DE与⊙O的位置关系,并证明你的结论.【分析】(1)连接CD,如图,根据圆周角定理,由BC为直径得到∠BDC=90°,然后根据等腰三角形的性质得AD=BD;(2)连接OD,先得到OD为△ABC的中位线,再根据三角形中位线性质得OD∥AC,而DE⊥AC,则DE⊥OD,然后根据切线的判定定理可得DE为⊙O的切线.【解答】(1)证明:连接CD,如图,∵BC为直径,∴∠BDC=90°,∴CD⊥AB,∵AC=BC,∴AD=BD,即点D是AB的中点;(2)解:DE与⊙O相切.理由如下:连接OD,∵AD=BD,OC=OB,∴OD为△ABC的中位线,∴OD∥AC,而DE⊥AC,∴DE⊥OD,∴DE为⊙O的切线.【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.【变式3-3】如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.(1)求证:BC是⊙O的切线;(2)已知∠B=30°,CD=4,求线段AB的长.【分析】(1)连接OD,根据角平分线的定义得到∠BAD=∠CAD,而∠OAD=∠ODA,则∠ODA=∠CAD,于是判断OD∥AC,由于∠C=90°,所以∠ODB=90°,然后根据切线的判定定理即可得到结论;(2)由∠B=30°得到∠BAC=60°,则∠CAD=30°,在Rt△ADC中,根据含30度的直角三角形三边的关系得到AC=Rt△ABC中,根据含30度的直角三角形三边的关系可得到AB=【解答】(1)证明:连接OD,如图,∵∠BAC的平分线交BC于点D,∴∠BAD=∠CAD,∵OA=OD,∴∠OAD=∠ODA,∴∠ODA=∠CAD,∴OD∥AC,∵∠C=90°,∴∠ODB=90°,∴OD⊥BC,∴BC是⊙O的切线;(2)解:∵∠B=30°,∴∠BAC=60°,∴∠CAD=30°,在Rt△ADC中,DC=4,∴AC==在Rt△ABC中,∠B=30°,∴AB=2AC=【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了含30度的直角三角形三边的关系.【变式3-4】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)若∠DBC=30°,DE=1cm,求BD的长.【分析】(1)连接OA,根据角之间的互余关系可得∠OAE=∠DEA=90°,故AE⊥OA,即AE是⊙O的切线;(2)根据圆周角定理,可得在Rt△AED中,∠AED=90°,∠EAD=30°,有AD=2DE;在Rt△ABD中,∠BAD=90°,∠ABD=30°,有BD=2AD=4DE,即可得出答案.【解答】(1)证明:连接OA,∵DA平分∠BDE,∴∠BDA=∠EDA.∵OA=OD,∴∠ODA=∠OAD,∴∠OAD=∠EDA,∴OA∥CE.∵AE⊥CE,∴AE⊥OA.∴AE是⊙O的切线.(2)解:∵BD是直径,∴∠BCD=∠BAD=90°.∵∠DBC=30°,∠BDC=60°,∴∠BDE=120°.∵DA平分∠BDE,∴∠BDA=∠EDA=60°.∴∠ABD=∠EAD=30°.∵在Rt△AED中,∠AED=90°,∠EAD=30°,∴AD=2DE.∵在Rt△ABD中,∠BAD=90°,∠ABD=30°,∴BD=2AD=4DE.∵DE的长是1cm,∴BD的长是4cm.【点评】此题主要考查了切线的判定,角平分线的性质,含30°的直角三角形的性质,勾股定理,矩形的判定和性质,构造出直角三角形是解本题的关键,是一道中等难度的中考常考题.●●【典例四】(2022•城关区一模)如图,C是⊙O上一点,点P在直径AB的延长线上,⊙O的半径为6,PB=4,PC=8.求证:PC是⊙O的切线;【分析】可以证明OC2+PC2=OP2得△OCP是直角三角形,即OC⊥PC,PC是⊙O的切线;【解答】解:如图,连接OC、BC,∵⊙O的半径为6,PB=4,PC=8.∴OC=OB=6,OP=OB+BP=6+4=10,∴OC2+PC2=62+82=100,OP2=102=100,∴OC2+PC2=OP2,∴△OCP是直角三角形,∴OC⊥PC,∴PC是⊙O的切线;【点评】本题考查圆的切线的判定和勾股定理逆定理,利用勾股定理的逆定理证明垂直是解决问题的关键.【变式4-1】如图,AD, BD是⊙O的弦,AD⊥BD,且BD=2AD=8 ,点C是BD的延长线上的一点,CD=2,求证:AC是⊙O的切线.【分析】先由勾股定理的逆定理证明垂直,再由切线的判断进行解答即可.【解答】证明:连接AB,∵AD⊥BD,且BD=2AD=8 ,∴AB为直径,AB2 =82+42 =80,∵CD=2,AD=4 ,∴AC2 =22 +42=20,∵CD=2,BD=8,∴BC=102=100,∴AC2+AB2=CB2,∴∠BAC=90° ,∴AC是⊙O的切线【点评】本题考查切线的判定,圆周角定理的推论,勾股定理的逆定理,解题关键是作出辅助线构造直角三角形.【变式4-2】如图,AD,BD是⊙O的弦,AD⊥BD,且BD=2AD=8,点C是BD的延长线上的一点,CD=2,求证:AC是⊙O的切线.【分析】先根据圆周角定理得到AB为⊙O的直径,再利用勾股定理计算出AB、AC,接着利用勾股定理的逆定理证明△ABC为直角三角形,∠BAC=90°,所以AC⊥AB,然后根据切线的判定定理得到结论.【解答】证明:∵AD⊥BD,∴∠ADB=90°,∴AB为⊙O的直径,∵BD =2AD =8,∴AD =4,在Rt △ADB 中,AB 2=AD 2+BD 2=42+82=80,在Rt △ADC 中,AC 2=AD 2+CD 2=42+22=20,∵BC 2=(2+8)2=10,∴AC 2+AB 2=BC 2,∴△ABC 为直角三角形,∠BAC =90°,∴AC ⊥AB ,∵AB 为直径,∴AC 是⊙O 的切线.【点评】本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理、勾股定理和勾股定理的逆定理.●●【典例五】(2022•鄞州区校级开学)如图,AB 为⊙O 的直径,点C 和点D 是⊙O 上的两点,连接BC ,DC ,BC =CD ,CE ⊥DA 交DA 的延长线于点E .求证:CE 是⊙O 的切线;【分析】连接OD ,OC ,证得△COD ≌△COB ,可得∠OCD =∠BCO ,从而得到∠ADC =∠DCO ,进而得到DA ∥CO ,利用切线的判定定理即可求证;【解答】证明:连接OD ,OC,如图,在△COD和△COB中,OD=OBOC=OC,CD=CB∴△COD≌△COB(SSS),∴∠OCD=∠BCO,∵CO=BO,∴∠B=∠BCO,∵∠B=∠ADC,∴∠ADC=∠DCO.∴DA∥CO,∴∠E+∠ECO=180°.∵CE⊥EA,∴∠E=90°.∴∠ECO=90°,∴EC⊥CO,∵CO是⊙O的半径,∴EC是⊙O的切线;【点评】本题主要考查了切线的判定,圆周角定理等知识,熟练掌握切线的判定,相似三角形的判定和性质,圆周角定理等知识是解题的关键.【变式5-1】如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.求证:CD是⊙O的切线;【分析】连接OD,利用SAS得到三角形COD与三角形COB全等,利用全等三角形的对应角相等得到∠ODC 为直角,即可得证;【解答】证明:如图,连接OD.∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD,又∵OA=OD,∴∠DAO=∠ADO,∴∠COD=∠COB,在△COD和△COB中,OC=OC∠COD=∠COB,OD=OB∴△COD≌△COB(SAS),∴∠CDO=∠CBO=90°,∵OD是⊙O的半径,∴CD是⊙O的切线;【点评】此题考查了切线的判定和性质,以及全等三角形的判定与性质,熟练掌握各自的性质是解本题的关键.【变式5-2】(2022秋•新抚区期末)如图,AB为⊙O的直径,四边形OBCD是矩形,连接AD,延长AD 交⊙O于E,连接CE.求证:CE为⊙O的切线.【分析】连接OC、BE,根据矩形性质和圆半径相等,推出∠CDE=∠AEO,进而得到OP=CP,然后根据OB∥CD,可以推出∠COE=∠BOC,最后通过证明△BOC≌△EOC即可求解.【解答】证明:如图:连接OC、BE,OE,CD交于点P,∵四边形OBCD是矩形,∴OB∥CD,∠OBC=90°,OB=CD,∵OB∥CD,∴∠A=∠CDE,∵在⊙O中,OA=OB=OE,∴OE=CD,∵OA=OE,∴∠A=∠AEO,∴∠CDE=∠AEO,∴DP=PE,∵OE=CD,∴OP=CP,∴∠COE=∠DCO,∵OB∥CD,∴∠DCO=∠BOC,∴∠COE=∠BOC,在△BOC和△EOC中,OB=OECO=CO,∠BOC=∠COE∴△BOC≌△EOC(SAS),∴∠CEO=∠OBC=90°,∴CE⊥OE,又∵OE为⊙O的半径,∴CE为⊙O的切线.【点评】本题考查圆周角定理,全等三角形的判定和性质,矩形的性质等众多知识点,熟悉掌握以上知识点是解题关键.【变式5-3】(2022•建邺区二模)如图,四边形ABCD是菱形,以AB为直径作⊙O,交CB于点F,点E在CD上,且CE=CF,连接AE.(1)求证:AE是⊙O的切线;(2)连接AC交⊙O于点P,若AP BF=1,求⊙O的半径.【分析】(1)连接AF,根据菱形的性质得到∠ACF=∠ACE,根据全等三角形的性质得到∠AFC=∠AEC,推出OA⊥AE,根据切线的判定定理即可得到结论;(2)连接BP,根据圆周角定理得到∠APB=90°,求得AC=2AP=【解答】(1)证明:连接AF,∵四边形ABCD为菱形,∴∠ACF=∠ACE,在△ACF与△ACE中,CF=CE∠ACF=∠ACEAC=AC,∴△ACF≌△ACE(SAS),∴∠AFC=∠AEC,∵AB是⊙O的直径,∴∠AFB=∠AFC=90°,∴∠AEC=90°,∵AB∥DC,∴∠BAE+∠AEC=90°,∴∠BAE=90°,∴OA⊥AE,∵OA是⊙O的半径,∴AE是⊙O的切线;(2)解:连接BP,∵AB是⊙O的直径,∴∠APB=90°,∵AB=CB,AP=∴AC=2AP=设⊙O的半径为R,∵AC2﹣CF2=AF2,AB2﹣BF2=AF2,∴2−(2R−1)2=(2R)2−12,∴R=32(负值舍去),∴⊙O的半径为3 2.【点评】本题考查了切线的判定和性质,圆周角定理,菱形的性质,三角形全等的性质和判定,勾股定理等知识,解答本题的关键是根据勾股定理列方程解决问题.类型二:无公共点:作垂直,证半径●●【典例六】如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.【分析】过点O作OE⊥AC于点E,连接OD,OA,根据切线的性质得出AB⊥OD,根据等腰三角形三线合一的性质得出AO是∠BAC的平分线,根据角平分线的性质得出OE=OD,从而证得结论.【解答】证明:过点O作OE⊥AC于点E,连接OD,OA,∵AB与⊙O相切于点D,∴AB⊥OD,∵△ABC为等腰三角形,O是底边BC的中点,∴AO是∠BAC的平分线,∴OE=OD,即OE是⊙O的半径,∵圆心到直线的距离等于半径,∴AC是⊙O的切线.【点评】本题考查了切线的判定和性质,等腰三角形的性质,角平分线的性质,熟练掌握性质定理是解题的关键.【变式6-1】如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.【分析】利用正方形的性质得出AC平分角∠BCD,再利用角平分线的性质得出OM=ON,即可得出答案.【解答】证明:如图所示,连接OM,过点O作ON⊥CD于点N,∵⊙O与BC相切于点M,∴OM⊥BC,又∵ON⊥CD,O为正方形ABCD对角线AC上一点,∴OM=ON,∴ON为⊙O的半径,∴CD与⊙O相切.【点评】此题主要考查了正方形的性质以及角平分线的性质,得出OM=ON是解题关键.【变式6-2】如图,OC平分∠AOB,D是OC上任意一点,⊙D和OA相切于点E,连接CE.(1)求证:OB与⊙D相切;(2)若OE=4,⊙D的半径为3,求CE的长.【分析】(1)过点D作DF⊥OB于点F,先由切线的性质得DE⊥OA,则由角平分线的性质得DF=DE,即可证得结论;(2)过E作EG⊥OD于G,先由勾股定理求出OD=5,再由面积法求出EG=125,然后由勾股定理求出DG=95,最后由勾股定理求出CE即可.【解答】(1)证明:连接DE,过点D作DF⊥OB于点F,如图所示:∵⊙D与OA相切于点E,∴DE⊥OA,∵OC平分∠AOB,∴DF=DE,又∵DF⊥OB,∴OB与⊙D相切;(2)解:过E作EG⊥OD于G,如图所示:由(1)得:DE⊥OA,∴∠OED=90°,∵OE=4,DE=3,∴OD=5,∵EG⊥OD,∴12OD×EG=12OE×DE,∴EG=OE×DEOD=4×35=125,∴DG===9 5,∴CG=CD+DG=3+95=245,∴CE=【点评】此题考查了切线的判定与性质、勾股定理以及角平分线的性质等知识,解题的关键是准确作出辅助线.【变式6-3】如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.(1)求证:CD是⊙O的切线;(2)若AD=4,BC=9,求⊙O的半径R.【分析】(1)过O点作OE⊥CD于点E,通过角平分线的性质得出OE=OA即可证得结论.(2)过点D作DF⊥BC于点F,根据切线的性质可得出DC的长度,继而在Rt△DFC中利用勾股定理可得出DF的长,继而可得出半径.【解答】(1)证明:过O点作OE⊥CD于点E,∵AM切⊙O于点A,∴OA⊥AD,又∵DO平分∠ADC,∴OE=OA,∵OA为⊙O的半径,∴OE是⊙O的半径,且OE⊥DC,∴CD是⊙O的切线.(2)解:过点D作DF⊥BC于点F,∵AM,BN分别切⊙O于点A,B,∴AB⊥AD,AB⊥BC,∴四边形ABFD是矩形,∴AD=BF,AB=DF,又∵AD=4,BC=9,∴FC=9﹣4=5,∵AM,BN,DC分别切⊙O于点A,B,E,∴DA=DE,CB=CE,∴DC=AD+BC=4+9=13,在Rt△DFC中,DC2=DF2+FC2,∴DF=12,∴AB=12,∴⊙O的半径R是6.【点评】此题考查了切线的性质、角平分线的性质及勾股定理的知识,证明第一问关键是掌握切线的判定定理,解答第二问关键是熟练切线的性质.【变式6-4】(2022秋•清原县期末)如图,在△ABC中,∠ACB=90°,点D是AB边的中点,点O在AC边上,⊙O 经过点C 且与AB 边相切于点E ,∠FAC =12∠BDC .(1)求证:AF 是⊙O 的切线;(2)若BC =6,AB =10,求⊙O 的半径长.【分析】(1)作OH ⊥FA ,垂足为点H ,连接OE ,证明AC 是∠FAB 的平分线,进而根据OH =OE ,OE ⊥AB ,可得AF 是⊙O 的切线;(2)勾股定理得出AC ,设⊙O 的半径为r ,则OC =OE =r ,进而根据切线的性质,在Rt △OEA 中,勾股定理即可求解.【解答】(1)证明:如图,作OH ⊥FA ,垂足为点H ,连接OE ,∵∠ACB =90°,D 是AB 的中点,∴CD =AD =12AB ,∴∠CAD =∠ACD ,∵∠BDC =∠CAD +∠ACD =2∠CAD ,又∵∠FAC =12∠BDC ,∴∠FAC =∠CAD ,即AC 是∠FAB 的平分线,∵点O 在AC 上,⊙O 与AB 相切于点E ,∴OE ⊥AB ,且OE 是⊙O 的半径,∴OH =OE ,OH 是⊙O 的半径,∴AF 是⊙O 的切线;(2)解:如图,在△ABC中,∠ACB=90°,BC=6,AB=10,∴AC==8,∵BE,BC是⊙O的切线,∴BC=BE=6,∴AE=10﹣6=4设⊙O的半径为r,则OC=OE=r,在Rt△OEA中,由勾股定理得:OE2+AE2=OA2,∴16+r2=(8﹣r)2,∴r=3.∴⊙O的半径长为3.【点评】本题考查了切线的性质与判定,勾股定理,熟练掌握切线的性质与判定是解题的关键.1.如图,已知AB是⊙O的直径,AB=BE,点P在BA的延长线上,连接AE交⊙O于点D,过点D作PC⊥BE垂足为点C.求证:PC与⊙O相切;【分析】连接OD,根据等腰三角形的性质得到∠BAE=∠BEA,∠BAE=∠ODA,等量代换得到∠ODA=∠BEA,证明OD∥BE,根据平行线的性质得到PC⊥OD,根据切线的判定定理证明结论;【解答】证明:连接OD,∵AB=BE,∴∠BAE=∠BEA,∵OA=OD,∴∠BAE=∠ODA,∴∠ODA=∠BEA,∴OD∥BE,∵PC⊥BE,∴PC⊥OD,∵OD是⊙O的半径,∴PC与⊙O相切;【点评】本题考查的是切线的判定、解直角三角形,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.2.如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,点D是BC的中点,DE∥BC交AC的延长线于点E.(1)求证:直线DE与⊙O相切;(2)若⊙O的直径是10,∠A=45°,求CE的长.【分析】(1)连接OD,如图,先利用垂径定理得到OD⊥BC,再根据平行线的性质得到OD⊥DE,然后根据切线的判定方法得到结论;(2)先根据圆周角定理得到∠B=90°,则∠ACB=45°,再根据平行线的性质得到∠E=45°,则可判断△ODE 为等腰直角三角形,于是可求出OE,然后计算OE﹣OC即可.【解答】(1)证明:连接OD,如图,∵点D是BC的中点,∴OD⊥BC,∵DE∥BC,∴OD⊥DE,∴直线DE与⊙O相切;(2)解:∵AC是⊙O的直径,∴∠B=90°,∵∠A=45°,∴∠ACB=45°,∵BC∥DE,∴∠E=45°,而∠ODE=90°,∴△ODE为等腰直角三角形,∴OE==∴CE=OE﹣OC=5.【点评】本题考查了切线的性质与判定:圆的切线垂直于经过切点的半径.也考查了垂径定理、圆周角定理和等腰直角三角形的性质.3.(2023•东城区校级模拟)如图,⊙O的半径OC与弦AB垂直于点D,连接BC,OB.(1)求证:2∠ABC+∠OBA=90°;(2)分别延长BO、CO交⊙O于点E、F,连接AF,交BE于G,过点A作AM⊥BC,交BC延长线于点M,若G是AF的中点,求证:AM是⊙O的切线.【分析】(1)先根据垂径定理得到AC=BC,再根据圆周角定理得到∠BOC=2∠ABC,然后利用互余关系得∠BOD+∠OBD=90°,从而得到结论;(2)如图,连接OA,根据垂径定理得到BE⊥AF,再根据圆周角定理得到∠CAF=90°,则可判断BE ∥AC,所以∠ABE=∠BAC,接着证明∠BAO=∠CBA得到OA∥BC,根据平行线的性质得到AM⊥OA,然后根据切线的判断方法得到结论.【解答】证明:(1)∵OD⊥AB,∴AC=BC,∠ODB=90°,∴∠BOC=2∠ABC,∵∠BOD+∠OBD=90°,∴2∠ABC+∠OBA=90°;(2)如图,连接OA,∵G是AF的中点,∴BE⊥AF,∵CF为直径,∴∠CAF=90°,∴CA⊥AF,∴BE∥AC,∴∠ABE=∠BAC,∴AC=BC,∴∠CAB=∠CBA,∵OA=OB,∴∠BAO=∠ABO,∴∠BAO=∠CBA,∴OA∥BC,∵AM⊥BC,∴AM⊥OA,而OA为⊙O的半径,∴AM是⊙O的切线.【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理、垂径定理.4.(2022•思明区校级二模)如图,四边形ABCD是⊙O的内接四边形,AC是⊙O直径,BE∥AD交DC 延长线于点E,若BC平分∠ACE.(1)求证:BE是⊙O的切线;(2)若BE=3,CD=2,求⊙O的半径.【分析】(1)连接OB,由条件可以证明OB∥DE,从而证明OB⊥BE;(2)由垂径定理求出AD长,从而由勾股定理可求AC长.【解答】(1)证明:连接OB,∵″OB=OC,∴∠OBC=∠OCB,∵∠BCE=∠OCB,∴∠OBC=∠BCE,∴OB∥DE,∵AC是⊙O直径,∴AD⊥DE,∵BE∥AD,∴BE⊥DE,∴OB⊥BE,∵OB是⊙O半径,∴BE是⊙O切线;(2)解:延长BO交AD于F,∵∠D=∠DEB=∠EBF=90°,∴四边形BEDF是矩形,∴BF⊥AD,DF=BE=3,∴AD=2DF=6,∵AC2=AD2+CD2,∴AC2=62+22=40,∴AC=∴⊙O【点评】本题考查切线的判定,矩形的判定和性质,垂径定理,勾股定理,用到的知识点较多,关键是熟练掌握知识点,并能灵活应用.5.(2023•封开县一模)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)当AB=5,BC=6时,求DE的长.【分析】(1)连接OD,由AC=AB,根据等边对等角得到一对角相等,再由OD=OB,根据等边对等角得到又一对角相等,等量代换可得一对同位角相等,根据同位角相等两直线平行可得OD与AC平行,又EF垂直于AC,根据垂直于两平行线中的一条,与另一条也垂直,得到EF与OD也垂直,可得EF为圆O的切线;(2)连接AD,由AB为圆的直径,根据直径所对的圆周角为直角可得∠ADB=90°,即AD与BC垂直,又AC=AB,根据三线合一得到D为BC中点,由BC求出CD的长,再由AC的长,利用勾股定理求出AD的长,三角形ACD的面积有两种求法,AC乘以DE除以2,或CD乘以AD除以2,列出两个关系式,两关系式相等可求出DE的长.【解答】(1)证明:连接OD,∵AB=AC,∴∠C=∠OBD,∵OD=OB,∴∠1=∠OBD,∴∠1=∠C,∴OD∥AC,∵EF⊥AC,∴EF⊥OD,∴EF是⊙O的切线;(2)连接AD,∵AB为⊙O的直径,∴∠ADB=90°,又∵AB=AC,且BC=6,∴CD=BD=12BC=3,在Rt△ACD中,AC=AB=5,CD=3,根据勾股定理得:AD=4,又S△ACD =12AC•ED=12AD•CD,即12×5×ED=12×4×3,∴ED=12 5.【点评】此题考查了等腰三角形的性质,圆周角定理,平行线的性质,勾股定理,三角形面积的求法,以及切线的判定,其中证明切线的方法为:有点连接圆心与此点,证垂直;无点过圆心作垂线,证明垂线段长等于圆的半径.本题利用的是第一种方法.6.(2023•宁德模拟)如图,OM 为⊙O 的半径,且OM =3,点G 为OM 的中点,过点G 作AB ⊥OM 交⊙O 于点A ,B ,点D 在优弧AB 上运动,将AB 沿AD 方向平移得到DC ;连接BD ,BC .(1)求∠ADB 的度数;(2)如图2,当点D 在MO 延长线上时,求证:BC 是⊙O 的切线.【分析】(1)连接AO ,BO ,先根据特殊角的正弦值可得∠OAG =30°,再根据等腰三角形的性质可得∠OAG =∠OBG =30°,从而可得∠AOB =120°,然后根据圆周角定理即可得;(2)连接AO ,BO ,CO ,先证出四边形ABCD 是平行四边形,再根据等边三角形的判定与性质可得AB =AD ,根据菱形的判定可得四边形ABCD 是菱形,根据菱形的性质可得CB =CD ,然后根据SSS 定理证出△COB ≌△COD ,根据全等三角形的性质可得∠OBC =∠ODC =90°,最后根据圆的切线的判定即可得证.【解答】(1)解:如图1,连接AO ,BO .∵点G 为OM 的中点,且OM =3,∴OG =12OM =32,OA =OB =OM =3,∵AB ⊥OM ,在Rt △AOG 中,OG =12OA .∴∠OAG =30°,又∵OA =OB ,∴∠OAG=∠OBG=30°,∴∠AOB=120°,∴∠ADB=12∠AOB=60°.(2)证明:如图2,连接AO,BO,CO,由平移得:AB=DC,AB∥DC,∴四边形ABCD是平行四边形,∵OM⊥AB,点D在MO延长线上,∴DM⊥CD,∵OA=OB,AB⊥OM,∴AG=BG,∴DM垂直平分AB,∴AD=BD,∵∠ADB=60°,∴△ABD为等边三角形,∴AB=AD,∴平行四边形ABCD是菱形,∴CB=CD,在△COB和△COD中,CB=CDOB=ODOC=OC,∴△COB≌△COD(SSS),∴∠OBC=∠ODC=90°,又∵OB是⊙O的半径,。
证明圆的切线的两种方法

证明圆的切线的两种方法一、通过圆的性质证明圆的切线圆的切线是与圆相切且只与圆相交于切点的直线。
我们可以通过圆的性质来证明圆的切线。
1. 方法一:利用圆的切线垂直于半径的性质证明对于任意一点P在圆上,连接圆心O与点P,并延长线段OP。
根据圆的性质可知,线段OP是圆的半径。
假设有一条直线l与圆相交于点A,且线段OA是圆的半径。
我们要证明直线l是圆的切线。
我们可以得到三角形OAP。
根据直角三角形的性质可知,线段OP与线段AP垂直。
因此,直线l与线段OA垂直。
我们要证明直线l只与圆相交于点A。
假设直线l与圆相交于另一点B,连接线段OB。
根据圆的性质可知,线段OB是圆的半径。
由于线段OA与线段OB都是圆的半径,所以线段OA等于线段OB。
然而,根据直线的性质可知,直线l是直线OB的切线。
因此,线段OA与线段OB的长度相等,与直线l只与圆相交于点A的性质相矛盾。
所以,直线l只与圆相交于点A,即直线l是圆的切线。
因此,我们通过圆的切线垂直于半径的性质证明了直线l是圆的切线。
2. 方法二:利用圆的切线与半径的斜率关系证明对于任意一点P在圆上,连接圆心O与点P,并延长线段OP。
根据圆的性质可知,线段OP是圆的半径。
假设有一条直线l与圆相交于点A,且线段OA是圆的半径。
我们要证明直线l是圆的切线。
我们可以得到直线l的方程。
设直线l的斜率为k,直线l的方程为y = kx + b。
我们要证明直线l的斜率与线段OA的斜率相等。
由于线段OA是圆的半径,所以线段OA的斜率等于0。
根据直线的性质可知,直线l 与线段OA垂直,即直线l的斜率与线段OA的斜率的乘积为-1。
因此,直线l的斜率等于0的倒数,即k = 0。
因此,直线l的方程为y = b。
接下来,我们要证明直线l只与圆相交于点A。
假设直线l与圆相交于另一点B,连接线段OB。
根据圆的性质可知,线段OB是圆的半径。
由于线段OA与线段OB都是圆的半径,所以线段OA等于线段OB。
然而,根据直线的性质可知,直线l与线段OB平行,即线段OA与线段OB的长度相等。
圆的切线定理

圆的切线定理定理表述设有一个圆和一条直线,当这条直线与圆相切时,直线与圆的切点之间的线段与半径垂直。
证明过程证明圆的切线定理的方法主要有两种:几何法和代数法。
几何法几何法是通过几何构造来证明定理。
我们可以通过以下步骤进行证明:1. 假设有一个圆和一条直线,直线与圆相切于点P。
2. 以圆心为起点,作一条半径OP。
3. 连接直线上的点P和圆心O,得到线段OP。
4. 利用三角形的性质,我们可以得出线段OP与直线的斜率相等。
5. 因为直线与圆相切,所以线段OP与半径OP垂直。
6. 因此,根据直线斜率的性质,直线与半径垂直。
通过以上步骤,我们证明了圆的切线与半径垂直。
代数法代数法是通过代数计算来证明定理。
我们可以使用坐标系的方法进行证明:1. 假设圆的方程为(x-a)^2 + (y-b)^2 = r^2,其中(a,b)为圆心坐标,r为半径。
2. 假设直线的方程为y = mx + c,其中m为直线的斜率,c为截距。
3. 将直线方程代入圆的方程,得到(x-a)^2 + (mx + c - b)^2 - r^2 = 0。
4. 根据圆的定义,当直线与圆相切时,该方程只有一个解。
5. 解方程得到一个二次方程,利用判别式判断方程有一个解的特性。
6. 通过计算判别式,可以得到切线方程有唯一解的条件。
7. 根据等式等式的性质,解方程得到的根与圆的切点相对应。
8. 证明了切线方程与圆的切点正交。
通过以上代数计算,我们证明了圆的切线与半径垂直。
应用和实例圆的切线定理在几何学和应用数学中有着广泛的应用。
它在解析几何的证明和问题求解中起着重要的作用。
例如,通过圆的切线定理,我们可以解决求直线与圆的切点坐标和切线方程的问题。
这对于工程学和物理学中的曲线研究非常有用。
另外,圆的切线定理在计算机图形学和计算机模拟中也被广泛应用。
通过计算机算法,我们可以快速计算出圆与直线的切点坐标,从而实现更精确的模拟效果。
总之,圆的切线定理是解析几何中重要的定理之一,它在几何学和应用数学中有着广泛的应用价值。
过一点求圆的切线的方程

[练习]
1.下列方程各表示什么图形?
(1) x2 y2 0 原点(0,0)
x y (2)
2
2
2x 4y 6 0
圆心(1,-2),半径
11
(3) x2 y2 2ax b2 0,(ab 0)
圆心 ( a,0), 半径 a 2 b2
2.求下列各圆的半径和圆心坐标.
3、当D2 E2 4F 0时,方程(1)不表示任何图形。
当D2 E2 4F 0时,方程(1)表示以( D , E )为圆心,
1 D2 E2 4F为半径的圆。
22
2
圆的一般方程 判断以下方程是不是圆的方程: ① x2 + y2 - 2x + 4y + 1 = 0 ② X 2+ y 2- 2x + 4y + 5 = 0 ③ X2 + y 2- 2x + 4y + 6 =0
因为O、M1、M2在圆上,所以它们的坐标是方程的解
F 0
D
E
F
2
0
解得F=0,D=8,E=6
4D 2E F 20 0
圆的半径为 r D2 E2 4F 5 2
于是得到所求圆的方程x2+y28x+6y=0.
∴圆的半径为5、圆心坐标是(4,-3)
(ⅰ) 问题转化和分类讨论的思想(原则是不重复,不遗漏) (ⅱ)方程的思想 (待定系数法) (ⅲ)数形结合的思想 [如习题示例(2)] 11. [作业]
P826 , 7 , 8
(3)给出圆的一般方程,如何求圆心和半径? (用配方法求解)
(4)要学会根据题目条件,恰当选择圆方程形式:
①若知道或涉及圆心和半径,我们一般采用圆的标准方程较简单.
求圆的切线方程的几种方法

求圆的切线方程的几种方法圆的切线是通过圆上特定点并且与该点垂直于圆心的直径所确定的线段。
求圆的切线方程有多种方法,下面将介绍其中的几种常见方法。
【方法一:向径垂直于切线】设圆心为O,半径为r,圆上一点为P,切点为A,连接O和P。
由于切线与向径垂直,所以OP与PA垂直。
根据垂直关系,我们可以得到以下的条件:1.斜率关系:由于向径OP与切线的斜率相乘等于-1,即斜率m1*m2=-1、假设斜率为m,则有m*∞=-1(∞代表垂直线的斜率)即m=0。
所以切线的斜率为0。
2.切点坐标关系:假设切线方程为y = kx + b,由于切点A的坐标为(x1, y1),代入切线方程中即可求得切线的方程。
【方法二:利用切线的性质求斜率和截距】在方法一中,我们先求出了切线的斜率为0。
然后,我们可以利用切点的特性求出切线的截距。
1.斜率求解:由于切线的斜率为0,所以利用两点的斜率公式,我们可以得到以下的关系式:m=(y2-y1)/(x2-x1)=(y1-y1)/(x1-x1)=0即y1-y1=0,即y1=y12.求截距:假设切点坐标为(x1,y1),则切线方程为y=b。
因为切点A在切线上,所以代入切线方程中即可求出截距。
【方法三:利用切线与半径的垂直性质】由于切线与半径垂直,所以可以利用向径的特性求出切线的斜率和截距。
1.斜率求解:假设斜率m,则向径OP的斜率为m1=(y-y1)/(x-x1)。
根据垂直性质,切线的斜率m与向径的斜率m1满足m*m1=-12.求截距:设切线方程为y = kx + b。
代入切点(x1, y1)得到:y1 = k * x1 + b。
再根据切线与半径垂直的性质,可以利用点斜式的截距形式求解截距。
【方法四:坐标代入法】设圆的方程为(x-a)^2+(y-b)^2=r^2,切点坐标为(x1,y1)。
则可以把切线方程代入圆方程,将圆方程中的x和y替换成x1和y1,即可得到切线方程。
【方法五:利用直角三角形的性质】在方法一中,我们已经得到了切线与向径OP垂直,假设角POA为θ,则tanθ = m = (y1 - y) / (x1 - x)。
高中数学:求圆的切线方程的几种解法

高中数学:求圆的切线方程的几种解法求经过点且与圆相切的切线方程并作图。
解1:利用过圆上一点的切线方程如图1,设过点的直线与圆相切于,根据过圆上一点求切线方程的公式,得圆的切线方程为(1)因为切线过点所以(2)又因为点在圆上所以(3)联立(2)(3)得代入(1)即得所求圆的切线方程为和。
解2:利用勾股定理设所求切线与已知圆相切于点,因为圆的方程为,所以圆心O的坐标为,连接,则,所以由勾股定理,得,即,所以又因为点在圆上,所以(2),联立(1)(2)得代入切线方程中,即得所求圆的切线方程为和。
解3:利用互相垂直的两条直线的斜率互为负倒数的关系。
设所求直线与圆相切于,则。
因为,所以,所以切线的方程为。
因为过点,所以代入上式得(1)而(2)以下同解2。
解4:利用圆锥曲线切线的定义设是圆上任意一点,作割线交圆于另一点,则,又因为两点都在圆上。
所以(2)得代入(1),得,当Q 与重合时,即当,时,割线的斜率就变成过圆上一点的切线的斜率,所以。
以下仿解3。
解5:利用点到直线的距离公式设过点且与圆相切的切线的斜率为k,则所求切线方程为,即。
因为圆心O 的坐标为,半径,所以由点到直线的距离公式,得,解得。
所以切线方程,即,再结合图形知另一条切线方程为。
解6:利用斜率为k的圆的切线方程因为圆的方程为,所以,故根据圆的切线方程,得。
(1)因为点在切线上,所以。
解得,将k值代入(1)即得所求切线的方程为,再结合图形知另一条切线方程为。
解7:利用切线与圆只有一个公共点的性质设所求圆的切线方程为代入中,整理得。
(2)因为直线和圆相切,它们只有一个公共点,所以方程(2)有两相等实数根,所以,即,所以(3)又因为切线过点,所以由(1)得(4)解(3)、(4),得代入(1)得,再结合图形知另一条切线方程为。
解8:利用参数方程设所求切线的参数方程为(为参数,)(1)代入方程中,消去x、y,整理得。
因为直线和圆相切所以,即。
因为,所以。
过圆外一点作圆的切线的两种方法

过圆外一点作圆的切线是一个有趣且具有一定难度的几何问题。
在数学几何中,有两种方法可以用来找到过圆外一点作圆的切线,分别是几何构造法和解析几何法。
在本文中,我将探讨这两种方法,并对其进行全面评估,以帮助你深入理解这一概念。
1. 几何构造法几何构造法是通过几何图形的构造和推导来寻找问题的解。
在求解过圆外一点作圆的切线时,我们可以利用几何构造法来找到两种方法,即内切和外切。
我们来看内切的情况。
设圆的圆心为O,外点为P。
我们可以通过以下步骤来构造过外点P作圆的内切线:a. 以外点P为圆心,画一条与圆相切的直线L,相切点为T。
b. 连接PT,可得到过外点P作圆的内切线。
接下来,我们来看外切的情况。
同样假设圆的圆心为O,外点为P。
通过以下步骤可以构造过外点P作圆的外切线:a. 以外点P为圆心,画一条与圆相切的直线L,相切点为T。
b. 连接PT,可得到过外点P作圆的外切线。
通过几何构造法,我们可以清晰地看到过圆外一点作圆的内切线和外切线的构造过程,从而更好地理解这一概念。
2. 解析几何法解析几何法是通过坐标系和方程来寻找问题的解。
在求解过圆外一点作圆的切线时,我们同样可以利用解析几何法来找到两种方法。
设圆的方程为(x-a)²+(y-b)²=r²,外点P的坐标为(x₀, y₀)。
我们可以通过以下步骤来求解过外点P作圆的切线方程:a. 联立圆的方程和外点P到圆的距离公式,可得到切线方程。
b. 根据切线方程,可以求解出与圆相切的直线方程。
通过解析几何法,我们可以用数学的方式来推导出过圆外一点作圆的切线方程,从而更加深入地理解这一概念。
总结回顾通过本文的讨论,我们深入探讨了过圆外一点作圆的切线的两种方法,即几何构造法和解析几何法。
在几何构造法中,我们通过构造图形和推导过程来寻找切线;而在解析几何法中,我们通过坐标系和方程来求解切线方程。
这两种方法各有特点,可以帮助我们更全面、深刻地理解这一几何问题。
圆的切点弦方程的九种求法

圆的切点弦方程的解法探究在理解概念熟记公式的基础上,如何正确地多角度观察、分析问题,再运用所学知识解决问题,是解题的关键所在。
本文仅通过一个例题,圆的部分的基本题型之一,分别从不同角度进行观察,用不同的知识点和九种不同的解法,以达到介绍如何观察、分析、解决关于圆的切点弦的问题。
一、预备知识:1、在标准方程(x-a)2+(y-b)2=r2下过圆上一点P(x0,y0)的切线方程为:(x0-a ()x-a)+(y0-b)(y-b)=r2 ;在一般方程x2+y2+Dx+Ey+F=0 (D+E-4F>0)下过圆上一点P(x0,y0)的切线方程为: xx0+yy0+Dx+x0y+y0+E+F=0。
222222222、两相交圆x2+y2+D1x+E1y+F1=0 (D1+E1-4F1>0)与x2+y2+D2x+E2y+F2=0 (D2+E2-4F2>0)的公共弦所在的直线方程为:(D1-D2)x+(E1-E2)y+(F1-F2)=0 。
223、过圆x2+y2+Dx+Ey+F=0 (D+E-4F>0)外一点P(x1,y1)作圆的切线,其切线长公式为:|PA|=x12+y12+Dx1+Ey1+F。
224、过圆x+y+Dx+Ey+F=0 (D+E-4F>0)外一点22P(x1,y1)作圆的切线,切点弦AB所在直线的方程为:;(x1-a()x-a)+(y1-b)(y-b)=r2(在圆的标准方程下的形式)xx1+yy1+Dx+x1y+y1。
+E+F=0(在圆的一般方程下的形式)22二、题目已知圆x2+y2-2x-4y-4=0外一点P(-4,-1),过点P作圆的切线PA、PB,求过切点A、B的直线方程。
三、解法解法一:用判别式法求切线的斜率如图示1,设要求的切线的斜率为k(当切线的斜率存在时),那么过点P(-4,-1)的切线方程为:y-(-1)=k[x-(-4)]即 kx-y+4k-1=0 ⎧kx-y+4k-1=0由⎨2 消去y并整2⎩x+y-2x-4y-4=0理得 (1+k2)x2+(8k2-6k-2)x+(16k2-24k+1)=0 ①2222令∆=(8k-6k-2)-4(1+k)(16k-24k+1)=0 ②15解②得 k=0或k=81528分别代入①解得 x=1、x=- 8172858从而可得 A(-,)、B(1,-1), 1717再根据两点式方程得直线AB的方程为:5x+3y-2=0。
求圆的切线方程的几种方法

求圆的切线方程的几种方法切线是与曲线只有一个公共点且在该点处与曲线相切的直线。
对于圆来说,切线与圆只有一个公共点,并且在该点处切线垂直于半径。
在求圆的切线方程时,我们可以使用以下几种方法:1.隐式求解法:这是一种常见的方法,通过圆的方程和直线的一般方程,构建方程组并解方程组,求得切线方程。
设圆的方程为(x-a)^2+(y-b)^2=r^2,其中(a,b)为圆心坐标,r为半径。
直线的一般方程为Ax+By+C=0,其中A、B、C为常数。
将直线方程中的A、B、C代入圆的方程,得到带有未知数x和y的一元二次方程,解方程即可得到切点的坐标。
将切点的坐标代入直线的一般方程,可得到切线的方程。
2. 参数方程法:对于圆来说,可以使用参数方程表示。
圆的参数方程为x = a + r*cosθ,y = b + r*sinθ,其中(a,b)为圆心坐标,r为半径,θ为参数。
对参数方程求导,可得到切线的斜率。
以切点的坐标作为参数方程中的x和y的值,联立切线的斜率和切点坐标,可以得到切线的方程。
3.向切线方程法:设圆的方程为(x-a)^2+(y-b)^2=r^2,其中(a,b)为圆心,r为半径。
假设切线经过点P(x1,y1)与圆相切。
首先,计算该切点到圆心的距离,即为半径r。
然后,计算切线与圆心的连线的斜率,即为切线的斜率。
根据切点与切线的斜率和点斜式,可以得到切线的方程。
4.向圆心斜率法:设圆的方程为(x-a)^2+(y-b)^2=r^2,其中(a,b)为圆心坐标,r为半径。
切线的斜率等于切线与圆心连线的斜率的负倒数,即为圆心到切点连线的斜率的负倒数。
根据切点坐标和斜率,可以得到切线的方程。
这些方法是求解圆的切线方程的常用方法,选择何种方法取决于具体问题的要求和已知条件。
在实际应用中,可以根据具体情况选择最适合的方法。
三招求圆的切线方程

三招求圆的切线方程江西省永丰中学 吴全根求圆的切线方程主要分为已知切线的斜率k 或已知切线上一点两种情况,而已知切线上一点又可分为点在圆上和点在圆外两种情况,面对这几种情况各采用什么方法求圆的切线方程呢?下面教你三招。
一、公式法 可求过圆上一点的切线方程. 公式如下:① 过圆x 2+y 2= r 2上点P(x 0,y 0)的切线方程为x 0x+y 0y= r 2。
② 过圆(x —a)2+(y-b )2= r 2上点P(x 0,y 0)的切线方程为(x 0-a)(x —a)+(y 0-b)(y-b )= r 2.③ 过圆x 2+y 2+Dx+Ey+F=0上点P(x 0,y 0)的切线方程 x 0x+y 0y+D 20x x ++E 20y y ++F=0 。
点评:(1)公式②中当a=b=0时即为公式①.(2)上述公式是利用“圆的切线垂直过切点的半径”这一性质推导的,当切线的斜率不存在时公式也适用。
(3)当你忘记了这些公式,可利用公式推导方法求之.例1 求过点A (4,1)且与圆(x —2)2+(y+1)2=8 相切的切线方程。
解一:(公式法) (4-2)2 +(1+1)2=8 ∴ 点A (4,1)在圆上,∴ 圆的切线方程为(4-2)(x —2)+(1+1) (y+1)=8,即x+y-5=0.解二:(公式推导法) 圆心C (2,—1)∴k AC =1 ∴ 过点A 的切线的斜率k= —1.∴ 所求切线方程为y —1= —1(x — 4),即x+y-5=0。
二、待定系数法 可求过圆外一点P (x 0,y 0)的圆的切线方程或求已知切线的斜率k 的切线方程. 此时可设圆的切线方程为y-y 0=k (x —x 0)或y=kx+b,然后利用“圆心到直线的距离等于半径” 这一性质求k .例2 求过点M (2,4)向圆(x-1)2+(y+3)2=1所引的切线方程.解:设所求切线方程为y-4=k (x-2)即kx —y-2k+4=0 (倾斜角不为900), d=114232=++-+k k k ,∴k=724,∴切线方程为24x —7y-20=0。
圆的切线方程公式推导过程

圆切线方程公式推导过程
圆的切线方程公式推导过程如下:
1.设圆的标准方程为(x-a)X2}+(y-b)^{2}二d{2},其中(a,b)是圆心,r是半径。
2.设切线的斜率为k,则切线方程可以表示为y二kx+m o
3.将切线方程y=kx+m代入圆的方程(x-a)^{2}+(y-
b)λ{2}=r^{2},得到:(x-a)^{2}÷(kx+m-b)X2}=rX2}
4.展开并整理上述方程,得到:
(1+k{2})x{2}+2(km-b)x+11Γ⑵-2bm+/⑵-r^{2}=O
5.由于切线与圆只有一个交点,因此上述方程应该只有一个解,即判别式Delta应该等于0:
Delta=[2(km-b)]^{2}-4(1+k^{2})(m^{2}-2bm+b^{2}-
r^{2})=0
6.展开并整理上述方程,得到:
kX2}πΓ{2}-2kbm+b^{2}-kX2}πΓ⑵+2kbm-b^{2}+r^{2}二0
r^{2}=0
7.由于r^{2}显然不为0,因此上述方程可以简化为:
2kbm-2kbm=0
8.由于上述方程对所有的k和m都成立,因此我们可以得到切线的斜率k与圆的半径r、圆心(a,b)和切线在y轴上的截距
m无关。
9.最后,我们可以得到圆的切线方程为y=kx÷m,其中k是任意实数,m是切线在y轴上的截距。
由于切线与圆只有一个交点,因此m可以是任意实数。
求圆的切线方程的几种方法

求圆的切线方程的几种方法圆的切线方程是研究圆与直线的接触性质和切线的位置关系的基础,它在几何学和微积分等学科中具有重要的应用价值。
本文将介绍几种求解圆的切线方程的方法,包括几何法、代数法和向量法。
一、几何法几何法是最直观的方法,通过观察圆与切线的几何特点,即圆上的点到切线的距离等于圆心到切线的距离,可以得到切线方程。
以圆心为坐标原点O(r,r),半径为r的圆(r>0)为例,设圆上一点A(x1,y1)为切点,切线为l,过点A作圆心的垂直平分线交切线于点B(0,b)。
根据切线的性质,OB与OA平行,且OA与切线垂直,可以得到以下关系:1.切线的斜率等于OB的斜率:k1=(b-r)/0=∞,即切线的斜率不存在。
2.OA与切线的斜率的乘积等于-1:k1*k2=-1由于切线的斜率不存在,所以根据第2条关系可以求解k2,即切线的斜率。
将OA和切线之间的关系代入k1*k2=-1,可以得到:∞*k2=-1,即k2=0。
因此,切线的斜率为0,此时切线的方程为y=y1如此,根据切点的坐标和斜率为0即可得到切线的方程。
二、代数法代数法是一种基于圆和切线的方程性质的方法,通过构建圆的方程和切线的一般方程,利用解方程的方法求解交点,进而得到切线方程。
以圆心为坐标原点O(r,r),半径为r的圆(r>0)为例,设圆上一点A(x1,y1)为切点,切线为l。
首先,我们可以根据圆的定义得到圆的方程:(x-r)²+(y-r)²=r²然后,我们可以得到切线的一般方程:Ax+By+C=0由于切点(x1,y1)在切线上,所以我们可以得到切线的方程:Ax1+By1+C=0接下来,我们将圆的方程和切线的方程带入切线方程,即可得到两个方程:A(r-r)+B(r-r)+C=0Ax1+By1+C=0经过简化,可以得到C=-Ax1-By1,将其带入第一个方程可以得到A(r-r)+B(r-r)=0。
由于r≠r,所以我们得到A=0和B=0,即切线的方程为0x+0y-C=0,即y=C。
圆的切线公式大全总结

圆的切线公式大全总结
圆的切线是指与圆相切的直线,切线与圆的切点处于圆上的切线。
圆的切线公式如下:
1. 切线的斜率公式:
设圆的方程为(x-a)²+(y-b)²=r²,其中(a,b)为圆心坐标,r为半径,则切线的斜率k满足:
k = -(x-a)/(y-b)
2. 切线的方程公式:
设切线的斜率为k,切点坐标为(x0,y0),则切线的方程为:
y - y0 = k(x - x0)
3. 切线的长度公式:
设切线与圆的切点为P(x0,y0),圆心为O(a,b),切线的长度为L,则L满足:
L = √((x0-a)²+(y0-b)²) = √(r²-x0²-y0²+2ax0+2by0-a²-b²)
4. 外切线的判定:
如果一条直线与圆相切,且直线的直径等于圆的半径,则这条直线是圆的外切线。
5. 内切线的判定:
如果一条直线与圆相切,且直线通过圆的圆心,则这条直线是圆的内切线。
6. 公切线的判定:
如果两个圆相切,且这两个圆的切点与圆心连线共线,则这条连线为两个圆的公切线。
以上是一些常见的圆的切线公式和判定条件,可以帮助求解与圆相关的几何问题。
【高中数学】高中数学知识点:圆的切线方程

【高中数学】高中数学知识点:圆的切线方程
圆的切线方程:
1、已知圆
,
(1)若已知切点
在圆上,则切线只有一条,其方程是
;
(2)当
圆外时,
表示过两个切点的切点弦方程。
(3)过圆外一点的切线方程可设为
,再利用相切条件求k,这时必有两条切线。
(4)斜率为k的切线方程可设为y=kx+b,再利用相切条件求b,必有两条切线。
2、已知圆
,
(1)过圆上的
点的切线方程为
;
(2)斜率为k的圆的切线方程为。
圆的切线方程的求法:
①代数法:设出切线方程,利用切线与圆仅有一个交点,将直线方程代入圆的方程,从而△=0,可求解;
②几何法利用几何特征:圆心到切线的距离等于圆的半径,可求解.
过定点的圆的切线方程:
①过圆上一点的切线方程:
与圆
的切线方程是
与圆
的切线方程是
与圆
的切线方程是
与圆
的切线方程是
②过圆外一点的切线方程:设
外一点,求过P
点的圆的切线.
方法l:设切点是
,解方程组
求出切点P
1
的坐标,即可写出切线方程。
方法2:设切线方程是
,再由
求出待定系数k,就可写出切线方程.
特别提醒:一般说来,方法2比较简便,但应注意,可能遗漏k不存在的切线.因此,当解出的k值唯一时,应观察图形,看是否有垂直于x轴的切线.
感谢您的阅读,祝您生活愉快。
高中数学求过圆上的一点(x0,y0)的切线方程的方法

代数法
当斜率存在时,设为k,则切线方程为y-y0=k(x-x0),即y=kx-kx0+y0,代入圆的方程,得到一个关于x的一元二次方程,由Δ=0,求得k,切线方程即可求出
[提醒]当点(x0,y0)在圆外时,一定要注意斜率不存在的情况.
高中数学求过圆上的一点(x0,y0)的切线方程的方法
先求切点与圆心连线的斜率k,若k不存在,则结合图形可直接写出切线方程为y=y0;若k=0,则结合图形可直接写出切线方程为x=x0;若k存在且k≠0,则由垂直关系知切线的斜率为- ,由点斜式可写出切线方程.
求过圆外一点(x0,y0)的圆的切线方程的2种方法
如何求圆的切线方程

如何求圆的切线方程圆的切线方程是指切点在圆上,与圆的切线相切的直线方程。
求圆的切线方程可以使用两种方法:一种是几何法,一种是解析几何法。
下面我将详细介绍这两种方法。
一、几何法:1.切点坐标的确定:设圆的方程为x^2+y^2=r^2,其中圆心坐标为(a,b),切点坐标为(x0,y0)。
首先,我们需要找到切线过圆的切点坐标。
切点坐标的确定有多种方法,其中一种常用方法是使用相似三角形:a)过切点(x0,y0)作圆的半径的垂直向量,与x轴的夹角为θ1,与y轴的夹角为θ2b)设此向量的x轴分量为r*cosθ1,y轴分量为r*sinθ2c)由于切线与半径垂直,切线的斜率为-k,其中k为半径的斜率,k=tanθ1=tan(π/2-θ2)=-cotθ2d)则切线的斜截式方程为:y-y0=-k(x-x0)y=y0-k(x-x0)2.斜率的确定:接下来,我们需要确定切线的斜率k。
a)过切点(x0,y0)作圆的切线,与$x^2+y^2=r^2$的导数成正交关系。
求导并求导数的负倒数可以得到斜率:k=(dy/dx)=-x0/y0b)根据切点坐标的确定部分,我们可以将切线的斜率表示为:k=-cotθ2=-x0/y03.切线方程的确定:根据斜截式方程以及确定切点坐标的部分,我们可以得到切线方程的最终形式:y=y0-x0/y0(x-x0)二、解析几何法:使用解析几何法,我们可以根据给定的圆的方程以及切点坐标的确定方法来求解切线方程。
1.切点坐标的确定:根据几何法中的部分,我们可以确定切点的坐标。
2.切线斜率的确定:根据几何法中的部分,我们可以确定切线的斜率。
3.切线方程的确定:使用点斜式,我们可以得到切线方程的最终形式。
y-y0=-k(x-x0)y=y0-k(x-x0)需要注意的是,如果圆的方程不是以原点为圆心,可以通过平移变换将其变换到以原点为圆心的方程形式。
然后使用上述方法求解切线方程。
希望上述内容对于你理解如何求圆的切线方程有所帮助。
求圆的切线方程公式

求圆的切线方程公式
1. 圆的切线方程公式:
(1)定义:
圆的切线是切圆的一条直线,它也称作某点圆上的切线或某点垂切线,可以当作圆的零级曲线,是由该点的切点确定的直线,其切线公式方程可以用中心式表示出来。
(2)公式:
令C(x_0,y_0)为圆的圆心,令P(x,y)为圆上任意一点,则围绕C(x_0,y_0)由P(x,y)形成的圆的切线方程可以表示为:
y - y_0 = ±(1 + (x - x_0)^2 ÷ x^2 -
2x_0x+x_0^2 )^(1/2)
上式中,当±号取“+”时,是切线A(x,y)所在直线的方程;
当±号取“-”时,是切线B(x,y)所在直线的方程。
2. 例子:
以一个圆C(-1,1)为例,P(2,1)是C圆上任意一点,则圆C(-1,1)上P(2,1)点的切线方程是:
y - 1 = ±√(1+(x+1)²÷4-2x-2+1)
令±号取“+”,得:
y - 1 = √(1+(x+1)²÷4-2x-2+1)
令±号取“-”,得:
y - 1 = -√(1+(x+1)²÷4-2x-2+1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 /
2 求圆的切线方程的几种方法
四川省冕宁中学 谢玉
在高中数学人教版第二册第七章《圆的方程》一节中有一例题:求过已知圆上一点的切线方程,除了用斜率和向量的方法之外还有几种方法,现将这些方法归纳整理,以供参考。
例:已知圆的方程是x 2 + y 2 = r 2,求经过圆上一点M(x0,y 0)的切线的方程。
解法一:利用斜率求解
同样适用。
在坐标轴上时上面方程当点所求的直线方程为:在圆上,所以因为点整理得的切线方程是:经过点,则,设切线的斜率为如图M .
.
.
)(,.112002202020200000
000
00r y y x x r y x M y x y y x x x x y x y y M y x k x y k k k k OM OM =+=++=+--=--=∴=-=⋅ 解法二:利用向量求解
()
.
..
)(0
PM OM )
,(PM ),,OM PM OM ,p 22002202020200000000000r y y x x r y x M y x y y x x y y y x x x y y x x y x y x =+=++=+=-⨯+-⨯∴=•∴--==⊥所求的直线方程为:在圆上,所以因为点整理得:)((,∵的坐标,设切线上的任意一点如图
(这种方法的优点在于不用考虑直线的斜率存不存在)
解法三:利用几何特征求解
用。
重合时上面方程同样适和当所求的直线方程为:在圆上,所以因为点整理得:∵的一点,设直线上不同于如图M P r y y x x r y x M y x y y x x y x y y x x y x OP PM OM PM
OM y x P y x M .
..
)()()
,(),(2200220202020002
220
2020202
2200=+=++=++=-+-++∴=+∴⊥
解法四:用待定系数法求解
图1
图2
2 / 2 1、 利用点到直线的距离求解
程同样适用。
当斜率不存在时上面方所求的直线方程为:在圆上,所以因为点整理得 代入⑴式解得:所以⑵式可化为:因为 ⑵
化简整理得:
到切线的距离等于半径
原点 ⑴
即:则直线方程为:
为设所求直线方程的斜率.
.
.
202)(1)0,0(O 0),(,200220202020000020002202
2
02020200220220
00000r y y x x r y x M y x y y x x y x k x k y x k y r y x y r k y x k x r r k kx y kx y y kx x x k y y k =+=++=+-==++=+=-++-=+-=-+--=-
2、 利用直线与圆的位置关系求解:
程同样适用。
当斜率不存在时上面方所求的直线方程为:在圆上,所以因为点整理得 代入⑴式解得:所以⑵式可化为:因为 ⑵
整理得:得 消去 由)
(即:则直线方程为:
为设所求直线方程的斜率..
.
202)(0
)2)(1(4)(40
2)(2)1(010),(,200220202020000020002202
202020200220220020220220022002
02200022222000000r y y x x r y x M y x y y x x y x k x k y x k y r y x y r k y x k x r r x ky x k y k kx y k r x ky x k y x kx y k x k y r y x kx y y kx kx y y kx x x k y y k =+=++=+-==++=+=-++-=--++--=∆=--++-++⎩
⎨⎧=+=-+-=-+--=-
这是圆心在坐标原点的圆的切线方程的求法,若圆心不在原点,也可以用这些方法求解。
同样一道题,思路不同,方法不同,难易程度不同。
显然在以上的几种解法中,用向量法和几何特征求解相对来说简单一些。
实际上在圆这一章,很多时候用几何特征求解圆的方程和直线方程是教简单的方法,同学们下来可以尝试。
