石油大学大专2019《线性代数(文)》第2阶段在线作业

合集下载

(完整word版)线性代数习题集(带答案)

第一部分专项同步练习第一章行列式一、单项选择题1．下列排列是5阶偶排列的是 ( ）.（A) 24315 （B) 14325 （C ） 41523 (D)24351 2．如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是（）. (A ）k (B ）k n - （C)k n -2! （D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( ）项。

(A) 0 （B ）2-n （C ） )!2(-n (D) )!1(-n4．=0001001001001000( ）。

(A ） 0 (B)1- (C) 1 （D) 25. =0001100000100100( ）.(A) 0 (B)1- (C ） 1 (D) 26．在函数100323211112)(x x x x x f ----=中3x 项的系数是( ）.(A) 0 （B ）1- (C) 1 （D) 27。

若21333231232221131211==a a a a a a a a a D ，则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ）. (A ） 4 (B) 4- (C) 2 （D ） 2-8．若a a a a a =22211211，则=21112212ka a ka a ( ）。

（A)ka (B)ka - (C ）a k 2 (D)a k 2-9．已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-，则=x （ )。

（A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ). (A ）1- (B ）2- (C ）3- （D ）011. 若2235001011110403--=D ，则D 中第四行元的余子式的和为( ）。

中国地质大学远程与继续教育学院线性代数(专升本)阶段性作业2.docx

中国地质大学远程与继续教育学院线性代数（专升本）阶段性作业2单选题则下列运算没有意义的是.（6 分）(A): (?+(酬(B):(C):(D): AC:参考答案：D2.设.是「1矩阵-「，二是一「矩阵，则下列方阵.（6分）(A): AB(B): A r B r(C): B T A T(D):（硼参考答案：B3.设■' _都是〔阶方阵，则必有.（6分）(A):(B): AB = BA(C): |外1.设「是：1矩阵，二是」「矩阵，■是「矩阵,的运算结果是二阶(D):- --参考答案：C4. 下列命题中，正确的是_____ .(6分)(A):- -(B):若，则川W团(C):设「'是三角矩阵，则- 二也是三角矩阵(D)：:-一：-一： _ 一参考答案：D5. 设「'都是匚阶矩阵，AB-^，则必有__________ .(6分)(A) -去-〔：(B) : .1 一(C) :同或昨°(D):参考答案：C6. __________________________________________ 设丄B都是"阶方阵，下列结论正确的是_______________________________________ .(6分)(A) :若二「均可逆，贝U…二可逆(B) :若-；-均可逆，则A 可逆(C) :若-；-可逆，贝U广；一打可逆(D) :若-；-可逆，贝U二「均可逆参考答案：B7•设"阶方阵满足关系式」BC = E ,则必有.(6分)(A) :二1」二二(B) : I 二二二二(C) :二一二二(D) :二'.1 二二参考答案：D8. _________________________________________________________________ 设』月C均为"阶方阵，若B二E + 1B , C-A+CA则B-C =____________________ .(6分)(A) :-(B) : _】(C) :…(D) : 一-：参考答案：A(a b眄A- b a b\9. __________________________________________________________ 设三阶矩阵e 0 口丿，若』的伴随矩阵的秩为i，则必有____________________________ .(6分)(A) 沁］勺或=(B) :二-或一亠「(C) : 一：「且一」■'(D) :一•-一且.■：■：'：■仁.-.参考答案：B7•设"阶方阵满足关系式」BC = E ,则必有.(6分)参考答案：Cfl 210]3 -1 0 210. 矩阵1一1『一】-一二丿的秩为2，贝叮= ___ .(6分)(A) 3(B) 4(C) 5(D) 6参考答案：D11. 设二_都是•：阶非零矩阵，且贝U ：-的秩_______ .(6分)(A) :必有一个等于零(B) :都小于(C) : 一个小于，一个等于(D) :都等于参考答案：B12. 下列矩阵中， _____ 不是初等矩阵.(6分)(0 0 1)0 10(A) : U °°(°冷(B) :b 0 0丿fl 0 0A』3 0(C) : 01,fl 0 0A0 10(D) : b 0 1 丿彷1处口13厂a2l兔、S 1 (fA =B =如氐 1 0 013.设Si乐禺丿1Sl +坷1 ^32给 + 如/1, 1(0 0 1?fl 0 0、PL Q i oJ ° 1丿，则必有________ .(6分)(A):(B) :(D) : ■■--参考答案：C14. 设…为3阶矩阵，将…的第2行加到第1行得Y ,再将匸的第1列的】倍加到第(11 0、P= 0 1 02列得C,记卩0 1丿，则_____________ .(6分)(A) :- 一(B) :(C) : - - -z(D) :-参考答案：B15. 设-为3阶矩阵，将…的第1列与第2列交换得匸，再将二的第2列加到第3列得C ，则满足丿0二c 的可逆矩阵0为 ________ .(6分)ro i o]1 o o(A) : I 】0 1 一(0 1 0： (1 0 1(B) : I 。

中国石油大学高等数学(二)在线作业1-3

第7题
B
在线作业一答案
CCDCC BDBDD DCBCB CDCAC EBBCD DCAAB 错错对错错错对错错对
第二次在线作业
第1题
第2题
第3题
第4题
第5题
第6题
第7题
第8题
第9题
第10题
第11题
第12题
第13题
第14题
第15题
第16题
第17题
第18题
第19题
第20题
第21题
第22题
第23题
第24题
第25题
第26题
第27题
第28题
第29题
第30题
第31题
第32题
第33题
第34题
第35题
第36题
第37题
第38题
第39题
第40题
DCDCC BDCAB BACBC DACBC ABCAA BADCB 对错对错错对错错对对
第三次在线作业
第1题
第2题
第3题
第4题
第5题
第6题
第7题
第8题
第10题
第11题
第12题
第13题
第15题
第16题
第17题
第18题
第19题
第20题
第21题
第22题
第23题
第24题
第25题
第26题
第27题
第28题
第29题
第30题
第31题
第32题
第33题
第34题
第35题
第36题
第37题
第38题
第39题
40题
DABCB CCCBD BDABA BBACD BDABD BADDA 对错对对错对对错错对。

西安石油大学线代试题

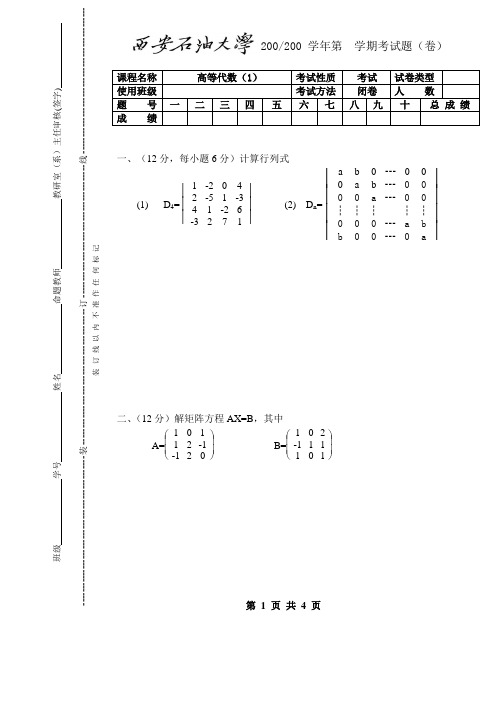
第 1 页共 4 页课程名称高等代数（1）考试性质考试试卷类型使用班级考试方法闭卷人数题号一二三四五六七八九十总成绩成绩一、（12分，每小题6分）计算行列式(1) D 4=⎪⎪⎪⎪⎪⎪1-2042-51-341-26-3271(2) D n=⎪⎪⎪⎪⎪⎪⎪⎪a b 0┅000a b ┅0000a ┅00┆┆┆┆┆000┅a b b 00┅0a二、（12分）解矩阵方程AX=B ，其中A=⎝ ⎛⎭⎪⎪⎫10112-1-120 B=⎝ ⎛⎭⎪⎪⎫102-111101班级学号姓名命题教师教研室（系）主任审核(签字)---------------------------------------------装-----------------------------------------订----------------------------------------线-------------------------------------------- 装订线以内不准作任何标记200/200 学年第学期考试题（卷）第 2 页共 4 页三、（12分）讨论a,b 取什么值时下面的线性方程组无解，有惟一解，有无穷多解？⎩⎪⎨⎪⎧x 1+x 2-x 3=2x 1+2x 2+x 3=3x 1+x 2+(a 2-5)x 3=b四、（12分）判别向量组α1=(0,0,2,3), α2=(1,2,3,4)，α3=(1,2,1,1)，α4=(1,0,1,0)是否线性相关，并求α1, α2, α3, α4的一个极大线性无关组．五、（12分）判别下列方程组是否有解，若有解，求出其通解．⎩⎪⎨⎪⎧2x 1+x 2-x 3+x 4=14x 1+2x 2-2x 3+x 4=22x 1+x 2-x 3-x 4=1第 3 页共 4 页六、（12分）求下面实二次型的正惯性指数和负惯性指数．f(x 1, x 2,x 3)= x 12+4x 1 x 2+2 x 1x 3+4x 22+4 x 2 x 3+3x 32 七、（14分，每小题7分）证明题（1）设B 是一个m ⨯r 矩阵,C 是一个r ⨯t 矩阵，rank(B)=r ，证明：如果BC=0,则C=0．（2）证明：rank((A,B))≤rank(A)+rank(B)．八、（14分，每小题7分）简答题（1）所有偶数所成的数集能否构成一个数域？所有奇数呢？说明理由．（2）简述n维向量组的“秩”与n维向量子空间的“维数”这两个概念的区别与联系．第 4 页共 4 页。

中国石油大学马克思主义基本原理第二阶段在线作业答案

1.（分）哲学的基本问题是•A、社会和自然的关系问题•B、思维和存在的关系问题•C、政治和经济的关系问题•D、理论和实践的关系问题我的答案：B 此题得分：分2.（分）“存在就是被感知”是•A、机械唯物主义观点•B、客观唯心主义观点•C、朴素唯物主义观点•D、主观唯心主义观点我的答案：D 此题得分：分3.（分）物质的唯一特性是它的•A、实物性•B、可知性•C、客观实在性•D、运动的绝对性我的答案：C 此题得分：分4.（分）机不可失，失不再来”可以说明•A、时间的连续性•B、空间的三维性•C、物质的客观性•D、时间的一维性我的答案：D 此题得分：分5.（分）哲学上的二元论是•A、唯物主义的一种形式•B、唯心主义的一种形式•C、超越于唯物主义和唯心主义的独立派别•D、主张物质和精神是两个相互独立的世界本原的哲学我的答案：D 此题得分：分6.（分）对立统一规律揭示了•A、事物发展的动力的源泉•B、事物发展的状态和过程•C、事物发展的方向和道路•D、事物发展的两种趋向我的答案：A 此题得分：分7.（分）事物的性质主要是由•A、矛盾的主要方面决定的•B、主要矛盾决定的•C、矛盾的普遍性决定的•D、矛盾的同一性决定的我的答案：A 此题得分：分8.（分）矛盾斗争的基本形式是•A、教育和惩罚•B、民主和专政•C、对抗和非对抗•D、同一性和斗争性我的答案：C 此题得分：分9.（分）矛盾的普遍性和特殊性的关系是•A、整体和部分的关系•B、运动和静止的关系•C、抽象和具体的关系•D、共性和个性的关系我的答案：D 此题得分：分10.（分）下列说法中属于矛盾的同一性含义的是•A、矛盾双方相互排斥和否定•B、矛盾双方相互依存和转化•C、矛盾双方相互对立和斗争•D、矛盾双方相互离异和冲突我的答案：B 此题得分：分11.（分）“沉舟侧畔千帆过，病树前头万木春”。

“芳林新叶摧陈叶，流水前波让后波”。

这两句诗包含的哲学道理是（）•A、矛盾是事物发展的动力•B、事物是本质和现象的统一•C、事物的发展是量变和质变的统一•D、新事物代替旧事物是事物发展的总趋势我的答案：D 此题得分：分12.（分）对不可知论最有力的驳斥是•A、客观真理•B、客观事实•C、客观规律•D、社会实践13.（分）真理是指•A、客观事物及其规律性•B、人们对客观事物及其规律性的正确认识•C、对人们有用的理论•D、先进阶级的进步观点我的答案：B 此题得分：分14.（分）绝对真理(真理的绝对性)和相对真理(真理的相对性)的关系是•A、两种性质不同的真理•B、真理的两种不同属性•C、真理的两种不同形式•D、真理的两个不同阶段我的答案：B 此题得分：分15.（分）“真理可以变成谬误，谬误也可以变成真理”，这是因为•A、真理和谬误没有确定的界限•B、真理是具体的有条件的，有一定的适用范围•C、真理和谬误的区别具有主观随意性•D、真理本身具有阶级性我的答案：B 此题得分：分16.（分）商品经济产生和存在的决定性条件是•A、社会分工•B、机器的出现•C、生产资料和产品属于不同所有者•D、货币的使用17.（分）在历史上，资本的最原始形式是•A、产业资本•B、商人资本•C、工业资本•D、可变资本我的答案：B 此题得分：分18.（分）商品价值量与劳动生产率的关系是•A、劳动生产率提高时价值量不变•B、劳动生产率降低时价值量不变•C、价值量同劳动生产率成反比•D、价值量同劳动生产率正比我的答案：C 此题得分：分19.（分）某资本家经营的企业通过改进技术、提高劳动生产率．使其生产商品花费的劳动时间比社会必要劳动时间少10％，由此形成商品个别价值低于社会价值的那部分是：( )•A、超额剩余价值•B、绝对剩余价值•C、相对剩余价值•D、剩余价值我的答案：A 此题得分：分20.（分）资本积聚和资本集中的区别在于，资本积聚的结果本身会使•A、社会资本总额增加•B、个别资本规律扩大•C、剩余价值数量增加•D、资本有机构成提高我的答案：A 此题得分：分21.（分）垄断的形成是•A、生产集中发展到一定阶段的结果•B、生产输出的结果•C、金融资本统治的结果•D、国家干预经济生活的结果我的答案：A 此题得分：分22.（分）垄断资本主义国家事实上的主宰者是•A、银行资本家•B、工业资本家•C、金融寡头•D、商业资本家我的答案：C 此题得分：分23.（分）金融寡头在经济上的统治主要是通过( )实现的•A、参与制•B、个人联合•C、建立政策研究咨询机构对政府施加影响•D、掌握舆论工具控制新闻媒介我的答案：A 此题得分：分24.（分）国家垄断资本主义是•A、国家政权与垄断资本相结合的垄断资本主义•B、国家政权与垄断资本相分离的垄断资本主义•C、消除了生产无政府状态的垄断资本主义•D、解决了资本主义基本矛盾的垄断资本主义我的答案：A 此题得分：分25.（分）第二次世界大战后，出现了一种新型的国际垄断组织•A、跨国公司•B、国际卡特尔•C、国际辛迪加•D、国际托拉斯我的答案：A 此题得分：分26.（分）生产力范畴反映了物质资料生产中•A、人与自然之间的关系•B、人与人之间的关系•C、人与生产资料之间的关系•D、人与劳动资料之间的关系我的答案：A 此题得分：分27.（分）生产力中的主导性要素是•A、劳动者•B、劳动资料•C、劳动对象•D、科学技术我的答案：A 此题得分：分28.（分）社会历史观的基本问题是•A、唯物史观与唯心史观的关系问题•B、历史主体与历史客体的关系问题•C、社会发展规律与社会发展动力的关系问题•D、社会存在与社会意识的关系问题我的答案：D 此题得分：分29.（分）社会意识相对独立性的最突出的表现是•A、社会意识的发展变化有自己的历史继承性•B、社会意识的发展变化与社会存在的发展变化具有不完全同步性•C、社会意识的发展水平与社会经济的发展水平具有不完全平衡性•D、社会意识对社会存在有反作用我的答案：D 此题得分：分30.（分）社会形态是•A、经济基础与上层建筑的统一•B、政治上层建筑与思想上层建筑的统一•C、政治法律制度与政治法律设施的统一•D、社会存在与社会意识的统一我的答案：A 此题得分：分31.（分）关于历史发展的动力，下列选项中表述错误的是•A、社会基本矛盾是社会发展的根本动力•B、阶级斗争是社会发展的直接动力•C、人民群众是历史的创造者•D、革命是历史的火车头我的答案：B 此题得分：分32.（分）关于社会形态演化的次序，正确的选项是•A、奴隶社会、原始社会、资本主义社会、社会主义及共产主义社会•B、奴隶社会、封建社会、资本主义社会、社会主义及共产主义社会•C、原始社会、奴隶社会、封建社会、资本主义社会、社会主义及共产主义社会•D、原始社会、奴隶社会、资本主义社会、封建社会、社会主义及共产主义社会我的答案：C 此题得分：分判断题(共8道题)收起33.（分）唯物主义是可知论，唯心主义是不可知论。

石大成人教育《线性代数(文)》期末考试复习题及参考答案

《线性代数（文）》课程综合复习资料一、填空题1．排列623451的逆序数为。

2．行列式2413635104D -=-=- 。

3．矩阵 12120000,000n n a a A a a a a ⋅⋅⋅⎛⎫ ⎪⋅⋅⋅ ⎪=⋅⋅⋅≠ ⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⎪⋅⋅⋅⎝⎭，则1A -= 。

4．设有矩阵2424,3612A B -⎛⎫⎛⎫== ⎪ ⎪---⎝⎭⎝⎭，则AB = 。

5．设有矩阵方程 AXB C =，其中A ,B 为可逆矩阵，则X = 。

6．若2-是三阶矩阵A 的特征值，则行列式|2|A E += 。

7．行列式1111211kD k -=-=-。

8．设矩阵110230003A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，则1A -=。

9．A 为 m n ⨯矩阵，齐次线性方程组0AX =仅有零解的充分必要条件是A 的列向量组是线性关的。

10．设矩阵 1201A ⎛⎫= ⎪⎝⎭，则k A =。

11. 向量组123139206317ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭，，一定是线性关的。

12．设有向量⎪⎪⎪⎭⎫ ⎝⎛-=121α，则α的长度为。

二、单项选择题1. 排列4123的逆序数为（）。

A ）1B ）2C ）3D ）42．设A, B 皆为n 阶矩阵，则必有 ( )。

A) A B A B +=+ B) AB BA = C) AB BA = D) 111()A B A B ---+=+3. 若矩阵111121231λ⎛⎫⎪ ⎪ ⎪+⎝⎭的秩为2，则λ= ( )。

A ）0B ）1C ）2D ）34．向量组1(1,1,1)α=，2(1,1,0)α=，3(0,0,1)α=的一个最大无关组为（）。

A ）1α； B ）2α； C ）12,αα； D ）123,,ααα5．三阶矩阵110110002A -⎛⎫⎪=- ⎪ ⎪-⎝⎭的特征值为（）。

A ）0, 2, 2-；B ）0, 2, 2；C ）0, 1, 1-；D ）0, 1, 16．若A 是n 阶正交矩阵，则有（）。

线性代数2019年4月自学考试试题+答案

2019年4月高等教育自学考试全国统一命题考试线性代数（课程代码02198）说明：在本卷中，A T表示矩阵A 的转置矩阵，A *表示矩阵A 的伴随矩阵，E 是单位矩阵，|A|表示方阵A 的行列式，r （A ）表示矩阵A 的秩。

第一部分选择题一、单项选择题：本大题共5小题，每小题2分，共10分。

在每小题列出的备选项中只有一项是最符合题目要求的，请将其选出。

1.设行列式k b b a a =2121，则=2121362b b a aA.KB.2KC.3KD.6k2.设A 为2阶矩阵，将A 的第1行与第2行互换得到矩阵B ，再将B 的第2行加到第1行得到单位矩阵，则A -1=A.⎪⎪⎭⎫ ⎝⎛0111 B ⎪⎪⎭⎫⎝⎛1011 C.⎪⎪⎭⎫⎝⎛1110 D.⎪⎪⎭⎫⎝⎛1101 3.设向量B=（2，1，b ）T可由向量组1α=（1，1.1）T，2α=（2，3,a ）T线性表出，则数a.b 满足关系式A.a-b=4B.a+b=4C.a-b=0D.a+b=04.设齐次线性方程组⎪⎩⎪⎨⎧=+-=++=++0002321321321x x x x x kx x x x 有非零解。

则数k 是=A.-2B.-1C.1D.25.设3阶实对称矩阵A 的秩为2，则A 的非零特征值个数为 A.0B.1C.2D.3第二部分非选择题二、填空题：本大题共10小题，每小题2分，共20分。

6.行列式702523300= .7.已知行列式111302c b a=1，则=-+-111111302c b a . 8.=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛102010001333231232221131211a a a a a a a a a .9.设矩阵A=⎪⎪⎭⎫⎝⎛-2022,若B=A 2-2A+E ，则B= . 10.设向量组α1=（1，l ，a ）T，α2=（1，a ，1）T，α3=（a ，1，1）T的秩为2，则数a= .11.设向量α=（1，l ）T，B=（1，-2）T，（α，β）表示α与β的内积，则β-()()=αααβα，， .12.设4元非齐次线性方程组Ax=b 的增广矩阵经初等行变换化为（A ，b ）→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----0000120011200011a 若该线性方程组有惟一解，则数a 的取值应满足 .13.设A 为n 阶矩阵，若非齐次线性方程组Ax=b 有无穷多解，则|A|= . 14.设A 为n 阶矩阵，且满足|3A+2E|=0，则A 必有一个特征值为 . 15.二次型f （x 1，x 2，x 3）=（x 1一x 2)2-（x 2+x 3)2的矩阵A= . 三、计算题：本大题共7小题，每小题9分，共63分。

线性代数(经济数学2)-习题集(含答案)

《线性代数(经济数学2）》课程习题集一、计算题11. 设三阶行列式为231021101--=D 求余子式M 11，M 12，M 13及代数余子式A 11，A 12，A 13．2. 用范德蒙行列式计算4阶行列式12534327641549916573411114--=D3. 求解下列线性方程组：⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++---1111322112132222111321211n n n n n n n n n x a x a x a x x a x a x a x x a x a x a x其中 ),,2,1,,(n j i j i a a j i =≠≠4. 问λ, μ取何值时, 齐次线性方程组1231231230020x x x x x x x x x λμμ++=⎧⎪++=⎨⎪++=⎩有非零解？5. 问λ取何值时, 齐次线性方程组123123123(1)2402(3)0(1)0x x x x x x x x x λλλ--+=⎧⎪+-+=⎨⎪++-=⎩有非零解？二、计算题26. 计算6142302151032121----=D 的值。

7. 计算行列式5241421318320521------=D 的值。

8. 计算0111101111011110=D 的值。

9. 计算行列式199119921993199419951996199719981999的值。

10. 计算4124120210520117的值。

11. 求满足下列等式的矩阵X 。

2114332X 311113---⎛⎫⎛⎫-=⎪ ⎪----⎝⎭⎝⎭12. A 为任一方阵，证明T A A +，T AA 均为对称阵。

13. 设矩阵⎪⎪⎭⎫⎝⎛-=212321A ⎪⎪⎪⎭⎫⎝⎛-=103110021B 求AB ．14. 已知⎪⎪⎭⎫⎝⎛--=121311A ⎪⎪⎪⎭⎫ ⎝⎛--=212211033211B 求T )(AB 和T T A B15. 用初等变换法解矩阵方程 AX =B 其中⎪⎪⎪⎭⎫ ⎝⎛--=011220111A ⎪⎪⎪⎭⎫⎝⎛-=121111B16. 设矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛--=2100430000350023A求1-A17. 求⎪⎪⎪⎭⎫⎝⎛=311121111A 的逆。

2019-2020学年线性代数期末考试题(含答案)

线性代数2019－2020学年第二学期期末考试试卷一、填空题（本大题共5个小题，每小题3分，共15分。

）1. 行列式11111111---x 的展开式中x 的系数是_________；2. 已知3阶矩阵A 的特征值为0，1，2，则=+-E A A 752__________；3. 向量组)0,0,1(),1,1,1(),1,1,0(),1,0,0(4321====αααα的秩为______；4. 设⎪⎪⎪⎭⎫ ⎝⎛-=12032211t A ，若3阶非零方阵B 满足0=AB ，则=t ；5. 设3阶可逆方阵A 有特征值2，则方阵12)(-A 有一个特征值为_________。

二、单项选择题（从下列各题四个备选答案中选出一个正确答案，并将其代号写在答题纸相应位置处。

答案错选或未选者，该题不得分。

每小题3分，共15分。

） 1. A 是n 阶方阵，*A 是其伴随矩阵，则下列结论错误的是【】A .若A 是可逆矩阵，则*A 也是可逆矩阵；B .若A 不是可逆矩阵，则*A 也不是可逆矩阵；C .若0||*≠A ，则A 是可逆矩阵；D .AE AA =||*。

2. 设⎪⎪⎪⎭⎫ ⎝⎛=333222111c b a c b a c b a A ，若⎪⎪⎪⎭⎫ ⎝⎛=333222111b c a b c a b c a AP ，则P =【】 A . ⎪⎪⎪⎭⎫ ⎝⎛010100001； B . ⎪⎪⎪⎭⎫ ⎝⎛010001100；C . ⎪⎪⎪⎭⎫ ⎝⎛001010100；D . ⎪⎪⎪⎭⎫ ⎝⎛010100000.3. n m >是n 维向量组m ααα,,,21 线性相关的【】.A 充分条件 .B 必要条件.C 充分必要条件 .D 必要而不充分条件4．设321,,ααα是0=Ax 的基础解系，则该方程组的基础解系还可以表示为【】A ．321,,ααα的一个等价向量组；B. 321,,ααα的一个等秩向量组；C. 321221,,αααααα+++；D . 133221,,αααααα---.5. s ααα,,,21 是齐次线性方程组0=AX (A 为n m ⨯矩阵)的基础解系，则=)(A R 【】A ．sB ．s n -C ．s m -D ．s n m -+三、计算题（要求在答题纸相应位置上写出详细计算步骤及结果。

石大在线《线性代数(文)》第一阶段在线作业(自测)答案

Biblioteka 8．第8题单选题()
A、a-1 B、-a-1 C、1-a D、a 1
标准答案：A
您的答案：
题目分数：10
此题得分：0.0
批注：
9．第9题单选题矩阵
的秩等于(
)
A、0 B、1 C、2 D、3
标准答案：D
您的答案：
mhtml:file://D:\用户数据\win8\Desktop\线性代数\《线性代数(文)》第一阶段在线作... 2013/5/9
标准答案：C
您的答案：
题目分数：10 此题得分：0.0 批注：
mhtml:file://D:\用户数据\win8\Desktop\线性代数\《线性代数(文)》第一阶段在线作... 2013/5/9
试题
页码，2/3
5．第5题单选题下列排列中是奇排列的是(
)
A、4321 B、1234 C、2314 D、4123
3．第3题单选题
4阶行列式D，其第3列的元素分别为1, 2, 3, 4.它们的余子式分别为4，3，2，1，
则行列式D = （
）
A、0
B、1
C、-1
D、2
标准答案：A
您的答案：
题目分数：10
此题得分：0.0
批注：
4．第4题单选题若
,则必有(
).
A、k=-1 B、k=3 C、k=-1或k=3 D、k≠-1且k≠3
试题
此题得分：0.0 批注：
10．第10题单选题若A是4阶方阵,|A|=2则|2A|=（
）
A、4 B、8 C、16 D、32
标准答案：D
您的答案：
题目分数：10
此题得分：0.0

中国石油大学安全系统工程第2阶段在线作业答案

中国石油大学平安系统工程在线作业第二阶段答案第1题采取举措使一个最小径集当中的所有事件都不发生,那么顶事件您的答案：B题目分数：0.5此题得分：0.0批注：最小径集的定义第2题事件树分析法与事故树分析法采用〔〕逻辑分析方法您的答案：B题目分数：0.5此题得分：0.5批注：事件树分析法与事故树分析法的分析原理第3题逻辑门是连接各事件并表示其逻辑关系的符号, 其中,表示输入事件中至少有一个发生,在满足条件A的情况下输出事件才发生的是您的答案：A题目分数：0.5此题得分：0.5批注：条件或门的定义第4题绘制事故事故时,事件B1与B2有一个发生,事件A就发生,那么应使用〔〕门来表示三者的逻辑关系您的答案：C题目分数：0.5此题得分：0.5批注：或门的定义第5题以下关于“事故树分析法〞正确的有您的答案：A题目分数：0.5此题得分：0.5批注：割集、最小割集、径集、最小径集的定义第6题系统寿命周期内开发研制阶段适合的平安分析方法为〔〕您的答案：C此题得分：0.5批注：只有预先危险性分析法适用于开发研制第7题在事故树中,导致其他事故发生、只是某个逻辑门的输入事件而不是任何逻辑门的输出事件的事件,称为您的答案：A题目分数：0.5此题得分：0.5批注：根本领件的定义第8题A* 〔A+B =人是布尔代数运算法那么的〔〕您的答案：C题目分数：0.5此题得分：0.5批注：分配律的定义第9题以下说法不正确的选项是您的答案：D题目分数：0.5此题得分：0.5批注：结构重要度的定义第10题按事故开展的时间顺序由初始时间开始推论可能的后果是您的答案：B题目分数：0.5此题得分：0.5批注：事件树分析法的分析原理第11题以下割集组合中,最符合最小割集定义的是您的答案：A题目分数：0.5此题得分：0.5批注：最小割集定义第12题在事故树分析中,某些根本领件都不发生那么导致顶事件不发生,这些根本领件的集合,称为事故树的您的答案：A题目分数：0.5此题得分：0.5批注：径集的定义第13题a和b某集合中的两个子集,根据布尔代数的运算定律,布尔代数式〔a+ab〕的简化式为题目分数：0.5此题得分：0.5批注：第14题对任意一个事故树,如各根本领件发生事件都是0.5,那么各根本领件的结构重要度系数I6与概率重要度Ig 在数值上存在如下关系您的答案：B题目分数：0.5此题得分：0.5批注：概率重要度的性质第15题在事故树分析中,反映根本领件发生概率的增减对顶事件发生概率影响的敏感程度的是您的答案：B题目分数：0.5此题得分：0.5批注：临界重要度的定义第16题某事故树的最小径集为P1={X1,X3},P2={X1,X4},P3={X2,X3,X5},P4={X2,X4,X6}, 那么根本领件X1,X2,X3的结构重要度从大到校排列正确的是您的答案：A题目分数：0.5此题得分：0.5批注：结构重要度的计算第17题一个最小径集中的节本领件都不发生,就可以使顶事件不发生,因此事故树的最小径集直接表示了系统的您的答案：D题目分数：0.5此题得分：0.5批注：最小径集的作用第18题以下不属于平安评价原理的是您的答案：A题目分数：0.5此题得分：0.5批注：平安评价的原理第19题以下不属于特种作业的是题目分数：0.5此题得分：0.5批注：特种作业的范围第20题平安治理在影响企业平安的因素中占有重要的位置.曾用于工厂安评方法中各个影响因素所占的比重一般是这样划分的：您的答案：A题目分数：0.5此题得分：0.5批注：工厂安评方法划分第21题系统的平安性评价是运用的方法对系统中存在的危险进行评价和预测的过程您的答案：C题目分数：0.5此题得分：0.5批注：平安评价的定义第22题进行建设工程平安验收评价的设计文件依据是项目〔〕您的答案：A题目分数：0.5此题得分：0.5批注：平安验收评价的依据第23题.事故发生的概率P和事故损失严重程度S的乘积称为您的答案：A题目分数：0.5此题得分：0.5批注：风险率的定义第24题在火灾爆炸指数法中,物质由燃烧或其他化学反应引起的火灾、爆炸中释放能量大小的内在特征,被称为您的答案：D题目分数：0.5此题得分：0.5批注：物质系数的定义第25题系统事故发生率P,风险率R,事故损失严重度S,那么题目分数：0.5此题得分：0.5批注：风险率的定义式第26题风险率=PX U其中U指的是您的答案：A题目分数：0.5此题得分：0.5批注：风险率的定义式第27题许多元件的故障率随时间变化成浴盆曲线,其中曲线上的平滑段指的是您的答案：B题目分数：0.5此题得分：0.5批注：故障率随时间变化曲线的考察第28题在道七版指数评价法中,工艺单元的危险系数F3 与一般工艺的危险系数F1及特殊的工艺危险系数F2的关系为您的答案：B题目分数：0.5此题得分：0.5批注：危险系数的计算第29题可修复系统的单元故障率q=X/〔入+仙〕,其中入指的是您的答案：B题目分数：0.5此题得分：0.5批注：可修复系统的单元故障率的定义式第30题火灾、爆炸指数F&EI与物质系数MF及单元危险系数F3的关系为您的答案：C题目分数：0.5此题得分：0.5批注：火灾、爆炸指数的求取方法第31题在事件树分析中,首先要确定初始事件,而初始事件是指事件树中在一定条件下造成的事故后果您的答案：错误此题得分：0.5批注：事件树分析的步骤第32题事故树中的底事件是导致其他事件的原因事件您的答案：正确题目分数：0.5此题得分：0.5批注：底事件的定义第33题在编制事故树的过程中,应将风险大的事故事件优先考虑您的答案：正确题目分数：0.5此题得分：0.5批注：编制事故树的规那么第34题事故树的顶事件的状态变量小,仅取1和0两种状态.您的答案：正确题目分数：0.5此题得分：0.5批注：顶事件只有发生〔1〕和不发生〔0〕两种状态第35题当事故树中根本领件都发生时,顶事件必然发生, 当所有根本领件都不发生时,顶事件必然不发生.您的答案：正确题目分数：0.5此题得分：0.5批注：结构函数的性质第36题在事故树中,我们把引起顶事件发生的根本领件的集合称为径集您的答案：错误题目分数：0.5此题得分：0.5批注：径集的定义第37题最小割集在事故树分析中,可以表示系统的平安性您的答案：错误题目分数：0.5批注：最小割集的作用第38题事故树中各根本领件的发生对顶事件的发生的影响主要取决于各根本时间发生概率的大小以及各根本领件在事故树模型结构中的位置您的答案：正确题目分数：0.5此题得分：0.5批注：根本时间的重要度分析第39题如果事故树中没有重复的根本领件,那么该事故树的最小割集间也必定没有重复事件.您的答案：正确题目分数：0.5此题得分：0.5批注：别离重复事件法的依据第40题事故树的最小径集是保证顶事件不发生的充分必要条件.您的答案：正确题目分数：0.5此题得分：0.5批注：最小径集的作用作业总得分：19.5作业总批注：0美闲。

石大线代(习题讲解)

4 2 3 见P71 1 设 A 1 1 0 ，且AB=A+2B，求 B 。习题4 1 2 3
1 解由 AB=A+2B，得 B ( A 2 E ) A
2 2 3 1 4 3 1 A 2E 1 1 0 ( A 2 E ) 1 5 3 1 2 1 1 6 4 1 4 3 4 2 3 3 8 6 B 1 5 3 1 1 0 2 9 6 1 6 4 1 2 3 2 12 9
1 Dn a1 a 2 a n (1 ) i 1 a i
n
解法 2 （加边法）
1 Dn 0 0 1 1 1 1 1 1 1 1 1 1 an 1 1 1 1 0 0 1 0 a2 0 1 0 0 an 0 1 a1 1 a1
解
( 3 A)
1
1 1 2A * A 2A * 3
1 A* 2 2 A * ( 2) A * 3 A 3
4 ( ) A * 3
64 2 4 A A* 27 3
3
64 1 16 27 4 27
2. (P59习题4) 设方阵A满足 A A 2 E 0 ，证明 A 及A+2E都可逆,并求 A 1 及( A 2 E ) 1 。
Dn xDn1 a n x 2 Dn 2 xan1 a n

x n 2 D2 xan1 a n .
x
n 2
x a2
1 x a1
xan1 a n .

2019年秋季石油大学计算机网络应用基础网考练习+在线作业答案

∙一、单选题目∙特别注意，考试答案与练习题答案顺序不一致，一定要看清楚答案在答题；∙1、计算机网络安全体系结构是指（C ）？∙ A.各种网络的协议的集合 B.网络安全基本问题应对措施的集合∙ C.网络层次结构与各层协议的集合 D.网络的层次结构的总称∙2、RSA算法是一种基于（C ）的公钥体系。

∙ A.素数不能分解 B.大数没有质因数的假设∙ C.大数不可能质因数分解的假设 D.公钥可以公开的假设∙3、现在计算机及网络系统中常用的身份认证的方式主要有以下四种，其中（B ）是最简答也是最常用的身份认证方法。

∙ A.IC卡认证 B.用户名/密码方式∙ BKey认证 D.动态密码∙4、常见的拒绝服务攻击不包括以下哪一项（D）∙ A.广播风暴 B.SYN淹没 C.OoB攻击 D.ARP 攻击∙5、防火墙截取内网主机与外网通信，由防火墙本身完成与外网主机通信，然后把结果传回给内网主机，这种技术称为（D）。

∙ A.地址转换 B.内容过滤 C.内容中转 D.透明代理∙6、下列对子网系统的防火墙的描述错误的是（A ）。

∙ A.防止内部和外部的威胁 B.增强保密性∙ C.集中的安全管理 D.控制对系统的访问∙7、仅设立防火墙系统，而没有（B），防火墙就形同虚设。

∙ A.安全操作系统 B.安全策略 C.防毒系统 D.管理员∙8、主要用于加密机制的协议是（C）∙ A.FTP B.TELNETD C.SSLD.HTTP∙9、在4种常见的防火墙系统构建模型中，最不安全的模型是（A ）∙ A.屏蔽主机模型 B.双宿主堡垒主机模型∙ C.屏蔽防火墙系统模型 D.屏蔽子网模型∙10、PKI的全称是（A ）。

∙ A.Public Key Infrastructure B.Private Key Infrastructure∙ C.Public KeyIntrusion D.Private Key Intrusion∙11、PKI管理对象不包括（D ）。

西安石油大学函授《线性代数》作业3

作业3 向量组的线性相关性方程组可解性判断1 / 25 单选题（4分）正确答案 B设为维向量组,且秩为(),则( ).A线性无关B线性相关C任一向量都可以表示为其余向量的线性组合D任一向量都不可以表示为其余向量的线性组合2 / 25 单选题（4分）正确答案 C若向量组线性无关,向量组线性相关,则( ).A必可由线性表示B必不可由线性表示C必可由线性表示D必不可由线性表示3 / 25 单选题（4分）正确答案 C若矩阵中个列向量线性无关,则的秩( ).A大于B大于C等于D等于4 / 25 单选题（4分）正确答案 C至多为( ).A1B2C3D45 / 25 单选题（4分）正确答案 CA若向量与正交,则对任意实数,与也正交B若向量与向量都正交,则与的任一线性组合也正交C若向量与正交,则,中至少有一个是零向量D若向量与任意同维向量正交,则是零向量6 / 25 单选题（4分）正确答案 A若为阶方阵,,则齐次线性方程组的基础解系含有的解向量个数为( ).A1BCD不确定7 / 25 单选题（4分）正确答案 A设矩阵,方程组仅有零解的充分必要条件是( ).A的列向量组线性无关B的列向量组线性相关C的行向量组线性无关D的行向量组线性相关8 / 25 单选题（4分）正确答案 B齐次线性方程组,其中为矩阵,且,是该方程组的三个线性无关的解向量,则下列选项中哪个是的基础解系( ).ABCD9 / 25 单选题（4分）正确答案 B已知是非齐次线性方程组的两个不同解,是其对应的齐次线性方程组的基础解系,为任意常数,则方程组的通解为( ).ABCD10 / 25 单选题（4分）正确答案 C设为阶方阵,且的秩,是的两个不同的解,则的通解为( ).ABCD11 / 25 单选题（4分）正确答案 D已知齐次线性方程组有非零解,则为( ).A3B4CD12 / 25 单选题（4分）正确答案 D设为阶方阵,且的秩,则的基础解系( ).A仅有唯一向量B有有限个向量C有无限个向量D不存在13 / 25 单选题（4分）正确答案 D为阶方阵,则可逆的充要条件是( ).A任一行向量都是非零向量B任一列向量都是非零向量C有解D14 / 25 单选题（4分）正确答案 D元线性方程组有唯一解的充要条件是( ).ABC为方阵且D,且可由的列向量线性表示15 / 25 单选题（4分）正确答案 D设是矩阵,是非齐次线性方程组所对应的齐次线性方程组,则下列结论正确的是( ).A若仅有零解,则有唯一解B若有非零解,则有无穷多个解C若有无穷多个解,则仅有零解D若有无穷多个解,则有非零解16 / 25 单选题（4分）正确答案 C设为4元非齐次线性方程组的三个解向量,且,若,,为任意常数,则线性方程组的通解为( ).ABCD17 / 25 单选题（4分）正确答案 B若方程组无解,则( ).A1BCD18 / 25 单选题（4分）正确答案 D设是齐次线性方程组的一个基础解系,则该方程组的基础解系也可以是( ).A用表示出的向量组B与秩相同的向量组C与等价的一个向量组D与等价的一个线性无关向量组19 / 25 单选题（4分）正确答案 C与向量都正交的全部向量为( ).ABCD20 / 25 单选题（4分）正确答案 B若为阶方阵,,则齐次线性方程组的基础解系含有的向量个数为( ).A1B3CD21 / 25 判断题（4分）若两个维向量组等价,则这两个向量组的秩相等.( )正确错误正确答案正确22 / 25 判断题（4分）若两个维向量组的秩相等,则这两个向量组等价.( )正确错误正确答案错误23 / 25 判断题（4分）量.( )正确错误正确答案错误24 / 25 判断题（4分）若向量组线性相关,则必含有零向量.( )正确错误正确答案错误25 / 25 判断题（4分）若向量组线性无关,则必不含有零向量.( )正确错误正确答案正确。

奥鹏中石油线性代数作业及答案

奥鹏中石油线性代数（文）2014年秋学期在线作业1.2答案2014年秋学期在线作业1.试卷总分：100 测试时间：--单选题一、单选题（共 10 道试题，共 100 分。

）V1.题目选项如下：A.B.C.D. D满分：10 分2.题目和选项如下:A.B. BC.D.满分：10 分3.题目和选项如下：A.B.C.D.满分：10 分4.题目和选项如下：A.B.C. CD.满分：10 分5.题目和选项如下：A.B.C.D.满分：10 分6.题目和选项如下：A.B.C.D. D满分：10 分7.题目和选项如下：A.B.C.D. D满分：10 分8.题目如下：A.B.C.D.满分：10 分9.题目和选项如下：A.B.C.D. D满分：10 分10.题目和选项如下：一、单选题（共 10 道试题，共 100 分。

）V1.题目和选项如下：A.B.C.D.满分：10 分2.题目和选项如下：A.B.C.D.满分：10 分3.题目和选项如下：A.B.C.D.满分：10 分4.题目和选项如下：A.B.C.D.满分：10 分5.题目和选项如下：A.B.C.D.满分：10 分6.题目和选项如下：A.B.C.D.满分：10 分7.题目和选项如下：A.B.C.D.满分：10 分8.题目和选项如下：A.B.C.D.满分：10 分9.题目和选项如下：A.B.C.D.满分：10 分10.题目和选项如下：A.B.C.D.。

2019年自考历年线性代数考试试题及答案解析精选

自考历年线性代数考试试题及答案解析精选第一部分选择题(共28分)一、单项选择题[本大题共14小题,每小题2分,共28分]在每小题列出的四个选项中只有一个是符合题目要求的,请将其代码填在题后的括号内.错选或未选均无分.1、设行列式=m, =n,则行列式等于[] A 、m+n B 、-(m+n) C 、n -m D 、m -n2、设矩阵A=,则A -1等于[]A 、B 、C 、D 、3、设矩阵A=,A *是A 的伴随矩阵,则A *中位于[1,2]的元素是[] A 、–6 B 、6 C 、2 D 、–24、设A 是方阵,如有矩阵关系式AB=AC,则必有[] A 、A=0 B 、BC 时A=0 C 、A0时B=C D 、|A|0时B=C5、已知3×4矩阵A 的行向量组线性无关,则秩[A T ]等于[] A 、1 B 、2 C 、3 D 、46、设两个向量组α1,α2,…,αs 和β1,β2,…,βs 均线性相关,则[]A 、有不全为0的数λ1,λ2,…,λs 使λ1α1+λ2α2+…+λs αs =0和λ1β1+λ2β2+…λs βs =0B 、有不全为0的数λ1,λ2,…,λs 使λ1[α1+β1]+λ2[α2+β2]+…+λs [αs +βs ]=0C 、有不全为0的数λ1,λ2,…,λs 使λ1[α1-β1]+λ2[α2-β2]+…+λs [αs -βs ]=0D 、有不全为0的数λ1,λ2,…,λs 和不全为0的数μ1,μ2,…,μs 使λ1α1+λ2α2+…+λs αs =0和μ1β1+μ2β2+…+μs βs =0 7、设矩阵A 的秩为r,则A 中[]A 、全部r -1阶子式都不为0B 、全部r -1阶子式全为0C 、至少有一个r 阶子式不等于0D 、全部r 阶子式都不为08、设Ax=b 是一非齐次线性方程组,η1,η2是其任意2个解,则下面结论错误的是[]A 、η1+η2是Ax=0的一个解B 、η1+η2是Ax=b 的一个解C 、η1-η2是Ax=0的一个解D 、2η1-η2是Ax=b 的一个解 9、设n 阶方阵A 不可逆,则必有[]A 、秩(A)<nB 、秩(A)=n -1C 、A=0D 、方程组Ax=0只有零解 10、设A 是一个n(≥3)阶方阵,下面陈述中正确的是[]A 、如存在数λ和向量α使A α=λα,则α是A 的属于特点值λ的特点向量B 、如存在数λ和非零向量α,使(λE -A)α=0,则λ是A 的特点值C 、A 的2个不同的特点值能够有同一个特点向量D 、如λ1,λ2,λ3是A 的3个互不相同的特点值,α1,α2,α3依次是A 的属于λ1,λ2,λ3的特点向量,则α1,α2,α3有可能线性相关11、设λ0是矩阵A 的特点方程的3重根,A 的属于λ0的线性无关的特点向量的个数为k,则必有[]A 、k ≤3B 、k<3C 、k=3D 、k>3 12、设A 是正交矩阵,则下面结论错误的是[] A 、|A|2必为1 B 、|A|必为1C 、A -1=A TD 、A 的行[列]向量组是正交单位向量组 13、设A 是实对称矩阵,C 是实可逆矩阵,B=C T AC 、则[] A 、A 和B 相似 B 、A 和B 不等价C 、A 和B 有相同的特点值D 、A 和B 合同14、下面矩阵中是正定矩阵的为[] A 、 B 、 C 、 D 、第二部分非选择题[共72分]二、填空题[本大题共10小题,每小题2分,共20分]不写解答过程,将正确的答案写在每小题的空格内.错填或不填均无分. 15、、16、设A=,B=、则A+2B= 、17、设A=(a ij )3×3,|A|=2,A ij 表示|A|中元素a ij 的代数余子式[i,j=1,2,3],则(a 11A 21+a 12A 22+a 13A 23)2+(a 21A 21+a 22A 22+a 23A 23)2+(a 31A 21+a 32A 22+a 33A 23)2= 、18、设向量[2,-3,5]和向量[-4,6,a]线性相关,则a= 、19、设A 是3×4矩阵,其秩为3,若η1,η2为非齐次线性方程组Ax=b 的2个不同的解,则它的通解为、20、设A 是m ×n 矩阵,A 的秩为r(<n),则齐次线性方程组Ax=0的一个基础解系中含有解的个数为、21、设向量α、β的长度依次为2和3,则向量α+β和α-β的内积[α+β,α-β]= 、22、设3阶矩阵A 的行列式|A|=8,已知A 有2个特点值-1和4,则另一特点值为、23、设矩阵A=,已知α=是它的一个特点向量,则α所对应的特点值为、 24、设实二次型f(x 1,x 2,x 3,x 4,x 5)的秩为4,正惯性指数为3,则其规范形为、三、计算题[本大题共7小题,每小题6分,共42分] 25、设A=,B=、求[1]AB T ；[2]|4A|、 26、试计算行列式、27、设矩阵A=,求矩阵B 使其满足矩阵方程AB=A+2B 、 28、给定向量组α1=,α2=,α3=,α4=、试判断α4是否为α1,α2,α3的线性组合；若是,则求出组合系数. 29、设矩阵A=、求:[1]秩[A]；[2]A 的列向量组的一个最大线性无关组.30、设矩阵A=的全部特点值为1,1和-8、求正交矩阵T 和对角矩阵D,使T -1AT=D 、 31、试用配方法化下面二次型为标准形 f(x 1,x 2,x 3)=,并写出所用的满秩线性变换.四、证明题[本大题共2小题,每小题5分,共10分]32、设方阵A 满足A 3=0,试证明E -A 可逆,且[E -A]-1=E+A+A 2、33、设η0是非齐次线性方程组Ax=b 的一个特解,ξ1,ξ2是其导出组Ax=0的一个基础解系、试证明[1]η1=η0+ξ1,η2=η0+ξ2均是Ax=b 的解； [2]η0,η1,η2线性无关. 答案:一、单项选择题[本大题共14小题,每小题2分,共28分]1、D2、B3、B4、D5、C6、D7、C8、A9、A 10、B 11、A 12、B 13、D 14、C 二、填空题[本大题共10空,每空2分,共20分] 15、6 16、 17、4 18、–1019、η1+c(η2-η1)[或η2+c(η2-η1)],c 为任意常数 20、n -r 21、–5 22、–2 23、1 24、三、计算题[本大题共7小题,每小题6分,共42分] 25、解[1]AB T = =、[2]|4A|=43|A|=64|A|,而|A|=、所以|4A|=64·[-2]=-128 26、解= =27、解AB=A+2B 即[A -2E]B=A,而 [A -2E]-1=所以B=(A -2E)-1A==28、解一所以α4=2α1+α2+α3,组合系数为[2,1,1]、解二考虑α4=x 1α1+x 2α2+x 3α3, 即方程组有唯一解[2,1,1]T ,组合系数为[2,1,1]、29、解对矩阵A施行初等行变换A=B、[1]秩[B]=3,所以秩[A]=秩[B]=3、[2]由于A和B的列向量组有相同的线性关系,而B是阶梯形,B的第1、2、4列是B的列向量组的一个最大线性无关组,故A的第1、2、4列是A的列向量组的一个最大线性无关组.[A的第1、2、5列或1、3、4列,或1、3、5列也是]30、解A的属于特点值λ=1的2个线性无关的特点向量为ξ1=[2,-1,0]T,ξ2=[2,0,1]T、经正交标准化,得η1=,η2=、λ=-8的一个特点向量为ξ3=,经单位化得η3=所求正交矩阵为T=、对角矩阵D=[也可取T=、]31、解f(x1,x2,x3)=[x1+2x2-2x3]2-2x22+4x2x3-7x32=[x1+2x2-2x3]2-2[x2-x3]2-5x32、设,即,因其系数矩阵C=可逆,故此线性变换满秩.经此变换即得f(x1,x2,x3)的标准形y 12-2y22-5y32、四、证明题[本大题共2小题,每小题5分,共10分]32、证由于[E-A][E+A+A2]=E-A3=E,所以E-A可逆,且[E-A]-1=E+A+A2、33、证由假设Aη0=b,Aξ1=0,Aξ2=0、[1]Aη1=A[η+ξ1]=Aη+Aξ1=b,同理Aη2=b,所以η1,η2是Ax=b的2个解.[2]考虑l0η+l1η1+l2η2=0,即[l0+l1+l2]η+l1ξ1+l2ξ2=0、则l0+l1+l2=0,否则η将是Ax=0的解,矛盾.所以l 1ξ1+l2ξ2=0、又由假设,ξ1,ξ2线性无关,所以l1=0,l2=0,从而l=0、所以η0,η1,η2线性无关.线性代数期末考试题一、填空题[将正确答案填在题中横线上.每小题2分,共10分]1、若,则__________.2、若齐次线性方程组只有零解,则应满足 .3、已知矩阵,满足,则和分别是阶矩阵.4、矩阵的行向量组线性 .5、阶方阵满足,则 .二、判断正误[正确的在括号内填”√”,错误的在括号内填”×”.每小题2分,共10分]1、若行列式中每个元素都大于零,则.[]2、零向量一定能够表示成任意一组向量的线性组合.[]3、向量组中,假如和对应的分量成比例,则向量组线性相关.[]4、,则.[]5、若为可逆矩阵的特点值,则的特点值为.<>三、单项选择题(每小题仅有一个正确答案,将正确答案题号填入括号内.每小题2分,共10分)1、设为阶矩阵,且,则[].①②③④42、维向量组[3≤s≤n]线性无关的充要条件是[].①中任意两个向量都线性无关②中存在一个向量不能用其它向量线性表示③中任一个向量都不能用其它向量线性表示④中不含零向量3、下面命题中正确的是<>.①任意个维向量线性相关②任意个维向量线性无关③任意个维向量线性相关④任意个维向量线性无关4、设,均为n阶方阵,下面结论正确的是<>.①若,均可逆,则可逆②若,均可逆,则可逆③若可逆,则可逆④若可逆,则,均可逆5、若是线性方程组的基础解系,则是的[]①解向量②基础解系③通解④A的行向量四、计算题(每小题9分,共63分)1、计算行列式.解·2、设,且求.解、,3、设且矩阵满足关系式求.4、问取何值时,下面向量组线性相关?.5、为何值时,线性方程组有唯一解,无解和有无穷多解?当方程组有无穷多解时求其通解.①当且时,方程组有唯一解；②当时方程组无解③当时,有无穷多组解,通解为6、设求此向量组的秩和一个极大无关组,并将其它向量用该极大无关组线性表示.7、设,求的特点值及对应的特点向量.五、证明题(7分)若是阶方阵,且证明.其中为单位矩阵.×××大学线性代数期末考试题答案一、填空题1、52、3、4、相关5、二、判断正误1、×2、√3、√4、√5、×三、单项选择题1、③2、③3、③4、②5、①四、计算题1、2、,3、4、当或时,向量组线性相关.5、①当且时,方程组有唯一解；②当时方程组无解③当时,有无穷多组解,通解为6、则,其中构成极大无关组,7、特点值,对于λ1＝1,,特点向量为五、证明题∴,∵【线性代数】复习提纲第一部分:基本要求[计算方面]四阶行列式的计算；N阶特殊行列式的计算[如有行和、列和相等]；矩阵的运算[包含加、减、数乘、乘法、转置、逆等的混合运算]；求矩阵的秩、逆[两种方法]；解矩阵方程；含参数的线性方程组解的情况的讨论；齐次、非齐次线性方程组的求解[包含唯一、无穷多解]；讨论一个向量能否用和向量组线性表示；讨论或证明向量组的相关性；求向量组的极大无关组,并将多余向量用极大无关组线性表示；将无关组正交化、单位化；求方阵的特点值和特点向量；讨论方阵能否对角化,如能,要能写出相似变换的矩阵及对角阵；通过正交相似变换[正交矩阵]将对称矩阵对角化；写出二次型的矩阵,并将二次型标准化,写出变换矩阵；判定二次型或对称矩阵的正定性.第二部分:基本知识一、行列式1、行列式的定义用n^2个元素aij组成的记号称为n阶行列式.[1]它表示全部可能的取自不同行不同列的n个元素乘积的代数和；[2]展开式共有n!项,其中符号正负各半；2、行列式的计算一阶|α|=α行列式,二、三阶行列式有对角线法则；N阶[n>=3]行列式的计算:降阶法定理:n阶行列式的值等于它的任意一行[列]的各元素和其对应的代数余子式乘积的和.方法:选取比较简单的一行[列],保保留一个非零元素,其它元素化为0,利用定理展开降阶.特殊情况上、下三角形行列式、对角形行列式的值等于主对角线上元素的乘积；[2]行列式值为0的几种情况:Ⅰ行列式某行[列]元素全为0；Ⅱ行列式某行[列]的对应元素相同；Ⅲ行列式某行[列]的元素对应成比例；Ⅳ奇数阶的反对称行列式.二、矩阵1、矩阵的基本概念[表示符号、一些特殊矩阵――如单位矩阵、对角、对称矩阵等]；2、矩阵的运算[1]加减、数乘、乘法运算的条件、结果；[2]关于乘法的几个结论:①矩阵乘法通常不满足交换律[若AB＝BA,称A、B是可交换矩阵]；②矩阵乘法通常不满足消去律、零因式不存在；③若A、B为同阶方阵,则|AB|=|A|*|B|；④|kA|=k^n|A|3、矩阵的秩[1]定义非零子式的最大阶数称为矩阵的秩；[2]秩的求法通常不用定义求,而用下面结论:矩阵的初等变换不改变矩阵的秩；阶梯形矩阵的秩等于非零行的个数[每行的第一个非零元所在列,从此元开始往下全为0的矩阵称为行阶梯阵].求秩:利用初等变换将矩阵化为阶梯阵得秩.4、逆矩阵[1]定义:A、B为n阶方阵,若AB＝BA＝I,称A可逆,B是A的逆矩阵[满足半边也成立]；[2]性质: (AB)^-1=(B^-1)*(A^-1),(A')^-1=(A^-1)'；(AB的逆矩阵,您懂的)[注意顺序][3]可逆的条件:①|A|≠0；②r(A)=n;③A->I;[4]逆的求解伴随矩阵法A^-1=(1/|A|)A*；(A*A的伴随矩阵~)②初等变换法[A:I]->(施行初等变换)[I:A^-1]5、用逆矩阵求解矩阵方程:AX=B,则X=[A^-1]B；XB=A,则X=B(A^-1)；AXB=C,则X=(A^-1)C(B^-1)三、线性方程组1、线性方程组解的判定定理:(1)r(A,b)≠r(A)无解；(2)r(A,b)=r(A)=n有唯一解；(3)r(A,b)=r(A)<n有无穷多组解；特别地:对齐次线性方程组AX=0(1)r(A)=n只有零解；(2)r(A)<n有非零解；再特别,若为方阵,(1)|A|≠0只有零解(2)|A|=0有非零解2、齐次线性方程组[1]解的情况:r(A)=n,[或系数行列式D≠0]只有零解；r(A)<n,[或系数行列式D＝0]有无穷多组非零解.[2]解的结构:X=c1α1+c2α2+…+Cn-rαn-r.[3]求解的方法和步骤:①将增广矩阵通过行初等变换化为最简阶梯阵；②写出对应同解方程组；③移项,利用自由未知数表示全部未知数；④表示出基础解系；⑤写出通解.3、非齐次线性方程组[1]解的情况:利用判定定理.[2]解的结构: X=u+c1α1+c2α2+…+Cn-rαn-r.[3]无穷多组解的求解方法和步骤: 和齐次线性方程组相同.[4]唯一解的解法:有克莱姆法则、逆矩阵法、消元法[初等变换法].四、向量组1、N维向量的定义注:向量实际上就是特殊的矩阵[行矩阵和列矩阵].2、向量的运算:[1]加减、数乘运算[和矩阵运算相同]；[2]向量内积α'β=a1b1+a2b2+…+anbn；[3]向量长度|α|=√α'α=√(a1^2+a2^2+…+an^2)(√根号)[4]向量单位化(1/|α|)α；5]向量组的正交化[施密特方法]设α1,α2,…,αn线性无关,则β1=α1,β2=α2-[α2’β1/β1’β]*β1,β3=α3-[α3’β1/β1’β1]*β1-[α3’β2/β2’β2]*β2,……….3、线性组合[1]定义若β=k1α1+k2α2+…+knαn,则称β是向量组α1,α2,…,αn的一个线性组合,或称β能够用向量组α1,α2,…,αn的一个线性表示.[2]判别方法将向量组合成矩阵,记A＝(α1,α2,…,αn),B=(α1,α2,…,αn,β)若r(A)=r(B),则β能够用向量组α1,α2,…,αn的一个线性表示；若r(A)≠r(B),则β不能够用向量组α1,α2,…,αn的一个线性表示.[3]求线性表示表达式的方法:将矩阵B施行行初等变换化为最简阶梯阵,则最后一列元素就是表示的系数.4、向量组的线性相关性[1]线性相关和线性无关的定义设k1α1+k2α2+…+knαn=0 若k1,k2,…,kn不全为0,称线性相关；若k1,k2,…,kn全为0,称线性无关.[2]判别方法:①r(α1,α2,…,αn)<n,线性相关；r(α1,α2,…,αn)=n,线性无关.②若有n个n维向量,可用行列式判别: n阶行列式aij＝0,线性相关[≠0无关](行列式太不好打了)5、极大无关组和向量组的秩[1]定义极大无关组所含向量个数称为向量组的秩[2]求法设A＝(α1,α2,…,αn),将A化为阶梯阵,则A的秩即为向量组的秩,而每行的第一个非零元所在列的向量就构成了极大无关组.五、矩阵的特点值和特点向量1、定义对方阵A,若存在非零向量X和数λ使AX＝λX,则称λ是矩阵A的特点值,向量X称为矩阵A的对应于特点值λ的特点向量.2、特点值和特点向量的求解: 求出特点方程|λI-A|=0的根即为特点值,将特点值λ代入对应齐次线性方程组(λI-A)X＝0中求出方程组的全部非零解即为特点向量.3、重要结论:[1]A可逆的充要条件是A的特点值不等于0；[2]A和A的转置矩阵A'有相同的特点值；[3]不同特点值对应的特点向量线性无关.六、矩阵的相似1、定义对同阶方阵A、B,若存在可逆矩阵P,使P^-1AP=B,则称A和B相似.2、求A和对角矩阵∧相似的方法和步骤[求P和∧]:求出全部特点值；求出全部特点向量；若所得线性无关特点向量个数和矩阵阶数相同,则A可对角化[否则不能对角化],将这n个线性无关特点向量组成矩阵即为相似变换的矩阵P,依次将对应特点值构成对角阵即为∧.3、求通过正交变换Q和实对称矩阵A相似的对角阵:方法和步骤和通常矩阵相同,只是第三歩要将所得特点向量正交化且单位化.七、二次型1、定义n元二次多项式f(x1,x2,…,xn)=∑aijxixj称为二次型,若aij=0(i≠j),则称为二交型的标准型.i,j=12、二次型标准化: 配方法和正交变换法.正交变换法步骤和上面对角化完全相同,这是由于对正交矩阵Q,Q^-1=Q',即正交变换既是相似变换又是合同变换.3、二次型或对称矩阵的正定性:[1]定义[略]；[2]正定的充要条件:①A为正定的充要条件是A的全部特点值都大于0；②A为正定的充要条件是A的全部顺序主子式都大于0高等教育自学考试试题部分说明:本卷中,A T表示矩阵A的转置,αT表示向量α的转置,E表示单位矩阵,|A|表示方阵A的行列式,A-1表示方阵A的逆矩阵,r[A]表示矩阵A的秩、一、单项选择题[本大题共10小题,每小题2分,共30分]在每小题列出的四个备选项中只有一个是符合题目要求的,请将代码填写在题后的括号内.错选、多选或未选均无分.1、设行列式[]A、B、1C、2D、2、设A,B,C为同阶可逆方阵,则[ABC]-1=[]A、A-1B-1C-1B、C-1B-1A-1C、C-1A-1B-1D、A-1C-1B-13、设α1,α2,α3,α4是4维列向量,矩阵A=[α1,α2,α3,α4]、假如|A|=2,则|-2A|=[]A 、-32B 、-4C 、4D 、32 4、设α1,α2,α3,α4是三维实向量,则[]A 、α1,α2,α3,α4一定线性无关B 、α1一定可由α2,α3,α4线性表出C 、α1,α2,α3,α4一定线性相关D 、α1,α2,α3一定线性无关 5、向量组α1=[1,0,0],α2=[1,1,0],α3=[1,1,1]的秩为[] A 、1 B 、2 C 、3 D 、46、设A 是4×6矩阵,r[A]=2,则齐次线性方程组Ax=0的基础解系中所含向量的个数是[]A 、1B 、2C 、3D 、47、设A 是m ×n 矩阵,已知Ax=0只有零解,则以下结论正确的是[] A 、m ≥n B 、Ax=b[其中b 是m 维实向量]必有唯一解 C 、r[A]=m D 、Ax=0存在基础解系 8、设矩阵A=,则以下向量中是A 的特点向量的是[] A 、[1,1,1]T B 、[1,1,3]T C 、[1,1,0]T D 、[1,0,-3]T9、设矩阵A=的三个特点值分别为λ1,λ2,λ3,则λ1+λ2+λ3=[] A 、4 B 、5 C 、6 D 、7 10、三元二次型f[x 1,x 2,x 3]=的矩阵为[] A 、 B 、 C 、 D 、二、填空题[本大题共10小题,每小题2分,共20分] 请在每小题的空格中填上正确答案.错填、不填均无分. 11、行列式=_________、 12、设A=,则A -1=_________、13、设方阵A 满足A 3-2A+E=0,则[A 2-2E]-1=_________、14、实数向量空间V={[x 1,x 2,x 3]|x 1+x 2+x 3=0}的维数是_________、15、设α1,α2是非齐次线性方程组Ax=b 的解、则A[5α2-4α1]=_________、 16、设A 是m ×n 实矩阵,若r[A T A]=5,则r[A]=_________、 17、设线性方程组有无穷多个解,则a=_________、18、设n 阶矩阵A 有一个特点值3,则|-3E+A|=_________、19、设向量α=[1,2,-2],β=[2,a,3],且α和β正交,则a=_________、 20、二次型的秩为_________、三、计算题[本大题共6小题,每小题9分,共54分] 21、计算4阶行列式D=、22、设A=,判断A 是否可逆,若可逆,求其逆矩阵A -1、 23、设向量α=[3,2],求[αT α]101、24、设向量组α1=[1,2,3,6],α2=[1,-1,2,4],α3=[-1,1,-2,-8],α4=[1,2,3,2]、 [1]求该向量组的一个极大线性无关组；[2]将其它向量表示为该极大线性无关组的线性组合、线性代数试题课程代码:04184一、单项选择题[本大题共20小题,每小题1分,共20分]在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内.错选、多选或未选均无分.1、已知2阶行列式=m, =n,则=[]A、m-nB、n-mC、m+nD、-[m+n]2、设A,B,C均为n阶方阵,AB=BA,AC=CA,则ABC=[]A、ACBB、CABC、CBAD、BCA3、设A为3阶方阵,B为4阶方阵,且行列式|A|=1,|B|=-2,则行列式||B|A|之值为[]A、-8B、-2C、2D、84、已知A=,B=,P=,Q=,则B=[]A、PAB、APC、QAD、AQ5、已知A是一个3×4矩阵,下面命题中正确的是[]A、若矩阵A中全部3阶子式都为0,则秩[A]=2B、若A中存在2阶子式不为0,则秩[A]=2C、若秩[A]=2,则A中全部3阶子式都为0D、若秩[A]=2,则A中全部2阶子式都不为06、下面命题中错误．．的是[]A、只含有一个零向量的向量组线性相关B、由3个2维向量组成的向量组线性相关C、由一个非零向量组成的向量组线性相关D、两个成比例的向量组成的向量组线性相关7、已知向量组α1,α2,α3线性无关,α1,α2,α3,β线性相关,则[]A、α1必能由α2,α3,β线性表出B、α2必能由α1,α3,β线性表出C、α3必能由α1,α2,β线性表出D、β必能由α1,α2,α3线性表出8、设A为m×n矩阵,m≠n,则齐次线性方程组Ax=0只有零解的充分必要条件是A 的秩[]A、小于mB、等于mC、小于nD、等于n9、设A为可逆矩阵,则和A必有相同特点值的矩阵为[]A、A TB、A2C、A-1D、A*10、二次型f[x1,x2,x3]=的正惯性指数为[]A、0B、1C、2D、3二、填空题[本大题共10小题,每小题2分,共20分]请在每小题的空格中填上正确答案.错填、不填均无分.11、行列式的值为_________________________、12、设矩阵A=,B=,则A T B=____________________________、13、设4维向量[3,-1,0,2]T,β=[3,1,-1,4]T,若向量γ满足2γ=3β,则γ=__________、14、设A为n阶可逆矩阵,且|A|=,则|A-1|=___________________________、15、设A为n阶矩阵,B为n阶非零矩阵,若B的每一个列向量都是齐次线性方程组Ax=0的解,则|A|=__________________、16、齐次线性方程组的基础解系所含解向量的个数为________________、17、设n阶可逆矩阵A的一个特点值是-3,则矩阵必有一个特点值为_____________、18、设矩阵A=的特点值为4,1,-2,则数x=________________________、19、已知A=是正交矩阵,则a+b=_______________________________.20、二次型f[x1,x2,x3]=-4x1x2+2x1x3+6x2x3的矩阵是_______________________________.三、计算题[本大题共6小题,每小题9分,共54分] 21、计算行列式D=的值.22、已知矩阵B=[2,1,3],C=[1,2,3],求[1]A=B T C ；[2]A 2.23、设向量组求向量组的秩及一个极大线性无关组,并用该极大线性无关组表示向量组中的其它向量.24、已知矩阵A=,B=、[1]求A -1；[2]解矩阵方程AX=B.25、问a 为何值时,线性方程组有惟一解?有无穷多解?并在有解时求出其解[在有无穷多解时,要求用一个特解和导出组的基础解系表示全部解].26、设矩阵A=的三个特点值分别为1,2,5,求正的常数a 的值及可逆矩阵P,使P -1AP=.四、证明题[本题6分]27、设A,B,A+B 均为n 阶正交矩阵,证明[A+B]-1=A -1+B -1. 全国2016年7月高等教育自学考试试卷说明:在本卷中,A T 表示矩阵A 的转置矩阵；A *表示A 的伴随矩阵；R(A)表示矩阵A 的秩；|A|表示A 的行列式；E 表示单位矩阵.1、设3阶方阵A=[α1,α2,α3],其中αi (i=1,2,3)为A 的列向量, 若|B|=|[α1+2α2,α2,α3]|=6,则|A|=[]A 、-12 B 、-6C 、6 D 、122、计算行列式[]A 、-180 B 、-120C 、120 D 、1803、设A=,则|2A *|=[]A 、-8 B 、-4C 、4 D 、8 4、设α1,α2,α3,α4都是3维向量,则必有A 、α1,α2,α3,α4线性无关B 、α1,α2,α3,α4线性相关C 、α1可由α2,α3,α4线性表示D 、α1不可由α2,α3,α4线性表示5、若A 为6阶方阵,齐次线性方程组Ax=0的基础解系中解向量的个数为2,则R(A)=[]A 、2 B3C 、4 D 、56、设A 、B 为同阶矩阵,且R(A)=R(B),则[]A 、A 和B 相似 B 、|A|=|B|C 、A 和B 等价 D 、A 和B 合同7、设A 为3阶方阵,其特点值分别为2,l,0则|A+2E|=[]A 、0 B 、2C 、3 D 、24 8、若A 、B 相似,则下面说法错误．．的是[]A 、A 和B 等价 B 、A 和 B 合同C 、|A|=|B|D 、A 和B 有相同特点9、若向量α=(1,-2,1)和β=(2,3,t)正交,则t=[]A 、-2 B 、0C 、2 D 、4 10、设3阶实对称矩阵A 的特点值分别为2,l,0,则[]A 、A 正定 B 、A 半正定C 、A 负定 D 、A 半负定二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案.错填、不填均无分.1l 、设A=,B=,则AB=________、12、设A 为3阶方阵,且|A|=3,则|3A -l |=________、 13、三元方程x 1+x 2+x 3=0的结构解是________、14、设α=(-1,2,2),则和α反方向的单位向量是______、15、设A 为5阶方阵,且R(A)=3,则线性空间W={x|Ax=0}的维数是______、 16、设A 为3阶方阵,特点值分别为-2,,l,则|5A -1|=_______、17、若A 、B 为同阶方阵,且Bx=0只有零解,若R(A)=3,则R(AB)=________、 18、二次型f(x 1,x 2,x 3)= -2x 1x 2+-x 2x 3所对应的矩阵是________、19、设3元非齐次线性方程组Ax=b 有解α1=,α2=,且R(A)=2,则Ax=b 的通解是________、20、设α=,则A=ααT 的非零特点值是_____、三、计算题(本大题共6小题,每小题9分,共54分) 21、计算5阶行列式D=22、设矩阵X 满足方程X=求X 、 23、求非齐次线性方程组的结构解、24、求向量组α1=[1,2,3,4],α2=[0,-1,2,3],α3=[2,3,8,11], α4=[2,3,6,8]的秩、25、已知A=的一个特点向量=[1,1,-1]T ,求a,b 及所对应的特点值,并写出对应于这个特点值的全部特点向量、26、用正交变换化二次型f(x 1,x 2,x 3)=为标准形,并写出所用的正交变换、四、证明题[本大题共1小题,6分]27、设α1,α2,α3是齐次线性方程组Ax=0的一个基础解系、证明α1,α1+α2,α2+α3也是Ax=0的基础解系、全国2016年10月高等教育自学考试线性代数(经管类)试题课程代码:04184说明:在本卷中,A T 表示矩阵A 的转置矩阵,A *表示矩阵A 的伴随矩阵,E 是单位矩阵,|A|表示方阵A 的行列式,r(A)表示矩A 的秩、一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内.错选、多选或未选均无分. 1、设A 为3阶矩阵,|A|=1,则|-2A T |=<> A 、-8B 、-2C 、2 D 、8 2、设矩阵A=,B=(1,1),则AB=<> A 、0B 、(1,-1)C 、 D 、3、设A 为n 阶对称矩阵,B 为n 阶反对称矩阵,则下面矩阵中为反对称矩阵的是<> A 、AB-BAB 、AB+BAC 、ABD 、BA4、设矩阵A 的伴随矩阵A *=,则A -1=<> A 、 B 、 C 、 D 、5、下面矩阵中不是．．初等矩阵的是<> A 、 B 、 C 、 D 、6、设A,B 均为n 阶可逆矩阵,则必有<>A 、A+B 可逆B 、AB 可逆C 、A-B 可逆D 、AB+BA 可逆 7、设向量组α1=(1,2),α2=(0,2),β=(4,2),则<> A 、α1,α2,β线性无关B 、β不能由α1,α2线性表示C 、β可由α1,α2线性表示,但表示法不惟一D 、β可由α1,α2线性表示,且表示法惟一8、设A 为3阶实对称矩阵,A 的全部特点值为0,1,1,则齐次线性方程组(E-A)x=0的基础解系所含解向量的个数为<>A 、0B 、1C 、2D 、3 9、设齐次线性方程组有非零解,则为<> A 、-1B 、0C 、1 D 、210、设二次型f(x)=x TAx 正定,则下面结论中正确的是<>A 、对任意n 维列向量x,x T Ax 都大于零B 、f 的标准形的系数都大于或等于零C 、A 的特点值都大于零D 、A 的全部子式都大于零二、填空题(本大题共10小题,每小题2分,共20分) 请在每小题的空格中填上正确答案.错填、不填均无分.11、行列式的值为_________、12、已知A=,则|A|中第一行第二列元素的代数余子式为_________、13、设矩阵A=,P=,则AP3=_________、14、设A,B都是3阶矩阵,且|A|=2,B=-2E,则|A-1B|=_________、15、已知向量组α1,=(1,2,3),α2=(3,-1,2),α3=(2,3,k)线性相关,则数k=_________、16、已知Ax=b为4元线性方程组,r(A)=3,α1,α2,α3为该方程组的3个解,且则该线性方程组的通解是_________、17、已知P是3阶正交矩,向量_________、18、设2是矩阵A的一个特点值,则矩阵3A必有一个特点值为_________、19、和矩阵A=相似的对角矩阵为_________、20、设矩阵A=,若二次型f=x T Ax正定,则实数k的取值范围是_________、三、计算题(本大题共6小题,每小题9分,共54分)21、求行列式D=22、设矩阵A=求满足矩阵方程XA-B=2E的矩阵X、23、若向量组的秩为2,求k的值、24、设矩阵(1)求A-1;(2)求解线性方程组Ax=b,并将b用A的列向量组线性表出、25、已知3阶矩阵A的特点值为-1,1,2,设B=A2+2A-E,求(1)矩阵A的行列式及A的秩、(2)矩阵B的特点值及和B相似的对角矩阵、26、求二次型f(x1,x2,x3)=-4x1x2+2x1x3+2x2x3经可逆线性变换所得的标准形、四、证明题(本题6分)27、设n阶矩阵A满足A2=E,证明A的特点值只能是、。