灾情巡视路线最优化的方案(刘)
铁路部门在洪水期间的线路巡查与险情处置方案

铁路部门在洪水期间的线路巡查与险情处置方案在洪水期间,铁路部门的线路巡查与险情处置方案具有重要的意义。
洪水可能对铁路线路造成严重影响,如路基冲毁、桥梁损毁、铁轨被冲毁等,会给铁路运输安全带来极大威胁。
因此,及时进行线路巡查和灾情处置显得尤为重要,能够及时发现问题并采取相应措施,保障铁路运输的安全与稳定。
本文将从洪水期间的线路巡查和险情处置方案两个方面来详细讨论铁路部门的措施。
一、线路巡查方案在洪水期间,铁路部门的线路巡查是保障铁路安全运行的基础工作。
以下是一些常用的线路巡查方案:1.定期巡查:铁路部门应建立一套定期巡查制度,按照规定的频率对铁路线路进行巡查。
尤其是在洪水期间,巡查的频率应更加密切,确保及时发现洪水对线路造成的潜在威胁。
2.重点部位巡查:针对洪水容易造成损害的重要部位,如桥梁、隧道等,应加大巡查力度。
同时,要加强对路基、铁轨等基础设施的巡查,确保其完好,不受洪水侵害。
3.科技手段辅助:可以利用无人机、遥感技术等高新技术手段进行线路巡查,通过空中监测,提前发现洪水对线路的潜在威胁。
这样可以节省人力物力,提高巡查效率。
4.实时监测:通过灾害监测系统,实时监测线路的变化。
一旦发现问题,能够及时采取应急措施,避免事故的发生。
5.人员培训:铁路部门应对相关人员进行培训,提高其对洪水期间线路巡查的专业知识和技能水平,使其能够按照规程进行巡查工作。
二、险情处置方案一旦发现洪水对线路产生了潜在威胁,铁路部门应采取有效措施进行险情处置。
以下是一些常用的险情处置方案:1.立即停运:一旦发现线路存在严重险情,如路基冲毁、桥梁损毁等,必须立即停运,确保列车和乘客的安全。
解决险情前,不得恢复运营。
2.设置警示标志:在险情处置期间,铁路部门应在险情点和周边区域设置明显的警示标志,提醒人员注意安全。
3.紧急修复:一旦确定险情,铁路部门应立即组织专业人员进行紧急修复。
修复过程中,需采取合理的施工措施,确保施工安全。
加强地震监测预警提升应急能力巡视整改方案

加强地震监测预警提升应急能力巡视整改方案地震作为一种不可预测且具有巨大破坏力的自然灾害,给人类的生命和财产安全带来了严重威胁。
为了有效应对地震灾害,加强地震监测预警,提升应急能力,特制定本巡视整改方案。
一、背景与目标(一)背景近年来,地震活动频繁,造成了不同程度的人员伤亡和财产损失。
尽管在地震监测和应急响应方面取得了一定的成绩,但仍存在一些亟待解决的问题,如监测设备老化、预警信息传递不畅、应急救援队伍建设不足等。
(二)目标通过本次巡视整改,全面提升地震监测预警的准确性和及时性,完善应急响应机制,提高应急救援能力,最大限度地减少地震灾害造成的损失,保障人民群众的生命财产安全。
二、存在的问题(一)地震监测网络不完善部分地区监测站点分布稀疏,监测手段相对单一,难以全面、准确地捕捉地震活动信息。
(二)预警信息传递效率低预警信息发布渠道有限,未能覆盖到所有潜在受影响区域和人群,导致预警信息传递不及时、不准确。
(三)应急救援队伍专业化程度不高救援人员缺乏系统的培训和实战经验,装备配备不足,影响救援效率和效果。
(四)公众防震减灾意识淡薄公众对地震的危害认识不足,缺乏应急避险和自救互救的知识和技能。
(五)应急物资储备不足应急物资种类不全、数量不够,储备地点布局不合理,导致在灾害发生时无法及时满足救援需求。
三、整改措施(一)优化地震监测网络1、增加监测站点的数量和密度,特别是在地震多发区域和重点防御区域,确保监测覆盖全面。
2、引入先进的监测技术和设备,如高精度地震仪、卫星遥感等,提高监测的精度和效率。
3、建立监测数据共享平台,实现不同地区、不同部门之间的监测数据互联互通,加强数据分析和处理能力。
(二)提高预警信息传递效率1、拓展预警信息发布渠道,包括广播、电视、手机短信、社交媒体等,确保预警信息能够快速、广泛地传播。
2、建立健全预警信息发布机制,明确发布主体、发布流程和发布标准,确保预警信息的准确性和权威性。
3、加强对公众的预警信息宣传和教育,提高公众对预警信息的认知和响应能力。
2024年防汛抗洪巡堤查险工作方案范文

2024年防汛抗洪巡堤查险工作方案范文____年防汛抗洪巡堤查险工作方案一、背景和目标近年来,全球气候异常,极端天气频繁发生,我国防汛抗洪任务越来越重。
堤防作为防洪的重要设施,其安全稳定性直接关系到人民群众的生命财产安全。
为了确保堤防的安全性,满足人民群众对防误抗灾的需求,我国每年都要对各级巡堤查险。
为了提高巡堤查险效率,确保任务的完成,特制定本工作方案,对____年防汛抗洪巡堤查险工作作出具体安排和指导。
二、工作内容和方法1. 工作内容(1)确认巡查区域:根据各地的具体情况,确定巡查区域。
根据堤防维护范围,逐级划分巡查区域。
(2)明确巡查时间:根据气象部门的天气预报,确定巡查时间。
尽量选择干燥、无降水的天气进行巡查。
(3)制定巡查路线:根据巡堤查险的要求,科学合理地规划巡堤路线。
在规划巡堤路线时,应考虑到堤防的特点和管护人员的工作范围,确保能够全面、高效地巡查。
(4)巡查内容:巡查内容包括但不限于下列方面:a. 检查堤体和堤坡的稳定性,是否存在塌方、滑坡等情况;b. 检查堤面上的杂草、杂物等是否清理干净;c. 检查堤内和堤外的水位,是否存在渗漏现象;d. 检查堤背、堤顶的防护措施,是否完好;e. 检查堤防上的生态环境,是否存在破坏现象。
(5)整理巡查记录:在巡堤过程中,对发现的问题进行详细记录,包括问题的性质、位置、严重程度等。
并对问题进行分类整理,提出相应的处理措施,并及时上报相关部门。
(6)评估巡查结果:根据巡查结果,评估巡查的效果,为下一步的工程设计和管理提供参考。
2. 工作方法(1)综合利用现代化技术手段,如卫星遥感、无人机、激光雷达等,对巡查区域进行快速、全面的调查,以提高巡查效率和准确性。
(2)加强巡查人员的培训,提高其巡查能力和技术水平。
(3)借鉴其他地区的经验,推广先进的巡查管理制度和工作方法。
三、工作计划和组织1. 工作计划(1)年度工作计划:根据气象部门的天气预报,提前确定巡查的时间。
复习案例:最佳灾情巡视路线.ppt

最新.课件
166
18 4.74
22.74 19
组名 I II III IV
表3
路
线
(路程单位:公里;时间单位:小时) 路 线 停留 行走 完成巡视 总长度 时间 时间 的总时间
O—2—5—6—7—E—8—E—11—G—12—H—12 —F—10—F—9—E—7—6—5—2—O
195.8
17
5.59
最新.课件
191.1
241.9 125.5
558.5 13
因为该分组的均衡度
0
(C1) (C2) max (Ci )
241.9 125.5 241.9
54.2%
.
i1,2,3
所以此分法的均衡性很差.
为改善均衡性,将第Ⅱ组中的顶点C,2,3,D,4
分给第Ⅲ组(顶点2为这两组的公共点),重新分
分组后的近似最优解见表2.
均分配给4个组,每个组约需17/4=4.25小时<6.75小
小时,故分成4组是可能最办新.课到件的.
17
现在尝试将顶点分为4组.分组的原则:除遵从 前面准则1、2、3外,还应遵从以下准则:
准则4 尽量使各组的停留时间相等. 用上述原则在下图上将图分为4组,同时计算 各组的停留时间,然后用算法一算出各组的近似最 最佳旅行售货员巡回,得出路线长度及行走时间, 从而得出完成巡视的近似最佳时间. 用算法一计 计算时,初始圈的输入与分三组时同样处理. 这4组的近似最优解见表3.
最新.课件
6
近证第因似最能2二)算佳得,边法旅到3逐)求行,较次其售4优修)一货步的正个员分计法近问别算的似题用结结最是三果果优N种. 与P解方—初,法完始来产全圈代生问有替初题关最始,,采故优圈用本解,一算.以种法保
灾区巡视路线答案
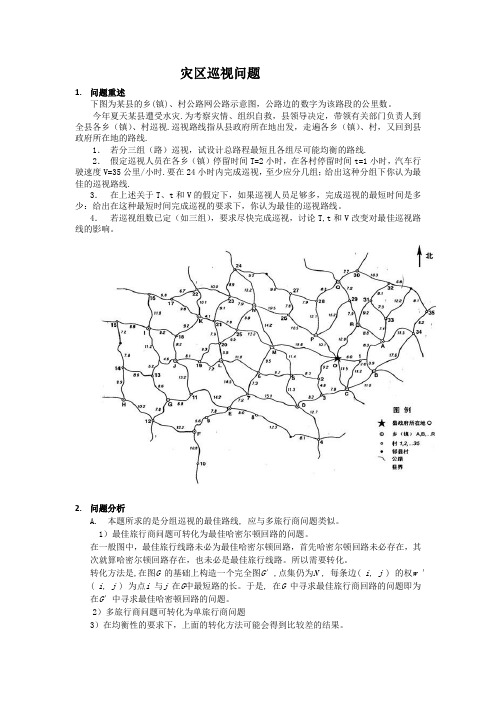
灾区巡视问题1.问题重述下图为某县的乡(镇)、村公路网公路示意图,公路边的数字为该路段的公里数。
今年夏天某县遭受水灾.为考察灾情、组织自救,县领导决定,带领有关部门负责人到全县各乡(镇)、村巡视.巡视路线指从县政府所在地出发,走遍各乡(镇)、村,又回到县政府所在地的路线.1.若分三组(路)巡视,试设计总路程最短且各组尽可能均衡的路线.2.假定巡视人员在各乡(镇)停留时间T=2小时,在各村停留时间t=1小时,汽车行驶速度V=35公里/小时.要在24小时内完成巡视,至少应分几组;给出这种分组下你认为最佳的巡视路线.3.在上述关于T、t和V的假定下,如果巡视人员足够多,完成巡视的最短时间是多少:给出在这种最短时间完成巡视的要求下,你认为最佳的巡视路线。
4.若巡视组数已定(如三组),要求尽快完成巡视,讨论T,t和V改变对最佳巡视路线的影响。
2.问题分析A.本题所求的是分组巡视的最佳路线, 应与多旅行商问题类似。
1)最佳旅行商问题可转化为最佳哈密尔顿回路的问题。
在一般图中,最佳旅行线路未必为最佳哈密尔顿回路,首先哈密尔顿回路未必存在,其次就算哈密尔顿回路存在,也未必是最佳旅行线路。
所以需要转化。
转化方法是,在图G 的基础上构造一个完全图G′,点集仍为N , 每条边( i, j ) 的权w ′( i, j ) 为点i 与j 在G中最短路的长。
于是, 在G 中寻求最佳旅行商回路的问题即为在G′中寻求最佳哈密顿回路的问题。
2)多旅行商问题可转化为单旅行商问题3)在均衡性的要求下,上面的转化方法可能会得到比较差的结果。
因此,这个问题应该先分组,再用单旅行商问题的方法求解。
B.第一问的分析1)分组方法和依据地理位置、最小生成树、最短路生成树、最优单旅行商路线2)均衡性的度量a=(max (Ci) - min (Ci))/ m ax (Ci)3)调整策略及依据各路线的长度、相邻点的数量、两组点间的距离C.第二问的分析1)确定最少组数停留时间:17*2+35*1=692)停留时间与路程的转化3)解法类似第一问,顶点数、转移点D.第三问的分析1)确定最短时间2)分组理论证明、设计算法21E.第四问3.模型假设与符号说明✧假设路面情况一切正常,汽车保持恒定速度行驶;✧分组完成后,小组内部不得在进行分组,需统一行动;✧第二次经过的城镇,第二次不停留;✧公共城镇停留时间只计算一次;✧小组行动后,无任何特殊事情影响进程;✧Pi表示个巡视组的巡视路程长度,i=1,2,3,…,n;✧Ti表示各巡视组的巡视时间,i=1,2,3,…,n;✧N表示分组数;✧Y表示距离均衡度函数;✧U表示时间均衡度函数;4.模型建立与求解问题可以转化为最佳旅行商问题,求加权图G(V,E)的旅行商回路。
灾情巡视路线

各组所走的路程分别为(单位:km) :212.2、125.5、215.9, 各组所走的路程总和为(单位:km) :553.6, 并求出其均衡度为:0.49。 4.2 问题二 4.2.1 问题分析 与第一题相同, 将巡视人员分为几组便将区域划分为几个部分。因此我们首 先确定在 24 小时内至少需要将巡视人员分为几组。在划分区域的过程中,经过 观察与计算发现,图中乡、村的分布十分的均匀,不存在某个区域集中出现乡或 者镇, 因此可以忽略停留时间对最小生成树与深度搜索的影响。所以我们套用第 一问的模型。 先进行粗略的分割得到大致所需的路程,然后根据最小生成树进行 深度优先算法,得到精确的路径,根据路径算出各组所需时间以及总时间。 4.2.2 模型的求解 首先计算需要把巡视人员分为几组: 乡镇停留时间:T=2 小时,村镇停留时间:t=1 小时,车速:V=35 公里/小时,乡 镇共有 17 个,村镇有 35 个, 总停留时间为 17×2+35=69 小时,要在 24 小时内 完成巡回,若不考虑汽车行驶时间,由 69/i<24(i 为分的组数)得到 i 最小为 4, 故至少要分 4 组。 由于该网络的乡(镇)、村分布较为均匀,故有可能找出停留时间尽量均衡的 分组,当分 4 组时各组停停留时间大约为 69/4=17.25 小时, 则每组分配在路途上 的时间大约为 24-17.25=6.75 小时。 根据第一问, 分三组时有个总巡视路程 602 公里,分 4 组时的总路程不会 比 603 公里大太多 , 不妨以 603 公里作为第二问的巡视总路程。路上约花 603/35=17 小时,若平均分配给 4 个组,每个组约需 17/4=4.25 小时小于 6.75 小 时,故巡视路线分成 4 组是合理的。 接下来套用第一题的最小生成树的 DFS 模型,得出了以下四个分组的路径:
数模论文之灾情巡视路线

数模论文之灾情巡视路线(相对优化方案)嘿,各位亲爱的数模爱好者,今天我们来聊聊灾情巡视路线的优化方案。
这个问题可是关系到救援效率和灾民生命安全的头等大事,咱们可得好好研究研究。
先来分析一下现有的巡视路线。
一般来说,现有的路线都是按照行政区域划分,从A点到B点,再到C点,看似合理,但实际上存在很多问题。
比如说,路线过长,导致救援队伍无法在第一时间赶到现场;路线规划不合理,有时候会绕弯路,浪费时间;还有,巡视路线上的重点区域划分不清,容易导致救援资源分配不均。
那怎么办呢?咱们得来个相对优化方案。
下面我就用意识流的方式,给大家详细讲解一下这个方案。
我们要运用图论的知识,对初步的巡视路线进行优化。
具体操作如下:1.将受灾点视为图的节点,受灾点之间的距离视为图的边,建立一张灾情巡视图。
2.运用Dijkstra算法,计算从救援队伍出发点到各个受灾点的最短路径。
3.对最短路径进行排序,优先考虑受灾程度较高的区域。
4.根据道路状况和救援队伍的行动速度,调整路径顺序,使得救援队伍在巡视过程中能够高效地到达各个受灾点。
5.对优化后的巡视路线进行评估,包括救援时间、救援成本、救援效果等方面,确保方案的科学性和实用性。
在这个过程中,我们还要考虑到一些特殊情况。
比如说,有些受灾点因为地形原因,无法直接到达,这时候我们可以采用无人机等先进设备进行巡视。
再比如,有些受灾点之间可能存在交通管制,这时候我们需要及时调整路线,确保救援队伍能够顺利到达。
优化方案有了,就是实施阶段。
我们要与政府部门、救援队伍、志愿者等各方密切配合,确保方案的顺利实施。
具体操作如下:1.制定详细的实施方案,明确各部门的职责和任务。
2.建立一个灾情信息共享平台,实时更新受灾点的受灾情况和救援进度。
3.对救援队伍进行培训,提高他们的救援技能和应对突发事件的能力。
4.加强宣传,提高公众对灾情巡视路线优化方案的认识和支持。
5.定期对方案进行评估和调整,以适应不断变化的灾情和救援需求。
线路设备灾后巡查制度范本

线路设备灾后巡查制度范本一、总则为确保自然灾害后电力线路及设备的安全稳定运行,及时发现和消除安全隐患,预防事故发生,制定本制度。
本制度适用于我国范围内遭受自然灾害后的电力线路及设备灾后巡查工作。
二、组织机构1. 成立灾后巡查领导小组,由公司领导、相关部门负责人及运维人员组成,负责灾后巡查工作的组织、协调和监督。
2. 设立巡查小组,成员由具备丰富经验的运维人员组成,负责具体巡查工作。
三、巡查内容1. 线路设备:杆塔、导线、绝缘子、塔基、拉线、配电设备等。
2. 附属设施:标识牌、防护网、驱鸟装置、接地装置等。
3. 环境因素:沿线地形、地貌、气象条件、交叉跨越、附近建筑物等。
4. 安全隐患:杆塔倾斜、拉线松动、绝缘子破损、导线断股、设备故障等。
四、巡查周期1. 自然灾害发生后立即开展首次巡查。
2. 首次巡查后,根据灾害程度和天气情况,制定后续巡查计划。
3. 重点区域和关键设备应增加巡查频率。
五、巡查流程1. 巡查前准备:检查巡查工具、仪器设备、安全防护用品等。
2. 巡查中执行:按照预定的巡查路线和内容进行逐项检查,发现问题及时记录。
3. 巡查后汇报:将巡查发现的问题及时上报领导小组,并提出整改建议。
4. 整改落实:领导小组根据巡查报告,制定整改措施,落实整改责任人和整改时间。
5. 整改验收:整改完成后,进行验收,确保问题得到有效解决。
六、巡查要求1. 巡查人员应具备相应的专业知识和技能,熟悉线路设备结构和工作原理。
2. 巡查过程中,严格遵守安全规程,确保人身和设备安全。
3. 巡查记录应详细、准确,涉及到的设备编号、位置、问题描述等信息要完整。
4. 领导小组要密切关注天气变化,及时调整巡查计划和策略。
5. 对于重大隐患问题,要立即采取临时措施,确保不影响电力供应。
七、考核与奖惩1. 对认真负责、及时发现和报告问题的巡查人员进行表彰和奖励。
2. 对巡查不到位、漏报重要问题的责任人进行批评教育,严重者依法依规处理。
灾情巡视路线地数学模型

word灾情巡视路线的数学模型摘要本文是解决灾情巡视路线最优安排方案的问题。
某县领导将带人下乡巡视灾情,打算从县城出发,视察所有乡、村后返回县城。
为确定安排巡视路线,本文将此安排问题转化为旅行售货员问题,建立了四个最优化模型解决问题。
对于问题一,建立了双目标最优化模型。
首先将问题一转化为三个售货员的最优旅行售货员问题,得到以总路程最短和路程均衡度最小的目标函数,采用最短路径的Dijkstra算法,并用MATLAB软件编程计算,得到最优树图,然后按每块近似有相等总路程的标准将最优树分成三块,最后根据最小环路定理,km km km km,路程均衡度为2.47%,具体巡视路线安排见表1。
对于问题二,建立了单目标最优化模型。
首先根据条件计算可确定至少要分4组巡视,于是可将问题转化为四个售货员的最优旅行售货员问题,采用Kruskal 算法求出巡视路线的最小生成树。
再根据求最优哈密顿圈的方法,运用LINGO 软件编程计算,求出了各组的最优巡视路线。
各组巡视的路程分别为154.3km、184km、km、km,时间分别为h、h、h、h,时间均衡度为4.82%,具体巡视路线安排见表2。
对于问题三,建立了以最少分组数为目标函数的单目标最优化模型。
运用问题一中最短路径的Dijkstra算法,运用LINGO软件编程计算,得到从县城到各点的最短距离,再经过计算可得到本问的最短巡视时间为6.43小时。
最后采用就近归组的搜索方法,逐步优化,最终得到最少需要分22组进展巡视,具体的巡视方案见表3。
对于问题四,建立了单目标优化模型,并且对变量进展讨论。
在分析乡〔镇〕停留时间T,村庄停留时间t和汽车行驶速度V的改变对最优巡视路线的影响时,我们通过控制变量的变化,初步的得出了当T与t变化时和V变化时对最优巡视路线的影响。
关键词最优化模型旅行售货员问题最优哈密顿圈今年夏天某县遭受水灾,为考察灾情、组织自救,县领导决定,带领有关部门负责人到全县各乡、村巡视。
5灾情巡视路线

灾情巡视路线第十二组(原十三组)李江南江云胜樊明瑾摘要本题给出了某县的乡(镇)、村公路网示意图, 要求的是在不同条件下的灾情巡视的最佳分组方案和路线。
是一个最佳推销员回路问题,运用最小生成树、动态规划等模型成功地解决了分组数、时间、最佳路线等问题问题一,先用图论软件包求出从O点到其他顶点的最短路,得到一以O为根,有6条干枝的二叉树,然后分为三组,将每组中的点看作是一加权无向图的一系列顶点, 得到一完备图,再将该完备图拓展成增广完备图。
然后确立初始H圈(哈密尔顿圈),利用二边逐次修正法和矩阵翻转法,并在MATLAB中编程求解出该增广完备图上的近似最优H圈,即巡视路线。
三组的路线长度分别为191.1km,215.3km 和192.2km。
巡视路线的总长度为598.6km,均衡度为11.2%。
问题二,先根据问题一的结果及题给条件,可求得至少要分4组,然后将图一的二叉树按照四个准则分为4组,得四个子图。
用问题一的算法求得每个子图的近似最优H圈。
四组的巡视路线长度分别为154.3km,185km,140.1km和230.6km。
巡视路线的总长度为710km,巡视路线的均衡度为39.2%,巡视时间的均衡度为2.59% 问题三,该问是要求在T,t和V的假定下,完成巡视的最短时间及在此条件下的最佳巡视路线。
由第一问中所求出的最小树,可得距O最远的点为H点,距T=2+77.5*2/35=6.4286h。
离为77.5km。
由此可求得,完成巡视的最短时间为:minT。
最后可分为23组来巡视。
按照相关的准则分组,使得每组的巡视时间不超过min问题四,讨论了分组一定时,停留时间T、t及车辆行进速度V的变化对总巡视时间的影响,判断了三者在不同大小时对总时间影响的主次权重。
关键词:图论二边逐次修正法矩阵翻转法近似最优H圈均衡度问题重述下图为某县的乡(镇)、村公路网示意图,公路边的数字为该路段的公里数。
今年夏天该县遭受水灾。
为考察灾情、组织自救,县领导决定,带领有关部门负责人到全县各乡(镇)、村巡视。
灾情巡视问题

三峡大学12组最优灾情巡视路线摘要本文解决的是灾情巡视路线的最佳安排问题,我们将其转化为多个推销员回路问题,并针对灾情巡视的不同要求,用哈密顿回路法求出了各情况下的近似最优解。
针对问题一:本文采用Kruskal 法求出最小生成树图,然后以最小生成树为依据将该县分为三个区域,分别对应三组巡视人员。
然后利用哈密顿法求解出各组最短的巡视路程,分别为第一组197.6km 、第二组196.8km 、第三组206.8km ,总路程为601.2km 。
最后用本文中自定义的路程均衡度来衡量分组的均衡性,路程均衡度为5.0%,各组的均衡性很好。
针对问题二:本文在解决问题一的基础上,将该县分为四个区域。
然后利用哈密顿法求解出四个区域的最短巡视路程,进而求出巡视时间和停留时间,得到各组的巡视总时间,分别为第一组21.1小时、第二组22.5小时、第三组23.0小时、第四组21.5小时。
其中时间均衡度为8.6%,满足题目要求。
针对问题三:本文分析得出,巡视的最短时间为6.43小时,然后我们根据最短时间并依据最小生成树图将巡视人员分为七组,在新的巡视规则下很好的完成了巡视任务。
各组的巡视路线和停留点时间如下表: 针对问题四:本文在不破坏原来分组均衡性的条件下,讨论了,,T t V 对分组的影响,并得出,,T t V 的最大变化范围。
最后根据得出的结论对分三组的实例进行定量分析,验证了结论的可行性。
组号 巡视路线时间/小时1 2567912141297652O E F H H F E O --------------------6.432 252021181518212025O M K L L K M O ---------------- 5.873 2561913111319652O L J G G J L O ------------------ 6.154 234891098432O D E F F E D O ------------------ 6.385 282726242322171617222324262728O P N N P O -------------------- 6.376 123133341123133341O R A B C O R A B C O -------------------- 5.38 72930323534129303235341O R Q A O R Q A O -------------------- 5.48关键字:哈密顿回路 最小生成树 F l o y d 算法1问题重述下图为某县的乡(镇)、村公路网示意图,公路边的数字为该路段的公里数。
灾情巡视路线的最优化方案(刘)

约束最优路线的模拟退火一、问题描述今年夏天该县遭受水灾。
为考察灾情、组织自救,县领导决定,带领有关部门负责人到全县各乡(镇)、村巡视。
巡视路线指从县政府所在地出发,走遍各乡(镇)、村,又回到县政府所在地的路线。
1.若分三组(路)巡视,试设计总路程最短且各组尽可能均衡的巡视路线。
2.假定巡视人员在各乡(镇)停留时间T=2小时,在各村停留时间t=1小时,汽车行驶速度V=35公里/小时。
要在24小时内完成巡视,至少应分几组;给出这种分组下你认为最佳的巡视路线。
3.在上述关于T,t和V的假定下,如果巡视人员足够多,完成巡视的最短时间是多少;给出在这种最短时间完成巡视的要求下,你认为最佳的巡视路线。
4.若巡视组数已定(如三组),要求尽快完成巡视,讨论T,t和V改变对最佳巡视路线的影响。
二、问题分析及模型的建立因为是分组巡视(不妨设分N组),要直接确定一个组巡视哪些地点是困难的。
由于将各组巡视的路线连接起来可看成一条N次相继从县城出发又回到县城的路线,这样,多组巡视就化成了单组巡视。
经分析,我们认为前3问及第4问计算部分都是组合规划中的约束优化问题,均属以模型()()()nj x g mi x h st x f j i ,,2,1,0,,2,1,0.min ⋯=≥⋯== (I ) 为基础的约束最优路线模型。
下面根据各问的要求,分别对4个问题进行具体讨论。
对于问题1,如果选取总路程最短的所有巡视路线中最均衡的,一般这一路线仍会很不均衡。
故除了要总路程短,另需“均衡”提出一定的要求,即组间巡视路线的长度差不大于某给定值L 。
还有路线能够分成3次从县城O 出发再回到O 、各组经过地点的并集为所有顶点的集合只之约束。
模型如下:()APLf f Nn st f f F n i i =≤-=-+≤≤ 1min max min max .min λ (II) 其中F 为巡视总路程,N 为要求的分组数(本问N=3),n 是优化过程中路线的实际分组数,f max 和f min 分别为n 组中最长和最短组的巡视路程,P i 为第i 组巡视地点的集合,A 是所有顶点的集合。
灾情巡视路线选择

根据上述的问题分析,先把 6 个干枝编号①-⑥,把①②分为一组,③④分 为一组,⑤⑥分为一组。分组如下:
计算其总距离与均衡度,计算结果如下:
均衡度α
=
241.9−125.5 241.9
= 48.12%
由上面的计算结果可以看出, 其总距离较短但是均衡度较大, 所以这种划分不合 理要进行优化。所以要将现有的路线进行手工改进,稍稍改变其路线,调整均衡 度,改进后的结果如下:
195.8
22.59
Ⅱ
162.4
22.64
Ⅲ
156.9
21.48
Ⅳ
186.6
22.33
我们可以看出 4 条路线的巡视都在 24 小时内完成,而且都控制在 23 小时内,路 线划分合理。
问题三 3.3.1 问题分析 对于问题三,我们可以从题目得到,巡视的人员足够多,但是务必要求在最 短的时间内完成巡视。 要求最短的时间, 就应该求出离县委政府 O 最远的乡 (镇) 或村所需的时间,且在途经的乡(镇)或村不作停留,这样才能求出最短的巡视 时间。我们要得到最佳的巡视路线,尽管人员足够多,我们还是应当避免不必要 的人力物力的浪费, 每组完成巡视的时间应当尽量差不多。根据最小生成树及该 县地图还有求出的最短的巡视时间,我们将整个巡视路线进行统筹规划,合理分 组。 3.3.2 问题解答 我们通过计算可得离县委政府 O 最远的乡 (镇) 为 H, 到 H 所需的时间至少是 6.43 小时。并通过最小生成树及该县的地图进行合理的分组。显然,其余组的时间要 小于第一组 O-H-O 的时间 6.43 小时,根据统筹学,我们进行了合理的划分和计 算。详细如下表: 小组名 称 第一组 第二组 第三组 第四组 第五组 第六组 第七组 第八组 第九组 第十组 第十一 组 第十二 组 第十三 组 第十四 组 第十五 组 路线 O-H-O O-3-D-4-D-3-2-O O-2-5-6-M-O O-2-5-6-7-E-9-F-12-F-9-E-7-6-5-2-O O-2-5-6-7-E-9-F-10-F-9-E-7-6-5-2-O O-2-5-6-E-11-G-11-E-6-5-2-O O-2-5-6-7-E-9-F-9-E-7-6-5-3-O O-2-5-6-7-E-11-E-8-E-8-E-11-E-7-6-5-2-O O-2-5-6-L-20-L-6-5-2-O O-2-5-6-L-19-J-13-14-13-J-19-L-6-5-2-O O-2-5-6-L-19-J-19-L-6-5-2-O O-M-25-21-K-17-16-17-K-21-25-M-O O-M-25-21-K-18-I-15-I-18-K-21-25-M-O O-M-25-21-K-18-I-18-K-21-25-M-O O-M-25-21-K-21-25-M-O 所用时间 (h) 6.43 5.99 6.34 5.85 5.76 5.58 6.15 5.65 5.54 6.15 6.10 5.45 5.99 5.49 5.49 停留地 时间差 点 (h) H 0 3、4、D 0.44 2、3、5、 0.09 M 9、12 0.58 7、10 0.67 G 0.85 F、E 0.28 8、11 0.78 L、20 0.89 13、14 0.28 19、J 16、17 15、18 I 21、K 0.33 0.98 0.44 0.94 0.94
灾情巡视路线程序

9附录附录一:Kruskal最小树成法程序clear all%图论最小生成树Kruskal避圈算法%w为邻接矩阵w=[0 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 10.3 5.9 11.2 inf inf inf inf inf inf inf inf inf inf inf 6 inf inf inf ; inf 0 4.8 inf 8.3 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 8.2 inf inf inf ;inf 4.8 0 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 7.8 8.2 inf inf inf inf inf inf inf inf inf inf inf inf inf inf ;inf inf inf 0 inf inf inf 20.4 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 12.7 inf inf inf inf inf inf inf inf inf inf inf inf inf inf ; inf 8.3 inf inf 0 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 11.3 inf inf inf inf inf inf inf inf 11.4 inf inf inf inf inf ; inf inf inf inf 9.7 0 7.3 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 11.8 9.5 inf inf inf inf inf ; inf inf inf inf inf 7.3 0 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 15.1 7.2 inf inf inf inf inf inf 14.5 inf inf inf inf inf inf ; inf inf inf 20.4 inf inf inf 0 inf inf inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 8 inf inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf 0 inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 7.8 5.6 inf inf infinf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf 0 infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 10.8 inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf 0 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 14.2 inf 6.8 infinf 13.2 inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf inf0 inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 12.2 7.8 10.2 inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf 0 8.6 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 8.8 inf 16.4 9.8 inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf 8.6 0 15 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf 9.9 infinf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf 15 0 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 8.8inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf 0 6.8 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 11.8 inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf 6.8 0 inf inf inf inf 6.7inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 9.8 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 0 inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 8.28.2 9.2 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 0 9.3 inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf8.1 inf 7.2 inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 9.3 0 7.9 infinf inf 6.5 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf 5.5 inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 7.9 0 inf9.1 inf 7.8 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 4.1 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf 6.7 inf inf inf inf 0 10 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf 10.1 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf 9.1 100 8.9 inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 7.9 inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf8.9 0 inf inf 18.8 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf 13.2 inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 6.5 7.8 infinf inf 0 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf 12 8.8 inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf 0 7.8 inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 10.5 inf 10.5 infinf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 18.8 inf 7.8 0 7.9 inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 7.9 0 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 12.1 8.3 inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 0 inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 15.2 7.2 7.8 ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 0 inf inf 10.3 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 7.7 inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 0 8.1 7.3inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 9.2 ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 8.1 0 19 inf 14.9 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf 10.3 7.3 190 inf inf 7.4 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf0 8.2 11.5 17.8 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf 14.9 inf 8.2 0 inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;10.3 inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf7.4 11.5 inf 0 inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 8.8 ;5.9 inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf 17.8 inf inf 0 11 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf ;11.2 inf 7.8 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 11 0 inf inf inf inf infinf inf inf inf inf inf 11.5 inf inf inf ;inf inf 8.2 12.7 11.3 inf 15.1 infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 0 inf infinf inf inf inf inf inf inf inf inf inf infinf ;inf inf inf inf inf inf 7.2 8 7.8 inf 14.2 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf 0 inf inf inf infinf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf 5.6 10.8 inf 12.2 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf 0 infinf inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf 6.87.8 8.8 inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf 0 inf infinf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf inf 10.2 inf 9.9 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf 0 inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf 16.4 inf inf 11.8 inf 8.2 inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 0 inf inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf 13.2 inf 9.8 inf inf inf inf 8.2 8.1 inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf0 inf inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf 9.8 9.2 inf inf 4.1 10.1 inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf 0 inf inf inf inf inf inf inf ;inf inf inf inf inf 11.8 14.5 inf infinf inf inf inf inf 8.8 inf inf inf 7.2 5.5inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 0 inf inf inf inf inf inf ;inf inf inf inf 11.4 9.5 inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf 12 inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf 0 14.2 19.8 inf infinf ;inf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf inf inf inf inf inf inf7.9 13.2 8.8 10.5 inf inf inf inf infinf inf inf inf inf inf inf inf inf inf infinf inf inf inf inf 14.2 0 inf inf infinf ;6 8.2 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 11.5 inf inf inf inf inf inf inf inf inf 19.8 inf 0 10.1 inf 12.8 ;inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 10.5 inf 12.1 15.2 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 10.1 0 inf inf ;inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 8.3 7.2 7.7 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 0 inf ;inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 7.8 inf 9.2 inf inf inf inf 8.8 inf inf inf inf inf inf inf inf inf inf inf inf inf 12.8 inf inf 0 ;];n=53;%有53个点k=1;for i=1:n-1for j=i+1:nif w(i,j)~=infx(1,k)=w(i,j);%记录边x(2,k)=i;%记录起点x(3,k)=j;%记录终点k=k+1;endendendk=k-1;%统计边数 k为边数%步骤一%冒泡法给边的大小排序for i=1:kfor j=i+1:kif x(1,i)>x(1,j)a=x(1,i);x(1,i)=x(1,j);x(1,j)=a;a=x(2,i);x(2,i)=x(2,j);x(2,j)=a;a=x(3,i);x(3,i)=x(3,j);x(3,j)=a;endendend%给各点标号赋初值for i=1:nl(i)=i;end%初始时选e1加入集合EE(1,1)=x(1,1); %E矩阵的第一行记录最小生成树的边长E(2,1)=x(2,1); %E矩阵的第二行记录边的起点E(3,1)=x(3,1); %E矩阵的第三行记录边的终点a=min([l(E(2,1)),l(E(3,1))]);l(E(2,1))=a;l(E(3,1))=a;b=1;%记录E中边数for i=2:k%步骤四if b==n-1 %如果树中边数达到n-1break%算法终止end%步骤二if l(x(2,i))~=l(x(3,i)) %如果两顶点标号不同b=b+1; %将这条边加入EE(1,b)=x(1,i);E(2,b)=x(2,i);E(3,b)=x(3,i);%步骤三for j=1:n %对于所有顶点if l(j)==max([l(E(2,b)),l(E(3,b))])%如果该顶点的标号,等于=,新加入边中的顶点标号较大的值l(j)=min([l(E(2,b)),l(E(3,b))]);%将其改为较小的那一个以避圈endendendendE附录二:问题一的求解程序1、计算强加权矩阵程序%floyd 算法通用程序,输入a为赋权邻接矩阵%输出为距离矩阵D,和最短路径矩阵pathfunction [D,path]=floyd(a)a=[0 inf inf inf inf inf inf inf inf inf inf inf inf 10.3 5.9 inf 6 inf inf inf ; inf 0 8.9 inf inf inf inf inf inf inf inf inf inf inf inf 7.9 inf inf inf inf ;inf 8.9 0 inf 18.8 inf inf inf inf inf inf inf inf inf inf 13.2 inf inf inf inf ; inf inf inf 0 7.8 inf inf inf inf inf inf inf inf inf inf 10.5 inf 10.5 inf inf ;inf inf 18.8 7.8 0 7.9 inf inf inf inf inf inf inf inf inf inf inf inf inf inf ;inf inf inf inf 7.9 0 inf inf inf inf infinf inf inf inf inf inf 12.1 8.3 inf ;inf inf inf inf inf inf 0 inf inf inf infinf inf inf inf inf inf 15.2 7.2 7.8 ;inf inf inf inf inf inf inf 0 inf 10.3 inf inf inf inf inf inf inf inf 7.7 inf ;inf inf inf inf inf inf inf inf 0 8.1 7.3inf inf inf inf inf inf inf inf 9.2 ;inf inf inf inf inf inf inf 10.3 8.1 0 19 inf 14.9 inf inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf 7.3 19 0inf 20.3 7.4 inf inf inf inf inf inf ;inf inf inf inf inf inf inf inf inf inf inf0 8.2 11.5 17.8 inf inf inf infinf ;inf inf inf inf inf inf inf inf inf 14.9 20.3 8.2 0 inf inf inf inf inf inf inf ; 10.3 inf inf inf inf inf inf inf inf inf7.4 11.5 inf 0 inf inf inf inf inf 8.8 ;5.9 inf inf inf inf inf inf inf inf inf inf 17.8 inf inf 0 inf inf inf inf inf ;inf 7.9 13.2 10.5 inf inf inf inf inf inf inf inf inf inf inf 0 inf inf inf inf ;6 inf inf inf inf inf inf inf inf inf inf inf inf inf inf inf 0 10.1 inf 12.8 ;inf inf inf 10.5 inf 12.1 15.2 inf inf inf inf inf inf inf inf inf 10.1 0 inf inf ;inf inf inf inf inf 8.3 7.2 7.7 inf inf inf inf inf inf inf inf inf inf 0 inf ;inf inf inf inf inf inf 7.8 inf 9.2 inf inf inf inf 8.8 inf inf 12.8 inf inf 0 ;];n=size(a,1);D=a;path=zeros(n,n);for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j;endendendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendend2、第1组巡视最短路线程序(第2,3组只变换数据)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
约束最优路线的模拟退火解法说明:以98年全国大学生数模竞赛中的B 题(即“灾情巡视路线”)为例,介绍能解一类较广泛的约束最优路线问题的方法−−模拟退火法[1]。
该法对“灾情巡视路线”这类有约束以及“(一般)旅行推销员”、“中国邮递员”等无约束组合优化问题均能求得较好的近似解,具有适用范围广和可拓展的优点。
一、问题描述对于最短路、最大流、中国邮递员、旅行推销员等最优路线问题,常采用各自不同的方法求解。
若在这些问题中再加入一些约束条件,则原方法往往不再有效,如98年大学生数模竞赛中的B 题就是如此。
我们设计的方法较好地解决了这一问题。
现以98年B 题为例,介绍该法及其实现。
下面为该题文字部分,并称其四问分别为问题1至问题4: 下图(略)为某县的乡(镇)、村公路网示意图,公路边的数字为该路段的公里数。
今年夏天该县遭受水灾。
为考察灾情、组织自救,县领导决定,带领有关部门负责人到全县各乡(镇)、村巡视。
巡视路线指从县政府所在地出发,走遍各乡(镇)、村,又回到县政府所在地的路线。
1.若分三组(路)巡视,试设计总路程最短且各组尽可能均衡的巡视路线。
2.假定巡视人员在各乡(镇)停留时间T=2小时,在各村停留时间t=1小时,汽车行驶速度V=35公里/小时。
要在24小时内完成巡视,至少应分几组;给出这种分组下你认为最佳的巡视路线。
3.在上述关于T ,t 和V 的假定下,如果巡视人员足够多,完成巡视的最短时间是多少;给出在这种最短时间完成巡视的要求下,你认为最佳的巡视路线。
4.若巡视组数已定(如三组),要求尽快完成巡视,讨论T ,t 和V 改变对最佳巡视路线的影响。
二、问题分析及模型的建立因为是分组巡视(不妨设分N 组),要直接确定一个组巡视哪些地点是困难的。
由于将各组巡视的路线连接起来可看成一条N 次相继从县城出发又回到县城的路线,这样,多组巡视就化成了单组巡视。
经分析,我们认为前3问及第4问计算部分都是组合规划中的约束优化问题,均属以模型()()()n j x g mi x h st x f j i ,,2,1,0,,2,1,0.min ⋯=≥⋯== (I )为基础的约束最优路线模型。
下面根据各问的要求,分别对4个问题进行具体讨论。
对于问题1,如果选取总路程最短的所有巡视路线中最均衡的,一般这一路线仍会很不均衡。
故除了要总路程短,另需“均衡”提出一定的要求,即组间巡视路线的长度差不大于某给定值L 。
还有路线能够分成3次从县城O 出发再回到O 、各组经过地点的并集为所有顶点的集合只之约束。
模型如下:()AP Lf f Nn st f f F n i i =≤-=-+≤≤ 1min max min max .min λ (II) 其中F 为巡视总路程,N 为要求的分组数(本问N=3),n 是优化过程中路线的实际分组数,f max 和f min 分别为n 组中最长和最短组的巡视路程,P i 为第i 组巡视地点的集合,A 是所有顶点的集合。
约束条件(f max -f min )≤L 用来保证各组路程基本均衡,目标函数中加入λ(f max -f min )是为了使各组的路程尽可能均衡,这是一个约束多目标规划。
权重λ的取值应远小于目标函数中F 的权系数1,否则会因离散问题函数值的跳跃现象而导致优化困难。
这里,我们取λ=1/L 。
对问题2和3,因在原图中不是任意两顶点间均有边,故在多组巡视时可能存在二组以上经过的公共点,从而使顶点赋权遇到如下困难:若先赋点权,则这些公共点的权会被重复计算;而若在优化过程中赋点权,则又有公共点究竟应该由哪次(组)巡视的问题。
对此,我们采用Dijkstra 法算出任意两点间的最短路程并除以速度V 转化为时间,并用其作为两顶点间边的权构造一新图。
第三个约束条件保证了每点至少经过一次,而这时若路线中含除县城外的重复地点将至少增加1个小时(除县城为0外,其它点权为1或2小时),因而能保证优化结果中不出现县城以外的重复点。
经分析,我们认为这两问同属分组数和路线双重优化问题,具体模型如下:AP TMAXf N n st F n i i =≤=≤≤U 1max .min (III) 其中N 、n 、A 、P i 与模型(II )相同,F 为各组巡视时间之和, f max 为n 组中时间最长组的巡视时间,TMAX 是巡视允许的最长时间。
对问题2,TMAX=24;对问题3,因人员足够多,故每个地点可由一组单独巡视,因此完成巡视的最短时间是这些单点巡视的最佳路线中花时间最长的组对应的巡视时间,其值TMAX 由程序计算确定。
对最少分组数的优化,模型中没有体现,我们是通过主程序与辅助控制函数协同工作来实现该目的的,即在优化过程中,若路线调整发现最短与次短组的时间之和不大于TMAX ,且满足约束,则记录该路线后返回,并由主程序将分组数减1后重新优化,如果重新优化找不到满足约束的可行路线,则认为找到了最优解;而若优化函数没有找到满足约束的可行路线,主程序则将分组数加1后进行下一轮优化。
我们用m 和M 分别表示求解时尝试的最小和最大分组数,对问题2,取m=4,M=8,而对问题3,m=20,M=35。
对于问题4,其最佳路线是指在分组数N 已确定的情况下,巡视时间最长的组所对应的时间尽量短的路线。
下面给出其模型,各参数的含义同模型(III ),关于T 、t 和V 对路线的影响,我们将在结果与分析部分给出。
A P Nn st f ni i ==≤≤U 1max.min (IV) 三、模型的求解(一)算法选择由以上分析可知,本题的所有问题都可视为“在一定约束下,从一点出发再回到该点的最优路线寻求问题”。
如问题1可看成有约束的“一般旅行推销员”问题,但即使是无约束的“旅行推销员”问题,也尚未找到解这类问题最优解的多项式算法[3],对本题n=53这种情形,无论是“分枝与界限法”[4]还是动态规划[5]等方法,想得到最优解一般是不可能的,只能用近似算法。
选择模拟退火法,是因为它不同于一般的单纯下降法,它具有一定条件下的随机上升过程,有可能从一极小区域跃过波峰到过另一极小区域,因而具有解更接近全局最优解的优点。
(二)计算方法与步骤1.方法概述 下面介绍模拟退火法函数,主函数部分略。
模拟退火法是一种较新的算法,尚无固定的计算步骤[1]。
我们设计的基本操作包括路线调整、约束条件判断、调整许可预测、内部优化、与已有最佳路线的比较和最佳路线及相关数据的记录等。
路线调整在给定的工作点集序列上进行,其前部分为当前路线,后部分为剩余点集。
如此设计是因为在许多问题中某些点在路线中可能出现多次,如“田”字型图的“一般旅行推销员”问题,此时可将每一可能重复的点或所有点以最大可能重复出现的次数置于工作点集中。
路线的调整有5种(所有操作对象都是随机选取的):交换−路线内两路段(含点)互换;反转−路线中选取一路段反向;删除−路线内一路段移至路线外;插入−路线外一路段插入到路线中;替换−路线内外各取一路段互换。
约束条件判断由用户函数完成;调整允许预测由内部函数完成,它决定是否接受一上升过程;内部优化是仅有交换和反转操作的优化过程,与上层模拟退火法函数基本相同。
2.基本步骤(1) 由主程序传送工作点集、初始路线终点、记录器数目、温度初值t0、温度下降率FT、温度循环上限maxtk、每个温度的最大循环次数maxk和最多成功次操作次数max_suc、连续温度无改进时结束优化参数K等,并设置寻找可行路线的不成功次数n_suc:=0、最优路线条数rec_n:=0、优化值fx0:=maxfx、温度循环变量tk:=1,优化连续无改进温度次数same_tn:=0等内部变量初值;(2) 计算初始路线的目标函数值fx、优化控制函数值fx1。
若fx1<maxfx,则记录路线并置fx0:=fx+fx1、rec_n:=0;(3) 如果tk==maxtk或same_tn==K,转步(15);否则,置循环变量kk:=1,成功操作次数计数器sucn:=0等;(4) 如果kk==maxk或sucn==max_suc,转步(14);否则,计算当前路线的优化控制函数值fx1、在复制路线上调整路线并计算目标函数值fx和优化控制函数值fx2,得到两者的改变量dfx和dfx1,置dfx12:=dfx+dfx1,kk:=kk+1;(5) 若fx2<maxfx,转步(7);否则,若rec_n>0或rec_n==0且fx2>fx1,转步(4);(6) 执行100次内部优化并更改路线,若某次内部优化后fx2<maxfx,则跳出循环转步(7);否则n_suc:=n_suc+1,当n_suc>30时,转步(15);其它情况转步(4);(7)计算路线的辅助控制函数值fx3,若fx3<=-maxfx,则路线及相关数据记入记录器第一个位置,转步(15);否则,用dfx12和t为参数调用预测函数,若返回值为0,即不允许更改路线时转步(4);(8)进行若干次内部优化(次数动态调整),更新路线和目标函数值fx,重算优化控制函数值fx2,sucn:=sucn+1;(9)若fx+fx2>fx0,即比已有的最佳路线差,转步(4);否则检查是否与记录的路线重复,若重复则转步(4);(10)若fx+fx2<fx0,则记录器中原最佳路线后移,最佳路线数rec_n:=1,更新优化值fx0:=fx+fx2,路线及相关数据记入第一个位置,转步(4);(11) rec_n:=rec_n+1,并计算记录器中最后一条最优路线的辅助控制函数值fx4;(12)若fx3<fx4,与记录器中各路线的辅助控制函数值比较并据此确定记录器指针,当前路线插入相应位置,转步(4);(13)若记录器没满,则路线及相关参数记在已有最优路线之后;转步(4);(14)若tk<maxtk,则tk:=tk+1,t:=FT*t;若fx0比前一温度有改进,则same_tn:=0,否则same_tn:=sam_tn+1;转步(3);(15)算法终止。
此时若rec_n>0,则找到了最优路线,可从记录器中获取最优和次优路线及相关数据。
3.编程提示对分组的处理及模型中的变量n、P i、f max、f min、F和下面用到的次短组巡视时间f min1均由分组处理函数完成,因此它是解决分组问题的关键,分组方法是:当自然分组数不大于N时,取自然分组;否则将最短两组合并,直到组数等于N为止。
与总的设计思想相对应,程序设计应考虑多功能与通用性,以适应起点与终点相同和不同、单组和多组等各种要求。
由于有上升过程,故需一组变量存放当前最佳路线、最优值和路线终点位置等。
记录器参数组可满足人们想获取多条最优路线的要求。
