苏州大学2020届高考考前指导卷数学试卷(含附加题)

合集下载

江苏省2020年高考名师押题信息卷数学试题+附加题+答案+全解全析2020.6.29

江苏省2020年高考名师押题信息卷数学2020.6.29Ⅰ卷一. 填空题：本大题共14小题，每小题5分共计70分1．设集合A ＝{x |（x +1）（x ﹣2）＜0}，集合B ＝{x |1＜x ＜3}，则A ∪B ＝__________．2．i 是虚数单位，则|2+i 1−i|的值为__________． 3．若执行如图所示的算法流程图，则输出的结果是__________．4．（如图是一组样本数据的频率分布直方图，则依据图形中的数据，可以估计总体的平均数与中位数分别是__________5．有5支彩笔（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫．从这5支彩笔中任取2支不同颜色的彩笔，则取出的2支彩笔中含有红色彩笔的概率为__________．6.已知cos 6πα⎛⎫-= ⎪⎝⎭，则sin 26πα⎛⎫+= ⎪⎝⎭_____________.7．设S n 是等比数列{a n }的前n 项的和，S 3，S 9，S 6成等差数列，则a 2+a 5a 8的值为__________．8．在平面直角坐标系xoy 中，若双曲线22221(0,0)x y a b a b-=>>的一条准线与两条渐近线恰能围成一个等边三角形，则该双曲线的离心率为______．9．在平面直角坐标系xOy 中，已知A ，B 两点在圆x 2+y 2＝1上，若直线x +y −√6=0上存在点C ，使△ABC 是边长为1的等边三角形，则点C 的横坐标是__________．10．如图，是一个四棱锥的平面展开图，其中间是边长为2的正方形，上面三角形是等边三角形，左、右三角形是等腰直角三角形，则此四棱锥的体积为__________．11．已知函数f （x ）＝x 2﹣2x +3a ，g （x ）=2x−1．若对∀x 1∈[0，3]，总∃x 2∈[2，3]，使得f （x 1）≤g （x 2）成立，则实数a 的取值集合为__________． 12．在ABC ∆中，3,2,AB AC D ==为边BC 上一点．若25,3AB AD AC AD ⋅=⋅=-u u u v u u u v u u u v u u u v ，则AB AC ⋅u u u v u u u v 的值为_________．13．已知向量()1,3a =v ，(),1b x y =-v 且//a b v v ，若实数,x y 均为正数，则31x y+最小值是______ 14．已知f （x ）是R 上的偶函数，且f(x)={3x ，0≤x ＜1(13)x +1，x ≥1，若关于x 的方程f 2（x ）﹣mf （x ）＝0有三个不相等的实数根，则m 的取值范围__________．二、解答题：（本大题共6道题，计90分．解答应写出必要的文字说明、证明过程或演算步骤）15. (本小题满分14分)已知函数()221()cos sin cos ()2f x x x x x x R =+-∈. (1)求()f x 的单调递增区间.(2)在ΔABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若f (A )=1，c =10，cosB =17，求ΔABC 的中线AD 的长.16. (本小题满分14分)如图，在四棱锥P ﹣ABCD 中，四边形ABCD 为平行四边形，∠BAP ＝∠CDP ＝90°，E 为PC 中点．（Ⅰ）求证：AP ∥平面EBD ；（Ⅱ）若△P AD 是正三角形，且P A ＝AB ．（i ）当点M 在线段P A 上什么位置时，有DM ⊥平面P AB ；（ii ）在（i ）的条件下，点N 在线段PB 什么位置时，有平面DMN ⊥平面PBC ．17. (本小题满分14分) 如图，在平面直角坐标系xOy 中，椭圆2222:1(0)x y C a b a b+=>>的下顶点为B ，点,M N 是椭圆上异于点B 的动点，直线,BM BN 分别与x 轴交于点,P Q ，且点Q 是线段OP 的中点．当点N 运动到点处时，点Q 的坐标为(,0)3．（1）求椭圆C 的标准方程；（2）设直线MN 交y 轴于点D ，当点,M N 均在y 轴右侧，且2DN NM =u u u v u u u u v时，求直线BM 的方程．。

江苏省2020届高考数学考前押题卷含附加题(附解析)

8
概率为9.本题考查了列举法求概率．本题属于容易题． 6. 7 解析：当 S<20 时执行，S＝21 时，i＝7.本题考查了伪代码知识．本题属于容易
题． 7. 3 解析：抛物线焦点坐标为(2，0)，则双曲线中 c＝2，a＝1.由 c2＝a2＋b2，得 b＝
3.本题考查了抛物线与双曲线焦点．本题属于容易题． 11
则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．
段 PC 的中点．
A. (选修 42：矩阵与变换)
[ ] [ ] 2 －2
1 0
已知矩阵 A＝ 1 －3 ，B＝ 0 －1 ，设 M＝AB.
(1) 求矩阵 M；
(1) 求异面直线 AP 与 BE 所成角的大小；
3 PF (2) 若点 F 在线段 PB 上，使得二面角 FDEB 的正弦值为 3 ，求PB的值．
已知数列{an}，{bn}都是单调递增数列，若将这两个数列的项按由小到大的顺序排成一列 (相同的项视为一项)，则得到一个新数列{cn}．
(1) 设数列{an}，{bn}分别为等差、等比数列，若 a1＝b1＝1，a2＝b3，a6＝b5，求 c20； (2) 设{an}的首项为 1，各项为正整数，bn＝3n，若新数列{cn}是等差数列，求数列{cn}的前 n 项和 Sn； (3) 设 bn＝qn－1(q 是不小于 2 的正整数)，c1＝b1，是否存在等差数列{an}，使得对任意的 n∈N*，在 bn 与 bn＋1 之间数列{an}的项数总是 bn？若存在，请给出一个满足题意的等差数列 {an}；若不存在，请说明理由.
S20＝__________．
5. 甲、乙两组各有三名同学，他们在一次测试中的成绩分别为甲组：88，89，90；乙组： 87，88，92.如果分别从甲、乙两组中随机选取一名同学，则这两名同学的成绩之差的绝对值不超过 3 的概率是________．

苏州大学2020届高三考前指导卷

苏州大学2020届高三考前指导卷1、若()i b i i a +=+3，其中R b a ∈,，i 是虚数单位，则=-b a 。

2、已知集合{}Zx x x x A ∈≤-=,042，(){}A x x y y B ∈+==,1log 2，则=B A 。

3.右面茎叶图表示的是甲，乙两人在5次综合测评中的成绩，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为4、若某算法流程图如右图所示，则输出的n 值是。

5、双曲线C ：1422=-my x （m ＞0）的离心率等于2，则该双曲线渐近线的斜率是。

6.设等比数列{}n a 的前n 项和为n S ，若0852=+a a ，则35S S 的值为7．已知(),,sin R x x x f ∈=()x g 的图像与()x f 的图像关于点⎪⎭⎫⎝⎛0,4π对称，则在区间[]π2,0上满足()()x g x f ≤的x 的取值范围是8.已知322322=+，833833=+，15441544=+，，若ta t a 66=+。

（t a ,均为正整数且t a ,互质）类比以上等式，可推测t a ,的值，则=+t a 9．过直线x y l 2:=上一点P 做圆()()5443M 22=-+-y x ：的两条切线21,l l ，A ，B 为切点，当直线21,l l 关于直线l 对称时，则=∠APB10、已知函数()62-=x x f ，若a ＜b ＜0，且()()b f a f =，则b a 2的最小值是。

11、点()00,y x P 是曲线C ：xy 1=（x ＞0）上的一个动点，曲线C 在点P 处的切线与x 轴、y 周分别交与B A ,两点，点O 是坐标原点。

给出三个命题：①PB PA =；②OAB ∆的面积为定值；③ 曲线C 上存在两点N M ,，使得OMN ∆为等腰直角三角形。

其中真命题的个数是。

12在AB C ∆中，F E ,分别是边AB AC ,的中点，且AC AB 23=，若t CFBE<恒成立，则t 的最小值为13、对于函数()x f y =，若存在区间[]b a ,，当∈x []b a ,时，()x f 的值域为[]kb ka ,(k ＞0），则称()x f y =为k 倍值函数。

2020年高考(江苏卷)数学附加题训练三(含答案)

2020年高考（江苏卷）数学附加题训练三21、已知矩阵M121a⎡⎤=⎢⎥⎣⎦，其中Ra∈，若点(1,7)P在矩阵M的变换下得到点(15,9)P'，（1）求实数a的值；（2）求矩阵M的特征值及其对应的特征向量.22、以坐标原点为极点，x轴的正半轴为极轴，且在两种坐标系中取相同的长度单位，建立极坐标系，判断直线12:12x tly t=+⎧⎨=-⎩（t为参数）与圆2:2cos2sin0Cρρθρθ+-=的位置关系．23、甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为21与p ，且乙投球2次均未命中的概率为1.16（Ⅰ）求乙投球的命中率p ；（Ⅱ）若甲投球1次，乙投球2次，两人共命中的次数记为ξ，求ξ的分布表和数学期望.24、设n 是给定的正整数，有序数组1(22n a ，a ，⋅⋅⋅ ，a )同时满足下列条件：①{1 ，1}i a ∈-,i =1 ，2 ，⋅⋅⋅ ，2n ；②对任意的1≤k ≤l ≤n ,都有212li i =2k a -∑≤．（1）记A n 为满足“对任意的1≤k ≤n ，都有a 2k -12k a +=0”的有序数组1(22n a ，a ，⋅⋅⋅ ，a )的个数，求n A ；（2）记B n 为满足“存在1≤k ≤n ，使得a 2k -12k a +≠0”的有序数组1(22n a ，a ，⋅⋅⋅ ，a )的个数，求n B ．数学附加题训练三答案21、已知矩阵M 121a ⎡⎤=⎢⎥⎣⎦，其中R a ∈，若点(1,7)P 在矩阵M 的变换下得到点(15,9)P '，（1）求实数a 的值；（2）求矩阵M 的特征值及其对应的特征向量.解：（1）由121a ⎡⎤⎢⎥⎣⎦17⎡⎤⎢⎥⎣⎦=159⎡⎤⎢⎥⎣⎦，∴1715a +=，解得2a =.………4分（2）由（1）知M 1221⎡⎤=⎢⎥⎣⎦，则矩阵M 的特征多项式为212()(1)(1)42321f λλλλλλλ--==---=----令0)(=λf ，得矩阵M 的特征值为1-与3.…………6分当1-=λ时，220220x y x y --=⎧⎨--=⎩，解得0x y +=∴矩阵M 的属于特征值1-的一个特征向量为11⎡⎤⎢⎥-⎣⎦;…………8分当3λ=时，220220x y x y -=⎧⎨-+=⎩，解得x y=∴矩阵M 的属于特征值3的一个特征向量为11⎡⎤⎢⎥⎣⎦.…………10分22、以坐标原点为极点，x 轴的正半轴为极轴，且在两种坐标系中取相同的长度单位，建立极坐标系，判断直线12:12x tl y t=+⎧⎨=-⎩（t 为参数）与圆2:2cos 2sin 0C ρρθρθ+-=的位置关系．解：把直线方程12:12x tl y t =+⎧⎨=-⎩化为普通方程为2x y +=．…………………3分将圆:C 22cos 2sin 0ρρθρθ+-=化为普通方程为22220x x y y ++-=，即22(1)(1)2x y ++-=．………………………………………………………………6分圆心C 到直线l的距离d =-------8分所以直线l 与圆C 相切.…………………………………………………………………10分23、甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为21与p ，且乙投球2次均未命中的概率为161.（Ⅰ）求乙投球的命中率p ；（Ⅱ）若甲投球1次，乙投球2次，两人共命中的次数记为ξ，求ξ的分布表和数学期望.解：（Ⅰ）设“甲投球一次命中”为事件A ，“乙投球一次命中”为事件B 由题意得()()()1611122=-=-p B P 解得43=p 或45（舍去），所以乙投球的命中率为43--------3分（Ⅱ）由题设和（Ⅰ）知()()()()41,43,21,21====B P B P A P A P ξ可能的取值为0，1，2，3，-----------------4分故()()()321412102=⎪⎭⎫ ⎝⎛⨯=⋅==B B P A P P ξ---------------5分()()()()()()32721414324121321412112212=⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯==⎪⎭⎫ ⎝⎛⨯=+⋅==A P B P B P C B B P A P P ξ--------------6分()()()329432132=⎪⎭⎫ ⎝⎛⨯=⋅==B B P A P P ξ------------7分()()()()321531012==-=-=-==ξξξξP P P P ---------------8分ξ的分布表为ξ123P3213273215329--------------9分ξ的数学期望232933215232713210=⨯+⨯+⨯+⨯=ξE ----------------10分24、设n 是给定的正整数，有序数组122( )n a a a ⋅⋅⋅，，，同时满足下列条件：①{}1 1i a ∈-，,1 2 2i n =⋅⋅⋅，，，；②对任意的1k l n ≤≤≤,都有2212li i k a =-∑≤．（1）记n A 为满足“对任意的1k n ≤≤，都有2120k k a a -+=”的有序数组122( )n a a a ⋅⋅⋅，，，的个数，求n A ；（2）记n B 为满足“存在1k n ≤≤，使得2120k k a a -+≠”的有序数组122( )n a a a ⋅⋅⋅，，，的个数，求n B ．解：（1）因为对任意的1k n ≤≤，都有2120k k a a -+=，所以22222n n n A =⨯⨯⋅⋅⋅⨯=个相乘；（3分）（2）因为存在1k n ≤≤，使得2120k k a a -+≠，所以2122k k a a -+=或2122k k a a -+=-，设所有这样的k 为12(1)m k k k m n ⋅⋅⋅≤≤, , ，不妨设2122(1)j j k k a a j m -+=≤≤，则112122j j k k a a ++-+=-（否则12212j j k i i k a +=->∑=4）；同理，若2122(1)j j k k a a j m -+=-≤≤，则112122j j k k a a ++-+=，------5分这说明212j j k k a a -+的值由11212k k a a -+的值（2或-2）确定，又其余的()n m -对相邻的数每对的和均为0，所以，11222C 22C 22C n n n n n n n B --=⨯+⨯+⋅⋅⋅+------7分11222(2+C 2C 2C )22n n n n nn n n --=⨯+⨯+⋅⋅⋅+-⨯2(12)22n n =+-⨯2(32)n n =-．（------10分）。

江苏省苏州大学高考指导测试 (二)(数学)

江苏省苏州大学高考指导测试 (二)（数学）考生注意：1．本试卷共4页，包括（第1题—第12题）、（第13题—第17题）两部分。

本试卷满分150分，考试时间1。

2．答将填空题答案和解答题的解答过程写在答题卷上，在本试卷上答题无效。

3．答题前，务必将自己的姓名、学校、准考证号写在答卷纸的规定位置。

一、填空题（本大题共14小题，每小题5分，共90分。

请把答案填写在答题卡相应位置上） 1. 若2(31)i 25i a a a -+-=+，其中i 是虚数单位，则实数a 的值为 ▲ ．2. 在平面直角坐标系xOy 中，“方程22113x y k k +=--表示焦点在x 轴上的双曲线”的充要条件是“实数k ∈ ▲ ”．3. 某地区在连续7天中，新增某种流感的数据分别为4，2，1，0，0，0，0，则这组数据的方差s 2= ▲ ． 4. 已知角α是锐角，求sin α＋3cos α的取值范围 ▲ ．5. 设m ，n 是两条不同的直线，α，β，γ是两个不同的平面，有下列四个命题：①⎩⎨⎧α∥ββ∥γ⇒α∥γ； ②⎩⎨⎧α⊥βm ∥α⇒m ⊥β； ③⎩⎨⎧m ⊥αm ∥β⇒α⊥β； ④⎩⎨⎧m ∥n n ⊂α⇒m ∥α．其中真命题的是 ▲ (填上所有真命题的序号)．6. 将A ，B ，C ，D 四个人平均分成两组，则“A ，B 两人恰好在同一组”的概率为 ▲ ．7. 右图是一个算法的流程图，最后输出的n ＝ ▲ ．8. 设S n 表示等差数列{a n }的前n 项和，已知a 5＝3a 3，则95S S = ▲ ．9. 已知函数()f x 是定义在(0,)+∞上的单调增函数，当n *∈N 时，()f n *∈N ，若[()]3f f n n =，则f (5)的值等于 ▲ ．10. 已知f (x )＝x 3－3x ，过A (1，m )可作曲线y ＝f (x )的三条切线，则m 的取值范围是 ▲ ．11. 已知D 是由不等式组⎩⎨⎧x －2y ≥0，x ＋3y ≥0所确定的平面区域，则圆x 2＋y 2＝4 围成的区域与区域D 的公共部分的面积为 ▲ ．12. 在平面直角坐标系xOy 中，设直线l ：10kx y -+=与圆C ：224x y +=相交于A 、B 两点，以OA ，OB 为邻边作□OAMB，若FC点M 在圆C 上，则实数k ＝ ▲ ．13. 在正六边形ABCDEF 中，AB ＝1，AP xAB y AF =+，则x ＋y 的取值范围是 ▲ ．14. 将所有3的幂，或者是若干个3的幂之和，由小到大依次排列成数列1，3，4，9，10，12，13，…，则此数列的第100项为 ▲ ．二、解答题（本大题共6小题，共90分．解答题应写出文字说明、证明过程或演算步骤）15. （本小题满分14分）已知向量m ＝(a ，cos2x )，n ＝(1＋sin2x ，3)，x ∈R ，记f (x )＝m ⋅n ．若y ＝f (x )的图象经过点(π4，2 )．（1）求实数a 的值；（2）设x ∈[－π4，π4]，求f (x )的最大值和最小值；（3）将y ＝f (x )的图象向右平移π12，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到y ＝g (x )的图象，求y ＝g (x )的单调递减区间． 16.（本小题满分14分）在四棱锥P －ABCD 中，∠ABC ＝∠ACD ＝90°，∠BAC ＝∠CAD ＝60°，PA ⊥平面ABCD ，E 为PD 的中点，PA ＝2AB ＝2．（Ⅰ）求四棱锥P －ABCD 的体积V ；（Ⅱ）若F 为PC 的中点，求证PC ⊥平面AEF ；（Ⅲ）求证CE ∥平面PAB ．17.（本小题满分15分）某企业有两个生产车间分别在A ，B 两个位置，A 车间有100名员工，B 车间有400名员工，现要在公路AC 上找一点D ，修一条公路BD ，并在D 处建一个食堂，使得所有员工均在此食堂用餐，已知A ，B ，C 中任意两点间的距离均有1km ，设∠BDC ＝α，所有员工从车间到食堂步行的总路程为S ．（1）写出S 关于α的函数表达式，并指出α的取值范围；（2）问食堂D 建在距离A 多远时，可使总路程S 最少？PA BCDEF18.（本小题满分15分）已知椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)，直线l 过点A (a ，0)和B (0，b )．（1）以AB 为直径作圆M ，连接MO 并延长，与椭圆C 的第三象限部分交于N ，若直线NB 是圆M 的切线，求椭圆的离心率；（2）已知三点D （4，0），E （0，3），G （4，3），若圆M 与△DEG 恰有一个公共点，求椭圆方程．19.（本小题满分16分）已知数列{}n a 的前n 项和n S 满足：(1)1n n aS a a =--（a 为常数，且0,1a a ≠≠）．（1）求{}n a 的通项公式；（2）设21=+nn nS b a ，若数列{}n b 为等比数列，求a 的值；（3）在满足条件（2）的情形下，设111211n n n c a a +=-++-（），数列{}n c 的前n 项和为T n ．求证：13n T ＜．本小题满分16分）已知关于x 的函数f (x )＝x 2＋2ax ＋b （其中a ，b ∈R ）．（1）求函数｜f (x )｜的单调区间；（2）对于一切a∈[0，1]，若存在实数m，使得1|()|4f m≤与1|(1)|4f m ≤能同时成立，求b－a的取值范围．参考答案1．2．2．3．4．（1，2]4－2若函数tan y x ω=在区间π(,π)2上单调递增，则实数ω的取值范围是________．13(0,][1,]22⋃．5．①③6．137． 100． 8．275 9． 8 10．（－3，－2）． 11．π2． 12． 0． 12－2在直角坐标平面内，点A （1，2）到直线l 的距离为1，且点B （4，1）到直线l 的距离为2，则这样的直线l 最多的条数为_________．4． 13．无13—2已知|a |＝2，|b |＝3，|c |＝4，且a ＋b ＋c ＝0 ，则向量a 与b 的夹角的余弦值＝．13－3在Rt △ABC 中，∠A ＝90°，AB ＝AC ＝2，点D 为AC 中点，点E 满足13BE BC =，则AE BD ⋅＝__________．13－4设点O 为△ABC 的外心，AB ＝13，AC ＝12，则BC AO ⋅＝_____． 14． 981．二、解答题 15． 16．无17．（1）在△BCD 中，∵sin 60sin sin(120)BD BC CDαα==︒︒-，∴2sin BD α=，sin(120)sin CD αα︒-=．则sin(120)1sin AD αα︒-=-．S＝sin(120)2400100[1]sin sin ααα︒-⋅+⋅-＝cos 450sin αα--．其中π3≤α≤2π3．（2）2sin sin (cos 4)cos sin S ααααα-⋅--'=-CA＝214cos sin αα-．令S '＝0，得1cos 4α=．当1cos 4α>时，S '＜0，S 是α的单调减函数；当1cos 4α<时，S '＞0，S 是α的单调增函数． ∴当1cos 4α=时，S 取得最小值．此时，sin α=，1sin sin(120)12211sin sin 2AD ααααα+︒-=-=-=-＝11122=-（答） 18已知椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)，直线l 过点A (a ，0)和B (0，b )．（1）以AB 为直径作圆M ，连接MO 并延长，与椭圆C 的第三象限部分交于N ，若直线NB 是圆M 的切线，求椭圆的离心率；（2）已知三点D （4，0），E （0，3），G （4，3），若圆M 与△DEG 恰有一个公共点，求椭圆方程．数列问题19－1解 (1)11(1),1－=-aS a a ∴1,=a a 当2n ≥时，11,11n n n n n a aa S S a a a a --=-=---1nn a a a -=，即{}n a 是等比数列．∴1n n n a a a a -=⋅=； (2)由(1)知，2(1)(31)211(1)n n n n n aa a a a ab a a a ⋅----=+=-，若{}n b 为等比数列，则有2213,b b b =而21232323223,,,a a a b b b a a +++===故22232322()3a a a a a +++=⋅，解得13a =，再将13a =代入得3n n b =成立，所以13a =．(3)证明：由(2)知1()3n n a =，所以11111332111131311()1()33n n n n n n n c +++==+-+-－－－＋－1113131n n +=-+-，由111111,313313n n n n ++<>+-得111111,313133n n n n ++-<-+- 所以11133n n n c +-＜，从而122231*********())33333333n n n n n T c c c ++=+++--++-=-＜＋（＜13．函数问题已知关于x 的函数f (x )＝x 2＋2ax ＋b （其中a ，b ∈R ）．（1）求函数｜f (x )｜的单调区间；（2）对于一切a ∈[0，1]，若存在实数m ，使得1|()|4f m ≤与1|(1)|4f m +≤能同时成立，求b －a 的取值范围．。

2020年江苏省高考数学预测押题试卷(含附加题及答案) (2)

由全国各地一线教师精心编制《高考终极预测押题卷》对近十年全国各地高考试题的全方位精确分析，把握命题规律，找出命题趋势。

全网首发！百位名师呕血专研，只为高考最后一搏！江苏省高考数学预测押题试卷【考试时间：120分钟分值：160分】参考公式：样本数据12,,,n x x x L 的方差2211()n i i s x x n ==-∑，其中11n i i x x n ==∑；一、填空题：本大题共14小题，每小题5分，计70分.不需写出解答过程，请把答案写在答题纸的指定位置上.1、集合{}3,6A =，{}3,9B =，则A B =U ▲ ．2、若复数1(4),()z a a i a R =++-∈是实数，则a = ▲ ．3、如果22sin 3α=，α为第一象限角，则sin()2πα+= ▲ ． 4、已知正六棱锥ABCDEF P -的底面边长为1cm ，高为1cm ，则棱锥的体积为 ▲ 3cm ．5、高三（1）班共有56人，学号依次为1，2，3，…，56，现用系统抽样的办法抽取一个容量为4的样本，已知学号为6，34，48的同学在样本中，那么还有一个同学的学号应为 ▲ ．6、已知某一组数据8,9,10,11,12，则其方差为 ▲ ．7、阅读下列程序框图，运行相应程序，则输出的S 值为 ▲ ．8、若)(x f y =是定义在R 上周期为2的偶函数，当[]1,0∈x 时，12)(-=xx f ，则函数3()()log g x f x x =-的零点个数为 ▲ ．9、若命题“R x ∃∈，使得2(1)10x a x +-+≤”为假命题，则实数a 的范围 ▲ ． 10、在△ABC 中，AH 为BC 边上的高，tan C ＝43，则过点C ，以A ，H 为焦点的双曲线的离心率为 ▲ ．11、设等比数列{}n a 的公比1q ≠，n S 表示数列{}n a 的前n 项的和，n T 表示数列{}n a 的前n 项的乘积，()n T k 表示{}n a 的前n 项中除去第k 项后剩余的1n -项的乘积，即()(),,n n kTT k n k N k n a *=∈≤，则当11a =，2q =，数列()()(){}12n n n n n S T T T T n +++L 的前n 项的和是 ▲ ．12、已知)(),(x g x f 都是定义在R 上的函数，()0,()()()()g x f x g x f x g x ''≠>, ()(),x f x a g x =⋅（01a a >≠且）,(1)(1)5,(1)(1)2f fg g -+=- 在有穷数列)10,,2,1}()()({Λ=n n g n f 中，任意取正整数k （110k ≤≤），则前k 项和不小于1615的概率是 ▲ ． 13、设A ,B ,C 为单位圆O 上不同的三点，则点集{(,)|,A x y OC xOA yOB ==+u u u r u u u r u u u r开始 n=1,S=1S=S·cos126n π-⋅n ≥3输出S 结束n=n+1是否02,02}x y <<<<所对应的平面区域的面积为 ▲ ．14、函数21()23ln 2f x x tx x =-+，2()3x tg x x +=+，函数()f x 在,x a x b ==处取得极值（0a b <<）， ()g x 在[,]b a --上的最大值比最小值大13，若方程()f x m =有3个不同的解，则函数152m y e +=的值域为 ▲ ．二、解答题：本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内. 15、(本小题满分14分)在ABC ∆中，c b a ,,分别是∠A 、∠B 、∠C 的对边, c b a ,,满足222b a c ac =+- (Ⅰ）求角B 的大小；(Ⅱ)在区间(0,)B 上任取θ，求2cos 12θ<<的概率；（Ⅲ）若AC ＝23，求ΔABC 面积的最大值.16、(本小题满分14分)直三棱柱111C B A ABC -中，11===BB BC AC ，31=AB ．（Ⅰ）求证：平面⊥C AB 1平面CB B 1； (Ⅱ)求三棱锥C AB A 11-的体积．17、(本小题满分14分)工厂生产某种零件，每天需要固定成本100元，每生产1件，还需再投入资金2元，若每天生产的零件能全部售出，每件的销售收入()P x （元）与当天生产的件数x （*x N ∈）A B C C 1A 1B 1之间有以下关系：()23183,01035201331,10x x P x x xx ⎧-<≤⎪⎪=⎨⎪->⎪⎩ ,设当天利润为y 元.（Ⅰ）写出y 关于x 的函数关系式；（Ⅱ)要使当天利润最大，当天应生产多少零件？（注：利润等于销售收入减去总成本）18、(本小题满分16分)设等比数列{}n a 的首项为12a =，公比为(q q 为正整数），且满足33a 是18a 与5a 的等差中项；等差数列{}n b 满足2*32()0(,)2n n n t b n b t R n N -++=∈∈. （Ⅰ）求数列{}n a ，{}n b 的通项公式；（Ⅱ) 若对任意*n N ∈，有111n n n n n n a b a a b a λ++++≥成立，求实数λ的取值范围; （Ⅲ）对每个正整数k ，在k a 和1k a +之间插入k b 个2，得到一个新数列{}n c .设n T 是数列{}n c 的前n 项和，试求满足12m m T c +=的所有正整数m .19、(本小题满分16分)已知椭圆2222:1(0)x y C a b a b +=>>过点3(3,)2，椭圆C 左右焦点分别为21,F F ，上顶点为E ，21F EF ∆为等边三角形.定义椭圆C 上的点00(,)M x y 的“伴随点”为00(,)x y N a b.（Ⅰ）求椭圆C 的方程；(Ⅱ)若圆1C 的方程为2(2)x a +＋2y ＝2a ，圆1C 和x 轴相交于A ，B 两点，点P 为圆1C 上不同于A ，B 的任意一点，直线PA ，PB 交y 轴于S ，T 两点．当点P 变化时，以ST 为直径的圆2C 是否经过圆1C 内一定点？请证明你的结论；（Ⅲ）直线l 交椭圆C 于H 、J 两点,若点H 、J 的“伴随点”分别是L 、Q ,且以LQ 为直径的圆经过坐标原点O .椭圆C 的右顶点为D ，试探究ΔOHJ 的面积与ΔODE 的面积的大小关系,并证明.20、(本小题满分16分)已知函数2()ln(1),()f x ax x a R =++∈．（Ⅰ）设函数(1)y f x =-定义域为D ①求定义域D ；②若函数41()[()ln(1)]()h x x f x x x x=+-++2(0)cx f '++在D 上有零点，求22a c +的最小值； (Ⅱ) 当12a =时，2()(1)(1)(1)2g x f x bf x ab x a '=-+---+，若对任意的],1[e x ∈，都有2()2g x e e≤≤恒成立，求实数b 的取值范围；（注：e 为自然对数的底数）（Ⅲ）当[0,)x ∈+∞时，函数()y f x =图象上的点都在0,0x y x ≥⎧⎨-≤⎩所表示的平面区域内，求实数a 的取值范围．2013届高三年级第三次模拟考试数学试题（附加题）（满分40分，考试时间30分钟）21、[选做题]本题包括A 、B 、C 、D 四小题，请选定其中两题，并在相应的答题区域内作答．．．．．．．．．．．．．．．．．．．．．．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤． A 、[选修4 - 1：几何证明选讲]（本小题满分10分）如图，AD 是⊙O 的直径，AB 是⊙O 的切线，M, N 是圆上两点，直线MN 交AD 的延长线于点C ，交⊙O 的切线于B ，BM ＝MN ＝NC ＝1，求AB 的长和⊙O 的半径．B 、[选修4 - 2：矩阵与变换]（本小题满分10分）已知矩阵213122A -⎡⎤⎢⎥=⎢⎥-⎣⎦（Ⅰ）求矩阵A 的逆矩阵B ；（Ⅱ）若直线经过矩阵B 变换后的直线方程为730x y -=，求直线的方程.C 、[选修4 - 4：坐标系与参数方程]（本小题满分10分）已知圆C 的极坐标方程是2cos ρθ=，以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，直线的参数方程为11,525x t y a t ⎧⎪⎪⎨⎪⎪⎩=+=+（为参数）.若直线与圆C相交于P ,Q 两点，且455PQ =. （Ⅰ）求圆C 的直角坐标方程，并求出圆心坐标和半径；（Ⅱ）求实数a 的值.D 、[选修4 - 5：不等式选讲]（本小题满分10分）已知函数()|3|f x x =-，()|4|g x x m =-++（Ⅰ）已知常数2a <，解关于x 的不等式()20f x a +->；（Ⅱ）若函数()f x 的图象恒在函数()g x 图象的上方，求实数m 的取值范围.【必做题】第22题、第23题，每题10分，共计20分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤． 22、（本小题满分10分）已知12310,,,,A A A A L 等10所高校举行的自主招生考试，某同学参加每所高校的考试获得通过的概率均为12. （Ⅰ）如果该同学10所高校的考试都参加，试求恰有2所通过的概率；（Ⅱ）假设该同学参加每所高校考试所需的费用均为a 元，该同学决定按12310,,,,A A A A L 顺序参加考试，一旦通过某所高校的考试，就不再参加其它高校的考试，试求该同学参加考试所需费用ξ的分布列及数学期望.23、（本小题满分10分）已知,m n 为正整数.（Ⅰ）用数学归纳法证明：当1x >-时，(1)1m x mx +≥+；（Ⅱ）对于6n ≥，已知11(1)32n n -<+，求证：1(1)()32n m m n -<+， (1,2,,)m n =L ；（Ⅲ）求出满足等式345(2)(3)n n n n nn n +++++=+L 的所有正整数n .2013届高三年级第三次模拟考试参考答案1、{}3,6,92、43、13 4、32 5、20 6、2 7、38-8、2 9、(1,3)- 10、2 11、21n- 12、710 13、25 14、4(27,)e15、解：(Ⅰ）由222b a c ac =+-得3B π= -------------------4分；(Ⅱ) 由2cos 12θ<<，得(0,)4πθ∈，--------------6分所以2cos 12θ<<的概率为34-------------8分（Ⅲ）由23b =，22212b a c ac ac ==+-≥.3334ABC S ac ∆=≤，ΔABC 面积的最大值为33.--------------14分 16、(Ⅰ）略；--------------8分 (Ⅱ)三棱锥C AB A 11-的体积为16．--------------14分 17、解：(1) 当0＜x ≤10时，y ＝x (83－13x 2)－100－2x ＝－13x 3＋81x －100；当x ＞10时，y ＝x (520x －1 331x 3)－2x －100＝－2x －1 331x2＋420.∴ y ＝⎩⎪⎨⎪⎧－13x 3＋81x －100，0＜x ≤100，x ∈N ，－2x －1 331x2＋420，x ＞10，x ∈N . ------- (6分)(2) 设函数y ＝h (x )＝⎩⎪⎨⎪⎧－13x 3＋81x －100，0＜x ≤100，x ∈N ，－2x －1 331x2＋420，x ＞10，x ∈N .① 当0＜x ≤10时，y ′＝81－x 2，令y ′＝0，得x ＝9 ------- .(9分)当x ∈(0,9)时，y ′＞0；当x ∈(9,10)时，y ′＜0. ∴ 当x ＝9时，y max ＝386；(10分)② 当x ＞10时，y ′＝－－2×1 331t3－2，令y ′＝0，得x ＝11. ------- (12分) 当x ∈(10,11)时，y ′＞0；当x ∈(11，＋∞)时，y ′＜0. ∴ 当x=11时，y max ＝387.(14分)∵ x ∈N *，∴ 综合①②知：当x ＝11时，y 取最大值．故要使当天利润最大，当天应生产11件零件．------- (14分)18、解：（1）由题意31568a a a =+，则2468q q =+，解得24q =或22q =因为q 为正整数，所以2q =，又12a =，所以*2()n n a n N =∈------3分2n b n =。

苏州大学2020届高考考前指导卷(附加)

苏州大学2020届高考考前指导卷数学Ⅱ（附加题）21．【选做题】本题包括A 、B 、C 三小题，请选定其中两题．．．．．．，并在相应的．．．．．答题区域．．．．内作．．答．，若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤． A ．选修4 2：矩阵与变换（本小题满分10分）在平面直角坐标系xOy 中，设点(5)P x ，在矩阵M 1234对应的变换下得到点(2)Q y y ，，求1x yM ．B ．选修4 4：坐标系与参数方程（本小题满分10分）在直角坐标系xOy 中，以坐标原点O 为极点，以x 轴非负半轴为极轴，建立极坐标系，直线l 的极坐标方程为sin()4C 的参数方程为2cos 3()sin 22x y，≤≤，求l 与曲线C 交点的直角坐标．C ．选修4 5：不等式选讲（本小题满分10分）已知00x y ，，且满足2211274x y x y ，求1534x y的最小值．【必做题】第22题、第23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）在四棱锥P ABCD 中，//AB CD ，2224AB CD BC AD ，60DAB ，AE BE ，PAD △为正三角形，且平面PAD 平面ABCD ．（1）求二面角P EC D 的余弦值；（2）线段PC 上是否存在一点M ，使得异面直线DM 和PE指出点M 的位置；若不存在，请说明理由．23．（本小题满分10分）已知非空集合M 满足{012}M n ，，，，*(2)n n N ≥，．若存在非负整数 ()k k n ≤，使得当a M 时，均有2k a M ，则称集合M 具有性质P ．记具有性质P 的集合M 的个数为()f n ．（1）求(2)f 的值；（2）求()f n 的表达式．（第22题图）。

2020年江苏省高考数学附加题专项7套含答案

专题一请同学从下面所给的三题中选定两题作答【题目1】选修4－2：矩阵与变换设矩阵A ＝⎣⎡⎦⎤m 00 n ，若矩阵A 的属于特征值1的一个特征向量为⎣⎡⎦⎤10，属于特征值2的一个特征向量为⎣⎡⎦⎤01，求矩阵A .【题目2】选修4－4：坐标系与参数方程已知直线l ：⎩⎨⎧x ＝1＋t ，y ＝－t (t 为参数)与圆C ：⎩⎨⎧x ＝2cos θ，y ＝m ＋2sin θ(θ为参数)相交于A ，B 两点，m 为常数. (1)当m ＝0时，求线段AB 的长；【题目1】甲、乙两人投篮命中的概率分别为23与12，各自相互独立.现两人做投篮游戏，共比赛3局，每局每人各投一球.(1)求比赛结束后甲的进球数比乙的进球数多1个的概率；(2)设ξ表示比赛结束后甲、乙两人进球数的差的绝对值，求ξ的分布列和数学期望E (ξ).解 (1)比赛结束后甲的进球数比乙的进球数多1个有以下几种情况：甲进1球，乙进0球；甲进2球，乙进1球；甲进3球，乙进2球.所以比赛结束后甲的进球数比乙的进球数多1个的概率为【题目2】在(1＋x ＋x 2)n ＝D 0n ＋D 1n x ＋D 2n x 2＋…＋D r n x r ＋…＋D 2n －1n x 2n －1＋D 2n n x 2n 的展开式中，把D 0n ，D 1n ，D 2n，…，D 2n n 叫做三项式系数. (1)当n ＝2时，写出三项式系数D 02，D 12，D 22，D 32，D 42的值；(2)类比二项式系数性质C m n ＋1＝C m －1n ＋C m n (1≤m ≤n ，m ∈N ，n ∈N )，给出一个关于三项式系数 .专题二请同学从下面所给的三题中选定两题作答【题目1】选修4－2：矩阵与变换已知曲线C ：y 2＝12x ，在矩阵M ＝⎣⎡⎦⎤1 00 －2对应的变换作用下得到曲线C 1，C 1在矩阵N ＝⎣⎡⎦⎤0 11 0对应的变换作用下得到曲线C 2，求曲线C 2的方程.【题目2】选修4－4：坐标系与参数方程在平面直角坐标系xOy 中，圆的参数方程为⎩⎨⎧x ＝2＋2cos α，y ＝2sin α(α为参数)，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系.求： (1)圆的普通方程；(2)圆的极坐标方程.必做部分【题目1】如图，在多面体ABCDEF中，ABCD为正方形，ED⊥平面ABCD，FB∥ED，且AD＝DE＝2BF＝2.(1)求证：AC⊥EF；(2)求二面角C－EF－D的大小.【题目2】已知k，m∈N*，若存在互不相等的正整数a1，a2，…，a m，使得a1a2，a2a3，…，a m－1a m，a m a1同时小于k，则记f(k)为满足条件的m的最大值.(1)求f(6)的值；(2)对于给定的正整数n (n ＞1)，(ⅰ)当n (n ＋2)＜k ≤(n ＋1)(n ＋2)时，求f (k )的解析式；(ⅱ)当n (n ＋1)＜k ≤n (n ＋2)时，求f (k )的解析式.专题三请同学从下面所给的三题中选定两题作答【题目1】选修4－2：矩阵与变换设二阶矩阵A ，B 满足A －1＝⎣⎡⎦⎤1 23 4，(BA )－1＝⎣⎡⎦⎤1 00 1，求B －1.【题目2】选修4－4：坐标系与参数方程在极坐标系中，已知曲线C ：ρ＝2sin θ，过极点O 的直线l 与曲线C 交于A ，B 两点，且AB ＝3，求直线l 的方程.必做部分【题目1】某校高一、高二两个年级进行乒乓球对抗赛，每个年级选出3名学生组成代表队，比赛规则是：①按“单打、双打、单打”顺序进行三盘比赛；②代表队中每名队员至少参加一盘比赛，但不能参加两盘单打比赛.若每盘比赛中高一、高二获胜的概率分别为37，4 7.(1)按比赛规则，高一年级代表队可以派出多少种不同的出场阵容？(2)若单打获胜得2分，双打获胜得3分，求高一年级得分ξ的概率分布列和数学期望.【题目2】已知抛物线C ：x 2＝2py (p ＞0)过点(2，1)，直线l 过点P (0，－1)与抛物线C 交于A ，B 两点.点A 关于y 轴的对称点为A ′，连接A ′B .(1)求抛物线C 的标准方程；(2)问直线A ′B 是否过定点？若是，求出定点坐标；若不是，请说明理由. 专题4请同学从下面给的三题中选定两题作答【题目1】选修4－2：矩阵与变换已知矩阵A ＝⎣⎡⎦⎤1 2c d (c ，d 为实数).若矩阵A 属于特征值2，3的一个特征向量分别为⎣⎡⎦⎤21，⎣⎡⎦⎤11，求矩阵A 的逆矩阵A －1.【题目2】选修4－4：坐标系与参数方程已知直线l 的极坐标方程为ρsin ()θ－π3＝3，曲线C 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝2sin θ(θ为参数)，设点P 是曲线C 上的任意一点，求P 到直线l 的距离的最大值.必做部分【题目1】如图，在直三棱柱ABC －A 1B 1C 1中，已知CA ＝CB ＝1，AA 1＝2，∠BCA ＝90°.(1)求异面直线BA 1与CB 1夹角的余弦值；(2)求二面角B－AB1－C平面角的余弦值.【题目2】在数列{a n}中，已知a1＝20，a2＝30，a n＋1＝3a n－a n－1(n∈N*，n≥2).(1)当n＝2，3时，分别求a2n－a n－1a n＋1的值，并判断a2n－a n－1a n＋1(n≥2)是否为定值，然后给出证明；(2)求出所有的正整数n，使得5a n＋1a n＋1为完全平方数.专题五2.(2018·江苏省盐城中学调研)已知矩阵M ＝⎣⎡⎦⎤0 ab 0满足：Ma i ＝λi a i ，其中λi (i ＝1,2)是互不相等的实常数，a i (i ＝1,2)是非零的平面列向量，λ1＝1，a 2＝⎣⎡⎦⎤11，求矩阵M .3.(2018·苏州、南通等六市模拟)在极坐标系中，求以点P ()2，π3为圆心且与直线l: ρsin ()θ－π3＝2相切的圆的极坐标方程.5.已知点A(1,2)在抛物线F：y2＝2px上.(1)若△ABC的三个顶点都在抛物线F上，记三边AB，BC，CA所在直线的斜率分别为k1，k2，k3, 求1k1－1k2＋1k3的值；(2)若四边形ABCD的四个顶点都在抛物线F上，记四边AB，BC，CD，DA所在直线的斜率分别为k1，k2，k3，k4，求1k1－1k2＋1k3－1k4的值.6.已知f n (x )＝C 0n x n －C 1n (x －1)n ＋…＋(－1)k C k n (x －k )n ＋…＋(－1)n C n n (x －n )n ，其中x ∈R ，n ∈N *，k ∈N ，k ≤n .(1)试求f 1(x )，f 2(x )，f 3(x )的值；(2)试猜测f n (x )关于n 的表达式，并证明你的结论. .专题六2.(2018·苏州、南通等六市模拟)在平面直角坐标系xOy 中，已知A ()0，0，B ()3，0，C ()2，2.设变换T 1, T 2对应的矩阵分别为M ＝⎣⎡⎦⎤1 02， N ＝⎣⎡⎦⎤2 00 1，求对△ABC 依次实施变换T 1, T 2后所得图形的面积.3.已知两个动点P ，Q 分别在两条直线l 1：y ＝x 和l 2：y ＝－x 上运动，且它们的横坐标分别为角θ的正弦，余弦，θ∈[0，π]，记OM →＝OP →＋OQ →，求动点M 的轨迹的普通方程.5.甲、乙两人轮流投篮，每人每次投一次篮，先投中者获胜，投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为25，乙每次投篮命中的概率为23，且各次投篮互不影响.现由甲先投.(1)求甲获胜的概率；(2)求投篮结束时甲的投篮次数X的概率分布与数学期望.6.设n 个正数a 1，a 2，…，a n 满足a 1≤a 2≤…≤a n (n ∈N *且n ≥3). (1)当n ＝3时，证明：a 1a 2a 3＋a 2a 3a 1＋a 3a 1a 2≥a 1＋a 2＋a 3；(2)当n ＝4时，不等式a 1a 2a 3＋a 2a 3a 4＋a 3a 4a 1＋a 4a 1a 2≥a 1＋a 2＋a 3＋a 4也成立，请你将其推广到n (n ∈N *且n ≥3)个正数a 1，a 2，…，a n 的情形，归纳出一般性的结论并用数学归纳法证明.专题七2.若二阶矩阵M 满足⎣⎢⎡⎦⎥⎤－2122－1M ＝⎣⎡⎦⎤－3 0 4－1，求曲线4x 2＋4xy ＋y 2－12x ＋12y ＝0在矩阵M 所对应的变换作用下得到的曲线的方程.3.已知直线的极坐标方程为ρsin ()θ＋π4＝22，圆M 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝－2＋2sin θ(其中θ为参数).(1)将直线的极坐标方程化为直角坐标方程； (2)求圆M 上的点到直线的距离的最小值.5.如图，在直三棱柱ABC －A 1B 1C 1中，AA 1＝AB ＝AC ＝2，AB ⊥AC ，M 是棱BC 的中点，点P 在线段A 1B 上.(1)若P 是线段A 1B 的中点，求直线MP 与直线AC 所成角的大小；(2)若N 是CC 1的中点，直线A 1B 与平面PMN 所成角的正弦值为77，求线段BP 的长度.6.已知()1＋12xn展开式的各项依次记为a 1(x )，a 2(x )，a 3(x )，…，a n(x )，an ＋1(x ).设F (x )＝a 1(x )＋2a 2(x )＋3a 3(x )＋…＋na n (x )＋(n ＋1)·a n ＋1(x ).(1)若a 1(x )，a 2(x )，a 3(x )的系数依次成等差数列，求n 的值； (2)求证：对任意x 1，x 2∈[0,2]，恒有|F (x 1)－F (x 2)|≤2n －1(n ＋2)－1专题一请同学从下面所给的三题中选定两题作答【题目1】选修4－2：矩阵与变换设矩阵A ＝⎣⎡⎦⎤m 0n ，若矩阵A 的属于特征值1的一个特征向量为⎣⎡⎦⎤10，属于特征值2的一个特征向量为⎣⎡⎦⎤01，求矩阵A .解由题意得⎣⎡⎦⎤m 00 n ⎣⎡⎦⎤10＝1⎣⎡⎦⎤10，⎣⎡⎦⎤m 00 n ⎣⎡⎦⎤01＝2⎣⎡⎦⎤01，所以⎩⎨⎧m ＝1，n ＝2，故A ＝⎣⎡⎦⎤1 00 2. 【题目2】选修4－4：坐标系与参数方程已知直线l ：⎩⎨⎧x ＝1＋t ，y ＝－t (t 为参数)与圆C ：⎩⎨⎧x ＝2cos θ，y ＝m ＋2sin θ(θ为参数)相交于A ，B 两点，m 为常数.(1)当m ＝0时，求线段AB 的长；(2)当圆C 上恰有三点到直线的距离为1时，求m 的值. 解 (1)直线l ：x ＋y －1＝0，曲线C ：x 2＋y 2＝4，圆心到直线的距离d ＝12，故AB ＝2r 2－d 2＝14. (2)圆C 的直角坐标方程为x 2＋(y －m )2＝4，直线l ：x ＋y －1＝0，由题意，知圆心到直线的距离d ＝|m －1|2＝1，∴m ＝1± 2. 必做部分【题目1】甲、乙两人投篮命中的概率分别为23与12，各自相互独立.现两人做投篮游戏，共比赛3局，每局每人各投一球.(1)求比赛结束后甲的进球数比乙的进球数多1个的概率；(2)设ξ表示比赛结束后甲、乙两人进球数的差的绝对值，求ξ的分布列和数学期望E (ξ). 解 (1)比赛结束后甲的进球数比乙的进球数多1个有以下几种情况：甲进1球，乙进0球；甲进2球，乙进1球；甲进3球，乙进2球. 所以比赛结束后甲的进球数比乙的进球数多1个的概率为P ＝C 13×23×()132×()123＋C 23×()232×()13×C 13×()123＋C 33×()233×C 23×()123＝1136.(2)ξ的取值为0，1，2，3，则P(ξ＝0)＝()133×()123＋C13×23×()132×C13×()123＋C23×()232×13×C23×()123＋()233×()123＝724，P(ξ＝1)＝()133×C13×()123＋C13×23×()132×()123＋C13×23×()132×C23×()123＋C23×()232×13×C13×()123＋C23×()232×13×()123＋()233×C23×()123＝1124，P(ξ＝2)＝()133×C23×()123＋C23×()232×13×()123＋C13×23×()132×()123＋()233×C13×()123＝524，P(ξ＝3)＝()133×()123＋()233×()123＝124，所以ξ的分布列为所以数学期望E(ξ)＝0×724＋1×1124＋2×524＋3×124＝1.【题目2】在(1＋x＋x2)n＝D0n＋D1n x＋D2n x2＋…＋D r n x r＋…＋D2n－1n x2n－1＋D2n n x2n的展开式中，把D0n，D1n，D2n，…，D2n n叫做三项式系数.(1)当n＝2时，写出三项式系数D02，D12，D22，D32，D42的值；(2)类比二项式系数性质C m n＋1＝C m－1n＋C m n(1≤m≤n，m∈N，n∈N)，给出一个关于三项式系数D m＋1n＋1(1≤m≤2n－1，m∈N，n∈N)的相似性质，并予以证明.解(1)因为(1＋x＋x2)2＝1＋2x＋3x2＋2x3＋x4，所以D02＝1，D12＝2，D22＝3，D32＝2，D42＝1.(2)类比二项式系数性质C m n＋1＝C m－1n＋C m n(1≤m≤n，m∈N，n∈N)，三项式系数有如下性质：D m＋1n＋1＝D m－1n＋D m n＋D m＋1n(1≤m≤2n－1).证明如下：因为(1＋x＋x2)n＋1＝(1＋x＋x2)·(1＋x＋x2)n，所以(1＋x ＋x 2)n ＋1＝(1＋x ＋x 2)·(D 0n ＋D 1n x ＋D 2n x 2＋…＋D 2n －1n x 2n －1＋D 2n nx 2n ). 上式左边x m＋1的系数为D m ＋1n ＋1，上式右边xm＋1的系数为D m ＋1n ＋D m n ＋D m －1n ，于是D m ＋1n ＋1＝D m －1n ＋D m n ＋D m ＋1n (1≤m ≤2n －1).专题二请同学从下面所给的三题中选定两题作答【题目1】选修4－2：矩阵与变换已知曲线C ：y 2＝12x ，在矩阵M ＝⎣⎡⎦⎤1 00 －2对应的变换作用下得到曲线C 1，C 1在矩阵N ＝⎣⎡⎦⎤0 11 0对应的变换作用下得到曲线C 2，求曲线C 2的方程. 解设A ＝NM ，则A ＝⎣⎡⎦⎤0 110⎣⎡⎦⎤1－2＝⎣⎡⎦⎤0 －210，设P (x ′，y ′)是曲线C 上任一点，在两次变换下，在曲线C 2上对应的点为P (x ，y )，则⎣⎡⎦⎤xy ＝⎣⎡⎦⎤0 －21 0⎣⎡⎦⎤x ′y ′＝⎣⎡⎦⎤－2y ′ x ′，即⎩⎨⎧x ＝－2y ′，y ＝x ′，∴⎩⎨⎧x ′＝y ，y ′＝－12x . 又点P (x ′，y ′)在曲线C ：y 2＝12x 上，∴()－12x2＝12y ，即x 2＝2y . 【题目2】选修4－4：坐标系与参数方程在平面直角坐标系xOy 中，圆的参数方程为⎩⎨⎧x ＝2＋2cos α，y ＝2sin α(α为参数)，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系.求： (1)圆的普通方程； (2)圆的极坐标方程.解 (1)根据sin 2α＋cos 2α＝1，得(x －2)2＋y 2＝4cos 2α＋4sin 2α，所以圆的普通方程为(x －2)2＋y 2＝4.(2)把⎩⎨⎧x ＝ρcos θ，y ＝ρsin θ代入圆的普通方程得圆的极坐标方程为ρ＝4cos θ.必做部分【题目1】如图，在多面体ABCDEF 中，ABCD 为正方形，ED ⊥平面ABCD ，FB ∥ED ，且AD ＝DE ＝2BF ＝2.(1)求证：AC ⊥EF ；(2)求二面角C －EF －D 的大小.(1)证明连接BD ，∵FB ∥ED ，∴F ，B ，E ，D 共面，∵ED ⊥平面ABCD ，AC 平面ABCD ，∴ED ⊥AC ，又ABCD 为正方形， ∴BD ⊥AC ，而ED ∩DB ＝D ，ED ，DB 平面DBFE ，∴AC ⊥平面DBFE ，而EF平面DBFE ，∴AC ⊥EF .(2)解如图建立空间直角坐标系.则A (2，0，0)，B (2，2，0)，C (0，2，0)，F (2，2，1)，E (0，0，2)，由(1)知AC →为平面DBFE 的法向量，即AC →＝(－2，2，0)，又CE →＝(0，－2，2)，CF →＝(2，0，1)，设平面CEF 的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧CE →·n ＝0，CF →·n ＝0，即⎩⎨⎧－2y ＋2z ＝0，2x ＋z ＝0，取z ＝1，则x ＝－12，y ＝1，∴n ＝()－12，1，1.设二面角C －EF －D 的大小为θ，则cos 〈n ，AC →〉＝n ·AC →|n ||AC →|＝1＋232×22＝22，又二面角C －EF －D 为锐角，所以θ＝π4.【题目2】已知k ，m ∈N *，若存在互不相等的正整数a 1，a 2，…，a m ，使得a 1a 2，a 2a 3，…，a m －1a m ，a m a 1同时小于k ，则记f (k )为满足条件的m 的最大值. (1)求f (6)的值；(2)对于给定的正整数n (n ＞1)，(ⅰ)当n (n ＋2)＜k ≤(n ＋1)(n ＋2)时，求f (k )的解析式； (ⅱ)当n (n ＋1)＜k ≤n (n ＋2)时，求f (k )的解析式. 解 (1)由题意，取a 1＝1，a 2＝2，a 1a 2＜6，满足题意，若a 3≥3，则必有a 2a 3≥6，不满足题意，综上所述，m 的最大值为2，即f (6)＝2. (2)由题意，当n (n ＋1)＜k ≤(n ＋1)(n ＋2)时，设A 1＝{1，2，…，n }，A 2＝{n ＋1，n ＋2，n ＋3，…}，显然，a i ，a i ＋1∈A 1时，满足a i a i ＋1≤n (n －1)＜n (n ＋1)＜k ，所以从集合A 1中选出的a i 至多有n 个，a j ，a j ＋1∈A 2时，a j a j ＋1≥(n ＋1)(n ＋2)≥k ，不符合题意，所以从集合A 2中选出的a j 必不相邻，又因为从集合A 1中选出的a i 至多有n 个，所以从集合A 2中选出的a j 至多有n 个，放置于从集合A 1中选出的a i 之间，所以f (k )≤2n .(ⅰ)当n (n ＋2)＜k ≤(n ＋1)(n ＋2)时，取一串数a i 为：1，2n ，2，2n －1，3，2n －2，…，n －1，n ＋2，n ，n ＋1，或写成a i ＝⎩⎪⎨⎪⎧i ＋12，i 为奇数，2n ＋1－i2，i 为偶数(1≤i ≤2n )，此时a i a i ＋1≤n (n ＋2)＜k (1≤i ≤2n －1)，a 2n a 1＝n ＋1＜k ，满足题意，所以f (k )＝2n . (ⅱ)当n (n ＋1)＜k ≤n (n ＋2)时，从A 1中选出的n 个a i ：1，2，…，n ，考虑数n 的两侧的空位，填入集合A 2的两个数a p ，a q ，不妨设na p ＞na q ，则na p ≥n (n ＋2)≥k ，与题意不符，所以f (k )≤2n －1，取一串数a i 为1，2n －1，2，2n －2，3，2n －3，…，n －2，n ＋2，n －1，n ＋1，n 或写成a i ＝⎩⎪⎨⎪⎧i ＋12，i 为奇数，2n －i 2，i 为偶数(1≤i ≤2n－1)，此时a i a i ＋1≤n (n ＋1)＜k (1≤i ≤2n －2)，a 2n －1a 1＝n ＜k ，满足题意，所以f (k )＝2n －1.专题三请同学从下面所给的三题中选定两题作答【题目1】选修4－2：矩阵与变换设二阶矩阵A ，B 满足A －1＝⎣⎡⎦⎤1 234，(BA )－1＝⎣⎡⎦⎤1 01，求B －1.解设B －1＝⎣⎡⎦⎤a bcd ，因为(BA )－1＝A －1B －1，所以⎣⎡⎦⎤1 01＝⎣⎡⎦⎤1 23 4⎣⎡⎦⎤a b c d ，即⎩⎪⎨⎪⎧a ＋2c ＝1，b ＋2d ＝0，3a ＋4c ＝0，3b ＋4d ＝1，解得⎩⎪⎨⎪⎧a ＝－2，b ＝1，c ＝32，d ＝－12，所以B－1＝⎣⎢⎡⎦⎥⎤－2 132 －12.【题目2】选修4－4：坐标系与参数方程在极坐标系中，已知曲线C ：ρ＝2sin θ，过极点O 的直线l 与曲线C 交于A ，B 两点，且AB ＝3，求直线l 的方程.解设直线l 的方程为θ＝θ0(ρ∈R )，A (0，0)，B (ρ1，θ0)，则AB ＝|ρ1－0|＝|2sin θ0|.又AB ＝3，故sin θ0＝±32. 解得θ0＝π3＋2k π或θ0＝－π3＋2k π，k ∈Z .所以直线l 的方程为θ＝π3或θ＝2π3(ρ∈R ).【题目3】选修4－5：不等式选讲已知a ≥0，b ≥0，求证：a 6＋b 6≥ab (a 4＋b 4).证明 ∵a 6＋b 6－ab (a 4＋b 4)＝a 5(a －b )－(a －b )b 5＝(a －b )(a 5－b 5). 又a ≥0，b ≥0，当a －b ≥0时，a 5－b 5≥0；当a －b ＜0时，a 5－b 5＜0，即(a －b )(a 5－b 5)≥0，所以a 6＋b 6－ab (a 4＋b 4)≥0，即a 6＋b 6≥ab (a 4＋b 4).必做部分【题目1】某校高一、高二两个年级进行乒乓球对抗赛，每个年级选出3名学生组成代表队，比赛规则是：①按“单打、双打、单打”顺序进行三盘比赛；②代表队中每名队员至少参加一盘比赛，但不能参加两盘单打比赛.若每盘比赛中高一、高二获胜的概率分别为37，47.(1)按比赛规则，高一年级代表队可以派出多少种不同的出场阵容？(2)若单打获胜得2分，双打获胜得3分，求高一年级得分ξ的概率分布列和数学期望.解 (1)先安排参加单打的队员有A 23种方法，再安排参加双打的队员有C 12种方法，所以，高一年级代表队出场共有A 23C 12＝12种不同的阵容.(2)ξ的取值可能是0，2，3，4，5，7. P (ξ＝0)＝()1－373＝64343，P (ξ＝2)＝C 12×37×()1－372＝96343， P (ξ＝3)＝()1－372×37＝48343，P (ξ＝4)＝()372×()1－37＝36343，P (ξ＝5)＝C 12×37×()1－37×37＝72343，P (ξ＝7)＝()373＝27343， ξ的概率分布列为所以E (ξ)＝0×64343＋2×96343＋3×48343＋4×36343＋5×72343＋7×27343＝3.【题目2】已知抛物线C ：x 2＝2py (p ＞0)过点(2，1)，直线l 过点P (0，－1)与抛物线C 交于A ，B 两点.点A 关于y 轴的对称点为A ′，连接A ′B .(1)求抛物线C 的标准方程；(2)问直线A ′B 是否过定点？若是，求出定点坐标；若不是，请说明理由. 解 (1)将点(2，1)代入抛物线C 的方程得p ＝2，所以抛物线C 的标准方程为x 2＝4y .(2)设直线l 的方程为y ＝kx －1，又设A (x 1，y 1)，B (x 2，y 2)，则A ′(－x 1，y 1)，由⎩⎨⎧y ＝14x 2，y ＝kx －1得x 2－4kx ＋4＝0，则Δ＝16k 2－16＞0， x 1＝2k －2k 2－1，x 2＝2k ＋2k 2－1，所以k A ′B ＝y 2－y 1x 2－（－x 1）＝x 224－x 214x 1＋x 2＝x 2－x 14，于是直线A ′B 的方程为y －x 224＝x 2－x 14(x －x 2)，所以y ＝x 2－x 14(x －x 2)＋x 224＝k 2－1x ＋1，当x ＝0时，y ＝1，所以直线A ′B 过定点(0，1).专题4请同学从下面给的三题中选定两题作答【题目1】选修4－2：矩阵与变换已知矩阵A ＝⎣⎡⎦⎤1 2cd (c ，d 为实数).若矩阵A 属于特征值2，3的一个特征向量分别为⎣⎡⎦⎤21，⎣⎡⎦⎤11，求矩阵A 的逆矩阵A －1.解由题意知⎣⎡⎦⎤1 2cd ⎣⎡⎦⎤21＝⎣⎡⎦⎤ 42c ＋d ＝2⎣⎡⎦⎤21，⎣⎡⎦⎤1 2c d ⎣⎡⎦⎤11＝⎣⎡⎦⎤ 3c ＋d ＝3⎣⎡⎦⎤11，所以⎩⎨⎧2c ＋d ＝2，c ＋d ＝3，解得⎩⎨⎧c ＝－1，d ＝4.所以A ＝⎣⎡⎦⎤1 2－1 4，所以A －1＝⎣⎢⎢⎡⎦⎥⎥⎤23－131616.【题目2】选修4－4：坐标系与参数方程已知直线l 的极坐标方程为ρsin ()θ－π3＝3，曲线C 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝2sin θ(θ为参数)，设点P 是曲线C 上的任意一点，求P 到直线l 的距离的最大值.解由ρsin ()θ－π3＝3，可得ρ⎝⎛⎭⎫12sin θ－32cos θ＝3.所以y －3x ＝6，即3x －y ＋6＝0，由⎩⎨⎧x ＝2cos θ，y ＝2sin θ得x 2＋y 2＝4，圆的半径为r ＝2，所以圆心到直线l 的距离d ＝62＝3，所以P 到直线l 的距离的最大值为d ＋r ＝5.【题目3】选修4－5：不等式选讲已知x ，y ，z ∈R ，且x ＋2y ＋3z ＋8＝0.求证：(x －1)2＋(y ＋2)2＋(z －3)2≥14. 证明因为[(x －1)2＋(y ＋2)2＋(z －3)2](12＋22＋32)≥[(x －1)＋2(y ＋2)＋3(z －3)]2 ＝(x ＋2y ＋3z －6)2＝142，当且仅当x －11＝y ＋22＝z －33，即x ＝z ＝0，y ＝－4时，取等号，所以(x －1)2＋(y ＋2)2＋(z －3)2≥14.必做部分【题目1】如图，在直三棱柱ABC －A 1B 1C 1中，已知CA ＝CB ＝1，AA 1＝2，∠BCA ＝90°.(1)求异面直线BA 1与CB 1夹角的余弦值； (2)求二面角B －AB 1－C 平面角的余弦值.解如图，以{CA →，CB →，CC 1→}为正交基底，建立空间直角坐标系C －xyz ，则A (1，0，0)，B (0，1，0)，A 1(1，0，2)，B 1(0，1，2)，所以CB 1→＝(0，1，2)，AB →＝(－1，1，0)，AB 1→＝(－1，1，2)，BA 1→＝(1，－1，2). (1)因为cos 〈CB 1→，BA 1→〉＝CB 1→·BA 1→|CB 1→||BA 1→|＝35×6＝3010，所以异面直线BA 1与CB 1夹角的余弦值为3010. (2)设平面CAB 1的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧m ·AB 1→＝0，m ·CB 1→＝0，即⎩⎨⎧－x ＋y ＋2z ＝0，y ＋2z ＝0，取平面CAB 1的一个法向量为m ＝(0，2，－1)；设平面BAB 1的法向量为n ＝(r ，s ，t )，则⎩⎪⎨⎪⎧n ·AB 1→＝0，n ·AB →＝0，即⎩⎨⎧－r ＋s ＋2t ＝0，－r ＋s ＝0，取平面BAB 1的一个法向量为n ＝(1，1，0)，则cos 〈m ，n 〉＝m·n|m ||n |＝25×2＝105，易知二面角B －AB 1－C 为锐角，所以二面角B －AB 1－C 平面角的余弦值为105. 【题目2】在数列{a n }中，已知a 1＝20，a 2＝30，a n ＋1＝3a n －a n －1(n ∈N *，n ≥2).(1)当n ＝2，3时，分别求a 2n －a n －1a n ＋1的值，并判断a 2n －a n －1a n ＋1(n ≥2)是否为定值，然后给出证明；(2)求出所有的正整数n ，使得5a n ＋1a n ＋1为完全平方数.解 (1)由已知得a 3＝70，a 4＝180.所以当n ＝2时，a 2n －a n －1a n ＋1＝－500；当n ＝3时，a 2n －a n －1a n ＋1＝－500.猜想：a 2n－a n －1a n ＋1＝－500(n ≥2). 下面用数学归纳法证明： ①当n ＝2时，结论成立.②假设当n ＝k (k ≥2，k ∈N *)时，结论成立，即a 2k －a k －1a k ＋1＝－500. 将a k ＋1＝3a k －a k －1代入上式，可得a 2k －3a k a k ＋1＋a 2k ＋1＝－500.则当n ＝k ＋1时，a 2k ＋1－a k a k ＋2＝a 2k ＋1－a k (3a k ＋1－a k )＝a 2k ＋1－3a k a k ＋1＋a 2k ＝－500.故当n ＝k ＋1结论成立，根据①②可得a 2n －a n －1a n ＋1＝－500(n ≥2)成立. (2)将a n －1＝3a n －a n ＋1代入a 2n －a n －1a n ＋1＝－500，得a 2n ＋1－3a n a n ＋1＋a 2n ＝－500，则5a n ＋1a n ＝(a n ＋1＋a n )2＋500，5a n a n ＋1＋1＝(a n ＋1＋a n )2＋501，设5a n ＋1a n ＋1＝t 2(t ∈N *)，则t 2－(a n ＋1＋a n )2＝501，即[t －(a n ＋1＋a n )](t ＋a n ＋1＋a n )＝501，又a n ＋1＋a n ∈N ，且501＝1×501＝3×167，故⎩⎨⎧a n ＋1＋a n －t ＝－1，a n ＋1＋a n ＋t ＝501或⎩⎨⎧a n ＋1＋a n －t ＝－3，a n ＋1＋a n ＋t ＝167，所以⎩⎨⎧t ＝251，a n ＋1＋a n ＝250或⎩⎨⎧t ＝85，a n ＋1＋a n ＝82，由a n ＋1＋a n ＝250解得n ＝3；由a n ＋1＋a n ＝82得n 无整数解，所以当n ＝3时，满足条件.专题五2.(2018·江苏省盐城中学调研)已知矩阵M ＝⎣⎡⎦⎤0 ab 0满足：Ma i ＝λi a i ，其中λi (i ＝1,2)是互不相等的实常数，a i (i ＝1,2)是非零的平面列向量，λ1＝1，a 2＝⎣⎡⎦⎤11，求矩阵M .解由题意，λ1，λ2是方程f (λ)＝⎪⎪⎪⎪⎪⎪ λ－a －bλ＝λ2－ab ＝0的两根. 因为λ1＝1，所以ab ＝1.又因为Ma 2＝λ2a 2，所以⎣⎡⎦⎤0 a b 0 ⎣⎡⎦⎤11＝λ2⎣⎡⎦⎤11，从而⎩⎨⎧a ＝λ2，b ＝λ2，所以λ22＝ab ＝1.因为λ1≠λ2，所以λ2＝－1，从而a ＝b ＝－1，故矩阵M ＝⎣⎢⎡⎦⎥⎤ 0 －1－10. 3.(2018·苏州、南通等六市模拟)在极坐标系中，求以点P ()2，π3为圆心且与直线l: ρsin ()θ－π3＝2相切的圆的极坐标方程.解以极点为原点，极轴为x 轴的正半轴，建立平面直角坐标系xOy .则点P 的直角坐标为()1，3.将直线l: ρsin ()θ－π3＝2的方程变形为： ρsin θcos π3－ρcos θsin π3＝2，化为普通方程得3x －y ＋4＝0.∴P ()1，3到直线l: 3x －y ＋4＝0的距离为4()32＋()－12＝2.∴所求圆的普通方程为()x －12＋()y －32＝4，化为极坐标方程得ρ＝4sin ()θ＋π6.4.已知实数x >0，y >0，z >0，证明：()1x ＋2y ＋3z ()x 2＋y 4＋z 6≥92. 证明因为x >0，y >0，z >0，所以1x ＋2y ＋3z 3≥36xyz ，x 2＋y 4＋z 63≥ 3xyz 48，所以()1x ＋2y ＋3z()x 2＋y 4＋z 6≥92. 当且仅当x ∶y ∶z ＝1∶2∶3时，等号成立. 5.已知点A (1,2)在抛物线F ：y 2＝2px 上.(1)若△ABC 的三个顶点都在抛物线F 上，记三边AB ，BC ，CA 所在直线的斜率分别为k 1，k 2，k 3, 求1k 1－1k 2＋1k 3的值；(2)若四边形ABCD 的四个顶点都在抛物线F 上，记四边AB ，BC ，CD ，DA 所在直线的斜率分别为k 1，k 2，k 3，k 4，求1k 1－1k 2＋1k 3－1k 4的值. 解 (1)由点A (1,2)在抛物线F 上，得p ＝2， ∴抛物线F ：y 2＝4x ，设B ()y 214，y 1，C ()y 224，y 2， ∴1k 1－1k 2＋1k 3＝y 214－1y 1－2－y 224－y 214y 2－y 1＋1－y 2242－y 2＝y 1＋24－y 2＋y 14＋2＋y 24＝1. (2)另设D ()y 234，y 3，则1k 1－1k 2＋1k 3－1k 4＝y 1＋24－y 2＋y 14＋y 3＋y 24－2＋y 34＝0.6.已知f n (x )＝C 0n x n －C 1n (x －1)n ＋…＋(－1)k C k n (x －k )n ＋…＋(－1)n C n n (x －n )n ，其中x ∈R ，n ∈N *，k ∈N ，k ≤n .(1)试求f 1(x )，f 2(x )，f 3(x )的值；(2)试猜测f n (x )关于n 的表达式，并证明你的结论.解 (1)f 1(x )＝C 01x －C 11(x －1)＝1，f 2(x )＝C 02x 2－C 12(x －1)2＋C 22(x －2)2＝x 2－2(x －1)2＋(x －2)2＝2，f 3(x )＝C 03x 3－C 13(x －1)3＋C 23(x －2)3－C 33(x －3)3＝x 3－3(x －1)3＋3(x －2)3－(x －3)3＝6.(2)猜测f n (x )＝n ！，n ∈N *. 以下用数学归纳法证明.①当n ＝1时，f 1(x )＝1，等式成立.②假设当n ＝m (m ≥1，m ∈N *)时，等式成立，即f m (x )＝∑k ＝0m(－1)k C k m(x －k )m ＝m ！. 当n ＝m ＋1时，则f m ＋1(x )＝∑k ＝0m ＋1(－1)k C k m ＋1·(x －k )m ＋1. 因为C k m ＋1＝C k m ＋C k －1m ，k C k m ＋1＝(m ＋1)·C k －1m，其中k ＝1,2，…，m ，且C 0m ＋1＝C 0m ，C m ＋1m ＋1＝C m m ，所以f m ＋1(x )＝∑k ＝0m ＋1(－1)k C k m ＋1(x －k )m ＋1＝x ∑k ＝0m ＋1(－1)k C k m ＋1(x －k )m－∑k ＝0m ＋1(－1)k k C km ＋1(x －k )m＝x ∑k ＝0m(－1)k C k m(x －k )m ＋x ∑k ＝1m ＋1(－1)k C k －1m(x －k )m －(m ＋1)∑k ＝1m ＋1(－1)k C k－1m (x －k )m ＝x ·m ！＋(－x ＋m ＋1)∑k ＝0m(－1)k C k m ·[(x －1)－k ]m ＝x ·m ！＋(－x ＋m ＋1)·m!＝(m ＋1)·m ！＝(m ＋1)！. 即当n ＝m ＋1时，等式也成立. 由①②可知，对n ∈N *，均有f n (x )＝n ！.专题六2.(2018·苏州、南通等六市模拟)在平面直角坐标系xOy 中，已知A ()0，0，B ()3，0，C ()2，2.设变换T 1, T 2对应的矩阵分别为M ＝⎣⎡⎦⎤1 02， N ＝⎣⎡⎦⎤2 00 1，求对△ABC 依次实施变换T 1, T 2后所得图形的面积.解依题意，依次实施变换T 1, T 2所对应的矩阵NM ＝ ⎣⎡⎦⎤2 01 ⎣⎡⎦⎤1 00 2＝⎣⎡⎦⎤2 00 2.则⎣⎡⎦⎤2 02 ⎣⎡⎦⎤00＝⎣⎡⎦⎤00， ⎣⎡⎦⎤2 00 2 ⎣⎡⎦⎤30＝⎣⎡⎦⎤60，⎣⎡⎦⎤2 00 2 ⎣⎡⎦⎤22＝⎣⎡⎦⎤44.∴A ()0，0，B ()3，0，C ()2，2分别变为点A ′()0，0，B ′()6，0，C ′()4，4. ∴所得图形的面积为12×6×4＝12.3.已知两个动点P ，Q 分别在两条直线l 1：y ＝x 和l 2：y ＝－x 上运动，且它们的横坐标分别为角θ的正弦，余弦，θ∈[0，π]，记OM →＝OP →＋OQ →，求动点M 的轨迹的普通方程.解设M (x ，y )，则⎩⎨⎧x ＝sin θ＋cos θ，y ＝sin θ－cos θ，两式平方相加得x 2＋y 2＝2.又x ＝2sin ()θ＋π4，y ＝2sin ()θ－π4， θ∈[0，π]，所以x ∈[－1，2]，y ∈[－1，2].所以动点M 轨迹的普通方程为x 2＋y 2＝2(x ，y ∈[－1，2]).4.(2018·江苏省盐城中学质检)已知a >0，b >0，证明：(a 2＋b 2＋ab )(ab 2＋a 2b ＋1)≥9a 2b 2.证明因为a >0，b >0，所以a 2＋b 2＋ab ≥33a 2·b 2·ab ＝3ab >0，ab 2＋a 2b ＋1≥33ab 2·a 2b ·1＝3ab >0，所以(a 2＋b 2＋ab )(ab 2＋a 2b ＋1)≥9a 2b 2.5.甲、乙两人轮流投篮，每人每次投一次篮，先投中者获胜，投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为25，乙每次投篮命中的概率为23，且各次投篮互不影响.现由甲先投.(1)求甲获胜的概率；(2)求投篮结束时甲的投篮次数X 的概率分布与数学期望.解 (1)设甲第i 次投中获胜的事件为A 1(i ＝1,2,3)，则A 1，A 2，A 3彼此互斥. 甲获胜的事件为A 1＋A 2＋A 3. P (A 1)＝25，P (A 2)＝35×13×25＝225，P (A 3)＝()352×()132×25＝2125. 所以P (A 1＋A 2＋A 3)＝P (A 1)＋P (A 2)＋P (A 3)＝25＋225＋2125＝62125.(2)X 的所有可能取值为1,2,3. 则P (X ＝1)＝25＋35×23＝45，P (X ＝2)＝225＋35×13×35×23＝425，P (X ＝3)＝()352×()132×1＝125. 即X 的概率分布为所以数学期望E (X )＝1×45＋2×425＋3×125＝3125.6.设n 个正数a 1，a 2，…，a n 满足a 1≤a 2≤…≤a n (n ∈N *且n ≥3). (1)当n ＝3时，证明：a 1a 2a 3＋a 2a 3a 1＋a 3a 1a 2≥a 1＋a 2＋a 3；(2)当n ＝4时，不等式a 1a 2a 3＋a 2a 3a 4＋a 3a 4a 1＋a 4a 1a 2≥a 1＋a 2＋a 3＋a 4也成立，请你将其推广到n (n ∈N *且n ≥3)个正数a 1，a 2，…，a n 的情形，归纳出一般性的结论并用数学归纳法证明. 证明 (1)因为a n (n ∈N *且n ≥3)均为正实数，左—右＝12()a 1a 3a 2＋a 1a 2a 3－2a 1＋12()a 2a 3a 1＋a 1a 2a 3－2a 2＋12()a 2a 3a 1＋a 1a 3a 2－2a 3≥12⎝⎛⎭⎫2a 1a 3a 2×a 1a 2a 3－2a 1＋12⎝⎛⎭⎫2a 2a 3a 1×a 1a 2a 3－2a 2＋12⎝⎛⎭⎫2a 2a 3a 1×a 1a 3a 2－2a 3＝0，所以原不等式a 2a 3a 1＋a 1a 3a 2＋a 1a 2a 3≥a 1＋a 2＋a 3成立. (2)归纳的不等式为：a 1a 2a 3＋a 2a 3a 4＋…＋a n －2a n －1a n ＋a n －1a n a 1＋a n a 1a 2≥a 1＋a 2＋…＋a n (n ∈N *且n ≥3). 记F n ＝a 1a 2a 3＋a 2a 3a 4＋…＋a n －2a n －1a n ＋a n －1a n a 1＋a n a 1a 2－(a 1＋a 2＋…＋a n )，当n ＝3(n ∈N *)时，由(1)知，不等式成立；假设当n ＝k (k ∈N *且k ≥3)时，不等式成立，即F k ＝a 1a 2a 3＋a 2a 3a 4＋…＋a k －2a k －1a k ＋a k －1a k a 1＋a k a 1a 2－(a 1＋a 2＋…＋a k )≥0. 则当n ＝k ＋1时，F k ＋1＝a 1a 2a 3＋a 2a 3a 4＋…＋a k －2a k －1a k ＋a k －1a k a k ＋1＋a k a k ＋1a 1＋a k ＋1a 1a 2－(a 1＋a 2＋…＋a k ＋a k ＋1) ＝F k ＋a k －1a k a k ＋1＋a k a k ＋1a 1＋a k ＋1a 1a 2－a k －1a k a 1－a k a 1a 2－a k ＋1＝F k ＋a k －1a k ⎝⎛⎭⎫1ak ＋1－1a 1＋a k ＋1()a k a 1－1＋a 1a 2(a k ＋1－a k )≥0＋a 2k ⎝⎛⎭⎫1a k ＋1－1a 1＋a k ＋1()a k a 1－1＋a 1a k (a k ＋1－a k )＝(a k ＋1－a k )⎝ ⎛⎭⎪⎫a k a 1＋a 1a k －a k ＋1＋a k a k ＋1，因为a k ＋1≥a k ，a k a 1＋a 1a k ≥2，a k ＋1＋a k a k ＋1≤a k ＋1＋a k ＋1a k ＋1＝2，所以F k ＋1≥0，所以当n ＝k ＋1时，不等式成立.综上所述，不等式a 1a 2a 3＋a 2a 3a 4＋…＋a n －2a n －1a n ＋a n －1a n a 1＋a n a 1a 2≥a 1＋a 2＋…＋a n (n ∈N *且n ≥3)成立.专题七2.若二阶矩阵M 满足⎣⎢⎡⎦⎥⎤－2122－1M ＝⎣⎡⎦⎤－3 0 4－1，求曲线4x 2＋4xy ＋y 2－12x ＋12y ＝0在矩阵M 所对应的变换作用下得到的曲线的方程.解记矩阵A ＝⎣⎢⎢⎡⎦⎥⎥⎤－2122 －1，det(A )＝(－2)×(－1)－2×12＝1≠0，故A －1＝⎣⎢⎢⎡⎦⎥⎥⎤－1 －12－2 －2，所以M ＝A －1⎣⎢⎡⎦⎥⎤－30 4 －1＝⎣⎢⎢⎡⎦⎥⎥⎤－1－12－2－2 ⎣⎢⎡⎦⎥⎤－30 4－1＝⎣⎢⎢⎡⎦⎥⎥⎤ 112－22，即矩阵M ＝⎣⎢⎢⎡⎦⎥⎥⎤ 112－2 2.设曲线4x 2＋4xy ＋y 2－12x ＋12y ＝0上任意一点P (x ，y )在矩阵M 对应的变换作用下得到点P ′(x ′，y ′).所以⎣⎡⎦⎤x ′y ′＝⎣⎢⎢⎡⎦⎥⎥⎤ 112－22 ⎣⎡⎦⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤ x ＋12y －2x ＋2y ，所以⎩⎪⎨⎪⎧x ′＝x ＋12y ，y ′＝－2x ＋2y ，所以⎩⎨⎧x ＝4x ′－y ′6，y ＝2x ′＋y ′3，又点P (x ，y )在曲线4x 2＋4xy ＋y 2－12x ＋12y ＝0上，代入整理得2x ′2＋3y ′＝0，由点P (x ，y )的任意性可知，所求曲线的方程为2x 2＋3y ＝0.3.已知直线的极坐标方程为ρsin ()θ＋π4＝22，圆M 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝－2＋2sin θ(其中θ为参数).(1)将直线的极坐标方程化为直角坐标方程； (2)求圆M 上的点到直线的距离的最小值. 解 (1)极点为直角坐标原点O ，ρsin ()θ＋π4＝ρ⎝⎛⎭⎫22sin θ＋22cos θ＝22，∴ρsin θ＋ρcos θ＝1，其直角坐标方程为x ＋y －1＝0.(2)将圆的参数方程化为普通方程为x 2＋(y ＋2)2＝4，圆心为M (0，－2)，∴点M 到直线的距离为d ＝|0－2－1|2＝32＝322，∴圆上的点到直线距离的最小值为32－42.4.已知函数f (x )＝|x ＋m |＋|x －2|(m >0)的最小值为4，正实数a ，b 满足1a ＋1b ＝ 3.求证：1a 2＋2b2≥m .证明易知|x ＋m |＋|x －2|≥|(x ＋m )－(x －2)|＝|m ＋2|，故由f (x )的最小值为4得|m ＋2|＝4，又m >0，所以m ＝2. 又()1a 2＋2b 2⎣⎡⎦⎤12＋⎝⎛⎭⎫122≥⎝⎛⎭⎫1a ×1＋2b ×122＝3，当且仅当a ＝32，b ＝3时等号成立，故1a 2＋2b2≥2＝m ，即结论成立. 5.如图，在直三棱柱ABC －A 1B 1C 1中，AA 1＝AB ＝AC ＝2，AB ⊥AC ，M 是棱BC 的中点，点P 在线段A 1B 上.(1)若P 是线段A 1B 的中点，求直线MP 与直线AC 所成角的大小；(2)若N 是CC 1的中点，直线A 1B 与平面PMN 所成角的正弦值为77，求线段BP 的长度. 解分别以AB ，AC ，AA 1所在直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则A (0,0,0)，B (2,0,0)，C (0,2,0)，A 1(0,0,2)，M (1,1,0).(1)若P 是线段A 1B 的中点，则P (1,0,1)，MP →＝(0，－1,1)，AC →＝(0,2,0). 所以cos 〈MP →，AC →〉＝MP →·AC →||MP →·||AC→＝－22.又〈MP →，AC →〉∈[0，π]，所以〈MP →，AC →〉＝3π4.所以直线MP 与直线AC 所成的角的大小为π4.(2)由N (0,2,1)，得MN →＝(－1,1,1). 设P (x ，y ，z )，BP →＝λBA 1,0≤λ≤1，则(x －2，y ，z )＝λ(－2,0,2)，所以⎩⎨⎧x ＝2－2λ，y ＝0，z ＝2λ，所以P (2－2λ，0,2λ)，所以MP →＝(1－2λ，－1,2λ). 设平面PMN 的法向量n ＝(x 1，y 1，z 1)，则n ⊥MN →，n ⊥MP →，所以⎩⎨⎧－x 1＋y 1＋z 1＝0，(1－2λ)x 1－y 1＋2λz 1＝0，取n ＝()1＋12λ，12λ，1.因为BA 1＝(－2,0,2)，设直线A 1B 与平面PMN 所成的角为θ.由sin θ＝||cos 〈n ，BA 1〉＝|n ·BA 1|||n ·||BA 1＝⎪⎪⎪⎪(－2)×()1＋12λ＋2()1＋12λ2＋()12λ2＋1·22＝77，得λ＝14(舍负). 所以BP →＝14BA 1，所以BP ＝14BA 1＝22.6.已知()1＋12xn展开式的各项依次记为a 1(x )，a 2(x )，a 3(x )，…，a n(x )，an ＋1(x ).设F (x )＝a 1(x )＋2a 2(x )＋3a 3(x )＋…＋na n (x )＋(n ＋1)·a n ＋1(x ).(1)若a 1(x )，a 2(x )，a 3(x )的系数依次成等差数列，求n 的值； (2)求证：对任意x 1，x 2∈[0,2]，恒有|F (x 1)－F (x 2)|≤2n －1(n ＋2)－1. (1)解依题意a k (x )＝C k －1n ()12x k －1，k ＝1,2,3，…，n ＋1，a 1(x )，a 2(x )，a 3(x )的系数依次为C 0n ·()12＝1，C 1n ·12＝n 2，C 2n ·()122＝n (n －1)8，所以2×n2＝1＋n (n －1)8，解得n ＝8或n ＝1(舍去).(2)证明 F (x )＝a 1(x )＋2a 2(x )＋3a 3(x )＋…＋na n (x )＋(n ＋1)a n ＋1(x )＝C 0n ＋2C 1n ()12x ＋3C 2n()12x 2＋…＋n C n －1n()12x n －1＋(n ＋1)C n n ()12x n，F (2)＝C 0n ＋2C 1n ＋3C 2n ＋…＋n C n －1n ＋(n ＋1)C nn ，设S n ＝C 0n ＋2C 1n ＋3C 2n ＋…＋n C n －1n ＋(n ＋1)C n n ，则S n ＝(n ＋1)C n n ＋n C n －1n ＋…＋3C 2n ＋2C 1n ＋C 0n ，考虑到C k n ＝C n －k n ，将以上两式相加得2S n ＝(n ＋2)(C 0n ＋C 1n ＋C 2n ＋…＋C n －1n ＋C n n )，所以S n ＝2n －1(n ＋2)，又当x ∈[0,2]时，F ′(x )>0恒成立，从而F (x )是[0,2]上的单调递增函数，所以对任意x 1，x 2∈[0,2]，|F (x 1)－F (x 2)|≤F (2)－F (0)＝2n －1(n ＋2)－1。

江苏省苏州大学2020届高三数学考前指导试题(含解析)

2020年江苏省苏州大学高考数学考前指导试卷
一、填空题：（本大题共14小题，每小题5分，共70分）
1．已知集合A={﹣1，0，2}，B={2，a2}，若BA，则实数a的值为．
2．已知（2﹣i）（m+2i）=10，i是虚数单位，则实数m的值为．
3．一个总体分为A，B两层，用分层抽样方法从总体中抽取一个容量为10的样本．已知B层
中每个个体被抽到的概率都为，则总体中的个体数为．
4．已知双曲线的离心率为，则b=．
5．如图是一个算法流程图，则输出的k值是
6．若a，b∈{0，1，2}，则函数f（x）=ax2+2x+b有零点的概率为．
7．设变量x，y满足约束条件，则目标函数z=2x+y的最小值为．
8．九章算术》商功章有题：一圆柱形谷仓，高1丈3尺寸，容纳谷2000斛（1丈=10尺，
定值，则=．
12．若a＞0，b＞0，且
，若对于直线3x+y﹣4=0上任意一点P，恒为
，则a+2b的最小值为．
13．已知函数，若f（x1）=f（x2）=f（x3）（x1＜x2＜x3），则的
取Байду номын сангаас范围为．
14．在△ABC中，若3sinC=2sinB，点E，F分别是AC，AB的中点，则
的取值范围为．
1尺=10寸，斛为容积单位，1斛≈1.62立方尺，π≈3），则圆柱底面周长约为丈．
9．等比数列{an}的前n项和为Sn，公比q≠1，若，则q的值为．
10．已知圆C：（x﹣1）2+（y﹣a）2=16，若直线ax+y﹣2=0与圆C相交于AB两点，且CA⊥CB，
则实数a的值是．
11．设点A（1，2），非零向量

【附加15套高考模拟试卷】苏州大学2020届高考数学考前指导卷【1】含答案

苏州大学2020届高考数学考前指导卷【1】一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在三棱锥S ABC -中，底面ABC △是直角三角形，其斜边4AB =，SC ⊥平面ABC ，且3SC =，则三棱锥的外接球的表面积为（） A ．25π B ．20π C ．16π D ．13π2．数列{}n a 的前n 项和为n S ，24,n n S a n N *=-∈，则n a =（）A ．12n + B ．2n C ．12n - D ．22n -3．已知双曲线C ：22221x y a b-=（0a >，0b >），1F ，2F 分别为其左、右焦点，O 为坐标原点，若点2F 关于渐近线的对称点恰好落在以1F 为圆心，1OF 为半径的圆上，则双曲线C 的离心率是（） A ．2 B ．3 C ．2D ．34．在ABC ∆中，角A ，B ，C 对应边分别为a ，b ，c ，已知三个向量(,cos)2A m a =r，(,cos )2B n b =r，(,cos )2C p c =r共线，则ABC ∆形状为（）A ．等边三角形B ．等腰三角形C ．直角三角形D ．等腰直角三角形5．唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在区域为221x y +≤，若将军从点(2,0)A 处出发，河岸线所在直线方程为3x y +=，并假定将军只要到达军营所在区域即回到军营，则“将军饮马”的最短总路程为（）A ．101-B ．221-C ．22D ．106．下列图象中，可能是函数()(e e )()a x x f x x a -=+∈Z 的图象的是( )A ．B ．C ．D ．7．已知平面向量a r 与b r 的夹角为23π，若(3,1)a =-r，2213a b -=r r ，则b r （）A ．3B ．4C ．3D ．28．已知椭圆22:143x y C +=的左、右焦点分别为1F 、2F ，过2F 且斜率为1的直线l 交椭圆C 于A 、B 两点，则1F AB ∆的内切圆半径为( )A ．2B ．22C ．32D ．429．当动点P 在正方体1111ABCD A B C D -的体对角线1A C 上运动时，异面直线BP 与1AD 所成角的取值范围是（）A ．,64ππ⎡⎤⎢⎥⎣⎦ B ．,63ππ⎡⎤⎢⎥⎣⎦ C ．,43ππ⎡⎤⎢⎥⎣⎦ D ．,32ππ⎡⎫⎪⎢⎣⎭ 10．设()f x 为定义在R 上的奇函数，当0x ≥时，()2(xf x m m =+为常数），则 ()1f -= （）A ．3B ．1C ．1-D ．3-11．将函数()4cos 2f x x π⎛⎫=⎪⎝⎭和直线()1g x x =-的所有交点从左到右依次记为1A ，2A ，…，5A ，若P 点坐标为(0,3)，则125...PA PA PA +++=u u u r u u u u r u u u r（）A ．0B ．2C ．6D ．1012．某几何体的三视图如图所示，则该几何体的表面积为（）A ．240B ．220C ．200D ．260二、填空题：本题共4小题，每小题5分，共20分。

江苏省苏州市2020届高三数学考前指导卷(二)含附加题含答案解析

A．选修 4—2：矩阵与变换
已知矩阵
A=
1 0 0 2
，
B
=
ห้องสมุดไป่ตู้
1 2
01
，若直线ｌ依次经过变换
TA , TB
后得到直线ｌ ˊ:
2x + y − 2 = 0 ，求直线ｌ的方程．
B．选修 4—4：坐标系与参数方程
已知直线ｌ的参数方程为
x
=
2
+
1 2
t
（t 为参数），点 P(1，2)在直线ｌ上．
7．已知an 为等差数列， Sn 为其前 n 项和，若 a2 + 5 = 2a5 ，则 S15 的值是________．
8．圆柱形容器的内壁底面半径是 10cm，有一个实心铁球浸没于容器的水中，若取出这个铁
1
球，测得容器的水面下降了 5 cm ，则这个铁球的表面积为________ cm2 ． 3
江苏省苏州市 2020 届高三考前指导卷（二）
数学Ⅰ试题
一、填空题：不需要写出解答过程，请把答案直接填在答题卡相应位置上．
1．已知集合 A = x x 1 ， B = 1, 2,3 ，则 A B = ________．
2．已知复数 z = 2 + i （其中 i 为虚数单位），若 z = a + bi (a,b R) ，则 ab 的值为________．
x
（1）求函数 f ( x) 的单调区间；
（2）若函数 f ( x) 在定义域内有两个零点，求 a 的取值范围；
( ) （3）若对任意 x (0, +) ，不等式 m( xln x +1) + (e −1) x≥ 2x − x2 ex 恒成立，求 m 的取值

2020年6月苏州大学2020届高三高考考前指导卷(一)数学答案(含附加题)

1 绝密★启用前江苏省苏州大学2020届高三高考考前指导卷(一)数学试题参考答案解析2020年6月一、填空题：本大题共14小题，每小题5分，共计70分．1．{|12}x x <≤ 2．23．280 4．1(0]2， 5．2 6．527．56 8．π2- 9．13 10．12- 11．5306612．4 13．4[1]33-， 14解答与提示：1．{|12}A B x x =<≤．2． 2i (2i)(1i)22i 1i 222a a a a z +++-+===+-．因为z 为纯虚数,所以2020a a -=⎧⎨+≠⎩，，解得2a =． 3．由图可知,时速在区间[8090)[110120)，，，的频率为(0.010.02)100.3+⨯=,所以时速在区间[90110)，的频率为10.3-,所以时速在区间[90,110)的车辆约为4000.7280⨯=辆． 4．由1200x x -⎧⎨>⎩≥，，解得102x <≤,即函数()f x 的定义域为1(0]2，． 5．离心率c e a =所以2λ=． 6．执行第一次循环105S i ==，；执行第二次循环207S i ==，；执行第三次循环349S i ==，；执行第四次循环5211S i ==，,终止循环．所以52S =．7．记方案一与方案二坐到“3号”车的概率分别为P 1,P 2,三辆车的出车顺序可能为：123,132,213,231,312,321．方案一坐“3号”车可能：132,213,231,所以136P =；方案二坐“3号”车可能：312,321,所以226P =．则该嘉宾坐到“3号”车的概率1256P P P =+=． 8．()cos sin f x x x x '=-,所以在π2x =处的切线的斜率为ππ()22k f '==-．。

2020苏大指导卷

的值是 ▲ ．
（第 6 题图）
8．圆柱形容器的内壁底面半径是10 cm ，有一个实心铁球浸没于
容器的水中，若取出这个铁球，测得容器的水面下降了 5 cm ， 3
则这个铁球的表面积为 ▲ cm2 ．
（第 6 题图）
1
9．若直线 y kx 1与曲线 y x 相切，则实数 k 的值为 ▲ ．
10．计算：
高三数学练习卷（一）
数学 Ⅰ 试题
2020．6
注意事项
在答题前请认真阅读本注意事项及各题答题要求 1. 本试卷共 4 页，包含填空题（第 1 题第 14 题）、解答题（第 15 题第 20 题）．本卷满分 160
分，考试时间为 120 分钟．考试结束后，请将答题卡交回． 2. 答题前，请您务必将自己的姓名、调研序列号用 0.5 毫米黑色墨水的签字笔填写在答题卡的规定
都成立，则称数列{cn} 为“ t 倍等阶差数列”．已知数列{an} 为“t 倍等阶差数列”．
（1）若
a1
0 ，a2
Hale Waihona Puke 1 2，a31 ，求实数 t
的值；
（2）在（1）的条件下，设 bn a2n1 a2n1 (n N* ) ．
①求数列{bn} 的通项公式；
②设数列{ 1 } 的前 bnbn1
n
项和为
（第 17 题图）
18．（本小题满分 16 分）
如图，点 F
为椭圆
C
x2 ：
a2
y2 b2
1
(a
b 0) 的左焦点，点 A，B 分别为椭圆 C 的右顶
点和上顶点，点 P( 2 ， 6 ) 在椭圆 C 上，且满足 OP∥AB ． 2
（1）求椭圆 C 的方程；（2）过定点 T (m ，0) (| m | 2) 且与 x 轴不重合的直线 l 交椭圆 C 于 M ，N 两点，直线

苏州大学2020届高考考前指导卷数学试题

苏州大学2020届高考考前指导卷数学 Ⅰ一、填空题：本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请把答案直接填在答题卡相应位置上．．．．．．．．． 1．已知集合{|12}A x x =-≤≤，{|1}B x x =>，则A B =I ▲ ． 2．已知纯虚数z 满足(1i)2i z a -=+，则实数a 等于 ▲ ．3．某高速公路移动雷达测速检测车在某时段对某段路过往的400辆汽车的车速进行检测，根据检测的结果绘制出如图所示的频率分布直方图，根据直方图的数据估计400辆汽车中时速在区间[90110)，的约有 ▲ 辆． 4．函数()12lg f x x x =-+的定义域为 ▲ ． 5．在直角坐标系xOy 中，已知双曲线221 (0)y x λλ-=>的离心率为3，则λ的值为 ▲ ． 6．执行如图所示的程序框图，输出的S 的值为 ▲ ．7．展览会会务组安排了分别标有序号为“1号”、“2号”、“3号”的三辆车，采用等可能随机的顺序前往酒店接嘉宾．某与会嘉宾设计了两种乘车方案．方案一：不乘坐第一辆车，若第二辆车的车序号大于第一辆车的车序号，就乘坐此车，否则乘坐第三辆车；方案二：直接乘坐第一辆车．则该嘉宾坐到“3号”车的概率是 ▲ ． 8．已知函数()cos f x x x =，则()f x 在点(())22f ππ，处的切线的斜率为 ▲ ． 9．已知n S 是等比数列{}n a 前n 项的和，若公比2q =，则1356a a a S ++的值是 ▲ ． 10．已知2sin cos()4ααπ=+，则tan()4απ-的值是 ▲ ．11．《九章算术》是我国古代著名数学经典．里面对勾股定理的论述比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深一寸，锯道长一尺．问这块圆柱形木料的直径是多少？长为1丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示（阴影部分为镶嵌在墙体内的部分）．已知弦1AB =尺，弓形高1CD =寸，估算该木材的体积约为 ▲ （立方寸）．（注：1丈10=尺100=寸，π 3.14≈）开始输出S结束i ≤10i ←3N YS ←S +2i （第6题图）i ←i ＋2S ←4 墙体CDFEB A O（第11题图）12．已知函数2|log 2|01()3 1x x f x x +<⎧⎪=⎨>⎪⎩，≤，，若存在互不相等的正实数123x x x ，，，满足123x x x <<且123()()()f x f x f x ==，则31()x f x 的最大值为 ▲ ．13．已知点P 为正方形ABCD 内部一点（包含边界），E F ，分别是线段BC CD ，中点．若0CP DP ⋅=u u u r u u u r，且AP AE AF λμ=+u u u r u u u r u u u r，则λμ+的取值范围是 ▲ ．14．已知D 是ABC △边AC上一点，且1s 43co C B D A B D D A C ∠==，，则3AB BC +的最大值为▲ ．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）ABC △的内角A B C ，，的对边分别为a b c ，，，且1a =sin C c A =．（1）求C ；（2）若3b =，D 是AB 上的点，CD 平分ACB ∠，求ACD △的面积．16．（本小题满分14分）如图，在四棱锥P ABCD中，底面ABCD是矩形，点E在棱PC上（异于点P C，），平面ABE与棱PD交于点F．（1）求证：AB EF∥；（2）若AF⊥EF，求证：平面P AD⊥平面ABCD．EFA BC DP（第16题图）17．（本小题满分14分）如图，某公园内有一半圆形人工湖，O为圆心，半径为1千米．为了人民群众美好生活的需求，政府为民办实事，拟规划在OCD△区域种荷花，在OBD△区域建小型水上项目．已知AOC CODθ∠=∠=．（1）求四边形OCDB的面积（用θ表示）；（2）当四边形OCDB的面积最大时，求BD的长（最终结果可保留根号）．18．（本小题满分16分）如图，已知椭圆22221 (0)x ya ba b+=>>的离心率为22，短轴长为2，左、右顶点分别为A B，．设点(2) (0)M m m>，，连接MA交椭圆于点C．D C（1）求该椭圆的标准方程；（2）若OC CM，求四边形OBMC的面积．（第18题图）19．（本小题满分16分）已知函数2()2ln f x x ax x =-+（其中a 为常数）．（1）求函数()f x 的单调区间；（2）设函数()f x 有两个极值点1212 ()x x x x <，，若12()f x mx ＞恒成立，求实数m 的取值范围．20．（本小题满分16分）对于数列{}n a ，若从第二项起的每一项均大于该项之前的所有项的和，则称{}n a 为P 数列．（1）若{}n a 的前n 项和32n n S =+，试判断{}n a 是否是P 数列，并说明理由；（2）设数列12310a a a a L ，，，，是首项为1-，公差为d 的等差数列，若该数列是P 数列，求d 的取值范围；（3）设无穷数列{}n a 是首项为a 、公比为q 的等比数列，有穷数列{}{}n n b c ，是从{}n a 中取出部分项按原来的顺序所组成的不同数列，其所有项和分别为12T T ，，求{}n a 是P 数列时a 与q 所满足的条件，并证明命题“若0a >且12T T =，则{}n a 不是P 数列”．苏州大学2020届高考考前指导卷数学Ⅰ（附加题）21．【选做题】本题包括A 、B 、C 三小题，请选定其中两题．．．．．．，并在相应的．．．．．答题区域．．．．内作答．．．，若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．A ．选修4 - 2：矩阵与变换（本小题满分10分）在平面直角坐标系xOy 中，设点(5)P x ，在矩阵M 1234⎡⎤=⎢⎥⎣⎦对应的变换下得到点(2)Q y y -，，求1x y -⎡⎤⎢⎥⎣⎦M ．B ．选修4 - 4：坐标系与参数方程（本小题满分10分）在直角坐标系xOy 中，以坐标原点O 为极点，以x 轴非负半轴为极轴，建立极坐标系，直线l 的极坐标方程为sin()4ρθπ-C 的参数方程为2cos 3()sin 22x y ααα=-+⎧ππ⎨=⎩，≤≤，求l 与曲线C 交点的直角坐标．【必做题】第22题、第23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）在四棱锥P ABCD-中，//AB CD，2224AB CD BC AD====，60DAB∠=︒，AE BE=，PAD△为正三角形，且平面PAD⊥平面ABCD．（1）求二面角P EC D--的余弦值；（2）线段PC上是否存在一点M，使得异面直线DM和PE所成的角的余弦值为6？若存在，指出点M的位置；若不存在，请说明理由．ACDPB （第22题图）23．（本小题满分10分）已知非空集合M 满足{012}M n ⊆L ，，，，*(2)n n ∈N ≥，．若存在非负整数 ()k k n ≤，使得当a M ∈时，均有2k a M -∈，则称集合M 具有性质P ．记具有性质P 的集合M 的个数为()f n ．（1）求(2)f 的值；（2）求()f n 的表达式．苏州大学2020届高考考前指导卷参考答案一、填空题：本大题共14小题，每小题5分，共计70分．1．{|12}x x <≤ 2．2 3．280 4．1(0]2，5．2 6．527．568．π2-9．13 10．12-11．5306612．4 13．24[1]3-， 14．165解答与提示：1．{|12}A B x x =<I ≤． 2． 2i (2i)(1i)22i 1i 222a a a az +++-+===+-．因为z 为纯虚数，所以2020a a -=⎧⎨+≠⎩，，解得2a =． 3．由图可知，时速在区间[8090)[110120)，，，的频率为(0.010.02)100.3+⨯=，所以时速在区间[90110)，的频率为10.3-，所以时速在区间[90,110)的车辆约为4000.7280⨯=辆．4．由1200x x -⎧⎨>⎩≥，，解得102x <≤，即函数()f x 的定义域为1(0]2，．5．离心率13c e a λ+===，所以2λ=． 6．执行第一次循环105S i ==，；执行第二次循环207S i ==，；执行第三次循环349S i ==，；执行第四次循环5211S i ==，，终止循环．所以52S =．7．记方案一与方案二坐到“3号”车的概率分别为P 1，P 2，三辆车的出车顺序可能为：123，132，213，231，312，321．方案一坐“3号”车可能：132，213，231，所以136P =；方案二坐“3号”车可能：312，321，所以226P =．则该嘉宾坐到“3号”车的概率1256P P P =+=． 8．()cos sin f x x x x '=-，所以在π2x =处的切线的斜率为ππ()22k f '==-．9．2312135616[1()]111(1)131a q a a a q a q S q q-++-===-+-． 10．因为π2sin cos()4αα=+，解得1tan 3α=，所以11π13tan()14213α--==-+． 11．如图，10AB =（寸），则5AD =（寸），1CD =（寸），设圆O 的半径为x （寸），则(1)OD x =-（寸）．在Rt ADO △，由勾股定理可得2225(1)x x +-=，解得13x =（寸），则该木材的体积约为221001316900x 100π=π⨯=π≈53066（立方寸）． 12．函数()f x 的图象如右图所示，由题意，30()2f x <<，即319x <<，因为123()()()f x f x f x ==，所以3133()(3)x f x x x =-，令3(1,3)t x =∈，构造函数32()3g t t t =-+，2()36g t t t '=-+，所以当2t =时，max ()(2)4g t g ==，所以31()x f x 的最大值为4．13．设正方形ABCD 的边长为a ，以A 为原点，AB AD ，所在直线为分别为x y ，轴建立平面直角坐标系，则(00)(0)()(0)A B a C a a D a ，，，，，，，．设()P x y ，，因为0CP DP ⋅=u u u r u u u r，所以()()0x a y a x y a --⋅-=，，，即222()()24a a x y a -+-=，设cos 22sin 2a a x a y a θθ⎧=+⎪⎪⎨⎪=+⎪⎩，．又因为()()22a a E a F a ，，，，AP AE AF λμ=+u u u r u u u r u u u r ，所以()()()22a a x y a a λμ=+，，，，即22a x a a y a λμλμ⎧=+⎪⎪⎨⎪=+⎪⎩，，所以223()[(sin cos )]1)33224a a x y a a λμθθθπ+=+=++=+，由P 为正方形ABCD 内部一点（包含边界），可得[2]θ∈ππ，，所以[]444θπ5π9π+∈，，所以41)[1]43λμθπ+=+∈，． 14．法一：设AD t =，则3CD t =，4AC t =，在ABD △中，222cos ADB ∠=在BDC △中，cos BDC ∠=又cos cos ADB BDC ∠=-∠，=2221238t c a =+-，①在ABC △中，2222(4)2cos AC t a c ac B ==+-，即2221162t a c ac =+-，②由①②可得2239322a c ac ++=．所以2222333532(3)(3)(3)()(3)2228a c a c a c a c a c +=+-+-⨯=+≥，即2832(3)5a c ⨯+≤，所以3a c +，当且仅当3a c =，即a c =所以3AB BC +．法二：因为3CD AD =，所以3CD DA =u u u r u u u r，即3()BD BC BA BD -=-u u u r u u u r u u u r u u u r ，整理得到3144BD BA BC =+u u u r u u u r u u u r ，两边平方后有22291316168BD BA BC BA BC =++⋅u u u r u u u r u u u r u u u r u u u r，DCBA所以22913216168BA BC BA BC =++⋅u u u r u u u r u u u r u u u r 即2291312||||161684BA BC BA BC =++⋅⨯u u u r u u u r u u u r u u u r ，整理得到223329||||||||2BA BC BA BC =++⋅u u u r u u u r u uu r u u u r ，设||||c BA a BC ==u u u r u u u r ，，所以22239329(3)22c a ac c a ac =++=+-，因为293333()2222ac a c c a ⋅⋅+=≤，所以222293532(3)(3)(3)(3)288c a ac c a c a c a =+-+-+=+≥，3c a +，当且仅当a c 所以3AB BC +．二、解答题：本大题共6小题，共计90分． 15．（本小题满分14分）解：（1）因为1a =sin C c A =cos sin C c A =， ····················· 2分在ABC △中，由正弦定理sin sin a cA C=，所以sin sin a C c A =，cos sin sin A C C A =． ·························································· 4分因为(0)A ∈π，，所以sin 0A ≠sin C C =，因为(0)C ∈π，，所以sin 0C ≠，所以cos 0C ≠，所以tan C ············· 6分因为(0)C ∈π，，所以3C π=． ······························································ 8分（2）由（1）知，3ACB π∠=，因为1a =，3b =，所以ABC △的面积13sin sin 223ABC S ab ACB π=∠==△， ························ 10分因为D 是AB 上的点，CD 平分ACB ∠，所以1sin12613sin 26BCDACDa CD S a Sb b CD π⋅⋅===π⋅⋅△△， ···················································· 12分因为ABC ACD BCD S S S =+△△△，所以3344ACD ABC S S ==△△． ············· 14分 16．（本小题满分14分）证：（1）因为四边形ABCD 是矩形，所以AB CD ∥．··································································································· 2分又AB ⊄平面PDC ，CD ⊂平面PDC ，所以AB ∥平面PDC ， ····································································· 5分又因为AB ⊂平面ABE ，平面ABE ∩平面PDC EF =，所以AB EF ∥． ················································································· 7分（2）因为四边形ABCD 是矩形，所以AB ⊥AD ．因为AF ⊥EF ，（1）中已证AB EF ∥，所以AB ⊥AF ， ·················································································· 9分因为AB ⊥AD ，由点E 在棱PC 上（异于点C ），所以F 点异于点D ，所以AF AD A =I ，又AF AD ，⊂平面P AD ，所以AB ⊥平面P AD ， ······································· 12分又AB ⊂平面ABCD ，所以平面P AD ⊥平面ABCD ． ·································· 14分 17．（本小题满分14分）解：（1）由题意AOC COD θ∠=∠=，设四边形OCDB 的面积为()S θ，因为四边形OCDB 可以分为OCD △和OBD △两部分，所以11()sin sin(2)22OCD OBD S S S OC OD OB OD θθθ=+=⋅+⋅π-△△， ··············· 3分因为1OB OC OD ===，所以1()(sin sin 2)2S θθθ=+．因为020θθ>π->，，所以02θπ<<．所以四边形OCDB 的面积1()(sin sin 2)(0)22S θθθθπ=+∈，，． ······················ 6分（2）由（1）1()(sin sin 2)(0)22S θθθθπ=+∈，，，所以2211()(sin )(sin cos )cos cos sin 22S θθθθθθθ'''=+=+-21(4cos cos 2)2θθ=+-，令()0S θ'=，即24cos cos 20θθ+-=，解得cos θcos θ= 因为02θπ<<，所以存在唯一的0θ，使得0cos θ= ····················· 10分当00θθ<<时，()0S θ'>，()S θ在0(0)θ，单调递增；当02θθπ<<时，()0S θ'<，()S θ在0()2θπ，单调递减，所以0θθ=时，max 0()()S S θθ=， ·························································· 12分此时22202cos(2)BD OB OD OB OD θ=+-⋅π-22000112cos 222(2cos 1)4cos θθθ=++=+-=，从而02cos BD θ=（千米）．答：当四边形OCDB 的面积最大时，BD·················· 14分 18．（本小题满分16分）解：（1）因为椭圆22221(0)x y a b a b+=>>，短轴长为2，所以222222b a b c c a⎧⎪=⎪⎪=+⎨⎪⎪=⎪⎩，，解得1a b ==，所以该椭圆的标准方程为2212x y +=．···················································· 4分（2）因为点) (0)(0)M m m A >，，所以直线AM的方程为y x =+，即y x ．由2212x y y x ⎧+=⎪⎪⎨⎪=⎪⎩，，消去y得2222(4)280m x x m +++-=． ·············· 7分设00()C x y ，，则202284m m -=+，所以0x =，所以0244my m =+．连接OM ，取OM 的中点R，则)2mR ，， ········································· 10分连接CR ，因为OC CM =，所以CR OM ⊥．又30OM CRmy k k -===31=-，即42280m m +-=，因为0m >，所以m = ································································· 13分所以四边形OBMC的面积114223ABM AOC S S S =-=⨯=△△． ····································································································· 16分 19．（本小题满分16分）解：（1）因为2()2ln f x x ax x =-+，所以222() (0)x ax f x x x-+'=>． ··············· 2分令2()22p x x ax =-+，216a ∆=-，当0∆≤即44a -≤≤时，()0p x ≥，即()0f x '≥，所以函数()f x 单调递增区间为(0)+∞，．当0∆>即4a <-或4a >时，12x x ==．若4a <-，则120x x <<，所以()0p x >，即()0f x '>，所以函数()f x 的单调递增区间为(0)+∞，．若4a >，则210x x >>，由()0f x '>即()0p x >，得10x x <<或2x x >；由()0f x '<，即()0p x <得12x x x <<．所以函数()f x 的单调递增区间为12(0)()x x +∞，，，；单调递减区间为12()x x ，．综上，当4a ≤时，函数()f x 的单调递增区间为(0)+∞，，无减区间；当4a >时，函数()f x 的单调递增区间为12(0)()x x +∞，，，，单调递减区间为12()x x ，． ······································· 6分（2）由（1）得222() (0)x ax f x x x-+'=>，若()f x 有两个极值点12x x ，，则12x x ，是方程2220x ax -+=的两个不等正实根，由（1）知4a >．则1212212ax x x x +=>=，，故1201x x <<<，···················· 8分要使12()f x mx >恒成立，只需12()f x m x >恒成立．因为222311111111111221()2ln 222ln 22ln 1f x x ax x x x x x x x x x x x -+--+===--+， ········ 10分令3()22ln (01)h t t t t t t =--+<<，则2()32ln h t t t '=-+， ·························· 12分当01t <<时，()0h t '<，()h t 为减函数，所以()(1)3h t h >=-． ·················· 14分由题意，要使12()f x mx >恒成立，只需满足3m -≤．所以实数m 的取值范围(3]-∞-，． ······················································· 16分 20．（本小题满分16分）解：（1）由32n n S =+，可知1123n n n n a S S ++=-=⨯，故1320n n n a S +-=->对一切正整数n 都成立，故{}n a 是P 数列． ················ 3分（2）由题意知，该数列的前n 项和为(1)2n n n S n d -=-+，11n a nd +=-+，由数列12310a a a a L ，，，，是P 数列，可知211a S a >=，故公差0d >．213(1)1022n n d S a n d n +-=-++<对满足19n ≤≤中的每一个正整数n 都成立，即23(1)1022d n d n -++<对于19n ≤≤都成立．······································· 6分由2231(1)1022399(1)1022d d d d ⎧⋅-++<⎪⎪⎨⎪⋅-++<⎪⎩，，可得8027d <<，故d 的取值范围是8(0)27，． ····· 8分（3）若{}n a 是P 数列，则12a S a aq =<=，若0a >，则1q >，又由1n n a S +>对一切正整数n 都成立，可知11n nq aq a q ->-，即12()n q q-<对一切正整数n 都成立，由1()0n q>，1()(01)n q ∈，，故20q -≤，可得2q ≥．若0a <，则1q <，又由1n n a S +>对一切正整数n 都成立，可知11nnq aq a q->-，即(2)1n q q -<对一切正整数n 都成立，又当(1]q ∈-∞-，时，(2)1n q q -<当2n =时不成立，故有(01)(2)1q q q ∈⎧⎨-<⎩，，，或2(10)(2)1q q q ∈-⎧⎨-<⎩，，，解得0)(01)q ∈U ，．所以{}n a 是P 数列时，a 与q 所满足的条件为02a q >⎧⎨⎩，≥，或0(01)0)a q <⎧⎪⎨∈⎪⎩U ，，．12分下面用反证法证明命题“若0a >且12T T =，则{}n a 不是P 数列”．假设{}n a 是P 数列，由0a >，可知2q ≥且{}n a 中每一项均为正数，若{}n b 中的每一项都在{}n c 中，则由这两数列是不同数列，可知12T T <，若{}n c 中的每一项都在{}n b 中，同理可得12T T >．若{}n b 中至少有一项不在{}n c 中且{}n c 中至少有一项不在{}n b 中，设{}{}n n b c ''，是将{}{}n n b c ，中的公共项去掉之后剩余项依次构成的数列，它们的所有项和分别为12T T ''，，不妨设{},{}n n b c ''中的最大项在{}n b '中，设为m a ，则2m ≥，则21211m m T a a a a T -''+++<L ≤≤，故21T T ''<，所以21T T <，故总有12T T ≠，与12T T =矛盾．故{}n a 不是P 数列． ································· 16分数学Ⅰ（附加题）21．【选做题】本题包括A 、B 、C 三小题，请选定其中两题．．．．．．，若多做，则按作答的前两题评分． A ．选修4 - 2：矩阵与变换（本小题满分10分）解：依题意1234⎡⎤⎢⎥⎣⎦5x ⎡⎤=⎢⎥⎣⎦2y y -⎡⎤⎢⎥⎣⎦，即102320 x y x y +=-⎧⎨+=⎩，，解得4 8 x y =-⎧⎨=⎩，， ···················· 3分由逆矩阵公式知，矩阵M 1234⎡⎤=⎢⎥⎣⎦的逆矩阵1213122--⎡⎤⎢⎥=⎢⎥-⎣⎦M ， ··················· 7分所以1x y -⎡⎤⎢⎥⎣⎦M 213122-⎡⎤⎢⎥=⎢⎥-⎣⎦48-⎡⎤⎢⎥⎣⎦1610⎡⎤=⎢⎥-⎣⎦． ··············································· 10分 B ．选修4 - 4：坐标系与参数方程（本小题满分10分）解：直线)l ρθθ=：，所以直线l 的直角坐标方程为20x y -+=． ············································· 3分曲线C 的普通方程为22(2) 1 (32)x y x ++=--≤≤， ································· 6分 2220(2) 1 (32)x y x y x -+=⎧⎨++=-⎩，≤≤-，消去y 整理得22870x x ++=，则22x =--，所以交点坐标为(2)22---． ································· 10分【必做题】第22题、第23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）解：设O 是AD 中点，PAD △为正三角形，则PO AD ⊥．因为平面PAD ⊥平面ABCD ，平面PAD I 平面ABCD AD =，PO ⊂平面PAD ，所以PO ABCD ⊥面．又因为2AD AE ==，60DAB ∠=︒，所以ADE △为正三角形，所以OE AD ⊥．建立如图所示空间直角坐标系O xyz -，则(00(00)(20)(100)P E C D --，，，，，，，于是(2(0(10PC PE DP =-=-=u u u r u u u r u u u r，，，． ··················· 2分（1）设平面PEC 的法向量为1()x y z =，，n ，由110,0PC PE ⋅=⋅=u u u r u u u rn n ，得一个法向量为1(011)=，，n ，平面EDC 的一个法向量为2(001)=，，n ，所以12cos <>==，n n ，又由图可得二面角P EC D --为锐角，所以二面角P EC D --． ················································ 4分（2）设 (01)PM PC λλ=u u u u r u u u r ≤≤，则(2)PM λ=--u u u u r，，(12)DM DP PM λ=+=-u u u u r u u u r u u u u r，(0PE =-u u u r， ················ 6分所以|cos |||||||DM PE DM PE DM PE ⋅<>===u u u u r u u u ru u u u r u u u r u u u u r u u u r ，， ················· 8分解得13λ=或23，所以存在点M 为线段PC 的三等分点． ··························· 10分23．（本小题满分10分）解：（1）当2n =时，{0}{1}{2}{02}{012}M =，，，，，，，具有性质P ，对应的k 分别为01211，，，，，故(2)5f =． ·············································· 3分（2）设当n t =时，具有性质P 的集合M 的个数为()f t ，则当1n t =+时，(1)()(1)f t f t g t +=++，x其中(1)g t +表示1t M +∈时也具有性质P 的集合M 的个数，下面计算(1)g t +关于t 的表达式，此时应有21k t +≥，即12t k +≥，故对n t =分奇偶讨论． ①当t 为偶数时，1t +为奇数，故应该有22t k +≥，则对每一个k ，1t +和21k t --必然属于集合M ，且t 和2k t -，L ，k 和k 共有1t k +-组数，每一组数中的两个数必然同时属于或不属于集合M ，故对每一个k ，对应具有性质P 的集合M 的个数为01111112t k t kt k t k t k C C C +-+-+-+-+-+++=L ，所以21222(1)2221221tt tg t -+=++++=⨯-L ．········································· 5分 ②当t 为奇数时，1t +为偶数，故应该有12t k +≥，同理111222(1)222121t t t g t +-+=++++=-L ， ···································· 7分综上，可得22()221(1)()21t tf t t f t f t t ⎧+⨯-⎪+=⎨⎪+-⎩，为偶数，，为奇数，又(2)5f =，由累加法解得212625()425t t t t f t t t +⎧⨯--⎪=⎨⎪⨯--⎩，为偶数，，为奇数，即212625()425nn n n f n n n +⎧⨯--⎪=⎨⎪⨯--⎩，为偶数，，为奇数． ······················································· 10分。

江苏省苏州大学2020届高考考前指导卷数学试题含解析

序所组成的不同数列，其所有项和分别为 T1 ，T2 ，求{an} 是 P 数列时 a 与 q 所满足的条件，并证明命题“若 a 0 且 T1 = T2 ，则{an} 不是 P 数列”．
8．已知函数 f (x) = xcos x ，则 f (x) 在点 ( ，f ()) 处的切线的斜率为 ▲ ．
22
9．已知
Sn
是等比数列{an} 前
n
项的和，若公比
q
=
2
，则
a1
+
a3 S6
+
a5
的值是
▲
．
开始
S←4
i←3
S←S+2i i←i＋2
i≤10 Y N
输出 S 结束（第 6 题图）
10．已知 2 sin = cos( + ) ，则 tan( − ) 的值是 ▲ ．
△ABC 的内角 A，B ，C 的对边分别为 a ，b，c ，且 a = 1， 3 cosC = csin A ．
（1）求 C ；（2）若 b = 3 ， D 是 AB 上的点， CD 平分 ACB ，求 △ACD 的面积．
16．（本小题满分 14 分）
如图，在四棱锥 P − ABCD 中，底面 ABCD 是矩形，点 E 在棱 PC 上（异于点 P ，C ），平面 ABE 与棱 PD 交于
14．已知 D 是 △ABC 边 AC 上一点，且 CD = 3AD ，BD = 2 ，cos ABC = 1 ，则 3AB + BC 的最大值为
4
▲．
二、解答题：本大题共 6 小题，共计 90 分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．
15．（本小题满分 14 分）

2020年江苏省高考押题卷数学试题(详解版)

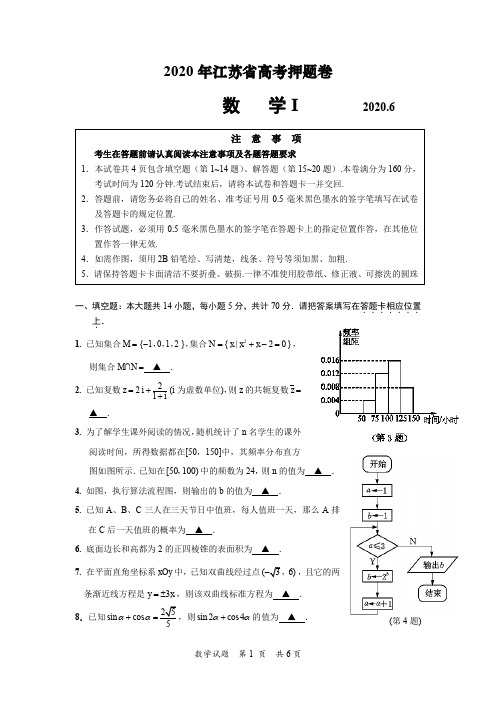
12. 已知正实数 x，y 满足 x (x 1 )2 1, 则 x 1 的最小值为 ▲ ．
yy
y
13．如图，在平行四边形 ABCD 中，AB=2AD，E, F 分别
D
为 AD，DC 的中点，AF 与 BE 交于点 O．若
E
O
12AD AB 5OF OB ，则∠DAB 的余弦值为 ▲ ．A
F
条渐近线方程是 y 3x ，则该双曲线标准方程为 ▲ ． 8．已知 sin cos 2 5 ，则 sin 2 cos 4 的值为 ▲ ．
5
(第 4 题)
数学试题第 1 页共 6 页
9. 设 Sn 为等差数列{an}的前 n 项和，若 2a3 a5 1， S10 100 ，则 S20 的值为 ▲ ． 10. 埃及数学中有一个独特现象：除 2 用一个单独的符号表示以外，其它分数都要写成若干
，2 7
1 4
1 28
，2 9
1 5
1 45
，
按此规律，
2 n
▲ (n 5，7，9，11，„) ．
11. 在平面直角坐标系 xOy 中，已知圆 C : (x 2)2 y2 4 ，点 P 是圆 C 外的一个动点，
直线 PA，PB 分别切圆 C 于 A，B 两点．若直线 AB 过定点(1，1)，则线段 PO 长的最小值为 ▲ ．
1. 已知集合 M {1，0，1，2 }，集合 N { x | x2 x 2 0 }，
则集合 M∩N ▲ ．
2.
已知复数
z
2
i
1
2
i
(i 为虚数单位)，则 z 的共轭复数 z
▲．
3. 为了解学生课外阅读的情况，随机统计了 n 名学生的课外

2020年高考(江苏卷)数学附加题训练八(含答案)

2020年高考（江苏卷）数学附加题训练八21．已知矩阵11a A b ⎡⎤=⎢⎥-⎣⎦，A 的一个特征值2λ=，其对应的一个特征向量是121α⎡⎤=⎢⎥⎣⎦（1）求矩阵A ；（2）设直线l 在矩阵1A -对应的变换作用下得到了直线:4m x y -=，求直线l 的方程．22、在极坐标系中，直线l 的极坐标方程为()4R πθρ=∈，以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，曲线C 的参数方程为4cos ,(1cos 2x y ααα=⎧⎨=+⎩为参数），求直线l 与曲线C 的交点P 的直角坐标．分析：化直线l 的极坐标方程为直角坐标方程，化曲线C 的参数方程为普通方程，联立求解得答案．23、如图，在直四棱柱1111ABCD -A B C D 中，底面四边形A B C D 为菱形，A 1A =AB =2，3ABC ∠=π，E ，F 分别是B C ，1A C 的中点．（1）求异面直线E F ，A D 所成角的余弦值；（2）点M 在线段A 1D 上，1A 1M A D =λ．若C M //平面AEF ，求实数λ的值．24．已知袋中装有大小相同的2个白球、2个红球和1个黄球．一项游戏规定；每个白球、红球和黄球的分值分别是0分、1分和2分，每一局从袋中一次性取出三个球，将3个球对应的分值相加后称为该局的得分，计算完得分后将球放回袋中．当出现第n 局得n 分(n ∈N *)的情况就算游戏过关，同时游戏结束，若四局过后仍未过关，游戏也结束．（1）求在一局游戏中得3分的概率；（2）求游戏结束时局数X 的分布列和数学期望E (X )．分析：（1）根据相互独立事件的概率公式求出对应的概率值；（2）由题意知随机变量X 的可能取值，计算在一局游戏中得2分的概率值，求出对应的概率值，写出分布列，计算数学期望．数学附加题训练八答案21．分析：（1）由111211a A b αλα⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦即可求出a ，b ；（2）设直线:4m x y -=上的任意一点(,)x y 在矩阵A 对应的变换作用下得到点(,)x y ''，根据122144x x x y y y x y '+⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'--+⎣⎦⎣⎦⎣⎦⎣⎦，可得2,3.6x y x x y y '-'⎧=⎪⎪⎨'+'⎪=⎪⎩进而得到l 的方程；．解：（1）1122112a a A b b α+⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥--+⎣⎦⎣⎦⎣⎦，124212λα⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦，∴24,22,a b +=⎧⎨-+=⎩解得2,4,a b =⎧⎨=⎩故1214A ⎡⎤=⎢⎥-⎣⎦；（2）1214A ⎡⎤=⎢⎥-⎣⎦ ，121331166A -⎡⎤-⎢⎥∴=⎢⎥⎢⎥⎢⎥⎣⎦，设直线:4m x y -=上的任意一点(,)x y 在矩阵1A -对应的变换作用下得到点(,)x y ''，则2121333311116666x y x x y y x y ⎡⎤⎡⎤--⎢⎥⎢⎥'⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'⎢⎥⎢⎥⎣⎦⎣⎦+⎢⎥⎢⎥⎣⎦⎣⎦∴21,3311,66x x y y x y ⎧'=-⎪⎪⎨⎪'=+⎪⎩∴2,4.x x y y x y ''=+⎧⎨''=-⎩4x y -= ，23y ∴'=，∴直线l 的方程为23y =．22解：直线l 的直角坐标方程为y x =．由方程4cos ,1cos 2x y αα=⎧⎨=+⎩，可得22212cos 2(48x y x α===，又1cos 1α- ，44x ∴- ．∴曲线C 的普通方程为21(44)8y x x =- ．将直线l 的方程代入曲线方程中，得218x x =，解得0x =，或8x =（舍去）．∴直线l 与曲线C 的交点P 的直角坐标为(0,0)．23分析：（1）建立坐标系，求出直线的向量坐标，利用夹角公式求异面直线E F ，A D 所成角的余弦值；（2）点M 在线段1A D 上，11A M A D λ=．求出平面AEF 的法向量，利用//C M 平面AEF ，即可求实数λ的值．解：因为四棱柱1111ABCD A B C D -为直四棱柱，所以1A A ⊥平面A B C D ．又AE ⊂平面A B C D ，A D ⊂平面A B C D ，所以1A A AE ⊥，1A A AD ⊥．在菱形A B C D 中3ABC π∠=，则A B C ∆是等边三角形．因为E 是B C 中点，所以B C A E ⊥．因为//B C A D ，所以AE AD ⊥．建立空间直角坐标系．则(0A ，0，0)，C 1，0)，(0D ，2，0)，1(0A ，0，2)，E 0，0)，3(2F ，12，1)．（1）(0AD = ，2，0)，3(2EF =，12，1)，所以异面直线E F ，A D 4=．（2）设(M x ，y ，)z ，由于点M 在线段1A D 上，且11A M A D λ=，则(x ，y ，2)(0z λ-=，2，2)-．则(0M ，2λ，22)λ-，(CM = ，21λ-，22)λ-．设平面AEF 的法向量为0(n x = ，0y，0)z ．因为AE = ，0，0)，AF = 12，1)，由000001022x y z =++=⎩，得00x =，00102y z +=．取02y =，则01z =-，则平面AEF 的一个法向量为(0n =，2，1)-．由于//C M 平面AEF ，则0n CM = ，即2(21)(22)0λλ---=，解得23λ=．24分析：（1）根据相互独立事件的概率公式求出对应的概率值；（2）由题意知随机变量X的可能取值，计算在一局游戏中得2分的概率值，求出对应的概率值，写出分布列，计算数学期望．解：（1）设在一局游戏中得3分为事件A，则P（A）1112213525C C CC==；（2）由题意随机变量X的可能取值为1，2，3，4；且在一局游戏中得2分的概率为1221222135310C C C CC+=；则2122351 (1)5C CP XC===，436(2)51025P X==⨯=，43228(3)(15105125P X==⨯-⨯=，43342(4)(15105125P X==⨯-⨯=，X∴的分布列为：X1234P156252812542125162842337 ()1234525125125125E X=⨯+⨯+⨯+⨯=．。

苏州大学2020届高考考前指导卷(答案)

苏州大学2020届高考考前指导卷参考答案一、填空题：本大题共14小题，每小题5分，共计70分．1．{|12}x x <≤ 2．2 3．280 4．1(0]2，5．2 6．52 7．56 8．π2- 9．1310．12-11．5306612．413．4[1]3-， 14解答与提示：1．{|12}A B x x =<I ≤． 2． 2i (2i)(1i)22i 1i 222a a a az +++-+===+-．因为z 为纯虚数，所以2020a a -=⎧⎨+≠⎩，，解得2a =． 3．由图可知，时速在区间[8090)[110120)，，，的频率为(0.010.02)100.3+⨯=，所以时速在区间[90110)，的频率为10.3-，所以时速在区间[90,110)的车辆约为4000.7280⨯=辆． 4．由1200x x -⎧⎨>⎩≥，，解得102x <≤，即函数()f x 的定义域为1(0]2，．5．离心率c e a ==2λ=． 6．执行第一次循环105S i ==，；执行第二次循环207S i ==，；执行第三次循环349S i ==，；执行第四次循环5211S i ==，，终止循环．所以52S =．7．记方案一与方案二坐到“3号”车的概率分别为P 1，P 2，三辆车的出车顺序可能为：123，132，213，231，312，321．方案一坐“3号”车可能：132，213，231，所以136P =；方案二坐“3号”车可能：312，321，所以226P =．则该嘉宾坐到“3号”车的概率1256P P P =+=． 8．()cos sin f x x x x '=-，所以在π2x =处的切线的斜率为ππ()22k f '==-．9．2312135616[1()]111(1)131a q a a a q a q S q q-++-===-+-．10．因为π2sin cos()4αα=+，解得1tan 3α=，所以11π13tan()14213α--==-+． 11．如图，10AB =（寸），则5AD =（寸），1CD =（寸），设圆O的半径为x （寸），则(1)OD x =-（寸）．在Rt ADO △，由勾股定理可得2225(1)x x +-=，解得13x =（寸），则该木材的体积约为221001316900x 100π=π⨯=π≈53066（立方寸）． 12．函数()f x 的图象如右图所示，由题意，30()2f x <<，即319x <<，因为123()()()f x f x f x ==，所以3133()(3)x f x x x =-，令3(1,3)t x =∈，构造函数32()3g t t t =-+，2()36g t t t '=-+，所以当2t =时，max ()(2)4g t g ==，所以31()x f x 的最大值为4．13．设正方形ABCD 的边长为a ，以A 为原点，AB AD ，所在直线为分别为x y ，轴建立平面直角坐标系，则(00)(0)()(0)A B a C a a D a ，，，，，，，．设()P x y ，，因为0CP DP ⋅=u u u r u u u r，所以()()0x a y a x y a --⋅-=，，，即222()()24a a x y a -+-=，设cos 22sin 2a a x a y a θθ⎧=+⎪⎪⎨⎪=+⎪⎩，．又因为()()22a a E a F a ，，，，AP AE AF λμ=+u u u r u u u r u u u r ，所以()()()22a ax y a a λμ=+，，，，即22a x a a y a λμλμ⎧=+⎪⎪⎨⎪=+⎪⎩，，所以2232()[(sin cos )]1sin()33224a a x y a a λμθθθπ+=+=++=++，由P 为正方形ABCD 内部一点（包含边界），可得[2]θ∈ππ，，所以[]444θπ5π9π+∈，，所以2241sin()[1]3433λμθπ+=++∈-，． 14．法一：设AD t =，则3CD t =，4AC t =，在ABD △中，222(2)cos 22t c ADB t +-∠=，在BDC △中，222(3)(2)cos 223t a BDC t+-∠=⋅，又cos cos ADB BDC ∠=-∠，所以222222(2)(3)(2)22223t c t a tt+-+-=-⋅，解得2221238t c a =+-，①DCBA在ABC △中，2222(4)2cos AC t a c ac B ==+-，即2221162t a c ac =+-，②由①②可得2239322a c ac ++=．所以2222333532(3)(3)(3)()(3)2228a c a c a c a c a c +=+-+-⨯=+≥，即2832(3)5a c ⨯+≤，所以3a c +当且仅当3a c =，即a c =所以3AB BC +．法二：因为3CD AD =，所以3CD DA =u u u r u u u r，即3()BD BC BA BD -=-u u u r u u u r u u u r u u u r ，整理得到3144BD BA BC =+u u u r u u u r u u u r ，两边平方后有22291316168BD BA BC BA BC =++⋅u u u r u u u r u u u r u u u r u u u r，所以22913216168BA BC BA BC =++⋅u u u r u u u r u u u r u u u r 即2291312||||161684BA BC BA BC =++⋅⨯u uu r u u u r u u u r u u u r ，整理得到223329||||||||2BA BC BA BC =++⋅u u u r u u u r u uu r u u u r ，设||||c BA a BC ==u u u r u u u r ，，所以22239329(3)22c a ac c a ac =++=+-，因为293333()2222ac a c c a ⋅⋅+=≤，所以222293532(3)(3)(3)(3)288c a ac c a c a c a =+-+-+=+≥，3c a +a c所以3AB BC +．二、解答题：本大题共6小题，共计90分． 15．（本小题满分14分）解：（1）因为1a =sin C c A =cos sin C c A =， ······················ 2分在ABC △中，由正弦定理sin sin a cA C=，所以sin sin a C c A =，cos sin sin A C C A =． ·························································· 4分因为(0)A ∈π，，所以sin 0A ≠sin C C =，因为(0)C ∈π，，所以sin 0C ≠，所以cos 0C ≠，所以tan C = ············· 6分因为(0)C ∈π，，所以3C π=． ······························································ 8分（2）由（1）知，3ACB π∠=，因为1a =，3b =，所以ABC △的面积13sin sin 223ABC S ab ACB π=∠==△， ························ 10分因为D 是AB 上的点，CD 平分ACB ∠，所以1sin12613sin 26BCD ACD a CD S a S b b CD π⋅⋅===π⋅⋅△△， ···················································· 12分因为ABC ACD BCD S S S =+△△△，所以3344ACD ABC S S ==△△． ············· 14分 16．（本小题满分14分）证：（1）因为四边形ABCD 是矩形，所以AB CD ∥． ································································· 2分又AB ⊄平面PDC ，CD ⊂平面PDC ，所以AB ∥平面PDC ， ··································· 5分又因为AB ⊂平面ABE ，平面ABE ∩平面PDC EF =，所以AB EF ∥． ············································ 7分（2）因为四边形ABCD 是矩形，所以AB ⊥AD ．因为AF ⊥EF ，（1）中已证AB EF ∥，所以AB ⊥AF ， ·················································································· 9分因为AB ⊥AD ，由点E 在棱PC 上（异于点C ），所以F 点异于点D ，所以AF AD A =I ，又AF AD ，⊂平面P AD ，所以AB ⊥平面P AD ， ······································· 12分又AB ⊂平面ABCD ，所以平面P AD ⊥平面ABCD ． ·································· 14分 17．（本小题满分14分）解：（1）由题意AOC COD θ∠=∠=，设四边形OCDB 的面积为()S θ，因为四边形OCDB 可以分为OCD △和OBD △两部分，所以11()sin sin(2)22OCD OBD S S S OC OD OB OD θθθ=+=⋅+⋅π-△△， ··············· 3分因为1OB OC OD ===，所以1()(sin sin 2)2S θθθ=+．因为020θθ>π->，，所以02θπ<<．所以四边形OCDB 的面积1()(sin sin 2)(0)22S θθθθπ=+∈，，． ······················ 6分（2）由（1）1()(sin sin 2)(0)22S θθθθπ=+∈，，，所以2211()(sin )(sin cos )cos cos sin 22S θθθθθθθ'''=+=+-21(4cos cos 2)2θθ=+-，令()0S θ'=，即24cos cos 20θθ+-=，解得cos θ=或cos θ= 因为02θπ<<，所以存在唯一的0θ，使得0cos θ= ····················· 10分当00θθ<<时，()0S θ'>，()S θ在0(0)θ，单调递增；当02θθπ<<时，()0S θ'<，()S θ在0()2θπ，单调递减，所以0θθ=时，max 0()()S S θθ=， ·························································· 12分此时22202cos(2)BD OB OD OB OD θ=+-⋅π-22000112cos 222(2cos 1)4cos θθθ=++=+-=，从而02cos BD θ=（千米）．答：当四边形OCDB 的面积最大时，BD·················· 14分 18．（本小题满分16分）解：（1）因为椭圆22221(0)x y a b a b+=>>的离心率为2，短轴长为2，所以22222b a b c c a⎧⎪=⎪⎪=+⎨⎪⎪=⎪⎩，，解得1a b ==，所以该椭圆的标准方程为2212x y +=． ···················································· 4分（2）因为点) (0)(0)M m m A >，，所以直线AM的方程为y x =+，即(4y x =．由2212(4x y y x ⎧+=⎪⎪⎨⎪=⎪⎩，，消去y得2222(4)280m x x m +++-=． ··············· 7分设00()C x y ，，则202284m m -=+，所以0x =，所以0244my m =+．连接OM ，取OM 的中点R，则)2mR ，， ········································· 10分连接CR ，因为OC CM =，所以CR OM ⊥．又30OM CR m y k k -==31=-，即42280m m +-=，因为0m >，所以m = ································································· 13分所以四边形OBMC的面积114223ABM AOC S S S =-=⨯=△△． ····································································································· 16分19．（本小题满分16分）解：（1）因为2()2ln f x x ax x =-+，所以222() (0)x ax f x x x-+'=>． ··············· 2分令2()22p x x ax =-+，216a ∆=-，当0∆≤即44a -≤≤时，()0p x ≥，即()0f x '≥，所以函数()f x 单调递增区间为(0)+∞，．当0∆>即4a <-或4a >时，12x x ==若4a <-，则120x x <<，所以()0p x >，即()0f x '>，所以函数()f x 的单调递增区间为(0)+∞，．若4a >，则210x x >>，由()0f x '>即()0p x >，得10x x <<或2x x >；由()0f x '<，即()0p x <得12x x x <<．所以函数()f x 的单调递增区间为12(0)()x x +∞，，，；单调递减区间为12()x x ，．综上，当4a ≤时，函数()f x 的单调递增区间为(0)+∞，，无减区间；当4a >时，函数()f x 的单调递增区间为12(0)()x x +∞，，，，单调递减区间为12()x x ，． ····· 6分（2）由（1）得222() (0)x ax f x x x-+'=>，若()f x 有两个极值点12x x ，，则12x x ，是方程2220x ax -+=的两个不等正实根，由（1）知4a >．则1212212ax x x x +=>=，，故1201x x <<<， ···················· 8分要使12()f x mx >恒成立，只需12()f x m x >恒成立．因为222311111111111221()2ln 222ln 22ln 1f x x ax x x x x x x x x x x x -+--+===--+， ········ 10分令3()22ln (01)h t t t t t t =--+<<，则2()32ln h t t t '=-+， ·························· 12分当01t <<时，()0h t '<，()h t 为减函数，所以()(1)3h t h >=-． ·················· 14分由题意，要使12()f x mx >恒成立，只需满足3m -≤．所以实数m 的取值范围(3]-∞-，． ······················································· 16分 20．（本小题满分16分）解：（1）由32n n S =+，可知1123n n n n a S S ++=-=⨯，故1320n n n a S +-=->对一切正整数n 都成立，故{}n a 是P 数列． ················ 3分（2）由题意知，该数列的前n 项和为(1)2n n n S n d -=-+，11n a nd +=-+，由数列12310a a a a L ，，，，是P 数列，可知211a S a >=，故公差0d >． 213(1)1022n n d S a n d n +-=-++<对满足19n ≤≤中的每一个正整数n 都成立，即23(1)1022d n d n -++<对于19n ≤≤都成立． ······································· 6分由2231(1)1022399(1)1022d d d d ⎧⋅-++<⎪⎪⎨⎪⋅-++<⎪⎩，，可得8027d <<，故d 的取值范围是8(0)27，． ····· 8分（3）若{}n a 是P 数列，则12a S a aq =<=，若0a >，则1q >，又由1n n a S +>对一切正整数n 都成立，可知11n nq aq a q ->-，即12()n q q-<对一切正整数n 都成立，由1()0n q>，1()(01)n q ∈，，故20q -≤，可得2q ≥．若0a <，则1q <，又由1n n a S +>对一切正整数n 都成立，可知11nnq aq a q->-，即(2)1n q q -<对一切正整数n 都成立，又当(1]q ∈-∞-，时，(2)1n q q -<当2n =时不成立，故有(01)(2)1q q q ∈⎧⎨-<⎩，，，或2(10)(2)1q q q ∈-⎧⎨-<⎩，，，解得0)(01)q ∈U ，．所以{}n a 是P 数列时，a 与q 所满足的条件为02a q >⎧⎨⎩，≥，或0(01)0)a q <⎧⎪⎨∈⎪⎩U ，，．12分下面用反证法证明命题“若0a >且12T T =，则{}n a 不是P 数列”．假设{}n a 是P 数列，由0a >，可知2q ≥且{}n a 中每一项均为正数，若{}n b 中的每一项都在{}n c 中，则由这两数列是不同数列，可知12T T <，若{}n c 中的每一项都在{}n b 中，同理可得12T T >．若{}n b 中至少有一项不在{}n c 中且{}n c 中至少有一项不在{}n b 中，设{}{}n n b c ''，是将{}{}n n b c ，中的公共项去掉之后剩余项依次构成的数列，它们的所有项和分别为12T T ''，，不妨设{},{}n n b c ''中的最大项在{}n b '中，设为m a ，则2m ≥，则21211m m T a a a a T -''+++<L ≤≤，故21T T ''<，所以21T T <，故总有12T T ≠，与12T T =矛盾．故{}n a 不是P 数列． ································· 16分数学Ⅱ（附加题）21．【选做题】本题包括A 、B 、C 三小题，请选定其中两题．．．．．．，若多做，则按作答的前两题评分．A ．选修4 - 2：矩阵与变换（本小题满分10分）解：依题意1234⎡⎤⎢⎥⎣⎦5x ⎡⎤=⎢⎥⎣⎦2y y -⎡⎤⎢⎥⎣⎦，即102320 x y x y +=-⎧⎨+=⎩，，解得4 8 x y =-⎧⎨=⎩，， ···················· 3分由逆矩阵公式知，矩阵M 1234⎡⎤=⎢⎥⎣⎦的逆矩阵1213122--⎡⎤⎢⎥=⎢⎥-⎣⎦M ， ···················· 7分所以1x y -⎡⎤⎢⎥⎣⎦M 213122-⎡⎤⎢⎥=⎢⎥-⎣⎦48-⎡⎤⎢⎥⎣⎦1610⎡⎤=⎢⎥-⎣⎦． ··············································· 10分 B ．选修4 - 4：坐标系与参数方程（本小题满分10分）解：直线)l ρθθ=：，所以直线l 的直角坐标方程为20x y -+=． ············································· 3分曲线C 的普通方程为22(2) 1 (32)x y x ++=--≤≤， ································· 6分 2220(2) 1 (32)x y x y x -+=⎧⎨++=-⎩，≤≤-，消去y 整理得22870x x ++=，则22x =--，所以交点坐标为(2)22---． ································· 10分 C ．选修4 - 5：不等式选讲（本小题满分10分）解：由00x y >>，，2211274x y x y +++=，得2215316127444x y x y x y -=+++-27327126444=+-=≥． ································· 6分当且仅当22818x x y y ⎧=⎪⎪⎨⎪=⎪⎩，，即122x y ==，时等号成立．故1534x y-的最小值为6． ··································································· 10分【必做题】第22题、第23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）解：设O 是AD 中点，PAD △为正三角形，则PO AD ⊥．因为平面PAD ⊥平面ABCD ，平面PAD I 平面ABCD AD =，PO ⊂平面PAD ，所以PO ABCD ⊥面．又因为2AD AE ==，60DAB ∠=︒，所以ADE △为正三角形，所以OE AD ⊥．建立如图所示空间直角坐标系O xyz -，则(00(00)(20)(100)P E C D --，，，，，，，于是(2(0(10PC PE DP =-=-=u u u r u u u r u u u r，，，． ··················· 2分（1）设平面PEC 的法向量为1()x y z =，，n ，由110,0PC PE ⋅=⋅=u u u r u u u rn n ，得一个法向量为1(011)=，，n ，平面EDC 的一个法向量为2(001)=，，n ，所以12cos <>==，n n ，又由图可得二面角P EC D --为锐角，所以二面角P EC D --． ················································ 4分（2）设 (01)PM PC λλ=u u u u r u u u r ≤≤，则(2)PM λ=--u u u u r，，(12)DM DP PM λ=+=-u u u u r u u u r u u u u r，(0PE =-u u ， ················ 6分x所以|cos|||||||DM PEDM PEDM PE⋅<>===u u u u r u u u ru u u u r u u u ru u u u r u u u r，，·················8分解得13λ=或23，所以存在点M为线段PC的三等分点． ···························10分23．（本小题满分10分）解：（1）当2n=时，{0}{1}{2}{02}{012}M=，，，，，，，具有性质P，对应的k分别为01211，，，，，故(2)5f=． ··············································3分（2）设当n t=时，具有性质P的集合M的个数为()f t，则当1n t=+时，(1)()(1)f t f tg t+=++，其中(1)g t+表示1t M+∈时也具有性质P的集合M的个数，下面计算(1)g t+关于t的表达式，此时应有21k t+≥，即12tk+≥，故对n t=分奇偶讨论．①当t为偶数时，1t+为奇数，故应该有22tk+≥，则对每一个k，1t+和21k t--必然属于集合M，且t和2k t-，L，k和k共有1t k+-组数，每一组数中的两个数必然同时属于或不属于集合M，故对每一个k，对应具有性质P的集合M的个数为01111112t k t kt k t k t kC C C+-+-+-+-+-+++=L，所以21222(1)2221221t t tg t-+=++++=⨯-L．·········································5分②当t为奇数时，1t+为偶数，故应该有12tk+≥，同理111222(1)222121t t tg t+-+=++++=-L， ····································7分综上，可得22()221(1)()21ttf t tf tf t t⎧+⨯-⎪+=⎨⎪+-⎩，为偶数，，为奇数，又(2)5f=，由累加法解得212625()425ttt tf tt t+⎧⨯--⎪=⎨⎪⨯--⎩，为偶数，，为奇数，即212625()425nnn nf nn n+⎧⨯--⎪=⎨⎪⨯--⎩，为偶数，，为奇数．·······················································10分。