冶金传输原理吴铿编(动量传输部分)习题参考答案
冶金传输原理考研试题及答案

冶金传输原理考研试题及答案一、选择题(每题2分,共10分)1. 在冶金过程中,下列哪项不是影响金属传输速率的因素?A. 温度B. 压力C. 金属的化学性质D. 金属的物理状态答案:B2. 冶金传输原理中,扩散系数与温度的关系通常可以用以下哪个方程描述?A. D = D0 * exp(-Q/RT)B. D = D0 * exp(Q/RT)C. D = D0 / (1 + exp(Q/RT))D. D = D0 * (1 + exp(-Q/RT))答案:A3. 在冶金过程中,金属的传输主要通过哪种机制?A. 对流B. 扩散C. 过滤D. 电迁移答案:B4. 下列哪项不是影响金属溶解速率的因素?A. 金属的晶格结构B. 溶液的浓度C. 金属的表面粗糙度D. 溶液的pH值答案:C5. 在冶金传输原理中,哪种类型的边界条件通常用于描述固体表面的传输现象?A. 狄利克雷边界条件B. 诺伊曼边界条件C. 罗宾边界条件D. 周期性边界条件答案:C二、简答题(每题10分,共30分)1. 简述冶金过程中对流传输和扩散传输的区别。
答案:对流传输是指流体中的物质由于整体运动而发生的宏观传输,它与流体的流动速度直接相关,通常发生在流体中,传输速率较快。
扩散传输是指由于分子或原子的热运动导致的微观传输,它不需要整体运动,可以在静止的介质中发生,传输速率相对较慢。
2. 描述冶金传输原理中的菲克第一定律及其物理意义。
答案:菲克第一定律描述了稳态扩散过程中,单位时间内通过单位面积的扩散通量与浓度梯度成正比的关系,即J = -D * (dc/dx),其中J是扩散通量,D是扩散系数,dc/dx是浓度梯度。
这一定律的物理意义在于,它表明了物质从高浓度区域向低浓度区域传输的速率与浓度梯度的大小成正比,且与介质的扩散性质有关。
3. 解释为什么在冶金过程中需要考虑金属的热力学性质和动力学性质。
答案:在冶金过程中,金属的热力学性质决定了反应的方向和平衡状态,而动力学性质则决定了反应的速率。
冶金传输原理习题答案

冶金传输原理习题答案冶金传输原理习题答案冶金传输原理是冶金学中的一个重要分支,研究金属和合金在加热、冷却和变形过程中的传输规律和机制。
在学习和研究冶金传输原理时,习题是不可或缺的一部分,通过解答习题可以加深对该学科的理解和掌握。
下面将给出一些常见的冶金传输原理习题及其答案。
1. 请简述热传导的基本原理。
热传导是指物质内部由于温度差异而传递热量的过程。
其基本原理是热量从高温区传递到低温区,传递过程中热量通过物质内部的分子或电子的碰撞和传递完成。
热传导的速率与温度差、物质的导热性质和传热距离有关。
2. 什么是对流传热?请举例说明。
对流传热是指通过流体(气体或液体)的传热方式。
当物体表面与流体接触时,流体会受热膨胀,形成对流循环,将热量从高温区传递到低温区。
例如,热水器中的水受热后上升,冷水下降,形成对流循环,使整个水体均匀受热。
3. 请解释辐射传热的特点。
辐射传热是指通过电磁波的传热方式。
辐射传热不需要介质,可以在真空中传递热量。
辐射传热的特点是传热速率与温度差的四次方成正比,与物体表面特性和距离的平方成反比。
例如,太阳辐射的热量可以通过真空传递到地球上。
4. 请简述固体变形的原理。
固体变形是指固体在外力作用下发生形状和尺寸的改变。
固体变形的原理是固体内部的晶格结构发生变化,从而使整个固体发生形变。
固体变形可以分为弹性变形和塑性变形两种。
弹性变形是指在外力作用下,固体发生形变后能够恢复原状;塑性变形是指在外力作用下,固体发生形变后不能恢复原状。
5. 请解释扩散的基本原理。
扩散是指物质在非均匀温度和浓度条件下的自发性传递过程。
扩散的基本原理是物质分子或原子的热运动引起的碰撞和交换。
扩散的速率与温度、浓度差、物质的扩散系数和距离有关。
扩散在冶金过程中起着重要的作用,如金属中的杂质扩散、合金的相变等都与扩散有关。
通过以上习题的解答,我们可以更加深入地理解和掌握冶金传输原理。
在实际应用中,冶金传输原理的理论和方法可以帮助我们解决金属加工和冶炼过程中的问题,提高生产效率和产品质量。
冶金传输原理课后答案

1、什么是连续介质,在流体力学中为什么要建立连续介质这一理论模型?答:(1)连续介质是指质点毫无空隙的聚集在一起,完全充满所占空间的介质。
(2)引入连续介质模型的必要性:把流体视为连续介质后,流体运动中的物理量均可以看为空间和时间的连续函数,就可以利用数学中的连续函数分析方法来研究流体运动,实践表明采用流体的连续介质模型,解决一般工程中的流体力学问题是可以满足要求的。
1-9 一只某液体的密度为800kg/,求它的重度及比重。
解: 重度:γ=ρg=800*9.8=7840kg/(˙)比重:ρ/=800/1000=0.8注:比重即相对密度。
液体的相对密度指该液体的密度与一个大气压下4℃水的密度(1000 kg/)之比课本p4。
1-11 设烟气在标准状态下的密度为1.3kg/m3,试计算当压力不变温度分别为1000℃和1200℃时的密度和重度解:已知:t=0℃时,0=1.3kg/m3,且=则根据公式当t=1000℃时,烟气的密度为kg/m3=0.28kg/m3烟气的重度为kg/m3=2.274kg/m3当t=1200℃时,烟气的密度为kg/m3=0.24kg/m3烟气的重度为kg/m3=2.36kg/m31—6答:绝对压强:以绝对真空为起点计算的压力,是流体的实际,真实压力,不随大气压的变化而变化。
表压力:当被测流体的绝对压力大于外界大气压力时,用压力表进行测量。
压力表上的读数(指示值)反映被测流体的绝对压力比大气压力高出的数值,称为表压力。
既:表压力=绝对压力-大气压力真空度:当被测流体的绝对压力小于外界大气压力时,采用真空表测量。
真空表上的读数反映被测流体的绝对压力低于大气压力的差值,称为真空度。
既:真空度=︱绝对压力-大气压力︱=大气压力-绝对压力1-81 物理大气压(atm)= 760 mmHg = 10332 mm H2O1 物理大气压(atm) = 1.033 kgf/cm2 = 101325 Pa1mmH20 = 9.81 Pa1-21 已知某气体管道内的绝对压力为117kPa,若表压为70kPa,那么该处的绝对压力是多少(已经当地大气压为98kPa),若绝对压力为68.5kPa 时其真空度又为多少?解:P 绝=P 表+P 大气=70kPa+98kPa=168kPaP 真=-(P 绝-P 大气)=-(68.5kPa-98kPa)=29.5kPa1、气体在什么条件下可作为不可压缩流体?答:对于气体,在压力变化不太大(压力变化小于10千帕)或流速不太高(V<70米/秒)条件下(如流速较低的通风道),气体压缩程度很小,可忽略气体密度变化而作为不可压缩流体来处理。
《冶金传输原理》吴铿编质量传输习题参考答案

第十六章习题参考答案(仅限参考)1. 解:(1)44444262638382290.27%CH CH CH CH CH C H C H C H C H CO CO y M y M y M y M y M ω==+++(2)44262638382216.82CH CH C H C H C H C H CO CO M y M y M y M y M =+++= (3)4449.6210CH CH p y p Pa ==⨯2. 解:52AB 1/31/3A B1.5610/D m s p V V -==⨯+3. 解:CH 4的扩散体积24.42,H2的扩散体积7.072AB 1/31/3A B 3.1910/D m s p V V ==⨯+-54. 解:(1)22222222 3.91/CO CO O O H O H O N N v v v v v m s ωωωω=+++= (2)22222222 4.07/m CO CO O O H O H O N N v y v y v y v y v m s =+++= (3)()()()22222220.212/CO CO CO CO CO CO M p kg m s RT ρ=-=-=-⋅j υυυυ (4)()()()2222225.33/CO CO CO CO m CO m p c mol m s RT=-=-=-⋅J υυυυ5. 解:(1)21% (2)21%(3)15.46pVm nM M kg RT === (4)230.117/O mkg m V ρ==(5)230.378/N mkg m V ρ==(6)30.515/mkg m Vρ==空气(7)317.4/c mol m Mρ==空气空气(8)29.6g/mol(9)2247.910N N p y p Pa ==⨯6. 证明:A A A A AA A AB B A A B Bm n M x M m n M n M x M x M ω===++ 得证。
材料加工冶金传输原理习题答案(吴树森版)
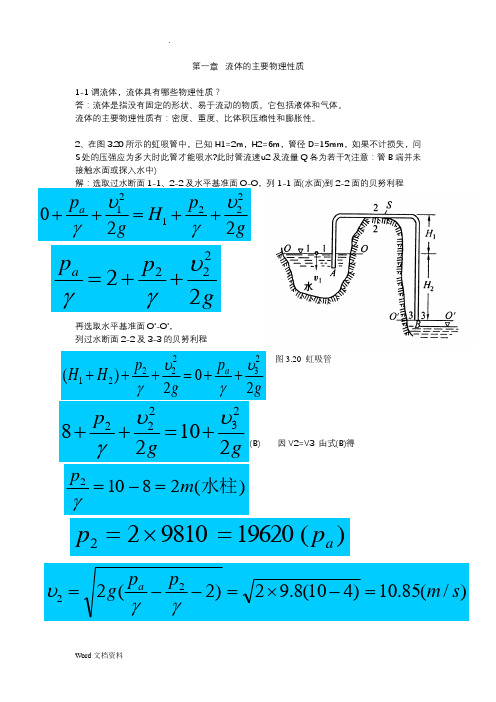
第一章 流体的主要物理性质1-1谓流体,流体具有哪些物理性质?答:流体是指没有固定的形状、易于流动的物质。
它包括液体和气体。
流体的主要物理性质有:密度、重度、比体积压缩性和膨胀性。
2、在图3.20所示的虹吸管中,已知H1=2m ,H2=6m ,管径D=15mm ,如果不计损失,问S 处的压强应为多大时此管才能吸水?此时管流速υ2及流量Q 各为若干?(注意:管B 端并未接触水面或探入水中)解:选取过水断面1-1、2-2及水平基准面O-O ,列1-1面(水面)到2-2面的贝努利程再选取水平基准面O ’-O ’,列过水断面2-2及3-3的贝努利程(B) 因V2=V3 由式(B)得 图3.20 虹吸管gpH gpa 220222121υγυγ++=++gppa 22222υγγ++=gp g p H H a 202)(2322221υγυγ++=+++ggp2102823222υυγ+=++)(28102水柱m p=-=γ)(19620981022a p p =⨯=)/(85.10)410(8.92)2(222s m ppg a =-⨯=--=γγυ)/(9.1)/(0019.085.104)015.0(3222s L s m A Q ==⨯⨯==πυ5、有一文特利管(如下图),已知d 1 =15cm ,d 2=10cm ,水银差压计液面高差∆h =20cm 。
若不计阻力损失,求常温(20℃)下,通过文氏管的水的流量。
解:在喉部入口前的直管截面1和喉部截面2处测量静压力差p 1和p 2,则由式const v p=+22ρ可建立有关此截面的伯努利程: ρρ22212122p v p v +=+ 根据连续性程,截面1和2上的截面积A 1和A 2与流体流速v 1和v 2的关系式为2211v A v A =所以 ])(1[)(2212212A A p p v --=ρ 通过管子的流体流量为 ])(1[)(2212212A A p p A Q --=ρ )(21p p -用U 形管中液柱表示,所以074.0))15.01.0(1(10)1011055.13(2.081.92)1.0(4])(1[)(22223332212'2=-⨯⨯-⨯⨯⨯⨯=--∆=πρρρA A h g A Q (m 3/s)式中 ρ、'ρ——被测流体和U 形管中流体的密度。
冶金传输原理课后习题答案

冶金传输原理课后习题答案【篇一:冶金传输原理课后答案(朱光俊版,第一章)】/m3 10001?273prtprtprt1-16 , r=(1) (2)1-21 dvxdy65010.5?0.0012dvx dy=vd1-23,,o=vx=hdy0.181.3?0.001=0.1385?1000 1/sdvx dy=1.011?1030.1385?107.2 pa.s【篇二:《冶金传输原理》吴铿编质量传输习题参考答案】s=txt>1. 解:(1)?ch4?ych4mch4ych4mch4?yc2h6mc2h6?yc3h8mc3h8?yco2mco2?90.27%(2)?ych4mch4?yc2h6mc2h6?yc3h8mc3h8?yco2mco2?16.82 (3)pch4?ych4p?9.62?104pa2. 解:dab?1/3b1/3pva?v?1.56?10?5m2/s3. 解:ch4的扩散体积24.42,h2的扩散体积7.07dab?1/3b1/3pva?v?3.19?10-5m2/s4. 解:(1)v??co2vco2??o2vo2??h2ovh2o??n2vn2?3.91m/s (2)vm?yco2vco2?yo2vo2?yh2ovh2o?yn2vn2?4.07m/s (3)jco2??co2?co2?????mco2pco2rtpco2rt??co2????0.212kg/?m2?s? ?(4)jco2?cco2?co2??m?????co2??m??5.33mol/?m2?s? ?5. 解:(1)21% (2)21%pvm?15.46kg (3)m?nm?rtm(4)?o2??0.117kg/m3vm(5)?n2??0.378kg/m3vm(6)?空气??0.515kg/m3v(7)c空气??空气m?17.4mol/m3(8)29.6g/mol(9)pn2?yn2p?7.9?104pa6. 证明:?a?manamaxama??mnama?nbmbxama?xbmb得证。
材料加工冶金传输原理习题答案

第一章 流体的主要物理性质1-1何谓流体,流体具有哪些物理性质?答:流体是指没有固定的形状、易于流动的物质。
它包括液体和气体。
流体的主要物理性质有:密度、重度、比体积压缩性和膨胀性。
1-2某种液体的密度ρ=900 Kg /m 3,试求教重度y 和质量体积v 。
解:由液体密度、重度和质量体积的关系知:)m /(88208.9900g 3N VG=*===ργ ∴质量体积为)/(001.013kg m ==ρν1.4某种可压缩液体在圆柱形容器中,当压强为2MN /m 2时体积为995cm 3,当压强为1MN /m 2时体积为1000 cm 3,问它的等温压缩率k T 为多少? 解:等温压缩率K T 公式(2-1): TT P V VK ⎥⎦⎤⎢⎣⎡∆∆-=1 ΔV=995-1000=-5*10-6m 3注意:ΔP=2-1=1MN/m 2=1*106Pa将V=1000cm 3代入即可得到K T =5*10-9Pa -1。
注意:式中V 是指液体变化前的体积1.6 如图1.5所示,在相距h =0.06m 的两个固定平行乎板中间放置另一块薄板,在薄板的上下分别放有不同粘度的油,并且一种油的粘度是另一种油的粘度的2倍。
当薄板以匀速v =0.3m/s 被拖动时,每平方米受合力F=29N ,求两种油的粘度各是多少?解:流体匀速稳定流动时流体对板面产生的粘性阻力力为YA F 0y x νητ==平板受到上下油面的阻力之和与施加的力平衡,即hh F 0162/22/h νηνηνητ=+==合代入数据得η=0.967Pa.s第二章 流体静力学(吉泽升版)2-1作用在流体上的力有哪两类,各有什么特点? 解:作用在流体上的力分为质量力和表面力两种。
质量力是作用在流体内部任何质点上的力,大小与质量成正比,由加速度产生,与质点外的流体无关。
而表面力是指作用在流体表面上的力,大小与面积成正比,由与流体接触的相邻流体或固体的作用而产生。
冶金传输原理-动量传输-第2章 流体静力学 试题库
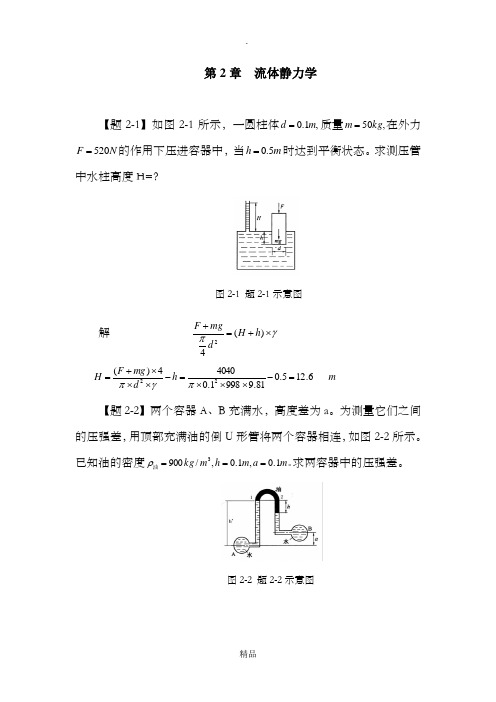
第2章 流体静力学【题2-1】如图2-1所示,一圆柱体,1.0m d =质量,50kg m =在外力N F 520=的作用下压进容器中,当m h 5.0=时达到平衡状态。
求测压管中水柱高度H=?图2-1 题2-1示意图解 γπ⨯+=+)(42h H d mg F m h d mg F H 6.125.081.99981.040404)(22=-⨯⨯⨯=-⨯⨯⨯+=πγπ【题2-2】两个容器A 、B 充满水,高度差为a 。
为测量它们之间的压强差,用顶部充满油的倒U 形管将两个容器相连,如图2-2所示。
已知油的密度。
油m a m h m kg 1.0,1.0,/9003===ρ求两容器中的压强差。
图2-2 题2-2示意图解 :(略)参考答案:Pa p p B A 1075=-【题2-3】如图2-3所示,直径m d m D 3.0,8.0==的圆柱形容器自重1000N ,支撑在距液面距离m b 5.1=的支架上。
由于容器内部有真空,将水吸入。
若,9.1m b a =+求支架上的支撑力F 。
图2-3 题2-3示意图解: 略【题2-4】如图2-4所示,由上下两个半球合成的圆球,直径d=2m,球中充满水。
当测压管读数H=3m 时,不计球的自重,求下列两种情况下螺栓群A-A 所受的拉力。
(1) 上半球固定在支座上;(2) 下半球固定在支座上。
图2-4 题2-4示意图解 :略【题2-5】矩形闸门长1.5m,宽2m(垂直于图面),A 端为铰链,B 端连在一条倾斜角045=α的铁链上,用以开启此闸门,如图2-5所示。
量得库内水深,并标在图上。
今欲沿铁链方向用力T 拉起此闸门,若不计摩擦与闸门自重,问所需力T 为若干?图2-5 题2-5示意图解 :略【题2-6】 如图2-6所示测量装置,活塞直径,35mm d =油的密度3/918m kg =油ρ,水银的密度3/13600m kg Hg =ρ,活塞与缸壁无泄露和摩擦。
冶金传输原理-动量传输-第3章试题库.doc

第3章流体动力学【题3-1】在生产过程中常用设备位置的高度差来使流体以一定的流速或流量流动,如水塔、高位槽或虹吸等。
这类计算可归纳为已知高度差求流速或流量;或者求出欲达到某一流量须保持若干高度差。
如图3-1所示,水槽液面至管道出U的垂直距离保持在6.2m,水管全长330m,管径为如果此流动系统中压头损失为6mH 20 ,试求管路中每分钟可达到的流量。
解取水槽液面为1 一1截面,水流出口为2—2截面,取水平基准面通过水管中心。
列出1一1截面至2—2截面之间的伯努利方程式为4 + 1 + 4 =i + A + z2+,<2^ gp 2g gp -因为水平基准而通过截面2—2,所以Z2=0,z1=6.2m。
液面因为水流出口均与大气相通,故A=p2=l大气压。
因截面1一1比2—2要大的多,所以可近似认为%=0。
己知/Av=6mH2O,将这些数值代入得6.2= 4 +6,解出u2 = ^/0.2x2g = 1.98m/ s于是水的流量Q = u,x-d2 =\.9Sx-x0.0922 =0.013m31s = 0.79m3 /min 2 4 4【题3-2】采用如图3-2所示的集流器测量离心风机的流量。
己知风机吸入管道的直径d=350mm,插入水槽中的玻璃管内水升高h= 100mm,空三的密度/?二1.2知/ m3,水的密度为p = 1000^ / ,不考虑损失,求空气的流量。
o图3-2题3-2不意图解取吸水玻璃管处为过流断面1 一1,在吸入U前的一定距离,空气为受干扰处,取过流断面0—0,其空气压力为大气压,空气流速近似为0,v0^Oo取管轴线为基准线,且/^_,=0,则列出0—0 和1 一1两个缓变流断面之间的能量方程为0 + 1 + 0 = 0 + -^ + 1 SP8PPi = P a-Pghf所以v, = 2g Pa ~ Pl = 2g= 2^/z^- =(2x9.807 x0.1 x= 40.43m3 / 5 \ SP \ SP V P V 1-2q v =v,-d2 = 40.42x-x0.352 = 3.89m3 /s v 1 44【题3-3】如图3-3所示,求单位宽度二维槽道内水的流量,忽略能量损失。
材料加工冶金传输原理(吴树森版)习题答案共19页word资料

第一章 流体的主要物理性质1-1何谓流体,流体具有哪些物理性质?答:流体是指没有固定的形状、易于流动的物质。
它包括液体和气体。
流体的主要物理性质有:密度、重度、比体积压缩性和膨胀性。
1-2某种液体的密度ρ=900 Kg /m 3,试求教重度y 和质量体积v 。
解:由液体密度、重度和质量体积的关系知: ∴质量体积为)/(001.013kg m ==ρν1.4某种可压缩液体在圆柱形容器中,当压强为2MN /m 2时体积为995cm 3,当压强为1MN /m 2时体积为1000 cm 3,问它的等温压缩率k T 为多少?解:等温压缩率K T 公式(2-1): TT P V V K ⎥⎦⎤⎢⎣⎡∆∆-=1 ΔV=995-1000=-5*10-6m 3注意:ΔP=2-1=1MN/m 2=1*106Pa将V=1000cm 3代入即可得到K T =5*10-9Pa -1。
注意:式中V 是指液体变化前的体积1.6 如图1.5所示,在相距h =0.06m 的两个固定平行乎板中间放置另一块薄板,在薄板的上下分别放有不同粘度的油,并且一种油的粘度是另一种油的粘度的2倍。
当薄板以匀速v =0.3m/s 被拖动时,每平方米受合力F=29N ,求两种油的粘度各是多少?解:流体匀速稳定流动时流体对板面产生的粘性阻力力为平板受到上下油面的阻力之和与施加的力平衡,即代入数据得η=0.967Pa.s第二章 流体静力学(吉泽升版)2-1作用在流体上的力有哪两类,各有什么特点?解:作用在流体上的力分为质量力和表面力两种。
质量力是作用在流体内部任何质点上的力,大小与质量成正比,由加速度产生,与质点外的流体无关。
而表面力是指作用在流体表面上的力,大小与面积成正比,由与流体接触的相邻流体或固体的作用而产生。
2-2什么是流体的静压强,静止流体中压强的分布规律如何?解: 流体静压强指单位面积上流体的静压力。
静止流体中任意一点的静压强值只由该店坐标位置决定,即作用于一点的各个方向的静压强是等值的。
材料加工冶金传输原理习题答案-19页文档资料

第一章 流体的主要物理性质1-1何谓流体,流体具有哪些物理性质?答:流体是指没有固定的形状、易于流动的物质。
它包括液体和气体。
流体的主要物理性质有:密度、重度、比体积压缩性和膨胀性。
1-2某种液体的密度ρ=900 Kg /m 3,试求教重度y 和质量体积v 。
解:由液体密度、重度和质量体积的关系知: ∴质量体积为)/(001.013kg m ==ρν1.4某种可压缩液体在圆柱形容器中,当压强为2MN /m 2时体积为995cm 3,当压强为1MN /m 2时体积为1000 cm 3,问它的等温压缩率k T 为多少?解:等温压缩率K T 公式(2-1): TT P V V K ⎥⎦⎤⎢⎣⎡∆∆-=1 ΔV=995-1000=-5*10-6m 3注意:ΔP=2-1=1MN/m 2=1*106Pa将V=1000cm 3代入即可得到K T =5*10-9Pa -1。
注意:式中V 是指液体变化前的体积1.6 如图1.5所示,在相距h =0.06m 的两个固定平行乎板中间放置另一块薄板,在薄板的上下分别放有不同粘度的油,并且一种油的粘度是另一种油的粘度的2倍。
当薄板以匀速v =0.3m/s 被拖动时,每平方米受合力F=29N ,求两种油的粘度各是多少?解:流体匀速稳定流动时流体对板面产生的粘性阻力力为平板受到上下油面的阻力之和与施加的力平衡,即代入数据得η=0.967Pa.s第二章 流体静力学(吉泽升版)2-1作用在流体上的力有哪两类,各有什么特点?解:作用在流体上的力分为质量力和表面力两种。
质量力是作用在流体内部任何质点上的力,大小与质量成正比,由加速度产生,与质点外的流体无关。
而表面力是指作用在流体表面上的力,大小与面积成正比,由与流体接触的相邻流体或固体的作用而产生。
2-2什么是流体的静压强,静止流体中压强的分布规律如何?解: 流体静压强指单位面积上流体的静压力。
静止流体中任意一点的静压强值只由该店坐标位置决定,即作用于一点的各个方向的静压强是等值的。
冶金传输原理第六章课后习题及解答

第六章 可压缩气体的流动例6-1 空气缸中的绝对压强40,/700020==t m kN p ℃,通过一喉部直径mm d 25=的拉瓦喷管向大气中喷射,大气压强22/1.98m kN P =,求: (1) 质量流量G ;(2) 喷管出口断面直径d 2; (3) 喷管出口的马赫数M 2。
解:由于02528.0P P <,喷管喉部可达到音速,由已知喉部条件,决定质量流量。
(1)33000/793.731328710700m kg RT p =⨯⨯==ρ由公式(6-19)()0012112ρKp K A G K K C -+⎪⎭⎫ ⎝⎛+=792.7107004.14.22105.243342⨯⨯⨯⎪⎭⎫⎝⎛⨯⨯=-πs kg /785.0=(2)由公式(6-19)计算喷管出口断面直径:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛-=-KK Kp P p P p K Kd G 10220200221124ρπ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-KK K p P p P p K KGd 10220200221124ρπ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯=286.043.137001.9817001.98792.7107007785.04π3100037.1-⨯=mm m d 7.310317.02==(3)37143.010202/914.17001.98792.7m kg p P K=⎪⎭⎫⎝⎛⨯=⎪⎪⎭⎫⎝⎛=ρρs m p K a /268914.1101.984.13222=⨯⨯==ρs m A G V /5201017.3914.1785.0442222=⨯⨯⨯⨯==-πρ 914.1268520222===a V M 例6-2 空气(K=1.4,R=287J/kg ·k )在400K 条件下以声速流动,试确定:(1)气流速度;(2)对应的滞止音速;(3)对应的最大可能速度;(4)滞止焓;(5)克罗克数max V V C r =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章习题参考答案(仅限参考)1.d2.c3.a(题目改成单位质量力的国际单位)4.b5.b6.a9. c (不能承受拉力)10.a 11.d 12.b(d为表现形式)13•解:由体积压缩系数的定义,可得:14•解:由牛顿内摩擦定律可知,A f dl■ dVx . vF = J A x - Ldl — : 8.57N7.c 8.a1 dVV dp1 995 — 1000 1031000 10“__106__-5 10^1/Pa式中由此得dydy &第二章参考习题答案(仅限参考)1.a 2.c 3.b 4.c5•解:P厂P a ‘油g0 、水gh?二'汞gh P a兀h =—F p 7油gh< ?水gh,2r d=0.4mPg(测压计中汞柱上方为标准大气压,若为真空结果为1.16m )6•解:(测压管中上方都为标准大气压)(1)P l = P a '油g h3 - ?水g ®-h i P a3p =833kg/m3(2)P 厂P a '油g % 一0 二 ^水g h, - h l P a h3=1.8m.D2 2S 0.1256m2V水=S0 =0.1256 0.5 = 0.0628m3V由=S h^h^ 7-0.1256 1.^0.16328m37 •解:设水的液面下降速度为为dzV, V =-一dt3T单位时间内由液面下降引起的质量减少量为:V「一4则有等式:v^2",代入各式得:4豈汙巾274」5整理得:-P 二d21 tz°5dz=0.274 dt =0.274t2 08•解:P i 二 P o YghP 2 二 P o 7gh卩二 P i _P2 二 0 -「s gh =248.7Pa解得:t 1 0.274 二d 242(1—忑)=1518s第三章习题参考答案(仅限参考)1.b2.c3.c4.c5•答:拉格朗日法即流体质点法必须首先找出函数关系 x(a,b,c,t), y(a,b,c,t), z(a,b,c,t), p (a,b,c,t)等。
实际上就是要跟踪每一个流体质点,可见这个方法在方 程的建立和数学处理上将是十分困难的。
因而除研究波浪运动等个别情况外很少 采用。
实际上,在大多数的工程实际问题中,通常并不需要知道每个流体质点至始 至终的运动过程,而只需要知道流体质点在通过空间任意固定点时运动要素随时 间变化状况,以及某一时刻流场中各空间固定点上流体质点的运动要素, 然后就 可以用数学方法对整个流场进行求解计算。
6•答:流体在运动过程中,若每一空间点的物理量(运动参数)不随时间改变, 则称为恒定流动(又称定常流动),否则称为非恒定流动(又称非定常流动) 流体质点的运动轨迹称为迹线。
流线是速度场的矢量线,是某瞬时在流场中所作 的一条空间曲线。
7.解:(1) R e = V md 」2002 1052300,湍流v 1^108 .答:v=Q/A ,断面平均流速是一种假想的流速,即过断面上每一点的平均流 速都相同。
断面平均流速的概念十分重要,它将使我们的研究和计算大为简化。
9.答:不正确。
均匀流是相对于空间分布而言,恒定流是相对于时间而言。
均匀 流的不同时刻的速度可以不同,也可以相同。
恒定流的不同空间点上的速度可以 不同,也可以相同。
当流量不变时,通过一变直径管道,显然是恒定流,但不是 均匀流。
10. 解:根据欧拉法中速度的定义: Vx(x,y,z,t )= —ct V y x,y,z,ty得: ctVz(x,y,z,t 尸乎R e 二V m d 0.2 150 10’ 28 10*= 107.1 :: 2300,层流. dx 如飞k1^dydtk 2』 • dt右边第一个式子,两边对t 求导,联合第二个式子可得:d 2x牙k i 2x = 0,解这个常微分方程得:dt 2x cos(k |t) c 2 sin(k |t)将 x 带入原方程得:y =C |Sin(k j t) -q cos(k (t), k 2t c 3再根据初始条件,得:G =a, q = -b, c 3 = c 于是得到拉格朗日法表示为:x =acos(k j t) -bsin(k 1t) y 二 asin(k 1t) bcos(k 1t) z = k 2t c11. 解:根据随体导数定义:第四章习题参考答案(仅限参考)1.错、错、错2.a3.ca x■:Vx■:Vx.:tV x —vy■:Vx■:y V z■:Vxay.:t V x —.x vy-Vy'V y Vz —;z az.v z .:tV xVy■:yV z.:v z将速度代入随体导数中,得:22 3 2 2a x =0 x y 2xy ]亠[3y ][ x 0 = 2x y -3x y ay =0-3y -30 0 =9ya z =0 0 0 8z 3=8z 3代入点(1,2,3)得:ax=2a y -18、a z =2164 •解:根据平面不可压缩流体连续性的性质: (1) 2 Y z =o ;连续 x ;z(2)^Vz =1 0=1 ;不连续 x ;z(3) 乞•昱 =2x • 1 ;当x=0.5时连续,其他情况不连续cX cZ 5•解:同题4,av x----- =Ay cos (xy )/x(1M :;当x=y 时,连续;其他情况不连续:VyAxcos (xy )6. 解:应用伯努利方程:' 2R 丄+o 亠+o+o ;g 2g : g解得 v =J"|(p — p ) = 20.98m/s 1 233流量 Q 3.14d v =2.37 10 m /s47. 解:根据流体静力学知识得到以下关系式:Pl 「gh = P 2「水gh 2「g :h根据左右两管水的体积相等,有:d 2D 2h d 2 :h —44Ay;连续Ay/ 口 d 2得E 莎h ,代入可解得:h= ---------- 9^02 0伽2::水 g - “ 2 2 亍8•解:选取圆柱坐标系,假设流动是沿 z 轴方向进行,且为充分发展的层流流 动。
根据已知条件可知,流动是轴对称,B 方向可不考虑,仅z 方向有流动。
由 连续性方程、稳定流动,忽略质量力,则有:二-0 ;.:z ::二化简得:1 ? ?. 7 1 ;:P(r 「) =常数1-. 、 1-. 'I If-.r :丁 :丁z进行第一次积分,并将边界条件r=0处,代入,算得积分常数 C1;再进行第 次积分,并将r=R 处,u z=0代入,算得出C2。
最后得到:z 二VdF (R 2-r 2)—RdF 【1-(R )2] 4」dz 4」dz R式中r 为管截面上速度为u z 处到管中心的距离,R 为圆管半径。
显然其速度分 布呈抛物线形。
下面很容易推导出 u z 与u zmax 的关系为:r 2z = zmax[1 -(匸)2]R9.解:列1-2处的伯努力方程:(以2处为0基点),用相对压强计算:2 20 A gh 2 = 0 空 02 2由于水槽的直径比虹吸管的直径大很多,那么就可以近似设 W 等于0代入可得 V 2 二.2^2 =8.86m/sd 2 __ d 2流量 Q =v 2 宜 3.14h ;〕2gh 2 丄 3.14=6.26 10^m 3/s4 4同理列2-3处的伯努利方程(P 2为什么为0):(以2处为0基点)2 2:z:t+vr汽zF_z2 z.仁z .丄匚.二 .:r 2 r ;r r 2 :r 2jz 20 ;.:t(r 二) 丁直仏 g (h h 2)=0 V^0 P 22根据质量守恒:3处和2处的速度满足:吃d 22,得 v 3 = v =2.215m/s4 4 4代入得:负号表示C 处的压强低于一个大气压,处于真空状态。
正是由于这一真空,才 可将水箱中的水吸起。
用绝对压强表示:101325-22024.3=79300.7 Pa.S -Vi 2、\ 1+h 2)1 2g 丿5 -■g - -22024.3Pa第五章习题参考答案(仅限参考)1.a2.b3.d4.c5.d扎..L PVm6.解:"d 264 64假设雷诺数小于2300,有乙矿不,代入上式得:64 L ‘V m 264 L v m V m d d 2 2d 22d 2心p 2江 0.152沃 0.965X06,则V m64 L 「 64 4 10^ 920 1000.山 Sv d 184 x 0 15 R 「4=E^69"2300,符合假设另一种简单计算方法: 假设雷诺数小于2300,有Re 二騒二1.84°?5二 690 :: 2300,符合假设 v 4 汉107.解:V m =程 4 0.032 = 0.425 m s兀 d 3.14乂0.32 坐=0.06 Re:dV m3.14 0.1521.844 =0.03 m : sr2、L PV m P 二dV mP R2 _ d 2p 8l L 321、0.1520.965 10632 4 10“ 920 10001.84m/sQ二Avm:dV m3.14 0.1521.844= 0.03 m 3s0.425 0.31.2 10,-1063 :: 2300-hf =L v m2 30 0.4252 —=0.06 0.06m 0.3 2x9.81d 2g &解:V m 4Q_ 4 0.05 二d 2 一 3.140.252= 1.02 m s v m d 1.02 925 Re 二 1.007 10-6= 2.5 105 105 皿"0052 ; 0.25查莫迪图得 心 0.031h f I 2 LV^=0.031 d 2g 2 100 1.02 c “ 0.66m0.25 2 9.81 9•解: 4Q‘ 0.3292 60 2 = 1.4 msPg L 2 父102 -0.03 沃 -6.29 - 6 - 0.29d 1000 汉 1.4 0.05匚、L、 2 vm700、S U +扎一2.9沃3+0.02ii d 2g0.15 10.解:二h = 1.132X -----------------2 汇 9.81i 匚-r L I d 丿 2g _ 2 p =7v m 2 6.64m11•解:Re 二 V m dV 0.25 0.305 1.231.78 10°二 5269 105* / 0.037R e2 (2)d 2 21—v(2)乞g)33 210.305 0.037 1.23 0.25 8 1-0.390.39365.58 Pa0.001212.解:v 4Q 60 603.14 d225 m s解得d=1.3m25 1.3 =2.07 10610551.57 100.0005 =0.000385 ;杳莫迪图得店0.01551.32Vm h - - /.-d / 2g 二 2.5 11 0.0155120I 1.3丿252921.57 m2 9.81p= 'g h= 1.23 9.81 921.57 = 11120PaPip a- p 二1.569 1.01325-0.11 10^ 2.471 105Pa13 .解:v m4Q 260——=11.9 m,s23.14 0.72Re V m d 11.9 0.72 50.157 10^ 5.46 100.2(1) d 720 = 0.000278 ;查莫迪图得X= 0.01472 L vm d 2g228.6 11.9= 0.0147 4.21m0.72 2 汉9.81h f720■ 2L V md 2g= 0.00278 ;查莫迪图得入二0.026528.6 11.92二0.0365 7.60m0.72 2 981第六章习题参考答案(仅限参考)6 5x ReT, 5x 5^3j36 =才=i= 8.13汉10 mRe< 3.4 10x = 0.1m丄=50 3 =1.0 10715 10 =Cf L1.292 ^0.41 汩C f T 0.074 = 2.95 10,Re L0.2C f T _ C f L Re x cr 二7620(若查表,则A*=8700)F f J 2bl二20.074RqA*仏Re.」2bl 二9.86N2(查附录1,对应的p =1.205kg/m3)1 •解: Re*..x 17 3OU二—15"0出=3.4 1062•解: Re x %x = 30.17x—=15 10"6=2 1053•解:50 0.915 10"=3 106 Re x crbl 2 1.70 NF f 二2。
