计算机图形学_第六章
《计算机图形学》课件第六章

(2) 两点透视。投影平面和二个坐标轴相交, 即投影 平面与一个坐标轴平行。 所生成的物体投影图具有较好 的真实性, 比较容易构造。 常用于建筑工程、 工业设计和
(3) 三点透视。投影平面和三个坐标轴相交, 这类透 视投影的构造比两点透视难一些, 用的较少。
6.2.2 透视投影的确定
令 z′=0, 得
(1) 绕 z 轴旋转-θ2角, 其变换矩阵为: (6.14)
(2) 绕y轴旋转-θ1角, 其变换矩阵为: (6.15)
(3) 绕 z 轴旋转θ角, 其变换矩阵为: (6.16)
(4) 绕y轴旋转θ1角, 其变换矩阵为: (6.17)
(5) 绕 z 轴旋转θ2角, 其变换矩阵为: (6.18)
(6.38)
oz 轴的单位方向向量为 而 ox 轴的方向和向量U×N一致, 所以
(6.39) (6.40)
根据右手规则, oy 轴的单位方向向量为
(6.41) 从而, 从用户坐标系到观察坐标系的坐标变换公式是
(6.42)
写成齐次坐标表示, 则有 其中
(6.43) (6.44)
3. 设透视中心C在用户坐标系oxyz中的坐标为(xc, yc, zc), 那么由式(6.43)可知, C在观察坐标系中的坐标 (xc,yc,zc)确定式为
(6.32)
其中A、 B为常数。 显然, 射影变换把三维空间的直线也变 成了直线。
6.2.3 平行投影及其分类
1. (1) 正投影。 投影平面垂直于某一坐标轴, 因此, 该坐标轴方向就是投影方向。 最常见的正投影有六种: 前 (主)视图、 后视图、 左(侧)视图、 右视图、 顶(俯)视图、 底(仰)视图, 工程制图中常用前视图、 侧视图和顶视图三 种。 正投影能较好地描述物体的一个面, 但却丢失了物体 的许多三维信息, 即使使用所有的六种正视图, 有时也难 以重构该物体的三维结构。
计算机图形学6(陈永强)

Y
X (e)关于x=-y对称
X (d)关于x=y对称
11
基本几何变换——对称变换
(1)关于x轴对称
Y
1a 0 b 0 1 c d m 0l 0
0 p 0 q s 1
P(x,y) X P'(x,-y)
图6-5 关于x轴对称
12
基本几何变换——对称变换
24
复合变换——二维复合旋转
cos1 sin 1 0 cos 2 Tr Tr1 Tr 2 sin 1 cos1 0 sin 2 0 1 0 0 cos(1 2 ) sin(1 2 ) 0 sin(1 2 ) cos(1 2 ) 0 0 0 1 sin 2 cos 2 0 0 0 1
1 b 0 c 1 0 0 0 1
(3)两个方向错切
18
二维图形几何变换的计算
几何变换均可表示成P’=P*T的形式。 1. 点的变换
x'
y ' 1 x
a b y 1 c d l m
p q r
19
二维图形几何变换的计算
2. 直线的变换
0 cos 0 0 0 1
1 0 tg 1 0
0
tg 1 0
0 1
0
26
6.3.5相对任一参考点的二维几何变换
相对某个参考点(xF,yF)作二维几何变换,其变 换过程为: (1) 平移; (2) 针对原点进行二维几何变换; (3) 反平移。
27
相对任一参考点的二维几何变换
P' P T P (T1 T2 T3 Tn ) P T1 T2 T3 Tn (n 1)
计算机图形学_完整版 ppt课件

发展趋势:与信息技术、大数据、人工智能等新兴 技术相结合,推动健康服务与管理的智能化、精细 化发展
专业定位与目标
定位:培养具备公共管理、健康服务与管理专业 知识和技能的人才
目标:提高公共管理水平,促进健康服务与管理 领域的发展
培养目标:具备公共管理、健康服务与管理专业 知识和技能,能够从事相关工作的人才
04
健康服务与管理专业能够促 进医疗资源的合理配置和利 用
2
专业课程设置
核心课程
公共管理学
卫生信息管理
卫生服务人力 资源管理
卫生服务领导 力
健康服务与管 理
卫生服务营销
卫生服务财务 管理
卫生服务创新 与变革
卫生经济学
卫生服务组织 与管理
卫生服务战略 管理
卫生服务研究 方法
卫生政策与法 规
卫生服务评估 与质量管理
有效沟通
02
具备良好的团队 协作能力,能够 与团队成员共同
完成工作任务
03
具备良好的组织 协调能力,能够 协调和管理各种
资源
04
具备良好的学习 能力,能够不断 更新自己的知识
和技能
05
具备良好的心理 素质,能够应对 工作中的压力和
挑战
感谢您的观看
4
就业前景与职业 发展
主要就业领域
1
2
3
4
5
6
Hale Waihona Puke 政府部门:卫 生、社保、医
保等
医疗机构:医 健康管理机构: 企业:人力资
院、诊所、康 健康咨询、体 源、员工健康
复中心等
检中心等
福利管理等
教育机构:高 校、职业院校
等
科研机构:公 共卫生、健康
计算机图形学第6章课后习题参考答案

第六章1.请简述朗伯(Lambert )定律。
设物体表面在P 点法线为N ,从P 点指向光源的向量为L ,两者夹角为θ,则点P 处漫反射光的强度为:I d =I p k d cos θ式中 : I d ——表面漫反射光的亮度;I p ——入射光的光亮度;K d ——漫射系数(决定于表面材料及入射光的波长) 0≤K d ≤l ; θ——入射光线与法线间的夹角,0≤θ≤π/2。
并且,当物体表面垂直于入射光方向时(N 、L 方向一致)看上去最亮,而θ越来越大,接近90°时,则看上去越来越暗。
2.试写出实现哥罗德(Gouraud )明暗处理的算法伪代码。
deltaI = (i2 - i1) / (x2 - x1);for (xx = x1; xx < x2; xx++){ int offset = row * CScene.screenW + xx;if (z < CScene.zBuf[offset]){ CScene.zBuf[offset] = z;CScene.frameBuf[offset] = i1;}z += deltaZ; i1 += deltaI;} 3. 在Phong 模型n s p d p a a V R K I N L K I K I I )()(⋅+⋅+=中,三项分别表示何含义?公式中的各个符号的含义指什么?三项分别代表环境光、漫反射光和镜面反射光。
a I 为环境光的反射光强,p I为理想漫反射光强,a K 为物体对环境光的反射系数,d K 为漫反射系数,s K 为镜面反射系数,n 为高光指数,L 为光线方向,N 为法线方向,V 为视线方向,R 为光线的反射方向。
4.试写出实现Phong (冯)明暗方法的伪代码。
for (xx = x1; xx < x2; xx++){ int offset = row * CScene.screenW + xx;if (z < CScene.zBuf[offset]){ CScene.zBuf[offset] = z;pt = face.findPtInWC(u,v);float Ival = face.ptIntensity;CScene.frameBuf[offset] = Ival;}u += deltaU;z += deltaZ;p1.add(deltaPt);n1.add(deltaN);}5.请简述自身阴影的生成方法。
《计算机图形学》课件第6章

第 6 章 真实感图形
1. Gouraud 1) 一个顶点由3个及以上的面汇集, 将这些面的法向平均值 近似为该顶点的法向量(此法向与该多边形物体近似的曲面的 切平面法向比较接近)。 假设顶点V相邻的多边形有k个, 法向 量分别为N1, N2, …, Nk, 则顶点V的法向量取为
第 6 章 真实感图形
第 6 章 真实感图形
扫描线Z缓存算法的流程如下: for (各条扫描线) {
扫描线帧缓冲器置为背景色; 扫描线Z缓冲器置为最小z值; for(每一个多边形) { 将该多边形进行投影变换; 求多边形与当前扫描线的二维投影之间的交点;
for(每一对交点之间所含像素)
第 6 章 真实感图形 { if(该像素的z值大于Z缓冲器在该处的z值) {
Ie=IaKa 其中, Ia是环境光的光强, Ka是物体对环境光的反射系数。
第 6 章 真实感图形
4. 已知简单光照模型为
I=IaKa+IpKd cosθ+IpKs(cosα)n 也就是说, 物体表面上一点P反射到视点的光强I为环境光的反 射光强Ie、 漫反射光强Id和镜面反射光强Is的总和。 简单光照 模型中的几何量分布如图6-3所示。
第 6 章 真实感图形
此凸多面体在以视点为顶点的视图四棱锥内,视点与第i个 面上一点连线的方向为(li, mi, ni)。 那么第i个面为自隐藏面的 判断方法是
(ai, bi, ci)×(li, mi, ni)>0 对于任意凸多面体, 可先求出所有隐藏面, 然后检查每条边, 若 相交于某条边的两个面均为自隐藏面, 那么根据任意两个自隐 藏面的交线为自隐藏线可知该边为自隐藏边。
第 6 章 真实感图形 上面的五项只要有一项成立, P就不遮挡Q。 如果所有测 试都失败, 就必须对两个多边形在xy平面上的投影作求交运算。 计算时不必具体求出重叠部分, 在交点处进行深度比较, 只要能 判断出前后顺序即可。 若遇到多边形相交或循环重叠的情况, 还必须在相交处分割多边形, 然后进行判断。
第六章路径与矢量图形的概念

矢量图
位图
2.路径的创建和编辑
钢笔工具可创建和编辑矢量图形,它是最基本的路径绘制工 具,工具调板中提供了包括钢笔工具、自由钢笔工具、添加锚点 工具、删除锚点工具和转换点工具,如图所示。
钢笔工具
(1)钢笔工具 使用钢笔工具可以勾画出平滑的曲线路径,在缩放或者变形之 后仍能保持平滑效果,钢笔工具提供了最佳的绘图控制和最高的绘 图准确度,其选项栏如下图所示。
多边形工具的选项栏
(5)直线工具 使用直线工具可绘制直线和箭头的路径和形状。通过设置箭头 参数,可以得到箭头图案。
直线工具选项栏
箭头图案
(6)自定形状工具 使用自定形状工具可绘制出多种复杂图案的路径和形状。
自定义形状工具的选项栏
6.上机练习
(1)制作标志
操作步骤:
A.绘制圆形路径
在“工具”调板中选择椭圆工具,按Shift键的同时,在页面上 拖动出一个圆形路径;拖动圆形路径,按Alt键复制出第2个、第3个 和第4个圆形路径,使用路径选择工具,将所有圆形路径选中,将4个 路径进行对齐和平均分布。
(2)自由钢笔工具 使用自由钢笔工具就像使用铅笔在纸上绘画一样随意,绘制 路径时可自动添加锚点,图6-5为自由钢笔工具选项栏。
自由钢笔工具选项栏
在选项栏中点按形状按钮旁边的反向箭头按钮,勾选磁性的复 选框,可绘制与图像中所定义区域的边缘对齐的路径,然后为 “曲线拟合”输入介于0.5~10.0像素之间的值,此值越高,创建 的路径锚点越少,路径越简单。
C.将选区部分进行复制 执行“编辑”→“拷贝”命令,接着执行“编辑→粘贴”命令, 或者在键盘上依次按下Ctrl+C、Ctrl+V组合键,此时图层调板中将新 生成“图层1”。 D.锁定透明像素 选择“图层1”,在图层调板上点按“锁定透明像素”按钮,透 明区域部分将不可编辑。
计算机图形学-第六章讲义

DC与NC之间的关系 ➢ 对每一个物理设备而言,DC与NC仅仅 是坐标值相差一个比例因子 ➢ NC可以看成是一个抽象的图形设备, 要输出到具体的设备时,只需乘上一个 比例因子即可
计算机图形学-第六章讲义
6.1 2D 观察变换
考察一个图形时,往往采用两种模型:
➢ 物理模型:是用户在WC中描述的 ➢ 逻辑模型:是在显示器上呈现的物体的图形,
计算机图形学-第六章讲义
线段的裁剪
Cohen-Sutherland直线裁剪(CS算法) Liang-Barsky 直线裁剪(LB算法) Nicholl-Lee-Nicholl 直线裁剪(NLN算法) 非矩形裁剪窗口
计算机图形学-第六章讲义
Cohen-Sutherland 线段裁剪
思想:
视口: 显示设备上用于窗口映射的坐标 区域,也叫视区。
观察变换:世界坐标系中部分场景映射到 设备坐标系的过程称为观察变换,也叫视 像变换,或称为从窗口到视口的变换。
计算机图形学-第六章讲义
2D 的观察流程
MC 使用建模坐标变换 WC 将世界坐标转
构造世界坐标场景
换为观察坐标
VC
DC 将规范化视口 NVC 使用窗口-视区描述
计算机图形学-第六章讲义
坐标系
1. 世界坐标系(World Coordinates) 用户处理自己的图形时所采用的坐标系,坐标的 大小和尺寸由用户确定。
2. 设备坐标系(Device Coordinates) 与一个图形设备相关的坐标系叫设备坐标系。如 显示器或打印机有它们自己的坐标系。
3. 规格化坐标系(Normal Device Coordinates) 它是独立于具体物理设备的一种坐标系,具有显 示空间在X和Y方向上都是从0到1
计算机图形学PPT教学课件

2020/10/16
19
• 多边形裁剪 • 双边裁剪——遇到交点向右拐
2020/10/16
20
• 1)进行初步深度排序,可按各多边形z最小值(或最 大值、平均值)排序;
• 2)选择当前深度最小(离视点最近)的多边形为裁剪 多边形;
• 3)用裁剪多边形对那些深度值更大的多边形进行裁剪
• 4)比较裁剪多边形与各内部多边形的深度,检查裁剪 多边形是否是离视点最近的多边形。若裁剪多边形深 度大于某个内部多边形的深度,则恢复被裁剪的各多 边形,选择新的裁剪多边形,回到3),否则做5);
➢该算法多用于线消隐,也用于面消隐。
➢算法的简单描述如下: ➢对于三维场景中的每一个物体:
➢判定场景中的所有可见表面;
➢用可见表面的颜色填充相应的像素以构成图形;
2020/10/16
9
假定:垂直投影
•隐藏线和隐藏面消除所讨论的对象是一个三维 图形,消隐后要在二维空间中表示出来,因此消 隐后显示的图形将和三维空间至二维空间的投影 方式有关。 •下面讨论消隐算法时,都假定投影平面是oxy平 面,投影方向为负z轴方向的垂直投影。
• 2)对多边形P,计算它在点(i,j)处的深度值 zi,j,
• 3)若zi,j< ZB(i,j),则ZB(i,j)=zi,j,CB(i,j)=多 边形P的颜色;
• 4)对每个多边形重复(2)、(3)两步,最 终在CB中存放的就是消隐后的图形。
2020/10/16
23
• 如何求深度
设某个多边形所在的平面方程为
• 5)择选下一个深度最小的多边形作为裁剪多边形,从 3)开始做,直到所有的多边形都处理过为止。在得到 的多边形中,所有的内部多边形是不可见的,其余多 边形均为可见多边形。
计算机图形学 抛物及三次样条曲线

第六章 曲线
一为什么要学习曲线? (用曲线能作什么?) 应用很广泛: 汽车制造,多媒体应用,飞机外形设计, 计算机辅助设计等方面被大量使用. 如: 用B样条曲线绘制汽车. 用抛物样条曲线绘制鱼(靠型值点来画)
二 汽车的传统设计方法和计算机辅助设计方法的比较: 汽车的制造过程: 1 素描车身草图,挑选其中的最佳方案。
6.2 曲线表示的基础知识:
一 曲线的表示方法:
1.显示方式:
一条平面曲线的一般式:
y=f (x)
如正弦曲线:f=sin(x)
一条直线的一般式:
y=m*x+b
特点:一个x表示一个y.
2.隐式方式:
一条平面曲线的一般式:
f (x, y)=0
一条直线的一般式:
ax+by+c=0
一个圆心在原点的圆:
x2+y2+1 =0
特点:与坐标轴无关,仅与参数有关,易于编程。
例如:圆的参数方程:x=cosθ, y=sinθ 绘制的1/4圆的各点弧长相等,见下图a。 以显示方式绘制的1/4圆的各点弧长不等,见下图b。
a
b
用参数方程可以非常均匀地画出来 即:参数方程控制形状的能力强
X等分取,y值不均匀
分析: 参数方程与非参数方程的比较:
和Δc(弧长变化量), 通常使用|Δφ/Δc来衡量弯曲程度。 曲线P(c)在r点的曲率为:k=lim|Δφ/Δc| 曲率半径:ρ= 1/ k
曲率大,则曲率半径小,曲线弯曲得厉害,如A点; 曲率小,则曲率半径大,曲线弯曲得不厉害,如B点。 圆的曲率半径等于它的半径。
B
A
(四) 型值点和控制点:
型值点: 通过测量或计算得到的曲线上少量描述曲线几何形状 的数据(如:鱼)
计算机图形学内容整理

计算机图形学第一章计算机图形学概论(4)【计算机图形学定义】计算机图形学是研究计算机图形的表示、生成、处理、显示的学科。
计算机图形学是计算机科学中最为活跃、得到广泛应用的分支之一。
1982年国际标准化组织(ISO)的定义:计算机图形学是研究通过计算机将数据转换为图形,并在专门显示设备上显示的原理、方法和技术的学科。
它是建立在传统的图学理论、应用数学和计算机科学基础上的一门边缘学科。
IEEE(Institute of Electrical and Electronics Engineers,美国电气及电子工程师学会)定义:Computer graphics is the art or science of producing graphical images with the aid of computer.计算机图形学是借助计算机产生图形影像的一门艺术或科学。
美国的James Foley在其著作中定义:计算机图形学是运用计算机描述、输入、表示、存储、处理(检索/变换/图形运算)、显示、输出图形的一门学科。
【图形和图像】图形(Figure、Graphic):是构成图像的要素,表示图像中的某一个具体形状。
图形含有几何属性,更强调场景的几何表示,是由场景的几何模型和景物的物理属性共同组成的。
图形主要分为两类:基于线条信息表示;明暗图(Shading)。
图形是指用计算机绘制工具绘制的画面,包括直线、曲线,圆/圆弧,方框等成分。
图形一般按各个成分的参数形式存储,可以对各个成分进行移动、缩放、旋转和扭曲等变换,可以在绘图仪上将各个成分输出。
图像(Image):绘图、照片、影像的总称。
图像纯指计算机内以位图(Bitmap)形式存在的灰度信息。
图像是由输入设备捕捉的实际场景或以数字化形式存储的任意画面。
图像可以用位图或矢量图形式存储。
数字图像(Digital Image)【计算机图形学的研究对象】图形:能在人的视觉系统中产生视觉印象的客观对象,包括自然景物、拍摄到的图片、用数学方法描述的图形等等。
计算机图形学 第六章 计算机动画(2)

应用实例
《史酷比2:怪兽偷跑》
整体和局部变形方法
由Alan Barr于1984年提出,是最早的变形方法
。包括渐细变形(Tapering)、螺旋形变形 (Twisting)等。
(a)变形前的茶壶
(b) 渐细变形
(c) 螺旋形变形
Alan Barr的变形类别
应用例子
自由变形方法FFD
1986年,Sederderg等提出了一种非常适合于柔 性物体动画的一般化的变形方法,该方法不直 接操作物体,而是将物体嵌入一空间,当所嵌 的空间变形时,物体也随之变形。
群组层次
群 —— Crowd behaviors
组 —— Group behaviors 个体 —— Individual behavior
为什么需要群组动画?
得到大场面的视觉震撼效果
动漫设计和影视特技中,不可避免地会遇到各种大 规模群体动作场面的制作。例如,两军对垒中的数 十万大军冲锋的效果、兽群、鸟群等。
茶壶的FFD变形 (a) 变形前 (b) 变形后
FFD的数学原理
Q (u, v, w) Pijk Bi (u ) B j (v) Bk ( w)
i 0 j 0 k 0 3 3 3
轴变形方法
轴变形是一种通过参数曲线来控制物体自由变 形的方法。该方法把物体嵌入轴线的局部参数 空间中来实施变形,当轴线变形时,嵌入其参 数空间中的各点的位置随之发生变化。
两个元球靠近时的形变过程
动画演示
过程动画技术
过程动画是指采用一个过程来描述物体的运动 或变形。 最简单的过程动画是设立一个数学模型去控制 物体的几何形状和运动,如旗帜迎风招展、水 波随风荡漾等。
计算机图形学2010_06三维图形变换
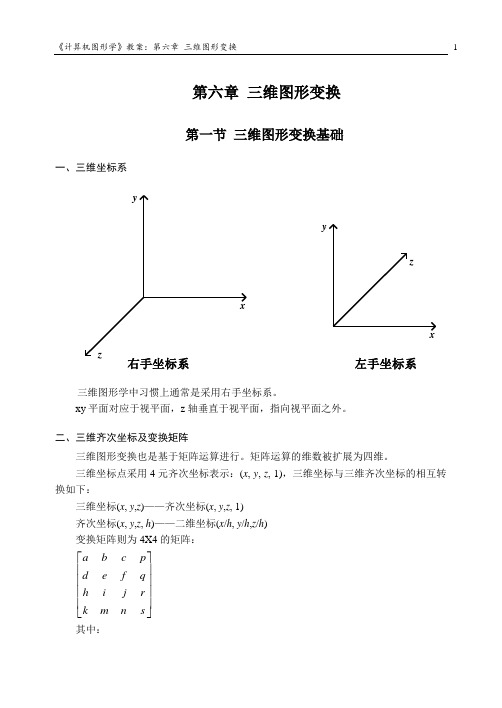
第六章 三维图形变换第一节 三维图形变换基础一、三维坐标系xyzxyz右手坐标系左手坐标系三维图形学中习惯上通常是采用右手坐标系。
xy 平面对应于视平面,z 轴垂直于视平面,指向视平面之外。
二、三维齐次坐标及变换矩阵三维图形变换也是基于矩阵运算进行。
矩阵运算的维数被扩展为四维。
三维坐标点采用4元齐次坐标表示:(x , y , z , 1),三维坐标与三维齐次坐标的相互转换如下:三维坐标(x , y ,z )——齐次坐标(x , y ,z , 1) 齐次坐标(x , y ,z , h )——二维坐标(x /h , y /h ,z /h ) 变换矩阵则为4X4的矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s nm kr j i h q f e d p c b a 其中:平移变换第二节 三维几何变换一、三维基本变换 1. 平移变换⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1010000100001nmk T )1,,,()1,,,(n z m y k x T z y x +++=⋅2. 比例变换)1,,,()1,,,(1000000000000jz ey ax T z y x j e a T =⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 3. 旋转变换三维的基本旋转变换分为三种,即绕三个坐标轴的旋转变换。
(1)绕z 轴旋转γ角旋转后z 值不变,x,y 值将发生改变,x,y 值的计算公式与平面旋转相同,即:zz y x y y x x ='+='-='γγγγcos sin sin cos 则变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000010000cos sin 00sin cos γγγγT 有:)1,1,cos sin ,sin cos ()1,,,(γγγγy x y x z y x +-=T(2)绕x 轴旋转α角则旋转后x 的坐标值不变,y 和z 的坐标值将改变,相当于在yz 平面上绕平面原点进行旋转变换。
平面转转变换的公式为:ααααcos sin sin cos y x y y x x +='-='对应而来,这里y 对应于x ,z 对应y ,有:ααααcos sin sin cos z y z z y y +='-='则变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10000cos sin 00sin cos 00001ααααT )1,cos sin ,sin cos ,()1,,,(ααααz y z y x z y x +-=T(3)绕y 轴旋转β角这时,z 对应于x ,x 对应于y 。
计算机图形学第二版(陆枫)课后习题答案部分

计算机图形学第二版(陆枫)课后习题集第一章绪论概念:计算机图形学、图形、图像、点阵法、参数法、图形的几何要素、非几何要素、数字图像处理;计算机图形学和计算机视觉的概念及三者之间的关系;计算机图形系统的功能、计算机图形系统的总体结构。
第二章图形设备图形输入设备:有哪些。
图形显示设备:CRT的结构、原理和工作方式。
彩色CRT:结构、原理。
随机扫描和光栅扫描的图形显示器的结构和工作原理。
图形显示子系统:分辨率、像素与帧缓存、颜色查找表等基本概念,分辨率的计算第三章交互式技术什么是输入模式的问题,有哪几种输入模式。
第四章图形的表示与数据结构自学,建议至少阅读一遍第五章基本图形生成算法概念:点阵字符和矢量字符;直线和圆的扫描转换算法;多边形的扫描转换:有效边表算法;区域填充:4/8连通的边界/泛填充算法;内外测试:奇偶规则,非零环绕数规则;反走样:反走样和走样的概念,过取样和区域取样。
5.1.2 中点 Bresenham 算法(P109)5.1.2 改进 Bresenham 算法(P112)习题解答习题5(P144)5.3 试用中点Bresenham算法画直线段的原理推导斜率为负且大于1的直线段绘制过程(要求写清原理、误差函数、递推公式及最终画图过程)。
(P111)解: k<=-1 |△y|/|△x|>=1 y为最大位移方向故有构造判别式:推导d各种情况的方法(设理想直线与y=yi+1的交点为Q):所以有: y Q-kx Q-b=0 且y M=y Qd=f(x M-kx M-b-(y Q-kx Q-b)=k(x Q-x M)所以,当k<0,d>0时,M点在Q点右侧(Q在M左),取左点 P l(x i-1,y i+1)。
d<0时,M点在Q点左侧(Q在M右),取右点 Pr(x i,y i+1)。
d=0时,M点与Q点重合(Q在M点),约定取右点 Pr(x i,y i+1) 。
所以有递推公式的推导:d2=f(x i-1.5,y i+2)当d>0时,d2=y i+2-k(x i-1.5)-b 增量为1+k=d1+1+k当d<0时,d2=y i+2-k(x i-0.5)-b 增量为1=d1+1当d=0时,5.7 利用中点 Bresenham 画圆算法的原理,推导第一象限y=0到y=x圆弧段的扫描转换算法(要求写清原理、误差函数、递推公式及最终画图过程)。
第06章 相机模型

第六章相机模型在第一章里,我们描述了计算机图形学中常用的针孔相机模型。
这种模型易于描述和模拟,但有严重的缺陷。
例如,用针孔相机所拍摄出的所有景物都在锐聚焦区(sharp focus)中,所得到的图像就像是计算机生成的。
为了使图像更具真实感,有必要更好地模拟真实世界中成像系统的特性。
跟第三章中Shape类一样,在pbrt中,相机也是用一个抽象类来表达的。
本章介绍Camera类及其唯一的函数:Camera::GenerateRay()。
该函数计算图像平面上任一点所对应的世界空间中的光线。
生成光线的方式因成像模型的不同而不同,所以pbrt中的相机可以对同一个三维场景生成不同的图像。
这里我们要介绍Camera接口的几个实现,每个实现的光线生成方法都不同。
6.1 相机模型Camera抽象基类包含相机的通用选项并定义了所有相机实现的共同的接口。
<Camera Declarations> =class COREDLL Camera {public:<Camera Interface><Camera Public Data>protected:<Camera Protected Data>};Camera的子类必须实现函数Camera::GenerateRay(),该函数根据给定的图像采样点生成光线。
注意Camera对所返回的光线的方向向量进行了正规化,因为系统的许多其它部分需要正规化的光线方向。
这个函数还返回一个浮点数的权值,用来控制光沿着所生成的光线到达胶片平面上的效果。
大多数情况下该函数返回1,但那些模拟真实物理透镜系统的相机需要根据虚拟透镜系统的光学和几何性质来设置该值。
<Camera Interface> =virtual float GenerateRay(const Sample &sample, Ray *ray) const = 0;Camera基类的构造器需要几个通用的相机参数,其中包括把相机放置到场景中的变换,在相机空间中决定可见区域的近裁剪面和远裁剪面。
第6章图形裁剪

下面假定裁剪是针对用户坐标系中窗口边界进行的, 裁剪完成后,再把窗口内图形映射到视区。所以裁剪的 目的是显示可见点和可见部分,删除视区外的部分。
第六章 图形裁剪(Clipping)
在用户坐标系中定义的图形往往是大而复杂的,而 输出设备如显示屏幕的尺寸及其分辨率却是有限的,为 了能够清晰地观察某一部分或对其进行某些绘图操作, 就需要将所关心的这一局部区域的图形从整个图形中区 分出来,这个区分指定区域内和区域外的图形过程称为裁 剪,所指定的区域称为裁剪窗口。
在用户坐标中设置观察坐标系,在观察坐标系中定 义一个观察窗口。观察坐标系用来任意设置矩形窗口的 方向。一旦建立了观察参考系,就可以将用户坐标系下 的描述变换到观察坐标系下。
2019/11/18
计算机图形学演示稿 纪玉波制作
2
(C)
2019/11/18
计算机图形学演示稿 纪玉波制作
3
(C)
3.规范化设备坐标系(Normalized Device Coordinates) 在规范化坐标系下(取值范围从0到1)定义视区,将
设备坐标定义,一般也定义成矩形,由其左下角和右上角两
点坐标来定义。所以,用户可以利用窗口来选择需要观察那
一部分图形,而利用视图区来指定这一部分图形在屏幕上显
示的位置。标准的窗口区和视图区一般都是矩形,其各边分
别与坐标轴平行。
2019/11/18
计算机图形学演示稿 纪玉波制作
6
(C)
用户定义的图形从窗口区到视图区的输出过程如下: 从 应 用 程 序 得 到 图 形 的 用 户 坐 标 (WC-World Coordinates)→对窗口区进行裁剪(WC)→窗口区到视图区的 规格化变换(NDC-Normalized Device Coordinate) →视图区 从 规 格 化 设 备 系 到 设 备 坐 标 系 的 变 换 (DC-Device Coordinate)→在图形设备上输出图形。
计算机图形学课件第六章交互式绘图技术

5、菜单方式
6、图标方式 6.5.3 交互式用户接口的实现
6.5.1 界面布置 6.5.2 交互式工作方式 6.5.3 交互式用户接口的实现
1、交互式输出界面设计
(1)设计原则
①要全盘考虑显示信息内容,布局和格式等;
②反馈信息和屏幕输出应面向用户,指导用户,以满足
用户需求为目标;
③反馈信息内容应准确、简洁;
④屏幕显示和布局应美观、清楚、合理;
⑤合理安排信息在屏幕上显示顺序;
⑥显示方式一致性;
⑦合理选择文本方式和图形方式显示;
⑧使用图形、多窗口方式显示。
17
(2)屏幕显示技术
①文本式屏幕显示一般格式
a.标题引。
标题
屏幕号
b.屏幕主体。
屏幕体
c.出错信息区。
错误信息
d.状态和提示行。
状态、提示行
②问答式屏幕设计
4、减少出错的可能性
5、提供改错能力
6、面向多种技术层次
第六章 交互式绘图技术
7、减少记忆量
6.2 交互式绘图系统
6.2.1 交互式绘图系统组成
6.2.2 交互式绘图系统交互任务
6.2.3 交互式绘图系统设计原则
9
6.3 交互式绘图的交互技术
交互式绘图技术是一种处理用户输入图形数据的技术, 可分为三类:
第六章 交互式绘图技术 6.5 交互式绘图系统构造方法 6.5.1 界面布置 6.5.2 交互式工作方式 6.5.3 交互式用户接口的实现
14
6.5.1 界面布置
界面布置包括屏幕划分、显示内容、颜色搭配等
1、屏幕划分:如图
菜单区 图形显示区
提示区
图形 显示区
提示区
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 yvmax yvmin 2 0
OpenGL中的二维观察变换 (1)指定矩阵栈 glMatrixMode(GL_PROJECTION); glLoadIdentity();
(2)指定裁剪窗口 gluOrtho2D(0,w, 0, h); (3)指定视口 glViewport(0,0,w,h);
Liang-Barsky算法(参数方程法)
u x x1 xw min u x xw max x1 u y y1 yw min u y yw max y1
令:
有不等式:
Liang-Barsky算法(参数方程法)
直线与窗口边界的相对位置: 1、直线段与窗口边界平行,其 ,k 表示取哪一条边(k=1,2,3,4,分别对应左、 右、下、上)。如果对某一k值,还满 足 ,则此直线完全在边界外,可不 考虑;如果 ,此线段在边界内。
Liang-Barsky算法(参数方程法)
2、如果 pk 0,此时把直线从 到 的连线方向作为正向,将此直线无限延伸, 同时把把窗口边界无限延伸;然后分以下 两种情况进行讨论
Liang-Barsky算法(参数方程法) (a)当 pk 0 时,则是由窗口边界延伸线 的外部发出的一条直线进入相应窗口边 界延伸线的内部。
二维点裁剪 二维点裁剪 点的裁剪是图形裁剪的基础,点在窗口内的条件如下:
xwmin x xwmax ywmin y ywmax
二维线裁剪 直线段与裁剪窗口的关系 完全落在窗口内、完全落在窗口外或者与窗口边界相交
二维线裁剪 实交点与虚交点 实交点是直线段与窗口矩形边界的交点。虚交点则是直 线段与窗口矩形边界延长线或直线段的延长线与窗口矩 形边界的交点。
世界坐标系到观察坐标系的变换矩阵 世界坐标系到摄像坐标系的变换 (1)点变换等于坐标系相反方向的变换 (2)将摄像坐标系原点移动到世界坐标系原点 (3)绕原点旋转使两坐标系重合
M world view R T
世界坐标系到观察坐标系的变换矩阵 已知: (1)观察坐标系的原点在世界坐标系中的位置是(x0,y0) (2)观察坐标系x轴在世界坐标系中的单位向量是u (3) 观察坐标系y轴在世界坐标系中的单位向量是v
二维线裁剪
Cohen-Sutherland算法 中点分割算法 Liang-Barsky算法
Cohen-Sutherland算法 基本思想 对每条直线段p1(x1, y1)p2(x2, y2)分三种情况处理: (1)直线段完全可见,“简取”之。 (2)直线段完全不可见,“简弃”之。 (3)直线段既不满足“简取”的条件,也不满足“简弃” 的条件,需要对直线段按交点进行分段,分段后重复上 述处理。
Cohen-Sutherland算法 求交 假定直线的端点坐标为(x1, y1)和(x2, y2) (1)左、右边界交点的计算:y=y1+k(x-x1); 其中:x是窗口左边界或右边界的值 (2)上、下边界交点的计算:x=x1+(y-y1)/k。 其中:y是窗口下边界或上边界的值 特点 用编码方法实现了对完全可见和不可见直线段的快速接 受和拒绝
设备坐标系(Device Coordinates) 与图形显示设备相关的坐标系。如显示器或打印机的坐标 系。
规范化坐标系(Normal Device Coordinates ) 它是独立于具体的物理设备的一种坐标系,其坐标空间限 定在(0.0,0.0)到(1.0,1.0)的坐标范围内。
坐标系
第六章、二维观察 已知,有两个坐标系a、b。构造一个矩阵,将坐标系a蓝 色矩形框中的点(xw,yw)映射到坐标系b中蓝色矩形框中。 注意,矩阵变换使用列向量。
( xwmax , ywmax ) ( xvmax , yvmax )
( xw, yw)
( xwmin, ywmin )
( xv, yv)
( xvmin, yvmin )
(a)
(b)
第六章、二维观察
二维观察流水线 裁剪窗口 规范化和视口变换 OpenGL二维观察函数 裁剪算法 二维点裁剪 二维线裁剪 多边形填充区裁剪 曲线裁剪
坐标系 世界坐标系(World Coordinates) 用户处理自己的对象时所采用的坐标系,坐标系的大小及 尺寸由用户自己定义。
规范化和视口变换 变换方法
sx S 0 0 0 sy 0
xwmin (1 s x ) ywmin (1 s y ) 1 xvmin xwmin yvmin ywmin 1 sx T S 0 0 0 sy 0 tx ty 1
规范化和视口变换 裁剪窗口到规范化坐标系的映射 在这种映射中规范化坐标系对应裁剪窗口
裁剪窗口
视口
规范化坐标系
规范化和视口变换 变换方法
( ቤተ መጻሕፍቲ ባይዱwmax , ywmax )
( xvmax , yvmax )
(1,1)
( xw, yw)
( xv, yv)
( xwmin, ywmin )
(1, 1)
y v (x0,y0) u v
y
(xv,yv)
x
u (xu,yu) x
1 0 x0 T 0 1 y0 0 0 1
xu R xv 0
yu yv 0
0 0 1
规范化和视口变换 裁剪窗口到规范化视口的映射 在这种映射中,规范化坐标系对应显示设备。
Cohen-Sutherland算法 编码 对于任一端点(x, y),根据其坐标所在的区域,赋予一个 位的二进制码D3D2D1D0。编码规则如下图所示: (1) 若 x xwmin ,则D0=1,否则D0=0; (2) 若 x xwmax ,则D1=1,否则D1=0; (3) 若 y ywmin ,则D2=1,否则D2=0; (4) 若 y ywmax ,则D3=1,否则D3=0。
Cohen-Sutherland算法 算法步骤
(1)输入直线段的两端点坐标:p1(x1, y1)、p2(x2, y2),以及窗口的 四条边界坐标。 (2)对p1、p2进行编码:点p1的编码为code1,点p2的编码为code2。 (3)若code1|code2=0,对直线段应简取之,转(6);否则,若 code1&code2≠0,对直线段可简弃之,转(7);当上述两条均不满 足时,进行步骤(4)。 (4)确保p1在窗口外部:若p1在窗口内,则交换p1和p2的坐标值和 编码。 (5)根据p1编码从低位开始找码为1处,从而确定p1在窗口外的哪一 侧,然后求出直线段与相应窗口边界的交点,并用该交点的坐标值 替换p1的坐标值。也即在交点s处把线段一分为二,并去掉p1s这 一段。考虑到p1是窗口外的一点,因此可以去掉p1s。转(2)。 (6)用直线扫描转换算法画出当前的直线段p1p2。 (7)算法结束。
二维观察流水线 变焦距效果
整体放缩效果
漫游效果
把固定大小的裁剪窗口在一幅大图形上移动,视口不变,可以产生漫 游的效果。
二维观察流水线 二维观察变换流水线
MC
使用建模坐 标变换构造 世界坐标系 场景
WC
将世界坐标 转换为摄像 坐标
VC
DC
将规范化设备 坐标映射到设 备坐标
NC
将摄像坐标 转换为规范 化设备坐标
2 xw xw min max M window normsquare 0 0 xvmax xvmin 2 M normsquare viewport 0 0 0 2 ywmax ywmin 0 xwmax xwmin xwmax xwmin ywmax ywmin ywmax ywmin 1 xvmax xvmin 2 yvmax yvmin 2 1
(3)如另一点在窗口内,则经(2)即确定了该线段在窗口内的部分。 如另一点不在窗口内,则该点和所求出的在窗口上的那一点构成一 条线段,重复步骤(2),即可求出落在窗口内的另一点。
Liang-Barsky算法(参数方程法)
直线的参数方程 设线段的两个端点为
参数方程如下:
其中, 。,参数u取[0,1] 之间的值。当u=0时 ,当u=1 时 。如果点 处于裁剪窗 口内:
中点分割算法 算法步骤
(1)若code1|code2=0,对直线段应简取之,结束;否则,若 code1&code2≠0,对直线段可简弃之,结束;当这两条均不满足 时,进行步骤(2)。 (2)找出该直线段离窗口边界最远的点和该直线段的中点。判中点 是否在窗口内:若中点不在窗口内,则把中点和离窗口边界最远点 构成的线段丢掉,以线段上的另一点和该中点再构成线段求其中点; 如中点在窗口内,则又以中点和最远点构成线段,并求其中点,直 到中点与窗口边界的坐标值在规定的误差范围内相等,则该中点就 是该线段落在窗口内的一个端点坐标。
裁剪窗口
视口
规范化坐标系
规范化和视口变换 变换方法
( xwmax , ywmax ) ( xvmax , yvmax )
( xw, yw)
( xwmin, ywmin )
( xv, yv)
( xvmin, yvmin )
1.以点 ( xwmin, ywmin ) 为中心进行缩放变换,将裁剪窗口变换 成视口大小 2.将 ( xwmin, ywmin ) 移动到 ( xvmin, yvmin )
( xv, yv)
( xvmin, yvmin )
摄像坐标系和裁剪窗口 (a)
标准化设备坐标系 (b)
设备坐标系和视口 (c)
1.以点 ( xwmin, ywmin ) 为中心进行缩放变换,将裁剪窗口变换成 标准化正方形大小 2.将标准化正方形映射到平面指定的视口中。
