第五章 多序列比对
05多序列比对和进化树分析

common carp
zebrafish
rainbow trout teleost
Orthologs: members of a gene (protein) family in various organisms. This tree shows RBP(视黄醇结合蛋白) orthologs.
Multiple sequence alignment programs How to get multiple sequences?
Sequence format BLAST Program
Multiple sequence alignment programs
Genedoc
Clustal X Clustal W Align X MultAlin T-Coffee MAFFT
Definitions: two types of homology Orthologs Homologous sequences in different species that arose from a common ancestral gene during speciation; may or may not be responsible for a similar function.
2.采用ClustalW在线分析( AAQ84722.1 )
来的各分类单位间的相互关系。
离散特征法则主要包括 MP 法(最大简约法)和 ML 法(最大 似然法)。 距离法在构成距离矩阵(故而也称距离矩阵法)后,要么通过 某个标准来筛选出进化树的最佳估计,可以用最小二乘标准来 估计进化树,称最小二乘进化树;或者根据某种算法得到一个 聚类的树形图,不必对每个树都进行比较,计算量小,因此也 不一定是最佳的树,常见的有UPGMA法(类平均法)和NJ法 (neighbor-joining method,邻接法)。
chapter-5多重序列比对PPT课件

2 整合算法MUSCLE
算法分为三个部分,每个部分相对独立; 1. Draft progressive:
(1) 对两条序列,计算距离采用k-mer的思想; (2) 用UPGMA算法构建引导树 (3) 使用渐进算法进行多序列比对
优点:两条序列之间的距离不采用动态规 划算法进行比对,节省时间
1.在线MAP2的网址以及两种输入数据提供方式。在本例中
数据被贴入提供的窗口,数据与ClustalX2.0中相同,是23
个动物中的miR-B1io9in。formatics, 2010-2011, Semester 1, HUST
34
2.主要的参数及其缺省值。DNA block penalty(Linux版本的参
数major_diff)影响非保守区块的大小,mismatch score、gap
open penalty和gap extension penalty只影响保守区中的全局
比对。
35
Bioinformatics, 2010-2011, Semester 1, HUST
3.MAP2以两种方式返回三个结果 —— 在线窗口
23
Bioinformatics, 2010-2011, Semester 1, HUST
产生输出 的DND文 件,它是 系统的种 系树
24
Bioinformatics, 2010-2011, Semester 1, HUST
ClustalW/X:存在的问题 1. 距离最近的,有两组序列AB和CD,哪 组最先比对?两种方案:
多序列比对的意义
用于描述一组序列之间的相似性关系, 以便了解一个基因家族的基本特征,寻 找motif,保守区域等。
用于描述一个同源基因之间的亲缘关系 的远近,应用到分子进化分析中。
生物信息学中的多序列比对算法研究

生物信息学中的多序列比对算法研究一、引言生物信息学是利用计算机及统计学方法来研究生物学问题的新兴领域。
在生物大数据时代,生物信息学的发展进入了一个快速发展的阶段。
在生物序列比对中,多序列比对(Multiple sequence alignment,MSA)是一个非常重要的问题。
多序列比对的研究及其算法的不断完善,对于研究生物学问题有着重要的意义。
二、多序列比对的定义多序列比对是指在多个序列之间查找相似性并对齐的过程。
在多种生物学研究中,多个同源或各异的序列的比对是相当常见和有意义的。
三、多序列比对的应用多序列比对在生物信息学中有着重要的应用,它可以用于以下几个方面:1. 生物系统学:由于多序列比对可以获得序列进化模型,因此多序列比对是解决生物系统学问题的重要工具。
2. 同源性分析:通过分析多序列比对结果,可以推断不同物种中相似序列的同源性,即是否来自于共同的祖先。
3. 结构预测:多序列比对可以用来预测蛋白质结构。
4. 动物分类学:由于时空因素影响,不同物种中的同源序列经过不同速率的进化,因此多序列比对的结果可以用于物种分类。
四、多序列比对的挑战多序列比对过程面临各种挑战,如序列长度、序列间差异、计算时间等。
序列长度:随着序列长度的增加,多序列比对算法的计算时间和空间开销也随之增加。
因此,序列长度的增加往往会给计算带来极大的压力。
序列间差异:多序列比对要求不同序列间具有相同或相似的部分,但同时要处理序列间差异性的问题,这增加了多序列比对的复杂度。
计算时间:多序列比对是一个复杂的计算问题,需要大量的计算时间和计算资源。
因此,如何降低计算时间和计算资源的开销也是多序列比对需要解决的问题。
五、多序列比对算法1. 基于局部比对的算法:局部比对算法是一种快速的多序列比对算法,该算法从每个序列的局部匹配开始,并在此基础上扩展。
其中,CLUSTALW算法就是一种基于局部比对的算法。
2. 基于全局比对的算法:全局比对算法是一种精确的多序列比对算法。
生物信息学中的多序列比对算法与分析

生物信息学中的多序列比对算法与分析生物信息学是一门交叉学科,将计算机科学和生物学相结合,通过计算机技术和方法研究生物学问题。
生物信息学包括生物序列比对、蛋白质结构预测、基因组分析等领域。
其中,生物序列比对算法是生物信息学中的重要组成部分。
随着技术的发展和数据量的不断增长,生物序列比对变得越来越重要,多序列比对算法及分析应运而生。
1. 多序列比对算法的概念多序列比对是将多个序列进行比对和对齐,找出它们之间的相同、不同和共同进化点。
多序列比对可以为生物学家提供大量的信息,例如基因识别、蛋白质功能预测、基因家族分类等。
多序列比对算法的基础是对于序列之间相似性的度量和序列的对齐。
多序列比对算法可以分为两大类:进化驱动的方法和多序列比对的区域被动方法。
2. 进化驱动的方法进化驱动的多序列比对方法基于序列的进化关系设计,主要包括进化修复和迭代模型。
进化修复方法基于序列的生物进化关系,构建出带权多层次基因族生成模型或者MCMC,利用多个序列的生物进化关系来比对序列。
该方法能够快速准确地对齐序列,并且在宏基因组学中得到广泛应用。
生命病理学家利用这种方法,找出了人类微核症和某些动物DNA片段的进化传播过程。
迭代模型是进化驱动的方法的另一类。
该方法基于多序列比对的思想,先生成初始的序列对齐,然后迭代循环地提高序列的可比性及对齐质量。
迭代模型可以应用于大规模的数据处理和基因家族的比较分析。
3. 多序列比对的区域被动方法多序列比对的区域被动方法是不考虑序列的进化关系,根据区域的相似性来生成序列的对齐。
这种方法主要有二分策略、滑动窗口和局部多序列比对等。
二分策略将序列分成长度相等或相近的子序列,用一棵二叉树将子序列进行比对,然后将比对结果合并成最终序列对齐结果。
二分策略速度快,但是对于高变异的序列处理得不太好。
滑动窗口法则是采用滑动窗口的方式,将一个序列拆分成长度相近的几个子序列进行比对。
该方法可以处理单个序列中不同区域的变异,但是算法耗时较长。
生物信息学中的多序列比对技术

生物信息学中的多序列比对技术生物信息学是一门应用多学科知识,研究生物信息的科学,其涉及到生命科学、计算机科学、数学等多个学科。
在生物学精确分子分析中,多序列比对技术是一种重要的分析工具。
下面本文将介绍多序列比对技术在生物信息学中的应用及其技术发展。
一、多序列比对技术基础多序列比对技术可以比较多个序列间相同或不同的特征,从而评估这些序列之间的相似性及可能的进化关系。
其基本原理是对多个序列中的每个对应位点进行相互比较分析,并在不同序列之间找出潜在的相互关系。
在多序列比对中,序列数量越多、相似性越高,比对过程就越困难,因此为了提高准确性,比对程序通常都采用“多步骤”策略。
这个策略的核心思想是尽量减少可能的误差影响和减小比对算法的复杂度,达到更高的准确性和高效性。
二、多序列比对技术的主要应用1.演化关系分析演化关系分析是生物信息学中的一个重要研究领域,其中多序列比对技术是十分不可或缺的工具。
通过比对多个物种的核酸、蛋白质序列,可以推断物种之间的演化关系。
比如使用多序列比对技术可以分析多个动物物种的基因序列,从而揭示它们之间更准确深入的发育进化关系。
2.序列结构分析序列结构分析是生物信息学中另一个广泛应用的研究领域。
通过多序列比对,可以分析序列间的结构和功能差异,发掘存在于多个序列间共同存在的结构和功能模式。
例如在蛋白质序列比对中,可以找到共同的功能区域和结构折叠模式。
3.疾病研究多序列比对技术在疾病研究领域也有广泛的应用。
病理相似性、病因的分子机制等都可以通过比对不同个体的序列得到。
例如,通过匹配患有同种疾病的患者之间的DNA序列,可以确定患者之间是否具有共同遗传因素。
可以显而易见的认为,多序列比对的应用领域十分广泛,相关的研究对于不同领域的生物学研究都有着重要的意义和作用。
三、多序列比对技术的技术发展随着科技的进步和计算机计算速度的提升,多序列比对技术的发展也呈现出不同的阶段。
1.初期阶段早期的多序列比对技术主要依靠人工干预,通过手工调整每一个测试序列,逐一比对得到更准确的结果。
生物信息学中的多序列比对方法

生物信息学中的多序列比对方法生物信息学是一门研究生命科学数据的计算机科学学科,主要用于从大量基因组、蛋白质组、代谢组等生命组学数据中发现、分析和研究基因、蛋白质、代谢途径等生命过程的规律。
其中的多序列比对(Multiple Sequence Alignment,MSA)技术是一个比较重要的研究方法,其主要应用于多种生物信息学研究方向,如物种分类、基因结构和功能研究、蛋白质结构和功能研究等。
本文就生物信息学中的多序列比对方法进行简要介绍。
一、多序列比对的意义及难点多序列比对是将多条生物序列进行比对,在把它们对齐之后确定它们之间的共同位点及其差异位点的过程,从而分析出序列间的相似性和异质性等结构、功能上的关联。
这一过程主要分为四步:选择序列、生成比对矩阵、进行比对分析和生成比对结果。
通过多序列比对可以揭示序列进化、注释微小RNA、寻找共同结构域、定位功能残基等关键性生物学问题。
多序列比对的难点主要包括以下几个方面:(1)大数据量。
由于生物序列的数据量是非常庞大的,比如对于人和马之间的比对,需要对他们的约3000万个碱基进行比对,而且每个人的基因组或每个生物的蛋白质组都是高度复杂和大量重复的,因此进行多序列比对的计算复杂度非常大,需要使用高效的计算方法,充分利用计算资源。
(2)序列多样性。
生物序列相互之间具有高度的多样性,包括同一物种内的不同个体、不同物种之间的比对和不同基因家族的比对等,这些差异给多序列比对带来很大的挑战,需要使用不同的比对算法、策略和参数,才能得到最优的结果。
(3)精度和可信度。
生物序列不同的比对方法可能会得到不同的结果,因此必须对比和评估多种方法的参数和性能指标,同时要考虑到数据的来源、质量和格式等,以提高比对结果的精度和可信度。
(4)效率和实时性。
多序列比对通常是大数据、高计算量的任务,因此需要使用高性能计算环境或分布式计算架构,同时要考虑到任务的时间复杂度、并行度和负载均衡等问题,从而提高比对效率和实时性。
生物信息学 第五章 多序列比对

多序列比对有时用来区分一组序列之间的差异,但其主要用于描述一组序列之间的相 似性关系,以便对一个基因家族的特征有一个简明扼要的了解。与双序列比对一样,多序列 比对的方法建立在某个数学或生物学模型之上。因此,正如我们不能对双序列比对的结果得 出“正确或错误”的简单结论一样,多序列比对的结果也没有绝对正确和绝对错误之分,而 只能认为所使用的模型在多大程度上反映了序列之间的相似性关系以及它们的生物学特征。 显然,多序列比对需要使用许多专门的分析工具。除了一些已经广泛使用并仍在不但 改进的多序列计算机程序外,还需要有一个开发方便实用的多序列比对手工编辑工具。 可以从多个不同角度出发构建多序列比对模型。这里,主要指建立比对模型的生物学 基础,而不仅是具体的比对方法,如自动比对或手动比对等。目前,构建多序列比对模型的 方法大体可以分为两大类。第一类是基于氨基酸残基的相似性,如物化性质、残基之间的可 突变性等。另一类方法则主要利用蛋白质分子的二级结构和三级结构信息,也就是说根据序 列的高级结构特征确定比对结果。显然,这两种方法所得结果可能有很大差别。一般说来, 很难断定哪种方法所得结果一定正确,应该说,它们从不同角度反映蛋白质序列中所包含的 生物学信息。 基于序列信息和基于结构信息的比对都是非常重要的比对模型,但它们都有不可避免 的局限性,因为这两种方法都不能完全反映蛋白质分子所携带的全部信息。我们知道,蛋白 质序列是经过 DNA 序列转录翻译得到的。从信息论的角度看,它应该与 DNA 分子所携带 的信息更为“接近”。而蛋白质结构除了序列本身带来的信息外,还包括经过翻译后加工修 饰所增加的结构信息,包括残基的修饰,分子间的相互作用等,最终形成稳定的天然蛋白质 结构。因此,这也是对完全基于序列数据比对方法批评的主要原因。显然,如果能够利用结 构数据,对于序列比对无疑有很大帮助。不幸的是,与大量的序列数据相比,实验测得的蛋 白质三维结构数据实在少得可怜。在大多数情况下,并没有结构数据可以利用,我们只能依 靠序列的相似性和一些生物化学特性建立一个比较满意的多序列比对模型。
多序列比对方法

多序列比对方法多序列比对是生物信息学中一个常见的分析方法,用于比较多个序列之间的相似性和差异性。
本文将介绍多序列比对的基本原理、常用方法和软件工具,以及其在生物学研究中的应用。
一、多序列比对的基本原理多序列比对是指对多个生物序列进行比较和分析。
生物序列可以是蛋白质序列、DNA序列或RNA序列等。
多序列比对的主要目的是确定序列之间的保守区域和变异区域,并发现序列之间的结构和功能相关性。
多序列比对的基本原理是通过构建序列之间的相似性矩阵,确定最佳的比对结果。
相似性矩阵用于测量两个序列之间的相似性,通常使用BLOSUM、PAM或Dayhoff矩阵等。
基于相似性矩阵和动态规划算法,可以计算序列之间的最佳比对路径,以及比对的得分。
二、常用的多序列比对方法1. 基于全局比对的方法:该方法适用于序列之间的整体相似性比较,常用的算法有Needleman-Wunsch算法和Smith-Waterman算法。
这两种算法都采用动态规划策略,通过计算各种可能的比对路径来确定最佳比对结果。
全局比对方法的主要缺点是在序列相似性较低的情况下,比对结果可能不准确。
2. 基于局部比对的方法:该方法适用于序列之间的部分相似性比较,常用的算法有BLAST和FASTA。
局部比对方法主要通过搜索局部相似片段来进行比对,可以提高比对的敏感性和准确性。
BLAST和FASTA是两种常用的快速局部比对工具,可以快速比对大规模序列数据库。
3. 基于多重比对的方法:该方法适用于多个序列之间的比较和分析,常用的算法有ClustalW和MAFFT。
多重比对方法通过构建多个序列的比对结果,可以识别序列之间的共同保守区域和变异区域,以及序列的结构和功能相关性。
ClustalW和MAFFT是两种常用的多重比对工具,具有较高的准确性和可靠性。
三、常用的多序列比对软件工具1. ClustalW:ClustalW是一个常用的多重比对软件,主要用于比对蛋白质和DNA序列。
多序列比对 简书

多序列比对1. 引言多序列比对是生物信息学中的一个重要问题,它可以用于比较多个生物序列之间的相似性和差异性。
通过多序列比对,我们可以揭示序列之间的共同特征、功能和进化关系,从而深入理解生物学中的重要问题。
本文将介绍多序列比对的基本概念、常用方法和应用领域,并对其进行详细的解析和讨论。
2. 多序列比对的概念和意义多序列比对是将多个生物序列(如DNA、RNA或蛋白质序列)进行对齐,找到它们之间的相似性和差异性。
相似性指的是序列之间的保守区域,而差异性则指的是序列之间的变异区域。
多序列比对的意义在于:•揭示序列的功能和结构:通过比对多个序列,我们可以找到它们之间的共同特征和保守区域,从而推断出序列的功能和结构。
•研究进化关系:多序列比对可以揭示序列之间的进化关系,帮助我们理解物种的演化历史和亲缘关系。
•寻找突变位点:多序列比对可以帮助我们找到序列之间的差异性,从而揭示突变位点和突变类型。
•设计引物和探针:多序列比对可以用于设计引物和探针,用于检测特定序列的存在和变异。
3. 多序列比对的方法多序列比对有多种方法,常见的包括:•基于序列相似性的方法:这种方法通过比对序列之间的相似性来进行对齐。
常见的算法包括Smith-Waterman算法和Needleman-Wunsch算法。
•基于基因组比对的方法:这种方法通过比对整个基因组的序列来进行对齐。
常见的算法包括BLAST和BLAT。
•基于结构比对的方法:这种方法通过比对序列的二级结构来进行对齐。
常见的算法包括RNA二级结构比对和蛋白质结构比对。
•基于进化模型的方法:这种方法利用进化模型来推断序列的对齐关系。
常见的算法包括MUSCLE和ClustalW。
每种方法都有其优缺点,选择合适的方法取决于具体的研究目的和数据特点。
4. 多序列比对的应用领域多序列比对在生物信息学和生物学研究中有广泛的应用,包括:•基因组比较:多序列比对可以用于比较不同物种的基因组,揭示基因组之间的相似性和差异性,从而推断物种的进化关系和基因家族的演化历史。
多序列比对结果

多序列比对结果多序列比对是生物信息学中的一项重要任务,其目的是找出多个生物序列之间的相似性和差异性。
多序列比对结果包含了许多有用的信息,可以帮助我们更好地理解生物学现象和进化规律。
本文将详细介绍多序列比对结果的相关内容。
一、多序列比对的基本概念1.1 多序列比对的定义多序列比对是指将三个或三个以上的生物序列进行比较,找出它们之间的相同和不同之处,并将它们分别放置在同一条直线上,以便于进行分析和研究。
1.2 多序列比对的意义多序列比对可以帮助我们更好地理解不同种类生物之间的进化关系、基因功能以及蛋白质结构与功能等方面。
同时,它也是进行系统发育分析、遗传变异研究以及药物设计等领域中必不可少的工具。
二、多序列比对结果中常见术语解释2.1 序列标识符(Sequence identifier)指每个输入序列所属生物体或基因名称等信息,通常用于区分不同来源的数据。
2.2 序列长度(Sequence length)指每个输入序列的长度,通常以碱基或氨基酸数量为单位。
2.3 序列相似度(Sequence similarity)指两个或多个序列之间的相同比例,通常用百分比表示。
2.4 序列同源性(Sequence homology)指两个或多个序列之间的共同祖先,通常用BLAST等工具进行判定。
2.5 序列保守性(Sequence conservation)指在比对结果中多个序列中某一位点上具有相同碱基或氨基酸的频率,可以反映出该位点在进化过程中的重要性。
三、多序列比对结果展示方式3.1 线性展示方式线性展示方式是将所有输入序列按照从左到右的顺序排成一条直线,并在每个位置上标注相应的碱基或氨基酸。
这种展示方式简单明了,易于理解和分析。
但是当输入序列较多时,会导致图形混乱不清晰。
3.2 矩阵展示方式矩阵展示方式将所有输入序列以矩阵形式呈现,并通过颜色等方式标注相应位点上的差异和保守性。
这种展示方式可以更清晰地显示不同位置上的差异和保守性,但是当输入序列较长时,会导致图形过于庞大和复杂。
多序列比对名词解释

多序列比对名词解释多序列比对(sequence-to-sequence matching)是指在一组图像中选择少数代表性的图像序列进行相应的代数处理,使用这些被选出来的图像序列来改善另一些样本。
它与主成分分析方法类似,不同之处是它把图像看成由许多图像块组成的,每个块都包含着所研究目标特征的信息,因此,它更加注重局部细节信息。
在研究目标周围,我们常常发现有一些特殊的值域,这些值域可以很好地反映该目标的一些属性,因此我们就可以通过统计这些区域的特征点来识别某个特定目标。
例如:某次考试总共有20题, 10题为选择题, 10题为填空题,且只有2题为单项选择题。
有5道题得分较低,因此采用统计这些区域特征点的分布来鉴别学生的正确答案,效果较好。
相关多序列比对方法有同一个数据的谱形态空间内的多样性分析和从几何学角度建立样本的子集合关系等。
在考试复习阶段,把所给的问题作为训练集合,并按照教学大纲要求给每个题目设置权值,并训练不同的特征,其他的题目或者删除,或者进行合并。
1、将试卷中每一道题的答案提取出来,写在黑板上;2、将答案分类,再将各题的答案写在白纸上;3、再按照上述步骤,从训练集中随机抽取10份,分别将其他的80份试卷当做对照组; 4、将原始答案放到正确答案集中,重新计算各个特征点在答案中的权值。
基于空间变换方法的多序列比对(geographical-invariant pattern-basedsubset-to-subset matching)又称为图像中的空间域分析法。
它在已知图像的光谱信息后,直接利用原始图像的邻域特征,计算某些空间特征点,并与光谱特征进行比较,进而确定其目标的位置。
因此,在数字图像的研究中,我们把这种方法称为空间域的方法,而图像的光谱特征则称为频率域的方法。
这种方法的优点是:基本不需要光谱的专门知识,而且处理的结果精确可靠。
在图像的多序列比对过程中,图像分割是非常重要的一个环节。
多序列比对 简书

多序列比对简书
摘要:
1.多序列比对的概念
2.多序列比对的方法
3.多序列比对的应用
4.简书的介绍
5.简书中的多序列比对应用案例
正文:
一、多序列比对的概念
多序列比对是一种生物信息学技术,用于比较两个或多个生物序列之间的相似性。
这种技术广泛应用于基因组学、蛋白质组学等领域,以研究基因和蛋白质的演化关系。
二、多序列比对的方法
多序列比对的方法主要包括以下几种:
1.基于最长公共子序列(LCS)的比对方法:通过寻找输入序列中最长的公共子序列来计算相似性。
2.基于动态规划的比对方法:通过动态规划算法来计算输入序列之间的相似性。
3.基于概率模型的比对方法:通过建立概率模型来计算输入序列之间的相似性。
三、多序列比对的应用
多序列比对在生物信息学领域具有广泛的应用,主要包括:
1.基因组学:通过比较不同物种或不同个体的基因组序列,研究基因演化关系。
2.蛋白质组学:通过比较不同物种或不同个体的蛋白质序列,研究蛋白质演化关系。
3.基因预测:通过比较已知基因序列和新发现的序列,预测新序列中可能存在的基因。
四、简书的介绍
简书是一个知识分享社区,用户可以在该平台上分享自己的知识、经验和见解。
简书旨在帮助用户更好地学习和成长,同时也为知识传播提供了一个便捷的平台。
五、简书中的多序列比对应用案例
在简书上,有篇文章详细介绍了多序列比对的概念、方法和应用。
作者通过实例阐述了多序列比对在基因组学和蛋白质组学研究中的重要作用,为广大读者提供了一个学习多序列比对的良好资源。
多序列比对 简书

多序列比对介绍多序列比对是一种在生物信息学领域中常用的方法,用于比较多个生物序列之间的相似性和差异性。
通过多序列比对,可以揭示生物序列的结构和功能信息,帮助科学家理解生物进化、基因功能和蛋白质结构等重要问题。
本文将详细介绍多序列比对的原理、方法和应用。
原理多序列比对的基本原理是将多个生物序列进行对齐,找出它们之间的共同模式和差异。
通过比较序列之间的相似性和差异性,可以推断它们的进化关系、功能和结构等信息。
方法多序列比对的方法主要分为两类:全局比对和局部比对。
全局比对是将整个序列进行对齐,适用于序列相似性较高的情况。
常用的全局比对算法包括Needleman-Wunsch算法和Smith-Waterman算法。
局部比对是将序列的一部分进行对齐,适用于序列相似性较低的情况。
常用的局部比对算法包括BLAST和FASTA。
应用多序列比对在生物信息学中有广泛的应用。
以下是一些常见的应用场景:进化分析通过比较不同物种的基因序列,可以推断它们的进化关系和演化过程。
多序列比对可以帮助科学家重建物种的进化树,揭示物种之间的亲缘关系。
基因功能预测通过比较不同基因的序列,可以推断它们的功能和作用机制。
多序列比对可以帮助科学家鉴定基因家族、识别保守区域和预测功能位点。
蛋白质结构预测通过比较不同蛋白质的序列,可以推断它们的结构和功能。
多序列比对可以帮助科学家预测蛋白质的二级结构、三级结构和功能域。
疾病研究通过比较病毒或细菌的基因序列,可以揭示它们的变异和毒力机制。
多序列比对可以帮助科学家研究疾病的起源、传播和治疗。
常用工具多序列比对的计算复杂度较高,因此需要使用专门的软件和工具。
以下是一些常用的多序列比对工具:1.ClustalW:一种经典的多序列比对工具,支持全局比对和局部比对。
2.MAFFT:一种快速而准确的多序列比对工具,适用于大规模序列比对。
3.MUSCLE:一种高效的多序列比对工具,适用于大规模序列比对和高质量比对结果。
多序列比对 简书

多序列比对简书摘要:一、多序列比对简介1.多序列比对的概念2.多序列比对的作用3.多序列比对的应用领域二、多序列比对方法1.传统的多序列比对方法2.基于进化树的多序列比对方法3.基于统计模型的多序列比对方法三、多序列比对软件1.Clustal Omega2.MUSCLE3.MAFFT4.ProbCons四、多序列比对的结果分析1.一致性序列的确定2.进化树构建3.功能域分析五、多序列比对在生物学研究中的应用1.基因进化分析2.蛋白质结构预测3.基因组注释正文:多序列比对(Multiple Sequence Alignment, MSA)是一种将多个氨基酸或核苷酸序列在同一坐标系中进行比较的方法,通过比较不同序列之间的相似性和差异性,探讨它们的进化关系和生物学功能。
多序列比对在分子进化、蛋白质结构预测、基因组注释等领域有着广泛的应用。
多序列比对方法主要分为传统的多序列比对方法和基于统计模型的多序列比对方法。
传统的多序列比对方法通常采用基于距离的方法,例如最长公共子序列(Longest Common Subsequence, LCS)方法和动态规划方法(例如Needleman-Wunsch 算法和Smith-Waterman 算法)等。
基于统计模型的多序列比对方法则通过建立序列间的统计模型来进行比对,例如利用核苷酸或氨基酸的组成、序列长度分布、局部序列比对等特征来建模。
多序列比对软件有很多,其中比较常用的有Clustal Omega、MUSCLE、MAFFT 和ProbCons 等。
这些软件在算法原理和实现上有所不同,但都能有效地完成多序列比对任务。
Clustal Omega 是一个基于迭代算法和优化聚类的软件,适用于大规模的多序列比对;MUSCLE 是一个采用简化分子进化模型和逐步比对策略的软件,适用于中等规模的多序列比对;MAFFT 是一个基于增量比对和优化搜索策略的软件,适用于小规模的多序列比对;ProbCons 是一个基于概率模型和蒙特卡洛搜索策略的软件,适用于高质量的多序列比对。
多序列比对 简书

多序列比对简书摘要:1.多序列比对的概念和意义2.多序列比对的方法3.多序列比对的应用实例4.多序列比对的未来发展趋势正文:一、多序列比对的概念和意义多序列比对是一种生物信息学技术,用于比较两个或多个生物序列之间的相似性。
在生物学研究中,多序列比对有着重要的应用价值,它可以帮助研究者了解生物序列之间的进化关系、功能和结构特征。
多序列比对可以为基因组学、蛋白质组学、代谢组学等领域的研究提供有力支持。
二、多序列比对的方法多序列比对的方法主要分为两类:基于距离的比对方法和基于相似性的比对方法。
1.基于距离的比对方法:这类方法通过计算序列之间的距离来衡量它们的相似性。
常见的距离计算方法有欧氏距离、曼哈顿距离、皮尔逊距离等。
2.基于相似性的比对方法:这类方法通过比较序列之间的相似性来衡量它们的相似性。
常见的相似性计算方法有PAM 矩阵、BLOSUM 矩阵等。
三、多序列比对的应用实例多序列比对在生物信息学领域有着广泛的应用,以下是一些典型的应用实例:1.基因组学:通过多序列比对,可以研究基因组之间的差异和进化关系,揭示物种间的亲缘关系。
2.蛋白质组学:通过多序列比对,可以研究蛋白质序列之间的相似性和功能保守性,为蛋白质功能预测和药物设计提供依据。
3.代谢组学:通过多序列比对,可以研究代谢物之间的相似性和生物活性,为代谢性疾病的诊断和治疗提供依据。
四、多序列比对的未来发展趋势随着生物信息学技术的不断发展,多序列比对在未来将呈现出以下发展趋势:1.算法的优化和提高:随着计算能力的提升,未来的多序列比对方法将更加高效、准确。
2.跨学科的应用:多序列比对技术将在生物学、医学、药物学等多个领域发挥更大的作用。
第五章 多序列比对

p78的所有得对于所得到的多重序列比对我们往往需要进行归纳分析总结这些序列的特征或者给出这些序列共性的表示hlvvgvlvggnlvvlhclvvhcl1保守序列表示序列每个位置上最可能出现的字符或者所有可能出现的字符atntscp表示在的每一列上各种字符出现的概率分布a代表字母表pjk代表字母表a中第k个字符在第列出现的概率
六、统计特征分析
• 对于所得到的多重序列比对,我们往往需要进行归纳分析, 总结这些序列的特征,或者给出这些序列共性的表示
—H—LVV G—VLVG GN—LVV LHCLVVHCL--
(1)保守序列 表示序列每个位置上最可能出现的字符(或者所有可能出 现的字符) ATNTSC (N - A,T,C,G ; S - G,C)
前趋节点的个数等于2k - 1
假设以k维数组A存放超晶格,则计算过程如下: a[ 0, 0, … ,0 ] = 0
a[ i ] = max {a[ i - b ] + SP-score(Column(s, i, b))}
Colum n ( s , i , b ) (c j ) j k s j [i j ] cj
6
-5 -16 -27 -38
-16
-27
多序列比对:最优算法
多项式时间复杂度:≤O(n3) 三条序列:时间复杂度:O(lmn) = O(n3)
第五章 序列比对(mine new)
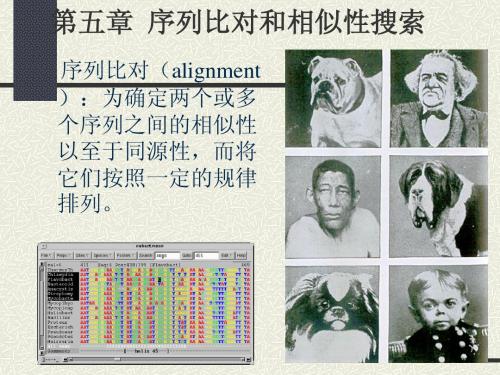
51 LFLQDNIVAEFSVDETGQMSATAKGRVR.LLNNWD..VCADMVGTFTDTE 97 RBP : | | | | :: | .| . || |: || |. 45 ISLLDAQSAPLRV.YVEELKPTPEGDLEILLQKWENGECAQKKIIAEKTK 93 lactoglobulin
D Asp
10 0 36 9859 0 5 56 11 3 1
C Cys
3 1 0 0 9973 0 0 1 1 2
Q Gln
8 10 4 6 0 9876 35 3 20 1
E Glu
17 0 6 53 0 27 9865 7 1 2
G Gly
21 0 6 6 0 1 4 9935 0 0
H His
遵循的规则为,每个单元格的值加上该单元格的对角右下格及 其下边列、右边行单元格的最大值
After you’ve filled in the matrix, find the optimal path(s) by a “traceback” procedure Page 66
sequence 1 ABCNJ-RQCLCR-PM sequence 2 AJC-JNR-CKCRBP-
1)、简单分组
将20种氨基酸分为6组: 第一组 C 第二组 S、T、P、A、G 第三组 N、D、E、Q(酸性) 第四组 H、R、K(碱性) 第五组 M、I、L、V (脂肪族) 第六组 F、Y、W (芳香族)
同一组的残基一律等量齐观,这样把20种符号简化为6种, 往往在不需要精确分析时能获得理想的结果。
2)、PAM打分矩阵
Dayhoff等在20世纪70年代后期引入了PAM(Accepted Point Mutation,可接受点突变)概念:在蛋白质中被 自然选择接受的单个氨基酸替换,取一个蛋白质序列中 的氨基酸变异1%作为演化距离的单位,称为1个PAM 。Dayhoff等用手工比较了当时数目有限的同源蛋白质 序列,取实际观察所得的代换频率与随机背景序列的相 应频率比值的对数,用统计方法得到对应1PAM的数据 ,再外推到250 PAM。实际计算中针对不同的演化距离 ,使用从PAMl00到PAM500不等的打分矩阵。亲缘关 系近者用PAMl00到PAMl50,亲缘关系远者用更高号 的矩阵,相当于容许更高的噪声背景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
前趋节点的个数等于2k - 1
假设以k维数组A存放超晶格,则计算过程如下: a[ 0, 0, … ,0 ] = 0
a[ i ] = max {a[ i - b ] + SP-score(Column(s, i, b))}
Colum n ( s , i , b ) (c j ) j k s j [i j ] cj
(2)特征统计图(Profile) 令P=(P1,P2,…,PL),P表示在的每一列上 各种字符出现的概率分布
Pj=(pj0,pj1,…,pj|A|)
A代表字母表,Pjk代表字母表A中第k个字符在第 j 列出现的概率。 第0个字符是特殊的空位符号“-”。
ATTAT AACTT CTTAT ACTTT AGAAT
if bj = 1 if bj = 0
(3-37) (3-38)
问题:
计算量巨大
时间复杂度为O(2ki=1,...,k si) ↓ O(2kNk)
图3.17 三维晶格节点计算依赖关系
2、 优化计算方法
标准动态规划算法存在的问题: 搜索空间大 剪枝技术:将搜索空间限定在一个较小的区域 范围内。 若问题是搜索一条得分最高(或代价最小)的 路径,则在搜索时如果当前路径的得分低于某 个下限(或累积代价已经超过某个上限),则 对当前路径进行剪枝,即不再搜索当前路径的 后续空间。
六、统计特征分析
• 对于所得到的多重序列比对,我们往往需要进行归纳分析, 总结这些序列的特征,或者给出这些序列共性的表示
—H—LVV G—VLVG GN—LVV LHCLVVHCL--
(1)保守序列 表示序列每个位置上最可能出现的字符(或者所有可能出 现的字符) ATNTSC (N - A,T,C,G ; S - G,C)
两两比对 多重比对
(sc, s1) (sc, s2) … (sc, sk)
sc
s1 s2 … sk
如何选择核心序列?
– 尝试将每一个序列分别作为核心序列,进行星形 多重序列比对,取比对结果最好的一个。 – 另一种方法是计算所有的两两比对,取下式值最 大的一个:
sim( si, sc )
例如,有5个序列: s1 = ATTGCCATT s2 = ATGGCCATT s3 = ATCCAATTTT s4 = ATCTTCTT
A T C G (碱基)
1 0.8 0.0 0.2 0.0
2 0.2 0.4 0.2 0.2
3 0.2 0.6 0.2 0.0
4 0.6 0.4 0.0 0.0
5 (位置) 0.0 1.0 0.0 0.0
• 利用保守序列或者特征统计图可以判断一个序列 是否满足一定的特征 一条序列与特征统计图相对照,如果代价值小, 说明该序列具有相应的特征,否则该序列不具备 相应的特征。 • 利用特征统计矩阵搜索数据库时,可以考察家族 的成员关系。
— 用一个k维数组来表示该显式函数(类似于打分矩阵)
期望: 函数在形式上应该简单 具有统一的形式 不随序列的个数而发生形式变化
逐对加和SP(sum-of-pairs)函数
SP score(c1 , c2 ,...,ck ) p(ci , c j )
i 1 j i 1
k 1
k
第四章 多序列比对
多序列比对
Made by GENEDOC
一、多序列比对:简介
• 1. 不同物种中,许多基因的功能保守,序列 相似性较高,通过多条序列的比较,发现保守 与变异的部分; • 2. 可构建统计学模型(如HMM) ,搜索更多 的同源序列; • 3. 构建进化树的必须步骤; • 4. 比较基因组学研究;
l: 双序列比对
Gap Gap V 0 -11
4
V -11 4
2
D -22 -7
S -33 -18
C -44 -29 -1 9 8 -3
Y -55 -40 -12 -3 7 15
时间复杂度:O(n2)
-5
10 -1 -12 -23
E
S L C Y
-22
-33 -44 -55 -66
-7
-18 -29 -40 -51
二、多序列比对的方法
• 手工比对方法(包括对结果进行修饰) • 同步法 • 步进法 动态规划算法 优化计算方法 • 星形比对 • 其它多序列比对算法
二、步进法
• 动态规划算法 • 优化计算方法
1、多重比对的动态规划算法
多重序列比对的最终目标是通过处理得 到一个得分最高(或代价最小)的序列 对比排列,从而分析各序列之间的相似 性和差异。
6
-5 -16 -27 -38
-16
-27
多序列比对:最优算法
多项式时间复杂度:≤O(n3) 三条序列:时间复杂度:O(lmn) = O(n3)
四条序列:时间复杂度:O(n4),非多项式时间! … m条序列:时间复杂度:O(nm),指数时间!
动态规划算法:全空间
/CBBresearch/Schaffer/msa.html
其中,c1,c2,…,ck是一列中的k个字符,p是关于一对字符相似性的打分函数。
L L A P SP score 26 G S G
逐对计算p(1,2),p (1,3),..., p(1,8),p (2,3),p(2,4),..., p (2,8),...,p (7,8) 的所有得 分 -6-6-5-4-2-2-1 = -26
(3-44)
多序列比对的方法
• 手工比对方法(包括对结果进行修饰) • 同步法 • 步进法 动态规划算法 优化计算方法 • 星形比对 • 其它多序列比对算法
五、MSA: 多序列比对的打分和评价
1、SP(Sum-of-Pairs)模型
评价多重序列比对的结果
按照每个对比的列进行打分,然后加和 处理每一列: — k个变量的打分函数
动态规划算法:优化算法
Sequence B
搜索有限空 间,类似于 BLAST算法
/CBBresearch/Schaffer/msa.html
多序列比对的方法
• 手工比对方法(包括对结果进行修饰) • 同步法 • 步进法 动态规划算法 优化计算方法 • 星形比对 • 其它多序列比对算法
• 星形比对是一种近似的方法,可以证明,用该方法 所得到多重序列比对的代价不会大于最优多重序列 比对代价的两倍
引理3.1: 对于所有的1≤i,j≤k,,ij, 有 dc(si, sj) ≤ D(si, sc) + D(sc, sj) (3-43)
定理3.2
V ( c ) 2(k 1) 2 V ( ) k
星形比对
• 星形比对的基本思想是:在给定的若干序列中, 选择一个核心序列,通过该序列与其它序列的 两两比对形成所有序列的多重比对,从而使 得在核心序列和任何一个其它序列方向的投 影是最优的两两比对。 • 利用标准的动态规划方法求出所有si和sc的最 优两两比对 –时间为O(kn2) –将这些两两比对聚集起来 –并采用“只要是空白, 则永远是空白”的原则。
s5 = ACTGACC
sc=s1
ATTGCCATT ATGGCCATT ATTGCCATT-ATC-CAATTTT ATTGCCATT ATCTTC-TT ATTGCCATT ACTGACC--
ATTGCCATT-ATGGCCATT-ATC-CAATTTT ATCTTC-TT-ACTGACC----
