《数字逻辑》 白中英 第六版 习题解答
数字逻辑课后题答案

习题一1.1 把下列不同进制数写成按权xx:⑴ (4517.239)10=4×103+5×102+1×101+7×100+2×10-1+3×10-2+9×10-3⑵(10110.0101)2=1×24+0×23+1×22+1×21+0×20+0×2-1+1×2-2+0×2-3+1×2-4⑶ (325.744)8=3×82+2×81+5×80+7×8-1+4×8-2+4×8-3⑷ (785.4AF)16=7×162+8×161+5×160+4×16-1+A×16-2+F×16-31.2 完成下列二进制表达式的运算:1.3 将下列二进制数转换成十进制数、八进制数和十六进制数:⑴ (1110101)2=(165)8=(75)16=7×16+5=(117)10⑵(0.110101)2=(0.65)8=(0.D4)16=13×16-1+4×16-2=(0.828125)10⑶ (10111.01)2=(27.2)8=(17.4)16=1×16+7+4×16-1=(23.25)101.4 将下列十进制数转换成二进制数、八进制数和十六进制数,精确到小数点后5位:⑴ (29)10=(1D)16=(11101)2=(35)8⑵ (0.207)10=(0.34FDF)16=(0.001101)2=(0.15176)8⑶ (33.333)10=(21.553F7)16=(100001.010101)2=(41.25237)81.5 如何判断一个二进制正整数B=b6b5b4b3b2b1b0能否被(4)10整除?解: 一个二进制正整数被(2)10除时,小数点向左移动一位, 被(4)10除时,小数点向左移动两位,能被整除时,应无余数,故当b1=0和b0=0时, 二进制正整数B=b6b5b4b3b2b1b0能否被(4)10整除.1.6 写出下列各数的原码、反码和补码:⑴ 0.1011[0.1011]原=0.1011; [0.1011]反=0.1011; [0.1011]补=0.1011⑵ 0.0000[0.000]原=0.0000; [0.0000]反=0.0000; [0.0000]补=0.0000⑶ -10110[-10110]原=110110; [-10110]反=101001; [-10110]补=1010101.7 已知[N]补=1.0110,求[N]原,[N]反和N.解:由[N]补=1.0110得: [N]反=[N]补-1=1.0101, [N]原=1.1010,N=-0.10101.8 用原码、反码和补码完成如下运算:⑴ 0000101-0011010[0000101-0011010]原=10010101;∴0000101-0011010=-0010101。
数字逻辑第六版习题答案2
W= AB+ACD X = BC+BD+BCD Y = CD+CD Z=D
A 0 0 0 0 0 1 1 1 1 1
B 0 1 1 1 1 0 0 0 0 1
C 1 0 0 1 1 0 0 1 1 0
D 1 0 1 0 1 0 1 0 1 0
W 0 0 0 0 0 0 0 0 1 1
X 0 0 0 0 1 1 1 1 0 0
Y 0 0 1 1 0 0 1 1 0 0
Z 0 1 0 1 0 1 0 1 0 1
这是一个余三码 至 8421 BCD 码转换的电路
7. 下图是一个受 M 控制的 4 位二进制码和格雷码的相互转换电路。M=1 时,完 成自然二进制码至格雷码转换;M=0 时,完成相反转换。请说明之
解:Y3=X3
Y2 X2 X3
F=F1F2 F1 F1 F1 F1
S3 S2 S1 S0 × × × × × × × × 0 0 1 1 0 1 0 1
F=F1F2 A AB AB 0
3. 分析下图所示逻辑电路,列出真值表,说明其逻辑功能。
解: F1= AB C 真值表如下:
ABC A BC B C = A B C A BC ABC
Y2 0 0 0 1 0 1 1 1
Y3 1 0 0 0 0 0 0 0
Y1 A B C Y 2 BC A( B C )
于是得: Y 3 A B C A B C
10. 用两片双四选一数据选择器和与非门实现循环码至 8421BCD 码转换。
解:(1)函数真值表、卡诺图如下;
十进制数 0 1 2 3 4 5 6 7 8 9 8421码 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 余三码 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100
数字逻辑课本习题答案
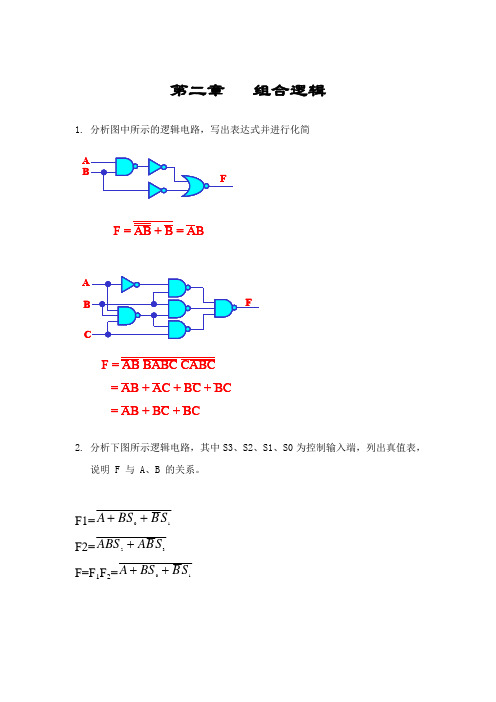
习 题 五1. 简述时序逻辑电路与组合逻辑电路的主要区别。
解答组合逻辑电路:若逻辑电路在任何时刻产生的稳定输出值仅仅取决于该时刻各输入值的组合,而与过去的输入值无关,则称为组合逻辑电路。
组合电路具有如下特征:②信号是单向传输的,不存在任何反馈回路。
时序逻辑电路:若逻辑电路在任何时刻产生的稳定输出信号不仅与电路该时刻的输入信号有关,还与电路过去的输入信号有关,则称为时序逻辑电路。
时序逻辑○1○2 电路中包含反馈回路,通过反馈使电路功能与“时序”○3 电路的输出由电路当时的输入和状态(过去的输入)共同决定。
2. 作出与表1所示状态表对应的状态图。
表 1解答根据表1所示状态表可作出对应的状态图如图1所示。
图13.已知状态图如图2所示,输入序列为x=11010010,设初始状态为A,求状态和输出响应序列。
图 2解答状态响应序列:A A B C B B C B输出响应序列:0 0 0 0 1 0 0 14. 分析图3所示逻辑电路。
假定电路初始状态为“00”,说明该电路逻辑功能。
图 3 解答○1根据电路图可写出输出函数和激励函数表达式为 xK x,J ,x K ,xy J y xy Z 1111212=====○2 根据输出函数、激励函数表达式和JK 触发器功能表可作出状态表如表2所示,状态图如图4所示。
表2图4○3由状态图可知,该电路为“111…”序列检测器。
5. 分析图5所示同步时序逻辑电路,说明该电路功能。
图5解答○1根据电路图可写出输出函数和激励函数表达式为 )(D ,x y x D y y x Z 21112121212y x y y y y y x ⊕=+=+=○2 根据输出函数、激励函数表达式和D 触发器功能表可作出状态表如表3所示,状态图如图6所示。
表3图6○3由状态图可知,该电路是一个三进制可逆计数器(又称模3可逆计数器),当x=0时实现加1计数,当x=1时实现减1计数。
6.分析图7所示逻辑电路,说明该电路功能。
《数字逻辑》(白中英)(第六版)习题解答教学提纲

《数字逻辑》(白中英)(第六版)习题解答《数字逻辑》(白中英)(第六版)习题解答第1章开关理论基础1、将下列十进制数化为二进制数和八进制数:十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.011111100 7.37479.43 1001111.0110110 117.332、将下列二进制数转换成十进制数和八进制数:二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153、将下列十进制数转换成8421BCD码:1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014、一个电路有三个输入端A 、B 、C ,当其中有两个输入端为高电平时,输出X 为高电平,试列出真值表,并写出X 的逻辑表达式。
[解]: 先列出真值表,然后写出X 的逻辑表达式C AB C B A BC A X ++=5、求下列函数的值:当A,B,C 为0,1,0时: BC B A +=1 ))((C B A C B A ++++=1 B C A B A )(+=1当A,B,C 为1,1,0时: BC B A +=0 ))((C B A C B A ++++=1 B C A B A )(+=1当A,B,C 为1,0,1时: BC B A +=0 ))((C B A C B A ++++=1 B C A B A )(+=06、用真值表证明恒等式 C B A C B A ⊕⊕=⊕⊕ 成立。
证明:所以由真值表得证。
7、证明下列等式 (1)B A B A A +=+证明:左边=B A A + =B A B B A ++)(=B A AB B A ++=B A AB AB B A +++ =B A A B B A )()(+++ =B A + =右边(2)BC AB C AB C B A ABC +=++证明:左边= C AB C B A ABC ++ = ABC C AB C B A ABC +++ =)()(C C AB B B AC +++ =AB AC + =右边(3)E CD A E D C CD A C B A A ++=++++)( 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++ =C B A C AB C B A B A +++)( =C B C A B A ++=右边8、用布尔代数简化下列逻辑函数(1)B C CB C B A ABC A F ++++= B C CB C B A ABC A ++++=)( B C CB A ++= C B A ⊕+=(2)C B A D A B A D C AB CD B A F ++++= )D A D C AB ()C B A B A CD B A (++++= D A B A +=(3)C B ABCD D BC ABD D ABC F ++++= C B D BC ABD ABC +++= C B D B ABD ABC +++= )(C D AD AC B +++= )(D A C A B +++= D B C B AB ++=(4)C AB C B BC A AC F +++= C AB C B )BC A AC (⋅⋅+= )C B A )(C B )(BC AC (++++= )C B A )(BC ABC (+++= )BC ABC BC A (++= BC =10、用卡诺图化简下列各式 (1)C AB C B BC A AC F +++=C F =说明:卡诺图中标有0的格子代表C B BC A AC F 1++=,1F 则是标有0之外的其余格子。
数字逻辑 课后习题答案

4. 最简电路是否一定最佳?为什么?
解答
一个最简的方案并不等于一个最佳的方案。最佳方案应满足全面的性能指标 和实际应用要求。所以,在求出一个实现预定功能的最简电路之后,往往要根据 实际情况进行相应调整。
2. 数字逻辑电路具有哪些主要特点?
解答
数字逻辑电路具有如下主要特点:
● 电路的基本工作信号是二值信号。 ● 电路中的半导体器件一般都工作在开、关状态。 ● 电路结构简单、功耗低、便于集成制造和系列化生产。产品价格低
廉、使用方便、通用性好。 ● 由数字逻辑电路构成的数字系统工作速度快、精度高、功能强、可
第二章
1 假定一个电路中,指示灯 F 和开关 A、B、C 的关系为 F=(A+B)C
试画出相应电路图。 解答
电路图如图 1 所示。
图1
2 用逻辑代数的公理、定理和规则证明下列表达式:
(1) AB + AC = AB + AC (2) AB + AB + AB + AB = 1 (3) AABC = ABC + ABC + ABC
= (A + B) ⋅ (A + B) =B
( ) F = BC + D + D ⋅ B + C ⋅ (AC + B)
= BC + D + (B + C)(AC + B) = BC + D + BC(AC + B) = BC + D + AC + B = B + D + AC
数字逻辑课后习题答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制491100016153110101651271111111177635100111101111737.493111.11117.7479.4310011001.0110111231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010101211110161751011100921340.100110.593750.4610111147570110113153.将下列十进制数转换成8421BCD码1997=000110011001011165.312=01100101.0011000100103.1416=0011.00010100000101100.9475=0.10010100011101014.列出真值表,写出X的真值表达式A B C X00000010010001111000101111011111X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1)(A⊕B)⊕C=A⊕(B⊕C)A B C(A⊕B)⊕C A⊕(B⊕C)0000000111010110110010011101001100011111所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C00011001000100001111100001011111011111007.证明下列等式(1)A+A B=A+B 证明:左边=A+A B=A(B+B )+A B =AB+A B +A B =AB+A B +AB+A B =A+B =右边(2)ABC+A B C+AB C =AB+AC 证明:左边=ABC+A B C+AB C=ABC+A B C+AB C +ABC =AC(B+B )+AB(C+C )=AB+AC =右边(3)E D C CD A C B A A )(++++=A+CD+E证明:左边=ED C CD A C B A A )(++++=A+CD+A B C +CDE =A+CD+CD E =A+CD+E =右边(4)C B A C B A B A ++=CB C A B A ++证明:左边=CB AC B A B A ++=C B A C AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1)F=A+ABC+A C B +CB+C B =A+BC+C B (2)F=(A+B+C )(A+B+C)=(A+B)+C C =A+B (3)F=ABC D +ABD+BC D +ABCD+B C =AB+BC+BD (4)F=C AB C B BC A AC +++=BC(5)F=)()()()(B A B A B A B A ++++=B A 9.将下列函数展开为最小项表达式(1)F(A,B,C)=Σ(1,4,5,6,7)(2)F(A,B,C,D)=Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式(1)CAB C B BC A AC F +++=0 ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111AB CD 00 01 11 1000011110化简得F=DA B A +(3)F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111ABCD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4)F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑题目及其答案和解析(1)一共60道题

第一部分:1.在二进制系统中,下列哪种运算符表示逻辑与操作?A) amp;B) |C) ^D) ~解析:正确答案是 A。
在二进制系统中,amp; 表示逻辑与操作,它仅在两个位都为1时返回1。
2.在数字逻辑中,Karnaugh 地图通常用于简化哪种类型的逻辑表达式?A) 与门B) 或门C) 异或门D) 与非门解析:正确答案是B。
Karnaugh 地图通常用于简化或门的逻辑表达式,以减少门电路的复杂性。
3.一个全加器有多少个输入?A) 1B) 2C) 3D) 4解析:正确答案是 C。
一个全加器有三个输入:两个加数位和一个进位位。
4.下列哪种逻辑门可以实现 NOT 操作?A) 与门B) 或门C) 异或门D) 与非门解析:正确答案是 D。
与非门可以实现 NOT 操作,当且仅当输入为0时输出为1,输入为1时输出为0。
5.在数字逻辑中,Mux 是指什么?A) 多路复用器B) 解码器C) 编码器D) 多路分配器解析:正确答案是 A。
Mux 是指多路复用器,它可以选择输入中的一个,并将其发送到输出。
6.在二进制加法中,下列哪个条件表示进位?A) 0 + 0B) 0 + 1C) 1 + 0D) 1 + 1解析:正确答案是 D。
在二进制加法中,当两个位都为1时,会产生进位。
7.在数字逻辑中,一个 JK 触发器有多少个输入?A) 1B) 2C) 3D) 4解析:正确答案是 B。
一个 JK 触发器有两个输入:J 和 K。
8.下列哪种逻辑门具有两个输入,且输出为两个输入的逻辑与?A) 与门B) 或门C) 异或门D) 与非门解析:正确答案是 A。
与门具有两个输入,只有当两个输入都为1时,输出才为1。
9.在数字逻辑中,下列哪种元件可用于存储单个位?A) 寄存器B) 计数器C) 锁存器D) 可编程逻辑门阵列解析:正确答案是 C。
锁存器可用于存储单个位,它可以保持输入信号的状态。
10.一个带有三个输入的逻辑门,每个输入可以是0或1,一共有多少种可能的输入组合?A) 3B) 6C) 8D) 12解析:正确答案是 C。
数字逻辑(第六版 白中英)课后习题答案

第四章习题答案1.设计4个寄存器堆。
解:2. 设计具有4个寄存器的队列。
解:3.设计具有4个寄存器的堆栈解:可用具有左移、右移的移位寄存器构成堆栈。
4.SRAM、DRAM的区别解:DRAM表示动态随机存取存储器,其基本存储单元是一个晶体管和一个电容器,是一种以电荷形式进行存储的半导体存储器,充满电荷的电容器代表逻辑“1”,“空”的电容器代表逻辑“0”。
数据存储在电容器中,电容存储的电荷一般是会慢慢泄漏的,因此内存需要不时地刷新。
电容需要电流进行充电,而电流充电的过程也是需要一定时间的,一般是0.2-0.18微秒(由于内存工作环境所限制,不可能无限制的提高电流的强度),在这个充电的过程中内存是不能被访问的。
DRAM拥有更高的密度,常常用于PC中的主存储器。
SRAM是静态的,存储单元由4个晶体管和两个电阻器构成,只要供电它就会保持一个值,没有刷新周期,因此SRAM 比DRAM要快。
SRAM常常用于高速缓冲存储器,因为它有更高的速率;5. 为什么DRAM采用行选通和列选通解:DRAM存储器读/写周期时,在行选通信号RAS有效下输入行地址,在列选通信号CAS有效下输入列地址。
如果是读周期,此位组内容被读出;如果是写周期,将总线上数据写入此位组。
由于DRAM需要不断刷新,最常用的是“只有行地址有效”的方法,按照这种方法,刷新时,是在RAS有效下输入刷新地址,存储体的列地址无效,一次选中存储体中的一行进行刷新。
每当一个行地址信号RAS有效选中某一行时,该行的所有存储体单元进行刷新。
6. 用ROM实现二进制码到余3码转换解:真值表如下:8421码余三码B B2B1 B0G G2G 1G00 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 03310 1 1 00 1 1 11 0 0 01 0 0 1 01 0 0 11 0 1 01 0 1 11 1 0 0最小项表达式为:G=∑)9,8,7,6,5(G2=∑)9,4,3,2,1(G1=∑)8,7,4,3,0(G0=∑)8,6,4,2,0(阵列图为:7. 用ROM实现8位二进制码到8421码转换解:输入为8位二进制数,输出为3位BCD码,12位二进制数,所以,所需ROM的容量为:28*12=30728.ROM、EPROM和EEPROM的区别解:ROM 指的是“只读存储器”,即Read-Only Memory。
(完整版)数字逻辑课后习题答案
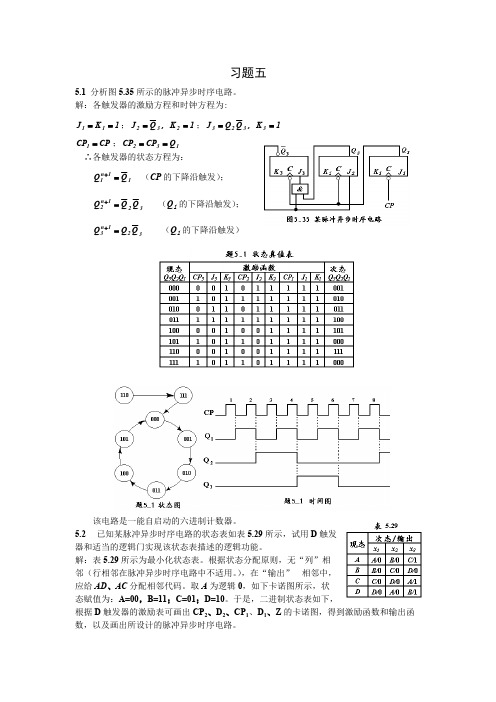
习题五5.1 分析图5.35所示的脉冲异步时序电路。
解:各触发器的激励方程和时钟方程为:;;1K J 11==1K ,Q J 232==1K ,Q Q J 3323==;CP CP 1=132Q CP CP == ∴各触发器的状态方程为:(CP 的下降沿触发);11n 1Q Q =+ (Q 1的下降沿触发);321n 2Q Q Q =+ (Q 1的下降沿触发)321n 3Q Q Q =+该电路是一能自启动的六进制计数器。
5.2 已知某脉冲异步时序电路的状态表如表5.29所示,试用D 触发器和适当的逻辑门实现该状态表描述的逻辑功能。
解:表5.29所示为最小化状态表。
根据状态分配原则,无“列”相邻(行相邻在脉冲异步时序电路中不适用。
),在“输出” 相邻中,应给AD 、AC 分配相邻代码。
取A 为逻辑0,如下卡诺图所示,状态赋值为:A=00,B=11;C=01;D=10。
于是,二进制状态表如下,根据D 触发器的激励表可画出CP 2、D 2、CP 1、D 1、Z 的卡诺图,得到激励函数和输出函数,以及画出所设计的脉冲异步时序电路。
得激励方程和输出方程:;22x CP =;32212x x Q x D ++=;3221x x Q CP +=;31211x Q x Q D +=。
)Q Q (x Q x Q x Z 2132313+=+=5.3 设计一个脉冲异步时序电路,该电路有三个输入端x 1、x 2和x 3,一个输出端Z 。
仅当输入序列x 1-x 2-x 3出现时,输出Z 产输出脉冲,并且与输入序列的最后一个脉冲重叠。
试作出该电路的原始状态图和状态表。
解:5.4 分析图5.36所示的电平异步时序电路。
解:(一)写出激励函数和输出函数表达式:;1112122y x y y x x Y ++=;1221121y x y x x x Y ++=12y x Z = (二)作状态流程表。
(三) 作时间图。
设输入状态的变化序列为00→01→11→10→00→10→11→01,初始总态为(12x x 12x x ,12y y )=(00,00)。
数字逻辑第6章习题参考解答

第6章习题参考解答6-3 画出74x27三输入或非门的德摩根等效符号。
解:图形如下6-10 在图X6.9电路中采用74AHCT00替换74LS00,利用表6-2的信息,确定从输入端到输出端的最大时间延迟。
解:该图中从输入到输出需要经过6个NAND2;每个NAND2(74AHCT00)的最大时间延迟为9 ns;所以从输入端到输出端的最大时间延迟为:54 ns。
6-31 BUT门的可能定义是:“如果A1和B1为1,但A2或B2为0,则Y1为1;Y2的定义是对称的。
”写出真值表并找出BUT门输出的最小“积之和”表达式。
画出用反相门电路实现该表达式的逻辑图,假设只有未取反的输入可用。
你可以从74x00、04、10、20、30组件中选用门电路。
解:真值表如下A1 B1 A2 B2 Y1 Y2 A1 B1 A2 B2 Y1 Y20 0 0 0 0 0 1 0 0 0 0 00 0 0 1 0 0 1 0 0 1 0 00 0 1 0 0 0 1 0 1 0 0 00 0 1 1 0 1 1 0 1 1 0 10 1 0 0 0 0 1 1 0 0 1 00 1 0 1 0 0 1 1 0 1 1 00 1 1 0 0 0 1 1 1 0 1 00 1 1 1 0 1 1 1 1 1 0 0利用卡诺图进行化简,可以得到最小积之和表达式为Y1=A1·B1·A2’+A1·B1·B2’ Y2=A1’·A2·B2+B1’·A2·B2Y 2采用74x04得到各反相器 采用74x10得到3输入与非 采用74x00得到2输入与非 实现的逻辑图如下:6-32 做出练习题6-31定义的BUT 门的CMOS 门级设计,可以采用各种反相门逻辑的组合(不一定是二级“积之和”),要求使用的晶体管数目最少,写出输出表达式并画出逻辑图。
解:CMOS 反相门的晶体管用量为基本单元输入端数量的2倍;对6-31的函数式进行变换:()()()()'2211'2'211'211'2111B A B A B A B A B B A A B A Y ⋅⋅⋅=+⋅⋅=⋅⋅+⋅⋅= ()()()()'1122'1'122'122'1222B A B A B A B A B B A A B A Y ⋅⋅⋅=+⋅⋅=⋅⋅+⋅⋅= 利用圈-圈逻辑设计,可以得到下列结构:()()()'''22'111B A B A Y ⋅+⋅= ()()()'''11'222B A B A Y ⋅+⋅=此结构晶体管用量为20只 (原设计中晶体管用量为40只)6-20 采用一片74x138或74x139二进制译码器和NAND 门,实现下列单输出或多数出逻辑函数。
数字逻辑(白中英)(第六版)习题解答

《数字逻辑》(白中英)(第六版)习题解答/ 第1章开关理论基础1、将下列十进制数化为二进制数和八进制数:十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 11 11732、将下列二进制数转换成十进制数和八进制数:二进制十进制八进制1010 10 12111101 61 751011100 92 134101111 47 5701101 13 153、将下列十进制数转换成8421BCD码:1997=0001 1001 1001 0111=0110 0001 0010=0100 0001 0110=0100 0111 01014、一个电路有三个输入端A、B、C,当其中有两个输入端为高电平时,输出X为高电平,试列出真值表,并写出X的逻辑表达式[解]:先列出真值表,然后写出X的逻辑表达式ABC X /0 0 0 P 00 0 1/■ 00 1 0 /00 1 1 11 0 0 01 0 1 1/1 1 0 11 1 1 0X ABC ABC ABC5、求下列函数的值:当A,B,C 为0,1,0 时:AB BC =1(A B C)(A B C) =1(AB AC)B =1当A,B,C 为1,1,0 时:AB BC =0(A B C)(A B C) =1(AB AC)B =1当A,B,C 为1,0,1 时:AB BC =0\ (A B C)(A B C) =1\ (AB AC)B =06用真值表证明恒等式A B C A B C成立。
证明:------- ■------------------------ --------------------------ABC ABC ABC0 0 0、0 00 0 1 \ 1 10 1 0 \ 1 10 1 1 、0 01 0 0 1 1 /1 0 1 0 \0 /1 1 0 0 \01 1 1 1 1所以由真值表得证。
数字逻辑(第六版 白中英)课后习题答案

第五章 习题答案1. 画出与阵列编程点解:---2. 画出或阵列编程点解:----X 1X 2X 3X 43. 与、或阵列均可编程,画出编程点。
解;1A-BB -F 324. 4变量LUT 编程解:A 0A 1A 2A 3SOP 输出5. 用VHDL 写出4输入与门解: 源代码:LIBRARY IEEE ;USE IEEE .STD_LOGIC_1164.ALL ;ENTITY and4 ISPORT (a ,b ,c ,d :IN STD_LOGIC ;x :OUT STD_LOGIC );END and4;ARCHITECTURE and4_arc OF and4 ISBEGINx <=a AND b AND c AND d ;END and4_arc ;6. 用VHDL 写出4输入或门解:源代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY or4 ISPORT (a,b,c,d:IN STD_LOGIC;x:OUT STD_LOGIC);END or4;ARCHITECTURE or4_arc OF or4 ISBEGINx<=a OR b OR c OR d;END or4_arc;7.用VHDL写出SOP表达式解:源代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY sop ISPORT (a,b,c,d,e,f:IN STD_LOGIC;x:OUT STD_LOGIC);END sop;ARCHITECTURE sop_arc OF sop ISBEGINx<=(a AND b) OR (c AND d) OR (e AND f);END sop_arc;8.用VHDL写出布尔表达式解:源代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY boolean ISPORT (a,b,c:IN STD_LOGIC;f:OUT STD_LOGIC);END boolean;ARCHITECTURE boolean_arc OF boolean ISBEGINf<=(a OR (NOT b) OR c) AND (a OR b OR (NOT c)) AND ((NOT a) OR (NOT b) OR (NOT c));END boolean_arc;9.用VHDL结构法写出SOP表达式解:源代码:――三输入与非门的逻辑描述LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY nand3 ISPORT (a,b,c:IN STD_LOGIC;x:OUT STD_LOGIC);END nand3;ARCHITECTURE nand3_arc OF nand3 ISBEGINx<=NOT (a AND b AND c);END nand3_arc;――顶层结构描述文件LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY sop ISPORT (in1,in2,in3,in4,in5,in6,in7,in8,in9:IN STD_LOGIC;out4:OUT STD_LOGIC);END sop;ARCHITECTURE sop_arc OF sop ISCOMPONENT nand3PORT (a,b,c:IN STD_LOGIC;x:OUT STD_LOGIC);END COMPONENT;SIGNAL out1,out2,out3:STD_LOGIC;BEGINu1:nand3 PORT MAP (in1,in2,in3,out1);u2:nand3 PORT MAP (in4,in5,in6,out2);u3:nand3 PORT MAP (in7,in8,in9,out3);u4:nand3 PORT MAP (out1,out2,out3,out4);END sop;10.用VHDL数据流法写出SOP表达式解:源代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY sop ISPORT (in1,in2,in3,in4,in5,in6,in7,in8,in9:IN STD_LOGIC;out4:OUT STD_LOGIC);END sop;ARCHITECTURE sop_arc OF sop ISBEGINout4<=(in1 AND in2 AND in3) OR (in4 AND in5 AND in6 ) OR (in7 AND in8 AND in9);END sop_arc;13.用VHDL设计3-8译码器解:源代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY decoder_3_to_8 ISPORT(a,b,c,g1,g2a,g2b:IN STD_LOGIC;y:OUT STD_LOGIC _VECTOR(7 downto 0));END decoder_3_to_8;ARCHITECTURE rt1 OF decoder_3_to_8 ISSIGNAL indata:STD_LOGIC _VECTOR(2 downto 0);BEGINindata<=c & b & a;PROCESS(indata,g1,g2a,g2b)BEGINIF(g1=′1′ AND g2a=′0′ AND g2b=′0′)THENCASE indata ISWHEN "000"=>y<="11111110";WHEN "001"=>y<="11111101";WHEN "010"=>y<="11111011";WHEN "011"=>y<="11110111";WHEN "100"=>y<="11101111";WHEN "101"=>y<="11011111";WHEN "110"=>y<="10111111";WHEN others=>y<="01111111";END CASE;ELSEy<="11111111";END IF;END PROCESS;END rt1;14.用VHDL设计七段显示译码器解:源代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY segment7 ISPORT(xin:IN STD_LOGIC _VECTOR(3 downto 0);lt,rbi:IN STD_LOGIC;yout:OUT STD_LOGIC _VECTOR(6 downto 0);birbo:INOUT STD_LOGIC);END segment7;ARCHITECTURE seg7448 OF segment7 ISSIGNAL sig_xin:STD_LOGIC _VECTOR(3 downto 0);BEGINsig_xin<=xin;PROCESS(sig_xin,lt,rbi,birbo)BEGINIF(birbo=′0′)THENyout<="0000000";ELSIF (lt=′0′)THENyout<="1111111";birbo<=′1′;ELSIF (rbi=′0′AND sig_xin="0000")THENyout<="0000000";birbo<=′0′;ELSIF (rbi=′1′ AND sig_xin="0000")THENyout<="1111110";birbo<=′1′;ELSEbirbo<=′1′;CASE sig_xin ISWHEN "0001"=>yout<="0110000";WHEN "0010"=>yout<="1101101";WHEN "0011"=>yout<="1111001";WHEN "0100"=>yout<="0110011";WHEN "0101"=>yout<="1011011";WHEN "0110"=>yout<="0011111";WHEN "0111"=>yout<="1110000";WHEN "1000"=>yout<="1111111";WHEN "1001"=>yout<="1110011";WHEN others=>yout<="0100011";END CASE;END IF;END PROCESS;END seg7448;15.用VHDL设计8/3优先编码器解:源代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY priorityencoder ISPORT(din:IN STD_LOGIC _VECTOR(7 downto 0);ei:IN STD_LOGIC;yout:OUT STD_LOGIC _VECTOR(2 downto 0);eo,gs:OUT STD_LOGIC);END priorityencoder;ARCHITECTURE cod74148 OF priorityencoder ISBEGINPROCESS(ei,din)BEGINIF(ei=′1′)THENyout<="111";eo<=′1′;gs<=′1′;ELSEIF(din(7)=′0′ ) THENyout<="000";eo<=′1′;gs<=′0′;ELSIF(din(6)=′0′ ) THENyout <="001";eo<=′1′;gs<=′0′;ELSIF(din(5)=′0′ ) THENyout<="010";eo<=′1′;gs<=′0′;ELSIF(din(4)=′0′ ) THENyout<="011";eo<=′1′;gs<=′0′;ELSIF(din(3)=′0′ ) THENyout<="100";eo<=′1′;gs<=′0′;ELSIF(din(2)=′0′ ) THENyout<="101";eo<=′1′;gs<=′0′;ELSIF(din(1)=′0′ ) THENyout<="110";eo<=′1′;gs<=′0′;ELSIF(din(0)=′0′ ) THENyout<="111";eo<=′1′;gs<=′0′;ELSIF(din="11111111") THENyout<="111";eo<=′0′;gs<=′1′;END IF;END IF;END PROCESS;END cod74148;16.用VHDL设计BCD码至二进制码转换器。
数字逻辑 白中英 第六版 答案
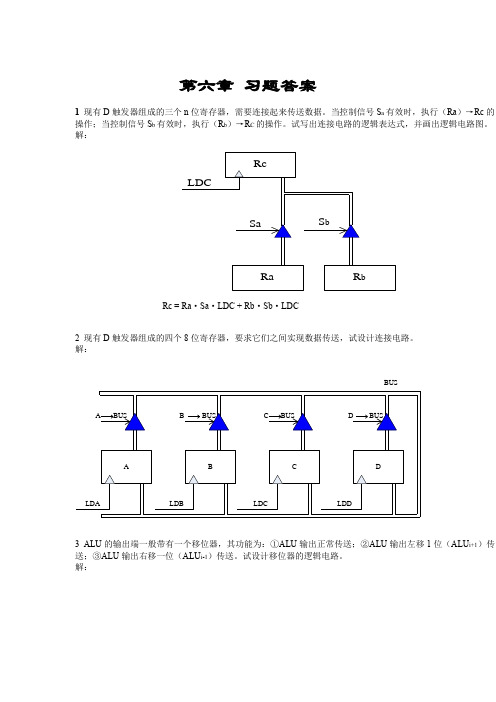
第六章习题答案1现有D触发器组成的三个n位寄存器,需要连接起来传送数据。
当控制信号S a有效时,执行(Ra)→Rc的操作;当控制信号S b有效时,执行(R b)→R C的操作。
试写出连接电路的逻辑表达式,并画出逻辑电路图。
解:Rc = Ra·Sa·LDC + Rb·Sb·LDC2 现有D触发器组成的四个8位寄存器,要求它们之间实现数据传送,试设计连接电路。
解:BUS3 ALU的输出端一般带有一个移位器,其功能为:①ALU输出正常传送;②ALU输出左移1位(ALU i+1)传送;③ALU输出右移一位(ALU i-1)传送。
试设计移位器的逻辑电路。
解:4 一个系统有A,B两条总线,为了接收来自任何一条总线上的数据并驱动任何一条总线,需要一个总线缓冲寄存器。
请用D触发器和三态门设计一个总线缓冲寄存器。
解:5 试构造能完成下列程序操作的ASM图:(a)if X = N, then … 。
(b)if X≠N, then …, else …。
解:(c)for X from A to B, step C, do… 。
解:(d)while X = Y, do …。
解:(e)if X > N OR X < O, then …, else …。
解:6 有一个数字比较系统,它能对两个8位二进制进行比较。
其操作过程如下:先将两个8位二进制数存入寄存器A和B, 然后进行比较,最后将大数移入寄存器A中。
要求:⑴画出此系统方框图,并构造ASM流程图。
⑵设计一个计数器型控制器。
解:(1)②状态转移真值表PS NSB A B( D ) A( D )转移条件 C0 00 11 0 1 10 11 01 11 00 1无条件转移无条件转移无条件转移( A > B ) = 1A >B = 0根据 NS = PS·C 公式,激励方程表达式为:B ( D ) = BA + BA + BA·( A > B )A ( D ) = BA + BA + BA·( A >B ) = A + BA ·( A > B )③电路图④ 控制信号表达式:7. 根据题6的条件,设计一个MUX 型控制器。
《数字逻辑》白中英第六习题解答

《数字逻辑》(白中英)(第六版)习题解答第1章开关理论基础1、将下列十进制数化为二进制数和八进制数:十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 11737.493 111.011111100 7.37479.43 1001111.0110110 117.332、将下列二进制数转换成十进制数和八进制数:二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153、将下列十进制数转换成8421BCD码:1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014、一个电路有三个输入端A、B、C,当其中有两个输入端为高电平时,输出X为高电平,试列出真值表,并写出X的逻辑表达式。
[解]:先列出真值表,然后写出X的逻辑表达式5、求下列函数的值:当A,B,C 为0,1,0时: BC B A +=1))((C B A C B A ++++=1 B C A B A )(+=1当A,B,C 为1,1,0时: BC B A +=0))((C B A C B A ++++=1 B C A B A )(+=1当A,B,C 为1,0,1时: BC B A +=0))((C B A C B A ++++=1 B C A B A )(+=06、用真值表证明恒等式 C B A C B A ⊕⊕=⊕⊕ 成立。
证明:所以由真值表得证。
7、证明下列等式(1)B A B A A +=+证明:左边=B A A +=B A B B A ++)(=B A AB B A ++=B A AB AB B A +++ =B A A B B A )()(+++ =B A + =右边(2)BC AB C AB C B A ABC +=++证明:左边= C AB C B A ABC ++= ABC C AB C B A ABC +++ =)()(C C AB B B AC +++ =AB AC + =右边 (3)E CD A E D C CD A C B A A ++=++++)(证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++ =C B A C AB C B A B A +++)( =C B C A B A ++=右边 8、用布尔代数简化下列逻辑函数 (1)B C CB C B A ABC A F ++++= (2)C B A D A B A D C AB CD B A F ++++= (3)C B ABCD D BC ABD D ABC F ++++= (4)C AB C B BC A AC F +++= 10、用卡诺图化简下列各式 (1)C AB C B BC A AC F +++=说明:卡诺图中标有0的格子代表C B BC A AC F 1++=,1F 则是标有0之外的其余格子。
数字逻辑 课后习题答案

1. 什么是模拟信号?什么是数字信号?试举出实例。
解答 模拟信号-----指在时间上和数值上均作连续变化的信号。例如,温度、压
力、交流电压等信号。 数字信号-----指信号的变化在时间上和数值上都是断续的,阶跃式的,或
者说是离散的,这类信号有时又称为离散信号。例如,在数 字系统中的脉冲信号、开关状态等。
第二章
1 假定一个电路中,指示灯 F 和开关 A、B、C 的关系为 F=(A+B)C
试画出相应电路图。 解答
电路图如图 1 所示。
图1
2 用逻辑代数的公理、定理和规则证明下列表达式:
(1) AB + AC = AB + AC (2) AB + AB + AB + AB = 1 (3) AABC = ABC + ABC + ABC
= (A + B) ⋅ (A + B) =B
( ) F = BC + D + D ⋅ B + C ⋅ (AC + B)
= BC + D + (B + C)(AC + B) = BC + D + BC(AC + B) = BC + D + AC + B = B + D + AC
(3) (33.33)10 =(?)2 =(?)8 =(?)16
23
3
21
6………… .1
2
8…………..0
2
4…………..0
2 2…………..0
2 1 ………. 0
0…………1
0.3 3
×
2
0.6 6
数字逻辑参考答案

数字逻辑参考答案数字逻辑参考答案数字逻辑是计算机科学中的一个重要分支,它研究的是数字信号和数字电路的设计与实现。
在数字逻辑中,我们常常需要解决各种逻辑问题,包括逻辑运算、逻辑门电路的设计和分析等。
本文将为大家提供一些常见数字逻辑问题的参考答案,希望能对大家的学习和研究有所帮助。
1. 逻辑运算逻辑运算是数字逻辑中最基础的概念之一。
常见的逻辑运算包括与运算、或运算、非运算等。
下面是一些逻辑运算的参考答案:- 与运算(AND):输入A和B,输出为A与B的逻辑与结果。
逻辑表达式为:C = A AND B。
- 或运算(OR):输入A和B,输出为A与B的逻辑或结果。
逻辑表达式为:C = A OR B。
- 非运算(NOT):输入A,输出为A的逻辑非结果。
逻辑表达式为:B = NOT A。
2. 逻辑门电路逻辑门电路是数字逻辑中常见的电路实现方式,可以用于实现各种逻辑功能。
常见的逻辑门包括与门、或门、非门等。
下面是一些逻辑门电路的参考答案:- 与门(AND Gate):输入A和B,输出为A与B的逻辑与结果。
逻辑表达式为:C = A AND B。
可以使用两个晶体管和一个电阻来实现与门电路。
- 或门(OR Gate):输入A和B,输出为A与B的逻辑或结果。
逻辑表达式为:C = A OR B。
可以使用两个晶体管和一个电阻来实现或门电路。
- 非门(NOT Gate):输入A,输出为A的逻辑非结果。
逻辑表达式为:B = NOT A。
可以使用一个晶体管和一个电阻来实现非门电路。
3. 布尔代数布尔代数是数字逻辑中的一种代数系统,它由三个基本运算符(与、或、非)和一些基本规则组成。
布尔代数可以用来描述和分析逻辑运算和逻辑门电路。
下面是一些布尔代数的参考答案:- 分配律:对于任意的A、B和C,有A AND (B OR C) = (A AND B) OR (A AND C) 和 A OR (B AND C) = (A OR B) AND (A OR C)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数字逻辑》(白中英)(第六版)
习题解答
第1章开关理论基础
1、将下列十进制数化为二进制数和八进制数:
十进制二进制八进制
49 110001 61
53 110101 65
127 1111111 177
635 1173
7.493 111.011111100 7.374
79.43 1001111.0110110 117.33
2、将下列二进制数转换成十进制数和八进制数:
二进制十进制八进制
1010 10 12
111101 61 75
1011100 92 134
0.10011 0.59375 0.46
101111 47 57
01101 13 15
3、将下列十进制数转换成8421BCD码:
1997=0001 1001 1001 0111
65.312=0110 0101.0011 0001 0010
3.1416=0011.0001 0100 0001 0110
0.9475=0.1001 0100 0111 0101
4、一个电路有三个输入端A、B、C,当其中有两个输入端为高电平时,输出X为高电平,试列出真值表,并写出X的逻辑表达式。
[解]:先列出真值表,然后写出X的逻辑表达式
5、求下列函数的值:
当A,B,C 为0,1,0时: BC B A +=1
))((C B A C B A ++++=1 B C A B A )(+=1
当A,B,C 为1,1,0时: BC B A +=0
))((C B A C B A ++++=1 B C A B A )(+=1
当A,B,C 为1,0,1时: BC B A +=0
))((C B A C B A ++++=1 B C A B A )(+=0
6、用真值表证明恒等式 C B A C B A ⊕⊕=⊕⊕ 成立。
证明:
所以由真值表得证。
7、证明下列等式
(1)B A B A A +=+
证明:左边=B A A +
=B A B B A ++)(
=B A AB B A ++
=B A AB AB B A +++ =B A A B B A )()(+++ =B A + =右边
(2)BC AB C AB C B A ABC +=++
证明:左边= C AB C B A ABC ++
= ABC C AB C B A ABC +++ =)()(C C AB B B AC +++ =AB AC + =右边
(3)E CD A E D C CD A C B A A ++=++++)( 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边
(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++ =C B A C AB C B A B A +++)( =C B C A B A ++=右边 8、用布尔代数简化下列逻辑函数 (1)B C CB C B A ABC A F ++++= (2)C B A D A B A D C AB CD B A F ++++= (3)C B ABCD D BC ABD D ABC F ++++= (4)C AB C B BC A AC F +++= 10、用卡诺图化简下列各式 (1)C AB C B BC A AC F +++=
说明:卡诺图中标有0的格子代表C B BC A AC F 1++=,1F 则是标有0之外
的其余格子。
(2)C B A D A B A D C AB CD B A F ++++=
(3)F(A,B,C,D)=∑m(0,1,2,5,6,7,8,9,13,14)
(4)F(A,B,C,D)=∑m(0, 13,14,15)+∑φ(1,2,3,9,10,11)
11 (1)C B A C AB F += (2))D C )(B A (F ++=
12、画出F
1和F
2
的波形图
A
B C
F
1
F
2
第2章 组合逻辑
1、分析图P2.1所示的逻辑电路。
1)B A B A B AB B AB F =+=+=+= 2)B A F =1
4、分析P2.3所示逻辑电路图的功能。
1)用逐级电平推导法:
F=0 ✍ F i =0 ✍ i A =1 ✍ A i =0 2)列写布尔代数法:
可见,当A 0~A 15均为0时,F=1。
5、分析图P2.5所示的逻辑电路。
显然,这是一个四选一数据选择器,其中A 1、A 0为选择控制输入: A 1A 0=00时,F=X 0 A 1A 0=01时,F=X 1 A 1A 0=10时,F=X 2 A 1A 0=11时,F=X 3
6、图P2.6为两种十进制代码转换器,输入为余三码,分析输出是什么代码? 1)逻辑表达式: 2)真值表:
由真值表可知,该电路为余三码到8421BCD 码转换电路。
7、分析图P2.7所示代码转换电路的功能。
1)逻辑表达式: 当M=1时: 33X Y = 当M=0时: 33X Y =
2)真值表
M=1时的真值表 M=0时的真值表
8421码 ✍ 循环码 循环码 ✍ 8421码
8、已知输入信号A, B, C, D 信号的波形如图P2.8所示,设计产生输出F 波形的组合逻辑电路。
1)真值简表(只列出F=1的情况)
2)逻辑表达式
F=∑m (1,3,4,5,8,9,10,11,12)
3)逻辑电路图(略)
9、【解】
1)真值表(输入“1”表示不正常,输出“1”表示亮)
2)逻辑表达式
3)逻辑电路图(略)
19、【解】
1)真值表(输入“1”表示按下,输出F=表示开锁,G=1表示报警)
2)逻辑表达式
3)逻辑电路图(略)
第3章 时序逻辑
7.【解】 1)激励方程 2)状态转移表
3)状态转移图(简图)
由状态转移表可知,电路只形成一个封闭的循环,因此能够自启动。
101✍010┐ ✍
000✍001✍011✍111✍110✍100 ┐ ✍ │
└──────────┘
8.【解】 1)状态方程 2)状态转移表
3)状态转移图(简图)
111┐ ┌101✍010 ✍ ✍ 000✍001✍011✍110✍100┐ ✍ │ └──────────┘
9.【解】
1)状态编码
采用常规的计数器法,须3个触发器。
2)状态转移表
计数器有6个状态,状态010和110未使用,可令这2个状态的次态为已使用的6个状态之一。
3)激励方程
4)电路图(略)
13.【解】
1)输出方程
2)激励方程
3)状态转移表
4)状态转移图(简图)
x=0时,为加法计数器
x=1时,为减法计数器
16.【解】
1)由波形图可知,电路有7个状态。
2)状态表
3)状态转移表
状态000没有在波形图中出现,为了让电路能够自启动,可令上述7个状态中任意一个作为状态000的次态。
4)激励函数(下边表达式中的φ为最小项000)
D
3=∑(3,7,6,2) + φ =
2
3
1
3
Q
Q
Q
Q+
D
2=∑(3,7,4,1) + φ =
1
2
1
2
1
3
Q
Q
Q
Q
Q
Q+
+
D
1=∑(3,2,5,1) + φ =
1
2
3
Q
Q
Q+
在利用卡诺图化简中,D
2和D
1
使用了任意项“000”,故状态000的次态为011。
5)电路图(略)19.【解】
1)状态编码
时序机有4个状态,用2个D触发器表示,并设S
0=00,S
1
=01,S
2
=10,S
3
=11。
2)状态转移表
3)激励函数
4)逻辑电路图(略)。
