水准高程平差计算表
南方平差易水准网平差实例.

水准平差实例实例1 符合水准路线平差(单一水准路线)实例2 三角高程平差实例3 水准网平差(多条水准路线)实例1、符合水准路线平差这是一条符合水准的测量数据和简图,A和B是已知高程点,2、3和4是待测的高程点。
测站点高差(米) 距离(米)高程(米)A -50.440 1474.4440 96.06202 3.252 1424.71703 -0.908 1749.32204 40.218 1950.4120B 88.1830水准原始数据表水准路线图(模拟)图中h为高差。
在平差易中输入以上数据,如下图“水准数据输入”所示:水准数据输入在测站信息区中输入A、B、2、3和4号测站点,其中A、B为已知高程点,其属性为01,其高程如“水准原始数据表”;2、3、4点为待测高程点,其属性为00,其它信息为空。
因为没有平面坐标数据,故在平差易软件中没有网图显示。
根据控制网的类型选择数据输入格式,此控制网为水准网,选择水准格式,如下图“选择格式”所示:选择格式注意:1、在“计算方案”中要选择“一般水准”,而不是“三角高程”。
“一般水准”所需要输入的观测数据为:观测边长和高差。
“三角高程”所需要输入的观测数据为:观测边长、垂直角、站标高、仪器高。
2、在一般水准的观测数据中输入了测段高差就必须要输入相对应的观测边长,否则平差计算时该测段的权为零,因此导致计算结果错误。
在观测信息区中输入每一组水准观测数据测段A点至2号点的观测数据输入(观测边长为平距)如下图“A->2观测数据”所示:A->2观测数据测段2号点至3号点的观测数据输入如下图“2->3观测数据”所示:2->3观测数据测段3号点至4号点的观测数据输入如下图“3->4观测数据”所示:3->4观测数据测段4号点至B点的观测数据输入如下图“4->B观测数据”所示:4->B观测数据以上数据输入完后,点击菜单“文件\另存为”,将输入的数据保存为平差易数据格式文件(格式内容详见附录A):[STATION]A,01,,,96.062000B,01,,,88.1830002,003,004,00[OBSER]A,2,,1474.444000,-50.44002,3,,1424.717000,3.25203,4,,1749.322000,-0.90804,B,,1950.412000,40.2180平差计算选择菜单“平差->闭合差计算”,计算该水准路线的高差闭合差。
四等水准测量平差计算
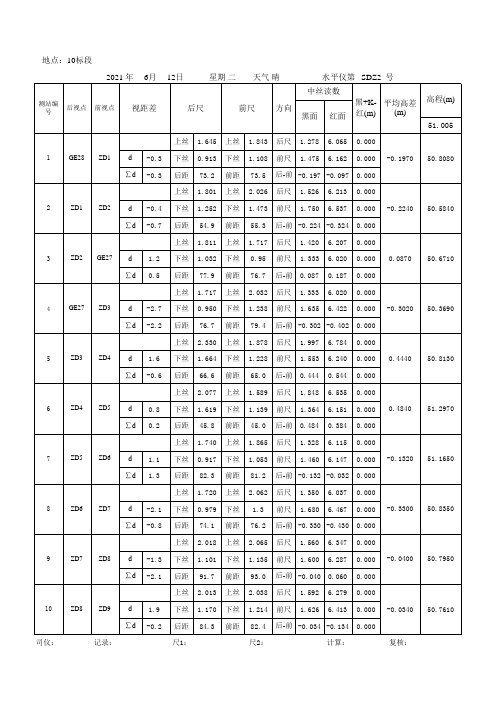
∑d 3.8 后距 51.4 前距 50.7 后-前 0.036 0.136 0.000
上丝 1.538 上丝 1.540 后尺 1.294 5.981 0.000
28 ZD19 D157 d -1.5 下丝 1.050 下丝 1.037 前尺 1.288 6.075 0.000 0.0060
∑d 2.3 后距 48.8 前距 50.3 后-前 0.006 -0.094 0.000
∑d -2.2 后距 76.7 前距 79.4 后-前 -0.302 -0.402 0.000
上丝 2.330 上丝 1.878 后尺 1.997 6.784 0.000
5
ZD3 ZD4 d 1.6 下丝 1.664 下丝 1.228 前尺 1.553 6.240 0.000 0.4440 50.8130
∑d -2.1 后距 91.7 前距 93.0 后-前 -0.040 0.060 0.000
上丝 2.013 上丝 2.038 后尺 1.592 6.279 0.000
10
ZD8 ZD9
d 1.9 下丝 1.170 下丝 1.214 前尺 1.626 6.413 0.000 -0.0340 50.7610
上丝 1.760 上丝 1.784 后尺 1.433 6.220 0.000
29 D157 ZD20 d 0.1 下丝 1.105 下丝 1.13 前尺 1.457 6.144 0.000 -0.0240
∑d 2.4 后距 65.5 前距 65.4 后-前 -0.024 0.076 0.000
上丝 1.706 上丝 1.736 后尺 1.400 6.087 0.000
14 D154 ZD12 d -0.7 下丝 1.091 下丝 0.921 前尺 1.249 6.036 0.000 0.1640
高程平差方法 举例说明

高程平差方法举例说明引言在工程建设中不免要对高程控制网进行高精度计算,手工计算对于较为简单的控制网还可适应,但对于较为复杂、节点较多的高程控制网来讲使用手工计算容易出现误差且非常耗时,因此我们针对高程控制网的平差计算原理进行了分析,并利用这一原理结合计算机技术进行了高效的控制网平差计算。
1 平差模型的建立1. 1 平差原理下面以一个水准网的算例来说明水准网间接平差原理,水准网如图1 所示:已知A 点高程HA=237. 483m,为求B、C、D 三点的高程,进行了水准测量,观测结果为见图1, h1、h2、h3、h4、h5 分别为观测值,对应的水准路线长度为S1、S2、S3、S4、S5。
取B、C、D 三点的高程值平差值为参数,其近似值为X01、X02、X03 其中:X01=HA+h1; X02=HA+h3; X03=HA+h5 于是观测值误差方程为v:常数项l:权P:如下:其中:改正数V= 系数阵A= 参数x= 常数项l=可以解出由此可以计算出高程平差值由上可知,水准网间接平差主要分为三个步骤:(1)高程近似值的计算;(2)列立观测值的误差方程;(3)解误差方程并求高程平差值。
1. 2 常数项矩阵的问题在求近似高程时,同一个未知点的近似高程并不是唯一的一个确定值,它的值随着计算时选择的线路不同而改变,因此得出的常数项矩阵L 也并不是唯一的,在下面的程序计算里面,输入已知数据时线路的排序不同,得出的常数项矩阵L 也不同,当然最后得到的高程改正数也不一样,由于进行平差计算时设的未知数就是未知点高程的近似值,因此在最后得到的未知点的高程平差值跟计算高程近似值时选择的线路无关,只要计算正确,最终得到的高程平差值也是正确的。
这一点可以在使用程序的过程中进行检验,无论线路排序如何改变,只要数据输入正确,得到的结果是一样的。
2 平差程序设计2. 1 关于程序语言的选用考虑到本软件所要解决的问题主要是数据的处理与计算,不涉及到计算机系统底层的操作,因此选用相对简单的Visual Basic 6. 0 来进行程序的编写,使用间接平差模型,在保证计算精度的同时,一来减少了代码编写的难度,二来提高了代码执行的效率。
水准测量平差计算

水准测量平差计算
水准测量平差计算是水准测量中的一项重要工作,主要是对测量数据进行分析处理,消除误差和残差,以求得较为准确的高程结果。
具体步骤如下:
1. 建立观测方程
在水准测量中,设定起点高程为0,然后逐站向前观测,求出每个站点的高程。
建立每个站点高程的观测方程,包括自由高差和永久高差的影响。
2. 矩阵方程式
将所有观测方程进行矩阵变换,消除自由高差,得到纯高差矩阵方程组。
3. 固定高程点的影响
将所有观测方程加上固定高程点的影响,消除永久高差,得到纯高差矩阵方程组。
4. 最小二乘方法
利用最小二乘方法解出平差后的高差平差值,分别确定每个站点的高程。
5. 残差分析
对于每个观测方程都会有一个残差,其代表了实际测量值与计算值之间的差异。
进行残差分析,可发现数据中的误差规律和存在的误差来源,为后续的测量和处理提供参考和改进。
6. 高程精度分析
通过对整个水准测量的误差分析和精度分析,得出测量结果的可靠性和精度,为后续的工作提供指导和帮助。
水准测量及其平差

2)高差闭合差的分配和计算改正后的高差
当高差闭合差在容许范围内时,可进行高差闭合差的分
配,分配原则是:对于闭合或附合水准路线,按与路线长
度L或分配。用数学公式表示为
水准仪及其使用
§1水准测量原理
水准测量是测出地面点高程的方法之一。已知A点高 程为HA,欲测定B点的高程。首先测出A、B两点之间的高 差。则B点的高程为:HB= HA + hAB
一、水准测量的原理
为测出AB两点之间的高差,可在AB两点上分别竖立两 根标尺,在两点之间安置一架能提供水平视线的仪器,使 视线水平照准A点标尺读数,设为a,再照准B点标尺读数, 设为b,则AB两点间的高差为 :hAB =a-b
一、水准点
§2普通水准测量
水准测量的主要目的是测出一系列点的高程。通常称 这些点为水准点。我国水准点的高程是从青岛水准原点起 算的。
为了进一步满足工程建设和地形测图的需要,以国家 水准测量的三、四等水准点为起始点,尚需布设工程水准 测量或图根水准测量,通常统称为普通水准测量(也称等 外水准测量)。普通水准测量的精度较国家等级水准测量 低一些,水准路线的布设及水准点的密度可根据具体工程 和地形测图的要求而有较大的灵活性。
每次读数时均应使符合水准气泡严密吻合,每个转点 均应安放尺垫,但所有已知水准点和待求高程点上不能放 置尺垫。
四、水准测量成果整理
普通水准测量外业观测结束后,首先应复查与检核记录 手簿,并按水准路线布设形式进行成果整理,其内容包括: 水准路线高差闭合差计算与校核;高差闭合差的分配和计 算改正后的高差;计算各点改正后的高程。
水准测量平差

·85·
1—7—1 1957 年中国东南部精密水准平差图(安徽省部分)
·86·
〔长(委)办 二、三 、四等 水准 平 差〕 长(委)办在完成宜昌以下沿江两岸,精密水准测量后进行 7 个水准路线环平差(简称
7 环平差),起算点为镇江 Y .R .C .BM 308’,属吴淞高程系。 中 国东 南 部精 密水 准 平差 后,长(委)办 又在 长 江流 域增 测 新线 ,省境 内 新布 设两 条 二
第二轮全国二等水准网平差,以 1986 年平差的一等水准成果为起算 数据,以一 等水 准路线环为单位,安徽省内及周边地区有 66、33、34、35、38 环参加平差。此项工作由国家 测绘局西安数据处理中心承担,至 1989 年还未结束。
·87·
〔安 徽省 水利 厅 勘测 设计 院 三、四 等水 准 平差〕 1959 年,安徽省水利厅勘测设计院对 前淮委、前水 利厅、长办、总 参测绘 局及本单 位 在省内所测的三、四等水准资料整理分析后,以国家二等水准路线环为单 位,用逐次 趋近 法进行整体平差。全省有 13 个二等环,由北向南依次编号,平差结果载于 1959 年 10 月编 印的《安徽省三、四等水准成果表》中,系 1956 年黄海高程。为了比较和应用方便,表内大 部分 点同 时载 有 1956 年 黄海 高程 和初 算高 程,表内 载有 安徽 省内 三、四等 水 准点 6367 个。 1978 年,该院会同阜阳、宿县地区水利局,整理了 1976 年前,各测量单位在淮北地区 布设的各级水准点,共 3421 个(包括接测水准的三角点),1978 年 6 月,以县为单位,编制 出版《淮 北地 区水 准 成果 表》。表 中绘 有 以县 为单 位 的水 准路 线 图,部 分点 载 有废 黄河 系 统 的高程值。其新、旧高程系统(1956 年黄海高程值减去废黄河高程值)的差值,在+0.100 ~+0.153 米之间,中数为+0.130 米。
条件平差算例

一、水准网条件平差示例 范例:有一水准网(如图8-3所示),已知点A ,B 的高程为: HA=50.000m , HB=40.000 m ,观测高差及路线长度见表8-1。
试用条件平差求:(1) 各观测高差的平差值;(2) 平差后P 1到P 2点间高差的中误差。
图8-3【解】1)、求条件方程个数;由图易知:n=7,t=3,条件式r=4。
故应列4个平差值条件方程,三个闭合环,一个附和路线2)、列平差值条件方程; 所列4个平差值条件方程为:⎪⎪⎭⎪⎪⎬⎫=-+-=--=-+=+-0ˆˆ0ˆˆˆ0ˆˆˆ0ˆˆˆ31643765521BA H H h h h h h h h h h h h 3)、转换成改正数条件方程;以ii i V L L +=ˆ代入上式可得: ⎪⎪⎭⎪⎪⎬⎫=-+-+-=--+--=-++-+=+-++-00003131643643765765521521B A H H h h v v h h h v v v h h h v v v h h h v v v 化简可得:⎪⎪⎭⎪⎪⎬⎫=--=+--=+-+=++-0403070731643765521mm mm mm mm v v v v v v v v v v v 可知条件方程系数阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----000101010110011100000010011⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=2101001000210000210000010000001称对P ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=2010010002000020000010000001称对Q ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----=320125100141101300100110001101001100000110010002010102200211000000100114)、组成法方程; 先求权阵P ;以1km 观测高差为单位权观测高差,则: 11=P ,12=P ,213=P ,214=P ,15=P ,16=P ,217=P ,而各观测高差两两相互独立,所以权阵为:,则协因数阵为:则,法方程的系数阵Naa 为:⎥⎥⎦⎤⎢⎢⎣⎡-----⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----==-=00010101011001110000001001120100100020000200000100000010001010101100111000000100111TT AQA T A AP aa N 称对所以,法方程为:043773212510014110134321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----k k k k 5)、解算法方程,求出联系数K⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡34831.213483.002247.177528.2437758427.025843.012360.023596.025843.032584.011236.012360.012360.011236.031461.014607.023596.012360.014608.046067.04377320125100141101314321k k k k 6)、求V 及高差平差值Lˆ 所以4210.212.118.3213.0214.418.214.0ˆ22222220⨯+⨯-+⨯-+⨯-+⨯-+⨯+⨯-==)()()()()(r PV V T σ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-----=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡==045.2157.1798.3270.0427.4775.2427.034831.213483.002247.177528.2002001100011020022000001100134831.213483.002247.177528.200001010101100111000000100112010010002000020000010000001m m T K T QA V 称对mmmm v v v v v v v h h h h h h h h h h h h h h L ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=5020.108548.56472.45007.143556.200028.153556.100.22.18.33.04.48.24.0500.10856.5651.4501.14360.20000.15356.10ˆˆˆˆˆˆˆˆ7654321765432176543217)、精度评定1)、单位权方差估值计算mm 98.24605.35±==2)、建立所求精度的平差值函数的算式,并按误差传播律求平差值函数的精度 依题意列平差值函数为: 5ˆh =ϕ 则:[]Tf 0010000=[][][][]51687.048313.01)16853.3146.0(1001111236.001124.016853.03146.0100110011111ˆˆ=-=+-=⨯---=-=-=--TTT T T aaaa N AQf N QA f Qf fQ ϕϕ所以:mm Q 14.251687.098.2ˆˆ0ˆ±=⨯==ϕϕϕσσ【答】:各观测高差的平差值为:}{m m m m m m m5020.108548.56472.45007.143556.200028.153556.10平差后P1到P2点间高差的中误差为:±2.14mm987654321ACPB 图8-11二、测角网条件平差 范例:有一测角网(如图8-11所示),A 、B 、C 三点为已知三角点,P 为待定点。
高程控制网平差

1.单位权中误差的计算公式:
m0 ˆ0
PVV
r
2.每km高差中误差:
m m0
C
3.最弱点的高程中误差
最弱点是指误差最大的待定水准点,一般为离开已知水准点 最远的点。首先要列出最弱点的权函数式:
V F f 1V1 f 2V 2 f nV n
利用m f
1
m0式P计f 算最弱点高程中误差。
V 1 V 7 V 8 W b 0
V 2 V 8 V 7 W c 0
V 3 V 5 V 8 W d 0
V 4 V 6 V 5 W e 0
2.闭合水准路线的条件数和条件方程式的组 成
图(c)是四边形状水准网,网中有4个待定点,没有已知点, 在平差计算时,只能确定个待定水准点之间的相互关系,如 果确定一个水准点的高程,就可以确定其他点的高程。因此, 该网的必要观测是3个,观测值总数是6个,又3个多余观测, 可以列出3个条件方程。为了让所列立的条件方程式互相独 立,没个条件方程都要求有一个其他方程没有用到的观测值, 即:
在水准网中,把3条或3条以 上水准路线的交点称为结点。 两条水准路线的交点称为节点。
(一)按间接平差法对结点进行平差
1.误差方程式的列立
不考虑水准路线中的节点,将水准路线的高差作为独立观测 值,取结点的近似高程改正数为未知数,列立每条水准路线 高差观测值的误差方程。
如图,路线高差观测值以表示,已知
(一)按间接平差法对结点进行平差
3.法方程式的解算 法方程式系数阵的逆阵为:
Q
N Q QQ 1
11
XX
21
31
Q 12
Q 22
Q 32
Q
13
Q Q23
附合水准路线测量成果计算表

附合水准路线测量成果计算表
1. 测量点编号,记录测量点的编号,以便对应不同的测量点。
2. 测站,测量所在的测站名称或编号。
3. 观测日期,进行水准观测的日期。
4. 观测时间,记录每次观测的具体时间。
5. 基准点高程,基准点的已知高程。
6. 测点高程,测量点的高程测量值。
7. 线路长度,测量线路的长度。
8. 观测方法,使用的水准观测方法,例如闭合回路、三角测量等。
9. 仪器,使用的水准仪器的型号和规格。
10. 观测人员,参与水准观测的人员姓名或编号。
在计算表中,通常会包括以下计算内容:
1. 观测数据处理,包括观测数据的校核、平差和处理过程。
2. 高程改正数,根据观测数据计算得出的高程改正数。
3. 最终高程,根据高程改正数修正后得出的最终高程值。
4. 精度评定,对测量结果的精度进行评定,包括精度等级和误
差限等信息。
以上是一般情况下附合水准路线测量成果计算表可能包括的内容。
针对具体的测量项目和要求,表格的具体内容可能会有所不同。
