简单六方格子-坐标纸-方便绘图
上册微专题七网格坐标系中的旋转作图及旋转证明人教版九年级数学全一册精品系列PPT

上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
变形3答图
上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
微专题七 网格(坐标系)中的旋转作图及旋转证明
一 二
一 网格(坐标系)中的旋转作图 (教材 P62 习题 23.1 第 4 题) 如图 1,分别画出△ABC 绕点 O 逆时针旋转 90°和 180°后的图形.
图1
解:如答图,△A1B1C1 是△ABC 绕点 O 逆时针旋转 90°后的图形;△A2B2C2 是 旋转 180°后的图形.
上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
二 旋转证明 (教材 P63 习题 23.1 第 10 题) 如图 5,△ABD,△AEC 都是等边三角形.BE 与 DC 有什么关系?你能用旋转 的性质说明上述关系成立的理由吗?
图人 教版九 年级数 学全一 册课件 (共27 张PPT)
顶点与原点重合,直角顶点 C 在第二象限,将 Rt△OCB 绕原点顺时针旋转 120°后得
到△OC′B′,则 B 点的对应点 B′的坐标是( A )
A.( 3,-1)
B.(1,- 3)
C.(2,0)
D.( 3,0)
上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
六年级数学上册教学设计-数形结合-人教版

六年级数学上册教学设计数形结合人教版教学内容本节课将引导学生深入理解数学中“数形结合”的概念,通过直观的图形来理解和解决数学问题。
课程内容主要围绕人教版六年级数学上册中关于“数形结合”的相关章节,包括但不限于:坐标平面、函数图像、几何图形的量化分析等。
教学目标1. 知识与技能:使学生能够正确理解数形结合的基本概念,掌握坐标平面上的点与二元组的关系,能够绘制简单的函数图像,并利用图形解决实际问题。
2. 过程与方法:通过观察、操作、分析等实践活动,培养学生运用数形结合思想解决问题的能力,增强学生的空间想象力和逻辑思维能力。
3. 情感态度与价值观:激发学生对数学学习的兴趣,培养学生合作交流、探索创新的意识,让学生体验到数学与实际生活的紧密联系。
教学难点1. 概念理解:学生对“数形结合”这一抽象概念的理解和内化。
2. 图形与数值转换:学生将具体图形中的信息转换为数值计算,或将数值计算结果通过图形表现出来的能力。
3. 问题解决策略:如何引导学生运用数形结合思想,找到解决数学问题的有效策略。
教具学具准备教师准备:多媒体教学设备、PPT课件、坐标纸、绘图工具。
学生准备:坐标纸、直尺、圆规、彩笔等绘图工具。
教学过程1. 导入新课:通过展示生活中的数形结合实例,如温度变化图、股票走势图等,引起学生的兴趣,导入新课。
2. 探究新知:引导学生观察坐标平面,探讨坐标点与二元组的对应关系。
通过绘制简单的函数图像,让学生直观感受数与形的结合。
3. 实践操作:学生分组进行图形绘制和数据分析,合作完成数形结合的实践任务。
5. 巩固练习:布置相关的练习题,让学生独立完成,巩固所学知识。
6. 课堂小结:回顾本节课的学习内容,强调数形结合的重要性。
板书设计板书将简洁明了地呈现本节课的主要内容和关键知识点,包括数形结合的定义、坐标平面的介绍、函数图像的绘制方法等。
同时,通过图表和示例,直观展示数形结合在解决实际问题中的应用。
作业设计作业将包括基础题、提高题和拓展题三个层次,旨在巩固学生对数形结合概念的理解,提高学生运用数形结合解决问题的能力。
十四种空间格子

同学们,再见!
的平行六面体的体积力求最小。
十四种空间格子
空间格子的划分
划分7种平行六面体
对应于7个晶系
形状及参数?
4mm
十四种空间格子
十四种空间格子
2.平行六面体中结点的分布
1)原始格子( primitive, P):结点分布于平行六面体的八个角顶。 2)底心格子( end-centered, C、A、B):结点分布于平行六面体 的角顶及某一对面的中心。 3)体心格子( body-centered, I):结点分布于平行六面体的角顶和 体中心。
4)面心格子( face-centered, F):结点分布于平行六面体的角顶和
三对面的中心。
十四种空间格子
以下两个平面点阵图案,画出其空间格子:
mm2(L22P) 4mm(L44P)
十四种空间格子
4mm
十四种空间格子
mm2 引出问题:空间格子可以有带心的格子; 另外请思考:如果上面的图案对称为3m,该怎么画?
十四种空间格子
总结: 在四种格子类型当中,其中底心、
体心、面心格子称带心的格子,这是因为有 些晶体结构在符合其对称的前提下不能画出 原始格子,只能画出带心的格子。
十四种空间格子
七个晶系—七套晶体常数—七种平行六面体种形状。 每种形状有四种类型,那么就有7×4=28种空间格子?
但在这28种中,某些类型的格子彼此重复并可转换,还有
一些不符合某晶系的对称特点而不能在该晶系中存在,因 此,只有14种空间格子,也叫14种布拉维格子。(A.Bravis
于1848年最先推导出来的)
结构化学第七章课件

Laue方程的推导
a (cos -cos0 )= h h为整数 即在入射角为0 时,在方向产
生衍射。
直线点阵上衍射圆锥的形成
Laue 方程组: 对于空间点阵,应同时满足以下三式,
h、k、l为整数(但并不都是互质整数)--衍射指标。
Laue 方程把衍射方向和晶胞参数联系在一起。
Laue方程组决定了衍射方向的分立性,因为空间点阵的 衍射方向是以三个互不平行的直线点阵为轴的的三组圆 锥面的共交线,所以只有某些特定方向上才会出现衍射。
h k l=nh* nk* nl* 才能产生反射。 如果某一晶面(h*k*l*)产生n级衍射,则可把其看作是晶 面(nh*nk*nl*)的一级衍射。晶面(h*k*l*)的面间距为d, 则晶面(nh*nk*nl*)的面间距就是d/n,于是Bragg方程可 写成:
2 (dh*k*l*)/n sinn = 即:2 dhkl sin =
d hkl
a h2 k2 l2
正交晶系
dh*k*l*
1 ( h* )2 ( k )2 (l )2
abc
六方晶系
dh*k*l*
1
4( h*2
hk 3a2
k
2
)
l 2 c2
Bragg方程表明,晶面指标为(h*k*l*)的晶面只对某些
角的入射线产生反射。可以证明,对于这些晶面,只有 衍射方向hkl和晶面指标(h*k*l*)满足:
1. 宏观对称元素和对称操作 晶体的理想外形在宏观表现出来的对称性
对称元素 旋转轴 (n或n) 反映面 (m) 对称中心 (i)
反轴 ( n )
对称操作
旋转 L() =2/n
反映 M 反演 I
旋转反演L()I
AutoCAD快速入门

AutoCAD快速入门AutoCAD快速入门(一):界面布局:点击查看AutoCAD快速入门(二):图形窗口:点击查看AutoCAD快速入门(三):捕捉栅格绘制直线:点击查看AutoCAD快速入门(四):使用坐标绘图:点击查看AutoCAD快速入门(五):对象捕捉:点击查看AutoCAD快速入门(六):绘制圆:点击查看AutoCAD快速入门(七):打开、新建和保存文件:点击查看AutoCAD快速入门(八):选择对象:点击查看AutoCAD快速入门(九):绘制多段线:点击查看AutoCAD快速入门(十):移动、旋转和复制:点击查看AutoCAD快速入门(十一):删除、修剪和延伸:点击查看AutoCAD快速入门(十二):偏移:点击查看AutoCAD快速入门(十三):倒角和圆角:点击查看AutoCAD快速入门(十四):夹点编辑:点击查看AutoCAD快速入门(十五):图层基础操作:点击查看AutoCAD快速入门(十六):修改颜色、线型和线宽:点击查看AutoCAD快速入门(十七):利用图层控制对象属性:点击查看AutoCAD快速入门(十八):填充:点击查看AutoCAD快速入门(十九):添加文字:点击查看AutoCAD快速入门(二十):文字样式:点击查看AutoCAD快速入门(二十一):修改文字:点击查看AutoCAD快速入门(二十二):添加标注:点击查看AutoCAD快速入门(二十三):标注样式:点击查看AutoCAD快速入门(二十四):修改标注:点击查看AutoCAD快速入门(二十五):图块:点击查看AutoCAD快速入门(二十六):图像:点击查看AutoCAD快速入门(二十七):外部参照:点击查看AutoCAD快速入门(二十八):布局:点击查看AutoCAD快速入门(二十九):视口:点击查看AutoCAD快速入门(三十):打印:点击查看一界面布局对于CAD初学者来说,了解操作界面的布局至关重要,因为只有了解软件的界面布局,才能方便地与他人交流,才有可以正确领会各种教程和技巧,才能在操作时迅速地找到目标功能,提高学习的兴趣和效率。
第六章 空间点阵
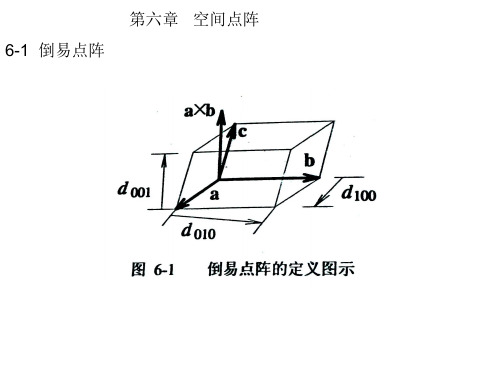
3
4 正点阵空间的位矢 R uvw u a v b w c 长度表示为 a u u 2 R uvw R uvw R uvw u , v , w b a b c v u , v , w G v w w c 5 h1 k 1l1 与 h 2 k 2 l 2 两平面夹角为两倒易矢 rh1 k 1 l1 * 与 rh 2 k 2 l 2 * 间
7
实际晶体中出现几率大
的是 Miller 指数小的晶面。
定义 2:一族晶面中离原点最 近的平面点阵在轴 a , b , c 上的 1 1 1 截距分别为 a , b , c 的 , , ,整数数组即为该晶面 的 Miller 指数。 h k l 定义 3:设一族点阵平面分别 将基矢 a , b , c 分为 h 段 , k 段 , l 段,则 该晶面的 Miller 指数为 hkl 。
a x a y a z a x a y a z ax ay az ax ay az 2 v a b c a b c bx by bz bx b y bz bx b y bz bx b y bz c c c c c c cx cy cz cx cy cz x y z x y z a a a b a c 2 1 b a b b b c det G 同理 v * det G * det G c a c b c c
Fourier
( x ua , y vb , z wc ) F hkl e
hkl
hkl
六角图的画法

六⾓图的画法所谓六⾓图就是利⽤功率表测量电流相位的⼀种⽅法,它是⼀种简单有效的相位检测⽅法。
利⽤六⾓图能正确的判断出:1)同⼀组电流互感器三相电流之间的相位是否正确。
2)功率⽅向继电器接线是否正确。
3)差动保护中不同组别电流互感器的电流相位是否正确。
4)电流互感器变⽐是否正确。
因此,向量六⾓图在实际应⽤中具有相当⼴泛的⽤途。
六⾓图的原理在⼀定坐标系统中,任何相量都可以⽤它在任何两个相交轴上的垂直投影来表⽰。
根据这⼀原理,我们采⽤的坐标系统是互成120’的三相对称电压系统。
由于线电压不受零序电压的⼲扰,所以采⽤三相线电压作为测量三相电流相位的基准量。
在相量图中,被测电流在⼀个电压相量上的投影,可以确定该电流相量端点的轨迹;在两个电压相量上的投影,可以确定被测电流相量端点的位置(即电流的相位和⼤⼩);⽤此⽅法得出不同⽅向的电流数值,进⾏⽮量计算,即可检验结果的准确性。
六⾓图实验将被测电流Ia按规定极性接⼊功率表的电流端⼦,再将同⼀系统的电压Uab、U bc、Uca按规定极性依次接⼊同⼀功率表的电压端⼦,分别读取Uab、Ubc、Uca 电压下的功率表的读数(其读数有正、负),再依次将Ib、Ic接⼊功率表重复上述试验。
⼀、绘制差动相量六⾓图,我们⼀般⽤的试验⼯具是钳形电流相位表,这个表可以测量电流、电压幅值,和电压与电流之间的夹⾓,两个电流之间的夹⾓。
要绘制六⾓图,我们只需要测量电流的幅值,与电流和电压(固定选取⼀相电压,如Uan)的夹⾓。
钳形电流表可取U1,I2,这样电压超前电流30度。
取U2, I1这样电压滞后电流30度。
在保护屏后边测量差动电流的幅值,以及电流和选定的电压的夹⾓,然后以选⽤的电压为基准(设为0度)画出测量所得的电流量,就绘制出了差动相量六⾓图。
⼆、在继电保护回路中,对有相位要求的电流回路,⼀般⽤电流相量六⾓图来判断电流回路接线是否正确。
从电流相量六⾓图可以直观反映出:同⼀组电流互感器三相电流IA、IB、Ic之间的关系;差动保护中不同组别电流互感器的电流之间的关系;阻抗或⽅向元件的电流和电压之间的相位关系。
chap8-晶体结构的几何理论

4mm(L44P)
mm2(L22P)
4mm
mm2
引出: 引出:空间格子可以有带心的格子
平行六面体中结点的分布
1)原始格子(P):结点分布于平行六面体的八个角顶。 )原始格子( ) 结点分布于平行六面体的八个角顶。 2)底心格子( C、A、B):结点分布于平行六面体的角 )底心格子( ) 顶及某一对面的中心。 顶及某一对面的中心。 3)体心格子(I ):结点分布于平行六面体的角顶和体中心。 )体心格子 :结点分布于平行六面体的角顶和体中心。 4)面心格子(F):结点分布于平行六面体的角顶和三对 )面心格子( ) 面的中心。 面的中心。
第八章 晶体结构的几何理论
主要教学内容
• • • • • • • 十四种空间格子* 十四种空间格子 空间格子中点的坐标、行列及面网符号* 空间格子中点的坐标、行列及面网符号 晶胞* 晶胞 晶体内部结构的对称要素* 晶体内部结构的对称要素 空间群(符号 符号)* 空间群 符号 等效点系 晶格缺陷
思考题: 思考题:
8.1 十四种空间格子 十四种空间格子(space lattice)
回顾: 回顾: • 空间格子是表示晶体结构中质点重复规 律的立体几何图形。 律的立体几何图形。 • 空间格子要素包括结点、行列、面网、 空间格子要素包括结点、行列、面网、 单位平行六面体。 单位平行六面体。
1.平行六面体的选择
平行六面体是空间格子中最小重复单位 对于每一种晶体结构而言,其结点的分布是客观存在的, 对于每一种晶体结构而言,其结ቤተ መጻሕፍቲ ባይዱ的分布是客观存在的, 但平行六面体的选择是人为的。 但平行六面体的选择是人为的。 空间格子是无限图形。在一个空间格子中可以划分出无数 空间格子是无限图形。 种不同形状和大小的平行六面体。如何划分? 种不同形状和大小的平行六面体。如何划分?
第五章 轴测图
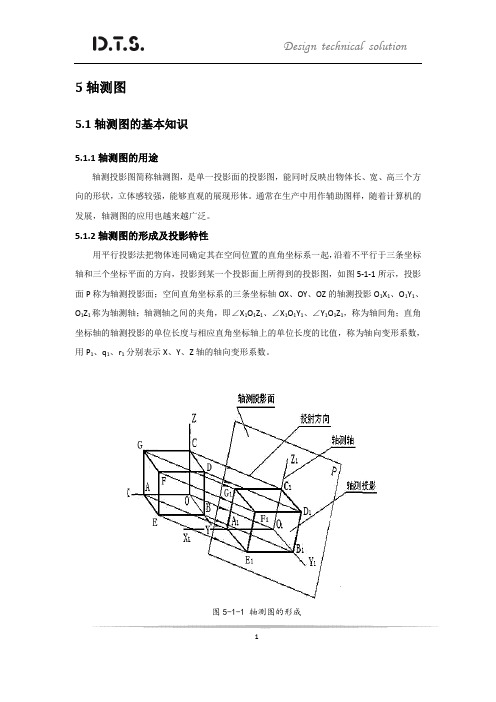
轴测图5.1轴测图的基本知识5.1.1轴测图的用途轴测投影图简称轴测图,是单一投影面的投影图,能同时反映出物体长、宽、高三个方向的形状,立体感较强,能够直观的展现形体。
通常在生产中用作辅助图样,随着计算机的发展,轴测图的应用也越来越广泛。
5.1.2轴测图的形成及投影特性用平行投影法把物体连同确定其在空间位置的直角坐标系一起,沿着不平行于三条坐标轴和三个坐标平面的方向,投影到某一个投影面上所得到的投影图,如图5-1-1所示,投影面P称为轴测投影面;空间直角坐标系的三条坐标轴OX、OY、OZ的轴测投影O1X1、O1Y1、O1Z1称为轴测轴;轴测轴之间的夹角,即∠X1O1Z1、∠X1O1Y1、∠Y1O1Z1,称为轴间角;直角坐标轴的轴测投影的单位长度与相应直角坐标轴上的单位长度的比值,称为轴向变形系数,Z轴的轴向变形系数。
用P1、q1、r1分别表示X、Y、5-1-1 轴测图的形成轴测图是用平行投影法得到的,具有以下投影特性:1. 平行性。
空间相互平行的直线,它们的轴测投影仍相互平行。
如图中BE∥DF∥OX,则B1E1∥D1F1∥O1X1。
2. 定比性。
物体上平行于坐标轴的线段的轴测投影与原线段之比,等于相应的轴向变形系数。
图中B1E1/BE=D1F1/DF=p1。
5.1.3轴测图的分类根据投射方向和轴测投影面的相对关系,轴测图分为正轴测投影图和斜轴测投影图两大类。
(1)当投影方向垂直于轴测投影面时,称为正轴测图。
(2)当投影方向倾斜于轴测投影面时,称为斜轴测图。
按轴向变形系数的选取不同,可得到多种轴测投影图。
国家标准中推荐使用的是正等轴测图和斜二轴测图。
本章仅介绍这两种轴测图的画法。
5.2正等轴测图的画法5.2.1 正等轴测图的形成,轴间角和轴向伸缩系数。
1. 形成当三根坐标轴与轴测投影面倾斜的角度相同时,用正投影法得到的投影图称为正等轴测图,简称正等测。
2. 轴间角正等轴测图的轴间角均为120º,即∠X1O1Y1=∠X1O1Z1=∠Y1O1Z1=120º。
2.2.4 晶体的14种Bravais格子简介

Bravais格子之惯用元胞的几何特征为:
a b c,
有 格点的分布方式只有一种:分布于惯用元胞的八个顶点上
一种Bravais格子:简单三斜Bravais格子
Pearson 记法 aP, 惯用
元胞如图2.2.2-1中的(a)图所示
背景音乐:
2°单斜(Monoclinic)晶系 Bravais格子之惯用元胞的几何特征为:
分布于惯用元胞的八个顶点上一种bravais格子称为简单六方bravais格子hp平行六面体元胞不能显示出点对称性常选用正六方棱柱体作为惯用元胞如图2221中的j图所示12090记法pearson背景音乐
2.2.4
晶体的十四种Bravais格子简介
就目前所知,晶体多达20000多种以上,它们的几何
外形更是多姿多彩、精美绝伦、奥妙无比,足以让所有 的能工巧匠叹为观止!然而,种类繁多、形状各异的晶 体在微观结构的周期性特征上却是极其简单的,描述晶 体微观结构周期性特征的Bravais格子总共只有十四种不
背景音乐:
5°六方(Hexagonal)晶系或六角晶系
Bravais格子之惯用元胞的几何特征为:
a b c, 90 0 , 120 0 有 格点的分布方式只有一种:分布于惯用元胞的八个顶点上 一种Bravais格子,称为简单六方
Bravais格子 Pearson 记法 hP, 平行六面体元胞不能显示出点对 称性,常选用正六方棱柱体作为
方Bravais格子。另一方面,惯用元
胞也可选用简单六方Bravais格子的 平行六面体元胞,只是除顶点外格点 还分布于体内(2/3,1/3,1/3)处 和(1/3,2/3,2/3)处,如图2.2.2 -1中的(k)图所示。因此,简单三 角Bravais格子通常又称为六方菱面 体 背景音乐:
浙教版初中数学九年级下册3.4简单几何体的表面展示图(12页)课件

3.4 简单几何体的表面展开图
几何体的展开图在生产时间中有着广泛的应用.通过 几何体的展开图可以确定和制作立体模型,也可以计算 相关集合体的侧面积和表面积.
观察与思考
某外包装盒的形状是棱柱(图3-1),它的两底面都是 水平的,侧棱都是竖直的(这样的棱柱叫做直棱柱).沿它的 棱剪开、铺平,就得到了它的平面展开图(图3-2).
关系?
做一做
1.制作圆锥并计算其相关的量. (1)在纸上画一个半径为6 cm,圆心角为216°的扇形. (2)将这个扇形剪下来,按图37-36所示围成一个圆锥. (3)指出这个圆锥的母线长,并求圆锥的高和底面的半径(
粘合部分忽略不计).
216° 6 cm
S
A
OB
做一做
2. 图3-3是四个几何体的平面展开图,请用纸分别复制下来,猜想下列展 开图可折成什么立体图形,实际动手折一下,并指出围成的几何体的 形状.
的表面积,就是图3-5中的两个主视图、两个左视 图和一个府视图的面积的和.你认为小明的想法正 确吗?为什么?
一起探究
—— 40 —— —— 40 —— —— 40 —— —20—
—20—
—20—
主 视 图
俯 视 图
—20—
—20—
左 视 图
主 视 图
—20—
俯 视 图
—20—
左 视 图
—— 40 ——
观察与思考
底面
侧棱 侧面
底面
图3-1
图3-2
观察与思考
1.这个棱柱有几个侧面?每个侧面是什么形状的? 2.这个棱柱的上、下底面的形状一样吗?他们各有几条边? 3.侧面的个数与底面图形的边数有什么关系? 4.这个棱柱有几条侧棱?它们的长度之间有什么关系? 5.侧面展开图的长和宽分别与棱柱底面的周长和侧棱长有什么
方格坐标纸模板

方格坐标纸模板
格子坐标纸是一种模板,它通常用于建筑设计、绘图、标注、数学计算或其他相关任务。
它可以用作方便准确的坐标系统,使您能够跟踪或记录点或线段,并帮助规划图形和建模。
由于格子坐标纸比竖直坐标纸具有更低的数字混乱,它可以比较容易地把点放在特定的位置上,制定统一的设计风格和尺寸标准,这使它成为一种重要的设计工具,已经在建筑、绘画、教育科研中得到人们的广泛推崇和应用。
格子坐标纸常用作A4或A3纸张大小,外观上,格子坐标纸主要由横向和纵向的格线组成,以直角形格栅为主,格线由小方格组成,一般情况下,单个小方格为2mm至5mm,格线也有不同的宽度,如0.5mm粗,表示粗线作为基准线,0.25mm细,表示细线分隔两个centered小方格,一般,格线的颜色是黑色的,和纸张的颜色相对比,容易对比观察,除此之外,还有半透明的图表,方便用户在覆盖整个纸张上绘制图形。
格子坐标纸的每个格线都代表着特定的补贴,即横向的线以水平方向表示,纵向的线以垂直方向表示,在将线表示为坐标轴时,上面的线标记为(X,0),右边的线标记为(0,Y),坐标系是指系统中所有点的集合,这些点代表了它们之间的关系,坐标轴相互垂直平行。
格子坐标纸是一种特定的坐标系统,可以有效地安排点和线,建立一个清晰的统计图表,而不易失真。
它主要适用于教学,使学生可以更精确地表示出点和线的位置。
它还可以应用于绘制精确的图纸,帮助建筑师或设计师绘制设计,也可以用作拼图游戏,游戏容易管理,使人们可以更容易地看到拼图的完成形状。
总之,格子坐标纸是一种实用工具,它有助于不同界面或媒体之间的定位和导航,减少拼图或寻找对象的时间,使图的清晰精确以及图画的连贯性,并便于观察和使用。
六年级下数学-数学好玩 绘制校园平面图 北师大版(24张)

作品欣赏
课后画一画
课外拓展
你能在家人或同学的帮助下,绘制出你家住房或小区的平 面图吗?
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
校门左侧为五层综合办公楼
在这次(活动把中计,我算的后表现的是数(请据把,每项记后在面的草☆图涂上上颜)色,涂满5个为做得最好的):
(尽量科学、合理、醒目)
实地测量(用卷尺、指南针等)并将数据及时记录在草图上。
我校绘图信息汇总
• 我校坐北朝南。南北长约250m,东西 180m。
• 校门左侧为五层综合办公楼 • 校门右侧为面积4631m2的图书实验楼 • 校门后方为面积2600m2的四层中心教学
数学好玩
绘制校园平面图
北师大版六年级下册
新课导入
推进新课
活动任务 绘制校园平面图。
设计方案
1.观察上面两张平面图,说说这些平面图有什么 共同的地方。
2.想一想,绘制校园平面图前,要先做哪些方面的 准备?
⑴在校园平面图中需要绘制哪些主要建筑物? ⑵需要收集哪些数据?如何收集这些数据呢? ⑶如何确定这幅图的比例尺?
小组内同学先分工,并填写分工表格。
南北长约250m,东西180m。
分工 校门右侧为面积4631m2的图书实验楼
正式绘制校园平面图。
测量
记录
教学楼后左侧为学校食堂和2幢住宿楼,正后
人员 ⑵需要收集哪些数据?如何收集这些数据呢?
你能在家人或同学的帮助下,绘制出你家住房或小区的平面图吗?
确定校园各建筑物在图上所处的方向
楼 和面积1700m2的电教综合楼 • 中心教学楼后是607m2的2层教学楼 • 教学楼后左侧为学校食堂和2幢住宿楼,
通用技术专用教室建设方案

通用技术专用教室建设方案
通用技术专用教室是学生进行技术设计、技术试验、技术制作、技术探究的实践活动场所,是保证通用技术课程方案的有效实施的必备硬件,《山东普通中小学基本办学条件标准(试行)》中对通用技术教学专用设备的要求是:学校须按照教育行政部门颁布的课程设置方案和课程标准的要求配置通用技术教学设备,应能满足中学开展通用技术教学的需要,便于教师灵活组织教学和学生有效学习。
通用技术教学设备主要包括教学活动所需要的教具、实践工具、道具、模型、图表、文献检索软件、图书卡片等。
通用技术教学设备按国家最新颁布的《普通高级中学理科教学仪器配备标准》进行配备。
其中必修模块所需设备为必配,选配设备由学校依据所用教材和所选模块进行配备。
现结合我市具体实际及国家《普通高级中学理科教学仪器配备标准》现对通用技术专用教室做出了如下基础性设计:
一、专用教室场地、功能
至少提供一间能供60人左右(6-10人/组)进行技术实践的通用技术专用教室。
可完成技术设计的方案构思、设计草图绘制、进行模型或产品的制作、装配以及技术试验等活动,同时该教室也可做为学生作品的展示室。
二、工具仪器配备
配备遵循“合理投入、充分利用、因地制宜、量力而行”的原则,按需选购,杜绝浪费。
暂拟定配备以下八类仪器设备和工具:技术设计工具、技术制作工具、学生试验工具仪器、技术测试仪器、教具模型、安全防护工具、消耗性材料、橱柜。
其中技术制作工具包括木工、钳工、电工三类,根据学校实际情况,可有所侧重。
另外,有些仪器设备教学中仅用一两次,可借用其他学科的教学设施,这样可以避免造成浪费。
通用技术专用教室设计方案配备目录。
六年级上数学教案-位置与方向1-人教新课标

六年级上数学教案位置与方向1人教新课标教学内容本节课为《位置与方向1》,选自人教新课标六年级上册数学教材。
教学内容主要包括:理解坐标平面上的点与位置的关系,掌握坐标的表示方法;学会使用方位角描述物体间的相对位置;能够通过给定的方向和距离确定物体的具体位置。
教学目标1. 知识与技能:学生能够准确描述物体在平面上的位置,并能运用方位角和距离确定物体的具体坐标。
2. 过程与方法:通过观察、操作和思考,培养学生空间想象力和逻辑思维能力。
3. 情感态度与价值观:激发学生对数学学习的兴趣,培养合作学习的意识和能力。
教学难点教学难点在于让学生理解方位角的概念,并能够将其应用于实际问题中,准确地描述和确定物体的位置。
教具学具准备1. 教具:多媒体教学设备,用于展示坐标平面和方位角的相关知识。
2. 学具:学生用坐标纸、直尺、量角器等绘图工具。
教学过程1. 导入:通过日常生活实例引入位置与方向的概念,激发学生的学习兴趣。
2. 新授:讲解坐标平面的概念,引导学生认识坐标轴和坐标点。
引入方位角,并通过实例演示其应用。
3. 实践操作:学生分组进行实践活动,使用坐标纸和工具测量并标记物体位置。
4. 巩固练习:完成教材中的练习题,加深对位置与方向知识的理解。
板书设计板书设计将围绕坐标平面、方位角和位置确定方法展开,通过图表和示例直观展示教学内容。
作业设计作业设计包括基础练习题和拓展思考题,旨在巩固学生对位置与方向的理解,并提高其解决实际问题的能力。
课后反思课后反思将围绕教学效果、学生接受程度和教学方法的适应性进行。
根据学生的反馈和学习情况,及时调整教学策略,以提高教学效果。
本教案遵循人教新课标的教学要求,注重理论与实践相结合,旨在通过多样化的教学方法,帮助学生掌握位置与方向的基本知识,培养其空间思维能力和解决问题的能力。
通过本节课的学习,学生将能够更好地理解和应用数学知识,为未来的学习打下坚实的基础。
重点细节:教学难点详细补充和说明教学难点是教学过程中的关键环节,它直接关系到学生对新知识的理解和掌握。
正六面体贴图

目录【设计题目及说明】 (2)设计需求 (2)设计分析 (3)【程序代码】 (3)【程序流程图】 (9)【参考文献】 (12)【设计题目及说明】设计需求以3维坐标xyz的原点为正方形体体心绘制一个正方体,任选六张图片,将图片作为纹理贴图映射到旋转的立方体的6个表面上。
我选用的图片是一下6个图:实现的效果图:具体说明:(1)导入6张图片,分别读取图片的信息,作为正方体表面的纹理。
(2)将每张图片绑定在正方体表面上,以图片每个像素的颜色填充正方体表面。
(3)使用键盘:“1”暂停正方体旋转,“2”开始旋转,“esc”退出播放。
(4)位图图片存放在data文件夹中。
(5)运行环境需安装opengl库函数。
(6)开发工具:visual C++ 6.0。
设计分析本次设计的目的是对正六面体进行纹理映射,使用六张不同的图片作为纹理,分别映射到六面体的六个面上。
设计步骤:(1)创建纹理对象并指定纹理。
(2)指定纹理应用。
(3)启用纹理。
(4)指定纹理坐标。
纹理映射需要建立纹理(u,v)与物体空间坐标(x,y,z的映射关系,也就是把物体空间的x,y,z和,u,v建立等式关系。
【程序代码】#include <windows.h>#include <gl\GL.h>#include <gl\GLU.h>#include <gl\GLAux.h>#include <stdio.h>#include <gl\glut.h>#pragma comment (lib,"glaux")GLfloat xrot=0;GLfloat yrot=0;GLfloat zrot=0;GLuint texture[6];bool flag = true;void Reshape(int w, int h){glViewport(0,0,w,h); // 重置当前的视口glMatrixMode(GL_PROJECTION);glLoadIdentity( );gluPerspective(45.0f, (GLfloat)w/(GLfloat)h,0.1f, 100.0f); //// 设置视口的大小glMatrixMode(GL_MODELVIEW);glLoadIdentity( );}//获得位图AUX_RGBImageRec *LoadBMP(cha r *Filename){FILE *File=NULL;if (!Filename){return NULL;}File=fopen(Filename,"r");if (File){fclose(File);return auxDIBImageLoad(Filename);}return NULL;}// 位图转换成纹理int LoadGLTextures(){int Status=FALSE;AUX_RGBImageRec *TextureImage[6];memset(TextureImage,0,sizeof(AUX_RGBImageRec *)*6);if((TextureImage[0] = LoadBMP("data/image1.bmp"))&&(TextureImage[1] = LoadBMP("data/image2.bmp"))&&(TextureImage[2] = LoadBMP("data/image3.bmp"))&&(TextureImage[3] = LoadBMP("data/image4.bmp"))&&(TextureImage[4]= LoadBMP("data/image5.bmp"))&&(TextureImage[5] = LoadBMP("data/image6.b mp"))){Status=TRUE;glGenTextures(6, &texture[0]); // 创建纹理for (int i=0; i<6; i++){glBindTexture(GL_TEXTURE_2D, texture[i]);glTexImage2D(GL_TEXTURE_2D, 0, 3, TextureImage[i]->sizeX, TextureImage[i]->sizeY, 0, GL_RGB, GL_UNSIGNED_BYTE, TextureImage[i]->data);glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_LINEAR);glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_LINEAR);}}for (int i=0; i<6; i++){if (TextureImage[i]){if (TextureImage[i]->data){free(TextureImage[i]->data);}free(TextureImage[i]);}}return Status;}void Display(){glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);glLoadIdentity();glTranslatef(0.0f, 0.0f,-5.0f);glRotatef(xrot,1.0f,0.0f,0.0f);glRotatef(yrot,0.0f,1.0f,0.0f);glRotatef(zrot,0.0f,0.0f,1.0f);//frontglBindTexture(GL_TEXTURE_2D,texture[0]);glBegin(GL_QUADS);glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f);glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, 1.0f);glEnd();glFlush();//backglBindTexture(GL_TEXTURE_2D,texture[1]);glBegin(GL_QUADS);glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, -1.0f); glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f); glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f); glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, -1.0f); glEnd();glFlush();//topglBindTexture(GL_TEXTURE_2D,texture[2]);glBegin(GL_QUADS);glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f); glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, 1.0f, 1.0f); glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, 1.0f, 1.0f); glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f); glEnd();glFlush();//bottomglBindTexture(GL_TEXTURE_2D,texture[3]);glBegin(GL_QUADS);glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, -1.0f, -1.0f); glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, -1.0f, -1.0f); glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f); glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f); glEnd();glFlush();//rightglBindTexture(GL_TEXTURE_2D,texture[4]);glBegin(GL_QUADS);glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, -1.0f, -1.0f); glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f); glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, 1.0f, 1.0f); glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f); glEnd();glFlush();//leftglBindTexture(GL_TEXTURE_2D,texture[5]);glBegin(GL_QUADS);glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, 1.0f, 1.0f);glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f);glEnd();glFlush();glutSwapBuffers( );}boolean init(){if (!LoadGLTextures()){return FALSE;}glEnable(GL_TEXTURE_2D);glShadeModel(GL_SMOOTH);glClearColor(0.0f, 0.0f, 0.0f,0.0f);glClearDepth(1.0f);glEnable(GL_DEPTH_TEST);glDepthFunc(GL_LEQUAL);glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST);return TRUE;}void keyfun(unsigned char key,int x,int y){GLfloat light[] = {0.5f, 1.0f, 1.0f, 0.0f};GLfloat mtrxSpecular[] = {0.8f, 1.0f, 1.0f, 1.0f};switch (key){case'1':flag=false;break;case '2':flag = true;break;case '\033':exit(0);break;default:break;}glutPostWindowRedisplay(1);}void roate(int rot){if(flag==true){xrot += 1.0f;yrot += 2.0f;zrot += 3.0f;}glutPostWindowRedisplay(1);glutTimerFunc(30,roate,1);}void main( ){int i=1;glutInitDisplayMode(GLUT_DOUBLE|GLUT_RGBA);glutInitWindowPosition(0,0);glutInitWindowSize(800,600);glutCreateWindow("纹理映射");init();glutKeyboardFunc(keyfun);glutReshapeFunc(Reshape);glutDisplayFunc(Display);glutTimerFunc(30,roate,1);glutMainLoop( );}【程序流程图】int main(in t argc,char *argv) voi d Reshape()void roate(int rot) void Display()voidboolean init()AUX_RGBImageRec *LoadBMP(cha r *Filename)[1] : 清华大学出版社,2006.[2] 北京:清华大学出版社,2008.[3] 北京:清华大学出版社,2008.[4] :化学工业出版社,2010.!)。
