医学统计学分析计算题答案

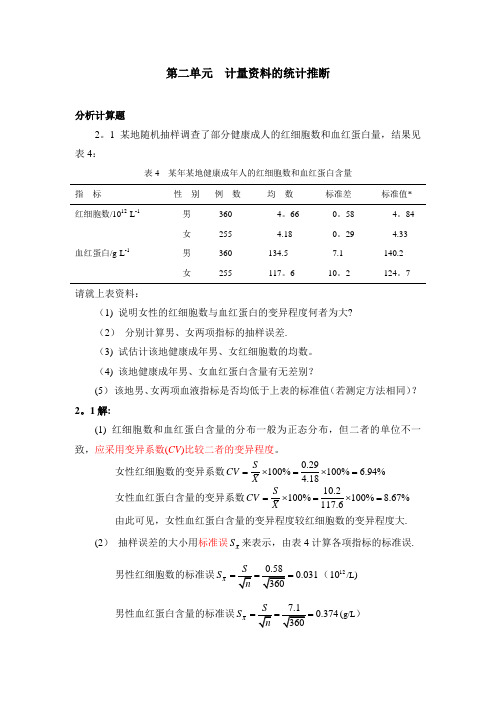
第二单元计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指标性别例数均数标准差标准值* 红细胞数/1012·L-1男360 4.66 0.58 4.84女255 4.18 0.29 4.33血红蛋白/g·L-1男360 134.5 7.1 140.2女255 117.6 10.2 124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？(2) 分别计算男、女两项指标的抽样误差。

(3) 试估计该地健康成年男、女红细胞数的均数。

(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV)比较二者的变异程度。

女性红细胞数的变异系数女性血红蛋白含量的变异系数由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。

(2) 抽样误差的大小用标准误来表示，由表4计算各项指标的标准误。

男性红细胞数的标准误(/L)男性血红蛋白含量的标准误(g/L)女性红细胞数的标准误(/L)女性血红蛋白含量的标准误(g/L)(3) 本题采用区间估计法估计男、女红细胞数的均数。

样本含量均超过100，可视为大样本。

未知，但足够大，故总体均数的区间估计按()计算。

该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)/L。

该地女性红细胞数总体均数的95%可信区间为：(4.18－1.96×0.018 , 4.18＋1.96×0.018)，即(4.14 , 4.22)/L。

(4) 两成组大样本均数的比较，用u检验。

1) 建立检验假设，确定检验水准H0：，即该地健康成年男、女血红蛋白含量均数无差别H1：，即该地健康成年男、女血红蛋白含量均数有差别2) 计算检验统计量3) 确定P值，作出统计推断查t界值表(ν＝∞时)得P<0.001，按水准，拒绝H0，接受H1，差别有统计学意义，可以认为该地健康成年男、女的血红蛋白含量均数不同，男性高于女性。

(5) 样本均数与已知总体均数的比较，因样本含量较大，均作近似u检验。

1) 男性红细胞数与标准值的比较①建立检验假设，确定检验水准H0：，即该地男性红细胞数的均数等于标准值H1：，即该地男性红细胞数的均数低于标准值单侧②计算检验统计量③确定P值，作出统计推断查t界值表(ν＝∞时)得P<0.0005，按水准，拒绝H0，接受H1，差别有统计学意义，可以认为该地男性红细胞数的均数低于标准值。

2) 男性血红蛋白含量与标准值的比较①建立检验假设，确定检验水准H0：，即该地男性血红蛋白含量的均数等于标准值H1：，即该地男性血红蛋白含量的均数低于标准值单侧②计算检验统计量③确定P值，作出统计推断查t界值表(ν＝∞时)得P<0.0005，按水准，拒绝H0，接受H1，差别有统计学意义，可以认为该地男性血红蛋白含量的均数低于标准值。

3) 女性红细胞数与标准值的比较①建立检验假设，确定检验水准H0：，即该地女性红细胞数的均数等于标准值H1：，即该地女性红细胞数的均数低于标准值单侧②计算检验统计量③确定P值，作出统计推断查t界值表(ν＝∞时)得P<0.0005，按水准，拒绝H0，接受H1，差别有统计学意义，可以认为该地女性红细胞数的均数低于标准值。

4) 女性血红蛋白含量与标准值的比较①建立检验假设，确定检验水准H0：，即该地女性血红蛋白含量的均数等于标准值H1：，即该地女性血红蛋白含量的均数低于标准值单侧②计算检验统计量③确定P值，作出统计推断查t界值表(ν＝∞时)得P<0.0005，按水准，拒绝H0，接受H1，差别有统计学意义，可以认为该地女性血红蛋白含量的均数低于标准值。

2.2 为了解某高寒地区小学生血红蛋白含量的平均水平，某人于1993年6月随机抽取了该地小学生708名，算得其血红蛋白均数为103.5g/L，标准差为1.59g/L。

试求该地小学生血红蛋白均数的95%可信区间。

2.2解：未知，足够大时，总体均数的区间估计可用()。

该地小学生血红蛋白含量均数的95％可信区间为：()，即(103.38 , 103.62)g/L 。

2.3 一药厂为了解其生产的某药物（同一批次）之有效成分含量是否符合国家规定的标准，随机抽取了该药10片，得其样本均数为103.0mg，标准差为2.22mg。

试估计该批药剂有效成分的平均含量。

2.3解：该批药剂有效成分的平均含量的点值估计为103.0 mg。

未知且很小时，总体均数的区间估计可用估=2.262，该批药剂有效成分的平均含量的95％可信区间计。

查t界值表得t0.05/2,9为：()，即(101.41 , 104.59)mg。

2.4 152例麻疹患儿病后血清抗体滴度倒数的分布如表5，试作总体几何均数的点值估计和95%区间估计。

表5 152例麻疹患儿病后血清抗体滴度倒数的分布滴度倒数 1 2 4 8 16 32 64 128 256 512 1024 合计人数0 0 1 7 10 31 33 42 24 3 1 152 2.4解：将原始数据取常用对数后记为X，则，用()估计，则滴度倒数对数值的总体均数的95％可信区间为：()，即(1.7893 , 1.9301)。

所以滴度倒数的总体几何均数的点估计值为：，滴度倒数的总体几何均数的95%区间估计为()，即(61.56 , 85.13)。

SPSS操作数据录入：打开SPSS Data Editor窗口，点击Variable View标签，定义要输入的变量x和f；再点击Data View标签，录入数据（见图2.4.1，图2.4.2）。

图2..4.1 Variable View窗口内定义要输入的变量x和f图2.4.2 Data View窗口内录入数据分析：Transform Compute…Target Variable：键入 logxNumeric Expression： LG10(x) 将原始数据取对数值OKData Weight Cases…Weight cases by Frequency Variable： f 权重为fOKAnalyze Descriptive Statistics Explore… 探索性分析Dependent list：logx 分析变量logxDisplay： StatisticsS tatistics…：Descriptives 统计描述ContinueOK注：最后得到结果是原始数据对数值的均数及其95%可信区间。

2.5 某口腔医生欲比较“个别取模器龈下取模技术”与“传统硅橡胶取模方法”两种取模技术精度的差异，在12名病人口中分别用两种方法制取印模，在体视显微镜下测量标志点到龈沟底的距离，结果如表6，问两种取模方法结果有无差异？表6 12个病人口腔某测量标志点到龈沟底的距离/cm病例号个别取模器龈下取模技术传统硅橡胶取模方法1 0.626 0.6142 0.627 0.6263 0.670 0.6544 0.548 0.5495 0.590 0.5746 0.603 0.5877 0.605 0.6028 0.347 0.3389 0.768 0.75910 0.576 0.57211 0.330 0.31812 0.233 0.2192.5解：本题为配对设计的两样本均数的比较，采用配对检验。

表2.5.1 12个病人口腔某测量标志点到龈沟底的距离/cm 病例号个别取模器龈下取模传统硅橡胶取模法1 0.626 0.614 0.0122 0.627 0.626 0.0013 0.670 0.654 0.0164 0.548 0.549 -0.0015 0.590 0.574 0.0166 0.603 0.587 0.0167 0.605 0.602 0.0038 0.347 0.338 0.0099 0.768 0.759 0.00910 0.576 0.572 0.00411 0.330 0.318 0.01212 0.233 0.219 0.014(1) 建立检验假设，确定检验水准H0：，即两种取模方法结果无差异H1：，即两种取模方法结果有差异(2) 计算检验统计量两种取模方法结果的差值d的计算见表2.5.1。

(3) 确定P值，作出统计推断查t界值表得P<0.001，按水准，拒绝H0，接受H1，差别有统计学意义，可以认为两种取模方法结果有差异，个别取模器龈下取模法标志点到龈沟底的距离略高于传统硅胶取模法。

SPSS操作数据录入：打开SPSS Data Editor窗口，点击Variable View标签，定义要输入的变量x1和x2；再点击Data View标签，录入数据（见图2.5.1，图2.5.2）。

图2.5.1 Variable View窗口内定义要输入的变量x1和x2图2.5.2 Data View窗口内录入12对数据分析：Analyze Compare Means Paired-samples T Test…配对设计均数比较t检验Paired Variables： x1 x2 配对变量为x1和x2OK2.6 将钩端螺旋体病人的血清分别用标准株和水生株作凝溶试验，测得稀释倍数如表7，问两组的平均效价有无差别？表7 钩端螺旋体病患者血清作凝溶试验测得的稀释倍数标准株(11人) 100 200 400 400 400 400 800 1600 1600 1600 3200 水生株(9人) 100 100 100 200 200 200 200 400 4002.6解：本题为成组设计的两小样本几何均数的比较，采用成组检验。

将原始数据取常用对数值后分别记为、，则(1) 建立检验假设，确定检验水准H0：两种株别稀释倍数的总体几何均数的对数值相等H1：两种株别稀释倍数的总体几何均数的对数值不等(2) 计算检验统计量(3) 确定P值，作出统计推断查t界值表得0.005<P<0.01，按水准，拒绝H0，接受H1，差别有统计学意义，可以认为二者稀释倍数的总体几何均数的对数值不等，即两种株别的平均效价有差别，标准株的效价高于水生株。

SPSS操作数据录入：打开SPSS Data Editor窗口，点击Variable View标签，定义要输入的变量g和x；再点击Data View标签，录入数据（见图2.6.1，图2.6.2）。