试验设计与数据分析第一次作业习题答案
实验设计与数据分析作业
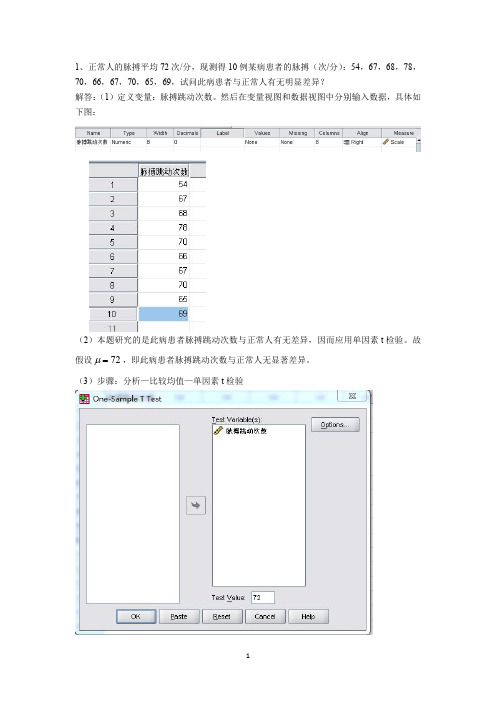
1、正常人的脉搏平均72次/分,现测得10例某病患者的脉搏(次/分):54,67,68,78,70,66,67,70,65,69,试问此病患者与正常人有无明显差异?解答:(1)定义变量:脉搏跳动次数。
然后在变量视图和数据视图中分别输入数据,具体如下图:(2)本题研究的是此病患者脉搏跳动次数与正常人有无差异,因而应用单因素t 检验。
故假设72=μ,即此病患者脉搏跳动次数与正常人无显著差异。
(3)步骤:分析—比较均值—单因素t 检验得到输出结果:Sig=0.037<0.05,故拒绝原假设,接受备择假设,即此病患者脉搏跳动次数与正常人由于.有显著差异。
2、比较两种茶多糖提取工艺的试验,分别从两种工艺中各取1个随机样本来测定其粗提取物中茶多糖的含量,问两种工艺的粗提物中茶多糖含量(单位:%)有无显著差异?醇沉淀法(x1)27.5227.7828.0328.8828.7527.94超滤法(x2)29.3228.1528.0028.5829.0029.32解答:(1)分别定义变量:工艺方法、茶多酚含量。
然后在变量视图和数据视图中分别输入数据,具体如下图:(2)本题研究的是醇沉淀法和超滤法这两种工艺的粗提物中茶多糖含量(单位:%)有无显著差异,因而应用独立样本t 检验。
故假设21μμ=,即这两种工艺的粗提物中茶多糖含量无显著性差异。
(3)步骤:分析—比较均值—独立样本t 检验。
得到输出结果:由于F检验.Sig=0.766>0.05,故方差相等,即Equal variances assumed,选择第一行的数据。
对于t检验.Sig=0.104大于0.05,故接受原假设,即这两种工艺的粗提物中茶多糖含量无显著性差异。
3、用四种不同型号的仪器对某种机器零件的七级光洁表面进行检查,每种仪器分别在同一表面上反复测四次,得数据如下,试从这些数据推断四种型号的仪器对测量结果有无显著差异?仪器号数据1 2 3 4-0.21-0.06-0.17-0.14 0.160.080.030.11 0.10-0.070.15-0.02 0.12-0.04-0.020.11解答:(1)分别定义变量:仪器号、光滑度。
实验设计与数据处理第一章例题及课后习题答案

1、 根据三组数据的绝对误差计算权重:12322211110000,25,400000.010.20.005w w w ====== 因为123::400:1:1600w w w = 所以1.54400 1.71 1.53716001.53840011600pH ⨯+⨯+⨯==++2、 因为量程较大的分度值也较大,用量程大的测量数值较小的物理量会造成很大的系统误差。
3.、含量的相对误差为0.2g ,所以相对误差为:0.20.99790525.3Rx E x ∆===。
4、 相对误差18.20.1%0.0182x mg mg ∆=⨯= 故100g 中维生素C 的质量范围为:18.2±0.0182。
5、1)、压力表的精度为1.5级,量程为0.2,则max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2)、1的汞柱代表的大气压为0.133,所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3)、1水柱代表的大气压为gh ρ,其中29.8/g m s =则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯6、样本测定值算术平均值 3.421666667 3.48 几何平均值 3.421406894 3.37 调和平均值 3.421147559 3.47 标准差s 0.046224092 3.38 标准差 0.04219663 3.4 样本方差 0.002136667 3.43 总体方差0.001780556 算住平均误差 0.038333333极差 0.117、依题意,检测两个分析人员测定铁的精密度是否有显著性差异,用F双侧检验。
根据试验值计算出两个人的方差及F值:221221223.733, 2.3033.7331.621232.303s s s F s ===== 而0.9750.025(9,9)0.248386,(9,9) 4.025994F F ==, 所以0.9750.025(9,9)(9,9)F F F << 两个人的测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
实验设计与数据处理课后答案

《试验设计与数据处理》专业:机械工程班级:机械11级专硕学号:S110805035 姓名:赵龙第三章:统计推断3-13 解:取假设H0:u1-u2≤0和假设H1:u1-u2>0用sas分析结果如下:Sample StatisticsGroup N Mean Std. Dev. Std. Error----------------------------------------------------x 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 = 0Alternative: Mean 1 - Mean 2 ^= 0If Variances Are t statistic Df Pr > t----------------------------------------------------Equal 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05,可认为拒绝原假设,即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。
3-14 解:用sas分析如下:Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1Alternative: Variance 1 / Variance 2 ^= 1- Degrees of Freedom -F Numer. Denom. Pr > F----------------------------------------------2.27 7 9 0.2501由p值为0.2501>0.05(显著性水平),所以接受原假设,两方差无显著差异第四章:方差分析和协方差分析4-1 解:Sas分析结果如下:Dependent Variable: ySum ofSource DF Squares Mean Square F Value Pr > FModel 4 1480.823000 370.205750 40.88 <.0001Error 15 135.822500 9.054833Corrected Total 19 1616.645500R-Square Coeff Var Root MSE y Mean0.915985 13.12023 3.009125 22.93500Source DF Anova SS Mean Square F Value Pr > Fc 4 1480.823000 370.205750 40.88 <.0001由结果可知,p值小于0.001,故可认为在水平a=0.05下,这些百分比的均值有显著差异。
试验设计和数据分析第一次作业习题答案解析

习题答案1.设用三种方法测定某溶液时,得到三组数据,其平均值如下:x1̅=(1.54±0.01)mol/Lx2̅=(1.7±0.2)mol/Lx3̅=(1.537±0.005)mol/L试求它们的加权平均值。
解:根据数据的绝对误差计算权重:w1=10.012,w2=10.22,w3=10.0052因为w1:w2:w3=400:1:1600所以w̅̅̅=1.54×400+1.7×1+1.537×1600400+1+1600=1.5376812.试解释为什么不宜用量程较大的仪表来测量数值较小的物理量。
答:因为用量程较大的仪表来测量数值较小的物理量时,所产生的相对误差较大。
如3.测得某种奶制品中蛋白质的含量为(25.3±0.2)g/L,试求其相对误差。
解:E w=∆ww =0.225.3=0.79%4.在测定菠萝中维生素C含量的测试中,测得每100g菠萝中含有18.2mg维生素C,已知测量的相对误差为0.1%,试求每100g菠萝中含有维生素C的质量范围。
解:E w=∆ww=0.1%,所以∆m=m×E w=18.2×0.1%=0.0182ww所以m的范围为18.1818mg<m<18.2182ww或依据公式w w=w×(1±|w w|)=18.2×(1±0.1%)mg5.今欲测量大约8kPa(表压)的空气压力,试验仪表用1)1.5级,量程0.2MPa 的弹簧管式压力表;2)标尺分度为1mm的U型管水银柱压差计;3)标尺分度为1mm的U形管水柱压差计。
求最大绝对误差和相对误差。
解:1)压力表的精度为1.5级,量程为0.2MPa,则|∆w|www=0.2×1.5%=0.003www=3wwww w=∆ww×100%=38×100%=3.75×10−1=37.5%2)1mm汞柱代表的大气压为0.133KPa,所以|∆w|www=0.133wwww w=∆ww×100%=0.1338×100%=1.6625×10−2=1.6625%3)1mm水柱代表的大气压:ρgh,其中g=9.80665m/s2,通常取g=9.8m/s2则|∆w|www=9.8×10−3wwww w=∆ww×100%=9.8×10−38×100%=1.225×10−36.在用发酵法生产赖氨酸的过程中,对产酸率(%)作6次评定。
试验设计与数据分析(答案)
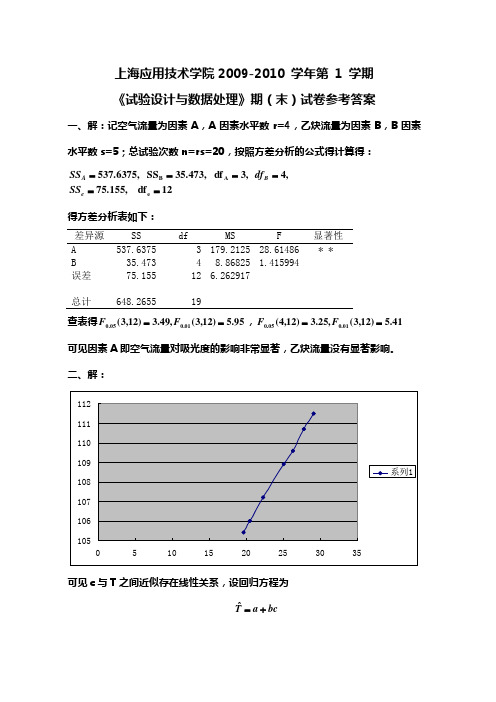
上海应用技术学院2009-2010 学年第 1 学期 《试验设计与数据处理》期(末)试卷参考答案一、解:记空气流量为因素A ,A 因素水平数r=4,乙炔流量为因素B ,B 因素水平数s=5;总试验次数n=rs=20,按照方差分析的公式得计算得:12df 75.155,,4 ,3df 35.473,SS 537.6375,e A B ======e B A SS df SS得方差分析表如下: 差异源 SS df MS F 显著性A 537.6375 3 179.2125 28.61486 * *B 35.473 4 8.86825 1.415994误差 75.155 12 6.262917 总计 648.2655 19查表得95.5)12,3(,49.3)12,3(01.005.0==F F ,41.5)12,3(,25.3)12,4(01.005.0==F F 可见因素A 即空气流量对吸光度的影响非常显著,乙炔流量没有显著影响。
二、解:可见c 与T 之间近似存在线性关系,设回归方程为bc a T+=ˆ 代入回归计算公式可得:a=92.911,b=0.6381,相关系数R ×R=0.9995说明所建立的回归方程与试验数据拟合得很好。
三、解:采用分数法,试验区间为[3,8],以1为单位可等分为5份,设桶数为x 时试验指标值为f(x),则:第一次试验点在3/5即6桶处,得试验指标值f(6); 第二次试验点在2/5即5桶处,得试验指标值f(5),比较两次试验结果f(6)>f(5),舍掉区间[3,5];第三次试验点在区间[5,8]的2/3即7桶处,得试验指标f(7),比较试验指标得f(6)>f(7),试验结束,最优结果为6桶。
四、解:(1)这是一个4因素2水平的试验,但还有一个交互作用,为5因素2水平,可将因素A,B,C,D分别放在正交表的第1,2,4,7列,交互作用A×(2)按照直观分析法得计算结果如下:因素主次 C A×B B A D(3)根据上一步排出的因素主次,可知交互作用A×B比因素B,A对试验指标的影响更大,所以确定A、B的水平应按A、B各水平搭配的好坏来确定。
试验设计与数据分析试题1

A.反映全部观察值的离散程度B.度量了一组数据偏离平均数的大小
C.反映了均数代表性的好坏D.不会小于算术均数
4.某地调查20岁男大学生100名,身高标准差为4.09cm,体重标准差为4.10kg,比较两
者的变异程度,结果()。
A.体重变异度大B.身高变异度较大
C.两者变异度相同D.由单位不同,两者标准差不能直接比较
xi1 3 4 5 6 7 8 9 10
yi2 7 8 10 11 12 10 9 8
1以下为excel作出的散点图,请问是否宜配二次项和三次项?理由何在?
如果采用添加趋势线法来确定回归参数,选择何种类型?阶数多少?截距该设定为0吗?
②写出求解多项式方程系数的正规方程组,并交代方程组来由。附:以下为计算表。
5、我们试验研究的目的是为了尽可能的解释自然界。成功的实验设计应该包括考虑到尽可能的减少的方差。两个基本的方法是a.在分析中增加;b.加入一个或更多的。
6.在多数情况下很多影响试验结果的因素自然的变化着,我们无法控制。因此,我们必须了解,如果没有采取处理措施,结果会是怎样。这就是的作用。
7、在有些实验中,被重复抽取的样本仅仅是而非真正的重复,我们通常这种情况称为伪重复。
得分
二、判断题:(每题1分,共10分,判断错误倒扣1分)
1.主成分分析的主要特点在于通过主成分转换消除性状间的相关的干扰。()
2.单纯形重心设计就是将试验点安排在单纯形的重心上,其中4维的单纯形重心设计的重心共有16个重心,即试验点为16个。()
3.配方试验设计的约束条件可以简单的表示为:xj>0, x1+x2+…+xm=1。()
专业:生物工程
试验设计与数据分析第一次作业习题答案
分析人员 A 8
分析人员 B 7.5
8
7.5
10
4.5
10
4
6
5.5
6
8
4
7.5
6
7.5
6Leabharlann 5.588
F-检验 双样本方差分析
分析人员 A 分析人员 B
平均
7.2
6.55
方差
3.733333333 2.302778
观测值
10
10
df
9
9
F
1.621230398
P(F<=f) 单尾 0.24144058
(
)
解:工艺的稳定性可用精密度来表征,而精密度可由极差、标准差或方差等表征,这里依据
方差来计算。 更稳定。
,由于
,所以新的冶炼工艺比旧工艺生产
(依据极差:
,
,同样可以得到上述结论)
(依据标准差
)
检验两种工艺之间是否存在系统误差,采用 t 检验法。
1)先判断两组数据的方差是否有显著性差异。根据试验数据计算出各自的平均值和方
标准差 s、标准差 、样本方差 、总体方差 解:
、算术平均误差 和极差 。
数据 计算公式
3.48 算术平均值
计算结果 3.421667
3.37 几何平均值
3.421407
调和平均值 3.47
或
3.421148
3.38 标准样本差
3.40 总体标准差
3.43 样本方差 总体方差
算术平均误差 极差
0.046224
试问 A 与 B 两人测定铁的精密度是否有显著性差异?(
)
解:依题意,检验 A 与 B 两人测定铁的精密度是否有显著性差异,采用 F 双侧检验。根据 试验值计算出两种方法的方差以及 F 值:
《试验设计与数据处理》上机练习-1

《试验设计与数据处理》上机练习-1《实验设计与数据处理》上机练习1、用Excel作出下表数据带数据点的折线散点图:(1)分别作出加药量和余浊、总氮T-N、总磷T-P、COD的变化关系图(共四张图,要求它们的格式大小一致,并以两张图并列的形式排版到Word中,注意调整图形的大小);(2)在一张图中作出加药量和浊度去除率、总氮T-N去除率、总磷T-P去除率、COD 去除率的变化关系折线散点图。
加药量 (mg/L) 50 75 100 125 150 加药量 (mg/L)50 75 100 125 150 总磷T-P T-P(mg/L) 去除率(%) 1.09 0.57 0.27 0.32 0.42 16.15 56.15 79.23 75.38 67.69 COD COD(mg/L) 去除率(%) 53 52 51 52 56 73.09 73.61 74.11 73.61 71.57 浊度余浊(NTU)去除率(%) 11.9 7.5 6.8 6.2 5.6 80.17 87.51 88.67 89.67 90.67 总氮T-N T-N(mg/L) 去除率(%) 11.01 14.01 14.38 13.01 10.08 52.05 38.98 37.37 43.34 56.11 2、对离心泵性能进行测试的实验中,得到流量Qv、压头H和效率η的数据如表所示,绘制离心泵特性曲线。
将扬程曲线和效率曲线均拟合成多项式。
(要求作双Y轴图)流量Qv、压头H和效率η的关系数据序号1 0.0 15.002 0.4 14.843 0.8 14.564 1.2 14.335 1.6 13.966 2.0 13.65Qv(m3/h) H/m1η序号0.0 7 2.4 13.28 0.3850.085 8 2.8 12.81 0.4160.156 9 3.2 12.45 0.4460.224 10 3.6 11.98 0.4680.277 11 4.0 11.30 0.4690.333 12 4.4 10.53 0.431Qv(m3/h) H/m η3、用荧光法测定阿司匹林中的水杨酸(SA),测得的工作曲线和样品溶液的数据如下表:C(SA)/μg.mL-1 F(荧光强度) 0.50 1.00 1.50 2.00 3.00 样品1 样品2 10.9 22.3 33.1 43.5 65.4 38.2 39.2 (1)列出一元线性回归方程,求出相关系数,并给出回归方程的精度;(2)求出未知液(样品)的水杨酸(SA)浓度。
试验设计及数据分析第一次作业习题答案

习题答案1.设用三种方法测定某溶液时,得到三组数据,其平均值如下:x1̅̅̅=(1.54±0.01)mol/Lx2̅̅̅=(1.7±0.2)mol/Lx3̅̅̅=(1.537±0.005)mol/L试求它们的加权平均值。
解:根据数据的绝对误差计算权重:w1=10.012,w2=10.22,w3=10.0052因为w1:w2:w3=400:1:1600所以w̅=1.54×400+1.7×1+1.537×1600400+1+1600=1.5376812.试解释为什么不宜用量程较大的仪表来测量数值较小的物理量。
答:因为用量程较大的仪表来测量数值较小的物理量时,所产生的相对误差较大。
如3.测得某种奶制品中蛋白质的含量为(25.3±0.2)g/L,试求其相对误差。
解:E w=∆ww =0.225.3=0.79%4.在测定菠萝中维生素C含量的测试中,测得每100g菠萝中含有18.2mg维生素C,已知测量的相对误差为0.1%,试求每100g菠萝中含有维生素C的质量范围。
解:E w=∆ww=0.1%,所以∆m=m×E w=18.2×0.1%=0.0182ww所以m的范围为18.1818mg<m<18.2182ww或依据公式w w=w×(1±|w w|)=18.2×(1±0.1%)mg5.今欲测量大约8kPa(表压)的空气压力,试验仪表用1)1.5级,量程0.2MPa 的弹簧管式压力表;2)标尺分度为1mm的U型管水银柱压差计;3)标尺分度为1mm的U形管水柱压差计。
求最大绝对误差和相对误差。
解:1)压力表的精度为1.5级,量程为0.2MPa,则|∆w|www=0.2×1.5%=0.003www=3wwww w=∆w w×100%=38×100%=3.75×10−1=37.5%2)1mm汞柱代表的大气压为0.133KPa,所以|∆w|www=0.133wwww w=∆w w×100%=0.1338×100%=1.6625×10−2=1.6625%3)1mm水柱代表的大气压:ρgh,其中g=9.80665m/s2,通常取g=9.8m/s2则|∆w|www=9.8×10−3wwww w=∆w w×100%=9.8×10−38×100%=1.225×10−36.在用发酵法生产赖氨酸的过程中,对产酸率(%)作6次评定。
实验设计与数据处理第一章例题及课后习题(附答案)

1、 根据三组数据的绝对误差计算权重:12322211110000,25,400000.010.20.005w w w ====== 因为123::400:1:1600w w w = 所以1.54400 1.71 1.53716001.53840011600pH ⨯+⨯+⨯==++2、 因为量程较大的分度值也较大,用量程大的测量数值较小的物理量会造成很大的系统误差。
3.、含量的相对误差为0.2g ,所以相对误差为:0.20.99790525.3Rx E x ∆===。
4、 相对误差18.20.1%0.0182x mg mg ∆=⨯= 故100g 中维生素C 的质量范围为:18.2±0.0182。
5、1)、压力表的精度为1.5级,量程为0.2,则max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2)、1的汞柱代表的大气压为0.133,所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3)、1水柱代表的大气压为gh ρ,其中29.8/g m s =则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯6、样本测定值算术平均值 3.421666667 3.48 几何平均值 3.421406894 3.37 调和平均值 3.421147559 3.47 标准差s 0.046224092 3.38 标准差 0.04219663 3.4 样本方差 0.002136667 3.43 总体方差0.001780556 算住平均误差 0.038333333极差 0.117、依题意,检测两个分析人员测定铁的精密度是否有显著性差异,用F双侧检验。
根据试验值计算出两个人的方差及F值:221221223.733, 2.3033.7331.621232.303s s s F s ===== 而0.9750.025(9,9)0.248386,(9,9) 4.025994F F ==, 所以0.9750.025(9,9)(9,9)F F F <<两个人的测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
《研究设计与数据分析》答案最终版

《研究设计与数据分析》【问】:相比美国人,中国人更不喜欢排队,请结合所学的研究中变量类型来解释。
【答】:所谓变量,就是具有一个以上不同取值(不同的子范畴、不同的属性、或不同的亚概念)的概念。
1. 根据变量取值的性质不同,可以把变量分为类别变量、顺序变量、间距变量和比率变量四种类型。
2. 按照是否可以直接观测分为直接测量变量和间接测量变量,直接测量变量如身高,体重,反应时等,间接测量变量如动机,态度,价值观等。
在本题中有两个变量,一个是国籍(美国人,中国人),一个是对排队的态度(喜欢,不喜欢)。
这两个变量中,国籍是直接测量变量,对排队的态度是间接测量变量。
3. 根据变量之间的关系及在研究中的地位划分,又可以把变量分为自变量、因变量以及中介变量。
自变量多为属性变量,而因变量多为行为或态度变量。
自变量是原因,因变量是结果,中介变量是过程。
调节变量是边界条件,控制变量是其他的原因。
本题中的两个变量,国籍是自变量,对排队的态度是因变量,但是不能简单的说国籍是导致排队态度的唯一原因,这其中会有其他因素的干扰,这个就是第三变量。
比如社会文化因素,教育水平等。
相比美国人,中国人更不喜欢排队,是否排队取决于:是否有规则意识;对别人的预期;管理措施等中介变量的影响。
【问】:在一份合格的问卷设计中应秉持什么原则,又有什么具体方法可操作,请阐述。
【答】:一、问卷设计的基本原则:1.明确问卷设计的出发点,注意问卷调查的目的与内容一致;2.调查对象是问卷设计考虑的重点;明确阻碍问卷调查的各种因素(1) 调查对象的性别、年龄、文化程度、职业分布(2) 调查对象的精力、能力(3) 调查问题的敏感性(4) 调查问卷形式(呆板,使被调查者失去兴趣)(5) 过滤性问题(太多但又指示不明)3.考虑问卷的处理方式、填答方式、调查方式等因素;(1) 手工/计算机,(2) 自填/访谈员填写(3) 集体分发、当场填写/邮寄填写(封面信);4.问卷的修改和试测。
试验设计与数据处理课后习题

试验设计与数据处理课后习题机械工程6120805019 李东辉第三章3-7分别使用金球和铂球测定引力常数(单位:)1. 用金球测定观察值为 6.683,6.681, 6.676, 6.678, 6.679, 6.6722. 用铂球测定观察值为 6.661, 6.661,6.667, 6.667, 6.664设测定值总体为N(u,)试就1,2两种情况求u的置信度为0.9的置信区间,并求的置信度为0.9的置信区间。
用sas分析结果如下:第一组:第二组:3-13下表分别给出两个文学家马克吐温的8篇小品文以及斯诺特格拉斯的10篇小品文中由3个字母组成的词的比例:马克吐温:0.225 0.262 0.217 0.240 0.230 0.229 0.235 0.217斯诺特格拉斯:0.209 0.205 0.196 0.210 0.202 0.207 0.224 0.223 0.220 0.201设两组数据分别来自正态总体,且两个总体方差相等,两个样本相互独立,问两个作家所写的小品文中包含由3个字母组成的词的比例是否有显著差异(a=0.05)取假设H0:u1-u2≤0和假设H1:u1-u2>0用sas分析结果如下:Sample StatisticsGroup N Mean Std. Dev. Std. Error----------------------------------------------------x 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 = 0Alternative: Mean 1 - Mean 2 ^= 0If Variances Are t statistic Df Pr > t----------------------------------------------------Equal 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05,可认为拒绝原假设,即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。
实验设计与分析知到章节答案智慧树2023年青岛农业大学

实验设计与分析知到章节测试答案智慧树2023年最新青岛农业大学第一章测试1.方差分析最早是由谁提出?()参考答案:Fisher2.哪位统计学家将试验设计中应用最广的正交设计表格化?()参考答案:田口玄一3.以下哪位数学家提出了均匀设计?()参考答案:王元和方开泰4.常用试验设计和数据处理软件哪些?()参考答案:MATLAB;SAS;Origin;SPSS5.试验数据处理在科学试验中的作用主要体现在以下哪些方面?()参考答案:获得试验因素对试验结果的影响规律;评判试验数据的可靠性;确定影响试验结果的因素主次;确定试验因素与试验结果之间存在的近似函数关系;确定最优试验方案或配方第二章测试1.用0.618法寻找某实验的最优加入量时,若当前“存优范围”是【568,714】,好点是“658”,则此时要做试验的加入点值是()参考答案:6242.常用的优选法有以下哪些?()参考答案:爬山法;分批试验法;黄金分割法;来回调试法3.用黄金分割法进行优选时,相互比较的两个实验点不一定都在所在区间的两个黄金分割点上。
()参考答案:错4.黄金分割法又称折纸法。
()参考答案:对5.用优选法处理多因素问题时,要把所有因素平等看待。
()参考答案:错第三章测试1.在表中,2水平的因素的每个水平做()次实验参考答案:62.L16(4 5)的5代表()参考答案:最多允许安排因素的个数3.等水平正交表中的任一列,不同的数字出现的次数相同。
()参考答案:对4.为了对试验条件全面考察,挑选的试验因素应尽可能多。
()参考答案:错5.交互作用被看做影响因素,在正交表中应占有相应的列,交互作用列同因素列一样可以随意安排。
()参考答案:错第四章测试1.U7(7 4)的4代表()参考答案:最多允许安排因素的个数2.等水平均匀表每个因素在每个水平仅做一次试验。
()参考答案:对3.均匀表任两列组成的试验方案是等价的。
()参考答案:错4.均匀设计结果可进行()。
实验设计和分析习题答案解析

- 1 -《实验设计与分析》习题与解答P41 习题一1.设用三种方法测定某溶液浓度时,得到三组数据,其平均值如下:1x (1.540.01)mol /L =± 2x (1.70.2)/mol L =± 3x (1.5370.005)mol /L =±试求它们的加权平均值。
解:①计算权重: 211100000.01w == 212250.2w == 213400000.005w == 1:2:310000:25:40000400:1:1600w w w ==②计算平均值1.54400 1.71 1.5371600 1.538 1.5/40011600x mol L ⨯+⨯+⨯==≈++5.今欲测量大约8kPa (表压)的空气压力,试验仪表用①1.5级,量程0.2MPa 的弹簧管式压力表;②标尺分度为1mm 的U 形管水银柱压差计;③标尺分度为1mm 的U 形管水柱压差计。
求最大绝对误差和相对误差解:①max 0.21000 1.5%3x kPa ∆=⨯⨯=R E =3100%37.5%8R E =⨯=②33max 1109.8113.610133.4160.133x Pa kPa -∆=⨯⨯⨯⨯== 0.133100% 1.66%8R E =⨯= ③33max 1109.81109.810.00981x Pa kPa -∆=⨯⨯⨯== 0.00981100%0.12%8R E =⨯=6.在用发酵法生产赖氨酸的过程中,对产酸率(%)作6次测定。
样本测定值为:3.48, 3.37, 3.47, 3.38, 3.40, 3.43,求该组数据的算术平均值、几何平均值、调和平均值、标准差s 、总体标准差σ、样本方差s 2、总体方差σ2、算术平均误差Δ和极差R 。
解:①算术平均值: 3.48 3.37 3.47 3.38 3.40 3.433.426x +++++==②几何平均值: 3.42G x =- 2 -③调和平均值:63.421111113.48 3.37 3.47 3.38 3.40 3.43H ==+++++④标准差:0.0463s =⑤总体标准差:0.0422σ=⑥样本方差:()()()()()()2222222 3.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.0021261s -+-+-+-+-+-==-⑦总体方差:()()()()()()22222223.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.001766σ-+-+-+-+-+-==⑧算术平均误差:3.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.03836-+-+-+-+-+-∆==⑨极差:R=3.48-3.37=0.117.A 与B 两人用同一分析方法测定金属钠中的铁,测得铁含量(μg/g )分别为: 分析人员A :8.0,8.0,10.0,10.0,6.0,6.0,4.0,6.0,6.0,8.0 分析人员B :7.5,7.5,4.5,4.0,5.5,8.0,7.5,7.5,5.5,8.0 试问A 与B 两人测定铁的精密度是否有显著性差异?(α=0.05) 解:①算术平均值:8.08.010.010.0 6.0 6.0 4.0 6.0 6.08.07.210A x +++++++++==7.57.5 4.5 4.0 5.58.07.57.5 5.58.06.5510B x +++++++++==②方差22222222222(8.07.2)(8.07.2)(10.07.2)(10.07.2)(6.07.2)(6.07.2)(4.07.2)(6.07.2)(6.07.2)(8.07.2) 3.7101A s -+-+-+-+-+-+-+-+-+-==-22222222222(7.5 6.55)(7.5 6.55)(4.5 6.55)(4.0 6.55)(5.5 6.55)(8.0 6.55)(7.5 6.55)(7.5 6.55)(5.57.2)(8.0 6.55) 2.3101B s -+-+-+-+-+-+-+-+-+-==-③统计量3.71.62.3F == ④临界值0.975(9,9)0.248F = 0.025(9,9) 4.03F =⑤检验∵0.9750.025(9,9)(9,9)F F F <<∴A 与B 两人测定铁的精密度是无显著性差异- 3 -8. 用新旧两种工艺冶炼某种金属材料,分别从两种冶炼工艺生产的产品中抽样,测定产品中的杂质含量(%),结果如下:旧工艺:2.69,2.28,2.57,2.30,2.23,2.42,2.61,2.64,2.72,3.02,2.45,2.95,2.51新工艺:2.26,2.25,2.06,2.35,2.43,2.19,2.06,2.32,2.34试问新冶炼工艺是否比旧工艺生产更稳定,并检验两种工艺之间是否存在系统误差?(α=0.05)解:(1)①算术平均值: 2.69 2.28 2.57 2.30 2.23 2.42 2.61 2.64 2.72 3.02 2.45 2.95 2.512.5713x ++++++++++++==旧2.26 2.25 2.06 2.35 2.43 2.19 2.06 2.32 2.342.259x ++++++++==新②方差(2.69-2.57)(2.28-2.57)(2.57-2.57)(2.30-2.57)(2.23-2.57)(2.42-2.57)(2.61-2.57)(2.64-2.57)(2.72-2.57)(3.02-2.57)(2.45-2.57)(2.95-2.57)(2.51-2.57)13-10.0586s++++++++++++==2222222222(2.26 2.25)(2.25 2.25)(2.06 2.25)(2.35 2.25)(2.43 2.25)(2.19 2.25)(2.06 2.25)(2.32 2.25)(2.34 2.25)0.016491s -+-+-+-+-+-+-+-+-==-新③F 统计量0.05863.570.0164F ==④F 临界值0.05(12,8) 3.28F =⑤F 检验 ∵0.05F>(12,8)F∴新冶炼工艺比旧工艺生产更稳定 (2)①t 统计量t x x -==②自由度22222222220.05860.0164139df -2-2=200.05860.01641391319111s s n n s s n n n n ⎛⎫⎛⎫+ ⎪+ ⎪⎝⎭⎝⎭==⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭+⎝⎭⎝⎭+++++新旧旧新新旧新旧旧新 ③t 临界值0.025t (20) 2.086=④t 检验 ∵0.025t >t (20)∴两种工艺之间存在系统误差- 4 -9. 用新旧两种方法测得某种液体的黏度(mPa ·s ),如下: 新方法:0.73,0.91,0.84,0.77,0.98,0.81,0.79,0.87,0.85 旧方法:0.76,0.92,0.86,0.74,0.96,0.83,0.79,0.80,0.75其中旧方法无系统误差,试在显著性水平α=0.05时,检验新方法是否可行。
实验设计和分析习题答案解析

《实验设计与分析》习题与解答P41 习题一1.设用三种方法测定某溶液浓度时,得到三组数据,其平均值如下:1x (1.540.01)mol /L =± 2x (1.70.2)/mol L =± 3x (1.5370.005)mol /L =±试求它们的加权平均值。
解:①计算权重:211100000.01w =="212250.2w ==213400000.005w == 1:2:310000:25:40000400:1:1600w w w ==②计算平均值1.54400 1.71 1.5371600 1.538 1.5/40011600x mol L ⨯+⨯+⨯==≈++5.今欲测量大约8kPa (表压)的空气压力,试验仪表用①级,量程的弹簧管式压力表;②标尺分度为1mm 的U 形管水银柱压差计;③标尺分度为1mm 的U 形管水柱压差计。
求最大绝对误差和相对误差解:①max 0.21000 1.5%3x kPa ∆=⨯⨯= &R E =3100%37.5%8R E =⨯=②33max 1109.8113.610133.4160.133x Pa kPa -∆=⨯⨯⨯⨯==0.133100% 1.66%8R E =⨯= ③33max1109.81109.810.00981x Pa kPa -∆=⨯⨯⨯==0.00981100%0.12%8R E =⨯=6.在用发酵法生产赖氨酸的过程中,对产酸率(%)作6次测定。
样本测定值为:, , , , , ,求该组数据的算术平均值、几何平均值、调和平均值、标准差s 、总体标准差σ、样本方差s 2、总体方差σ2、算术平均误差Δ和极差R 。
解:①算术平均值: 3.48 3.37 3.47 3.38 3.40 3.433.426x +++++==②几何平均值: 3.42G x == ③调和平均值:63.421111113.48 3.37 3.47 3.38 3.40 3.43H ==+++++…④标准差:0.0463s =⑤总体标准差:0.0422σ=⑥样本方差:()()()()()()22222223.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.0021261s-+-+-+-+-+-==-⑦总体方差:()()()()()()22222223.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.001766σ-+-+-+-+-+-==⑧算术平均误差:3.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.03836-+-+-+-+-+-∆==⑨极差:R=与B 两人用同一分析方法测定金属钠中的铁,测得铁含量(μg/g )分别为: 分析人员A :,,,,,,,,, 分析人员B :,,,,,,,,,试问A 与B 两人测定铁的精密度是否有显著性差异(α=) 解:①算术平均值:8.08.010.010.0 6.0 6.0 4.0 6.0 6.08.07.210A x +++++++++==7.57.5 4.5 4.0 5.58.07.57.5 5.58.06.5510B x +++++++++==②方差22222222222(8.07.2)(8.07.2)(10.07.2)(10.07.2)(6.07.2)(6.07.2)(4.07.2)(6.07.2)(6.07.2)(8.07.2) 3.7101As -+-+-+-+-+-+-+-+-+-==-22222222222(7.5 6.55)(7.5 6.55)(4.5 6.55)(4.0 6.55)(5.5 6.55)(8.0 6.55)(7.5 6.55)(7.5 6.55)(5.57.2)(8.0 6.55) 2.3101B s -+-+-+-+-+-+-+-+-+-==-③统计量 ~3.71.62.3F ==④临界值0.975(9,9)0.248F = 0.025(9,9) 4.03F =⑤检验∵0.9750.025(9,9)(9,9)F F F <<∴A 与B 两人测定铁的精密度是无显著性差异8. 用新旧两种工艺冶炼某种金属材料,分别从两种冶炼工艺生产的产品中抽样,测定产品中的杂质含量(%),结果如下: 旧工艺:,,,,,,,,,,,, (新工艺:,,,,,,,,试问新冶炼工艺是否比旧工艺生产更稳定,并检验两种工艺之间是否存在系统误差(α=)解:(1)①算术平均值: 2.69 2.28 2.57 2.30 2.23 2.42 2.61 2.64 2.72 3.02 2.45 2.95 2.512.5713x ++++++++++++==旧2.26 2.25 2.06 2.35 2.43 2.19 2.06 2.32 2.342.259x ++++++++==新②方差22222222222222(2.69-2.57)(2.28-2.57)(2.57-2.57)(2.30-2.57)(2.23-2.57)(2.42-2.57)(2.61-2.57)(2.64-2.57)(2.72-2.57)(3.02-2.57)(2.45-2.57)(2.95-2.57)(2.51-2.57)13-10.0586s++++++++++++==旧2222222222(2.26 2.25)(2.25 2.25)(2.06 2.25)(2.35 2.25)(2.43 2.25)(2.19 2.25)(2.06 2.25)(2.32 2.25)(2.34 2.25)0.016491s -+-+-+-+-+-+-+-+-==-新③F 统计量0.05863.570.0164F ==④F 临界值 0.05(12,8) 3.28F =:⑤F 检验∵0.05F>(12,8)F∴新冶炼工艺比旧工艺生产更稳定 (2)①t 统计量t x x -==②自由度22222222220.05860.0164139df -2-2=200.05860.01641391319111s s n n s s n n n n ⎛⎫⎛⎫+ ⎪+ ⎪⎝⎭⎝⎭==⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭+⎝⎭⎝⎭+++++新旧旧新新旧新旧旧新 ③t 临界值0.025t (20) 2.086=④t 检验:∵0.025t >t (20)∴两种工艺之间存在系统误差9. 用新旧两种方法测得某种液体的黏度(mPa ·s ),如下: 新方法:,,,,,,,, 旧方法:,,,,,,,,其中旧方法无系统误差,试在显著性水平α=时,检验新方法是否可行。
试验设计与分析课后习题解答及复习资料

田间试验与统计分析-习题集及解答1.在种田间试验设计方法中,属于顺序排列的试验设计方法为:对比法设计、间比法2.若要控制来自两个方面的系统误差,在试验处理少的情况下,可采用:拉丁方设计3.如果处理内数据的标准差或全距与其平均数大体成比例,或者效应为相乘性,则在进行方差分析之前,须作数据转换。
其数据转换的方法宜采用:对数转换。
4.对于百分数资料,如果资料的百分数有小于30%或大于70%的,则在进行方差分析之前,须作数据转换。
其数据转换的方法宜采用:反正弦转换(角度转换)。
5.样本平均数显著性测验接受或否定假设的根据是:小概率事件实际不可能性原理。
6.对于同一资料来说,线性回归的显著性和线性相关的显著性:一定等价。
7.为了由样本推论总体,样本应该是:从总体中随机地抽取的一部分8.测验回归和相关显著性的最简便的方法为:直接按自由度查相关系数显著表。
9.选择多重比较的方法时,如果试验是几个处理都只与一个对照相比较,则应选择:LSD法。
10.如要更精细地测定土壤差异程度,并为试验设计提供参考资料,则宜采用:空白试验11.当总体方差为末知,且样本容量小于30,但可假设==(两样本所属的总体方差同质)时,作平均数的假设测验宜用的方法为:t测验12.因素内不同水平使得试验指标如作物性状、特性发生的变化,称为:效应13.若算出简单相差系数大于1时,说明:计算中出现了差错。
14.田间试验要求各处理小区作随机排列的主要作用是:获得无偏的误差估计值15.正态分布曲线与轴之间的总面积为:等于1。
16.描述总体的特征数叫:参数,用希腊字母表示;描述样本的特征数叫:统计数,用拉丁字母表示。
17.确定分布偏斜度的参数为:自由度18.用最小显著差数法作多重比较时,当两处理平均数的差数大于LSD0.01时,推断两处理间差异为:极显著19.要比较不同单位,或者单位相同但平均数大小相差较大的两个样本资料的变异度宜采用:变异系数20.选择多重比较方法时,对于试验结论事关重大或有严格要求的试验,宜用:q测验。
试验设计和分析习题答案解析

6《实验设计与分析》习题与解答P41习题一1.设用三种方法测定某溶液浓度时,得到三组数据,其平均值如下: 方! =(1.54 ±0.01)mol / Lx 2 二(1.7 二0.2)mol / L X 3 =(1.537 ±0.005)mol / L试求它们的加权平均值。
解:①计算权重:1w1 2 =100000.012 1w2 2 =250.221w32=400000.005w1: w2: w3 =10000: 25: 40000 二 400:1:1600② 计算平均值5.今欲测量大约8kPa (表压)的空气压力,试验仪表用①1.5级,量程0.2MPa 的弹簧管式压力表;②标尺分度为1mm 的U 形管水银柱压差计;③标尺分度为 1mm 勺U 形管水柱压差计。
求最大绝对误差和相对误差 解:① |Ax|=0.2x1000".5% = 3kPamaxE R 二 E R =3 100% =37.5%8②AX =1 汉 10;汉9.81 汉 13.6汉 103 =133.416Pa = 0.133kPamax0 133E R100% =1.66% 8③Ax| =1><10;x9.81x103 =9.81Pa = 0.00981kPamax6.在用发酵法生产赖氨酸的过程中, 对产酸率(%作6次测定。
样本测X 」54 40047 1 侮71600400 1 1600=1.538 : 1.5mol/LE R0.009818100% =0.12%6定值为:3.48, 3.37,3.47, 3.38, 3.40, 3.43,求该组数据的算术平均值、几何平均值、调和平均值、标准差S 、2 2总体标准差b 、样本方差s 、总体方差(T 、算术平均误差 △和极差R 。
解:①算术平均值:-3.48 3.373.47 3.38 3.40 3.43x3.423.48 3.37 3.47 3.38 3.40 3.43②几何平均值: 心=6 3.48 3.37 3.47 3.38 3.40 3.43 =3.42匚•丄丄•丄•丄」= 3.42③调和平均值:H④标准差:--------------------------- 2 2 2 2 2 2(3.48—3.42 j +(3.37—3.42 j +(3.47—3.42)十(3.38—3.42) +(3.40—3.42)十(3.43_3.42 )o°4636-1⑤总体标准差:<j =I222222(3.48—3.42)+(3.37d.42)+(3.47d.42)+(3.38-3.42)+(3.40—3.42)+(3.43—3.42) °⑥样本方差:2 2 2 2 2 2s 2(3.48—3.42 $ +(3.37—3.42 j +(3.47—3.42 j +(3.38—3.42 卄(3.40—3.42)+(3.43—3.42)0 002[2s = —_i =.⑦总体方差:2 2 2 2 2 22(3.48-3.42)+(3.37 _3.42)+(3.47—3.42)+(3.38—3.42)+(3.40—3.42)+(3.43—3.42)二 6 =. ⑧算术平均误差: 3.48—3.42|+|3.37 —3.42|+|3.47 —3.42|+|3.38—3.42| +|3.40—3.42|+|3.43 —3.42| q ⑨极差:R=3.48-3.37=0.11 7.A 与B 两人用同一分析方法测定金属钠中的铁,测得铁含量( 卩g/g )分别为: 分析人员 A : 8.0 , 8.0 , 10.0 , 10.0 , 6.0 , 6.0 , 4.0 , 6.0 , 6.0 , 8.0 分析人员 B : 7.5 , 7.5 , 4.5 , 4.0 , 5.5 , 8.0 , 7.5 , 7.5 , 5.5 , 8.0试问A 与B 两人测定铁的精密度是否有显著性差异? ( a =0.05 ) 解:①算术平均值:仝° 8° 1°.° 1°.° 6.° 6° 4.° 6.0 6° 8.0 £ A 10 X B 7.5 7.5 4.5 4.0 5.5 8.0 7.5 7.5 5.5 8.0 10 = 6.55②方差 2(8.0 -/三)2 但。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题答案1.设用三种方法测定某溶液时,得到三组数据,其平均值如下:试求它们的加权平均值。
解:根据数据的绝对误差计算权重:因为所以2.试解释为什么不宜用量程较大的仪表来测量数值较小的物理量。
答:因为用量程较大的仪表来测量数值较小的物理量时,所产生的相对误差较大。
如3.测得某种奶制品中蛋白质的含量为,试求其相对误差。
解:4.在测定菠萝中维生素C含量的测试中,测得每100g菠萝中含有18.2mg维生素C,已知测量的相对误差为0.1%,试求每100g菠萝中含有维生素C的质量范围。
解:,所以所以m的范围为或依据公式5.今欲测量大约8kPa(表压)的空气压力,试验仪表用1)1.5级,量程0.2MPa 的弹簧管式压力表;2)标尺分度为1mm的U型管水银柱压差计;3)标尺分度为1mm的U形管水柱压差计。
求最大绝对误差和相对误差。
解:1)压力表的精度为1.5级,量程为0.2MPa,则2)1mm汞柱代表的大气压为0.133KPa,所以3)1mm水柱代表的大气压:,其中,通常取则6.在用发酵法生产赖氨酸的过程中,对产酸率(%)作6次评定。
样本测定值为3.48,3.37,3.47,3.38,3.40,3.43,求该组数据的算术平均值、几何平均值、调和平均值、标准差s、标准差、样本方差、总体方差、算术平均误差和极差。
解:准样本体标准7.A与B两人用同一种分析方法测定金属钠中的铁,测得铁含量()分别为:分析人员A:8.0,8.0,10.0,10.0,6.0,6.0,4.0,6.0,6.0,8.0分析人员B:7.5,7.5,4.5,4.0,5.5,8.0,7.5,7.5,5.5,8.0试问A与B两人测定铁的精密度是否有显著性差异?()解:依题意,检验A与B两人测定铁的精密度是否有显著性差异,采用F双侧检验。
根据试验值计算出两种方法的方差以及F值:根据显著性水平,,查F分布表得,。
所以,A与B两人测定铁的方差没有显著差异,即两人测定铁的精密度没有显著性差异。
分析人员A 分析人员B8 7.58 7.510 4.510 46 5.56 84 7.56 7.56 5.58 8F-检验双样本方差分析分析人员A 分析人员B平均7.2 6.55方差 3.733333333 2.302778观测值10 10df 9 9F 1.621230398P(F<=f) 单尾0.24144058F 单尾临界 3.1788931048.用新旧两种工艺冶炼某种金属材料,分别从两种冶炼工艺生产的产品中抽样,测定产品中的杂质含量(%),结果如下:旧工艺(1):2.69,2.28,2.57,2.30,2.23,2.42,2.61,2.64,2.72,3.02,2.45,2.95,2.51;新工艺(2):2.26,2.25,2.06,2.35,2.43,2.19,2.06,2.32,2.34试问新冶炼工艺是否比旧工艺生产更稳定,并检验两种工艺之间是否存在系统误差?()解:工艺的稳定性可用精密度来表征,而精密度可由极差、标准差或方差等表征,这里依据方差来计算。
,由于,所以新的冶炼工艺比旧工艺生产更稳定。
(依据极差:,,同样可以得到上述结论)(依据标准差)检验两种工艺之间是否存在系统误差,采用t检验法。
1)先判断两组数据的方差是否有显著性差异。
根据试验数据计算出各自的平均值和方差:故已知n1=13,n2=9,则,,根据显著性水平,查F分布表得,,两方差有显著差异。
旧工艺新工艺2.69 2.262.28 2.252.57 2.062.30 2.352.23 2.432.42 2.192.61 2.062.64 2.322.72 2.343.022.452.952.51F-检验双样本方差分析旧工艺新工艺平均 2.568461538 2.251111111标准差0.242103496 0.128105859方差0.058614103 0.016411111观测值13 9df 12 8F 3.571610854P(F<=f) 单尾0.039724983F 单尾临界 3.283939006t-检验: 双样本异方差假设旧工艺新工艺平均 2.568461538 2.251111111方差0.058614103 0.016411111观测值13 9假设平均差0df 19t Stat 3.988050168P(T<=t) 单尾0.000393697t 单尾临界 1.729132812P(T<=t) 双尾0.000787395t 双尾临界 2.0930240542)进行异方差t检验根据显著性水平,查单侧t分布表得,所以,则两种工艺的平均值存在差异,即两种工艺之间存在系统误差。
备注:实验方差分析是单侧检验:因为方差分析不像差异显著检验,方差分析中关心的只是组间均方是否显著大于组内均方或误差均方。
目的是为了区分组间差异是否比组内差异大的多,因为只有大得多,才能证明实验的控制条件是否造成了显著的差异,方差齐性中F检验要用到双侧检验,因为要看的是否有显著性差异,而没有说是要看有差异时到底是谁大于谁,所以没有方向性。
9.用新旧两种方法测得某种液体的黏度()如下:新方法:0.73,0.91,0.84,0.77,0.98,0.81,0.79,0.87,0.85旧方法:0.76,0.92,0.86,0.74,0.96,0.83,0.79,0.80,0.75其中旧方法无系统误差。
试在显著性水平时,检验新方法是否可行。
解:检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验。
先求出各数据的秩,如表所示。
秩 1 2 3 4 5 6.5 6.5 8 9 10 11 12 13 14 15 16 170.79 0.81 0.84 0.85 0.87 0.91新0.73 0.77旧0.74 0.75 0.76 0.79 0.80 0.83 0.86 0.92 0.9此时,n1=9,n2=9,n=18,对于,查秩和临界值表,得,由于,故,两组数据无显著差异,新方法无系统误差,可行。
T检验成对数据的比较新方法旧方法di0.73 0.76 -0.03 0.002075310.91 0.92 -0.01 0.000653090.84 0.86 -0.02 0.00126420.77 0.74 0.03 0.000208640.98 0.96 0.02 1.9753E-050.81 0.83 -0.02 0.00126420.79 0.79 0 0.000241980.87 0.8 0.07 0.00296420.85 0.75 0.1 0.007130860.14 0.015822220.0155560.044472210.34978145n=9 1.04934436对于,查表,所以,即两组数据无显著差异,新方法无系统误差,可行。
10.对同一铜合金,有10个分析人员分析进行分析,测得其中铜含量(%)的数据为:62.20,69.49,70.30,70.65,70.82,71.03,71.22,71.25,71.33,71.38(%)。
问这些数据中哪个(些)数据应被舍去,试检验?解:1)拉依达(P aǔta)检验法○1检验62.20计算包括62.20在内的平均值及标准偏差计算比较和,,依据拉依达检验法,当时,62.20应该舍去。
○2检验69.49计算包括69.49在内的平均值及标准偏差计算比较和,,依据拉依达检验法,当时,69.49应该舍去。
○3检验70.30计算包括70.30在内的平均值及标准偏差计算比较和,,依据拉依达检验法,当时,69.49不应该舍去。
○4检验71.38计算包括71.38在内的平均值及标准偏差计算比较和,,依据拉依达检验法,当时,71.38不应该舍去。
2)格拉布斯(Grubbs)检验法○1检验62.20计算包括62.20在内的平均值及标准偏差,查表得计算所以62.20应该舍去。
○2检验69.49计算包括69.49在内的平均值及标准偏差,查表得计算所以69.49应该舍去。
○3检验70.30计算包括70.30在内的平均值及标准偏差,查表得计算计算69.49不应该舍去。
○4检验71.38计算包括71.38在内的平均值及标准偏差,查表得计算计算当时,71.38不应该舍去。
3)狄克逊(Dixon)检验法应用狄克逊双侧情形检验:○1对于62.20和71.38,,计算当,对于双侧检验,查出临界值,由于,且,故最小值62.20应该被舍去。
○2舍去62.20后,对剩余的9个数据(n=9)进行狄克逊双侧检验:当,对于双侧检验,查出临界值,由于,且,没有异常值。
单侧检验时,查表得到临界值,,没有异常值。
11.将下列数据保留4位有效数字:3.1459,136653,2.33050,2.7500,2.77447解:3.146、1367×102、2.330、2.750、2.77412.在容量分析中,计算组分含量的公式为,其中V是滴定时消耗滴定液的体积,c是滴定液的浓度。
今用浓度为(1.000±0.001)mg/mL的标准溶液滴定某试液,滴定时消耗滴定液的体积为(20.00±0.02)mL,试求滴定结果的绝对误差和相对误差。
解:根据组分含量计算公式,各变量的误差传递系数分别为,所以组分含量的绝对误差为(mg)(mg)最大相对误差为13.在测定某溶液的密度ρ的试验中,需要测定液体的体积和质量,已知质量测定的相对误差≤0.02%,预使测定结果的相对误差≤0.1%,测量液体体积所允许的最大相对误差为多大?解:由公式,误差传递系数为,则绝对误差相对误差由于质量的相对误差,预使得,需要,即测量液体体积所允许的最大相对误差为0.08%。
