中考复习专题:求线段的长度课件19张
合集下载
线段的计算人教版七年级数学上册精品PPT1

线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
解:如图,BP+PC的最小值是BC=6.
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
10. 如图,点B,C把线段MN分成三部分,其比是 MB∶BC∶CN=2∶3∶4,P是MN的中点,且MN= 18 cm,求PC的长.
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
2. (例1)如图,小强出门从甲地到乙地有四条路 线,其中路线 ③ 最短.
(填“①”“②”“③”“④”中的一个)
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
3. 下列现象中,可用基本事实“两点之间,线段最短” 来解释的现象是( B ) A. 用两个钉子就可以把木条固定在墙上 B. 把弯曲的公路改直,就能缩短路程 C. 利用圆规可以比较两条线段的大小关系 D. 植树时,只要定出两棵树的位置,就能确定同一 行树所在的直线
线段的计算人教版七年级数学上册精 品课件1
解:如图,连接AB交直线m于点O, 则点O即为所求的点. 理由:根据连接两点的所有线中,线段最短, 可得OA+OB最短.
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
6. 如图,A,B,C三棵树在同一直线上,量得A树与B树 之间的距离是20米,B树与C树之间的距离是10米.
线段的计算人教版七年级数学上册精 品课件1
第四章 几何图形初步
第8课 线段的计算(3)
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学本事实及两点的距离
线段的计算人教版七年级数学上册精 品课件1
解:如图,BP+PC的最小值是BC=6.
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
10. 如图,点B,C把线段MN分成三部分,其比是 MB∶BC∶CN=2∶3∶4,P是MN的中点,且MN= 18 cm,求PC的长.
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
2. (例1)如图,小强出门从甲地到乙地有四条路 线,其中路线 ③ 最短.
(填“①”“②”“③”“④”中的一个)
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
3. 下列现象中,可用基本事实“两点之间,线段最短” 来解释的现象是( B ) A. 用两个钉子就可以把木条固定在墙上 B. 把弯曲的公路改直,就能缩短路程 C. 利用圆规可以比较两条线段的大小关系 D. 植树时,只要定出两棵树的位置,就能确定同一 行树所在的直线
线段的计算人教版七年级数学上册精 品课件1
解:如图,连接AB交直线m于点O, 则点O即为所求的点. 理由:根据连接两点的所有线中,线段最短, 可得OA+OB最短.
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学上册精 品课件1
6. 如图,A,B,C三棵树在同一直线上,量得A树与B树 之间的距离是20米,B树与C树之间的距离是10米.
线段的计算人教版七年级数学上册精 品课件1
第四章 几何图形初步
第8课 线段的计算(3)
线段的计算人教版七年级数学上册精 品课件1
线段的计算人教版七年级数学本事实及两点的距离
冀教版-数学-七年级上册-2.3 线段的长度 配套课件

4.5
●
●
A B 0
1
2
3
4
5
6
7
数的角度
8
9 10
3.3
●
●
C0 1
2
3D 4
5
6
7
8
9 10
∴ AB>CD
方法2:叠合法(用平移法比较) 形的角度
●
●
●
A
B
∴ AB>CD
●
●
C
D
观察下图中的几条线段,估 计一下,哪一条最长,哪一 条最短?
a d
b c
问题2:如何画线段等于已知线段
如图,已知线段MN你能用直尺和 圆规准确地画一条与MN相等的线 段吗?
①
·A
②
③
·B
④
⑤
你来做一做
在纸上任意点两点,用线联接它们,量 一下它们的长短,比较一下谁最短?
基本事实: 两点之间的所有连线中,
线段最短.
1.按要求画图,填空:
(1)画一条线段BC=2cm; (2)延长BC到D,使CD=BC; (3)反向延长BC到A,使AC= 2BC,则AB=______cm,AD= _____cm.
2.3线段的长度
知识海洋,追逐梦想.
快乐学习,快乐成长.
姚明和潘长江谁的个子高? 小明和小亮谁的个子高?
你哪有 我高啊!
小 明
我比你 高!
同么们学办量的们法比争一比你取一执量有消?什他
服了吧!
喔,原 来你比 我高!
小
亮
小
明
小 亮
问题1: 如何比较下面两条线段的长短?
●
●
●
●
A
冀教版-数学-七年级上册-2.3 线段的长度 参考课件
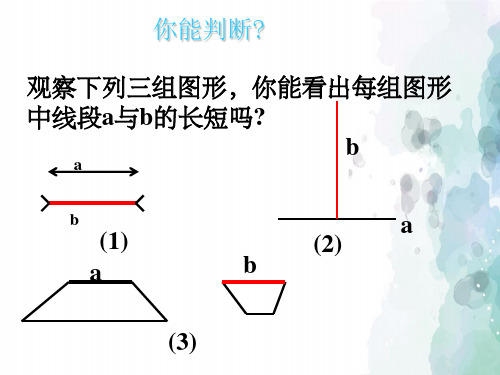
你能判断?
观察下列三组图形,你能看出每组图形 中线段a与b的长短吗?
b
a
b
(1)
a
a (2) b
(3)
2.3线段的长短
生活中长短的比较
怎样比较两个同学的高矮?
叠合法
度量法
思考:
我们能否借助于比较两位同学身高的 方法来比较两条线段的长短呢?
比较线段AB和CD的大小
方法(一)
度量法
A 3cm
B C 2.3cm D
练一练
1.下列说法正确的是( D ) A.过A、B两点的直线长是A、B两点间的距离 B.线段AB就是A、B两点间的距离 C.乘火车从杭州到上海要走210千米,这就是说
杭州站与上海站间的距离为210千米 D. 连结A、B两点的所有线中,其中最短的线的长度
就是A、B两点间的距离 2、课本71页A组1 3、课本71页B组1,单元本28页11 4、已知AB=5cm,BC=3cm,那AC两点间的距离是
先画一条线段,再画一条与它相等的线段, 怎么画?你能想出几种方法?
用圆规和直尺作一条线段等于已知线段
已知线段a,用直尺和圆规画一条线段等于已知线段。
① 画射线AB; ② 以A为圆心,a的长为半径画弧,交射线AB于点C。
注:尺规作图中: 1、直尺只能用来画直线,不能 量距离。 2、要求做出图形,说明结果, 并保留作图痕迹
a AC
B
线段AC即为所求线 段。
动手做一做
课本第70页 做一做 (1)、(2)
一个人过马路到对面的商店去。提 问:为什么有些人要直穿草坪过马 路到对面,却不愿走人行横道呢?
10
A·
12
7
·
15
B
基本事实:两点之间的所有连线中,
观察下列三组图形,你能看出每组图形 中线段a与b的长短吗?
b
a
b
(1)
a
a (2) b
(3)
2.3线段的长短
生活中长短的比较
怎样比较两个同学的高矮?
叠合法
度量法
思考:
我们能否借助于比较两位同学身高的 方法来比较两条线段的长短呢?
比较线段AB和CD的大小
方法(一)
度量法
A 3cm
B C 2.3cm D
练一练
1.下列说法正确的是( D ) A.过A、B两点的直线长是A、B两点间的距离 B.线段AB就是A、B两点间的距离 C.乘火车从杭州到上海要走210千米,这就是说
杭州站与上海站间的距离为210千米 D. 连结A、B两点的所有线中,其中最短的线的长度
就是A、B两点间的距离 2、课本71页A组1 3、课本71页B组1,单元本28页11 4、已知AB=5cm,BC=3cm,那AC两点间的距离是
先画一条线段,再画一条与它相等的线段, 怎么画?你能想出几种方法?
用圆规和直尺作一条线段等于已知线段
已知线段a,用直尺和圆规画一条线段等于已知线段。
① 画射线AB; ② 以A为圆心,a的长为半径画弧,交射线AB于点C。
注:尺规作图中: 1、直尺只能用来画直线,不能 量距离。 2、要求做出图形,说明结果, 并保留作图痕迹
a AC
B
线段AC即为所求线 段。
动手做一做
课本第70页 做一做 (1)、(2)
一个人过马路到对面的商店去。提 问:为什么有些人要直穿草坪过马 路到对面,却不愿走人行横道呢?
10
A·
12
7
·
15
B
基本事实:两点之间的所有连线中,
浙教版七年级上数学6.3 线段的长短比较课件(共18张PPT)

D C
AP B
∴点P就是所求的位置。
课堂小结: 这节课你学会了什么? 1.线段的基本性质:两点之间线段最短。 2.两点之间的距离:两点之间线段的长度。 3.线段的中点的概念及表示方法。
两点之间线段最短
走进生活
村庄A
两点之间线段最短
大桥P
河流
村庄B
(2)如图,村庄A, B之间有一条河流,要 在河流上建造一座大桥P, 为了使村庄A, B之 间的距离最短,请问:这座大桥P应建造在 哪里。为什么?请画出图形。
走进生活
(3)如图,A、B、C、D表示4个居民小区。现要 建一个牛奶供应站,使它到4个小区的距离之和最 小,你认为牛奶供应站应建在何处?标出牛奶供应 站的位置,并说明理由。
A B
D
测测眼力吧!
观察下列三组图形,你能看出每组图形中线段a与b的长短吗
b
a
b
(1) a
a (2) b
(3)
怎样表示两条绳子的长短?
1.直接比较 2.测量比较
怎样比较两条线段的长短?
线段的比较:
第一种方法是:度量法, 即用一把尺量出两条线段的长度, 再进行比较。
3.1cm
4.1cm
00
11
22
33
44
55
66
77
88
第二种方法是:叠合法 先把两条线段的一端重合,另一端 落在同侧,根据另一端落下的位置 来比较长短.
怎样比较多边形中各边的长短?
A
B
AC< CD
CD > AB
D C
可用圆规吗?
先画一条线段,再画一条与它相等的线段, 怎么画?你能想出几种方法?
例1 已知线段a,用直尺和圆规画一条 线段,使它等于已知线段a.
AP B
∴点P就是所求的位置。
课堂小结: 这节课你学会了什么? 1.线段的基本性质:两点之间线段最短。 2.两点之间的距离:两点之间线段的长度。 3.线段的中点的概念及表示方法。
两点之间线段最短
走进生活
村庄A
两点之间线段最短
大桥P
河流
村庄B
(2)如图,村庄A, B之间有一条河流,要 在河流上建造一座大桥P, 为了使村庄A, B之 间的距离最短,请问:这座大桥P应建造在 哪里。为什么?请画出图形。
走进生活
(3)如图,A、B、C、D表示4个居民小区。现要 建一个牛奶供应站,使它到4个小区的距离之和最 小,你认为牛奶供应站应建在何处?标出牛奶供应 站的位置,并说明理由。
A B
D
测测眼力吧!
观察下列三组图形,你能看出每组图形中线段a与b的长短吗
b
a
b
(1) a
a (2) b
(3)
怎样表示两条绳子的长短?
1.直接比较 2.测量比较
怎样比较两条线段的长短?
线段的比较:
第一种方法是:度量法, 即用一把尺量出两条线段的长度, 再进行比较。
3.1cm
4.1cm
00
11
22
33
44
55
66
77
88
第二种方法是:叠合法 先把两条线段的一端重合,另一端 落在同侧,根据另一端落下的位置 来比较长短.
怎样比较多边形中各边的长短?
A
B
AC< CD
CD > AB
D C
可用圆规吗?
先画一条线段,再画一条与它相等的线段, 怎么画?你能想出几种方法?
例1 已知线段a,用直尺和圆规画一条 线段,使它等于已知线段a.
中考复习专题:求线段的长度课件(共19张PPT)

2.如图,在△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB
的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为
10 3
.
类型二: 与四边形有关的线段长度的计算
例2 如图,在平行四边形ABCD中,对角线AC,BD相交于点O, AB=OB,点E,F分别是OA,OD的中点,连接EF,EM⊥BC于点M, EM交BD于点N.若∠CEF=45°,FN=5,则线段BC的长为 44 5 .
优秀ppt公开课ppt免费课件下载免费 课件20 20年 中考复 习专题 :求线 段的长 度课件( 共19张 PPT)
【思路分析】
由题意可知,在点E运动的过程中,始终有△BCE≌△CDF,则∠CGB始 终是90°,所以可得到点G的运动路线是以BC为直径的半圆O,当点O,G,D 共线时,DG的值最小.
人教版九年级数学
中考复习专题
求线段长度
专题解读:线段长度的计算是中考的必考题.此类试题通常以三
角形、四边形或圆为背景,结合图形的变换构造出较复杂的图形,然后 计算其中某特定线段的长度. 此类试题通常为填空题的压轴题,考查的 是各种图形的性质,要求学生具有较强的分解复杂图形、整合利用条件、 合理添加辅助线、构造基本图形的能力,综合性较强,难度较大.解决 此类问题需要熟练掌握求线段长的基本方法,如利用勾股定理、相似三 角形的对应边成比例以及直角三角形的边角关系等,要注意总结添加辅 助线、构造基本图形的方法,积累分析求解此类问题的经验.
5.(2019·安徽)如图,△ABB于点D.若⊙O的半径为2,则CD的长为 2 .
优秀ppt公开课ppt免费课件下载免费 课件20 20年 中考复 习专题 :求线 段的长 度课件( 共19张 PPT)
6.3 线段的长短比较 教学课件 (共28张PPT)
讲授新课
作一条线段等于已知线段 已知:线段 a,作一条线段 AB,使 AB=a. 第一步:用直尺画射线 AF; 第二步:用圆规在射线 AF 上截取 AB = a. 所以线段 AB 为所求线段.
a Aa B F
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
讲授新课
尺规作图的要点: 1.直尺只能用来画线,不能量距; 2.尺规作图要求作出图形,说明结果,并保留作图痕迹.
生活中我们常常会比较两个物体的长短。如图两支铅笔 谁长?
我们可以把两支铅笔看成两条线段,这样我们就把实际 问题转化为了几何问题.
讲授新课
思考:怎样比较两条线段的长短??
Aa B
(1)度量法 用刻度尺量出它们的 长度,再进行比较.
Cb
D
(2) 叠合法 将其中一条线段“移动”, 使其一端点与另一线段的 一端点重合,两线段的另 一端点均在同一射线上.
(2)连接两点的线段叫两点间的距离;
(3)两点之间所有连线中,线段最短;
(4)射个
C.3个
D.4个
当堂检测
2.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银
杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是(
)
A.两点之间线段最短 C.垂线段最短
解:作图步骤如下:
aa b
(1)作射线 AM;
A B1 B2
BM
(2)在 AM 上顺次截取 AB1=a,B1B2=a,
B2B=b,则线段 AB=2a+b.
讲授新课 知识点三 有关线段的基本事实
探究
我要去书店 怎么走呀?
商场
礼堂
书店
讲授新课
根据生活经验,容易发现: 两点之间的所有连线中,线段最短
最新部编人教版七年级上学期数学《线段的长短比较与运算》课件

a
b
A
a-b
D bB
C
课程讲授
3 线段的中点及和、差、倍、分
A
MB
定义:如图,点 M 把线段 AB 分成相等的两条
线段AM 与 BM,点 M 叫做线段 AB 的中点. AM= BM
线段的三等分点
线段的四等分点
课程讲授
3 线段的中点及和、差、倍、分
练一练:如图,下列关系式中与图形不符合的是( B )
④AB+BC=AC.
其中能表示点B是线段AC的中点的有( C )
A.1个
B.2个
C.3个 D.4个
课堂小结
线段的长 短比较与
运算
用尺规作一条线段等于已知线段
度量法
线段的长短比较
叠合法
线段的中点及和、差、倍、分
线段的基本事实及两 点间的距离
两点之间,线段最短.
第四章 几何图形初步
4.2 直线、射线、线段
第2课时 线段的长短比较与运算
新知导入
试一试:试着用简单的几何图形,画出下面的图画.
新知导入
试一试:试着用简单的几何图形,画出下面的图画.
课程讲授
1 用尺规作一条线段等于已知线段
问题1:画一条线段等于已知线段a.
a
先量出这条线段a的长度,再画出一条的等于这个 长度的线段.
a
a
b
b
课程讲授
2 线段的长短比较
问题1:我们在生活中如何比较两个人的身高?以此为 启发,想一想怎样比较两条直线的长短?
度量法 用尺分别度量出两个同学的 身高,将所得的数值进行比较.
课程讲授
2 线段的长短比较
问题1:我们在生活中如何比较两个人的身高?以此为 启发,想一想怎样比较两条直线的无刻度的直尺
第课时线段长短的比较与运算完整版课件PPT

AB
C
D
3.下列语句准确规范的是( D )
A.直线a、b相交于一点m B.延长直线AB C.反向延长射线OA D.延长线段AB到C,使BC=AB
4.如果点C在AB上,下列表达式
AC=1/2AB; AB=2BC; AC=BC; AC+BC=AB中,能
表示C是AB中点的有( C
)
A.1个
B.2个
C.3个
• A
• B
有关线段的基本事实
• A
• B
线段的性质:两点的所有连线中,线段最短. 简单说成:两点之间,线段最短. 两点间的距离:连接两点间的线段的长度,叫做 这两点间的距离.
三 初用新知,小试牛刀
例1 画线段的和与差:如图,已知两条线段a、b(a>b)
(1)画线段a+b
a
A
B
解:如图,∵AB=a, BC=b ∴AC=AB+BC=a+b
线段的四等分点
M 是线段 AB 的中点
a
a
A
M
B
几何语言:∵ M 是线段 AB 的中点 ∴ AM = MB = 1 AB 2 ( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = 1 AB 2
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
点 M , N 是线段 AB 的三等分点:
所以 BE 1 AB 3 x, CF 1 CD 5 x,
2
2
2
2
所以EF=BE+BC+CF=
3 2
x
2
x
5 2
x
6x.
因为EF=24,所以6x=24,解得x=4.
中考复习--圆中求线段长课件

∴OC= 5,∴AB=10.∵AB是⊙O直径,∴∠AEB=90° .在Rt△ABE中, ∵sin∠EAB= ,∴BE=6.∴AE=8.
例1 解:连接OC交AE于点H,连接OE ,BE.
∴sin∠OCD= sin∠BAE= .在Rt△COD中, OD=3,
8
构造直角三角形解直角三角形直线型图形的问题
31
2
(1)求证: AC是∠DAB的平分线;
分析:
H
27
∴AC是∠DAB的平分线.
例4 如图, AB是⊙O的直径,直线HC与⊙O相切于点C.过 点A作HC的垂线,垂足为D,线段AD与⊙O相交于点E.(1)求证: AC是∠DAB的平分线;
证明:连接OC. ∵直线HC与⊙O相切于点C, ∴∠OCH=90°. ∵AD⊥DH, ∴∠ADH=90°. ∴∠OCH=∠ADH. ∴OC/AD.
如图,(2)若AB=10 , 再探解法1: ∠1=∠2
连接EO∠EOC=∠BOC
,求AE的长.
例4
ED
H
33
矩形ONDCON=CD=4Rt△AON中 AO=5AN=3
例4 如图,(2)若AB=10,分析:
过点O作ON⊥AE于点N
,求AE的长.
解法2:
AE=2AN
AE
H
2
34
圆中求 转化成 线段长的问题
例1 反思:
解题关键:
9
例2 已知:如图,在△ABC中,以BC为直径的⊙O交AB于 点D, E为 的中点.延长DE ,CB交于点P,若PB=BO , DE=2,求PE的长.分析: 已知 可知 OC=OE∠1=∠2 ∠2=∠3∠1=∠3OE//CD10
∴DF=4.∴sin∠2= .在Rt△BOE中, sin∠BOE= sin∠2 = ,∴OB .
例1 解:连接OC交AE于点H,连接OE ,BE.
∴sin∠OCD= sin∠BAE= .在Rt△COD中, OD=3,
8
构造直角三角形解直角三角形直线型图形的问题
31
2
(1)求证: AC是∠DAB的平分线;
分析:
H
27
∴AC是∠DAB的平分线.
例4 如图, AB是⊙O的直径,直线HC与⊙O相切于点C.过 点A作HC的垂线,垂足为D,线段AD与⊙O相交于点E.(1)求证: AC是∠DAB的平分线;
证明:连接OC. ∵直线HC与⊙O相切于点C, ∴∠OCH=90°. ∵AD⊥DH, ∴∠ADH=90°. ∴∠OCH=∠ADH. ∴OC/AD.
如图,(2)若AB=10 , 再探解法1: ∠1=∠2
连接EO∠EOC=∠BOC
,求AE的长.
例4
ED
H
33
矩形ONDCON=CD=4Rt△AON中 AO=5AN=3
例4 如图,(2)若AB=10,分析:
过点O作ON⊥AE于点N
,求AE的长.
解法2:
AE=2AN
AE
H
2
34
圆中求 转化成 线段长的问题
例1 反思:
解题关键:
9
例2 已知:如图,在△ABC中,以BC为直径的⊙O交AB于 点D, E为 的中点.延长DE ,CB交于点P,若PB=BO , DE=2,求PE的长.分析: 已知 可知 OC=OE∠1=∠2 ∠2=∠3∠1=∠3OE//CD10
∴DF=4.∴sin∠2= .在Rt△BOE中, sin∠BOE= sin∠2 = ,∴OB .
秋七级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT(实用资料)ppt

秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT
湘教版习题课件小 专题七线段长度的 几种计算方法共19
张PPT
秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT 秋七年级数学上册湘教版习题课件小专题七线段长度的几种计算方法共19张PPT
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类型三:与圆有关的线段长度的计算
例3 (2019·遵义)如图,已知⊙O的半径为1,AB,AC是⊙O
的两条弦,且AB=AC,延长BO交AC于点D,连接OA,OC.若
AD2=AB·DC,则O5D2-=1
.
【思路分析】
由题意可证△AOB≌△AOC,推出∠ACO=∠ABD.由OA=OC,得∠OAC= ∠ACO=∠ABD,再结合∠ADO=∠ADB,即可证明△OAD∽△ABD.根据对应边 成比例,设OD=x,表示出AB,AD,根据AD2=AB·DC,列方程求解即可.
人教版九年级数学
中考复习专题
求线段长度
专题解读:线段长度的计算是中考的必考题.此类试题通常以三
角形、四边形或圆为背景,结合图形的变换构造出较复杂的图形,然后 计算其中某特定线段的长度. 此类试题通常为填空题的压轴题,考查的 是各种图形的性质,要求学生具有较强的分解复杂图形、整合利用条件、 合理添加辅助线、构造基本图形的能力,综合性较强,难度较大.解决 此类问题需要熟练掌握求线段长的基本方法,如利用勾股定理、相似三 角形的对应边成比例以及直角三角形的边角关系等,要注意总结添加辅 助线、构造基本图形的方法,积累分析求解此类问题的经验.
2.如图,在△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB
的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为
10 3
.
类型二: 与四边形有关的线段长度的计算
例2 如图,在平行四边形ABCD中,对角线AC,BD相交于点O, AB=OB,点E,F分别是OA,OD的中点,连接EF,EM⊥BC于点M, EM交BD于点N.若∠CEF=45°,FN=5,则线段BC的长为 44, 且晴朗 明澈, 但是缺 少深度 。也有 评论家 认为好 就好在 没有深 度,因 为没有 深度的 “看” 风景, 其实就 不为一 般的社 会价值 所局限 ,这样 也就抛 弃了自 以为是 的优越 感和置 身事外 的位置 ,而是 在宇宙 万汇的 动静之 中“看 ”。
•
5.一次眼光看风景万物,多了一份包 涵和宽 容,看 到的历 史也就 不是战 争、王 朝更迭 之类的 东西, 而是千 百年来 凡夫俗 子们的 哀乐、 努力和 命运。 它们代 表了更 为现实 逼真的 生存和 价值。
•
6.抒发的感情真诚感人,不写自己的 品学兼 优、勤 奋用功 ,而是 如实地 展现自 己的天 生的野 性,充 满了阅 读和学 习“生 活”这 本大书 所得到 的欢欣 鼓舞的 生命体 验,表 现了对 自然和 生命无 比好奇 和热爱 以及泰 然面对 一切残 忍和苦 难的生 活观。
【同步练习】
4.(2019·潍坊)如图,四边形 ABCD 内接于⊙O,AB 为直径,AD=CD,过点 D 作
DE⊥AB 于点 E,连接 AC 交 DE 于点 F.若 sin∠CAB=3,DF=5,则 BC 的长为( 5
C
)
A.8
B.10
C.12
D.16
5.(2019·安徽)如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,
【思路分析】 设 EF=x,根据三角形中位线定理,得 AD=2x,AD∥EF,可得∠CAD=∠CEF =∠ECM=45°,从而证明△EMC 是等腰直角三角形,则∠CEM=45°,连接 BE, 可知 BE⊥AO,从而△BCE 也是等腰直角三角形,根据三线合一可得 BM=CM=x,进 而证明△ENF≌△MNB,则 EN=MN=12x,BN=FN=5,最后在 Rt△BMN 中利用勾 股定理求得 x 的值,进一步可求得 BC 的长.
典例精讲
类型一:与三角形有关的线段长度的计算
例1 如图,在△ABC中,∠C=90°,∠BAC=60°,AC=1,D在BC 上,E在AB上,使得△ADE为等腰直角三角形,∠ADE=90°,则BE4-=2 43 -2
【思路分析】
求BE的长,考虑BE所在三角形的特征,而△BDE中只知∠B,无法求解, 所以考虑添加辅助线.过点E作EF∥AC,交BC于点F,易证△ADC和△DEF全 等,得出DF=AC=1,设CD=EF=x.然后利用CD+DF+BF=BC,进一步求出 BE的长.
例5 (2019·东营)如图,AC是⊙O的弦,AC=5,点B是⊙O上的一个动
点,且∠ABC=45°.若M,N分别是AC,BC的中点,则MN的最大值是 . 52
2
【思路分析】
根据中位线定理得到MN最大时,AB最大,当AB最大时是直径,从而求得直 径后就可以求得MN的最大值.
归纳总结 解决与动点有关的线段最值的计算,主要的依据是“两点之间线段最短 ”与“垂线段最短”这两个结论,关键是考虑清楚动点的运动路线,构造出 符合基本事实的图形.
•
7. 学习了这篇传记让我们了解到了沈 从文从 小如何 “读社 会这本 大书” ,感受 到他青 春期的 悲欢得 失。由 于传主 生活经 历的太 多苦难 ,加上 作者在 回忆中 不时融 入淳厚 的情感 ,让我 们读来 有某种 沉重与 辛酸, 也让我 们学生 受到启 发:对 于强者 ,生活 中的风 霜雨雪 也和阳 光雨露 一样, 都从不 同侧面 或者以 不同的 方式滋 润着我 们的生 命,现 实中的 曲折、 坎坷、 苦难可 能拓展 人的精 神空间 ,让人 能更加 以阔大 的心胸 与坚强 的意志 ,去感 受生命 ,理解 生活的 意义。
CD⊥AB于点D.若⊙O的半径为2,则CD的长为 2 .
类型四:动点问题中线段长度的计算
例4 如图,在正方形ABCD中,AB=3,点E,F分别在边CD,AD上,
CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG
3 5-3
的最小值2为
.
【思路分析】
由题意可知,在点E运动的过程中,始终有△BCE≌△CDF,则∠CGB始 终是90°,所以可得到点G的运动路线是以BC为直径的半圆O,当点O,G,D 共线时,DG的值最小.
归纳总结:在三角形中计算线段的长,要准确分析题目中所给三
角形的条件,从各个条件展开联想,分解基本图形并探究可得到的新的 条件,同时要从所求线段出发,理清可能用到的方法,从而添加辅助线 构造出相应的基本图形求解.
【同步练习】 1.如图,在边长为3的等边△ABC中,D是AB边上一点,BD= 1/3AB,AE∥BC,AE=BD,连接DE,则DE的7 长是 .
•
2.沈从文创作的小说主要有两类,一 种是以 湘西生 活为题 材,一 种是以 都市生 活为题 材,前 者通过 描写湘 西人原 始、自 然的生 命形式 ,赞美 人性美 ;后者 通过都 市生活 的腐化 堕落, 揭示都 市自然 人性的 丧失。
•
3. 从作者的描述看,作者的观察敏锐 ,记忆 超强, 对现象 世界十 分倾心 ,对大 自然的 声音、 气味, 社会上 的人与 事怀有 浓厚的 兴趣。 他把大 自然与 社会生 活称为 一本“ 大书” ,他从 这本“ 大书” 中学到 了许多 书本上 没有的 东西, 他在自 然和社 会中倾 心体验 ,尊重 生命本 真的做 法,并 非不爱 学习, 而是为 了更好 的学习 。
【同步练习】
6.(2019·兴化模拟)如图,在Rt△ABC中,∠ACB=90°,AB=2,D为线 段AB的中点,将线段BC绕点B顺时针旋转90°,得到线段BE,连接DE,则 DE的最大值是2+1+1 .
•
1.沈从文的创作风格趋向浪漫主义, 他要求 小说的 诗意效 果,融 写实、 纪梦、 象征于 一体, 语言格 调古朴 ,句式 简峭、 主干突 出,单 纯而又 厚实, 朴讷而 又传神 ,具有 浓郁的 地方色 彩,凸 现出乡 村人性 特有的 风韵与 神采。
