(完整版)遗传算法求解函数最大值(matlab)
完整的遗传算法函数Matlab程序

完整的遗传算法函数Matlab程序遗传算法是一种模拟自然进化过程的算法,通过遗传代数操作来搜索最优解。
它是一种优化算法,可以用于解决复杂问题,例如函数优化、组合优化、机器学习等。
在Matlab 中,遗传算法可以通过使用内置函数进行实现,也可以编写自己的遗传算法函数。
以下是一个完整的遗传算法函数Matlab程序的示例:function [x_best, f_best] = GA(fit_func, nvars)% fit_func: 适应度函数句柄% nvars: 变量个数% 遗传算法参数设置pop_size = 100; % 种群大小prob_crossover = 0.8; % 交叉概率prob_mutation = 0.02; % 变异概率max_gen = 1000; % 最大迭代次数% 初始化种群pop = rand(pop_size, nvars);for i = 1:max_gen% 计算适应度for j = 1:pop_sizefitness(j) = feval(fit_func, pop(j,:));end% 找到最优个体[f_best, best_idx] = max(fitness);x_best = pop(best_idx,:);% 交叉操作for j = 1:2:pop_sizeif rand < prob_crossover% 随机选择父代idx_parent1 = randi(pop_size);idx_parent2 = randi(pop_size);parent1 = pop(idx_parent1,:);parent2 = pop(idx_parent2,:);% 交叉idx_crossover = randi(nvars-1);child1 = [parent1(1:idx_crossover) parent2(idx_crossover+1:end)];child2 = [parent2(1:idx_crossover) parent1(idx_crossover+1:end)];% 更新种群pop(j,:) = child1;pop(j+1,:) = child2;endend% 变异操作for j = 1:pop_sizeif rand < prob_mutation% 随机选择变异个体idx_mutation = randi(nvars);pop(j,idx_mutation) = rand;endendendend在上述程序中,遗传算法的参数通过设定变量的值进行设置,包括种群大小、交叉概率、变异概率和最大迭代次数等。
使用Matlab进行遗传算法优化问题求解的方法

使用Matlab进行遗传算法优化问题求解的方法引言在现代科技发展的背景下,优化算法成为解决各种问题的重要工具之一。
遗传算法作为一种生物启发式算法,具有全局寻优能力和适应性强的特点,在许多领域中被广泛应用。
本文将介绍如何使用Matlab进行遗传算法优化问题求解,包括问题建模、遗传算子设计、遗传算法编码、适应度评价和求解过程控制等方面。
一、问题建模在使用遗传算法求解优化问题之前,我们首先需要将问题定义为数学模型。
这包括确定问题的目标函数和约束条件。
例如,假设我们要最小化一个多变量函数f(x),其中x=(x1,x2,...,xn),同时还有一些约束条件g(x)<=0和h(x)=0。
在Matlab中,我们可通过定义一个函数来表示目标函数和约束条件。
具体实现时,我们需要在目标函数和约束函数中设置输入参数,通过调整这些参数进行优化。
二、遗传算子设计遗传算法的核心是遗传算子的设计,包括选择(Selection)、交叉(Crossover)、变异(Mutation)和替代(Replacement)等。
选择操作通过一定的策略从种群中选择出适应度较高的个体,作为进行交叉和变异的父代个体。
交叉操作通过将两个父代个体的基因片段进行交换,产生新的子代个体。
变异操作通过改变个体某些基因的值,引入新的基因信息。
替代操作通过选择适应度较低的个体将其替换为新产生的子代个体。
三、遗传算法编码在遗传算法中,个体的编码方式决定了问题的解空间。
常见的编码方式有二进制编码和实数编码等。
当问题的变量是二进制形式时,采用二进制编码。
当问题的变量是实数形式时,采用实数编码。
在Matlab中,我们可以使用矩阵或向量来表示个体的基因型,通过制定编码方式来实现遗传算法的编码过程。
四、适应度评价适应度评价是遗传算法中判断个体优劣的指标。
在适应度评价过程中,我们将问题的目标函数和约束条件应用于个体的解,计算得到一个适应度值。
适应度值越大表示个体越优。
利用遗传算法求函数的极大值

利用遗传算法求函数的极大值该函数有两个局部极大值点,分别是f (2.048,-2.048)=3897.7342和f (2.048,-2.048)=3905.9262,其中,后者为全局最大点。
可以分别用二进制编码和十进制编码遗传算法求函数极大值遗传算法二进制编码求函数极大值程序%Generic Algorithm for function f(x1,x2) optimumclear all;close all;%Parameters 参数Size=80; %群体大小G=100; %终止进化代数CodeL=10; %代码长度umax=2.048;umin=-2.048;E=round(rand(Size,2*CodeL)); %Initial Code 最初代码%Main Program 主程序for k=1:1:Gtime(k)=k;222212121(,)100()(1)2.048 2.048(1,2)i f x x x x x x i ⎧=-+-⎨-≤≤=⎩for s=1:1:Sizem=E(s,:);y1=0;y2=0; %X对应的十进制代码%Uncodingm1=m(1:1:CodeL);for i=1:1:CodeLy1=y1+m1(i)*2^(i-1); %将y1转换为十进制数endx1=(umax-umin)*y1/1023+umin;m2=m(CodeL+1:1:2*CodeL);for i=1:1:CodeLy2=y2+m2(i)*2^(i-1); %将y2转换为十进制数endx2=(umax-umin)*y2/1023+umin; %求x对应的十进制数F(s)=100*(x1^2-x2)^2+(1-x1)^2; %个体适应度函数endJi=1./F; %个体适应度函数的倒数%****** Step 1 : Evaluate BestJ ******BestJ(k)=min(Ji);fi=F; %Fitness Function 适应函数[Oderfi,Indexfi]=sort(fi); %Arranging fi small to biggerBestfi=Oderfi(Size); %Let Bestfi=max(fi)BestS=E(Indexfi(Size),:); %Let BestS=E(m), m is the Indexfi belong to max(fi) %最佳样本bfi(k)=Bestfi;%****** Step 2 : Select and Reproduct Operation******fi_sum=sum(fi);fi_Size=(Oderfi/fi_sum)*Size;fi_S=floor(fi_Size); %Selecting Bigger fi valuekk=1;for i=1:1:Sizefor j=1:1:fi_S(i) %Select and ReproduceTempE(kk,:)=E(Indexfi(i),:);kk=kk+1; %kk is used to reproduceendend%************ Step 3 : Crossover Operation ************pc=0.60; %交叉概率n=ceil(20*rand); %种群大小for i=1:2:(Size-1)temp=rand;if pc>temp %Crossover Conditionfor j=n:1:20TempE(i,j)=E(i+1,j); %交换E(i,j)和E(i+1,j)TempE(i+1,j)=E(i,j);endendendTempE(Size,:)=BestS;E=TempE;%************ Step 4: Mutation Operation ************** %pm=0.001; %变异概率%pm=0.001-[1:1:Size]*(0.001)/Size; %Bigger fi, smaller Pm %pm=0.0; %No mutationpm=0.1; %Big mutationfor i=1:1:Sizefor j=1:1:2*CodeLtemp=rand;if pm>temp %Mutation Conditionif TempE(i,j)==0TempE(i,j)=1;elseTempE(i,j)=0;endendendend%Guarantee TempPop(30,:) is the code belong to the best individual(max(fi)) TempE(Size,:)=BestS;E=TempE;endMax_Value=BestfiBestSx1x2figure(1);plot(time,BestJ); %目标函数和时间的坐标系xlabel('Times');ylabel('Best J');figure(2);plot(time,bfi);xlabel('times');ylabel('Best F');遗传算法十进制编码求函数极大值程序%Generic Algorithm for function f(x1,x2) optimumclear all;close all;%Parameters参数Size=80;G=100; %迭代次数CodeL=10; %编码长度umax=2.048;umin=-2.048;E=round(rand(Size,2*CodeL)); %Initial Code ???%Main Programfor k=1:1:Gtime(k)=k;for s=1:1:Sizem=E(s,:);y1=0;y2=0;%Uncodingm1=m(1:1:CodeL); %???for i=1:1:CodeLy1=y1+m1(i)*2^(i-1);endx1=(umax-umin)*y1/1023+umin;m2=m(CodeL+1:1:2*CodeL);for i=1:1:CodeLy2=y2+m2(i)*2^(i-1);endx2=(umax-umin)*y2/1023+umin;F(s)=100*(x1^2-x2)^2+(1-x1)^2;endJi=1./F;%****** Step 1 : Evaluate BestJ ****** BestJ(k)=min(Ji);fi=F; %Fitness Function[Oderfi,Indexfi]=sort(fi); %Arranging fi small to biggerBestfi=Oderfi(Size); %Let Bestfi=max(fi)BestS=E(Indexfi(Size),:); %Let BestS=E(m), m is the Indexfi belong to max(fi)bfi(k)=Bestfi;%****** Step 2 : Select and Reproduct Operation******fi_sum=sum(fi);fi_Size=(Oderfi/fi_sum)*Size;fi_S=floor(fi_Size); %Selecting Bigger fi valuekk=1;for i=1:1:Sizefor j=1:1:fi_S(i) %Select and ReproduceTempE(kk,:)=E(Indexfi(i),:);kk=kk+1; %kk is used to reproduceendend%************ Step 3 : Crossover Operation ************ pc=0.60;n=ceil(20*rand);for i=1:2:(Size-1)temp=rand;if pc>temp %Crossover Conditionfor j=n:1:20TempE(i,j)=E(i+1,j);TempE(i+1,j)=E(i,j);endendendTempE(Size,:)=BestS;E=TempE;%************ Step 4: Mutation Operation ************** %pm=0.001;%pm=0.001-[1:1:Size]*(0.001)/Size; %Bigger fi, smaller Pm%pm=0.0; %No mutationpm=0.1; %Big mutationfor i=1:1:Sizefor j=1:1:2*CodeLtemp=rand;if pm>temp %Mutation Conditionif TempE(i,j)==0TempE(i,j)=1;elseTempE(i,j)=0;endendendend%Guarantee TempPop(30,:) is the code belong to the best individual(max(fi)) TempE(Size,:)=BestS;E=TempE;endMax_Value=BestfiBestSx1x2figure(1);plot(time,BestJ);xlabel('Times');ylabel('Best J');figure(2);plot(time,bfi);xlabel('times');ylabel('Best F');思考:通过改变群体大小、终止进化代数G、交叉概率P c和变异概率P m,分析群体大小、终止进化代数、交叉概率和变异概率对优化效果的影响。
matlab遗传算法 算例

下面是一个使用MATLAB实现的基本遗传算法算例。
本例用于解决简单的优化问题:寻找函数f(x) = x^2在[-10,10]范围内的最小值。
```matlab定义问题参数PopSize = 100; 种群数量Genes = -10:0.1:10; 基因范围FitnessFunc = @(x) -x.^2; 适应度函数(这里为了方便,使用了-x^2,即求最大值,实际应用中应改为-f(x))MaxGen = 50; 最大迭代次数初始化种群Pop = zeros(PopSize, length(Genes));for i = 1:PopSizePop(i,:) = rand(1,length(Genes))*2*Genes - Genes; 随机产生初始种群end开始迭代for gen = 1:MaxGen计算当前种群适应度Fitness = FitnessFunc(Pop);[BestFit, Index] = max(Fitness); 找到最佳适应度BestFitPos = Pop(Index,:); 找到最佳适应度对应的基因选择(轮盘赌选择)NewPop = zeros(PopSize, length(Genes));SumFitness = sum(Fitness);RandomFitness = rand(PopSize,1)*SumFitness; 随机生成每个个体的"随机适应度"for i = 1:PopSize[~, Index] = min(RandomFitness); 用随机适应度进行选择(越小被选中概率越大)NewPop(i,:) = Pop(Index,:); 将选择出的个体放入新种群RandomFitness(Index) = SumFitness; 将已选择的个体的随机适应度设为最大值,避免重复选择end交叉(杂交)for i = 1:PopSize/2随机选择两个父代个体Parent1 = NewPop(randi([1 PopSize]),:);Parent2 = NewPop(randi([1 PopSize]),:);生成新个体Child1 = (Parent1 + Parent2)/2; 中间值交叉Child2 = Parent1 + (Parent2 - Parent1)*rand; 一点交叉将新个体加入新种群NewPop((i-1)*2+1,:) = Child1;NewPop((i-1)*2+2,:) = Child2;end变异for i = 1:PopSizeif rand < 0.01 变异概率为0.01随机选择一个基因进行变异(取反)GeneIdx = randi(length(Genes));NewPop(i,GeneIdx) = ~NewPop(i,GeneIdx);endend更新种群Pop = NewPop;end输出结果BestFit = FitnessFunc(BestFitPos);fprintf('Best fitness: f\n', BestFit);fprintf('Best position: s\n', num2str(BestFitPos));```这个例子比较简单,只用了基本的遗传算法操作:选择、交叉和变异。
matlab遗传算法计算函数区间最大值和最小值

matlab遗传算法计算函数区间最大值和最小值下面是用matlab实现遗传算法计算函数区间最大值和最小值的示例代码:首先定义函数(此处以f(x)=x*sin(10*pi*x)+1为例):matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;end然后设置遗传算法参数:matlaboptions = gaoptimset('Generations', 1000, 'PopulationSize', 50,'StallGenLimit', 200, 'TolCon', 1e-10);其中,Generations表示遗传算法的迭代次数,PopulationSize表示种群大小,StallGenLimit表示在连续多少代没有改变时停止迭代,TolCon表示收敛精度。
接着,编写遗传算法主函数:matlab[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);其中,第一个参数为要优化的函数,第二个参数为变量维度,后面的参数为变量的取值范围。
最后,输出结果:matlabfprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);其中,-fval表示函数最大值,fval表示函数最小值。
完整代码如下:matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;endoptions = gaoptimset('Generations', 1000, 'PopulationSize', 50, 'StallGenLimit', 200, 'TolCon', 1e-10);[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);fprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);参考资料:[1][2]。
遗传算法优化的matlab案例

遗传算法优化的matlab案例以下是一个简单的遗传算法优化的Matlab 案例:假设我们想找到一个函数f(x) 的最大值,其中x 的取值范围为[0,10]。
我们可以使用遗传算法来找到最大值。
步骤如下:1. 定义适应度函数我们可以使用f(x) 来定义适应度函数。
在这个例子中,我们使用函数f(x) = x^2。
在Matlab 中,我们可以这样定义适应度函数:function y = fitness(x)y = x.^2;end2. 定义遗传算法参数我们需要定义一些遗传算法的参数,如种群大小、交叉概率、变异概率等。
在这个例子中,我们定义种群大小为50,交叉概率为0.8,变异概率为0.1。
pop_size = 50; % 种群大小crossover_rate = 0.8; % 交叉概率mutation_rate = 0.1; % 变异概率3. 执行遗传算法优化我们可以使用Matlab 自带的ga 函数来执行遗传算法优化。
我们需要传入适应度函数、变量的取值范围等参数。
lb = 0; % 变量下限ub = 10; % 变量上限nvars = 1; % 变量个数options =gaoptimset('Display','iter','PopulationSize',pop_size,'CrossoverFraction',c rossover_rate,'MutationFcn',@mutationadaptfeasible,'MutationRate',mut ation_rate,'StallGenLimit',50); % 遗传算法参数[x,fval] = ga(@fitness,nvars,[],[],[],[],lb,ub,[],options); % 执行遗传算法优化disp(['Optimal value: ',num2str(fval)]);disp(['Optimal solution: [',num2str(x),']']);在上面的代码中,我们使用了mutationadaptfeasible 函数来保证变异产生的新个体也满足变量取值范围。
用遗传算法求函数的最大值MATLAB程序

N2=initialize(); N3=initialize(); N4=initialize(); total=1; Num=0; MaN1=0; MaN2=0; flag=0; continue; else break; end end temp1=cal(N1,n1); temp2=cal(N2,n2); temp3=cal(N3,n3); temp4=cal(N4,n4); M=[temp1;temp2;temp3;temp4]; N1=M(1,:); N2=M(2,:); N3=M(3,:); N4=M(4,:); %交叉-crossover while 1 p=floor(1000*rand); if p>1 break; else continue; end end k=mod(p,3); switch k case 0 [N1,N2,N3,N4,ps]=crossover(N1,N2,N3,N4); case 1 [N1,N3,N2,N4,ps]=crossover(N1,N3,N2,N4); case 2 [N1,N4,N2,N3,ps]=crossover(N1,N4,N2,N3); end %变异-mutation U=[N1,N2,N3,N4]; pos=mod(floor(1000*rand),20)+1; if U(1 U(1,pos)=0; end N1=U(1,1:5); N2=U(1,6:10); N3=U(1,11:15); N4=U(1,16:20); %遗传算法结束条件:连续 10 代最大值均保持一致 if Num==10 disp('进化代数:') total-10 disp('现在的种群:') N1 N2 N3 N4 disp('最大值:') MaN1 break; end flag=mod(flag+1,2); total=total+1; end MATLAB 仿真结果:
遗传算法用matlab求函数极大值

遗传算法用matlab求函数极大值一、题目:寻找f(x)=x2,,当x在0~31区间的最大值。
二、源程序:%遗传算法求解函数最大值%本程序用到了英国谢菲尔德大学(Sheffield)开发的工具箱GATBX,该工具箱比matlab自带的GATOOL使用更加灵活,但在编写程序方面稍微复杂一些Close all;Clear all;figure(1);fplot('variable*variable',[0,31]); %画出函数曲线%以下定义遗传算法参数GTSM=40; %定义个体数目ZDYCDS=20; %定义最大遗传代数EJZWS=5; %定义变量的二进制位数DG=0.9; %定义代沟trace=zeros(2, ZDYCDS); %最优结果的初始值FieldD=[5;-1;2;1;0;1;1]; %定义区域描述器的各个参数%以下为遗传算法基本操作部分,包括创建初始种群、复制、交叉和变异Chrom=crtbp(GTSM, EJZWS); %创建初始种群,即生成给定规模的二进制种群和结构gen=0; %定义代数计数器初始值variable=bs2rv(Chrom, FieldD); %对生成的初始种群进行十进制转换ObjV=variable*variable; %计算目标函数值f(x)=x2 while gen<ZDYCDS %进行循环控制,当当前代数小于定义的最大遗传代数时,继续循环,直至代数等于最大遗传代数FitnV=ranking(-ObjV); %分配适应度值SelCh=select('sus', Chrom, FitnV, DG); %选择,即对个体按照他们的适配值进行复制SelCh=recombin('xovsp', SelCh, 0.7); %交叉,即首先将复制产生的匹配池中的成员随机两两匹配,再进行交叉繁殖SelCh=mut(SelCh); %变异,以一个很小的概率随机地改变一个个体串位的值variable=bs2rv(SelCh, FieldD); %子代个体的十进制转换ObjVSel=variable*variable; %计算子代的目标函数值[Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel);%再插入子代的新种群,其中Chrom为包含当前种群个体的矩阵,SelCh为包好当前种群后代的矩阵variable=bs2rv(Chrom, FieldD); %十进制转换gen=gen+1; %代数计数器增加%输出最优解及其序号,并在目标函数图像中标出,Y为最优解, I为种群的%序号[Y, I]=max(ObjV);hold on; %求出其最大目标函数值plot(variable(I), Y, 'bo');trace(1, gen)=max(ObjV); %遗传算法性能跟踪trace(2, gen)=sum(ObjV)/length(ObjV);end%以下为结果显示部分,通过上面计算出的数值进行绘图variable=bs2rv(Chrom, FieldD); %最优个体进行十进制转换hold on, grid;plot(variable,ObjV,'b*'); %将结果画出三、运行结果:由图可见该函数为单调递增函数,即当X=31时,该取得最大值f(x)max =961。
遗传算法求函数极大值(matlab实现)

遗传算法求函数最大值(matlab实现)一、题目:寻找f(x)=x2,,当x在0~31区间的最大值。
二、源程序:%遗传算法求解函数最大值%本程序用到了英国谢菲尔德大学(Sheffield)开发的工具箱GATBX,该工具箱比matlab自带的GATOOL使用更加灵活,但在编写程序方面稍微复杂一些Close all;Clear all;figure(1);fplot('variable*variable',[0,31]); %画出函数曲线%以下定义遗传算法参数GTSM=40; %定义个体数目ZDYCDS=20; %定义最大遗传代数EJZWS=5; %定义变量的二进制位数DG=0.9; %定义代沟trace=zeros(2, ZDYCDS); %最优结果的初始值FieldD=[5;-1;2;1;0;1;1]; %定义区域描述器的各个参数%以下为遗传算法基本操作部分,包括创建初始种群、复制、交叉和变异Chrom=crtbp(GTSM, EJZWS); %创建初始种群,即生成给定规模的二进制种群和结构gen=0; %定义代数计数器初始值variable=bs2rv(Chrom, FieldD); %对生成的初始种群进行十进制转换ObjV=variable*variable; %计算目标函数值f(x)=x2 while gen<ZDYCDS %进行循环控制,当当前代数小于定义的最大遗传代数时,继续循环,直至代数等于最大遗传代数FitnV=ranking(-ObjV); %分配适应度值SelCh=select('sus', Chrom, FitnV, DG); %选择,即对个体按照他们的适配值进行复制SelCh=recombin('xovsp', SelCh, 0.7); %交叉,即首先将复制产生的匹配池中的成员随机两两匹配,再进行交叉繁殖SelCh=mut(SelCh); %变异,以一个很小的概率随机地改变一个个体串位的值variable=bs2rv(SelCh, FieldD); %子代个体的十进制转换ObjVSel=variable*variable; %计算子代的目标函数值[Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel);%再插入子代的新种群,其中Chrom为包含当前种群个体的矩阵,SelCh为包好当前种群后代的矩阵variable=bs2rv(Chrom, FieldD); %十进制转换gen=gen+1; %代数计数器增加%输出最优解及其序号,并在目标函数图像中标出,Y为最优解,I 为种群的%序号[Y, I]=max(ObjV);hold on; %求出其最大目标函数值plot(variable(I), Y, 'bo');trace(1, gen)=max(ObjV); %遗传算法性能跟踪trace(2, gen)=sum(ObjV)/length(ObjV);end%以下为结果显示部分,通过上面计算出的数值进行绘图variable=bs2rv(Chrom, FieldD); %最优个体进行十进制转换hold on, grid;plot(variable,ObjV,'b*'); %将结果画出三、运行结果:由图可见该函数为单调递增函数,即当X=31时,该取得最大值f(x)max=961。
遗传算法matlab程序代码

遗传算法matlab程序代码遗传算法是一种优化算法,用于在给定的搜索空间中寻找最优解。
在Matlab中,可以通过以下代码编写一个基本的遗传算法:% 初始种群大小Npop = 100;% 搜索空间维度ndim = 2;% 最大迭代次数imax = 100;% 初始化种群pop = rand(Npop, ndim);% 最小化目标函数fun = @(x) sum(x.^2);for i = 1:imax% 计算适应度函数fit = 1./fun(pop);% 选择操作[fitSort, fitIndex] = sort(fit, 'descend');pop = pop(fitIndex(1:Npop), :);% 染色体交叉操作popNew = zeros(Npop, ndim);for j = 1:Npopparent1Index = randi([1, Npop]);parent2Index = randi([1, Npop]);parent1 = pop(parent1Index, :);parent2 = pop(parent2Index, :);crossIndex = randi([1, ndim-1]);popNew(j,:) = [parent1(1:crossIndex),parent2(crossIndex+1:end)];end% 染色体突变操作for j = 1:NpopmutIndex = randi([1, ndim]);mutScale = randn();popNew(j, mutIndex) = popNew(j, mutIndex) + mutScale;end% 更新种群pop = [pop; popNew];end% 返回最优解[resultFit, resultIndex] = max(fit);result = pop(resultIndex, :);以上代码实现了一个简单的遗传算法,用于最小化目标函数x1^2 + x2^2。
遗传算法求解函数最大值

人工智能遗传算法函数优化目录1引言1.1 摘要函数优化是遗传算法的经典应用领域,也是对遗传算法进行性能评价的常用算例。
本文将用一个详细的例子来说明用遗传算法解一个简单参数优化问题的过程。
这里求解的是一个函数的最大值的问题。
1.2 背景遗传算法采纳自然进化模型。
通过保持一个潜在解的群体执行了多方向的搜索并支持这些方向上的信息构成和交换。
群体经过一个模拟进化的过程:在每一代,相对“好”的解产生,相对“差”的解死亡。
为区别不同解,我们使用了一个目标(评价)函数,它起着一个环境的作用。
选择是用来确定管理费用或交叉个体,以及被选个体将产生多少个代个体。
杂交组合了两个亲代染色体的特征,并通过交换父代相应的片断形成了两个相似的后代。
杂交算子的意图是在不同潜在解之间进行信息交换。
变异是通过用一个等于变异率的概率随机地改变被选择染色体上的一个或多个基因。
变异算子的意图是向群体引入一些额外的变化性。
运用遗传算法解题必经的五个步骤:1.对问题潜在解的遗传表达。
2.产生潜在解初始群体的方法。
3.起环境作用的用“适应值”评价解的适应程度的评价函数。
4.改变后代组成的各种遗传算子。
5.遗传算法所使用的各种参数:群体规模、应用遗传算子的概率等。
2 实验过程2.1 程序目标在实验过程中,我们应用遗传算法来模拟一个函数优化的问题。
程序所要解决的问题是求f(x1,x2)=21.5+x1*sin(4pi*x1)+x2*sin(20pi*x2)的最大值,其中-3.0≤x1≤12.1及4.1≤x2≤5.8。
2.2 实验原理及步骤1 )首先确立变量x1的定义域长度为15.1;所要求的小数点以后第四位精度意味着区间[-3.0, 12.1]应该至少被分成15.1*10000个等距区间,即染色体的第一部分需要18位;自变量x2域长度为 1.7,精度要求区间[4.1, 5.8]应该至少被分成1.7*10000个等距区间,即染色体的第二部分需要15位。
编程实现利用遗传算法求解方程最值

编程实现利用遗传算法求解方程最值一.函数为:求函数y=x+3*sin(2*x)-7*cos(x) 在【-4 4】的最大值二.MATLAB 程序如下:1.主控制程序GA.m%求函数y=x+3*sin(2*x)-7*cos(x) 在【-4 4】的最大值%function main()clearclcpopsize=100chromlength=10pc=0.6pm=0.01%%pop=initpop(popsize,chromlength)for i=1:100[objvalue]=calobjvalue(pop)fitvalue=calfitvalue(objvalue)[newpop]=selection(pop,fitvalue)%选择操作[newpop]=crossover(pop,pc)%交叉操作[newpop]=mutation(pop,pm)%变异操作[bestindividaul,bestfit]=best(pop,fitvalue)%求出群体中适应值最大的个体及其适应值y(i)=max(bestfit)n(i)=ipop5=bestindividaulx(i)=decodechrom(pop5,1,chromlength)*8/1023-4pop=newpop;endx(i)y(i)fplot('x+3*sin(2*x)-7*cos(x)',[-4 4])grid onhold onplot(x,y,'r*')title('x+3*sin(2*x)-7*cos(x)的最大值')hold off2.子程序:初始化%初始化function pop=initpop(popsize,chromlength)pop=round(rand(popsize,chromlength)) %rand随机产生初始种群3. 子程序:计算目标函数%计算目标函数值function [objvalue]=calobjvalue(pop)temp1=decodechrom(pop,1,10)x=temp1*8/1023-4objvalue=x+3*sin(2*x)-7*cos(x)function pop2=decodechrom(pop,spoint,length)pop1=pop(:,spoint:spoint+length-1)pop2=decodebinary(pop1)function pop2=decodebinary(pop)[px,py]=size(pop)for i=1:pypop1(:,i)=2.^(py-1).*pop(:,i)py=py-1endpop2=sum(pop1,2)4. 子程序:选择操作%选择function [newpop]=selection(pop,fitvalue)totalfit=sum(fitvalue)fitvalue=fitvalue/totalfit%但个个体选择概率fitvalue=cumsum(fitvalue)[px,py]=size(pop)ms=sort(rand(px,1))fitin=1newin=1while newin<=pxif(ms(newin))<fitvalue(fitin)newpop(newin,:)=pop(fitin,:)newin=newin+1elsefitin=fitin+1endend5.子程序:交叉% 交叉function [newpop]=crossover(pop,pc)[px,py]=size(pop)newpop=ones(size(pop))for i=1:2:px-1if(rand<pc)cpoint=round(rand*py)newpop(i,:)=[pop(i,1:cpoint) pop(i+1,cpoint+1:py)]newpop(i+1,:)=[pop(i+1,1:cpoint) pop(i,cpoint+1:py)] elsenewpop(i,:)=pop(i,:)newpop(i+1,:)=pop(i+1,1)endend%6. 子程序:变异%变异function [newpop]=mutation(pop,pm)[px,py]=size(pop)newpop=ones(size(pop))for i=1:pxif(rand<pm)mpoint=round(rand*py)if mpoint<=0mpoint=1endnewpop(i,:)=pop(i,:)if any(newpop(i,mpoint))==0newpop(i,mpoint)=1elsenewpop(i,mpoint)=0endelsenewpop(i,:)=pop(i,:)endend7. 求出群体中适应值最大的个体及其适应值:%求出群体中最大适应值及其个体function [bestindividual,bestfit]=best(pop,fitvalue) [px,py]=size(pop)bestindividual=pop(1,:)bestfit=fitvalue(1)for i=2:pxif fitvalue(i)>bestfitbestindividual=pop(i,:)bestfit=fitvalue(i)endend三以上程序运行后的的结果如下图:(图)。
使用遗传算法求解函数最大值【精品毕业设计】(完整版)

使用遗传算法求解函数最大值题目使用遗传算法求解函数f(x,y)=x∗sin(6∗y)+y∗cos(8∗x)在x∈[1,2]及y∈[1,2]的最大值。
解答算法使用遗传算法进行求解,篇末所附源代码中带有算法的详细注释。
算法中涉及不同的参数,参数的取值需要根据实际情况进行设定,下面运行时将给出不同参数的结果对比。
定义整体算法的结束条件为,当种群进化次数达到maxGeneration时停止,此时种群中的最优解即作为算法的最终输出。
设种群规模为N,首先是随机产生N个个体,实验中定义了类型Chromosome表示一个个体,并且在默认构造函数中即进行了随机的操作。
然后程序进行若干次的迭代,在每次迭代过程中,进行选择、交叉及变异三个操作。
一选择操作首先计算当前每个个体的适应度函数值,这里的适应度函数即为所要求的优化函数,然后归一化求得每个个体选中的概率,然后用轮盘赌的方法以允许重复的方式选择选择N个个体,即为选择之后的群体。
但实验时发现结果不好,经过仔细研究之后发现,这里在x、y取某些值的时候,目标函数计算出来的适应值可能会出现负值,这时如果按照把每个个体的适应值除以适应值的总和的进行归一化的话会出现问题,因为个体可能出现负值,总和也可能出现负值,如果归一化的时候除以了一个负值,选择时就会选择一些不良的个体,对实验结果造成影响。
对于这个问题,我把适应度函数定为目标函数的函数值加一个正数,保证得到的适应值为正数,然后再进行一般的归一化和选择的操作。
实验结果表明,之前的实验结果很不稳定,修正后的结果比较稳定,趋于最大值。
二交叉操作首先是根据交叉概率probCross选择要交叉的个体进行交叉。
这里根据交叉参数crossnum进行多点交叉,首先随机生成交叉点位置,允许交叉点重合,两个重合的交叉点效果互相抵消,相当于没有交叉点,然后根据交叉点进行交叉操作,得到新的个体。
三变异操作首先是根据变异概率probMutation选择要变异的个体。
手把手教你学matlab遗传算法
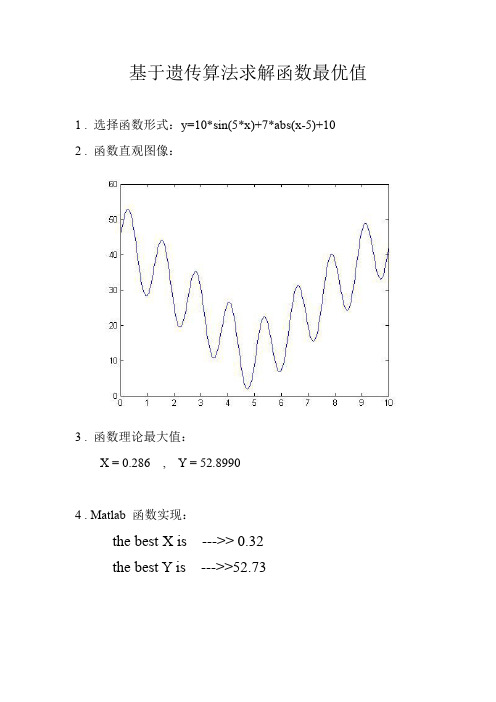
基于遗传算法求解函数最优值1.选择函数形式:y=10*sin(5*x)+7*abs(x-5)+102.函数直观图像:3.函数理论最大值:X=0.286,Y=52.89904.Matlab函数实现:the best X is--->>0.32the best Y is--->>52.735.Matlab程序5.1--------------------------------------------------------------%-------------函数说明----------------%%主函数%---------------------------------------function main()clearclcpopsize=100;%种群大小chromlength=10;%二进制编码长度pc=0.6;%交叉概率pm=0.001;%变异概率pop=initpop(popsize,chromlength);%初始种群for i=1:100[objvalue]=cal_objvalue(pop);%计算适应度值(函数值)fitvalue=objvalue;[newpop]=selection(pop,fitvalue);%选择操作[newpop]=crossover(newpop,pc);%交叉操作[newpop]=mutation(newpop,pm);%变异操作pop=newpop;%更新种群[bestindividual,bestfit]=best(pop,fitvalue);%寻找最优解x2=binary2decimal(bestindividual);x1=binary2decimal(newpop);[y1]=cal_objvalue(newpop);if mod(i,10)==0figure;fplot('10*sin(5*x)+7*abs(x-5)+10',[010]);hold on;title(['迭代次数为n='num2str(i)]);plot(x1,y1,'*');endendfprintf('the best X is--->>%5.2f\n',x2);fprintf('the best Y is--->>%5.2f\n',bestfit);5.2-----------------------------------%-------------函数说明----------------%初始化种群大小%输入变量:%popsize:种群大小%chromlength:染色体长度--》转化的二进制长度%输出变量:%pop:种群%---------------------------------------function pop=initpop(popsize,chromlength)pop=round(rand(popsize,chromlength));5.3--------------------------------------%-------------函数说明----------------%二进制转化十进制函数%输入变量:%二进制种群%输出变量:%十进制数值%---------------------------------------function pop2=binary2decimal(pop)[px,py]=size(pop);for i=1:pypop1(:,i)= 2.^(py-i).*pop(:,i);end%sum(.,2)对行求和,得到列的向量temp=sum(pop1,2);pop2=temp*10/1023;5.4--------------------------------------%-------------函数说明----------------%计算函数目标值%输入变量:%二进制数值%输出变量:%目标函数值%---------------------------------------function[objvalue]=cal_objvalue(pop)x=binary2decimal(pop);%转化二进制数为x变量的变化域范围的数值%x=temp*10/1023;%objvalue=10*sin(5*x)+7*cos(4*x);%objvalue=10*sin(x)+7*x+10objvalue=10*sin(5*x)+7*abs(x-5)+10;5.5------------------------------------------%-------------函数说明----------------%%输入变量:%pop:二进制种群%fitvalue:适应度值%输出变量:%newpop:选择以后的二进制种群%---------------------------------------function[newpop]=selection(pop,fitvalue) %构造轮盘[px,py]=size(pop);totalfit=sum(fitvalue);p_fitvalue=fitvalue/totalfit;p_fitvalue=cumsum(p_fitvalue);%概率求和排序%-------ms=sort(rand(px,1));%从小到大排列fitin=1;newin=1;while newin<=pxif(ms(newin))<p_fitvalue(fitin)newpop(newin,:)=pop(fitin,:);newin=newin+1;else fitin=fitin+1;endend5.6---------------------------------------%-------------函数说明----------------%%输入变量:%pop:二进制的父代种群数%pc:交叉的概率%输出变量:%newpop:交叉后的种群数%---------------------------------------function[newpop]=crossover(pop,pc)[px,py]=size(pop);newpop=ones(size(pop));for i=1:2:px-1if(rand<pc)cpoint=round(rand*py);newpop(i,:)=[pop(i,1:cpoint),pop(i+1,cpoint+1:py)];newpop(i+1,:)=[pop(i+1,1:cpoint),pop(i,cpoint+1:py)];elsenewpop(i,:)=pop(i,:);newpop(i+1,:)=pop(i+1,:);endend5.7------------------------------------------%-------------函数说明----------------%%输入变量:%pop:二进制种群%pm:变异概率%输出变量:%newpop:变异以后的种群%---------------------------------------function[newpop]=mutation(pop,pm)[px,py]=size(pop);newpop=ones(size(pop));for i=1:pxif(rand<pm)mpoint=round(rand*py);if mpoint<=0mpoint=1;endnewpop(i,:)=pop(i,:);if newpop(i,mpoint)==0newpop(i,mpoint)=1;else newpop(i,mpoint)=0;endelsenewpop(i,:)=pop(i,:);endend5.8----------------------------------------%-------------函数说明----------------%%输入变量:%pop:种群%fitvalue:种群适应度%%输出变量:%bestindividual:最佳个体(二进制个体)%bestfit:最佳适应度值%---------------------------------------function[bestindividual,bestfit]=best(pop,fitvalue) [px,py]=size(pop);bestindividual=pop(1,:);bestfit=fitvalue(1);for i=2:pxif fitvalue(i)>bestfitbestindividual=pop(i,:);bestfit=fitvalue(i);endend。
基于Matlab用遗传算法求一元函数最值问题(附源码)

基于Matlab⽤遗传算法求⼀元函数最值问题(附源码)问题:求y=10cos(5x x)+7sin(x-5)+10x x的最⼩值要求:(1)⽤遗传算法编程求解问题(2)编程语⾔⽤MATLAB 或C(3)输出问题的最优解及最⼤值,并绘图显⽰⽅法⼀function.mclear all;close all;clc;x=-1:0.01:0;y=10.*cos(5.*x.*x)+7.*sin(x-5.0)+10.*x.*x;figureplot(x,y)grid onxlabel('x')ylabel('f(x)')title('f(x)=10*cos(5*x*x)+7*sin(x-5)+10*x*x')%%f(x)=10*cos(5*x*x)+7*sin(x-5)+10*x*x1)运⾏结果函数取(-1,0)定义域,能够显⽰出的X=-0.7733时,Y=-0.4888,图像如下⽅法⼆func.mclear all;close all;clc;x=-1:0.01:0;y=10.*cos(5.*x.*x)+7.*sin(x-5.0)+10.*x.*x;figureplot(x,y)grid onxlabel('x')ylabel('f(x)')title('f(x)=10*cos(5*x*x)+7*sin(x-5)+10*x*x')%%f(x)=10*cos(5*x*x)+7*sin(x-5)+10*x*xmain.mclear all; %清除所有变量close all; %清图clc; %清屏nvars = 1;LB = -1;UB = 0;[t,fval] =ga(@test,1,[],[],[],[],LB,UB)fplot(@(x)(10.*cos(5.*x.*x)+7.*sin(x-5)+10.*x.*x),[-1 0]);hold on;plot(t,fval,'*');function y = test(x)y = 10*cos(5*x*x)+7*sin(x-5)+10*x*xendsimple_fitness.m%⽬标函数x = -1:0.01:0;%y=10*cos(5*x*x)+7*sin(x-5)+10*x*x;y=10.*cos(5.*x.*x)+7.*sin(x-5)+10.*x.*x;plot(x,y);%%%%%%%%%%%%%%%初始化参数%%%%%%%%%%%%%%%clear all; %清除所有变量close all; %清图clc; %清屏NP=50; %种群规模(数量)L = 20; %⼆进制位串长度Pc = 0.8; %交叉率Pm = 0.1; %变异率G = 100; %最⼤遗传代数Xs = 1; %上限Xx = -0; %下限f = randi([0,1],NP,L);%随机获得初始种群xB =[];%%%%%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%for k = 1:G%%%%%%%%%%%%%%%将⼆进制解码为定义域范围内⼗进制%%%%%%%%%%%%%%%for i = 1:NPU = f(i,:);m = 0;for j = 1:Lm = U(j)*2^(j-1)+m;endx(i) = Xx+m*(Xs-Xx)/(2^L-1);Fit(i) = 1/func1(x(i));endmaxFit = max(Fit);minFit = min(Fit);rr = find(Fit==maxFit);fBest = f(rr(1,1),:);xBest = x(rr(1,1));xB(i)=xBest;Fit = (Fit-minFit)/(maxFit-minFit);%%%%%%%%%%%%%%%基于轮盘赌的复制操作%%%%%%%%%%%%%%% sum_Fit = sum(Fit);fitvalue = Fit./sum_Fit;fitvalue = cumsum(fitvalue);ms = sort(rand(NP,1));fiti = 1;newi = 1;while newi <= NPif (ms(newi)) < fitvalue(fiti)nf(newi,:) = f(fiti,:);newi = newi + 1;elsefiti = fiti+1;endend%%%%%%%%%%%%%%%基于概率的交叉操作%%%%%%%%%%%%%%% for i=1:2:NPp = rand;if p < Pcq = randi(1,1,L);for j = 1:Lif q(j)==1;temp = nf(i+1,j);nf(i+1,j) = nf(i,j);nf(i,j) = temp;endendendend%%%%%%%%%%%%%%%基于概率的变异操作%%%%%%%%%%%%%%% i= 1;while i<= round(NP*Pm)h = randi([1,NP]);for j = 1:round(L*Pm)g = randi([1,L]);nf(h,g) =~ nf(h,g);endi=i+1;endf=nf;f(1,:) = fBest;trace(k) = maxFit;endxBest;fBestt=func1(xBest);subplot(1,2,1)plot(trace)xlabel('迭代次数')ylabel('⽬标函数值')title('适应度进化曲线')subplot(1,2,2)fplot(@(x)(10.*cos(5.*x.*x)+7.*sin(x-5)+10.*x.*x),[-1 0]);hold on;plot(xBest,func1(xBest),'*');%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%function result = func1(x)%fit = x+10*sin(5*x)+7*cos(4*x);fit = 10.*cos(5.*x.*x)+7.*sin(x-5)+10.*x.*x;result = fit;end1)运⾏结果适应度曲线函数图像。
matlab-遗传算法工具箱函数及实例讲解

matlab-遗传算法工具箱函数及实例讲解最近研究了一下遗传算法,因为要用遗传算法来求解多元非线性模型。
还好用遗传算法的工具箱予以实现了,期间也遇到了许多问题。
首先,我们要熟悉遗传算法的基本原理与运算流程。
基本原理:遗传算法是一种典型的启发式算法,属于非数值算法范畴。
它是模拟达尔文的自然选择学说和自然界的生物进化过程的一种计算模型。
它是采用简单的编码技术来表示各种复杂的结构,并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。
遗传算法的操作对象是一群二进制串(称为染色体、个体),即种群,每一个染色体都对应问题的一个解。
从初始种群出发,采用基于适应度函数的选择策略在当前种群中选择个体,使用杂交和变异来产生下一代种群。
如此模仿生命的进化进行不断演化,直到满足期望的终止条件。
运算流程:Step1:对遗传算法的运行参数进行赋值。
参数包括种群规模、变量个数、交叉概率、变异概率以及遗传运算的终止进化代数。
Step2:建立区域描述器。
根据轨道交通与常规公交运营协调模型的求解变量的约束条件,设置变量的取值范围。
Step3:在Step2的变量取值范围内,随机产生初始群体,代入适应度函数计算其适应度值。
Step4:执行比例选择算子进行选择操作。
Step5:按交叉概率对交叉算子执行交叉操作。
Step6:按变异概率执行离散变异操作。
Step7:计算Step6得到局部最优解中每个个体的适应值,并执行最优个体保存策略。
Step8:判断是否满足遗传运算的终止进化代数,不满足则返回Step4,满足则输出运算结果。
其次,运用遗传算法工具箱。
运用基于Matlab的遗传算法工具箱非常方便,遗传算法工具箱里包括了我们需要的各种函数库目前,基于Matlab的遗传算法工具箱也很多,比较流行的有英国设菲尔德大学开发的遗传算法工具箱GATB某、GAOT以及MathWork公司推出的GADS。
实际上,GADS就是大家所看到的Matlab中自带的工具箱。
matlab遗传算法求解二元函数最大值

遗传算法是一种模拟自然选择与遗传机制的优化算法,它具有全局寻优能力强、适用范围广等优点。
结合Matlab强大的数学计算能力,可以使用遗传算法求解二元函数的最大值,本文将对此进行详细讨论。
二、遗传算法概述遗传算法是一种基于生物进化的优化算法,它的基本思想是模拟自然界中生物的繁殖、变异、适应过程。
通过适应度函数对个体进行评估,然后通过选择、交叉和变异等操作产生新的个体,以达到寻优目的。
遗传算法具有全局寻优、适用范围广等优点,被广泛应用于解决数值优化问题。
三、Matlab中遗传算法的实现在Matlab中,可以使用遗传算法工具箱(GATool)来求解二元函数的最大值。
首先需要定义适应度函数、种裙大小、交叉概率、变异概率等参数,然后通过GATool提供的函数进行遗传算法的求解过程。
四、遗传算法求解二元函数最大值的步骤1. 定义适应度函数:在Matlab中,可以使用function关键字定义适应度函数,例如:```matlabfunction y = fitnessFunction(x)y = -x(1)^2 - x(2)^2;```2. 设置遗传算法参数:定义种裙大小、交叉概率、变异概率等参数,例如:```matlaboptions = gaoptimset('PopulationSize', 50,'CrossoverFraction', 0.8, 'Mutation', {mutationuniform, 0.1});```3. 调用遗传算法求解:使用Matlab提供的遗传算法函数对二元函数进行最大值求解,例如:```matlab[x, fval] = ga(fitnessFunction, 2, [], [], [], [], [-10, -10], [10, 10], [], options);```五、案例分析以二元函数f(x) = -x1^2 - x2^2为例,通过以上步骤在Matlab中进行遗传算法求解,可以得到最大值点为(0, 0),最大值为0。
遗传算法Matlab编程求函数的最大适应性及相应位置

遗传算法Matlab编程求函数的最大适应性及相应位置摘要:阐述了遗传算法的基本原理,探讨了matlab环境中实现遗传算法的编程方法,并以y yx xyx fs i ns i n), ( 1*=、]20)5()5(exp[999.0)10)5()5(exp(9.0),(2222 2-+--*++++*=yxyxyxfx,y∝[-10,10],要求种群数N=50,交换位数n/2,位置随机;变异位数统一为4。
交换的个数Nc=20、28、36、44;变异的个数Nm=1、5、10、15.两个函数的精度分别为0.001,0.0001两个简单的实例做了具体的分析。
关键词:遗传算法(GA)、matlab一、遗传算法概述遗传算法(Genetic Algorithm ,GA) 是借鉴生物界自然选择复制和群体进化机制形成的一种全局寻优算法。
与传统的优化算法相比,遗传算法具有如下优点[1 ] :1) 不是从单个点,而是从多个点构成的群体开始搜索;2) 在搜索最优解过程中,只需要由目标函数值转换得来的适应值信息,而不需要导数等其它辅助信息;3) 搜索过程不易陷入局部最优点。
目前,该算法已渗透到许多领域,并成为解决各领域复杂问题的有力工具[2 ]。
在遗传算法中,将问题空间中的决策变量通过一定编码方法表示成遗传空间的一个个体,它是一个基因型串结构数据;同时,将目标函数值转换成适应值,它用来评价个体的优劣,并作为遗传操作的依据。
遗传算法的应用,遗传算法在人工智能的众多领域便得到了广泛应用。
例如,机器学习、聚类、控制(如煤气管道控制)、规划(如生产任务规划)、设计(如通信网络设计、布局设计)、调度(如作业车间调度、机器调度、运输问题)、配置(机器配置、分配问题)、组合优化(如TSP、背包问题)、函数的最大值以及图像处理和信号处理等等。
另一方面,人们又将遗传算法与其他智能算法和技术相结合,使其问题求解能力得到进一步扩展和提高。
例如,将遗传算法与模糊技术、神经网络相结合,已取得了不少成果。
(完整版)遗传算法求解函数最大值(matlab)

遗传算法求解函数F(x1,x2)=100*(x1^2-x2)^2+(1-x1)^2;的最大值(MATLAB)%Generic Algorithm for function f(x1,x2) optimum (最大值)clear all;close all;%ParametersSize=80;G=100;CodeL=10;umax=2.048;umin=-2.048;E=round(rand(Size,2*CodeL)); %Initial Code%Main Programfor k=1:1:Gtime(k)=k;for s=1:1:Sizem=E(s,:);y1=0;y2=0;%Uncodingm1=m(1:1:CodeL);for i=1:1:CodeLy1=y1+m1(i)*2^(i-1);endx1=(umax-umin)*y1/1023+umin;m2=m(CodeL+1:1:2*CodeL);for i=1:1:CodeLy2=y2+m2(i)*2^(i-1);endx2=(umax-umin)*y2/1023+umin;F(s)=100*(x1^2-x2)^2+(1-x1)^2;endJi=1./(F+1);%****** Step 1 : Evaluate BestJ ******BestJ(k)=min(Ji);fi=F; %Fitness Function[Oderfi,Indexfi]=sort(fi); %Arranging fi small to biggerBestfi=Oderfi(Size); %Let Bestfi=max(fi)BestS=E(Indexfi(Size),:); %Let BestS=E(m), m is the Indexfi belong to max(fi)bfi(k)=Bestfi;%****** Step 2 : Select and Reproduct Operation******fi_sum=sum(fi);fi_Size=(Oderfi/fi_sum)*Size;fi_S=floor(fi_Size); %Selecting Bigger fi value (取整)kk=1;for i=1:1:Sizefor j=1:1:fi_S(i) %Select and ReproduceTempE(kk,:)=E(Indexfi(i),:);kk=kk+1; %kk is used to reproduceendend%************ Step 3 : Crossover Operation ************pc=0.60;n=ceil(20*rand);for i=1:2:(Size-1)temp=rand;if pc>temp %Crossover Conditionfor j=n:1:20TempE(i,j)=E(i+1,j);TempE(i+1,j)=E(i,j);endendendTempE(Size,:)=BestS;E=TempE;%************ Step 4: Mutation Operation **************%pm=0.001;%pm=0.001-[1:1:Size]*(0.001)/Size; %Bigger fi, smaller Pm%pm=0.0; %No mutationpm=0.1; %Big mutationfor i=1:1:Sizefor j=1:1:2*CodeLtemp=rand;if pm>temp %Mutation Conditionif TempE(i,j)==0TempE(i,j)=1;elseTempE(i,j)=0;endendendend%Guarantee TempPop(30,:) is the code belong to the best individual(max(fi)) TempE(Size,:)=BestS;E=TempE;endMax_Value=BestfiBestSx1x2figure(1);plot(time,BestJ);xlabel('Times');ylabel('Best J');figure(2);plot(time,bfi);xlabel('times');ylabel('Best F');轐行绒果Map_Falue =3.9059e+ 03BestS =0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Р0ɸ1 =-2&0480x2 =-2.0080。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
遗传算法求解函数F(x1,x2)=100*(x1^2-x2)^2+(1-x1)^2;
的最大值(MATLAB)
%Generic Algorithm for function f(x1,x2) optimum (最大值)
clear all;
close all;
%Parameters
Size=80;
G=100;
CodeL=10;
umax=2.048;
umin=-2.048;
E=round(rand(Size,2*CodeL)); %Initial Code
%Main Program
for k=1:1:G
time(k)=k;
for s=1:1:Size
m=E(s,:);
y1=0;y2=0;
%Uncoding
m1=m(1:1:CodeL);
for i=1:1:CodeL
y1=y1+m1(i)*2^(i-1);
end
x1=(umax-umin)*y1/1023+umin;
m2=m(CodeL+1:1:2*CodeL);
for i=1:1:CodeL
y2=y2+m2(i)*2^(i-1);
end
x2=(umax-umin)*y2/1023+umin;
F(s)=100*(x1^2-x2)^2+(1-x1)^2;
end
Ji=1./(F+1);
%****** Step 1 : Evaluate BestJ ******
BestJ(k)=min(Ji);
fi=F; %Fitness Function
[Oderfi,Indexfi]=sort(fi); %Arranging fi small to bigger
Bestfi=Oderfi(Size); %Let Bestfi=max(fi)
BestS=E(Indexfi(Size),:); %Let BestS=E(m), m is the Indexfi belong to max(fi)
bfi(k)=Bestfi;
%****** Step 2 : Select and Reproduct Operation******
fi_sum=sum(fi);
fi_Size=(Oderfi/fi_sum)*Size;
fi_S=floor(fi_Size); %Selecting Bigger fi value (取整)
kk=1;
for i=1:1:Size
for j=1:1:fi_S(i) %Select and Reproduce
TempE(kk,:)=E(Indexfi(i),:);
kk=kk+1; %kk is used to reproduce
end
end
%************ Step 3 : Crossover Operation ************
pc=0.60;
n=ceil(20*rand);
for i=1:2:(Size-1)
temp=rand;
if pc>temp %Crossover Condition
for j=n:1:20
TempE(i,j)=E(i+1,j);
TempE(i+1,j)=E(i,j);
end
end
end
TempE(Size,:)=BestS;
E=TempE;
%************ Step 4: Mutation Operation **************
%pm=0.001;
%pm=0.001-[1:1:Size]*(0.001)/Size; %Bigger fi, smaller Pm
%pm=0.0; %No mutation
pm=0.1; %Big mutation
for i=1:1:Size
for j=1:1:2*CodeL
temp=rand;
if pm>temp %Mutation Condition
if TempE(i,j)==0
TempE(i,j)=1;
else
TempE(i,j)=0;
end
end
end
end
%Guarantee TempPop(30,:) is the code belong to the best individual(max(fi)) TempE(Size,:)=BestS;
E=TempE;
end
Max_Value=Bestfi
BestS
x1
x2
figure(1);
plot(time,BestJ);
xlabel('Times');ylabel('Best J');
figure(2);
plot(time,bfi);
xlabel('times');ylabel('Best F');
轐行绒果
Map_Falue =
3.9059e+ 03
BestS =
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Р0
ɸ1 =
-2&0480
x2 =
-2.0080。
