管道包扎问题的数学建模

合集下载

制作管道的数学建模

制作管道的数学建模一、教学目标：1.通过学习探究与实践的课题四制作管道为载体让学生体验运用数学知识建模解决问题的过程。

2.活用三角知识解决实际问题。

3.增强学生实践动手能力通过参与问题解决的活动，逐步增强合作意识，形成数学知识的应用意识和综合意识。

二、教学重点、难点：重点：构建数学模型、运用三角知识解决实际问题。

难点：数学模型的建立。

三、教学过程：展示图片，解释课题四在实际生活中产生的背景，引出问题“大口径的管道用钢板卷曲焊接而成，请设计钢板切割方案，标出焊缝位置。

”学生实验操作：提供给学生圆柱形物体、可裁成任意宽度纸带的纸张、剪刀、胶带。

请同学动手实验探究。

生1：用纸带缠绕圆柱形物体，用铅笔在纸带上做好剪裁记号，摊开纸带裁去多余部分。

C A生2：用胶带包裹好圆柱体模型（无盖），将圆柱侧面沿胶带接缝螺旋线剪开。

学生操作后还可以将圆柱一边在黑板上滚动，一边将其剪开的侧面展开并粘于黑板上，让大家体会刚才的操作过程。

生3：缠绕一个长为圆柱高，宽为圆柱底面半周长的矩形。

启发：空调是把送风管、排冷凝水管、电线包裹缠绕在一起，形状不一定是圆柱，那会有什么不同呢？比如缠绕包裹的对象不是圆柱，而是一个正三棱柱、正四棱柱、任意直棱柱或者一把直尺呢？纸制的侧面即可以是一个圆柱的侧面，也可以折成任意等高，等底面周长的任意直棱柱侧面。

这样运用拓扑思想把立几问题平几化，思考起来更为简单。

A（黑色粗线条处为折痕。

）实际使用纸带的长度为：OG学生发现问题：切割方案主要由一个角度决定，（裁去直角三角形的一个锐角或者剪裁为平行四边形纸带的一个内角）。

纸带不同或圆柱不同得到的角度也不同。

学生提出问题：进一步关注这个角度与哪些变量有关。

学生解决问题：1、引导学生建模解决问题：角度的大小与纸带的宽度、圆柱底面周长有关。

故设纸带宽为d ，圆柱底面半径为r ，高为h 。

设纸带被裁为平行四边形后一个锐内角BAC θ∠=。

已知：纸带宽为d ，圆柱底面半径为r ，高为h 。

布条缠绕管道模型

布条缠绕管道模型
布条缠绕管道模型是一种描述管道流体运动的数学模型，它利用布条缠绕的方式来描述管道内的流体湍流和流动状态。

该模型广泛应用于工程和科学领域，用于研究流体运动的复杂性和相关问题。

布条缠绕管道模型的基本原理是利用一系列截然不同的布条模拟流体。

通常来说，这些布条是随机放置的，并且每个布条的位置和颜色都与随机标志相关联。

这些标志可用于定义流体的速度、流量和流动方向等参数，从而可以模拟不同条件下的流体运动。

布条缠绕管道模型的核心思想是建立一个具有一定复杂度的非线性动力学系统，其中包括尽可能多的自由变量来描述流体的运动。

在此过程中，需要考虑流体的粘性、密度、惯性等因素，并根据这些因素来模拟流体的运动。

模型的复杂性和准确性程度与计算量增加成正比关系，因此需要合理权衡模型的精度和计算效率。

在具体的应用中，布条缠绕管道模型可以用于研究管道流体运动的不同特性，如流体的速度分布、径向输运速度、阻力和能量消耗等。

此外，该模型还可用于优化管道设计，减少流体的能量损耗和阻力，提高流体的输送效率。

管道包扎问题的数学模型论文

管道包扎问题的数学模型论文管道包扎问题的数学模型摘要: 本篇论文讨论管道的包扎问题.是一个三维空间的问题我采用剪切的方法把空间问题转化为平面问题建立刚好全部包扎所用带子最短模型和管道包扎出现接缝处重叠模型然后利用数学软件Matlab 求解.在图1 中，求得最短带子包扎的通用表达式并代入题目给出的数据得到第一个问题的最短长度为50.4 米。

在图2 和图3 中，采用近似的处理方法求出管道包扎接缝处重叠带子宽度的表达式代入第二个问题的数据得到带子的重叠宽度为0.004 米.论文的最后对临界角0 和截面是正多边形的管道的情况作进一步的讨论并得到更一般的模型.关键词: 临界角临界点临界长度等量关系1 问题的提出用宽度为0.3m 的带子缠绕包扎圆柱型管道，管道长30m，截面周长为0.5m. 1 如果用带子全部包住管道，最少要用多长的带子，请你给出计算这个最小长度的公式，并且依次计算出所需长度数值. 2 现有一条长度为51m 的带子，想将这条带子全部用于缠绕包扎这个管道，可以使带子的接缝处重叠瘩接.请你给出用这条带子缠绕包扎这个管道的方案.（计算结果精确到0.001m）3 如果管道截面是正三边形正四边形或边数更多的正多边形.2 问题的分析生活的经验告诉我们在包扎圆形管道的过程中如果开始包扎时带子边缘所在的直线与管道母线的夹角过小就可能出现不能把管道全部包扎的现象如果夹角过大就可能出现包扎带子在接缝处重叠的现象. 所以随着夹角的增大总会出现在接缝处恰好接合而没有重叠的情况.这种特殊的情况就是第一问的求解问题称此时包扎带子的长度为临界长度带子边缘所在的直线与管道母线的夹角为临界角管道任一端的带子截口所在边与管道截面的交点称为临界点.如果给定一段带子的长度大于临界长度则总能找到一种包扎方案使得整条带子全都包扎完其中接缝处有重叠. 当管道的截面为正多边形时我们把正多边形的直棱柱管道看作圆形管道的变形来处理即正多边形的直棱柱管道的平面展开图与圆形管道的平面展开图是同样的.3 模型的假设1 管道没有厚度即把管道剪开图看成平面不考虑空间结构2 管道是刚性物体带子也不具备弹性 3 管道截面是圆形或正多边形整条管道粗细均匀 4 包扎过程中带子的宽度不变，带子也不能切断 5 带子没有厚度且两端截口垂直于它的边.即把带子看成一个长方形不考虑空间结构4 符号的约定1）a -----带子的宽度2）b -----管道的长度；3 c -----管道截面的周长4）l ----- 带子的长度5 θ--- 带子截口所在的直线与管道母线的夹角 6 S1 ----- 直角三角形AED 的面积7 S 2 ----- 直角三角形OBF 的面积8 S 3 ---- 四边形COHG 的面积9 x ---- 带子重叠部分的宽度10 y --- 重叠部分的带子长度11 m---- 截面正多边形的边长12 n ---- 截面正多边形的边数.5 模型的建立和求解5.1 刚好全部包扎所用带子最短模型经过临界点沿着管道的母线切开得到矩形ABCD如下图1: 图1 其中矩形ABCD 为管道的侧面展开图三角形AED 为直角三角形四边形OHGC.定理1 直角三角形AED 的面积等于直角三角形OBF 和四边形OHGC 之和. 证明线段BF 和线段CG在空间图形中是重合的故这两线段相等. 把直角三角形OBF 向右移动使BF 与CG 重合则构成直角三角形O HO . 又EDOH OBOCAD 故AED O HO 即定理成立.推论1 沿着管道任一母线剪开得到的平面展开图中管道截面界线的两端分别能组成两个直角三角形且这两个直角三角形的面积相等.由上面的定理 1 和推论可以得出刚好包扎管道所用带子最短的模型: al S1 S 2 S 3 bc 1 S1 a c a 2 2 2 S1 S 2 S 3 求得一般表达式为: bc l c2 a2 a把题目中给出的数据代入一般表达式求得第一问题的临界长度为: 30 0.5 l 0 .5 2 0 .3 2 50.4 米0 .35.2 管道包扎出现接缝处重叠的模型按图1的剪开方法得到管道平面展开图如图2: 图2 其中阴影为带子重叠部分. 命题1 在带子宽度不变的条件下带子相接处重叠的宽度一定相等即图 2 中阴影部分的平行四边形的宽度不改变.5.2.1 求阴影部分的带子的长度. 命题 2 阴影部分的长度比整条包扎带子的长度短线段AE 的长度. 证明由推论 2 阴影部分的宽度相等故可以过图2 的 A 点垂直AE 剪切再把剪切的左边部分图形补到右边如下图3: 图3由图3 可以看出y l AE l c cos5.2.2 利用阴影部分的面积相等得到模型: xy al bc a x c 2 a x 2 y l c cos c 2 a x 2 cos c化简此方程组得: 2 x a c 2 a x 2 xl al bc 0 1利用Matlab 解方程1得到的结果过繁所以为了得到一个比较简单而又接近实际的答案我们作以下处理: 在生活和工作中为了节省材料包扎管道的带子一般不会比临界长度长太多所以可用 c 2 a 2 近似代替c 2 a x 2 求得结果为: a c 2 a 2 bc al x 2 2 c2 a2 l 把第二问题的数据代入方程1得: x 1 0.00357把第二问题的数据代入方程2得: x 2 0.0036由以上计算得到的结果可以看出当带子的长度不太长时用 a c 2 a 2 bc al x 2 c2 a2 l代替这个模型的结果是可以的.且取得第二问题的结果为: x0.004米5.3 截面为正多边形的直棱柱管道模型推理1 对于任何正多边直棱柱的包扎面从临界点沿棱柱的母线剪开得到的剪开平面如图 1 所示包扎方案为临界时如果有带子重合的情形如图 2.类似以上图 1 圆柱管道包扎方案的方法建立模型如下: 5.3.1 包扎正多边直棱柱的临界模型: al S1 S 2 S 3 bmn 1 S1 a mn a 2 2 2 S1 S 2 S 3 解得: mnb l mn 2 a 2 a 5.3.1 包扎正多边直棱柱的有重叠的模型: xy al mnb a x mn 2 a x 2 y l mn cos mn 2 a x 2 cos mn 以mn 2 a 2 代替mn 2 a x 2 解得a mn 2 a 2 mnb al x 2 mn 2 a 2 l6 模型的分析6.1 临界角的讨论 a 临界角0 arcsin 3 c 6.1.1 当0 时带子不能全部包扎整条管道.如果要在角增大即临界角增大的情况下实现全部包扎由3 式可以看出应加大带子的宽度或减小管道截面的周长. 6.1.2 当0 时带子在包扎过程中出现接缝处重叠.如果要在角减小即临界角减小的情况下实现全部包扎由3 式可以看出应减小带子的宽度或增加管道截面的周长.故有以下推理:推理 2 包扎管道的临界角0 随带子宽度的增大而增大管道截面周长的减小而增大随带子宽度的减小而减小管道截面周长的增大而减小.6.2 管道的讨论由推论1、命题1 和推理1可知无论求解模型是圆柱模型或是截面为正多边形的直棱柱其求解过程都是相同的故有以下推理.推理3 管道的包扎方案与管道截面是凸多边形不限边数不限每边的长度或连续的凸封闭曲线无关只与管道截面的周长C、管道长度l 和给定的带子的长度有关.参考文献:1 吕林根. 解析几何〔Ｍ〕. 北京:高等教育出版社，2000.2 刘来福. 数学模型与数学建模〔M 北京：北京师范大学出版社20023.姜启源等编.《数学模型》（第三版）.北京：高等教育出版社.2003. 》4.姜启源等编.《数学模型（第三版）习题参考解答. 北京：高等教育出版社.2003.5.刘来福，曾文艺.数学模型与数学建模.北京：北京师范大学出版社，19976.杨启帆，边馥萍.数学模型.杭州：浙江大学出版社，19907.叶其孝.中学数学建模M.长沙：湖南出版社.1998.9-108.冯跃峰.对数学教育若干问题的认识J.数学教育学报.1992（1）:64-659.卜月华.中学数学建模教与学M.东南大学出版社，2002，310.荆新大.足球中的数学J.数学教学，1993（3）11.廖运章.强调数学理解建模灵活开放.数学通报，2000，12 The study of pipeline bind up’s problem YE Feiwu（Department of mathematics 2000 grade Class Shaoguan College Shaoguan512005Guangdong）Abstract: we will discuss the bind up problems of pipeline in this paper. This problem is athree- figure problem. We can cut the pipeline open and change these plane problems intothree-figure problems. We set up the best of all shot model which use band shot of all and happen tobind up the pipeline entirely and set up the repeated model of which the joint locate appear repeatedthen take the mathematics software to work out the problem. In the fig1 we work out the currencyexpression of best of all bands and make use of the data of subject and gained the answer of thefirst problem is 50.4 meter. In the fig2 and fig3 adopt approximate method to seek out theexpression of the band’s width superposed and make use of the data of subject and gained theanswer of the second problem is 0.004 meter. At the end of the paper we will discuss the critical angle 0 and pipeline of which section ispositive polygon and gained the even more model.Key words: critical angle critical point critical length grade measure relation。

管道包扎

管道包扎一、摘要家庭中的煤气管道或暖气管道以及化工厂中大量的管道在室外的部分经常需要从外部用很长的带子缠绕包扎，从而对管道加以保护。

在包扎过程中总会考虑到材料最省时需要带子的总量，以及在材料稍微多余的情况下如何包扎才能将材料全部用完的问题。

在这里，我们将建立简单的数学模型并借助数学软件MATLAB求解，利用一些参数可以算出所需最短带子的长度为50.400m，这就解决了第一个问题。

在第二个问题中，带子总长M=51.000m，由此我们算出包扎时每次重叠0.004m 就能刚好把带子用完。

二、问题已知直圆管道的长度，用缠绕的方法包扎管道，需用多长的带子？1、设管道长L = 30m , 圆管截面周长C = 50cm, 带子宽W = 30cm,则最少要用多长M的带子才能将管道缠绕包扎上?2、现有带长M=51m，计划将这条带子全部用来缠绕包扎上面的管道。

缠绕时允许带子互相重叠一部分。

应该如何包扎这个管道？(计算结果精确到0.001)三、问题的分析这是一个很实际化、很生活化的问题，但是题目给得很粗糙，在建立数学模型时为了能顺利解决问题，我们需要作出一些假设，如假设管道是直圆管、带子无弹性等。

根据生活经验，我们需要将带子斜着缠绕在管道上，于是为了使带子全部包住管道而且带子间互不重叠就必须得选择一个适当的角度，为此我们将建立一个简单的数学模型来解决这个问题。

但是，实际生活我们又会遇到这样一个问题，买来的带子通常要稍微多于实际所需要的，这时，我们就得另外建立一个模型，来考虑如何将买来的材料用完并且包扎得比较完美的问题。

四、假设1）. 管道是直圆管，粗细一致；2）. 带子等宽，无弹性，并且带宽要小于圆管截面周长；3）. 为保持包扎过程的连续性以减少劳动量，在包扎过程中昼不将带子剪短；4）.针对问题1，假设在包扎过程中带子包住管道且带子互不重叠、边缘衔接处没有空隙：5）.针对问题2，假设包扎时带子每次重叠的部分相等；6）.为表达更加方便，我们假设一些符号表示——W：带宽，C：截面周长，：倾斜角，W*:问题2中模型上的带宽，L:管长，M:带长五、模型的建立及求解1、问题1模型我们设想将带子已经缠绕在管道上使它包住管道且带子互不重叠、边缘衔接处没有空隙，并且从带子一角的A 点沿圆管母线的方向画一条辅助线l ，再在辅助线与带子边缘的交点处画出圆管的横截面的切口线c ，将画有辅助线的带子剪下一段展开。

钢管的运输与订购问题(数学建模)

管道订购与运输问题摘要：本文通过研究了题目所给图并结合题目所给条件信息，理解到钢管的订购与运输问题可通过合理假并简化为单一的公路运输问题，构架了产量未定的单一运输优化模型。

运用运筹学原理求得钢管厂到铺设点的最小距离，通过线性规划的思想列出目标函数，在求得目标函数的同时，我们要考虑到目标最小费用函数中管道的铺设费用，在从铺设点向两边铺设的过程两端开始的1千米是不需要铺设费的，运用等差数列的思想构造一个子函数作为目标函数的一部分，从而得到优化的数学模型，运用lingo软件求得最小运费为1274296。

我们的数学模型是综合考虑运费与钢管单价及铺设费用问题，是整个钢管订购铺设总费用最小。

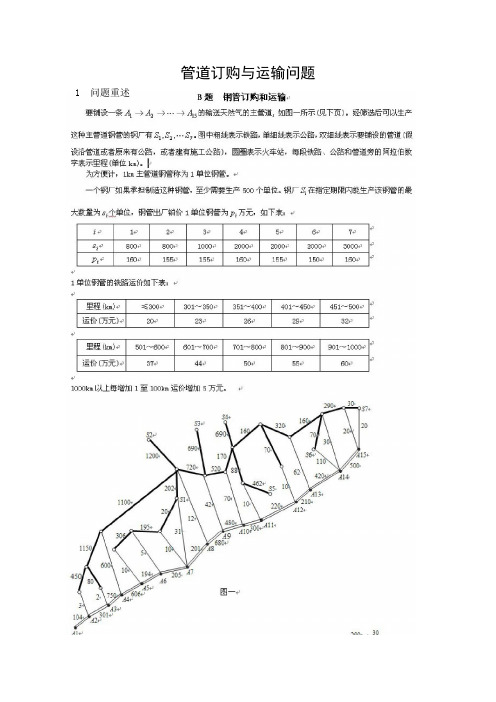
关键词：管道订购与运输；运筹学；LINGO软件；产量未定的运输模型；线性规划（一）问题重述：要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见附录一)筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。

图中粗线表示铁路，单细线表示公路，双细线表示要铺设的管道(假设沿管道或者原来有公路，或者建有施工公路)，圆圈表示火车站，每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。

为方便计，1km 主管道钢管称为1单位钢管。

一个钢厂如果承担制造这种钢管，至少需要生产500个单位。

钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位，钢管出厂销价1单位钢管为i p 万元，如下表：i1 2 3 4 5 6 7 i s800 800 1000 2000 2000 2000 3000 i p1601551551601551501601单位钢管的铁路运价如下表：里程(km) ≤300 301～350 351～400 401～450 451～500 运价(万元) 2023262932里程(km) 501～600 601～700 701～800 801～900 901～1000运价(万元)37445055601000km 以上每增加1至100km 运价增加5万元。

研究生几个数学模型及建模方法

第一、二章数学模型与建模数学模型是架于数学与实际问题之间的桥梁在数学发展的进程中无时无刻不留下数学模型的印记。

一.模型为了一定的目的，人们对原型的一个抽象例如：航空模型对飞机的一个抽象，城市交通图对交通系统的一个抽象二.数学模型用数学语言，对实际问题的一个近似描述，以便于人们用数学方法研究实际问题。

例1 :牛顿定律假设：1. 物体为质量为m的质点，忽略物体的大小和形状。

2. 没有阻力、摩擦力及其他外力，只有沿物体运动方向的作用力F。

引入变量x(t)表示在t时刻物体的位置，则受力物体满足如下运动规律，这就是牛顿定律的数学模型。

例2:哥尼斯堡七桥问题问题：能否从某地出发，通过每座桥恰好一次，回到原地？由4个结点7条边组成的图构成解决这个问题的数学模型。

三.数学模型的特征1. 实践性：有实际背景，有针对性。

接受实践的检验。

2. 应用性：注意实际问题的要求。

强调模型的实用价值。

3. 综合性：数学与其他学科知识的综合。

四.建模举例数学建模(Mathematical modelling)是一种数学的思考方法，用数学的语言和方法，通过抽象、简化建立能近似刻画并—军决实际问题的强有力的数学工具。

下面给出几个数学建模的例子，重点说明：如何做出合理的、简化的假设；如何选择参数、变量，用数学语言确切的表述实际问题；如何分析模型的结果，解决或解释实际问题，或根据实际情况改进模型。

例1.管道包扎问题：用带子包扎管道，使带子全部包住管道，且用料最省。

假设：1. 直圆管，粗细一致。

2. 带子等宽，无弹性。

3. 带宽小于圆管截面周长。

4. 为省工，用缠绕的方法包扎管道.参量、变量：W :带宽，C:圆管截面周长， K倾斜角 (倾斜角)包扎模型W二Csin ■■(截口)包扎模型|0B | —C2-W 2进一步问，如果知道直圆管道的长度，用缠绕的方法包扎管道，需用多长的带子?设管道长带长模型问题：L,圆管截面周长C,带子宽W,带子长M. M 二LC /W C2 -W21•若L = 30m, C = 50cm, W = 30cm ,则最少要用多长的带子才能将管道缠绕包扎上？2. 现有带长M i=51m，计划将这条带子全部用来缠绕包扎上面的管道。

布条缠绕圆形管道模型

布条缠绕圆形管道班级：12数学（1）班学号：1207021028 姓名：许菁菁摘要：本文通过将三维空间上的问题转化为二维平面上的问题，在已知布条宽度以及管道直径、长度且不考虑布条厚度情况下，通过一些简单的计算将布条与管道轴心的夹角计算出来，然后根据布条的表面积与管道的表面积相等，考虑到是否考虑管道两端影响这两种情况，最后给出管道截面是三角形的情况分析。

关键词：表面积紧贴转化1 问题重述用宽为W的布条缠绕直径为d的圆形管道，如果用布条全部包住管道，问布条应该如何缠绕，才能使所用的布条长度最小（如图所示）。

若知道管道长度为L，需要多长布条（可考虑管道两端影响），如果管道是其他形状呢？2 问题分析对于已知管道长度L，在考虑两端影响的情况下，需要用多长布条问题，我们首先需要将布条包围圆形管道这个三维空间上的问题转化为平面上的问题，其次我们考虑布条与圆形管道中心轴线的夹角α，利用边角关系求出布条长度。

此时，我们还需附加考虑管道两端的影响。

再根据前面问题的求解过程，考虑管道是其他形状的情况。

3 模型假设3.1假设布条的厚度不3.2假设布条没有弹性3.3假设布条紧密缠绕且没有重叠3.4假设不考虑其它外界因素的影响4 符号系统表1 符号错误！未找到引用源。

错误！未找到引用源。

5 模型建立与求解5.1不考虑两端影响图1 管道展开图根据需要我们将三维空间中布条包围管道的问题转化成平面中布条包围管道问题。

由于布条不重叠而且完全缠绕，那么布条的长度/sin CD t d πα==5.2考虑两端影响由于布条是完全缠绕而且不重叠的，因此，我们考虑管道的表面积与布条的表面积相等。

则S dL s tWπ== 由于S=s则dLt W π=由于布条必须完全包住管道，因此管道两端都有浪费，浪费的长度为2AE 的长度，则浪费的长度为 ()2222AE t d W π=- 此时，布条的总长度为 ()2222AE dLT t t d W W ππ=+=+-5.3考虑管道是其他形状如图，若管道横截面是三角形的，周长为c ，考虑方法相同，只要将πd 改为c 即可。

带子缠绕包扎圆柱形管道模型处理

浙江师范大学首届数学建模竞赛一等奖参赛小组负责人: 刘海华组员: 黄敏组员: 陈斌学院: 生命与环境科学学院系别与班级: 生物科学012 班主办：浙师范师范大学团委承办：数理信息工程学院目录题目 1模型一 2模型二 3模型三 4模型分析 6 带子缠绕包扎圆柱形管道模型处理摘要讨论了几种带子缠绕包扎圆柱形管道的模型，并经分析比较择优处理后，确认出最佳模型。

问题的提出用宽度为0.3的带子缠绕包扎圆柱形管道，管道长30m，截面周长为0.5m。

（1）如果用带子全部包住管道，最少要用多长的带子，请你给出计算这个最小长度的公式，并且依次计算出所需长度数值。

(2) 现有一条长度为51m的带子，想将这条带子全部用于缠绕包扎这个管道，可以使带子的接缝处重叠瘩接。

请你给出用这条带子缠绕包扎这个管道的方案。

（计算结果精确到0.001m）在现代社会，随着科技的发展，产品的包装的重要性甚至可以与产品的质量相抗衡，一些圆柱形产品的包装曾经困绕了不少人，在产品质量相同的情况下，如何让外表既美观有省材成为竞争的关键，在此，我们以带子残缠绕包扎圆柱形管道问题为例进行讨论几种处理模型问题的分析不同类型的包扎有不同的特点，在此不赘述，而是先按题目的要求假设几种模型，在分析问题的过程中，不可能通过一次假设就建立起完善的数学模型因此，我有如下思路：先做简单的假设，对结果进行分析，针对结果不合理之处，逐步进行修改，最终得到较好的模型。

模型一纵向缠绕包扎模型模型假设在研究建立模型时，需要作一些假设，目的是使模型简单、利于理解、便于计算，为此我们考虑四种费用，即剪切费用、粘贴费用、缠绕费用和带子总费用，归纳假设条件如下：（1）带子可以根据需要任意剪切（2）剪切费用为a 元/m （3）粘贴费用为b 元/m 2 （4）螺型缠绕费用为c 元/m 2 （5）带子价格d 元/m 2(6) 由于切过程需要精确测量计算.因此耗费较大.粘贴过程要用粘贴剂也许花费较大成本而且为了保证粘贴效果要精细的劳动,而缠绕则较为简单.因此可以作如下近似估计： d ≈a ≈b ＞＞c模型构建和求解将带子均分为两段.用以包住圆柱即:纵向包扎模型如图(1) 设：带长为L,带宽为i,管长为N,管道横切面周长为n,带子面积s 1, 管道侧面积s 2要使带子能完全缠绕包扎住管道则：s 1≥s 2 即L×i ≥N×n 所以L ≥N×n/i=30×0.5/0.3=50m 图(1)取一根长为m 的带子分两段同为25m 将圆柱侧面贴满 1则先转化为将圆柱侧面展开图贴满如图(2)D 阴影部分GHIJ 即是重叠部分剪下来再分段贴满BCFE 区域从矩形IJHG 和矩形BCFE 边长关系看可将矩形剪成5段每段长5m 宽0.1m 由于矩形长BCFE5m 宽0.5m 因此五段恰好贴满矩形BCFE设模型总耗费是Y 经计算, 剪切总长度 P=0.3+25+4×0.1=25.7m粘贴总面积 q= s 2=15m 2C螺旋缠绕面积 K=0 图(2)带子面积s 1=15m 2 所以, Y 1=25.7a+15b+15d……….(A 1) 现所给带子长为51m 即赋值于L=51m 用与上述同样方法即有如图所示展开图(3)阴影部分是带子重叠部分阴影部分面积s 3=51×0.3-50×0.3=0.3m 2经计算剪切总长： p=0.3+2505+4×0.1=26.2m 粘贴总面积： q=s 2=51×0.3=15.3m 2螺旋缠绕总面积： k=0 带子总面积： s 1=51×0.3=15.3m 2 图(3) 在此模型下L=51时的总费用：y 1=26.2a+15.3b+15.3d …………(a 1)1模型二横向缠绕包扎模型模型假设：在研究建立模型时，需要作一些假设，目的是使模型简单、利于理解、便于计算，为此我们考虑四种费用，即剪切费用、粘贴费用、缠绕费用和带子总费用，归纳假设条件如下：（1）带子可以根据需要任意剪切（2）带子价格d元/m2（3）剪切费用a元/m（4）粘贴费用b元/m2（5）螺旋缠绕费用c元/m2（6）由于剪切过程需要精确测量计算.因此耗费较大.粘贴过程要用粘贴剂也许花费较大成本而且为了保证粘贴效果要精细的劳动,而缠绕则较为简单.因此可以作如下近似估计：d≈a≈b＞＞c构模与求解：将带子剪成多段，横向缠绕包扎，如图（4）设：管道长度为N ,横切面周长n；i带子宽为i；带子长为L；相邻的带子之间缠绕是覆盖的宽度e(即图中黑实线的宽度)由于管道口周长n=0.5m因此被截断的带子总条数为L/n ,则有：未被覆盖带子表面积S3=管道侧面积S2图4即：L(i-e)/i=S2L=i×S2/(i-e)=i×N×n/(i-e)=15/(0.3-e)由于e≥0 得L≥50(m)所以此时将带子截成长0.5m宽0.3m的100小段.设模型总耗费为Y2经计算得：剪切总长度p=99×0.3=29.7(m)粘贴总面积q=S2=15m2螺型缠绕面积k=0带子面积S1=15m2所以：Y2=29.7a+15b+15d………….(A2)题中所给带子长为51m 即：赋值于L=51m又：L=15/(0.3-e)得e=0.3-15/L将L=51代入上式得a=3/510=0.0059当带子长51m时设模型总耗费为y2经计算剪切总长度p=99×0.3=29.7(m)粘贴总面积q=51×0.3=15.3(m2)螺型缠绕面积k=0带子面积S=51×0.3=15.3(m2)所以：y 2=29.7a+15.3b+15.3d………….(a2)模型三斜向螺旋包扎模型模型假设：在研究建立模型时，需要作一些假设，目的是使模型简单、利于理解、便于计算，为此我们考虑四种费用，即剪切费用、粘贴费用、缠绕费用和带子总费用，归纳假设条件如下：（7）带子不需要剪切和大面积粘贴（8）带子价格d元/m2（9）剪切费用a元/m（10）粘贴费用b元/m2（11）螺旋缠绕费用c元/m2(6) 由于剪切过程需要精确测量计算.因此耗费较大.粘贴过程要用粘也许花费较大成本而且为了保证粘贴效果要精细的劳动,而缠绕则较为简单.因此可以近似估计d≈a≈b＞＞c模型构建与求解：不需剪切，让带子与管道以x角度斜向包扎即：斜向螺旋缠绕包扎如图（5）先假设缠绕过程中不重叠。

数学建模2000B题

i 1
m
ai

ji
n
bj
从发点A到收点B的距离（或单位运费）是已知的，设为
c ij ( i 1, 2 ,..., m , j 1, 2 ,..., n )
。
问题：寻求一个调运方案，使总运输费用达到最小。
一个调运方案主要由一组从发点
Ai
到收点 B j 的输
送量来描述。
发点
收点
B1
B2
290 S4 S3 S2 320 160 70 30 70 170 720 202 1100 20 12 195 1150 600 306 0 10 31 201 A8 480 680 A10 S1 70 42 10 520 88 462 S5 10 220 300 A11 S2 S6 110
30
70
A1
480
31
1150
A9 680
A10
300
A11
201
205 A7
A8
450
80 2 750 A4 606
图二
3
104 A1 301 A2
A3
问题
所属类型做题思路和关键点结果表示形式
优化模型
1、问题的分析
优化问题
1）优化模型的数学描述
求函数
u f (x)
x ( x 1 , x 2 , x 3 ,..., x n )
在约束条件 h i ( x ) 0 , i 1, 2 ,..., m . 和
g i ( x ) 0 ( g i ( x ) 0 ), i 1, 2 ,..., p .
下的最大值或最小值，其中设计变量（决策变量） x

管道包扎问题中正弦函数模型的实验探究与教学设计

管道包扎问题中正弦函数模型的实验探究与教学设计
何宇;谭代伦
【期刊名称】《福建中学数学》
【年(卷),期】2022()9
【摘要】《普通高中数学课程标准(2017年版)》将数学建模活动与数学探究活动这一主题列入必修课程之中,并且提出数学建模活动是基于数学思维运用模型解决实际问题的一类综合实践活动,是高中阶段数学课程的重要内容[1].高中数学学习的过程中,学生往往被动接受数学知识,数学问题通常是给定条件信息,求解目标问题.而数学建模活动是给定一个现实情境,教师通过教学引导学生开拓思维,把数学和生活紧密联系在一起,从实际生活中寻找数学问题,从而通过建模的方法解决问题,养成遇到问题从数学模型角度思考的良好学习习惯.
【总页数】4页(P24-27)
【作者】何宇;谭代伦
【作者单位】西华师范大学数学与信息学院
【正文语种】中文
【中图分类】G63
【相关文献】
1.浅谈LC正弦振荡器在实验教学中相关问题的探索
2.浅谈LC正弦振荡器在实验教学中相关问题的探索
3.化学实验教学中探究性实验问题的类型与过程的设计
4.基于实验探究核心素养的创新实验设计——以“利用DISlab验证正弦交流电电流
有效值的教学”为例5.真实问题情境中探究实验的教学设计——以“探究熟石灰变质”一课为例
因版权原因，仅展示原文概要，查看原文内容请购买。

全国数模竞赛优秀论文钢管订购与运输的优化模型(浙江师范大学胡国英柯懿张惠锋) 精品

（1）如果要铺设的管道不是一条线，而是一个树形图，铁路、公路和管道构成网络，请就这种更一般的情形给出一种解决办法，并对图二（见附录一）按（1）的要求给出模型和结果。

（二）问题的分析本题要铺设一条A1~A15的天然气管道，使得总费用最小。

可以这样考虑问题：我们可以先把钢厂生产的钢管运到各个站点Ai(i≠1)再往两边运送，再计算出总的费用使之最小。

事实上我们并不知道每个站点上要运去多少货，所以设每个钢厂运往站点的数量为一变量及站点运往两边的钢管量也为变量，再通过图中已知信息相应的列出一些恒等式和约束条件。

为了使问题便于求解，我们把铁路费用及销价相应转换为公路费用（其简化的图示见附录一的图三），又因为铁路运费为一分段函数，故要对一些点之间加线使运费相当。

转换完毕后再利用赋权图的性质求出厂到站点的最短路。

（其具体数据见附录三）（三）模型的假设（１）运钢管过程中若用火车则可直接把钢管运到公路与铁路交接处,即下了火车不上火车。

（２）假设运输单位可提供足够的火车与汽车。

（３）费用计算时按照钢管数量来算，不考虑其他计费方法及因素。

（４）运费中不足整公里部分按整公里计。

（５）假设向每个钢管厂都订购钢管。

（６）设１Ｋm主管道钢管为１单位钢管。

（７）路中铺设的钢管只允许由其相邻站点提供。

（８）不计各个环节中的装卸费用。

（四）符号说明Ｓi: 表示生产钢管的钢厂（i=1,2…7）。

Ai：表示暂存钢管的站点。

(i=1,2…15)Ｘ1,+kk 与Ｘ1,-kk：分别表示Ａk运往Ａ1+k方向的钢管的数量和Ａk运往Ａ1-k方向的钢管的数量。

（其中Ｋ=2,3…15 X21=104, X16,15=0）Ｂk ：表示存放在Ａk处的钢管数量（k=2,3…15）.Yij : 表示从Ｓi－>Aj所运的钢管数量。

Ｆ(Xij ,Yij): 表示总的费用。

（单位:万元）△Ｐi :表示钢管销价的变化量。

（五）模型的建立与求解题Ⅰ：为了使问题简化，我们可采取如下原则：(1)总费用公路化原则：就是将铁路运费及钢管销价恰当的转换为公路运费。

数学建模钢管问题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1. 闫诺2. 谭斌3. 赵莹指导教师或指导教师组负责人(打印并签名)：日期： 2011 年 07 月 11 日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：钢管订购和运输问题的数学模型摘要本文根据对钢管订购和运输问题的条件和要求，建立了两个模型，模型一为单目标非线性规划模型；模型二为双容量最小费用循环流模型，并通过求解这两个模型，得到路线最优的钢管订购运输方案，使成本达到最小。

对于问题一，由于铁路运输费用函数具有不可加性，不能直接应用现有的最短路算法来求铁路和公路交通网中任意两点间最小费用路问题。

本文采用了一种启发式递推算法，巧妙的解决了这个问题。

对于问题二，根据要求改变钢厂钢管的销价和钢厂钢管的产量上限，然后用lingo 求解，观察得到的图表，对改变以上两个条件后总运费及方案受到的影响进行分析。

对于问题三，其与问题一相似不同之处在于问题三中的钢管铺设路线变成了树形，因此我们仍然采用问题一的建模思路，对于特殊之处进行修改。

采用图论中的floyd 算法，求得总体最小运输费用矩阵C(i,j)。

【例4-3】在外径为140mm的蒸气管道外包扎保温材料，以减少热损失

&我们所做的一切就是为了把这门课程学好、学扎实。

因为它将是从事本专业的重要基础课程之一，我们将用它来解决实际问题。

在过程工业中，实际问题千变万化，但提炼之后，能上升至理论高度的内容并不多，本课程讲了许多实用的理论。

但由于课时有限，我们只能再选择一些更基础的内容来讲授和练习。

正因为是基础知识，大家必须学扎实，多看书、多做练习。

我一直为你们以优异的成绩考入本校而骄傲。

在人生的整个历程中，大学是学习地方，大学时期是我们精力与能力的顶峰时期，但我们的经验与阅历不足以建功立业，最适宜我们的事情便是认真学习，从书本中学习前人优秀的经验。

现代社会，我们不可能都学，我们有所选择，这便有了专业的概念。

我们的专业属工科，研究对象为工程技术。

事实上，工科的理论基础有许多相通之处，其关键在于一个“通”字。

这要求在低年级时，重视基础理论的学习，它将是以后专业学习与解决问题的钥匙。

回顾一下我们的学习阶段，大学所学的知识丰富多彩，有点是课堂上的，有的是自学的，有的来自于同学间的交流……它远远超过以前的所有学过的知识。

从另一角度来看，用心的同学与糊涂的同学之间人生的分水岭也从此产生。

随便写几句。

后面的答案供参考：【例4-3】在外径为140mm 的蒸气管道外包扎保温材料，以减少热损失。

蒸气管外壁温度为390℃，保温层外表面温度不大于40℃。

保温材料的λ与t 的关系为λ=0.1+0.0002t （t 的单位为℃，λ的单位为W/（m ·℃））。

若要求每米管长的热损失Q/L 不大于450W/m ，试求保温层的厚度以及保温层中温度分布。

解：此题为圆筒壁热传导问题，已知：r 2=0.07m t 2=390℃ t 3=40℃ 先求保温层在平均温度下的导热系数，即143.024********.01.0=⎪⎭⎫ ⎝⎛++=λW/（m ·℃）（1）保温层温度（课本中公式）改写为()L Q t t r r /2ln 3223-=πλ()07.0ln 45040390143.02ln 3+-⨯=πr得 r 3=0.141m 故保温层厚度为b =r 3－r 2=0.141－0.07=0.071m=71mm（2）保温层中温度分布设保温层半径r 处的温度为t ，代入式（4-15）可得 ()45007.0ln390143.02=-⨯r t π解上式并整理得t =－501ln r －942计算结果表明，即使导热系数为常数，圆筒壁内的温度分布也不是直线而是曲线。

管道订购与运输问题-2000年全国数学建模竞赛B题优秀论文

管道订购与运输问题1 问题重述2 基本假设(1)只考虑订购费用和运输费用，不考虑装卸等其它费用． (2)钢管单价与订购量、订购次数、订购日期无关．(3)订购汁划是指对每个厂商的定货数量；运输方案是指具有如下属性的一批记录：管道区间，供应厂商，具体运输路线．(4)将每一单位的管道所在地看成一个需求点，向一单位管道的所在地运输钢管即为向一个点运输钢管．3 符号说明M ：钢厂总数. n ：单位管道总数.:i S 第i 个钢厂 :i S 第i 个钢厂的产量上限。

:i p 第i 个钢厂单位钢管的销售价 i A 管道线上第i 个站点。

i d 管道线上第i 个单位管道的位置。

F ：总费用。

:ij C 从钢厂(1,2,,)i S i m =到点(1,2,,)j d j n =的最低单位费用。

4 问题的简化求 S AP 矩阵的基本思路是图的最短路算法 . 由于铁路的运输费用与线路的长度不是线性关系 ,必须对铁路网做一些预处理才能套用图的标准最短路算法 . 下面叙述求 S AP 矩阵的过程:1.利用图的标准最短路算法 ,从铁路网络得出图中任两个点之间的最短路径表 T (如果两个点之间不连通 ,认为它们之间的最短路长度为+ ∞ ) .2.利用题中的铁路运价表将 T 中的每个元素 (即最短距离 )转化为运输费用 ,将运输费用表记为 C.3.将公路的长度换算为运输费用 ,由公路路程图 (包括要沿线铺设管道的公路 )得出公路费用图 G,若 i, j 不连通 ,则令 Gij = + ∞ .4.对于任一组 ( i , j)∈ { 1,… n }× { 1,… m } 如果 Cij <+ ∞ ,且小于 Gij ,那么就在公路费用图中加一条边. 即令 Gij = min{Cij , Gij } .5.利用图的标准最短路算法 ,求公路费用图中任一个 S 点到任一个 A 点的最小费用路径 ,得出 S AP 矩阵. 如表 1所示:SAP 矩阵A123 4 5 6 7 8 9 10 11 12 13 14 15 S1 170716031402986 380 205 31 212 642 920 960 1060 1212 1280 14202 215720531902 1716 1110 955 860 712 1142 1420 1460 1560 1712 1780 19203 230722032002 1816 1210 1055 960 862 482 820 860 960 1112 1180 13204 260725032352 2166 1560 1405 1310 1162 842 620 510 610 762 830 9705 255724532252 2066 1460 1305 1210 1112 792 570 330 510 712 730 8706 265725532352 2166 1560 1405 1310 1212 842 620 510 450 262 110 2807 275726532452 2266 1660 1505 1410 1312 992 760 660 560 382 260 205问题分析运输费用等价转换法则：按单位运费相等原则将任意两点间的最短铁路线转换为公路线．对于铁路线上的任意两点,i j V V ，用F1oyd 算法找出两点间最短铁路路线的长度ij L 查铁路运价表求得ij L ，对应的铁路单位运费ij f ;又设与该段铁路等费用的公路长度为ij l ，则：0.1ij ij f l =⨯由此，我们就在,i j V V 之间用一条等价的公路线来代替,i j V V 间的最短铁路线．如果,i j V V 之间原来就有公路，就选择新旧公路中较短的一条．这样，我们就把铁路运输网络转换成了公路运输网络．销价等价转换法则：按单位费用相等将任意钢厂的单位销价转换为公路单位运价．对于钢厂S i 的销售单价P i ，我们可以虚设一条公路线，连接钢厂S i 及另一虚拟钢厂'i s ，其长度为i l ，并且满足0.1i i l p =⨯；从而将钢厂的销售单价转换成公路运输单价，而新钢厂'i s 的销售价为0.将铁路和销价转换为公路的过程可以由计算机编程实现．通过上述的分析，我们可以将原问题化为一个相对简单的产量未定的运输问题，利用115A A 到之间的管道距离和钢厂和站点之间的公路距离建立一个产量未定的运输问题的模型．但是由于1215,A A A ,并不能代表所有的实际需求点(实际需求点是n 个单位管道)，因此，我们可以用F1oyd 算法进一步算出7个钢厂到所有实际的n 个需求点(对于问题一，n ＝5171;对于问题三，n ＝5903)的最短路径，并由此得出一个具有7个供应点、n 个需求点的产址未定的运输模型．6 模型的建立产量未定的运输模型根据假设4，我们可以将每一单位的管道看成一个需求点，向一单位管道的所在地运输钢管即为向一个点运输钢管．对每个点，我们可以根据该点的位置和最短等价公路距离，求出各钢厂与该点之间最小单位运输费用ij C (销价已经归人运输费用之中了)．设总共有m 个供应点(钢厂)，n 个需求点，我们就可以得到一个产量未定的运输模型：有m 个供应点、n 个需求点，每个供应点的供应量{0}{500,}i i u s ∈；每个需求点需要1单位，运输单价矩阵为C ，求使得总运输费用最小的运输方案．其数学规划模型： 11minmnij ij i j F C x ===∑∑11{0}{500,}1,2,,..11,2,01nij i j mij i ij x S i ms tx j n x ==⎧∈=⎪⎪⎪==⎨⎪⎪=⎪⎪⎩∑∑或其中： 1112112n m m mn C C C C CC C ⎛⎫⎪=⎪ ⎪⎝⎭为单位费用矩阵 1112112n m m mn x x x X x x x⎛⎫⎪=⎪ ⎪⎝⎭为决策矩阵，也为0-1矩阵代码如下7 模型的求解对于本题，上述0-1规划规模宏大，现有的一些算法不能胜任，我们必须具体问题具体分析，结合本题实际情况，寻找行之有效的算法．(1)初始方案的改进的最小元素法和改进的伏格尔法 *改进的最小元素法改进的最小元素法又称为贪婪法或瞎子爬山法，它的宗旨是每一步都取当前的最优值算法步骤为，对费用矩阵C 作n 次下列循环：①C 中找一个最小值ij C ； ②令1;ij x =③C 的第j 的所有数据改为+∞；④如果1nij i j x s ==∑，第i 个供应点的供应量已达上限，将C 的第i 行数据全改为+∞。

布条缠绕圆形管道的问题模型1

布条缠绕圆形管道数学模型学号：1407022005 班级：14数学二班姓名：朱文艳摘要：本文在已知布条宽度和圆形管道直径的情况下，建立相应的数学模型，通过确定重合点，运用一些简单的几何知识解决了布条与管道轴线的夹角问题。

同时，从管道表面积和布条面积相等的角度，在已知管道长度的情况下，求出了布条的长度。

同时也考虑到了布条两端的影响。

此外，分两种情况考虑了其他形状的管道的布条缠绕问题：布条紧贴于管道缠绕和布条不紧贴贴于管道缠绕。

关键词：重合点表面积紧贴管道缠绕正文1问题重述用宽为W的布条缠绕直径为d的圆形管道，如果用布条全部包住管道，问布条应该如何缠绕，才能使所用布条长度最小。

若知道管道长度为L。

需用多长布条（可考虑管道两端影响），如果管道是其他形状呢？2合理假设与变量约定2.1管道粗细一样且足够长；2.2管道外表面光滑；2.3缠绕时布条没有重叠或重叠部分忽略不计；2.4布条的厚度可忽略不计；2.5布条没有弹性；2.6变量限定W：布条的宽度（厘米）S: 布条的面积（平方厘米）h: 布条的长度（不考虑两端影响时）（厘米）H：布条的长度（考虑两端影响时）（厘米）L：管道长度（厘米）C: 管道横截面周长（厘米）d：管道直径（厘米）θ：布条与管道的缠绕角度，见图1（度）S：管道的表面积（平方厘米）3模型建立与求解模型一：夹角α的模型不妨将管道表面展开如图1，黄色部分为缠绕的布条。

由于要求布条完全缠绕于管道上且不重叠，那么A 、B 应该在管道上重合。

则cos d παω=故arccosdωαπ=模型二：布条长度L 的模型由于布条是完全缠绕于管道上的，且没有重叠，可以从管道表面积和布条面积相等来考虑。

0S dh π=S l ω=且 0S S =，即dh l πω=也即dh l πω=但由于布条两端都成πα-弧度，会有所浪费，因此也考虑两端的影响，即多加上图中AC 段的长度。

222sin AC l d d παπω==-故所需布条长度为222AC dh L l l d ππωω=+=+-4模型优化优化一：布条厚度的考虑既然布条厚度为一个影响结果的因素，不妨考虑一下布条的厚度。

管道包扎问题的数学模型

管道包扎问题的数学模型潘龙飞[摘要]:本论文讨论管道的包扎问题.此问题是一个三维空间问题,我们采用剪切的方法把空间问题变为平面问题,建立刚好全部包扎所用带子最短模型和管道包扎出现接缝处重叠模型,然后利用数学软件Matlab 求解。

在图1中，求得最短带子包扎的通用表达式,并代入题目给出的数据得到第一个问题的最短长度为50.4 米。

在图2和图3中，采用近似的处理方法求出管道包扎接缝处重叠带子宽度的表达式,代入第二个和截面是正多边形的管道的情况作问题的数据,得到带子的重叠宽度为 0.004 米。

论文的最后对临界角进一步的讨论,并得到更一般的模型。

关键词:临界角；临界点；临界长度；等量关系1 问题的提出用宽度为0.3m的带子缠绕包扎圆柱型管道，管道长30m，截面周长为0.5m.(1) 如果用带子全部包住管道，最少要用多长的带子，请你给出计算这个最小长度的公式，并且依次计算出所需长度数值.(2) 现有一条长度为51m的带子，想将这条带子全部用于缠绕包扎这个管道，可以使带子的接缝处重叠瘩接.请你给出用这条带子缠绕包扎这个管道的方案.（计算结果精确到0.001m）(3) 如果管道截面是正三边形,正四边形,或边数更多的正多边形.2 问题的分析生活的经验告诉我们,在包扎圆形管道的过程中, 如果开始包扎时带子边缘所在的直线与管道母线的夹角过小,就可能出现不能把管道全部包扎的现象; 如果夹角过大,就可能出现包扎带子在接缝处重叠的现象. 所以, 随着夹角的增大,总会出现在接缝处刚好接合而没有重叠的情况.这种特殊的情况就是第一问的求解问题,称此时包扎带子的长度为临界长度, 带子边缘所在的直线与管道母线的夹角为临界角,管道任一端的带子截口所在边与管道截面的交点称为临界点.如果给定一段带子的长度大于临界长度,则总能找到一种包扎方案,使得整条带子全都包扎完,其中接缝处有重叠.当管道的截面为正多边形时,我们把正多边形的直棱柱管道看作圆形管道的变形来处理,即正多边形的直棱柱管道的平面展开图与圆形管道的平面展开图是同样的.3 模型的假设3.1管道没有厚度(即把管道剪开图看成平面,不考虑空间结构)；3.2管道是刚性物体,带子也不具备弹性；3.3管道截面是圆形,整条管道粗细均匀，带子的宽度也不变；3.4包扎过程中带子不能切断；3.5带子两端截口垂直于它的边：4 符号的约定a -----带子的宽度；b -----管道的长度；c -----管道截面的周长；l----- 带子的长度；θ--- 带子截口所在的直线与管道母线的夹角；1S ----- 直角三角形AED 的面积；2S ----- 直角三角形OBF 的面积；S 3---- 四边形COHG 的面积；x ---- 带子重叠部分的宽度；y --- 重叠部分的带子长度；m---- 截面正多边形的边长；n ---- 截面正多边形的边数.5 模型的建立和求解5.1 刚好全部包扎所用带子最短模型经过临界点,沿着管道的母线切开得到截面,如下图1:图1 其中矩形ABCD 为管道的侧面展开图,三角形AED 为直角三角形.定理1 直角三角形AED 的面积等于直角三角形OBF 和四边形OHGC 之和.证明线段BF 和线段CG 在空间图形中是重合的,故这两线段相等.把直角三角形OBF 向右移动,使BF 与CG 重合,则构成直角三角形O 'HO .又 ED=OHOB+OC=AD故HO O AED '∆≅∆,即定理成立.推论1 沿着管道任一母线剪开得到的平面展开图中,管道截面界线的两端分别能组成两个直角三角形, 且这两个直角三角形的面积相等.由上面的定理1和推论可以得出刚好包扎管道所用带子最短的模型:⎪⎩⎪⎨⎧+=-=+++=32122132121S S S a c a S bc S S S al求得一般表达式为:a bca c l +-=22把题目中给出的数据代入一般表达式求得第一问题的临界长度为:3.05.0303.05.022⨯+-=l =50.4 (米) 5.2 管道包扎出现接缝处重叠的模型按图1的剪开方法,得到管道平面展开图,如图2:图2 其中阴影为带子重叠部分.命题1 在带子宽度不变的条件下,带子相接处重叠的宽度一定相等(即图2中阴影部分的平行四边形的宽度不改变).5.2.1求阴影部分的带子的长度.命题2 阴影部分的长度比整条包扎带子的长度短线段AE 的长度.证明由推论2, 阴影部分的宽度相等, 故可以过图2的A 点,垂直AE 剪切, 再把剪切的左边部分图形补到右边,如下图3:图3由图3可以看出, ⨯-=-=c l AE l y θcos5.2.2 利用阴影部分的面积相等得到模型: ⎪⎪⎩⎪⎪⎨⎧--=⨯-=-----=c x a c c l y x a c x a bc al xy 2222)(cos cos )()(θθ 化简此方程组得:0)()2(22=-+----bc al xl x a c a x (1)利用Matlab 解方程(1)得到的结果过繁,所以为了得到一个比较简单而又接近实际的答案,我们作以下处理: 在生活和工作中,为了节省材料,包扎管道的带子一般不会比临界长度长太多,所以可用22a c -近似代替22)(x a c --,求得结果为: l a c albc a c a x ---+-=22222 (2)把第二问题的数据代入方程(1)得:x 1=0.00357把第二问题的数据代入方程(2)得:x 2=0.0036由以上计算得到的结果可以看出,当带子的长度不太长时,用 l a c albc a c a x ---+-=22222代替这个模型的结果是可以的.且取得第二问题的结果为:x=0.004 (米)5.3 截面为正多边形的直棱柱管道模型推理1 对于任何正多边直棱柱的包扎面,从临界点沿棱柱的母线剪开得到的剪开平面如图1所示(包扎方案为临界时),如果有带子重合的情形如图2. 类似以上图1 圆柱管道包扎方案的方法建立模型如下:5.3.1、包扎正多边直棱柱的临界模型:⎪⎩⎪⎨⎧+=-=+++=321221321)(21S S S a mn a S bmn S S S al 解得: amnb a mn l +-=22)(5.3.2、包扎正多边直棱柱的有重叠的模型:⎪⎪⎩⎪⎪⎨⎧--=-=-----=m n x a m n m n l y x a m n x a m nb al xy 2222)()(cos cos )()()(θθ 以22)(a mn -代替22)()(x a mn --解得, l a mn almnb a mn a x ---+-=2222)(2)(6 模型的分析6.1、临界角的讨论临界角 c a arcsin0=θ (3) 6.1.1 当0θθ>时,带子不能全部包扎整条管道.如果要在θ角增大(即临界角增大的情况下实现全部包扎,由(3) 式可以看出应加大带子的宽度或减小管道截面的周长.6.1.2 当0θθ<时,带子在包扎过程中出现接缝处重叠.如果要在θ角减小(即临界角减小的情况下实现全部包扎,由(3) 式可以看出应减小带子的宽度或增加管道截面的周长.故有以下推理:推理2 包扎管道的临界角0θ随带子宽度的增大而增大,管道截面周长的减小而增大;随带子宽度的减小而减小,管道截面周长的增大而减小.6.2、管道的讨论由推论1、命题1和推理1,可知无论求解模型是圆柱模型或是截面为正多边形的直棱柱,其求解过程都是相同的,故有以下推理.推理3 管道的包扎方案与管道截面是凸多边形(不限边数,不限每边的长度)或连续的凸封闭曲线无关,只与管道截面的周长C 、管道长度l 和给定的带子的长度有关.参考文献:[1] 吕林根. 解析几何［Ｍ］. 北京:高等教育出版社，２０００.[2] 刘来福. 数学模型与数学建模［M ］. 北京：北京师范大学出版社，２００２.。

数学建模之管道包扎

数学建模之管道包扎【摘要】：本文讨论用带子包扎管道，使带子全部包住管道，且用料最省的问题，即在管长一定，带宽一定，管道底边周长一定的情况下，求解出带子如何包扎才能用料最少并建立具体的模型首先，取用一张细长的纸条，毫无缝隙的绕在一根适当的圆棍上;其次，用笔画出缠绕后多出管道边缘的部分，并划出一条母线；然后，展开纸条；最后, 综合各种模型的优点和缺点,建立模型。

在本文结尾,对模型进行了进一步的改进和优化,使模型更加贴合实际。

【关键词】：管道包扎、化三维为二维、勾股定理、平移、相似定理１问题的重述与分析用带子包扎管道，使带子全部包住管道，且用料最省即（１）求出缠绕时的角度（2）求出带长２问题的假设（1）. 直圆管，粗细一致。

（3）. 带宽小于圆管截面周长。

（4）. 为省工, 用缠绕的方法包扎管道３模型建立的假设首先，取用一张细长的纸条，毫无缝隙的绕在一根适当的圆棍上;其次，用笔画出缠绕后多出管道边缘的部分，并划出一条母线；然后，展开纸条；４符号说明W----带宽L----管长 l----母线在纸带上的长度C----管的底面周长α----缠绕的角度５模型建立与分析求解（１）纸带展开模型：DO关键是如何在带子起端减去一个合适的直角三角形，使得斜边的长与管子的周长相等。

过B 点作AD 直线的垂线，且长度为W∴（倾斜角）sin α=C W∴ OB=22W C - 即在纸带一端剪去一条直角长度为ＯＢ，另一条直角边长度为Ｗ，的直角三角形（２）纸条的平移模型进一步如果知道直圆管道的长度，用缠绕的方法包扎管道，需用多长的带子？根据相似三角形定律；BF C L W =ＢＦ＝WLC 带长模型：ＯＦ＝ＢＦ＋ＯＢＯＦ＝22W C WLC -+ 即截一段长为22W C W LC -+的带子６模型检验模型并不太实用，因为毫无缝隙的缠绕在生活中很难实现７模型的进一步讨论展望讨论：如果缠绕时后带压前带的宽度为ｄ，带宽为Ｗ，底面周长为Ｃ，管长为Ｌ．数学模型,简单说就是用数学语言描述实际现象的过程.数学模型後两对很重拿来的属性,一是合理性,二揍简易性.建立数学模型的过程 B ＡＥＦ。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

问题：水管或煤气管道经常需要从外部用带子包扎以便对管道起到保护作用，包扎时用很长的带子缠绕在管道外部。

为节省材料，如何进行包扎才能使带子全部包住管道而且也没有发生重叠。

管道包扎
分析：在包扎时显然管道的形状，其粗细程度、带子的宽度和缠绕的角度是三个决定因素。

它们之间
应存在着一定的关系。

包扎的方式是什么样的？？？
需要考
虑哪些
因素？？
假设：
1. 直圆管，粗细一致。