遗传,模拟退火,蚁群三个算法求解TSP的对比

合集下载

几种M-TSP问题的解法

之差越小（定义为级差）。但是，仅仅考虑级差是不够的，因为级差的大小与各巡视组所走
路程总和（所用总时间）有关，在考虑均衡系数时，应该考虑到各巡视组所走路程总和（所
-2-

用总时间）这一因素，总路程（总时间）越大所允许的级差应该可以大一些，于是在均衡系
数的分母中引入了总路程（总时间）的均值来平衡级差与总路程的关系。可见，均衡系数越
分组第1组第2组第3组
表 1 遗传—蚁群算法得到的最佳巡视路线
巡视路线
乡镇数
村数
O-1-B-34-35-32-31-33-A-R-29-Q-30-2
4
12
8-27-24-23-21-25-M-O
O-2-5-6-7-E-9-F-10-12-H-14-13-G-11-
5
11
8-4-D-3-2-O
O-P-26-N-23-22-K-17-16-I-15-18-J-19-
-4-

基于以上分析，选择个体各个TSP回路路程中的最大值作为返回值，根据其中返回值大小分配适应度值，返回值小的适应度大。
3.遗传操作 (1)选择选择时以个体的适应度决定选择那个个体，以转轮法选择，对于适应度大的个体被选中的可能性也越大。（2)交叉按照给定的交叉率，进行交叉操作。交叉时对从种群中选择的2个个体作为母体进行交叉操作。 (3)变异为了保持群体的多样性，避免遗传寻优陷人局部最优，可以对种群中的个体以给定的变异率进行变异操作。变异操作就是对选中的母体上的某个基因的值进行随机改变，这意味着被改变的基因对应的顶点被划人到另外一个回路中，而原来回路中不再包含该顶点。设置变异率为0.007。上面的遗传操作将产生新的个体，为保持每一代种群中个体的规模，在完成一代操作时，要根据适应度的大小去掉适应度小的个体。这体现了遗传算法的适者生存的思想。在以上算法的基础上，遗传代数设为 200 代，利用 Matlab 编程实现，得到了总路程尽可能最短且各组尽可能均衡的巡视路线如表 1 所示。在最优的个体中，寻找最佳巡视路线的蚁群算法的寻优过程如图 2 所示

TSP的几种求解方法及其优缺点

TSP的几种求解方法及其优缺点一、什么是TSP问题旅行商问题，简称TSP，即给定n个城市和两两城市之间的距离，要求确定一条经过各城市当且仅当一次的最短路线。

其图论描述为：给定图G=（V，A），其中V为顶点集，A 为各顶点相互连接组成的边集，设D=（dij）是由顶点i和顶点j之间的距离所组成的距离矩阵，要求确定一条长度最短的Hamilton回路，即遍历所有顶点当且仅当一次的最短距离。

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，⋯，n）；2）非对称旅行商问题（dij≠dji，ϖi，j=1，2，3，⋯，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

若对于城市V={v1，v2，v3，⋯，v n}的一个访问顺序为T={t1，t2，t3，⋯，t i，⋯，t n}，其中t i∈V（i=1，2，3，⋯，n），且记t n+1=t1，则旅行商问题的数学模型为：minL=。

TSP是一个典型的组合优化问题，并且是一个NP完全难题，是诸多领域内出现的多种复杂问题的集中概括和简化形式，并且已成为各种启发式的搜索、优化算法的间接比较标准。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

但是，由于构造型算法优化质量较差，迄今为止已开发了许多性能较好的改进型搜索算法，主要有：1）模拟退火算法2）禁忌搜索算法3）Hopfield神经网络优化算法4）蚁群算法5）遗传算法6）混合优化策略2.1模拟退火算法方法1）编码选择：采用描述TSP解的最常用的一种策略——路径编码。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SWAP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

用蚁群算法解决TSP问题

用蚁群算法解决TSP 问题一、引言蚁群算法是一种受自然界生物行为启发而产生的“自然”算法，产生于对蚂蚁行为的研究。

蚁群中的蚂蚁以“信息素”为媒介，间接异步的相互联系。

蚂蚁在行动中，会在他们经过的地方留下一些化学物质，称为“信息素”。

这些物质能被同一种群众后来的蚂蚁感受到，并作为一种信号影响后者的行动，具体表现在后到的蚂蚁选择有这些物质的路径的可能性比选择没有这些物质的路径的可能性大的多。

后者留下的信息素会对原有的信息素进行加强，并循环下去。

这样，经过蚂蚁多的路径，后到蚂蚁选择这条路径的可能性就越来越大。

由于在一定的时间内，越短的路径会被越多的蚂蚁访问，因而积累的信息素就越多，在下一个时间内被其他的蚂蚁选中的可能性也越大。

这个过程会持续到所有的蚂蚁都走到最短的那一条路径为止。

二、关键技术（1）解的表达形式在应用蚁群优化算法时，只需要建立一个虚拟的始终点，相当于蚁群的巢穴和食物所在地，这样一个所经过城市的路径的排列就构成了一个解；（2）信息素的记忆和更新在算法开始时，由于从来没有蚂蚁去寻找过路径，因此可以认为是没有任何先验信息，即每条路上的信息相等。

客观地将，信息素应该都为0，但是由于在蚁群算法中，信息素决定了蚂蚁选择这条路径的概率，因此可以认为初始信息素矩阵为：1/(*(1))0ij N N p -⎧=⎨⎩i j i j ≠=其中N 为城市数当算法运行过程中，每次放出m 支蚂蚁，每只蚂蚁按照信息素选择路径，将其中路径最短的记录下来，对这条最短路进行信息素的加强；而对于其他路径，因为信息素的挥发，信息素浓度将会降低，更新后的信息素矩阵为： 11(1)//(1)/k ij k ij k ij p N p p ρρρ--⎧-+⎪=⎨-⎪⎩i j i j →→经过路径不经过路径其中N 为城市数，ρ为挥发系数（3）蚁群的规模在一般应用中，蚁群中蚂蚁的个数m 是固定数，不超过TSP 图的节点数。

三、算法实现步骤1 设定蚁群规模m ，计算次数n ，挥发系数ρ，初始化信息素矩阵，设定变量best =+∞记录全局最优解；步骤2 若n =0，推出并输出结果；否则n=n-1，分别放出m 只蚂蚁，按照信息素概率选择路径，并找出m 条路径中的当代最优路径cubest ；步骤3 根据当代最有路径更新信息素；步骤4 如果cubest<best ，best=cubest ，执行步骤2；否则直接执行步骤2；四、结果及分析通过五个城市节点的TSP 问题的求解，其城市间的距离矩阵为：01015621008139158020156132005291550⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭蚁群算法找到的最优路径为A C B D E →→→→，总路程为43；通过试验结果发现，对于小规模的ＴＳＰ问题，蚁群算法和禁忌搜索、模拟退火算法的计算结果相似，而且耗时很短，因此该算法是合理的。

TSP问题的几种解法对比

城市旅行问题之路程短摘要城市旅行问题即旅行商(TSP)问题，要从图G的所有周游路线中求取最小成本的周游路线，而从初始点出发的周游路线一共有(n-1)!条，即等于除初始结点外的n-1个结点的排列数，因此旅行商问题是一个排列问题。

排列问题比子集合的选择问题通常要难于求解得多，这是因为n个物体有n!种排列，只有子集合(n!>O( n2))。

通过枚举(n-1)!条周游路线，从中找出一条具有最小成本的周游路线的算法，其计算时间显然为O(n!)。

这种枚举法运算量相当庞大，随着城市数量呈指数增长。

为此，我们对比应用随机探索的模拟退火算法，线性规划和蚁群算法三种方法：模拟退火算法，利用物理退火达到平衡态时的统计思想，建立数学模型，编写该算法的MATLAB程序，进行求解，得出最短旅行的最短距离为422.13；对TSP的约束条件和目标函数编写LINGO程序，经过多次迭代，得出最短旅行的最短距离也为422.13；蚁群算法：基于自然界蚂蚁觅食的最短路径原理，建立模型，通过MATLAB程序，得出最短旅行距离为427.8971。

关键词模拟退火算法线性规划蚁群算法一．问题重述一个人要到30个不同的城市游玩，每两个城市i和j之间的距离为d ij，如何选择一条路径使得此人走遍所有城市后又回到起点，要求所走路径最短。

二.符号说明三．问题分析与处理便于我们说明和解决问题，先将题中给出的城市编号：表一30座城市的坐标3.1模拟退火方法这是一个典型的TSP组合优化问题[1]，并且是一个N-P难问题。

传统的解决此类问题的方法包括：分枝定界法、线性规划法和动态规划法等等。

随着人工智能的发展，一些智能优化的算法逐渐产生，这其中模拟退火算法因具有高效、稳定、通用、灵活的优点备受专家和学者的青睐。

将模拟退火算法引入STP问题求解，可以有效的避免在求解过程中陷入局部最优。

下面就是我们用模拟退火算法具体解决这个问题。

算法设计步骤：（1）问题的解空间和初始值城市旅行问题的解空间S 是遍访36个城市恰好一次的所有回路，是所有城市排列的集合。

求解TSP问题的几种算法比较

求解TSP问题的几种算法比较侯淑静【摘要】The traveling salesman problem (TSP) is an important problem for the classical discrete optimization, which is very important to study the solving algorithm. After the introduction of the greedy algorithm, taboo search algorithm, simulated annealing algorithm, genetic algorithm, the author put forward the corresponding algorithm. Aiming at the four typical examples in the test base, we realized implementation of these algorithms with procedures, and the running time and the results of these algorithms are compared. The results show that the greedy algorithm can draw the solution in a short time, the taboo search algorithm and genetic algorithm have the same effect, and the results of simulated annealing algorithm is better than those of genetic algorithm.%旅行售货商问题(简称TSP )是离散优化的一个经典的重要问题，对求解算法的研究非常重要。

物流网络优化中的遗传算法与模拟退火算法性能比较分析

物流网络优化中的遗传算法与模拟退火算法性能比较分析物流网络优化是当今物流行业中关键的问题之一。

如何通过优化物流网络，提高货物的运输效率和降低成本，一直是物流行业从业者努力解决的难题。

而在物流网络优化中，遗传算法和模拟退火算法被广泛应用于解决复杂的物流网络优化问题。

本文将对这两种算法的性能进行比较分析，以评估它们在物流网络优化中的适用性和优劣。

首先，我们来了解一下遗传算法和模拟退火算法的基本原理。

遗传算法是受到自然进化原理启发的一种优化算法。

它通过模拟生物进化的过程，使用遗传操作（如选择、交叉和变异）来搜索最优解。

而模拟退火算法则是模拟金属热退火过程推导而来的全局优化算法，通过模拟随机的粒子运动来寻找全局最优解。

在物流网络优化中，遗传算法通常用于解决TSP（旅行商问题）和VRP（车辆路径问题）等NP-hard问题。

遗传算法通过建立一个基因编码方案，并运用适应度函数来评估解的质量。

接着，通过选择、交叉和变异操作，生成新的解，并用新解替换旧的解。

这个过程将不断迭代，直到满足停止条件。

相对而言，模拟退火算法适用于连续优化问题，比如最小化总运输时间、最小化总运输成本等。

模拟退火算法通过引入一个控制参数，控制粒子跳出局部最优解的概率，以便更好地搜索全局最优解。

在搜索过程中，模拟退火算法接受任何比当前解更好的解，并且还以一定的概率接受比当前解更差的解，以避免陷入局部最优解。

接下来，我们将对遗传算法和模拟退火算法在物流网络优化中的性能进行比较分析。

首先是算法的搜索能力。

遗传算法通过基因编码和遗传操作，能够搜索到较好的解，尤其是在解空间较大且多峰值的问题中。

而模拟退火算法作为一种全局搜索算法，能够在搜索过程中接受一定概率的劣解，从而有机会跳出局部最优解，但相对于遗传算法，其搜索能力稍弱一些。

其次是算法的收敛速度。

遗传算法需要进行多次迭代和大量的选择、交叉和变异操作，因此收敛速度相对较慢。

而模拟退火算法通过不断调整控制参数，根据一定的概率接受劣解，能够更快地朝着全局最优解方向收敛。

TSP的几种求解方法及其优缺点

v1.0 可编辑可修改TSP的几种求解方法及其优缺点一、什么是TSP问题旅行商问题，简称TSP，即给定n个城市和两两城市之间的距离，要求确定一条经过各城市当且仅当一次的最短路线。

其图论描述为：给定图G=（V，A），其中V为顶点集，A为各顶点相互连接组成的边集，设D=（dij）是由顶点i和顶点j之间的距离所组成的距离矩阵，要求确定一条长度最短的Hamilton回路，即遍历所有顶点当且仅当一次的最短距离。

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，⋯，n）；2）非对称旅行商问题（dij≠dji，ϖi，j=1，2，3，⋯，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

但是，由于构造型算法优化质量较差，迄今为止已开发了许多性能较好的改进型搜索算法，主要有：1）模拟退火算法2）禁忌搜索算法3）Hopfield神经网络优化算法4）蚁群算法5）遗传算法6）混合优化策略模拟退火算法方法1）编码选择：采用描述TSP解的最常用的一种策略——路径编码。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SWAP）；②逆序操作（INV）；③插入操作（INS）。

TSP的几种求解方法及其优缺点

其图论描述为：给定图G=（V，A），其中V为顶点集，A为各顶点相互连接组成的边集，设D=（dij）是由顶点i和顶点j之间的距离所组成的距离矩阵，要求确定一条长度最短的Hamilton回路，即遍历所有顶点当且仅当一次的最短距离。

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，?，n）；2）非对称旅行商问题（dij≠dji，?i，j=1，2，3，?，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

若对于城市V={v1，v2，v3，?，v n}的一个访问顺序为T={t1，t2，t3，?，t i，?，t n}，其中t i∈V（i=1，2，3，?，n），且记t n+1=t1，则旅行商问题的数学模型为：minL=。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SWAP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

TSP的几种求解方法及其优缺点

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，⋯，n）；2）非对称旅行商问题（dij≠dji，ϖi，j=1，2，3，⋯，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SW AP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

用于解决多目标旅行商问题的算法

多目标旅行商问题（MO-TSP）是指在多个目标地点之间找到最优路径，使得旅行商能够同时满足多个旅行目标的问题。

这是一个复杂的组合优化问题，涉及到时间、成本、距离等多个目标的平衡。

针对这一问题，已经有许多算法被提出，比如遗传算法、模拟退火算法、蚁群算法等。

在本文中，我将针对用于解决多目标旅行商问题的算法进行深入剖析和讨论。

1. 遗传算法遗传算法是一种模仿自然选择和遗传机制的优化方法，通过种群的进化来寻找问题的最优解。

在解决MO-TSP问题时，遗传算法可以通过不断进化种群中的路径来寻找最佳的解决方案。

在每一代进化中，选择、交叉和变异等操作都会对种群进行改进，直到找到最优的解。

2. 模拟退火算法模拟退火算法是一种启发式算法，模拟金属退火过程中的晶粒结构变化来寻找问题的最优解。

在解决MO-TSP问题时，模拟退火算法可以通过接受较差解的概率来跳出局部最优解，并在搜索空间中进行全局搜索，以找到更好的解。

3. 蚁群算法蚁群算法是一种基于蚁群寻食行为的启发式算法，模拟蚂蚁在搜索食物时释放信息素的过程。

在解决MO-TSP问题时，蚁群算法可以通过蚂蚁在路径上释放信息素的方式来寻找最优路径，蚁群不断更新信息素浓度，并通过信息素浓度来选择下一步的移动方向。

在实际应用中，这几种算法都有其优缺点，如何选择最合适的算法取决于实际问题的复杂度、目标要求和算法的性能。

在我看来，遗传算法在求解MO-TSP问题时具有良好的全局搜索能力，但对于大规模问题的收敛速度可能较慢；模拟退火算法适用于局部搜索和全局搜索的结合，但在处理多目标问题时需要合理设定参数；蚁群算法在求解路径优化问题时具有较好的鲁棒性和稳健性，但对于问题解空间的探索可能会存在过早收敛的问题。

MO-TSP问题是一个复杂的组合优化问题，需要综合运用各种启发式算法和元启发式算法，以及结合实际问题的特点和要求，才能找到最佳的解决方案。

通过对算法的深入理解和灵活运用，我们可以在实际问题中取得较好的优化效果。

TSP的几种求解方法及其优缺点

TSP的几种求解方法及其优缺点TSP（Traveling Salesman Problem）是一种NP-hard问题，其目标是找到一条路径，使得旅行商经过所有城市并返回原始城市的总距离最小。

由于TSP在实际应用中具有广泛的应用，很多研究者提出了多种方法来解决TSP问题。

本文将介绍几种常见的TSP求解方法及其优缺点。

1.枚举法枚举法是最简单直观的方法，它遍历所有可能的路径，并选择总距离最小的路径作为最优解。

由于TSP问题的解空间随问题规模呈指数级增长，这种方法只适用于规模较小的问题。

枚举法的优点是保证找到最优解，缺点是耗时较长。

2.最近邻法最近邻法从一个起始城市出发，每次选择与当前城市距离最近的未访问城市作为下一个城市。

直到所有城市都被访问一遍，并返回原始城市。

最近邻法的优点是简单易实现，缺点是容易陷入局部最优解，从而得不到整体最优解。

3.插入法插入法从初始路径开始，将未访问的城市不断插入到已访问城市之间，直到所有城市都被访问一遍。

插入方法有多种，比如最短边插入、最长边插入和最佳位置插入等。

插入法的优点是相对于最近邻法来说，可以得到更好的解。

缺点是算法复杂度较高，计算时间较长。

4.遗传算法遗传算法是一种群体智能算法，模拟生物进化的过程，通过遗传操作寻找优秀的解。

在TSP问题中，遗传算法可以将城市路径看作染色体，并通过选择、交叉和变异等操作进行优化。

遗传算法的优点是能够快速找到次优解，并且对于规模较大的问题也适用。

缺点是需要调节大量参数，算法收敛速度较慢。

5.动态规划动态规划是一种由上而下的分治思想，将原问题分解为若干子问题，通过求解子问题的最优解来求解原问题。

在TSP问题中，可以通过建立状态转移方程来求解最优路径。

动态规划的优点是求解过程中可以剪枝，避免重复计算，能够得到精确解。

缺点是算法时间复杂度较高，不适用于大规模问题。

以上是几种常见的TSP求解方法及其优缺点。

不同的方法适用于不同的问题规模和实际应用场景。

TSP的几种求解方法及其优缺点

其图论描述为：给定图G=（V，A），其中V 为顶点集，A为各顶点相互连接组成的边集，设D=（dij）是由顶点i和顶点j之间的距离所组成的距离矩阵，要求确定一条长度最短的Hamilton回路，即遍历所有顶点当且仅当一次的最短距离。

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，，n）；2）非对称旅行商问题（dij≠dji，i，j=1，2，3，，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

若对于城市V={v1，v2，v3，，v n}的一个访问顺序为T={t1，t2，t3，，t i，，t n}，其中t i∈V（i=1，2，3，，n），且记t n+1=t1，则旅行商问题的数学模型为：minL=。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SWAP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

蚁群算法、遗传算法、模拟退火算法介绍

蚁群算法、遗传算法、模拟退火算法介绍穷举法列举所有可能,然后一个个去,得到最优的结果。

如图一，需要从A点一直走到G点，才能知道，F是最高的（最优解）。

这种算法得到的最优解肯定是最好的，但也是效率最低的。

穷举法虽然能得到最好的最优解，但效率是极其低下的。

为了能提高效率，可以不要枚举所有的结果，只枚举结果集中的一部分，如果某个解在这部分解中是最优的，那么就把它当成最优解。

显然这样有可能不能得到真正的最优解，但效率却比穷举法高很多。

只枚举部分解的方法很多。

贪心法在枚举所有解时，当遇到的解在当前情况下是最优时，就认为它是最优解。

如图一，当从A 点到B点时，由于B点比A点的解更优，所以会认为B点是最优解。

显然这样的效率很高，但得到的最优解质量也很差。

爬山法贪心法是只和前面的一个比较，为了提高最优解的质量，可以不仅和前一个解比较，也和后一个解比较，如果比前面和后面的解都优，那么就认为它是最优解。

如图一，当到C点时，发现它比前面的B和后面的D点的解都好，所以认为它是最优解。

模拟退火算法爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。

如图一，搜索到A点后就停止了搜索。

如果能跳出局部最优解，那么得到的最优解的质量相对就会好很多。

如当搜索到A点时以一定的概率跳转到另外一个地方。

这样就有可能跳出局部最优解A。

如果经过一定次数的跳跃，跳到了E 点，那么就会找到全局的最优解了。

如果这个概率不变，那么就会一直跳跃下去，不会结束。

可以让这个概率逐渐变小，到最后趋于稳定。

这里的概率逐渐减小类似于金属冶炼的退火过程，所以称之为模拟退火算法。

模拟退火算法(Simulated Annealing，SA)最早由Kirkpatrick等应用于组合优化领域，它是基于Mente-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。

模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。

退火算法,蚁群算法,遗传算法

退火算法,蚁群算法,遗传算法1.引言1.1 概述退火算法、蚁群算法和遗传算法都是常见的启发式优化算法，用于解决复杂问题。

这些算法通过模拟自然界中生物的行为或物质的特性，寻找最优解或接近最优解。

退火算法是一种基于物理退火原理的优化算法。

它通过模拟金属在高温下冷却过程中晶格的调整过程，来寻找最优解。

退火算法首先在一个较高的温度下随机生成一个解，然后通过降温过程逐步调整解，并根据一个接受概率在解空间中进行随机搜索。

退火算法具有全局优化能力，可用于解决多种问题，如旅行商问题、图着色问题等。

蚁群算法模拟了蚂蚁在寻找食物时的集体行为。

蚂蚁通过释放信息素与其他蚂蚁进行通信，藉此找到最短路径。

蚁群算法主要包含两个重要步骤：信息素更新和状态转移规则。

信息素更新指的是蚂蚁在路径上释放信息素的过程，而状态转移规则决定了蚂蚁在搜索过程中如何选择路径。

蚁群算法被广泛应用于组合优化问题、路径规划等领域，取得了良好的效果。

遗传算法是模拟生物进化过程的一种优化算法。

它通过模拟自然界中的进化和遗传操作，逐代迭代地搜索最优解。

遗传算法通过编码个体、选择、交叉和变异等操作，形成新的个体，并根据适应度函数评估个体的优劣。

遗传算法以其并行性、全局寻优能力和对问题结构要求不高的特点而被广泛应用于各个领域，如函数优化、机器学习中的特征选取等。

这三种算法都是基于启发式思想的优化方法。

它们可以在解空间中进行搜索，并在搜索过程中逐步优化。

退火算法通过模拟金属冷却过程，蚁群算法通过模拟蚂蚁的集体行为，而遗传算法则模拟了生物的进化过程。

这些算法在不同领域和问题上都取得了较好的效果，为求解复杂问题提供了有效的解决方案。

1.2 文章结构文章结构部分的内容可以包括以下方面的介绍：文章结构本文将会包含三个主要的部分：退火算法、蚁群算法和遗传算法。

每个部分将会包括原理和应用两个小节的介绍。

这些算法是优化问题中常用的启发式算法，它们分别基于不同的思维方式和模拟自然界的现象。

求解TSP问题算法综述

求解TSP问题算法综述一、本文概述本文旨在全面综述求解旅行商问题（Traveling Salesman Problem, TSP）的各种算法。

TSP问题是一个经典的组合优化问题，自提出以来就引起了广泛的关注和研究。

该问题可以描述为：给定一系列城市和每对城市之间的距离，求解一条最短的可能路线，使得一个旅行商从某个城市出发，经过每个城市恰好一次，最后返回出发城市。

本文将首先介绍TSP问题的基本定义、性质及其在实际应用中的重要性。

接着，我们将综述传统的精确算法，如动态规划、分支定界法等，以及它们在求解TSP问题中的优缺点。

然后，我们将重点介绍启发式算法和元启发式算法，包括模拟退火、遗传算法、蚁群算法等，这些算法在求解大规模TSP问题时表现出良好的性能和效率。

本文还将探讨近年来新兴的机器学习算法在TSP问题求解中的应用，如深度学习、强化学习等。

我们将对各类算法进行总结和评价，分析它们在不同场景下的适用性和性能表现。

我们也将展望TSP问题求解算法的未来发展方向，以期为相关领域的研究和实践提供有益的参考和指导。

二、经典算法求解旅行商问题（TSP）的经典算法多种多样，每种算法都有其独特的优缺点和适用场景。

本节将对一些代表性的经典算法进行综述。

暴力穷举法（Brute-Force）：暴力穷举法是最简单直观的TSP求解算法。

其基本思想是生成所有可能的旅行路径，计算每条路径的总距离，然后选择最短的那条。

虽然这种方法在理论上可以找到最优解，但由于其时间复杂度为O(n!)，对于大规模问题来说计算量极大，因此并不实用。

动态规划（Dynamic Programming, DP）：动态规划是一种通过将问题分解为更小的子问题来求解的优化方法。

对于TSP问题，DP算法可以将一个大循环中的多个子问题合并成一个子问题，从而减少重复计算。

然而，TSP的DP算法仍面临“维度灾难”的问题，即当城市数量增多时，所需存储空间和计算时间呈指数级增长。

tsp实验报告

tsp实验报告《TSP实验报告》摘要：本实验旨在通过对旅行商问题（TSP）的实验研究，探讨不同算法在解决TSP问题上的表现。

我们使用了蚁群算法、遗传算法和模拟退火算法进行实验，并对比它们的效果和性能。

实验结果表明，不同算法在解决TSP问题上有着各自的优势和局限性，为解决实际问题提供了一定的参考价值。

引言：旅行商问题（TSP）是一个经典的组合优化问题，其目标是寻找一条最短的路径，使得旅行商可以经过每个城市一次并回到起点城市。

TSP问题在实际中有着广泛的应用，如物流配送、电路板布线等领域。

为了解决TSP问题，人们提出了多种算法，如蚁群算法、遗传算法和模拟退火算法等。

本实验旨在比较这些算法在解决TSP问题上的表现，为实际问题的解决提供参考。

实验方法：本实验采用了三种经典的优化算法：蚁群算法、遗传算法和模拟退火算法。

我们使用Python语言编写了相应的程序，并在TSP问题的不同数据集上进行了实验。

实验中，我们记录了每种算法的运行时间、最优解和收敛性等指标，并进行了对比分析。

实验结果：通过实验，我们得到了以下结论：1. 蚁群算法在大规模TSP问题上表现较好，具有较快的收敛速度和较高的解的质量。

2. 遗传算法适用于中等规模的TSP问题，其具有较好的全局搜索能力和较高的稳定性。

3. 模拟退火算法在解决TSP问题上表现一般，其收敛速度较慢，但能够找到较优的解。

结论：不同算法在解决TSP问题上有着各自的优势和局限性。

在实际应用中，需要根据具体问题的规模和特点选择合适的算法。

本实验为解决实际问题提供了一定的参考价值。

展望：未来可以进一步研究和改进现有的TSP算法，提高其求解效率和解的质量。

同时，也可以探索新的算法和方法，为TSP问题的解决提供更多的选择。

TSP的几种求解方法及其优缺点

TSP的几种求解方法及其优缺点旅行商问题（TSP）是一个组合优化问题，目的是找到一条最短的路径，使得旅行商能够访问一系列城市并返回起始点。

TSP由于其复杂性而被广泛研究，已经发展出了许多求解方法。

本文将讨论几种主要的TSP求解方法，包括贪婪算法、局部算法、遗传算法和蚁群算法，并分析它们的优缺点。

1.贪婪算法贪婪算法是一种基于贪心策略的求解方法。

它从一个起始城市开始，每次选择距离当前城市最近的未被访问过的城市作为下一步的目标城市，直到所有的城市都被访问过。

贪婪算法的优点是简单易于理解和实现，并且在处理小规模问题时效果显著。

然而，贪婪算法没有考虑全局最优解，很容易陷入局部最优解，不能保证找到最优解。

2.局部算法局部算法是一类启发式算法，它通过不断优化当前解来逐步接近最优解。

其中最典型的是2-opt算法，它通过交换路径中的两个顶点位置来改进解的质量。

局部算法的优点是可以找到局部最优解，且计算时间较短。

然而，局部算法容易陷入局部最优解，而且计算开销随问题规模增加而增加，且不能保证找到全局最优解。

3.遗传算法遗传算法是一种模拟生物进化的随机算法。

它通过模拟遗传、交叉和变异等基因操作来生成和改进解。

遗传算法的优点是可以处理大规模问题，且不容易陷入局部最优解。

同时，遗传算法能够在空间中探索多个解，提高解的多样性。

然而，遗传算法的计算开销相对较高，需要大量的迭代和种群更新。

此外，遗传算法的性能与参数设置相关，需要进行调整。

4.蚁群算法蚁群算法是一种模拟蚂蚁觅食行为的算法。

它通过模拟蚂蚁在路径上释放信息素的过程，来引导蚂蚁选择路径。

蚁群算法的优点是能够找到较好的解并具有一定的自适应性。

它适用于处理大规模问题，且能够处理问题中的不确定性。

然而，蚁群算法的计算开销较高，并且参数设置对结果影响较大。

综上所述，TSP的求解方法包括贪婪算法、局部算法、遗传算法和蚁群算法等。

每种方法都有自己的优点和缺点。

选择适合问题规模、问题特征和求解时间的方法是关键。

遗传算法与其他优化算法的对比分析

遗传算法与其他优化算法的对比分析近年来，随着计算机科学的快速发展，优化算法在解决实际问题中扮演着越来越重要的角色。

优化算法旨在找到问题的最优解，以提高效率和性能。

在众多的优化算法中，遗传算法因其独特的思想和广泛的应用领域而备受关注。

本文将对遗传算法与其他优化算法进行对比分析，以探讨它们的优缺点和适用范围。

首先，我们来介绍一下遗传算法。

遗传算法是受到达尔文的进化论启发而发展起来的一种优化算法。

它模拟了自然界中的进化过程，通过模拟遗传、变异和选择等操作，逐步优化问题的解。

遗传算法的基本流程包括初始化种群、评估适应度、选择、交叉、变异和更新种群等步骤。

遗传算法具有全局搜索的能力，能够在复杂的问题空间中找到较优的解。

与遗传算法相比，其他优化算法也有各自的特点和优势。

例如，模拟退火算法是一种基于物理退火原理的优化算法。

它通过模拟金属在退火过程中的结晶行为，以一定的概率接受劣解，从而避免陷入局部最优解。

模拟退火算法具有较好的全局搜索能力，适用于解决连续优化问题。

另一个常见的优化算法是粒子群算法。

粒子群算法模拟了鸟群觅食的行为，通过不断调整粒子的位置和速度，寻找最优解。

粒子群算法具有较快的收敛速度和较强的局部搜索能力，适用于解决连续和离散优化问题。

此外，蚁群算法也是一种常见的优化算法。

蚁群算法模拟了蚂蚁在觅食过程中的信息交流和合作行为。

蚁群算法通过蚂蚁在解空间中的移动和信息素的更新，逐步找到问题的最优解。

蚁群算法具有较好的全局搜索能力和鲁棒性，适用于解决组合优化问题。

虽然遗传算法、模拟退火算法、粒子群算法和蚁群算法等都是优化算法，但它们在应用领域和求解效果上存在一些差异。

遗传算法适用于解决复杂的组合优化问题，如旅行商问题和车辆路径问题。

模拟退火算法适用于解决连续优化问题，如函数最优化和参数优化。

粒子群算法适用于解决连续和离散优化问题，如函数最优化和图着色问题。

蚁群算法适用于解决组合优化问题，如旅行商问题和背包问题。

五种典型启发式算法对比总结

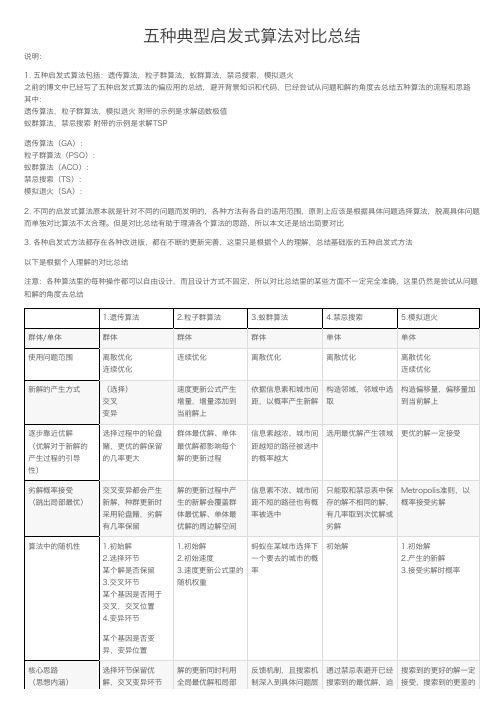
五种典型启发式算法对⽐总结说明：1. 五种启发式算法包括：遗传算法，粒⼦群算法，蚁群算法，禁忌搜索，模拟退⽕之前的博⽂中已经写了五种启发式算法的偏应⽤的总结，避开背景知识和代码，已经尝试从问题和解的⾓度去总结五种算法的流程和思路其中：遗传算法，粒⼦群算法，模拟退⽕附带的⽰例是求解函数极值蚁群算法，禁忌搜索附带的⽰例是求解TSP遗传算法（GA）：粒⼦群算法（PSO）：蚁群算法（ACO）：禁忌搜索（TS）：模拟退⽕（SA）：2. 不同的启发式算法原本就是针对不同的问题⽽发明的，各种⽅法有各⾃的适⽤范围，原则上应该是根据具体问题选择算法，脱离具体问题⽽单独对⽐算法不太合理。

但是对⽐总结有助于理清各个算法的思路，所以本⽂还是给出简要对⽐3. 各种启发式⽅法都存在各种改进版，都在不断的更新完善，这⾥只是根据个⼈的理解，总结基础版的五种启发式⽅法以下是根据个⼈理解的对⽐总结注意：各种算法⾥的每种操作都可以⾃由设计，⽽且设计⽅式不固定，所以对⽐总结⾥的某些⽅⾯不⼀定完全准确，这⾥仍然是尝试从问题和解的⾓度去总结1.遗传算法2.粒⼦群算法3.蚁群算法4.禁忌搜索5.模拟退⽕群体/单体群体群体群体单体单体使⽤问题范围离散优化连续优化连续优化离散优化离散优化离散优化连续优化新解的产⽣⽅式（选择）交叉变异速度更新公式产⽣增量，增量添加到当前解上依据信息素和城市间距，以概率产⽣新解构造邻域，邻域中选取构造偏移量，偏移量加到当前解上逐步靠近优解（优解对于新解的产⽣过程的引导性）选择过程中的轮盘赌，更优的解保留的⼏率更⼤群体最优解、单体最优解都影响每个解的更新过程信息素越浓、城市间距越短的路径被选中的概率越⼤选⽤最优解产⽣领域更优的解⼀定接受劣解概率接受（跳出局部最优）交叉变异都会产⽣新解，种群更新时采⽤轮盘赌，劣解有⼏率保留解的更新过程中产⽣的新解会覆盖群体最优解、单体最优解的周边解空间信息素不浓、城市间距不短的路径也有概率被选中只能取和禁忌表中保存的解不相同的解，有⼏率取到次优解或劣解Metropolis准则，以概率接受劣解算法中的随机性 1.初始解2.选择环节某个解是否保留3.交叉环节某个基因是否⽤于交叉，交叉位置4.变异环节某个基因是否变异，变异位置1.初始解2.初始速度3.速度更新公式⾥的随机权重蚂蚁在某城市选择下⼀个要去的城市的概率初始解 1.初始解2.产⽣的新解3.接受劣解时概率核⼼思路（思想内涵）选择环节保留优解，交叉变异环节解的更新同时利⽤全局最优解和局部反馈机制，且搜索机制深⼊到具体问题层通过禁忌表避开已经搜索到的最优解，迫搜索到的更好的解⼀定接受，搜索到的更差的（算法特⾊）产⽣新解最优解信息⾯使算法搜索新的最优解以概率接受解。