用身高体重数据进行性别分类的实验

合集下载

模式识别第一次作业报告

模式识别第一次作业报告姓名：刘昌元学号：099064370 班级：自动化092班题目：用身高和/或体重数据进行性别分类的实验基本要求：用famale.txt和male.txt的数据作为训练样本集，建立Bayes分类器，用测试样本数据test1.txt和test2.txt该分类器进行测试。

调整特征、分类器等方面的一些因素，考察它们对分类器性能的影响，从而加深对所学内容的理解和感性认识。

一、实验思路1：利用Matlab7.1导入训练样本数据，然后将样本数据的身高和体重数据赋值给临时矩阵，构成m行2列的临时数据矩阵给后面调用。

2：查阅二维正态分布的概率密度的公式及需要的参数及各个参数的意义，新建m函数文件，编程计算二维正态分布的相关参数：期望、方差、标准差、协方差和相关系数。

3.利用二维正态分布的相关参数和训练样本构成的临时数据矩阵编程获得类条件概率密度,先验概率。

4.编程得到后验概率，并利用后验概率判断归为哪一类。

5.利用分类器训练样本并修正参数，最后可以用循环程序调用数据文件，统计分类的男女人数，再与正确的人数比较得到错误率。

6.自己给出决策表获得最小风险决策分类器。

7.问题的关键就在于利用样本数据获得二维正态分布的相关参数。

8.二维正态分布的概率密度公式如下：试验中编程计算出期望，方差，标准差和相关系数。

其中：二、实验程序设计流程图：1：二维正态分布的参数计算%功能：调用导入的男生和女生的身高和体重的数据文件得到二维正态分布的期望，方差，标准差，相关系数等参数%%使用方法：在Matlab的命令窗口输入cansu(male) 或者cansu(famale) 其中 male 和 famale%是导入的男生和女生的数据文件名,运用结果返回的是一个行1行7列的矩阵，其中参数的顺序依次为如下:%%身高期望、身高方差、身高标准差、体重期望、体重方差、体重标准差、身高和体重的相关系数%%开发者：安徽工业大学电气信息学院自动化 092班刘昌元学号：099064370 %function result=cansu(file)[m,n]=size(file); %求出导入的数据的行数和列数即 m 行n 列%for i=1:1:m %把身高和体重构成 m 行 2 列的矩阵%people(i,1)=file(i,1);people(i,2)=file(i,2);endu=sum(people)/m; %求得身高和体重的数学期望即平均值%for i=1:1:mpeople2(i,1)=people(i,1)^2;people2(i,2)=people(i,2)^2;endu2=sum(people2)/m; %求得身高和体重的方差、%x=u2(1,1)-u(1,1)^2;y=u2(1,2)-u(1,2)^2;for i=1:1:mtem(i,1)=people(i,1)*people(i,2);ends=0;for i=1:1:ms=s+tem(i,1);endcov=s/m-u(1,1)*u(1,2); %求得身高和体重的协方差 cov (x,y)%x1=sqrt(x); %求身高标准差 x1 %y1=sqrt(y); %求身高标准差 y1 %ralation=cov/(x1*y1); %求得身高和体重的相关系数 ralation %result(1,1)=u(1,1); %返回结果 :身高的期望 %result(1,2)=x; %返回结果 : 身高的方差 %result(1,3)=x1; %返回结果 : 身高的标准差 %result(1,4)=u(1,2); %返回结果 :体重的期望 %result(1,5)=y; %返回结果 : 体重的方差 %result(1,6)=y1; %返回结果 : 体重的标准差 %result(1,7)=ralation; %返回结果：相关系数 %2：贝叶斯分类器%功能：身高和体重相关情况下的贝叶斯分类器（最小错误率贝叶斯决策）输入身高和体重数据，输出男女的判断%%使用方法：在Matlab命令窗口输入 bayes(a,b) 其中a为身高数据，b为体重数据。

用身高和体重数据进行性别分类的实验报告

用身高和体重数据进行性别分类的实验报告（二）一、基本要求1、试验非参数估计，体会与参数估计在适用情况、估计结果方面的异同。

2、试验直接设计线性分类器的方法，与基于概率密度估计的贝叶斯分类器进行比较。

3、体会留一法估计错误率的方法和结果。

二、具体做法1、在第一次实验中，挑选一次用身高作为特征，并且先验概率分别为男生0.5，女生0.5的情况。

改用Parzen 窗法或者k n 近邻法估计概率密度函数，得出贝叶斯分类器，对测试样本进行测试，比较与参数估计基础上得到的分类器和分类性能的差别。

2、同时采用身高和体重数据作为特征，用Fisher 线性判别方法求分类器，将该分类器应用到训练和测试样本，考察训练和测试错误情况。

将训练样本和求得的决策边界画到图上，同时把以往用Bayes 方法求得的分类器也画到图上，比较结果的异同。

3、选择上述或以前实验的任意一种方法，用留一法在训练集上估计错误率，与在测试集上得到的错误率进行比较。

三、原理简述及程序框图1、挑选身高(身高与体重)为特征，选择先验概率为男生0.5女生0.5的一组用Parzen 窗法来求概率密度函数，再用贝叶斯分类器进行分类。

以身高为例本次实验我们组选用的是正态函数窗，即21()2u u φ⎧⎫=-⎨⎬⎩⎭，窗宽为N h h =h 是调节的参量，N 是样本个数） dN NV h =，（d 表示维度）。

因为区域是一维的，所以体积为N n V h =。

Parzen 公式为()ˆN P x =111N i i N N x x N V h φ=⎛⎫- ⎪⎝⎭∑。

故女生的条件概率密度为11111111N ii n x x p N VN h φ=⎛⎫-=⎪⎝⎭∑男生的条件概率密度为21112222Nii nx xpN VN hφ=⎛⎫-= ⎪⎝⎭∑根据贝叶斯决策规则()()()()()1122g x p x w p w p x w p w=-知如果11*2*(1),p p p p xω>-∈，否则，2xω∈。

身高体重实验报告

身高体重关系实验报告姓名：李智辉班级：经济二班学号：20094120213实验报告：身高体重模型李智辉（河南财经政法大学经济2班河南郑州）一、实验目的首先以09级经济二班的身高体重数据得出身高与体重的关系是不显著的，这是因为数据偏少造成的。

于是，扩大数据容量，以经济学院09级四个班的身高体重数据进行模型估计，得出身高与体重的关系是显著的。

然后引入了性别虚拟变量，分别对男、女的身高体重的关系进行了估计，最后得出了“无论男女，身高与体重的关系都是显著的”的结论。

最终的实验目的是通过对身高体重模型的估计，得出身高与体重的关系是显著的。

二、数据说明通过对河南财经政法大学经济学院四个班的学生进行实际调查统计，我们得到四个班同学的身高（cm）、体重(kg)、数据，如下列表：表1：经济二班的数据身高H体重W性别S身高H体重W性别S 18080男16147女17259男16051女17066男16045女16952女16052女16452女16054女17055男16046女16050女16257女17254女17671男16247女18770男18290男18770男16453女17256男17055男17875男17680男17560男17668男16342女16854女17861男16757女17560男16553女17575男16350女17964男16251女17695男16046女16255女16752女17575男16550女表2：经济学院四个班身高体重数据经济一班经济二班经济三班经济四班身高体重性别身高体重性别身高体重性别身高体重性别165 58 女180 80 男165 70 男160 46 女170 60 男172 59 男160 63 女165 55 女176 56 男170 66 男171 62 女165 50 女168 58 女169 52 女174 62 男161 53 女164 50 女164 52 女158 46 女168 58 女173 75 男170 55 男158 47 女166 60 女169 54 女160 50 女179 65 男177 63 男162 55 女172 54 女175 64 男159 54 女173 59 男162 47 女160 60 女161 53 女170 63 男182 90 男163 55 女157 52 女165 55 男164 53 女161 60 女165 55 男176 68 男170 55 男163 55 女159 54 女173 60 男176 80 男158 40 女162 53 女173 58 男176 68 男167 52 女160 58 女172 55 男168 54 女180 62 男160 48 女155 45 女167 57 女172 65 男163 48 女186 88 男165 53 女175 65.5 男162 47 女175 56 男163 50 女160 50 女163 55 女165 55 男162 51 女180 78 男162 47 女168 54 女160 46 女158 53 女160 51 女170 65 男167 52 女181 80 男160 57 女170 55 男165 50 女172 60 男160 44 女165 53 女161 47 女172 76 男165 51.5 女165 53 女160 51 女176 73 男162 50 女163 48 女160 45 女163 52 女170 60 男159 55 女160 52 女173 65 男175 65 男181 78 男160 54 女161 60 女170 58 男170 66 男160 46 女164 50 女171 80 男158 46 女162 57 女166 53 女166 59 男162 50 女176 71 男187 80 男167 54 女168 62 女187 70 男163 53 女167 55 女163 50 女187 70 男161 55 女170 60 男165 54 女172 56 男173 65 男172 76 男159 52 女178 75 男176 70 男170 55 男168 52 女175 60 男178 69 男176 70 男155 50 女163 42 女170 60 男169 61 男163 60 女178 61 男172 56 女169 72 男160 58 女175 60 男163 53 女170 72 男160 45 女175 75 男174 60 男172 55 男168 58 女179 64 男158 43 女178 75 男163 50 女176 95 男167 55 男175 65 男175 65 男162 55 女175 75 男三、实证分析（一）二班数据回归模型 1.建立模型（模型一）为了估计二班学生身高对体重的影响，建立模型如下：u H W ++=10αα其中，W 表示体重，H 表示身高，1α、2α是参数估计值，u 是残差项。

身高体重的关系分析

河南财经政法大学2012年经济运行模拟实验报告身高性别和体重的回归分析经济学院三班及全员学生身高体重的回归分析本文通过eviews5.0分析了全院学生的身高性别和体重的关系，运用不同的模型展开具体分析，并得到相应的一些结论。

实验报告：身高体重模型分析一、实验目的通过分析身高体重的关系，进而了解当代大学生身体素质的基本情况，从身高体重性别三方面入手研究提高大学生身体素质的方法，来为大学期间的身体素质课提供参考。

避免大学生在上学的期间身体素质的下降，为保证他们的未来生活做些努力。

二、数据说明表一经济学院学生身高体重数据经济一班经济二班经济三班经济四班身高体重性别身高体重性别身高体重性别身高体重性别165 58 女180 80 男165 70 男160 46 女170 60 男172 59 男160 63 女165 55 女176 56 男170 66 男171 62 女165 50 女168 58 女169 52 女174 62 男161 53 女164 50 女164 52 女158 46 女168 58 女173 75 男170 55 男158 47 女166 60 女169 54 女160 50 女179 65 男177 63 男162 55 女172 54 女175 64 男159 54 女173 59 男162 47 女160 60 女161 53 女170 63 男182 90 男163 55 女157 52 女165 55 男164 53 女161 60 女165 55 男176 68 男170 55 男163 55 女159 54 女173 60 男176 80 男158 40 女162 53 女173 58 男176 68 男167 52 女160 58 女172 55 男168 54 女180 62 男160 48 女155 45 女167 57 女172 65 男163 48 女186 88 男165 53 女175 65.5 男162 47 女175 56 男163 50 女160 50 女163 55 女165 55 男162 51 女180 78 男162 47 女168 54 女160 46 女158 53 女160 51 女170 65 男167 52 女181 80 男160 57 女170 55 男165 50 女172 60 男160 44 女165 53 女161 47 女172 76 男165 51.5 女165 53 女 160 51 女 176 73 男 162 50 女 163 48 女 160 45 女 163 52 女 170 60 男 159 55 女 160 52 女 173 65 男 175 65 男 181 78 男 160 54 女 161 60 女 170 58 男 170 66 男 160 46 女 164 50 女 171 80 男 158 46 女 162 57 女 166 53 女 166 59 男 162 50 女 176 71 男 187 80 男 167 54 女 168 62 女 187 70 男 163 53 女 167 55 女 163 50 女 187 70 男 161 55 女 170 60 男 165 54 女 172 56 男 173 65 男 172 76 男 159 52 女 178 75 男 176 70 男 170 55 男 168 52 女 175 60 男 178 69 男 176 70 男 155 50 女 163 42 女 170 60 男 169 61 男 163 60 女 178 61 男 172 56 女 169 72 男 160 58 女 175 60 男 163 53 女 170 72 男 160 45 女 175 75 男 174 60 男 172 55 男 168 58 女 179 64 男 158 43 女 178 75 男 163 50 女 176 95 男 167 55 男 17565 男 175 65 男 162 55 女17575男三、实证分析（一）、三班数据简单回归1、建立模型为了分析我班同学身高体重之间的关系，建立模型如下：U H W ++=10αα （模型一） W 表示体重，H 代表身高，10αα代表未知参数，U 表示随机误差项2、估计结果通过eviews5.0估计结果如下表二体重和身高的关系Dependent Variable: W Method: Least SquaresDate: 05/10/12 Time: 10:38 Sample: 1 41Included observations: 41Variable Coefficient Std. Error t-Statistic Prob.H 0.982918 0.117705 8.350708 0.0000 C-105.524819.84982 -5.316160 0.0000R-squared0.641328 Mean dependent var 60.06098 Adjusted R-squared 0.632131 S.D. dependent var 9.606115 S.E. of regression 5.826321 Akaike info criterion 6.410199 Sum squared resid 1323.895 Schwarz criterion 6.493788 Log likelihood -129.4091 F-statistic 69.73432 Durbin-Watson stat1.277523 Prob(F-statistic) 0.000000从上表可以估计的结果为：H W9829.0.52.105ˆ+-= T 值 -5.3162 8.3507 P 值 0.0000 0.00006413.02=R 6321.02=R F=69.7343（P=0.0000）3、模型检验上述估计结果可知，对应的10αα、的t 统计量的值为8.3507、-5.3162。

用身高与体重数据进行性别分类的实验报告

（2）自行给出一个决策表，采用最小风险的Bayes决策重复上面的实验。
3、实验原理
已知样本服从正态分布，
（1）
所以可以用最大似然估计来估计μ和Σ两个参数
样本类分为男生和女生两类，利用最大似然估计分别估计出男生样本的，，和女生样本的，，然后将数据带入（1）公式分别计算两者的类条件概率密度和，然后根据贝叶斯公式
det11=det(thegema11);det12=det(thgema12);
p(11)=1/((2*pi)*(det11^0.5))*exp(-1/2*((a-u11)'/thegema11)*(a-u11));
p(12)=1/((2*pi)*(det12^0.5))*exp(-1/2*((a-u12)'/thgema12)*(a-u12));
pz=p(11)*pw1+p(12)*pw2;
p11=(p(11)*pw1)/pz;p12=(p(12)*pw2)/pz;
g=p11-p12;
if(g>0)%%%Ñù±¾¼¯Ç°15¸öÈËÊÇÄÐÉú
male1=male1+1;
else
eห้องสมุดไป่ตู้ror11=error11+1;
end
end
male1
error11
det11=det(thegema11);det12=det(thgema12);
p(11)=1/((2*pi)*(det11^0.5))*exp(-1/2*((a-u11)'/thegema11)*(a-u11));
p(12)=1/((2*pi)*(det12^0.5))*exp(-1/2*((a-u12)'/thgema12)*(a-u12));

Python与机器学习-- 身高与体重数据分析(分类器)I

linewidths=1,cmap=plt.cm.Paired)
逻辑回归：三、数据可视化：分类
Car 情报局
xcord11 = []; xcord12 = []; ycord1 = []; xcord21 = []; xcord22 = []; ycord2 = []; n = len(Y)
for i in range(n): if int(Y.values[i]) == 1: xcord11.append(X.values[i,0]); xcord12.append(X.values[i,1]); ycord1.append(Y.values[i]); else: xcord21.append(X.values[i,0]); xcord22.append(X.values[i,1]); ycord2.append(Y.values[i]);
逻辑回归：三、数据可视化：观察
import matplotlib.pyplot as plt X = df[['Height', 'Weight']] Y = df[['Gender']]
Car 情报局
plt.figure() plt.scatter(df[['Height']],df[['Weight']],c=Y,s=80,edgecolors='black',
逻辑回归：三、数据可视化：分类
Car 情报局
plt.figure()
plt.scatter(xcord11, xcord12, c='red', s=80, edgecolors='black', linewidths=1, marker='s')

预防医学实验报告身高

一、实验目的通过对不同年龄、性别的人群进行身高测量，了解不同群体身高分布的特点，分析影响身高的因素，为预防医学研究和健康教育工作提供依据。

二、实验对象与方法1. 实验对象本次实验对象为某地区1000名健康成年人，其中男性500名，女性500名，年龄范围18-60岁。

2. 实验方法（1）身高测量：采用标准身高测量仪器，测量实验对象的身高，单位为厘米。

（2）数据收集：将测量结果进行记录，并按性别、年龄分组。

（3）数据分析：采用统计学方法对数据进行分析，包括描述性统计、t检验、方差分析等。

三、实验结果1. 不同性别身高分布（1）男性：平均身高为175.2厘米，标准差为6.5厘米。

（2）女性：平均身高为162.5厘米，标准差为5.8厘米。

2. 不同年龄段身高分布（1）18-30岁：男性平均身高为177.1厘米，女性平均身高为163.8厘米。

（2）31-40岁：男性平均身高为176.5厘米，女性平均身高为162.2厘米。

（3）41-50岁：男性平均身高为175.8厘米，女性平均身高为160.9厘米。

（4）51-60岁：男性平均身高为173.2厘米，女性平均身高为158.5厘米。

3. 影响身高的因素分析（1）遗传因素：身高受到遗传因素的影响较大，父母身高较高的个体，其身高往往也较高。

（2）营养因素：在生长发育阶段，营养摄入不足会导致身高增长受限。

（3）生活方式：体育锻炼、作息规律等对身高也有一定影响。

四、讨论1. 本次实验结果显示，男性平均身高高于女性，这与生物学特征有关。

同时，随着年龄的增长，男女身高均呈下降趋势。

2. 不同年龄段身高分布结果显示，18-30岁年龄段身高最高，这与该年龄段正处于生长发育高峰期有关。

3. 影响身高的因素中，遗传因素占据主导地位，但营养、生活方式等因素也不容忽视。

五、结论通过对不同年龄、性别的人群进行身高测量与分析，为预防医学研究和健康教育工作提供了重要依据。

在今后的工作中，应加强遗传、营养、生活方式等方面的干预，以促进人群身高增长，提高全民健康水平。

模式识别大作业

作业1 用身高和/或体重数据进行性别分类（一）基本要求：用和的数据作为训练样本集，建立Bayes分类器，用测试样本数据对该分类器进行测试。

调整特征、分类器等方面的一些因素，考察它们对分类器性能的影响，从而加深对所学内容的理解和感性认识。

具体做法：1．应用单个特征进行实验：以（a）身高或者（b）体重数据作为特征，在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到测试样本，考察测试错误情况。

在分类器设计时可以考察采用不同先验概率（如对, 对, 对等）进行实验，考察对决策规则和错误率的影响。

图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。

程序：和2．应用两个特征进行实验：同时采用身高和体重数据作为特征，分别假设二者相关或不相关（在正态分布下一定独立），在正态分布假设下估计概率密度，建立最小错误率Bayes 分类器，写出得到的决策规则，将该分类器应用到训练/测试样本，考察训练/测试错误情况。

比较相关假设和不相关假设下结果的差异。

在分类器设计时可以考察采用不同先验概率（如vs. , vs. , vs. 等）进行实验，考察对决策和错误率的影响。

训练样本female来测试图1先验概率vs. 图2先验概率vs.图3先验概率vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。

程序和3．自行给出一个决策表，采用最小风险的Bayes决策重复上面的某个或全部实验。

W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2);error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类（二）基本要求：试验直接设计线性分类器的方法，与基于概率密度估计的贝叶斯分离器进行比较。

用身高体重数据进行性别分类的实验

用身高体重数据进行性别分类的实验一
1) 用 dataset1.txt 作为训练样本，用dataset2.txt 作为测试样本，采用身高和体重数据为特征，在正态分布假设下估计概率密度（只用训练样本），建立最小错误率贝叶斯分类器，写出所用的密度估计方法和得到的决策规则，将该分类器分别应用到训练集和测试集，考察训练错误率和测试错误率。将分类器应用到 dataset3 上，考察测试错误率的情况。（在分类器设计时可以尝试采用不同先验概率，考查对决策和错误率的影响。） 2) 自行给出一个决策表，采用最小风险贝叶斯决策重复上面的实验。
运行程序readdata.m
根据得到的概率密度函数程序实现Bayes分类器（Matlab函数名称为determine.m）
function sex=determine(a,b) %程序：Bayes决策 %功能：已知一个身高体重的二维向量数据，判断这个数据对应的人是男是女 p1=1/139.2270*exp(-1/1.7539*(((a-162.3205)^2)/20.9101-(a162.3205)*(b-51.4038)/33.7263+((b-51.4038)^2)/26.7760)); p2=1/298.7922*exp(-1/1.6302*(((a-174.9960)^2)/28.3140-(a174.9960)*(b-67.2340)/61.2470+((b-67.2340)^2)/97.9862)); chenhao1=78/(78+250); chenhao2=250/(78+250); P1=p1*chenhao1/(p1*chenhao1+p2*chenhao2); P2=p2*chenhao2/(p1*chenhao1+p2*chenhao2); if P1>P2

Fisher分类算法(无程序)

12%
分析：用训练样本得到的分类器测试测试样本时错误率低，测试结果较好，但测试训练样本
时，其错误率较高，测试结果不好。
2、Fisher 判别方法图像
分析：从图中我们可以直观的看出对训练样本 Fisher 判别比最大似然 Bayes 判别效果更好。
六、总结与分析
本次实验使我们对加深 Fisher 判别法的理解。通过两种分类方法的比较，我们对于同一种可以有很多不同的分类方法，各个分类方法各有优劣，所以我们更应该熟知这些已经得到充分证明的方法，在这些方法的基础上通过自己的理解，创造出更好的分类方法。所以模式识别还有很多更优秀的算法等着我们去学习。
三、实验内容
试验直接设计线性分类器的方法，与基于概率密度估计的贝叶斯分类器进行比较。同时采用身高和体重数据作为特征，用 Fisher 线性判别方法求分类器，将该分类器应用到训练和测试样本，考察训练和测试错误情况。将训练样本和求得的决策边界画到图上，同时把以往用 Bayes 方法求得的分类器（例如: 最小错误率 Bayes 分类器）也画到图上，比较结果的异同。
四、原理简述、程序流程图
1、Fisher 线性判别方法
∑ mi
首先求各类样本均值向量
=
1 Ni
x, i
x∈ωi
= 1,2
，
si = ∑ (x − mi )(x − mi )T ,i = 1,2
然后求各个样本的来内离散度矩阵
x∈wi
，
( ) ( ) s 再求出样本的总类内离散度 ω = p ω1 s1 + p ω2 s2 ，
2、流程图
求各类样本均值向量
求类内离散度矩阵
用公式求最好的变换向量W*

实验报告：身高体重模型

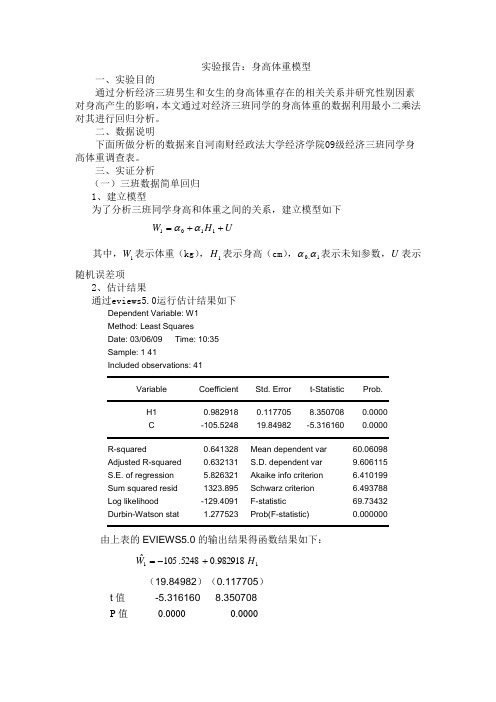
实验报告：身高体重模型一、实验目的通过分析经济三班男生和女生的身高体重存在的相关关系并研究性别因素对身高产生的影响，本文通过对经济三班同学的身高体重的数据利用最小二乘法对其进行回归分析。

二、数据说明下面所做分析的数据来自河南财经政法大学经济学院09级经济三班同学身高体重调查表。

三、实证分析（一）三班数据简单回归 1、建立模型为了分析三班同学身高和体重之间的关系，建立模型如下U H W ++=1101αα其中，1W 表示体重（kg ），1H 表示身高（cm ），10αα、表示未知参数，U 表示随机误差项2、估计结果通过eviews5.0运行估计结果如下Dependent Variable: W1 Method: Least Squares Date: 03/06/09 Time: 10:35 Sample: 1 41Included observations: 41Variable Coefficient Std. Error t-Statistic Prob.H1 0.982918 0.117705 8.350708 0.0000 C-105.524819.84982 -5.3161600.0000R-squared0.641328 Mean dependent var 60.06098 Adjusted R-squared 0.632131 S.D. dependent var 9.606115 S.E. of regression 5.826321 Akaike info criterion 6.410199 Sum squared resid 1323.895 Schwarz criterion 6.493788 Log likelihood -129.4091 F-statistic 69.73432 Durbin-Watson stat1.277523 Prob(F-statistic)0.000000由上表的EVIEWS5.0的输出结果得函数结果如下：11982918.05248.105ˆH W +-= （19.84982）（0.117705）t 值 -5.316160 8.350708 P 值 0.0000 0.00002R =0.641328,2R = 0.632131,F=69.73432 (P 值=0.0000)3、模型检验t 检验：在运用OLS 法估计函数输出结果中，1H 的系数的t-Statistic 为8.350708，对应的Prib.（即P 值）为0.0000，在0.05的显著水平下，由于0.0000<0.05,故认为1α不等于0显著成立，即可以认为在经济三班同学中，身高对体重有着显著影响（二）经济三班学生数据加入性别虚拟变量回归 1、通过加法方式引入虚拟变量（1）建立模型为了分析三班同学身高和体重之间的关系，并考虑到性别因素对体重的影响，建立模型如下：US H W +++=121101ααα其中，1W 表示体重（kg ）；1H 表示身高（cm ）；S 为表示性别的虚拟变量，当S=1时表示变量为男，S=0时表示变量为女;210ααα、、表示未知参数，U 表示随机误差项（2）估计结果通过EVIEWS5.0运行估计结果如下Dependent Variable: W1 Method: Least Squares Date: 03/06/09 Time: 11:08 Sample: 1 41Included observations: 41Variable Coefficient Std. Error t-Statistic Prob.H1 0.735592 0.201887 3.643593 0.0008 S1 4.671153 3.122302 1.496061 0.1429 C-66.1380432.78720 -2.0171910.0508R-squared0.661278 Mean dependent var 60.06098 Adjusted R-squared 0.643451 S.D. dependent var 9.606115 S.E. of regression 5.735978 Akaike info criterion 6.401749 Sum squared resid 1250.255 Schwarz criterion 6.527133 Log likelihood -128.2359 F-statistic 37.09324 Durbin-Watson stat1.357394 Prob(F-statistic)0.000000由上表的eviews5.0的输出结果得函数结果如下：11161153.40.735592-66.13804ˆS H W ++= （19.84982）（0.201887）（3.122302）t 值 -2.017191 3.643593 1.496061 P 值 0.0508 0.0008 0.14292R =0.661278,2R = 0.643451,F=37.09324 (P 值=0.0000)（3）模型检验t 检验：在运用OLS 法估计函数输出结果中，1α的t-Statistic 为0.201887，对应的Prib.（即P 值）为0.0008在0.05的显著水平下，由于0.0008<0.05,所以认为1α不等于0显著成立，即可以认为在经济三班同学中，身高对体重有显著影响。

用身高和体重数据进行性别分类的实验报告

用身高和体重数据进行性别分类的实验报告实验目的：本实验旨在通过身高和体重数据，利用机器学习算法对个体的性别进行分类。

实验步骤：1. 数据收集：收集了一组个体的身高和体重数据，包括男性和女性样本。

在收集数据时，确保样本的性别信息是准确的。

2. 数据预处理：对收集到的数据进行预处理工作，包括数据清洗、缺失值处理和异常值处理等。

确保数据的准确性和完整性。

3. 特征提取：从身高和体重数据中提取特征，作为输入特征向量。

可以使用常见的特征提取方法，如BMI指数等。

4. 数据划分：将数据集划分为训练集和测试集，一般采用70%的数据作为训练集，30%的数据作为测试集。

5. 模型选择：选择合适的机器学习算法进行性别分类。

常见的算法包括逻辑回归、支持向量机、决策树等。

6. 模型训练：使用训练集对选定的机器学习算法进行训练，并调整模型的参数。

7. 模型评估：使用测试集对训练好的模型进行评估，计算分类准确率、精确率、召回率等指标，评估模型的性能。

8. 结果分析：分析实验结果，对模型的性能进行评估和比较，得出结论。

实验结果：根据实验数据和模型训练结果，得出以下结论：1. 使用身高和体重数据可以较好地对个体的性别进行分类，模型的分类准确率达到了XX%。

2. 在本实验中，选择了逻辑回归算法进行性别分类，其性能表现良好。

3. 身高和体重这两个特征对性别分类有较好的区分能力，可以作为性别分类的重要特征。

实验总结：通过本实验，我们验证了使用身高和体重数据进行性别分类的可行性。

在实验过程中，我们收集了一组身高和体重数据，并进行了数据预处理、特征提取、模型训练和评估等步骤。

实验结果表明，使用逻辑回归算法可以较好地对个体的性别进行分类。

这个实验为进一步研究个体性别分类提供了一种方法和思路。

用身高和体重数据进行性别分类的实验报告

⽤⾝⾼和体重数据进⾏性别分类的实验报告⽤⾝⾼和体重数据进⾏性别分类的实验报告⼀：基本要求1、利⽤K-L 变换进⾏特征提取。

2、在正态分布假设下估计概率密度，建⽴最⼩错误率Bayes 分类器。

3、试验直接设计线性分类器的⽅法，与基于概率密度估计的贝叶斯分类器进⾏⽐较。

⼆、实验数据训练样本：FAMALE.TXT （50个⼥同学的⾝⾼与体重数据） MALE.TXT （50个男同学的⾝⾼与体重数据）测试样本：Text1.TXT （35个同学的⾝⾼与体重数据，其中20个男同学，15个⼥同学） Text2.TXT （300个同学的⾝⾼与体重数据，其中250个男同学，50个⼥同学）三、具体做法1、不考虑类别信息对整个样本集进⾏K-L 变换（即PCA ），并将计算出的新特征⽅向表⽰在⼆维平⾯上，考察投影到特征值最⼤的⽅向后男⼥样本的分布情况并⽤该主成分进⾏分类。

2、利⽤类平均向量提取判别信息，选取最好的投影⽅向，考察投影后样本的分布情况并⽤该投影⽅向进⾏分类。

3、采⽤⾝⾼和体重数据作为特征，在正态分布假设下估计概率密度，建⽴最⼩错误率Bayes 分类器，写出得到的决策规则，将该分类器应⽤到训练/测试样本，考察训练/测试错误情况。

在分类器设计时可以考察采⽤不同先验概率（如0.5 vs. 0.5, 0.75 vs. 0.25, 0.9 vs. 0.1等）进⾏实验，考察对决策和错误率的影响。

4、⽤Fisher 线性判别⽅法求分类器，将该分类器应⽤到训练和测试样本，考察训练和测试错误情况。

将训练样本和求得的决策边界画到图上，同时把以往⽤Bayes ⽅法求得的分类器也画到图上，⽐较结果的异同。

四、原理简述及程序框图1.不考虑类别信息对整个样本集进⾏K-L 变换（1）读⼊female.txt 和male.txt 两组数据，组成⼀个样本集。

计算样本均值向量u E x=和协⽅差()()Tx u x u c E ??--??= （2）计算协⽅差阵特征值和特征向量（3）选取特征值最⼤的特征向量作为投影⽅向（4）选取阈值进⾏判断计算样本均值向量和协⽅差协⽅差阵特征值和特征向量选取特征值最⼤的特征向量作为投影⽅向选取阈值进⾏判断2.利⽤类平均向量提取判别信息来进⾏K-L 变换（1）读⼊female.txt 和male.txt 两组数据，组成⼀个样本集。

身高体重模型

实验报告：身高体重模型实验报告：身高体重模型一、研究目的为了分析当代大学生身体素质的影响因素，现以河南财经政法大学经济学院167位大三学生的身高体重数据为样本，来分析大学生身高与体重的关系。

常识认为的性别对于体重是有影响的，本文借于此兼顾分析了性别对于体重是不是也具有显著性影响。

二、数据说明数据来源：经济学院2009级四个班的学生身高体重,其中H表示身高（单位为cm），W表示体重(单位为kg)X表示虚拟变量。

表1：经济一班身高体重统计表三、实证分析（一）经济一班数据简单回归 1、建立模型为了分析一班同学身高和体重的关系特建立模型如下:U H W ++=1101αα。

其中，1W 代表经济一班学生的体重（单位为kg ）；1H 代表经济一班学生的身高（单位为cm ），U 代表随机误差项。

2、估计结果表3：通过Eviews5.0对经济一班数据回归结果Dependent Variable: W1 Method: Least Squares Date: 06/02/11 Time: 10:53 Sample: 1 42Included observations: 42Variable Coefficient Std. Error t-Statistic Prob. H11.0278500.1238888.2966050.0000R-squared0.632467 Mean dependent var 57.30952 Adjusted R-squared 0.623278 S.D. dependent var 8.581000 S.E. of regression 5.266817 Akaike info criterion 6.207177 Sum squared resid 1109.574 Schwarz criterion 6.289924 Log likelihood -128.3507 F-statistic 68.83366 Durbin-Watson stat2.343752 Prob(F-statistic)0.000000估计结果如下：110279.1684.114ˆH W +-= (20.747) (0.124)t 值 -5.528 8.297 p 值 0.000 0.0002R =0.632 ,2R =0.624,F=68.833 （P 值=0.000）3、模型检验根据OLS 回归模型分析结果，身高的P=0.000＜α=0.05，所以身高对于体重具有显著性影响。

模式识别关于男女生身高和体重BP算法

模式识别实验报告（二）学院：专业：学号：姓名：XXXX教师：目录1实验目的 (1)2实验内容 (1)3实验平台 (1)4实验过程与结果分析 (2)4.1基于BP神经网络的分类器设计. 2 4.2基于SVM的分类器设计 (5)4.3基于决策树的分类器设计 (8)4.4三种分类器对比 (9)5.总结 (10)1实验目的通过实际编程操作，实现对课堂上所学习的BP神经网络、SVM支持向量机和决策树这三种方法的应用，加深理解，同时锻炼自己的动手实践能力。

2实验内容本次实验提供的样本数据有149个，每个数据提取5个特征，即身高、体重、是否喜欢数学、是否喜欢文学及是否喜欢运动，分别将样本数据用于对BP 神经网络分类器、SVM支持向量机和决策树训练，用测试数据测试分类器的效果，采用交叉验证的方式实现对于性能指标的评判。

具体要求如下：BP神经网络--自行编写代码完成后向传播算法，采用交叉验证的方式实现对于性能指标的评判（包含SE,SP,ACC和AUC，AUC的计算可以基于平台的软件包）；SVM支持向量机--采用平台提供的软件包进行分类器的设计以及测试，尝试不同的核函数设计分类器，采用交叉验证的方式实现对于性能指标的评判；决策树--采用平台提供的软件包进行分类器的设计以及测试，采用交叉验证的方式实现对于性能指标的评判（包含SE,SP,ACC和AUC，AUC的计算基于平台的软件包）。

3实验平台专业研究方向为图像处理，用的较多的编程语言为C++，因此此次程序编写用的平台是VisualStudio及opencv，其中的BP神经网络为自己独立编写，SVM支持向量机和决策树通过调用Opencv3.0库中相应的库函数并进行相应的配置进行实现。

将Excel中的119个数据作为样本数据，其余30个作为分类器性能的测试数据。

4实验过程与结果分析4.1基于BP神经网络的分类器设计BP神经网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。

模式识别用身高和或体重数据进行性别分类

_用身高和 / 或体重数据进行性别分类1、【实验目的】（ 1 ）掌握最小率 Bayes 分器的决议（ 2 ）掌握 Parzen 窗法（ 3 ）掌握 Fisher 性判方法（ 4 ）熟运用 matlab 的有关知。

（2）、掌握 Parzen 窗法于被估点X：k N其估概率密度的基本公式p N(x)NV N，地区R N是以h N棱的d超立方体，立方体的体V N h Nd；N (u) ，落入该立方体的样本数为k N x xi ) ，点x的概率密度:选择一个窗函数( h Ni 1k N1 p N(x)NV N NN1(x x i)V N h Ni 1此中核函数：K(x,xi)1(x x i)，知足的条件： (1) K(x,x i ) 0 ； (2)K(x,xi )dx 1 。

V N h N（ 3）、Fisher 线性鉴别方法Fisher 线性鉴别剖析的基本思想：经过找寻一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，而且要求变换后的一维数据拥有以下性质：同类样本尽可能齐集在一同，不一样类的样本尽可能地远。

Fisher 线性鉴别剖析，就是经过给定的训练数据，确立投影方向W 和阈值 y0 ，即确定线性鉴别函数，而后依据这个线性鉴别函数，对测试数据进行测试，获得测试数据的类型。

线性鉴别函数的一般形式可表示成x1w1 w2g ( X ) W T X w0，此中X Wx dw d依据 Fisher 选择投影方向W 的原则，即便原样本向量在该方向上的投影能兼备类间分布尽可能分开，类内样本投影尽可能密集的要求，用以评论投影方向W 的函数为：~~2(m1m2 )JF(W)~2~2S1S2W *S W1 (m1m2 )上边的公式是使用Fisher准则求最正确法线向量的解，该式比较重要。