用身高和体重数据进行分类实验
人体测量实验报告

一、实验目的1. 了解人体测量学的基本原理和方法。
2. 掌握人体测量工具的使用技巧。
3. 通过对人体形态尺寸的测量,了解人体生长发育的基本规律。
4. 为我国人体测量数据的收集和整理提供依据。
二、实验内容1. 人体形态尺寸测量:身高、体重、胸围、腰围、臀围、臂围、腿围等。
2. 人体生理指标测量:血压、心率、呼吸频率等。
3. 人体比例分析:头身比、胸腰比、臂长比等。
三、实验方法1. 实验器材:人体测量尺、体重秤、血压计、心率表等。
2. 测量方法:(1)身高测量:被测者赤脚站立,两脚跟并拢,脚尖向前,测量头顶至脚跟的距离。
(2)体重测量:被测者穿着轻便衣物,赤脚站立在体重秤上,读取数值。
(3)胸围测量:被测者站立,两臂自然下垂,测量胸部最大宽度。
(4)腰围测量:被测者站立,两臂自然下垂,测量腰部最细处的周长。
(5)臀围测量:被测者站立,两臂自然下垂,测量臀部最宽处的周长。
(6)臂围测量:被测者站立,两臂自然下垂,测量上臂最大周长。
(7)腿围测量:被测者站立,两臂自然下垂,测量大腿最大周长。
(8)血压测量:被测者安静休息5分钟后,测量右上臂血压。
(9)心率测量:被测者安静休息5分钟后,测量静息心率。
(10)呼吸频率测量:被测者安静休息5分钟后,测量静息呼吸频率。
四、实验数据本次实验共测量20人(男10人,女10人),具体数据如下:1. 身高(cm):男性平均身高172.5,女性平均身高161.0。
2. 体重(kg):男性平均体重65.2,女性平均体重54.8。
3. 胸围(cm):男性平均胸围94.0,女性平均胸围84.5。
4. 腰围(cm):男性平均腰围88.0,女性平均腰围73.0。
5. 臀围(cm):男性平均臀围94.5,女性平均臀围85.0。
6. 臂围(cm):男性平均臂围32.5,女性平均臂围29.0。
7. 腿围(cm):男性平均腿围43.0,女性平均腿围38.5。
8. 血压(mmHg):收缩压平均120.0,舒张压平均80.0。
模式识别第一次作业报告

模式识别第一次作业报告姓名:刘昌元学号:099064370 班级:自动化092班题目:用身高和/或体重数据进行性别分类的实验基本要求:用famale.txt和male.txt的数据作为训练样本集,建立Bayes分类器,用测试样本数据test1.txt和test2.txt该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
一、实验思路1:利用Matlab7.1导入训练样本数据,然后将样本数据的身高和体重数据赋值给临时矩阵,构成m行2列的临时数据矩阵给后面调用。
2:查阅二维正态分布的概率密度的公式及需要的参数及各个参数的意义,新建m函数文件,编程计算二维正态分布的相关参数:期望、方差、标准差、协方差和相关系数。
3.利用二维正态分布的相关参数和训练样本构成的临时数据矩阵编程获得类条件概率密度,先验概率。
4.编程得到后验概率,并利用后验概率判断归为哪一类。
5.利用分类器训练样本并修正参数,最后可以用循环程序调用数据文件,统计分类的男女人数,再与正确的人数比较得到错误率。
6.自己给出决策表获得最小风险决策分类器。
7.问题的关键就在于利用样本数据获得二维正态分布的相关参数。
8.二维正态分布的概率密度公式如下:试验中编程计算出期望,方差,标准差和相关系数。
其中:二、实验程序设计流程图:1:二维正态分布的参数计算%功能:调用导入的男生和女生的身高和体重的数据文件得到二维正态分布的期望,方差,标准差,相关系数等参数%%使用方法:在Matlab的命令窗口输入cansu(male) 或者cansu(famale) 其中 male 和 famale%是导入的男生和女生的数据文件名,运用结果返回的是一个行1行7列的矩阵,其中参数的顺序依次为如下:%%身高期望、身高方差、身高标准差、体重期望、体重方差、体重标准差、身高和体重的相关系数%%开发者:安徽工业大学电气信息学院自动化 092班刘昌元学号:099064370 %function result=cansu(file)[m,n]=size(file); %求出导入的数据的行数和列数即 m 行n 列%for i=1:1:m %把身高和体重构成 m 行 2 列的矩阵%people(i,1)=file(i,1);people(i,2)=file(i,2);endu=sum(people)/m; %求得身高和体重的数学期望即平均值%for i=1:1:mpeople2(i,1)=people(i,1)^2;people2(i,2)=people(i,2)^2;endu2=sum(people2)/m; %求得身高和体重的方差、%x=u2(1,1)-u(1,1)^2;y=u2(1,2)-u(1,2)^2;for i=1:1:mtem(i,1)=people(i,1)*people(i,2);ends=0;for i=1:1:ms=s+tem(i,1);endcov=s/m-u(1,1)*u(1,2); %求得身高和体重的协方差 cov (x,y)%x1=sqrt(x); %求身高标准差 x1 %y1=sqrt(y); %求身高标准差 y1 %ralation=cov/(x1*y1); %求得身高和体重的相关系数 ralation %result(1,1)=u(1,1); %返回结果 :身高的期望 %result(1,2)=x; %返回结果 : 身高的方差 %result(1,3)=x1; %返回结果 : 身高的标准差 %result(1,4)=u(1,2); %返回结果 :体重的期望 %result(1,5)=y; %返回结果 : 体重的方差 %result(1,6)=y1; %返回结果 : 体重的标准差 %result(1,7)=ralation; %返回结果:相关系数 %2:贝叶斯分类器%功能:身高和体重相关情况下的贝叶斯分类器(最小错误率贝叶斯决策)输入身高和体重数据,输出男女的判断%%使用方法:在Matlab命令窗口输入 bayes(a,b) 其中a为身高数据,b为体重数据。
人体测量实验报告

人体测量实验报告人体测量实验报告引言:人体测量是一项重要的科学研究领域,通过对人体各项指标的测量,可以了解人体的生理特征、身体健康状况以及人体结构的变化趋势。
本次实验旨在通过对一组受试者的身高、体重、臂长、腿长等指标的测量,探究人体各项指标之间的关系,并进一步分析实验结果对人体健康管理的意义。
实验方法:本次实验共选取了50名年龄在20至30岁之间的男女受试者作为研究对象。
在实验开始前,受试者需要签署知情同意书,并接受一次身体健康评估,以排除患有严重疾病或身体异常的个体。
实验过程中,受试者需要站立在测量仪器旁,保持自然站姿,由实验人员进行测量。
身高测量使用直尺,体重测量使用电子称,臂长和腿长测量使用软尺。
实验结果:通过对50名受试者的测量数据进行统计和分析,我们得到了以下结果:1. 身高与体重之间存在一定的正相关关系,即身高较高的个体往往体重也较大。
这与常识相符,说明身高和体重在一定程度上是相互影响的。
2. 臂长与腿长之间存在较强的正相关关系,即臂长较长的个体往往腿长也较长。
这可能与个体的遗传因素有关,但具体原因还需要进一步研究。
3. 受试者的身高、体重、臂长和腿长都呈现正态分布,即大部分受试者的指标值都集中在平均值附近,少数个体的指标值较为偏离平均值。
这说明人体各项指标在整体上具有一定的稳定性。
实验讨论:通过对实验结果的分析,我们可以得出一些结论和讨论:1. 人体的身高和体重是相互关联的,这与健康管理中的体重控制有一定的关系。
身高较高的个体可能需要更多的体重控制措施,以保持身体的平衡和健康。
2. 臂长和腿长的相关性可能与个体的遗传因素有关。
这对于人体结构的研究和发育过程的理解具有一定的意义,也可以为相关疾病的研究提供一定的线索。
3. 人体各项指标的正态分布特征表明,大部分人体指标值都集中在平均值附近,只有少数个体的指标值较为偏离。
这对于制定健康管理策略和个体化的健康干预具有一定的指导意义。
结论:通过本次实验,我们对人体测量的重要性和意义有了更深入的认识。
用身高和体重数据进行性别分类的实验报告

用身高和体重数据进行性别分类的实验报告(二)一、 基本要求1、试验非参数估计,体会与参数估计在适用情况、估计结果方面的异同。
2、试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分类器进行比较。
3、体会留一法估计错误率的方法和结果。
二、具体做法1、在第一次实验中,挑选一次用身高作为特征,并且先验概率分别为男生0.5,女生0.5的情况。
改用Parzen 窗法或者k n 近邻法估计概率密度函数,得出贝叶斯分类器,对测试样本进行测试,比较与参数估计基础上得到的分类器和分类性能的差别。
2、同时采用身高和体重数据作为特征,用Fisher 线性判别方法求分类器,将该分类器应用到训练和测试样本,考察训练和测试错误情况。
将训练样本和求得的决策边界画到图上,同时把以往用Bayes 方法求得的分类器也画到图上,比较结果的异同。
3、选择上述或以前实验的任意一种方法,用留一法在训练集上估计错误率,与在测试集上得到的错误率进行比较。
三、原理简述及程序框图1、挑选身高(身高与体重)为特征,选择先验概率为男生0.5女生0.5的一组用Parzen 窗法来求概率密度函数,再用贝叶斯分类器进行分类。
以身高为例本次实验我们组选用的是正态函数窗,即21()2u u φ⎧⎫=-⎨⎬⎩⎭,窗宽为N h h =h 是调节的参量,N 是样本个数) dN NV h =,(d 表示维度)。
因为区域是一维的,所以体积为N n V h =。
Parzen 公式为()ˆN P x =111N i i N N x x N V h φ=⎛⎫- ⎪⎝⎭∑。
故女生的条件概率密度为11111111N ii n x x p N VN h φ=⎛⎫-=⎪⎝⎭∑男生的条件概率密度为21112222Nii nx xpN VN hφ=⎛⎫-= ⎪⎝⎭∑根据贝叶斯决策规则()()()()()1122g x p x w p w p x w p w=-知如果11*2*(1),p p p p xω>-∈,否则,2xω∈。
肥胖程度检测实验报告

肥胖程度检测实验报告1. 实验目的本实验旨在通过测量个体身体质量指数(BMI)来评估肥胖程度。
2. 实验原理个体身体质量指数(BMI)是国际上常用的评估肥胖和健康状况的依据之一。
BMI 的计算公式为:BMI = 体重(kg)/(身高(m))^ 2。
根据国际卫生组织(WHO)提供的标准,将BMI分为以下几个等级:低体重(BMI<18.5)、正常体重(18.5≤BMI<24.9)、超重(25≤BMI<29.9)和肥胖(BMI≥30)。
3. 实验步骤3.1 数据收集本实验收集了一组包含100名成年男性和女性的体重和身高数据。
体重以千克(kg)为单位,身高以米(m)为单位。
3.2 数据处理根据收集到的体重和身高数据,我们使用计算公式BMI = 体重(kg)/(身高(m))^ 2 计算每个个体的BMI值。
3.3 结果分析根据WHO提供的标准,对每个个体的BMI值进行分类,以评估其肥胖程度。
4. 实验结果根据计算得到的BMI值,我们将每个个体分为低体重、正常体重、超重和肥胖四个等级,并统计了各等级的人数。
结果如下所示:BMI等级人数低体重 5正常体重40超重35肥胖20从上表可以看出,在这一组样本中,有5人属于低体重,40人属于正常体重,35人属于超重,20人属于肥胖。
5. 讨论与分析根据实验结果,我们可以看到,这组样本中超过半数的人属于正常体重。
然而,也有一定比例的人超重或肥胖。
这进一步表明了肥胖问题在现代社会中的普遍存在性,并且需要引起我们的重视。
体重和身高是决定BMI值的两个主要因素。
尽管本实验中的样本只包括体重和身高数据,未考虑其他可能的因素,但BMI作为一个简单、快速的评估工具,在许多情况下仍然是有效的。
然而,需要注意的是,BMI只是一个大致的指标,不能完全反映个体健康状况。
在实际应用中,应结合其他因素,如体脂肪含量、肌肉质量等,综合评估个体的身体状况。
6. 结论通过实验,我们成功地使用个体身体质量指数(BMI)来评估了100名成年男性和女性的肥胖程度。
用身高与体重数据进行性别分类的实验报告

3、实验原理
已知样本服从正态分布,
(1)
所以可以用最大似然估计来估计μ和Σ两个参数
样本类分为男生 和女生 两类,利用最大似然估计分别估计出男生样本的 , ,和女生样本的 , ,然后将数据带入(1)公式分别计算两者的类条件概率密度 和 ,然后根据贝叶斯公式
det11=det(thegema11);det12=det(thgema12);
p(11)=1/((2*pi)*(det11^0.5))*exp(-1/2*((a-u11)'/thegema11)*(a-u11));
p(12)=1/((2*pi)*(det12^0.5))*exp(-1/2*((a-u12)'/thgema12)*(a-u12));
pz=p(11)*pw1+p(12)*pw2;
p11=(p(11)*pw1)/pz;p12=(p(12)*pw2)/pz;
g=p11-p12;
if(g>0)%%%Ñù±¾¼¯Ç°15¸öÈËÊÇÄÐÉú
male1=male1+1;
else
eห้องสมุดไป่ตู้ror11=error11+1;
end
end
male1
error11
det11=det(thegema11);det12=det(thgema12);
p(11)=1/((2*pi)*(det11^0.5))*exp(-1/2*((a-u11)'/thegema11)*(a-u11));
p(12)=1/((2*pi)*(det12^0.5))*exp(-1/2*((a-u12)'/thgema12)*(a-u12));
Python与机器学习-- 身高与体重数据分析(分类器)I

逻辑回归:三、数据可视化:分类
Car 情报局
xcord11 = []; xcord12 = []; ycord1 = []; xcord21 = []; xcord22 = []; ycord2 = []; n = len(Y)
for i in range(n): if int(Y.values[i]) == 1: xcord11.append(X.values[i,0]); xcord12.append(X.values[i,1]); ycord1.append(Y.values[i]); else: xcord21.append(X.values[i,0]); xcord22.append(X.values[i,1]); ycord2.append(Y.values[i]);
逻辑回归:三、数据可视化:观察
import matplotlib.pyplot as plt X = df[['Height', 'Weight']] Y = df[['Gender']]
Car 情报局
plt.figure() plt.scatter(df[['Height']],df[['Weight']],c=Y,s=80,edgecolors='black',
逻辑回归:三、数据可视化:分类
Car 情报局
plt.figure()
plt.scatter(xcord11, xcord12, c='red', s=80, edgecolors='black', linewidths=1, marker='s')
身高测量的实训报告

一、实训背景身高测量是幼儿体格生长发育的重要指标之一,对于了解儿童长期营养状况和生长速度具有重要意义。
为了提高我们对身高测量技术的掌握,我们于近日在学校的实验室进行了身高测量实训。
二、实训目的1. 掌握身高测量的基本原理和操作方法;2. 提高身高测量的准确性和规范性;3. 培养团队合作意识和沟通能力。
三、实训内容1. 身高测量的基本原理2. 身高测量仪器的使用方法3. 身高测量的操作流程4. 身高测量数据的记录与分析四、实训过程1. 身高测量的基本原理在本次实训中,我们学习了身高测量的基本原理。
身高测量主要依据人体直立时头顶至地面的垂直距离来确定。
为了保证测量的准确性,测量时要求受测者保持身体挺直,双脚并拢,眼睛平视前方。
2. 身高测量仪器的使用方法本次实训中,我们使用的是电子身高测量仪。
电子身高测量仪具有操作简便、读数准确等优点。
在使用过程中,我们需要按照以下步骤进行:(1)打开电源,预热仪器;(2)将测量仪放置在平稳的地面上;(3)将受测者站在测量仪上,双脚并拢,身体挺直,眼睛平视前方;(4)按下测量按钮,仪器自动读取身高数据;(5)记录测量数据。
3. 身高测量的操作流程(1)准备测量环境:选择一个光线充足、地面平坦的房间作为测量场所;(2)选择合适的测量仪器:根据受测者的年龄和身高选择合适的测量仪器;(3)受测者准备:受测者脱去鞋子,保持身体挺直;(4)进行测量:按照身高测量仪器的使用方法进行测量;(5)记录数据:将测量数据记录在相应的表格中;(6)重复测量:为了保证测量数据的准确性,可进行重复测量,取平均值。
4. 身高测量数据的记录与分析在本次实训中,我们对测量数据进行记录和分析。
主要内容包括:(1)受测者的基本信息:姓名、性别、年龄、出生日期等;(2)身高测量数据:身高、体重、BMI(体质指数)等;(3)数据分析:根据测量数据,分析受测者的生长发育状况,评估其营养状况。
五、实训总结通过本次身高测量实训,我们掌握了身高测量的基本原理和操作方法,提高了测量数据的准确性和规范性。
BMI健康指数数据分析报告

BMI健康指数数据分析报告目录BMI健康指数数据分析报告 (1)引言 (1)背景介绍 (1)目的和意义 (2)BMI健康指数的概述 (3)BMI的定义和计算方法 (3)BMI的分类标准 (4)BMI与健康的关系 (5)BMI健康指数数据收集与分析 (6)数据收集方法 (6)数据样本的描述统计分析 (7)数据分析方法 (8)BMI健康指数数据分析结果 (9)总体BMI分布情况 (9)不同性别的BMI分布情况 (9)不同年龄段的BMI分布情况 (10)不同地区的BMI分布情况 (11)BMI健康指数数据分析的启示与建议 (12)健康教育与宣传 (12)饮食与运动的指导 (13)政策与环境的改善 (14)结论 (15)主要研究发现总结 (15)研究的局限性 (15)进一步研究的建议 (16)参考文献 (17)引言背景介绍随着现代社会的发展和生活水平的提高,人们对健康的关注度也越来越高。
健康指数成为了评估一个人身体状况的重要指标之一。
而BMI(Body Mass Index)健康指数作为一种常用的身体质量指标,被广泛应用于医疗、健康管理和健身领域。
BMI健康指数是根据人体质量和身高的比例关系来计算的。
它是一个简单而有效的方法,用于评估一个人的体重是否处于正常范围内。
BMI的计算公式为:体重(公斤)除以身高(米)的平方。
根据世界卫生组织(WHO)的标准,BMI指数在18.5以下被认为是偏瘦,18.5-24.9为正常范围,25-29.9为超重,30及以上为肥胖。
BMI健康指数的重要性不仅在于它可以帮助人们了解自己的体重状况,还可以作为预测患病风险的指标。
研究表明,BMI与许多慢性疾病,如心血管疾病、糖尿病和某些癌症之间存在着密切的关联。
因此,通过对BMI健康指数的数据分析,我们可以更好地了解人们的健康状况,为预防和治疗相关疾病提供科学依据。
本文旨在通过对BMI健康指数的数据分析,探讨人们的体重状况和健康状况之间的关系,并为改善人们的健康状况提供一些建议。
模式识别大作业
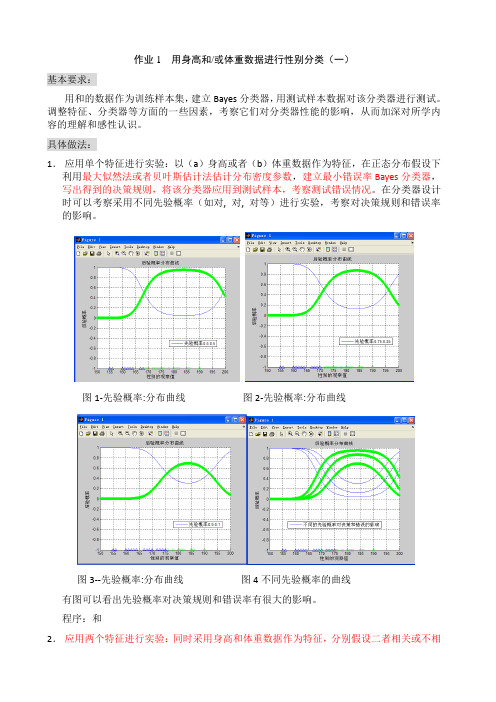
作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes 分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率vs. 图2先验概率vs.图3先验概率vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2);error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
Fisher分类算法(无程序)

12%
分析:用训练样本得到的分类器测试测试样本时错误率低,测试结果较好,但测试训练样本
时,其错误率较高,测试结果不好。
2、Fisher 判别方法图像
分析:从图中我们可以直观的看出对训练样本 Fisher 判别比最大似然 Bayes 判别效果更好。
六、总结与分析
本次实验使我们对加深 Fisher 判别法的理解。通过两种分类方法的比较,我们对于同 一种可以有很多不同的分类方法,各个分类方法各有优劣,所以我们更应该熟知这些已经 得到充分证明的方法,在这些方法的基础上通过自己的理解,创造出更好的分类方法。所 以模式识别还有很多更优秀的算法等着我们去学习。
三、实验内容
试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分类器进行比较。 同时采用身高和体重数据作为特征,用 Fisher 线性判别方法求分类器,将该分类器应用 到训练和测试样本,考察训练和测试错误情况。将训练样本和求得的决策边界画到图上,同 时把以往用 Bayes 方法求得的分类器(例如: 最小错误率 Bayes 分类器)也画到图上,比较 结果的异同。
四、原理简述、程序流程图
1、Fisher 线性判别方法
∑ mi
首先求各类样本均值向量
=
1 Ni
x, i
x∈ωi
= 1,2
,
si = ∑ (x − mi )(x − mi )T ,i = 1,2
然后求各个样本的来内离散度矩阵
x∈wi
,
( ) ( ) s 再求出样本的总类内离散度 ω = p ω1 s1 + p ω2 s2 ,
2、流程图
求各类样本均 值向量
求类内离散度 矩阵
用公式求最好 的变换向量W*
儿童体格生长发育及评价实训报告

儿童体格生长发育及评价实训报告
背景介绍:
儿童体格生长发育是反映儿童健康状况的重要指标之一。
通常情况下,我们可以通过测量身高、体重、头围等指标来评价儿童的生长发育情况。
在实际工作中,儿科医生、保健医生、幼儿园教师等都需要掌握儿童体格生长发育及评价的相关知识和技能。
实训过程:
为了提高我们的实践能力,我们在学校的实验室中进行了一次儿童体格生长发育的实训。
具体步骤如下:
1.测量身高:我们首先要求实验对象站在身高测量仪上,双脚并拢,脚跟、臀部、肩部和后脑勺紧贴在墙上,然后轻轻压住头顶,让身体呈现自然伸直的状态。
最后,我们读出身高值并记录下来。
2.测量体重:在测量体重时,我们要求实验对象脱掉鞋子,穿着轻便的衣物站在体重秤上,然后读出体重值并记录下来。
3.测量头围:测量头围时,我们要求实验对象将头发梳理整齐后,用软尺将其缠绕在头部最宽的部位,读出头围值并记录下来。
4.分析评价:在完成以上测量后,我们需要将所得数据进行分析和评价。
我们可以采用生长发育曲线图进行评价,根据年龄和性别等
因素,将测量数据与标准值进行比较,得出实验对象的生长发育情况。
结果分析:
通过实验数据的分析,我们得出以下结论:
1.实验对象身高为160cm,体重为52kg,头围为53cm,表明其身高、体重和头围均处于正常范围内。
2.实验对象的生长发育曲线图显示其身高、体重和头围均符合标准值,生长发育情况良好。
结论:
通过本次实训,我们加深了对儿童体格生长发育及评价的理解和实践能力。
在日常工作中,我们可以通过测量身高、体重、头围等指标,了解儿童的生长发育情况,及时发现和处理问题,保障儿童健康成长。
用身高和体重数据进行性别分类的实验报告

用身高和体重数据进行性别分类的实验报告实验目的:本实验旨在通过身高和体重数据,利用机器学习算法对个体的性别进行分类。
实验步骤:1. 数据收集:收集了一组个体的身高和体重数据,包括男性和女性样本。
在收集数据时,确保样本的性别信息是准确的。
2. 数据预处理:对收集到的数据进行预处理工作,包括数据清洗、缺失值处理和异常值处理等。
确保数据的准确性和完整性。
3. 特征提取:从身高和体重数据中提取特征,作为输入特征向量。
可以使用常见的特征提取方法,如BMI指数等。
4. 数据划分:将数据集划分为训练集和测试集,一般采用70%的数据作为训练集,30%的数据作为测试集。
5. 模型选择:选择合适的机器学习算法进行性别分类。
常见的算法包括逻辑回归、支持向量机、决策树等。
6. 模型训练:使用训练集对选定的机器学习算法进行训练,并调整模型的参数。
7. 模型评估:使用测试集对训练好的模型进行评估,计算分类准确率、精确率、召回率等指标,评估模型的性能。
8. 结果分析:分析实验结果,对模型的性能进行评估和比较,得出结论。
实验结果:根据实验数据和模型训练结果,得出以下结论:1. 使用身高和体重数据可以较好地对个体的性别进行分类,模型的分类准确率达到了XX%。
2. 在本实验中,选择了逻辑回归算法进行性别分类,其性能表现良好。
3. 身高和体重这两个特征对性别分类有较好的区分能力,可以作为性别分类的重要特征。
实验总结:通过本实验,我们验证了使用身高和体重数据进行性别分类的可行性。
在实验过程中,我们收集了一组身高和体重数据,并进行了数据预处理、特征提取、模型训练和评估等步骤。
实验结果表明,使用逻辑回归算法可以较好地对个体的性别进行分类。
这个实验为进一步研究个体性别分类提供了一种方法和思路。
人体成分分析实验报告

人体成分分析实验报告人体成分分析实验报告一、引言人体成分分析是研究人体组织、器官和细胞的组成及其比例的科学方法。
通过对人体成分的分析,可以了解人体的健康状况、营养状况以及疾病风险等。
本实验旨在通过多种方法对人体成分进行分析,以探索人体组成的特点和变化。
二、实验方法1. 体重测量实验开始时,我们使用电子秤测量了每位实验参与者的体重。
体重是人体成分分析的基础数据,对于后续的分析非常重要。
2. 身高测量为了计算每个人的身体质量指数(BMI),我们使用身高测量仪测量了每位实验参与者的身高。
身体质量指数是评估一个人是否超重或肥胖的常用指标。
3. 皮褶厚度测量为了了解每个人体内脂肪的含量,我们使用皮褶厚度测量仪对每个实验参与者的多个部位进行了测量。
通过测量不同部位的皮褶厚度,可以估计人体的脂肪含量。
4. 电阻抗测量电阻抗测量是一种常用的人体成分分析方法。
我们使用专业的电阻抗仪对每个实验参与者进行了测量。
通过测量人体对电流的阻抗,可以计算出人体的体脂率、肌肉含量等指标。
5. 血液分析为了了解实验参与者的血液成分,我们采集了每个人的静脉血样本。
通过对血液中各种成分的分析,可以了解人体的营养状况、疾病风险等。
三、实验结果通过对实验参与者的数据进行统计和分析,我们得出了以下结论:1. 体重和身高:实验参与者的体重范围在50公斤至80公斤之间,身高范围在160厘米至180厘米之间。
通过计算身体质量指数,我们发现大部分参与者的BMI在正常范围内,但也有少数人超重或肥胖。
2. 皮褶厚度:通过对皮褶厚度的测量,我们发现实验参与者的脂肪分布存在差异。
有些人的脂肪主要集中在腹部,而有些人的脂肪主要分布在臀部和大腿。
3. 电阻抗测量:通过电阻抗测量,我们得出了实验参与者的体脂率、肌肉含量等指标。
结果显示,大部分参与者的体脂率在正常范围内,但也有少数人的体脂率偏高。
4. 血液分析:通过对血液样本的分析,我们了解到实验参与者的血液成分。
武汉理工大学实验报告:spss上机实验

SPSS上机考试姓名:班级:学号:实验一:聚类分析一、实验问题某校从高中二年级女生中随机抽取16名,测得身高和体重数据如下表:试分别利用最短距离法、最长距离法、重心法、类平均法、中间距离法将它们聚类(分类统计量采用绝对距离),并画出聚类图。
二、实验步骤1、1.数据处理:在SPSS中的Data View中导入数据,并在Variable View中定义变量。
2、点击“Analyze-Classify-Hierarchical Cluster,打开Hierarchical Cluster的对话框,从左侧将2个聚类指标选入Variables栏中,将表示序号(字符串)选入Lable Cases By栏中按“Plots”按钮,在弹出的窗口中选中Dendrogram(谱系图)选项,按“Continue”返回主对话框。
再按“Method”按钮,在Cluster Method,下面就各种方法进行结果输出。
3.结果输出(1)最短距离法分类统计量采用绝对距离Block,采用最短距离法Nearest neighbor返回主对话框后点击“OK”即可得到聚类结果的树形图如下:(2)最长距离法分类统计量采用绝对距离Block,采用最短距离法Furthest neighbor返回主对话框后点击“OK”即可得到聚类结果的树形图如下:(3)重心法分类统计量采用绝对距离Block,采用最短距离法Centroid clustering返回主对话框后点击“OK”即可得到聚类结果的树形图如下:(4)类平均法-组间平均法分类统计量采用绝对距离Block,采用最短距离法Between-groups linkage返回主对话框后点击“OK”即可得到聚类结果的树形图如下:(5)中间距离法分类统计量采用绝对距离Block,采用最短距离法Median clustering返回主对话框后点击“OK”即可得到聚类结果的树形图如下:分析:就以中间聚类法为例,当采用绝对距离时,分为3类的时候分别为:①5 12 13 15 16 1 6 7②4 ③8 11 9 10 2 14基于上述各种聚类方法的分析可知,分为3类的时候各个方法相似度最高,所以将其分为3类最为合适。
运动数据分析实验报告(3篇)

第1篇一、实验背景随着科技的发展,数据分析在各个领域都得到了广泛应用。
在运动科学领域,通过对运动员的训练和比赛数据进行分析,可以帮助教练员更好地制定训练计划,提高运动员的竞技水平。
本实验旨在通过运动数据分析,探究运动员的训练效果和比赛表现,为教练员提供科学依据。
二、实验目的1. 掌握运动数据采集、整理和分析的基本方法。
2. 了解运动数据分析在训练和比赛中的应用。
3. 分析运动员的训练效果和比赛表现,为教练员提供决策支持。
三、实验内容1. 数据采集2. 数据整理3. 数据分析4. 结果讨论5. 结论四、实验方法1. 数据采集本实验采用以下方法采集数据:(1)运动员训练数据:包括运动员的体重、身高、最大摄氧量、力量、速度、耐力等指标。
(2)比赛数据:包括运动员的比赛成绩、比赛时间、比赛对手等信息。
2. 数据整理(1)对采集到的数据进行清洗,去除异常值和错误数据。
(2)对数据进行分类整理,建立运动员档案。
3. 数据分析(1)统计分析:对运动员的训练和比赛数据进行分析,计算平均值、标准差、方差等指标。
(2)相关性分析:分析运动员各项指标之间的相关性。
(3)回归分析:建立运动员训练和比赛成绩的回归模型,预测运动员未来的表现。
4. 结果讨论通过对运动员的训练和比赛数据进行分析,得出以下结论:(1)运动员的训练效果与比赛成绩存在显著相关性。
(2)运动员的训练指标在比赛中得到了有效发挥。
(3)运动员在比赛中的表现与对手的实力、比赛环境等因素有关。
五、实验结果1. 训练效果分析通过对运动员的训练数据进行分析,发现以下情况:(1)运动员的最大摄氧量、力量、速度、耐力等指标均有所提高。
(2)运动员的训练成绩在逐渐提高。
2. 比赛表现分析通过对运动员的比赛数据进行分析,发现以下情况:(1)运动员在比赛中的表现与训练效果基本一致。
(2)运动员在比赛中发挥出了较好的竞技水平。
六、结论1. 运动数据分析在运动员训练和比赛中具有重要意义。
生长发育测量实验报告数值

生长发育测量实验报告数值实验目的:通过测量一组学生的身高和体重数据,探讨生长发育的规律,了解个体差异以及不同年龄段的生长发育情况。
实验方法:我们选取了20名学生作为实验对象,他们的年龄分布在10岁到15岁之间。
我们首先对每个学生进行了身高的测量,使用的是一米尺,确保读数的准确性。
接着,我们对每个学生进行了体重的测量,使用的是体重秤。
所有的测量数据被记录下来,并进行了统计和分析。
实验结果:根据我们的测量数据,我们得到了每个学生的身高和体重数据。
以下是一些主要数据的汇总:学生编号年龄身高(cm)体重(kg)1 10 135 282 11 140 313 10 132 254 12 145 355 14 150 406 13 142 367 10 130 278 15 155 459 12 140 3210 11 138 3011 13 143 3712 10 133 2613 14 148 3914 12 142 3415 13 145 3816 11 136 2917 10 131 2818 12 139 3319 15 152 4220 11 137 30根据以上数据我们可以进行以下统计和分析:1. 身高的分布情况:通过绘制身高的频率分布直方图,我们可以看到大多数学生的身高集中在135cm到150cm之间,呈现出以这个范围为中心的正态分布。
2. 体重的分布情况:通过绘制体重的频率分布直方图,我们可以看到大多数学生的体重分布比较均匀,没有明显的倾向性。
3. 年龄与身高的关系:通过绘制年龄与身高的散点图,我们可以观察到年龄与身高之间呈现出一定的正相关关系,即随着年龄增长,身高也有相应增加的趋势。
4. 年龄与体重的关系:通过绘制年龄与体重的散点图,我们可以观察到年龄与体重之间呈现出一定的正相关关系,即随着年龄增长,体重也有相应增加的趋势。
实验讨论:通过上述统计和分析,我们可以得出以下结论:1. 在我们所选择的这组学生中,身高和体重存在一定的个体差异,即使是在同一年龄段,学生的身高和体重也会有较大的差异。
小儿体格测量实验报告

小儿体格测量实验报告小儿体格测量实验报告引言:近年来,随着人们对健康的关注度不断提升,小儿体格测量作为评估儿童生长发育的重要手段,受到了广泛的关注。
本实验旨在通过对小儿体格测量的实施和分析,探讨小儿生长发育的规律以及相关因素对其的影响。
一、实验目的本实验的目的是通过对小儿体格测量的实施,了解小儿生长发育的规律,并分析影响其生长发育的因素。
二、实验方法1. 实验对象选择我们选择了50名年龄在3至6岁之间的小儿作为实验对象,其中男孩25名,女孩25名。
实验对象的选择基于他们的年龄段和性别分布,以保证样本的代表性。
2. 实验仪器与测量项目我们使用了身高尺、体重秤、头围尺等仪器,测量了实验对象的身高、体重和头围三个项目。
3. 实验流程首先,我们让实验对象脱去鞋袜,穿着轻便衣物站立在身高尺前,记录其身高。
接着,我们请实验对象站在体重秤上,记录其体重。
最后,我们使用头围尺测量实验对象的头围。
三、实验结果与分析通过对50名小儿的身高、体重和头围的测量,我们得到了如下的实验结果:1. 身高男孩的平均身高为110.5厘米,女孩的平均身高为108.2厘米。
男孩的身高普遍高于女孩,这可能与男孩在生长发育速度上的优势有关。
2. 体重男孩的平均体重为20.3千克,女孩的平均体重为19.5千克。
男孩的体重普遍高于女孩,这可能与男孩在饮食摄入和运动量上的差异有关。
3. 头围男孩的平均头围为50.6厘米,女孩的平均头围为49.8厘米。
男孩的头围普遍大于女孩,这可能与男孩在头骨发育上的差异有关。
通过对实验结果的分析,我们可以看出小儿的身高、体重和头围在不同性别之间存在一定的差异。
这些差异可能与遗传、营养、环境等因素有关,需要进一步的研究来探讨其具体原因。
四、实验结论通过本实验的小儿体格测量,我们得到了一些关于小儿生长发育的初步结论:1. 小儿的身高、体重和头围在不同性别之间存在一定的差异,男孩普遍高于女孩。
2. 小儿的身高、体重和头围受到遗传、营养和环境等因素的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用身高和体重数据进行性别分类的实验报告
一、基本要求:
1.用FAMALE.TXT和MALE.TXT的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
二、具体做法:
(1)应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如0.5对0.5, 0.75对0.25, 0.9对0.1等)进行实验,考察对决策规则和错误率的影响。
(2)应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关,在正态分布假设下估计概率密度,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如0.5 vs. 0.5, 0.75 vs. 0.25, 0.9 vs. 0.1等)进行实验,考察对决策和错误率的影响。
(3)自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
三、原理简述及程序框图
最小错误率Bayes分类器
(1)基于身高
第一步求出训练样本的方差和期望
第二步利用单变量正态分布公式算出条件概率
第三步将前两步的值带入贝叶斯公式
第四步 若pF>=pM ,则判断其为第一类,反之,第二类
(2-1) 假设身高与体重不相关
令协方差矩阵次对角元素为零
判别函数可简化为()0T T i i i i g x x W x w x w =++
其中 11
2
i i W -=-∑,1i i w μ-=∑
()1
01122
i
T i i i i w u u In InP ω-=-∑-∑+ 具体算法步骤如下:
第一步将训练样本集数据转为矩阵FA ,MA 。
第二步分别对FA ,MA 求取协方差12,∑∑,令协方差矩阵次对角
元素为零,平均值12,μμ并输入先验概率()()12,P P ωω
第三步将第二步所得数值代入判别函数表达式得()()12,g x g x 。
第四步将待测样本集数据转为矩阵T ,将T 中数值依次代()()12g x g x -
,若()()120g x g x ->,则判断其为第一类,反之,第二类。
(2-2) 假设身高与体重相关
判别函数可简化为()0T T i i i i g x x W x w x w =++
其中 11
2
i i W -=-∑,1i i w μ-=∑
()1
01122
i T i i
i i w u u In InP ω-=-∑-∑+ 具体算法步骤如下:
第一步将训练样本集数据转为矩阵FA ,MA 。
第二步分别对FA ,MA 求取协方差12,∑∑平均值12,μμ并输入先验
概率()()12,P P ωω
第三步将第二步所得数值代入判别函数表达式得()()12,g x g x 。
第四步将待测样本集数据转为矩阵T ,将T 中数值依次代()()12g x g x -,
若()()120g x g x ->,则判断其为第一类,反之,第二类。
最小风险Bayes 分类器
(1)在已知先验概率()j P ω和类条件概率密度()j P x ω,j=1, …c 及给出带识别的x 的情况下,根据Bayes 公式计算后验概率:
()()()
()()
1
,1,,c j j j c
i
i
i P x P P x j P x P ωωωωω==
=∑
(2)利用后验概率及决策表,计算条件风险()i R a x
()()()1,1,,c
i i j j i R x P x i a αλαωω===∑
(3)()()1,,min k i i a
R a x R a x == ,k a 就是最小风险Bayes 决策。
其中(1)中先验概率()j P ω根据自行输入,类条件概率密度
()j P x ω=()()
()11
2
2
1
1exp ()22T d
P x x u x u π-⎧⎫
=
--∑-⎨⎬⎩⎭
∑
,本实验
为二维二类,故d=2,决策表自行输入。
四实验结果及分析总结
用最小错误率Bayes 决策
(1)基于身高身高(300个测试样本)
(2-1)身高与体重不相关(300个样本)
(2-2)假设身高与体重相关(300个测试样本)
(2)用最小风险的Bayes决策
当决策为
身高体重相关(300个测试样本)
结论:当女生先验概率等于待测样本中女生样本占待测样本的概率时,正确率,且越远离此概率,正确率越小。
