用身高和或体重数据进行性别分类的实验
模式识别第一次作业报告

模式识别第一次作业报告姓名:刘昌元学号:099064370 班级:自动化092班题目:用身高和/或体重数据进行性别分类的实验基本要求:用famale.txt和male.txt的数据作为训练样本集,建立Bayes分类器,用测试样本数据test1.txt和test2.txt该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
一、实验思路1:利用Matlab7.1导入训练样本数据,然后将样本数据的身高和体重数据赋值给临时矩阵,构成m行2列的临时数据矩阵给后面调用。
2:查阅二维正态分布的概率密度的公式及需要的参数及各个参数的意义,新建m函数文件,编程计算二维正态分布的相关参数:期望、方差、标准差、协方差和相关系数。
3.利用二维正态分布的相关参数和训练样本构成的临时数据矩阵编程获得类条件概率密度,先验概率。
4.编程得到后验概率,并利用后验概率判断归为哪一类。
5.利用分类器训练样本并修正参数,最后可以用循环程序调用数据文件,统计分类的男女人数,再与正确的人数比较得到错误率。
6.自己给出决策表获得最小风险决策分类器。
7.问题的关键就在于利用样本数据获得二维正态分布的相关参数。
8.二维正态分布的概率密度公式如下:试验中编程计算出期望,方差,标准差和相关系数。
其中:二、实验程序设计流程图:1:二维正态分布的参数计算%功能:调用导入的男生和女生的身高和体重的数据文件得到二维正态分布的期望,方差,标准差,相关系数等参数%%使用方法:在Matlab的命令窗口输入cansu(male) 或者cansu(famale) 其中 male 和 famale%是导入的男生和女生的数据文件名,运用结果返回的是一个行1行7列的矩阵,其中参数的顺序依次为如下:%%身高期望、身高方差、身高标准差、体重期望、体重方差、体重标准差、身高和体重的相关系数%%开发者:安徽工业大学电气信息学院自动化 092班刘昌元学号:099064370 %function result=cansu(file)[m,n]=size(file); %求出导入的数据的行数和列数即 m 行n 列%for i=1:1:m %把身高和体重构成 m 行 2 列的矩阵%people(i,1)=file(i,1);people(i,2)=file(i,2);endu=sum(people)/m; %求得身高和体重的数学期望即平均值%for i=1:1:mpeople2(i,1)=people(i,1)^2;people2(i,2)=people(i,2)^2;endu2=sum(people2)/m; %求得身高和体重的方差、%x=u2(1,1)-u(1,1)^2;y=u2(1,2)-u(1,2)^2;for i=1:1:mtem(i,1)=people(i,1)*people(i,2);ends=0;for i=1:1:ms=s+tem(i,1);endcov=s/m-u(1,1)*u(1,2); %求得身高和体重的协方差 cov (x,y)%x1=sqrt(x); %求身高标准差 x1 %y1=sqrt(y); %求身高标准差 y1 %ralation=cov/(x1*y1); %求得身高和体重的相关系数 ralation %result(1,1)=u(1,1); %返回结果 :身高的期望 %result(1,2)=x; %返回结果 : 身高的方差 %result(1,3)=x1; %返回结果 : 身高的标准差 %result(1,4)=u(1,2); %返回结果 :体重的期望 %result(1,5)=y; %返回结果 : 体重的方差 %result(1,6)=y1; %返回结果 : 体重的标准差 %result(1,7)=ralation; %返回结果:相关系数 %2:贝叶斯分类器%功能:身高和体重相关情况下的贝叶斯分类器(最小错误率贝叶斯决策)输入身高和体重数据,输出男女的判断%%使用方法:在Matlab命令窗口输入 bayes(a,b) 其中a为身高数据,b为体重数据。
用身高和体重数据进行性别分类的实验报告

用身高和体重数据进行性别分类的实验报告(二)一、 基本要求1、试验非参数估计,体会与参数估计在适用情况、估计结果方面的异同。
2、试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分类器进行比较。
3、体会留一法估计错误率的方法和结果。
二、具体做法1、在第一次实验中,挑选一次用身高作为特征,并且先验概率分别为男生0.5,女生0.5的情况。
改用Parzen 窗法或者k n 近邻法估计概率密度函数,得出贝叶斯分类器,对测试样本进行测试,比较与参数估计基础上得到的分类器和分类性能的差别。
2、同时采用身高和体重数据作为特征,用Fisher 线性判别方法求分类器,将该分类器应用到训练和测试样本,考察训练和测试错误情况。
将训练样本和求得的决策边界画到图上,同时把以往用Bayes 方法求得的分类器也画到图上,比较结果的异同。
3、选择上述或以前实验的任意一种方法,用留一法在训练集上估计错误率,与在测试集上得到的错误率进行比较。
三、原理简述及程序框图1、挑选身高(身高与体重)为特征,选择先验概率为男生0.5女生0.5的一组用Parzen 窗法来求概率密度函数,再用贝叶斯分类器进行分类。
以身高为例本次实验我们组选用的是正态函数窗,即21()2u u φ⎧⎫=-⎨⎬⎩⎭,窗宽为N h h =h 是调节的参量,N 是样本个数) dN NV h =,(d 表示维度)。
因为区域是一维的,所以体积为N n V h =。
Parzen 公式为()ˆN P x =111N i i N N x x N V h φ=⎛⎫- ⎪⎝⎭∑。
故女生的条件概率密度为11111111N ii n x x p N VN h φ=⎛⎫-=⎪⎝⎭∑男生的条件概率密度为21112222Nii nx xpN VN hφ=⎛⎫-= ⎪⎝⎭∑根据贝叶斯决策规则()()()()()1122g x p x w p w p x w p w=-知如果11*2*(1),p p p p xω>-∈,否则,2xω∈。
《数据分析》教学案例

《数据分析》教学案例作者:李增海高传忠来源:《中国信息技术教育》2016年第21期本节课是“数据的编辑加工”单元中的内容,本单元主要是表格数据的排序、筛选、分类汇总等概念及操作。
本节课的授课对象是七年级的学生,经过小学阶段和七年级上学期的学习,学生具备了一定的信息素养,掌握了网上搜索、文字录入和处理等操作技能。
但学生对数据的编辑和分析是第一次接触,比较有新鲜感。
但这部分内容七年级学生接触较少,而且具有一定的难度,需要认真学习,才能掌握。
创设情境,案例引入(5分钟)师:我们上节课学习了《数值计算》,通过公式法或函数法可以计算出一行或一列数的总和、平均数、最大值、最小值等数值。
我们计算这些数值的目的往往不只是计算数值,更重要的是想寻找一些规律或蕴含在这些数值中的信息为工作和生活服务。
这节课,我们一起来探究简单的数据分析方法,其中主要包括排序、筛选、分类汇总三种技术。
下面有三个案例,每个案例都含有三个问题,大家看看如何解决这些问题?案例1:为了庆祝“元旦”,学校举办了一场庆“元旦”演讲比赛,刘燕等同学承担了这次比赛的分数统计工作。
他们将评委的打分录入后,先按照评委会的要求,去掉一个最高分和一个最低分,得出每位选手的最后得分(如表1),你能通过自主探究和小组合作学习,利用本节课学习的内容,按得分高低计算出每位选手的总名次、级部名次和优胜级部吗?案例2:表2是咱们班所有同学的身高和体重统计表,你想不想知道你的身高或体重在我们班处于一个什么样的位次,在相同性别的同学中又处于什么位次呢?咱们班男生、女生的平均身高或体重又是多少呢?案例3:表3是2015-2016学年度第二学期班级卫生检查结果记录表,你能通过自主探究,利用本节课的知识计算出每个班级的总名次、每个班在本级部中的名次以及优胜级部吗?设计意图:教师通过精讲,让学生明确学习任务,理解有关专业术语的概念;以学生熟悉的三个真实案例创设情境,导入新课,目的是激发学生的学习兴趣,培养他们分析问题、解决问题的能力。
贝叶斯决策理论与统计判决方法

=1X1/2+1/5X1/2
=0.6
例:考试有用吗?
利用贝叶斯公式可以得到:
这说明老师们依据试卷成绩来衡量学生平时的学习状况 还是有科学依据的。
仪器,经常被用于征兵、安全部门的 筛查、侦破、诉讼等领域。定义事件T={测谎仪检测到一个人在说谎}, L={一个人真正在说谎}。
p( x)P(i x) P(i ) p( x i )
条件概率 先验概率:P(i)表示类i出现的先验概率,简称类i的概率。 后验概率:P(i|x)表示x出现条件下类i出现的概率,称其为类别的后验概率, 对于模式识别来讲可理解为x来自类i的概率。 类条件概率密度: p(x|i)表示在类i条件下的概率密度,即类i模式x的概率 分布密度,简称为类条件概率密度。
A B4 B3
B2
划分示意图
例:考试有用吗?
老师出了一道5选题,5个选项中只有一个是正确的选择。 假定某学生知道正确答案的概率为1/2,如果他最后选对了, 问他确实知道答案的概率是多少? 解: 设 A事件为{知道答案},B事件为{选择正确}, 由题意可知:
P(B|~A)=1/5,P(B|A)=1, P(A)=1/2 由全概率公式: P(B)=P(B|A)XP(A)+P(B|~A)XP(~A)
两种鱼的长度特征直方图
例:鱼的分类
单凭长度特征很难将两类鱼很好地区分开,因此,我们 可以考虑别的特征,比如:平均光泽度。
例:鱼的分类
分别输入100组鲈鱼和鲑鱼的亮度、长度数据,作为训练集。输入400组数据作为测试 集,其中200组鲈鱼数据,100组鲑鱼数据。得到以下实验结果(设定鲈鱼先验概率为 0.5,鲑鱼先验概率为0.5): 鲈鱼错误分类(鲑鱼判决为鲈鱼):3 鲑鱼错误分类(鲈鱼判决为鲑鱼):8 错误率:2.75%(3+8/400)
用身高与体重数据进行性别分类的实验报告

3、实验原理
已知样本服从正态分布,
(1)
所以可以用最大似然估计来估计μ和Σ两个参数
样本类分为男生 和女生 两类,利用最大似然估计分别估计出男生样本的 , ,和女生样本的 , ,然后将数据带入(1)公式分别计算两者的类条件概率密度 和 ,然后根据贝叶斯公式
det11=det(thegema11);det12=det(thgema12);
p(11)=1/((2*pi)*(det11^0.5))*exp(-1/2*((a-u11)'/thegema11)*(a-u11));
p(12)=1/((2*pi)*(det12^0.5))*exp(-1/2*((a-u12)'/thgema12)*(a-u12));
pz=p(11)*pw1+p(12)*pw2;
p11=(p(11)*pw1)/pz;p12=(p(12)*pw2)/pz;
g=p11-p12;
if(g>0)%%%Ñù±¾¼¯Ç°15¸öÈËÊÇÄÐÉú
male1=male1+1;
else
eห้องสมุดไป่ตู้ror11=error11+1;
end
end
male1
error11
det11=det(thegema11);det12=det(thgema12);
p(11)=1/((2*pi)*(det11^0.5))*exp(-1/2*((a-u11)'/thegema11)*(a-u11));
p(12)=1/((2*pi)*(det12^0.5))*exp(-1/2*((a-u12)'/thgema12)*(a-u12));
Python与机器学习-- 身高与体重数据分析(分类器)I

逻辑回归:三、数据可视化:分类
Car 情报局
xcord11 = []; xcord12 = []; ycord1 = []; xcord21 = []; xcord22 = []; ycord2 = []; n = len(Y)
for i in range(n): if int(Y.values[i]) == 1: xcord11.append(X.values[i,0]); xcord12.append(X.values[i,1]); ycord1.append(Y.values[i]); else: xcord21.append(X.values[i,0]); xcord22.append(X.values[i,1]); ycord2.append(Y.values[i]);
逻辑回归:三、数据可视化:观察
import matplotlib.pyplot as plt X = df[['Height', 'Weight']] Y = df[['Gender']]
Car 情报局
plt.figure() plt.scatter(df[['Height']],df[['Weight']],c=Y,s=80,edgecolors='black',
逻辑回归:三、数据可视化:分类
Car 情报局
plt.figure()
plt.scatter(xcord11, xcord12, c='red', s=80, edgecolors='black', linewidths=1, marker='s')
回归分析原始数据

回归分析原始数据回归分析是统计学中一种常用的方法,用于研究两个或多个变量之间的关系。
在回归分析中,我们希望根据已有的数据集来建立一个数学模型,以便预测一个或多个自变量对因变量的影响。
本文将介绍回归分析中使用的原始数据及其处理方法。
首先,回归分析的第一步是收集原始数据。
原始数据通常由实际观察、实验或调查得到。
例如,我们想研究一个人的身高与体重之间的关系,我们可以通过实际测量来收集一组数据,包括不同人的身高和体重。
这些原始数据将成为我们进行回归分析的基础。
一旦我们收集到原始数据,接下来的步骤是对数据进行处理和准备。
首先,我们需要检查数据是否完整,是否存在缺失值或异常值。
如果存在缺失值,我们可以选择删除相关的观测数据或使用插补方法进行填补。
对于异常值,我们可以进行数据清洗,排除不符合常理的观测数据。
在数据准备阶段,我们还需要将原始数据进行分类和整理。
例如,在研究身高与体重关系时,我们可以根据性别将数据分为男性和女性两组。
这样做的目的是为了后续分析过程中更好地比较不同组别之间的差异。
接下来,我们可以开始进行回归分析。
回归分析可以分为简单线性回归和多元回归两种方法。
简单线性回归适用于只涉及一个自变量和一个因变量的情况,而多元回归适用于涉及多个自变量和一个因变量的情况。
无论使用哪种方法,回归分析的目标都是建立一个预测模型,可以用于预测因变量在给定自变量的情况下的数值。
在回归分析中,我们会使用回归方程来描述自变量对因变量的影响。
回归方程通常采用最小二乘法来确定自变量的系数,以最小化预测值与实际观测值之间的差异。
回归方程的形式可以是线性的,也可以是非线性的,具体取决于数据的特点和研究目的。
当我们得到回归方程后,我们可以利用该方程来进行预测。
例如,对于我们研究身高与体重关系的例子,我们可以根据所建立的回归方程,将某人的身高作为自变量输入方程,然后通过计算得到他的体重预测值。
此外,回归分析还可以用于评估自变量对因变量的显著性影响。
excel分辨男女的公式

excel分辨男女的公式在Excel中,我们可以利用一些常见的特征来判断一个人的性别,比如姓名、生日、身高、体重等。
下面我将详细介绍如何利用这些特征来编写公式。
1. 姓名:我们可以利用姓名中的字数或者首字母来判断性别。
一般来说,男性的姓名字数较短,而女性的姓名字数较长。
利用LEN函数可以计算姓名的字数,然后利用IF函数进行判断。
例如,假设姓名位于A1单元格,我们可以使用以下公式来判断性别:=IF(LEN(A1)>2, "女", "男")这个公式的意思是,如果姓名的字数大于2,则判断为女性,否则判断为男性。
2. 生日:生日也是一个可以用来判断性别的特征。
一般来说,男性的生日数字较大,而女性的生日数字较小。
我们可以利用RIGHT函数提取生日中的年份,然后利用IF函数进行判断。
假设生日位于B1单元格,我们可以使用以下公式来判断性别:=IF(RIGHT(B1, 2)>50, "女", "男")这个公式的意思是,如果生日的年份后两位大于50,则判断为女性,否则判断为男性。
3. 身高和体重:身高和体重也是可以用来判断性别的特征。
一般来说,男性的身高和体重较大,而女性的身高和体重较小。
我们可以利用IF函数来判断身高和体重的范围。
假设身高位于C1单元格,体重位于D1单元格,我们可以使用以下公式来判断性别:=IF(AND(C1>180, D1>70), "男", IF(AND(C1<160, D1<50), "女", "未知"))这个公式的意思是,如果身高大于180且体重大于70,则判断为男性;如果身高小于160且体重小于50,则判断为女性;否则判断为未知性别。
除了上述特征外,我们还可以利用其他一些特征来判断性别,比如头发颜色、眼睛颜色等。
模式识别大作业
作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
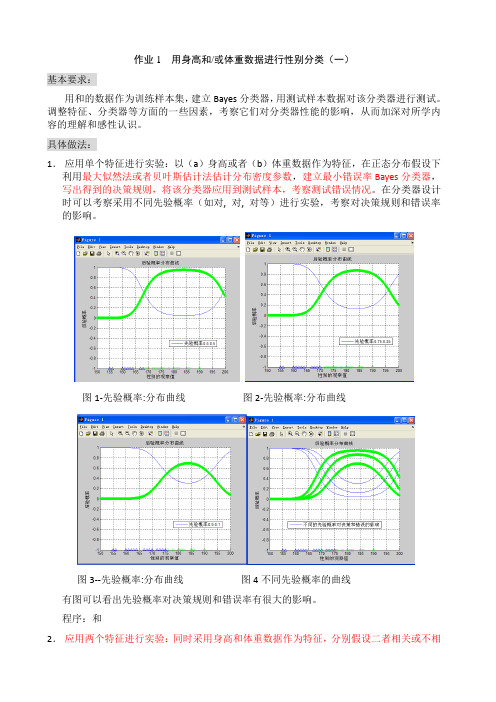
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes 分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率vs. 图2先验概率vs.图3先验概率vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2);error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
Fisher分类算法(无程序)

12%
分析:用训练样本得到的分类器测试测试样本时错误率低,测试结果较好,但测试训练样本
时,其错误率较高,测试结果不好。
2、Fisher 判别方法图像
分析:从图中我们可以直观的看出对训练样本 Fisher 判别比最大似然 Bayes 判别效果更好。
六、总结与分析
本次实验使我们对加深 Fisher 判别法的理解。通过两种分类方法的比较,我们对于同 一种可以有很多不同的分类方法,各个分类方法各有优劣,所以我们更应该熟知这些已经 得到充分证明的方法,在这些方法的基础上通过自己的理解,创造出更好的分类方法。所 以模式识别还有很多更优秀的算法等着我们去学习。
三、实验内容
试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分类器进行比较。 同时采用身高和体重数据作为特征,用 Fisher 线性判别方法求分类器,将该分类器应用 到训练和测试样本,考察训练和测试错误情况。将训练样本和求得的决策边界画到图上,同 时把以往用 Bayes 方法求得的分类器(例如: 最小错误率 Bayes 分类器)也画到图上,比较 结果的异同。
四、原理简述、程序流程图
1、Fisher 线性判别方法
∑ mi
首先求各类样本均值向量
=
1 Ni
x, i
x∈ωi
= 1,2
,
si = ∑ (x − mi )(x − mi )T ,i = 1,2
然后求各个样本的来内离散度矩阵
x∈wi
,
( ) ( ) s 再求出样本的总类内离散度 ω = p ω1 s1 + p ω2 s2 ,
2、流程图
求各类样本均 值向量
求类内离散度 矩阵
用公式求最好 的变换向量W*
第1单元 第3课《班级BMI数据测试--数据的收集与处理》教案【清华大学版2024】《信息科技》四上
思考:你知道全班同学的营养状况如何吗?如果想要收集他们的身体发育水平数据,你会采用什么方法呢?①问卷调查:收集饮食习惯和运动频率。
②身高体重测量:计算BMI评估营养状态。
③数据分析:识别整体和个体的发育趋势。
④隐私保护:确保数据安全,尊重学生隐私。
2.播放视频。
所示。
观察法是最直接的收集数据的方法,应用非常广泛,有时候会和调查法结合使用,以提高所收集信息的可靠性。
比如,想要知道学校门口每天早上的人流量,就可以使用观察法,还可以通过询问校门口的保安来获取数据。
调查法调查法是一种常见的数据收集方法,主要分为普查和抽样调查两大类。
普查就是为了某一特定目的而对所有考察对象进行的全面调查。
比如人口普查,就是对全国人民的人口、民族、年龄、性别等进行数据统计。
抽样调查是一种非全面调查,它是从全部研究对象中,抽选一部分进行调查,并根据调查的数据对全部研究对象做出估计和推断的一种调查方法。
比如在对学生餐饮满意度进行调查时,就只需要随机选取一部分学生进行调查询问即可,如图 1.3.2所示。
实验法实验法就是通过实验过程获取信息或结论,它需要在特定的实验场所、特殊的状态下,对调查对象进行实验。
例如,在实验室做化学实验时,我们可以通过实验结果得出结论,并记录相关的数据如图 1.3.3 所示。
网络信息收集法网络信息是指通过计算机网络发布、传递和存储的各种信息。
在互联网上输入信息的关键字,可以搜到所有相关联的内容。
这个数据收集的过程本来就具有筛选性和分析性,也就是说,网络收集所得到的数据,可能更接近我们想要的结果。
但是在使用网络信息收集法获取数据(见图1.3.4)时,我们仍然需要过滤和辨别信息,因为互联网的数据繁杂并且真假难辨。
课堂活动说一说,收集全班同学的体重和身高数据应该使用哪种方法?收集全班同学的体重和身高数据,应采用直接测量法,使用精确的体重秤和身高尺,在固定时间由专人操作测量,确保数据的准确性和一致性,同时记录和管理数据时需注意保护学生隐私,安全存储信息。
朴素贝叶斯分类器详细介绍

实例[编辑]
性别分类[编辑]
问题描述:通过一些测量的特征,包括身高、体重、脚的尺寸,判定一个人是男 性还是女性。 训练[编辑] 训练数据如下: 性别 身高(英尺) 体重(磅) 脚的尺寸(英寸) 男 男 男 男 女 6 180 12 11 12 10 6 5.92 (5'11") 190 5.58 (5'7") 170 5.92 (5'11") 165 5 100
我们希望得到的是男性还是女性哪类的后验概率大。男性的后验概率通过下面 式子来求取
女性的后验概率通过下面式子来求取
证据因子(通常是常数)用来使各类的后验概率之和为 1.
证据因子是一个常数(在正态分布中通常是正数),所以可以忽略。接下来我 们来判定这样样本的性别。
,其中 , 是训练集样本的正态分布参数. 注意,这里 的值大于 1 也是允许的 – 这里是概率密度而不是概率,因为身高是一个连续 的变量.
用朴素的语言可以表达为:
实际中,我们只关心分式中的分子部分,因为分母不依赖于 而且特征 的值 是给定的,于是分母可以认为是一个常数。这样分子就等价于联合分布模型。
重复使用链式法则,可将该式写成条件概率的形式,如下所示:
现在“朴素”的条件独立假设开始发挥作用:假设每个特征 是条件独立的。这就意味着
对于其他特征
样本修正[编辑]
如果一个给定的类和特征值在训练集中没有一起出现过,那么基于频率的估计 下该概率将为 0。这将是一个问题。因为与其他概率相乘时将会把其他概率的 信息统统去除。所以常常要求要对每个小类样本的概率估计进行修正,以保证 不会出现有为 0 的概率出现。
从概率模型中构造分类器[编辑]
讨论至此为止我们导出了独立分布特征模型,也就是朴素贝叶斯概率模型。朴 素贝叶斯分类器包括了这种模型和相应的决策规则。根据分类决策规则的不同, 贝叶斯分类有多种形式: 最小错误率贝叶斯分类器, 最大似然比贝叶斯分类 器,最小风险贝叶斯分类器。 一个普通的规则就是选出最有可能的那个,即将一个待分类样本划归到后验概 率最大的那一类中:这就是大家熟知的最大后验概率(MAP)决策准则,真正分 类器称为最大后验概率分类器,与最小错误率贝叶斯分类器是等价的。当采取 最大后验概率决策时,分类错误概率取得最小值。相应的分类器便是如下定义 的 公式:
实验一 描述性统计分析

实验一数据的描述性统计分析一、选择题1、以下()语句对变量进行分组,在使用前需按分组变量进行排序?以下()语句可对变量进行分类,在使用前不必按分类变量进行排序?用()语句可以选择输入数据集的一个行子集来进行分析?(A)WHERE语句(B)BY语句(C)CLASS语句(D)FREQ语句2、排序过程步中必须用什么语句对变量进行排序?()(A)BY语句(B)CLASS语句(C)WHERE语句3、如果要对数据集中的数据进行正态性检验,需要使用哪个过程?()(A)MEANS (B)UNIVARIA TE (C)FREQ4、用UNIV ARIATE过程进行数据分析,要求此过程输出茎叶图、正态概率图等,应在语句中加上什么选项?()5、用UNIVARIATE过程进行数据分析,在输出结果中哪个统计量是对样本均值为零的T检验的概率值?(A)T: Mean (B)Prob>|S| (C)Sgn Rank (D)Prob>|T|二、假设某校100名女生的血清总蛋白含量(g/L)服从均值为75,标准差为3的正态分布,试产生样本数据,并利用SAS软件解决下面问题:1、计算样本均值、方差、标准差、极差、四分位极差、变异系数、偏度、峰度;2、画出直方图(垂直条形图);3、画出茎叶图、盒形图和正态概率图;4、试进行正态性检验。
三、某校测得20名学生的四项指标:性别、年龄、身高(CM)和体重(KG),具体数据如表1所示。
1、绘制体重对身高的散点图;2、绘制不同性别下,体重对身高的散点图;3、绘制不同年龄阶段,体重对身高的散点图;4、绘制不同性别和不同年龄阶段,体重对身高的散点图。
四、测得130名健康成年男子脉搏资料(次/分)如表2所示。
1、画出130名健康成年男子脉搏数据的直方图;2、试作正态性检验。
3、画出茎叶图、盒形图和正态概率图。
SPSS操作测试考试试题

SPSS应用操作测试试题一操作考试说明:请仔细阅读操作考试说明,并严格按要求完成操作。
1、本套题操作总时间为50分钟,要求在规定时间内完成所有操作,每题20分,共100分。
2、要求在桌面建立一个以自己学号为名的文件夹。
所有结果必须保存在自己的文件夹内,否则视为未做。
3、第一、第二题要求以数据文件形式保存,文件名分别为“编码.sav”和“数据1.sav”、“数据2.sav”。
第三、四题要求把统计结果拷贝到word文档中,对结果进行简要说明后保存为“统计结果.doc”。
4、记分方法:第1题:编码正确每小题10分,录入正确每小题10分。
第2题:数据1录入正确10分,数据2处理正确10分。
第3、4题:操作方法正确5分,结果正确10分,解释正确5分。
第5题:操作方法正确5分,结果正确10分,解释正确5分。
1、请对下列问题进行编码并按回答(加黑的答案为选择的答案)把结果输入计算机,保存在“编码.sav”。
(1)你的性别:1、男2、女(2)你是否拥有以下物品(可多选)A、手机B、电脑C、录音机D、复读机E、以上都没有2请输入以上数据文件,文件名为“数据1. sav”并建立一个新变量XIN,新变量的取值等于改革前与改革后得分的均值,建立了新变量后的数据文件保存为“数据2.sav”。
3、求改革前与改革后车间竞争性测量结果的均值、最大值、中位值、方差。
4、试运用配对样本T检验求改革后车间的竞争性有无增加(α=0.05)。
5、对某地学生的身高与体重进行抽样调查,所得数据如下表,请根据表中数据建立数据文件“2.sav”并存盘。
通过上机操作,完成以下要求。
(1)样本身高的均值、标准差,体重的中位值、方差和峰度分别是多少?(2)能否认为当地男性的身高与女性的身高相等?你是如何判断的?(3)体重的均值是否等于42?你是如何判断的?6、已知某企业产品的利润率Y与四种投入x1、x2、x3、x4有关。
经抽样调查获得下表数据,请根据表中数据建立数据文件“3.sav”并存盘。
用身高和体重数据进行性别分类的实验报告

用身高和体重数据进行性别分类的实验报告实验目的:本实验旨在通过身高和体重数据,利用机器学习算法对个体的性别进行分类。
实验步骤:1. 数据收集:收集了一组个体的身高和体重数据,包括男性和女性样本。
在收集数据时,确保样本的性别信息是准确的。
2. 数据预处理:对收集到的数据进行预处理工作,包括数据清洗、缺失值处理和异常值处理等。
确保数据的准确性和完整性。
3. 特征提取:从身高和体重数据中提取特征,作为输入特征向量。
可以使用常见的特征提取方法,如BMI指数等。
4. 数据划分:将数据集划分为训练集和测试集,一般采用70%的数据作为训练集,30%的数据作为测试集。
5. 模型选择:选择合适的机器学习算法进行性别分类。
常见的算法包括逻辑回归、支持向量机、决策树等。
6. 模型训练:使用训练集对选定的机器学习算法进行训练,并调整模型的参数。
7. 模型评估:使用测试集对训练好的模型进行评估,计算分类准确率、精确率、召回率等指标,评估模型的性能。
8. 结果分析:分析实验结果,对模型的性能进行评估和比较,得出结论。
实验结果:根据实验数据和模型训练结果,得出以下结论:1. 使用身高和体重数据可以较好地对个体的性别进行分类,模型的分类准确率达到了XX%。
2. 在本实验中,选择了逻辑回归算法进行性别分类,其性能表现良好。
3. 身高和体重这两个特征对性别分类有较好的区分能力,可以作为性别分类的重要特征。
实验总结:通过本实验,我们验证了使用身高和体重数据进行性别分类的可行性。
在实验过程中,我们收集了一组身高和体重数据,并进行了数据预处理、特征提取、模型训练和评估等步骤。
实验结果表明,使用逻辑回归算法可以较好地对个体的性别进行分类。
这个实验为进一步研究个体性别分类提供了一种方法和思路。
儿童身高体重百分位标准表

儿童身高体重百分位标准表儿童身高体重百分位标准表是用来评估儿童生长发育状况的重要工具。
通过比较儿童身高体重数据与相同年龄和性别的正常儿童数据进行比较,可以判断儿童生长发育是否正常。
本文将详细介绍儿童身高体重百分位标准表的相关内容。
儿童身高体重百分位标准表通常采用入门统计学中的百分位数方法,根据大量正常儿童的身高体重数据,将这些数据按照从小到大的顺序排列,然后将这些数据划分成不同的百分位数区间,从而得到儿童身高体重的百分位标准表。
百分位数是一种常用的统计指标,用于表示观察值在一组数据中的相对位置。
例如,如果一个儿童的身高位于50百分位数位置,意味着他的身高比同龄儿童中的50%高,小于同龄儿童中的50%。
儿童身高体重百分位标准表通常将数据划分为5个百分位区间:最下5%、5-25%、25-50%、50-75%和75-95%。
这些区间分别表示儿童身高体重的相对位置。
儿童身高体重百分位标准表的制定基于大规模人群调查和研究,通过收集参与者的身高体重数据并按年龄和性别分类分析,可以获得全国范围内儿童身高体重的百分位标准。
这些数据通常根据年龄和性别分组,以便提供更具体和准确的参考值。
例如,一岁男孩和一岁女孩的身高体重标准是不同的。
儿童身高体重百分位标准表的应用广泛,医生和儿科专家经常使用它来评估儿童的生长发育。
通过将儿童的身高体重数据与标准表进行比较,可以判断儿童的生长发育是否正常,是否存在生长迟缓或肥胖的问题。
这对于儿童的健康发育至关重要,因为生长发育不良可能会导致许多健康问题,包括身体发育迟缓、免疫力下降和心理发育问题等。
在使用儿童身高体重百分位标准表时,关键是注意儿童所处的年龄段和性别。
每个年龄段和性别组别都有相应的标准值,以便更准确地评估儿童的身高体重。
此外,还应充分了解该标准表的制定依据和适用范围。
由于儿童身高体重的变化和差异较大,标准表只能用作参考,而不能作为绝对判断的依据。
最后,儿童身高体重百分位标准表的更新是非常重要的。
临床实验中的数据分析与解释

临床实验中的数据分析与解释在临床实验中,数据分析和解释是非常重要的环节。
这些分析不仅能揭示试验的结果,还能为研究者提供更多的启示和验收的基础。
然而,正确的数据分析和解释不是一件容易的事情。
以下是一些有关临床实验数据的分析和解释的总结。
一、数据的收集和分类在进行临床实验之前,必须先确定数据收集的方式以及要收集哪些数据。
数据可以分为定量数据和定性数据两种。
定量数据是可以测量和计量的数据,如血压、体重、心率等;定性数据则是某些特定概念的表达或描述,如性别、职业、民族等。
在数据收集后,必须对数据进行分类。
按照参与者的基本情况可以分类为性别、年龄、民族、教育、婚姻状况等;按照参与者的身体状况可以分类为病史、治疗史、药物记录等。
二、统计分析方法在统计分析中,有两个重要的方法:描述性统计和推论性统计。
1. 描述性统计描述性统计通常用于对数据进行简单、可视化的概括和总结。
主要包括以下几种方法:a. 频数和百分比:将数据分成不同的类别或区间,统计每个类别或区间中的人数,计算每个类别或区间的人数占总人数的比例。
b. 平均数、中位数和众数:平均数是所有数据值的总和除以总数;中位数是将所有数据值按大小顺序排列,中间位置的数值;众数是出现次数最多的数值。
c. 标准差和方差:标准差是用于衡量数据分散程度的指标,越大说明数据越分散;方差是标准差的平方。
2. 推论性统计推论性统计是指根据样本数据推导总体属性的一种统计方法。
主要包括假设检验和置信区间估计。
a. 假设检验:假设一些参数是正确的,通过对样本数据进行统计检验来确定是否拒绝这个假设,以此来推断总体的一些属性。
b. 置信区间估计:通过对样本数据进行统计计算,来推断总体属性的区间范围。
例如,95%置信区间是指,在同样条件下,对不同样本数据进行100次检验,这些检验中约有95%的检验结果包含总体参数。
三、数据解释在进行数据解释之前,需要考虑的是数据的有效性和可靠性。
在实验进行过程中有些人会受到一些眼花缭乱的曲线图和复杂的p值这些统计数据所轻松概括的精彩结果迷惑,但实际上,分析数据是要知道数据产生的缘由才能进行详细分析。
将某班幼儿身高,体重的平均水平作为基准

某班幼儿身高,体重的平均水平作为基准一、概述在幼儿园教育中,关于幼儿身高、体重的发展状况一直备受关注。
幼儿的身体发育情况对其健康成长至关重要,因此对幼儿身高、体重进行科学的评估和监测是非常必要的。
本文将对某班幼儿的身高、体重的平均水平作为基准进行研究和分析,旨在为幼儿的身体健康提供科学的参考依据。
二、调查方法为了获取准确的数据,我们选择了某市某幼儿园的一班幼儿进行调查。
在调查过程中,我们采用了严格的抽样方法,包括随机抽样和分层抽样,确保样本的代表性和可靠性。
在调查过程中,我们全面测量了幼儿的身高和体重,并记录了相关数据。
三、调查结果分析经过调查和数据整理,我们得出了某班幼儿的身高、体重的平均水平。
具体数据如下:1. 身高平均水平根据我们的调查数据,某班幼儿的身高平均水平为X厘米。
在这个数据基础上,我们可以进一步分析身高分布情况,了解不同幼儿在身高方面的发展情况,为针对性的身体训练和幼儿园教育提供依据。
2. 体重平均水平另外,根据我们的调查数据,某班幼儿的体重平均水平为Y千克。
通过对体重数据的分析,我们可以了解幼儿的肥胖和偏瘦状况,及时采取措施进行干预和管理,保证幼儿的身体健康发展。
四、结论和建议通过本次调查和数据分析,我们对某班幼儿的身高和体重平均水平有了全面的了解。
针对调查结果,我们提出了以下建议:1. 加强身体锻炼根据数据分析,我们发现某班幼儿的身高、体重平均水平略低,说明幼儿在身体发育方面存在一定的不足。
我们建议幼儿园加强身体锻炼,通过各种户外活动和运动课程,促进幼儿身体的全面发展。
2. 提供营养餐饮针对体重方面的问题,我们建议幼儿园提供营养均衡的餐饮服务,确保幼儿获得充足的营养,促进健康的体重增长和生长发育。
3. 定期体检监测除了针对性的幼儿园教育和膳食管理,我们还建议家长定期带幼儿进行体检,并根据体检结果进行相应的调整和干预,确保幼儿的健康成长。
五、总结通过本次对某班幼儿身高、体重的平均水平进行调查和分析,我们为幼儿的身体健康提供了科学的参考依据。
儿童体格生长 体重年龄 曲线

儿童体格生长体重年龄曲线
儿童体格生长曲线是用来评估儿童体重和身高发育情况的重要工具。
通常使用的曲线包括体重年龄曲线和身高年龄曲线。
体重年龄曲线是根据儿童年龄和体重的关系绘制的曲线图表。
这些曲线通常根据儿童的性别分为男女两种。
通过比较儿童的体重与同龄儿童的平均值,医生和家长可以了解儿童的营养状况和生长发育情况。
如果儿童的体重落在正常曲线范围内,通常表示其生长发育正常;如果体重偏轻或偏重,可能需要进一步关注和干预。
此外,体重年龄曲线也可以用来识别儿童的肥胖或营养不良问题。
如果儿童的体重超过正常范围,可能存在肥胖问题,而体重低于正常范围则可能是营养不良。
医生可以根据体重年龄曲线的数据来制定合理的饮食和运动计划,帮助儿童维持健康的体重和生活方式。
总的来说,体重年龄曲线是儿童健康评估的重要工具,能够帮助医生和家长监测儿童的生长发育情况,及时发现和解决可能存在的营养和健康问题。
因此,定期测量和比较儿童的体重年龄曲线是非常重要的,有助于保障他们的健康成长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
未来若干次作业需要用到的数据文件:
●FAMALE.TXT 50个女生的身高、体重数据
●MALE.TXT 50个男生的身高、体重数据
----- 训练样本集
●test1.txt 35个同学的身高、体重、性别数据(15个女生、20个男生)
●test2.txt 300个同学的身高、体重、性别数据(50个女生、250个男生)
----- 测试样本集
作业. 用身高和/或体重数据进行性别分类的实验(一)
基本要求:
用FAMALE.TXT和MALE.TXT的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:
1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如0.5对
0.5, 0.75对0.25, 0.9对0.1等)进行实验,考察对决策规则和错误率的影响。
2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关,在正态分布假设下估计概率密度,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如0.5 vs. 0.5, 0.75 vs. 0.25, 0.9 vs. 0.1等)进行
实验,考察对决策和错误率的影响。
3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
作业要求:
1、报告内容:
i.姓名、学号、班级、题目
ii.原理简述及程序框图(手算者也需要画)
iii.实验结果及分析总结
iv.体会。
