曲线拟合实验报告
曲线拟合实验报告[优秀范文5篇]
![曲线拟合实验报告[优秀范文5篇]](https://img.taocdn.com/s3/m/ed56c4cd0342a8956bec0975f46527d3240ca6e1.png)
曲线拟合实验报告[优秀范文5篇]第一篇:曲线拟合实验报告数值分析课程设计报告学生姓名学生学号所在班级指导教师一、课程设计名称函数逼近与曲线拟合二、课程设计目的及要求实验目的: ⑴学会用最小二乘法求拟合数据的多项式,并应用算法于实际问题。
⑵学会基本的矩阵运算,注意点乘与叉乘的区别。
实验要求: ⑴编写程序用最小二乘法求拟合数据的多项式,并求平方误差,做出离散函数与拟合函数的图形;⑵用MATLAB 的内部函数polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差,并用MATLAB的内部函数plot作出其图形,并与(1)结果进行比较。
三、课程设计中的算法描述用最小二乘法多项式曲线拟合,根据给定的数据点,并不要求这条曲线精确的经过这些点,而就是拟合曲线无限逼近离散点所形成的数据曲线。
思路分析 : 从整体上考虑近似函数)(x p 同所给数据点)(i iy x , 误差i i iy x p r -=)(的大小,常用的方法有三种:一就是误差i i iy x p r -=)(绝对值的最大值im ir≤≤ 0max ,即误差向量的无穷范数;二就是误差绝对值的与∑=miir0,即误差向量的 1成绩评定范数;三就是误差平方与∑=miir02的算术平方根,即类似于误差向量的 2 范数。
前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑 2 范数的平方,此次采用第三种误差分析方案。
算法的具体推导过程: 1、设拟合多项式为:2、给点到这条曲线的距离之与,即偏差平方与:3、为了求得到符合条件的 a 的值,对等式右边求偏导数,因而我们得到了:4、将等式左边进行一次简化,然后应该可以得到下面的等式5、把这些等式表示成矩阵的形式,就可以得到下面的矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑∑∑∑∑∑∑∑∑=====+==+====niininiiknikinikinikinikiniiniinikiniiyyyaax x xx x xx x11i11012111111211 1an MMΛM O M MΛΛ 6.将这个范德蒙得矩阵化简后得到⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡n kkn nkkyyyaaax xx xx x M MΛM O M MΛΛ21102 21 1111 7、因为 Y A X = * ,那么 X Y A / = ,计算得到系数矩阵,同时就得到了拟合曲线。
实验数据的拟合

一、实验目的
学会MATLAB软件中利用给定数据进行拟合运算的 方法。
二、相关知识
在上一个实验中,我们已经讨论了在生产和科学实 验中,需要利用插值和拟合的场合,本实验讨论拟 合。在MATLAB中,拟合也有相应的函数来完成。 我们首先来讨论拟合的数学定义。
已知离散点上的数据集 {(x1, y1), (x2, y2 ), , (xn, yn )},即 已知在点集 {x1, x2 , , xn}上的函数值 {y1, y2, , yn} , 构造一个解析函数 f (x)(其图形为一曲线),使 f (x)
T/C 31 32 31 29 27 25 24 22 20 18 17 16
考虑下列类型函数,得到残差。并作图比较效果: (1)二次多项式函数; (2)三次多项式函数; 3.简述插值与拟合的区别。 4.完成实验报告。
2.假定某天的气温变化记录如下表,试用最小二 乘法找出这一天的气温变化规律。
t/h 0 1 2 3 4 5 6 7 8 9 10 11 12
T/C 15 14 14 14 14 15 16 18 20 22 23 25 28
t/h 13 14 15 16 17 18 19 20 21 22 23 24
c=lsqcurvefit(fun,c0,x,y)
说明:polyfit求出已知数据x,y的n阶拟合多项式
f (x) 的系数p,x,y都是向量,x的分量必须单调。
lsqcurvefit用作各种类型曲线的拟合,用最小二乘 法寻找符合经验公式的最优曲线。可用非线性函数 的数据拟合。
例1:求如下给定数据的拟合曲线, x=[0.5,1.0,1.5,2.0,2.5,3.0], y=[1.75,2.45,3.81,4.80,7.00,8.60]。
计算方法实验三 不同曲线拟合比较讲解

计算方法C(2014-2015-2)【不同拟合曲线的比较】实验报告学号:******* 姓名:*****8课程教师:戴克俭教学班级:无实验三 不同拟合曲线的比较实验目的:掌握曲线拟合和最小二乘法的思想,比较不同拟合曲线的精度。
实验题目:下表给出了我国1949~1984年间的一些人口数据,分别按下述方案求最小二乘拟合函数及其偏差平方和Q ,求1969年人口并预测方案I 拟合函数取如下形式的三次多项式3322101)(x a x a x a a x F +++=方案II 用离散正交多项式求三次拟合多项式)(2x F 方案III 用离散正交多项式求四次拟合多项式)(3x F 方案IV 拟合函数为如下形式的函数10sin)(4xb a x F π+=算法流程图如下:i、方案1 ii、方案2iii、方案3iv、方案4源程序清单如下:i、方案1图1:求3次多项式图2:求偏差ii、方案2图3:求3次多项式iii、方案3图4:求4次多项式图5:求sin(π*X/10)图6:nafit函数M文件图7:命令行输入运算结果如下:⑴、方案1P(X)=745181.85611415-1135.160413656X+0.576328328X^2-0.000097520X^3 P(1969)= 11.4973750142380600 亿P(2000)=14.3408021503128110亿图8 拟合曲线:蓝色线表示拟合曲线P(X),红色线表示真实数据误差很大⑵、方案2P(X)=732370.3125-1115.615844727X+0.566389024X^2-0.000095836X^3P(1969)= 4.1277828774182126亿P(2000)= 6.7190460005076602亿图9 拟合曲线:蓝色线表示拟合曲线P(X),红色线表示真实数据误差很大⑶、方案3P(X)=30212.5+320.9404296875X-0.5357236862X^2+0.0002799341X^3-0.000000048X^4P(1969)= 627.7665998683078200 亿P(2000)= 671.4145749998278900 亿图10 拟合曲线:蓝色线表示拟合曲线P(X),红色线表示真实数据蓝色线的数值全是上百亿与实际严重不符误差巨大⑷、方案4P(X)=0.2414+7.7753sin(π*X/10)P(1969)= 2.6441006951177228 亿P(2000)= 0.2413990828363674 亿图11 拟合曲线:蓝色线表示拟合曲线P(X),整体看该曲线具有和sin近似的周期性质,与实际数据不是很符合。
黄酮规范标准曲线绘制的实验报告

黄酮规范标准曲线绘制的实验报告-/黄酮标准曲线绘制的实验报告1.总黄酮的测定1.1 实验仪器电⼦天平AR2140;紫外可见分光光度计UV2754;型数控超声波清洗器KQ3200DB;超级恒温槽;Rotavapor R200 旋转蒸发仪 ;FD21C250 冷冻⼲燥机21.2 试剂及药品芦丁标准品硝酸铝国产分析纯(配成5 %)亚硝酸钠国产分析纯(配成10 %)氢氧化钠国产分析纯配成(配成1mol/L)95%⼄醇,⽆⽔⼄醇国产分析纯(配成60%⼄醇 50%⼄醇)DPPH·(2,2-diphenyl-1-picrylhydrazyl,⼆苯代苦味肼基⾃由基)Vc(Ascrobic acid,维⽣素 C,抗坏⾎酸)没⾷⼦酸对照品:基准纯。
⼤青叶⼦采摘于海南⼤学东坡湖畔1.3实验步骤:1.3.1准备⼯作及波长的确定样品60℃烘⼲粉碎机粉碎,过20⽬筛,装⼊试剂瓶中备⽤。
根据查阅⽂献总黄酮在波长为510nm处吸收值最⼤。
1.3.2参照品芦丁标准溶液的制备精密称取120 ℃⼲燥⾄恒重的芦丁标准样品37.5mg置于100mL烧杯中,⽤60%⼄醇溶解后定容⾄25mL 容量瓶中,摇匀,即可得1.5mg/mL的芦丁标准溶液。
1.3.3标准品的测量及绘制标准曲线精密吸取芦丁标准溶液0.0、1.0、2.0、3.0、4.0、5.0、6.0mL ,分别置于、0.3mg/ml、0.15mg/ml、0.0mg/ml容量瓶中,并定容⾄刻度线。
得到10mL-/、0.6mg/ml、0.75mg/ml、0.45mg/ml0.9mg/ml的标准品溶液,分别取1ml到试管中各加5 %亚硝酸钠溶液0.3mL 摇匀,放置6min ,加10%硝酸铝溶液0.3mL 摇匀,放置6min ,加1mol /L氢氧化钠溶液4mL ,再⽤60%⼄醇溶液稀释⾄刻度,放置15min 后,分别在510nm 处测定其吸光度(Tai,Cai&Dai,2011)。
实验二函数逼近与曲线拟合

《数值分析》课程设计实验报告实验二函数逼近与曲线拟合一、问题提出从随机的数据中找出其规律性,给出其近似表达式的问题,在生产实践和科学实验中大量存在,通常利用数据的最小二乘法求得拟合曲线。
在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量与时间t 的拟合曲线。
二、实验步骤先写出线性最小二乘法的M文件function c=lspoly(x,y,m)% x是数据点的横坐标组成的向量,y是纵坐标组成的向量% m是要构成的多项式的次数,c是多项式由高到低次的系数所组成的向量n=length(x);b=zeros(1:m+1);f=zeros(n,m+1);for k=1:m+1f(:,k)=x.^(k-1);enda=f'*f;b=f'*y';c=a\b;c=flipud(c);方法一:近似解析表达式为:y(t)=a1t+a2t2+a3t3第二步在命令窗口输入:lspoly([0,5,10,15,20,25,30,35,40,45,50,55],[0,1.27,2.16,2.86,3.44 ,3.87,4.15,4.37,4.51,4.58,4.02,4.64],2)回车得到:ans =0.0000-0.00520.26340.0178即所求的拟合曲线为y=-0.0052t2+0.2634t+0.0178在编辑窗口输入如下命令:>>x=[0,5,10,15,20,25,30,35,40,45,50,55];y=[0,1.27,2.16,2.86,3.44, 3.87,4.15,4.37,4.51,4.58,4.02,4.64];>> t=0:0.1:55;>> z=-0.0052*t.^2+0.2634*t+0.0178;>> plot(x,y,'ro',t,z);grid命令执行得到如下图(图2-1)0102030405060拟合多项式与数据点的关系方法二:假设近似表达式为:y(t)=c0+c1t+c2t2第一步在命令窗口输入:>>lspoly([0,5,10,15,20,25,30,35,40,45,50,55],[0,1.27,2.16,2.86,3. 44,3.87,4.15,4.37,4.51,4.58,4.02,4.64],2)回车得到:ans =-0.00240.20370.2305即所求的拟合曲线为y=-0.0024t2+0.2037t+0.2305在编辑窗口输入如下命令:>>x=[0,5,10,15,20,25,30,35,40,45,50,55];y=[0,1.27,2.16,2.86,3.44,3.87,4.15,4.37,4.51,4.58,4.02,4.64];>> t=0:0.1:55;>> z=-0.0024*t.^2+0.2037*t+0.2305;>> plot(x,y,'ro',t,z);grid命令执行得到如下图(图2-2)拟合多项式与数据点的关系三、实验结论在利用数据的最小二乘法求拟合曲线时,选取合适的近似表达式很重要,应通过不断的试验找出较为合适的近似表达式,这样才能尽可能的提高拟合精度。
数学实验报告数据拟合

实验报告一·实验指导书解读本次实验是通过两个变量的多组记录数据利用最小二乘法寻求两个变量之间的函数关系!两个变量之间的函数关系要紧有两种:一是线性关系(一次函数);二是非线性关系(非一次的其它一元函数)。
因此本实验做两件事:一是线性拟合(练习1);二是非线性拟合(练习2、3、4)。
练习2是用多项式函数拟合,练习3是用指数函数、对数函数、双曲函数、三角函数、分式有理多项式函数等初等函数拟合,练习4是用分段函数(非初等函数)拟合。
二、实验打算1.用线性函数拟合程序线性拟合曲线ft1可由如下mathematica程序求出:lianxi1biao= { {100,45} , {110,51} , { 120,54} , {130,61} , {140,66} , {150,70} , {160,74} , {170,78} , {180,85} , {190,89} }ft1=Fit[lianxi1biao,{1,x},x]gp = Plot [ ft1 , {x,100,190} , PlotStyle -> { RGBColor[1,0,0]} ]fp = ListPlot [ lianxi1biao,PlotStyle->{PointSize[],RGBColor[0,0,1]} ]Show[fp,gp]a= ;b= ;f[x_]=a*x+b;dareta=Sum[(lianxi1biao[[i,2]]-f[lianxi1biao[[i,1]]])^2,{i,1,10}]修改、补充程序:要说明拟合成效,要紧从形(大多数散点是不是在拟合曲线上或周围)与量(残差是不是小)!计算残差的程序:假设对两个变量的多组记录数据已有程序biao={{x1,y1},{x2,y2},…,{xn,yn}}而且通过Fit取得线性拟合函数y=ax+b咱们能够先概念函数(程序)f[x_]:=a*x+b再给出计算残差的程序dareta=Sum[(biao[[i ,2]]-f[biao[[i ,1]]])^2,{i ,1, n}]程序说明:biao[[i]]是提取表biao的第i行,即{xi,yi}biao[[i ,1]] 是提取表biao的第i行的第一个数, 即xibiao[[i ,2]] 是提取表biao的第i行的第一个数, 即yibiao[[i ,2]]-f[biao[[i ,1]]] 即yi-(a*xi+b)实验思路1、先对练习1的十组数据线性拟合,并从形与量看拟合成效;2、对练习1的十组数据中的九组数据线性拟合,并从形与量看拟合成效;3、对练习1的十组数据中的八组数据线性拟合,并从形与量看拟合成效;4、对练习1的十组数据中的七组数据线性拟合,并从形与量看拟合成效;5、对练习1的十组数据中的六组数据线性拟合,并从形与量看拟合成效。
逻辑斯蒂增长曲线-实验报告

逻辑斯蒂增长曲线-实验报告实验⽬的:1、使学⽣们认识到环境资源是有限的,任何种群数量的动态变化都受到环境条件的制约。
2、加深对逻辑斯蒂增长模型的理解与认识,深刻领会该模型中⽣物学特性参数r与环境因⼦参数----⽣态学特性参数K的重要作⽤。
3、学会如何通过实验估计出r、K两个参数和进⾏曲线拟合的⽅法。
实验原理:种群在资源有限环境中的数量增长不是⽆限的,当种群在⼀个资源有限的空间中增长时,随着种群密度的上升,对有限空间资源和其他⽣活必需条件的种内竞争也将加强,必然影响到种群的出⽣率和存活率,从⽽降低了种群的实际增长率,直⾄种群停⽌增长,甚⾄使种群数量下降。
逻辑斯蒂增长是种群在资源有限环境下连续增长的⼀种最简单的形式,⼜称阻滞增长。
种群在有限环境中的增长曲线是S型的,它具有两个特点:1、S型增长曲线有⼀个上渐近线,即S型增长曲线逐渐接近于某⼀特定的最⼤值,但不会超过这个最⼤值的⽔平,此值即为种群⽣存的最⼤环境容纳量,通常⽤K表⽰。
当种群⼤⼩到达K值时,将不再增长。
2、S型曲线是逐渐变化的,平滑的,⽽不是骤然变化的。
逻辑斯蒂增长的数学模型:dN dt =rN(K?NK)或dN dt =rN(1?NK)式中:dNdt—种群在单位时间的增长率;N—种群⼤⼩;t—时间;r—种群的瞬时增长率;K—环境容纳量;)—“剩余空间”,即种群还可以继续利⽤的增长空间。
逻辑斯蒂增长模型的积分式:N=K1+e a?rt式中:a—常数;e—常数,⾃然对数的底。
实验器材:恒温光照培养箱、实体显微镜、凹拨⽚、1000毫升烧杯、100毫升量筒、移液枪(50微升),1千⽡电炉、普通天平、⼲稻草、鲁哥⽒固定液、50毫升锥形瓶、纱布、橡⽪筋、⽩胶布条、封⼝膜、标记笔、计数器、⾃制的观测数据记录表格⽅法与步骤:1、准备草履⾍原液从湖泊或⽔渠中采集草履⾍。
2、制备草履⾍培养液(1)制取⼲稻草5g,剪成3~4厘⽶长的⼩段。
(2)在1000毫升烧杯中加⽔800毫升,⽤纱布包裹好⼲稻草,放⼊⽔中煮沸10分钟,直⾄煎出液呈现淡黄⾊。
vegan曲线拟合

vegan曲线拟合首先,我们需要明确什么是vegan曲线。
Vegan曲线是一种用于描述物种多样性与环境梯度之间关系的曲线。
它是基于生态学中的物种多样性指数和环境因子之间的关联关系而建立的。
通过拟合vegan曲线,我们可以了解物种多样性如何随着环境变化而变化。
在进行vegan曲线拟合时,我们通常会采用统计学方法,比如广义线性模型(Generalized Linear Models, GLMs)或广义可加模型(Generalized Additive Models, GAMs)。
这些模型可以帮助我们分析物种多样性与环境因子之间的非线性关系,并进行曲线拟合。
在进行拟合时,我们需要收集相关的数据,包括物种多样性指数和环境因子的测量数据。
然后,我们可以使用适当的统计软件(如R语言中的vegan包)来拟合vegan曲线。
拟合vegan曲线的过程中,我们需要考虑一些因素。
首先是选择合适的物种多样性指数,例如Shannon多样性指数、Simpson多样性指数或Pielou均匀度指数。
其次是选择合适的环境因子,这可能涉及到地理位置、土壤性质、气候因素等。
还需要注意数据的质量和样本数量,以及是否存在其他可能影响物种多样性的因素。
此外,在拟合vegan曲线时,我们还可以考虑使用非参数方法,如核密度估计或局部回归方法。
这些方法可以更好地捕捉到非线性关系,并提供更准确的拟合结果。
总结起来,vegan曲线拟合是一种用于研究物种多样性与环境梯度之间关系的方法。
它涉及到统计学方法和数据分析技巧,需要收集相关数据并选择合适的模型来进行拟合。
通过拟合vegan曲线,我们可以更好地理解物种多样性的分布和变化规律。
数值计算方法实验报告5―温度分布的曲线拟合

数值计算方法实验报告5―温度分布的曲线拟合本报告是关于温度分布的曲线拟合的,望对大家有所帮助!!!数值计算方法实验报告标题:温度分布的曲线拟合1.实验描述:在科学技术工程和实验中,经常需要从大量的实验数据中寻找拟合曲线,最简单的是一维情形(一元函数),此时数据的形式为x和y坐标的有序对,如:(x1,y1),...,(xN,yN),这里的横坐标{x}是明确的。
数值计算方法的目的之一是求解一个将自变量与因变量联系起来的拟合函数。
求解拟合函数的方法有多种,常见的方法有:线性最小二乘拟合、多项式拟合(最小二乘抛物线拟合)、样条插值拟合(三次样条拟合)、三角多项式拟合、贝塞尔曲线拟合这五种方法。
本次实验分别利用上述五种方法对一组温度数据进行拟合,通过拟合的结果比较这五种方法的优缺点(主要考虑误差)。
2.实验内容:已知某地区一天的温度数据如下:时间,p.m***-**********午夜***-********-********-*****温度时间,a.m***-**********正午***-********-********-*****温度分别利用:线性最小二乘拟合、多项式拟合(最小二乘抛物线拟合)、样条插值拟合(三次样条拟合)、三角多项式拟合、贝塞尔曲线拟合这五种方法对这组温度数据进行拟合,通过拟合的结果比较这五种方法的优缺点。
3.实验原理及分析:本报告是关于温度分布的曲线拟合的,望对大家有所帮助!!!①线性最小二乘拟合法:设{(x,y)}有N个点,其中横坐标{x}是确定的。
最小二乘拟合曲线为:kkk=1kk=1y=Ax+B,其系数满足如下正规方程:(∑x)A+(∑xk)B=∑xkyk 2kNNNNNk=1k=1(∑xk)A+NB=∑yk k=1k=1N解得:A=N∑xk=1Nk=1Nkyk Nxy2k∑xkNxN2=∑(xNNkx)(yk y),B=y Axk∑(xk=1kx)2其中:x=∑xk=1N,y=∑yk=1N线性最小二乘法的本质是:多元函数(均方根误差函数)求极值问题。
《数学实验》实验报告——最小二乘法
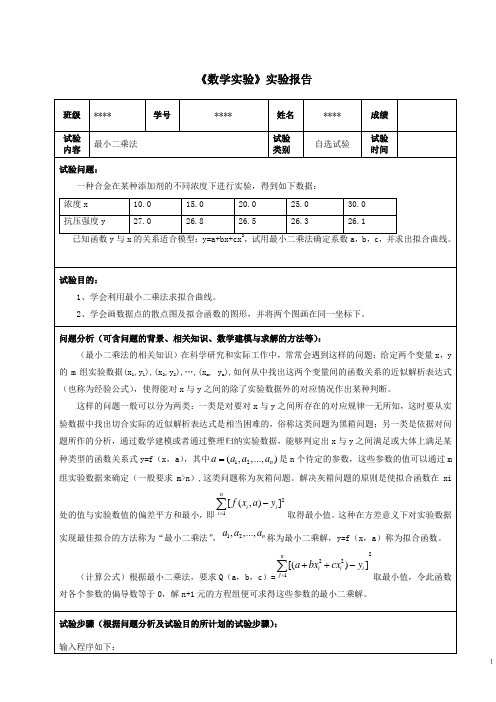
《数学实验》实验报告1x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02]];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25}];Show[t1,t2]首先得到a,b,c三个值: {{a->27.56,b->-0.0574286,c->0.000285714}}然后得到同一坐标系下的数据点散点图及拟合函数的图形:试验过程(含详细试验步骤、程序清单及异常情况记录等)输入以下mathematica语句求解参数a,b,c:运行后可得解:2为求得数据点的散点图及拟合函数的图形,输入以下语句,并将两个图画在同一坐标下:运行得:3在最开始时,我输入的程序是这样的:x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02],DisplayFunction->Identity];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25},DisplayFunction->Identity];Show[t1,t2, DisplayFunction->$ DisplayFunction]然而得到的结果没有图形(如下):我比照了老师的讲义,改动了“DisplayFunction->Identity”,可是,结果还是一样,没有图形。
实验一:拟合实验报告

实验报告
实验项目名称拟合实验所属课程名称数学建模实验类型综合性实验实验日期
班级
学号
姓名
成绩
【实验目的】
1、直观了解拟合基本内容。
2、掌握用数学软件求解拟合问题。
【实验原理】
1. 曲线拟合问题最常用的解法——线性最小二乘法的基本思路 第一步:先选定一组函数 r 1(x), r 2(x), …,r m (x), m<n, 令
f(x)=a 1r 1(x)+a 2r 2(x)+ …+a m r m (x) (1) 其中 a 1,a 2, …,a m 为待定系数.
第二步: 确定a 1,a 2, …,a m 的准则(最小二乘准则): 使n 个点(x i ,y i ) 与曲线 y=f(x) 的距离
i 的平方和最小 .
22
1211
2
1
1
(,,
)[()][()](2)
n
n
m i i i i i n
m
k k i i i k J a a a f x y a r x y δ======-=-∑∑∑∑
MATLAB 函数: p=polyfit(x,y,n) [p,s]= polyfit(x,y,n)
多项式曲线求值函数:polyval( ) 调用格式: y=polyval(p,x)
p 为幂次从高到低的多项式系数向量p 。
s 用于生成预测值的误差估计。
数据拟合与曲线拟合实验报告

数据拟合与曲线拟合实验报告【数据拟合与曲线拟合实验报告】1. 实验介绍数据拟合与曲线拟合是数学和统计学中非常重要的概念和方法。
在科学研究、工程技术和数据分析中,我们经常会遇到需要从一组数据中找到代表性曲线或函数的情况,而数据拟合和曲线拟合正是为了解决这一问题而存在的。
2. 数据拟合的基本原理数据拟合的基本思想是利用已知的一组数据点,通过某种数学模型或函数,找到一个能够较好地描述这组数据的曲线或函数。
常见的数据拟合方法包括最小二乘法、最小二乘多项式拟合、指数拟合等。
在进行数据拟合时,我们需要考虑拟合的精度、稳定性、可行性等因素。
3. 曲线拟合的实验步骤为了更好地理解数据拟合与曲线拟合的原理与方法,我们进行了一组曲线拟合的实验。
实验步骤如下:- 收集一组要进行拟合的数据点;- 选择合适的拟合函数或模型;- 利用最小二乘法或其他拟合方法,计算拟合曲线的参数;- 对拟合结果进行评估和分析;- 重复实验,比较不同的拟合方法和模型。
4. 数据拟合与曲线拟合的实验结果通过实验,我们掌握了数据拟合和曲线拟合的基本原理与方法。
在实验中,我们发现最小二乘法是一种简单而有效的数据拟合方法,能够较好地逼近实际数据点。
我们还尝试了多项式拟合、指数拟合等不同的拟合方法,发现不同的拟合方法对数据拟合的效果有着不同的影响。
5. 经验总结与个人观点通过这次实验,我们对数据拟合和曲线拟合有了更深入的理解。
数据拟合是科学研究和实践工作中不可或缺的一部分,它能够帮助我们从一堆杂乱的数据中提炼出有用的信息和规律。
曲线拟合的精度和稳定性对研究和实践的结果都有着重要的影响,因此在选择拟合方法时需要慎重考虑。
6. 总结在数据拟合与曲线拟合的实验中,我们深入探讨了数据拟合和曲线拟合的基本原理与方法,并通过实验实际操作,加深了对这一概念的理解。
数据拟合与曲线拟合的重要性不言而喻,它们在科学研究、工程技术和信息处理中发挥着重要的作用,对我们的日常学习和工作都具有重要的指导意义。
计算方法实验报告 拟合

南京信息工程大学实验(实习)报告
一、实验目的:
用最小二乘法将给定的十个点拟合成三次多项式。
二、实验步骤:
用matlab编制以函数为基的多项式最小二乘拟合程序,并用于对下列数据作三次多项式最小二乘拟合(取权函数wi=1)
给定直线方程为:y=1/4*x3+1/2*x2+x+1
三、实验结论:
最小二乘法:通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
一般地。
当测量数据的散布图无明显的规律时,习惯上取n次代数多项式。
程序运行结果为:
a =
0.9731
1.1023
0.4862
0.2238
即拟合的三次方程为:y=0.9731+1.1023x+0.4862*x2+0.2238*x3
x 轴
y 轴
拟合图
结论:
一般情况下,拟合函数使得所有的残差为零是不可能的。
由图形可以看出最小二乘解决了残差的正负相互抵消的问题,使得拟合函数更加密合实验数据。
优点:曲线拟合是使拟合函数和一系列的离散点与观测值的偏差平方和达到最小。
缺点:由于计算方法简单,若要保证数据的精确度,需要大量的数据代入计算。
ELISA实验报告(两篇)

引言概述:ELISA(酶联免疫吸附测定)是一种常用于测定抗体或抗原的定量和定性的快速、敏感和特异性的实验技术。
本文将继续讨论ELISA实验的一些重要内容,包括实验操作步骤、控制样品的使用、结果分析和解释。
通过深入了解这些实验细节,我们可以更好地理解ELISA的原理和应用。
正文内容:一. 实验操作步骤1. 准备样品和标准曲线- 收集所需的样品,可以是血清、尿液或细胞上清等。
- 确定需要测定的抗体或抗原,并准备相应的标准曲线。
2. 处理样品- 样品处理包括离心、稀释或加热等步骤,以去除可能干扰测定的物质。
3. 准备实验板- 将酶标板预先涂覆上抗体或抗原,然后用非特异性蛋白质阻断剂进行阻断。
4. 加入样品和标准曲线- 将处理后的样品和标准曲线加入预先涂覆抗体或抗原的孔中。
5. 孔洗涤和加入检测抗体- 通过洗涤孔来去除非特异性结合物质。
- 加入检测抗体,它可以是与标准曲线中的抗体相同的抗体或与待测物质结合的抗体。
6. 孔洗涤和加入底物- 通过洗涤孔来去除未结合的检测抗体。
- 加入底物,它会与酶结合并产生可测定的信号。
7. 信号检测和结果记录- 使用酶标仪测量底物的反应产物生成的光信号。
- 将光信号与标准曲线进行比较,得出待测样品中目标物质的含量。
二. 控制样品的使用1. 阳性对照样品- 阳性对照样品是已知含有目标抗体或抗原的样品,用于验证实验的准确性和可靠性。
2. 阴性对照样品- 阴性对照样品是未含目标抗体或抗原的样品,用于确定实验的特异性。
3. 反应性对照样品- 反应性对照样品是含有不同浓度目标抗体或抗原的样品,用于绘制标准曲线并进行定量测定。
4. 标准曲线的制备- 使用已知浓度的标准样品制备标准曲线,该曲线用于将光信号转换为目标物质的定量结果。
5. 控制实验条件- 控制实验条件,包括温度、时间和洗涤次数等,以确保实验的可重复性和可比性。
三. 结果分析1. 原始数据处理- 使用酶标仪测量的吸光度值为原始数据,在计算吸光度值之前,需要进行空白校正和标准曲线外推。
高等数学数学实验报告(两篇)2024

引言概述:高等数学数学实验报告(二)旨在对高等数学的相关实验进行探究与研究。
本次实验报告共分为五个大点,每个大点讨论了不同的实验内容。
在每个大点下,我们进一步细分了五到九个小点,对实验过程、数据收集、数据分析等进行了详细描述。
通过本次实验,我们可以更好地理解高等数学的概念和应用。
正文内容:一、微分方程实验1.利用欧拉法求解微分方程a.介绍欧拉法的原理和步骤b.详细阐述欧拉法在实际问题中的应用c.给出具体的实例,展示欧拉法的计算步骤2.应用微分方程建立模型求解实际问题a.介绍微分方程模型的建立方法b.给出一个具体的实际问题,使用微分方程建立模型c.详细阐述模型求解步骤和结果分析3.使用MATLAB求解微分方程a.MATLAB求解微分方程的基本语法和函数b.给出一个具体的微分方程问题,在MATLAB中进行求解c.分析结果的准确性和稳定性二、级数实验1.了解级数的概念和性质a.简要介绍级数的定义和基本概念b.阐述级数收敛和发散的判别法c.讨论级数的性质和重要定理2.使用级数展开函数a.介绍级数展开函数的原理和步骤b.给出一个函数,使用级数展开进行近似计算c.分析级数近似计算的精确度和效果3.级数的收敛性与运算a.讨论级数收敛性的判别法b.介绍级数的运算性质和求和法则c.给出具体的例题,进行级数的运算和求和三、多元函数极值与最值实验1.多元函数的极值点求解a.介绍多元函数的极值点的定义和求解方法b.给出一个多元函数的实例,详细阐述求解过程c.分析极值点对应的函数值和意义2.多元函数的条件极值与最值a.讨论多元函数的条件极值的判定法b.给出一个具体的多元函数,求解其条件极值和最值c.分析条件极值和最值对应的函数值和意义3.利用MATLAB进行多元函数极值与最值的计算a.MATLAB求解多元函数极值与最值的基本语法和函数b.给出一个多元函数的具体问题,在MATLAB中进行求解c.分析结果的准确性和可行性四、曲线积分与曲面积分实验1.曲线积分的计算方法与应用a.介绍曲线积分的定义和计算方法b.给出一个具体的曲线积分问题,详细阐述计算过程c.分析曲线积分结果的几何意义2.曲线积分的应用举例a.讨论曲线积分在实际问题中的应用b.给出一个实际问题,使用曲线积分进行求解c.分析曲线积分结果的实际意义和应用价值3.曲面积分的计算方法与应用a.介绍曲面积分的定义和计算方法b.给出一个具体的曲面积分问题,详细阐述计算过程c.分析曲面积分结果的几何意义五、空间解析几何实验1.空间曲线的参数方程表示与性质a.介绍空间曲线的参数方程表示和性质b.给出一个具体的空间曲线,转化为参数方程表示c.分析参数方程对应的几何意义和性质2.平面与空间直线的位置关系a.讨论平面与空间直线的位置关系的判定方法b.给出一个具体的平面与空间直线的问题,判定其位置关系c.分析位置关系对应的几何意义和应用实例3.空间直线与平面的夹角和距离计算a.介绍空间直线与平面的夹角和距离的计算方法b.给出一个具体的空间直线和平面,计算其夹角和距离c.分析夹角和距离计算结果的几何意义总结:通过本次高等数学数学实验报告(二),我们深入了解了微分方程、级数、多元函数极值与最值、曲线积分、曲面积分以及空间解析几何的相关概念和应用。
最小二乘法曲线拟合实验报告

竭诚为您提供优质文档/双击可除最小二乘法曲线拟合实验报告篇一:实验3曲线拟合的最小二乘法实验三曲线拟合的最小二乘法1、实验目的:在科学研究与工程技术中,常常需要从一组测量数据出发,寻找变量的函数关系的近似表达式,使得逼近函数从总体上与已知函数的偏差按某种方法度量能达到最小而又不一定过全部的点。
这是工程中引入最小二曲线拟合法的出发点。
充分掌握:1.最小二乘法的基本原理;2.用多项式作最小二乘曲线拟合原理的基础上,通过编程实现一组实验数据的最小二乘拟合曲线。
2、实验要求:1)认真分析题目的条件和要求,复习相关的理论知识,选择适当的解决方案和算法;2)编写上机实验程序,作好上机前的准备工作;3)上机调试程序,并试算各种方案,记录计算的结果(包括必要的中间结果);4)分析和解释计算结果;5)按照要求书写实验报告;3、实验内容:1)给定数据如下:x:0.15,0.4,0.6,1.01,1.5,2.2,2.4,2.7,2.9,3.5,3.8,4.4,4.6,5.1,6.6,7.6;y:4.4964,5.1284,5.6931,6.2884,7.0989,7.5507,7.5106,8.0756,7.8708,8.2403,8.5303,8.7394,8.9981,9.1450,9.5070,9.9115;试作出幂函数拟合数据。
2)已知一组数据:x:0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1y:-0.447,1.978,3.28,6.16,7.08,7.34,7.66,9.56,9.48,9.30,11.2;试用最小二乘法求多项式函数,使与此组数据相拟合。
4、题目:曲线拟合的最小二乘法5、原理:从整体上考虑近似函数同所给数据点(i=0,1,…,m)误差(i=0,1,…,m)的大小,常用的方法有以下三种:一是误差(i=0,1,…,m)绝对值的最大值,即误差向量的∞—范数;二是误差绝对值的和,即误差向量r的1—范数;三是误差平方和的算术平方根,即误差向量r的2—范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑2—范数的平方,因此在曲线拟常采用误差平方和来度量误差(i=0,1,…,m)的整体大小.。
数值分析拟合实验报告(3篇)

第1篇一、实验目的本次实验旨在通过数值分析方法对一组已知数据点进行拟合,掌握线性插值、多项式插值、样条插值等方法的基本原理和实现过程,并学会使用MATLAB进行数值拟合。
二、实验内容1. 线性插值线性插值是一种简单的插值方法,适用于数据点分布较为均匀的情况。
其基本原理是通过两个相邻的数据点,利用线性关系拟合出一条直线,然后通过该直线来估算未知的值。
2. 多项式插值多项式插值是一种较为精确的插值方法,通过构造一个多项式函数来逼近已知数据点。
其基本原理是利用最小二乘法求解多项式的系数,使得多项式在已知数据点上的误差最小。
3. 样条插值样条插值是一种更灵活的插值方法,通过构造一系列样条曲线来逼近已知数据点。
其基本原理是利用最小二乘法求解样条曲线的系数,使得样条曲线在已知数据点上的误差最小。
三、实验步骤1. 线性插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`linspace`生成插值点:xi = linspace(1, 5, 100);(3)使用MATLAB内置函数`interp1`进行线性插值:yi = interp1(x, y, xi, 'linear');(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');2. 多项式插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`polyfit`求解多项式系数:p = polyfit(x, y, 3);(3)使用MATLAB内置函数`polyval`进行多项式插值:yi = polyval(p, xi);(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');3. 样条插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`spline`进行样条插值:yi = spline(x, y, xi);(3)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');四、实验结果与分析1. 线性插值线性插值方法简单易行,但精度较低,适用于数据点分布较为均匀的情况。
数值计算(分析)实

数值计算(分析)实验报告2南昌航空大学数学与信息科学学院实验报告课程名称:《数值计算方法》实验名称:曲线拟合实验类型:验证性■综合性□设计性□实验室名称:数学实验室班级学号: 09072113学生姓名:邢宪平任课教师(教师签名):成绩:一、实验目的实验目的:实验目的:了解函数逼近与曲线拟合的基本原理,并且运用MATLAB 软件进行实践操作。
二、实验原理、程序框图、程序代码等 实验题目:题目1:试分别用抛物线2y a bx cx =++和指数曲线bxy ae =拟合下列数据并比较两个拟合函数的优劣。
题目2:已知实验数据如下:试用形如2y a bx =+的抛物线进行最小二乘拟合。
实验原理:1、逼近方式 假设()[,]f x C a b ∈,2{1,,,...,}n nHspan x x x =,()nnP x H ∈,称(,)|||||()()|max n n n a x bf P F P f x P x ≤≤=-=-V 为()f x 与()|nP x 在[,]a b 上的偏差。
若存在*()nnP x H ∈,使得**(,)|||||()()|max inf n nn nn P H a x bf P f Pf x P x ∞∈≤≤=-=-V 则称*()nP x 是()f x 在[,]a b 上的最佳一致逼近多项式。
假设()[,]f x C a b ∈及[,]C a b 的一个子集01{(),(),,...()}nspan x x x ϕ=ϕϕϕ,若存在*()S x ϕ∈,使*22222()()||()()||||()()||()[()()]min min bS x S x af x S x f x S x x f x S x dxϕϕρ∈∈-=-=-⎰则称*()S x 是()f x 在子集[,]C a b ϕ⊂中的最佳平方逼近数。
2、曲线拟合上述函数的最佳平方逼近法中,若()f x 是以一组离散点集的形式给出的,即给出了函数()f x 在一些离散点上的值{(,),0,1,...,}iix y i m =,则该方法就是所说的曲线拟合。
《数值分析》课程实验报告范文

《数值分析》课程实验报告范文《数值分析》课程实验报告姓名:学号:学院:机电学院日期:2022年某月某日目录实验一函数插值方法1实验二函数逼近与曲线拟合5实验三数值积分与数值微分7实验四线方程组的直接解法9实验五解线性方程组的迭代法15实验六非线性方程求根19实验七矩阵特征值问题计算21实验八常微分方程初值问题数值解法24实验一函数插值方法一、问题提出对于给定的一元函数的n+1个节点值。
试用Lagrange公式求其插值多项式或分段二次Lagrange插值多项式。
实验二函数逼近与曲线拟合一、问题提出从随机的数据中找出其规律性,给出其近似表达式的问题,在生产实践和科学实验中大量存在,通常利用数据的最小二乘法求得拟合曲线。
在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量与时间t的拟合曲线。
t(分)051015202530354045505501.272.162.863.443.874.154.374.51 4.584.024.64二、要求1、用最小二乘法进行曲线拟合;2、近似解析表达式为;3、打印出拟合函数,并打印出与的误差,;4、另外选取一个近似表达式,尝试拟合效果的比较;5、某绘制出曲线拟合图。
三、目的和意义1、掌握曲线拟合的最小二乘法;2、最小二乘法亦可用于解超定线代数方程组;3、探索拟合函数的选择与拟合精度间的关系四、实验步骤:第一步先写出线性最小二乘法的M文件functionc=lpoly(某,y,m)n=length(某);b=zero(1:m+1);f=zero(n,m+1); fork=1:m+1f(:,k)=某.^(k-1);enda=f'某f;b=f'某y';c=a\b;c=flipud(c);第二步在命令窗口输入:>>lpoly([0,5,10,15,20,25,30,35,40,45,50,55],[0,1.27,2.16,2.86,3.44,3.87,4.15,4.37,4.51,4.58,4.02,4.64],2)回车得到:an=-0.00240.20370.2305即所求的拟合曲线为y=-0.0024某2+0.2037某+0.2305在编辑窗口输入如下命令:>>某=[0,5,10,15,20,25,30,35,40,45,50,55];>>y=-0.0024某某.^2+0.2037某某+0.2305;>>plot(某,y)命令执行得到如下图五、实验结论分析复杂实验数据时,常采用分段曲线拟合方法。
硫酸标准曲线绘制实验报告

硫酸标准曲线绘制实验报告
以下是一份硫酸标准曲线绘制实验报告的模板:
硫酸标准曲线绘制实验报告
一、实验目的
通过绘制硫酸标准曲线,确定硫酸浓度与吸光度之间的关系。
二、实验原理
硫酸与特定指示剂反应后,会产生颜色变化。
通过测定吸光度,可以建立硫酸浓度与吸光度之间的标准曲线。
三、实验仪器和试剂
1. 分光光度计
2. 硫酸标准溶液
3. 指示剂
4. 蒸馏水
四、实验步骤
1. 准备一系列已知浓度的硫酸标准溶液。
2. 分别向每个硫酸标准溶液中加入指示剂,并充分混合。
3. 使用分光光度计测量每个溶液的吸光度。
4. 以硫酸浓度为横坐标,吸光度为纵坐标,绘制标准曲线。
五、实验结果
1. 记录每个硫酸标准溶液的浓度和对应的吸光度。
2. 根据实验数据绘制硫酸标准曲线。
六、结论
根据绘制的硫酸标准曲线,可以确定在一定范围内硫酸浓度与吸光度之间的关系。
这对于定量分析硫酸溶液的浓度提供了参考依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档
数值分析
课程设计报告
学生姓名
学生学号
所在班级
指导教师
一、课程设计名称
函数逼近与曲线拟合
二、课程设计目的及要求
实验目的:
⑴学会用最小二乘法求拟合数据的多项式,并应用算法于实际问题。
⑵学会基本的矩阵运算,注意点乘和叉乘的区别。
实验要求:
⑴编写程序用最小二乘法求拟合数据的多项式,并求平方误差,做出离散函
数和拟合函数的图形;
⑵用MATLAB 的内部函数polyfit 求解上面最小二乘法曲线拟合多项式的系
数及平方误差,并用MATLAB 的内部函数plot 作出其图形,并与(1)结果进行比较。
三、课程设计中的算法描述
用最小二乘法多项式曲线拟合,根据给定的数据点,并不要求这条曲线精确的经过这些点,而是拟合曲线无限逼近离散点所形成的数据曲线。
思路分析:从整体上考虑近似函数)(x p 同所给数据点
)(i i y x ,误差i i i y x p r -=)(的大小,常用的方法有三种:一是误差i i i y x p r -=)(绝对值的最大
值i m
i
r ≤≤0max ,即误差向量的无穷范数;二是误差绝对值的和∑=m
i i r 0
,即误差向量的1
范数;三是误差平方和∑=m
i i r 0
2的算术平方根,即类似于误差向量的2范数。
前两
种方法简单、自然,但不便于微分运算,后一种方法相当于考虑2范数的平方,此次采用第三种误差分析方案。
算法的具体推导过程: 1.设拟合多项式为:
2.给点到这条曲线的距离之和,即偏差平方和:
3.为了求得到符合条件的a 的值,对等式右边求偏导数,因而我们得到了:
4.将等式左边进行一次简化,然后应该可以得到下面的等式
5.把这些等式表示成矩阵的形式,就可以得到下面的矩阵:
⎥⎥⎥⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑∑∑∑∑∑∑∑∑=====+==+====n i i n i n i i k n i k i n
i k i
n
i k i n i k i n
i i
n i i
n
i k i
n
i i
y y y a a x x
x x x
x
x x 11i 1
10121
11
1112111
a n M M
Λ
M O M
M ΛΛ 6. 将这个范德蒙得矩阵化简后得到
⎥⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡n k k n n k k y y y a a a x x x x x x M M Λ
M
O
M M ΛΛ211022111
11
7.因为Y A X =*,那么X Y A /=,计算得到系数矩阵,同时就得到了拟合曲线。
四、课程设计内容
⑴实验环境:MATLAB2010
⑵实验内容:给定的数据点 0 0.5 0.6 0.7 0.8 0.9 1.0
1
1.75
1.96
2.19
2.44
2.71
3.00
1) 用最小二乘法求拟合数据的多项式; 2) 用MATLAB 内部函数polyfit 函数进行拟合。
⑶实验步骤
1)首先根据表格中给定的数据,用MATLAB 软件画出数据的散点图(图1)。
2)观察散点图的变化趋势,近似于二次函数。
则用二次多项式进行拟合,取一组基函数
,并令
,其中是待定系数。
3)用MATLAB 程序作线性最小二乘法的多项式拟合,求待定系数。
算法实现代码如下:
x=[0 0.5 0.6 0.7 0.8 0.9 1.0]; y=[1 1.75 1.96 2.19 2.44 2.71 3.00]; R=[(x.^2)' x' ones(7,1)]; A=R\y'
4) 用MATLAB 程序计算平均误差。
算法实现代码如下:
y1=[1 1.75 1.96 2.19 2.44 2.71 3.00]; x=[0 0.5 0.6 0.7 0.8 0.9 1.0]; y=x.^2+x+1; z=(y-y1).^2; sum(z)
5) 作出拟合曲线和数据图形(图2)。
6)用MATLAB的内部函数polyfit求解上面最小二乘法曲线拟合多项式的系数及平方误差。
算法实现代码如下:
x=[0 0.5 0.6 0.7 0.8 0.9 1.0];
y=[1 1.75 1.96 2.19 2.44 2.71 3.00];
A=polyfit(x,y,2);%二次多形式拟合%
z=polyval(A,x);
A
d=sum((z-y).^2)
7)绘制使用polyfit函数实现的拟合图形。
(图3)
五、程序流程图
图5-1 用最小二乘法求多项式拟合曲线流程图
输入初始数据点
调用polyfit函数,确定多形式的系数
调用polyval函数,进行多项式求值
调用plot函数进行绘图
图5-2 用polyfit函数求多项式拟合曲线流程图六、实验结果
图6-1 表中数据的散点图
图6-2. 最小二乘法实现的拟合曲线第1问
系数为
A = 1.0000 1.0000 1.0000
则多项式的方程为
平方误差和为
ans =1.9722e-031
图6-3. polyfit函数实现的拟合函数
第2问
系数为
A = 1.0000 1.0000 1.0000
则多项式的方程为
平方误差和为
ans = 1.9722e-031
七、实验结果分析
编写程序用最小二乘法求拟合曲线的多项式的过程中,求出的数据和拟合函数的平方误差很小,达到了很高的精度要求,以及通过散点求得的拟合曲线比较光滑。
而用MATLAB的内部函数求polyfit求解的曲线拟合多项式和平方误差与程序求得的相同,还有就是虽然求解过程简单了,但用MATLAB的内部函数做出的图形由明显的尖点,不够光滑。
此次实验数据较少,而且数据基本都是可靠数据。
但是在应用实际问题中,数据会很庞杂,此时对于最小为乘法的算法就需要进一步的细化。
例如在进行数
据采集时,由于数据采集器(各种传感器)或机器自身的原因及其外部各种因素的制约,导致数据偶尔会有大幅度的波动,及产生一些偏差极大的数据,不能真实反映数据的可靠性,所以会对数据进行筛选或修正。
而此时就可应用曲线拟合的最小二乘法的进行处理。
八、实验心得体会
在日常的学习和生活中,我们可能会遇到各种方面的跟数据有关的问题,并不是所有的数据都是有用,必须对数据进行适当的处理,然后找出数据之间的关系,然后进行分析得出结果。
此次实验结果基本没有大的区别,可是MATLAB提供给我们一个特别简洁的办法,应用一个函数即可实现相同的结果。
虽然很方便,但是对于初学者来说,我觉得打好基础才是关键,对于一个知识点,应该掌握其最基本的原理,然后在将它应用于实际。
通过这个实验我也理解到了,数值分析是一个工具学科,它教给了我们分析和解决数值计算问题得方法,使我从中得到很多关于算法的思想,从中受益匪浅。
附录:源代码
散点图:
x=[0 0.5 0.6 0.7 0.8 0.9 1.0];
y=[1 1.75 1.96 2.19 2.44 2.71 3.00];
plot(x,y,'r*')
title('实验数据点的散点图');
legend('数据点(xi,yi)');
xlable('x');
ylable('y');
最小二乘拟合:
x=[0 0.5 0.6 0.7 0.8 0.9 1.0];
y=[1 1.75 1.96 2.19 2.44 2.71 3.00];
R=[(x.^2)' x' ones(7,1)];
A=R\y'
x1=[0 0.5 0.6 0.7 0.8 0.9 1.0];
y1=[1 1.75 1.96 2.19 2.44 2.71 3.00]; x=[0 0.5 0.6 0.7 0.8 0.9 1.0];
y=x.^2+x+1;
plot(x1,y1,'k+',x,y,'r')
title('实验数据点的散点图及拟合曲线'); z=(y-y1).^2;
sum(z)
Polyfit函数拟合:
x=[0 0.5 0.6 0.7 0.8 0.9 1.0];
y=[1 1.75 1.96 2.19 2.44 2.71 3.00];
A=polyfit(x,y,2);%二次多形式拟合%
z=polyval(A,x);
A
d=sum((z-y).^2)
plot(x,y,'k+')
title('实验数据点的散点图及拟合曲线'); hold on
plot(x,z,'r')。
